和
则稀点阵总共有
天线数,其中稀疏阵列的位置由式(2)确定近年来对于5G(5th-Generation)技术的研究以井喷式的速度发展,其中大规模多输入多输出[1](Massive multiple-input multiple-output, Massive MIMO)在学术界和工业界均引起了很大的关注。Massive MIMO是一个在基站(Base Station, BS)配置极大的天线阵列,服务于多个单天线用户的系统。大规模天线阵列可以获得巨大的频谱效益、提高能量效率、提高空间分辨率、并且降低网络干扰[1-2]。考虑到天线的排列部署,将天线放置在二维网格中则会大大减少天线面板的尺寸,这样的大规模天线阵列的部署称为3D-MIMO(three dimension multiple-input multiple-output)。3D-MIMO技术不仅可以利用大规模发射天线的空间自由度,而且可以在水平和垂直维度上调整发射波束的方向,这有助于提高空间分辨率,从而提高信号功率,减少小区间干扰[3- 4]。理论研究可知,当基站天线数越多则系统的性能会越好,但是从实际的角度考虑,通信系统在基站部署大量的天线,会极大的增加成本,增加发送功率。因此不少研究者提出了在基站部署少量的非均匀二维阵列,不仅减少了平面阵列的天线数,降低了系统的复杂度,而且可以实现大规模均匀面阵的性能[5]。为了获得非均匀平面阵列潜在优点的收益,准确的获得基站和用户之间的信道状态信息(Channel State Information, CSI)变的尤为重要。
一部分的研究者利用Massive MIMO信道的稀疏性进行信道估计,从而降低系统的计算复杂度和减少导频开销[6- 8]。文献[6]作者将Massive MIMO信道估计问题表述成一个压缩感知(Compressed Sensing, CS)问题,但是在实际的操作中很难确定信道的稀疏程度,通常假设信道稀疏程度是已知的,即信道脉冲响应(Channel Impulse Response, CIR)的非零元素的个数是已知的[7]。文献[8]作者通过贝叶斯学习(Bayesian Learning)的方法利用少量的观测数据重建Massive MIMO系统的稀疏信道分量进行信道估计。除了上述研究方向外还有研究者提出利用信道协方差矩阵的低秩性进行信道估计[9-10]。文献[9-10]均是假设每个用户的到达角是窄角度,利用信道协方差矩阵的特征分解可以降低信道的维度,降低系统的计算复杂度。这些协方差感知方法被划分为空分复用,利用不同用户的非重叠空间信息实现正交传输[11]。文献[12]作者提出一种在多用户Massive MIMO系统中基于DFT(Discrete Fourier Transform)的空间基扩展模型(Spatial Basis Expansion Model, SBEM)方法,该方法依据均匀线阵的物理特性,将信道通过DFT变换到空域中,可以体现出信道的稀疏性,然后通过用户空间特征的不同进行信道估计。文献[13]作者提出一种在毫米波Massive MIMO系统下基于2D-DFT(two-dimensional Discrete Fourier Transform)的信道估计算法,该算法首先估计出每个用户不同径的到达角(the direction of arrival, DOA)信息,然后通过角度旋转技术增强DOA估计的准确性实现角度的超分辨率估计,再估计出每个径的增益信息,最后重构信道。
上述工作都是在均匀阵列的大规模 MIMO系统下进行研究,然而通信系统在基站部署大量的天线,会极大的增加成本和发送功率。文献[5]在蜂窝通信系统基站部署较少天线数的非均匀阵列,可以实现大规模MIMO,提高频谱利用率和信道容量,降低系统天线阵元数和计算开销。近几年提出的嵌套阵[14]和互素阵列[16]是最引人关注的阵列配置。文献[17]作者提出压缩阵元间距的互素阵列(co-prime arrays with compressed inter-element spacing, CACIS)和置换子阵列的互素阵列(co-prime arrays with displaced subarrays, CADiS)、文献[18-19]中提出超级嵌套阵(super nested arrays)以及文献[20]提出的增广嵌套阵列(augmented nested arrays)目的均是为了减少耦合,此外文献提出稀疏的互素阵列(thinned co-prime arrays)[21-22]为了进一步增加DOA估计的自由度(Degrees of freedom, DOFs)。有研究者基于空间平滑子空间方法[14-16]研究非均匀阵列的DOA估计,文献[15]在天线阵列信号处理领域,基于二维嵌套阵列的DOA估计首先对阵列接收信号做自相关处理,将二维嵌套阵列的接收信号转换为虚拟的差分阵列的接收信号,最后通过MUSIC(Multiple Signal Classification)算法进行角度估计。还有研究者在压缩感知框架下基于等效的差分阵列进行DOA估计[17,23-24]。
本文聚焦于研究文献[14]那样的,由二维嵌套阵组成的大规模3D MIMO系统信道估计问题。在基站端配置M个阵元的稀疏阵列和N个阵元的密集阵列,服务于配置单天线的用户。二维嵌套阵通过自相关处理可以转化为Ο(MN)自由度的连续阵元的差分阵列,此差分阵列是一个M×N的均匀平面阵列,并且信道在差分阵列具有稀疏性。然后,对基站的接收信号做自相关处理转化为差分阵列的接收信号,写成矩阵形式,通过2D-DFT估计每个上行信道的初始到达角,接着通过角度旋转技术增强角度估计的准确性,从而实现超分辨率DOA估计。再者从基站接收信号利用LS估计方法获得上行链路信道增益的估计值。最后通过获得的角度估计值和增益估计重构出上行信道。数值计算结果验证了该方法的有效性。
本文的其他部分组织如下。第2部分是二维嵌套阵列结构以及嵌套阵下3D MIMO系统的传输模型和信道模型的介绍。第3部分介绍基于2D-DFT的信道估计算法和算法的计算复杂度分析。第4部分给出数值仿真。第5部分给出结论。
本文的符号说明:小写黑体和大写黑体分别表示列向量和矩阵。上标(·)H、(·)T、(·)*、(·)-1分别表示矩阵的共轭转置、转置、共轭、求逆。[A]i, j表示矩阵A的第(i, j)的元素。diag{a}表示由列向量a元素构成的对角矩阵,vec(A)表示矩阵A的矢量化。
我们考虑在基站部署二维嵌套阵的TDD大规模MIMO系统,其中二维嵌套阵的结构基于史密斯形式设计[14]。N(s)和N(d)分别表示稀疏阵列和密集阵列的生成矩阵,并且满足N(s)=N(d)P,其中P为任意整数矩阵。对P进行史密斯分解
P=U1ΛU2
(1)
其中,U1和U2是幺模矩阵,Λ=diag{(λ1,λ2)}。给定正整数和则稀点阵总共有天线数,其中稀疏阵列的位置由式(2)确定
(2)
密集阵列总共有Nd=det(P)=λ1λ2天线数。他们的位置由文献[14]中配置二确定
-λ2+1≤n≤0
(3)
这种结构确保产生的差分阵列有
个连续的阵元,阵元位置由式(4)给出
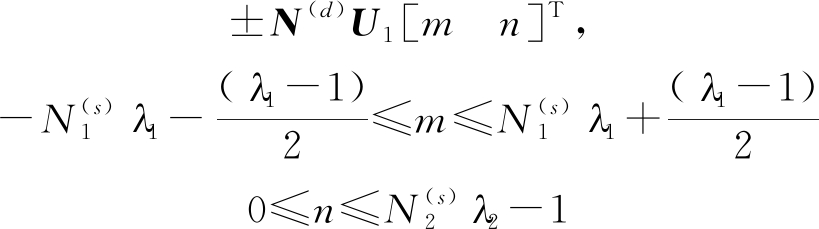
(4)
形成的差分阵列对应大小为M×N的均匀矩形天线阵列(Uniform Rectangular Array, URA),其中M和N满足式(5)
(5)
基站接收到的信号可以表示为
(6)
其中基站接收信号
是用户k的信道向量,其中Nd为密集阵列的阵元数目,Ns为稀疏阵列的阵元数目,
表示用户端发送的长度为导频长度Nl的导频序列,
是加性高斯白噪声。
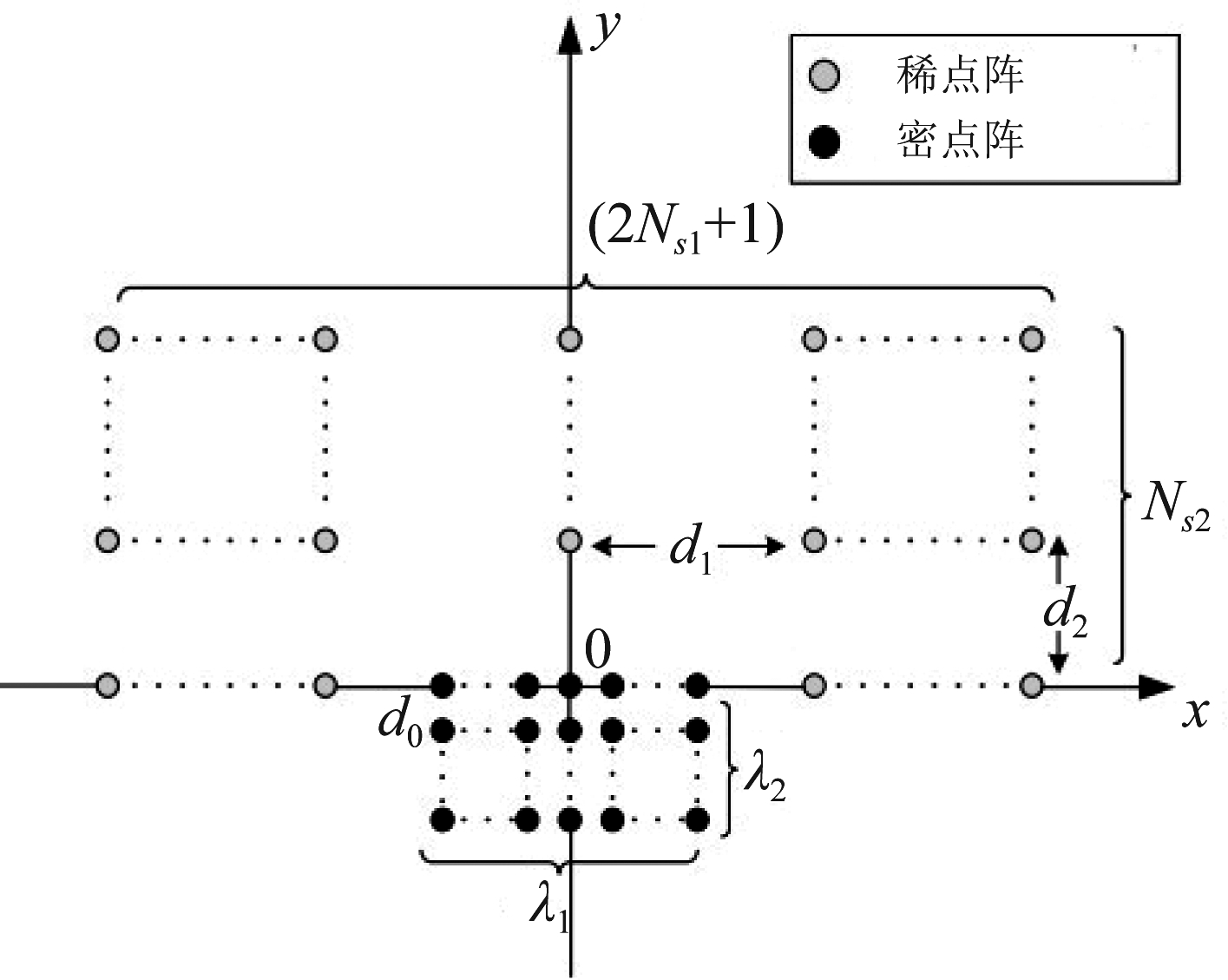
图1 基于史密斯形式设计的二维嵌套阵列
Fig.1 2D nested array based on Smith form design
如图1所示为基于史密斯形式的二维嵌套阵列结构,阵元位置由式(2)和式(3)确定,其密集阵列的阵元数目为Nd,稀疏阵列的阵元数目为Ns,密集阵列的阵元间隔为d=λ/2,稀疏阵列的阵元间隔沿着x轴方向为d1=λ1d0,沿着y轴方向为d2=λ2d0。单天线用户分布在基站端附近,假设信道为平坦衰落信道,用户到基站端(BS)的有效传播路径为L条,相应的上行链路信道可以表示为
(7)
其中,αkl表示用户k到基站第l路径的复增益,φkl∈(-p/2,p/2)和θkl∈(-p,p)分别表示用户k到基站第l条路径的俯仰角和水平角,
其有如下表示
(8)
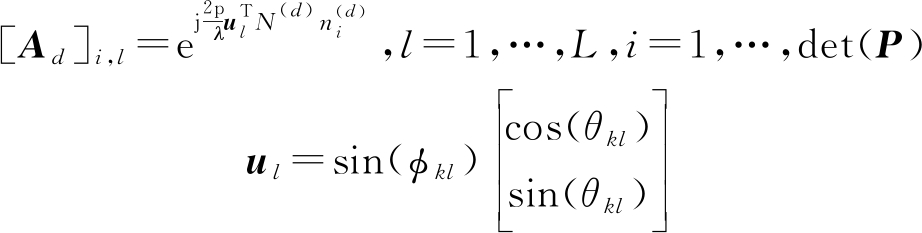
(9)
本文研究的二维嵌套阵列类似于文献[14]中基于史密斯形式设计,取
则对应的二维嵌套阵列结构图如图2所示,白色的空心圆表示稀疏阵列的阵元分布,黑色的实心圆表示密集阵列的阵元分布。
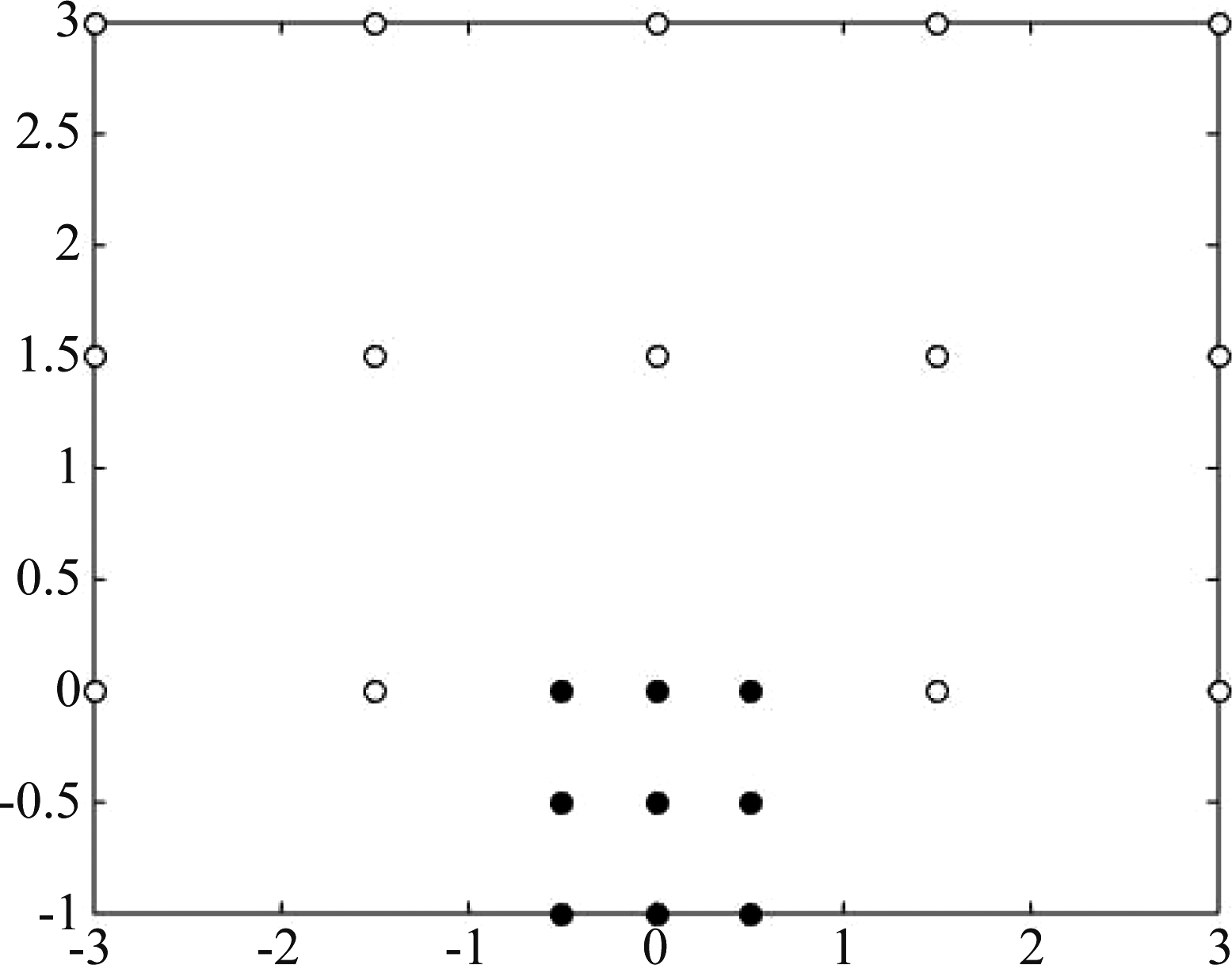
图2 二维嵌套阵列结构图
Fig.2 2D nested array structure
为了分析简单,假设小区中只有一个用户,用户发送的导频为s序列长度为Nl且发送的导频功率为σ。用户发送信号到达基站的二维嵌套阵路径有L条,每条路径的俯仰角和方位角表示为(φl,θl),l=1,2,…,L。基站接收到的信号表示为
(10)
其中,
是稀疏阵列N(s)的阵列流形矢量,
是密集阵列N(d)的阵列流形矢量,其中
是用户的第l条路径的信道复增益,是加性高斯白噪声。基站每一时刻接收到的信号表示为y(t),即Y={y(1),y(2),…,y(Nl)}。
接下来对基站接收信号y(t)做自相关处理,则y(t)的自相关矩阵可以表示为
(11)
其中,Rss为信号s(t)的自相关矩阵,σn是高斯噪声的功率。然后对Ryy进行向量化,可得
(12)
其中,vec(·)表示将矩阵中的元素按列的顺序拉直排列成一个列向量,⊙表示Khatri-Rao积,
是除了第i个元素为1其他元素全为0的列向量。
是类似于二维嵌套阵列的差分阵列的流形矩阵。
对应的差分阵列流形矢量的阵元结构如图3(a)所示,“菱形”表示差分阵列的阵元位置,仿真计算可知此差分阵列有很多冗余元素,且形成的差分阵列是不连续的。我们首先将冗余的元素去掉,然后选取阵元连续部分对应的元素进行排序,使得到的差分阵列的阵元位置与嵌套阵的元素一一对应,最后得到一个新的矩阵
即得到图3(b)所示的阵元位置的差分阵列。因此等效的阵列接收信号可以表示为
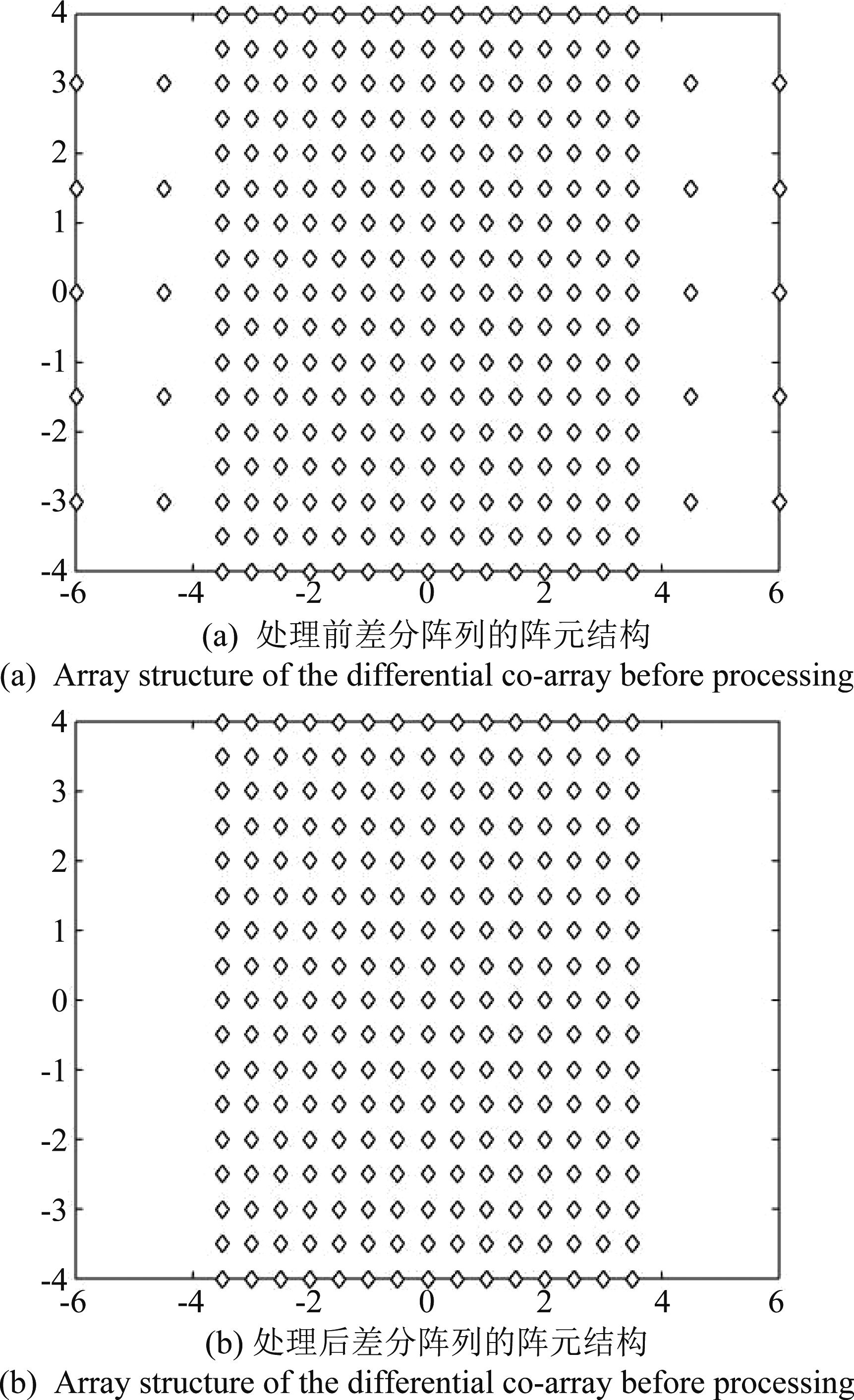
图3 差分阵列的阵元结构
Fig.3 Array structure of differential co-array
(13)
其中,
可以看作为所得差分阵列的接收信号,σ2可以看作入射到该差分阵列的等效信号,
是一个确定的矢量。
由z1的维度可知,z1是差分阵列接收信号向量化得到的,为了能对接收信号z1做后续处理,按照一定的要求,将其恢复成维数为M×N的矩阵zν,z1和zν之间有着如下关系
z1=vec(zν)
(14)
基于史密斯形式设计的嵌套阵列通过对接收信号自相关处理可以等效为虚拟均匀平面阵的接收信号,然后进行DOA估计,即首先通过2D-DFT变换估计出用户的初始到达角,然后通过角度旋转技术获得更加精确的到达角,下面详细阐述DOA估计过程。
(1)初始DOA估计
首先定义M点和N点的标准离散傅里叶变换矩阵FM和FN,其中FM是M×M的DFT矩阵,第(p,q)个元素可以表示为
是N×N的DFT矩阵,第(p′,q′)个元素可以表示为
然后,我们把接收信号zν的标准2D-DFT记做
其中
表示转化为差分阵列后基站接收信号zν的2D-DFT变换矩阵。它的第(p,q)个元素可以表示为
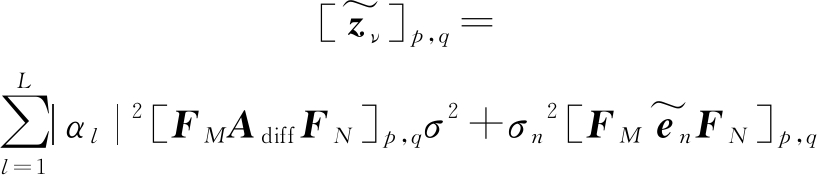
(15)
其中Adiff是虚拟阵列的流形矩阵,由等式adiff=vec(Adiff)来确定。定义
则
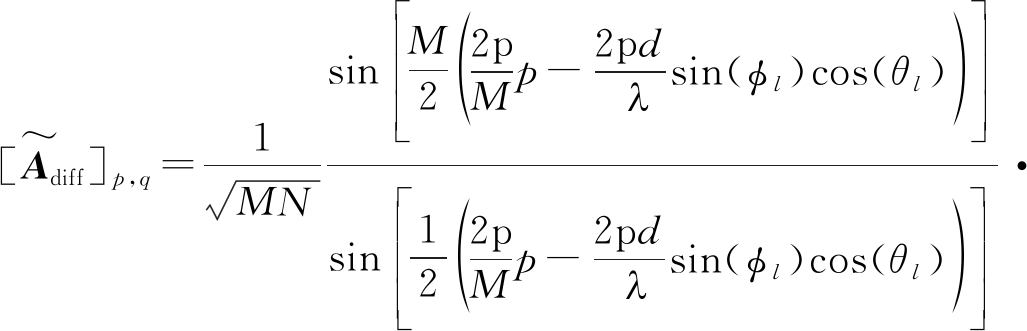
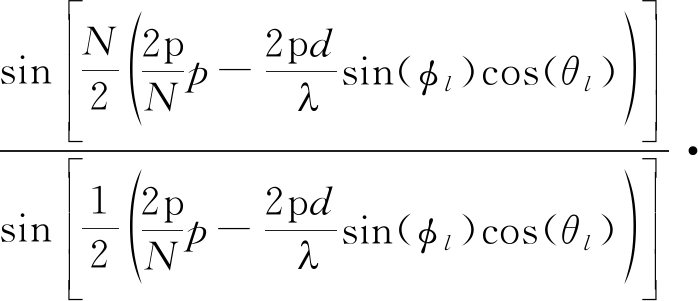
(16)
其中φl和θl表示用户第l条路径的垂直俯仰角和水平方位角。
需要注意的是当天线阵列数趋于无限时,即M→
,N→,存在一些整数点
其中
使得
而
其他元素的值全部为0。用户的所有功率集中在差分阵列的
位置处,即具有稀疏性,所以通过的非0元素的位置可以估计出用户的角度信息。但是在实际中,阵列天线个数是有限的,一般情况下有些角度不能满足
和
一定是整数,因此信道功率将会从第
个元素位置泄漏到它邻近的元素位置处。然而从式(16)可以看出当M和N比较大的时候,可以近似地认为
是一个稀疏矩阵,最大能量亦是聚集在第
个元素位置,因此根据能量泄露的位置仍然可以估计出用户的初始到达角信息[13]。即通过非0点的位置
可以初步估计出用户的垂直俯仰角和水平方位角
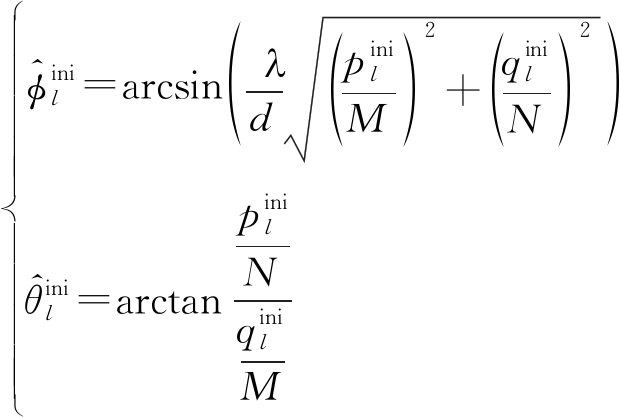
(17)
(2)精确的DOA估计
基于2D-DFT方法获得的到达角
分辨率受限于基站天线数和DFT间隔,例如当M=100,N=100时,DOA估计的最小的均方误差(MSE)大约是10-4。为了提高DOA估计的准确度,我们通过角度旋转技术进行补偿,实现超分辨率估计。
首先定义两个旋转矩阵,
φM(η)=diag{[1,ejη,…,ej(M-1)η]}
φN(γ)=diag{[1,ejγ,…,ej(N-1)γ]}
(18)
式中的η和γ是两个旋转角,它们的取值范围分别为
和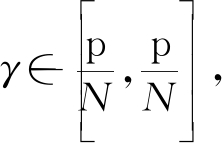
两个旋转角的取值范围是由DFT的分辨率决定的。基站嵌套阵列的虚拟阵列的接收矩阵的角度旋转可以表示为
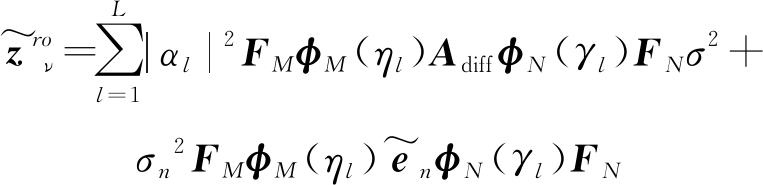
(19)
令
是虚拟阵列流形矩阵角度旋转的2D-DFT变换矩阵,它的第(p,q)元素可以表示为
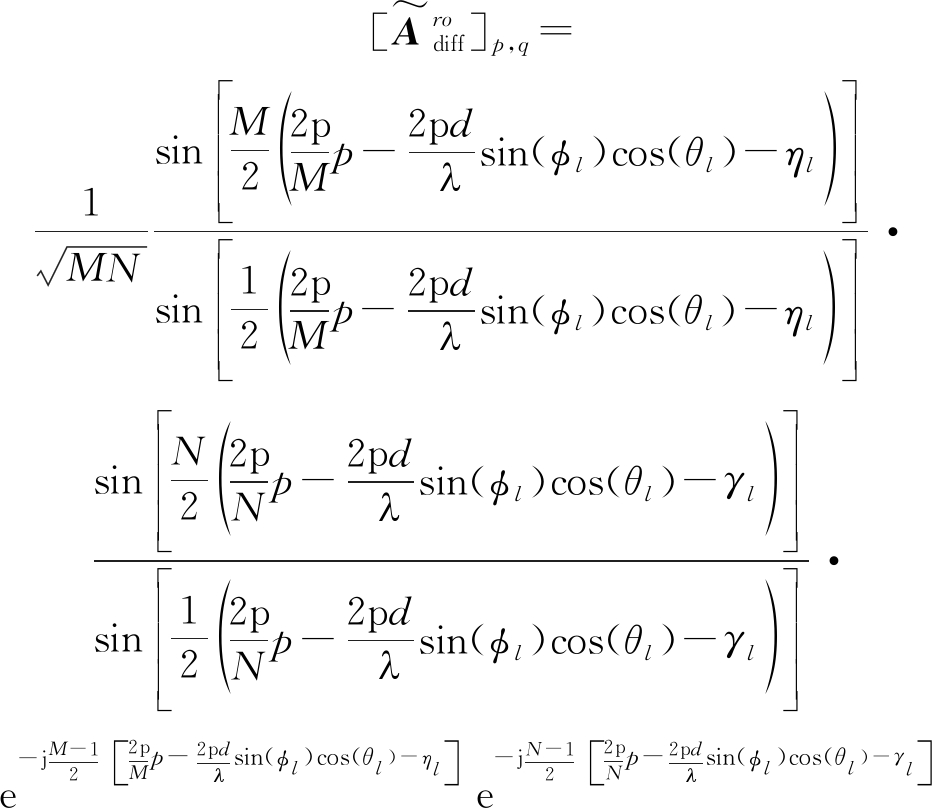
(20)
通过一维搜索的方法可以在
和
范围内寻找到用户第l条路径的最优旋转角度(Δηl,Δγl),使得用户信道能量更加的集中,即使得(Δηl,Δγl)满足式(21)
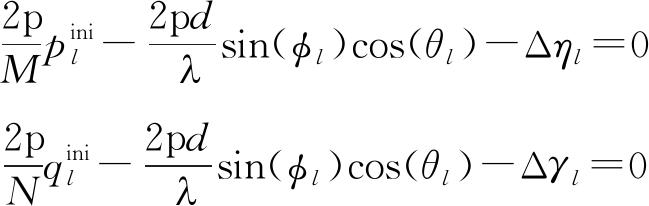
(21)
然后可以精确的估计出用户的第l条路径的俯仰角和方位角(φl,θl)
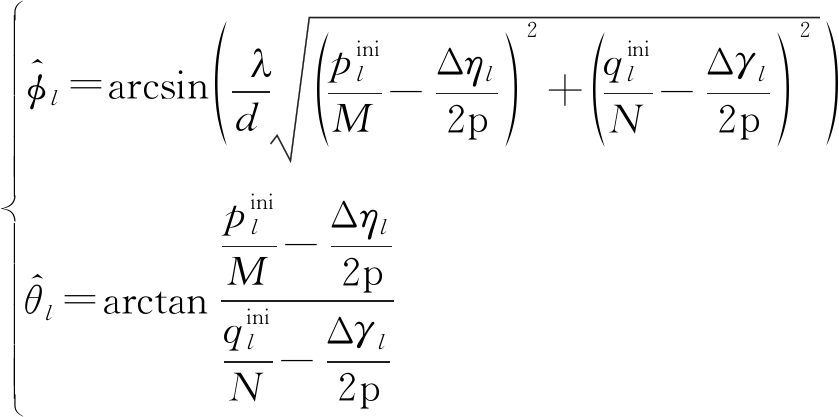
(22)
则可以估计出用户所有路径的到达角(φl,θl),l=1,2,…,L。
为了获得上行链路的信道增益,基站利用精确的DOA估计参数
基站接收信号可以重新表示为
(23)
然后基站可以通过最小二乘(LS)方法估计出信道增益
(24)
其中,
表示用户的第l条路径到基站的复增益估计值,s(t)为发送的训练序列,
和
表示用户到基站的垂直俯仰角和水平方位角的估计值。根据估计的角度信息
和信道增益信息
估计出的信道矩阵信息就可以表示为:
(25)
其中,
表示二维嵌套阵的阵列流形。
表1中的算法计算复杂度主要体现在步骤1,3,4中。步骤1涉及接收信号的自相关处理,复杂度为O(Ns2),其中Ns是稀疏阵列的天线数;步骤3中主要操作是2D-DFT变换,涉及矩阵乘法运算,因为2D-DFT变换可以通过快速傅里叶变换(fast Fourier transform, FFT)代替,复杂度为O(Mlog2M);步骤4主要操作是角度旋转技术,复杂度为O(G2),其中G为搜索次数。
表1 基于2D-DFT和角度旋转的信道估计算法
Tab.1 Channel estimation algorithm based on 2D-DFT and angle rotation
主要算法流程输入:y(t),s(t)输出:H^1.对接收信号做自相关处理Ryy=E{y(t)yH(t)},向量化得到z=vec(Ryy);2.差分阵列接收信号z1=∑Ll=1αl2adiffσ2+σn2e～n,将其矩阵化z1=vec(zν);3.z～ν=FMzνFN寻找出能量集中的点(pinil,qinil),l=1,2,…,L;4. ForΔη=-pM:pM,Δγ=-pN:pN5. For l=1:L6. (Δηl,Δγl)满足式(21)7. End for8. End for9.式(22)获得(ϕ^l,θ^l),l=1,2,…,L;10.式(24)获得α^l,l=1,2,…,L;11.式(25)重构信道H^=1L∑Ll=1α^lANA(ϕ^l,θ^l)。
综上所述,对于基于二维嵌套阵的3D MIMO系统,本文提出的信道估计算法的复杂度为O(N2)。文献[13]中提出非均匀阵列的DOA估计的基于空间平滑子空间的MUSIC算法,该算法的主要涉及的步骤是特征值分解,所以其复杂度为O(N3)。对比分析得出,本文所提算法复杂度低于后者。
仿真过程中,我们考虑二维嵌套阵下大规模3D MIMO系统模型, 二维嵌套阵有如下两种生成方案。方案一:考虑二维嵌套阵列是由矩阵
密点阵生成矩阵
令P和N(d)为对角矩阵的目的是为了使得最终生成的差分阵列有着矩形面阵的结构。假设
则稀点阵一共有
个天线阵元(不包含处于原点位置的阵元情况),密点阵一共有Nd=det(P)=λ1λ2=9个天线阵元,故整个二维嵌套阵的天线阵元总数为Nco=Ns+Nd=23个,最终获得差分阵列的天线阵元总数为
个。方案二:考虑二维嵌套阵列是由矩阵密点阵生成矩阵令P和N(d)为对角矩阵的目的是为了使得最终生成的差分阵列有着矩形面阵的结构。假设
则稀点阵一共有
个天线阵元(不包含处于原点位置的阵元情况),密点阵一共有Nd=det(P)=λ1λ2=9个天线阵元,故整个二维嵌套阵的天线阵元总数为Nco=Ns+Nd=62个,最终获得差分阵列的天线阵元总数为
个。在没有特殊说明的情况下仿真过程的嵌套阵列的数目是以方案一生成的。
假设用户到基站的路径总数有L=1条,导频序列默认的长度设置为Nl=16。传播路径的范围是俯仰角
和方位角θ∈(-p,p)。我们默认将区间
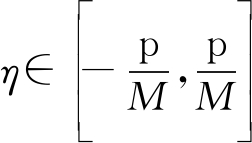等分为GM=10个小区间和
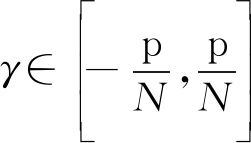等分为GN=10个小区间,区间的数量大小记为搜索网络G=GMGN,搜索网络默认为G=10×10,旋转角ηk和γk分别表示这两部等分区间的端点值。定义信噪比(signal to noise, SNR)
信道估计的性能指标为平均个体均方误差(the average individual MSE),即表示为
(26)
角度估计误差的性能指标平均单个用户单个路径的均方误差,可以表示为
RMSE
(27)
图4表示在二维嵌套阵背景下本文所提信道估计算法、传统的LS估计算法以及文献[15]中MUSIC估计算法上行链路MSE性能随信噪比变化曲线。从仿真图可以看出,在其他条件相同的情况下,本文所提方法基于2D-DFT信道估计方法的均方误差曲线随着信噪比的增加呈现出下降的趋势,且曲线始终位于基于LS信道估计算法和MUSIC估计算法的均方误差曲线下方,表明本文所提方法的估计性能要优于LS估计算法和MUSIC估计算法。
图4 三种信道估计方法的估计性能对比曲线
Fig.4 Estimation performance comparison curve of three channel estimation methods
图5表示本文所提DOA估计方法粗略估计,不同的搜索网络以及传统的MUSIC算法的角度均方误差随着信噪比变化的曲线。从图中可以看出,在没有进行角度旋转操作,即初步的粗略估计的时候,所求角度估计值的均方误差很大,和真实的角度值有着一定的差距。通过角度旋转操作,即精确的DOA估计,从图5中很明显可以看出DOA估计的角度均方误差(RMSE)要小很多,此时求得的角度估计值和真实值差距更小,更加符合预期要求。图5中还展现了在不同搜索网络G下的DOA估计误差曲线,可以看出,搜索网络G=30×30的情况下所求的角度值要比搜索网络G=10×10的情况下所求的角度更加准确,这是因为增大搜索网络G的时候,角度分辨率也相应的增大了。从曲线的变化趋势来看,若搜索网络G的值不断增大,DOA估计的性能将会越来越好。与传统的MUSIC算法比较,在不同的搜索网络下本文所提算法的DOA估计的准确性高于传统MUSIC算法,并且由3.4计算复杂度分析可知本文所提算法计算复杂度要低于传统MUSIC算法。
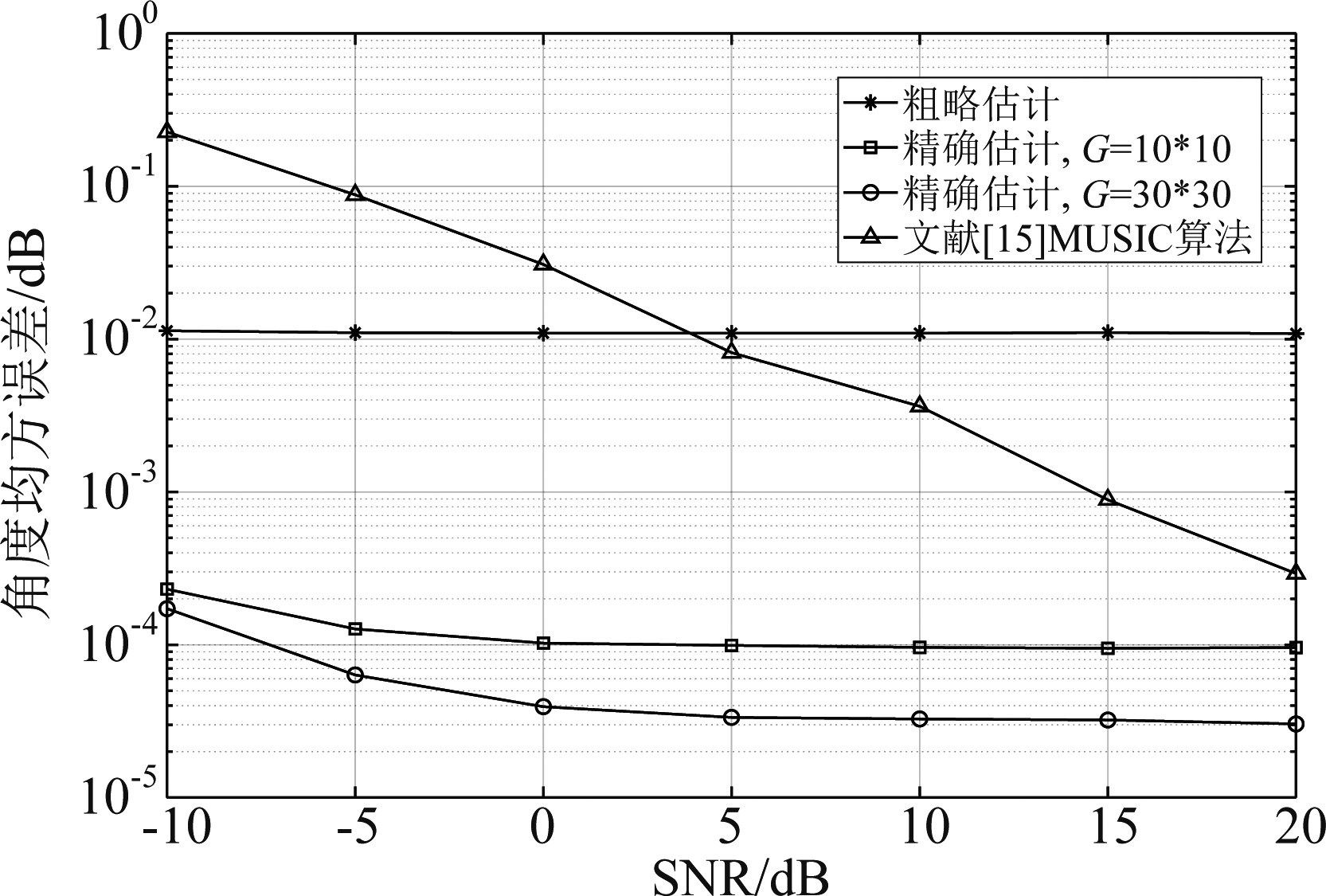
图5 不同搜索网络G下DOA初始粗略估计、精确估计以及传统MUSIC算法性能的对比图
Fig.5 Comparison of initial rough estimation, accurate estimation and conventional MUSIC algorithm performance of DOA under different search networks
图6表示本文所提DOA估计方法在二维嵌套阵不同天线数的情况,角度均方误差随信噪比变化的曲线。当二维嵌套阵列采用方案一生成时,其天线数为Nco=23时,与之对应的差分阵列的天线数为Nν=255;当二维嵌套阵列采用方案二生成时,其天线数Nco=23时,与之对应的差分阵列的天线数为Nν=945。从图6可以看出随着天线数量增加,DOA的初步粗略估计和精确估计的准确度都会相应的增加。本文所提DOA估计方法能够在确保估计准确度的前提下,还可以进一步减少基站端所需部署的天线数量。
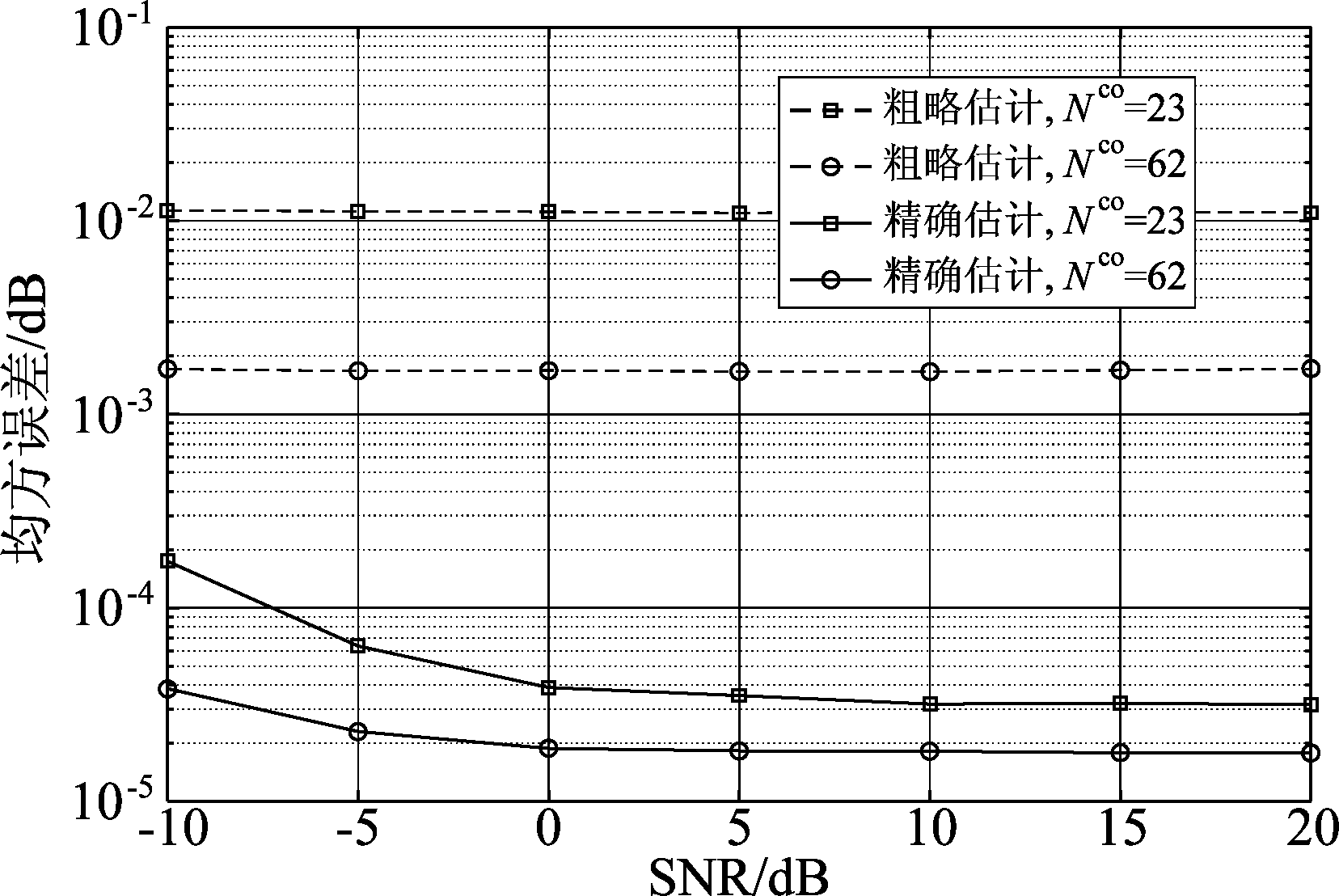
图6 不同天线数下DOA初始粗略估计和精确估计性能的对比图
Fig.6 Comparison of initial rough estimate and accurate estimation performance of DOA under different antenna numbers
图7表示本文所提信道估计算法、传统LS信道估计算法和理想信道的误码率(BER)随信噪比变化的曲线。仿真过程中,我们采用的是QPSK调制。为了保持公平性,每种信道估计方法所用训练序列的功率设置为一样的。从图7中可以看出本文所提方法的误码率始终要低于传统LS信道估计方法的误码率,而且更加接近理想信道状态下的误码率,这一结果也证实了所提方法的有效性。
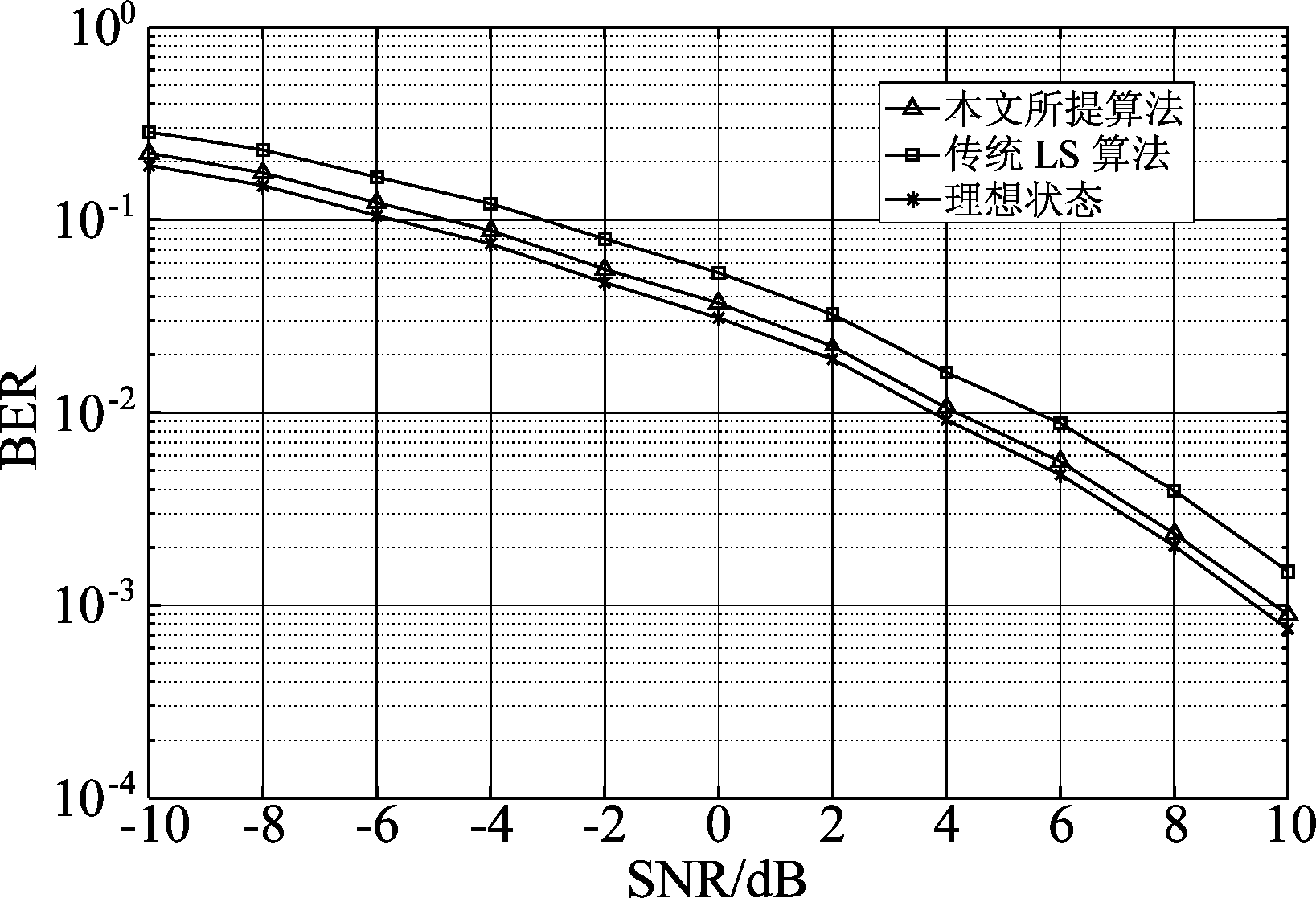
图7 理想状态信道和两种信道估计方法误码率的曲线对比图
Fig.7 Curve comparison of BER for ideal state channel and two channel estimation methods
本文探索了单小区单用户在基站配置二维嵌套阵列的3D-MIMO系统的信道估计问题。传统的3D-MIMO系统在基站端均是配置二维均匀平面阵列,在基站端配置大量的天线,极大的增加成本、发送功率以及计算复杂度。为解决这一问题,本文在基站端配置基于史密斯形式分解的二维嵌套阵列实现大规模MIMO从而降低成本,提高空间自由度。然而基于二维嵌套阵列的大规模MIMO基站接收信号很难直接获得用户和基站之间的信道,本文提出一种基于2D-DFT的信道重构算法。首先,对接收信号做自相关处理转化为Ο(MN)自由度的连续的差分阵列的接收信号;然后通过2D-DFT估计出用户的每一条路径的初始DOA,再利用角度旋转技术增强DOA估计实现超分辨率估计,其次根据精确的DOA估计通过传统的LS估计方法估计出信道增益;最后重构出用户的信道。数值仿真验证了算法的有效性。后续工作,我们将考虑多用户情况下二维嵌套阵3D-MIMO系统信道估计方法。
[1] Elijah O, Leow C Y, Rahman T A, et al. A Comprehensive Survey of Pilot Contamination in Massive MIMO—5G System[J]. IEEE Communications Surveys & Tutorials, 2016, 18(2): 905-923.
[2] Wang M, Gao F, Jin S, et al. An Overview of Enhanced Massive MIMO with Array Signal Processing Techniques[J]. IEEE Journal of Selected Topics in Signal Processing, 2019, 13(5): 886-901.
[3] 罗发龙, 张建中. 5G权威指南—信号处理算法及实现, 第12章大规模阵列3D-MIMO: 理论、实现和测试[M]. 北京: 机械工程出版社, 2018: 217-233.
Luo Falong, Zhang Charlie (Jianzhong). Signal Processing for 5G: Algorithms and Implementations, 12 3D-MIMO with Massive Antennas: Theory, Implementation and Testing[M]. Beijing: China Machine Press, 2018: 217-233.(in Chinese)
[4] 白帆, 李汀, 李飞, 等. 3D MIMO系统下水平和垂直维联合预编码的研究[J]. 信号处理, 2016, 32(9): 1093-1100.
Bai Fan, Li Ting, Li Fei, el al. Research on Joint Precoding of Horizontal and Vertical Dimension in 3D MIMO System[J]. Journal of Signal Processing, 2016, 32(9): 1093-1100.(in Chinese)
[5] Yuan S, Liang Q. To achieve Massive MIMO with much less antennas by nested placement[C]∥Computer Communications Workshops. IEEE, 2016: 668- 673.
[6] Wu L, Qi C. Uplink channel estimation for massive MIMO systems exploring joint channel sparsity[J]. Electronics Letters, 2014, 50(23): 1770-1772.
[7] Dai L, Wang Z, Yang Z. Compressive Sensing Based Time Domain Synchronous OFDM Transmission for Vehicular Communications[J]. IEEE Journal on Selected Areas in Communications, 2013, 31(9): 460- 469.
[8] Wen C K, Jin S, Wong K K, et al. Channel Estimation for Massive MIMO Using Gaussian-Mixture Bayesian Learning[J]. IEEE Transactions on Wireless Communications, 2015, 14(3): 1356-1368.
[9] Adhikary A, Nam J, Ahn J Y, et al. Joint Spatial Division and Multiplexing—The Large-Scale Array Regime[J]. IEEE Transactions on Information Theory, 2013, 59(10): 6441- 6463.
[10] Sun C, Gao X, Jin S, et al. Beam Division Multiple Access Transmission for Massive MIMO Communications[J]. IEEE Transactions on Communications, 2015, 63(6): 2170-2184.
[11] Xie H, Gao F, Zhang S, et al. A unified transmission strategy for TDD/FDD massive MIMO systems with spatial basis expansion model[J]. IEEE Transactions on Vehicular Technology, 2016, 66(4): 3170-3184.
[12] Xie H, Gao F, Zhang S, et al. UL/DL Channel Estimation for TDD/FDD Massive MIMO Systems Using DFT and Angle Reciprocity[C]∥IEEE Vehicular Technology Conference. IEEE, 2016.
[13] Fan D, Gao F, Liu Y, et al. Angle Domain Channel Estimation in Hybrid MmWave Massive MIMO Systems[J]. IEEE Transactions on Wireless Communications, 2018, 17(12): 8165- 8179.
[14] Pal P, Vaidyanathan P P. Nested Arrays in Two Dimensions, Part I: Geometrical Considerations[J]. IEEE Transactions on Signal Processing, 2012, 60(9): 4694- 4705.
[15] Pal P, Vaidyanathan P P. Nested Arrays in Two Dimensions, Part II: Application in Two Dimensionals Array Processing[J]. IEEE Transactions on Signal Processing, 2012, 60(9): 4706- 4718.
[16] Vaidyanathan P P, Pal P. Sparse Sensing With Co-Prime Samplers and Arrays[J]. IEEE Transactions on Signal Processing, 2011, 59(2): 573-586.
[17] Qin S, Zhang Y D, Amin M G. Generalized Coprime Array Configurations for Direction-of-Arrival Estimation[J]. IEEE Transactions on Signal Processing, 2015, 63(6): 1377-1390.
[18] Liu C L, Vaidyanathan P P. Super Nested Arrays: Linear Sparse Arrays With Reduced Mutual Coupling—Part I: Fundamentals[J]. IEEE Transactions on Signal Processing, 2016, 64(15): 3997- 4012.
[19] Liu C L, Vaidyanathan P P. Super Nested Arrays: Linear Sparse Arrays With Reduced Mutual Coupling—Part II: High-Order Extensions[J]. IEEE Transactions on Signal Processing, 2016, 64(16): 4203- 4217.
[20] Liu J, Zhang Y, Lu Y, et al. Augmented Nested Arrays with Enhanced DOF and Reduced Mutual Coupling[J]. IEEE Transactions on Signal Processing, 2017, 65(21): 5549-5563.
[21] Raza A, Liu W, Shen Q. Thinned Coprime Arrays for DOA Estimation[C]∥25th European Signal Processing Conference, 2017: 395-399.
[22] Raza A, Liu W, Shen Q. Thinned Coprime Array for Second-Order Difference Co-Array Generation With Reduced Mutual Coupling[J]. IEEE Transactions on Signal Processing, 2019, 67(8): 2052-2065.
[23] Shen Q, Liu W, Cui W, et al. Low-Complexity Direction-of-Arrival Estimation Based on Wideband Co-Prime Arrays[J]. IEEE/ACM Transactions on Audio, Speech, and Language Processing, 2015, 23(9): 1445-1456.
[24] Cui W, Shen Q, Liu W, et al. Low Complexity DOA Estimation for Wideband Off-Grid Sources Based on Re-Focused Compressive Sensing With Dynamic Dictionary [J]. IEEE Journal of Selected Topics in Signal Processing, 2019, 13(5): 918-930.
万应清 男, 1993年生, 甘肃白银人。南京邮电大学通信与信息工程学院, 硕士研究生, 研究方向为大规模MIMO信道估计技术等。
E-mail: 1824359705@qq.com
解培中 女, 1968年生, 江苏兴化人。南京邮电大学通信与信息工程学院, 副教授, 博士, 主要研究方向为MIMO预编码技术、干扰对齐、定位技术等。
E-mail: cas@njupt.edu.cn
李 汀 男, 1979年生, 江苏扬州人。南京邮电大学通信与信息工程学院, 副教授, 博士, 主要研究方向为5G无线通信技术、 基于人工智能的无线通信技术等。
E-mail: lit@njupt.edu.cn
曾 强 男, 1992年生, 湖北襄阳人。南京邮电大学通信与信息工程学院, 硕士研究生, 研究方向为大规模MIMO信道估计技术等。
E-mail: otrainbow530@163.com