随着4G、5G通信技术的深入发展,在C波段及以下频段,通信领域逐渐占据了原本属于雷达使用的频段,而雷达自然降为了第二用户[1]。近年来,随着各无线电服务自身的发展,像雷达与通信这样在某些频段主次用户地位发生变化的现象逐渐增多,这主要是因为传统的通过严格的频率划分方法已经不能保证各服务领域绝对互不交叠。而波形设计实现频谱共存是最近几年来很多的科研人员和工程师关注的热门研究领域。总之,频谱环境随着通信、雷达等无线电业务的迅猛发展变得越来越拥挤,射频频谱资源愈发珍贵。因此设计波形实现频谱共享对于提高频谱资源利用效率,具有重要意义。
雷达面临诸多挑战,射频频谱环境拥挤是诸多挑战中亟待解决的困难之一。文献[2]从雷达的角度全面回顾了频谱拥挤问题发展历程,从本质上说明了雷达与通信产生频谱交叠的原因。而波形设计作为重要的理论研究方向,文献[3]很早就提出了设计频谱“零陷”的思路。文献[4- 8]则延续了[3]的思路,通过设计单个“零陷”或者多个零陷形成很窄的阻带来“出让”某些频率给通信或者其他服务使用。与以上思路不同的是,文献[9]同时考虑雷达距离分辨率,设计低自相关旁瓣水平同时频谱指定频段带有凹陷的发射信号。该团队又在文献[10]中提出针对任意波形的“整形”算法。
此外,添加不同的时域和频域约束寻找满足特定目标函数的最优波形的凸优化方法,是目前有效地实现频谱共享的新思路,该方法在文献[11]中做了充分的论述,并且给出了很好的仿真实验说明。之后该团队又考虑精确控制各重叠频段频谱能量[12]。文献[13]则针对文献[11]中利用凸优化工具寻找优化信号所涉及的高计算复杂度的问题,提出了利用交替方向乘子法(ADMM)求解该问题。该方法的优点在于迭代过程中可以分解为几个二次规划的问题,因此,降低了计算复杂度。此后,文献[14]则将文献[11]研究的内容进一步发展,添加信号能量约束,同时将接收滤波器联合发射波形共同进行设计,并指出设计恒模波形问题,具有重要工程意义。最终在文献[15]中给出了联合接收滤波器设计实现频谱共享的波形设计理论框架,同时又一次指出设计恒模波形是重要的研究方向。针对MIMO雷达不考虑频谱兼容性设计恒模波形,文献[16]施加恒模约束和相似性约束并采用高斯随机化方法得到了效果很好的恒模波形。
杂波环境下恒模波形设计实现频谱共享是目前还没有很好解决的问题,针对这一问题,本文在文献[14]的框架下提出一种可行的方法解决杂波环境下设计恒模波形实现频谱共享的问题。本文在第2、3节里分别介绍模型建立,算法构建的问题。主要的过程是添加不同约束并以信干噪比作为目标函数得到优化问题模型,该模型涉及非凸问题的分式规划问题,通常不容易求解,利用分步优化的思想可以很好地解决该问题,而后又提出利用高斯随机化的方法求解优化信号。第4节中通过仿真实验验证了该方法的有效性。最后,第5节对全文加以总结。
在这一小节里,将对问题背景进行阐述,添加约束,确定目标函数,建立杂波环境下联合接收滤波器设计的波形设计实现频谱共享的问题模型。
假设雷达探测信号为M′维的离散时间信号,用s表示信号,即s∈CM′×1。当从雷达接收端考虑,考虑接收机接收杂波,令y为M′维的快时间维列向量,代表接收信号,那么有:
y=βs+c+n′
(1)
其中,β代表着从目标距离方位角范围内的后向散射效应,即βs表示目标反射回来的探测信号,而c表示进入接收机的杂波(clutter),与此同时,n′表示接收机内部热噪声和一些独立干扰源产生的干扰,建模为复高斯随机向量,其均值为零,协方差矩阵为M。对杂波c而言,它是来自受测试区域单元格的所有回波信号的叠加[14],满足:
(2)
βi表示目标区域单元的散射系数,与n′同理,将其建模为复高斯随机向量,其均值为零,协方差矩阵为
表示为特殊矩阵,满足
(3)
其中(p,q)∈{1,…,M′}2,假定该雷达系统工作在C波段以下频率,将通信作为该工作频段上的“主用户”,设计雷达探测信号与通信实现频谱共享。雷达作为“次用户”需要雷达探测信号尽可能地在重叠频段上减少对通信系统产生影响。可以假设
(k=1,…,K,其中K为重叠频带个数),而
分别表示第k个频带归一化的下边界和上边界频率。从频域的角度来看,可以将k个频带上发射的能量表示为:
s†RIs≤EI
(4)
其中,
rk≥0,k=1,…,K,(符号“†”表示共轭转置,下同),rk的不同代表着不同的频段允许相互干扰的能力不同。根据
为能量谱密度(energy spectral density,ESD),其中
为
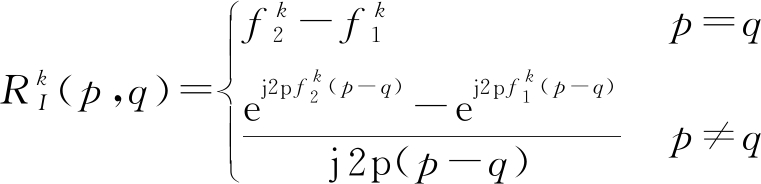
(p,q)∈{1,…,M′}2
(5)
从接收一侧考虑,信号经过滤波器被接收机接收。以雷达系统的检测性能为优化指标,选择输出信干噪比作为优化对象。假设信号通过线性系统,ω作为系统系数,由(1)知,有:
yout=βω†s+ω†c+ω†n′
(6)
yout表示接收滤波器输出的信号,进一步有
yout=βω†s+ω†(c+n′)
(7)
令Nc=c+n′ 则输出信干噪比:
sin r=|β|2|ω†s|2/E[(ω†Nc)2]=
|β|2|ω†s|2/E(ω†NcNc†ω)=
|β|2|ω†s|2/ω†E(NcNc†)ω
(8)
接收机内部热噪声与干扰以及外部杂波是相互独立的干扰源,则有:
E(NcNc†)=E(cc†)+E(n′n′†)
(9)
sin r=|β|2|ω†s|2/ω†[E(cc†)+E(n′n′†)]ω
(10)
根据(2)得
(11)
其中“* ”表示共轭操作,令
且
那么
(12)
在这里,假设信号总的能量为1,但在能量要求的基础上进一步约束信号为恒定幅度的,这主要是为了保证雷达发射机效率,应尽可能的使发射机放大器工作在饱和状态[10]。因此有:
(13)
另一方面,雷达发射信号为获得高距离分辨率通常需要保持较低的自相关旁瓣水平,为此,可以对信号施加相似性约束,即‖s-s0‖2≤κ,其中κ≥0,参考信号s0通常选为线性调频信号。那么便得到与文献[14]中类似的模型:
s†RIs≤EI
‖s-s0‖2≤κ
(14)
显然,(14)更进一步将能量约束进一步完善为恒模约束,使得问题更加复杂。约束条件中恒模约束(13)是非凸条件,并且目标函数也是非凸的,除此之外,求解该模型首先需要确定可行集合,即约束条件不相互矛盾的集合,同时,目标函数是由两个变量组成同时求最大值,属于分式规划问题。
文献[14]提出在针对任意幅度波形设计的问题,本文将恒模约束考虑之后,使得[14]的解决方法不再适用。讨论问题(14)的求解问题过程与[14]有类似也有重要区分。可以看到(14)是在恒模约束、相似性约束和频谱兼容性约束下关于ω与s的联合优化问题。如前所述,(14)是高度非凸问题模型,并属于分式规划问题,同[14]中方法一样利用分步优化的方法,将ω与s分别固定,求解问题。
当s固定时,(14)可以转化为
(15)
此时,该问题进一步等效为最小方差失真响应问题(MVDR)[16]
s.t|β|2|ω†s|2=1
(16)
那么得到
(17)
在ω固定时候,则问题(14)可以转化为
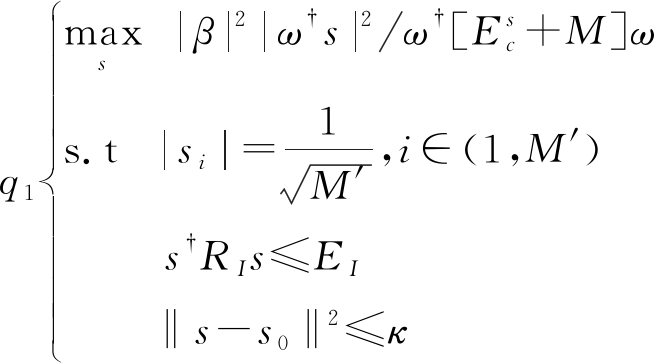
(18)
约束条件中恒模约束导致该问题只存在相位上的自由度,因此本文提出抛掉恒模约束松弛成为可解凸问题,即只对所求的矩阵对角线施加恒模约束,对(18)松弛处理,恒模约束是非凸条件,抛掉恒模约束(13),将约束条件写成迹的形式,得
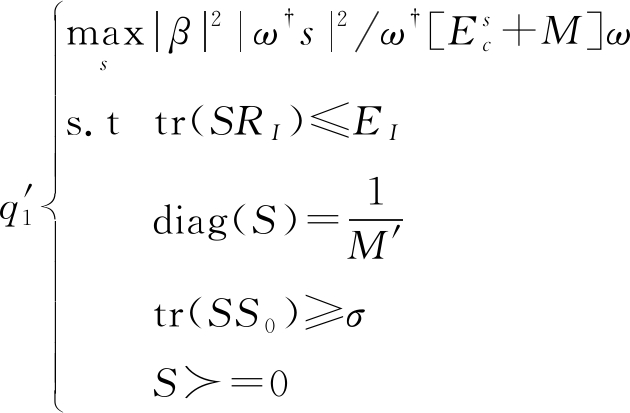
(19)
其中,S≻=0表示矩阵S是一个半正定矩阵,另外σ=(1-κ/2)2。
‖s-s0‖2=[2-2Re(s†s0)]
(20)
可以发现,当s=s′ejarg(s′†s0)时,Re(s†s0)等价于
因此假设s′是q′的解,那么s=s′ejarg(s′†s0)则是问题q1的解。
目标函数涉及分式规划问题,因此对于q′可以利用Charnes-Cooper变换将(19)转换为一个等效的可解的半正定规划(SDP)问题,如下:
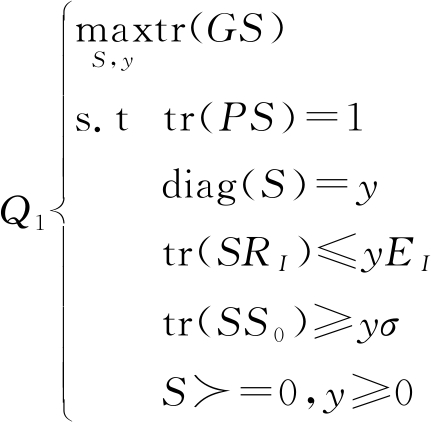
(21)
那么,假定(S△,y) 是(21)的解,那么可以得到(19)的解应为S=S△/y。
其中,S=ss†,S0=s0s0†,G=ωω†,并且
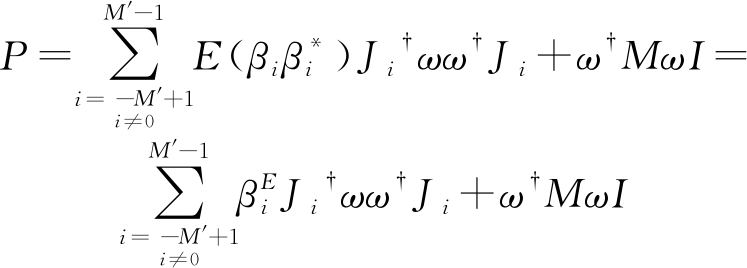
(22)
在求解整个问题之前,需要分析q1中约束条件构成的可行区域问题。具体的证明过程见文献[11]。约束条件构成的边界区域可以描述为
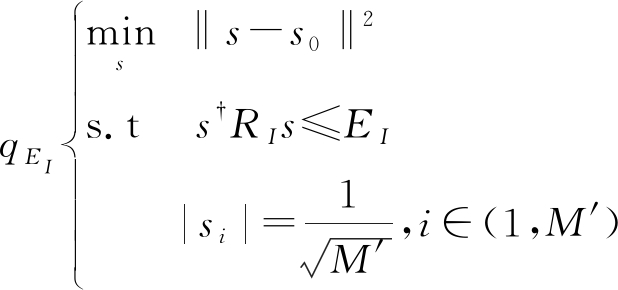
(23)
此外,解决(14)还需要利用分步优化,即固定s和ω中的一个变量,优化另外一个变量。
先固定s优化ω,假定s=s1,带入(17)得到ω1,并计算信干噪比SINR1,然后将ω1带入(21)得到s2,再得到ω2,并计算SINR2,然后循环以上步骤,直到优化得到信干噪比(SINR)与上一次经过循环步骤得到的SINR差距在既定范围之内,输出优化信号。
文献[14]针对能量约束问题在松弛分步优化过程中利用“秩一分解”理论得到优化信号,而该理论并不适用于恒模约束条件下的(14),本文提出利用高斯随机化方法恢复优化信号。
根据以上思路,详细的算法步骤如表1所示。
表1 波形优化算法
Tab.1 Waveform optimization algorithm
算法一 波形优化算法1. 给定初始信号s-1,设定循环次数N次或者算法退出条件值ζ,u=1。2. 根据(17)计算得到ωu,带入初始数据,利用凸优化工具求解Q1(21)模型并得到复矩阵S',以及优化值ν=tr(GS)和y。3. 令S'=S'/y,同时计算S'的秩。4. 若rank(S')=1,直接对S'进行特征值分解即得到最优解s',跳到步骤7。5. 若rank(S')>1,以均值为零,协方差矩阵为S'随机生成向量X组随机向量,同时代入信干噪比表达式。6. 在X组中选取使得信干噪比最大的随机向量作为优化信号s'u。令s'u(i)=1/M'angle(s'u(i))。7. 取s″u=s'uejarg(s'u†s0)。8. 信号s″u带入(17)计算得到ωu,带入(12)得到SINRu,若SINRu-SINRu-1<ζ(u=1时,SINR0利用步骤1中数据)或u=N,跳出执行步骤9,否则u=u+1并重复步骤2～8。9. 输出s″=s″u。
本节将根据前面及部分的阐述,添加具体的数值,并通过仿真实验验证算法效果,给出仿真结果截图。假设相似对象为线性调频信号,满足:
(24)
其中M′=120,kS=750×109/148 Hz/s,同时令fs=810 kHz。
假设在归一化频带上,存在以下三个重叠频带,
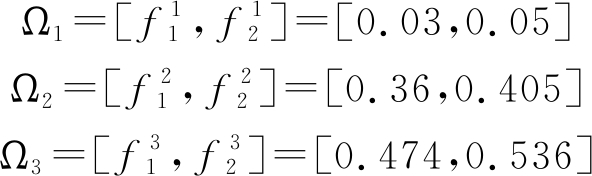
如前所述,复高斯随机向量n′表示接收机内部热噪声和一些独立干扰源产生的干扰,通常认为由接收机内部热噪声、已知的发射机干扰、敌对干扰。其均值为零,协方差矩阵为M,且
(25)
其中,σ0 代表内部热噪声,而且σ0=0 dB, σI,k=10 dB,k=1,2,…,K,K=3代表交叠的频带数量。而另一方面,σJ,1=25 dB,σJ,2=30 dB,并且假设
其中, fJ,k 代表干扰频率,同时fJ,1/fs=0.7, fJ,2/fs=0.75。另外,|β|2=10 
dB。
根据式(24)得到s0自相关函数仿真结果如下:
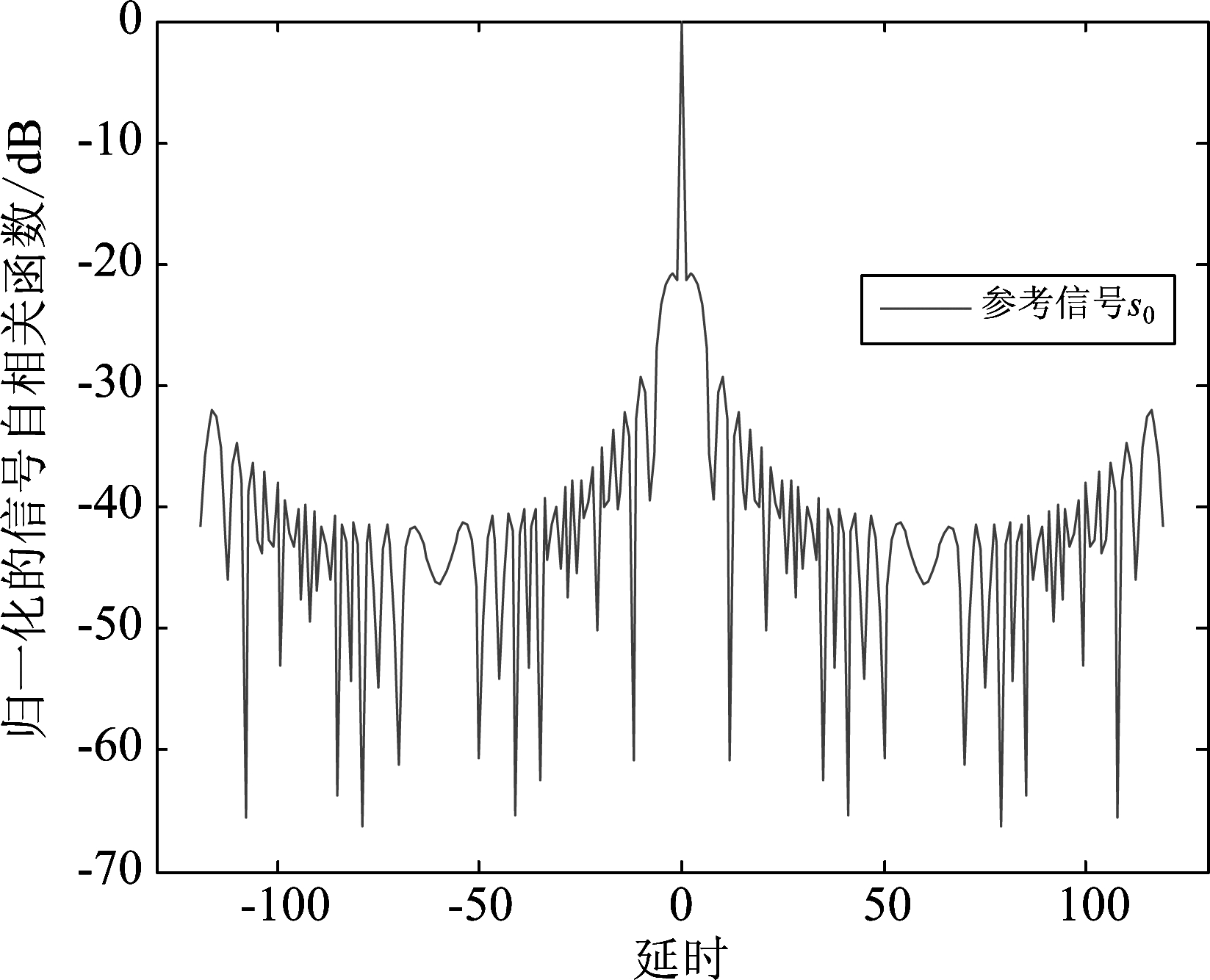
图1 参考信号s0的自相关函数
Fig.1 Autocorrelation function of reference signal
图2 干扰相似性区域
Fig.2 Interference and similarity achievable region
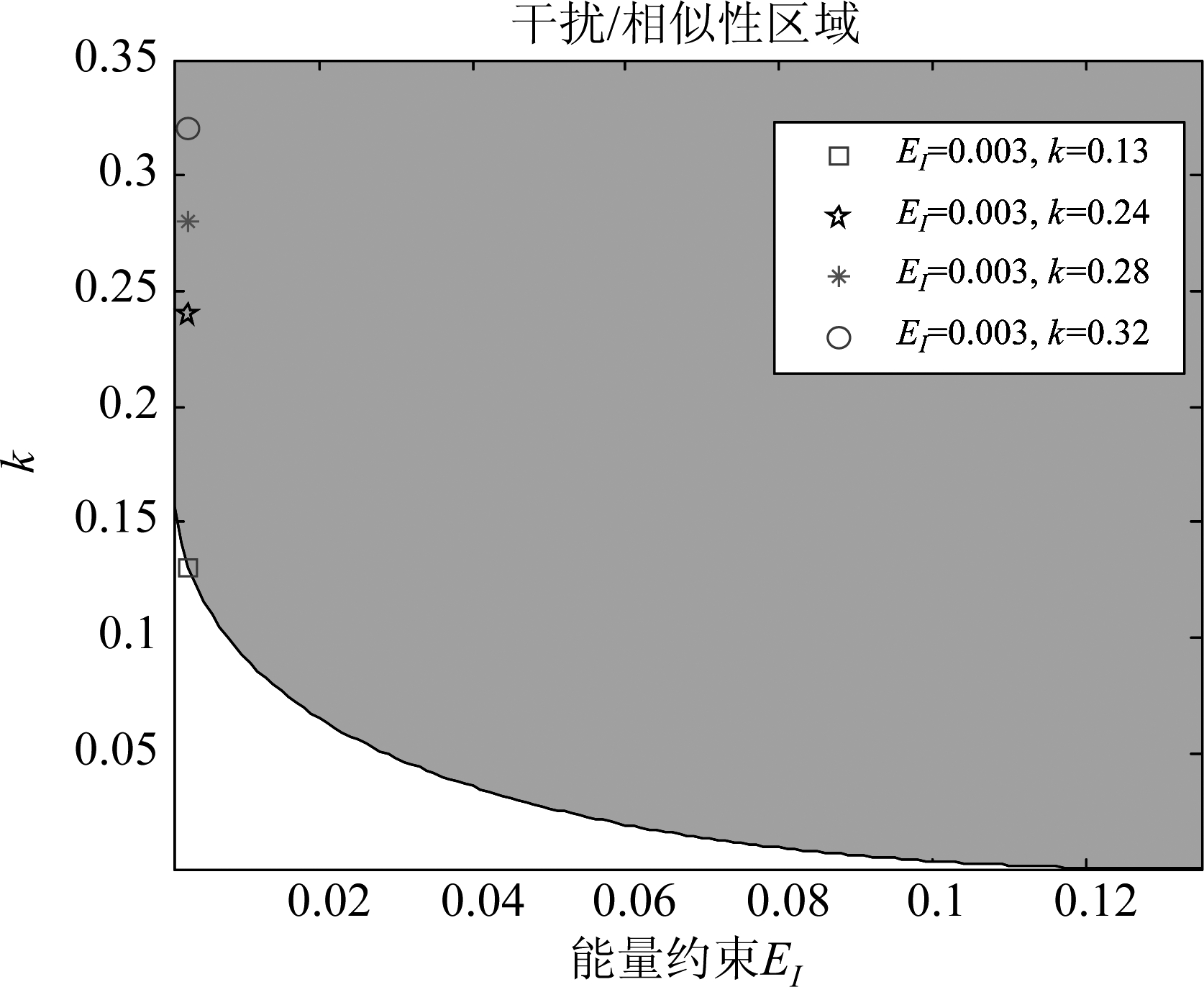
图3 干扰相似性区域
Fig.3 Interference and similarity achievable region
图3是根据式κ≥ν(qEI),将模型(23)中恒模约束更换为能量约束得到的可行集区域。可以看到图2、图3所描绘的边界线上区域为凸集,且图3比图2要小很多,这也正是因为在求解(23),松弛过程中抛掉恒模约束施加了矩阵对角线元素恒定,这说明恒模条件是十分苛刻的。
在图2中可行集内给出了几个数据点,即(EI=0.018,k=0.12)、(EI=0.018,k=0.15)、(EI=0.031,k=0.15)以及(EI=0.0626,k=0.15),下面根据提出的算法分别对这几个点进行实验仿真,寻找优化信号,设置随机化次数为2000次,观察其仿真结果,自相关函数(autocorrelative function,ACF)、信号幅度、ESD分别如下列图所示:
图4 信号的自相关函数仿真结果
Fig.4 Simulation results of signal ACF
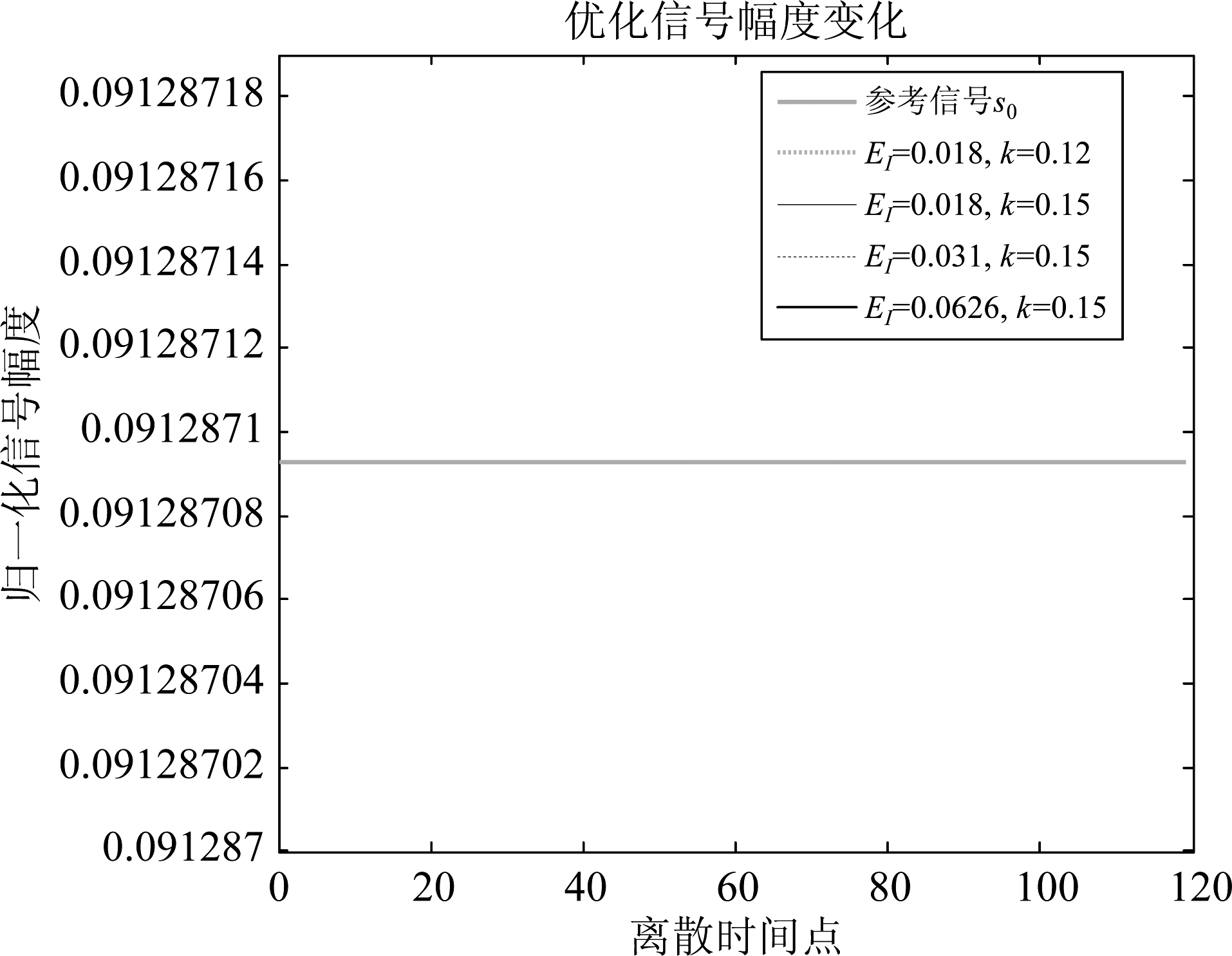
图5 信号幅度
Fig.5 Amplitude of signal obtained from algorithm 1
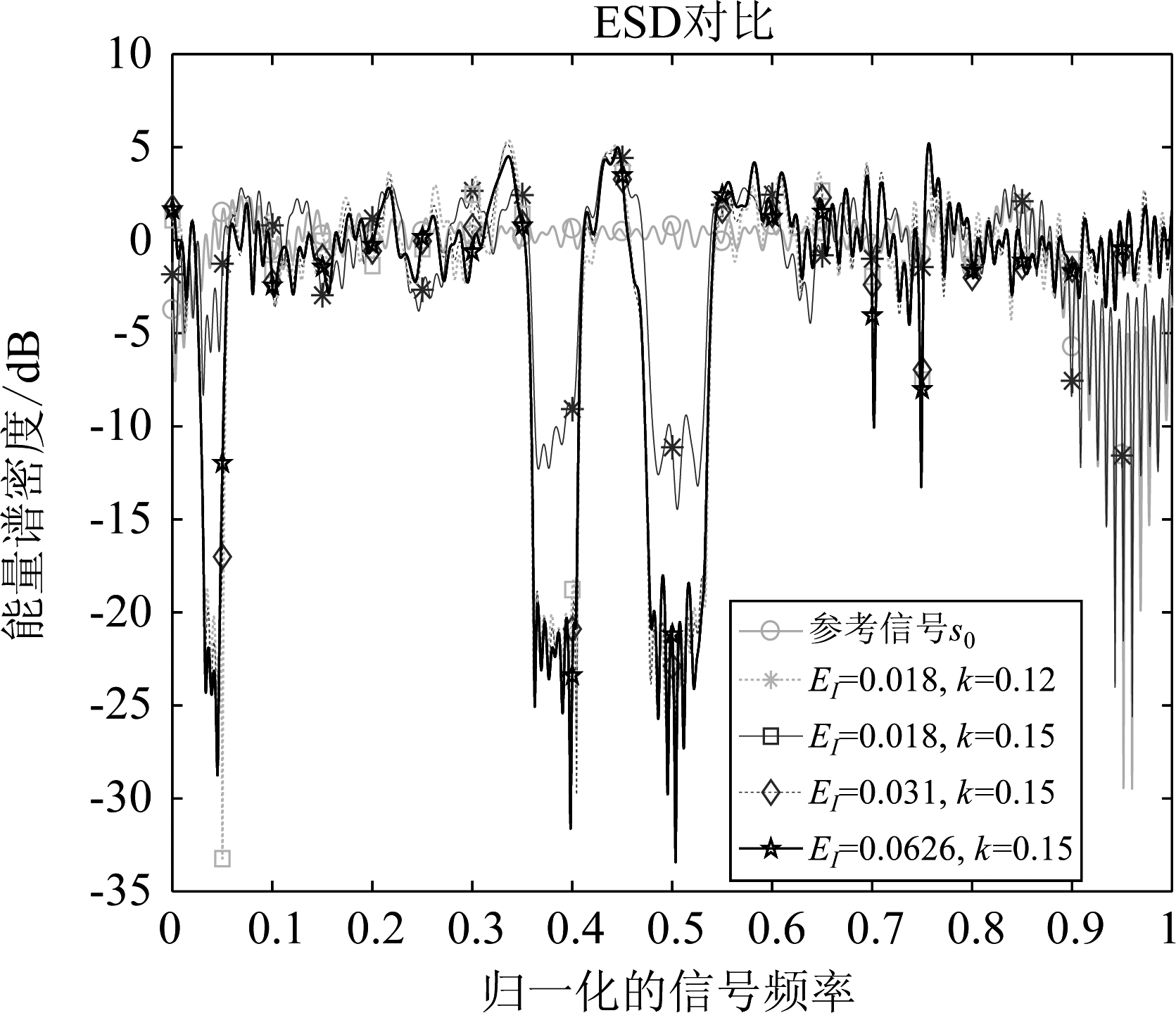
图6 能量谱密度比较效果图
Fig.6 Comparison of ESD
如图4所示,利用提出的算法得到的信号自相关旁瓣水平比参考信号大了很多,其中峰值旁瓣水平明显升高,自相关特性变差,但总体上自相关特性因为施加了相似性约束的原因得到了控制,峰值旁瓣水平仍然较低,所以本文提出的算法仍是很有效的。本文的目标是设计恒模波形,算法得到的信号幅度如图5所示,不同数据点得到的信号的幅度都是
因此,在仿真图中不同颜色的线被相互掩盖,只能看到一条线。图6显示,算法得到信号在指定的频段信号能量谱密度下降明显,已经达到了-20 dB,因此该算法效果十分明显。
不同数据点算法得到信干噪比随着算法循环次数的变化趋势作仿真结果如下:
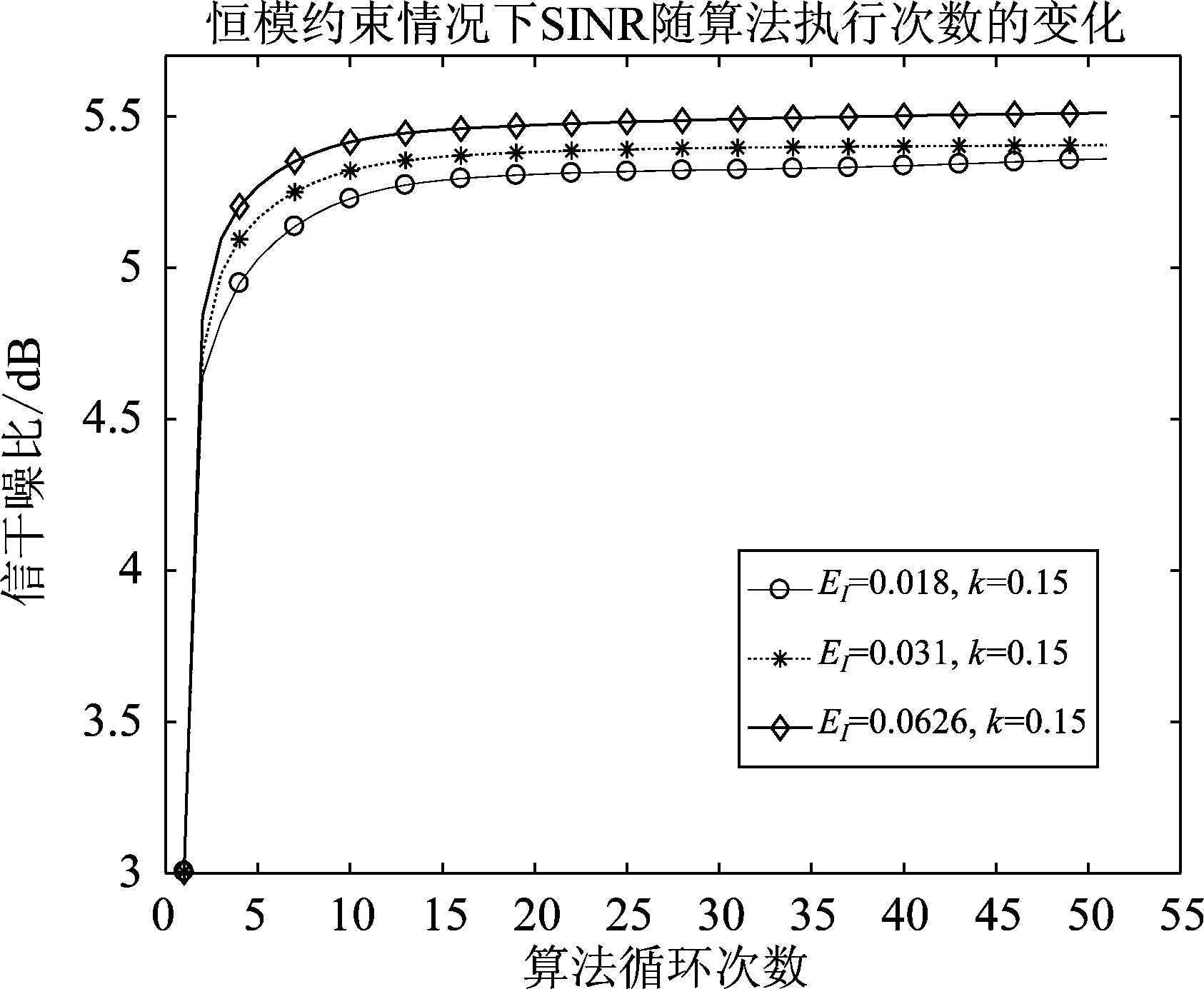
图7 信干噪比随循环次数的变化趋势
Fig.7 The trend of SINR with the number of cycles
从图7可以看出,随着循环次数的不断增加,目标函数即信干噪比稳步上升。可行集内不同点利用本文算法得到的信干噪比随循环次数增加收敛到不同值,而且变化趋势都是稳步提升的。
为全面地说明算法的有效性,下面将对表1中算法与文献[14]中杂波环境下,使用能量约束建立模型最终利用秩一分解理论的方法进行对比,重新选择对比点(EI=0.003,k=0.24)、(EI=0.003,k=0.28)、(EI=0.003,k=0.32)以及能量约束条件下算法初始点为可行区域的边界(EI=0.003,k=0.13),恒模约束条件下表1算法初始点(EI=0.003,k=0.22),得:
图8 可行区域内取点
Fig.8 The points in feasible areas
选取图3、图8中EI=0.003,k不同的点,得到图11、图12给出了对信号能量谱密度的仿真结果,其中本文恒模约束条件下高斯随机化方法得到的信号能量谱密度下降指定频段最多可以降到-20 dB,而能量约束条件下降较多。这种结果和上面的对自相关函数的仿真得到的比较结果结论一样,这不代表本文方法无效,而是本文研究的是设计恒定幅度模型的信号,而图11是针对任意幅度信号,所以本文研究的问题,本身自由度更小,得到的信号自然性能会打折扣。经过以上对比,可以得出虽然相比于能量约束时信号有所折扣,但是得到的信号满足了恒模,更适用于工程应用,另外,总体上看,信号的频谱兼容特性仍较好,比能量约束时差别并不大,也说明了本文算法的有效性。
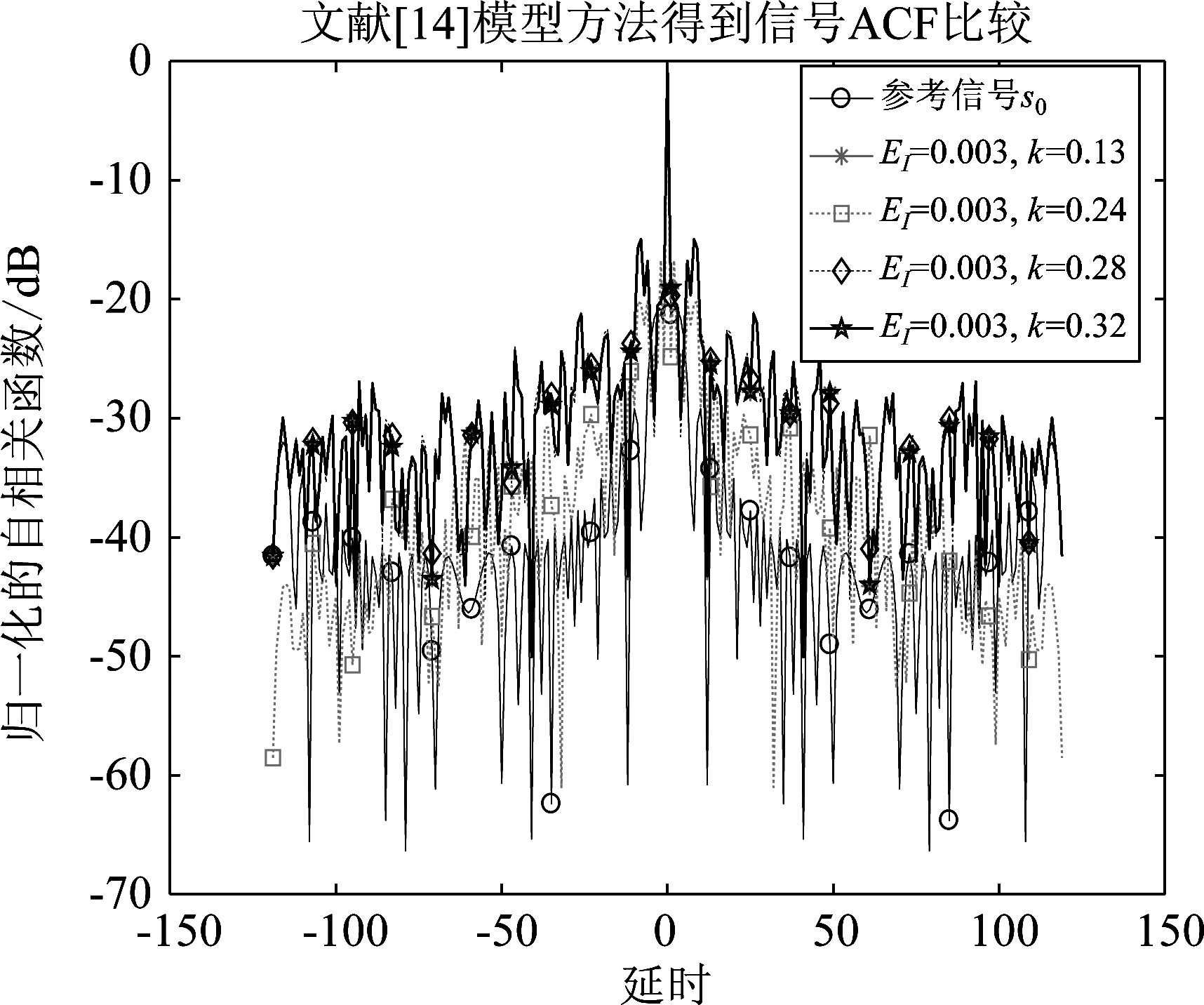
图9 文献[14]能量约束条件下信号自相关函数
Fig.9 ACF of signal under energy constraint in[14]
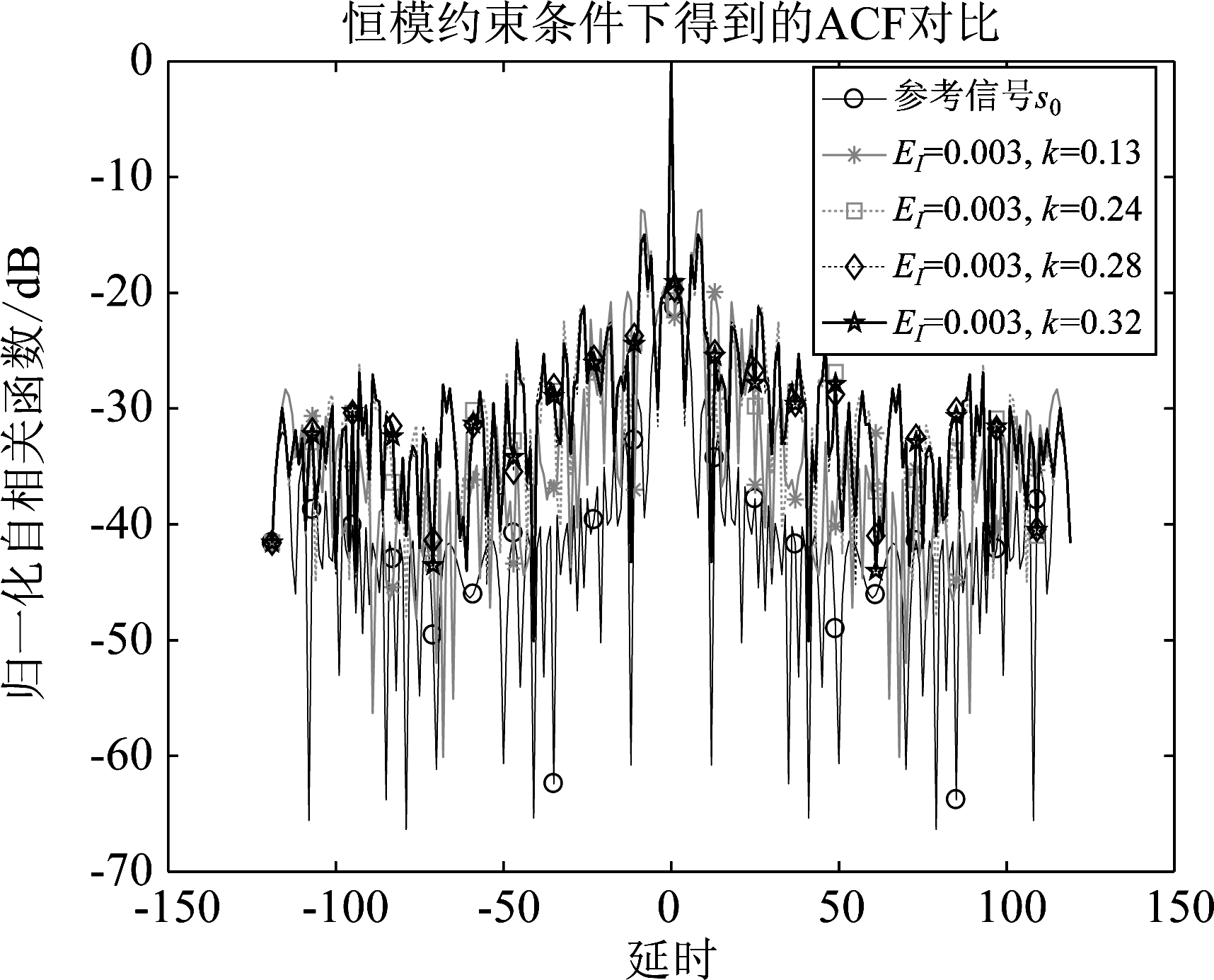
图10 本文恒模约束条件下信号自相关函数
Fig.10 Signal ACF under constant mode constraint
图11 文献[14]能量约束条件下信号ESD
Fig.11 ESD under energy constraint in reference[14]
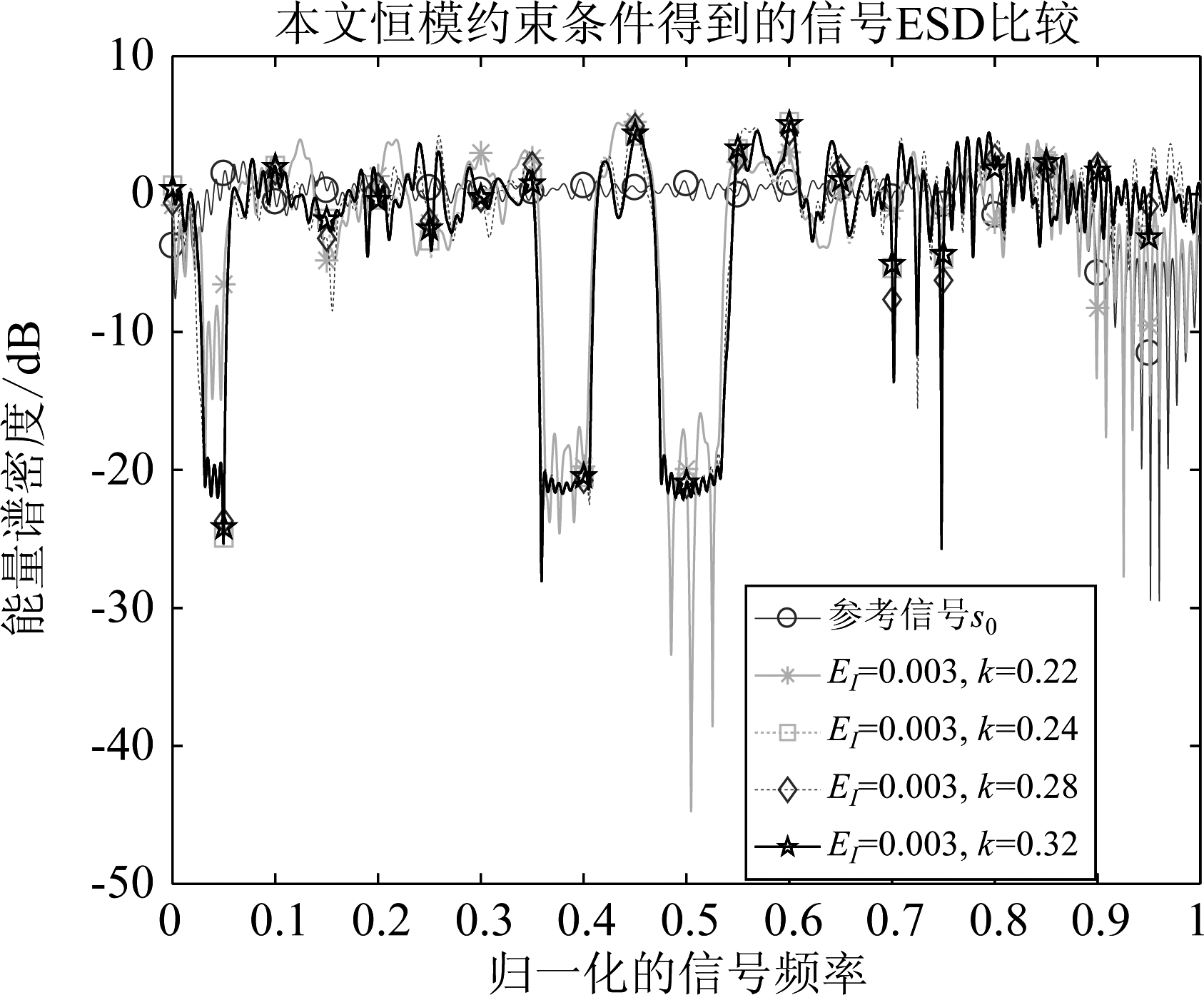
图12 本文恒模约束条件下信号ESD
Fig.12 ESD under constant mode constraint
图13 文献[14]能量约束条件下信号SINR变化
Fig.13 SINR under energy constraint in reference[14]
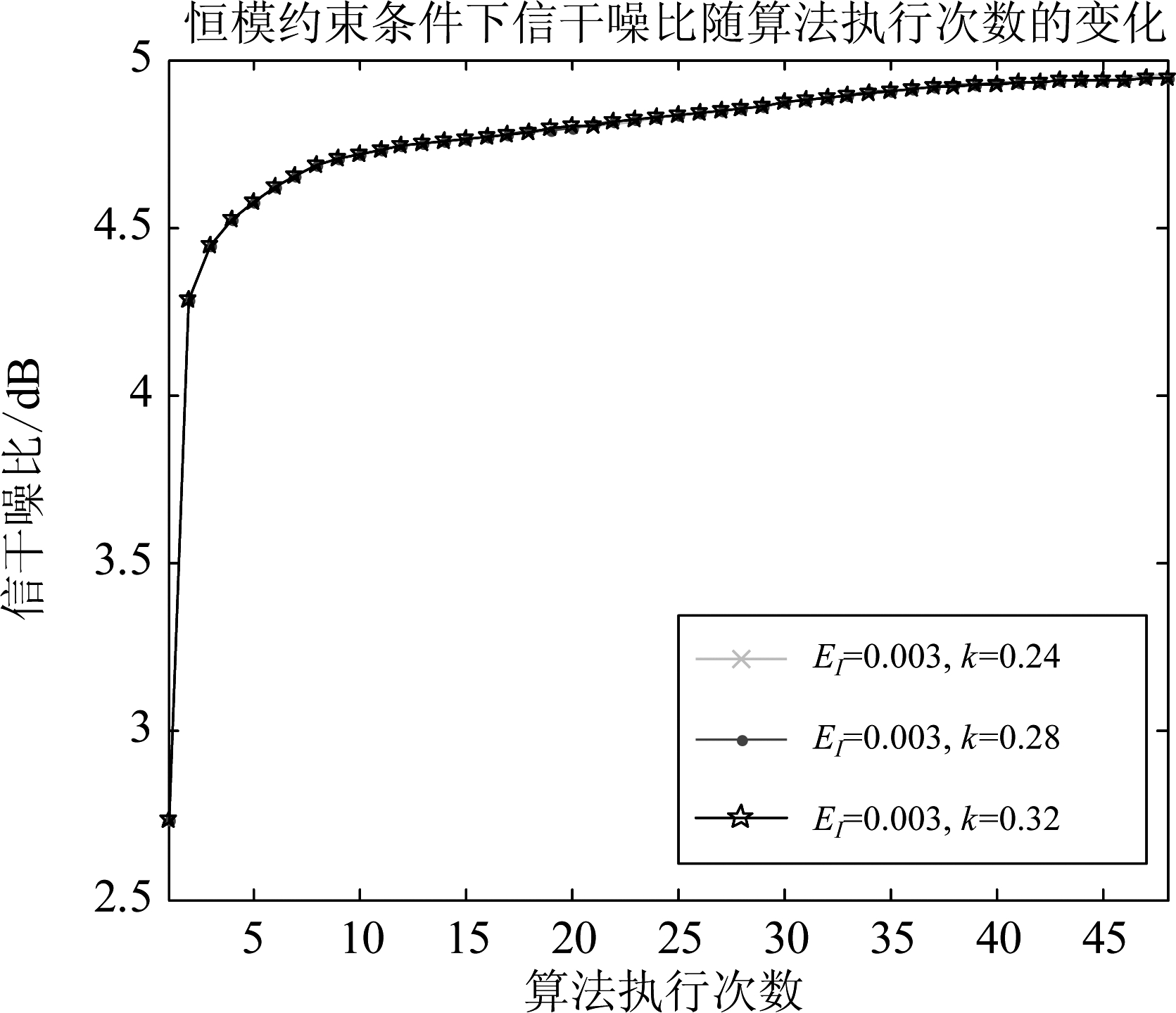
图14 恒模约束条件下信号SINR变化
Fig.14 SINR variation under constant mode constraint
另外,可以看到图13和图14相比,相同的EI,k不同时,最终得到下SINR几乎一致,而相同的k,EI不同时,得到SINR各不相同,EI越大时,SINR越高,这同时说明EI对优化解的影响更大。
设计波形实现频谱共享对于缓解频谱拥挤具有低成本、效果优良的特点。针对杂波环境下联合接收滤波器设计,本文提出了一种可行方法,在能量约束的基础上进一步解决恒定幅度信号设计实现共享频谱的问题。本文将接收滤波器纳入考虑,进行恒模波形设计。建立恒模约束、指定频段频谱能量约束、相似性约束下的非凸问题模型。在求解过程中涉及非凸问题松弛过程和分式规划问题。仿真结果表明,本文在杂波环境下考虑接收滤波器设计恒模波形的方法得到的信号自相关特性良好,峰值旁瓣水平得到有效控制,在指定的频段内能量谱密度下降20 dB以上,同[14]中能量约束时设计任意幅度波形共享频谱相比,信号性能下降不多。总之,本文方法达到了预期效果,实现了雷达通过控制发射波形在指定的频段与其他无线电服务共享频谱。另外,本文的方法算法复杂度仍有下降的空间,下一步将着重研究算法复杂度更低的可靠算法。
[1] Griffiths H, Blunt S, Cohen L, et al. Challenge problems in spectrum engineering and waveform diversity[C]∥2013 IEEE Radar Conference (Radar Con13). IEEE, 2013: 1-5.
[2] Radar Spectrum Engineering and Management: Technical and Regulatory Issues[J]. Proceedings of the IEEE, 2015, 103(1): 85-102.
[3] Haykin S. Cognitive Dynamic Systems: Radar, Control, and Radio[Point of View][J]. Proceedings of the IEEE, 2012, 100(7): 2095-2103.
[4] Nunn C, Moyer L R. Spectrally-compliant waveforms for wideband radar[J]. Aerospace & Electronic Systems Magazine IEEE, 2012, 27(8): 11-15.
[5] Gerlach K, Frey M R, Steiner M J, et al. Spectral Nulling on Transmit via Nonlinear FM Radar Waveforms[J]. IEEE Transactions on Aerospace and Electronic Systems, 2011, 47(2): 1507-1515.
[6] Selesnick I W, Pillai S U, Zheng R. An iterative algorithm for the construction of notched chirp signals[C]∥IEEE Radar Conference. IEEE, 2010: 200-203.
[7] Cook M R, Higgins T, Shackelford A K. Thinned spectrum radar waveforms[C]∥Waveform Diversity & Design Conference, 2010: 238-243.
[8] Selesnick I W, Pillai S U. Chirp-like transmit waveforms with multiple frequency-notches[C]∥Radar Conference (RADAR), 2011 IEEE. IEEE, 2011: 1106-1110.
[9] He H, Stoica P, Li J. Waveform design with stopband and correlation constraints for cognitive radar[C]∥International Workshop on Cognitive Information Processing. IEEE, 2010: 344-349.
[10] Rowe W, Stoica P, Jian L. Spectrally Constrained Waveform Design[sp Tips&Tricks][J]. IEEE Signal Processing Magazine, 2014, 31(3): 157-162.
[11] Aubry A, De Maio A, Piezzo M, et al. Radar waveform design in a spectrally crowded environment via nonconvex quadratic optimization[J]. IEEE Transactions on Aerospace and Electronic Systems, 2014, 50(2): 1138-1152.
[12] Maio A D, Aubry A, Carotenuto V. Forcing Multiple Spectral Compatibility Constraints in Radar Waveforms[J]. IEEE Signal Processing Letters, 2016, 23(4): 1-1.
[13] Tang B, Li J, Liang J. Alternating Direction Method of Multipliers for Radar Waveform Design in Spectrally Crowded Environments[J]. Signal Processing, 2017: S0165168417302852.
[14] Piezzo M, De Maio A, Aubry A, et al. Cognitive radar waveform design for spectral coexistence[C]∥Radar Conference. IEEE, 2014.
[15] Aubry A, Carotenuto V, Maio A D, et al. Optimization theory-based radar waveform design for spectrally dense environments[J]. IEEE Aerospace and Electronic Systems Magazine, 2016, 31(12): 14-25.
[16] Cui G, Li H, Rangaswamy M. MIMO Radar Waveform Design With Constant Modulus and Similarity Constraints[J]. IEEE Transactions on Signal Processing, 2014, 62(2): 343-353.
张令浩 男, 1994年生, 山东枣庄人。国防科技大学电子对抗学院硕士研究生, 研究方向为频谱共享雷达波形设计。
E-mail: zlh_0221@126.com
张剑云 男, 1963年生, 浙江龙泉人。国防科技大学电子对抗学院教授, 博士生导师, 中国电子学会高级会员, 雷达分委会委员, IEEE会员, 主要研究方向是雷达及目标环境模拟、雷达信号处理、高速信号处理。
E-mail: zjy921@sina.com
周青松 男, 1982年生, 安徽巢湖人。国防科技大学电子对抗学院讲师, 主要研究方向为高速数字信号处理和凸优化理论。
E-mail: zhouqingsong1207@gmail.com