跳频通信因其保密性好、抗干扰能力强、截获概率低和组网能力强等特点被广泛应用于军事通信中,因此针对跳频通信的侦查和对抗问题已经成为研究的重点[1-3]。
信号的波达方向(DOA)问题是阵列信号处理的基本问题之一,也是雷达、声呐等许多领域的重要任务之一。跳频信号的DOA估计对于跳频信号网台分选同样具有重要意义,因此如何快速精确地估计DOA成为研究热点之一。目前关于跳频信号DOA估计主要有基于空时频分析的方法以及以多重信号分类(MUltiple SIgnal Classification,MUSIC)算法和旋转不变子空间(Estimating Signal Parameter via Rotational Invariance Techniques,ESPRIT)算法为代表的子空间类估计算法[4-5]。文献[6-7]将空时频模型引入跳频信号来进行DOA估计,但其适用于超定条件,在欠定条件下性能不佳;文献[8-9]首先对跳频信号进行有效的时频变换,得到清晰稳健的全景时频图,在时频域提取有效跳(hop)后建立空时频矩阵,利用root-MUSIC算法进行DOA估计,但其性能在较少快拍数时下降明显;文献[10-12]在跳频信号参数估计问题中结合了空间极化时频分布思想,利用ESPRIT算法能同时实现信号的DOA和极化参数估计,但是该算法计算量大且对噪声敏感度高,在低信噪比条件下表现不佳;针对常规子空间类算法复杂度高的问题,国内外学者提出了一些方法。文献[13]将共轭子空间的思想引入到MUSIC算法中,利用噪声子空间降维的思想构造空间谱,通过半谱搜索实现信号的DOA估计,降低了算法复杂度。文献[14]首先利用形态学滤波对信号时频图进行修正,然后利用酉ESPRIT算法进行DOA估计,将接收数据从复数域转化到实数域,降低了算法复杂度;文献[15]基于阵列划分和矩阵重构的思想构造新的信号子空间,进而进行信号的DOA估计。该方法降低了算法复杂度,但是未能充分利用空域信息且只适用于连续信号。
综上所述,为了充分利用跳频信号的空域信息来进行信号的DOA估计,在信号空时频分析的基础上,本文提出了一种基于协方差矩阵重构的高效跳频信号DOA估计方法。首先将接收信号的均匀线阵(uniform linear array, ULA)平均划分成2个子阵,分别对每个子阵接收到的信号进行时频分析,在时频域选择有效跳,构造每跳的空时频矩阵(spatial time-frequency distribution, STFD),然后求得2个子阵的互协方差矩阵。将2个子阵的互协方差矩阵进行重构运算得到等效的信号子空间,最后构造空间谱多项式求根估计出信号的DOA。仿真结果表明该方法相比于以往改进类子空间算法能够有效提高估计精度和降低算法复杂度。
假设在观测时间T内有K个相互独立的远场跳频信号,K个跳频信号的DOA为θ=[θ1,θ2,...,θK]T。第k个跳频信号sk(t)的幅度为ak,跳周期为Tk,在观测时间内共有M跳,则sk(t)可表示为:
(1)
式中: fkm为sk(t)第m跳的载频,φkm为sk(t)第m跳的初相,t′=t-(m-1)Tk,rect表示单位矩形脉冲。
假设K个跳频信号被阵元数为2N的均匀线阵ULA接收,每个阵元都是全向阵元,增益均相等,相互之间的互耦忽略不计,阵列的间距为d,并且d<c/2fmax,fmax为接收机带宽的频率上限。将接收均匀线阵等分成2个子阵,每个子阵包含N个阵元,记为子阵U1 和子阵U2,阵元结构如图1所示。虽然跳频信号是宽带信号,每跳的载频随机跳变,阵列流型矩阵也是随机改变的,但是在分析每跳时,信号包络在各阵元上的差异可忽略,故可以当做窄带信号处理。以第一个阵元作为基准,则子阵U1的方向矩阵为A(θ)=[a(θ1),a(θ2),...,a(θK)],其中a(θk)=[1,ejτk,...,ej(N-1)τk]T为对应sk(t)的导向矢量。子阵U1的快拍矢量模型可以表示为
XU1(t)=A(θ)S(t)+V1(t)
(2)
子阵U2的快拍矢量模型可以表示为
XU2(t)=A(θ)ΦS(t)+V2(t)
(3)
式中:XU1(t)=[x1(t),x2(t),x3(t),…,xN(t)]T,XU2(t)=[xN+1(t),xN+2(t),xN+3(t),…,x2N(t)]T为子阵输出的数据矢量;S(t)=[s1(t),s2(t),…,sK(t)]T是跳频信号源数据矢量;τk=2pdsin(θk)/λ,λ为信号波长;Φ=diag(ejNτ1,ejNτ2,…,ejNτK,)是子阵U1和U2之间的关系矩阵;V1(t)=[ν1(t),ν2(t),…,νN(t)]T,V2(t)=[νN+1(t),νN+2(t),…,ν2N(t)]T为噪声数据矢量,假设阵元接收到的噪声均为平稳零均值高斯白噪声,各阵元间的噪声互不相关。
图1 阵列结构图
Fig.1 Array structure
Belouchrani和Amin等人最早将空时频分析方法应用于非平稳信号处理,并取得了不错的效果。其核心思想是将传统空时处理的一维时域分析扩展到二维的时频域分析。具体方法是先对时域信号做时频变换,然后在时频域上选择有效的时频点,最后利用时频域数据构造空时频矩阵。常用的时频分析方法主要包括线性变换和非线性变换,其中非线性变换的时频方法以平滑伪Wigner-Ville分布(SPWVD)为代表,具有较高的时频分辨率和抑制交叉项性能。众多的二次时频分布可以用式(4)来表示:
e-jp(τ ν+τ f-uν)dudνdτ
(4)
式中,φ(τ,ν)是核函数,当φ(τ,ν)≡1时,式(4)就变成了Wigner-Ville分布。SPWVD的表达式为
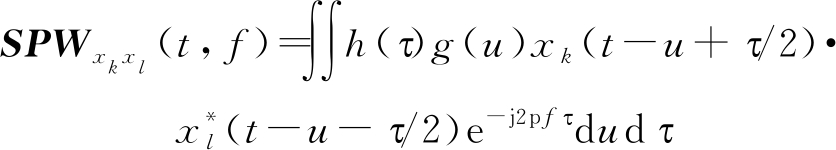
(5)
当信号时频分析采用二次时频分布时,子阵U1输出的STFD矩阵表示为:
DXU1XU1(t, f)=A(θ)×DSS(t, f)×
AH(θ)+DV1V1(t, f)
(6)
子阵U2输出的STFD矩阵表示为:
DXU2XU2(t, f)=A(θ)Φ×DSS(t, f)×
ΦHAH(θ)+DV2V2(t, f)
(7)
其中,
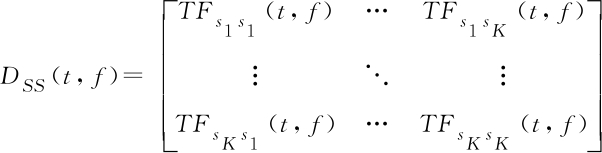
(8)
在得到各个子阵的STFD矩阵后,现定义矩阵DXU1XU2为子阵U1输出数据和子阵U2输出数据的前向互STFD,矩阵DXU2XU1为子阵U2输出数据和子阵U1输出数据的后向互STFD。表示如下:
DXU1XU2(t, f)=A(θ)×DSS(t, f)×ΦHAH+DV1V2(t, f)
(9)
DXU2XU1(t, f)=A(θ)Φ×DSS(t, f)×AH+DV2V1(t, f)
(10)
根据式(9)和式(10)可求得两个子阵时频域的前向协方差矩阵RXU1XU2和后向协方差矩阵RXU2XU1,表示为:
RXU1XU2=E[DXU1XU2]=A(θ)RsΦHAH(θ)
(11)
RXU2XU1=E[DXU2XU1]=A(θ)ΦRsAH(θ)
(12)
其中,Rs是跳频信号源的自协方差矩阵。因为信号源之间相互独立,所以Rs是一个对角阵,表示为:
Rs=diag(p1,p2,…,pK)
(13)
其中,pk(k=1,2,…,K)为第k个跳频信号源的能量。
为了充分利用两个子阵输出数据的相关性,将前向协方差矩阵RXU1XU2和后向协方差矩阵RXU2XU1相加构造一个新的矩阵RUN,表示为:
RUN=RXU1XU2+RXU2XU1=A(θ)RsΦHAH(θ)+
A(θ)ΦRsAH(θ)=A(θ)ΛAH(θ)
(14)
其中,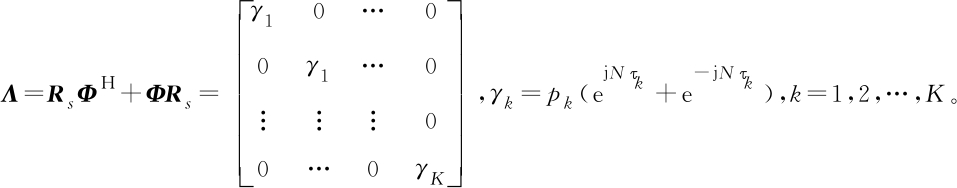
协方差矩阵重构的关键在于构造出和源信号等效的信号子空间。首先将取出RUN的第一列记为向量rUN1,表示为:
rUN1=A(θ)Λδ
(15)
式中,δ是K维的全1列向量。
现定义变换矩阵TN对rUN1进行变换,表示如下:
(16)
其中,TN为副对角线全为1,其余元素全为0的N×N维矩阵,
为N维列向量。由式(15)和式(16),将rUN1和组合成2N维列向量
表示为:
(17)
通过简单推算可知TNA*(θ)是A(θ)的共轭反对称矩阵,因此TNA*(θ)的最后一行元素与A(θ)的第一行元素相同,所以
的第N个元素和第N+1个元素是重复的。将其中重复的一个元素去除后得到新的向量rUN,表示为:
(18)
其中,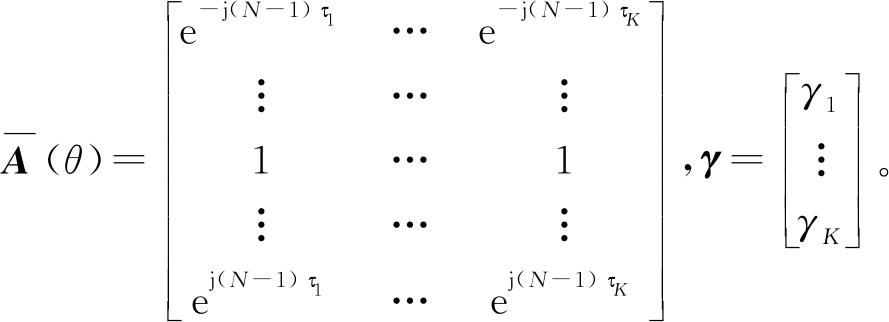
经过上述几步矩阵运算重构后,矩阵rUN变为由1个(2N-1)×K维矩阵
和向量γ乘积的结果。维度由N×K扩展为(2N-1)×K,这样可以补偿由于阵列均分造成的阵列孔径损失,从而提高DOA估计性能。
重构出矩阵rUN后,将rUN分解出与相对应的维(2N-K)×K信号子空间Us,表示为:
Us=[rUN(1),rUN(2),…,rUN(K)]
(19)
其中,rUN(i)=rUN(i:2N-K-1+i)为(2N-K)×1维列向量,取自rUN的第i至第2N-K-1+i个元素。
由式(18)和式(19),信号子空间Us可进一步表示为:
Us=HΛD
(20)
其中,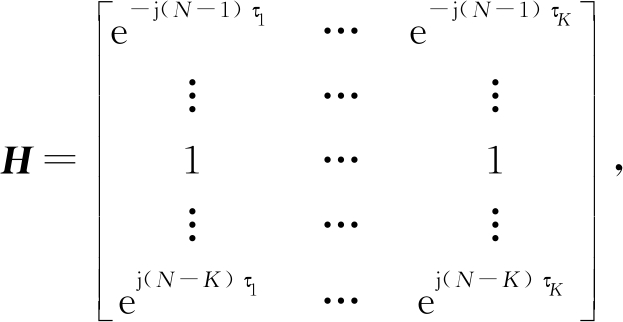
是(2N-K)×K维矩阵。
是K×K维矩阵。
由矩阵H和D的表达式可知,H和D都是Vandermonde矩阵,又因为K个源信号相互独立,互不相关,所以矩阵H和Λ都是列满秩,矩阵D为行满秩,它们的秩均为K。故可知span(Us)=span(H),即Us包含了信号的DOA信息。对Us进行施密特正交化处理可得到完备的信号子空间
在得到信号子空间
后,令
定义
给出求根多项式:
(21)
其中,
为(2N-K)×(2N-K)维单位矩阵。取
在单位圆上具有最大幅值的K个根
便可得到信号的DOA估计:
(22)
需要注意的是,在实际应用中信号的采样数是有限的,因此通常采用协方差矩阵的估计值
即:
(23)
为了确保式(15)能够成立,需要对
进行平滑处理,即:
(24)
考虑到在协方差矩阵重构的过程中只涉及到
的第一列元素,其他元素都未被应用即冗余。因此为了降低运算复杂度,可以只考虑的第一列元素。由式(24)可知,的第一列元素为的第一列元素与其最后一列元素共轭翻转后的平均值。因此可以简化为一个由第一列和最后一列元素组成的N×2维的矩阵,表示为:
(25)
其中,
是
的第一列和最后一列元素组成的矩阵。
是
的第一列和最后一列元素组成的矩阵。所以rUN1的估计值表示为:
(26)
基于以上分析,本文方法具体步骤如下:
步骤1 根据式(6)和式(7)求得两个子阵的STFD矩阵DXU1XU1(t,f)和DXU2XU2(t,f)。
步骤2 根据式(9)和式(10)求得两个子阵时频域的前向协方差矩阵
和后向协方差矩阵
步骤3 根据式(25)和式(26)求得
根据式(16)和式(17),去除相同的一行元素重构得到rUN。
步骤4 利用rUN构造出信号子空间Us,对Us进行施密特正交化处理可得到完备的信号子空间
步骤5 根据式(21)构造求根多项式
根据式(22)求得信号的DOA。
本文方法在充分利用跳频信号的空域信息的基础上,通过对接收阵列划分和协方差矩阵重构,只需对N×1维列向量
进行简单的线性运算便可得到等效的信号子空间Us。相比于传统的子空间类算法,本文方法不需要对全部阵元的2N×2N维协方差矩阵进行特征值分解,有效降低了算法复杂度。
假设阵列数据的快拍数为L,L≫N>K。Root-MUSIC算法在进行协方差矩阵分解时的计算量为O(4N2L+8N3)。文献[13]提出的MSCS方法通过半空间谱搜索降低了算法复杂度,其计算量为O(2N2L+8N3)。而本文方法对N×1维列向量
进行线性运算所需要的计算量为O(4NL),可以看出本文方法相比于Root-MUSIC算法可以明显降低运算量。
本节通过仿真实验来验证本文方法性能。阵列结构如图1所示,阵元间距d为半波长;空间中共有3个跳频信号源记为FH1,FH2,FH3,入射角分别为θ1=10°,θ2=40°,θ3=63°;跳周期为2 μs,采样率为100 MHz。每次进行200次蒙特卡洛实验,采用均方根误差(Root Mean Square Error,RMSE)和估计成功率作为性能指标,定义RMSE为:
(27)
其中,P为蒙特卡洛实验次数,K为跳频信号源的数量,
为第k个信号第p次角度估计值,θk为第k个信号的角度真实值。
定义估计值与真实值误差在1°即为估计成功,则估计成功率表示为:
η=P1/P
(28)
其中,P1为估计成功的次数。
为了验证阵元数对本文方法的估计性能的影响,假设存在3个跳频信号源FH1,FH2,FH3,快拍数固定为2000。均匀线阵ULA的阵元数以2为步进从4递增到16,SNR为0 dB。Root-MUSIC算法、MSCS方法和本文方法的估计性能如图2和图3所示。
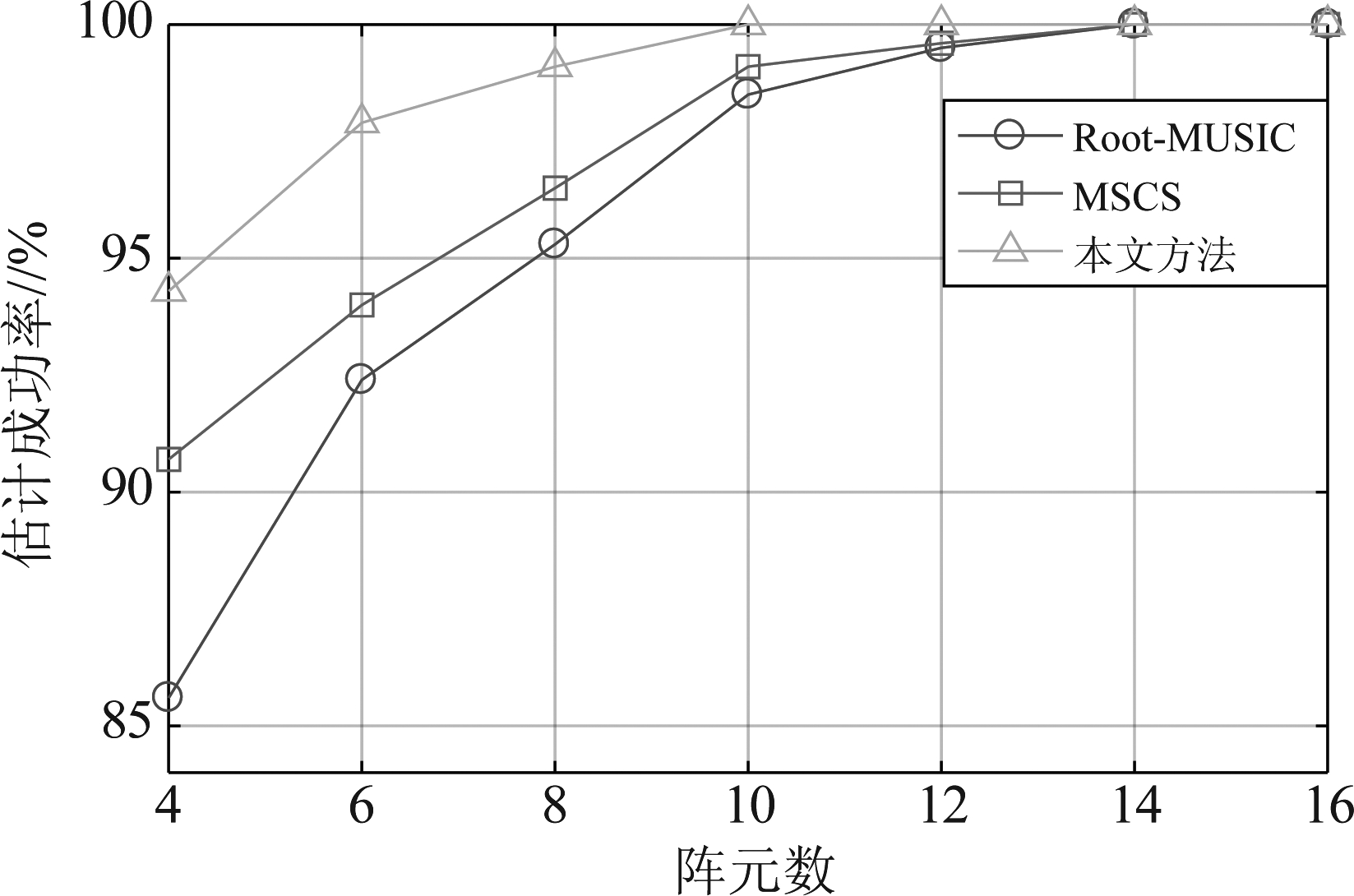
图2 实验1的估计成功率
Fig.2 Estimated success rate of experiment 1
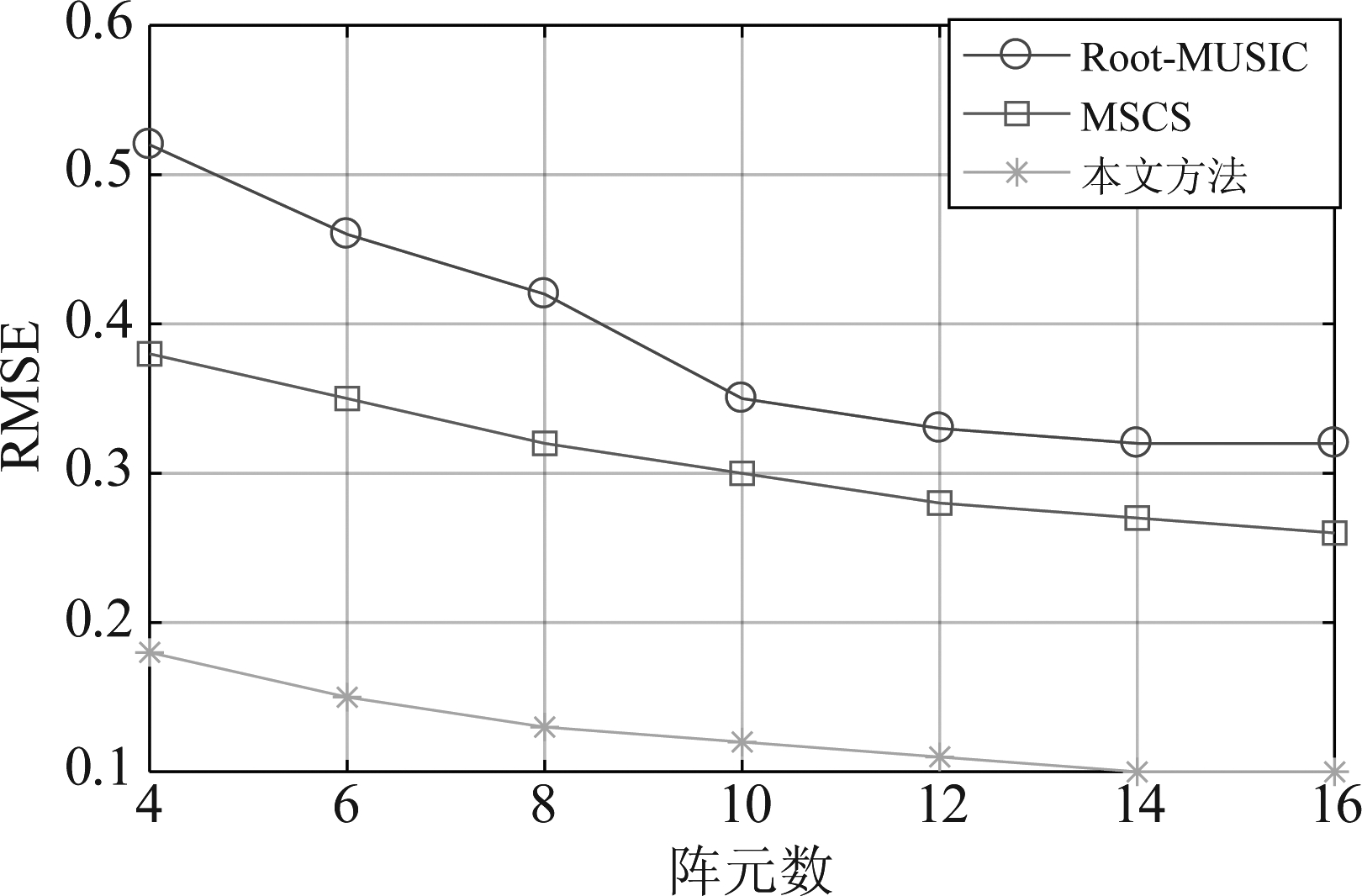
图3 实验1的均方根误差
Fig.3 Root mean square error of experiment 1
从图2可以看到,随着阵元数的增加,三种方法的估计成功率都随之增加。当快拍数相同,阵元数不超过10时,本文方法的估计成功率明显高于另外两种算法,尤其是当阵元数为8时,估计成功率已经接近100%。从图3可以看出,随着阵元数的增加,三种方法的RMSE都在降低,但本文方法估计性能始终优于另外两种方法。
为了验证信噪比对本文方法的估计性能的影响,假设存在3个跳频信号源FH1,FH2,FH3,快拍数固定为2000,均匀线阵ULA的阵元数为8,信噪比从-10 dB递增到10 dB。Root-MUSIC算法、MSCS方法和本文方法的估计性能如图4和图5所示。
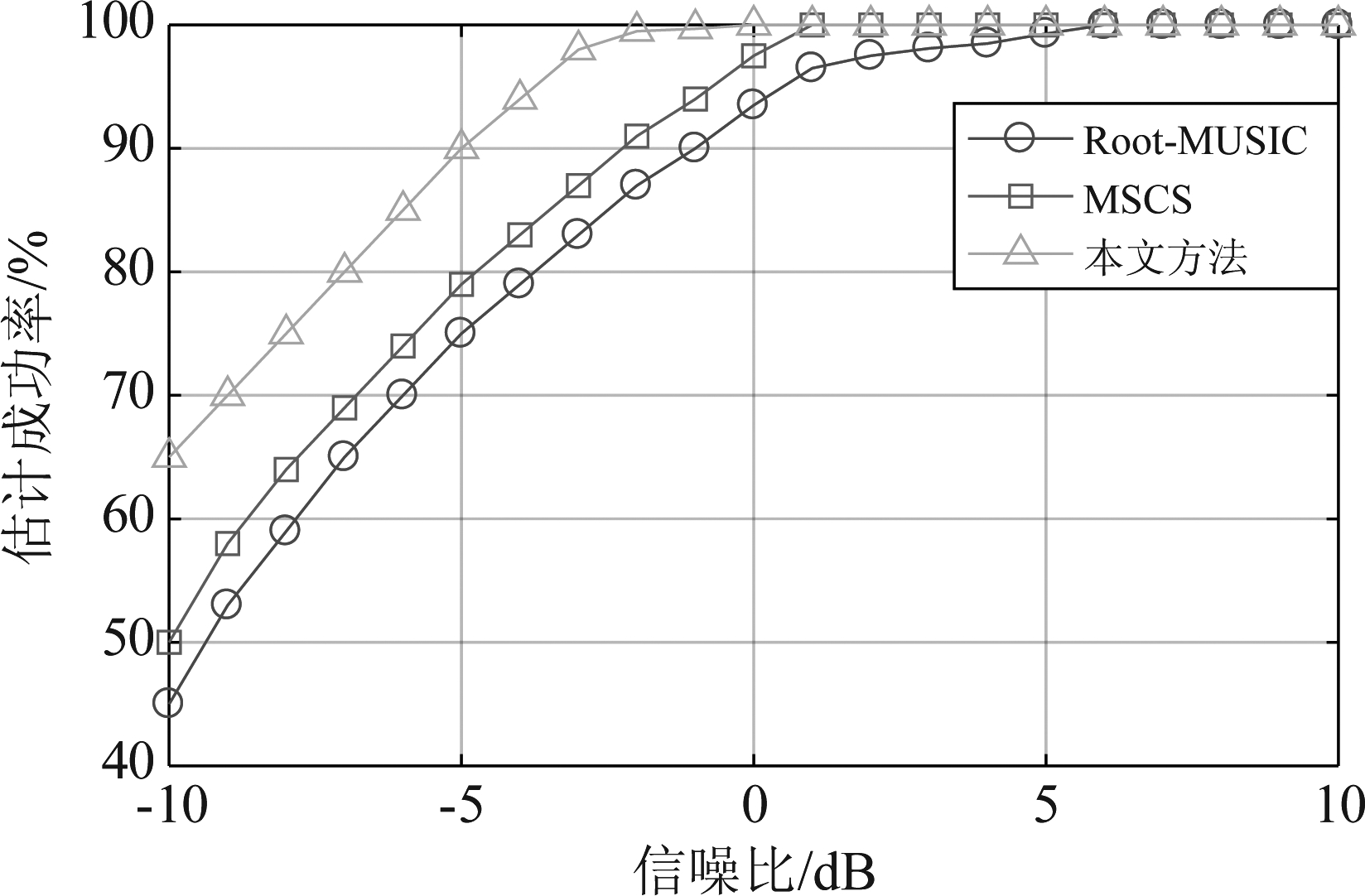
图4 实验2的估计成功率
Fig.4 Estimated success rate of experiment 2
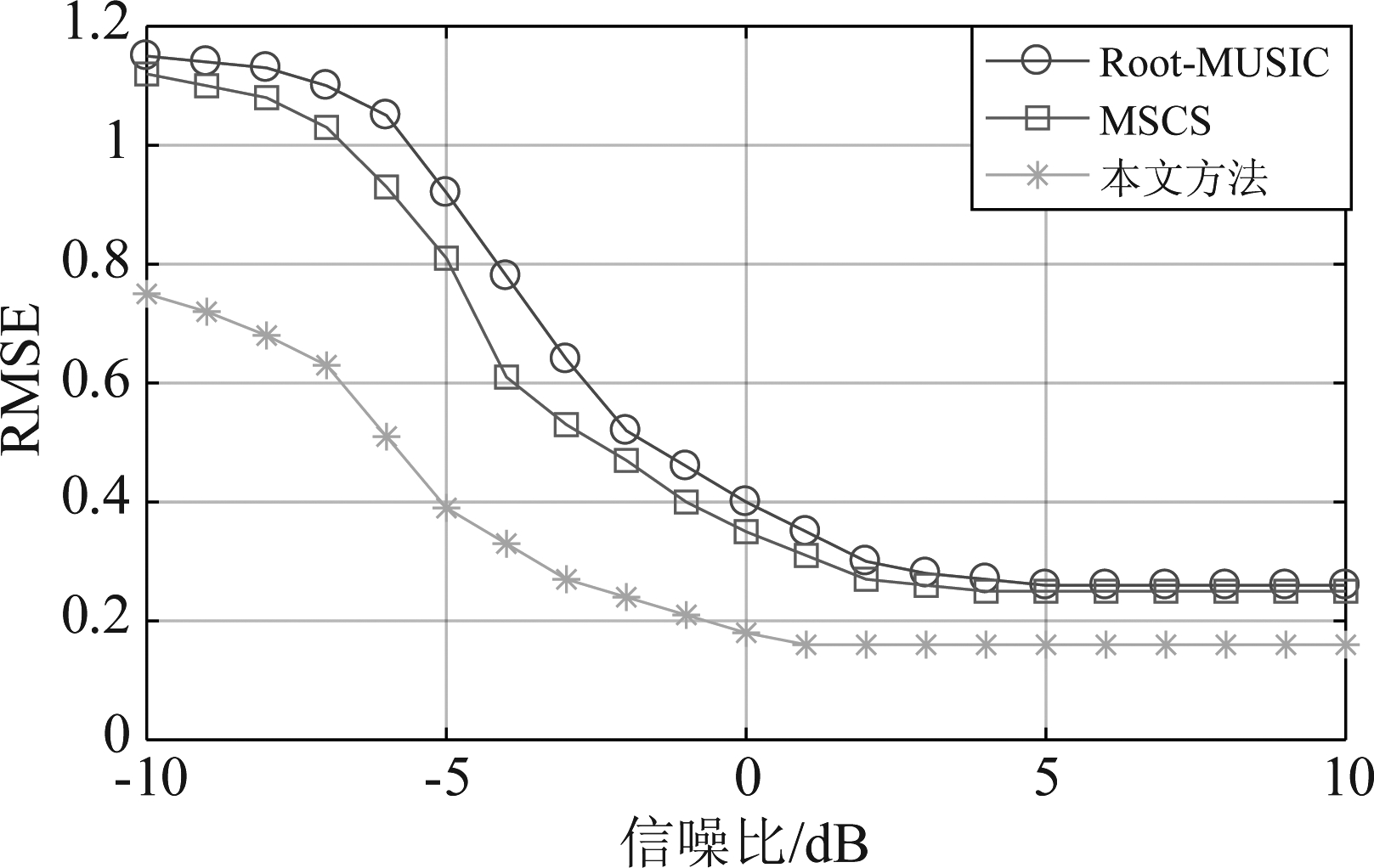
图5 实验2的均方根误差
Fig.5 Root mean square error of experiment 2
从图4可以看出,随着信噪比的增大,三种方法的估计成功率都在增加。整体上本文方法估计成功率要高于另外两种算法,尤其是在低信噪比情况下本文方法估计效果更佳,当信噪比为-3 dB时,估计成功率已经接近100%。由图5可以看出,随着信噪比的增大,三种方法的RMSE都在降低。当信噪比小于-5 dB时,本文方法RMSE明显低于另外两种算法;当信噪比大于-2 dB时,本文方法的RMSE曲线已经趋于平稳。
为了验证快拍数对本文方法的估计性能的影响,假设存在3个跳频信号源FH1,FH2,FH3,均匀线阵ULA的阵元数为8,信噪比为0 dB,快拍数从以200为步进从400递增到2000。Root-MUSIC算法、MSCS方法和本文方法的估计性能如图6和图7所示。
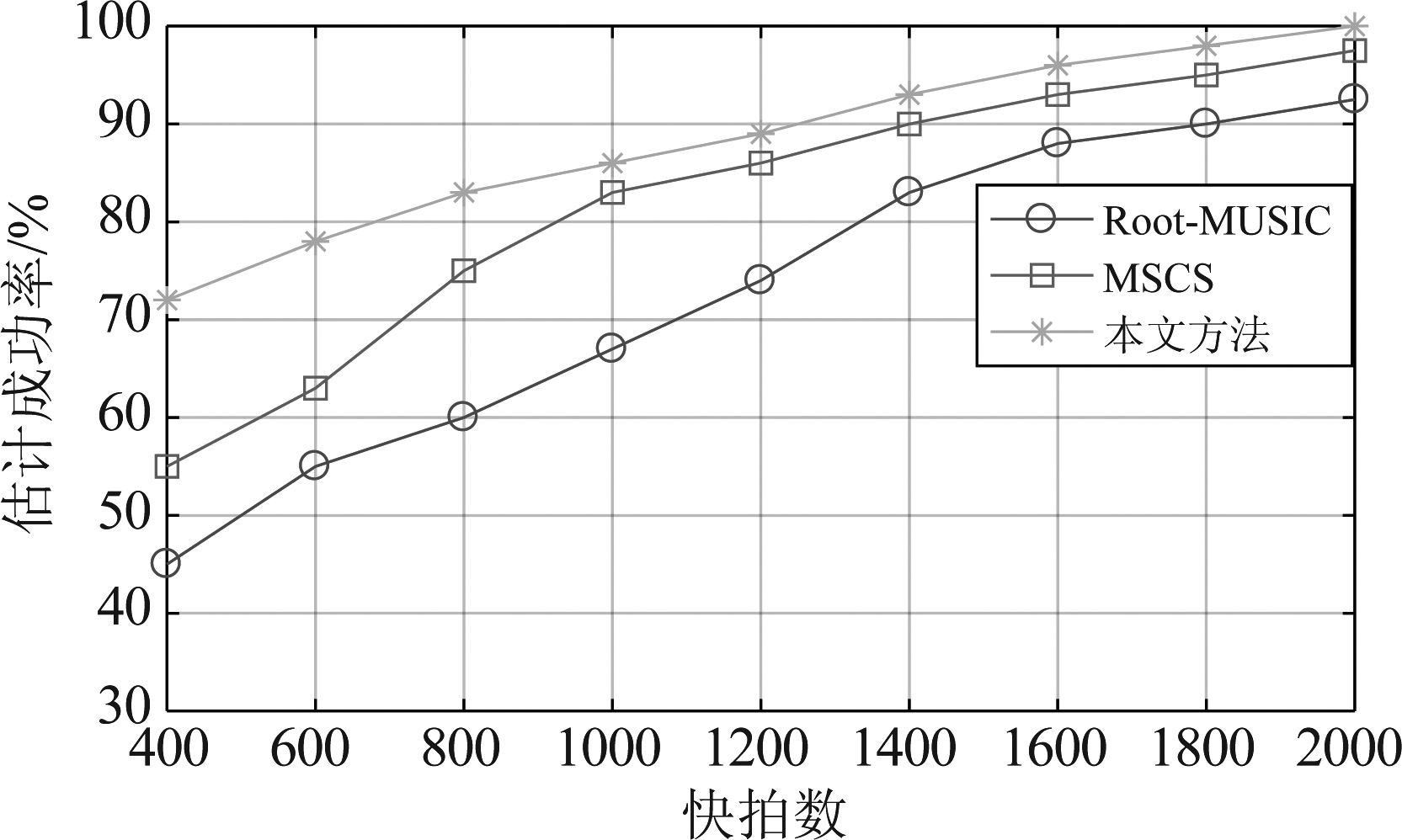
图6 实验3的估计成功率
Fig.6 Estimated success rate of experiment 3
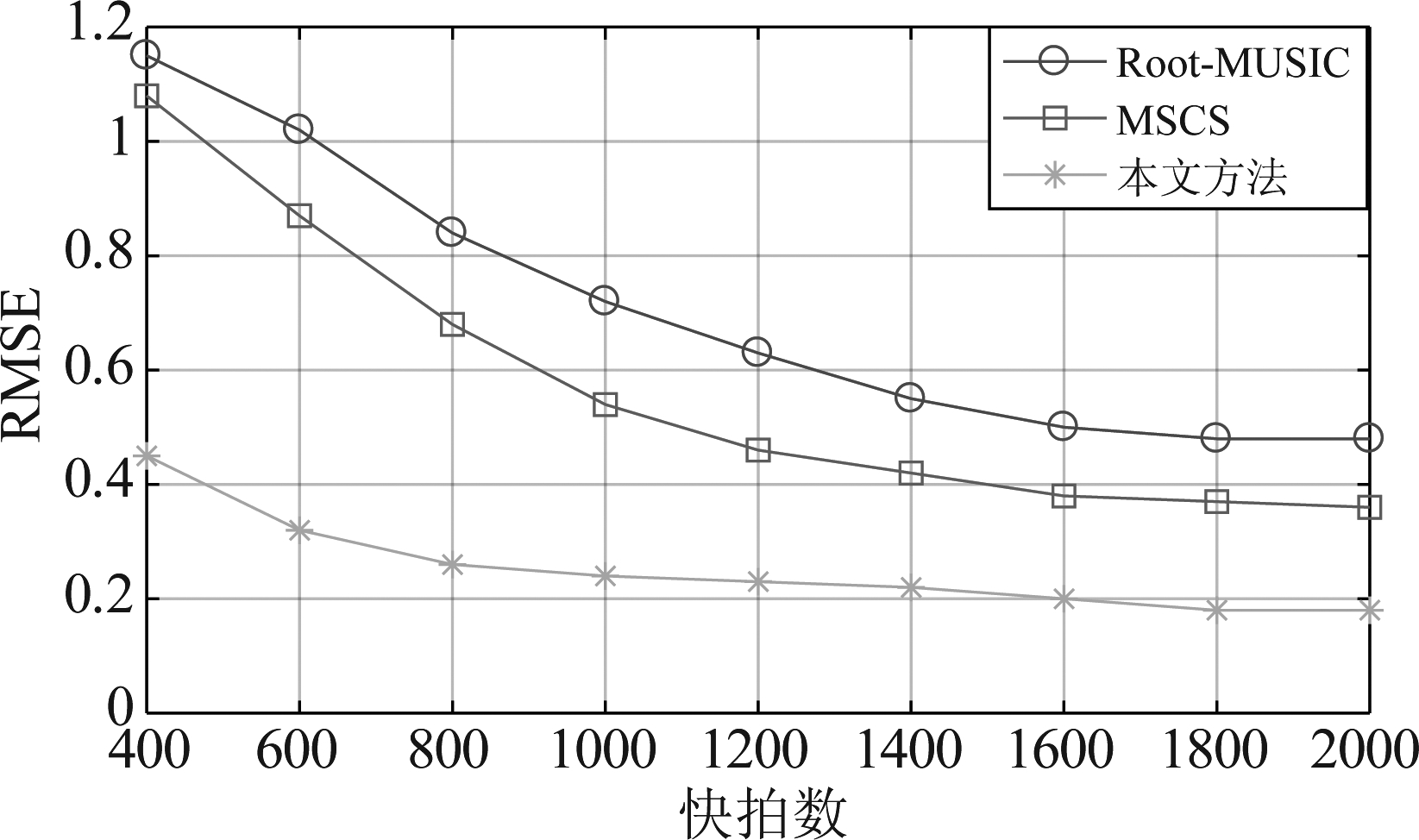
图7 实验3的均方根误差
Fig.7 Root mean square error of experiment 3
从图6可以看出,随着快拍数的增加,三种方法的估计成功率都在增加。在较低快拍数情况下,本文方法估计成功率高于另外两种算法;在高快拍数情况下,三种方法都能达到较高成功率。从图7可以看出,随着快拍数的增加,三种方法的RMSE都在降低。当快拍数低于1200时,本文方法估计精度要明显高于另外两种算法。
本文充分利用跳频信号的空域信息来进行信号的DOA估计,在信号空时频分析的基础上,提出了一种基于协方差矩阵重构的高效跳频信号DOA估计方法。首先构造跳频信号的空时频矩阵,通过协方差矩阵的重构得到了等效的信号子空间,进而实现DOA估计。与传统子空间类算法相比,本文方法不需要进行子空间分解,能够有效降低计算量。仿真结果表明相比于传统方法,本文方法估计性能更佳且提高了估计速度。
[1] Krim H, Viberg M. Two decades of array signal processing research: the parametric approach[J]. IEEE Signal Processing Magazine, 1996, 13(4): 67-94.
[2] Benesty J, Chen J, Huang Y. Microphone Array Signal Processing[J]. Journal of the Acoustical Society of America, 2003, 125(6): 4097- 4098.
[3] Gu Y, Goodman N A, Hong S, et al. Robust adaptive beamforming based on interference covariance matrix sparse reconstruction[J]. Signal Processing, 2014, 96(5): 375-381.
[4] Schmidt R. Multiple emitter location and signal parameter estimation[J]. IEEE Transactions on Antennas & Propagation, 1986, 34(3): 276-280.
[5] Friedlander B. The Root-MUSIC algorithm for direction finding with interpolated arrays[J]. Signal Processing, 1993, 30(1): 15-29.
[6] Lin C H, Fang W H. Joint Angle and Delay Estimation in Frequency Hopping Systems[J]. IEEE Transactions on Aerospace and Electronic Systems, 2013, 49(2): 1042-1056.
[7] Liu X, Li J, Ma X. An EM Algorithm for Blind Hop Timing Estimation of Multiple FH Signals Using an Array System With Bandwidth Mismatch[J]. IEEE Transactions on Vehicular Technology, 2007, 56(5): 2545-2554.
[8] 陈利虎, 张尔扬. 基于数字信道化和空时频分析的多网台跳频信号DOA估计[J]. 通信学报, 2009, 30(10): 68-74.
Chen Lihu, Zhang Eryang. Directions of arrival estimation for multi frequency-hopping signals based on digital channelized receiver and spatial time-frequency analysis[J]. Journal of Communications, 2009, 30(10): 68-74.(in Chinese)
[9] 陈利虎, 王永明, 张尔扬. 基于空时频分析的多FH/DS信号DOA估计[J]. 信号处理, 2009，25(8):1309-1313.
Chen Lihu, Wang Yongming, Zhang Eryang. Directions of Arrival Estimation of Multicomponent Frequency-Hopping/Direct Sequence Spread Spectrum Signals Based on Space Time-Frequency Analysis[J]. Signal Processing, 2009, 25(8):1309-1313.(in Chinese)
[10] 张东伟, 郭英, 齐子森, 等. 多跳频信号波达方向与极化状态联合估计算法[J]. 电子与信息学报, 2015,37(7): 1695-1701.
Zhang Dongwei, Guo Ying, Qi Zisen, et al. Joint Estimation Algorithm for Direction of Arrival and Polarization for Multiple Frequency-hopping Signals[J]. Journal of Electronics and Information, 2015, 37(7): 1695-1701.(in Chinese)
[11] 张东伟, 郭英, 张坤峰, 等. 多跳频信号频率跟踪与二维波达方向实时估计算法[J]. 电子与信息学报, 2016, 38(9): 2377-2384.
Zhang Dongwei, Guo Ying, Zhang Kunfeng, et al. Online Estimation Algorithm of 2D-DOA and Frequency Tracking for Multiple Frequency-hopping Signals[J]. Journal of Electronics and Information, 2016, 38(9): 2377-2384.(in Chinese)
[12] 张东伟, 郭英, 齐子森, 等. 跳频信号2D-DOA与极化参数的欠定估计[J]. 哈尔滨工业大学学报, 2016, 48(4): 121-128.
Zhang Dongwei, Guo Ying, Qi Zisen, et al. Underdetermined estimation of 2D-DOA and polarization for frequency hopping signals[J]. Journal of Harbin Institute of Technology, 2016, 48(4): 121-128.(in Chinese)
[13] 于欣永, 郭英, 张坤峰, 等. 基于STFD&SCMUSIC的多跳频信号DOA估计与网台分选[J]. 信号处理, 2017, 33(10):1344-1351.
Yu Xinyong, Guo Ying, Zhang Kunfeng, et al. DOA estimation and network sorting based on STFD&SCMUSIC of Mutil-FH Signal[J]. Journal of Signal Processing, 2017, 33(10): 1344-1351.(in Chinese)
[14] 杨银松, 郭英, 于欣永, 等. 多跳频信号的2D-DOA估计[J]. 信号处理, 2018, 34(5): 610-619.
Yang Yinsong, Guo Ying, Yu Xinyong, et al. 2D-DOA estimation of multiple frequency-hopping signals[J]. Journal of Signal Processing, 2018, 34(5): 610-619.(in Chinese)
[15] 闫锋刚, 荣加加, 刘帅, 等. 联合互协方差矩阵的快速波达方向估计[J]. 系统工程与电子技术, 2018, 40(4): 733-738.
Yan Fenggang, Rong Jiajia, Liu Shuai, et al. Joint cross-covariance matrix based fast direction of arrival estimation[J]. Systems Engineering and Electronics, 2018, 40(4): 733-738.(in Chinese)
杨 鑫 男, 1996年生, 安徽阜阳人。 空军工程大学硕士研究生, 主要研究方向为通信信号处理及网台分选。
E-mail: yyxxmelody@163.com
郭 英 女, 1961年生, 山西临汾人。 空军工程大学博士生导师, 博士, 主要研究方向为通信信号处理、自适应信号处理。
E-mail: yguo163@163.com