步入21世纪以来,全球卫星导航系统(Global Satellite Navigation System,GNSS)愈加蓬勃发展,卫星导航是一种集无线电导航、测绘于一体的高端技术,随着拥有卫星导航系统国家国际地位优势的体现,全球有一定能力基础的国家都在争先研究并发射卫星,这样造成了频带资源紧张的问题,为了解决该问题,二进制偏移载波调制(Binary offset carrier modulation,BOC)信号[1]及其衍生信号双二进制偏移载波调制(Dual binary offset carrier modulation,DBOC)信号被提出,新提出信号的频谱分裂特性相比传统BPSK调制的信号不仅提高了抗干扰能力、码跟踪精度和保密性,又充分利用了频段资源,解决了频带拥挤的问题,但由于增加了频谱分裂的特性,为捕获也增加了难度。目前BOC及其衍生信号被广泛应用在GPS、Galileo、BeiDou导航中, DBOC信号作为BOC信号的一种衍生信号,不失研究的一般性,并且现有的研究工作中,针对高动态下的DBOC捕获算法比较少,基于以上特点,本文以DBOC(1,3)信号为例对高动态环境下的捕获进行应用基础性研究(不特指其工作的具体频带及领域),DBOC(1,3)信号中的1表示以基准时钟归一化的子载波频率,3表示以基准时钟归一化的扩频码速率。DBOC信号与BOC及其他BOC衍生信号主要区别在于子载波的表达式不同。
目前有一些传统的卫星信号捕获算法,如分形重构算法[2]、ASPeCT算法[3]和PCF算法[4],但这些算法过程复杂且不适合捕获高动态环境下的DBOC信号。文献[5-9]通过部分匹配滤波器(Partial Matched Filter,PMF)与快速傅里叶变换(Fast fourier Transform,FFT)结合对含多普勒效应的高动态信号进行捕获,通过FFT过程将信号从时域卷积运算转换为频域的乘积运算,完成对信号多普勒频率的补偿的同时减少了码相位搜索维度,该算法一定意义上提高了捕获概率、节省了捕获时间、降低了硬件要求,但该方法会造成扇贝损失,为了解决这一问题有学者提出在该算法基础上加窗,在PMF过程和FFT过程均进行加窗,虽在一定程度上解决了扇贝损失问题,但由于时域截断又带来了频谱泄露问题。文献[10]通过离散chirp无法对高动态信号多普勒频偏进行补偿。文献[11]引入惯性导航辅助系统,增加了系统复杂度和成本。
针对目前信号捕获中存在的这些问题,通过文献[12]可知,由于接收机对捕获的信号动态阶数未知,需要对动态性先做判断,文献[12]中提出将高动态信号先通过离散多项式相位变换[13](DPT)结合傅里叶变换(FFT)进行定阶,进而对高动态信号通过DPT降阶,对降阶后的信号通过PMF-FFT结合频谱校正的方法进行捕获。本文在文献[12]的基础上,先通过DPT-FFT的定阶算法,根据定阶后的动态阶数,对只带有一阶多普勒变化率的高动态信号使用PMF-FRFT算法进行捕获,通过PMF减少FRFT[14-20]运算点数,减少了FRFT过程的运算量,再利用FRFT变换在特定时频面下旋转角度α形成易于捕获的单峰冲激波形,在支撑区以外很好的抑制了频谱泄露,能量损失基本可以忽略不计。对带有二阶多普勒变化率的高动态信号提出使用DPT-PMF-FRFT的算法进行捕获,通过先降一阶处理,降低动态阶数,再通过PMF-FRFT的算法进行捕获。
根据文献[12],高动态下带有一阶多普勒变化率的DBOC接收信号加高斯白噪声可表示如下
r(t)=s(t)+n0(t)
(1)
式(1)中:s(t)表示高动态环境下带有一阶多普勒变化率的DBOC接收信号,n0(t)表示加性高斯白噪声。s(t)可表示为
s(t)=Ad(t)c(t)sDBOC(t)x(t)
(2)
式(2)中:A为信号幅度,这里设A=1,d(t)为导航信息,c(t)为伪码序列,一阶高动态DBOC信号中的副载波sDBOC(t),载波信号x(t)及伪码c(t)可以分别表示为
sDBOC(t)=sign[sin(NBOC1NBOC2pt/Tc)]
(3)
x(t)=exp{j[2p(f0+fd)t+pkdt2+φ]}
(4)
(5)
上式中:NBOC1表示第一次BOC调制信号阶数,NBOC2表示第二次BOC调制阶数,Tc表示DBOC子载波的码元宽度,pTc(t)表示的是码元宽度值为Tc的扩频符号。f0是中频频率, fd是多普勒频偏,kd是加速度引起的多普勒频率变化率,φ是随机相位。
由于导航卫星和地面的监测站之间存在高速的相对运动,这样会导致信号在传输过程中产生多普勒效应。接收信号经过下变频和离散采样后,式(2)可以重新表示为
s(n)=Ad(n)sDBOC(n)c(n)x(n)
0≤n≤N-1
(6)
式(4)可重新被表示为
x(n)=exp{j[2p(f0+fd)nTs+pkd(nTs)2+φ]}
(7)
式中:N是采样点数,Ts是采样间隔,φ表示相位,本文中将sDBOC(n)·c(n)作为组合伪随机码。
由文献[12-13]知,多项式相位信号可通过式(8)来表示
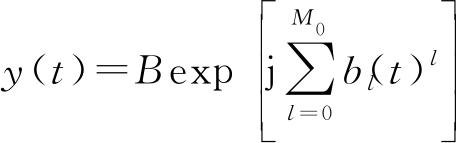
(8)
上式经过离散化采样后可表示为
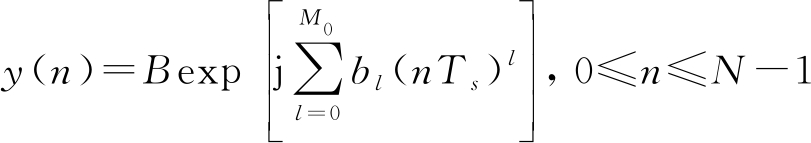
(9)
上式中,B表示多项式信号的幅度,为方便研究,取值B=1。bm表示实相位系数,N表示信号采样长度,Ts表示采样间隔,M0表示动态阶数。
M0阶多项式信号的一阶瞬态矩、二阶瞬态矩及M0阶瞬态矩可以分别表示为
DP1[y(n),τ]=y(n)
(10)
DP2[y(n),τ]=y(n)y*(n-τ)
(11)
DPM0[y(n),τ]=DP2[DPM0-1[y(n),τ],τ]
(12)
上式中,时延τ的取值可依据文献[12-13]确定。M0≤3时,τ=N/M0;M0>3时,τ=N/(M0+2)。
在式(7)中,载波中含多普勒频偏fd和加速度引起的一阶多普勒变化率kd,若接收到的高动态信号中还带有二阶多普勒变化率kf,则载波及信号模型可被重新表示为
x1(n)=
exp{j2p[(fd+f0)nTs+kd(nTs)2/2+kf(nTs)3/6+φ]}
(13)
s1(n)=Ad(n)c(n)sDBOC(n)x1(n)
(14)
对于含kf的高动态信号,增加了捕获的难度。所以本文提出将含kf的信号通过DPT的方法对其进行降阶处理,降阶后再结合FRFT算法对其进行捕获。在不考虑数据位跳变的情况下,含kf的高动态信号降阶后可表示为
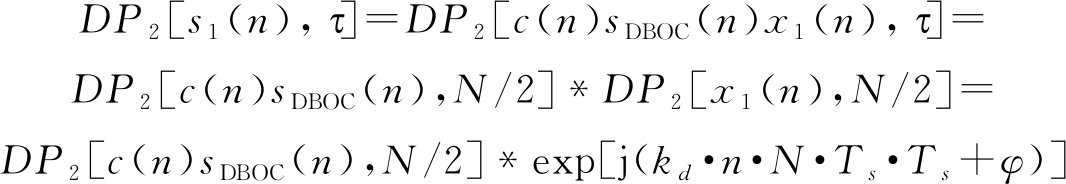
(15)
其中φ可表示为
φ=(M0-1)!(τTs)M0-1bM0-1-
0.5(M0-1)M0!(τTs)M0bM0
(16)
含kf的信号,通过降阶处理降低了动态性和捕获复杂度,便于下一步捕获。
接收机接收到信号时,无法预知其动态性,为捕获增加了难度。由参考文献[12]可知,通过DPT结合FFT的方法对接收信号进行定阶处理,达到判断接收信号阶数的目的,进而可以对高动态信号进行降阶处理。由文献[12]可得,可根据图1所示进行定阶判断。
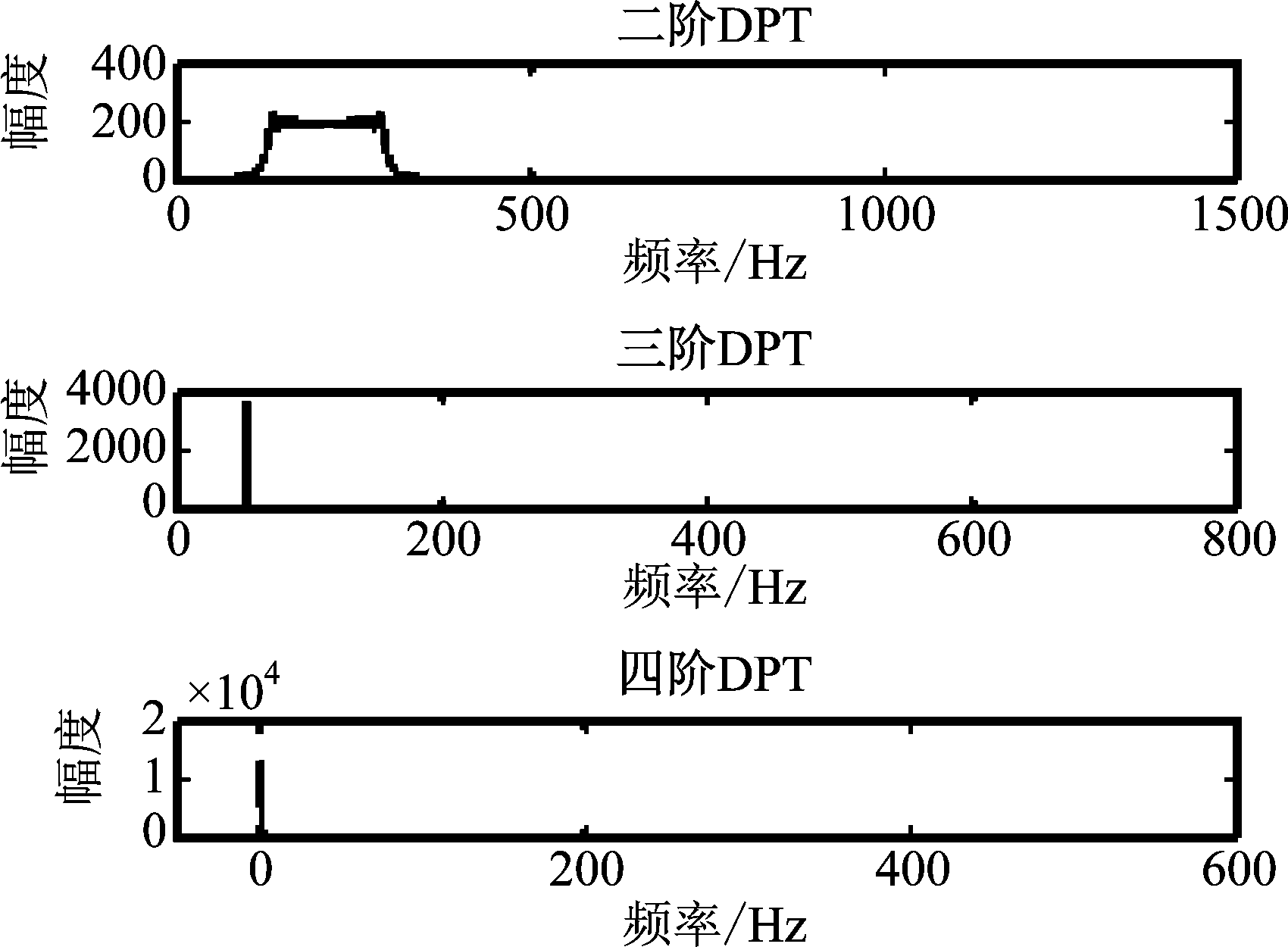
图1 定阶判断
Fig.1 Order judgment
可通过以下特征来判断接收信号的动态阶数:
(1)若m<M0,频谱图中出现凌乱的谱线。
(2)若m=M0,频谱图中出现单峰谱线。
(3)若m>M0,频谱图中出现直流分量。
接收信号定阶的基本流程为:可将m的初值设定为2,经m阶DPT处理后,频域出现直流分量则表明接收信号动态阶数M0=m-1;否则令m=m+1,继续进行DPT处理,直至频域出现直流分量。
通过以上分析,如果直接用PMF-FFT加窗算法对信号进行捕获,会导致扇贝损失、频谱泄露的问题,进而影响捕获概率。针对以上问题,本文提出了改进的基于PMF-FFT的捕获算法。
4.1.1 部分相关过程
由文献[5]可知,部分匹配滤波器是将经过下变频、采样后的接收信号与组合伪随机码进行分段相关运算,设信号长度为M,每个部分匹配滤波器的长度为X,部分匹配滤波器个数为N(N=M/X),N个部分匹配滤波器同时进行相关运算,最终得到长度为N的信号。部分匹配滤波器运算过程如图2所示。
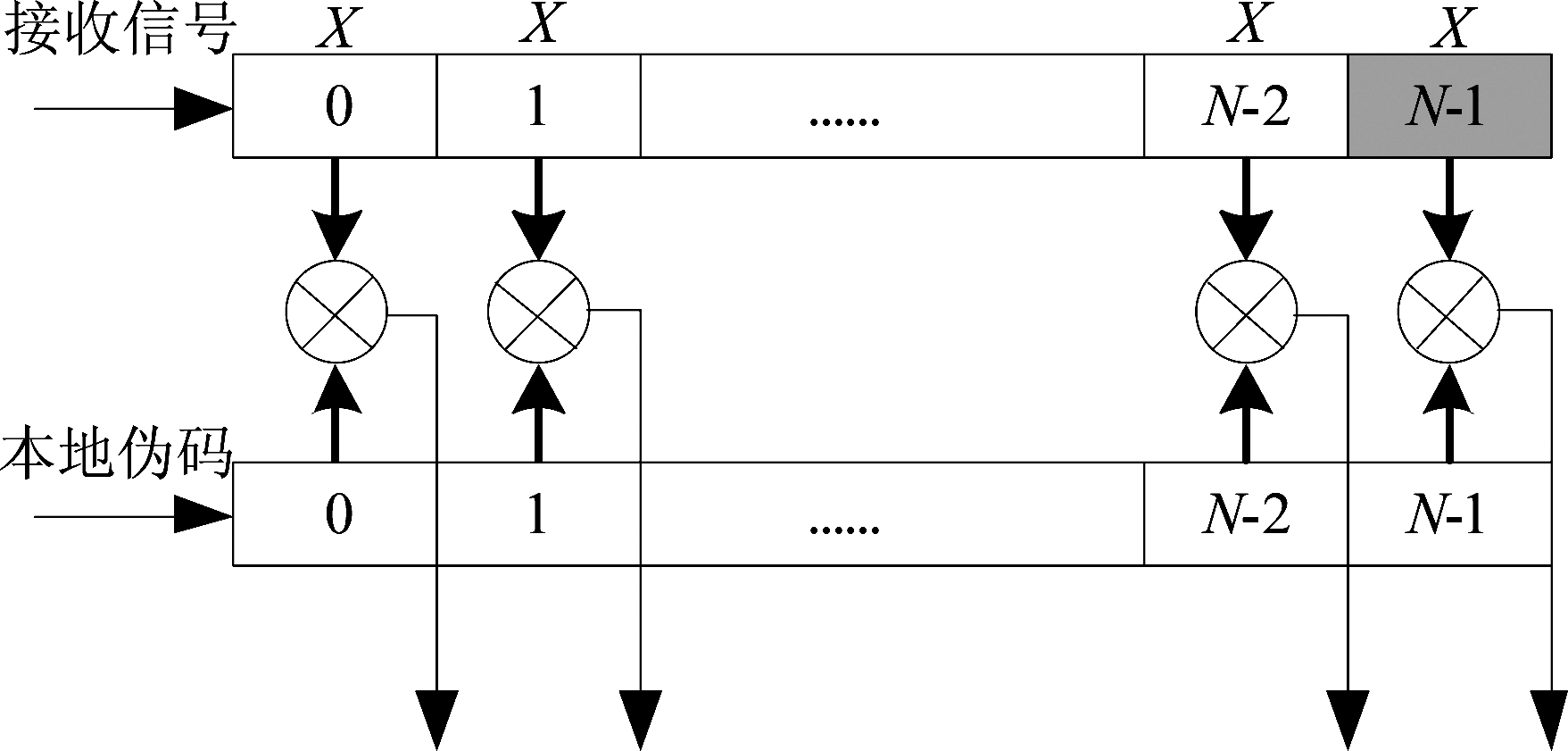
图2 PMF具体过程
Fig.2 PMF Specific process
在伪码相位对齐后,信号s(n)第k(1≤k≤N)个PMF可表示为
yPMF=
(17)
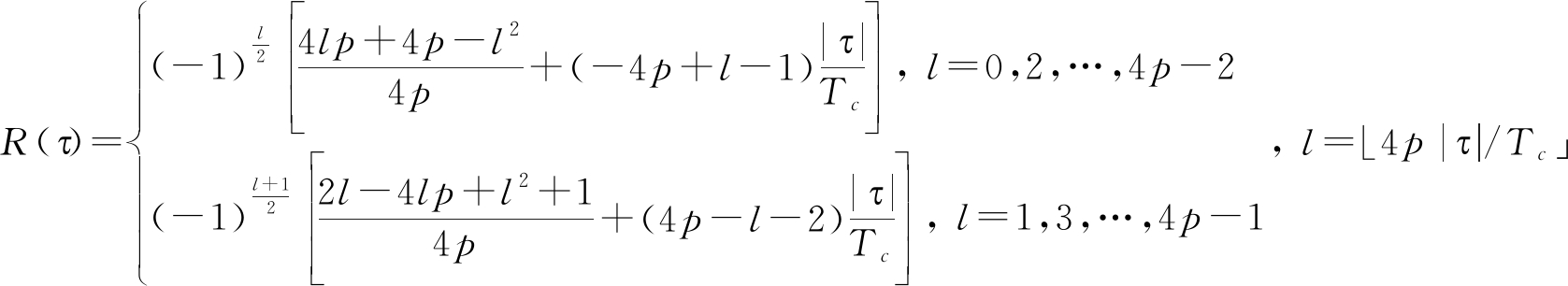
(18)
式中:Ps表示信号功率,R(τ)表示DBOC自相关结果,Ts表示采样间隔, fd表示多普勒频偏,kd表示多普勒变化率,X表示单个PMF的长度。
4.1.2 分数阶傅里叶变换
信号s(t)的分数阶傅里叶变换(FRFT)可定义为[14-20]
(19)
式(19)中FRFT的变换核Kp(t,u)表示如下
Kp(t,u)=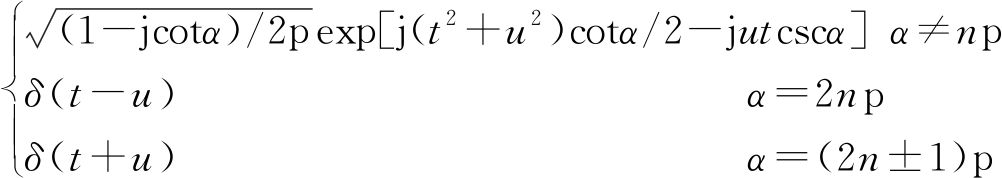
(20)
其中,n为整数,p表示FRFT变换的阶数,α表示旋转角度,δ(t)为单位冲击函数,Fp[]表示FRFT的算子符号。
FRFT的时移特性:
Fp[s(t-t1)]=![]()
(21)
信号s(t)的FRFT变换是一种线性变换,它和Wigner-Ville(简称WVD)分布的关系可解释为时频面的旋转算子,这个特性使得FRFT非常适合处理线性调频(LFM)信号。
由式(19)FRFT的定义,可知信号s(n)的p阶FRFT变换为
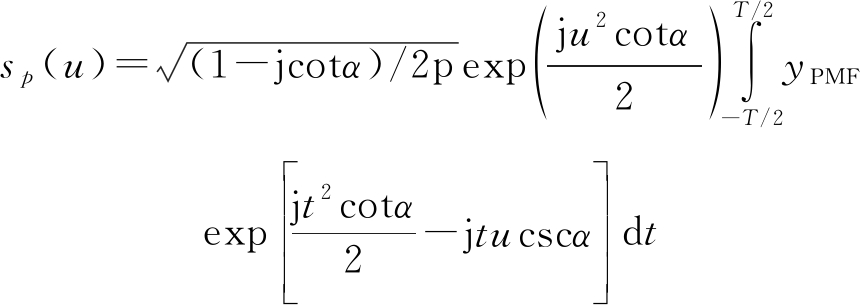
(22)
其中T表示观测时间。目前大部分文献在(α,u)平面上通过采用基于幅度一阶矩的方法确定最佳变换阶数,由文献[20]可知,当幅度一阶矩值最小时,表示对应旋转阶数下在FRFT域能量最为集中,幅度一阶矩可定义为:
(23)
通过比较每个旋转角度下幅度一阶矩的值,确定FRFT域能量值最大处对应的阶数。本文在该算法基础上进行改进,不需要经过幅度一阶矩的运算,直接通过逐精度搜索的方法确定最佳阶数,具体步骤如下:
(1)在[0,2]区间内,先以步长0.1为间隔进行FRFT运算,直接搜索最大幅值sp(u)对应的阶数p,记录为p1。
(2)在[p1-0.1,p1+0.1]区间内以0.01为步进量进行FRFT搜索运算,直接搜索最大幅值sp(u)对应的阶数p,记为p2。
(3)根据需要的精度按步骤2的方法继续搜索,最后得到最佳旋转角度α。
(24)
当旋转角度α=-arccotK时,sp(u)具有最佳的能量聚集,这里K表示调频斜率。高动态二阶DBOC信号在该旋转角度下具有最大的峰值。
(25)
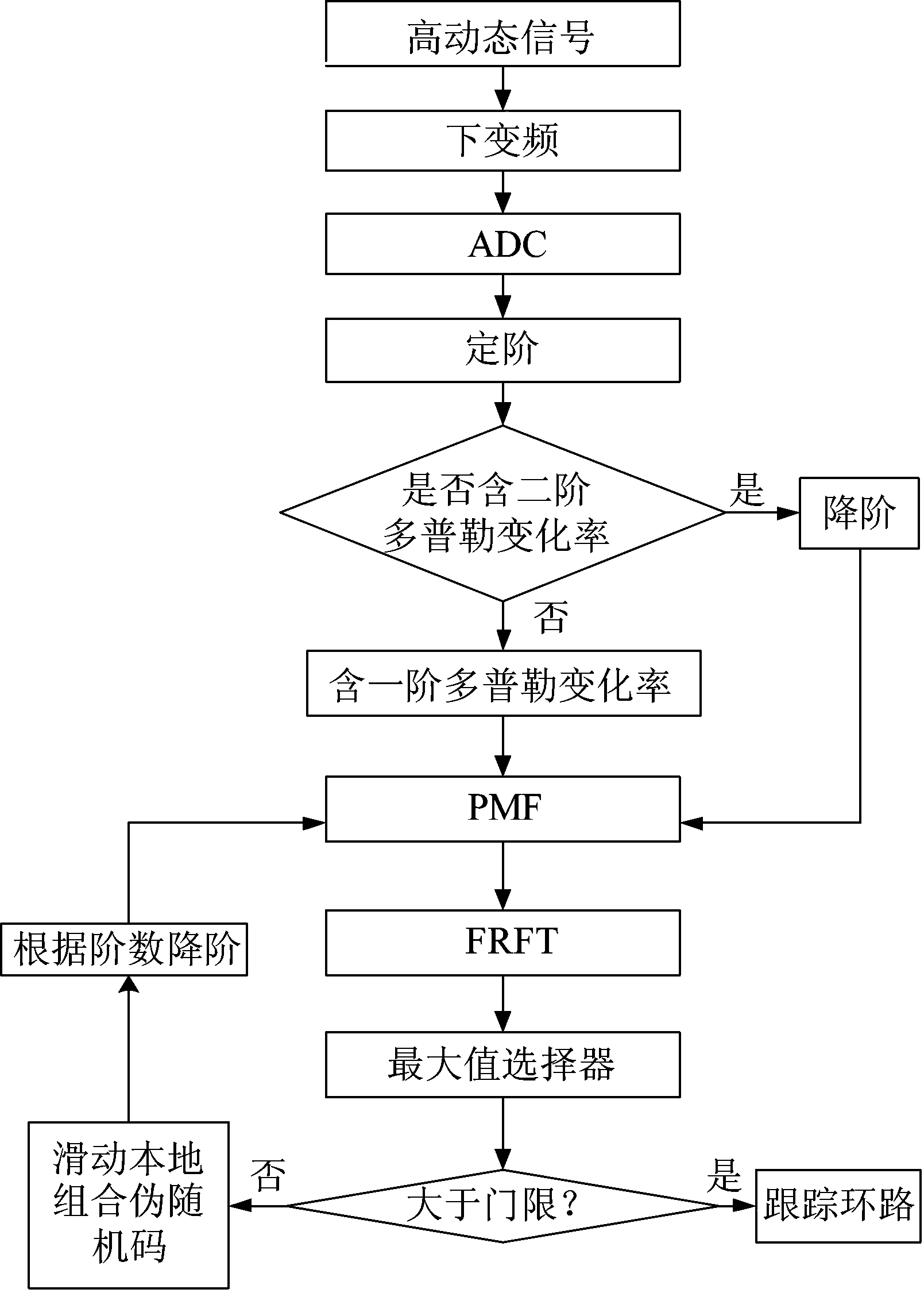
图3 接收机整体捕获算法框图
Fig.3 Receiver overall capture algorithm block diagram
捕获算法步骤:
步骤1 对接收到的信号进行下变频、模数转换、离散化采样。再对离散信号通过基于DPT的定阶算法进行定阶处理。
步骤2 对带有二阶多普勒变化率的高动态信号首先进行DPT降一阶,并对本地经过子载波调制后的伪码进行同样阶数的降阶,降阶后的信号与降阶后的组合伪随机码进行相关运算,最后通过FRFT算法对相关结果进行捕获。对带有一阶多普勒变化率的高动态信号,接收信号与本地组合伪随机码直接进行相关运算,然后使用FRFT算法对相关结果进行捕获。
步骤3 若经过步骤2之后的捕获结果大于预设门限β(可通过式(27)确定),则捕获成功,进入跟踪环节(本文只讨论捕获过程,跟踪环节不予讨论)。反之,滑动组合伪随机码,继续进行捕获操作。滑动组合伪随机码过程具体可以通过移位寄存器来实现,将接收信号送入L级移位寄存器,本地组合伪随机码按某一相位状态送入另一L级移位寄存器,然后对该信号和组合伪随机码进行步骤2的操作,如果捕获不成功,需要对组合伪随机码在移位寄存器中作一个切普(用Tc表示)的延迟移位,然后继续进行步骤2的捕获过程,直至捕获成功。
对于步骤3中滑动组合伪随机码对捕获时间的影响,从接收机开始接收信号到L级移位寄存器装载完L个码元,需要消耗时间LT0(这里T0表示每级延迟移位寄存器装载一个码元的时间,由于一个寄存器寄存一个码元,所以T0=Tc),所以,最小捕获同步时间为L级移位寄存器的装载时间,即,Tmin=LTc。如果捕获不成功,需要滑动组合伪随机码,最大需要的同步时间为Tmax=LTc+(M-1)Tc。
本文研究的是在高斯白噪声环境下DBOC信号的捕获,一般用H1表示存在有用信号,捕获过程中若只有高斯白噪声H0存在,会导致虚警情况发生。由文献[20]可知,通过计算接收信号的FRFT变换,将FRFT域的峰值与预设门限β进行比较,若峰值大于预设门限β,则表示捕获成功,反之,捕获失败。
本文通过采用聂孟-皮尔逊(Neyman-Pearson)准则确定预设门限β,检验统计量可以表示为:
I=|FRFT(α,μ)|
(26)
虚警概率表示为:
(27)
检测概率表示为:
(28)
门限β的求取可通过将预定的虚警概率和H0条件下I发生的概率密度函数p(I|H0)代入式(27)计算得到。再通过H1条件下I发生的概率密度函数p(I|H1)代入式(28)计算得到检测概率。
本文采用均值为0,方差为σ2的高斯白噪声,由于FRFT变换为线性变换,高斯白噪声经过FRFT变换后仍服从高斯分布,经过FRFT后的高斯白噪声n0(n)可表示为:
(29)
由于E[n0(n)]=0,E[|n0(n)|2]=σ2,所以可得:
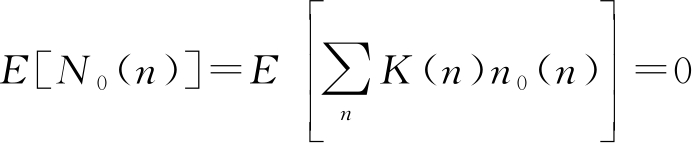
(30)
![]()
N·σ2
(31)
由以上表达式可知,H0条件下I服从正态分布N(0,N·σ2)。在H1条件下经FRFT后,可表示为:
FRFT[r(n)]=FRFT[s(n)+n0(n)]=![]()
(32)
由上式可得,H1条件下I服从正态分布N(N·A/2,N·σ2),这里N表示FRFT变换点数,A表示幅度。
本文通过MATLAB仿真检测本文所提算法的性能,实验中使用DBOC信号,信号采样频率fs为16.368 MHz,码片速率为1.023 MHz,多普勒频偏fd设置为10 kHz,多普勒变化率引起的加速度kd为5 kHz/s,多普勒变化率引起的加加速度kf为1 kHz/s2。
实验1 捕获性能仿真。对接收到的长度为2048,带有高斯白噪声的DBOC高动态信号和只有高斯白噪声的信号通过本文所提算法进行捕获,对比分析所提算法性能特性。
由图4可知,图(a)对应的是当接收信号中只有高斯白噪声时,通过PMF-FRFT算法对其进行捕获时,频谱均匀分布在时频面。图(b)、(c)分别对应的是用所提算法对含高斯白噪声的DBOC信号进行捕获,DBOC高动态信号通过基于FRFT的捕获算法后,在支撑区以外,信号频谱幅度非常小,频谱泄露基本可忽略不计,在支撑区内出现冲激函数波形,能量集中在支撑区。由此可以得出,对含多普勒变化率的高动态信号,由本文提出的算法首先可以抑制高斯白噪声的干扰,使噪声频谱均匀分布在频域范围,这是因为高斯白噪声经过FRFT线性变换后仍服从高斯分布。
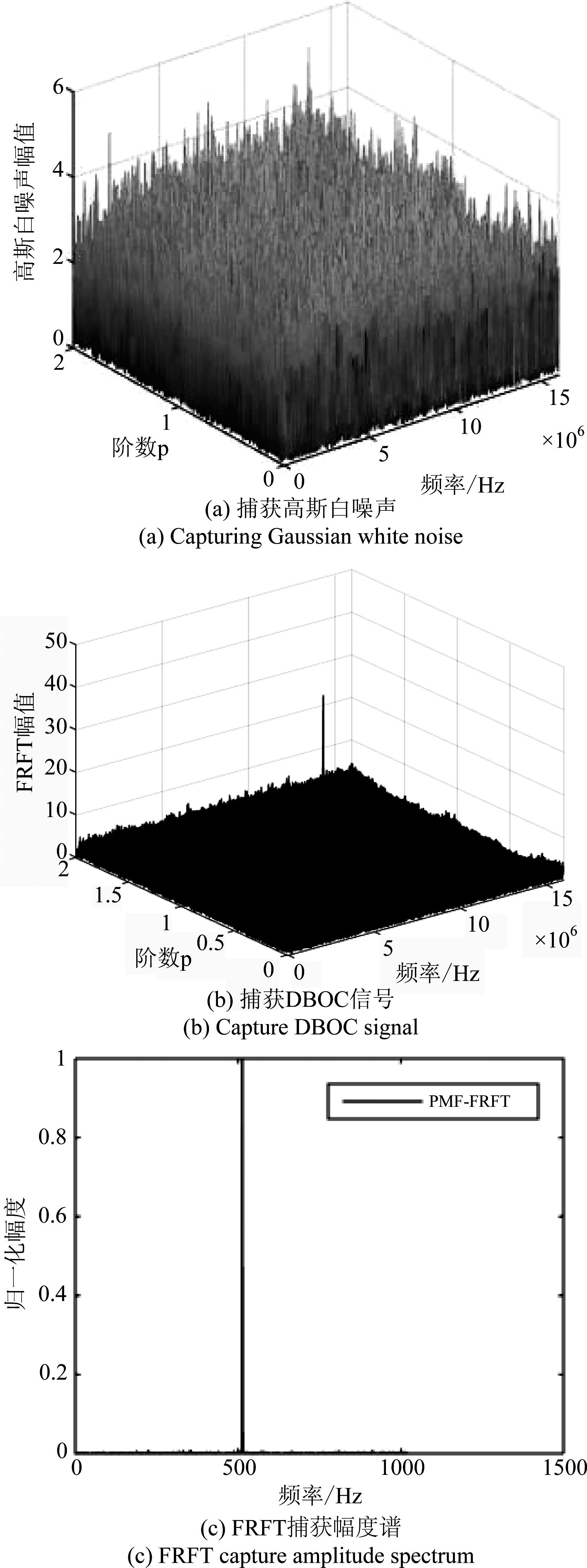
图4 FRFT捕获性能
Fig.4 FRFT capture performance
实验2 捕获概率分析。该实验分别对含一阶多普勒变化率的信号和含二阶多普勒变化率的信号进行了捕获概率仿真实验。该实验通过对长度为2048的接收信号分别采用基于PMF-FRFT、DPT-PMF-FFT-比值校正法及DPT-PMF-FFT算法进行捕获概率对比,实验中取N=1024,X=2。
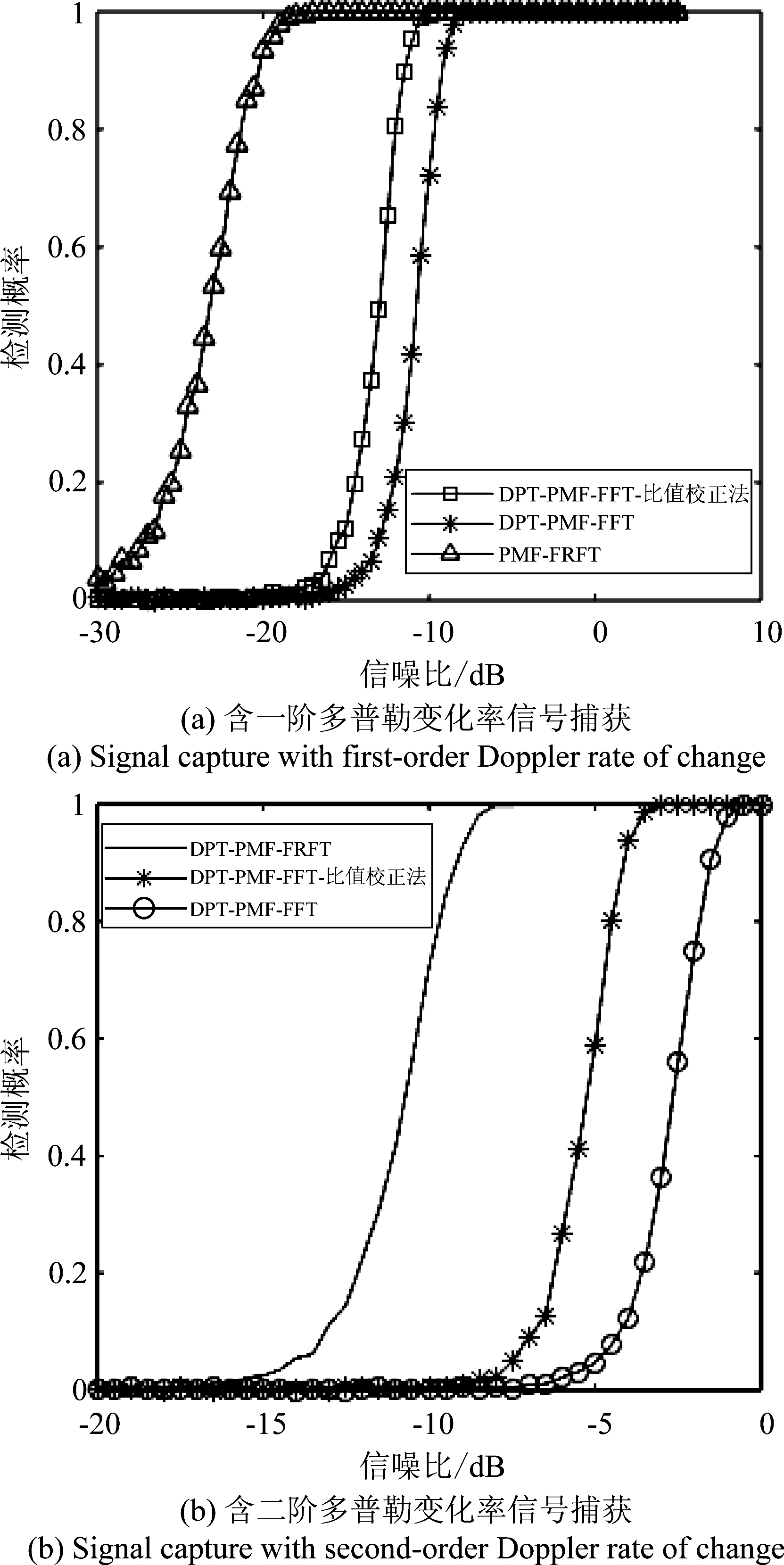
图5 捕获概率
Fig.5 Capture probability
由实验结果可知,对含一阶多普勒变化率的高动态信号使用DPT-PMF-FFT算法捕获时,在-8 dB时捕获概率达到1,经过文献[12]的算法后捕获概率有2 dB的提升,本文所提算法在-17.5 dB时捕获概率达到1,相比文献[12]算法捕获概率提高7.5 dB左右,相比DPT-PMF-FFT算法有9.5 dB的提升。对含二阶多普勒变化率的高动态信号使用DPT-PMF-FFT算法捕获时,在-0.5 dB时捕获概率达到1,经过文献[12]的算法后捕获概率有2.5 dB的提升,本文所提算法在-8 dB时捕获概率达到1,相比文献[12]算法捕获概率提高5 dB左右,相比DPT-PMF-FFT算法有7.5 dB的提升。由此可得在相同条件下,本文所提算法捕获概率较基于PMF-FFT的捕获算法性能有一些提升。
实验3 对不同长度信号的捕获概率分析。本实验中对含一阶多普勒变化率的信号,分别取长度为2048,512。取长度为2048时,N=1024,512,X=2,4。取长度为512时,令N=128,X=4。对含二阶多普勒变化率的信号分别取长度为1024,2048,4096,8192,其对应的PMF个数分别为N=512,1024,2048,4096。
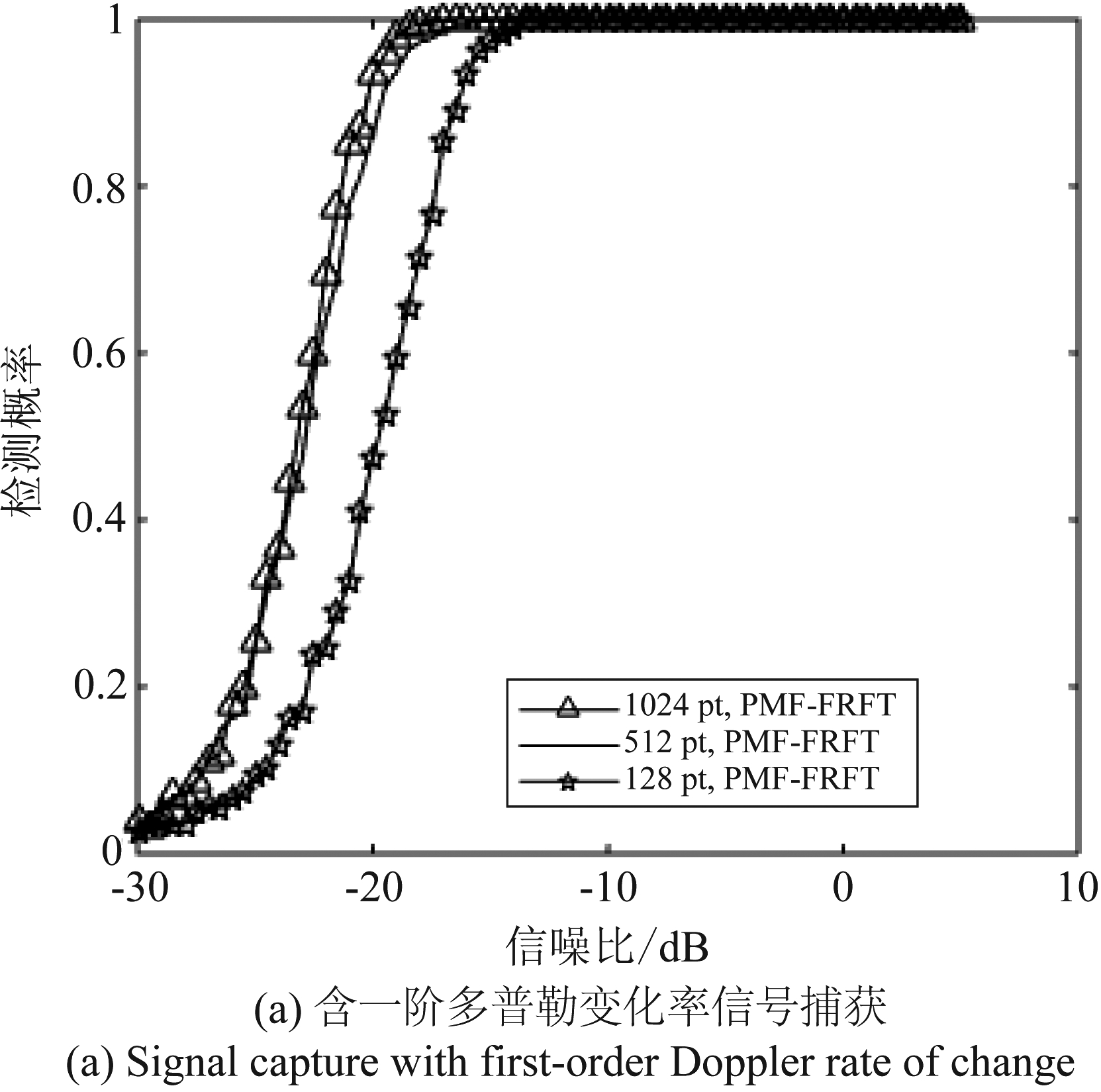
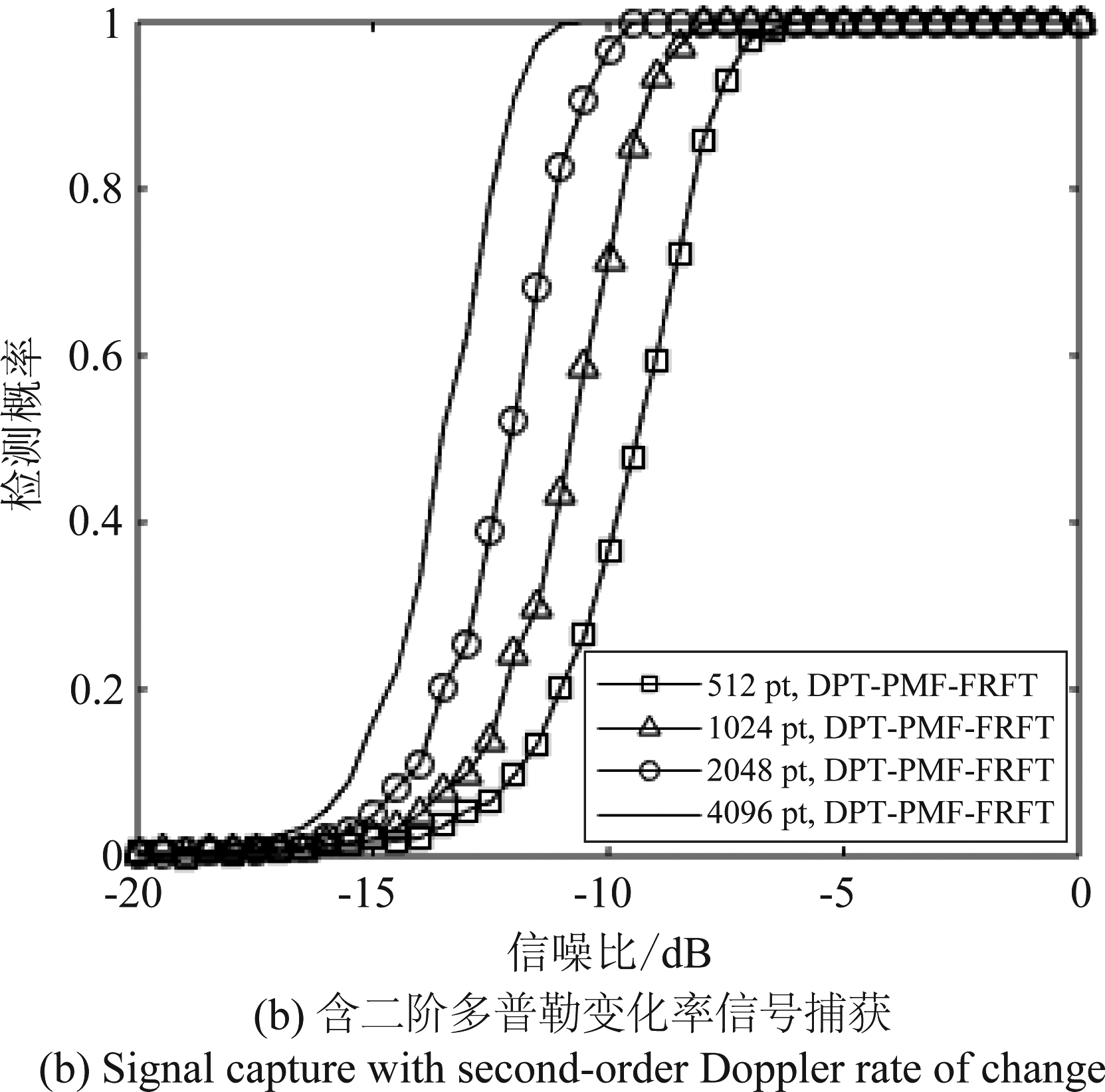
图6 捕获概率
Fig.6 Capture probability
由实验结果可知,图(a)中,随着接收信号长度的增加,捕获概率会有相应的提高,在信号长度为2048,FRFT点数为1024时,在-17.5 dB时捕获概率达到1。与信号长度为512,FRFT运算点数为128相比,捕获概率有4 dB的提升。图(b)中,对含二阶多普勒变化率的信号,长度为8192,FRFT运算点数为4096时,在-11 dB时捕获概率达到1,相比长度为1024,FRFT运算点数为512时,捕获概率有5 dB的提高。由此可得,无论对于只含一阶多普勒变化率和含二阶多普勒变化率的信号,随着接收信号长度的增加,捕获概率会有一定程度的提升。
实验4 加窗对本文算法捕获概率的影响。该实验取含二阶多普勒变化率的信号长度为2048,N=1024,实验中分别加哈明窗,凯赛窗和布莱克曼窗,进行1000次蒙特卡洛仿真实验。
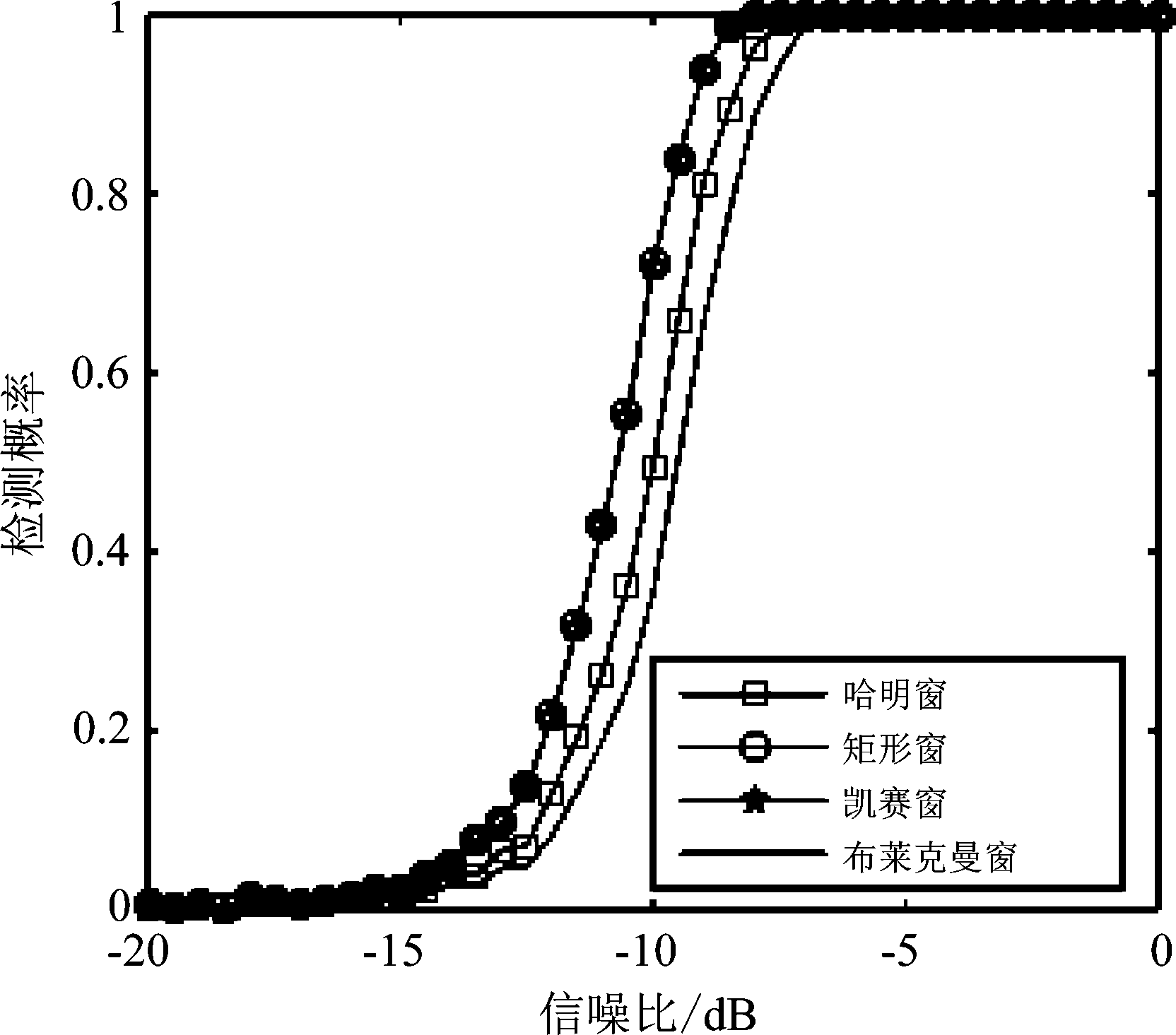
图7 捕获概率
Fig.7 Capture probability
由实验结果可知,在本文所用的算法中,加窗并没有使得捕获概率得以提高,加凯赛窗和不加窗捕获效果一样,加哈明窗、布莱克曼窗后捕获效果反倒不如不加窗的效果好。加窗一般是为了抑制频谱泄露,进而达到提高捕获概率的目的,但是由于FRFT算法的特殊性质,对含二阶多普勒变化率的高动态信号进行DPT降阶后,通过PMF-FRFT算法进行捕获,经过FRFT变换后只有一根冲击单峰,并且FRFT变换对高斯白噪声有很好的抑制效果,对频谱泄露问题有很好的抑制作用,所以该算法不需要再结合加窗处理也可以达到比较好的效果。
实验5 平均捕获时间。由文献[12]可知,平均捕获时间公式可以表示为:
(33)
式中:pd表示不同算法对应的检测概率;τd表示积分时间;Pfa表示虚警概率,本文取Pfa=0.05,K表示虚警代价因子,文中设K=1;N为部分匹配滤波器的个数。
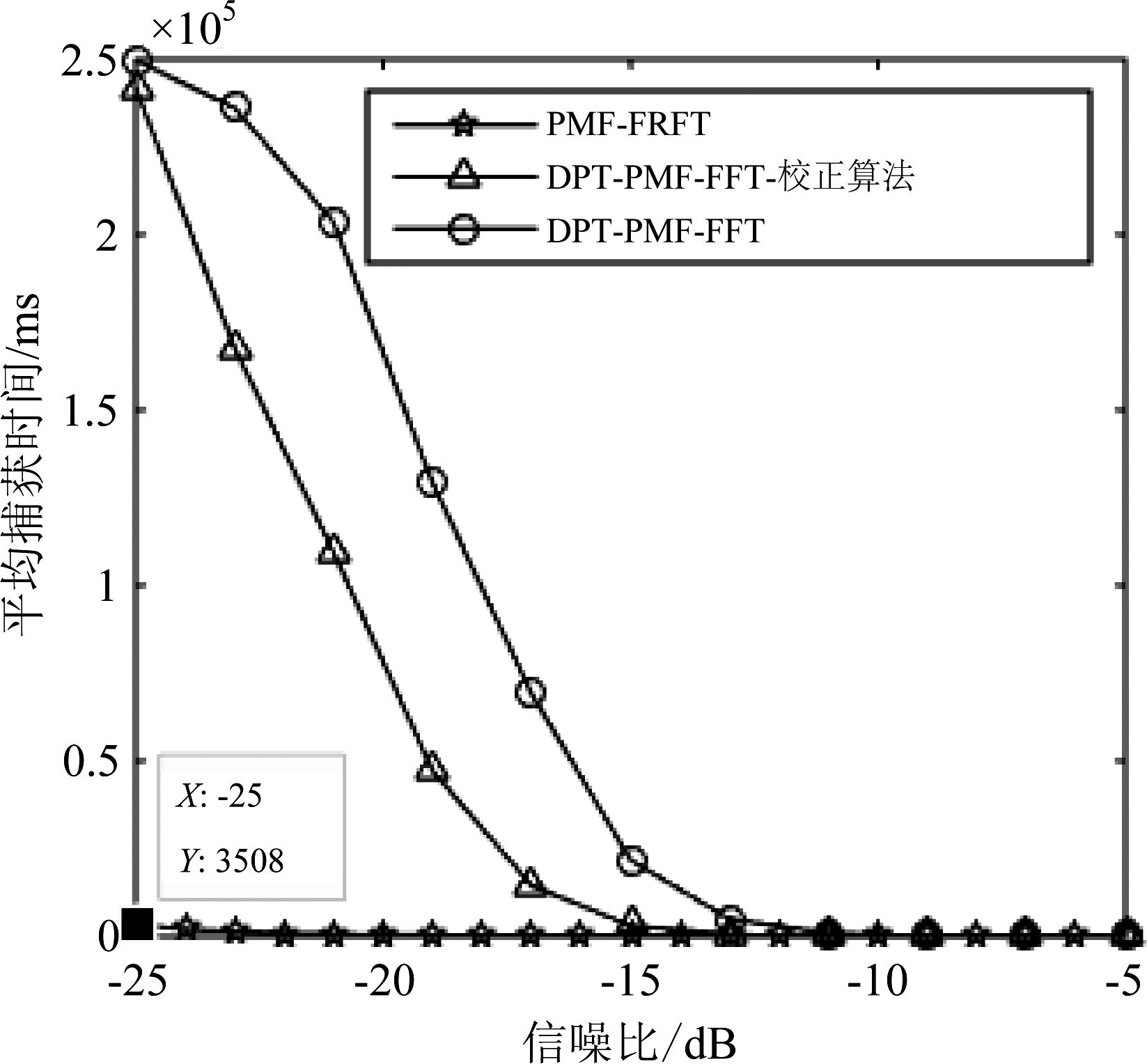
图8 平均捕获时间
Fig.8 Average capture time
由实验结果可知,在一定信噪比下,高动态环境下信号的平均捕获时间,本文所提的PMF-FRFT算法平均捕获时间要小于DPT-PMF-FFT结合频谱校正算法和DPT-PMF-FFT算法所用的平均捕获时间,相当于对比算法捕获时间的1%级别,更符合捕获的实时性。由结果知,DPT-PMF-FFT结合频谱校正算法所用平均捕获时间略小于DPT-PMF-FFT算法。由于线性调频信号经过FRFT变换后只出现一个冲击单峰,这样的特性提高了捕获概率,缩短了搜索时间。
通过MATLAB对本文所提算法和文献[12]算法及DPT-PMF-FFT算法在捕获概率和平均捕获时间方面进行性能对比,对带有一阶多普勒变化率的高动态信号,在信号长度为2048的情况下,本文算法可以在-17.5 dB时捕获概率达到1,较DPT-PMF-FFT结合频谱校正算法和DPT-PMF-FFT算法捕获概率分别提高7.5 dB、9.5 dB,对带有二阶多普勒变化率的信号,本文算法捕获性能也比对比算法要好,并且有效缩短了捕获时间。本文设计的算法不仅解决了针对传统算法无法有效实现对含有二阶多普勒变化率信号的捕获、同步,通过PMF过程减少了FRFT变换点数,缩短了捕获时间,并通过FRFT变换有效抑制了噪声干扰,进而提高捕获概率。总之,相比文献[12]算法,本文算法的优势主要体现在提高了捕获概率,缩短了捕获时间,更符合对高动态环境下信号捕获实时性的要求。主要区别在于本文算法利用了FRFT适合处理线性调频信号的特点,对只带有一阶多普勒变化率的信号不再需要降阶,而文献[12]算法对只带有一阶多普勒变化率的信号仍然需要降一阶处理,对带有二阶多普勒变化率的信号本文算法只需要降一阶处理,而文献[12]算法需要降二阶。
[1] 闫振华. BOC及MBOC调制信号的捕获与跟踪算法研究[D]. 重庆: 重庆邮电大学, 2016.
Yan Zhenhua. Study on the acquisition and tracking algorithm for BOC and MBOC modulation signals[D]. Chongqing: Chongqing University of Posts and Telecommunications, 2016.(in Chinese)
[2] 杨力, 潘成胜, 薄煜明, 等. 基于相关重构的BOC调制信号捕获新方法[J]. 宇航学报, 2009, 30(4): 1675-1679.
Yang Li, Pan Chengsheng, Bo Yuming, et al. A new method for acquisition of BOC modulation signal based on refactoring theory to cross-correlation [J]. Journal of Astronautics, 2009, 30(4): 1675-1679.(in Chinese)
[3] Julien O, Macabian C, Cannon M, et al. ASPeCT: unambiguous sine-BOC(n, n) acquisition/tracking technique for navigation applications[J]. IEEE Transactions on Aerospace and Electronic Systems, 2007, 43(1): 150-162.
[4] Kim S, Chong D, Yoon S, et al. A new GNSS synchronization scheme[C]∥2009 IEEE 69th Vehicular Technology Conference(VTC2009), Barcelona, Spain: IEEE, 2009: 1-5.
[5] 柳春. 基于PMF-FFT的高动态导航信息捕获设计与实现[D]. 成都: 电子科技大学, 2014.
Liu Chun. Design and implementation of high dynamic navigation signal acquisition based on PMF-FFT algorithm[D]. Chengdu: University of Electronic Science and Technology, 2014.(in Chinese)
[6] 廉昕, 王元钦, 侯孝民, 等. 一种脉冲超宽带测控信号捕获方法[J]. 电子与信息学报, 2017, 39(8): 2000-2006.
Lian Xin, Wang Yuanqin, Hou Xiaomin, et al. Acquisition scheme for impulse radio UWB TT&C signal[J]. Journal of Electronics and Information, 2017, 39(8): 2000-2006.(in Chinese)
[7] 杨秦彪, 王祖林, 黄勤, 等. 高动态链路中折叠PMF-FFT快速捕获方法[J]. 系统工程与电子技术, 2016, 38(8): 1723-1729.
Yang Qinbiao, Wang Zulin, Huang Qin, et al. Folded PMF-FFT fast acquisition method for high dynamic scenarios[J]. Systems Engineering and Electronics, 2016, 38(8): 1723-1729.(in Chinese)
[8] Guo Wenfei, Niu Xiaoji, Guo Chi, et al. A new FFT acquisition scheme based on partial matched filter in GNSS receivers for harsh environments[J]. Aerospace Science and Technology, 2017, 61: 66-72.
[9] 施荣华, 余畅, 董健, 等. 一种高动态环境下COMPASS卫星信号快速捕获算法[J]. 计算计应用研究, 2015, 32(5): 1454-1457.
Shi Ronghua, Yu Chang, Dong Jian, et al. Fast method for high dynamic COMPASS signal acquisition[J]. Calculation Application Research, 2015, 32(5): 1454-1457.(in Chinese)
[10] Fan B, Zhang K, Qin Y, et al. Discrete chirp-Fourier transform-based acquisition algorithm for weak global positioning system L5 signals in high dynamic environments[J]. IET Radar, Sonar & Navigation, 2013, 7(7): 736-746.
[11] 王野. 惯性辅助的GNSS捕获技术研究[D]. 哈尔滨: 哈尔滨工程大学, 2014.
Wang Ye. Research on inertial aided acquisition technique[D]. Harbin: Harbin Engineering University, 2014.(in Chinese)
[12] 张天骐, 袁帅, 刘董华, 等. 高动态环境下高阶双二进制偏移载波信号的精确捕获[J]. 电子与信息学报, 2018, 40(11): 2728-2735.
Zhang Tianqi, Yuan Shuai, Liu Donghua, et al. Accurate acquisition of high order Double Binary Offset Carrier signals for high dynamic environment[J]. Journal of Electronics and Information, 2018, 40(11): 2728-2735.(in Chinese)
[13] Peleg S, Friedlander B. The discrete polynomial-phase transform[J]. IEEE Transactions on Signal Processing, 1995, 43(8): 1901-1914.
[14] 徐会法, 刘锋. 线性调频信号分数阶频谱特征分析[J]. 信号处理, 2010, 26(12): 1897-1901.
Xu Huifa, Liu Feng. Spectrum characteristic analysis of linear frequency-modulated signal in the fractional fourier domain[J]. Signal Processing, 2010, 26(12): 1897-1901.(in Chinese)
[15] 黄明军, 王永民, 牛家红. 基于MF-FRFT伪码捕获算法研究[J]. 计算机应用研究, 2017, 31(1): 163-165.
Huang Mingjun, Wang Yongmin, Niu Jiahong. Pseudo-code acquisition algorithm based on MF-FRFT[J]. Application Research of Computers, 2017, 31(1): 163-165. (in Chinese)
[16] 仇兆炀, 陈蓉, 汪一鸣. 基于FRFT的线性调频信号欠采样快速检测方法[J]. 电子学报, 2012, 40(11): 2165-2170.
Qiu Zhaoyang, Chen Rong, Wang Yiming. Fast detection of LFM signal based on FRFT and sub-nyquist sampling[J]. Electronic Journal, 2012, 40(11): 2165-2170. (in Chinese)
[17] 王永. 基于分数阶傅里叶变换的线性调频信号参数估计[D]. 哈尔滨: 哈尔滨工业大学, 2012.
Wang Yong. Study on the feature analysis of the lenear frequency modulated signal based on the Fractional Fourier Transform [D]. Harbin: Harbin Institute of Technology, 2012.(in Chinese)
[18] 邵岩. 分数阶傅里叶变换的算法研究[D]. 哈尔滨: 哈尔滨理工大学, 2016.
Shao Yan. The application of Fractional Fourier Transform in signal analysis[D]. Harbin: Harbin University of Science and Technology, 2016.(in Chinese)
[19] 张永飞, 魏安全, 孙玉琦. DSSS系统LFM干扰抑制技术研究[J]. 电子质量, 2011(7): 1-3,6.
Zhang Yongfei, Wei Anquan, Sun Yuqi. Aresearch of the LFM interference suppression in DSSS system[J]. Electronic Quality, 2011(7): 1-3,6.(in Chinese)
[20] 马垒, 赵拥军, 赵闯, 等. STLFMCW信号的周期FRFT检测与参数估计[J]. 计算机工程与应用, 2017, 53(1): 134-141.
Ma Lei, Zhao Yongjun, Zhao Chuang, et al. Detection and parameter estimation of STLFMCW signal based on periodic FRFT[J]. Computer Engineering and Applications, 2017, 53(1): 134-141. (in Chinese)
赵健根 男, 1992年生, 山西人。重庆邮电大学通信与信息工程学院硕士研究生, 主要研究方向为导航信号的捕获。
E-mail: 2655910322@qq.com
张天骐 男, 1971年生, 四川人。重庆邮电大学通信与信息工程学院教授、博士生导师, 主要研究方向为通信信号的调制解调、盲处理、语音信号处理、神经网络实现以及FPGA、VLSL实现。
E-mail: zhangtq@cqupt.edu.cn
李鑫凯 男, 1993年生, 河南人。重庆邮电大学通信与信息工程学院硕士研究生, 主要研究方向为通信信号盲估计。
E-mail: 807934868@qq.com
葛宛营 男, 1994年生, 河南人。重庆邮电大学通信与信息工程学院硕士研究生, 主要研究方向为语音增强与盲分离。
E-mail: 472944688@qq.com