无线携能通信(Simultaneous Wireless Information and Power Transfer, SWIPT)是解决能量受限网络中能量稀缺问题的无线传输技术。与传统依靠外界电源供能的网络不同,SWIPT网络节点从接收到的射频信号中收集能量,将收集的能量用于信息传输,克服了信息传输对外界电源的依赖。同时,无线节点不便配置可靠电源的缺陷也得到了弥补[1-2]。在以往的研究中,无线能量传输(Wireless Power Transfer,WPT)和无线信息传输(Wireless Information Transfer,WIT)为了实现不同的研究目标,运用不同的性能指标来衡量系统的优劣:无线能量传输的侧重点偏向于能量传输效率(能效)的最大化,而无线信息传输的侧重点在于信息通过信道衰落与噪声干扰过程中的频谱效率(谱效)的最大化[3]。近年来,由于射频信号中同时蕴含信息和能量,学者们通过统一设计目标,探寻WPT和WIT的均衡点[3]。
L.R.Varshney首次定义了SWIPT中的“容量能量函数”(Capacity Energy Function),分别分析了二进制离散信道和幅度受限的加性高斯白噪声信道下的SWIPT能量效率和信息速率均衡性能[4]。随后,P.Grover和A.Sahai将SWIPT技术的研究延伸到AWGN信道中[5],提出了一种采用耦合电感电路来实现近距离无线信息与能量同时传输的电路模型,采用注水法实现最优功率分配,并给出了可达信息速率与能量转换效率间的最优均衡方案。然而,这种假设对于当前的电路技术是无法实现的[6- 8]。在文献[6]中,作者为了解决这个问题,研究了四种SWIPT系统实现方案,即:动态功率分割(Dynamic Power Splitting, DPS),开关功率分割(On-off Power Splitting, OPS),静态功率分割(Static Power Splitting, SPS)和时隙切换(Time Switching, TS)。不同文献研究了不同SWIPT系统的速率-能量(Rate-Energy, R-E)均衡关系。例如,文献[6]研究了分离/共址信息和能量接收器的多天线SWIPT系统的R-E均衡关系,文献[8]研究了有限码长的单天线SWIPT系统的R-E均衡关系。
目前,基于线性能量收集模型的R-E均衡已被广泛研究[6- 8]。在该模型中,SWIPT节点收集到的能量与能量收集电路的输入射频(Radio Frequency, RF)功率成线性关系[6- 8]。当能量(或功率)转换效率在输入功率的整个范围内恒定时,这种线性关系才能成立。但是,实际能量收集电路的能量转换效率和输入信号关系是非线性的[9-10]。因此,实际SWIPT节点的能量收集过程是非线性的。即,随着输入功率的增加,其转换效率首先增加,然后显著降低[11-12]。因此,简单的线性能量收集模型无法准确地描述SWIPT节点能量收集过程。
针对SWIPT节点实际采用非线性能量收集,论文首先建立非线性能量收集模型,提出了时隙切换与静态功率分割相结合的智能协同SWIPT传输方案(Intelligent Cooperation of Time Switching and Static Power Splitting, CoTP),推导了该传输方案的速率-能量(R-E)域,研究了接收端电路功耗情况下CoTP方案的速率-能量(R-E)均衡策略,通过仿真比较了所提CoTP策略与DPS、OPS、SPS与TS策略的R-E域性能,并分析了噪声以及接收端电路功耗对各策略R-E域性能的影响。CoTP方案可以智能地调整时间分割因子和功率分割因子,从而可以获得较高的可达速率。通过联合调整时间分割因子和功率分割因子,所提智能协同SWIPT传输方案使SWIPT节点收集能量与信息传输变得可调可控。
本文的其余部分安排如下:第2部分介绍了系统模型。第3部分研究了不同SWIPT传输方案下的R-E域及其均衡性能。 第4部分考虑在接收端电路功耗情况下,不同SWIPT传输方案的R-E域性能,并给出了仿真与性能分析。第5部分为全文总结。
考虑SWIPT网络中具有多个SWIPT收发节点,每个SWIPT节点可作发射端或接收端,收发节点均配备单天线。N表示每个时间块中发射符号的总数量。同时假设每个发射符号的发射功率均为P。h表示发射端与接收端之间的复信道功率增益,在每个时间块内h保持不变。根据文献[1],SWIPT节点仅在移动性较低的固定环境(例如,在固定距离范围内的室内场景)中可行,因此,SWIPT网络中均假设信道是准静态信道。
在接收端,第k个符号周期内接收到的RF信号被归一化功率分割因子ρk(0≤ρk≤1)分割成两个部分。其中,接收功率的(1-ρk)部分用于信息解码。因此,第k个信息符号的信道容量[5]为
(1)
其中
和
分别表示天线噪声和RF到基带转换噪声的方差(功率)。
考虑SWIPT节点线性能量收集模型[6- 8]。在线性能量收集模型中,接收功率的剩余部分ρk用于能量收集,SWIPT节点在第k个符号间隔内收集到的能量和输入功率ρkhP成线性比例,如下式所示
(2)
其中,ζ(0<ζ≤1)表示能量转换效率,通常假定为常数。
多个实验结果表明,SWIPT节点实际能量收集过程为非线性的。为了准确地给出实际非线性能量收集过程,文献[13]提出了一种非线性能量收集模型。与线性模型相比,该非线性模型能够较为精确地匹配实际实验结果。在该非线性模型中,SWIPT节点在第k个符号间隔内收集的能量建模为
(3)
其中,
是确保零输入零输出响应的常数,Y(ρk)的表达式如下
(4)
在式(3)中,Pmax表示能量收集电路饱和时的最大收集功率。A和B是与电路规格有关的常数且为正数,例如电阻值、电容值和二极管导通电压值。实际上,常数A反映了相对于输入功率的非线性充电速率,而常数B与EH电路开启阈值有关。当给定能量收集电路时,可以通过曲线拟合确定参数Pmax,A和B。
目前,SWIPT节点进行信息传输与能量收集的实现方案主要有:动态功率分割(DPS),开关功率分割(OPS),静态功率分割(SPS)和时隙切换(TS)。在此基础上,论文提出了时隙切换与静态功率分割相结合的智能协同SWIPT传输方案(CoTP)。各方案如图1所示。
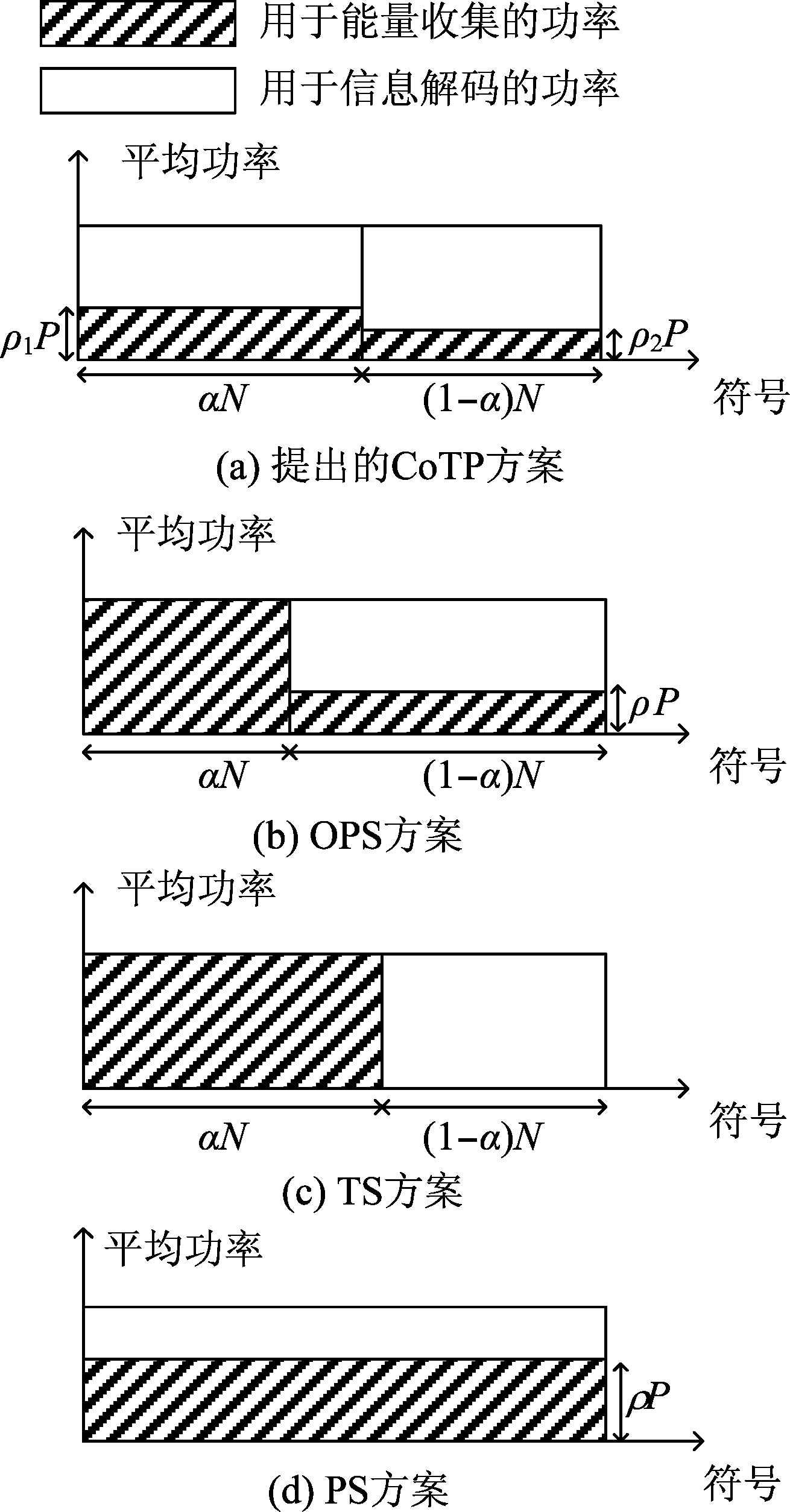
图1 SWIPT节点信息传输与能量收集实现方案
Fig.1 Information transmission and energy harvesting strategies for SWIPT nodes
(1)动态功率分割(DPS):SWIPT的通用方案是在文献[5]中提出的DPS。在DPS中,每个符号间隔的接收功率以功率分割比0≤ρk≤1,k=1,…,N进行动态分配。第k个接收功率的ρk和(1-ρk)部分分别用于能量收集和信息解码。
(2)智能协同时隙切换与静态功率分割相结合(CoTP):作为DPS的特例,我们结合TS与SPS,提出了CoTP,如图1(a)所示。在CoTP中,前α部分进行以ρk=ρ1的静态功率分配,剩余部分进行以ρk=ρ2的静态功率分配。
(3)On-Off功率分割(OPS):它是ρ1=1的CoTP的特例。文献[5]首先提出了OPS,如图1(b)所示。 在OPS中,α部分进行纯能量收集,在其余(1-α)部分进行静态功率分配。
(4)静态功率分割(SPS):SPS是α=0的OPS的特殊情况。在一个符号间隔用于收集能量和解码信息的分离信号功率比设为一个固定的常数ρ。 因此,对于SPS,我们有
ρk=ρ, k=1,…,N
(5)
(5)时隙切换(TS):TS是ρ=0的OPS的特殊情况。当信息接收器处于关闭模式时,前α部分,所有信号功率都用于能量收集。对于信息接收器在开启模式下工作时,剩余的(1-α)部分,所有信号功率都用于信息解码。因此,对于TS,我们有
(6)
首先,我们给出SWIPT节点信息传输与能量收集实现方案的R-E域表达式。其中,R为非线性能量收集下的平均可达速率,
为收集的能量。
DPS方案的R-E域定义为:
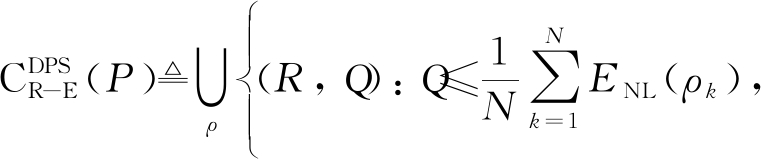
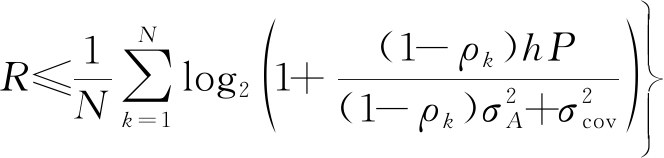
(7)
可以从式(7)获得CoTP的R-E域为:
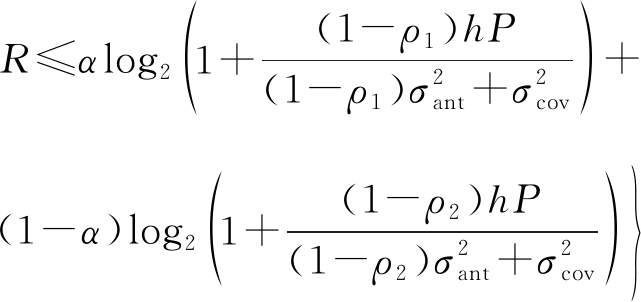
(8)
OPS的R-E域可以根据式(8),令ρ1=1获得,表示如下:
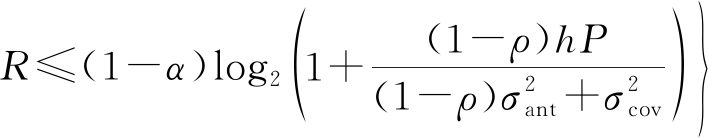
(9)
SPS和TS的R-E域可以根据式(9),分别令α=0和ρ=0,表示如下:
(10)
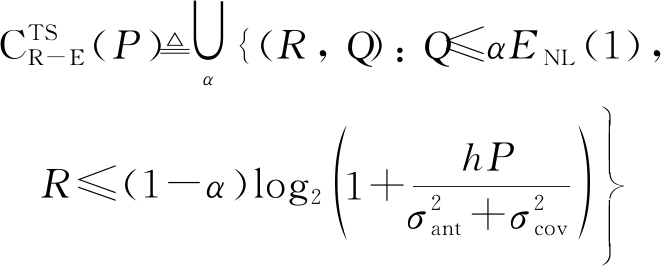
(11)
对于SPS和TS,可以通过将ρ和α分别从0变为1,来实现R-E区域的边界(即,考虑ρ和α的所有可能值)。 另一方面,要确定CoTP和OPS的R-E边界,需要通过对所有可能的收集能量来最大化速率R,以使R-E域最大化,从而优化参数。
针对所提CoTP方案的R-E域,我们考虑如下优化问题:
αlow≤α≤αup, ρlow≤ρ≤ρup
(12)
其中,
P0的解是在第一个约束条件严格相等的情况下获得。因此,边界点的
满足以下两式:
(13)
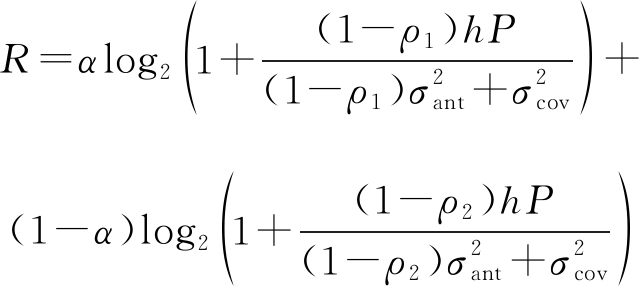
(14)
根据式(13),可以得到,
其中,
为ENL(x)=y的反函数,表示如下:
(15)
将
代入式(14),有:
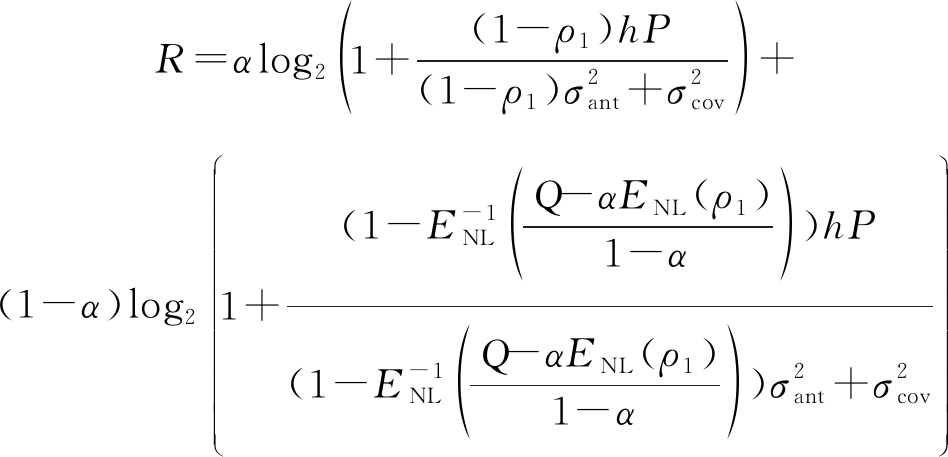
(16)
通过优化算法找到α和ρ1的最优解α*和
从而得出最优的可达速率R*。
综上,CoTP方案联合优化ρ和α的算法步骤如表1所示。
表1 CoTP方案联合优化算法
Tab.1 Joint optimization algorithm for CoTP scheme
联合优化α, ρ1. 初始化 设置ρ1=ρ;2. 循环;3. 当ρ'1-ρ1≥Δρ时;4. 将ρ1代入(16)计算最优的R和α;5. 将α代入(16)计算最优的R和ρ1;6. 结束循环;7. 返回最优的α*, ρ*1和R*作为最后的结果。
考虑OPS的R-E域。根据
ENL(ρ)可以得出,
因为
从而保证0≤ρ≤1,把
代入
中,运用一维搜索算法,即可求得最优的速率R*。
在上一节中,我们假设接收端信息解码所需的电路功耗是忽略不计的。然而,在实际中,接收端电路功耗是不可忽略的[8-9]。在本节中,我们考虑接收端存在电路功耗情况下SWIPT节点的R-E均衡策略。
假设Ps>0表示接收端用于信息解码的电路功耗。对于Ps>0,我们假定Ps<ENL(1)。在这种情况下,可以将上述SWIPT节点信息传输与能量收集实现方案的R-E域重新定义如下:
(17)
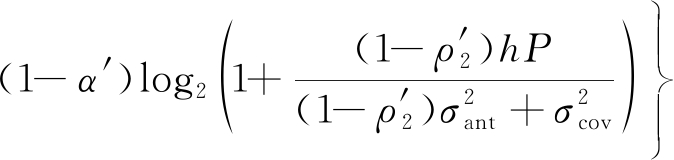
(18)
(1-α′)ENL(ρ′)-(1-α′)Ps,
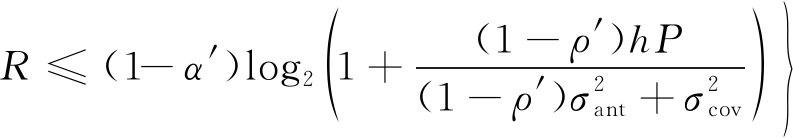
(19)
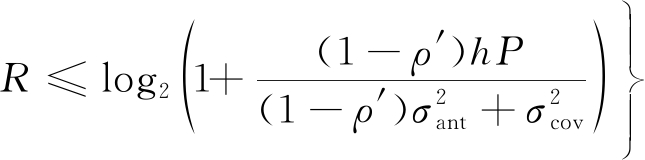
(20)
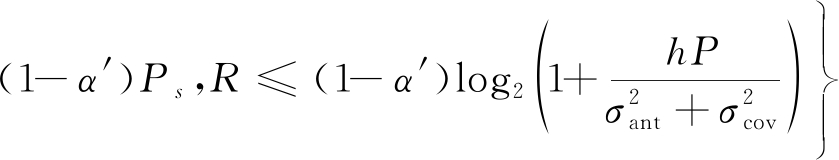
(21)
在式(17)～式(21)中,为收集到的能量与电路功率消耗的能量之差。
对于SPS和TS,可以通过分别将ρ′和α′从
和
变到1来实现R-E区域的边界。 另一方面,要确定CoTP和OPS的R-E边界,则需要计算对所有可能收集到的能量以最大化速率R,使得R-E域最大化,从而优化参数。
将
替代为
可以得到CoTP方案的R-E域,它与不考虑电路功率消耗的情况相同。
本节仿真SWIPT节点信息传输与能量收集实现方案的R-E域均衡性能,并仿真分析噪声以及接收端电路功耗对R-E域均衡性能的影响。
图2和图3分别给出了在不同参数下,不同SWIPT节点信息传输与能量收集实现方案的R-E域均衡性能。假设
图2中
图3中
由图2可知,TS方案相较于其他方案的R-E域较小;SPS方案在较高收集能量区域具有更好的R-E域性能。当每比特收集能量为0.6 mJ～2.4 mJ时,本文所提CoTP方案具有较高的可达速率。在该范围内,若增加相同的收集能量,CoTP的可达速率变化也较小。对比图2与图3可知,在相同的收集能量情况下,SWIPT节点接收信噪比的增加可以显著增加其可达速率。
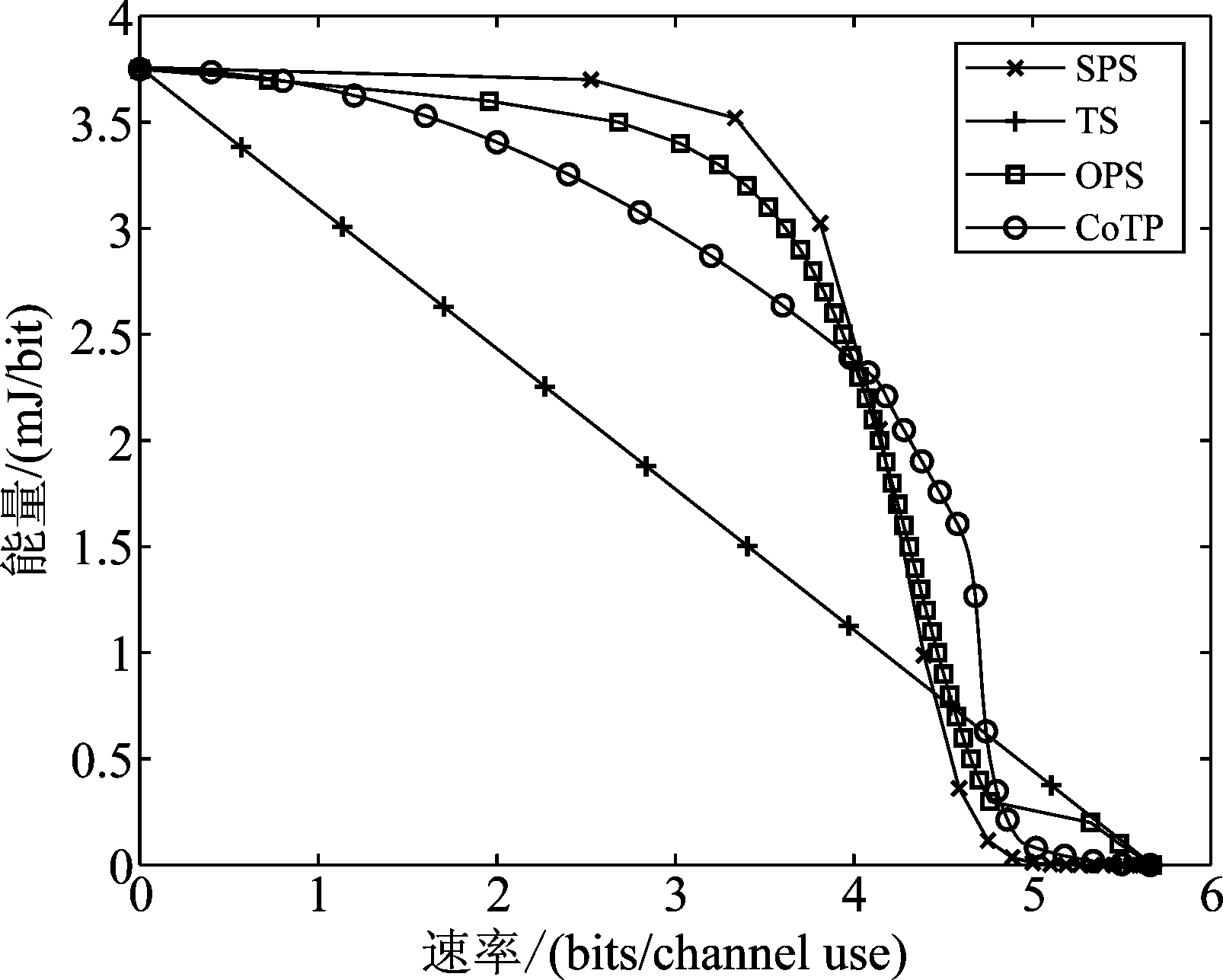
图2 不同SWIPT实现方案的R-E域
Fig.2 R-E region of different SWIPT schemes 
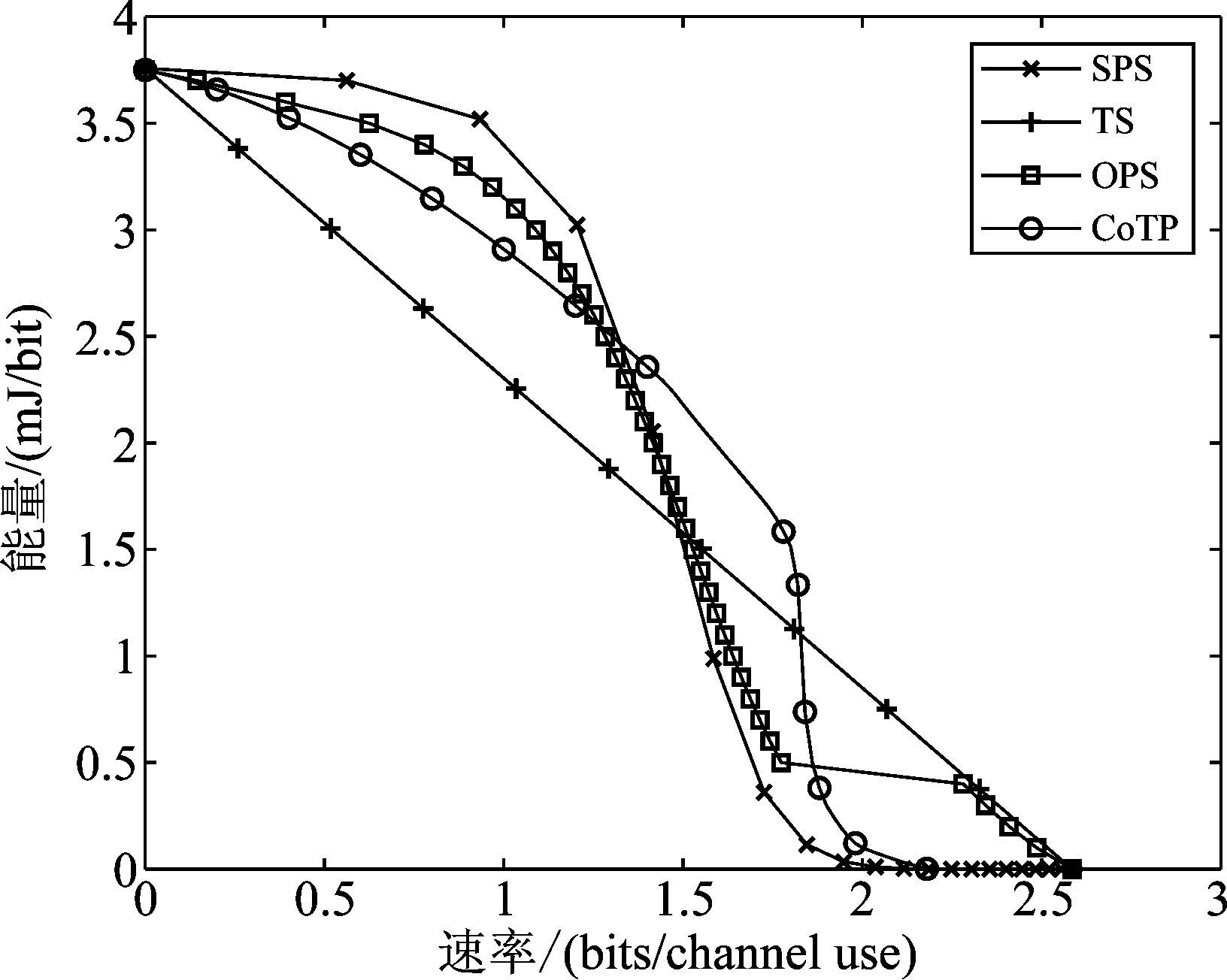
图3 不同SWIPT实现方案的R-E域
Fig.3 R-E region of different SWIPT schemes 
图4给出了考虑接收端存在电路功耗情况下,不同SWIPT节点信息传输与能量收集实现方案的R-E域均衡性能。假设
当考虑电路功耗时,由于SPS与CoTP方案均包含信息解码过程,故一直存在功率消耗,导致两种方案收集到的最大能量小于其他方案。同样,当每比特收集能量为0 mJ～1.5 mJ时,本文所提CoTP方案具有较高的可达速率。在该范围内,增加相同的收集能量,CoTP方案的可达速率变化较小。因此,所提CoTP策略在较少的收集能量情况下,具有较高的可达速率,可实现能量收集与信息传输的均衡。
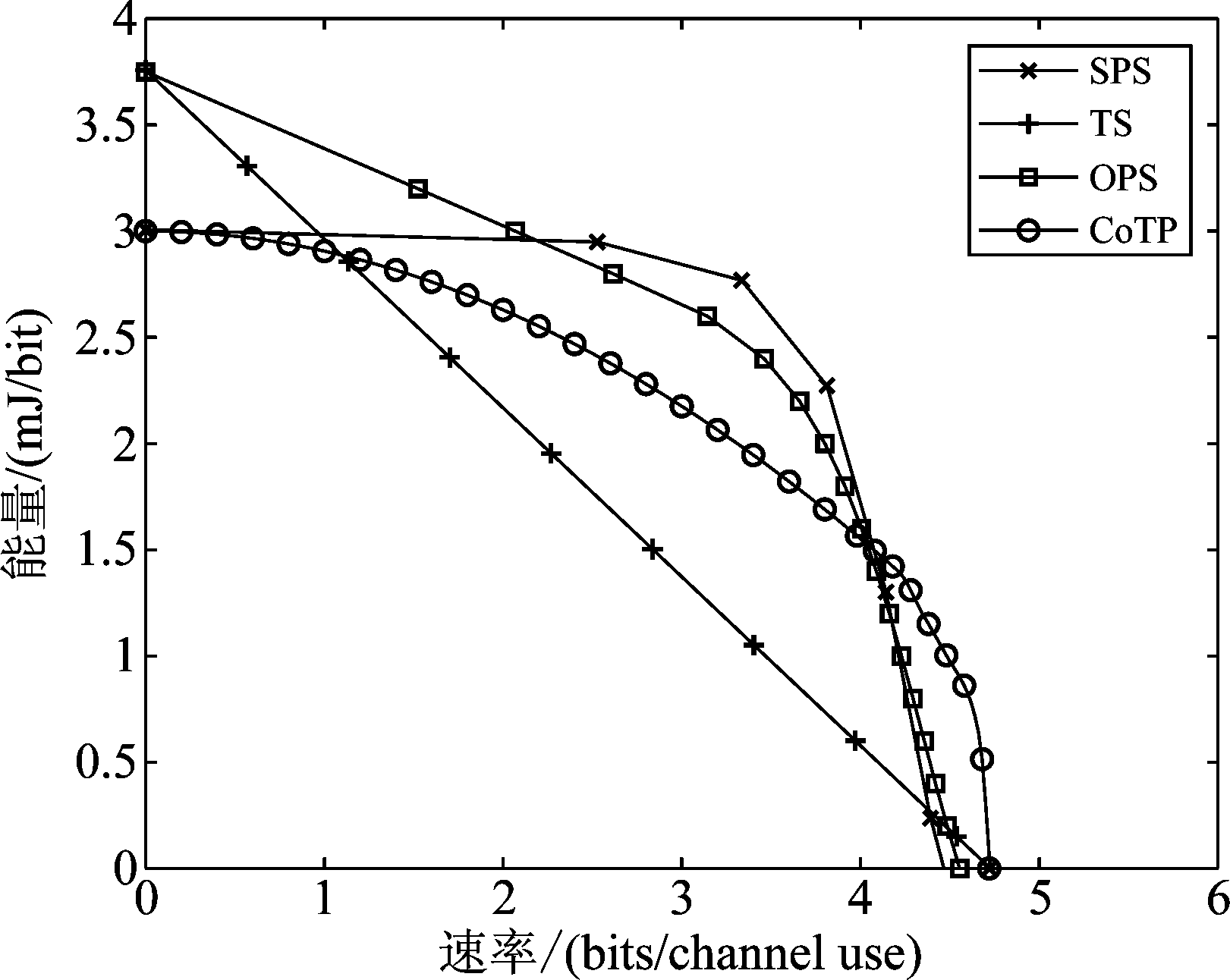
图4 考虑电路功耗情况下,不同SWIPT实现方案的R-E域
Fig.4 R-E region of different SWIPT schemes with the consideration of circuit power consumption
论文研究了SWIPT网络中节点非线性能量收集与信息传输均衡策略,研究了四种不同的SWIPT节点信息传输与能量收集实现方案,提出了时隙切换与静态功率分割相结合的智能协同SWIPT传输方案,并给出了该传输方案的R-E域。同时,分析了噪声与接收端电路功耗对各种策略的R-E域性能影响。通过对所提CoTP与OPS、SPS、TS方案的R-E域性能比较可知,所提CoTP策略在节点较少的收集能量情况下,可以实现能量收集与信息传输的有效均衡。CoTP方案通过联合调整时间分割因子和功率分割因子,可以获得较高的可达速率。所提智能协同SWIPT传输方案使SWIPT节点收集能量与信息传输变得可调可控。
[1] 石振波, 许晓荣, 孙明杭, 等. 携能网络中保障能效的缓存队列中继选择与能量分配方案[J]. 信号处理, 2019, 35(11): 1880-1887.
Shi Zhenbo, Xu Xiaorong, Sun Minghang, et al. Energy-efficiency priority based buffer-aided relay selection and power allocation strategy in SWIPT network[J]. Journal of Signal Processing, 2019, 35(11): 1880-1887.(in Chinese)
[2] Ku M, Li Wei, Chen Yan, et al. Advances in energy harvesting communications: past, present, and future challenges[J]. IEEE Communications Surveys and Tutorials, 2016, 18(2): 1384-1412.
[3] 洪鑫龙, 许晓荣, 石振波. 无线携能网络中一种基于时隙切换的中继辅助信能同传协议[J]. 信号处理, 2018, 34(12): 1467-1473.
Hong Xinlong, Xu Xiaorong, Shi Zhenbo. A relay-aided information and power transfer protocol based on time switching structure in SWIPT[J]. Journal of Signal Processing, 2018, 34(12): 1467-1473.(in Chinese)
[4] Varshney L R. Transporting information and energy simultaneously[C]∥IEEE International Symposium on Information Theory (ISIT), Toronto, 2008: 1612-1616.
[5] Gover P, Sahai A. Shannon meets Tesla: wireless information and power transfer[C]∥IEEE International Symposium on Information Theory (ISIT), Austin, 2010: 2363-2367.
[6] Zhou Xun, Zhang Rui, Ho C K. Wireless information and power transfer: architecture design and rate-energy tradeoff[J]. IEEE Transactions on Communications, 2013, 61(11): 4754- 4767.
[7] Zhang Rui, Ho C K. MIMO broadcasting for simultaneous wireless information and power transfer[J]. IEEE Transactions on Wireless Communications, 2013, 12(5): 1989-2001.
[8] Kim I M, Kim D I, Kang J. Rate-energy tradeoff and decoding error probability-energy tradeoff for SWIPT in finite code length[J]. IEEE Transactions on Wireless Communications, 2017, 16(12): 8220- 8234.
[9] Clerckx B, Bayguzina E. Waveform design for wireless power transfer[J]. IEEE Transactions on Signal Processing, 2016, 64(23): 6313- 6328.
[10] Zeng Yong, Clerckx B, Zhang Rui. Communications and signals design for wireless power transmission[J]. IEEE Transactions on Communications, 2017, 65(5): 2264-2290.
[11] Guo Jiapin, Zhu Xinen. An improved analytical model for RF-DC conversion efficiency in microwave rectifiers[C]∥IEEE/MTT-S International Microwave Symposium Digest, Montreal, QC, Canada, 2012: 1-3.
[12] Valenta C R, Durgin G D. Harvesting wireless power: survey of energy-harvester conversion efficiency in far-field, wireless power transfer systems[J]. IEEE Microwave Magazine, 2014, 15(4):108-120.
[13] Boshkovska E, Ng D W K, Zlatanov N, et al. Schober. Practical non-linear energy harvesting model and resource allocation for SWIPT systems[J]. IEEE Communications Letters, 2015, 19(12): 2082-2085.
[14] Kim I, Kin D I. Wireless information and power transfer: rate-energy tradeoff for equi-probable arbitrary-shaped discrete inputs[J]. IEEE Transactions on Wireless Communications, 2016, 15(6): 4393- 4407.
沈霖晖 男, 1995年生, 浙江舟山人。杭州电子科技大学硕士研究生, 主要研究方向为绿色携能网络中信息传输与能量收集均衡策略设计与优化等。
E-mail: 554855550@qq.com
许晓荣 男, 1982年生, 浙江杭州人。博士后, 杭州电子科技大学副教授, 硕士生导师。主要研究方向为SWIPT网络中继选择、资源调度与物理层安全; 基于能量有效性的认知无线网络物理层安全、资源分配与优化等。
E-mail:xuxr@hdu.edu.cn
孙明杭 男, 1995年生, 浙江温州人。杭州电子科技大学硕士研究生。主要研究方向为认知无线携能网络中保障能效的资源调度策略优化技术等。
E-mail: 410726517@qq.com