其中,N表示极化码的码长,K表示信息位长度。极化码的编码公式[1]可以写为:2009 年,极化码[1]的提出是信道编码领域的一个重大突破。极化码作为目前唯一一类可以在理论上实现二进制输入离散无记忆信道(Binary-Input Discrete Memoryless Channels, B-DMC)容量的编码方案,凭借较低的编译码复杂度,传输时延小等优点,可应用于无线通信[2-3]、窃听信道[4]和多址接入[5]等各类通信系统。2016年,极化码成功入选5G标准,3GPP最终确定极化码为5G增强移动宽带(Enhanced Mobile Broadband, eMBB)场景下控制信道的编码方案[6]。
极化码自研究以来,多使用二进制相移键控(BPSK)调制方式。近年来,极化码与高阶调制相结合的方式已经成为5G无线通信系统中的实用性方案[7- 8],通过交织器将编码与调制联合设计,以获得更高的频谱利用率,为此人们做了大量的研究工作。文献[9]对比特交织极化编码调制(Bit Interleaved Polar Coded Modulation,BIPCM)进行了系统性的描述与优化,其特征在于交织器的设计,Shin等人提出采用密度进化法计算搜索空间中映射方案的可靠性,选取有最大可靠性的映射方案作为系统的交织算法,然而在M-PAM调制下,搜索策略复杂度较高,难以找到最优的比特映射模式。基于此,Niu Kai等人通过对并行子信道容量进行均等划分,提供了等容量分割的信道映射方案[10],以实现并行子信道与编码比特之间的传输,从而降低了系统选择的复杂度。为了进一步提高高阶调制下极化码的频谱效率,文献[11]利用极化码的递归结构扩展了多级信道的信道极化定理,提出了一种适用于16QAM和64QAM调制的复合极化方案,相比于分离性的极化编码方案,[11]中所提出的极化码具有更好的纠错性能。文献[12]使用随机交织仿真了BIPCM系统在QPSK和16QAM调制方式下的误码率性能,但是在交织器的使用上未能充分将编码比特与极化子信道进行映射。此外,文献[13]提出了一种交织器辅助的逐次消除翻转译码算法,将交织后的信息比特和循环冗余校验(Cyclic Redundancy Check,CRC)比特共同作为检查节点。译码时,通过确定交织后CRC比特的前一部分是否发生错误,从而判定是否需要对所有的信息比特进行译码,从而有效地降低译码复杂度。
本文采用巴氏参数(Bhattacharyya)法[1]对极化码进行构造,设计出一种新型交织算法,将衡量比特信道可靠度参数进行大小交错排序,编码后的比特按照重排后的比特信道可靠度参数进行交织。最后在加性高斯白噪声(Additive White Gaussian Noise, AWGN)信道模型下,采用基于Gray映射的16QAM调制以及逐次消除(Successive Cancellation, SC)译码算法,在现有的BIPCM系统中,对不同的交织算法进行仿真比较,结果表明本文提出的交织方案具有更好的性能。在此基础上,与基于LDPC码的BICM系统性能相比,BIPCM系统在改进译码算法的辅助下具有更明显的性能增益。
极化码的核心是信道极化原理[1],信道极化包括信道组合和信道分解两部分。信道组合对应于极化码编码过程,信道分解原理应用于SC译码算法。当极化码的码长N足够大时,会出现极化现象:一部分比特信道的容量趋近于“1”,称为无噪信道;剩余部分的比特信道容量趋近于“0”,称为全噪信道。
在极化码的构造中,通常采用比特信道的巴氏参数值来评估信道的可靠度,比特信道的巴氏参数值越大,说明信道可靠度低;反之,巴氏参数值越小,则说明比特信道可靠度高。极化码的编码原理在于选取较为可靠的K个比特信道传输信源产生的信息比特,剩余N-K个比特信道传输收发端已知的冻结比特,得到混合矢量其中,N表示极化码的码长,K表示信息位长度。极化码的编码公式[1]可以写为:
(1)
式(1)中,
为编码矢量,生成矩阵GN由下式给出:
GN=BNF⊗n
(2)
其中,BN表示比特反转操作,且BN=RN(I2⊗BN/2),式中B2、I2为2维单位矩阵,RN为置换矩阵,将输入向量
经过RN操作,输出向量为
表示矩阵F的n次克罗内克积,
E.Arikan表示当极化码码长N足够大时,使用SC译码算法,系统能获得较好的渐进性能。在接收端,极化码译码器的作用在于,利用已知的信息位索引以及信道输出矢量
计算
的估计序列
其中
代表第i个译码比特。若为冻结比特,则
若为信息位,计算的对数似然比(Log-Likelihood Ratio, LLR):
(3)
再根据LLR值进行判决:
(4)
SC译码算法是一种贪婪算法,当极化码码长为有限长时,比特信道未能完全极化,若当前比特译码发生错误,将产生错误传播。针对这一缺陷,Tal等人提出了逐次消除列表(Successive Cancellation List , SCL)译码算法[14]。即在SC译码算法的过程中保留L条译码路径。选取L条路径中度量值最大的一条路径作为SCL译码结果输出。L为路径搜索宽度。当搜索路径宽度L=1时,SCL译码算法退化为SC译码算法。
为了进一步改善极化码译码算法的性能,Niu Kai等人提出将CRC技术应用到极化码的SCL(CA-SCL)译码算法[15],通过牺牲少量信息位,引入循环冗余校验元,以提高极化码的纠错性能。在发送端,将k比特的信息位送入到CRC编码器,产生一个r位的校验比特,此时的信息位为k+r比特,作为极化码编码器的输入;在接收端,极化码译码器经SCL译码算法筛选出L条译码路径之后,对每条译码路径执行一次CRC校验,若其中有一条路径通过校验,则译码正确,该译码路径作为最终的译码结果输出;反之,译码错误。
极化码的BICM系统是一种简单、实用的高阶编码调制方案,其主要特征是在极化码编码器后面增添一个比特交织器,最大程度地离散编码比特之间的相关性[16]。极化码的M=2m进制调制BICM系统模型如图1所示。图中,为信息比特与冻结比特混合的待编码矢量,
为编码矢量。
为编码矢量经过交织器后的比特序列,调制器采用M-QAM调制,将交织后的比特序列转化为符号序列
在接收端,
表示接收到信道输出的符号矢量,
表示符号经解调后得到的初始LLR序列。由于发送端增添了交织器,相应地在接收端设置一个解交织器,其输出矢量为作为译码器的输入。
表示极化码译码器输出的译码估计序列。
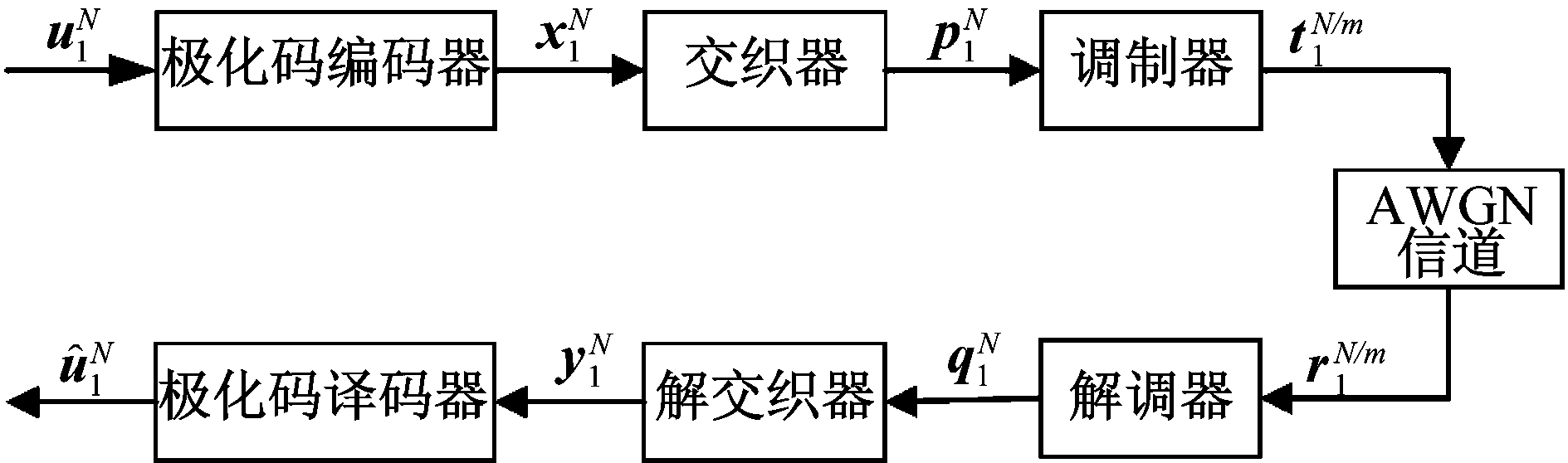
图1 极化码的BICM系统模型
Fig.1 BICM system model of polar codes
BICM系统的主要特征在于交织器的设计,利用交织器打乱编码比特序列,最大程度地减弱编码比特之间的相关性,分段编码序列映射到星座图上,从而将出现连续错误的编码比特映射到不同的调制符号中,离散化突发错误,改善系统性能。当交织器为理想交织器时,编码器与调制器可以分离设计,系统灵活性较大,从而有效提高编码分集增益。
文献[10]中,Chen Kai等人采用等容量分割的信道映射方案,对J个并行子信道{W1,W2,...,WJ}的信道容量值{I(W1),I(W2),...,I(WJ)}进行分组,使得参与到各分量变换中的每组子信道的信道容量之和尽可能相等,通过对该组并行信道排序,得到编码比特与并行信道之间的映射关系。本文将该算法运用到交织器中,通过计算极化码比特信道的可靠性衡量参数,对其进行均等化排序、分组,得到对应的目标索引序列,最终编码矢量按照目标序列完成等容量交织。具体步骤如下:使用巴氏参数法计算N个比特信道的可靠度Z(Wi)(i=1,2,…,N),根据巴氏参数与信道容量之间的关系[1],其比特信道容量表示为I(Wi)(i=1,2,…,N),对
进行分组,使得分组后的每组容量之和尽可能相等,并记录每次分组之后的索引序列
直到每组集合中只含有2个容量值I(Wi)(i=1,2),操作终止。示例一:当码长N=8时,使用巴氏参数法估计比特信道的可靠性,相应地得到其对称容量
及其初始状态索引号
经过第一次均等化排序、分组,得到
和
相应地索引序列转化为
经过再一次递归分组,对称容量I(Wi)(i=1,2,…,N)转化为
目标序列
最终编码矢量
根据等容量交织转化为{p1,p8,p4,p5,p2,p6,p3,p7}。
文献[12]采用随机交织算法作为比特交织器的工作原理。对于长度为N的极化码编码序列
对其产生N个在区间[0,1]内取值的随机数,且随机数与编码比特一一对应;将N个随机数按照某一规则(从大到小)进行排列,编码比特则按照对应的随机数序列依次读出,完成对原编码序列的随机交织。示例二,当码长N=4时,产生的随机数序列
和索引序列
将其按照从大到小规则排列为
得到目标序列
最终编码矢量
按照目标序列
实现随机交织为{p4,p1,p3,p2}。
相比于一般的随机交织,交错交织算法的提出是基于编码比特与极化子信道之间的映射关系,计算极化子信道的可靠性,将高可靠性的比特信道与低可靠性的比特信道交错设计,借助高可靠性的比特信道对低可靠性的比特信道辅助译码的方式,提高极化码的纠错性能。本文通过巴氏参数法衡量参与极化子信道的可靠度,得到对应比特信道的信道容量,将其按照从大到小的方式排序,并依次排列为首尾交错的顺序,即容量值最大者放在首位,最小者放在第二位,次大者放于第三位……依次下去,完成比特信道可靠性参数的位置交替。最终编码矢量按照上述交替方式实现交错交织。
具体步骤如下:使用巴氏参数法计算N个比特信道的可靠性Z(Wi)(i=1,2,…,N),相应地得到其对称容量,作为该组比特信道的可靠度衡量参数
任意比特信道的可靠度Qi(i=1,2,…,N)唯一对应码字中相应位置上的编码比特xi(i=1,2,…,N),对
按照从大到小的方式排序,所得序列
即为极化码比特信道可靠度排序的索引号,使得QX1≤QX2≤…≤QXN;将
按照首尾交错的方式排列,得到交织后的目标序列
编码矢量按照目标序列
完成比特交织。示例三,当码长N=4时,使用巴氏参数法估计其比特信道的可靠性为{Z1,Z2,Z3,Z4}={0.79,0.86,0.13,0.35},根据巴氏参数与信道容量之间的关系,得到该组比特信道的可靠度参数{Q1,Q2,Q3,Q4}={0.21,0.14,0.87,0.65},对
按照从大到小的方式排序,则比特信道可靠度排序的索引号为
并将其按照首尾交错的规则重新排列,得到目标序列
最终,编码矢量
根据目标序列
实现交错交织,转化为{p3,p2,p4,p1}。
BICM系统模型下极化码的编译码步骤如下:
(1)极化码编码:码长为N,长度为K的信息序列
经过CRC编码器,产生r位的校验比特。将长度的K+r的生成序列
与N-(K+r)个冻结比特混合后,得到长度为N的待编码矢量
乘以N维生成矩阵GN,即
(2)交织:根据提出的交错交织算法计算得到将编码后的比特序列与进行一对一映射得到
(3)调制:采用基于Gray映射的16QAM调制方式,即相邻4个比特映射成一个传输符号。比特序列经过调制器转换成一组符号序列
每个符号ti(i=1,2,…,N/4)映射为星座图上的一个点,用实部tre和虚部tim表示。
(4)AWGN信道:调制符号
经过服从高斯分布N(0,σ2)的AWGN信道传输后,接收端收到的符号矢量为r=t+z,其中z为信道噪声序列。
(5)解调:在接收端,解调器对矢量
进行软解调,由符号概率计算各比特的后验概率值,得到初始比特的LLR序列
(6)解交织:经软解调后的序列按照索引的逆序列
进行解交织后送入到极化码译码器。
(7)极化码译码:译码器的输入序列
经SCL译码器,选取保留L条路径作为译码备选路径。将L条备选序列送入CRC校验器,选取其中能通过校验的一条路径作为极化码译码器输出的估计序列
为验证交织器对BIPCM系统性能的影响,本文在AWGN信道模型下,码率固定为0.5时,采用16QAM调制,通过蒙特卡洛仿真误码率来分析系统的性能。其中,图2、图3分别是极化码码长为256、1024,在SC译码算法下,BIPCM系统中3种交织算法与极化码无联合编码调制系统的性能对比仿真图;图4是将BIPCM系统与采用随机交织算法的LDPC码编码的BICM系统性能进行对比,其中,码长均为256。在译码方式上,LDPC码使用置信传播译码,设置最大迭代次数为50,极化码采用CA-SCL译码算法,L=32。
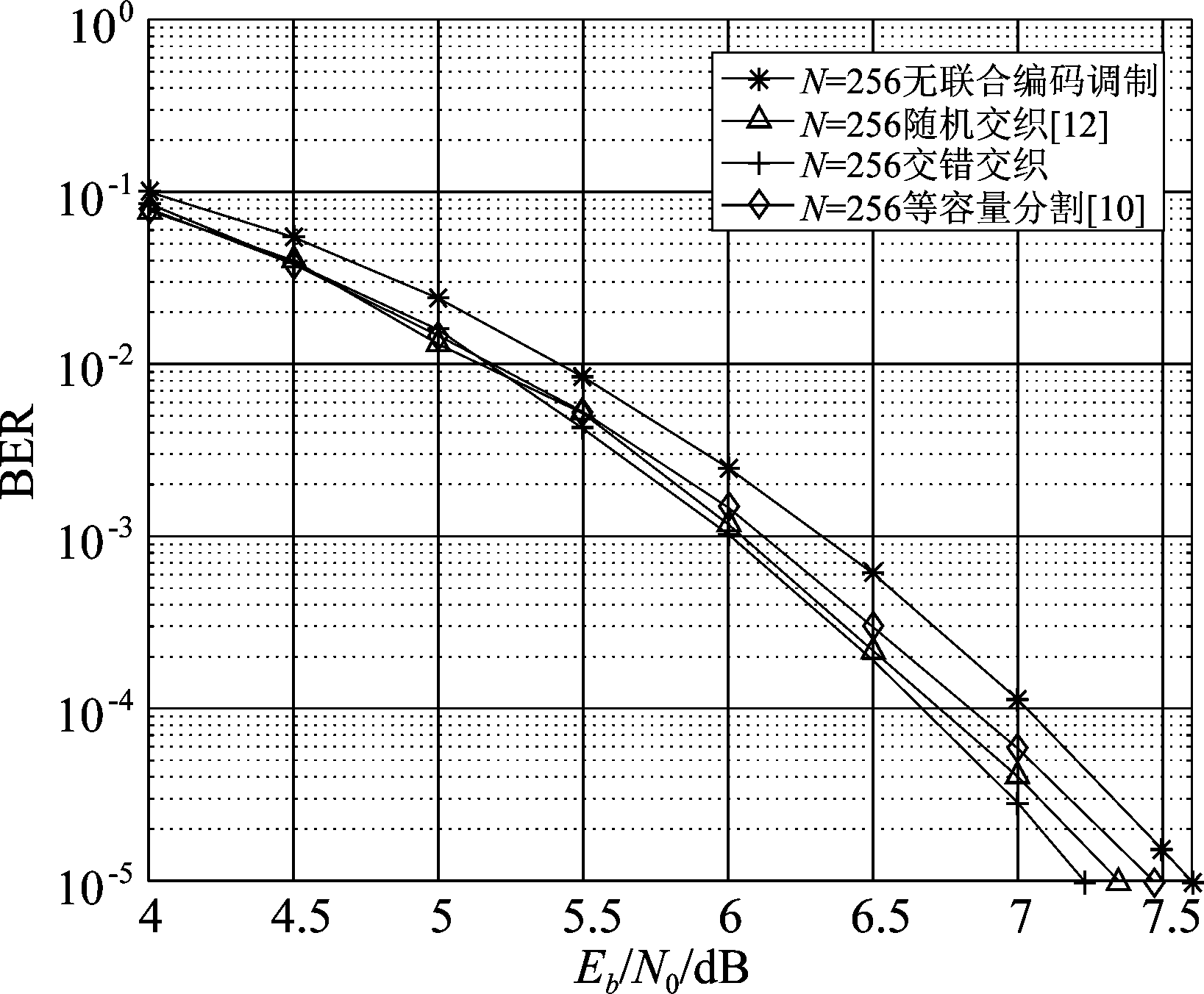
图2 码长为256时,BIPCM系统中交织器性能对比
Fig.2 Performance comparison of interleaver in BIPCM system when the code length is 256
如图2和图3所示,在相同码率的情况下,相对于极化码的无联合编码调制系统,当码长为256、1024时,本文提出的BIPCM系统分别具有0.35 dB与0.57 dB的性能增益,其主要原因在于交织器的引入极大程度地打乱了编码比特序列,将出现连续错误的比特映射至不同的调制符号中。本文提出的交错交织算法相比其他文献中的交织算法也存在0.1～0.4 dB的增益,且极化码码长越长,性能增益越大。当误码率为10-5,码长为1024时,本文所提出的BIPCM系统相比于基于随机交织、等容量分割算法的BIPCM系统也存在0.23 dB与0.4 dB的增益。这均表明采用交错交织算法的BIPCM系统具有良好的性能,打乱编码比特相关性的同时充分考虑极化子信道与编码比特之间的映射关系,以提高极化码译码的可靠性。
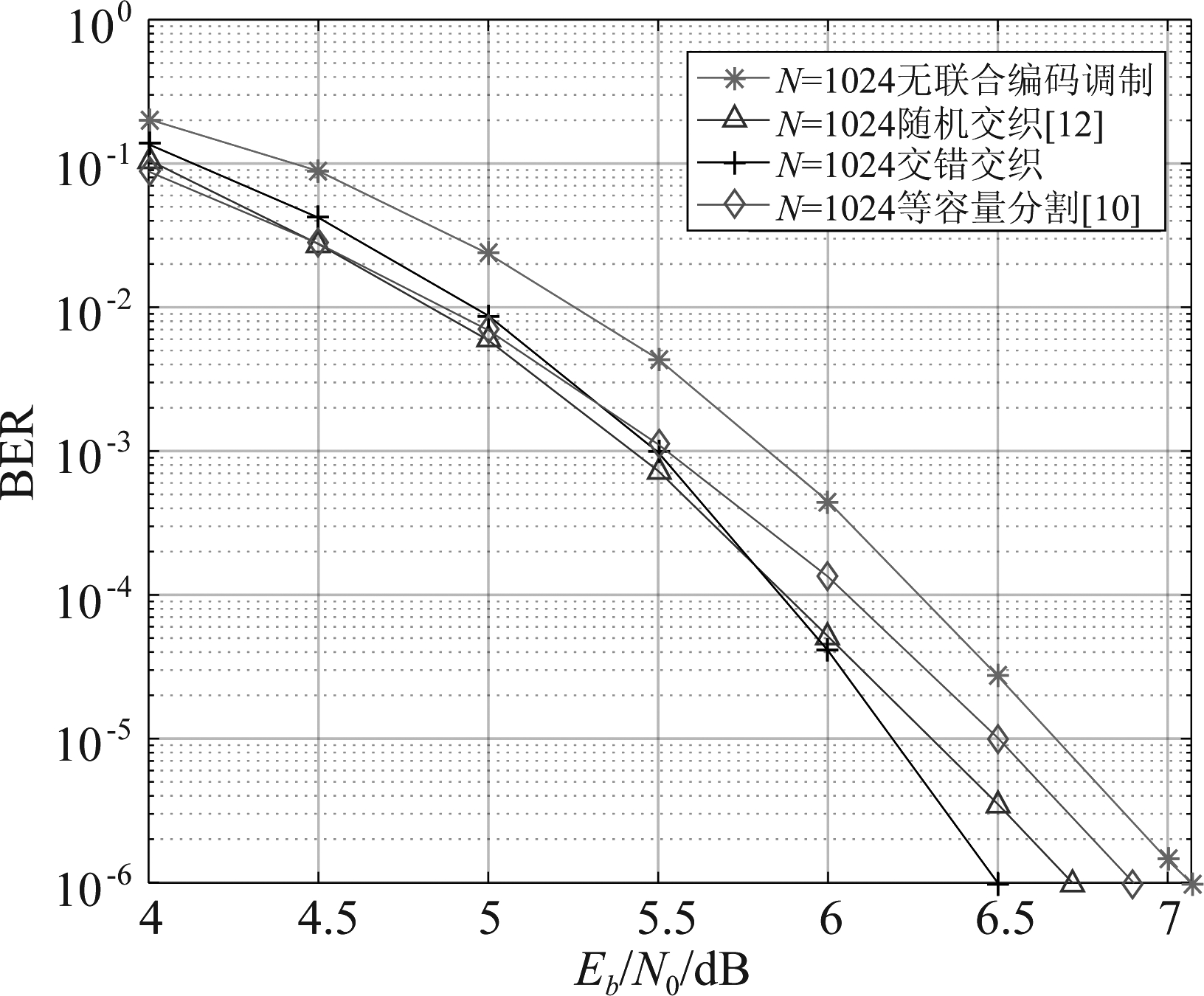
图3 码长为1024时,BIPCM系统中交织器性能对比
Fig.3 Performance comparison of interleaver in BIPCM system when the code length is 1024
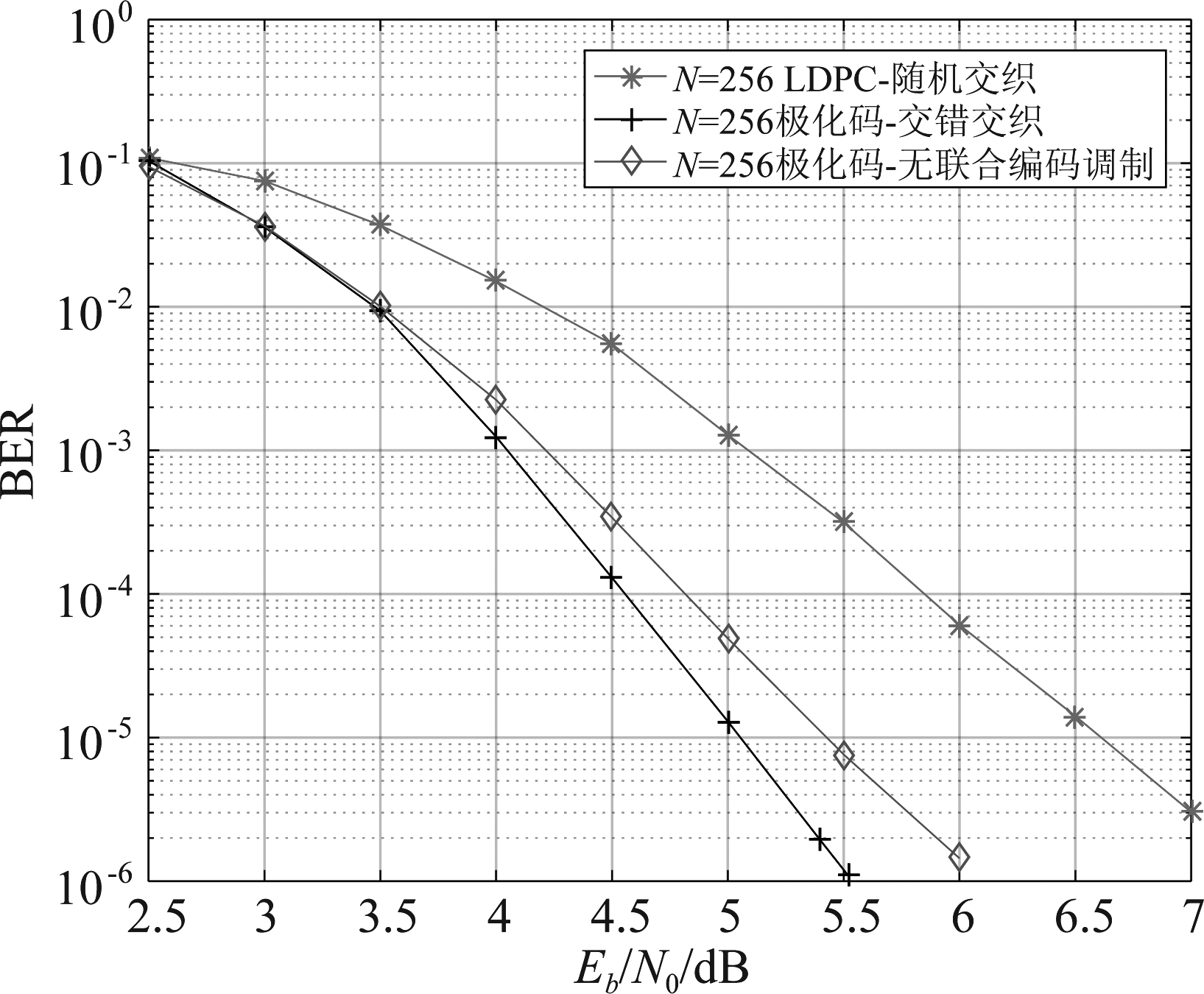
图4 极化码与LDPC码的BICM系统性能对比
Fig.4 Performance comparison of BICM system between Polar codes and LDPC codes
如图4所示,在短码方案上,BIPCM系统相比同等码长、码率的LDPC码编码的BICM系统具有更优异的性能。当误码率为10-5时,使用交错交织方案的BIPCM系统相比于LDPC码编码的BICM系统性能增益高达1.51 dB。在CA-SCL译码算法的辅助下,通过牺牲少量信息位,加入CRC校验比特,以提高极化码的纠错性能;同时计算比特信道的可靠性,寻找适合于编码比特与极化子信道之间的良好映射,借助于高可靠性的比特信道对低可靠性的比特信道进行译码,改善系统性能。特别地,相对于随机交织与等容量分割的交织算法,交错交织是针对比特信道可靠度衡量参数的简单排序操作,其算法实现复杂度较低,所以系统在复杂度方面几乎没有增加。
为了提高未来移动通信系统中的频带利用率,本文将极化码与高阶调制联合考虑,采用单层极化码高阶编码调制系统模型,通过排序比特信道可靠度衡量参数,提出了交错交织算法。在SC和CA-SCL译码算法下,分别比较高阶M-QAM调制下交织器对BIPCM系统性能的影响,并与采用随机交织算法的LDPC码编码的BICM系统进行仿真对比。结果表明,使用交错交织算法的BIPCM系统具有更好的性能,有望在未来移动通信系统中得到应用。
[1] Arikan E. Channel polarization: a method for constructing capacity-achieving codes for symmetric binary-input memoryless channels[J]. IEEE Transactions on Information Theory, 2009, 55(7): 3051-3073.
[2] 李晓磊, 石旭, 周林, 等. 新型级联Polar码设计[J]. 信号处理, 2019, 35(3): 516-521.
Li Xiaolei, Shi Xu, Zhou Lin, et al. Design of novel cascaded polar codes[J]. Journal of Signal Processing, 2019, 35(3): 516-521.(in Chinese)
[3] Kim J, Moon S, Kim Y, et al. Polar modulation with CR method for optical wireless communication MIMO system[C]∥2018 International Conference on Information and Communication Technology Convergence (ICTC). Jeju, South Korea: IEEE, 2018: 611-615.
[4] 张孝甜, 赵生妹, 郑宝玉. 无线信道中的Polar码协商[J]. 信号处理, 2018, 34(7): 793-798.
Zhang Xiaotian, Zhao Shengmei, Zheng Baoyu. Key reconciliation using polar code in wireless channel[J]. Journal of Signal Processing, 2018, 34(7): 793-798.(in Chinese)
[5] Dizdar O, Goken C, Yilmaz A. An uplink non-orthogonal multiple access method based on frozen bit patterns of polar codes[J]. IEEE Communications Letters, 2019, 23(6): 975-978.
[6] Gamage H, Rajatheva N, Latva-Aho M. Channel coding for enhanced mobile broadband communication in 5G systems[C]∥2017 European Conference on Networks and Communications (EuCNC). Oulu, Finland: IEEE, 2017: 1-6.
[7] Sharma A, Salim M. Polar code: the channel code contender for 5G scenarios[C]∥2017 International Conference on Computer, Communications and Electronics (Comptelix). Jaipur, India: IEEE, 2017: 676-682.
[8] Seidl M, Schenk A, Stierstorfer C, et al. Polar-coded modulation[J]. IEEE Transactions on Communications, 2013, 61(10): 4108-4119.
[9] Shin D M, Lim S C, Yang K. Mapping selection and code construction for 2^m-ary polar-coded modulation[J]. IEEE Communications Letters, 2012, 16(6): 905-908.
[10] Chen Kai, Niu Kai, Lin Jiaru. An efficient design of bit-interleaved polar coded modulation[C]∥2013 IEEE 24th Annual International Symposium on Personal, Indoor, and Mobile Radio Communications (PIMRC). London, UK: IEEE, 2013: 693-697.
[11] Mahdavifar H, El-Khamy M, Lee J, et al. Polar coding for bit-interleaved coded modulation[J]. IEEE Transactions on Vehicular Technology, 2016, 65(5): 3115-3127.
[12] 樊婷婷, 杨维, 许昌龙. 基于Polar码的BICM系统在AWGN信道中的性能[J]. 东南大学学报: 自然科学版, 2016, 46(1): 18-22.
Fan Tingting, Yang Wei, Xu Changlong. Performance of BICM system based on polar code in AWGN channel[J]. Journal of Southeast University: Natural Science Edition, 2016, 46(1): 18-22.(in Chinese)
[13] Kim H, Lee H, Park H. Interleaver-aided successive cancellation flip decoding algorithm for polar codes[C]∥2018 IEEE 4th International Conference on Computer and Communications (ICCC). Chengdu, China: IEEE, 2018: 2559-2563.
[14] Tal I, Vardy A. List decoding of polar codes[J]. IEEE Transactions on Information Theory, 2015, 61(5): 2213-2226.
[15] Niu Kai, Chen Kai. CRC-aided decoding of polar codes[J]. IEEE Communications Letters, 2012, 16(10): 1668-1671.
[16] Millar D, Kojima K, Sugihara K, et al. Bit-interleaved polar-coded modulation for low-latency short-block transmission[C]∥2017 Optical Fiber Communications Conference and Exhibition (OFC). Los Angeles, CA, USA: IEEE, 2017: 1-3.
石 旭 女, 1996年生, 湖南常德人。华侨大学信息科学与工程学院, 硕士研究生, 主要研究方向为信道编码与调制、5G移动通信。
E-mail: 757000739@qq.com
周 林(通信作者) 男, 1982年生, 河南南阳人。华侨大学信息科学与工程学院, 副教授, 博士学位, 主要研究方向为信道编码、无线通信和光通信等。
E-mail: linzhou@hqu.edu.cn
张树颖 男, 1997年生, 福建三明人。华侨大学信息科学与工程学院, 硕士研究生, 主要研究方向为信道编码、人工智能等。
E-mail: Zhangshuying@hqu.edu.cn
陈 辰 女, 1990年生, 福建莆田人。华侨大学信息科学与工程学院, 讲师, 博士学位, 主要研究方向为无线通信和信道编码等。
E-mail: chen_chen@hqu.edu.cn
傅玉青 女, 1984年生, 福建泉州人。华侨大学工学院, 讲师, 博士学位, 主要研究方向为光通信和信道编码等。
E-mail: fuyq@hqu.edu.cn
贺玉成 男, 1964年生, 山西太原人。华侨大学信息科学与工程学院, 教授, 博士学位, 主要研究方向为信道编码、协作通信、无线通信等。
E-mail: yucheng.he@hqu.edu.cn