近些年来,随着无线通信技术的迅速发展,无线用户的数量也随之急剧增加,由于频谱资源的不可再生性,另一方面已分配的频谱资源的利用率并不是很高,这些现象使得无线频谱资源变得越来越稀缺。为了能够更好的解决这一问题,认知无线电(Cognitive Radio,CR)技术应运而生[1-2]。认知无线电的基本概念是频谱复用,也即是在判断主用户没有充分利用其分配的频谱资源的情况下,它允许未分配权限的次级用户(认知用户)利用该频谱资源进行通信。实现这一过程就需要认知用户频繁的利用频谱感知技术[3],来判断主用户是否正在利用该频谱资源。
最初的单认知用户频谱感知算法有能量检测法[4- 6]、匹配滤波检测法[7]、循环平稳特征检测法[8]等。其中能量检测算法受噪声不确定性影响较大,难以适应低信噪比环境下的复杂的无线通信环境[9];匹配滤波检测由于要知道主用户信号的先验知识和严格的相位同步条件,使其实用性不高[7];循环平稳特征检测实现的复杂程度高,检测时间长[10],影响通信要求的实时性。
针对上述单用户频谱感知存在的问题,一些学者提出了协作频谱感知的思想[11-15],大的研究方向主要包括集中式和分布式协作频谱感知两大类[12-14]。传统的协作频谱感知算法确实能在一定程度上提高系统检测的准确性能,但不管是在算法本身的复杂度方面还是在低信噪比、低虚警概率的环境下依然存在着很多需要改进的地方。
随着频谱感知算法的成熟,越来越多高质量的研究成果相继发表。Sun Chenhao等人提出一种基于主成分分析和K-medoids聚类的协作频谱感知算法[16],Zhou Rikang 等人提出一种基于贝叶斯压缩感知的协同频谱感知算法[17]等,这些算法在减少感知时间的同时大大的提高了传统协作频谱感知算法检测概率。近些年来图像分类的方法日趋成熟,以及机器学习算法在图像分类方面的广泛应用且具有较高的可靠性,所以本文基于这个想法提出一种基于图像K-means聚类分析的频谱感知算法,相较于传统频谱感知算法可以提高认知用户在低信噪比情况下的检测概率。
频谱感知一般被抽象的认为是一个二元假设检验模型,其中H0和H1分别表示在信道中主用户信号空闲和忙碌的两种状态。如下所示:
(1)
其中t表示时间点,x(t)表示认知用户接收到的信号,s(t)表示主用户发射信号,n(t)表示信道中存在的噪声信号总和。当主用户信号空闲时,认知信号中只有噪声信号;当主用户信号忙碌时,认知信号是主用户信号和噪声信号之和。
由于认知用户接收到的信号x(t),在主用户存在和不存在时,二者信号采样点数据值的分布情况整体是有差别的,因此在图像上呈现到的亮度也是不同的。对x(t)信号进行N个点采样,由N个信号采样点的幅值构成一个m行n列的矩阵R,表示如下,
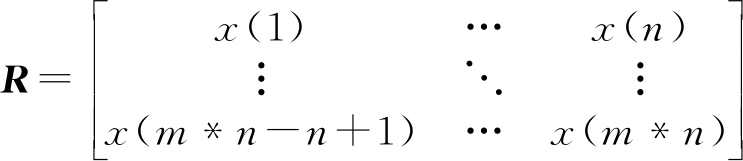
(2)
利用该数值矩阵R,实现由数值到图像的映射。每一个方块区域点均代表一个采样信号点,例如当采样点为100时,将100个信号采样值转化为10*10的矩阵,映射如图1所示。

图1(a)和图1(b)分别表示在信噪比为-15 dB时主用户信号不存在与存在的图像。由图可以看到主用户信号存在与否的差别是图像亮度的不同,本文的主要判断依据是根据亮度的差异区分出主用户是否存在。高信噪比时,差异较大区分效果明显;反之低信噪比时由于差异较小,区分效果相对于高信噪比不太明显,从而导致检测的正确率下降,影响算法的性能。为了解决在低信噪比时存在的上述问题,需要对原始映射图像作图像增强和高斯滤波预处理操作。
由于在低信噪比时,主用户存在与否的图像,区分效果不太明显,所以首先需要分别对两类图片进行图像预处理,本文通过对图像像素值的压缩和解压的方式增大两类图像之间的差异性。设定输入图片强度范围[i_min,i_max],以及输出图片的强度范围[o_min,o_max],读取原图像的结果用m表示,假设像素个数为n。
对图像数组进行预处理,首先是对图像像素值的压缩(截取),截取规则如下:

(3)
对像素数据压缩之后得到的图片强度范围为[i_min,i_max],对压缩之后的像素进行等比例的扩大使得图片强度范围为[o_min,o_max],解压公式如下:
![]()
(o_max-o_min)+o_min,i=1,2 ,…,n
(4)
通过对像素值的压缩和扩大的结果分析,输入像素值m[i]在小于i_min的范围内,输出像素值固定为o_min;在i_min和i_max之间的输入像素值m[i],输出像素值等比例扩大,图片的绝对像素值增大;输入像素值m[i]在大于i_max内,输出像素值固定为o_min。本文中主用户信号不存在时,映射成的图像像素值一般小于i_min,而主用户存在时的映射成的图像像素值一般在i_min和i_max之间,通过上述方法使得同一类图片像素分布均匀,不同类图片之间像素差异性较大,有利于图片特征向量的有效提取,进而提高检测正确率。本文中i_min和i_max分别为20和220,o_min和o_max分别为0和255。
高斯滤波(Gauss filter)是一种常用的线性平滑滤波算法,适用于平滑图像。高斯滤波算法可简化为对整幅图像的像素值进行加权平均计算。对于图像中的任意一个像素值,均是由其本身值和其邻域所在的全部像素值通过加权平均后计算得到。高斯滤波的具体过程是用一个带有范围的模板扫描图像中的每一个像素点,用模板规定的邻域内的所有像素值加权求和得到的像素值去替代模板中心像素点的值[18]。
在2.2增大图像的差异性的基础上,利用高斯滤波算法进一步将图像进行平滑滤波处理。由于图像中的每一个像素点的值都是由领域内的其他点加权求和得到。使得图像像素点关联性更高,分布更加均匀。进一步使同类图片像素分布均匀,不同类图片之间像素差异更大。
由于本文中处理的图像是二维平面的,所以要用二维高斯分布函数来计算模板范围内每一个像素点的权重。这里的二维高斯分布函数为:
(5)
其中(x,y)为点的坐标,将中心点视为原点,其他点按照其在高斯分布函数的位置来分配权重。得到权重与原本像素值进行加权求和并归一化得到中心点坐标值。由于参数σ的大小关系着远处像素对中心点像素的影响程度。σ值越大,生成的模板内各部分元素值比重相对差别不大,类似于平均模板。σ值越小,模板内越接近原点的元素值所占的比重越大。通过调节参数σ的大小来达到最好的平滑滤波效果,本文中依次对σ取值为1、3、5的平滑滤波效果进行模拟仿真,通过对检测结果的影响对比得出当σ设为3时效果较佳。
根据假定灰度级范围的个数可以求出一幅图像直方图,求直方图的步骤为:假设图像可以分为L个灰度级范围,统计高斯滤波后的图像各灰度级范围的像素总数nk,由此可得图像像素的直方图,而Gk(k=1,2,...,L)是每一个灰度级范围的中间值。通过灰度级范围的中间值Gk和对应灰度级范围的像素总数nk相乘提取该图片一个灰度级的特征值Tk。
Tk=Gk*nk
(6)
由L个灰度级提取出L个特征值Tk,构成出代表一幅图像信息的特征向量:
T=[T1,T2,...,TL]
(7)
k-means模型是最基本和最常见的聚类算法之一。该模型在欧几里得空间定义包含个n向量元素的数据集D={d1,…,dn},根据各个样本之间欧式距离的大小,将其划分为k个簇[19-20]。要求在簇内的样本之间的欧式距离都要尽可能的小,而让簇间样本的欧式距离都尽可能的大。即把n个元素分配到k个不同的聚类簇中S={S1,S2,…,Sk}其目标函数是最小化平方误差E:
(8)
其中x是簇S的任意元素,μi是簇S的均值向量,有时也称为质心,表达式为:
(9)
假设输入是样本集D={x1,x2,…,xn},聚类的簇数为k,迭代次数为N,输出是簇划分S={S1,S2,…,Sk},则K-means算法流程为:
表1 K-means算法流程
Tab.1 K-means algorithm steps

k-means算法流程1. 从数据集中随机选择初始的K个质心向量:{μ1,μ2,…,μk}。2. for n=1,2,…,N:1) 将k个簇初始化为空集,即:Sj=∅,j=1,2,…,k;2) 依次计算样本xi(i=1,2,…,m)跟每个质心μj(j=1,2,…,k) 之间的欧式距离:dij=‖xi-μj‖22(10)将xi划分到dij最小时所对应的簇Sj中。即更新,Sj=Sj∪{xi}(11)3)根据更新后的簇内样本点更新该簇的新质心,uj=1Sj∑x∈Sjx(12)4)当所有簇的质心均不变时结束循环迭代,否则继续循环。
本文中因为只需要判断主用户信号是否存在,属于K-means中的二分类情况,训练模型如图2所示。
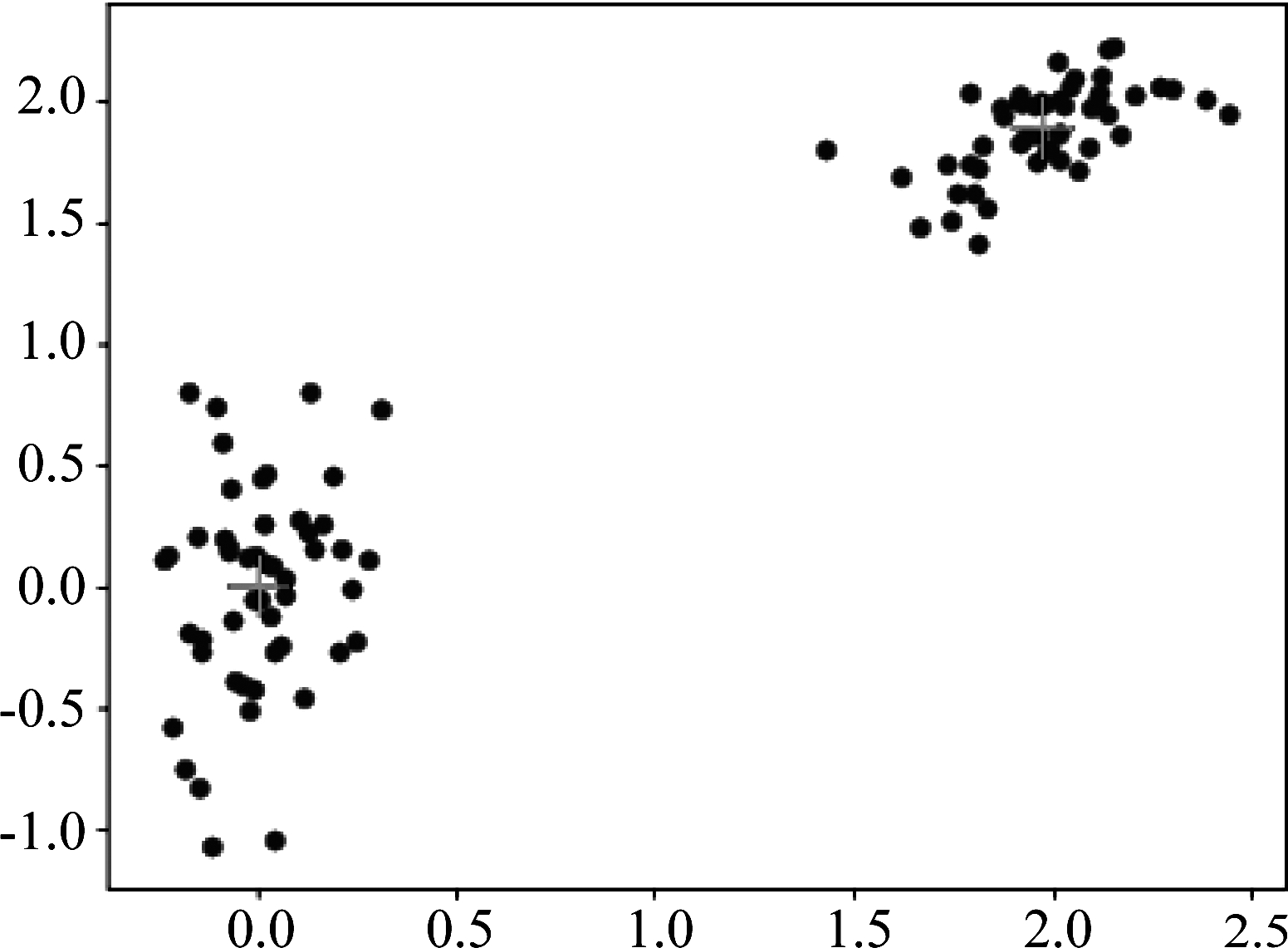
图2 基于K-means的二分类模型
Fig.2 K-means-based binary classification model
星号标记点则分别是两个簇的质心,两个簇内的圆点均满足最小化平方误差准则。本文在二分类模型训练完成获得两个簇的质心μ1、 μ2,由于K-means聚类算法是无监督学习,不能确定质心μ1、 μ2归属于主用户信号存在或是空闲状态,所以,需要对两个质心点进行1、0标记,其中主用户信号存在标记为1,空闲标记为0。
本文采用对欧式距离求和比较大小的方式进行标记。已知样本集D*={x1,x2,…,xM}是主用户信号空闲的情况下,分别依次对两个簇的质心求欧式距离之和。即计算:
(13)
以及,
(14)
通过比较E1和E2的大小,较大的为主用户忙(存在)时的质心μ1,较小的对应的即为主信号空闲时的质心μ2。
通过同样的特征提取方法对测试集数据进行处理,得到测试集数据的特征向量集T*={t1,t2,…,tN},依次计算每一个特征向量ti与质心μ1、 μ2之间的欧式距离。
o1=‖ti- μ1‖2
(15)
以及,
o2=‖ti- μ2‖2
(16)
比较o1和o2的大小进行判决,
(17)
当Re=H0表示主用户信号不存在,反之Re=H1则表示主用户信号存在。
评价频谱感知算法性能好坏常用的指标包括虚警概率Pf和检测概率Pd。相同信噪比的情况下Pf越小,Pd越大,算法的可靠性越高。本文利用matlab和python进行仿真实验。最先利用matlab生成的模拟信号进行等间隔采样并映射成对应的图片信息,把映射得到的图片分为训练样本集和测试样本集两部分;其次利用python中的skimage模块对样本图片提取特征向量,利用scipy中的whiten和k-means模块对特征向量进行无监督分类模型训练并进行1、0标记;最后利用训练好的分类器模型对测试样本进行测试统计。实验仿真假设主用户信号为BPSK信号,载波频率为100 kHz,采样频率为628 kHz,通过改变主用户信号的幅值来控制信噪比的变化,本文中主要以0 dB、-3 dB、-5 dB、-7 dB、-10 dB、-15 dB这六个信噪比的信号进行测试,为方便处理假设噪声信号为均值为0,方差为1的高斯白噪声。本文主要从算法的不同以及采样点数的不同对算法进行多维的比较。
分别对传统能量检测频谱感知、基于能量的协作频谱感知、以及本文提出的基于图像的K-means聚类分析的频谱感知算法以采样点数200进行模拟仿真,且该方法经测试在六个信噪比上对应的虚警概率分别为0.166、0.149、0.022、0.001、0.003、0、0。仿真结果如图3。
图3反应了当频谱感知算法不同时,检测概率随信噪比的变化曲线。由图可得,当信噪比和虚警概率均相同时,基于图像的K-means聚类频谱感知算法在检测性能上优于传统的能量检测法和基于能量检测的协作频谱感知算法。尤其在信噪比小于-7 dB时,检测性能得到明显提高,在信噪比为-15 dB时,能量检测算法检测概率为0.3263,基于能量检测的协作频谱感知算法的检测概率为0.3665,而基于图像的K-means聚类频谱感知算法的检测概率则达到了0.816。
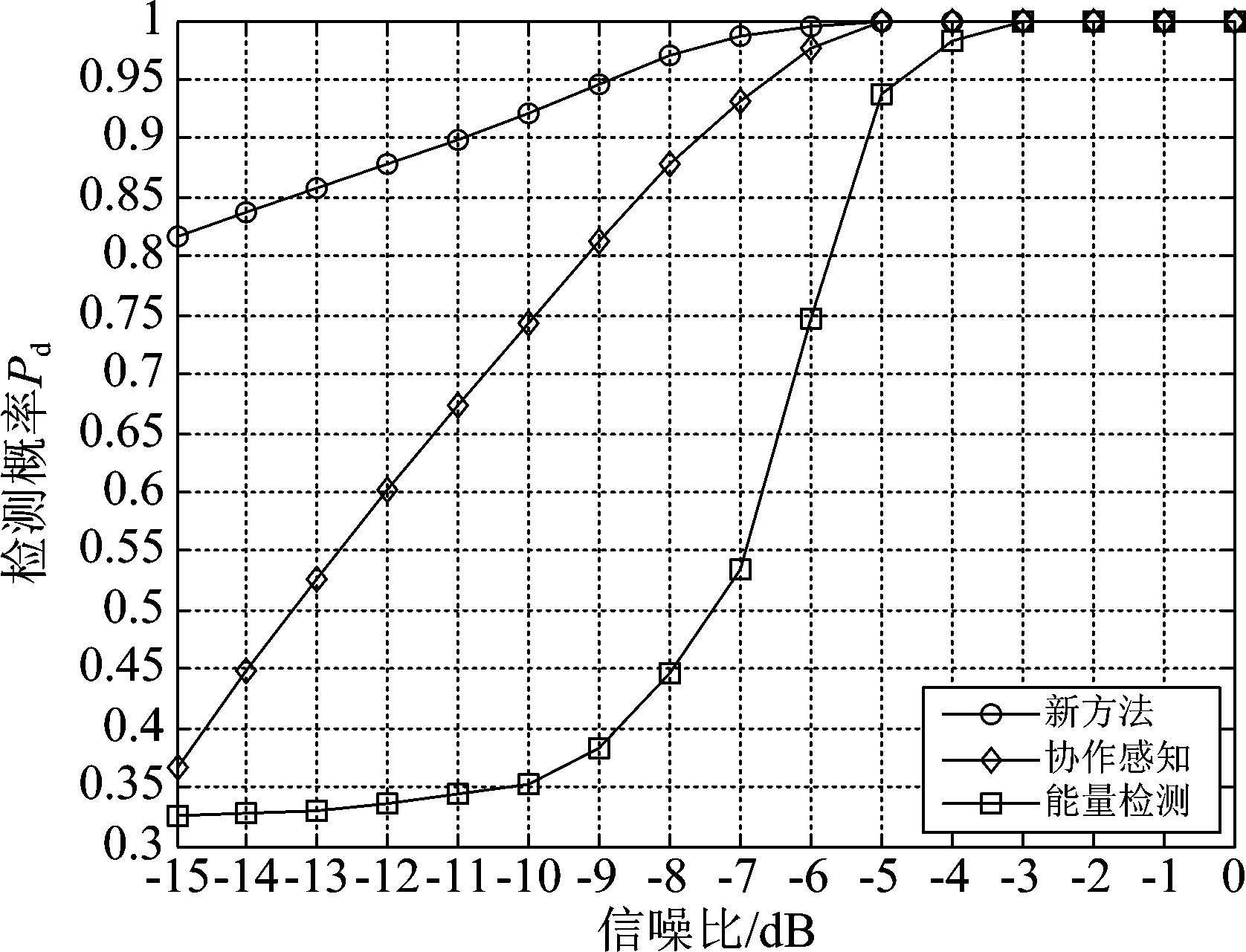
图3 不同检测算法的性能比较
Fig.3 Performance comparison of different detection algorithms
图4反映了当信号采样点数不同时对检测性能的影响。本文中以取采样点数N=50、100、200为例进行仿真,从图中可以得到,当信噪比大小相同的情况下,当采样点数越多时,算法的检测性能也就越好,且在低信噪比时效果尤其明显。
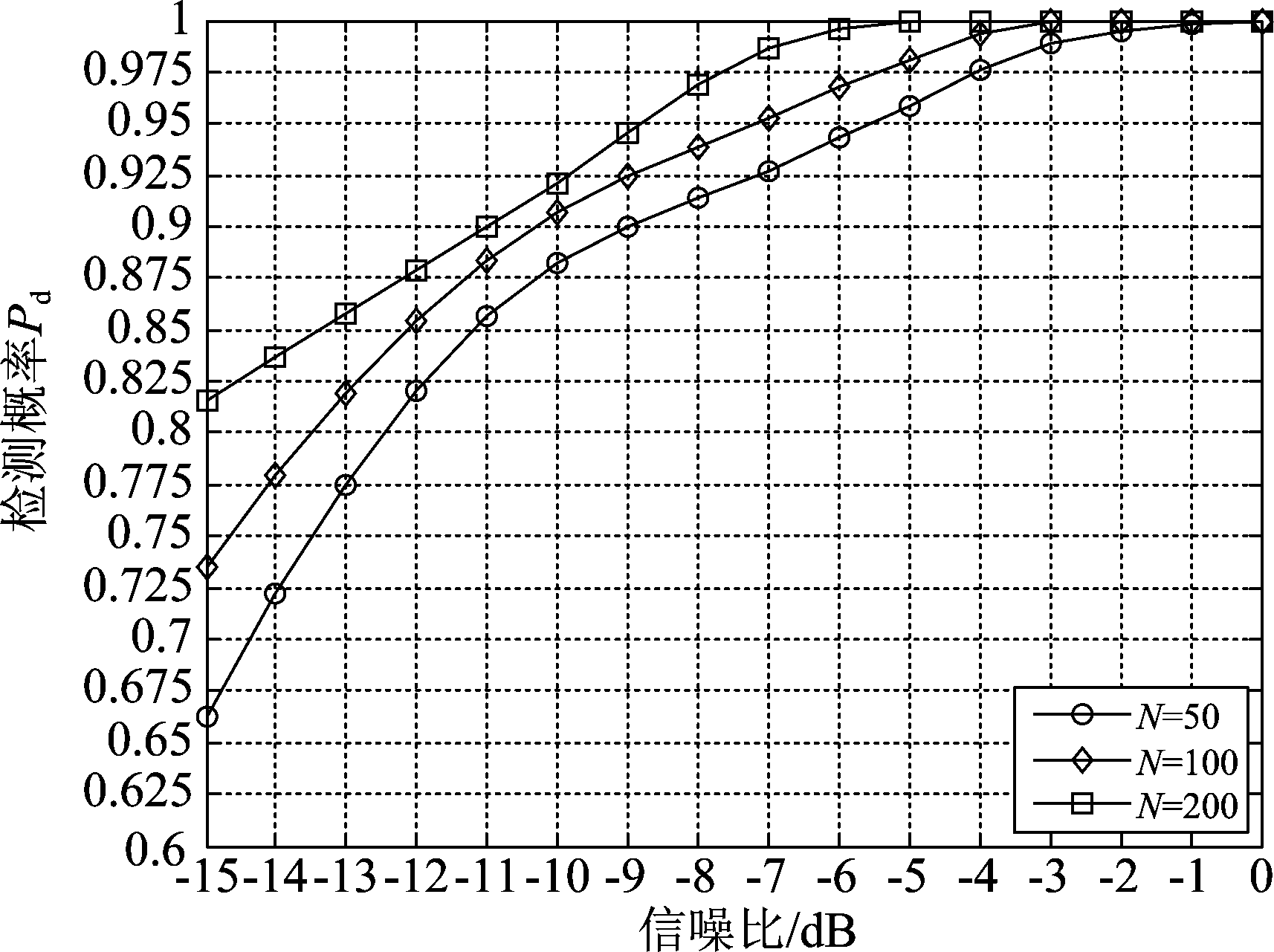
图4 不同采样点对检测性能的影响
Fig.4 Influence of different sampling points on detection performance
图5反应了在信号采样点不同时,基于图像的K-means聚类频谱感知算法的虚警概率的随信噪比变化的曲线。由于噪声信号的随机性,导致仿真结果会出现小范围的上下波动。从图中可以看到与检测概率Pd变化相反的情况,当信噪比越来越大,采样点越多时虚警概率Pf整体趋势越来越小,在信噪比为0 dB时虚警概率几乎为0。
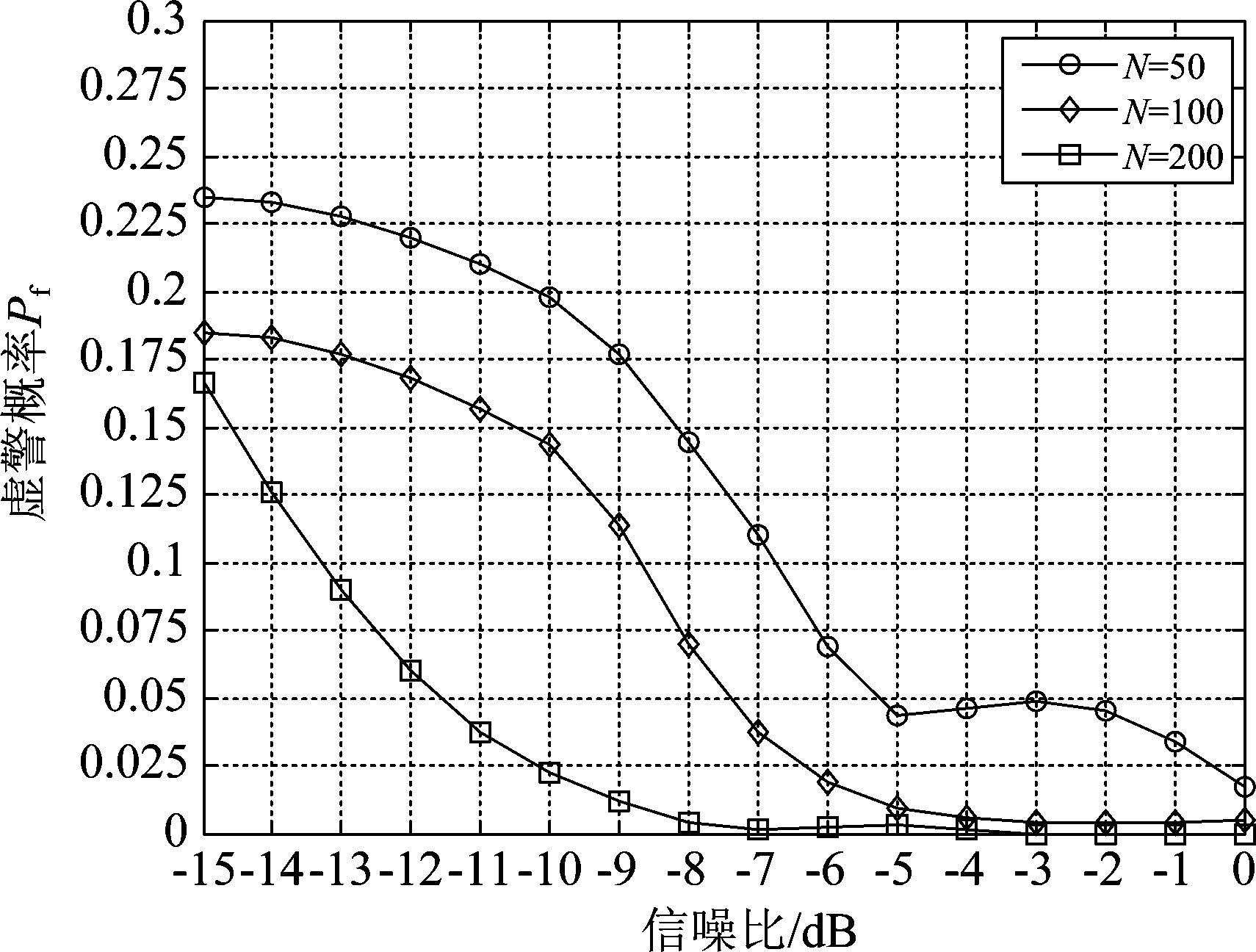
图5 不同采样点对虚警概率的影响
Fig.5 Influence of different sampling points on false alarm probability
传统的频谱感知算法,如提到的能量检测法和协作检测法,二者的检测性能前者比较依赖于检测门限的准确性,后者比较依赖在认知用户的数量,在检测门限不准确以及认知用户比较少时,系统的检测概率相对较低,检测性能将会很大受到影响。
本文中提出的基于图像的K-means聚类频谱感知算法则避免了上述方法的不足,在单用户检测时也能达到比较高的检测性能,通过对两种历史信号数据的训练学习,训练出分类器模型,利用该分类器从而实现频谱感知。模拟仿真实验也证明了该方法的可行性和较高的可靠性,且在相同虚警概率以及信噪比的情况下,该算法在检测性能上相较于传统频谱感知算法得到明显改善,并且检测性能随着采样点数的增加而提高,而虚警概率随着采样点数的增加而整体呈降低趋势。本文中在图像特征提取过程中用到图像处理方法,找到更有效的提取信号特征向量的方法以提高检测性能,减小图像处理的时间复杂度提供系统检测的实时性将是下一步工作的重点。
[1] Seshukumar K, Saravanan R, Suraj M S. Spectrum sensing review in cognitive radio[C]∥2013 International Conference on Emerging Trends in VLSI, Embedded System, Nano Electronics and Telecommunication System (ICEVENT). IEEE, 2013: 1- 4.
[2] 郭文祥, 余志勇, 逄晨, 等. 认知无线电频谱感知技术综述[J]. 通信技术, 2018, 51(2): 261-265.
Guo Wenxiang, Yu Zhiyong, Pang Chen, et al. Overview on Cognitive Radio Spectrum Sensing Technology[J]. Communications Technology, 2018, 51(2): 261-265.(in Chinese)
[3] Alom M Z, Godder T K, Morshed M N. A survey of spectrum sensing techniques in cognitive radio network[C]∥2015 International Conference on Advances in Electrical Engineering (ICAEE). IEEE, 2015: 161-164.
[4] Amrutha V, Karthikeyan K V. Spectrum sensing methodologies in cognitive radio networks: A survey[C]∥2017 International Conference on Innovations in Electrical, Electronics, Instrumentation and Media Technology (ICEEIMT). IEEE, 2017: 306-310.
[5] 姚迪, 刘会杰, 刘洁, 等. 基于支持向量机的认知无线电频谱感知[J]. 电子设计工程, 2018, 26(21): 1-5.
Yao Di, Liu Huijie, Liu Jie, et al. Support vector machine based spectrum sensing algorithm in cognitive radio[J]. Electronic Design Engineering, 2018, 26(21): 1-5.(in Chinese)
[6] Khan R T, Islam M I, Zaman S, et al. Comparison of cyclostationary and energy detection in cognitive radio network[C]∥2016 International Workshop on Computational Intelligence (IWCI). IEEE, 2016: 165-168.
[7] Salahdine F, El Ghazi H, Kaabouch N, et al. Matched filter detection with dynamic threshold for cognitive radio networks[C]∥2015 International Conference on Wireless Networks and Mobile Communications (WINCOM). IEEE, 2015: 1- 6.
[8] Cho D, Narieda S. A weighted diversity combining technique for cyclostationarity detection based spectrum sensing in cognitive radio networks[C]∥2015 IEEE 16th International Symposium on A World of Wireless, Mobile and Multimedia Networks (WoWMoM). IEEE, 2015: 1- 6.
[9] Rani R, Kumar K, Kumar R, et al. Evaluation of spectrum sensing process through energy detection technique[C]∥2017 International Conference on Computing and Communication Technologies for Smart Nation (IC3TSN). IEEE, 2017: 348-351.
[10] Ilyas I, Paul S, Rahman A, et al. Comparative evaluation of cyclostationary detection based cognitive spectrum sensing[C]∥2016 IEEE 7th Annual Ubiquitous Computing, Electronics & Mobile Communication Conference (UEMCON). IEEE, 2016: 1-7.
[11] Gupta M, Verma G, Dubey R K. Cooperative spectrum sensing for cognitive radio based on adaptive threshold[C]∥2016 Second International Conference on Computational Intelligence & Communication Technology (CICT). IEEE, 2016: 444- 448.
[12] 谢前英, 姚远程, 秦明伟. 基于集中式协作频谱感知的数据融合技术研究[J]. 微型机与应用, 2015, 34(12): 54-56, 60.
Xie Qianying, Yao Yuancheng, Qin Mingwei. Research of data fusion technologies based on centralized cooperative spectrum sensing[J]. Microcomputer & Its Applications, 2015, 34(12): 54-56, 60.(in Chinese)
[13] 许力, 黄毅杰, 林晖. 分布式协作频谱感知的信誉模型[J]. 北京邮电大学学报, 2015, 38(4): 53-57.
Xu Li, Huang Yijie, Lin Hui. Reputation Model for Distributed Collaborate Spectrum Sensing[J]. Journal of Beijing University of Posts and Telecommunications, 2015, 38(4): 53-57.(in Chinese)
[14] 刘乐. 协作频谱感知研究及其面临的问题和挑战[J]. 现代导航, 2019, 10(3): 223-227.
Liu Le. Cooperative Spectrum Sensing Research with Its Issues and Challenges[J]. Modern Navigation, 2019, 10(3): 223-227.(in Chinese)
[15] 岳文静, 郑宝玉, 孟庆民, 等. 衰落信道下提高协作频谱感知能力的方法[J]. 中国科学: 信息科学, 2011, 41(2): 207-218.
Yue Wenjing, Zheng Baoyu, Meng Qingmin, et al. Robust cooperative spectrum sensing schemes for fading channels in cognitive radio networks[J]. Scientia Sinica: Informationis, 2011, 41(2): 207-218.(in Chinese)
[16] Sun C, Wang Y, Wan P, et al. A cooperative spectrum sensing algorithm based on principal component analysis and K-medoids clustering[C]∥2018 33rd Youth Academic Annual Conference of Chinese Association of Automation (YAC). IEEE, 2018: 835- 839.
[17] Zhou R, Zhang Y, Sun X, et al. A cooperative spectrum sensing algorithm based on Bayesian compressed sensing[C]∥2017 3rd IEEE International Conference on Computer and Communications (ICCC). IEEE, 2017: 658- 662.
[18] 甄文奇. 基于多传感器的智能护理系统研究[D]. 南京理工大学, 2017.
Zhen Wenqi. Research on Intelligent Nursing System Based on Multisensor[D]. Nangjing University of Science & Technology, 2017.(in Chinese)
[19] Dehariya V K, Shrivastava S K, Jain R C. Clustering of image data set using k-means and fuzzy k-means algorithms[C]∥2010 International Conference on Computational Intelligence and Communication Networks. IEEE, 2010: 386-391.
[20] 张朝, 郭秀娟, 张坤鹏. K-means算法聚类中心选取[J]. 吉林大学学报: 信息科学版, 2019, 37(4): 437- 441.
Zhang Zhao, Guo Xiujuan, Zhang Kunpeng. Clustering Center Selection on K-means Clustering Algorithm[J]. Journal of Jilin University: Information Science Edition, 2019, 37(4): 437- 441.(in Chinese)
岳文静 女, 1982年生, 山西应县人。南京邮电大学通信与信息工程学院, 副教授, 硕士生导师, 主要研究方向为认知无线电网络、移动物联网、数据挖据。
E-mail: yuewj@njupt.edu.cn
刘文博 男, 1996年生, 河南鹿邑县人。南京邮电大学研究生, 研究方向为频谱感知、认知无线电网络等。
E-mail: 15603828297@163.com
陈 志(通讯作者) 男, 1978年生, 江苏淮安人。南京邮电大学计算机学院、软件学院、网络空间安全学院, 教授, 硕士生导师, 主要研究方向为移动物联网、无线传感器网络、软件工程、数据挖据。
E-mail: chenz@njupt.edu.cn