为了满足移动数据流量的急剧增长,未来无线通信系统需要具有更高的频谱效率和信道容量。带内全双工(In-Band Full-Duplex, IBFD)技术,使得通信设备可以在同一频谱资源上同时收发信号,理论上具有倍增频谱效率的潜力[1- 4]。由于同时同频收发信号,发射信号会在本地接收机处产生极强的自干扰(Self-interference, SI),其功率相比远端接收信号高出约99 dB[2]。因此,远端信号的可靠接收需要高效的自干扰抑制,先进的自干扰信号处理是发挥IBFD技术优势的关键。
现有自干扰抵消技术,根据其信号处理所处功能域,可以分为三类:天线域、模拟域和数字域自干扰抵消技术。由于受到接收机前端非线性器件影响,以及模数转换器(ADC)动态范围限制,一般认为,自干扰应在天线域和模拟域(射频域)进行抵消[5]。模拟域抵消电路结构包括:多抽头模拟抵消电路和数字域协助抵消电路[6-7]。多抽头抵消电路中,从发射机前端耦合的发射信号,经过多条支路对其时延、幅度和相位进行调整,再结合产生抵消信号。该方法可在发射机前端非线性器件之后耦合发射信号,有利于捕获自干扰信号中的非线性成分,但其抵消能力受限于抽头个数。理论上,抽头数量越多抵消效果越好,但过多的抽头数会极大地增加电路和控制算法的复杂度。
数字域协助的抵消方法,在数字域利用滤波器产生抵消参数,再反馈到模拟电路域进行抵消。该方法的优点是,数字滤波器系数可调并且阶数可以达到很大,技术关键是如何抵消自干扰信号所携带的噪声和非线性成分。
文献[8]采用16抽头的模拟抵消电路,可以抵消自干扰中的多径分量,并对80 MHz宽带信号获得了60 dB的抵消效果,但如此多的抽头数量极大地增加了抵消电路的复杂度和功耗。为了在保证抵消能力的同时减少抽头数量,文献[9]提出一种闭环数字调节的射频域抵消结构,将抵消电路抽头数减少到3个。实验测得,对于80 MHz的宽带自干扰信号可以抵消41 dB,但其所使用的闭环控制结构较为复杂,并且是非线性结构。
文献[10]采用数字域协助的抵消方法,需要额外的发射链路产生抵消信号。在数字域进行信号处理可以降低电路复杂度,但数字域的信道模型未考虑发射端非线性因素的影响,因此抵消性能受限。为此,文献[5- 6,11]在数字域引入非线性信道模型,以达到抵消自干扰中非线性成分的目的。
为了进一步提高模拟域抵消能力,文献[12]和[13]提出一种两阶段(two-stage)模拟域抵消结构,结合使用模拟域多抽头电路和数字域协助电路。多抽头电路采用较少的支路数,仅抵消直射径和强反射径自干扰分量;数字域协助电路用于抵消多径自干扰分量。相比于[12],文献[13]在数字域采用非线性模型,在抵消多径分量的同时还可以抵消非线性成分,抵消性能更优。
本文提出一种基于分段反变换法(Segment Inverse Transform Method, SITM)的数字域协助抵消方法,针对自干扰中由环境散射产生的多径分量进行消除。该方法根据瑞利衰落模型,利用SITM直接产生数字抵消信号,再转换到模拟域进行抵消。相比文献[12]和[13]的方案,该方法无需对自干扰信道进行估计或建立非线性模型,使抵消电路和控制算法得到简化。此外,本文方案可以结合使用文献[12]中的单抽头抵消电路,先对直射路径干扰进行抵消,可获得更好的抵消效果。
带内全双工系统的收发机结构如图1所示,xs(t)为本地发射信号,通过分离天线或共用天线辐射出去,yr(t)为本地接收机收到的远端信号。若采用共用天线结构,需要借助环形器实现单天线收发信号。由于收发天线间距离很近、环形器隔离度有限,本地发射信号通过天线间耦合或环形器耦合直接进入接收机,形成直射路径自干扰ydp(t)。此外,发射信号受到环境中反射物影响,形成多径自干扰ymp(t)。因此,近端接收机的接收信号可以表示为
ys(t)=yr(t)+ydp(t)+ymp(t)+n(t)
(1)
式中,n(t)为接收机处噪声信号。
根据文献[12],多径信道可以表示为
(2)
式中,M为多径数,hi和τi分别表示第i条路径的信道增益和时延。因此,多径自干扰可以表示为
(3)
图1中,模拟域自干扰抵消包括两部分:单抽头抵消电路和本文所提方案(虚线框内结构)。单抽头抵消电路只对直射路径自干扰进行抵消,可采用文献[12]中的单抽头抵消电路;本文方案用于抵消多径自干扰,根据瑞利分布模型,采用SITM直接产生抵消信号,无需耦合本地发射信号、估计信道,结构较为简单。接收信号经过模拟域自干扰抵消后,可以表示为
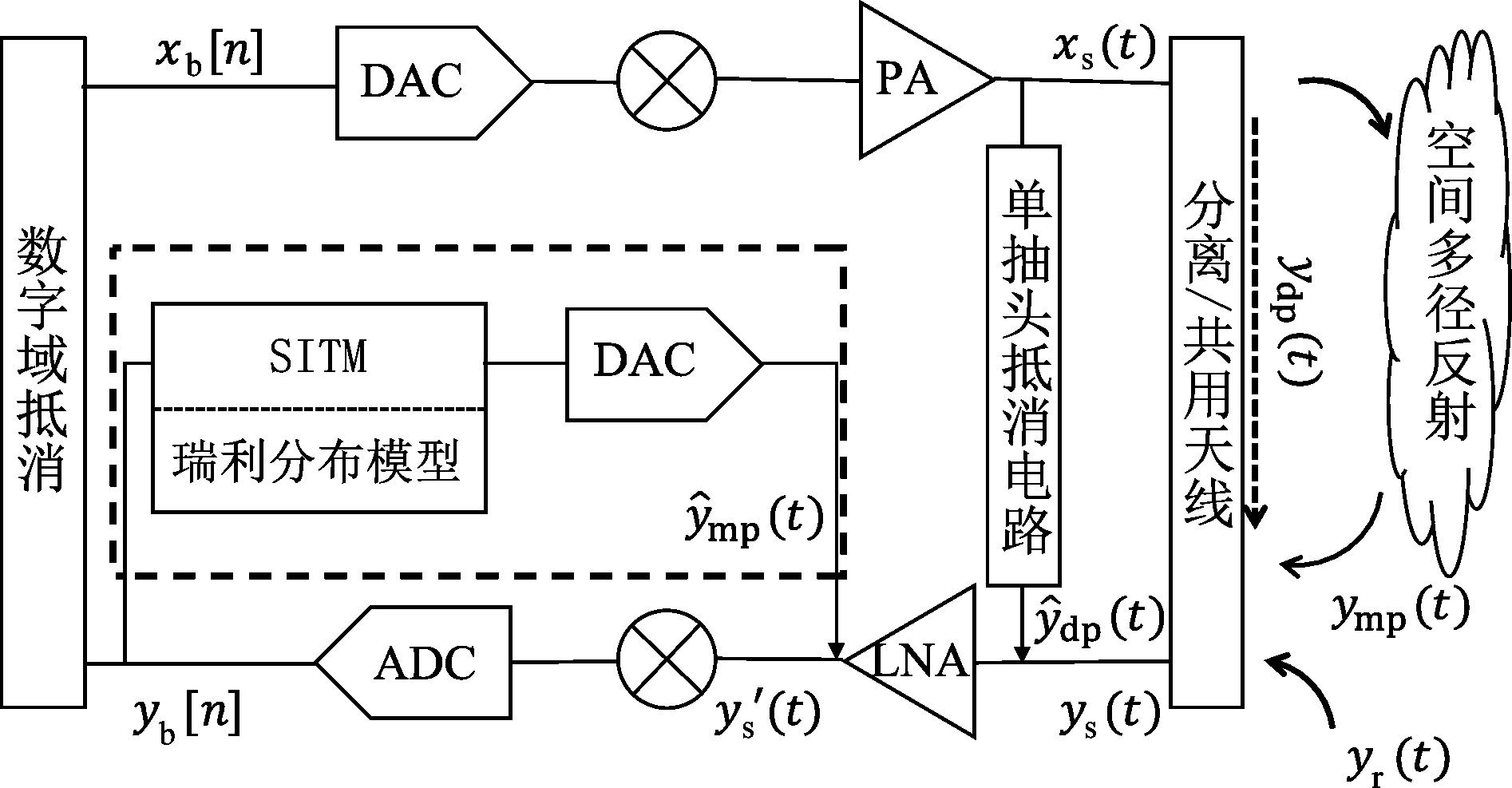
图1 全双工收发机结构示意图
Fig.1 Block diagram of full-duplex transceiver
(4)
式中,
为直射径自干扰抵消信号,
为多径自干扰抵消信号。
本文定义所提方案的自干扰抵消能力为
(5)
进行自干扰抵消后的接收信干比为
(6)
反变换法(Inverse Transform Method, ITM)是产生瑞利信号的常用方法[14-15]。反变换法是利用累积分布函数(cumulative distribution function, CDF)的反函数来产生具有某一类分布特征的随机变量的方法。
假设X是一个随机变量,其概率密度函数(probability density function, PDF)为fX(x),累积分布函数为FX(x)。如果FX(x)是一个非减函数,则其反函数定义为
0≤y≤1
(7)
如果y服从[0,1]之间的均匀分布,那么由式(7)产生的x,其概率密度函数服从fX(x)。利用反变换法产生具有某类分布特征的随机变量的前提是:该累积分布函数的反函数必须存在。
利用ITM产生瑞利信号。瑞利分布的概率密度函数为
(8)
式中,σ是参数,且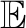
[r2]=2σ2。其累积分布函数为
(9)
因此,其累积分布函数的反函数存在,为
(10)
令F(r;σ)服从[0,1]均匀分布,则由式(10)产生的r服从瑞利分布。
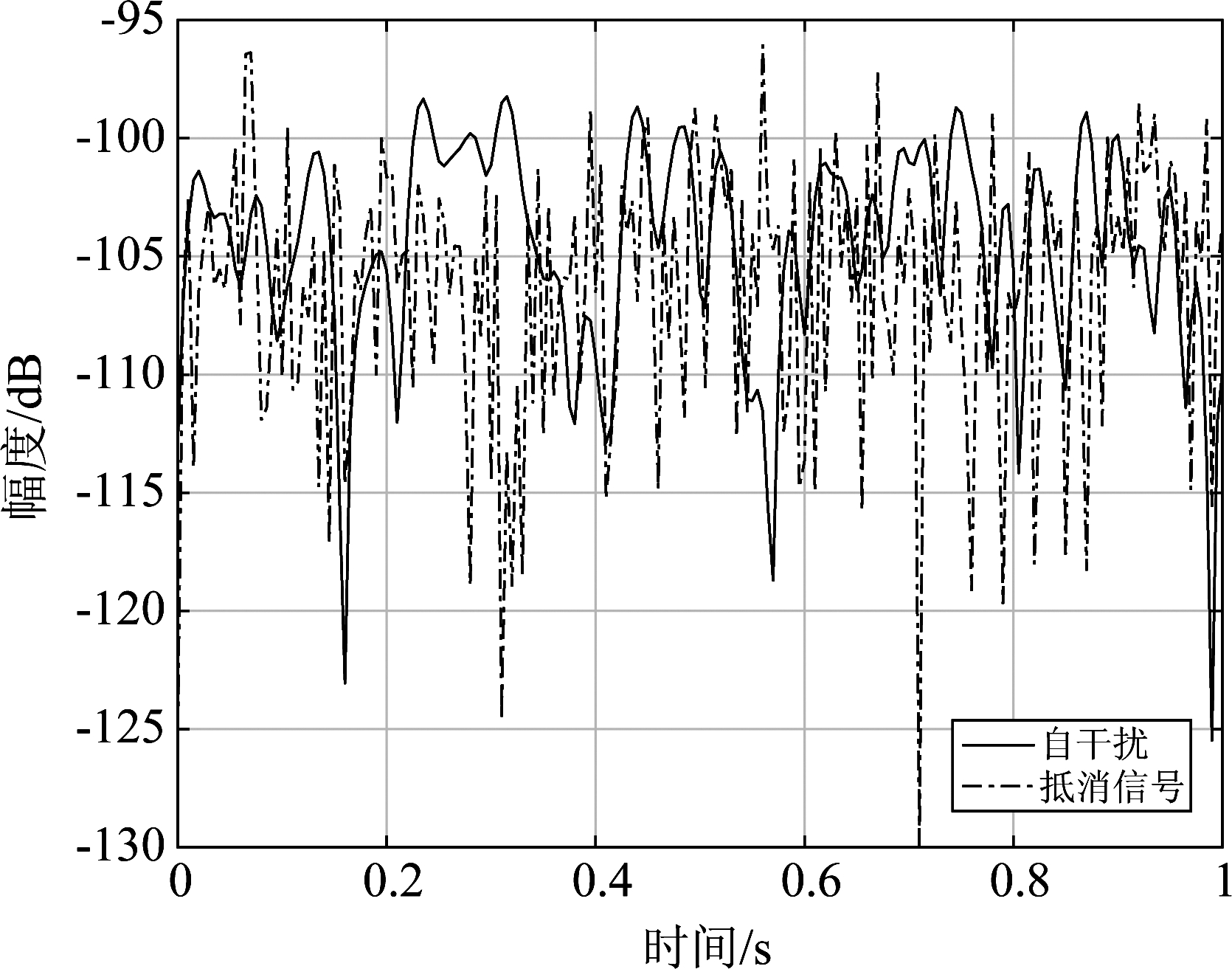
图2 自干扰信号与抵消信号比较(ITM)
Fig.2 Comparison of the SI signal and the cancellation signal generated by ITM
用ITM产生的抵消信号如图2所示,其衰落特性与实际信号相差较大。原因是,反变换法利用瑞利分布的反函数,仅包含跟幅度(功率)相关的参数σ,虽然能产生具有瑞利分布特征的信号,但对于特定的信号,不能很好地反映其衰落特性的细节,比如衰落快慢等。因此,下节提出一种改进ITM的方法——分段反变换法(SITM)。
为了使重构的自干扰信号能更加接近实际自干扰信号,以提高抵消效果,本文改进ITM,先根据幅度阈值对自干扰信号进行分段,估计相应的抵消参数,再利用抵消参数产生抵消信号,改进后的方法命名为分段反变换方法(SITM)。
电平通过率(level cross rate, LCR)是衡量瑞利信号衰落快慢的二阶统计量,它代表单位时间内信号幅度沿正向或反向穿越某个阈值的次数[16]。参考LCR,本文引入电平通过时间集(level cross time set, LCTS),定为信号沿正向和反向穿越某个幅度阈值的瞬时时刻的集合。SITM根据该时间集合对原始自干扰信号进行分段,估计各段信号的抵消参数,用于后续产生相应的抵消信号。
值得一提的是,抵消参数的估计可以在帧间间隙(inter-frame space, IFS)进行[17]。在该段时间内没有对端来的有用信号,通信终端可以发射训练信号,并接收该信号进行自干扰信道估计。此外,对于移动通信环境,认为抵消参数的有效性可以持续一个帧周期是合理的。以LTE信号为例,它的帧长为10 ms,若移动终端产生的最大多普勒频率为100 Hz(即移动速度为45 km/h),在一帧的时间内它移动的距离为0.125 m,这意味着在一个帧周期内,周围环境变化不明显。
以下对SITM具体实现步骤进行阐述,以设置2个幅度阈值为例:
Step 1 对某段自干扰信号R(t)(t∈[0,T]),设置2个幅度阈值,分别为
和
设置时间阈值tmth,用于控制信号分段的最短时长。
Step 2 根据幅度阈值得到两个LCTS时间集,分别为T1={t11,t12,…,t1m1}和T2={t21,t22,…,t2m2}(m1、m2分别为集合中元素个数)。
Step 3 合并时间集T1、T2,并加入起始和结束时刻,得到时间集合Ttot=T1∪T2∪{0,T};对Ttot中元素进行从小到大排序,得到Ttot={t0,t1,t2,…,tm1+m2,tm1+m2+1},下标表示元素在集合中的顺序号。
Step 4 计算每个时间段[ti,ti+1] (i∈{0,1,…,m1+m2})的长度li,如果li小于时间阈值tmth,则在时间集合Ttot中删去ti。最后得到更新的时间集合Ttot={t0,t1,t2,…,tm3}(0<m3≤m1+m2+1)。
Step 5 计算每个时间段[ti,ti+1] (i∈{0,1,…,m3-1})内信号幅度的均值和标准差,如下
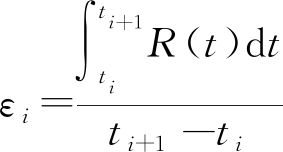
(11)
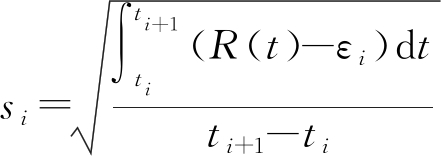
(12)
Step 6 根据每段信号的均值εi和标准差si(i∈{0,1,…,m3-1}),计算产生第i段抵消信号的累积分布函数的分布范围,
(13)
(14)
Step 7 产生第i (i∈{0,1,…,m3-1})段抵消信号
(15)
式中,F(r;σ)服从
上均匀分布,σ的值可以利用导频信号估计得到。
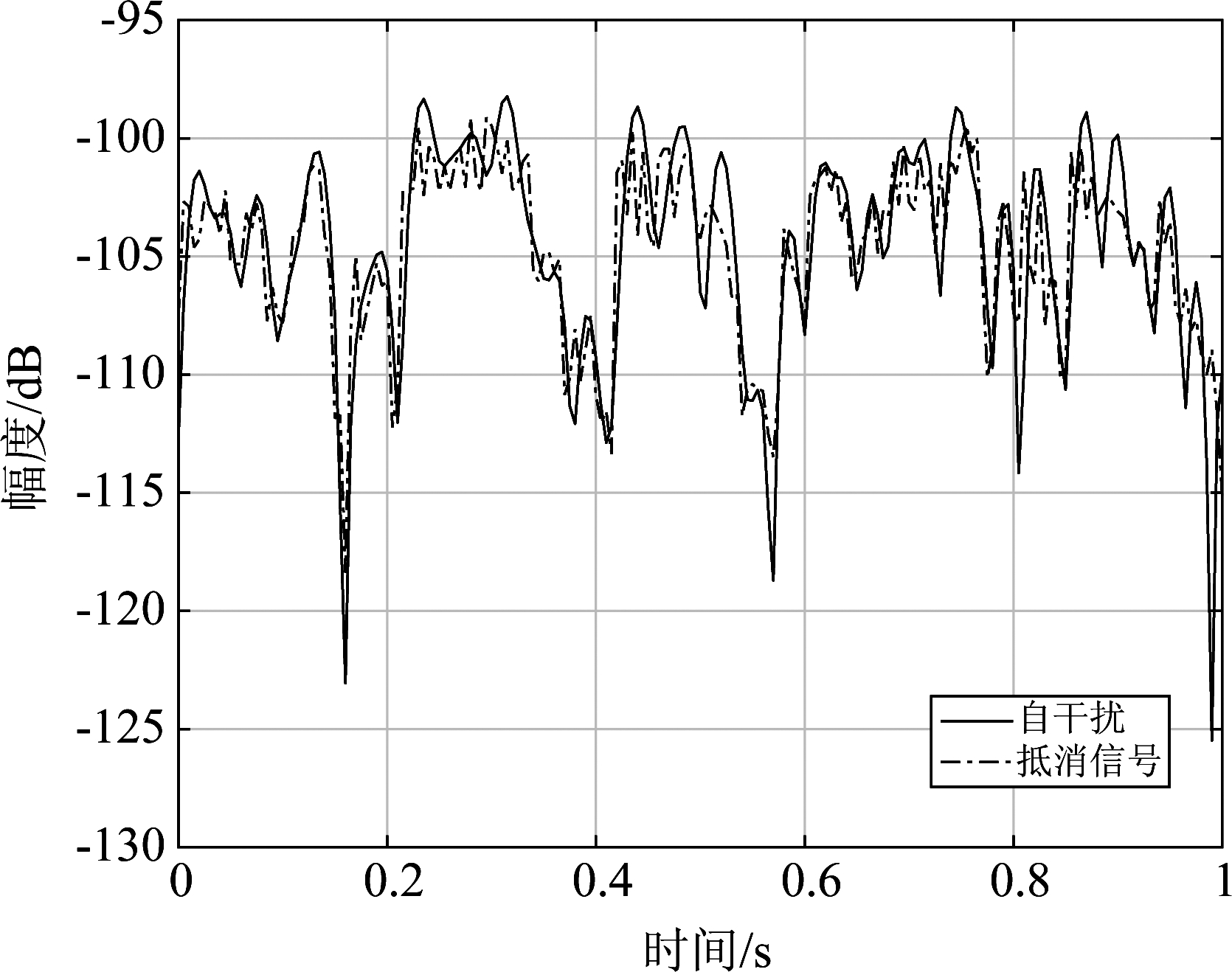
图3 自干扰信号与抵消信号比较(SITM)
Fig.3 Comparison of the SI signal and the cancellation signal generated by SITM
用SITM产生的抵消信号如图3所示。与ITM相比,SITM产生的抵消信号与实际信号相似程度更高,能更好地反映实际信号的衰落特性。
SITM产生的抵消信号更接近于实际自干扰信号,主要原因是,通过设置幅度阈值得到的LCTS与信号衰落频率有关,此外,根据时间分段估计信号功率,可以更好地确定衰落所处的时间范围。这些措施能更好地捕获原自干扰信号衰落特性的细节。因此,相比于用ITM直接根据整段信号的平均功率来产生估计信号,用SITM产生的估计信号与实际信号更加接近。
为验证本文所提抵消方法——SITM的有效性,本节进行无线多径信道场景下,全双工系统自干扰抵消的数值仿真实验。仿真中采用的多径信道模型为文献[18]中的椭圆模型,该模型可以通过改变空间反射体数量(即为多径数)和移动台运动速度(影响最大多普勒频移)来改变信道条件。本节研究不同信道条件和不同参数设置对SITM抵消性能的影响;同时,在本文仿真条件下,也对文献[12]方案的抵消能力进行计算,并与SITM比较。值得一提的是,尽管文献[13]中第二阶段的抵消方法也能抵消多径自干扰,但其总体抵消能力还包含了部分非线性成分的抵消,因此本文只将SITM的抵消性能与文献[12]方案进行比较。
由于文献[12]中没有对其实验参数进行明确阐述,但文献[13]给出了详细的实验参数,并对[12]和[13]两种方法的抵消能力都进行了测试,因此列出文献[13]中的实验参数和实验结果(表1),以便于与本文仿真参数和仿真结果(表2)进行直观的比较。表2中的抵消能力是根据4.1节中的仿真结果计算得到的平均值。
表1 文献实验参数和结果
Tab.1 Experimental parameters and results in the reference
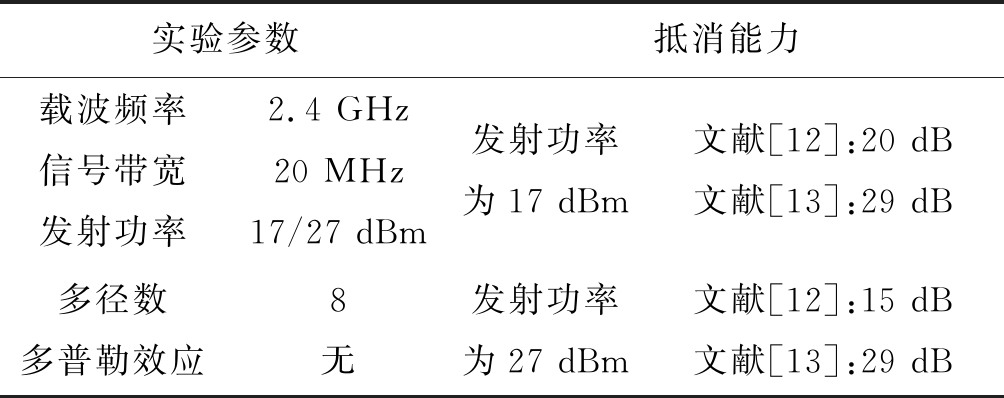
实验参数抵消能力载波频率信号带宽发射功率2.4 GHz20 MHz17/27 dBm发射功率为17 dBm文献[12]:20 dB文献[13]:29 dB多径数多普勒效应8无发射功率为27 dBm文献[12]:15 dB文献[13]:29 dB
表2 本文仿真参数和结果
Tab.2 Simulation parameters and results in this paper
仿真参数抵消能力载波频率信号带宽发射功率2.4 GHz20 MHz20 dBm文献[12]10.2 dB多径数多普勒效应10～5010～100 Hz文本方案14.2 dB
为了研究最大多普勒频率和多径数对SITM抵消性能和接收信干比的影响,分别改变信道最大多普勒频移和多径数量,其他参数保持不变,进行仿真实验。仿真结果如图4、图5所示。
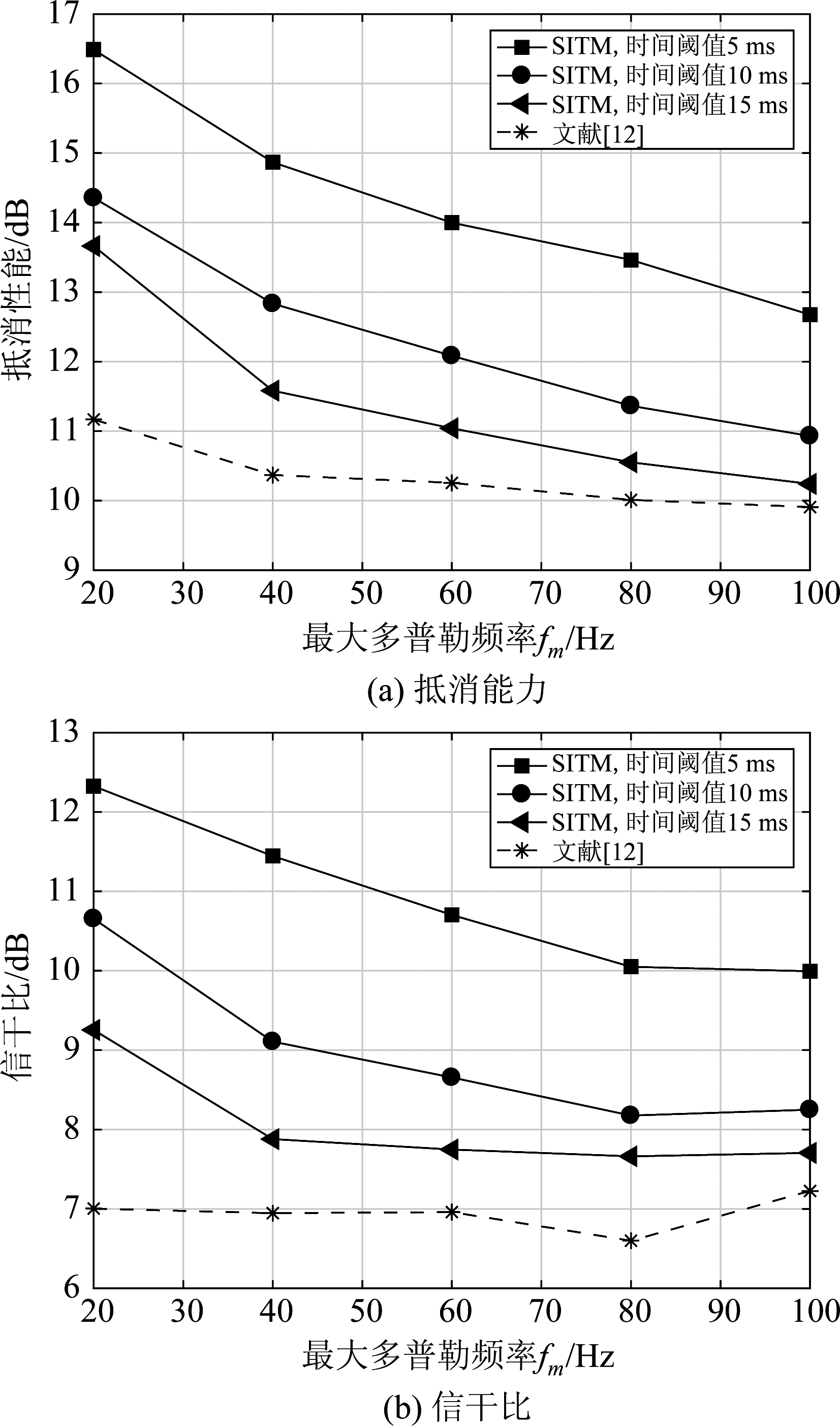
图4 最大多普勒频移对抵消性能和信干比影响
Fig.4 Impact of the maximum Doppler frequency on cancellation capability and signal-to-interference ratio
图4(a)、(b)分别是两种方案抵消性能以及接收信干比随最大多普勒频率变化曲线,仿真多径数为20。观察图(a)可知,随着最大多普勒频率(fm)增大,SITM抵消性能有明显下降;文献[12]抵消性能受最大多普勒频率影响较小,但始终低于SITM。此外,当时间阈值较小时,本文方案优势更明显,自干扰抵消性能最多可高出约5.3 dB。图(b)中,接收信干比的变化趋势与抵消能力的变化基本一致,在SITM方法下得到的信干比始终高于文献[12]方法,最多有5.3 dB的性能增益。
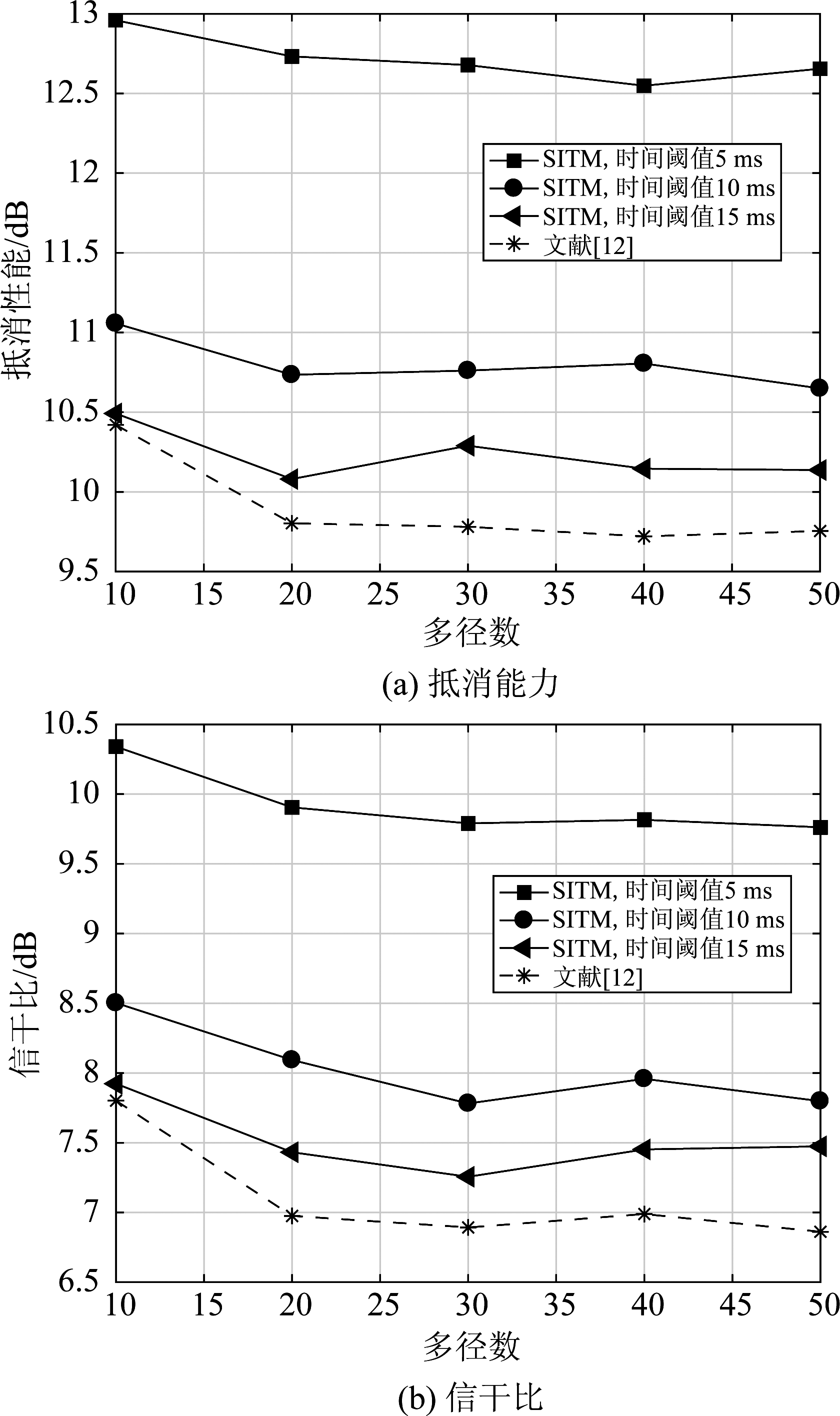
图5 多径数对抵消性能和信干比影响
Fig.5 Impact of the number of multiple paths on cancellation capability and signal-to-interference ratio
图5(a)、(b)分别是抵消性能以及接收信干比随多径数变化曲线,最大多普勒频率为100 Hz。从图(a)中可以看出,文献[12]抵消性能随多径数增加而下降。而对于SITM,当时间阈值小于15 ms时,其性能基本不受多径数影响;当时间阈值为15 ms时,其抵消性能不稳定。总体来看,SITM抵消性能优于文献[12],当时间阈值为5 ms时,抵消结果高出2.6 dB。在图(b)中,当多径数大于20时,多径数变化基本不影响接收信干比。同样地,使用SITM方法,当时间阈值设置较小时,接收信干比可以获得2～3 dB的增益。
为了研究算法参数设置对SITM抵消性能的影响,包括时间阈值的大小和幅度阈值的数量,改变仿真过程中SITM的参数,进行仿真实验。
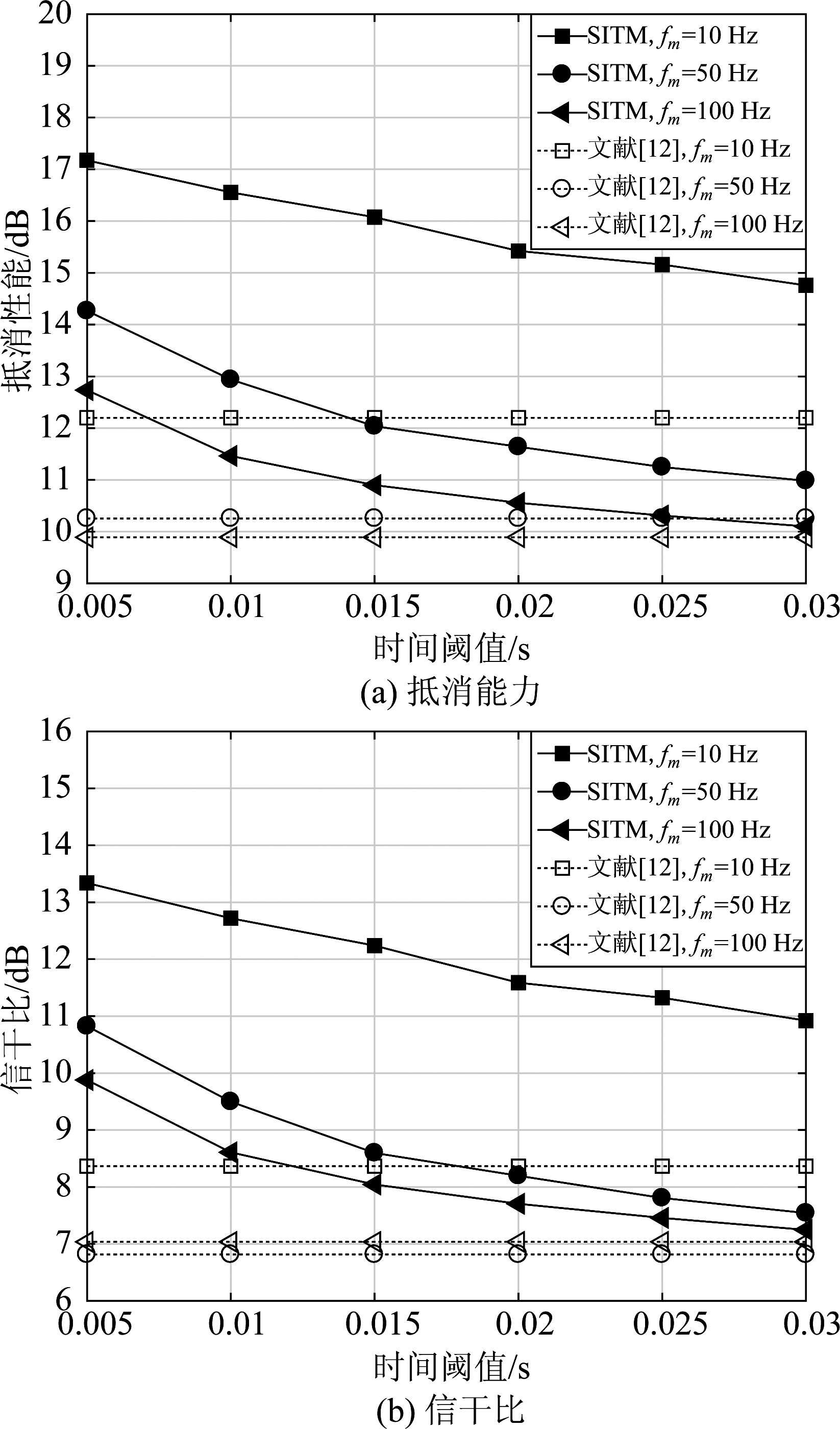
图6 时间阈值对抵消性能和信干比影响
Fig.6 Impact of the time threshold on cancellation capability and signal-to-interference ratio
图6(a)、(b)描绘了两种方案抵消性能以及接收信干比随时间阈值变化曲线,多径数为20。由图(a)可知,文献方案不受时间阈值影响,而SITM抵消性能随时间阈值增大而下降。时间阈值设置越小,SITM抵消效果越好,最多可比文献[12]高出5 dB。但是,当时间阈值为30 ms,最大多普勒频率为100 Hz时,SITM抵消性能与文献[12]基本相同。此外,图(b)所示的接收信干比的变化趋势与抵消能力的变化一致,当时间阈值和最大多普勒频率都较小时,采用SITM抵消方法,接收信干比可以有5 dB的增益。
图7给出了2幅度阈值和3幅度阈值情况下,SITM产生的抵消信号和实际自干扰信号的比较图(多径数为50)。从图中可以看出,设置3个幅度阈值时,产生的抵消信号在信号深衰处(虚线圈出)与实际信号更接近。因此,适当增加幅度阈值的数量有利于提高SITM抵消性能。
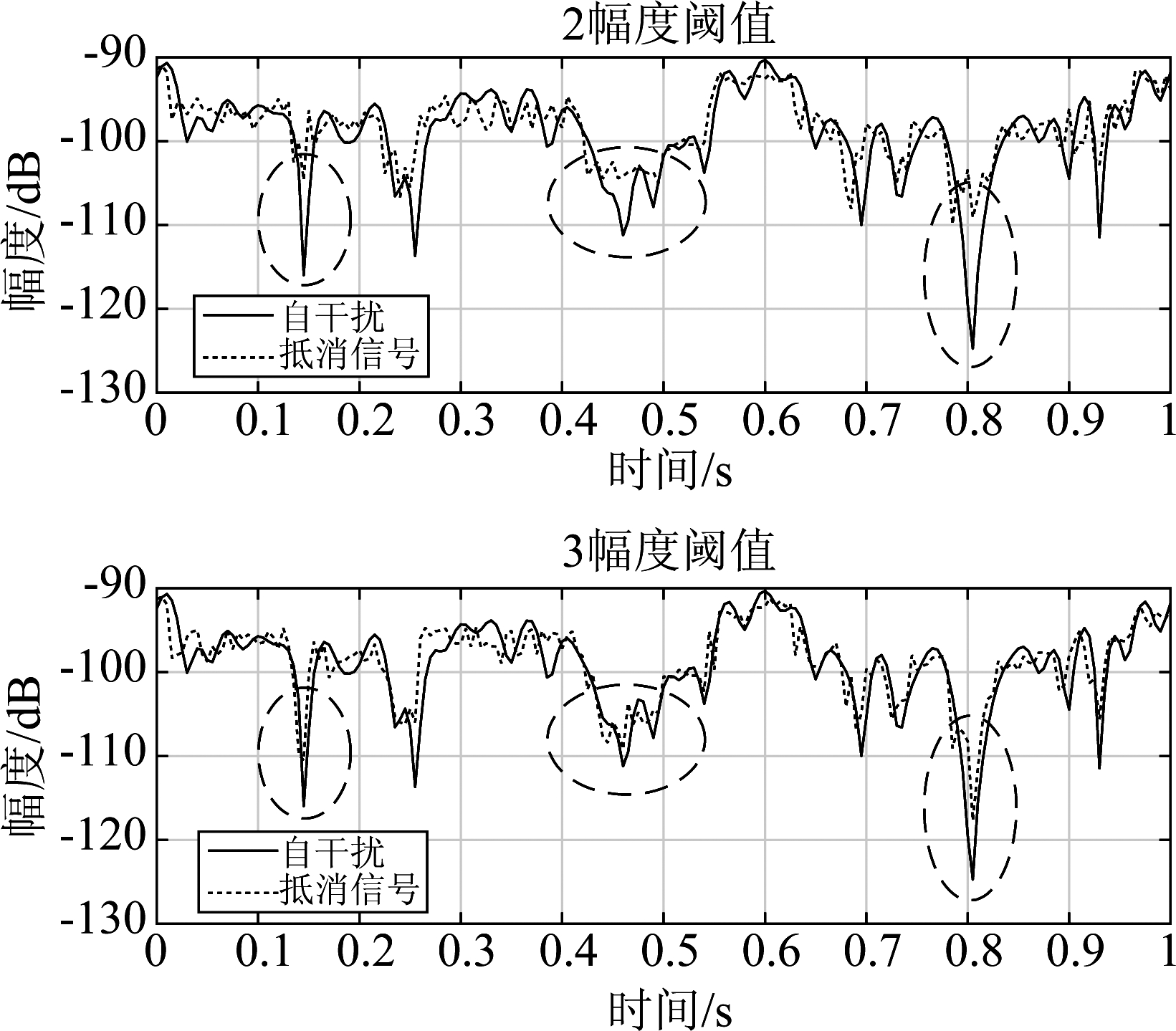
图7 幅度阈值数量对抵消性能影响
Fig.7 Impact of the number of amplitude thresholds on cancellation capability
本文提出了一种适用于全双工设备在无线多径环境下的模拟域自干扰抵消方法,该方法基于瑞利分布模型,利用SITM直接产生数字域抵消参数,并通过额外的发射链路将抵消信号转换到模拟域进行自干扰消除。相比于其他数字域协助的模拟域抵消方案,本文方案无需在数字域建立复杂的信道模型、估计信道参数,也不需要耦合发射端信号,结构上得到了简化。仿真结果显示,在最大多普勒频率和时间阈值都较小的情况下,本方案相比于文献[12]有5 dB的性能增益。此外,本方案抵消性能受传播路径数的影响较小,基本不随路径数增加而明显下降。为了获得更大数量的抵消,本文所提方案还可以结合文献[12]和[13]中结构较为简单的多抽头模拟抵消电路,先对直射路径干扰和强反射径干扰进行抵消。
[1] Sabharwal A, Schniter P, Guo Dongning, et al. In-band full-duplex wireless: challenges and opportunities[J]. IEEE Journal on Selected Areas in Communications, 2014, 32(9): 1637-1652.
[2] Kim D, Lee H, Hong D. A survey of in-band full-duplex transmission: from the perspective of PHY and MAC layers[J]. IEEE Communications Surveys & Tutorials, 2015, 17(4): 2017-2046.
[3] Liu Gang, Yu F R, Ji Hong, et al. In-band full-duplex relaying: a survey, research issues and challenges[J]. IEEE Communications Surveys & Tutorials, 2015, 17(2): 500-524.
[4] Kolodziej K E, Perry B T, Herd J S. In-band full-duplex technology: techniques and systems survey[J]. IEEE Transactions on Microwave Theory and Techniques, 2019, 67(7): 3025-3041.
[5] Ge Songhu, Meng Jin, Xing Jinling, et al. Digital-domain assisted RF cancellation of nonlinear wideband self-interference for co-site wireless communication systems[C]∥2018 IEEE International Symposium on Electromagnetic Compatibility and 2018 IEEE Asia-Pacific Symposium on Electromagnetic Compatibility (EMC/APEMC), Singapore, 2018: 98-103.
[6] Liu Ying, Quan Xin, Pan Wensheng, et al. Digitally assisted analog interference cancellation for in-band full-duplex radios[J]. IEEE Communications Letters, 2017, 21(5): 1079-1082.
[7] 邹亚州, 向新, 张婧怡. 全双工射频自干扰改进时变步长NLMS对消算法[J]. 信号处理, 2017, 33(10): 1360-1367.
Zou Yazhou, Xiang Xin, Zhang Jingyi. Improved time-varying step-size NLMS algorithm for RF self-interference cancellation in full-duplex[J]. Journal of Signal Processing, 2017, 33(10): 1360-1367.(in Chinese)
[8] Bharadia D, McMilin E, Katti S. Full duplex radios[J]. ACM SIGCOMM Computer Communication Review, 2013, 43(4): 375-386.
[9] Tamminen J, Turunen M, Korpi D, et al. Digitally-controlled RF self-interference canceller for full-duplex radios[C]∥2016 24th European Signal Processing Conference (EUSIPCO), Budapest, 2016: 783-787.
[10] Duarte M, Dick C, Sabharwal A. Experiment-driven characterization of full-duplex wireless systems[J]. IEEE Transactions on Wireless Communications, 2012, 11(12): 4296-4307.
[11] Kiayani A, Anttila L, Valkama M. Active RF cancellation of nonlinear TX leakage in FDD transceivers[C]∥2016 IEEE Global Conference on Signal and Information Processing (GlobalSIP), Washington, DC, 2016: 689- 693.
[12] Quan Xin, Liu Ying, Pan Wensheng, et al. A two-stage analog cancellation architecture for self-interference suppression in full-duplex communications[C]∥2017 IEEE MTT-S International Microwave Symposium (IMS), Honololu, HI, 2017: 1169-1172.
[13] Liu Ying, Roblin P, Quan Xin, et al. A full-duplex transceiver with two-stage analog cancellations for multipath self-interference[J]. IEEE Transactions on Microwave Theory and Techniques, 2017, 65(12): 5263-5273.
[14] Gomez-Deniz E, Gomez-Deniz L. A generalisation of the Rayleigh distribution with applications in wireless fading channels[J]. Wireless Communications and Mobile Computing, 2013, 13(1): 85-94.
[15] Rubinstein R. Simulation and the Monte Carlo method [M]. New York: John Wiley & Sons, 1981.
[16] Stüber G L. Principles of mobile communication [M]. New York: Springer, 2012.
[17] Li Yunxin. Blind SNR estimation of OFDM signals[C]∥2010 International Conference on Microwave and Millimeter Wave Technilogy, Chengdu, 2010: 1792-1796.
[18] Wu Wei, Zhuang Jincheng, Wang Wennai, et al. Geometry-based statistical channel models of reflected-path self-Interference in full-duplex wireless[J]. IEEE Access, 2019, 7: 48778- 48791.
吴 炜 女, 1993年生, 江苏常州人。南京邮电大学通信与信息工程学院博士研究生, 主要研究方向为宽带无线通信、下一代无线网络等。
E-mail: 2017010205@njupt.edu.cn
王文鼐 男, 1966年生, 江苏南京人。南京邮电大学通信与信息工程学院教授, 博士生导师, 主要研究方向为无线通信、网络工程等。
E-mail: wangwn@njupt.edu.cn
王 斌 男, 1970年生, 江西景德镇人。南京邮电大学通信与信息工程学院副教授, 硕士生导师, 主要研究方向为网络虚拟化、交换和路由技术、无线通信、网络编码等。
E-mail: wangbin7062@sohu.com