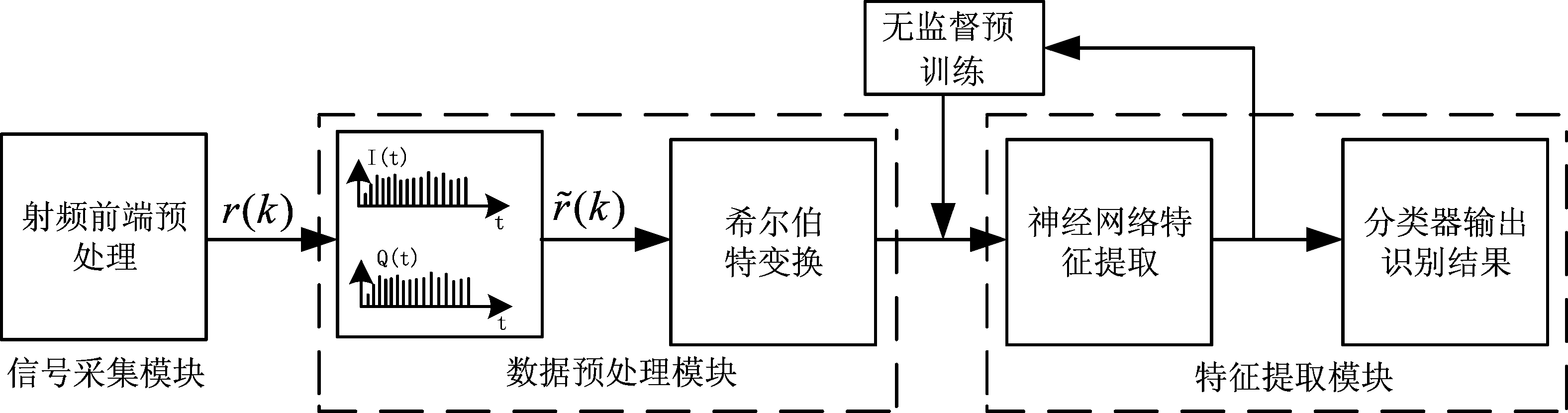
图1 自动调制识别分类模型框架
Fig.1 Classification model framework of automatic modulation recognition
通信信号的自动调制样式识别技术是信息侦察、通信对抗、电磁频谱监控、认知无线电领域的重要技术之一。传统自动调制识别主要分为决策判决和统计模式识别理论,统计模式识别框架下,根据专家经验利用特征工程构造特征,这方面国内外学者提出了很多调制信号特征工程的构造算法,有基于最大似然[1]、短时Fourier变换和小波变换[2,4-5]、高阶累积量[3-6]方法。这些算法主要针对特定调制方式,通过建立假设噪声的信号模型,从时域、频域或时频域[7]构造特征参数。这类方法的优点是建模准确,针对特定调制方式识别精度高,但算法受实际环境不确定因素影响很难匹配到预定特征空间,无法满足稳定的识别精度,而且存在判决门限不好设置、特征参数固定,特征数量受计算资源制约等不足。随着5G和物联网兴起,电磁空间信号样式日益复杂。因此,寻求一种适用范围更广、特征提取更加智能的方法是目前亟待解决的问题。
自动调制识别领域,人工神经网络(artificial neural network, ANN)最早被用来设计调制信号分类器[4- 6,8],随着深度学习算法在图像及自然语言等复杂对象特征提取方面取得重大突破,神经网络特征提取潜力被发掘出来,尤其在信号处理领域应用更为广泛。Tim O’Shea的文献[9]首次展示了浅层卷积神经网络对通信调制信号的识别能力。文献[10-11]使用深层卷积神经网络框架VGG(Visual Geometry Group)和残差神经网络(Deep residual network, ResNet)将识别数目提升到24种。文献[12]提出将长短期记忆神经网络(LSTM)[13]通过分布式计算部署在实时低功耗调制样式识别硬件平台上。以上文献均在有监督学习框架下进行,本文将考虑通过无监督学习实现小样本条件下调制识别任务。
无监督预训练[14]方法充分利用无标签样本为深层网络寻找最佳解空间,以达到更好的训练效果。对于调制信号识别任务,实际环境中可以获得大量未标记样本,这些样本通过人工标注代价过高,往往无法充分利用。传统无监督预训练使用在全链接结构的自编码器上,新型网络架构由于应用批归一化(Batch Normalization, BN)算法[15]、层归一化算法[16]、快捷连接[17]等新型深度学习技术,缓解了反向传播遇到的梯度弥散和梯度爆炸问题,但这些网络只能在有监督条件下训练。本文将无监督对比预测编码网络(Contrastive Predictive Coding, CPC)[18-19]应用于联合神经网络调制信号分类任务中,通过大量无标签数据预训练模型,初始化网络参数,再通过有监督学习微调网络参数训练分类器。经实验验证该方法可以有效减少对有标签数据的需求,提高网络训练速度,并获得更好的识别精度。
数据预处理是基于深度学习调制信号识别的常用方法,其中通过时频变换转为时频图再经过卷积神经网络[20-21]取得了较好效果,但同时增加了信号处理计算量。幅度、相位、频率是任何调制方式直接作用的对象,蕴藏着不同调制方式的细微差别。本文采用保留信号序列特征,通过希尔伯特变换(Hilbert Transform,HT)构造调制信号幅度、相位和频率瞬时参数作为训练数据。再通过设计联合神经网络映射原始信号到高维空间的特征表达,高维空间特征更能体现信号语义信息,能够更好的区分低维空间无法分离的信号,在抗噪声方面也有一定作用。经实验验证该方法具有低信噪比条件识别能力,有效识别调制种类数量明显多于传统人工特征提取方法并且具有极强的识别扩展能力。为减轻设备资源消耗,缓解系统设计复杂度和数据存储压力提供支持。
调制识别模型框架如图1所示。
图1 自动调制识别分类模型框架
Fig.1 Classification model framework of automatic modulation recognition
射频前端模块混频降采样得到中频/视频信号,经A/D变换得到离散化信号r(k),再通过加窗处理截取有限点数。记符号速率为RbBaud,采样速率SbHz,单位时间采样信号序列长度N=Rb×Sb。
数据预处理模块通过希尔伯特变换计算信号的瞬时参数构成训练序列。首先信号采集模块输出r(k)经希尔伯特变换得到
再构造解析信号
调制信号瞬时参数计算分别表示为:
瞬时幅度:
(1)
瞬时相位:
(2)
瞬时频率: f(k)=(φk-φk-1)Sb
(3)
数据预处理模块的另一功能是消除数值绝对大小带来的计算负担,因为神经网络系统学习数值间的相对变化关系,对数值的绝对大小并不敏感,所以对参数做归一化处理。根据范数理论,幅度向量经L2正则化为:
(4)
相位弧度值经归一化为:
θ∈(-p,p)→[-1,1]
(5)
瞬时频率经归一化为:
f∈(fmin, fmax)→[-1,1]
(6)
将瞬时幅度、相位、频率三者构成的3×N维矩阵记作D,作为神经网络的输入,N为一个训练样本的序列长度。
2.3.1 长短期记忆神经网络
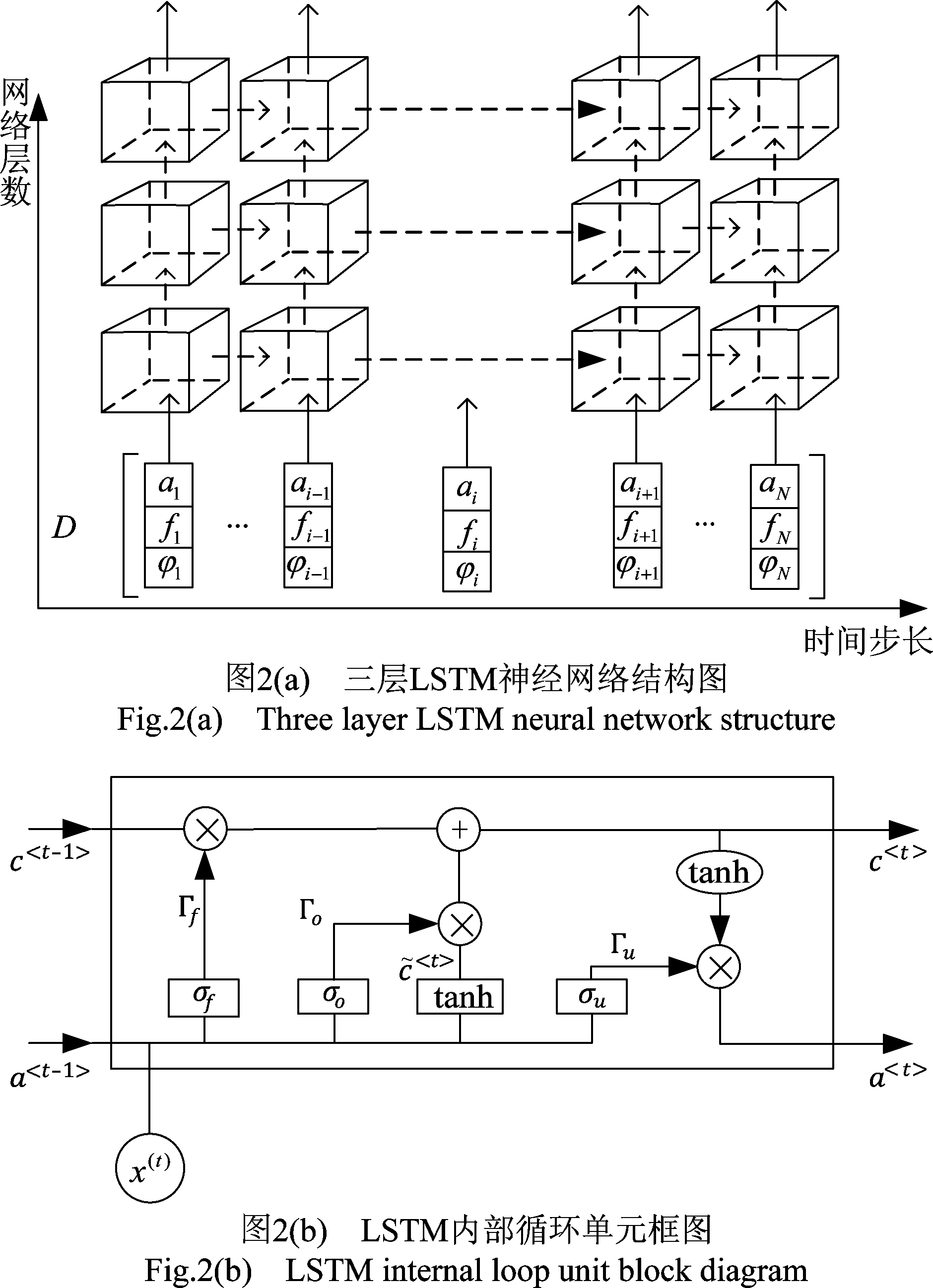
长短期记忆神经网络(long short term memory, LSTM)是循环神经网络(RNN)[22]的改进框架,使网络能够学习长期依赖特征并且不会在训练过程产生梯度消失和梯度爆炸。其原理通过添加门控单元使自循环的权重,累积的时间尺度可以动态改变。将前期状态传导至网络后端,本文根据LSTM神经网络的这一特点,学习信号数据分布的周期性特征和不同尺度的特征。LSTM框架如图2(a)、(b)所示,单元内部数学模型如下:
记忆细胞
(7)
遗忘门 Γf=σf(wf[a<t-1>,x<t>]+bf)
(8)
更新门 Γu=σu(wu[a<t-1>,x<t>]+bu)
(9)
输出门 Γo=σo(wo[a<t-1>,x<t>]+bo)
(10)
状态更新
(11)
a<t>=Γu×tanhc<t>
(12)
图2(a)表示时序长度为N的样本通过LSTM神经网络,神经元状态通过参数共享机制在同层和各层之间相互传递。LSTM内部通过门控机制实现t时刻状态量c<t>由三个阈值Γf、Γu、Γo控制,根据t-1时刻输出a<t-1>和输入数据x<t>,网络可以学习各个门上的权重。门控机制帮助LSTM单元可以在多种时间尺度上学习序列的稳定特征。
2.3.2 残差神经网络
网络深度对模型性能至关重要,网络加深可以提取更加复杂的特征模式,特征的“级别”可以通过堆叠层的数量来丰富,以获得高维解空间,这一点已经在图像识别领域得到很好的验证[23-24]。由于深层网络反向传播时,层数堆积的累积效应会造成梯度消失或梯度爆炸,导致深层网络退化问题[25]。残差神经网络(ResNet)通过建立深层网络间的恒等映射[17](identity mapping),将浅层特征通过快捷连接(shortcut connection)传导至深层,以克服深层网络难以训练问题,残差单元结构如图3(b)所示。
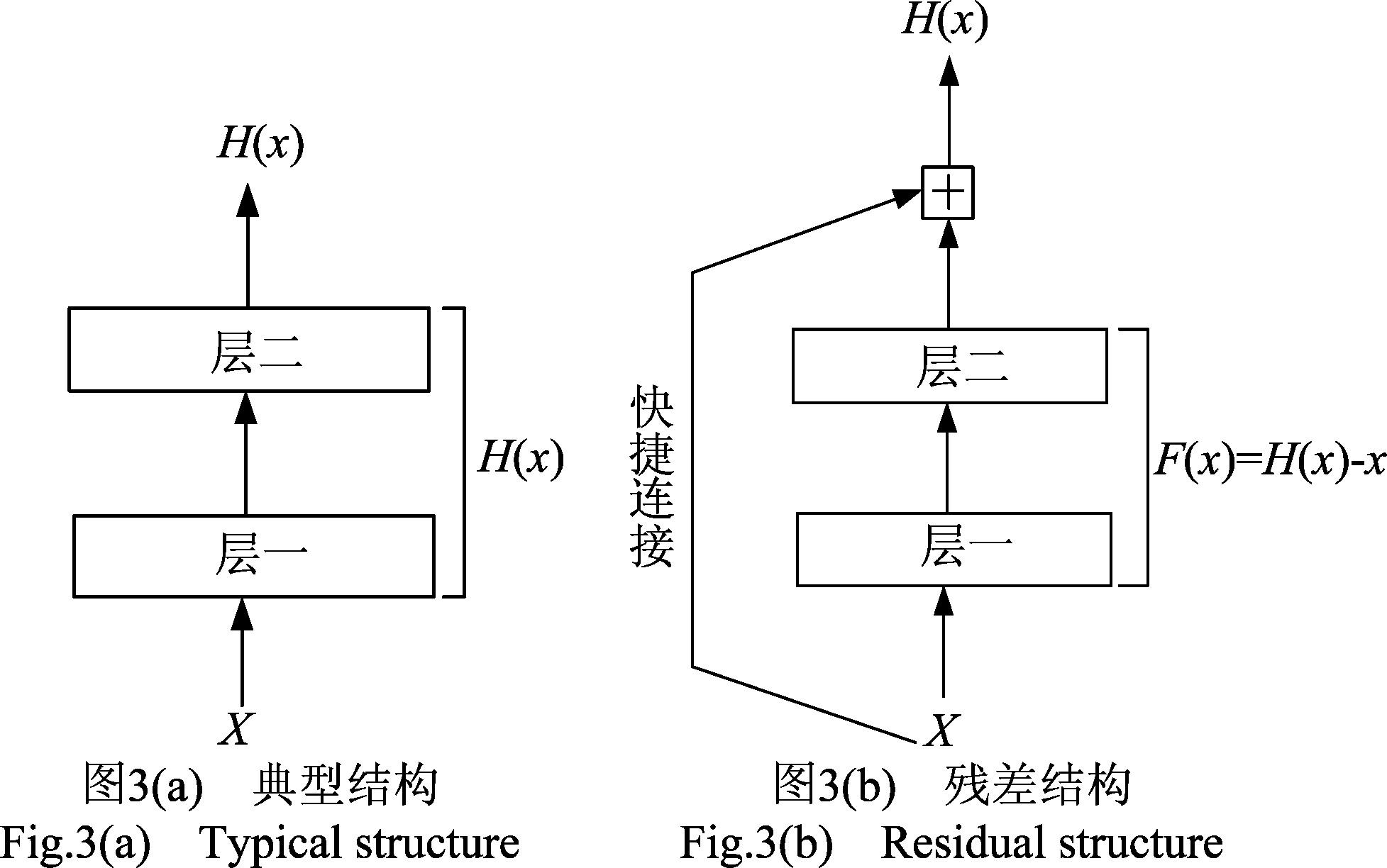
残差结构图3(b)与经典结构图3(a)相比,通过快捷连接避免多个相邻层直接拟合期望的基础映射H(x),将由输入X逼近目标函数H(x)的经典网络形式转化为F(x)=H(x)-x,这构成了残差学习结构。这样的好处在于,将堆叠的深层网络进行分块处理,每一个残差块相当于一个小的卷积网络,通过快捷连接将残差块连接起来,实现网络后端残差块同步训练,并消除逐层传递带来的梯度消失和梯度爆炸。
实际环境绝大多数样本未人工标注,为充分利用无标签数据,本文提出在LSTM-ResNet网络后连接CPC网络(结构如图4)。无标签数据通过无监督学习提取特征,根据基于噪声对比估计[26](Noise-Contrastive Estimation, NCE)损失函数,计算CPC网络预测特征和LSTM-ResNet提取特征的互信息量,通过损失函数寻优使LSTM-ResNet学习更有效的特征。无监督训练结束后用softmax替换CPC网络,再用带标签数据通过有监督学习训练分类器。因为LSTM-ResNet在无监督学习时已经对网络参数完成初始化,所以有监督学习训练样本数量大幅减小。算法设计步骤如下:
1.记
为特征提取模块LSTM-ResNet网络输出;
2.其中
部分输入到自回归网络gar,通过学习部分数据分布,自回归网络输出
并对
部分进行预测记为
本文根据文献[18]使用门控循环单元(gated recurrent unit, GRU)[27]作为自回归网络进行预测,Wk为t+k位置的预测矩阵;
(13)
3.自回归网络预测值
和LSTM-ResNet网络特征提取值
基于NCE建立损失函数,首先建立原始输入和自回归网络输出的互信息表达,
(14)
因为原始输入xt+k和自回归网络输出ct正比于自回归网络预测值
和特征提取值
(15)
建立关于自回归网络预测值和特征提取值
的损失函数,
图4 CPC网络结构
Fig.4 Structure of Contrastive Predictive Coding Network
(16)
表示一批样本中由神经网络所提取特征的集合;
4.通过最小化对比损失函数(CPC),使网络在无标签样本中学习样本最佳表示特征,初始化LSTM-ResNet网络参数;
5.用softmax替换CPC网络,用数量为N的有标签数据{x,y}训练分类器softmax,
(17)
gφ∘fθ*表示分类器gφ和初值为θ*的特征提取器fθ*构成的混合函数。通过有监督学习找到最佳参数φ。
本文从调制信号瞬时参数本质特征出发,提出一种联合神经网络框架,利用LSTM和ResNet神经网络提取差异性特征模式。如图5所示,第一部分结构由LSTM神经网络组成,从前文可知根据输入信号形式LSTM神经网络将在不同时间尺度上学习数据中具有周期性的特征,这一处理可以有效减少输入ResNet网络中的重复特征,实现特征的一次筛选,减少了模型学习复杂度。第二部分,残差神经网络将完成信号细粒特征提取,学习信号高维空间重构特征,将低维不可分问题转换到高维空间后有利于分类边界的形成。
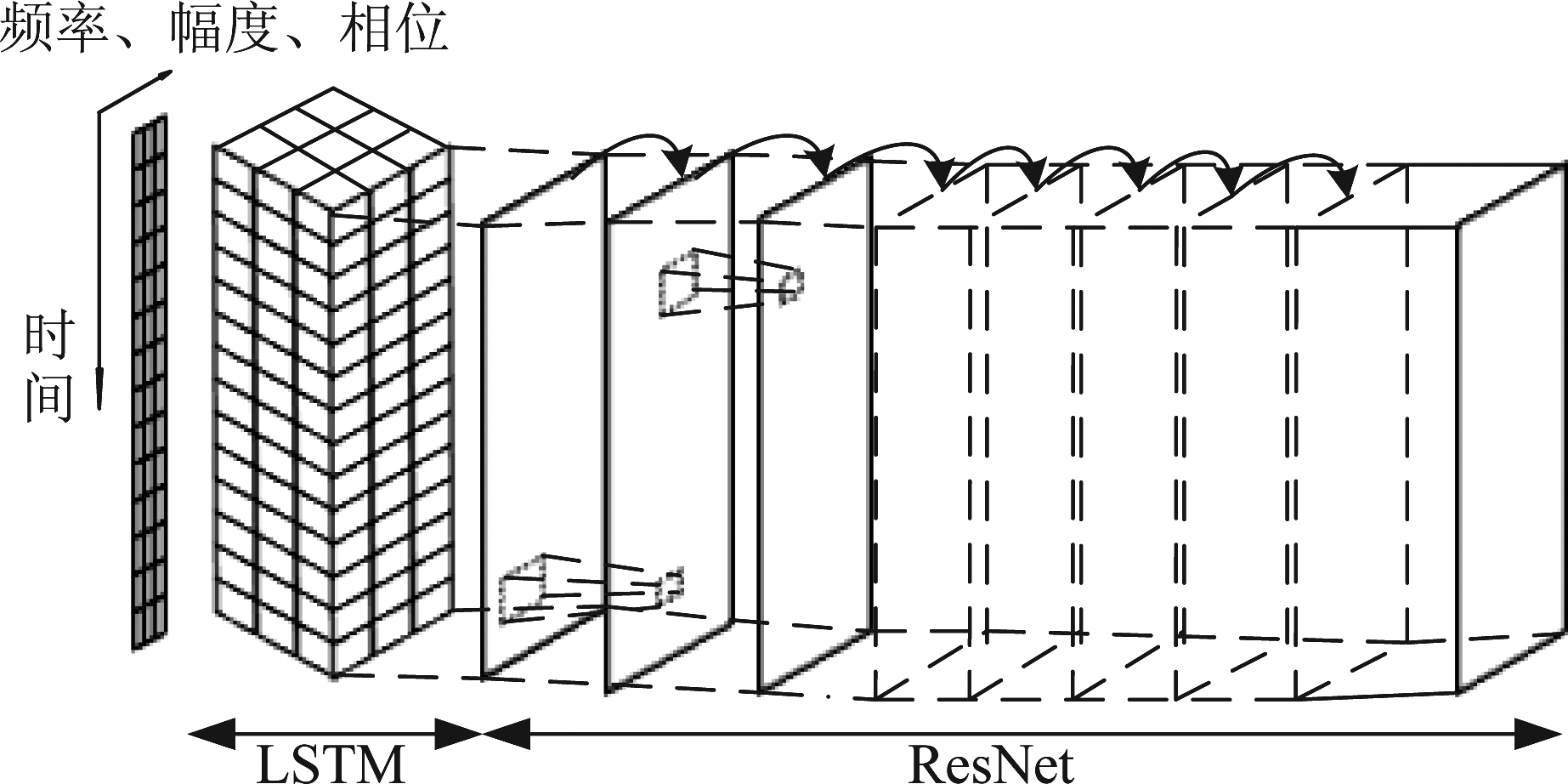
图5 LSTM-ResNet神经网络结构示意图
Fig.5 Schematic diagram of LSTM-ResNet neural network structure
本文通过实验对比和参考文献[10-12],第一部分为3层LSTM神经网络,第二部分为ResNet50神经网络,网络详细参数如表1所示。
表1 LSTM-ResNet联合神经网络参数
Tab.1 LSTM-ResNet joint neural network parameter
层名输出维度参数配置Input Layer3×128LSTM-1283×128tanh激活函数[28]LSTM-2563×256tanh激活函数LSTM-1283×128tanh激活函数Reshape[1×3×128]zero padding5×130(1,1)Res Stack15×1303×3,64步长(1,2)Res Stack2 3×643×3 Max Pooling步长(1,2)1×1643×3641×1256 ×4Res Stack33×641×1643×3641×1256 ×4Res Stack43×641×11283×31281×1512 ×6Res Stack53×641×12563×32561×11024 ×31×11average pool,11-d,softmax
实验中使用DeepSig的调制识别公开数据集[29],先将数据集的IQ样本通过希尔伯特变换得到信号的瞬时幅度A[a1,a2,...,an];瞬时相位φ[φ1,φ2,...,φn];瞬时频率S[f1,f2,...,fn]。本文使用调制信号数据集各项参数如表2所示。
实验平台为windows7,32GB内存,NVDIA P4000显卡。设置batchsize为128,迭代周期根据损失函数衰减趋势自动终止。将数据分为10份,采用交叉验证方式进行训练,具体实验步骤如下。
表2 调制信号数据集参数
Tab.2 Modulated signal data set parameters
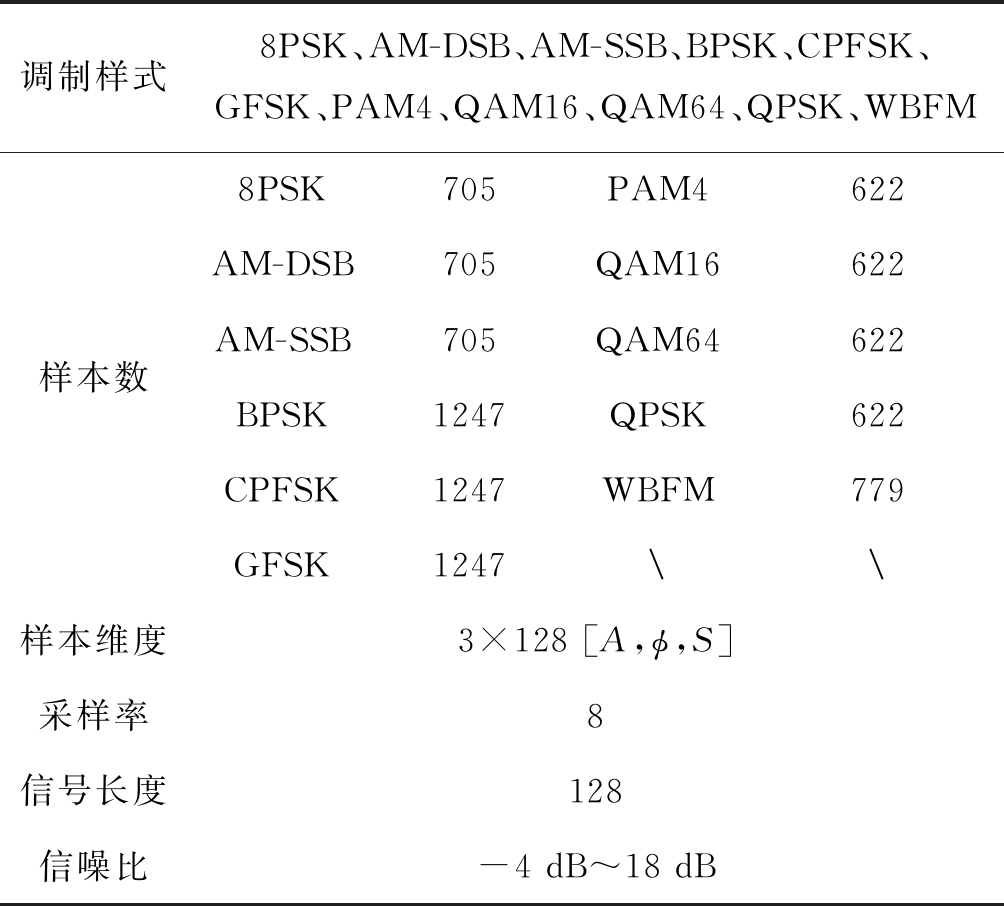
调制样式8PSK、AM-DSB、AM-SSB、BPSK、CPFSK、GFSK、PAM4、QAM16、QAM64、QPSK、WBFM样本数8PSK705PAM4622AM-DSB705QAM16622AM-SSB705QAM64622BPSK1247QPSK622CPFSK1247WBFM779GFSK1247\\样本维度3×128 [A,ϕ,S]采样率8信号长度128信噪比-4 dB～18 dB
实验1 考察文中算法特征提取能力和运行时间比较,首先对比有监督学习条件下LSTM-ResNet联合神经网络和其他调制信号分类神经网络在-4 dB～18 dB识别精度。文献[11]使用9层残差网络训练样本长度为128的IQ数据。文献[12]使用包含信号幅度和相位信息,长度为128的数据训练两层LSTM神经网络。本文使用包含信号瞬时幅度、相位、频率长度为128的数据训练LSTM-ResNet联合神经网络,网络结构如图5所示。三种方法均使用包含11种调制方式的带标签数据集通过交叉验证方式训练,结果如表3所示。
表3 比较不同信噪比条件下算法平均识别准确率
Tab.3 Algorithms average recognition accuracy of different SNR conditional
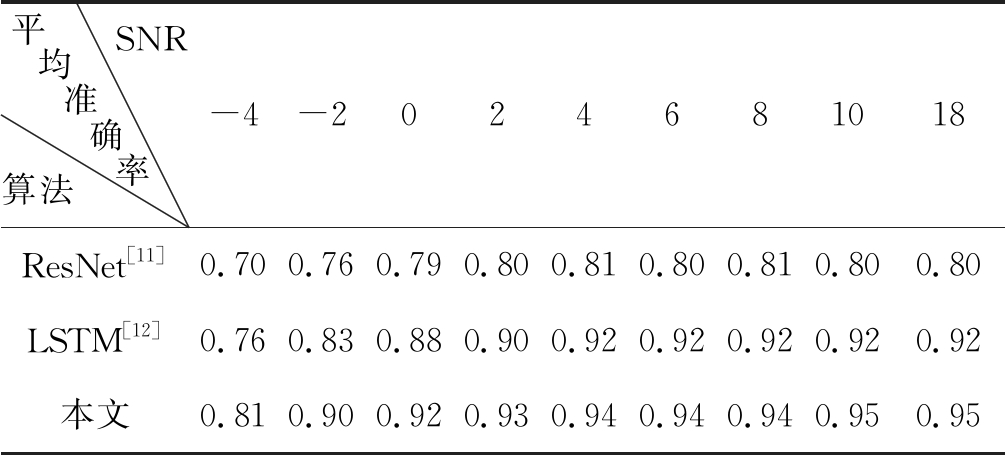
平均准确率 SNR算法 -4-2024681018ResNet[11]0.700.760.790.800.810.800.810.800.80LSTM[12]0.760.830.880.900.920.920.920.920.92本文0.810.900.920.930.940.940.940.950.95
从实验结果分析,与单一结构的神经网络调制识别方法相比,联合神经网络结构能够学习到更丰富的信号特征并且深层网络能够拟合出高维语义特征从而提高识别准确率。从训练样本所包含信号信息量角度看,通过数据预处理得到信号幅度、相位、频率信息相比直接使用IQ数据训练样本,更有助于网络学习到有用的特征。
表4列出三种神经网络在设置相同batchsize的条件下,测试训练一个epoch所花费的平均时长,考虑到有监督学习需要大量有标签数据使网络收敛并且联合神经网络使用深层网络模型ResNet50,模型收敛速度较慢,为此本文提出添加对比预测编码网络并实验验证。
表4 对比不同算法训练迭代的运行时间
Tab.4 Compare algorithm the running time of per training iterations
算法秒/epochResNet[11]560LSTM[12]420本文1800
实验2 考察半监督学习算法的小样本识别性能,验证文中联合神经网络结合对比预测编码(CPC)网络在小样本场景下的识别效果。分别测试半监督学习算法在-2 dB、0 dB、10 dB条件下的小样本识别准确率。第一步使用全部无标签数据集对连接有对比预测编码网络的LSTM-ResNet网络进行预训练;第二步随机抽取各类调制信号中不同信噪比的少量带标签样本通过有监督学习微调网络参数;第三步分别测试-2 dB、0 dB、10 dB信噪比条件下小样本识别11种调制信号的平均准确率,对照实验以完全通过有监督学习的LSTM-ResNet网络为基准。实验结果如图6所示。
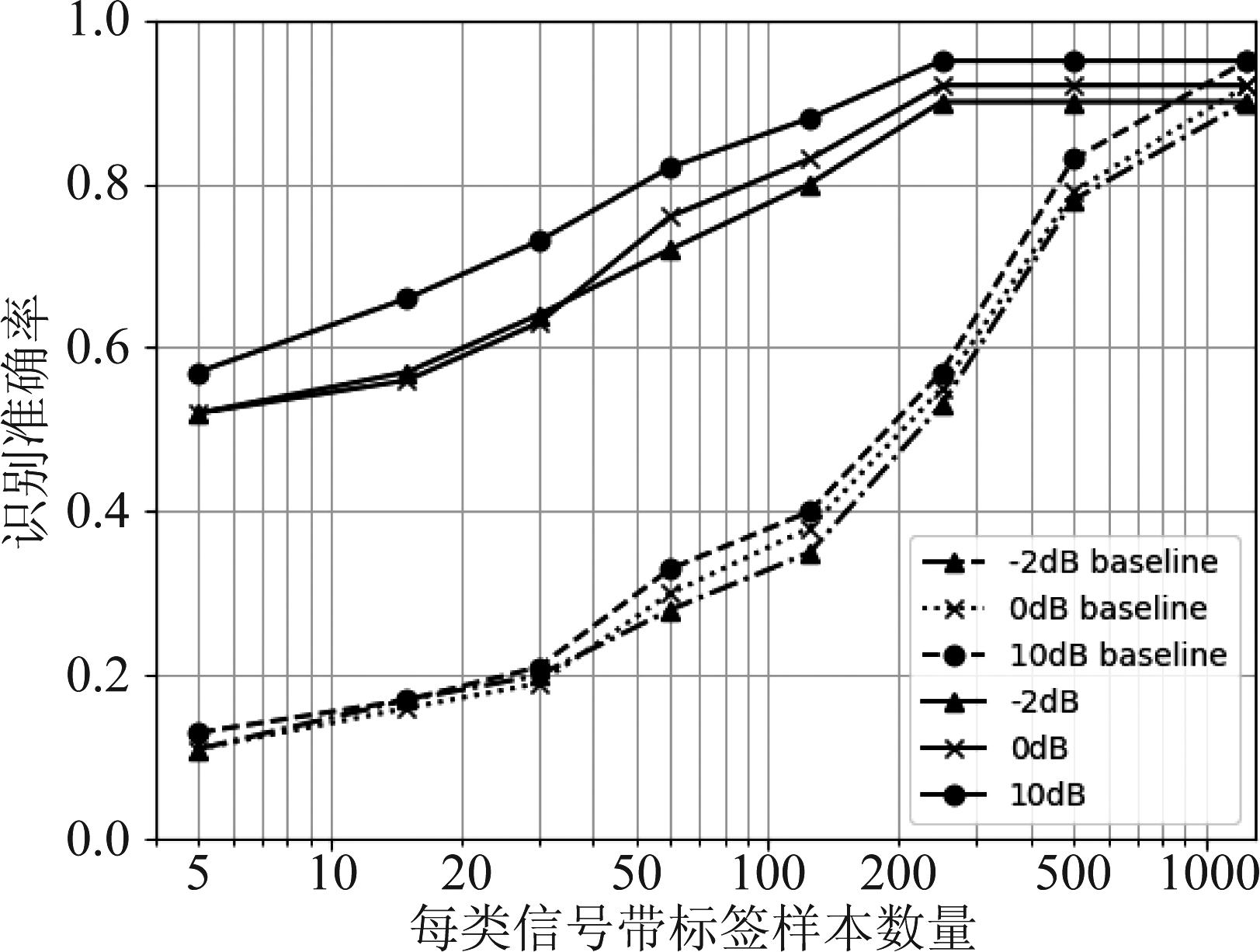
图6 半监督学习CPC算法-2 dB、0 dB、10 dB
条件下小样本识别准确率
Fig.6 Recognition accuracy comparison of semi-supervised learning with CPC at -2 dB、0 dB、10 dB SNR
由图6可以看出, 小样本条件下,采用基于CPC算法的半监督学习识别准确率显著高于有监督学习识别准确率。当使用每类信号200～300的带标签样本时半监督学习方法识别准确率能够达到有监督学习最佳效果。实验发现本文算法在低数据条件下仅通过无监督预训练对11种调制信号的识别精度接近60%,表明对比预测算法使用无标签样本通过对比损失函数能够学习到信号的有效特征。
时间性能方面,通过无监督预训练后的联合神经网络所需的数据量大幅减少,训练时间也随之减少,当本文方法识别率达到有监督学习识别率时,大约每epoch耗时约8 min。
图7 信噪比为-2 dB预测混淆矩阵
Fig.7 Confusion matrix for joint Neural Network at -2 dB SNR
实验3 考察文中算法对数据集中包含的11种模拟和数字调制样式在特定信噪比条件下的类间识别概率。由图7～图9可以看出本文算法具备一定的抗噪声能力,在-2 dB能够达到90%识别准确率。实验发现,8PSK、QPSK、WBFM、AM-DSB信号易出现混淆,分析可能因为IQ数据转为瞬时参数序列后,LSTM网络特征提取更倾向表达幅度、相位、频率的数值规律,对调制阶数相近的信号容易出现误识别,在QAM16和PAM4也体现这种情况,反而QAM16和QAM64这类调制阶数相差较大的信号区分效果较好。对于这种问题考虑可以采用变换域数据训练网络或采取在有监督学习阶段增加带标签样本损失权重加强标签对网络的约束能力,以更好区分相似的特征。实验验证特定信噪比条件下,11种调制样式的类间识别混淆矩阵如下图所示。
图8 信噪比为0 dB预测混淆矩阵
Fig.8 Confusion matrix for joint Neural Network at 0 dB SNR
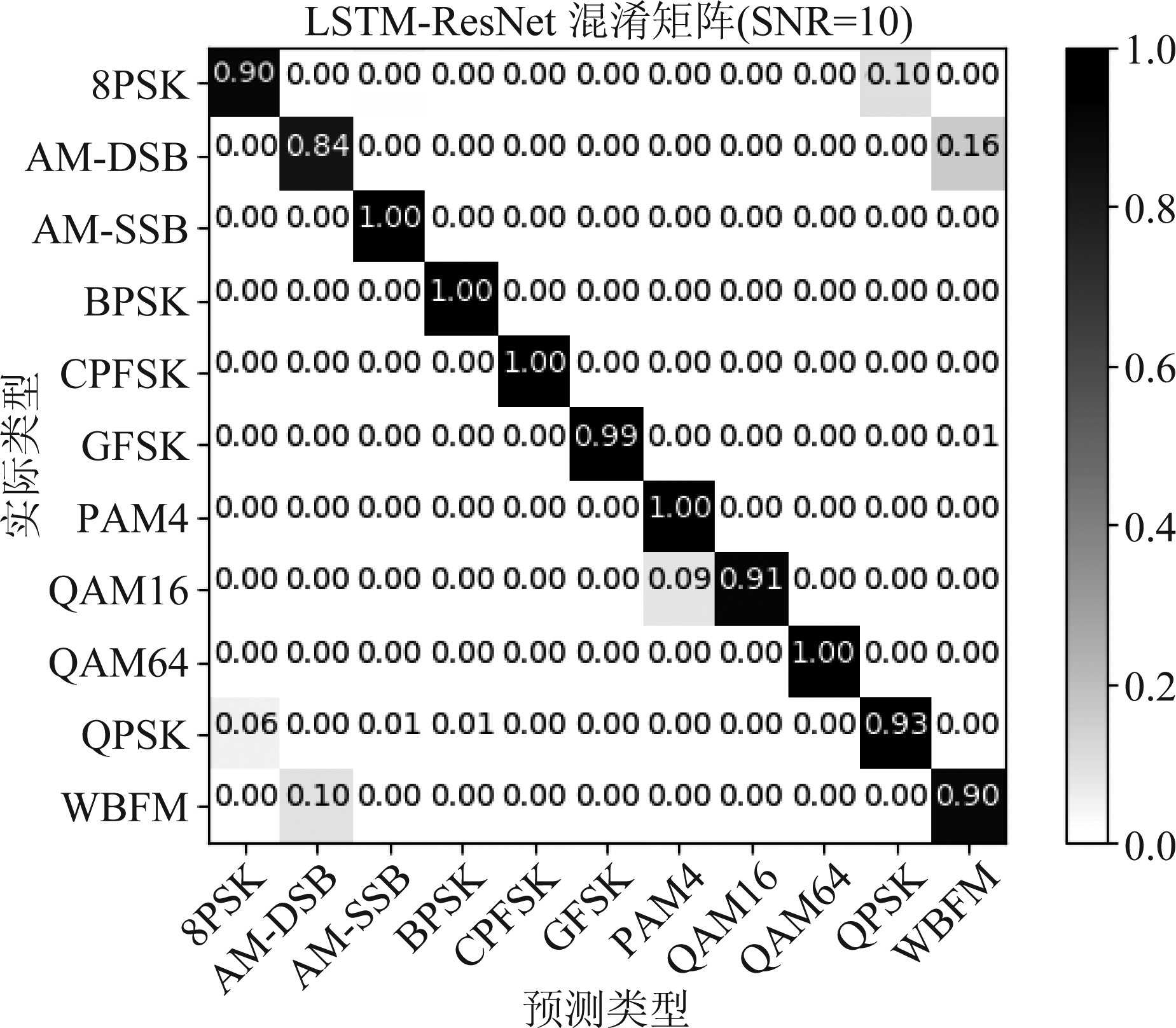
图9 信噪比为10 dB预测混淆矩阵
Fig.9 Confusion matrix for joint Neural Network at 10 dB SNR
文中利用不同调制信号的时域瞬时参数差异性特点,提出一种联合神经网络结构识别方法。该方法无需时频变换预处理,通过长短期记忆神经网络的尺度筛选和残差网络的高维特征提取,实现对时域特征较好拟合。在0 dB信噪比条件下,对11种调制信号的平均识别率达到92%。该方法将无监督预训练与有监督学习相结合,充分利用数据,以满足小样本条件需求。
[1] Boiteau D, Le Martret C. A general maximum likelihood framework for modulation classification[A]. In: Proc. of IEEE ICASSP’98[C]. Seattle, US: 1998, 4: 2165-2168.
[2] Maliatsos K, Vassaki S, Constantinou P. Interclass and Intraclass Modulation Recognition using the Wavelet Transform[C]∥Personal, Indoor and Mobile Radio Communications, 2007. PIMRC 2007. IEEE 18th International Symposium on, 2007: 1-5.
[3] Swami A, Sadler B M. Hierarchical digital modulation classification using cumulants[J]. IEEE Transactions on Communications, 2000, 48(3): 416- 429.
[4] 谭晓衡, 褚国星, 张雪静, 等. 基于高阶累积量和小波变换的调制识别算法[J]. 系统工程与电子技术, 2018, 40(1): 171-177.
Tan Xiaoheng, Chu Guoxing, Zhang Xuejing, et al. Modulation recognition algorithm based on high-order cumulants and wavelet transform[J]. Systems Engineering and Electronics, 2018, 40(1): 171-177.(in Chinese)
[5] 徐毅琼. 数字通信信号自动调制识别技术研究[D]. 郑州: 解放军信息工程大学, 2011.
Xu Yiqiong. Research on automatic modulation recognition of digital communication signals[D]. Zhengzhou: The PLA Information Engineering University, 2011.(in Chinese)
[6] 赵雄文, 郭春霞, 李景春. 基于高阶累积量和循环谱的信号调制方式混合识别算法[J]. 电子与信息学报, 2016, 38(3): 674- 680.
Zhao Xiongwen, Guo Chunxia, Li Jingchun. Mixed Recognition Algorithm for Signal Modulation Schemes by High-order Cumulants and Cyclic Spectium[J]. Journal of Electronice & Information Technology, 2016, 38(3): 674- 680.(in Chinese)
[7] 代翱, 张海剑, 孙洪. 联合时域和时频域特征的数字调制信号自动分类[J]. 信号处理, 2016, 32(11): 1283-1292.
Dai Ao, Zhang Haijian, Sun Hong. Digital Modulations Automatic Classification Using the Combination of Several Features Extracted from Time and Time-Frequence Domain[J]. Journal of Signal Processing, 2016, 32(11): 1283-1292.(in Chinese)
[8] Azzouz E E, Nandi A K. Modulation recognition using artificial neural networks[M]. Automatic Modulation Recognition of Communication Signals. Springer, Boston, MA, 1996: 132-176.
[9] O’Shea T J, Corgan J, Clancy T C. Convolutional radio modulation recognition networks[C]∥International conference on engineering applications of neural networks. Springer, Cham, 2016: 213-226.
[10] O’Shea T J, Roy T, Clancy T C. Over-the-air deep learning based radio signal classification[J]. IEEE Journal of Selected Topics in Signal Processing, 2018, 12(1): 168-179.
[11] West N E, O’Shea T. Deep architectures for modulation recognition[C]∥2017 IEEE International Symposium on Dynamic Spectrum Access Networks (DySPAN). IEEE, 2017: 1- 6.
[12] Rajendran S, Meert W, Giustiniano D, et al. Deep learning models for wireless signal classification with distributed low-cost spectrum sensors[J]. IEEE Transactions on Cognitive Communications and Networking, 2018, 4(3): 433- 445.
[13] Hochreiter S, Schmidhuber, Jürgen. Long Short-Term Memory[J]. Neural Computation, 1997, 9(8): 1735-1780.
[14] Erhan D, Bengio Y, Courville A, et al. Why does unsupervised pre-training help deep learning?[J]. Journal of Machine Learning Research, 2010, 11(Feb): 625- 660.
[15] Ioffe S, Szegedy C. Batch normalization: Accelerating deep network training by reducing internal covariate shift[J]. arXiv preprint arXiv: 1502.03167, 2015.
[16] Ba J L, Kiros J R, Hinton G E. Layer normalization[J]. arXiv preprint arXiv: 1607.06450, 2016.
[17] He K, Zhang X, Ren S, et al. Identity mappings in deep residual networks[C]∥European Conference on Computer Vision. Springer, Cham, 2016: 630- 645.
[18] Oord A, Li Y, Vinyals O. Representation learning with contrastive predictive coding[J]. arXiv preprint arXiv: 1807.03748, 2018.
[19] Hénaff O J, Razavi A, Doersch C, et al. Data-efficient image recognition with contrastive predictive coding[J]. arXiv preprint arXiv: 1905.09272, 2019.
[20] 白芃远, 许华, 孙莉. 基于卷积神经网络与时频图纹理信息的信号调制方式分类方法[J]. 西北工业大学学报, 2019, 37(4): 816- 823.
Bai Pengyuan, Xu Hua, Sun Li. A Recognition Algorithm for Modulation Schemes by Convolution Neural Network and Spectrum Texture[J]. Northwestern Polytechnical University, 2019, 37(4): 816- 823.(in Chinese)
[21] 吴灏, 周亮, 李亚星, 等. 基于卷积神经网络和稀疏滤波的调制识别方法[J]. 系统工程与电子技术, 2019, 41(9): 2114-2121.
Wu Hao, Zhou Liang, Li Yaxing, et al. Modulation classification based on convolutional neural network and sparse filtering[J]. Systems Engineering and Electronics, 2019, 41(9): 2114-2121.(in Chinese)
[22] Lipton Z C, Berkowitz J, Elkan C. A critical review of recurrent neural networks for sequence learning[J]. arXiv preprint arXiv: 1506.00019, 2015.
[23] He K, Zhang X, Ren S, et al. Deep residual learning for image recognition[C]∥Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2016: 770-778.
[24] He K, Zhang X, Ren S, et al. Delving deep into rectifiers: Surpassing human-level performance on imagenet classification[C]∥Proceedings of the IEEE International Conference on Computer Vision, 2015: 1026-1034.
[25] He K, Sun J. Convolutional neural networks at constrained time cost[C]∥Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2015: 5353-5360.
[26] Gutmann M, Hyvärinen A. Noise-contrastive estimation: A new estimation principle for unnormalized statistical models[C]∥Proceedings of the Thirteenth International Conference on Artificial Intelligence and Statistics, 2010: 297-304.
[27] Gers F A, Schmidhuber J. Recurrent nets that time and count[C]∥Proceedings of the IEEE-INNS-ENNS International Joint Conference on Neural Networks. IJCNN 2000. Neural Computing: New Challenges and Perspectives for the New Millennium. IEEE, 2000, 3: 189-194.
[28] Fan E. Extended tanh-function method and its applications to nonlinear equations[J]. Physics Letters A, 2000, 277(4-5): 212-218.
[29] O’shea T J, West N. Radio machine learning dataset generation with gnu radio[C]∥Proceedings of the GNU Radio Conference. 2016, 1(1).
苟泽中 男, 1995年生, 陕西咸阳人。空军工程大学硕士研究生, 主要研究方向为通信信号处理、机器学习、通信对抗。
E-mail: zezhonggou@126.com
许 华 男, 1976年生, 湖北枝江人。空军工程大学教授, 博士, 主要研究方向为通信信号处理、盲信号处理、通信对抗。
E-mail: 13720720010@139.com
郑万泽 男, 1985年生, 吉林辽源人。空军工程大学讲师, 硕士, 主要研究方向为通信工程、训练评估。
E-mail: 107011650@qq.com
冯 磊 男, 1997年生, 湖北随州人。空军工程大学硕士研究生, 主要研究方向为通信信号处理、机器学习、通信对抗。
E-mail: m13720621014@163.com
白芃远 男, 1995年生, 河南洛阳人。空军工程大学硕士研究生, 主要研究方向为通信信号处理、机器学习、通信对抗。
E-mail: 418503814@qq.com