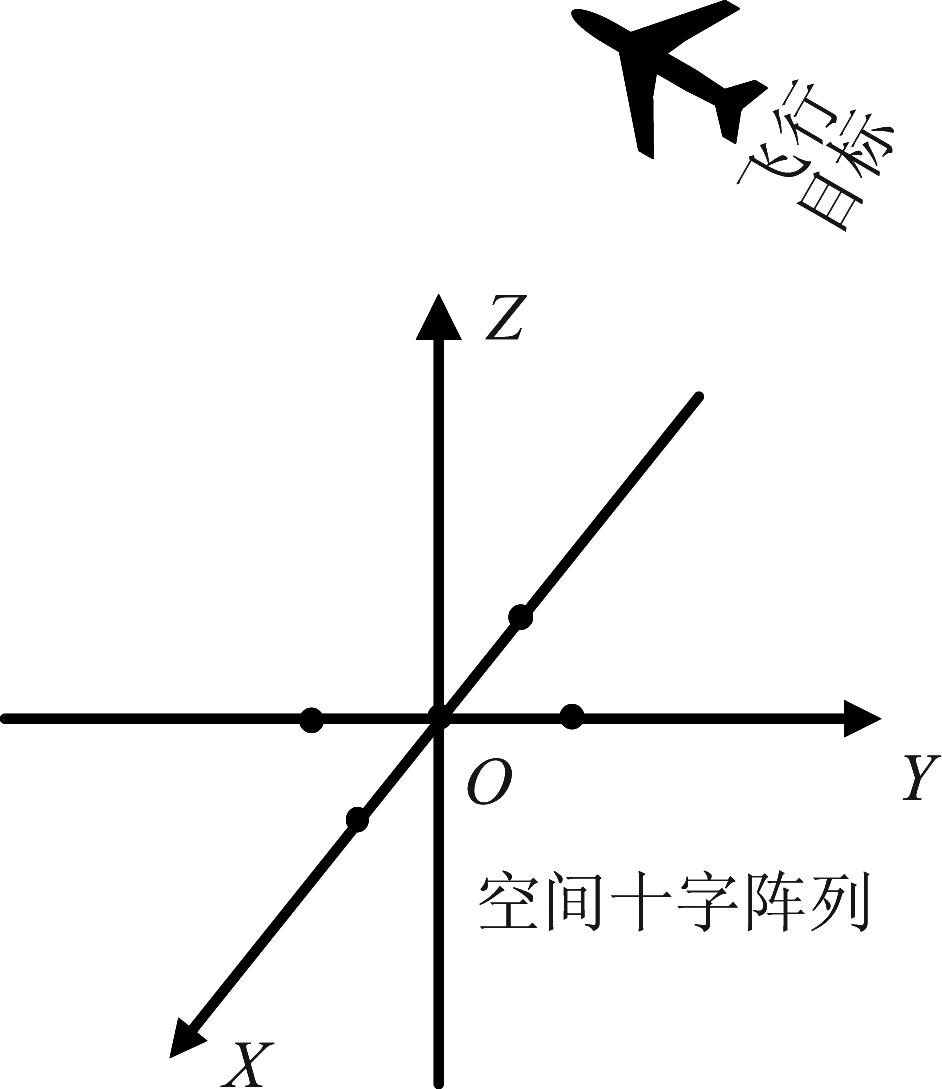
图1 均匀线性空间十字阵示意图
Fig.1 Distribution Diagram of Uniform Linear Baseline Arrays
Reference format: Chen Zhaonan, Wang Lei. The Time-Domain MSWF Rapid Bandwidth DOA Estimation of High Subsonic Flight Target Based on Acoustic Sensor Arrays[J]. Journal of Signal Processing, 2020, 36(12): 2116-2122. DOI: 10.16798/j.issn.1003- 0530.2020.12.018.
受到海面平台高度的制约,对海面低空飞行目标的超视距探测是常规雷达探测技术的难点。同时,由于海面平台附近电磁环境复杂、低仰角海杂波严重、多径效应影响等不利因素,对海面近程低空飞行目标的雷达探测也存在一定问题。声学探测方法通过接收海面目标的飞行噪声对其进行探测,具有不受电磁和光环境影响、全向监测、不受通视条件制约等优点,尤其是应用于海面平台时,其背景和环境噪声较为单一,杂波干扰较少,因此该方法在对海面低空飞行目标的探测方面具有独特优势。
以声速为界限,低空飞行目标可分为超声速目标和高亚声速目标两大类。超声速目标飞行时会对周边空气产生扰动而形成马赫波,马赫波的波前又叫激波,激波呈锥面传播且时域特征明显,因此对超声速目标的声学跟踪已经有相对成熟的理论和技术[1-3]。对于高亚音速飞行目标,其呈现宽带、瞬态和非平稳特性,对该类目标的声学跟踪方法研究相对较少。
对于声学探测方法而言,由于其不具备对目标距离的主动探测能力,且单个静止声阵列已被证明不能仅依靠波达方向估计目标的运动轨迹,实现对目标运动参数估计需要阵列中声传感器达到百米量级间距[4],因此目前主要通过单传感器实现对目标噪声的波达方向(Direction of Arrive, DOA)估计,在此基础上通过角度交汇等方式实现目标轨迹估计。同时,在海面低空飞行目标探测场景中,声学探测方法受限于其声波频率和波长,其DOA估计精度也受到制约,因此声学探测方法获得的目标方位信息主要用于为其他高精度探测系统提供引导信息,这就对声学DOA估计方法的实时性提出了较高的要求。
从目前宽带信号DOA估计方法的研究现状来看,目前所提出的方法包括宽带信号子空间方法[5]、宽带波束域方法[6]、宽带循环平稳DOA估计方法[7]以及基于时域模型的宽带阵列信号DOA估计[8]。宽带信号子空间方法需要对信号相关矩阵求逆,增加了其计算复杂度;宽带波束域方法主要针对多相关信号同时入射的场景,宽带循环平稳DOA估计方法一般针对持续出现的通信信号,海面高亚音速飞行目标噪声信号持续时间较短,不具有循环平稳特性。基于时域模型的宽带阵列信号DOA估计可同时适用于窄带和宽带信号,其一般采用马尔可夫链蒙特卡罗方法进行求解,也存在计算复杂度高的问题。
在对低空飞行目标的探测跟踪问题研究方面,佟建飞等研究了适用于窄带信号目标的低空目标单声阵列轨迹估计方法,首先利用多普勒效应估计目标飞行参数,结合波达方向估计目标轨迹方向、水平偏置和高度,依据几何模型确定其运动轨迹[9]。陈华伟等提出了基于五元十字阵的低空目标声测无源定位算法,在时延估计方面,提出了基于维纳加权的频域自适应时延估计算法和基于双谱的时延估计算法,在小尺寸高精度定向方面,首次将压差式矢量声传感器引入低空目标侧向研究中,提出基于矢量传感器阵的宽带相干信号子空间最优波束形成算法[10]。张君等针对低信噪比情况下的声源角度估计问题,提出了基于四阶累积量的阵列可扩展声矢量锥形阵测向算法[11]。
论文以利用布设于有限空间内的声传感器阵实现海面高亚音速目标角度的快速估计为背景,建立了基于均匀线性空间十字阵的宽带时域阵列信号模型,提出了宽带时域多级维纳滤波器(Multi-Stage Wiener Filtering, MSWF)的DOA快速估计方法,在降低系统计算复杂度的同时,保持了目标DOA的高分辨率估计。
由于目标运动方向未知,为实现对全方位飞行目标方向的有效估计,这里采用均匀线性空间十字阵阵列模型,同时以该阵列基线建立直角坐标系。对于声传感器阵型的优化设计,文献[12]中进行了详细的研究和讨论,本文方法对声传感器阵型设计没有特殊要求,具体的传感器阵型决定了信号方向矢量的表达式。基准传感器为坐标原点,声传感器均匀分布于x轴、y轴和z轴的正负半轴上,相邻传感器之间的距离,即基线长度均为d。声传感器阵布设位置如图1所示。

图1 均匀线性空间十字阵示意图
Fig.1 Distribution Diagram of Uniform Linear Baseline Arrays
在DOA估计中,如果信号带宽B满足:
(N-1)d/c≤1/B
(1)
其中,N为阵元中的传感器总数,c为声速,则认为该信号为窄带信号。根据实测的高亚音速飞行目标噪声数据,其信号带宽较宽,不满足式(1)条件,因此为宽带信号。
假设超短基线阵位于声源的远场,此时声波为平面波。假设目标入射波的方位角和俯仰角分别为φ和θ(俯仰角为与z轴正向的夹角),则入射波的单位方向向量k可表示为:
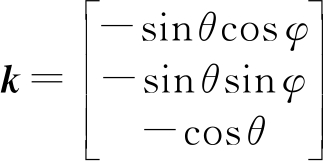
(2)
假设对于宽带入射信号s(t),其频率范围为[fl, fh], fh=fl+B。为避免测向模糊,传感器间距d应满足:
(3)
相邻传感器间接收信号的传输时延τ=αd/c,其中α为sin θcos φ、sin θsin φ和cos θ中之一,因此有
(4)
从而得到相邻传感器接收信号时延的取值范围为τ∈[-Tmax,Tmax]。
对于接收的宽带目标声源信号s(t),这里采用带通信号重构和采样方法,将其表示为[13]:
(5)
其中,τ为某传感器接收信号相对于基准传感器接收信号的时延,Ts为采样周期,ψ(t)为带通采样信号,其可采用sinc函数的带通形式或带通椭圆球面波函数,L表示窗函数的长度。
将上式进行时域离散采样,并用n-l代替l,得到传感器接收信号在nTs时刻的输出为:
(6)
其中,hl(τ)=ψ(l-τ)ω(l-τ),ω(l-τ)为窗函数。
对于均匀线性空间十字阵阵列,其可看做是由X轴,Y轴和Z轴三个均匀线性阵列构成。以X轴为例,原点传感器例外,假设X轴上共有2M个传感器,即左右半轴各有M个传感器,X轴上信源的时延矢量可表示为:
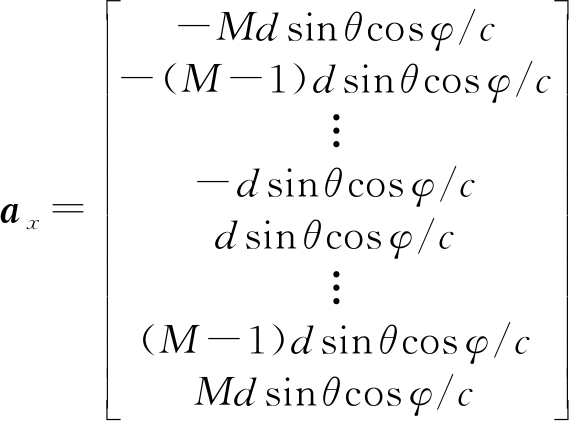
(7)
相应地,Y轴和Z轴的信源方向矢量可分别表示为:
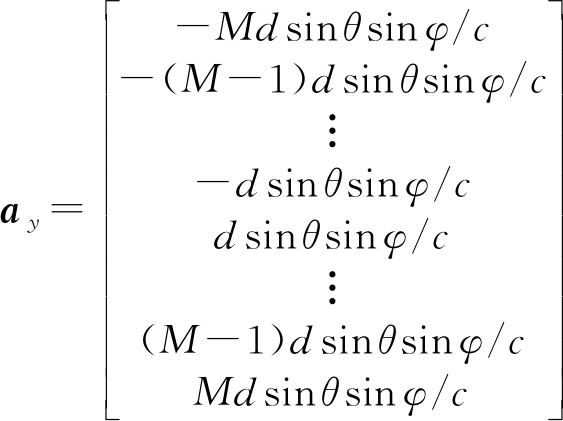
(8)
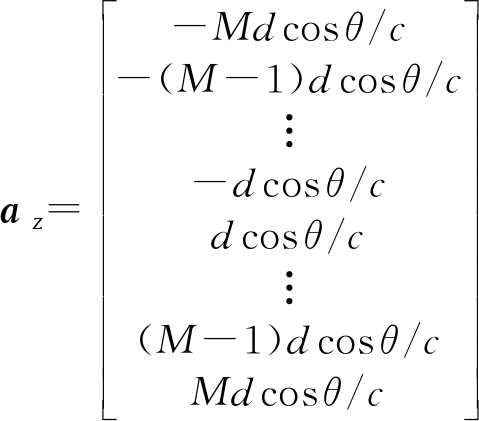
(9)
相应的,X轴阵元的接收信号向量可表示为:
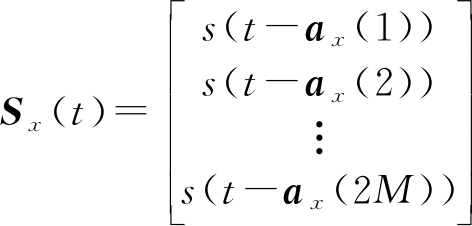
(10)
Sx(t)相应的离散形式可表示为:
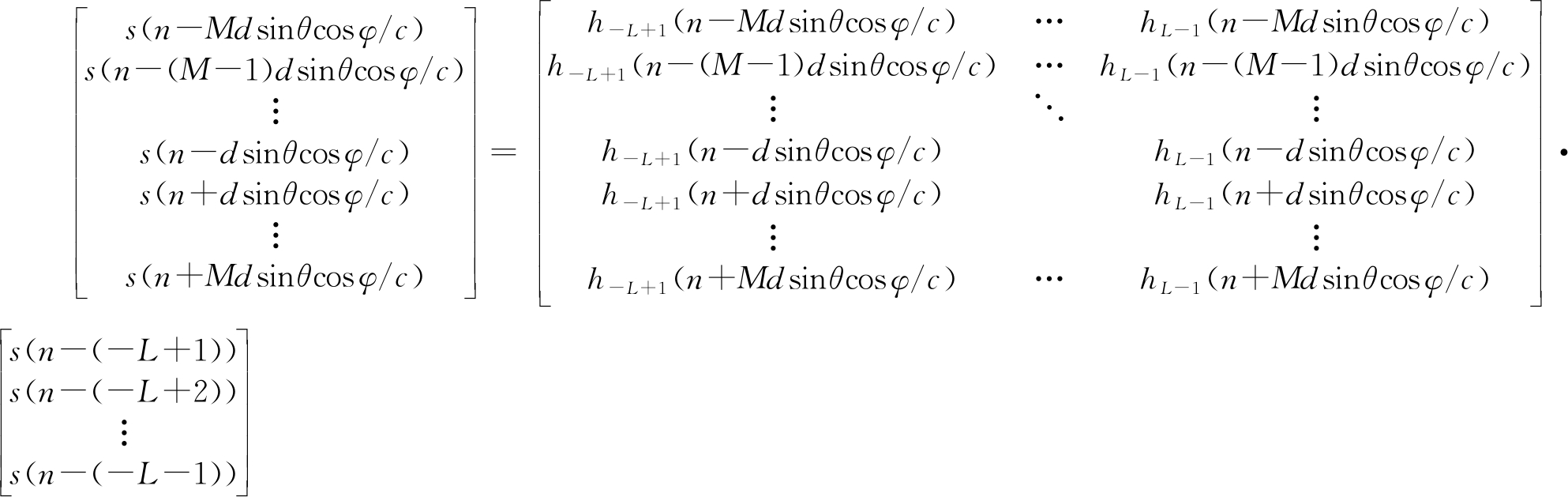
(11)
将上式表达为矩阵形式:
Sx(n)=Hx(n,τ)s(n)
(12)
其中,Sx(n)为n时刻X轴阵元的观测信号矢量,Hx(n,τ)为n时刻X轴阵元的时延差矩阵,s(n)为对基准传感器收到的信号以n时刻为中心、向前后各拓展L-1个采样时刻得到的离散信号向量。对于Y轴和Z轴阵元的接收信号向量,同样可以得到上述表示形式。
令所有非基准阵元接收信号矩阵Sτ(n)=[Sx(n);Sy(n);Sz(n)],时延差矩阵H(n,τ)=[Hx(n,τ);Hy(n,τ);Hz(n,τ)],从而得到所有非基准阵元接收信号的矩阵表达式:
Sτ(n)=H(n,τ)s(n)
(13)
所有非基准阵元接收信号值可由时延差矩阵中的向量对基准信号加权求和得到。
式(13)即为均匀线性空间十字阵阵列的时域宽带信号模型。
在宽带信号的DOA估计方法中,特征子空间类方法(非相干信号子空间算法和相干信号子空间算法[14])具有良好的分辨率和鲁棒性,但其求解过程中需要进行矩阵特征值分解和谱峰搜索运算,尤其在阵元数目较大的情况下,导致其实现复杂度较高,难以满足海面高亚音速飞行目标的实时探测需求。基于多级维纳滤波器(MSWF)的快速子空间估计方法不需要进行矩阵协方差估计和特征值分解运算,且其运算过程均是复矩阵相乘运算,尤其适合高速DSP平台实时实现,因此该方法目前得到了广泛应用。本文基于接收阵列的时域宽带信号模型,提出了时域MSWF快速估计方法。
在经典的维纳滤波器的求解过程中,需要通过求解观测数据协方差矩阵的逆来获得滤波器的最优权值,在观测数据维数较高时具有较大的实现复杂度,MSWF将高维观测数据变为低维数据,其降维的主要思路是对观测信号进行多次正交投影分解,分解得到两个子空间:一个平行于参考信号与上一次观测信号的互相关矢量的子空间,一个正交于第一子空间的空间,然后对第二子空间再进行正交投影分解,第一子空间向量构成匹配滤波器组,第二子空间向量构成合成滤波器组,由匹配滤波器组和合成滤波器组的嵌套,即利用相关相减来实现矩阵的求逆运算。在MSWF算法用于快速子空间时,信号子空间可以由匹配滤波器组快速生成,因此在实现过程中只需要计算其匹配滤波器组,而不需计算合成滤波器组,从而进一步减少了计算量。
MSWF是由多个维纳滤波器嵌套构成的,其所包含的滤波器组可分为匹配滤波器组和合成滤波器组。在时域MSWF快速估计方法中,首先将所有非基准阵元接收信号的离散采样值,划分为K段,每段有Nk个快拍,计算所有段数据协方差矩阵的均值:
(14)
将协方差矩阵R代入作为多级维纳滤波器的输入,通过MSWF的p+2级分解求得R的信号子空间H=[h1,h2,…,hp+2],p为入射信号个数,在本文的应用场景中,一般取p=1。
在完成上述工作后,按照如下步骤完成目标DOA估计:
(1)选择基准传感器接收信号为参考信号,即d0(k)=s(k),非基准传感器接收信号为参考信号,即X0(k)=X(k),rX0d0为初始参考信号和初始接收信号的互相关向量,令h0=rX0d0/|rX0d0|;
(2)进行前向递推,令i=1,2,3,...,6M,
Xi(k)=Xi-1(k)-hidi(k)
(3)计算信号子空间US或噪声子空间UN:
US=span{h1,h2,…,hp+2},
UN=span{hp+3,hp+4,…,h6M}
(4)利用噪声子空间,构造二维空间谱函数:
(15)
按照设定步长对其谱函数进行谱峰搜索,得到信号的二维达到角最优估计值为:
(16)
在硬件实现过程中,为减少二维谱峰搜索的计算量,可采用粗搜索和细搜索相结合的方式进行,文献[15]给出了优化空间谱搜索过程的相关策略,可直接用于本文方法中。
对典型布站情况下使用本文提出的方法,对二维入射角度估计进行了仿真。假设阵列长度L=0.5 m,每个坐标轴上采用8个非基准阵元,目标入射角度[φ,θ]=[60°,80°],快拍数为200,采用基于MSWF的时域宽带DOA快速估计方法,对目标波达方向进行了估计,搜索步长为0.5°,在信噪比为10 dB时,得到的二维空间谱如图2所示。
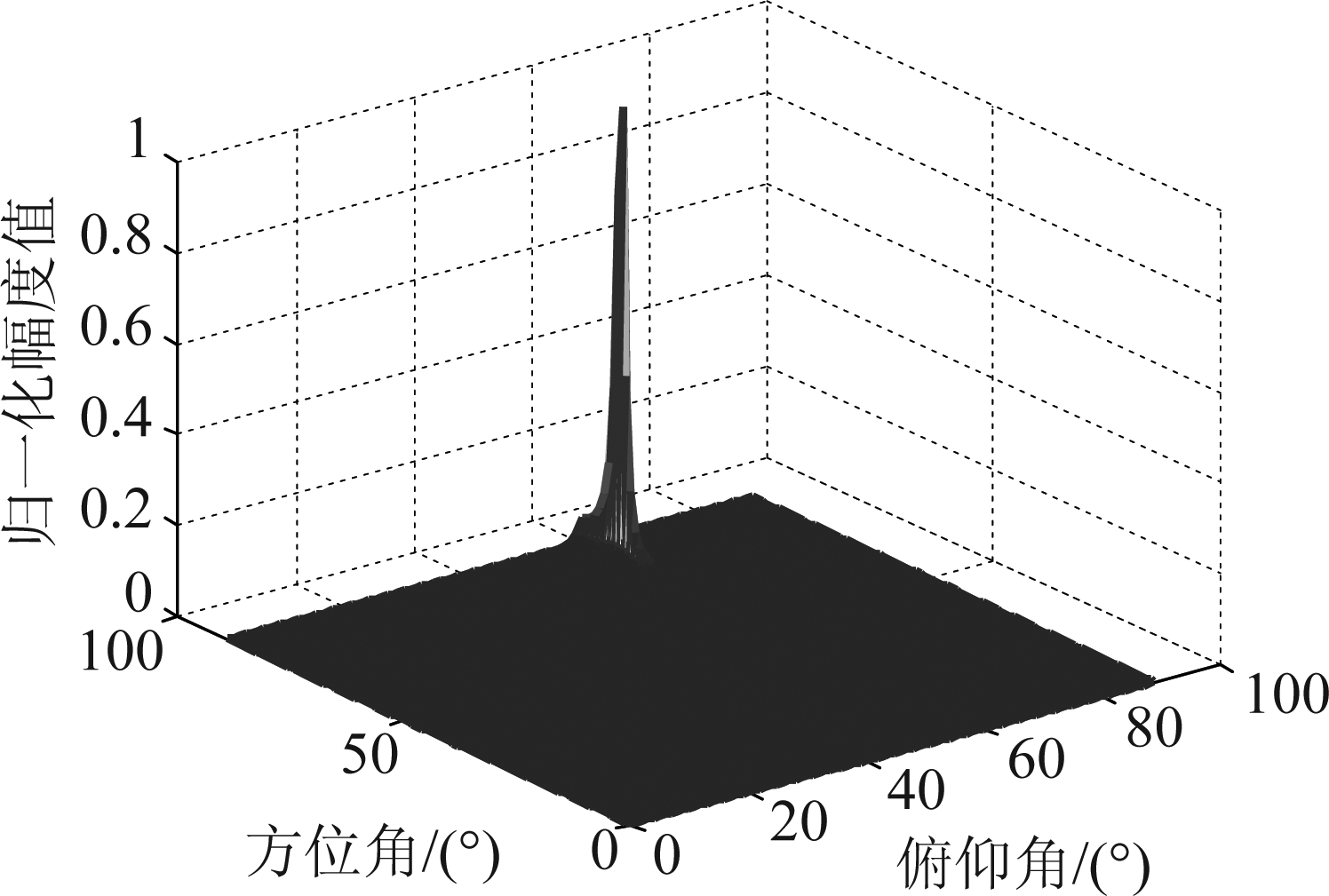
图2 信噪比10 dB时得到的二维空间谱
Fig.2 The two-dimensional spatial spectrum for SNR=10 dB
由图2可见,该方法估计得到的空间谱中谱峰非常尖锐,且估计值为[60°,80°],能够准确地实现目标二维波达方向估计。
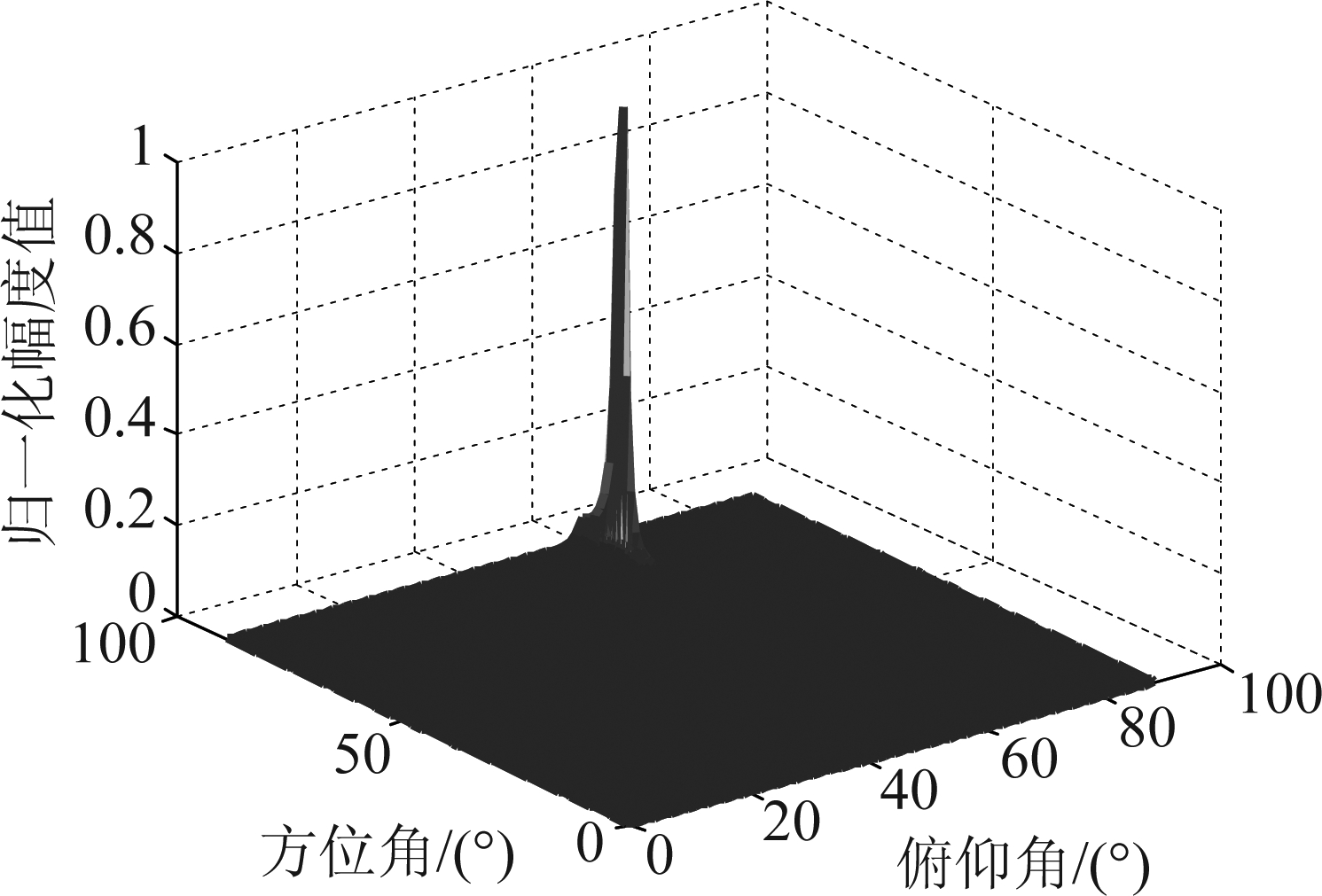
图3 信噪比0 dB时得到的二维空间谱
Fig.3 The two-dimensional spatial spectrum for SNR=0 dB
由图3可见,该方法估计得到的空间谱中谱峰呈现一定程度的下降,且估计值为[60°,80.5°],能够较为准确地实现目标二维波达方向估计。
下面对不同参数取值下,本文方法和MUSIC(Multiple Signal Classification, MUSIC)方法的性能进行了比较。在阵元数分别为8和16、快拍数为200、阵元基线长度为0.5 m、信噪比为-10 dB至5 dB、角度搜索步长为0.5°时,MSWF算法中的参考信号取基准传感器的接收信号,目标入射角度为[φ,θ]=[60.5°,80.5°],每个信噪比条件下进行50次仿真,得到了本文方法和MUSIC方法的角度估计均方差,结果如图4所示。
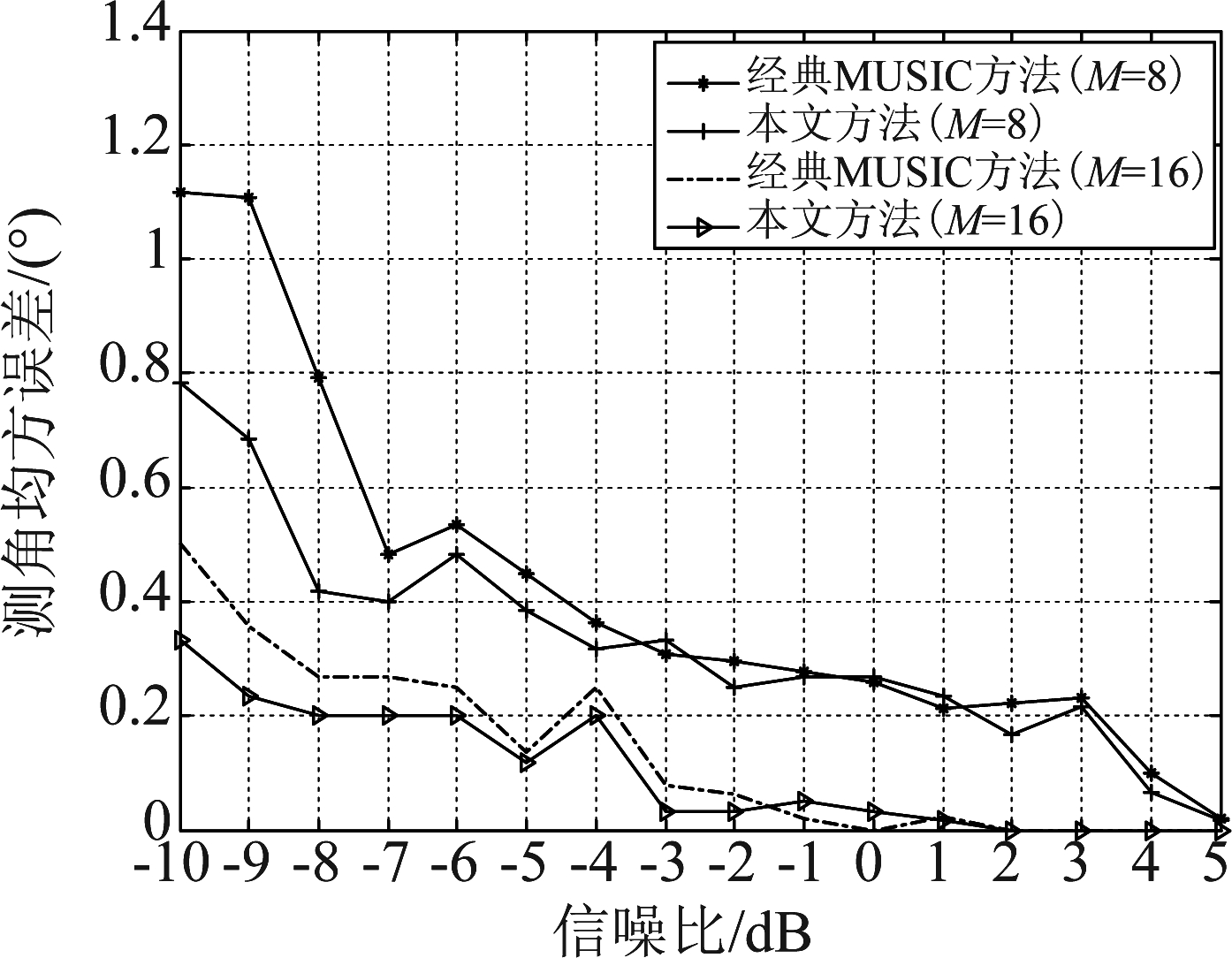
图4 不同信噪比下两种方法的测角均方误差仿真结果
Fig.4 The angle estimation results of two methods for different SNRs
在与图4同样的参数设置条件下,对MSWF算法中的参考信号分别取基准传感器的接收信号、各路接收信号的均值、接收信号互相关均值的第一行、接收信号互相关均值的列平均值,对其测角精度进行了仿真分析,得到的角度估计均方差如图5所示。
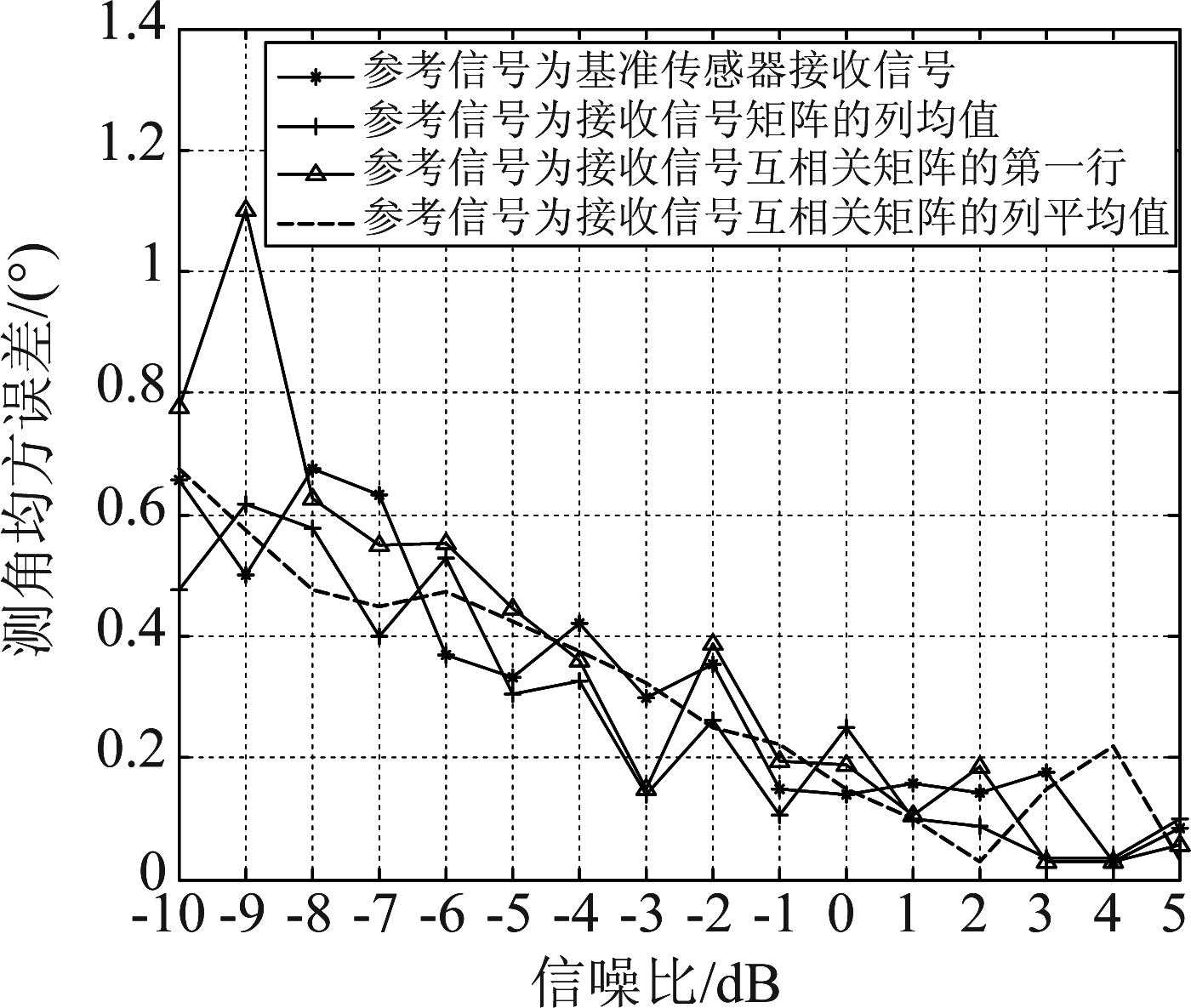
图5 不同信噪比下本文方法采用不同参考信号时的测角均方误差仿真结果
Fig.5 The angle estimation results of two methods with different reference signals for different SNRs
由图4可见,在阵元数目为16时,信噪比大于等于0 dB时,两种方法都可以达到较高的测角精度,总体而言,两种方法的测角精度在同一量级,在低信噪比情况下,本文方法具有比MUSIC方法更高的估计性能。由图5可见,在MSWF算法中,当其参考信号为接收信号矩阵的列均值时,本方法具有更高的测角精度。总体而言,取不同的参考信号,对MSWF算法的测角精度影响不大。
基于MSWF的时域宽带DOA快速估计方法,对于N个快拍、M个阵元、P个目标情况下,MSWF方法的计算量约为O(NPM2),常规MUSIC方法中的运算量主要体现在特征值分解过程,该过程需要计算维度为M的信号协方差矩阵并对其进行特征值分解,其计算量约为O(NM2+M3),因此,对于单目标探测的场景,在阵元数较低的情况下,两种方法的计算量相当,随着阵元数的增加,常规MUSIC方法的运算量迅速增加;在快拍数较大的情况下,两种方法的计算量差距并不明显。考虑到本文方法是基于海面单个高亚音速飞行目标的探测场景提出,其目标数为1且快拍数目也不会太大,因此本文方法在计算量方法比常规MUSIC方法具有明显优势。
在单个目标时,不同阵元数和快拍数下本文方法和MUSIC方法的理论计算量如图6所示。
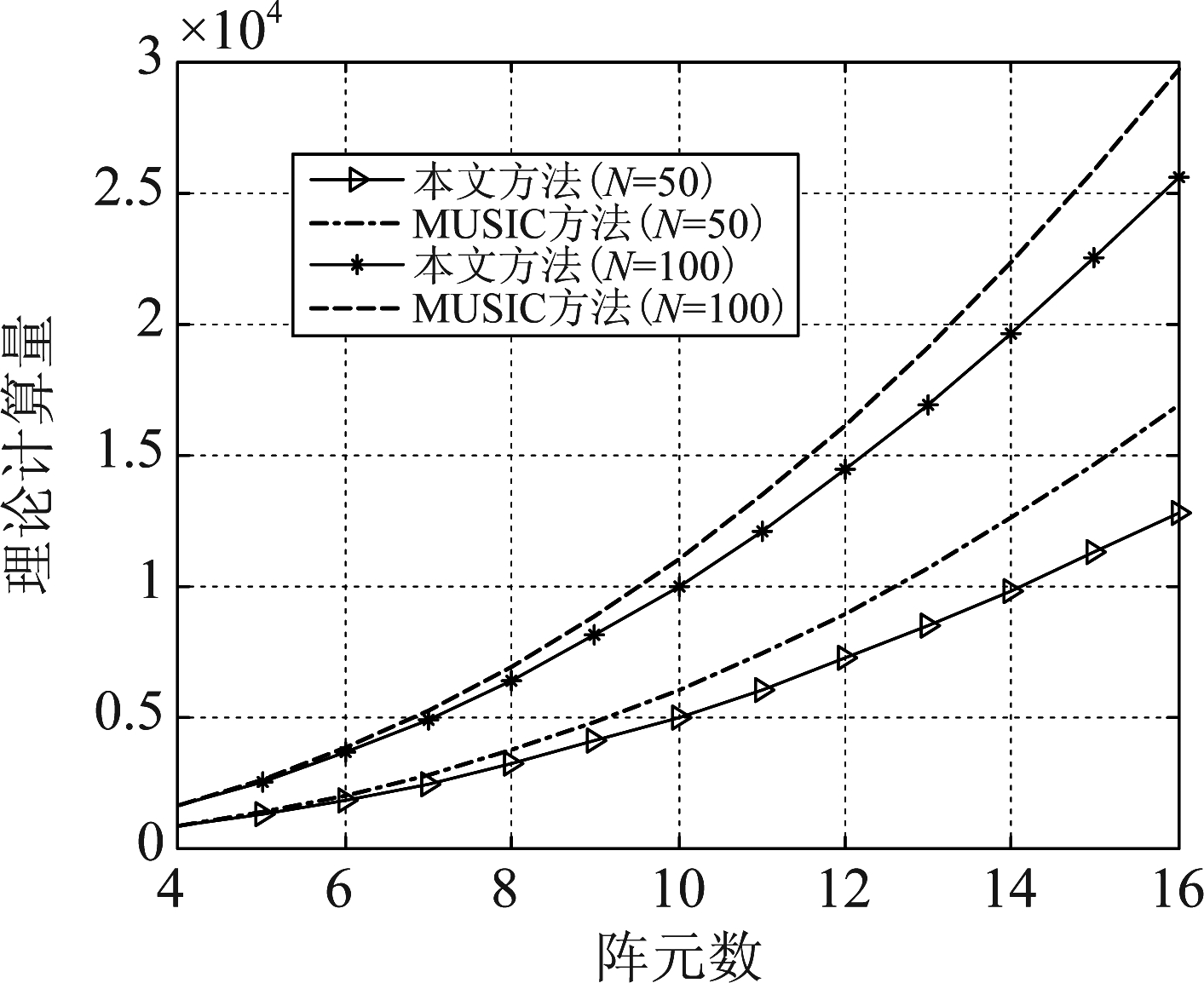
图6 本文方法和MUSIC方法的理论计算量比较图
Fig.6 The Theoretical Computations of the Proposed Method and MUSIC Method
如图6所示,在阵元数较大的情况下,本方法较MUSIC方法在计算量上具有明显优势;在快拍数较少的情况下,本方法在计算量上的优势更加明显。在阵元数为4、8、12、16和20,目标为1个,信噪比为0 dB,快拍数为100和200,阵元间距为0.5,搜索步长为0.5°的情况下,对两种方法运算所需的机器周期数进行了仿真,结果如图7所示。
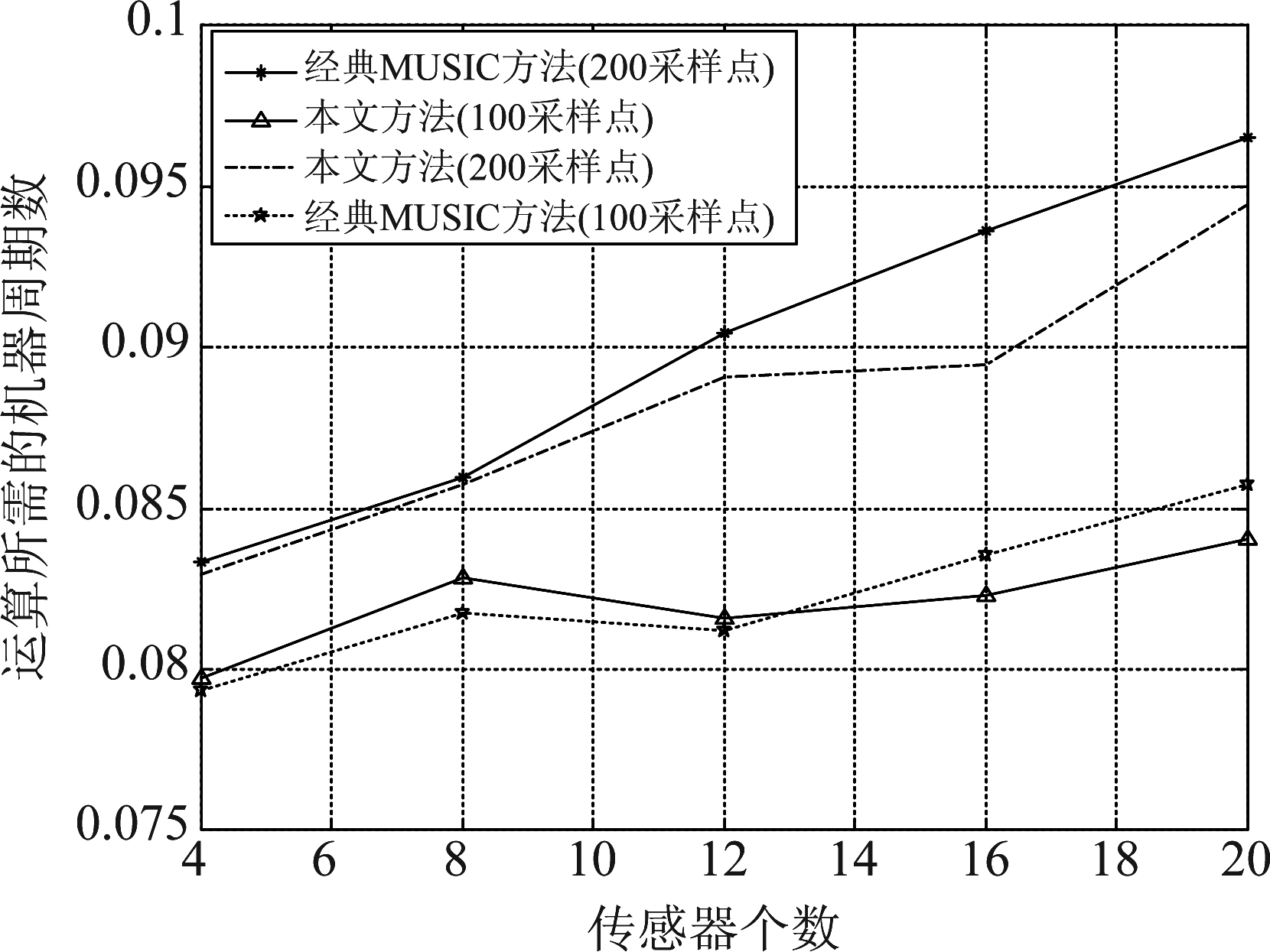
图7 本文方法和MUSIC方法的实际计算量仿真比较结果
Fig.7 The Computation Simulations of the Proposed Method and MUSIC Method
图7中给出的实际运算量变化趋势与理论结果吻合。在阵元个数较少时,考虑到变量定义及存储等相关过程,两种方法所需的实际机器周期数基本相同;随着阵元数量的增加,本文方法所需的实际机器周期数更少。同时,随着快拍数的减少,两种方法所需的实际机器周期数也逐渐减少。
本文方法的优势在于:① 本文通过构建均匀线性空间十字阵阵列的时域宽带信号模型,并采用基于MSWF的时域宽带DOA快速估计方法,有效降低了系统的计算复杂度,提高了高亚音速飞行目标估计的实时性;② 本文通过在时域构建宽带接收模型,有效拓展了MSWF的DOA估计方法的应用范围,为有效实现海上高亚音速飞行目标的声学探测提供了技术基础。
[1] 谢维, 刘小睿, 佟建飞, 等. 低信噪比下激波信号奇点检测方法[J]. 声学学报, 2018, 43(3): 495-503.
Xie Wei, Liu Xiaorui, Tong Jianfei, et al. Detection of Shock Wave Signals Using Singularity under Low SNR Conditions[J]. Acta Acustica, 2018, 43(4): 495-503.(in Chinese)
[2] 刘德耀, 陈志菲, 郭心伟, 等. 基于声学传感网络的弹着点定位系统[J]. 弹道学报, 2017, 29(2): 85- 89.
Liu Deyao, Chen Zhifei, Guo Xinwei, et al. Measurement System for Projectile Impact-Points Based on Acoustic Sensor Network[J]. Journal of Ballistics, 2017, 29(2): 85- 89.(in Chinese)
[3] 王磊, 陈昭男. 基于被动声学的超声速武器脱靶量解算方法研究[J]. 应用声学, 2018, 37(3): 385-390.Wang Lei, Chen Zhaonan. Supersonic anti-ship weapon miss-distance using passive acoustic location[J]. Journal of Applied Acoustics, 2018, 37(3): 385-390.(in Chinese)
[4] Kam W L, Brian G F. Flight Path Estimation Using Frequency Measurements from a Wide Aperture Acoustic Array[J]. IEEE Transactions on Aerospace and Electronic Systems, 2001, 37(2): 685- 694.
[5] 黄可生, 周一宇, 张国柱, 等. 基于Krylov子空间的宽带信号DOA快速估计方法[J]. 宇航学报, 2005, 26(4): 461- 465.
Huang Kesheng, Zhou Yiyu, Zhang Guozhu, et al. A Fast DOA Estimating Method of Wideband Signals Based on Krylov Subspace[J]. Journal of Astronautics, 2005, 26(4): 461- 465.(in Chinese)
[6] 智婉君, 李志舜. 一种宽带源高分辨率测向的降维处理方法[J]. 声学学报, 1999, 24(3): 288-294.
Zhi Wanjun, Li Zhishun. The Dimension reduction approach to direction finding of wide-band sources[J]. Acta Acustica, 1999, 24(3): 288-294.(in Chinese)
[7] 黄知涛, 王炜华, 姜文利, 等. 一种基于循环互相关的非相干源信号方向估计方法[J]. 通信学报, 2003, 24(2): 108-113.
Huang Zhitao, Wang Weihua, Jiang Wenli, et al. A Cyclic Cross-correlation Based Direction-of-arrival Estimation Approach[J]. Journal of China Institute of Communications, 2003, 24(2): 108-113.(in Chinese)
[8] William N G, James P R. Wideband Array Signal Processing Using MCMC Methods[J]. IEEE Transactions on Signal Processing, 2005, 50(2): 350-354.
[9] 佟建飞, 谢维, 胡小青, 等. 单声阵列的低空目标轨迹估计方法[J]. 声学学报, 2016, 41(5): 665- 673.
Tong Jianfei, Xie Wei, Hu Xiaoqing, et al. Fight path estimation of low altitude target with a single acoustic array[J]. Acta Acustica, 2016, 41(5): 665- 673.(in Chinese)
[10] 陈华伟. 低空目标声测无源定向理论与算法研究[D]. 西安: 西北工业大学, 2004: 77-102.
Chen Huawei. On passive acoustic direction finding for low altitude targets[D]. Xi’an: Northwestern Polytechnical University, 2004: 77-102.(in Chinese)
[11] 张君, 陈志菲, 常继红, 等. 声矢量锥形阵的高阶累积量波达方向估计[J]. 声学学报, 2019, 44(6): 970-985.
Zhang Jun, Chen Zhifei, Chang Jihong, et al. Direction-of-arrival estimation algorithm of pyramid-shaped acoustic vector sensor array based on higher-order cumulants[J]. Acta Acustica, 2019, 44(6): 970-985.(in Chinese)
[12] 王强, 何培宇. 具有高测向精度的最优麦克风对称阵设计研究[J]. 信号处理, 2015, 31(10): 1366-1371.
Wang qiang, He Peiyu. Study on the Design of Optimal Microphone Symmetrical Array with High Direction-Finding Accuracy[J]. Journal of Signal Processing, 2015, 31(10): 1366-1371.(in Chinese)
[13] 黄有方. 带通信号的直接采样和重构[J]. 信号处理, 1994, 10(1): 194-198.
Huang Youfang. Direct Sampling and Reconstruction of Bandpass signals[J]. Signal Processing, 1994, 10(1): 194-198.(in Chinese)
[14] 赵拥军, 李冬海, 赵闯, 等. 宽带阵列信号波达方向估计理论与方法[M]. 北京: 国防工业出版社, 2013: 176-179.
Zhao Yongjun, Li Donghai, Zhao Chuang, et al. Wideband Array Signal Direction of Arrive Estimation Theory and Methods[M]. Beijing: National Defense Industry Press, 2013: 176-179.(in Chinese)
[15] 刘剑, 宋爱民, 郭兴阳, 等. MUSIC测向算法的入射方向确定方法[J]. 信号处理, 2015, 31(8): 896-900.
Liu Jian, Song Aimin, Guo Xingyang, et al. Estimating Directions of Incident Signals in MUSIC Algorithm for Direction-finding[J]. Journal of Signal Processing, 2015, 31(8): 896-900.(in Chinese)
陈昭男 男, 1985年生, 山东烟台人。中国人民解放军91550部队工程师, 主要研究方向为阵列信号处理、目标探测与跟踪、信息融合处理等。
E-mail: chzhnan12@163.com
王 磊 男, 1979年生, 辽宁抚顺人。中国人民解放军91550部队高级工程师, 主要研究方向为目标探测与跟踪、信息融合处理等。
E-mail: 13793598901@163.com