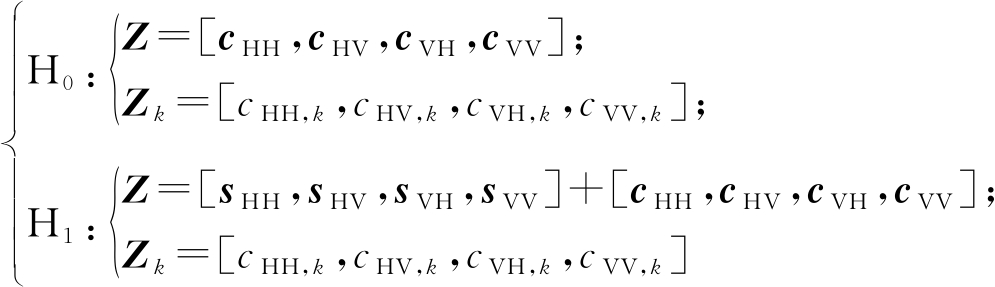
Reference format: Shi Sainan, Yang Jing, Wang Jie. Detection of Sea-surface Small Target Based on Multi-domain and Multi-dimensional Feature Fusion[J]. Journal of Signal Processing, 2020, 36(12): 2099-2106. DOI: 10.16798/j.issn.1003- 0530.2020.12.016.
随着隐身技术的发展以及探测目标的小型化趋势,海面小目标是对海雷达执行预警、探测和跟踪的重点和难点对象[1-3]。相对于军舰、轮船等目标,小船、潜望镜、漂浮物等小尺寸的海面目标回波弱,使得信杂比(Signal-to-Clutter Ratio, SCR)处于临界可检测状态。在多普勒频域,低速运动小目标的多普勒偏移落在海杂波主杂波带内,这加大了高分辨海杂波背景下的小目标检测的难度。
长时间观测积累是提升目标回波SCR和检测性能的有效途径[4-5],适用于岸基、舰载等低速运动平台。在几百毫秒甚至秒级观测时间下,海杂波在时间上非平稳且纹理具有时变特性[6-7],传统的基于杂波模型的最优检测器性能损失严重。为此,学者引入分形理论描述海面回波的粗糙和不规则程度,提出了基于Hurst指数的检测器[8-9],打破了能量为主的传统检测框架。分形类方法结构简单,但需要几秒以上的观测时间。针对单一特征检测概率低的问题,Shui提出了基于相对幅度、相对多普勒峰高和相对向量熵的三特征检测器[10],联合了时域、频域的特征优势,开启了多维特征的检测框架。Shi提出了时频域的三特征检测器,充分挖掘了目标和海杂波在二维时频域的特性[11]。依据不同极化的散射物理机理,Xu提出了基于极化三特征的检测器[12],反映了海杂波和含目标回波在面散射、二面角散射、体散射上的能量差异性;针对回波在极化四通道的不同特性,Xu提出了基于四通道融合的三特征检测器[13],对四种极化通道的数据进行融合后提取时域、频域特征。更多特征的联合带来了检测性能的提升,但同时带来了高维分类器设计的难点。Zhou提取了时域分形特征和频域分形特征以及频域相对峰高比特征,提出基于决策树的三特征检测器,在3D特征空间中采用决策树实现虚警可控的判决区域,但未涉及更高维度的运用。Shui提出了基于B氏距离的特征压缩的特征检测器[14],将多维特征压缩到3D特征空间,采用快速凸包算法实现分类器判决区域划分。因此,多维特征检测方法的关键在于特征提取和特征域分类器设计[15-16],需要进一步平衡维度信息的增加和高维分类器设计困难两者之间的矛盾。
本文提出基于多域多维特征融合的检测方法,从时域、频域、时频域、极化域等多域提取多维特征,以扩展维度信息。通过极化域特征线性加权融合和特征域基于主成分分析的线性融合,将高维特征压缩成3D特征,实现异常检测判决。基于IPIX实测数据[17]验证了所提检测器性能的高效性和稳健性,可运用于岸基、舰载等满足长时观测要求的平台。
假设对海雷达系统具有HH、HV、VH、VV四种全极化通道,并且能同时接收到四个极化通道的回波数据。当四个极化通道的接收回波向量Z=[zHH,zHV,zVH,zVV]进行联合检测时,雷达目标检测问题归为以下的二元假设检验[2- 6]:
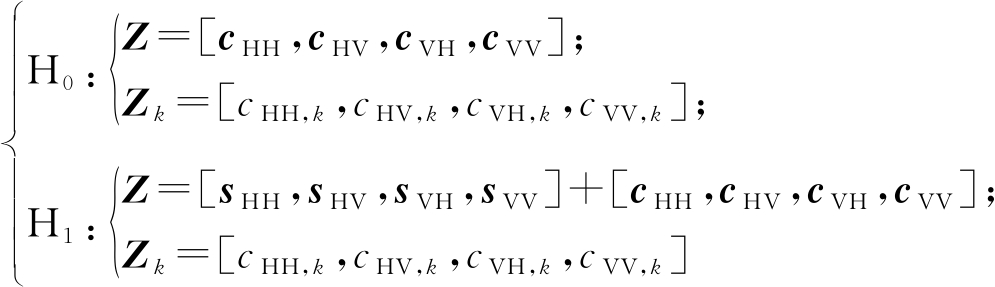
(1)
其中,Z表示四极化通道待检测单元(Cell Under Test, CUT)的观测矩阵,Zk=[zHH,k,zHV,k,zVH,k,zVV,k],k=1,2,...,K,表示第k个距离单元的参考矩阵,K表示CUT周围的参考单元数目,cHH、cHV、cVH、cVV分别表示四种极化下的海杂波向量,sHH、sHV、sVH、sVV分别表示四种极化下的含目标回波向量。注意,所有向量的维度为N,N表示脉冲数目。在H0假设下,观测矩阵为纯杂波数据;在H1假设下,观测矩阵为含目标回波数据。检测的本质就是判别观测矩阵属于哪种假设。
在长时观测下,高分辨海杂波具有非均匀、非平稳和非高斯特性,很难建立简单的数学模型进行描述。因此,长时观测下不适合直接采用短时下的自适应相干检测算法[18-20]。基于多维特征的检测方法是一种可行的有效途径。该方法从时域、频域、时频域等多个域提取海杂波和含目标回波的差异性,并通过多维特征表征这些差异性,将检测问题转换到高维特征空间中的判决区域划分,进而实现海杂波背景下的小目标检测。多维特征提取是多维特征检测的关键和前提。下面,给出2个幅度特征、2个频域特征和3个时频特征的提取方式。
(1)幅度特征
从雷达回波幅度角度,海杂波和含目标回波在几何粗糙程度和能量上具有很大的差异性。对于回波向量z=[z(1),z(2),...,z(N)]T可看作是一个“随机游走过程”[8-9]。在尺度区间m∈[24,212]上,满足以下关系
![]()
m∈[24,212]
(2)
其中,Hurst在对数域中为拟合直线的斜率,称为观测向量幅度的Hurst指数。Hurst指数反映海杂波和含目标回波序列的粗糙程度差异性,记为第一个特征ξ1(z)。
相对平均幅度定义为
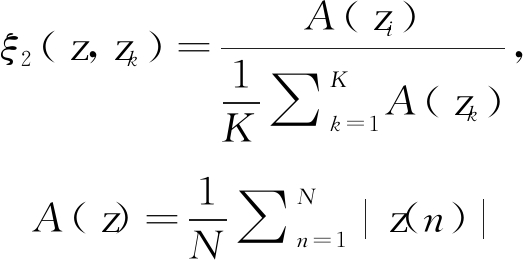
(3)
表明海杂波和含目标回波在能量上的差异性。
(2)频谱特征
雷达回波向量的多普勒幅度频谱为
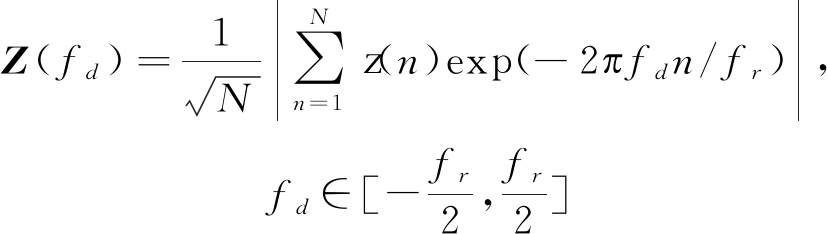
(4)
其中, fr为雷达的脉冲重复频率。针对海杂波频谱带宽和目标带宽的不同,相对多普勒峰高(Doppler Peak Height, DPH)定义为
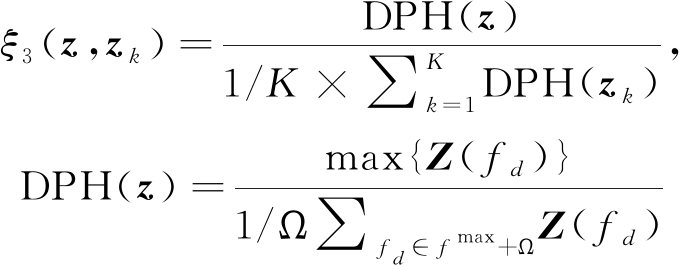
(5)
其中,DPH描述峰高值与周围局部区域Ω的比值。
相对向量熵(Vector Entropy, VE)描述的是归一化频谱的混乱程度,即
![]()
![]()
(6)
(3)时频特征
在一维频谱的基础上,二维时频描述了频谱随着时间的变化信息。为了增大含目标回波和海杂波在时频图上的差异性,归一化时频分布(Normalized Time-frequency Distribution, NTFD)定义为
NTFD(n,l|z,zk)=![]()
(7)
其中,TFD表示时频分布计算,均值函数的估计值为![]()
时频脊能量定义为
(8)
为了描述几何特征,在NTFD上生成一个二值图像,可获得的连通区域记为{Ω1,Ω2,...,ΩW}。那么,连通区域数目和最大区域尺寸特征定义为
(9)
综上,不同的特征描述了海杂波和含目标回波在时域、频域、时频域的不同特性。将多个特征进行联合,构建多维特征空间
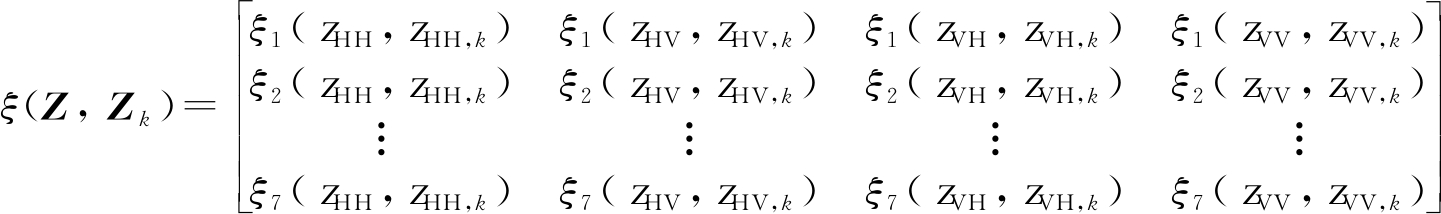
(10)
式(10)建立了不同极化通道下的特征空间矩阵。若将所有通道的特征构建为一个特征向量,将得到28维的高维特征向量,反映了海杂波和含目标回波在时域、频域、时频域、极化域等多域的差异性。
在高维特征空间中,分析各个特征之间的相关性和独立性。在概率统计中,采用相关系数ρ描述x和y两个量之间的相关性
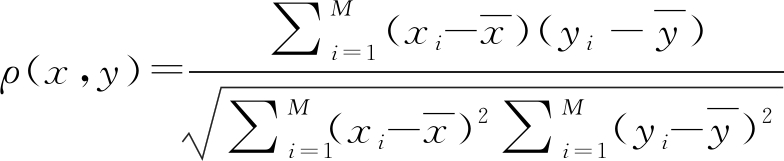
(11)
其中,M表示样本的总个数。为了更好的描述各个特征之间的关系,引入相关系数矩阵
Rρ=ρ(ξi,ξj),i, j=1,2,...,7
(12)
按照相关系数的值,在0.8~1.0之间具有极强相关,在0.6~0.8之间具有强相关,在0.4~0.6具有中等程度相关,在0.2~0.4属于弱相关,在0.0~0.2属于极弱相关或无相关。图1是7个特征的相关系数矩阵,可以发现,特征2和特征5之间存在强相关性;特征2和特征6存在中等程度相关。因此,可以进行特征融合,去除特征信息的冗余,同时减少高维空间的计算代价。
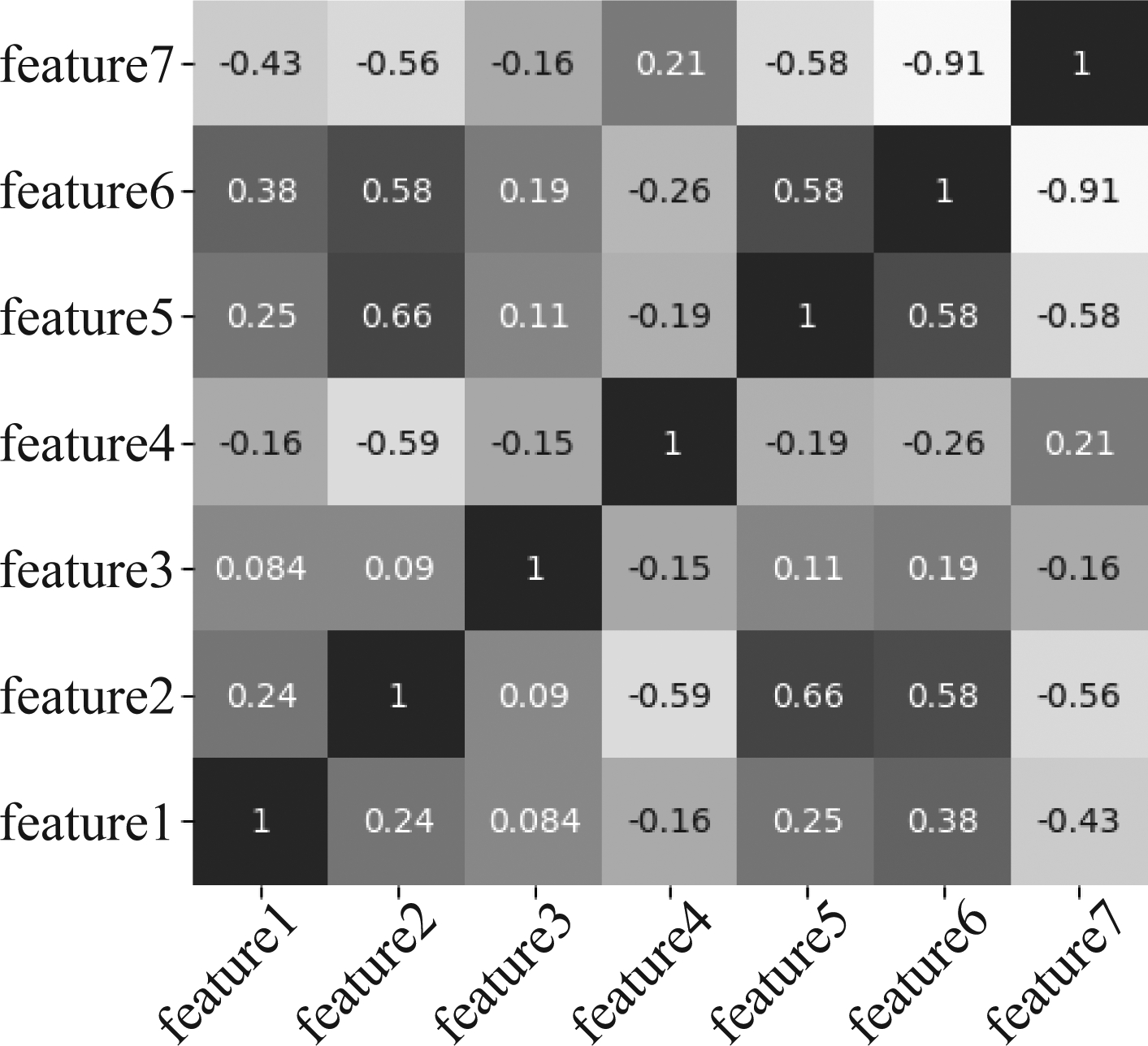
图1多维特征的相关系数
Fig.1 Correlation coefficient of multidimensional features
当雷达工作在不同极化方式下时,海杂波和含目标回波的特性会有较大的不同[6-21]。通常,HV和VH交叉极化下的SCR要比HH和VV同极化的SCR高,且海杂波谱的特性也随极化方式改变而改变。因此,本文提出先在各个极化通道独立提取多维特征,再采用极化域和特征域的特征线性融合的方法,旨在降低高维计算代价的同时获得多维高保真信息量。
针对每个极化通道内的特征尺度不同,采用归一化预处理将特征投影在同一尺度上。由于海杂波数据可大量获得,采用H0假设下大量海杂波数据的多维特征对每个极化方式下各个特征进行归一化处理,使得海杂波具有零均值和单位标准差。假设在第i特征维和第j个极化下存在M个H0样本,记为ξi, j(m|H0),m=1,2,…,M;i=1,2,…,7;j=HH,HV,VH,VV。因此,归一化预处理按如下计算
![]()
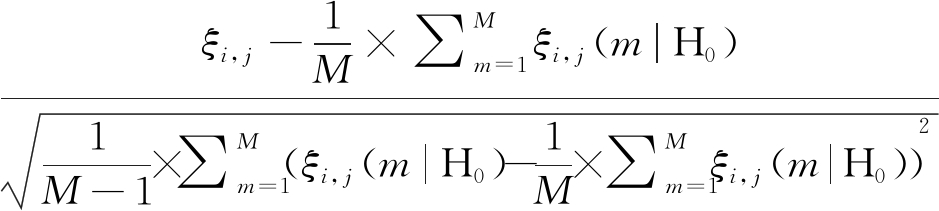
(13)
下面,从极化域和特征域出发,提出多域多维特征融合的方法,将检测问题从高维特征域转换到低维特征域,进而解决高维特征域判决区域设计问题。
(1)极化域
针对四通道的极化特性,在归一化预处理后,采用线性加权进行特征融合
![]()
i=1,2,...,7
(14)
其中,ω1,ω2,ω3,ω4∈[0,1]表示加权系数,满足ω1+ω2+ω3+ω4=1。加权系数的选择是特征融合的关键所在,这与四个极化通道的特性有关。通过极化域的特征融合,将式(10)中的高维特征矩阵融合到七维特征向空间。
(2)特征域
考虑到特征域中高维计算量大和判决区域设计难,通过主成分分析(Principal Component Analysis,PCA)的方法[22-23],将高维特征向量降到低维特征空间,即进一步实现多域特征线性融合。
假设高维特征向量Y=[ξ1,ξ2,...,ξ7]T存在一个线性矩阵A能够将之投影到低维特征向量YL=[ξ1,ξ2,ξ3]T空间中,满足
YL=A×Y
(15)
其中,矩阵A称为投影矩阵,维度为3×7。值得注意的是,必须保证海杂波和含目标杂波采用相同的投影矩阵。由于海杂波样本可大量获得,采用H0假设下M个特征向量样本获得投影矩阵A。
下面给出投影矩阵A的计算方法,在高维特征空间中,记H0假设下的M个特征向量样本为{Ym,m=1,2,…,M},计算采样协方差矩阵为
(16)
其中,D和Σ分别是协方差矩阵R的特征向量矩阵和对角矩阵,Σ对角线上对应的是特征值。假设Σ的特征值分别为λ1,λ2,…,λ7且满足λ1>λ2>…>λ7,对应的特征向量分别为d1,d2,…,d7。那么,PCA的投影矩阵A由前3个最大特征值对应的特征向量构成,即A=[d1,d2,d3]T。PCA方法是按照类内最大方差进行线性投影降维,进一步实现特征域的特征融合。
通常,海杂波数据可大量获得。由于海面小目标空间分布的稀疏性、军事保密性以及随海况变化的多变性,很难获得大量的含目标回波数据。因此,海面目标检测不得不归于异常检测问题。在异常检测中,将大量海杂波看成正常样本,获取具有虚警可控的判决区域,而含目标回波为非正常样本。至此,检测问题转换为高维特征空间域的单分类器设计。
图2给出了基于多域多维特征融合(Multi-domain and Multi-dimensional Feature Fusion, MMFF)检测器的流程图。不同于传统的特征检测器,将四种极化下的回波数据进行联合处理,提取了时域、频域、时频域、极化域的多维特征。并且,联合极化域和特征域的线性融合,将高维特征空间降到3D特征空间中,保证维度信息量的同时解决高维分类器设计问题。在3D特征空间中,采用快速凸包算法[10-13]获得虚警可控的判决区域。整个检测框架是一个开放式的特征架构,可以进一步提取其他维度的特征或者改变融合方式,甚至可以直接进行高维特征域的单分类器设计。
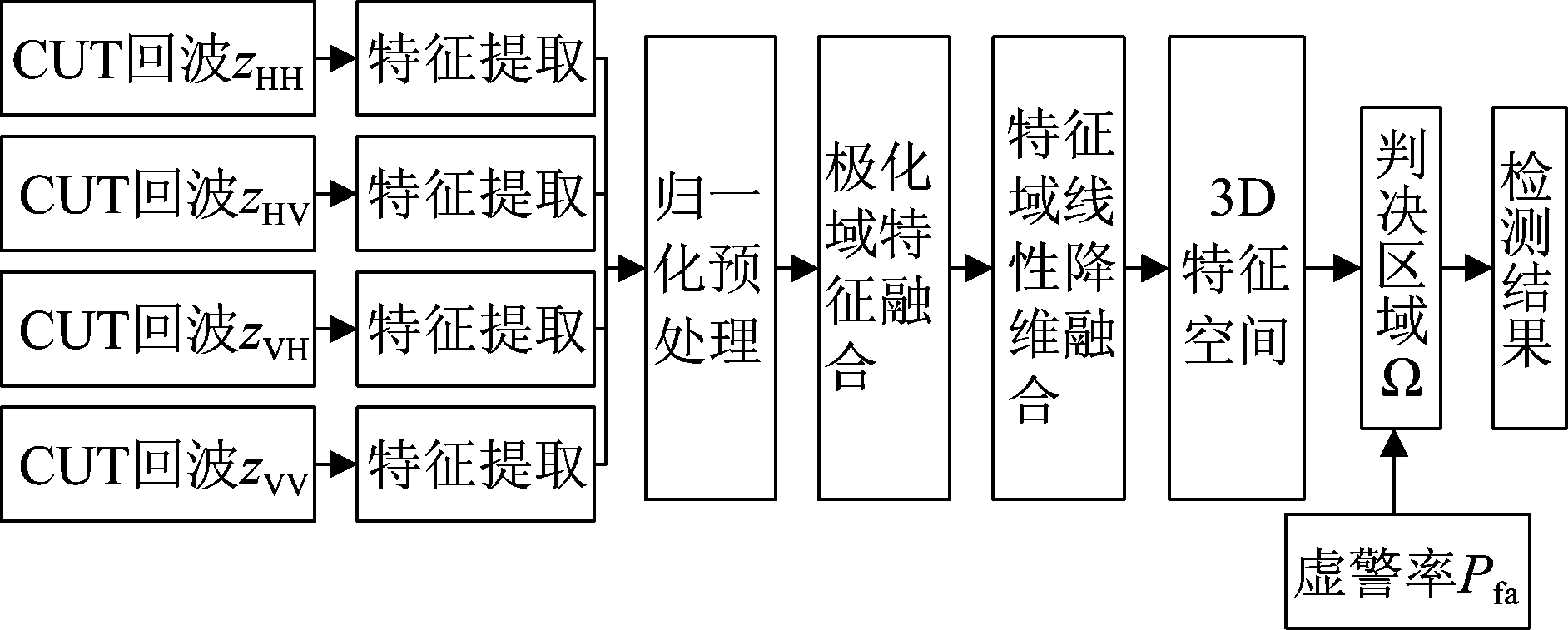
图2 基于多域多维特征融合的算法流程图
Fig.2 Flow diagram of algorithm based on multi-domain and multi-dimensional feature fusion
在3D特征空间中,双重融合后的3个特征受到信杂比、雷达工作参数、海洋环境等多个因素影响。图3演示了判决区域获取过程的示意图,红色圆圈代表含目标回波,蓝色方块代表海杂波,判决区域由多面体凸包构成。从图3中可知,判决区域将大量的海杂波包围,在判决区域外面的海杂波为虚警样本。检测时,当CUT的融合特征向量处于判决区域之外时,则判定为含目标回波;否则,判定为无目标。
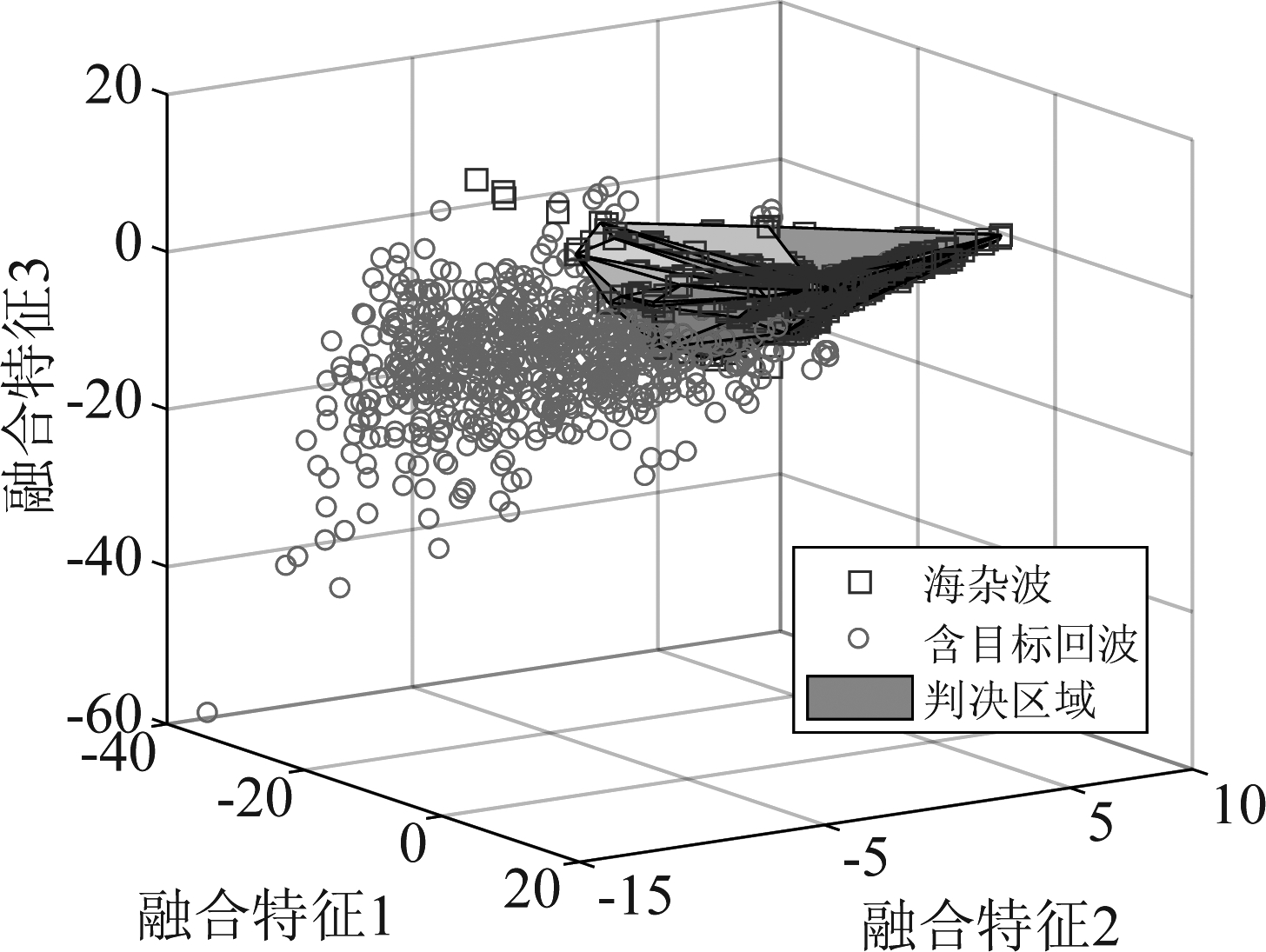
图3 3D特征空间中判决区域
Fig.3 Decision region in 3D feature space
在进行极化域线性加权特征融合时,需要确定最优的加权系数。在给定虚警率Pfa=10-3下,MMFF检测器的最优加权系数将获得最大检测概率Pd,即满足如下的优化问题
max{Pd}
st.0≤ω1,ω2,ω3,ω4≤1;ω1+ω2+ω3+ω4=1;Pfa=10-3
(17)
由于无法获得Pd和Pfa的具体数学解析表达式,因而无法采用数学优化方法进行求解。所以,式(17)只能借助全局遍历搜索方法求解。但是,全局搜索多个变量的值具有很大的计算开销。注意到多个特征在归一化预处理时已去中心化,所有特征处于同一尺度。因此,从理论上来说,可近似地将不同极化下的特征看成具有相同的权值。
实验中,采用网上公认的IPIX雷达小目标测试数据库[17]。该数据采集于1993年的加拿大东海岸,X波段实验雷达具有HH、HV、VH和VV四种极化方式,距离分辨率30 m,脉冲重复频率fr=1000 Hz。测试目标为锚固定的漂浮小球,直径1 m。
(1)不同探测环境下检测性能对比
设置累积脉冲数为N=512,对应观测时间0.512 s,参考单元数目K=10,虚警率Pfa=10-3。10组IPIX实测数据代表不同的海洋环境,具体的风速、浪高等环境参数可参考文献[13-17]。
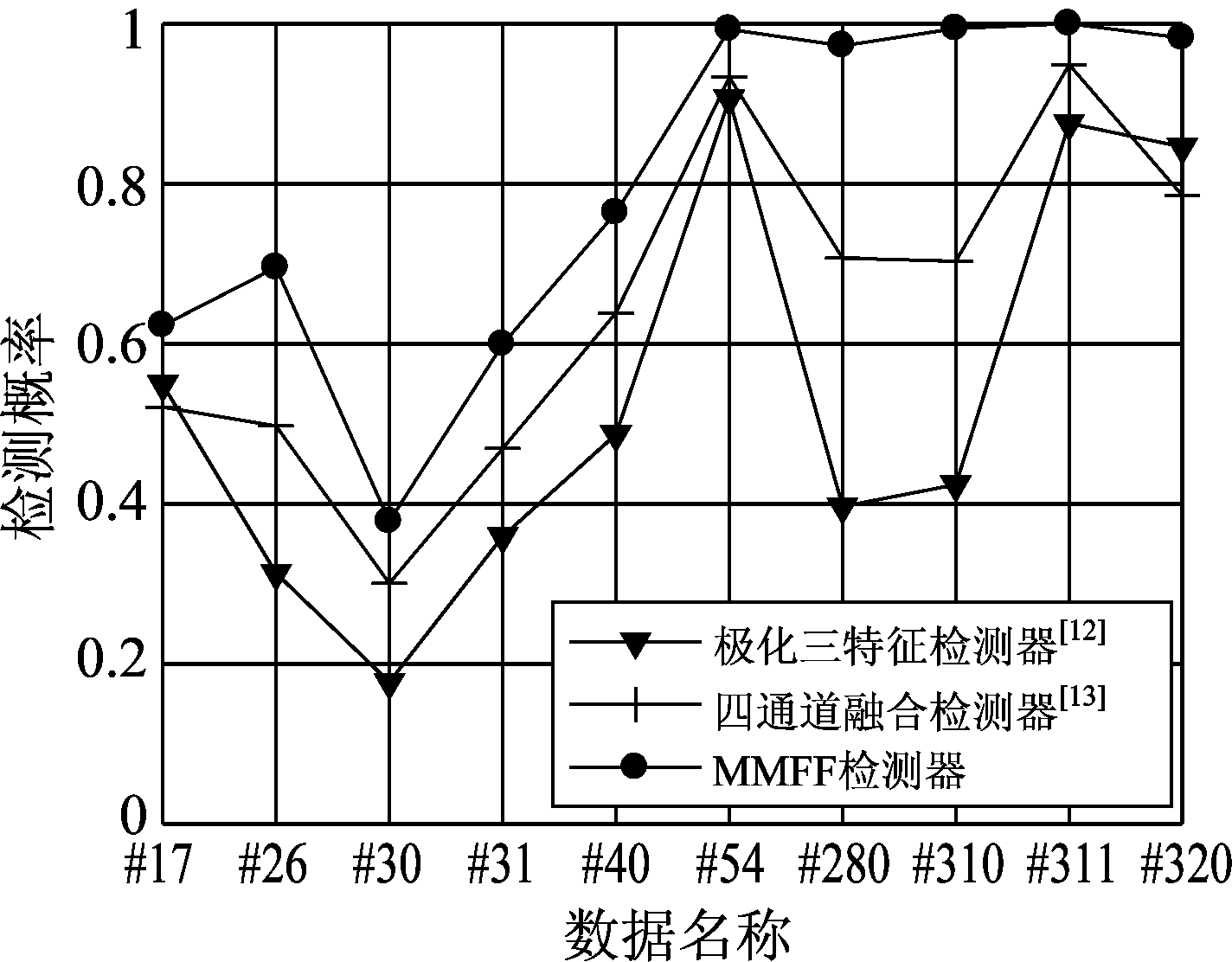
图4 三种极化检测器的检测结果(N=512, Pfa=10-3)
Fig.4 Detection results of three polarization detectors (N=512, Pfa=10-3)
图4是三种极化检测器的检测结果。从整体上来看,基于极化三特征的检测器[10]的检测性能最差,平均检测概率为0.533。事实上,从面散射、体散射和二面角散射的极化散射机理出发,基于极化三特征的检测器[12]提取了这三种散射方式的能量信息,缺少了频域信息。基于四通道融合的检测器[13]的性能次优,平均检测概率为0.621,这得益于该检测器提取了时域、频域、极化域的多维特征。相对于上述两种检测器,本文提出的基于多域多维特征融合的检测器的性能最优,平均检测概率为0.801,性能提升显著。在时域、频域、极化域三个维度的基础上,MMFF检测器进一步提取了含目标回波和海杂波在时频域上的差异性,具有4个域的信息量。值得注意的是,三种极化检测器最终都转换到3D特征空间中进行判别。因而,相对于现有的这两种极化检测器,MMFF检测器只增加了少量多维特征提取和线性特征融合的计算代价,不会额外增加高维度的计算代价。
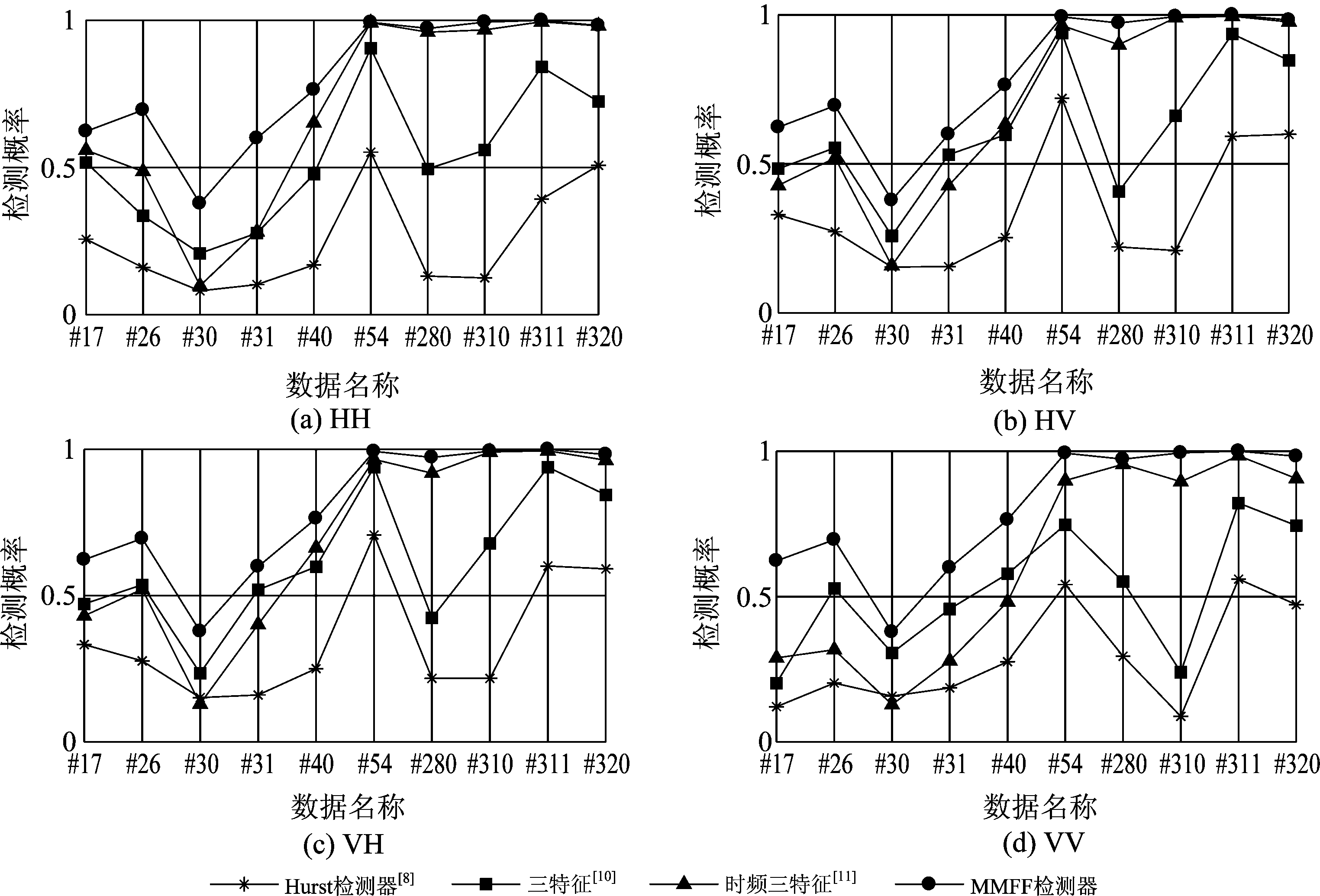
图5 不同极化下四种检测器性能对比(N=512, Pfa=10-3)
Fig.5 Performance comparison of four detectors at different polarization (N=512, Pfa=10-3)
图5是不同极化下四种检测器的性能对比。基于Hurst指数的检测器[8]的检测性能最差,HH、HV、VH、VV四种极化下10组数据的平均检测概率分别为0.248、0.351、0.351、0.290,其主要原因在于Hurst指数的提取需要秒级以上观测时间并且受制于单一特征的局限。在四种极化下,基于三特征的检测器[10]的平均检测概率分别为0.534、0.622、0.619、0.518,基于时频三特征的检测器[11]为0.698、0.699、0.698、0.614。前者提取了时域和频域两个域的特征,在前五组数据性能较好;后者提取了时频域的3个特征,在后五组数据性能较好。从实验结果表明:这两种检测器具有互补特性,适用于不同的海洋环境下。然而,本文提出的MMFF检测器在10组数据条件下保持最佳性能,平均检测概率为0.801,充分挖掘了时域、频域、时频域、极化域等多域的特性,满足实际雷达探测环境下的稳健性和高效性要求。
(2)不同参数下性能对比分析
图6是三种极化检测器的接收机性能(Receive Of Characteristic, ROC)曲线。设置脉冲累积数N=512,参考单元数目K=10,虚警率Pfa从0.001到0.1,纵轴表示10组数据的平均检测概率。本文提出的MMFF检测器具有最优的检测性能,整体平均检测概率在0.8以上。相对于四通道融合检测器[13]和极化三特征检测器[12],MMFF检测器的平均检测性能提升了25%和50%,充分展现了时域、频域、时频域、极化域等多域特征联合的优势。
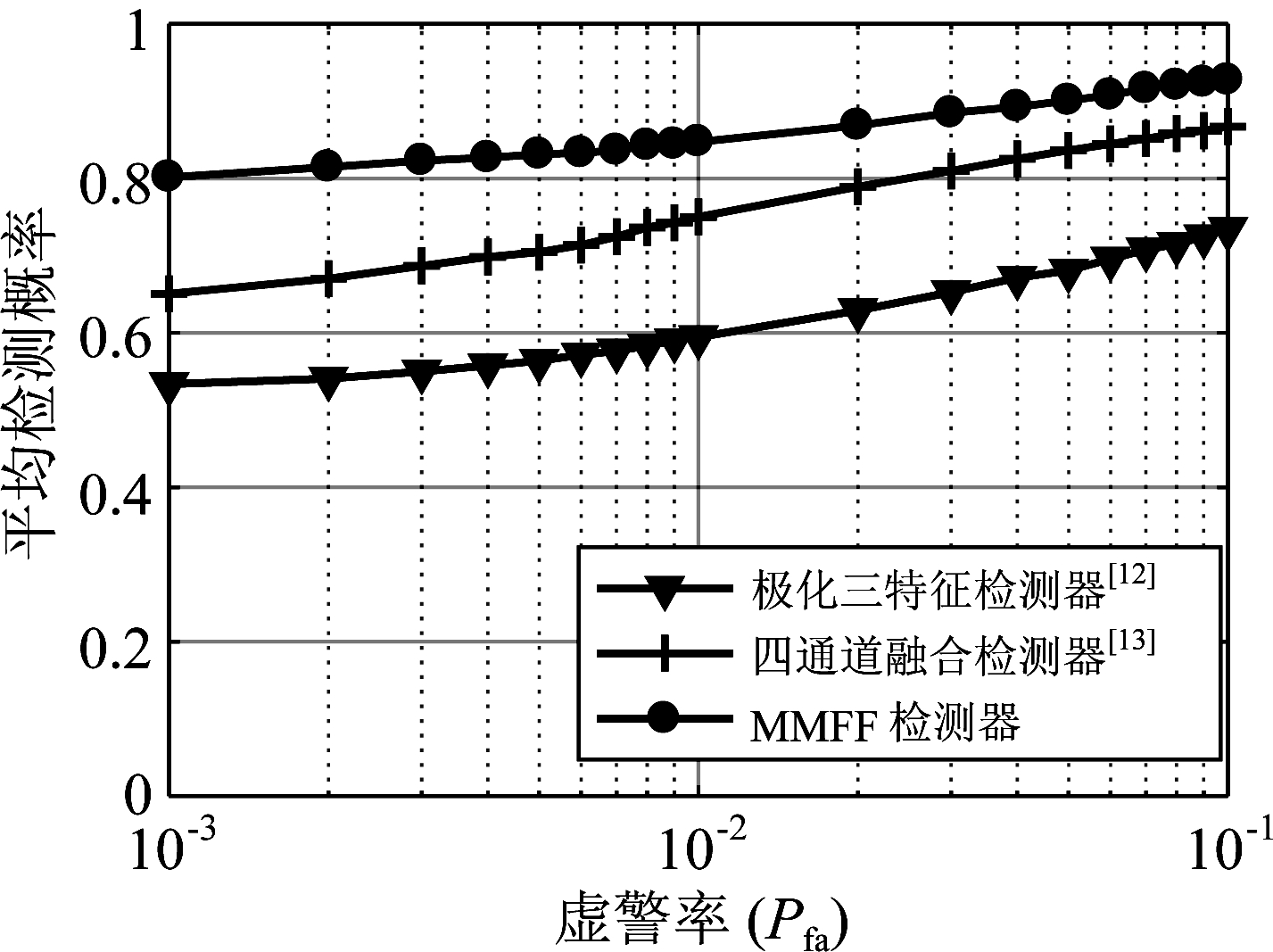
图6 三种极化检测器的ROC曲线(N=512)
Fig.6 ROC curves of three polarization detectors (N=512)
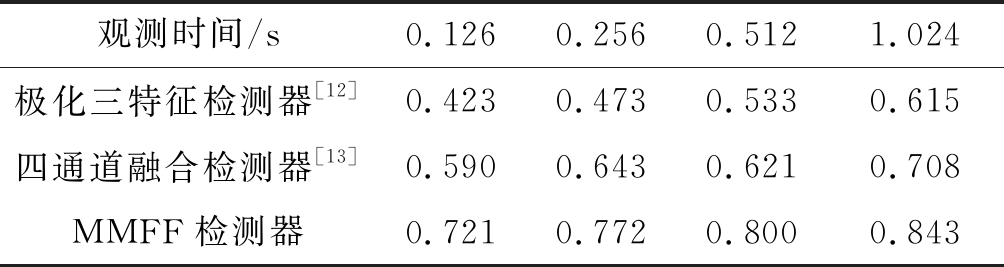
表1列出了不同观测时间下三种极化检测器的性能对比,观测时间分别从0.128 s、0.256 s、0.512 s到1.024 s依次增加。从表中结果可知,随着观测时间的不断增加,所有检测器的性能都有所改善,证实了长时累积观测是提高小目标性能的有效途径。同时,随着观测时间的增加,本文提出的MMFF检测器始终保持最优检测性能,10组数据的平均检测概率从0.721提升到0.843。对比极化三特征检测器[12]和四通道融合检测器[13],MMFF检测器性能提升的幅度最少,这主要由于后5组数据的检测概率在观测时间为0.128 s时已接近1。
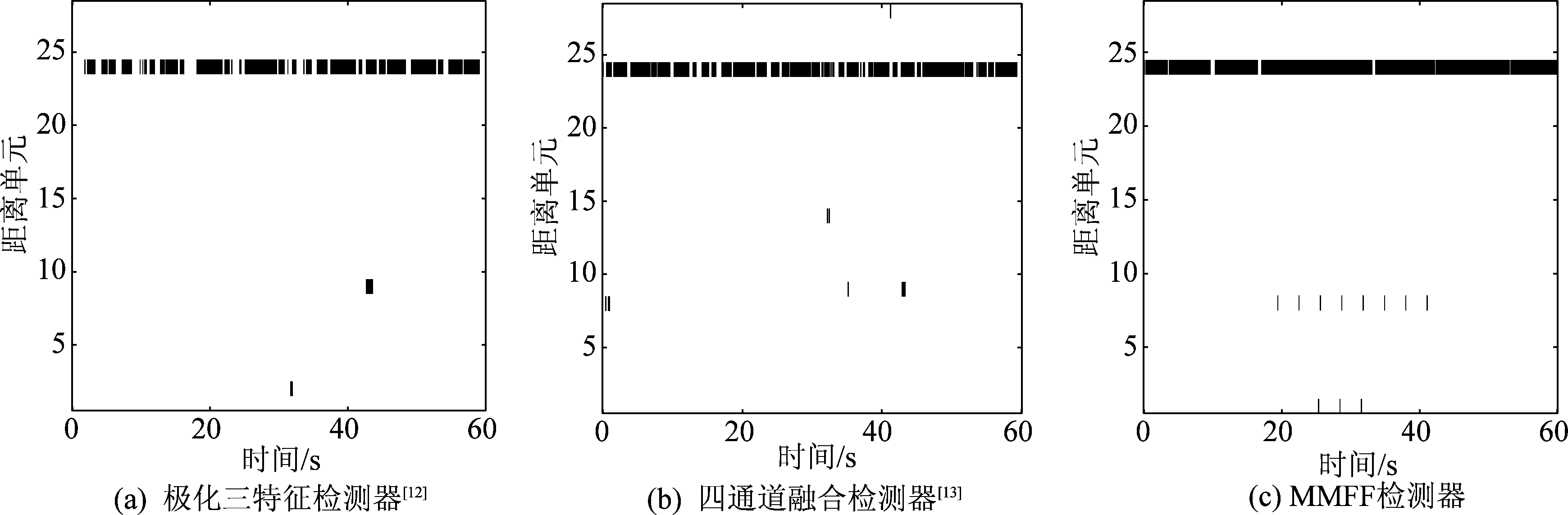
图7 三种检测器对运动小船的检测结果(N=512, Pfa=10-3)
Fig.7 Performance results of three detectors to small maneuvering boat (N=512, Pfa=10-3)
表1 不同观测时间下性能对比
Tab.1 Comparison performance at different observation time
观测时间/s0.1260.2560.5121.024极化三特征检测器[12]0.4230.4730.5330.615四通道融合检测器[13]0.5900.6430.6210.708MMFF检测器0.7210.7720.8000.843
(3)不同小目标类型下检测性能对比
下面进一步验证检测器对于不同类型小目标的检测性能。实验数据来自1998年采集的IPIX雷达数据库,数据名称为19980204_163113_ANTSTEP。测试目标为运动小船,观测时间内位于第24个距离单元。图7给出了极化三特征检测器[12]、四通道融合检测器[13]和MMFF检测器的检测结果,检测概率分别为0.684、0.794、0.985。因此,所提出的MMFF检测器能够运用于漂浮类物体、机动类小船等海面低速运动小目标的检测。
最后,从实验层面,讨论加极化域权系数对MMFF检测器的性能影响。考虑到HV和VH交叉极化的对称性,设定ω2=ω3。通过调整不同的加权系数,获得5种典型的融合情况,分别为HH极化占优(ω1=0.7)、HV极化占优(ω2=0.4)、VV极化占优(ω3=0.7)、HH和VV同时占优(ω1=ω4=0.4)、四种极化均衡情况(ω1=ω2=ω3=ω4=0.25)。图8是上述5种情况下的检测结果,10组数据的平均检测概率分别为0.783、0.791、0.762、0.785、0.801。结果表明:在四种极化均衡的情况下,MMFF检测器获得最优性能。此外,单一极化占优时,MMFF检测器的性能在某些情况下具有较大的波动,影响雷达性能的鲁棒性。这也验证了极化域的特征间具有互补性,在极化域占有相同的比重,均衡融合后实现整体稳健性能。因此,从更多域提取多维特征,有利于全面提升海面小目标的探测性能。
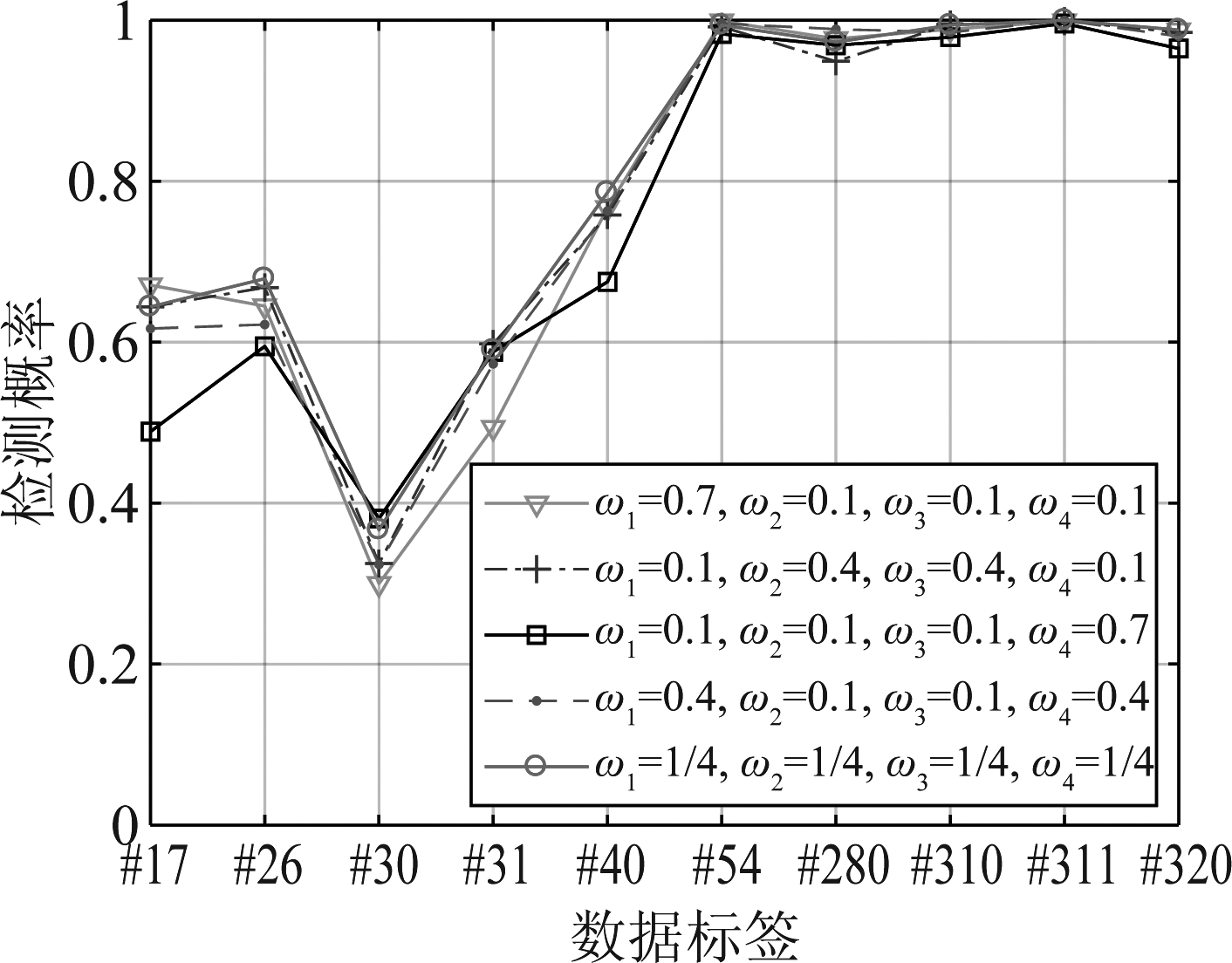
图8 加权系数对性能的影响(N=512, Pfa=10-3)
Fig.8 Influence of weighting coefficient on performance (N=512, Pfa=10-3)
针对高分辨海杂波下具有临界SCR的小目标检测问题,从时域、频域、时频域、极化域等多域提取多维特征,并通过极化域和特征域的双重线性融合,保证3维特征向量具有高维信息量和低维度计算代价。虽然特征融合减少了高维计算代价,但高维压缩到低维不可避免会损失一部分特征信息。后续可进一步研究高维特征域中的分类器设计问题,尽可能地保证特征信息的完整性,实现海面小目标探测性能的进一步提升。
[1] Li Y, Yang Y, Zhu X. Target detection in sea clutter based on multifractal characteristics after empirical mode decomposition[J]. IEEE Geoscience and Remote Sensing Letters, 2017, 14(9): 1547-1551.
[2] Petrov N, Chevalier Le F, Yarovoy A G. Detection of range migrating targets in compound-Gaussian clutter[J]. IEEE Transactions on Aerospace and Electronic Systems, 2018, 54(1): 37-50.
[3] Shi S, Liang X, Shui P, et al. Low-velocity small target detection with Doppler-guided retrospective filter in High-resolution radar at fast scan mode[J]. IEEE Transactions on Geoscience and Remote Sensing, 2019, 57(11): 8937- 8953.
[4] Li X, Cui G, Yi W, et al. Coherent integration for maneuvering target detection based on Radon-lv’s distribution[J]. IEEE Signal Processing Letters, 2015, 22(9): 1467-1471.
[5] Li X, Sun Z, Yi W, et al. Computationally efficient coherent detection and parameter estimation algorithm for maneuvering target[J]. Signal Processing, 2019, 155: 130-142.
[6] Ward K, Tough R, Watts S. Sea clutter scattering: the K distribution and radar performance[M]. London: The Institution of Engineering and Technology, 2013.
[7] 张玉石, 许心瑜, 尹雅磊, 等. L波段小擦地角海杂波幅度统计特性研究[J]. 电子与信息学报, 2014, 36(5): 1044-1048.
Zhang Yushi, Xu Xinyu, Yin Yalei, et al. Research on amplitude statistics of L-band low grazing angle sea clutter[J]. Journal of Electronics & Information Technology, 2014, 36(5): 1044-1048.(in Chinese)
[8] Hu J, Tung W, Gao J. Detection of low observable targets within sea clutter by structure function based multifractal analysis[J], IEEE Transactions on Antennas and Propagation, 2006, 54(1): 136-143.
[9] Li D, Shui P. Floating small target detection in sea clutter via normalised hurst exponent[J]. Electronics Letters, 2014, 50(17): 1240-1242.
[10] Shui P, Li D, Xu S. Tri-feature-based detection of floating small targets in sea clutter[J]. IEEE Transactions on Aerospace and Electronic Systems, 2014, 50(2): 1416-1430.
[11] Shi S, Shui P. Sea-surface floating small target detection by one-class classifier in time-frequency feature space[J]. IEEE Transactions on Geoscience and Remote Sensing, 2018, 56(11): 6395- 6411.
[12] Xu S, Zheng J, Pu J. Sea-surface floating small target detection based on polarization features[J]. IEEE Geoscience and Remote Sensing Letters, 2018, 15(10): 1505-1509.
[13] 许述文, 蒲佳. 基于四极化通道融合的海面漂浮微弱目标特征检测[J]. 信号处理, 2017, 33(3): 324-329.
Xu Shuwen, Pu Jia. Floating small targets detection in sea clutter based on Four-polarization-channels fusion[J]. Journal of Signal Processing, 2017, 33(3): 324-329.(in Chinese)
[14] Shui P, Guo Z, Shi S. Feature-compression-based detection of sea-surface small targets[J]. IEEE Access, 2020, 8: 8371- 8385.
[15] Zhou H, Jiang T. Decision tree based Sea-surface weak target detection with false alarm rate controllable[J]. IEEE Signal Processing Letters, 2019, 26(6): 793-797.
[16] 楼奇哲, 刘乐, 姚元. 采用卷积神经网络的海面多目标检测研究[J]. 信号处理, 2018, 34(9): 1053-1059.
Lou Qizhe, Liu Le, Yao Yuan. Multi-target detection in sea clutter with convolutional neural network[J]. Journal of Signal Processing, 2018, 34(9): 1053-1059.(in Chinese)
[17] Cognitive Systems Laboratory, McMaster University, Canada. The IPIX radar database[OL]. http:∥soma.mcmaster.ca∥ipix.php.2012.10.11.
[18] Sang K J, Gini F, Greco M V. Coherent radar target detection in heavy-tailed compound-Gaussian clutter[J]. IEEE Transactions on Aerospace and Electronic Systems, 2012, 48(1): 64-77.
[19] Zhou W, Xie J, Li G, et al. Robust CFAR detector with weighted amplitude iteration in nonhomogeneous sea clutter[J]. IEEE Transactions on Aerospace and Electronic Systems, 2017, 53(3): 1520-1535.
[20] Zuo L, Li M, Zhang X, et al. An efficient method for detecting slow-moving weak targets in sea clutter based on time-frequency iteration decomposition[J]. IEEE Transactions on Geoscience and Remote Sensing, 2013, 51(6): 3659-3672.
[21] 刘玉静, 张晓峰, 金威, 等. 基于实测数据的Ka波段海杂波极化特性研究[J]. 电波科学学报, 2019, 34(6): 687- 692.
Liu Yujing, Zhang Xiaofeng, Jin Wei, et al. Polarization characteristics of Ka-band sea clutter based on measured data[J]. Chinese Journal of Radio Science, 2019, 34(6): 687- 692.(in Chinese)
[22] Moore B. Principal component analysis in linear systems: controllability, observability, and model reduction[J]. IEEE Transactions on Automatic Control, 1981, 26(1): 17-32.
[23] Gu T. Detection of small floating targets on the sea surface based on multi-features and principal component analysis[J]. IEEE Geoscience and Remote Sensing Letters, 2020, 17(5): 809- 813.
施赛楠 女, 1990年生, 江苏南通人。南京信息工程大学讲师, 主要研究方向为雷达信号处理、微弱目标检测。
E-mail: snshi@nuist.edu.cn
杨 静 男, 1996年生, 江苏泰州人。南京信息工程大学硕士研究生, 主要研究方向为海面目标检测、人工智能识别。
E-mail: 2223032190@qq.com
王 杰 男, 1986年, 江苏泰州人。南京信息工程大学讲师, 主要研究方向为MIMO雷达信号处理、雷达通信一体化波形设计。
E-mail: wangjie110@nuist.edu.cn