低掠射微波雷达的海杂波多方位幅度特性分析
曹成会1,2 张 杰1,2 张 晰2 孟俊敏2 毛兴鹏1
(1. 哈尔滨工业大学电子与信息工程学院, 黑龙江哈尔滨 150001; 2. 自然资源部第一海洋研究所, 山东青岛 266100)
摘 要: 雷达处于低掠射角探测时,干涉、衍射以及遮挡等效应导致电磁波与海面的相互作用更加复杂,海杂波的非均匀、非高斯、非线性特性明显,使得海杂波建模难度大,同时,雷达海杂波在多方位下的特性是否存在差异也是一个问题,进一步增大了低掠射条件下海杂波的认知难度。为了提高海杂波的建模精度和多方位特性的认知,亟需开展低掠射雷达海杂波的多方位幅度特性分析。利用低掠射机载雷达数据,围绕雷达的低掠射和多方位两个特点,开展了多方位海杂波的幅度特性差异分析,在此基础上,利用多个海杂波模型对低掠射、多方位下的海杂波进行拟合优度分析。实现了低掠射角条件下海杂波的多方位特性差异认知,包括不同方位下的带宽和最优海杂波模型。实验结果表明,雷达前视状态带宽最窄,侧视最宽;对于多方位下的最优海杂波拟合,雷达前视时推荐G0分布,而侧视模式下,海杂波更接近K和GΓD分布。
关键词:低掠射角;海杂波;多方位;图形化拟合优度;直方图表示
中图分类号:TP732
文献标识码:A
DOI: 10.16798/j.issn.1003- 0530.2020.12.015
引用格式: 曹成会, 张杰, 张晰, 等. 低掠射微波雷达的海杂波多方位幅度特性分析[J]. 信号处理, 2020, 36(12): 2085-2098. DOI: 10.16798/j.issn.1003- 0530.2020.12.015.
Reference format: Cao Chenghui, Zhang Jie, Zhang Xi, et al. Multi-azimuth Amplitude Analysis of Sea Clutter At Low Grazing Angle[J]. Journal of Signal Processing, 2020, 36(12): 2085-2098. DOI: 10.16798/j.issn.1003- 0530.2020.12.015.
文章编号: 1003-0530(2020)12-2085-14
收稿日期:2020-11-11;修回日期:2020-12-24
基金项目:国家重点研发计划项目(2017YFC1×××201);国家自然科学基金项目(U2006207,61971455)
Multi-azimuth Amplitude Analysis of Sea Clutter At Low Grazing Angle
Cao Chenghui1,2 Zhang Jie1,2 Zhang Xi2 Meng Junmin2 Mao Xingpeng1
(1.School of Electronics and Information Engineering, Harbin Institute of Technology, Harbin, Heilongjiang 150001, China; 2. First Institute of Oceanography, Ministry of Natural Resources, Qingdao, Shandong 266100, China)
Abstract: At low grazing angle, the interaction of electromagnetic wave and the sea surface is more complex due to the interference, diffraction and shade effect. The non-uniform, non-Gaussian and nonlinear characteristics of sea clutter make it difficult to model. Furthermore, the characteristic difference of radar sea clutter under multi-azimuth angle increase the cognitive difficulty. To better understand sea clutter, multi-azimuth amplitude analysis of sea clutter was carried out at low grazing angle by using the airborne radar data. On the basis, the goodness of fit of sea clutter models was analyzed at different azimuth angles. The results show that the bandwidth is the narrowest at forward-looking and widest at side-looking. For multi-azimuth sea clutter modeling, G0 distribution is recommended in forward -looking, and K and GΓD are recommended in side-looking.
Key words: low grazing angle; sea clutter; multi-azimuth; graphical goodness of fit; histogram distribution
1 引言
雷达进行海上探测时,接收的回波信号中除了感兴趣的目标回波外,还包含噪声、干扰、海杂波等,其中海杂波功率水平较高,非高斯、非平稳特性显著,且其影响因素复杂多变,是制约雷达海上探测性能的主要因素。因此,开展海杂波特性的研究,掌握海杂波的变化规律是改进和发展海杂波抑制和目标检测算法的基础。
为了准确的描述海杂波的幅度特性,研究者们开展了许多海杂波探测实验[1],并基于实验数据发展了一系列的分布模型,如Log-normal[2]、Weibull[3]、K[4]、G0和广义伽马分布(GΓD)[5]等,广泛应用于中等分辨率雷达的海杂波幅度建模,进而进行目标检测[6- 8]。其中,K和G0分布是基于物理模型推导的,考虑了海面后向散射的物理机制,而Log-normal分布、Weibull分布和GΓD为实验得到的经验模型。Log-normal分布适用于动态范围较大、拖尾程度较重情况下的海杂波建模问题,Ai等人[9]利用Log-normal分布描述海杂波,并基于此提出了一种新的双参数恒虚警率检测器,得到了较好的目标检测性能。Weibull分布[10]也是用于描述海杂波非瑞利特性的模型,实验结果表明其拖尾程度介于瑞利模型和对数正态模型之间,适用于较均匀情况下的海杂波建模问题。Jakeman等人[4]提出的K分布模型能够表示海杂波的时间和空间相关性,是表征非均匀海杂波的理想分布模型。Wackermann等人[11]利用K分布对海杂波的概率密度函数(PDF)进行拟合,证明了K分布可用于沿海地区的船舶自动检测。Xin等人[12]利用瑞利分布、威布尔分布和K分布对机载圆扫低分辨率海杂波数据建模,并对其拟合优度进行分析。G0分布的参数对区域的均匀程度非常敏感,实验证明G0分布模型适合于非均匀或极其非均匀区域的杂波建模[13]。对于GΓD,Martín-de-Nicol s等人[14]和Gao等人[15]的实验结果证明,在不同极化和海况下GΓD的拟合精度优于瑞利分布、对数-正态分布和K分布等。由于海杂波是非常复杂的,上述海杂波模型并不总是准确的,海况、风速、掠射角、方位角和频率等的变化会导致某些模型失配[16]。为了进一步提高海杂波的建模精度,Alpha-stable分布、KA分布和复合高斯分布等模型被用于海杂波建模。Alpha-stable分布是基于广义中心极限定理发展而来,能很好地描述非高斯分布的概率模型,Liu等人[17]利用Alpha-stable分布推导了不同CFAR检测器的表达式,并评估了各个检测器的目标检测性能,且性能优于移动目标检测方法(MTD)。Watts等人[18]将带有海尖峰的海杂波建模为KA分布,KA分布在尾部区域具有较好的拟合性能,但是KA分布的主要缺点是其概率密度函数(PDF)不能显式表示,需要对其进行数值计算,计算成本较高。Balleri等人[19]将实测杂波数据建模为逆伽马纹理的复合高斯模型,并对逆伽马分布的参数进行估计。丁昊等人[20]综述了海杂波的特性,以及典型幅度分布模型的适用性。
s等人[14]和Gao等人[15]的实验结果证明,在不同极化和海况下GΓD的拟合精度优于瑞利分布、对数-正态分布和K分布等。由于海杂波是非常复杂的,上述海杂波模型并不总是准确的,海况、风速、掠射角、方位角和频率等的变化会导致某些模型失配[16]。为了进一步提高海杂波的建模精度,Alpha-stable分布、KA分布和复合高斯分布等模型被用于海杂波建模。Alpha-stable分布是基于广义中心极限定理发展而来,能很好地描述非高斯分布的概率模型,Liu等人[17]利用Alpha-stable分布推导了不同CFAR检测器的表达式,并评估了各个检测器的目标检测性能,且性能优于移动目标检测方法(MTD)。Watts等人[18]将带有海尖峰的海杂波建模为KA分布,KA分布在尾部区域具有较好的拟合性能,但是KA分布的主要缺点是其概率密度函数(PDF)不能显式表示,需要对其进行数值计算,计算成本较高。Balleri等人[19]将实测杂波数据建模为逆伽马纹理的复合高斯模型,并对逆伽马分布的参数进行估计。丁昊等人[20]综述了海杂波的特性,以及典型幅度分布模型的适用性。
针对海杂波建模难度大的问题,虽然取得了一系列的成果,但是还存在一些问题,主要表现在:(1)现有的分布模型大多是在中高等掠射角条件下提出的,当雷达处于低掠射角探测时,海面的干涉、衍射以及遮挡等效应使得海杂波建模难度增大,现有的海杂波模型是否适用于低掠射角海杂波建模是一个问题;(2)主要研究的是单一海杂波模型在不同环境下的海杂波建模问题,面对越来越多的海杂波模型,业务化应用中如何选择最优模型进行目标检测也是一个问题。(3)另外,现有的模型主要是针对侧视雷达的海杂波统计分析得到,而雷达前视探测时,多普勒带宽变窄,方位分辨率下降,模型是否适用于前视雷达的海杂波建模又是一个问题。(4)当海杂波样本较少或者直方图波动较大时,直方图的准确性较差,导致基于直方图的拟合优度评估方法误差增大。为此,本文基于低掠射微波雷达的海杂波数据,选取了6个海杂波模型对海杂波数据进行拟合,并结合多种拟合优度评估方法对6个模型的拟合精度进行评价,给出了最优的海杂波模型。此外,针对雷达的多方位探测特点,从海杂波带宽和模型的拟合优度两方面对比分析了雷达侧视、前视和斜前视模式下的海杂波幅度建模结果,得到了不同探测方位下的最优海杂波模型,可以为目标探测的业务化应用提供参考。针对直方图拟合误差大的问题,本文采用图形化拟合优度方法,该方法无需计算概率直方图,直接对样本数据构建统计量,将假设分布的样本数据和期望数据转化为图形特征,实现样本任意区域的拟合优度评估。
论文第2部分为雷达数据的介绍,工作于低掠射角模式;第3部分为本文用到的海杂波模型和评估方法;第4部分分析了不同方位角下的海杂波幅度特性,主要从海杂波带宽和海杂波最优拟合模型方面分析;第5部分为结论。
2 数据
本文采用的数据为机载雷达的实测海杂波数据,数据采集于2018年10~12月中国广东阳江附近海域,海况为中等。经统计,实验飞行总时长29.5小时,飞行里程超过4500公里,获取机载雷达数据共5.7T。雷达扫描模式的实验区域如图1所示,每个框代表一次实验探测到的海面范围,共计15个框,即获取了15次实验数据。机载雷达工作示意图如图2所示,O点表示机下点,θ表示方位角,为斜距在水平面的投影线与飞行方向的夹角(机身方向为0°,向右为正,向左为负),φ表示掠射角,为斜距与水平地面的夹角。在飞行过程中天线通过连续的周期性扫描来增大海上的监视范围,实现-120°~120°范围内的探测,并利用惯性导航系统记录飞行姿态。雷达的系统参数设置如表1所示,其中掠射角为5.3°,属于低掠射角条件下的雷达探测。
表1 机载雷达的工作参数
Tab.1 The parameters of airborne radar
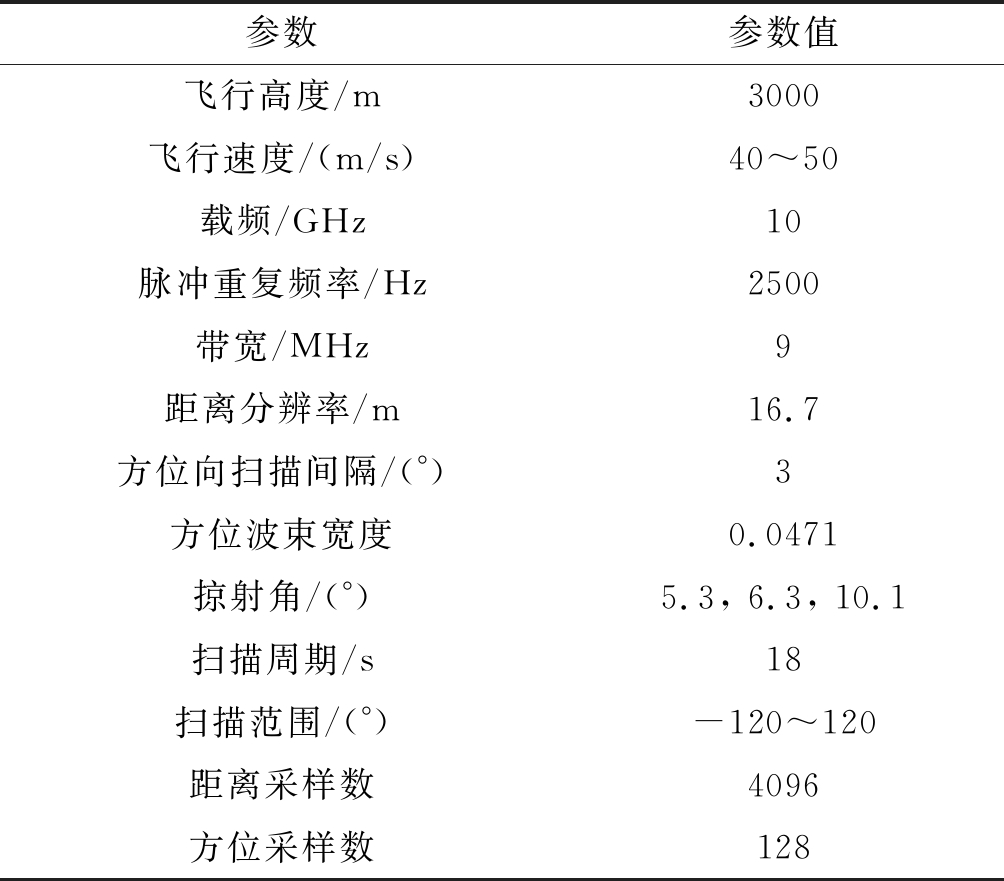
参数参数值飞行高度/m 3000飞行速度/(m/s)40~50载频/GHz10脉冲重复频率/Hz2500带宽/MHz9距离分辨率/m16.7方位向扫描间隔/(°)3方位波束宽度0.0471掠射角/(°)5.3, 6.3, 10.1扫描周期/s18扫描范围/(°)-120~120距离采样数4096方位采样数128
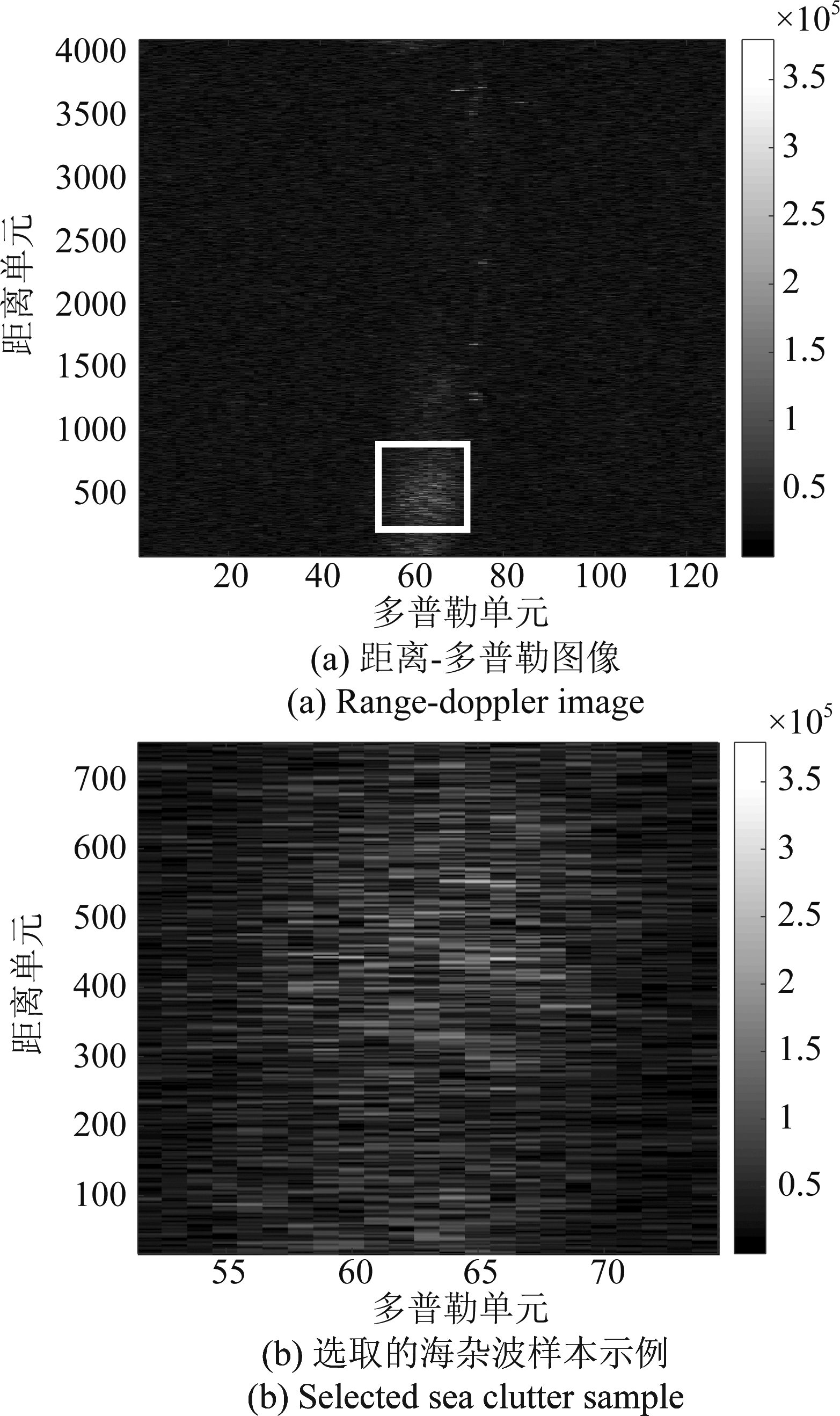
采集的机载雷达数据在使用前需要进行预处理,以保证距离维和多普勒维信息的准确性。预处理包括距离压缩、距离单元徙动校正和方位向傅里叶变换三步。其中,第三步傅里叶变换时,由于杂波的多普勒中心随波束扫描角度的变化而变化,造成多普勒中心发生偏移,所以需要同时利用系统参数补偿扫描角引起的多普勒中心偏移。预处理得到的雷达数据为复数值,通过取绝对值计算其幅度,得到用于海杂波幅度特性分析的距离-多普勒图像。距离-多普勒图像可以同时提供距离域和多普勒域的海杂波信息,图3为一个距离-多普勒图像的示例,方位角为9.5°,掠射角为5.3°,其中图3(a)红色方框内表示选取的海杂波样本,图3(b)为(a)中选取的海杂波样本数据。
对于每个距离-多普勒图像,利用多普勒中心对称截断得到用于杂波分析的主瓣杂波。随着斜视角的增大,主瓣宽度减小,截断多普勒单元的数量也相应减少。截断的多普勒单元数随着主瓣多普勒宽度的增大而增大,而距离单元数不变。不同方位角下截取的多普勒单元数不同,当扫描角度非常接近0度时(-20°~20°),主瓣多普勒宽度最小,多普勒单元数设置为24。侧视与前视之间的角度范围内,即方位角范围为[-70°,-20°]和[20°,70°]时,多普勒单元数设置为28。当工作模式接近侧视时,多普勒单元数设为32。
3 海杂波拟合模型与评估方法
3.1 分布模型及参数估计方法
对海杂波进行建模,需要先给定分布模型,然后对直方图拟合,估计出概率密度函数所需的参数,进而确定出概率密度函数表达式f(x)。本文选用了六种海杂波模型,分别为Weibull、Log-normal、G0、K、GΓD和Alpha-stable分布。利用直方图进行参数估计的主要方法有矩估计法(MoM)、最大似然法(ML)、对数累量法(MoLC),其中MoLC方法已经被证明具有较好的估计一致性,适用于各种复杂模型的参数估计[21]。各模型的概率密度函数表达式及其参数MoLC估计方程如表2所示。其中,Alpha-stable分布由于没有显式解,表2列出了该分布的特征函数,其概率密度函数的求解参考文献[22]和[23]。
3.2 模型精度评估方法
本文使用的模型精度评估方法主要有MSE、K-L距离、巴氏距离、阈值误差和图形化拟合优度[24-27]。
(1)均方误差(MSE)
MSE的表达式为
(1)
其中, f(·)为假设分布的概率密度函数,其参数由样
表2 各模型的概率密度函数及参数方程
Tab.2 The PDF and MoLC equation of sea clutter models

注:Φ0(1,L)表示多伽马函数。
本数据获得,g(·)为直方图的概率。MSE越小,模型的拟合精度越高。
(2)K-L散度
K-L散度的表达式为
(2)
其中0<g(x)<1,0<f(x)<1。K-L散度越小,模型的拟合精度越高。
(3)巴氏距离(BD)
巴氏距离(BD)的表达式为
(3)
巴氏距离的取值范围为[0,∞),巴氏距离越小,模型的拟合优度越好,当两个概率密度函数完全相同时,得到最小值0。
(4)阈值误差(Te)
MSE、K-L距离和BD都能评估总的拟合优度,但是无法获得不同数据区域的局部匹配程度,特别是在幅度值大的区域。而互补累计分布函数(CCDF)曲线可以显示任何数据区域的匹配程度,通过比较样本与假设分布的CCDF的趋近程度,可以得到最拟合的分布。该方法不仅能判断出最优分布,还能反映出不同数据范围内的匹配程度。通过计算恒定虚警率PFA下样本数据与假定分布的水平差,可以得到基于CCDF的阈值误差Te,表达式为
Te=|xreal-xsimu|
(4)
其中,xreal和xsimu分别为给定PFA对应的真实样本和假设分布值,这两个值都可以通过它们对应的CCDF求得。
(5)图形化拟合优度
以上拟合优度评价方法需要进行直方图统计,且无法反应某一位置处的拟合优度-在这种情况下,可以使用图形化拟合优度来选择最适合样本数据的分布模型,该方法属于有序统计,首先,将样本数据按递增顺序排序,为x1, x2,..., xn;然后,假设给定分布为零假设,构造检验统计量。在获得有序样本数据和期望数据后,给出了图形曲线。利用有序样本数据x1, x2,..., xn构造连接向量Q1(U1, V1),..., Qi (Ui, Vi),..., Qn(Un, Vn),其中Qi (Ui, Vi)的定义为
(5)
(6)
其中F0(xj)=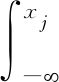 f0(x)dx, f0(·)为零假设的PDF。
f0(x)dx, f0(·)为零假设的PDF。
从原点开始,我们画出终点为点Q1(U1, V1)的第一个向量。类似地,其他向量依次在二维平面上画出来。然后将这些向量逐个连接,得到连接向量图。同样,可以使用期望数据来获得连接向量。连接向量图形成后,需要利用期望数据构造置信椭圆。然后利用样本图上各点的位置与置信椭圆的关系来判断是否接受原假设。该方法的整个过程如下:
1)按递增顺序对样本数据进行排序。
2)根据样本数据估计对应原假设的参数,并利用参数生成期望数据。
3)获取样本与期望数据的关联向量。
4)对于给定的样本点Qn,构造100(1-e)%的置信椭圆。
5)如果Qn位于置信椭圆内,则接受假设,否则拒绝假设。
通过蒙特卡罗实验得到Qn对应的期望数据和置信椭圆。在得到Qn(Un, Vn)点的均值和方差后,可以得到置信椭圆。假设Qn(Un, Vn)的均值和方差分别为E(Un)=mu,E(Vn)=mν和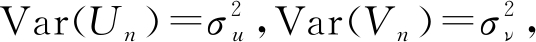 则置信水平为1-e的置信椭圆可以表示为
则置信水平为1-e的置信椭圆可以表示为
(7)
置信椭圆的大小取决于置信水平的大小。置信水平越高,置信椭圆越大。一般取置信水平为90%、95%或99%,观察该点是否落在相应的置信椭圆内,因此e的值为0.1、0.05或0.01。在本文中,为了提高置信水平,我们将e的值设为0.01。
4 不同方位角下的海杂波幅度特性分析
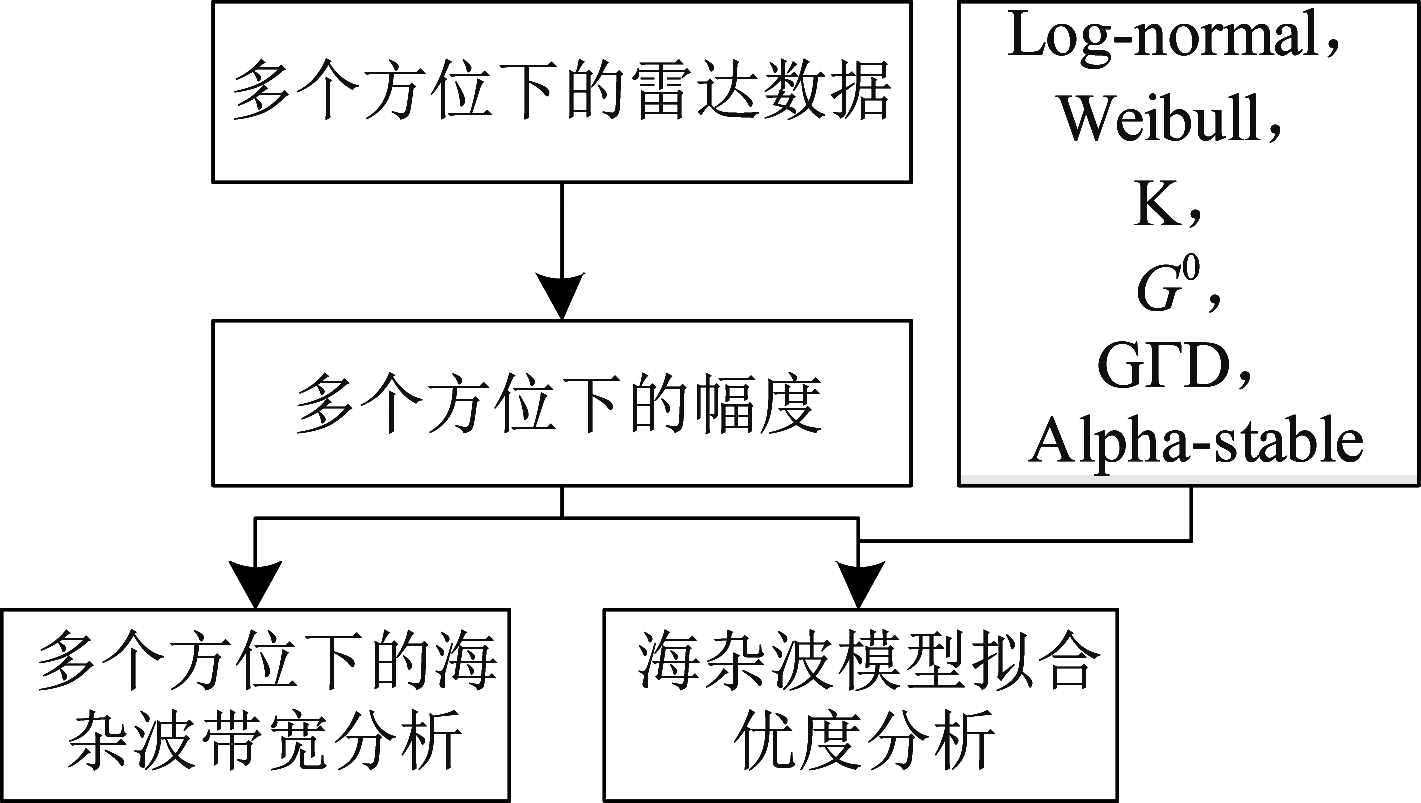
针对机载雷达小掠射角下的海杂波幅度建模问题,本文开展了不同方位角下的海杂波幅度特性分析。首先分析了不同方位角下的海杂波带宽差异;其次,利用6种典型的海杂波模型对不同方位角下的海杂波进行拟合,并利用不同评估方法得到最优的幅度分布模型,海杂波多方位特性分析的总体框图见图4。
4.1 不同方位角下的海杂波差异分析
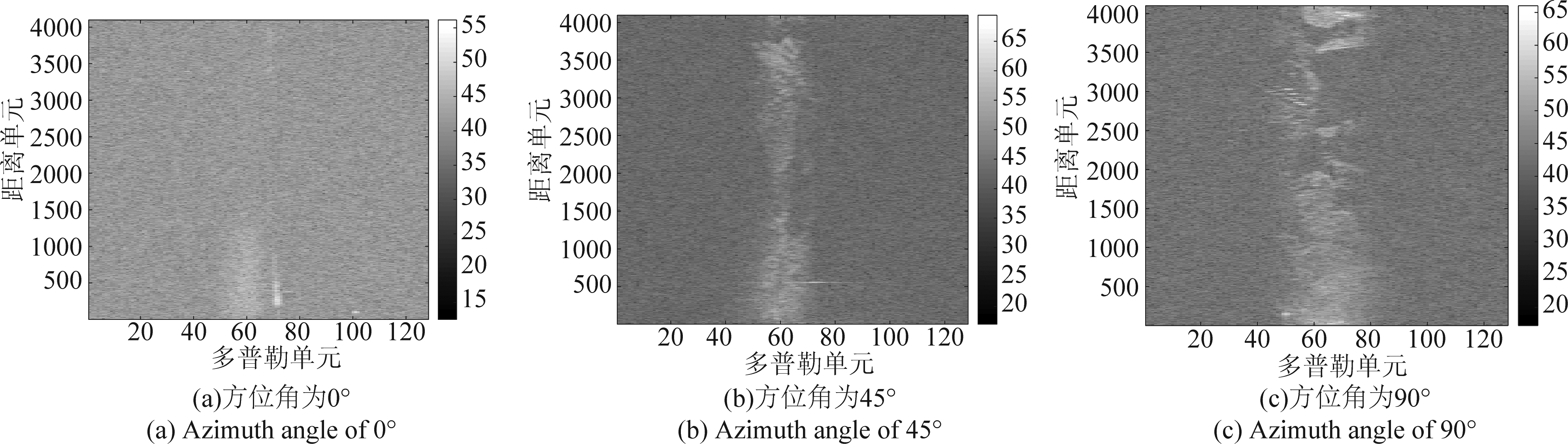
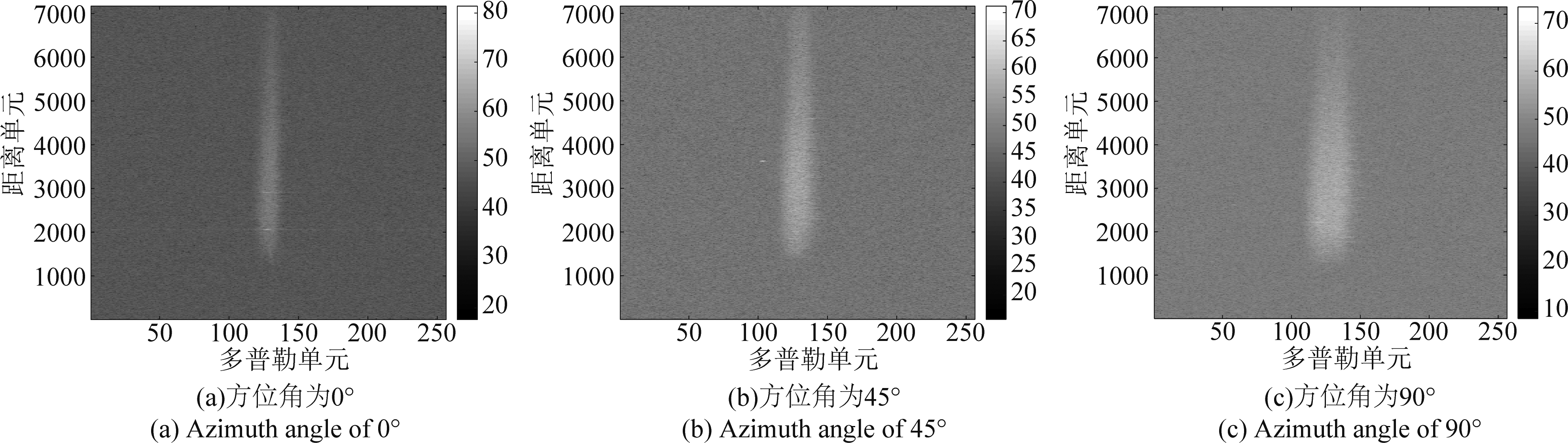
图5~图7为不同方位角下的距离-多普勒图像,图5和图6中的(a)~(c)分别表示方位角为0°、45°和90°,图7中的(a)~(c)分别表示方位角为0°、-45°和-90°。对于不同方位向,补偿了平台运动引起的多普勒中心偏移,所以固定杂波的多普勒中心应为零。由于海面的运动,海杂波的多普勒中心可能会从零频率发生偏移,但对统计分析没有影响。由图5~图7的结果可知,主瓣多普勒宽度随方位角的变化而变化,当方位角为0°时,雷达为前视探测,多普勒带宽最窄,当方位角为±90°时主瓣多普勒带宽最宽,方位角为±45°时介于两者之间。
4.2 不同方位角下的海杂波幅度模型分析
利用Log-normal、Weibull、K、G0、GΓD和Alpha-stable六种分布,开展了低掠射角不同方位角下海杂波幅度模型的拟合优度分析。首先对机载雷达不同方位角下的海杂波数据进行拟合,然后利用多种评估方法对拟合结果进行评价,得到对应于不同方位角下的最优分布模型。
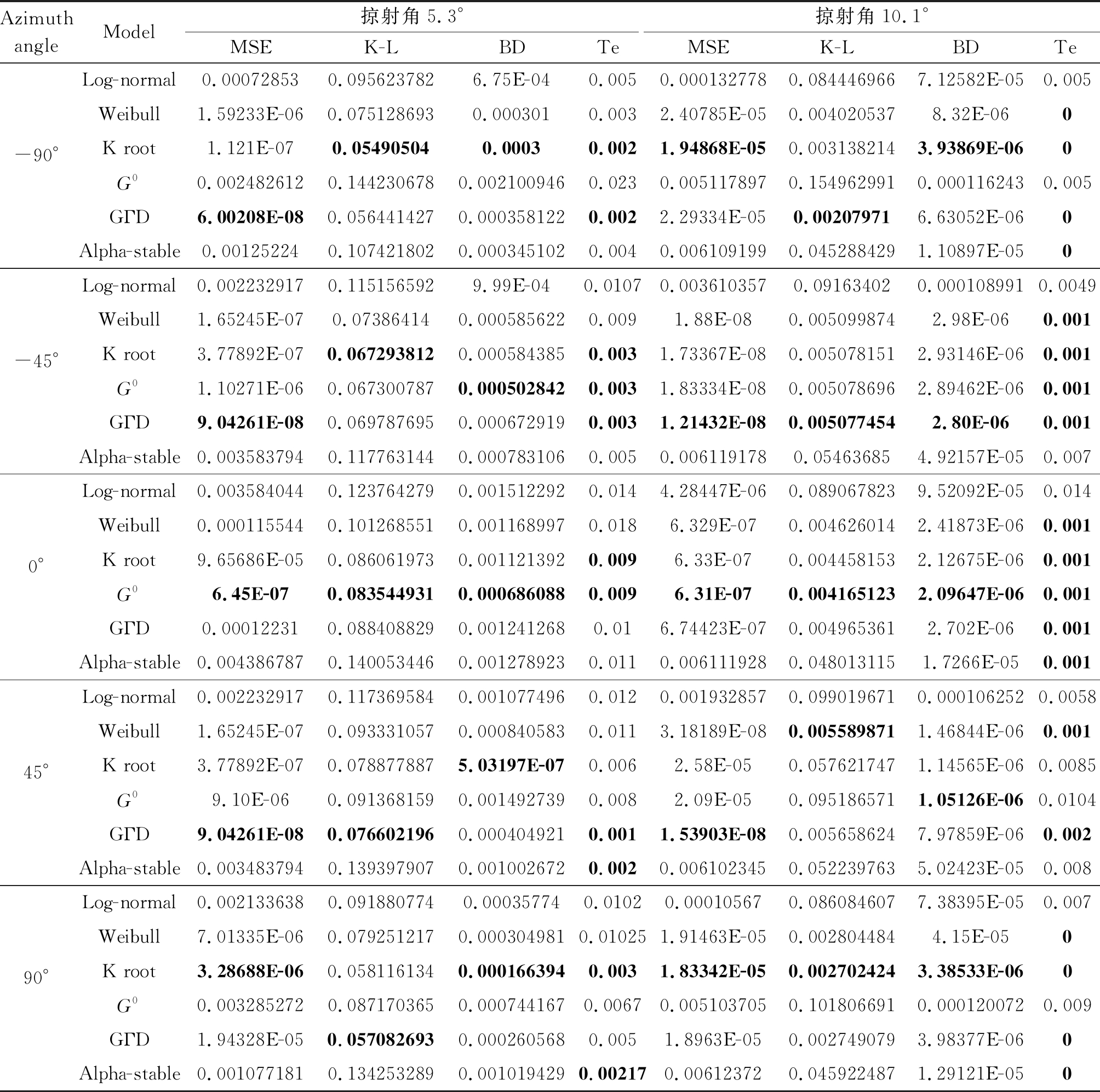
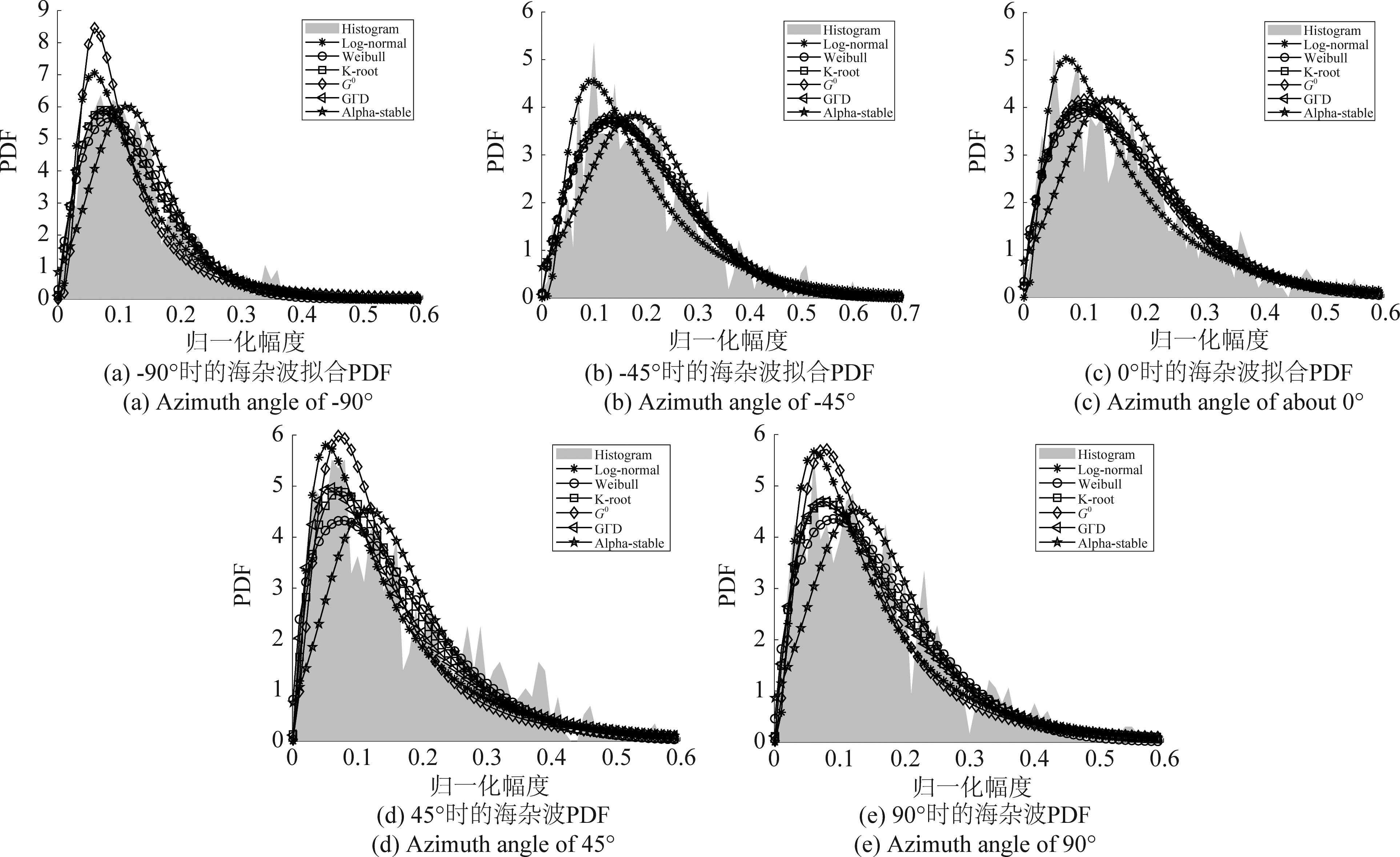
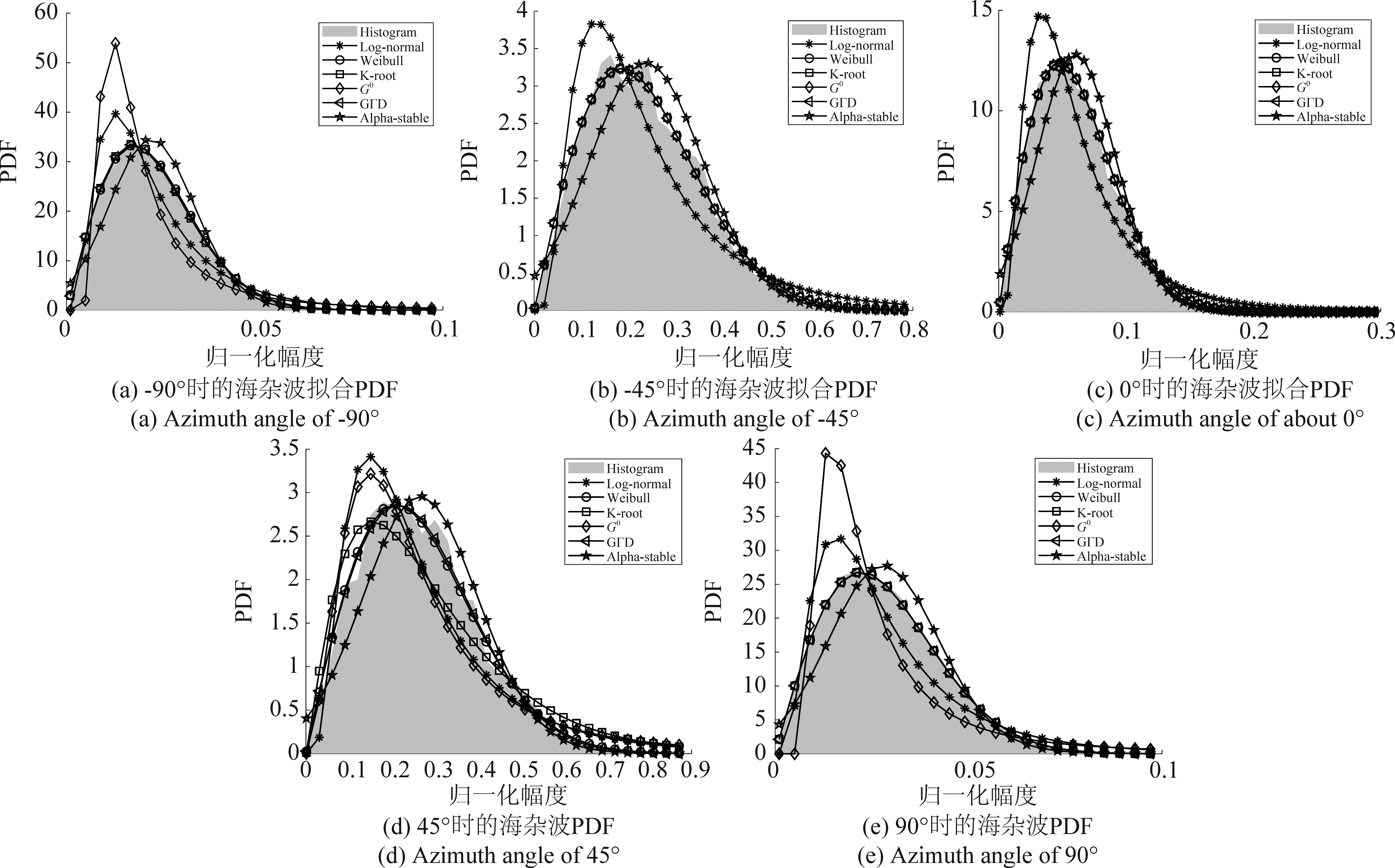
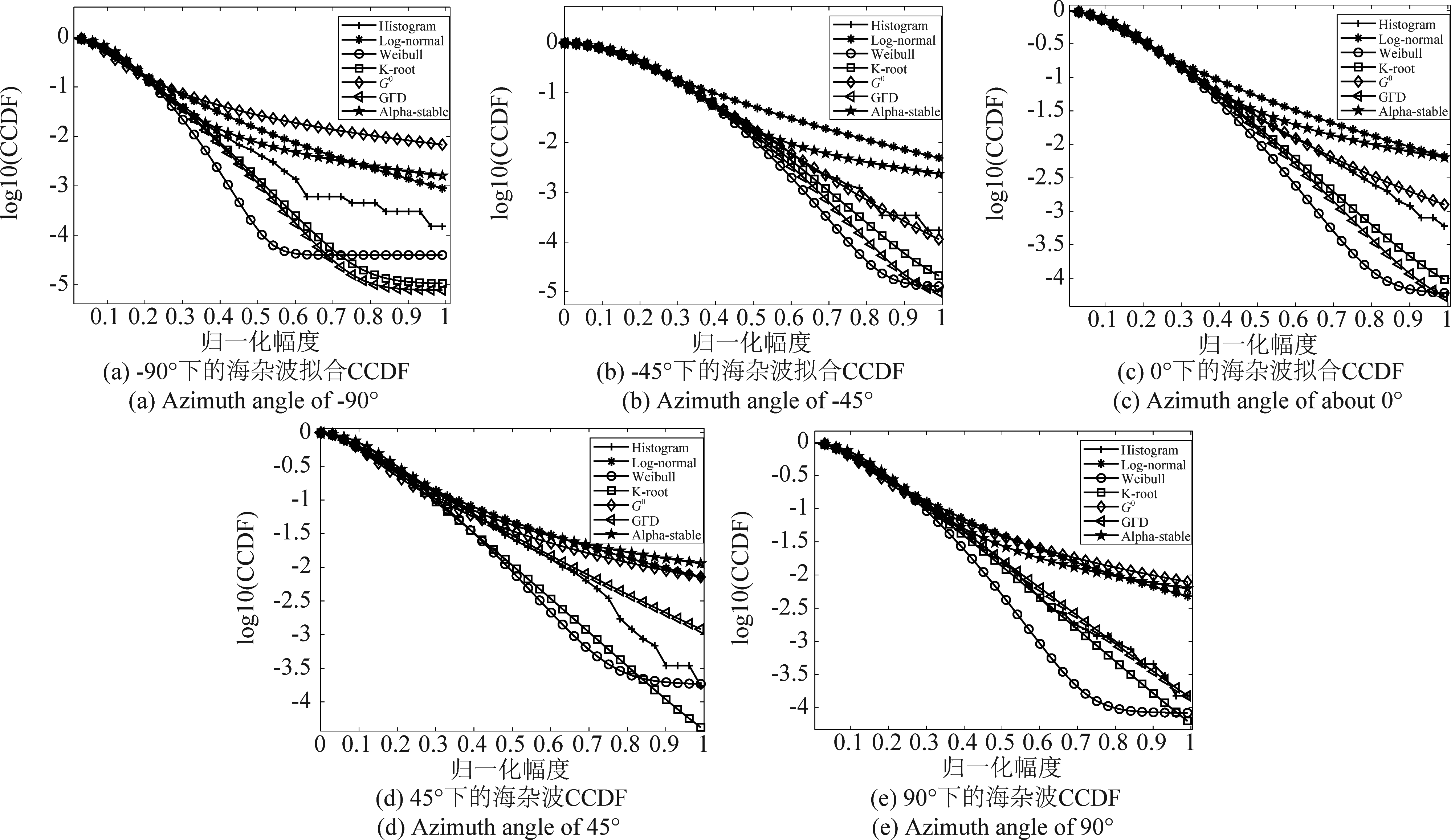
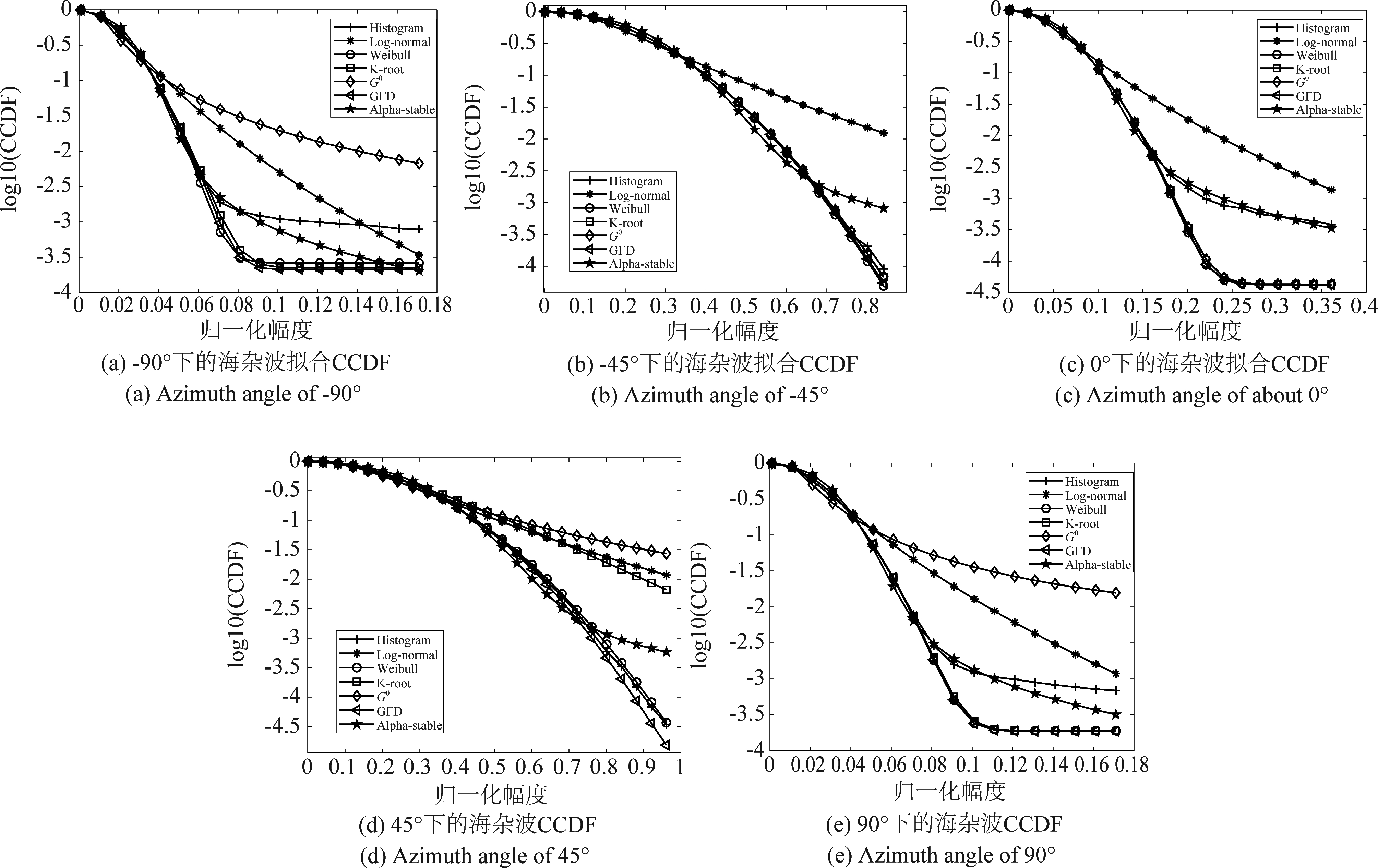
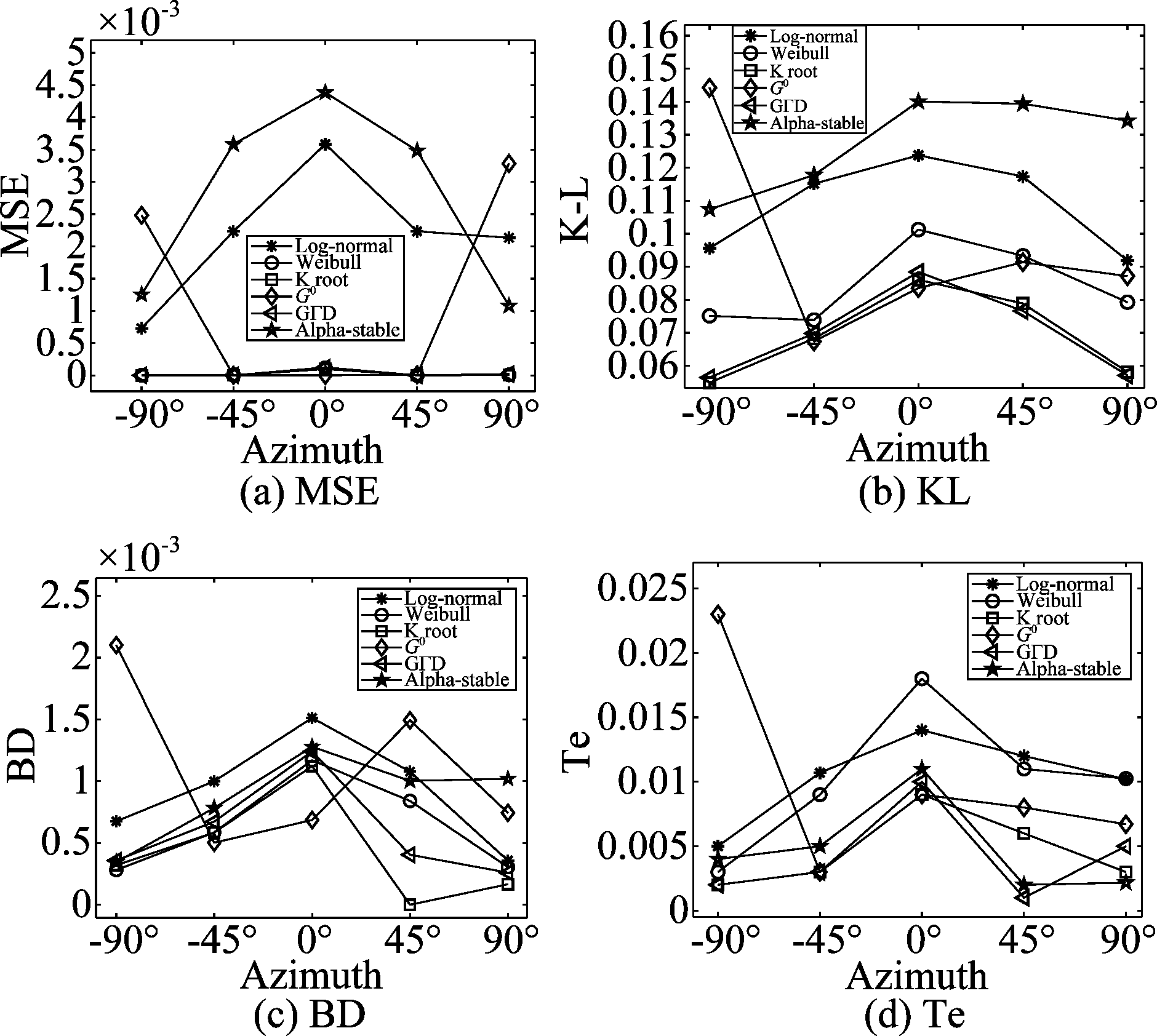
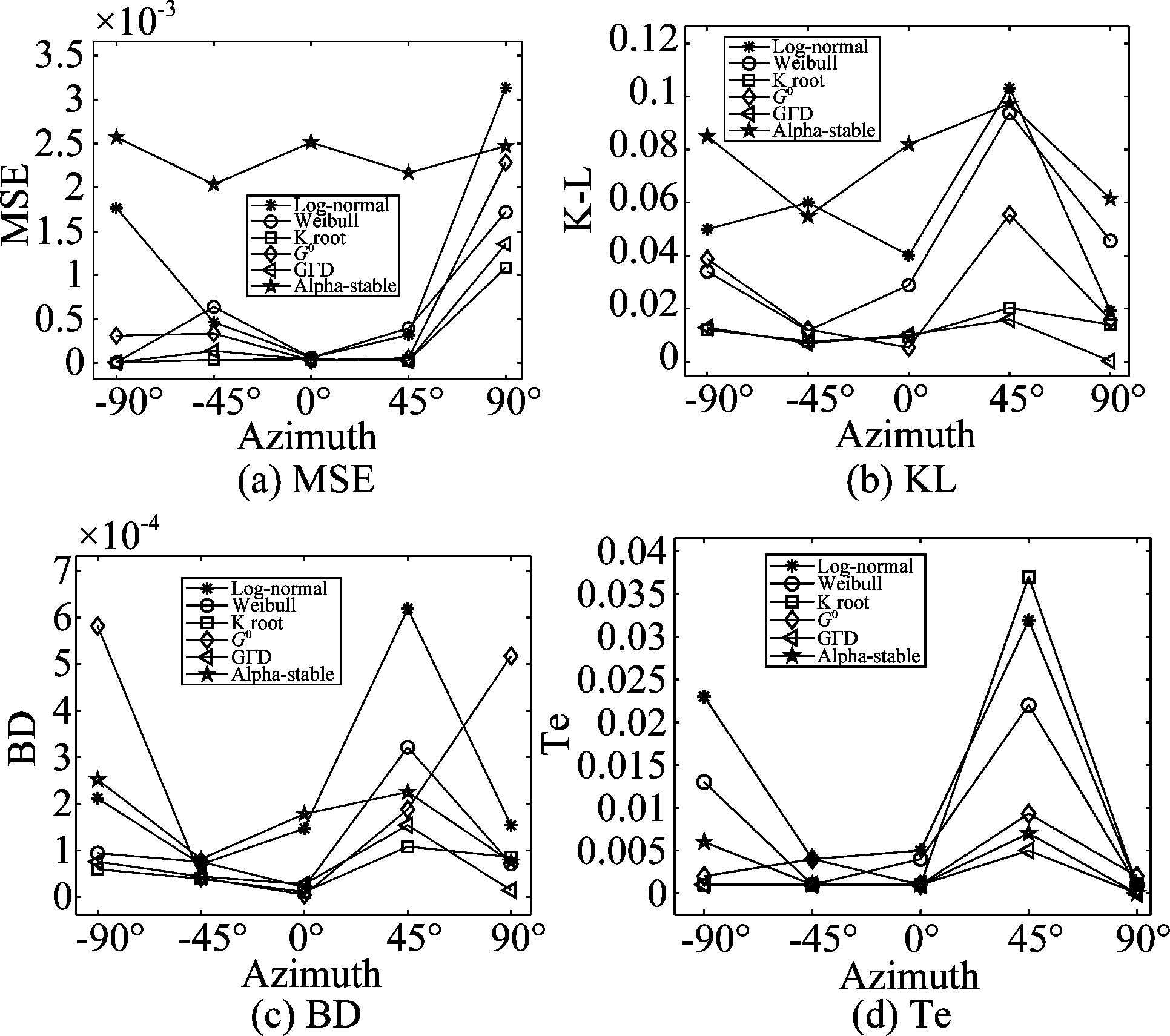
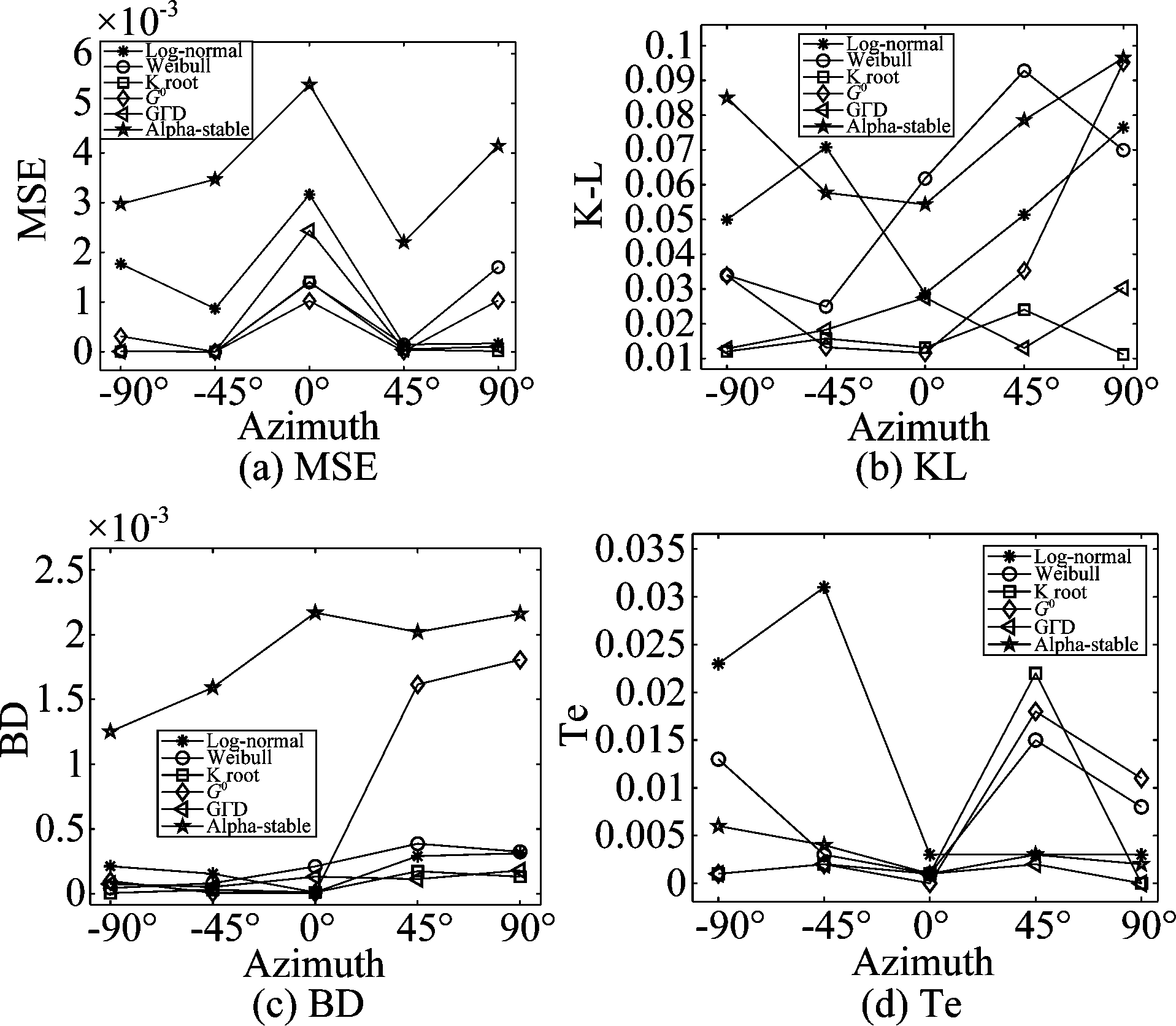
图8和图9列举了5.3°和10.1°掠射角下的海杂波拟合结果,(a)~(e)分别表示-90°,-45°,0°,45°和90°时的概率密度函数,横坐标表示海杂波幅度的归一化值。可以看到,海杂波出现了长拖尾现象,这是因为雷达处于低掠射角探测,“海尖峰”等效应增强,造成海杂波强度增大。由(a)~(e)可知,对于整体的拟合,K和GΓD分布在各个方位角下均能实现很好地拟合,Weibull和G0分布次之,其中G0分布在方位角为0°和-45°时的拟合性能很好,Log-normal和Alpha-stable分布在各个方位角下的拟合性能均较差,尤其是对海杂波峰值处的拟合。图10和图11分别为5.3°和10.1°掠射角下海杂波拟合的互补累计分布函数(CCDF)值,该值可以清楚的反应海杂波尾部的拟合优度,(a)~(e)分别对应-90°,-45°,0°,45°和90°方位角时的CCDF值。结果可知,-90°和90°时,海杂波的尾部主要符合K和GΓD分布,-45°和45°时,海杂波尾部主要符合G0、K和GΓD分布,0°时,尾部主要符合G0分布。图12和图13分别为5.3°和10.1°掠射角下不同评估方法得到的海杂波拟合误差曲线,表3为对应的海杂波拟合误差值,评估方法包括MSE、K-L距离、BD和Te值。结果可知,方位角为-90°和90°时,整体的拟合精度排序为:K > GΓD > Weibull > Log-normal > Alpha-stable > G0,尾部最优模型为K和GΓD分布;方位角为-45°和45°时,整体的拟合精度排序为:G0/GΓD/K > Weibull > Log-normal > Alpha-stable,尾部的最优模型为G0、GΓD和K分布;方位角为0°时,整体的拟合精度排序为:G0 > K > GΓD > Weibull > Log-normal > Alpha-stable,尾部的最优模型为G0和K分布。-90°和90°方位角下,GΓD和K分布均最优,说明左侧视(-90°)和右侧视(90°)模式下的海杂波拟合结果无差异,而0°时,G0分布最优,与侧视模式下的最优分布不同,因为当方位角为0°时雷达处于前视工作模式,其回波的多普勒带宽有限,方位分辨率下降,所以海杂波的幅度特性与侧视模式下不同。
表3 MMTI不同方位角下海杂波幅度拟合的误差
Tab.3 The errors of sea clutter models at different azimuth angles
Azimuth angleModel掠射角5.3°MSEK-LBDTe掠射角10.1°MSEK-LBDTe-90°Log-normal0.000728530.0956237826.75E-040.0050.0001327780.0844469667.12582E-050.005Weibull1.59233E-060.0751286930.0003010.0032.40785E-050.0040205378.32E-060K root1.121E-070.054905040.00030.0021.94868E-050.0031382143.93869E-060G00.0024826120.1442306780.0021009460.0230.0051178970.1549629910.0001162430.005GΓD6.00208E-080.0564414270.0003581220.0022.29334E-050.002079716.63052E-060Alpha-stable0.001252240.1074218020.0003451020.0040.0061091990.0452884291.10897E-050-45°Log-normal0.0022329170.1151565929.99E-040.01070.0036103570.091634020.0001089910.0049Weibull1.65245E-070.073864140.0005856220.0091.88E-080.0050998742.98E-060.001K root3.77892E-070.0672938120.0005843850.0031.73367E-080.0050781512.93146E-060.001G01.10271E-060.0673007870.0005028420.0031.83334E-080.0050786962.89462E-060.001GΓD9.04261E-080.0697876950.0006729190.0031.21432E-080.0050774542.80E-060.001Alpha-stable0.0035837940.1177631440.0007831060.0050.0061191780.054636854.92157E-050.0070°Log-normal0.0035840440.1237642790.0015122920.0144.28447E-060.0890678239.52092E-050.014Weibull0.0001155440.1012685510.0011689970.0186.329E-070.0046260142.41873E-060.001K root9.65686E-050.0860619730.0011213920.0096.33E-070.0044581532.12675E-060.001G06.45E-070.0835449310.0006860880.0096.31E-070.0041651232.09647E-060.001GΓD0.000122310.0884088290.0012412680.016.74423E-070.0049653612.702E-060.001Alpha-stable0.0043867870.1400534460.0012789230.0110.0061119280.0480131151.7266E-050.00145°Log-normal0.0022329170.1173695840.0010774960.0120.0019328570.0990196710.0001062520.0058Weibull1.65245E-070.0933310570.0008405830.0113.18189E-080.0055898711.46844E-060.001K root3.77892E-070.0788778875.03197E-070.0062.58E-050.0576217471.14565E-060.0085G09.10E-060.0913681590.0014927390.0082.09E-050.0951865711.05126E-060.0104GΓD9.04261E-080.0766021960.0004049210.0011.53903E-080.0056586247.97859E-060.002Alpha-stable0.0034837940.1393979070.0010026720.0020.0061023450.0522397635.02423E-050.00890°Log-normal0.0021336380.0918807740.000357740.01020.000105670.0860846077.38395E-050.007Weibull7.01335E-060.0792512170.0003049810.010251.91463E-050.0028044844.15E-050K root3.28688E-060.0581161340.0001663940.0031.83342E-050.0027024243.38533E-060G00.0032852720.0871703650.0007441670.00670.0051037050.1018066910.0001200720.009GΓD1.94328E-050.0570826930.0002605680.0051.8963E-050.0027490793.98377E-060Alpha-stable0.0010771810.1342532890.0010194290.002170.006123720.0459224871.29121E-050
综上,5.3°、6.3°和10.1°掠射角下的海杂波多方位拟合结果是一致的,雷达接近侧视模式时,海杂波的整体和尾部最优拟合模型均为K和GΓD分布,雷达接近前视模式时,海杂波的整体和尾部最优拟合模型为G0和K分布;当雷达处于前视和侧视模式之间时,G0、GΓD和K分布在整体和尾部的拟合上均表现出了很好的性能。
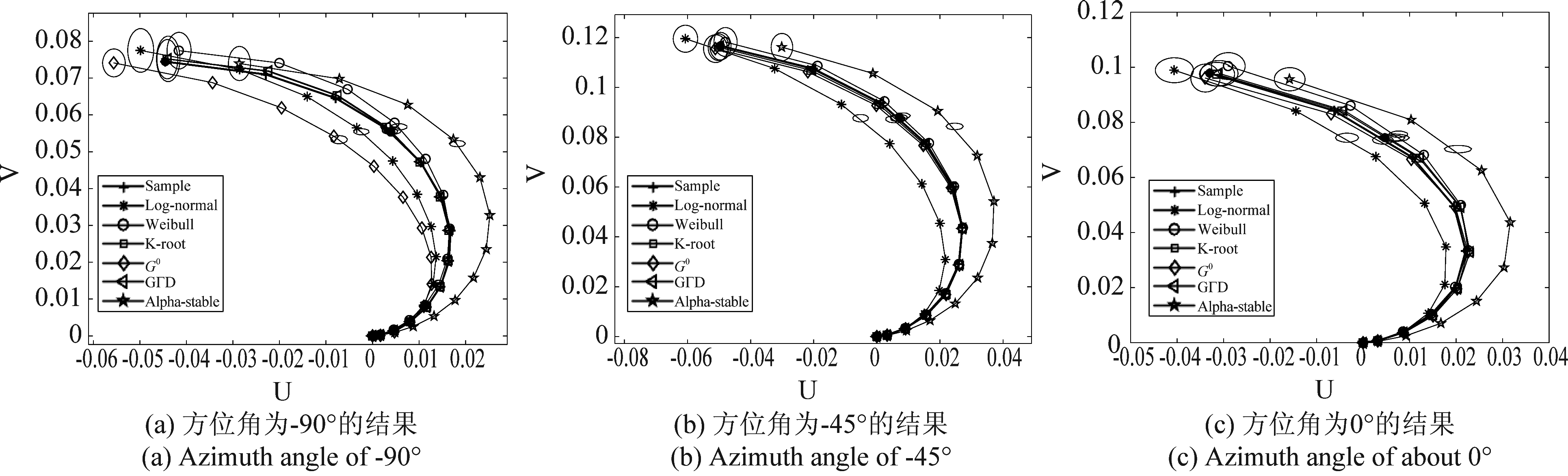
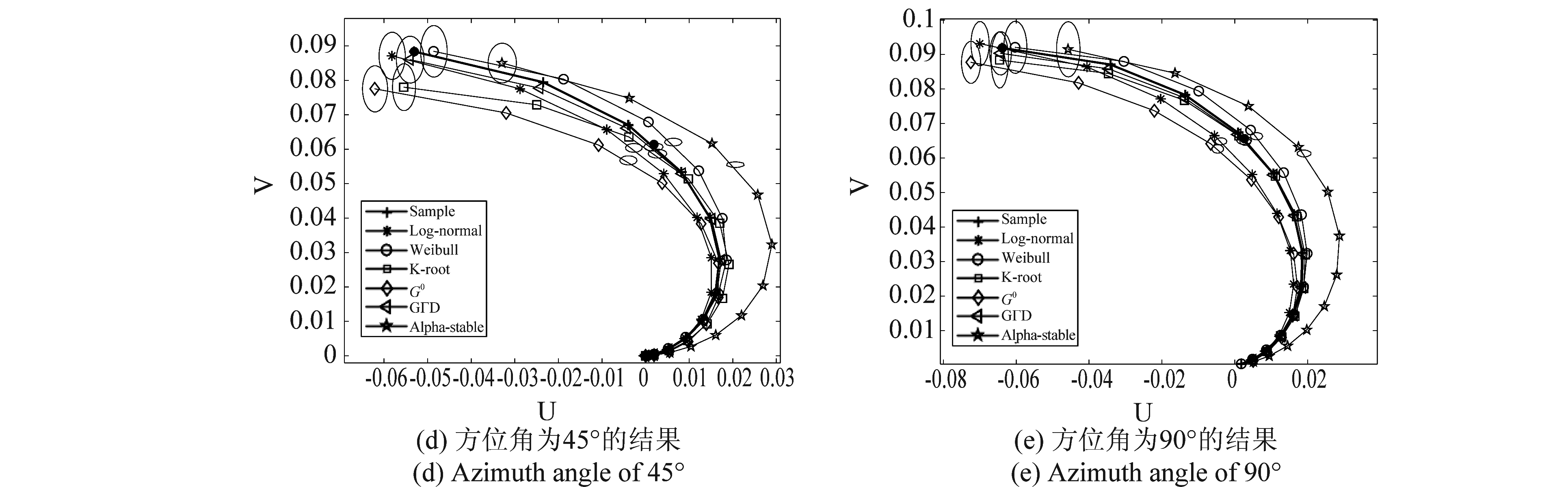
下面利用图形化拟合优度方法对各个分布的拟合结果进行评价,置信水平设为0.99,蒙特拉罗实验次数设置为样本数量的10倍[13]。图形化拟合优度方法无需统计海杂波的分布直方图,直接利用有序样本构建统计量,实现任一点处的拟合误差检验,一般利用有序样本的3/4点和端点的置信椭圆来判断模型的拟合优度。图14列举了5.3°掠射角条件下方位角为-90°、-45°、0°、45°和90°时各个模型的图形化拟合优度结果,“+”号表示的曲线为有序样本数据的结果,三个圆点分别表示有序样本的初始点、3/4点和终点。结果显示,-90°和90°方位角下,GΓD和K分布的三个点都落在置信椭圆内,表示样本满足GΓD和K分布,而Weibull分布的端点落入置信椭圆,3/4点在置信椭圆之外,说明样本的PDF不符合Weibull分布,同理,也不满足Log-normal、G0和Alpha-stable分布;0°方位角下,样本数据满足G0、K和GΓD分布;-45°方位角下,样本数据满足Weibull、K、G0和GΓD分布,而45°方位角下,样本数据仅满足GΓD分布,这可能与样本的选择有关;图形化拟合优度的结果与上述MSE、KL、BD和Te方法的结论一致,具有很好的一致性,增大了海杂波拟合的准确性,可为海上目标检测的海杂波模型选择提供参考。
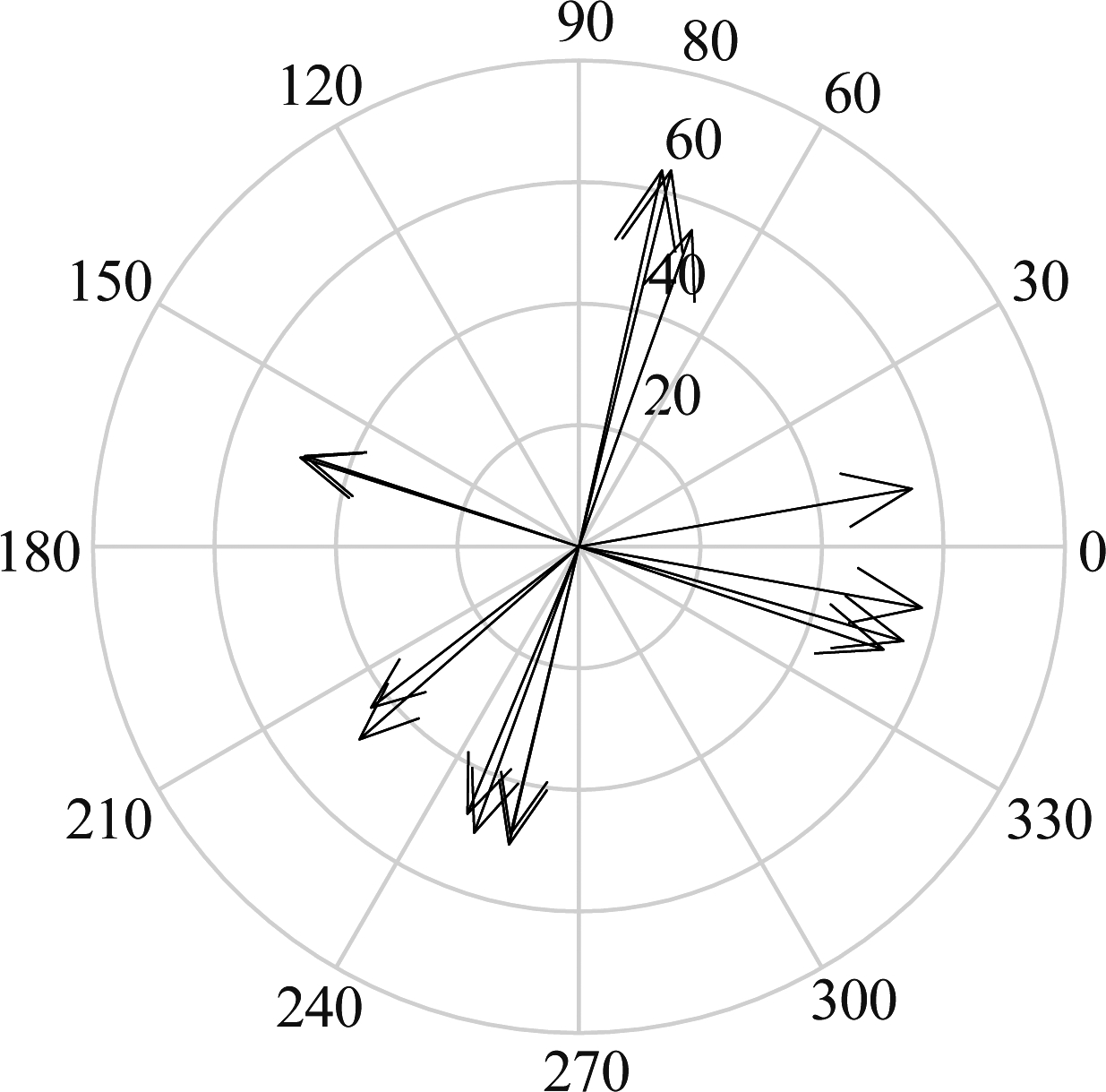
另外,需要讨论的是不同方位海杂波谱的特性差异是否与海浪方向有关。雷达天线的扫描方向为-120°~120°,所以数据包含了不同的方向,且-120°~120°角度范围涵盖了海浪的180°模糊现象。每次实验的飞行方向设置是不同的,图15给出了15次飞行实验中飞机的飞行方向(雷达数据以正北方向为参考,顺时针方向0°~360°),可以看到飞机的飞行方向涵盖了0°~360°的不同方向,包含了不同的海浪方向。结合海洋气象监测资料,在所有结果都是包含了不同海浪方向的情况下,海杂波多方位海杂波谱特性的差异分析结果是一致的。图16和图17列举了5.3°掠射角下,飞机飞行方向为161.7°和217.7°的海杂波拟合误差曲线,结合图12(飞机飞行方向为256.8°),结果可知,不同飞行方向下海杂波的多方位特性结果是一致的。雷达处于侧视探测时,K和GΓD分布最优;雷达接近前视模式时,最优拟合模型为G0和K分布;当雷达处于前视和侧视模式之间时,G0、GΓD或者K分布均表现出了很好的拟合性能,所以海杂波的多方位特性差异不受雷达照射方向和海浪运动方向夹角的影响,是与海浪方向无关的。
5 结论
掌握海杂波的变化规律,实现目标与海杂波的分离,是海上目标探测的关键。雷达处于低掠射探测时,电磁波与海表面的相互作用非常复杂,海杂波的建模难度大,此外,海杂波幅度在多个方位下表现出不同的特性,如何选择合适的海杂波模型进行目标检测是一个问题。因此,针对低掠射雷达海杂波的多方位特性以及建模问题,我们结合雷达的扫描模式,开展了低掠射角不同方位角下的海杂波幅度特性分析。数据为广东阳江附近海域采集的机载雷达数据,雷达工作在X波段、低掠射角条件下。首先对低掠射多个方位下的海杂波特性差异进行对比分析,主要体现在海杂波带宽,其次利用Log-normal、Weibull、K、G0、GΓD和alpha-stable模型对不同低掠射角、不同方位角下的海杂波幅度进行全面的建模分析,并分别采用直方图对应的拟合优度和图形化拟合优度评价方法选取了最优的海杂波分布模型。主要结论如下:
(1)针对低掠射角的海杂波建模问题,基于不同掠射角、方位角雷达数据和多种海杂波模型及评估方法,实验结果表明雷达前视时,海杂波统计直方图更尖,海杂波模型推荐G0分布;侧视模式下,海杂波模型推荐K和GΓD分布;而斜前视模式下,推荐K、GΓD和G0分布,可为业务化应用提供参考。
(2)针对海杂波幅度在多个方位下的特征差异,实验结果表明海杂波前视条件下海杂波带宽最窄,侧视模式下带宽最宽,斜前视时带宽居中,可用于指导主杂波带宽内海杂波样本的选取。
(3)针对海杂波样本量小或者直方图波动较大时,选取最优海杂波模型难度大的问题,发展了图形化拟合优度的评估方法,直接利用原始数据构建统计量,简单、准确,无需进行直方图统计分析,实验结果表明,与直方图对应的GoF相比,图形化GoF在评估海杂波拟合性能方面具有明显的优势。
参考文献
[1] 丁昊, 刘宁波, 董云龙, 等. 雷达海杂波测量试验回顾与展望[J]. 雷达学报, 2019, 8(3): 5-26.
Ding Hao, Liu Ningbo, Dong Yunlong, et al. Overview and Prospects of Radar Sea Clutter Measurement Experiments[J]. Journal of Radars, 2019, 8(3): 5-26.(in Chinese)
[2] Sayama S, Sekine M. Log-Normal, Log-Weibull and K-Distributed Sea Clutter[J]. Ice Trans Commun B, 2002, 85: 1375-1381.
[3] Ravid R, Levanon N. Maximum-likelihood CFAR for Weibull background[J]. Radar & Signal Processing Iee Proceedings F, 1992, 139(3): 256-264.
[4] Jakeman E, Pusey P. A model for non-Rayleigh sea echo[J]. IEEE Transactions on Antennas & Propagation, 1976, 24(6): 806-814.
[5] Li Hengchao, Hong Wen, Wu Yirong, et al. On the Empirical-Statistical Modeling of SAR Images With Generalized Gamma Distribution[J]. IEEE Journal of Selected Topics in Signal Processing, 2011, 5(3): 386-397.
[6] Chen Xiaolong, Guan Jian, Bao Zhonghua, et al. Detection and Extraction of Target With Micromotion in Spiky Sea Clutter Via Short-Time Fractional Fourier Transform[J]. IEEE Transactions on Geoence & Remote Sensing, 2013, 52(2): 1002-1018.
[7] 周超, 刘泉华. Ku波段实验雷达海杂波实测数据分析[J]. 信号处理, 2015, 31(12): 1573-1578.
Zhou Chao, Liu Quanhua. Analysis of field Sea Clutter Data of Ku Band[J]. Journal of Signal Processing, 2015, 31(12): 1573-1578.(in Chinese)
[8] 时艳玲, 杜宇翔, 蒋锐, 等. 部分均匀海杂波中分组加权的协方差矩阵估计[J]. 信号处理, 2019, 35(7): 1170-1179.
Shi Yanling, Du Yuxiang, Jiang Rui, et al. A Grouped Weighted Covariance Matrix Estimator in Partially Homogeneous Sea Clutter[J]. Journal of Signal Processing, 2019, 35(7): 1170-1179.(in Chinese)
[9] Ai Jiaqiu, Yang Xuezhi, Dong Zhangyu, et al. A new two parameter CFAR ship detector in Log-Normal clutter[C]∥2017 IEEE Radar Conference (RadarConf17). IEEE, 2017.
[10] Qin Xianxiang, Zhou Shilin, Zou Huanxin, et al. Statistical modeling of sea clutter in high-resolution SAR images using generalized gamma distribution[C]∥International Conference on Computer Vision in Remote Sensing. IEEE, 2013.
[11] Wackerman C C, Friedman K S, Pichel W G, et al. Automatic Detection of Ships in RADARSAT-1 SAR Imagery[J]. Canadian Journal of Remote Sensing, 2001, 27(5): 568-577.
[12] Xin Zhihui, Liao Guisheng, Yang Zhiwei, et al. Analysis of Distribution Using Graphical Goodness of Fit for Airborne SAR Sea-Clutter Data[J]. IEEE Transactions on Geoscience & Remote Sensing, 2017(10): 1-10.
[13] Frery A C, Muller H J. A model for extremely heterogeneous clutter[J]. IEEE Transactions on Geoence & Remote Sensing, 1997, 35(3): 648-659.
[14] Martín-de-Nicol s J, Jarabo-Amores M P, Mata-Moya D, et al. Statistical Analysis of SAR Sea Clutter for Classification Purposes[J]. Remote Sensing, 2014, 6: 9379-9411.
s J, Jarabo-Amores M P, Mata-Moya D, et al. Statistical Analysis of SAR Sea Clutter for Classification Purposes[J]. Remote Sensing, 2014, 6: 9379-9411.
[15] Gao Gui, Ouyang K, Luo Y, et al. Scheme of Parameter Estimation for Generalized Gamma Distribution and Its Application to Ship Detection in SAR Images[J]. IEEE Transactions on Geoence & Remote Sensing, 2017, 55(3): 1812-1832.
[16] Kourti N, Shepherd I, Schwartz G, et al. Integrating Spaceborne SAR Imagery into Operational Systems for Fisheries Monitoring[J]. Canadian Journal of Remote Sensing, 2001, 27(4): 291-305.
[17] Liu Xu, Xu Shuwen, Tang Shiyang. CFAR Strategy Formulation and Evaluation Based on Fox’s H-function in Positive Alpha-Stable Sea Clutter. Remote Sensing, 2020, 12: 1273.
[18] Watts S, Ward K, Tough R. The physics and modelling of discrete spikes in radar sea clutter[C]∥Radar Conference, 2005 IEEE International, IEEE, 2005.
[19] Balleri A, Nehorai A, Wang J. Maximum likelihood estimation for compound-gaussian clutter with inverse gamma texture[J]. IEEE Transactions on Aerospace & Electronic Systems, 2007, 43(2): 775-779.
[20] 丁昊, 董云龙, 刘宁波, 等. 海杂波特性认知研究进展与展望[J]. 雷达学报, 2016, 5(5): 499-516.
Ding Hao, Dong Yunlong, Liu Ningbo, et al. Overview and Prospects of Research on Sea Clutter Property Cognition[J]. Journal of Radars, 2016, 5(5): 499-516.(in Chinese)
[21] Cui S, Schwarz G, Datcu M. A Comparative Study of Statistical Models for Multilook SAR Images [J]. IEEE Geoscience & Remote Sensing Letters, 2014, 11(10): 1752-1756.
[22] Ozturk A. A general algorithm fob, univariate and multivariate goodness of pit tests based on graphical representation[J]. Communication in Statistics-Theory and Methods, 2007, 20(10): 3111-3137.
[23] Ozturk A. An application of a distribution identification algorithm to signal detection problems[C]∥Asilomar Conference on Signals. IEEE Computer Society, 1993: 248-252.
[24] Fiche A, Angelliaume S, Rosenberg L, et al. Analysis of X-Band SAR Sea-Clutter Distributions at Different Grazing Angles[J]. IEEE Transactions on Geoence & Remote Sensing, 2015, 53(8): 4650- 4660.
[25] Pan Xueli, Liao Guisheng, Yang Zhiwei, et al. Experimental analysis of sea clutter using airborne circular scanning SAR in medium grazing angle[J]. Journal of Systems Engineering and Electronics, 2019.
[26] Angelliaume S, Rosenberg L, Ritchie M. Modeling the Amplitude Distribution of Radar Sea Clutter[J]. Remote Sensing, 2019, 11(3).
[27] Kil D, Shin F, Pattern Recognition and Prediction With Applications to Signal Processing[M]. New York, NY, USA: Springer-Verlag, 1998.
作者简介
曹成会 女, 1990年生, 山东人。哈尔滨工业大学电子与信息工程学院, 博士研究生。主要研究方向为雷达海杂波特性分析和船只目标检测。
E-mail: chenghui_cao@126.com
张 杰 男, 1963年生, 内蒙古人。自然资源部第一海洋研究所, 研究员, 博士。主要研究方向为海洋动力过程的SAR反演与海洋目标的SAR探测、海洋高光谱遥感、高频地波雷达海洋探测技术和海洋遥感应用系统集成。
E-mail: zhangjie@fio.org.cn
张 晰 男, 1981年生, 山东人。自然资源部第一海洋研究所, 副研究员, 博士。主要研究方向为海冰微波遥感、海冰散射数值模拟、合成孔径雷达数据分析。
E-mail: xi.zhang@fio.org.cn
孟俊敏 男, 1973年生, 山西人。自然资源部第一海洋研究所, 研究员, 博士。主要研究方向为微波遥感海洋参数反演。
E-mail: mengjm@fio.org.cn
毛兴鹏 男, 1972年生, 辽宁人。 哈尔滨工业大学电子与信息工程学院, 教授, 博士。主要研究方向为无线通信与雷达中的信号处理。
E-mail: mxp@hit.edu.cn
 s等人[14]和Gao等人[15]的实验结果证明,在不同极化和海况下GΓD的拟合精度优于瑞利分布、对数-正态分布和K分布等。由于海杂波是非常复杂的,上述海杂波模型并不总是准确的,海况、风速、掠射角、方位角和频率等的变化会导致某些模型失配[16]。为了进一步提高海杂波的建模精度,Alpha-stable分布、KA分布和复合高斯分布等模型被用于海杂波建模。Alpha-stable分布是基于广义中心极限定理发展而来,能很好地描述非高斯分布的概率模型,Liu等人[17]利用Alpha-stable分布推导了不同CFAR检测器的表达式,并评估了各个检测器的目标检测性能,且性能优于移动目标检测方法(MTD)。Watts等人[18]将带有海尖峰的海杂波建模为KA分布,KA分布在尾部区域具有较好的拟合性能,但是KA分布的主要缺点是其概率密度函数(PDF)不能显式表示,需要对其进行数值计算,计算成本较高。Balleri等人[19]将实测杂波数据建模为逆伽马纹理的复合高斯模型,并对逆伽马分布的参数进行估计。丁昊等人[20]综述了海杂波的特性,以及典型幅度分布模型的适用性。
s等人[14]和Gao等人[15]的实验结果证明,在不同极化和海况下GΓD的拟合精度优于瑞利分布、对数-正态分布和K分布等。由于海杂波是非常复杂的,上述海杂波模型并不总是准确的,海况、风速、掠射角、方位角和频率等的变化会导致某些模型失配[16]。为了进一步提高海杂波的建模精度,Alpha-stable分布、KA分布和复合高斯分布等模型被用于海杂波建模。Alpha-stable分布是基于广义中心极限定理发展而来,能很好地描述非高斯分布的概率模型,Liu等人[17]利用Alpha-stable分布推导了不同CFAR检测器的表达式,并评估了各个检测器的目标检测性能,且性能优于移动目标检测方法(MTD)。Watts等人[18]将带有海尖峰的海杂波建模为KA分布,KA分布在尾部区域具有较好的拟合性能,但是KA分布的主要缺点是其概率密度函数(PDF)不能显式表示,需要对其进行数值计算,计算成本较高。Balleri等人[19]将实测杂波数据建模为逆伽马纹理的复合高斯模型,并对逆伽马分布的参数进行估计。丁昊等人[20]综述了海杂波的特性,以及典型幅度分布模型的适用性。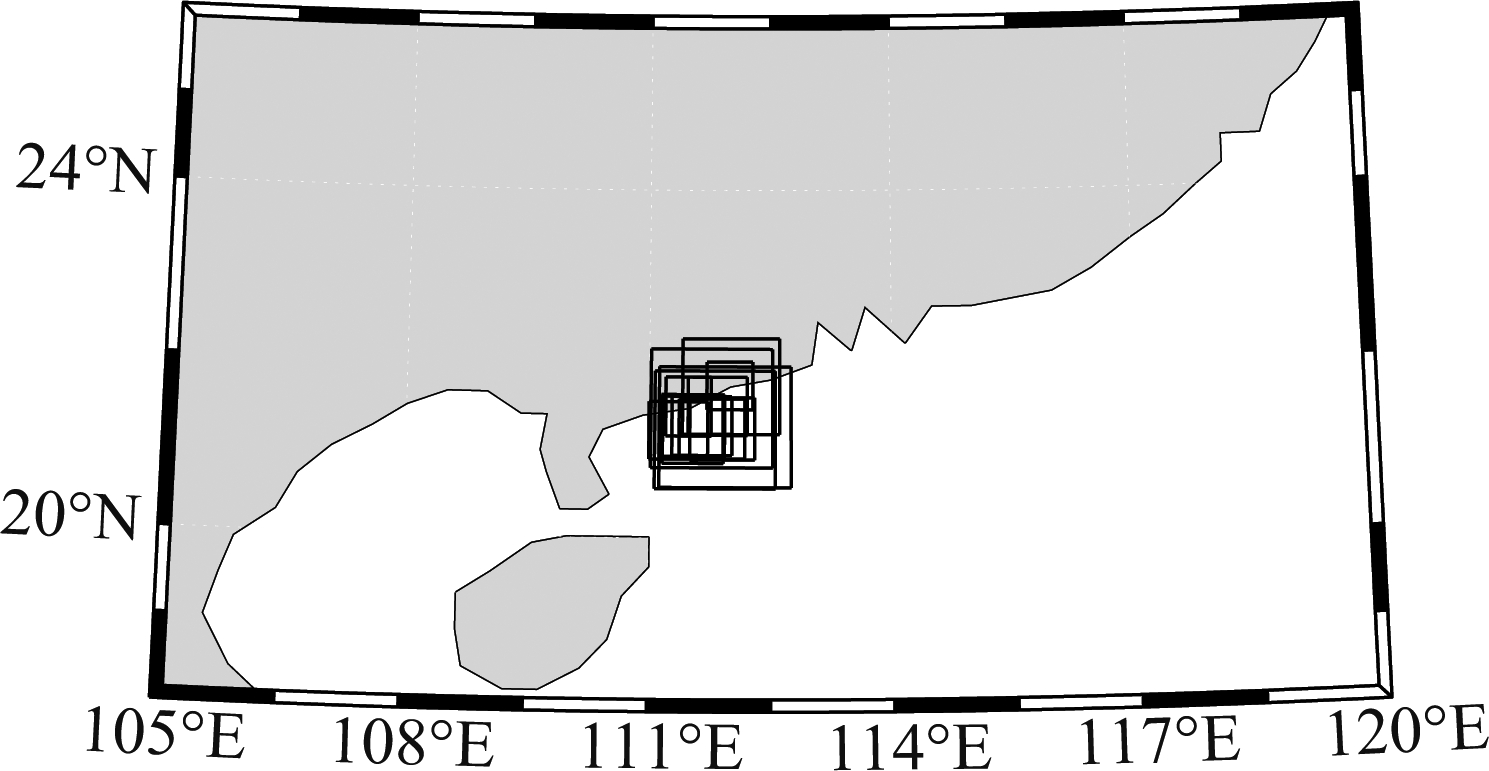






 s J, Jarabo-Amores M P, Mata-Moya D, et al. Statistical Analysis of SAR Sea Clutter for Classification Purposes[J]. Remote Sensing, 2014, 6: 9379-9411.
s J, Jarabo-Amores M P, Mata-Moya D, et al. Statistical Analysis of SAR Sea Clutter for Classification Purposes[J]. Remote Sensing, 2014, 6: 9379-9411.



