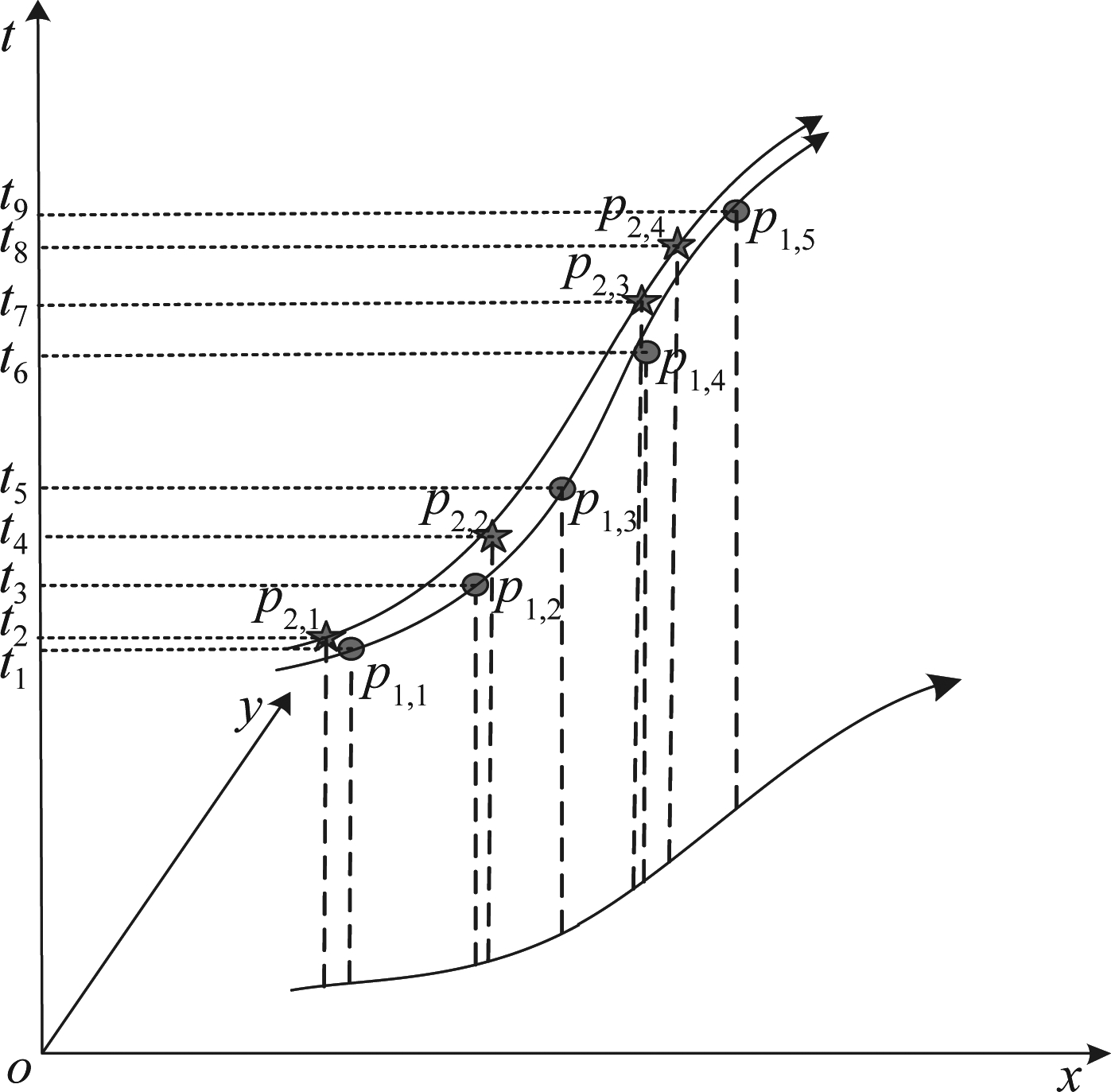
图1 航迹示意图
Fig.1 Trajectories
Reference format: Jin Jialong, Zhou Wei, Jiang Baichen. Trajectory Segmentation Algorithm Based on Behavior Pattern[J]. Journal of Signal Processing, 2020, 36(12): 2074-2084. DOI: 10.16798/j.issn.1003- 0530.2020.12.014.
海上目标探测与识别通常基于目标的声光电磁特性,容易受海上环境等因素影响,探测识别难度大。例如,雷达信号容易受到海杂波、大气扰动以及目标运动特性[1-2]等因素影响,船舶的类型和分布也影响着雷达的成像质量[3]。这些传统的海上目标探测与识别手段对目标的轨迹考虑较少,通过挖掘分析海上目标监视系统实时获取和长期积累的大量轨迹数据,提取特定区域典型目标的行为特征,对于提升传统的基于声光电磁等特性的海上目标探测技术性能具有重要意义。由于海上目标轨迹数据来自不同类型的主被动传感器,通常存在定位精度不一致、时空粒度不均匀、局部缺失不连续等突出问题,轨迹数据分段能够在简化数据的同时保留轨迹特征,广泛用于轨迹聚类[4-5]、预测和行为分析等轨迹数据挖掘应用的预处理中。
轨迹分段算法的分段质量和精细程度直接影响着轨迹数据挖掘的质量,大量文献对轨迹分段进行了研究。文献[6]提出了轨迹处理经典的Douglas-Peucker(DP)算法,通过限制位置点的Perpendicular Distance(PD)达到轨迹分段和简化的目的。文献[7-9]通过限制Synchronized Euclidean Distance(SED),考虑时间维度对轨迹进行分段,提出了Directed Acyclic Graph(DAG)算法。受此启发,为了解决DAG算法不能在线应用,处理即时数据流的问题,文献[10]提出了一种复杂度更低、能够对流数据处理的Directed acyclic graph based On Trajectory Simplification (DOTS)算法。DOTS算法对实时输入的位置点进行计算并同时保存计算结果,每次进行DAG搜索,在合适的时候进行编码输出,达到数据实时处理的效果,降低了算法复杂度。
在应用层面,利用DOTS算法,文献[11]提出了一种轨迹分段和聚类方法,并与采用Minimum Description Length(MDL)分段方法的轨迹聚类框架Trajectory Clustering(TRACLUS)[12]进行比较。文献[13]提出了一种(Parition Cluster Extract Trajectory Clustering)PCETC聚类算法与TRACLUS具有相近的效果。此外,基于TRACLUS框架,文献[14]提出了一种异常检测算法。同时,文献[15]利用分段子轨迹提出一种滤波算法得到高质量的GPS数据。文献[16]利用分段轨迹检测兴趣点和频繁的运动序列。但是,上述算法仅从距离度量的角度达到轨迹压缩的目的,尽可能使压缩后的损失较小,没有从语义层面研究分段轨迹所代表的更深含义。本文从海上目标行为模式入手,制定优先级对轨迹进行分段,在分段和压缩轨迹的同时,赋予每一段轨迹语义内涵,使得本文提出的算法具有更高的工程价值。
轨迹Ti是采样数据按时间顺序排列的序列,记为Ti=〈pi,1,pi,2,…,pi,l〉,其中pi,k=(xi,k,yi,k,ti,k)表示目标在ti,k时刻的位置(xi,k,yi,k)(k=1,2,…,l)。采样数据是一种三维时空结构[17],在xoy平面的投影代表目标平面运动轨迹。图1所示为两种不同传感器对某个目标的采样航迹,分别表示为T1和T2。受工作条件等各方面因素影响,同一传感器的采样数据间隔ti,k+1-ti,k不尽相同。以AIS(Automatic Identification System)为例,在港口等船舶密集区域,设备最短2秒进行一次采样;在外海等航行条件良好、船舶稀少的区域,设备的采样间隔可达数小时。采样频率不一致导致目标轨迹时空粒度不均匀,增加了时间因素对轨迹数据挖掘质量的影响。不同传感器受工作原理等因素的影响,同一时刻采样点的位置(xi,k,yi,k)不尽相同。以雷达和AIS为例,雷达用微波原理计算目标与雷达的相对位置,AIS根据GPS主动发送位置给AIS接收设备,两者的工作原理存在显著差异,导致采样数据存在不同程度的测量误差。此外,由于故障、人为等因素导致传感器数据缺失或错误,增加了海上目标监管和轨迹分析的难度。
图1 航迹示意图
Fig.1 Trajectories
针对上述问题,通常采用一些预处理的方法降低其对轨迹数据挖掘质量的影响。海上目标轨迹分段是在xoy平面内根据轨迹空间特征进行预处理的手段,在损失可接受的范围内,减少数据量。轨迹分段在简化和压缩轨迹后,降低了时空粒度不均匀对轨迹数据挖掘质量的影响。同时,轨迹分段的处理方式保留了主要的轨迹特征,可以通过轨迹特征层面进行多源航迹关联,解决定位精度不一致对轨迹挖掘质量的影响。通过分段轨迹及轨迹特征,可在一定程度上还原目标的真实轨迹,为解决数据缺失问题、提升数据质量提供重要途径。
假设T=〈p1,p2,…,pl〉为一条海上目标轨迹,其中l代表轨迹T的长度。对海上目标轨迹进行分段,实质上是找到一些关键点p1,p2,…,pm∈{p1,p2,…,pl}(m<l)作为轨迹段之间的分界点,这些关键点按时间顺序组成新的序列,将轨迹T分成m-1条分段轨迹。其中,航迹起点与航迹终点是原始轨迹中必不可少的点,也是分段轨迹中的航迹起点与航迹终点,记为 p1=p1,pm=pl,如图2所示。
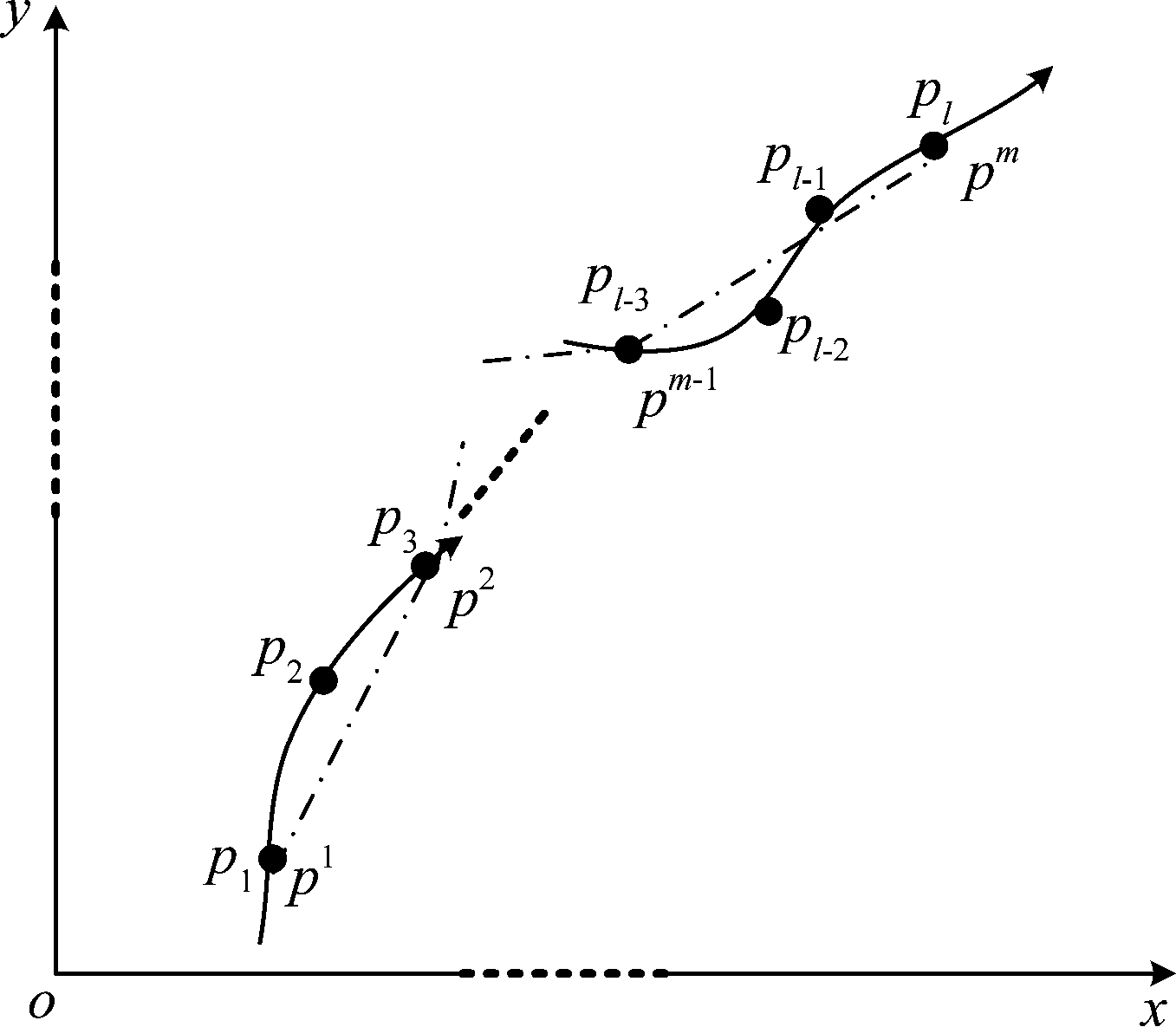
图2 轨迹分段示意图
Fig.2 Trajectories segmentation
图2所示为一条长度为l的海上目标轨迹压缩为m-1条分段轨迹。大多数轨迹分段算法会采用距离度量的方式进行轨迹分段,如DP算法采用最小PD距离作为分段准则,DAG算法采用最小SED距离作为分段准则。这种以最小距离作为分段准则是为了在以直线轨迹代替曲线轨迹时,最大限度的还原原始轨迹,使分段后的轨迹损失最小。
但是,以直线轨迹代替曲线轨迹不仅会造成不可避免的损失,还会损失大量的空间特征。要想尽可能保留空间特征,就要选取更多的关键点,使得分段的原始轨迹无限逼近直线轨迹。因此,这种分段方式的损失与压缩率是成反比的。由于以最小距离作为分段准则,分段后的轨迹并无实际含义,对后续更深入挖掘分析没有太大作用。为了解决上述存在的问题,可以根据目标的行为模式进行分段,通过引入轨迹特征代替曲线轨迹,以增加数据维度来提高压缩比,同时带有行为模式信息,为后续的轨迹挖掘提供基础。
轨迹T=〈p1,p2,…,pl〉由一组关键点p1,p2,…,pm∈{p1,p2,…,pl}(m<l)分成m-1段轨迹段,依次记为T1,T2,…,Tm-1。对应每条分段轨迹,有一组特征值Γ1,Γ2,…,Γm-1,其中Γk=[αk,βk](k∈[1,m-1])为第k段轨迹段的特征值,αk代表行为模式,βk为特征向量。
为了使算法具有普适性,行为模式应选取易于理解并被广泛接受的基础描述。本文涉及七种行为模式:直线航行、小左转、小右转、小S航行、大左转、大右转以及大S航行。为了能更好的还原原始轨迹,降低损失,本文选取曲线拟合参数作为特征向量,将在4.2节进行介绍。
行为模式是算法的核心与关键,通过定义行为模式并进行分段,能够使分段轨迹在具有语义内涵的同时得到简化压缩。不同的行为模式复杂程度不尽相同,本文需要对定义的行为模式进行优先级划分,解决在算法执行过程中可能存在的一些矛盾。
对于海上目标,大多数传感设备主要是获取目标位置、速度信息,通过AIS或成像设备,还可以获取目标的船首向等信息。作为行为模式的判别依据,船首向等方位信息受洋流等环境因素的影响较大,而位置信息是大多数传感设备可获取的,并具有一定的可靠性。因此,本文主要通过位置信息来判别目标的行为模式。
实质上,判断目标具有何种行为模式是依据目标前后所处的相对状态来判定的,当获取目标单个位置信息时,是无法独立判断目标的行为模式。因此,本文通过获取连续的位置点来判定目标的行为模式,称为子轨迹。
定义1 子轨迹:连续的位置点pk,pk+1,…,pk+λ-1组成的一段轨迹。在轨迹T=〈p1,p2,…,pl〉中,从第k个轨迹点pk起,连续λ个轨迹点组成轨迹T的第k段子轨迹,记为T(k)=〈pk,pk+1,…,pk+λ-1〉。
子轨迹从起始点开始,对长度为l的航迹,能产生l-λ+1条子轨迹,在同一子轨迹中,所有航迹点具有同一种行为模式,因此,子轨迹是判断目标行为模式的基础和基本单元。在2.2节中,本文介绍了七种行为模式,定义如下:
定义2 直线航行、小机动、大机动:设a、b为距离阈值,
为平均垂直距离。当
时,目标为直线行驶;当
时,目标为小机动;当
时,目标为大机动。
其中,a、b为距离阈值,为子轨迹的平均垂直距离,计算方式如下:
(1)
其中,di为第i个轨迹点到直线Lk的垂直距离。Lk为子轨迹起点pk和子轨迹终点pk+l-1连成的直线,直线方程为:
Lk∶ y=(yk+λ-1-yk)(x-xk)/(xk+λ-1-xk)+yk
(2)
定义3 左转弯机动、右转弯机动、S形机动:假设num+为第k段子轨迹中,位于直线Lk上方轨迹点个数,即Lk(x=xi)<=yi(i=k+1,k+2,…,k+λ-1);num-为直线Lk下方轨迹点的个数,即Lk(x=xi)>yi(i=k+1,k+2,…,k+λ-1)。当num+=num-时,目标的行为模式为S形机动;当num+>num-时,根据目标的相对运动位置判定,如图3所示,有四种情况。其中,图3(a)、(c)为左转弯机动、图3(b)、(d)为右转弯机动;当num+<num-时,同理有四种情况,如图4所示。其中图4(a)、(c)为右转弯机动、图4(b)、(d)为左转弯机动。
图3 num+>num-时,行为模式判定
Fig.3 Behavior patterns when num+>num-
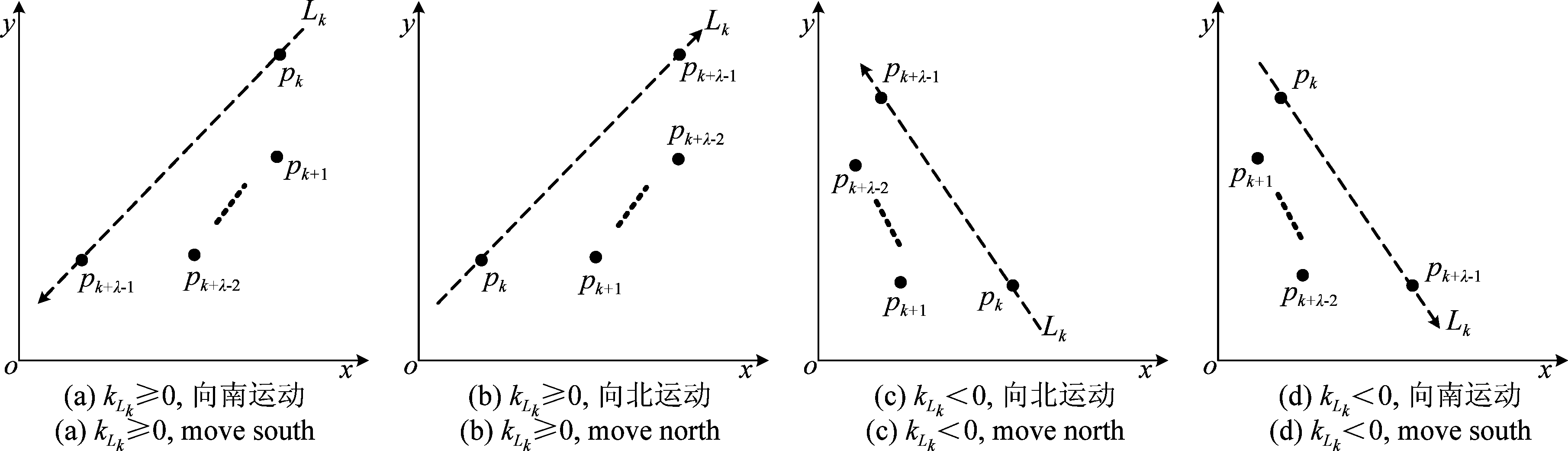
图4 num+<num-时,行为模式判定
Fig.4 Behavior patterns when num+<num-
根据定义1、定义2,目标进行直线航行时,不应该具有方位变换。因此,本文组合定义1和定义2中的行为模式得到目标在机动过程中的其中行为模式,分别如下:
①当目标满足直线航行定义时,目标的行为模式为直线航行;②当目标同时满足小机动和右转弯机动的定义时,目标的行为模式为小右转;③当目标同时满足小机动和左转弯机动的定义时,目标的行为模式为小左转;④当目标同时满足小机动和S形机动转弯机动的定义时,目标的行为模式为小S形航行;⑤当目标同时满足大机动和右转弯机动的定义时,目标的行为模式为大右转;⑥当目标同时满足大机动和左转弯机动的定义时,目标的行为模式为大左转;⑦当目标同时满足大机动和S形机动时,目标的行为模式为大S形航行。
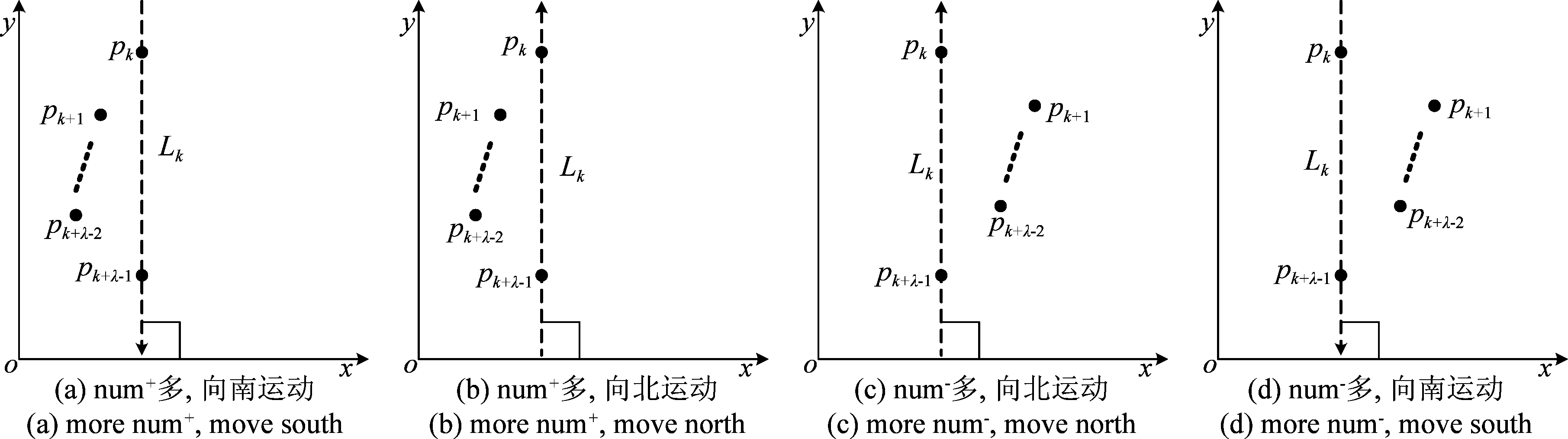
图5 kLk=
时,行为模式判定
Fig.5 Behavior patterns when kLk=
上述行为模式根据日常描述用词定义,是一种基础性的行为描述。在判定方式上,采用阈值分割的方式,涵盖了绝大部分的情况。为了覆盖所有的情况,本文对仅存的一种特殊情况进行讨论。当直线Lk的斜率为无穷大(kLk=
)时,无法通过y值计算num+和num-,此时应根据xi(i=k+1,k+2,…,k+λ-2)与xk的大小进行判定。此时,num+为在Lk左侧的轨迹点数量,即xi<xk,num-为在Lk右侧的轨迹点数量,判定左右转向时的四种情况如图5所示。其中图5(a)、(c)为左转弯机动,图5(b)、(d)为右转弯机动,行为模式的判定方法相同。
本文讨论了如何利用子轨迹判断目标在某个位置具有的行为模式。根据定义1可知,对于长度为l的子轨迹,相邻的两条子轨迹会有l-1个重合轨迹点,当行为模式相同时,可以将这些轨迹点划分在同一条轨迹段中;当行为模式不同时,我们需要为重合的轨迹点选择一种行为模式。在本文的轨迹分段算法中,通过引入行为模式优先级为轨迹点寻找更高优先级的行为模式。
海上目标的航行条件比较宽松,在大部分区域,为了节省能源和时间,目标会尽可能的选择简单快捷的直线航行方式。因此,处于直线航行模式的轨迹点在整条轨迹中占大多数,这种多数的轨迹点不会因为失去了部分轨迹点而出现只有少量轨迹点的情况。相反,在定义S形轨迹时,需要满足num+=num-的条件,在所有行为模式中属于最为严苛的定义,只会在少量的子轨迹中出现。因此,S形轨迹应具有最高优先级。最后,转向模式(左转、右转)是相似的行为,具有同等优先级。但是,目标在条件满足的情况下,会选择小机动模式进行航行,因此大右转和大左转因具有更高的优先级。综上所述,七种行为模式的优先级如式(3)所示。
直线航行<小左转=小右转<大左转=
大右转<小S形航行=大S形航行
(3)
行为模式和特征提取是增加分段轨迹的数据维度,行为模式属于轨迹分段算法的核心,特征提取是在分段完成后进行,目的是为了尽可能的还原真实轨迹,降低算法的轨迹损失。
根据定义的行为模式以及优先级,本文给出一种基于行为模式的轨迹分段算法,通过从航迹起点开始遍历,为每一个航迹点匹配行为模式,算法核心过程如图6所示。
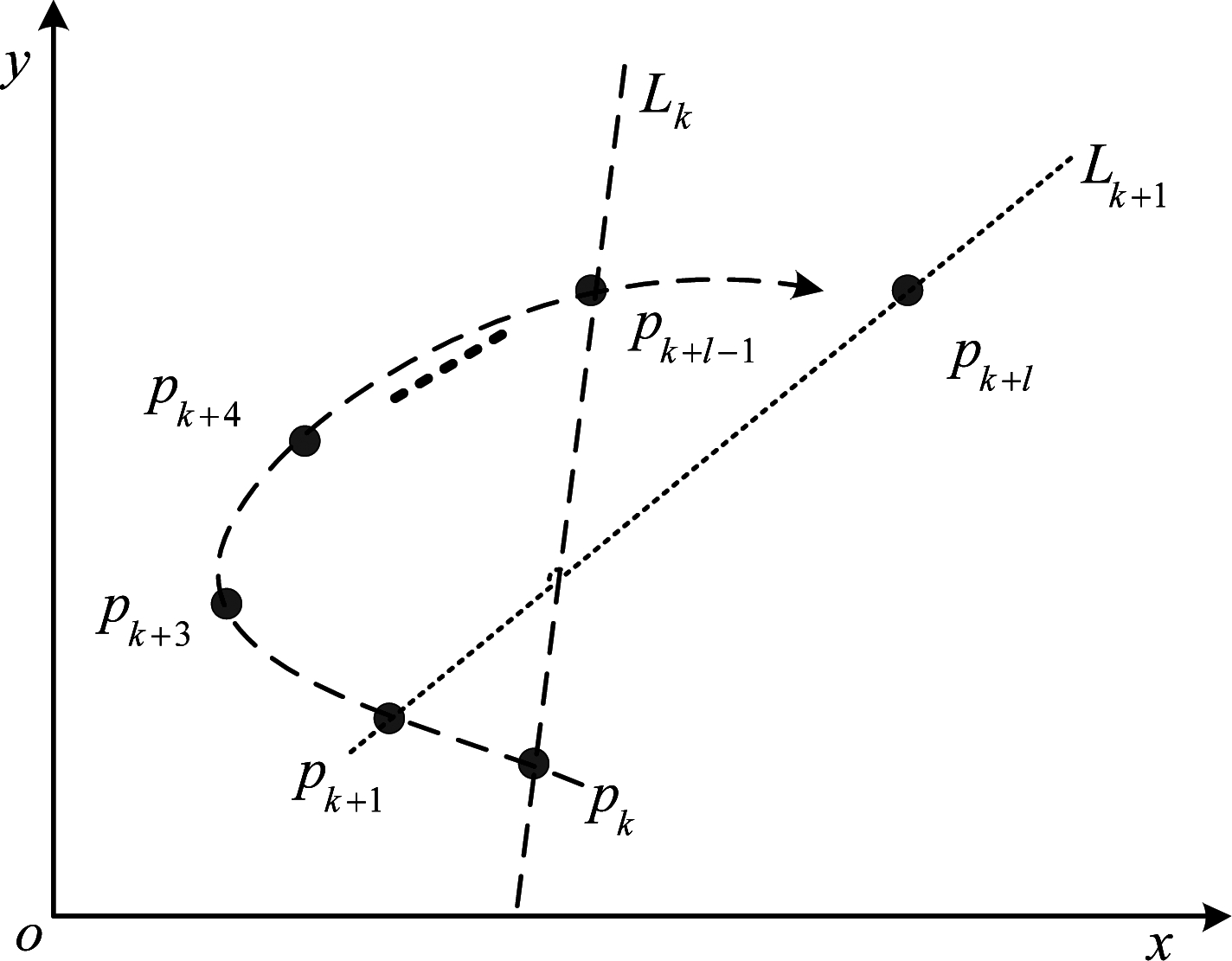
图6 算法过程图
Fig.6 Process of algorithm
图6所示为轨迹T遍历过程中连续的两段子轨迹,当前是遍历到航迹点pk,子轨迹T(k)具有的行为模式记为typek,即pk,pk+1,…,pk+λ-1都应该具有行为模式typek。当遍历到航迹点pk+1,子轨迹T(k+1)具有的行为模式记为typek+1,即pk+1,pk+2,…,pk+λ。对于重合的轨迹点pk+1,pk+2,…,pk+λ-1,有以下几种情况:
(1) typek与typek+1为同一类型,继续遍历下一个航迹点pk+2直到pk+λ;
(2) typek比typek+1具有更高的优先级,继续遍历下一个航迹点pk+2直到pk+λ-1;
(3) typek比typek+1具有更低的优先级或为同一优先级的不同行为模式,记录子轨迹类型和关键点pk+1,遍历重新从pk+1开始。
其中k=1,2,…,l-λ+1。根据上述核心过程,从起始点p1开始遍历,直到pl-λ+1结束,分别保存行为模式和关键点。最后,对于较短的轨迹,可以将其合并到相邻的轨迹段中,提高轨迹的压缩比。算法的具体流程如图7所示。
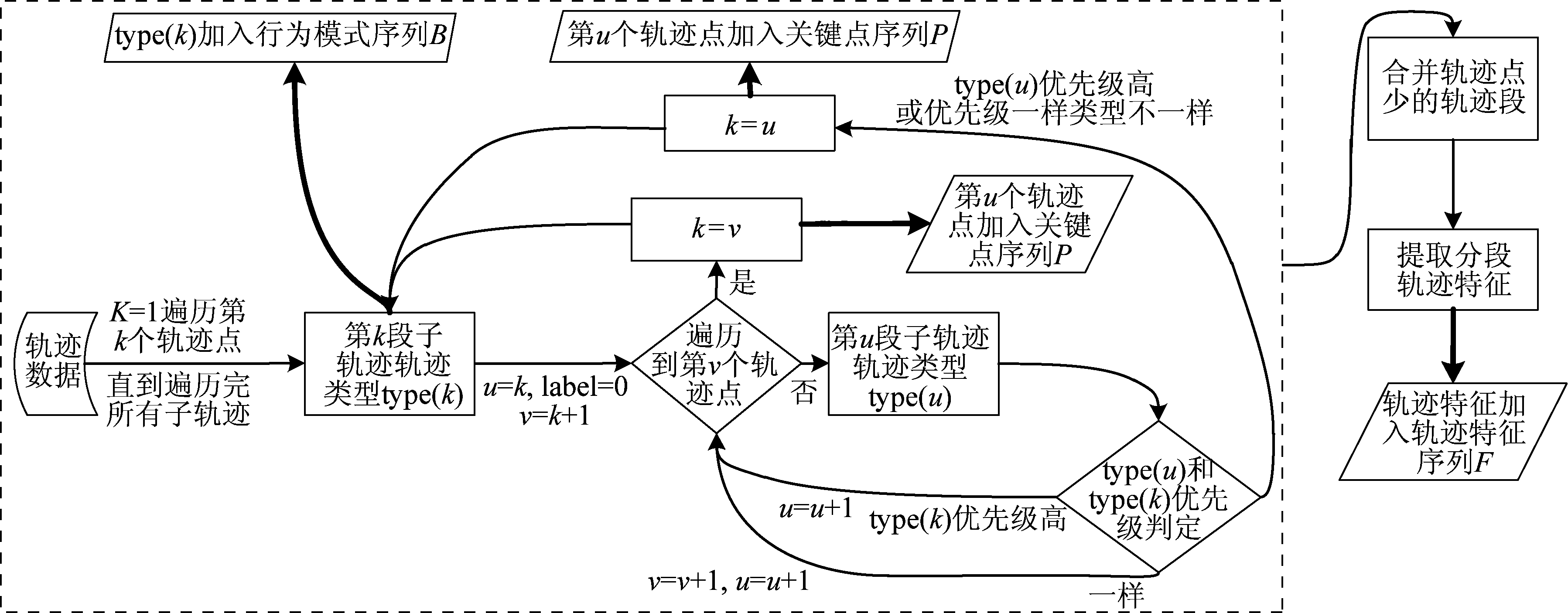
图7 算法流程图
Fig.7 Process of algorithm
分段完成的轨迹与子轨迹不同,是长度不等的轨迹段,这种根据行为模式的分段与常用的距离度量原理不同,分段完成的轨迹与直线轨迹相差很大,甚至大机动轨迹弯曲程度很大。因此,根据行为模式分段的轨迹不能以分段点连接的直线代替原始轨迹,需要找到分段轨迹的特征值。海上目标轨迹无论进行何种程度的机动,航向一定是渐变的,目标轨迹也一定是一条光滑的轨迹。在这种认知的启发下,本文根据原始航迹进行非线性拟合,将拟合参数作为分段轨迹的轨迹特征。为了使分段后数据量尽可能小、分段后轨迹的损失尽可能小,本文对直线行驶的轨迹采用线性拟合,对其余的行为模式采用三次非线性拟合,拟合表达式如式(4)、式(5)所示。
线性拟合: y=a2x+a1
(4)
三次非线性拟合: y=a4x3+a3x2+a2x+a1
(5)
其中x、y分别为轨迹点的横纵坐标。
根据式(4)、式(5)可知,直线行驶的轨迹具有2个特征值a1和a2,分别为常数项和一次项系数。其他行为模式具有4个特征值a1、a2、a3和a4,分别为常数项、一次项系数、二次项系数和三次项系数。从表达式可知,这种拟合方式只能拟合常规的曲线,对于拟合图8所示的曲线,误差会很大。因此,本文利用坐标旋转的方式将其变为可以拟合的常规曲线。
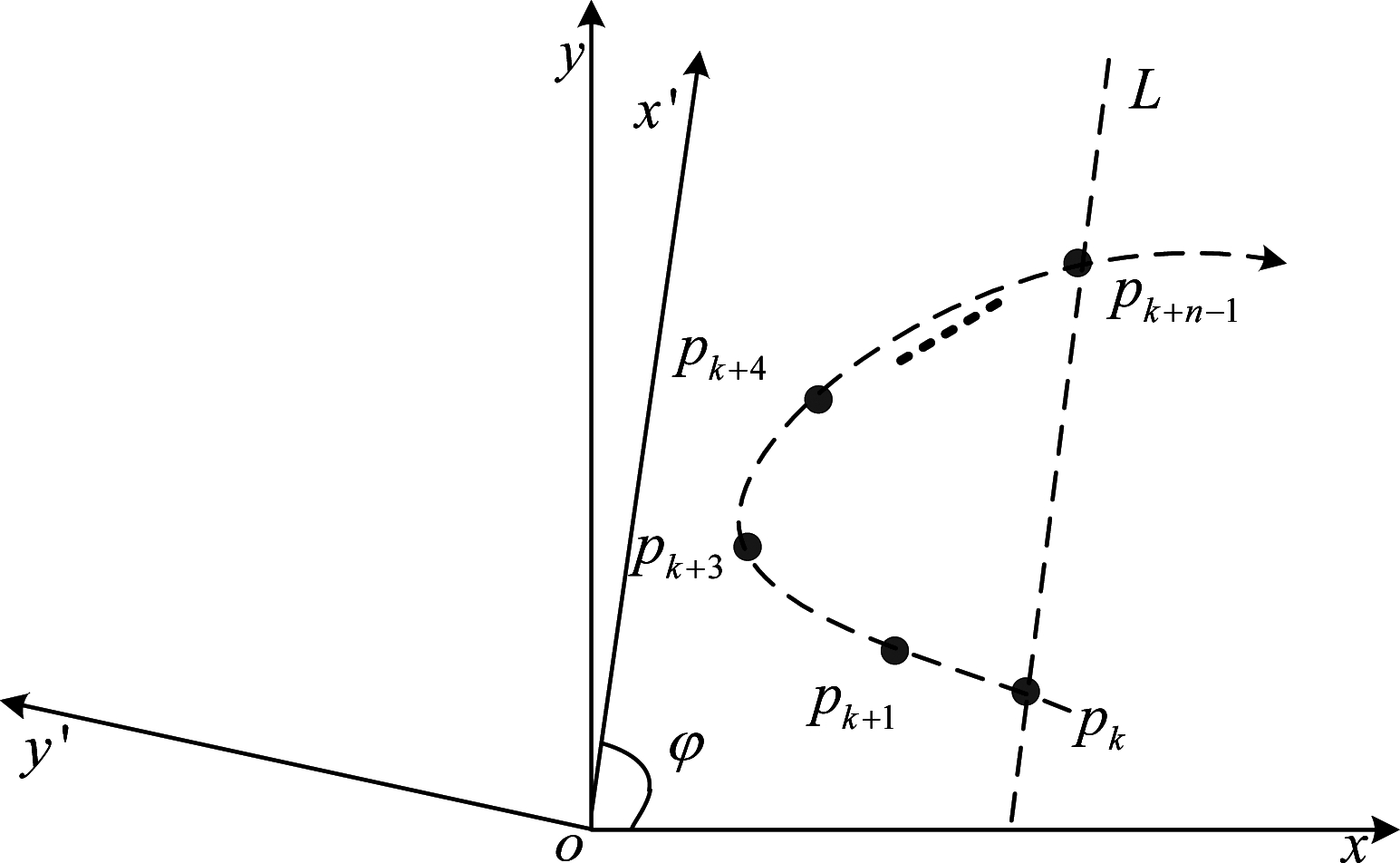
图8 特殊曲线
Fig.8 Special curve
图8所示为一条分段轨迹,具有n个轨迹点,L为轨迹段起始点和结束点连成的直线。从图中可以看出,这种曲线在原坐标系下一个横坐标对应两个纵坐标值,如果不进行坐标旋转,将会出现严重的误差,不能还原真实轨迹。因此,本文将坐标系进行旋转,使旋转后的横轴ox′平行于直线L,旋转角为φ,旋转后纵坐标轴为oy′,坐标旋转公式为:
(6)
其中x′、y′为旋转后的坐标,x、y为原坐标。进行坐标变换后,由于要对此类特殊曲线进行标记,为了尽量减少数据量,采用二次非线性拟合,如式(7)所示。
二次非线性拟合: y=a3x2+a2x+a1
(7)
经过式(7)的拟合,这类特殊曲线具有3个特征值a1、a2、a3,分别为常数项、一次项系数和二次项系数。为了能够真实的还原轨迹,最终需要根据式(6)进行反变换,由于分段后保存的是旋转后曲线的特征值,为了与其他特征值区分,还需引入标记δ,表示在还原轨迹时需要对坐标进行反变换。最终,这类特殊的曲线也具有四个特征值,分别为δ、a1、a2和a3。
基于行为模式的轨迹分段重点考虑到给不同轨迹段赋予行为模式,其目的不仅是针对轨迹的简化和压缩。最终,我们的算法得到的是有具体意义的轨迹段,能够辅助其他研究者或用户进行理解。实际上,很多实际应用过程中,用户想要接受的并不是特征值,这些数据对于他们来说是难以具体理解的,某些情况下,他们只关心目标进行了何种运动？从哪里到哪里？速度多少？路程多远？等信息。这种基于行为模式的轨迹分段也正是基于这种考虑。
在研究中,针对于汽车进行过总结性摘要的生成,例如某段轨迹汽车行驶的平均速度为70 km/h,对于普通的道路,70 km/h是很快的,而对于高速公路是比较慢的,为了帮助用户进行类似的理解,文献[18]设计了一种模板,包含汽车轨迹段的出发地、目的地、道路类型和速度等。相对于陆上交通,海上目标行驶在辽阔的海域,缺少道路约束,也很少有地标性的参考,只能通过目标的一些静态、动态信息理解目标的行为。对于摘要的生成,大多数是靠人工完成的。
本文的研究为这种摘要做了一些基础性的工作。例如目标轨迹分段、行为模式挖掘和轨迹特征提取。实际上,借助本文的结果结合地理环境信息,给一些轨迹点和一部分特殊轨迹段赋予类似于地标性建筑和道路名称的实际含义,结合目标的行为模式和轨迹特征,就能够生成目标行为的摘要。这种摘要将来可以利用本文处理技术进行文本聚类等挖掘分析,进一步提高海上目标轨迹数据挖掘的深度。
本文的算法与常用的轨迹分段算法不同,根据行为模式分段是本文算法的核心也是亮点。首先,通过行为模式定义、优先级设置和轨迹分段算法,使分段轨迹具有语义内涵。然后,根据原始轨迹进行非线性拟合,降低压缩损失。最终,本文分段轨迹用于定量和定性的轨迹数据挖掘,与常用的轨迹分段算法差别较大,没有比较的必要性。因此,本文仅对算法的参数和分段的性能指标进行讨论。
为了验证本文算法的有效性,本文选取了两种需求下的情景,可以更直观的表现本文算法在实际应用中的效果。实验数据选取AIS数据中1条典型航迹,如图9所示。
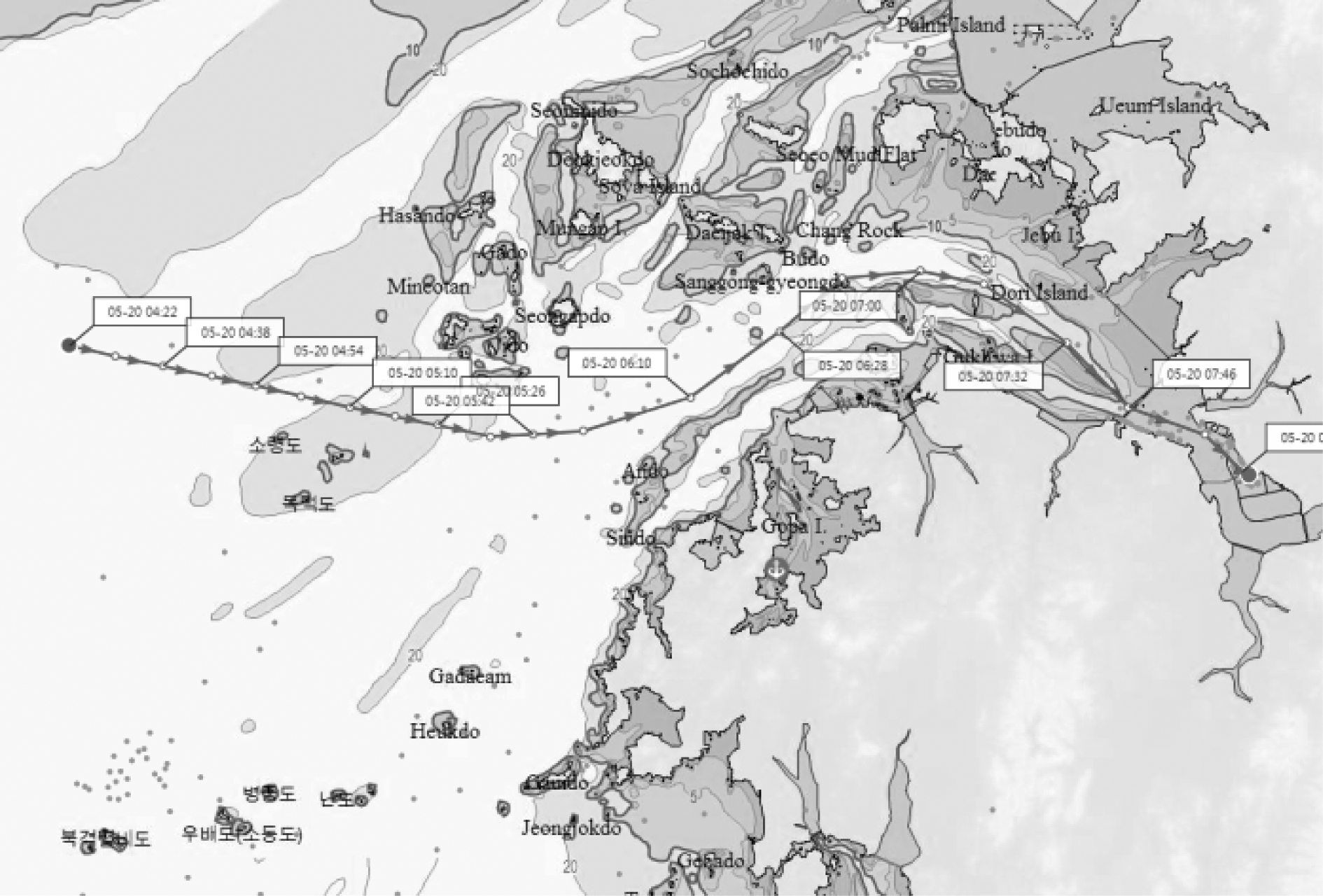
图9 实验轨迹
Fig.9 Experiment trajectory
图9所示为MMSI(Maritime Mobile Service Identify)号为636017754的客船从2019年5月20日4:20到8:36进入韩国平泽市港口的轨迹数据,共计53个轨迹点。由于算法是建立在平面直角坐标系下,AIS数据采用经纬度坐标,需要将经纬度进行投影,本文采用UTM(Universal Transverse Mercator Grid)坐标系统。
图9转换后以(120°E,35°N)为坐标原点建立直角坐标系,得到UTM坐标系统中的轨迹,如图10所示。
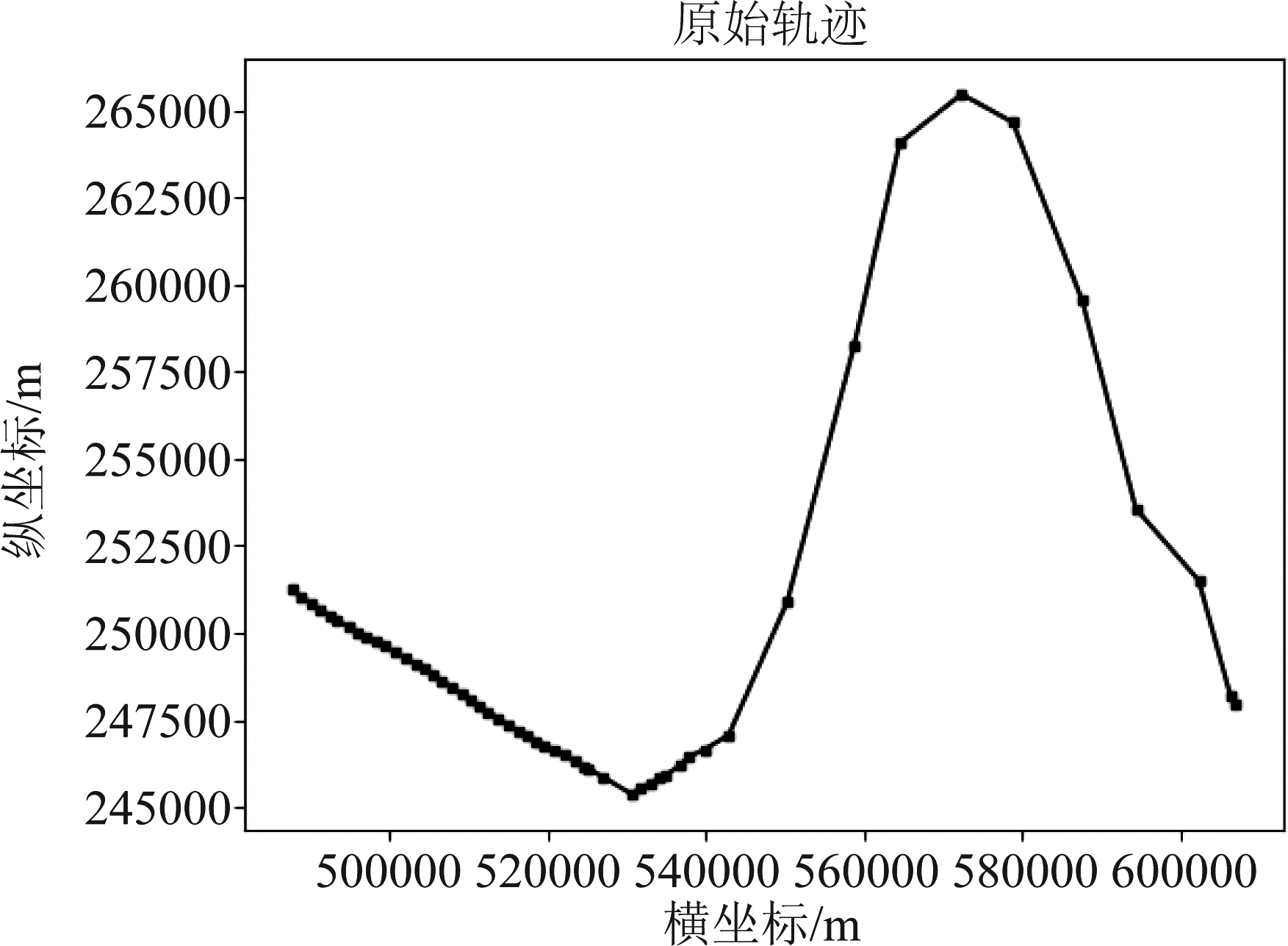
图10 坐标转换后的轨迹
Fig.10 Transform trajectory
实验运行在计算机上,操作系统为Windows7,CPU为Intel Core I7- 4710MQ,内存为8G,所有算法均使用Python语言编写,软件环境为PyCharm4.0.4。
5.2.1 性能评价指标
为了衡量算法的性能,本文采取两种评价指标分析算法的实际分段能力。在常用的轨迹简化算法中,压缩比和损失是最常用的两种评价指标。其中,压缩比是衡量轨迹简化和压缩性能的重要指标,压缩比越大,轨迹的简化和压缩性能越强;损失是衡量轨迹还原能力的重要指标,是定义真实轨迹点与压缩轨迹之间的数学量,本文采用同一横坐标下的平均纵向偏移距离(以下简称偏移距离)作为压缩轨迹的损失。
π=l/m
(8)
(9)
式(8)为压缩比的表达式,l为压缩前轨迹点的数量,m为压缩后轨迹点的数量。
式(9)为偏移距离的表达式,
表示第k条轨迹段的偏移距离,n为第k条轨迹段的长度,xk，i,yk，i分别表示第k条轨迹段第i个轨迹点的原始横纵坐标,C为根据特征参数拟合的曲线,C(x=xk，i)表示曲线C上横坐标xk，i对应的纵坐标。
5.2.2 子轨迹长度λ的选取
子轨迹作为判断行为模式的基础,在分段算法中具有重要作用。根据定义3可知,要计算子轨迹正负偏离点的个数,子轨迹长度必须λ>2;子轨迹为了能判断S形轨迹,存在满足num+=num-的可能,子轨迹长度λ必须为偶数。因此,λ的取值为大于等于4的偶数。
考虑到子轨迹的长度不能很大(如λ=60),这种情况是不现实的,子轨迹的长度应该受到原始轨迹长度等因素的限制。受不同需求的影响,λ取值不同,本文选取了λ=4,6,8,10,12,14进行实验。实验轨迹如图9所示,为韩国平泽市港口入港时轨迹,范围较小,设定一个较小的阈值a=50(m)、b=100(m)。
图11所示为λ=4时的分段结果,图中虚线部分为由特征参数还原的轨迹,实线部分为原始航迹点的折线图,图11中几段主要的航迹如图12所示。通过视觉检查可以发现,利用行为模式进行分段,提取特征参数后,还原的轨迹更加光滑,符合目标的运动规律。例如图12(b)所示的大左转轨迹段,目标由低纬度向高纬度运动,呈光滑的曲线状,相对于原始轨迹的折线图更加符合目标渐变航行的规律。
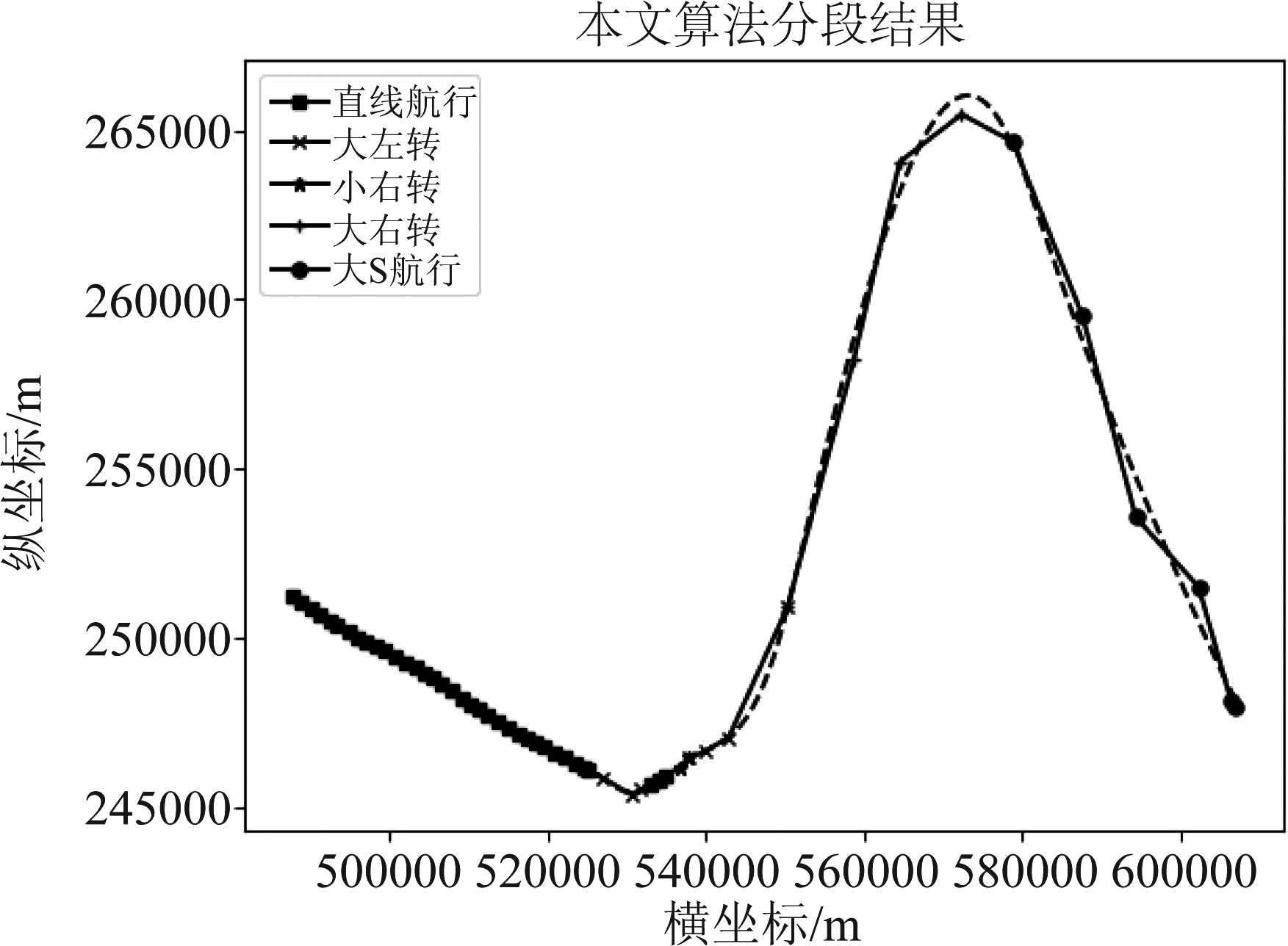
图11 分段轨迹
Fig.11 Segmentation
通过对图11、图12的视觉检查发现,在λ=4是分段算法的效果比较好。根据本文给定的性能评价指标,本文对λ=4,6,8,10,12,14时的分段效果进行对比,图13所示为不同λ取值时压缩比的变化图,表1所示为不同λ取值下每段轨迹的偏移距离。
图12 轨迹段
Fig.12 Part of Segmentation
表1 不同子轨迹长度的偏移距离
Tab.1 Error of different length
注:(a, b)中a表示行为模式:直线航行0,小右转1,小左转2,小S航行3,大右转4,大左转5,大S航行6;b表示平均纵向偏移距离,单位为m。
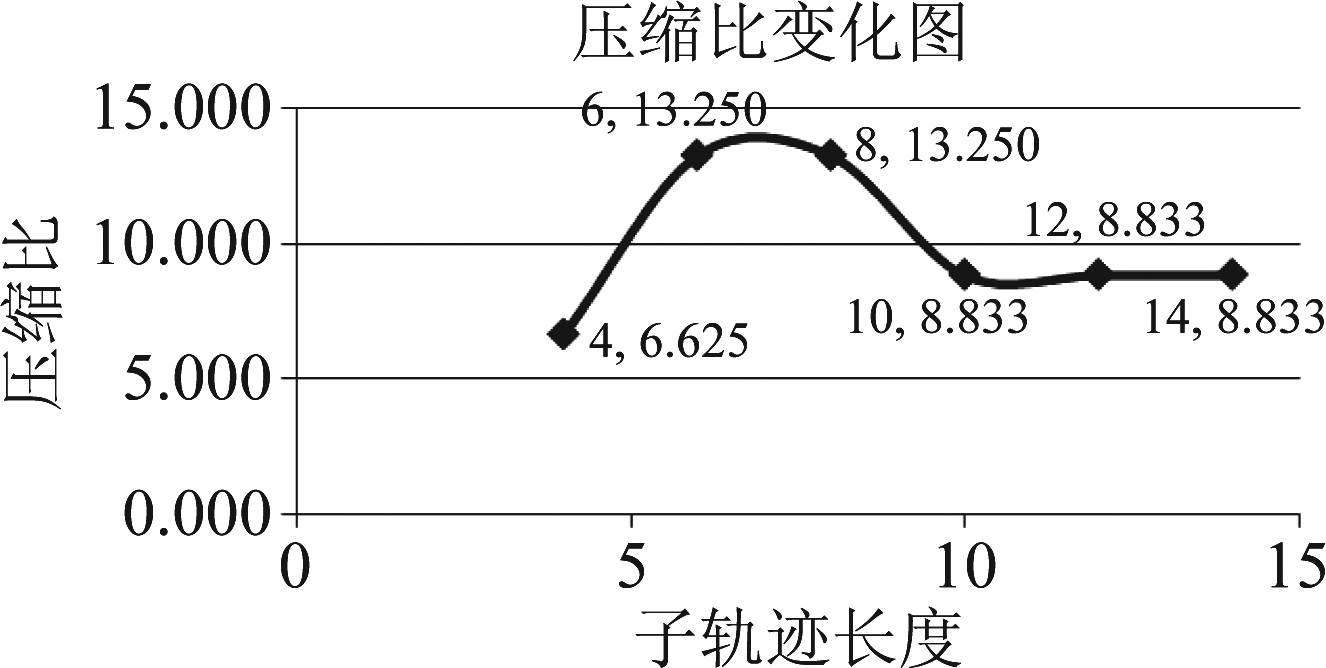
图13 不同子轨迹长度的轨迹压缩比
Fig.13 Compression ratio of different length
结合图13和表1发现,当子轨迹长度取值较小时,分段轨迹数量最多,压缩比最小;当子轨迹长度取值适中时,分段轨迹数量最少,压缩比最大;当子轨迹长度取较大值时,子轨迹数量较少,压缩比较大。从表1中可以发现,随着子轨迹长度的变化,轨迹点的类型在发生变化,这并不代表着目标的行为模式是不定的,也不是在分段的过程中发生错误。
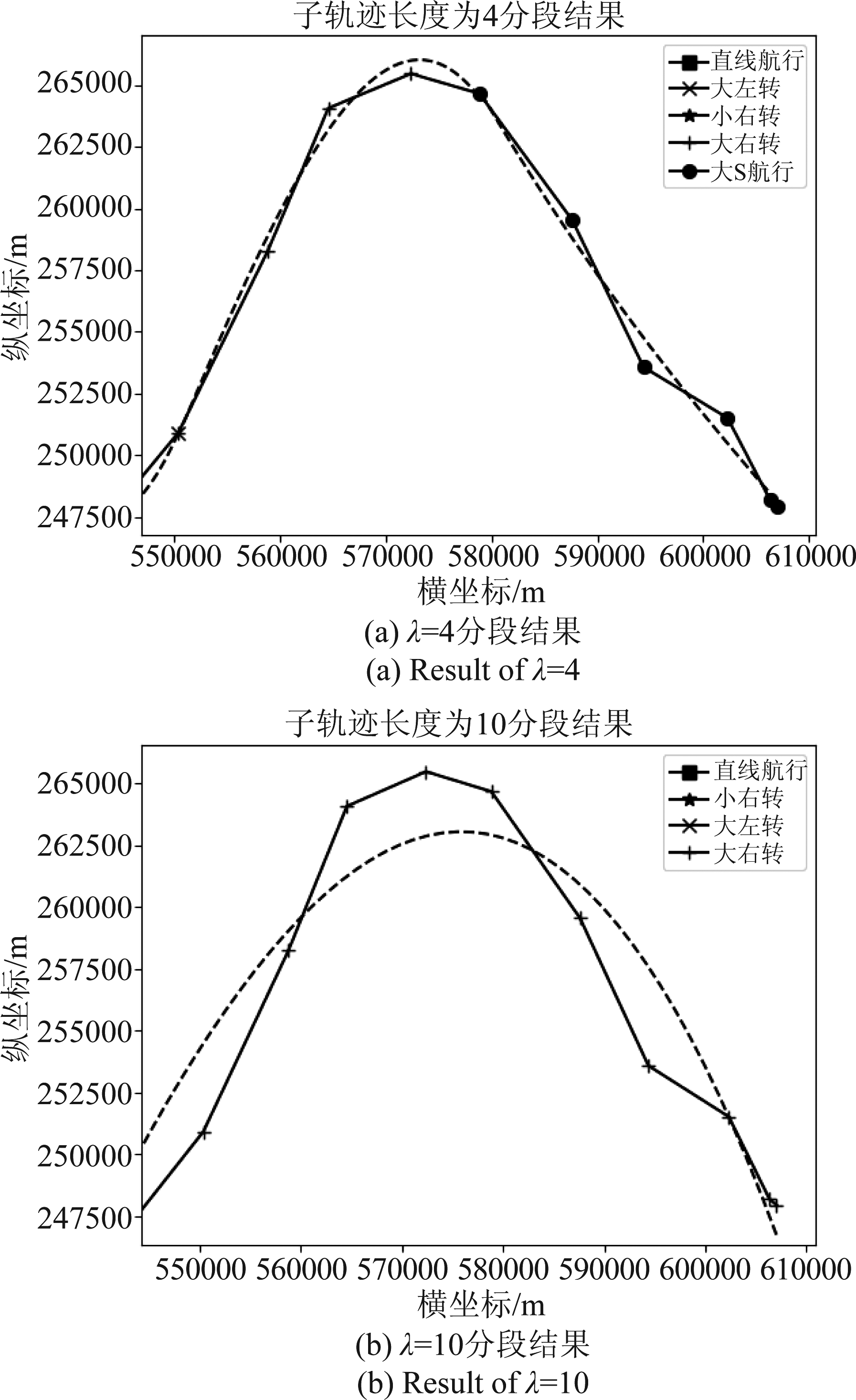
图14 不同子轨迹长度分段结果
Fig.14 Result of different length
图14所示为同一局部区域,子轨迹长度λ=4和λ=10的分段结果。从视觉检查上,两种分段方式都是符合行为模式的,但分段的数量不同。当子轨迹长度较小时,划分较为细致,适合于用于较为精确的研究;当子轨迹长度较大时,主要考虑总体的走向,会忽略一些局部细节,主要适合于对目标大方向的整体掌握。结合表1和图14可以发现,随着子轨迹长度的增加,部分轨迹的偏移距离减小,如图14所示的轨迹偏移距离增大,这也是与考虑的轨迹长度和应用需求息息相关的。从偏移距离上来分析,当子轨迹长度较小时,偏移距离是分布较为均匀的;当子轨迹长度增加,偏移距离的两极化越来越严重。
综上所述,子轨迹长度λ取值不同,应用场景不同,轨迹的损失也不同。较小的子轨迹长度可用于精确度较高的研究,例如目标短时动向分析;较长的子轨迹用于掌握目标的总体动向,例如用于关键点等长时预测方向。但是,子轨迹的长度不宜过长,建议取值范围为[4,16]。
5.2.3 阈值a、b的选取
阈值a、b是本文算法的核心,是决定行为模式的关键参数。实际上,阈值是根据用户的需求以及经验决定的,是可调可变的。当子轨迹长度λ=6时,分别取两组参数a=50(m),b=100(m)和a=500(m),b=1000(m)进行对比。
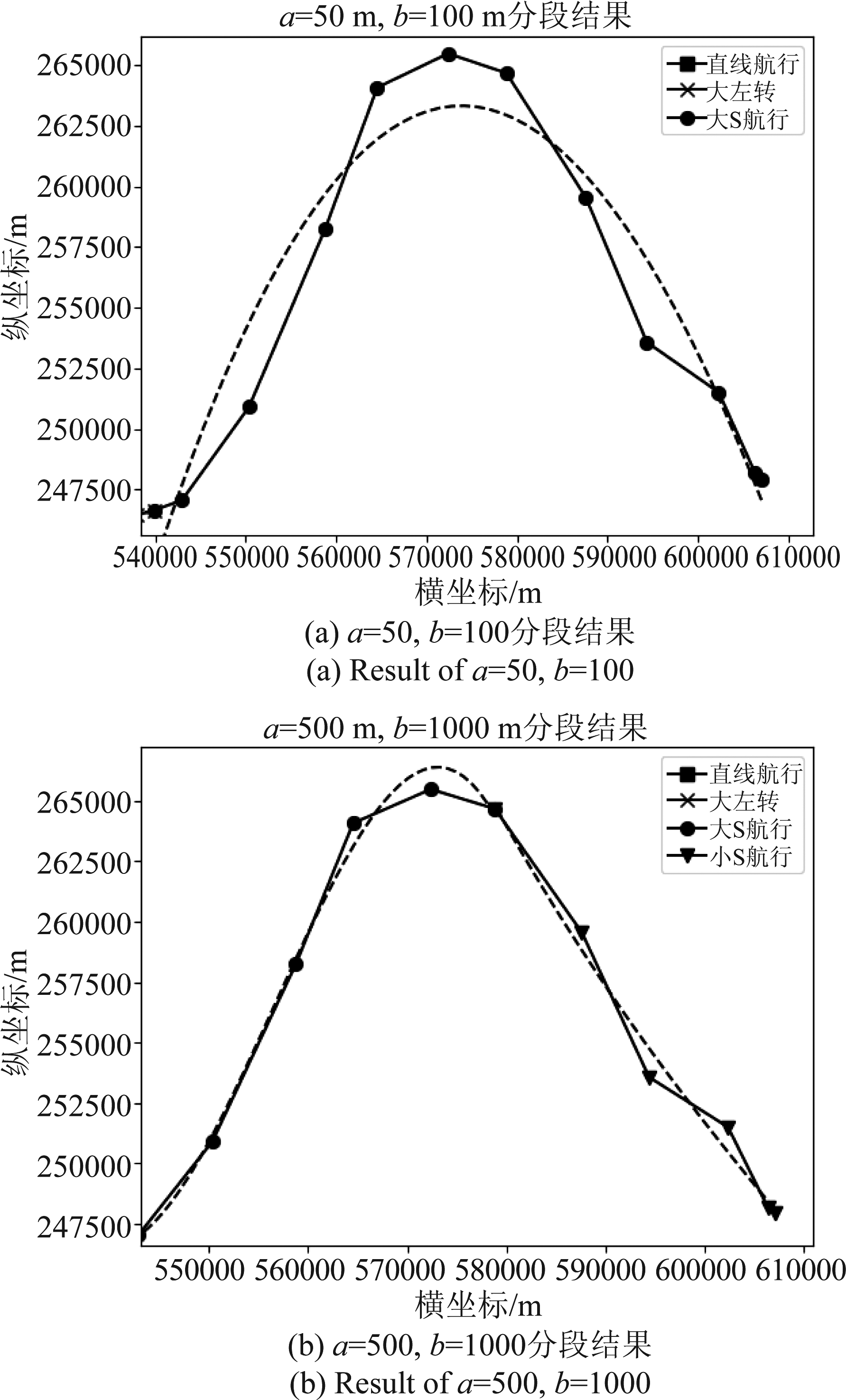
图15 不同阈值分段结果
Fig.15 Result of different threshold
图15所示为a=50(m),b=100(m)和a=500(m),b=1000(m)时的局部分段结果。当a=50(m),b=100(m)时,目标进行了连续的大S机动;但是,当阈值增大a=500(m),b=1000(m)时,第二段大S航行变成了小S航行。因为,大机动和小机动的界限并没有明确的界定,根据不同的需求,例如进行整体动向研究时,可以忽略很多小的局部机动,例如遇到海浪、渔网等不可抗力。但是,这种忽略小的局部机动不影响目标整体动向的研究。
综上所述,在取值范围内,子轨迹长度λ和阈值a、b是根据实际的研究内容决定的,在利用分段算法时,结合专家经验和调试确定合适的取值。
5.2.4 总结性摘要示例
根据4.3节的介绍,可以通过与地理环境信息的结合生成总结性摘要,是对分段结果中行为模式这种语义内涵的应用。摘要根据分段后的轨迹生成,通过对拟合的曲线进行积分,求解轨迹段的总航程;通过时间信息,求解平均航速;结合地理环境信息,给用户位置参考,使得摘要的描述更加的具体。以本文的分段结果(如图11所示)为例,给出一段示范性的文本摘要信息:
目标MMSI号为636017754,从2019年5月20日4:20到2019年5月20日8:36,出发地为(125.51°E,37.07°N),目的地为韩国平泽市。目标从出发地出发,经过直线航行于2019年5月20日5:24到达(125.93°E,37.00°N),总航程约20海里;经过大左转航行于2019年5月20日5:36到达(126.01°E,36.99°N),总航程约4.2海里,平均航速19.4节;而后经过直线航行、小右转于2019年5月20日5:46到达(126.08°E,36.99°N),总航程约3.5海里;经过大左转航行于2019年5月20日6:10到达(126.22°E,37.02°N),总航程约7.7海里,平均航速19.5节,到达瑞山市海域;经过大右转航行于2019年5月20日7:14到达(126.55°E,37.12°N),总航程约18.4海里,平均航速18.4节,到达入海口;经过大S形航行于2019年5月20日8:36到达目的地平泽市。
本文给出的示范仅供参考,在进行摘要生成时,应该重点关注于大机动、大航程的轨迹段和有环境参考信息的轨迹段,进行详细描述,例如经过 于 到达 ,总航程约 ,平均航速 ,到达 。对于“而后经过 于 到达 ,总航程约 ;”这类机动性不强,航程较短的轨迹段,可以使用简化描述的模板。
本文提出了一种基于行为模式优先级的轨迹分段算法,以子轨迹作为基本单元,从起始点进行遍历。通过定义7种行为模式,对目标当前的行为进行描述,在分段过程中,依据行为模式的优先级顺序决定轨迹点最终的行为模式。最终,本文对分段完成的轨迹进行特征提取,降低轨迹损失,还原原始轨迹。实验表明,本文的分段算法能够准确的进行分段、简化和压缩。我们在对本文三个重要参数的讨论中发现,在实际过程中,不同的参数设置对应不同的应用需求。
在应用上,本文的分段结果还可以有很多的应用展望,例如,分段轨迹可以通过TRACLUS聚类框架进行聚类,挖掘有用的航道信息;通过特征层面的聚类探索某个区域或某类目标普遍的行为模式;通过组合不同类型的行为模式,辅助识别特定目标的特定任务等。最后,本文也对分段轨迹和行为模式等信息在总结性文本生成上的应用前景进行展望。
[1] 陈小龙, 关键, 何友, 等. 高分辨稀疏表示及其在雷达动目标检测中的应用[J]. 雷达学报, 2017, 6(3): 239-248.
Chen Xiaolong, Guan Jian, He You, et al. High-resolution Sparse Representation and Its Applications in Radar Moving Target Detection[J]. Journal of Radars, 2017, 6(3): 239-248.(in Chinese)
[2] 陈小龙, 关键, 黄勇, 等. 雷达低可观测目标探测技术[J]. 科技导报, 2017, 35(11): 32- 40.
Chen Xiaolong, Guan Jian, Huang Yong, et al. Radar low-observable target detection[J]. Science & Technology Review, 2017, 35(11): 32- 40.(in Chinese)
[3] Zhang Xiaohan, Wang Haipeng, Xu Congan, et al. A Lightweight Feature Optimizing Network for Ship Detection in SAR Image[J]. IEEE Access, 2019.
[4] Lamba S, Nain N. Segmentation of crowd flow by trajectory clustering in active contours[J]. The Visual Computer, 2019(10).
[5] Tasnim S, Caldas J, Pissinou N, et al. Semantic-Aware Clustering-based Approach of Trajectory Data Stream Mining[C]∥2018 International Conference on Computing, Networking and Communications (ICNC). IEEE Computer Society, 2018.
[6] Dodge M. Algorithms for the Reduction of the Number of Points Required to Represent a Digitized Line or its Caricature[J]. Cartographica: The International Journal for Geographic Information and Geovisualization, 1973, 10(2): 112-122.
[7] Imai H. Polygonal approximations of a curve-Formulation and algorithms[J]. Computational Morphology, 1988.
[8] Daescu O, Mi N. Polygonal chain approximation: a query based approach[J]. Computational Geometry: Theory and Applications, 2005, 30(1): 41-58.
[9] Kolesnikov A, Fränti, Pasi. A fast near-optimal algorithm for approximation of polygonal curves[C]∥International Conference on Pattern Recognition. IEEE, 2002.
[10] Cao Weiquan, Li Yunzhao. DOTS: An online and near-optimal trajectory simplification algorithm[J]. Journal of Systems and Software, 2017.
[11] 曹卫权, 李智翔, 魏强, 等. 基于区域分布概率密度估计的轨迹分类方法[J]. 计算机工程, 2018, 44(4): 268-273.
Cao Weiquan, Li Zhixiang, Wei Qiang, et al. Trajectory Classification Method Based on Probability Density Estimation of Regional Distribution[J]. Computer Engineering, 2018, 44(4): 268-273.(in Chinese)
[12] Lee Jae-Gil, Han Jiawei, Whang Kyu-Young. Trajectory Clustering: A Partition-and-Group Framework[J]. ACM, 2007.
[13] Chen Jiashun, Pi D. A New Trajectory Clustering Based on Paritition-Cluster-Extration[C]∥The Fifth International Conference on Computational and Information Sciences(ICCIS2013), 2013.
[14] Lee J G, Han Jiawei, Li Xiaolei. Trajectory Outlier Detection: A Partition-and-Detect Framework[C]∥IEEE International Conference on Data Engineering. IEEE Computer Society, 2008.
[15] Yang X, Tang L. CROWDSOURCING BIG TRACE DATA FILTERING: A PARTITION-AND-FILTER MODEL[J]. ISPRS-International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, 2016.
[16] Yuan Hua, Qian Yu, Ma Baojun, et al. From Trajectories to Path Network: An Endpoints-Based GPS Trajectory Partition and Clustering Framework[M]. Web-Age Information Management.Springer International Publishing, 2014: 740-743.
[17] 孙璐, 周伟, 姜佰辰, 等. 一种时空联合约束的多源航迹相似性度量模型[J]. 系统工程与电子技术, 2017(11): 19-27.
Sun Lu, Zhou Wei, Jiang Baichen, et al. Multi-source trajectories similarity measure model with spatial and temporal constraints[J]. System Engineering and Electronics, 2017(11): 19-27.(in Chinese)
[18] Su Han, Zheng Kai, Zeng Kai, et al. Making sense of trajectory data: A partition-and-summarization approach[C]∥2015 IEEE 31st International Conference on Data Engineering, 2015.
金佳龙 男, 1996年生, 四川绵阳人。海军航空大学硕士研究生, 主要研究方向为时空轨迹数据挖掘。
E-mail: jjldwb@sina.cn
周 伟 男, 1980年生, 湖北黄石人。海军航空大学副教授, 主要研究方向为多源信息融合、大数据技术及应用。
E-mail: yeaweam@163.com
姜佰辰 男, 1991年生, 山东烟台人。海军航空大学博士研究生, 主要研究方向为时空轨迹数据挖掘。
E-mail: 704011136@qq.com