图1 通信成功率预测网络
Fig.1 Transmission success rate prediction network
Reference format: Yang Hang, Li Honglie, Fang Fang, et al. Depth Learning Model for RDSS Emission in Maritime Aviation Distress[J]. Journal of Signal Processing, 2020, 36(12): 2061-2066. DOI: 10.16798/j.issn.1003- 0530.2020.12.012.
战斗机飞行员海上遇险卫星求救装备通常以预先设置的时间周期进行位置报告,但由于受恶劣气象、设备浸水、天线难以对星等多种因素影响,选择恰当的时机快速发起遇险位置报告的相关能力较弱,成功率较低,且与长时工作的矛盾难以调和。
影响卫星信号质量的因素多种多样,包括经度、纬度、高度、方向、俯仰角、速度、加速度、浸水、卫星信号强度、设备电量等[1-2]。上述因素往往是交叉和迭代的,比如湿度和浸水使信号传输性能变差,为了降低误码率,需要加大发射功率或提高发射频度,但这又加快了能量耗损,导致电池电量快速下降,电池瞬时放电能力变差,功率效率进一步降低,从而进入恶性循环。
飞行员穿戴式设备体积和重量严格受限,很难通过增加电池电量来解决有效发射与工作时长指标的矛盾,因此希望通过发掘环境条件与卫星信号质量之间的关系,得到一种可能的预测模型,减少对卫星信号质量实时监控的开窗口时间,减少无效发射,以增加平时数据分析复杂度为代价,换取紧急情况下设备位置报告成功率。文献[3]给出了深度学习的定义,文献[4]将深度神经网络(DNN:Deep Neural Network)应用于浅水环境中的源定位,文献[5]详细论述了将机器学习方法应用于水声被动定位的关键理论基础,文献[6]给出了输入降维方法,文献[7]给出了水下目标被动识别中常用的深度神经网络结构、深度学习对特征提取环节产生的影响以及数据匮乏条件下的建模方法,但由于环境因素的复杂性,传统的机器学习可从以往的数据中挖掘规律仍然需要人为指定特征,技术理论分析难度较大。本文分析了影响发射效率的主要因素,提出了一种基于DNN的自学习报位策略预测模型,无需行业专家指定特征,通过自学习实现报位策略的动态调整,该策略区别于以往固定周期的工作方式,可根据设备多维度实时传感器数据自动调整到最优或次优报位时刻,在增加报位成功率的同时,节省电量,延长设备工作时间。
遇险现场的多种条件因素会对报位成功率产生影响。这些因素的组合需要列为决定是否发射求救报位信号的参数条件。
(1) 自由空间损耗
可通过自身卫星定位模块获取经纬度、高度、方向数据,通过陀螺仪获取仰角数据,与卫星星历结合估算链路路径损耗。
(2) 链路附加损耗
部分终端设备可检测卫星实时下行波束数量及信号强度,但受大气、雨衰等因素影响,信号强度难以作为是否适合进行信号发射的严格判断标准,当前气象条件,如温度、湿度、气压等数据,可用于间接估算雨衰对卫星信号的影响,且不能精确地预测,仅能做出估计。上述条件在不同的仰角、温度、湿度、云层、雾气、电离层不连续性等因素影响下难以估计。但时间与星食、日凌等因素对卫星信号的影响具有对应关系。
(3) 发射功率
设备的发射功率需要动态调整,因此,电量与环境温度也是影响信号发射的重要因素。但由于电池加工工艺不同,该影响在不同电池上的表现并不一致,其影响力难以准确估计。
(4) 运动规律
随机海浪理论认为,随机海面中的海浪是由多个不同振幅、不同频率、不同方向、不同相位的谐波叠加组成[8]。终端设备只能根据过去一段时间内方向、俯仰角及加速度的变化获得当前海浪的变化规律。可根据该规律预测合适的对星角度出现的时机,以便选择合适的发射时刻。
(5) 浸水和结冰
水和冰会阻断电磁波的传播,但规律不同。设备浸在水中或表面覆冰时会极大地影响信号发射和接收。因此,如果检测到设备处于浸水或厚覆冰状态,则不适宜进行发射。
(6) 多普勒频移
终端设备在进行星间切换时也会产生多普勒频移突变,它是少数可计算的影响因素。
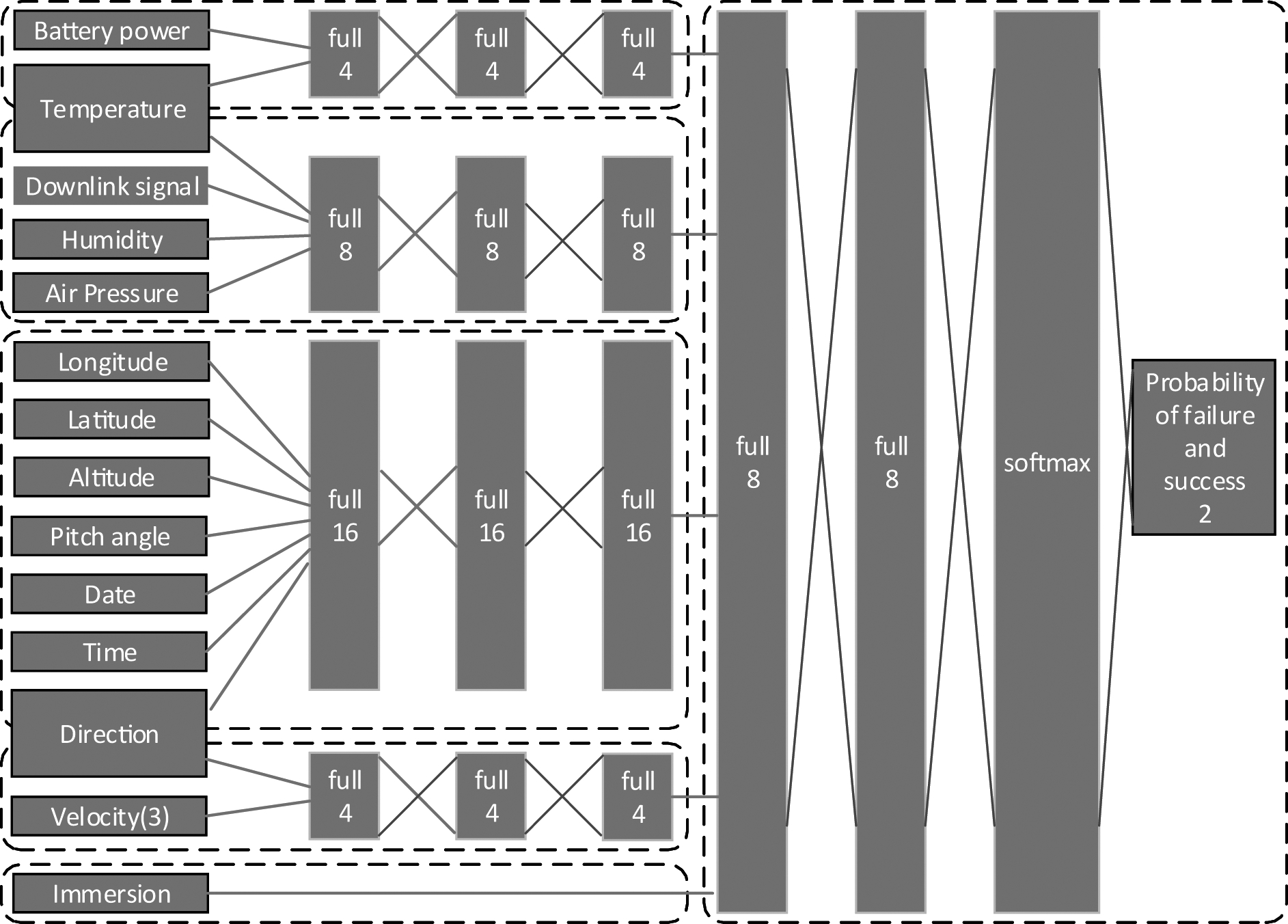
在发射成功率影响因素分析基础上,设计DNN模型(图1),该模型为全连接网络,包含两个子网络共6个分支结构,左侧5分支用于拟合链路特性及影响因素;右侧网络整合各分支结构,计算得最终结果。

图1 通信成功率预测网络
Fig.1 Transmission success rate prediction network
模型以传感器获取的实时参数作为输入条件,包括俯仰角、经纬度、高度、信号强度、速度、方向、浸水、湿度、温度、气压、剩余电量、时间等,其中的温度和方向数据被两个子网络共享。根据太阳日及恒星年对卫星轨道及信号影响的不同,将日期与时间拆分为两个数据;运动速度数据用含有3个元素的向量表示;浸水用0、1两种状态表示。所有参数转换为单精度浮点数输入网络,经过10个隐层,每层32个神经元,最终以softmax层输出,得到互斥的预测结果。为了便于扩展更多发射功率等级,使用2个(0,1)区间的浮点数输出结果,分别表示发射失败及成功的概率,使用纠正线性单元(ReLU) 作为激活函数[9],以有效避免梯度消失或梯度爆炸问题,提高训练速度。
(1)
使用交叉熵计算该网络的loss值[10-11]。
(2)
图2为发射延时预测子网络。输入的序列化加速度及俯仰角数据经过RNN后,可以得到中间结果o表示海浪谱的周期,然后使用设备最后一次在海浪中的相位(加速度、俯仰角、方向),结合海浪谱周期,计算得到下一次设备处于波峰和波谷的时间段。在制作训练数据集时,下一次设备处于波峰或波谷的时刻即为设备在Y方向速度趋近于0,且俯仰角亦趋近于0的时刻,由于已预先得知输入数据的后续所有相位数据,因此,该时刻已知,可用于训练数据的输出。故以过去10 s为计算周期,每秒采集到的1次加速度和俯仰角格式化为浮点数,之后将3×10的矩阵塑为1×30的可视数据输入递归神经网络(RNN:Recurrent Neural Network)[12-13],经过10个隐层后,将位于(0,1)区间的输出结果放大10倍,预测得下一时刻对星角度最好的最小延时时间。为了提高训练速度,需要对左侧子网络进行预训练后再进行整体训练。
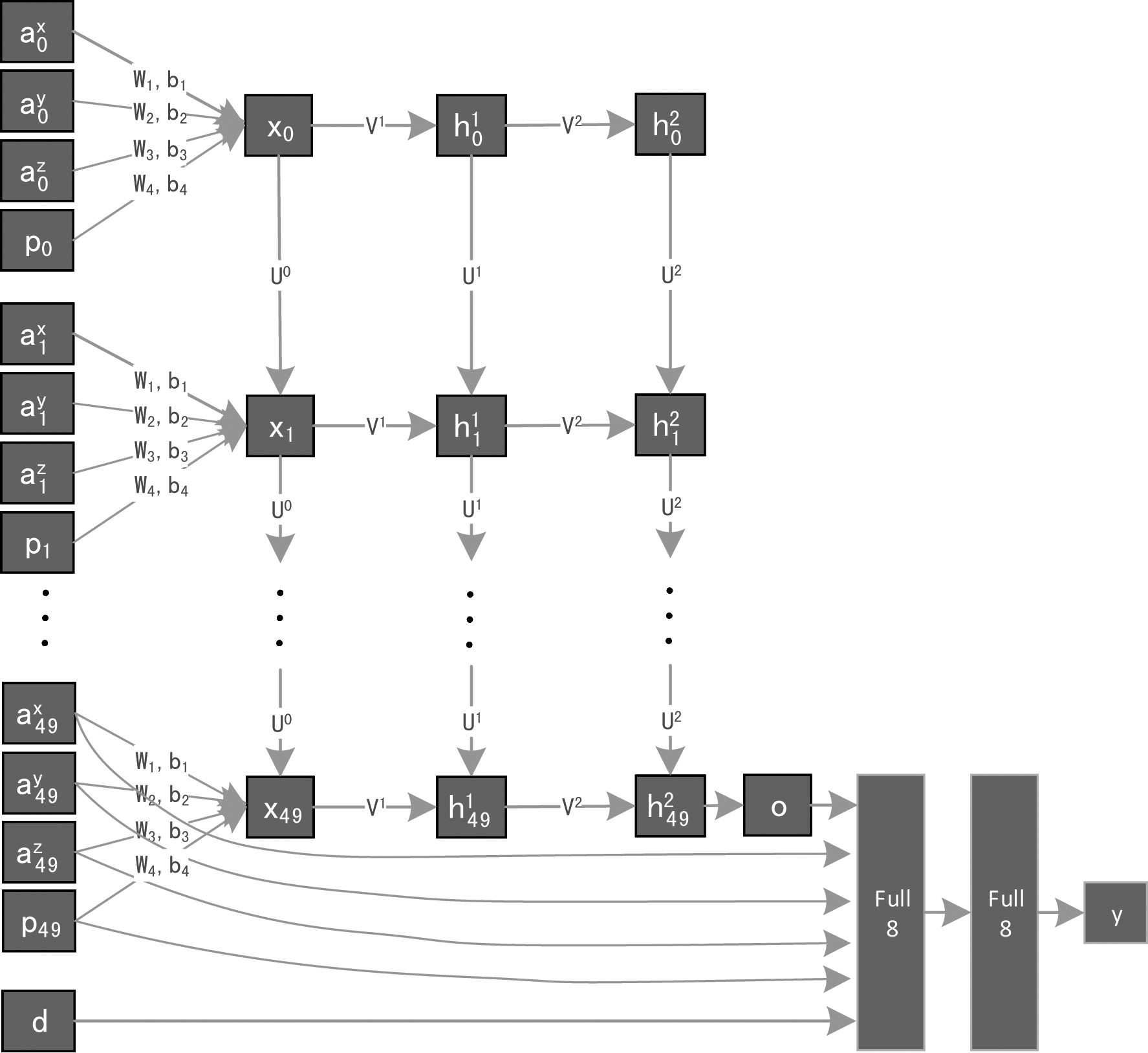
图2 发射延时预测网络
Fig.2 Transmitting delay prediction network
依据当前时刻发射成功率及延时时间的预测,承载的北斗短报文装备会周期性执行以下流程:
(1)基于发射成功率预测网络预测当前条件下的发射成功率;
(2)成功率超过阈值P,则发射;
(3)若成功率低于阈值P,预测延时时间T,T时间后重新预测成功率;
(4)为避免进入死循环,增加重试次数N限制。
海浪包括风浪、涌浪、近岸浪等,远海海浪主要是风浪,由风产生的波动,其周期为0.5~25 s,其中频率高于2 Hz的海浪其波长较小,逐渐由表面张力起主导作用,成为毛细波,对设备俯仰影响较小。因此,仅考虑频率小于等于2 Hz的海浪波。根据香农采样定理,将采样率设定为5 Hz。
估算海浪周期需要历史序列化数据。因此以0.2 s为周期,采集过去10 s内的设备加速度(ax/ay/az)以及俯仰角(p)数据。首先将每个时间点的数据![]() 通过一层全连接计算得到矢量波动幅度xi。
通过一层全连接计算得到矢量波动幅度xi。
(3)
从而得到一组序列化数据向量x:
x=[x0,x1,…,x49]
(4)
由于该层中所有时间点使用相同的拟合方法,该层共享神经元参数w1、b1、w2、b2、w3、b3、w4、b4。然后以向量x作为输入,使用循环神经网络(RNN)[12-13]提取序列化数据中的海浪谱周期。其RNN神经元输出计算方法为:
(5)
(6)
其中l为RNN层数,ReLU为激活函数,每层的U、V、B参数共享,经过RNN,得到唯一输出海浪谱o。最后将海浪谱、当前设备加速度、俯仰角及方向数据输入全连接网络,预测合适的发射延时y。其中y的取值范围为(0, 1),精度为0.1 s。使用二次代价函数计算网络的Loss值[13]。
(7)
根据装备佩戴情况,飞行员落水后,装备会随人员在海中沉浮。装备天线采用塔式结构的面天线,天线露出水面是发送成功的必要条件。正常安装条件下,天线高度、盒壁厚度及间隙、安装包吸水后厚度之和约为9 mm,在3级海况实际测试中,能够保证装备天线间歇露出水面。因安装包存在吸水和兜水情况,还需实时采集天线露出水面时的真实信号情况如下(截短数据)。
05:51.102: RD_BoShu:1220220000;05:51.103: Acceleration:X=-67
05:51.103: 8mg;Y=249mg;Z=908mg;
05:52.242: RD_BoShu:2300020300;05:52.332: Acceleration:X=-60
05:52.333: 5mg;Y=159mg;Z=705mg;
05:53.202: RD_BoShu:2410220310;05:53.262: Acceleration:X=-64
05:53.263: 3mg;Y=31mg;Z=963mg;05:53.286: 05:54.132: RD_BoShu:2432330210
参数RD_BoShu值代表了北斗1-10号波束格式化后的信号强度,其同行左边的数字为时间戳。
通过观察造浪池3级海况下的实测数据,发现在实测过程中,设备的功率信号按照一定规律进行变化,其变化规律与人员在水中沉浮的频率具有相关性。在此条件下,在一定时间内具备短报文发送条件,满足发送门限的时间窗口短且呈现出间歇状态。对数据进行平滑滤波处理后,其统计变化规律如下。
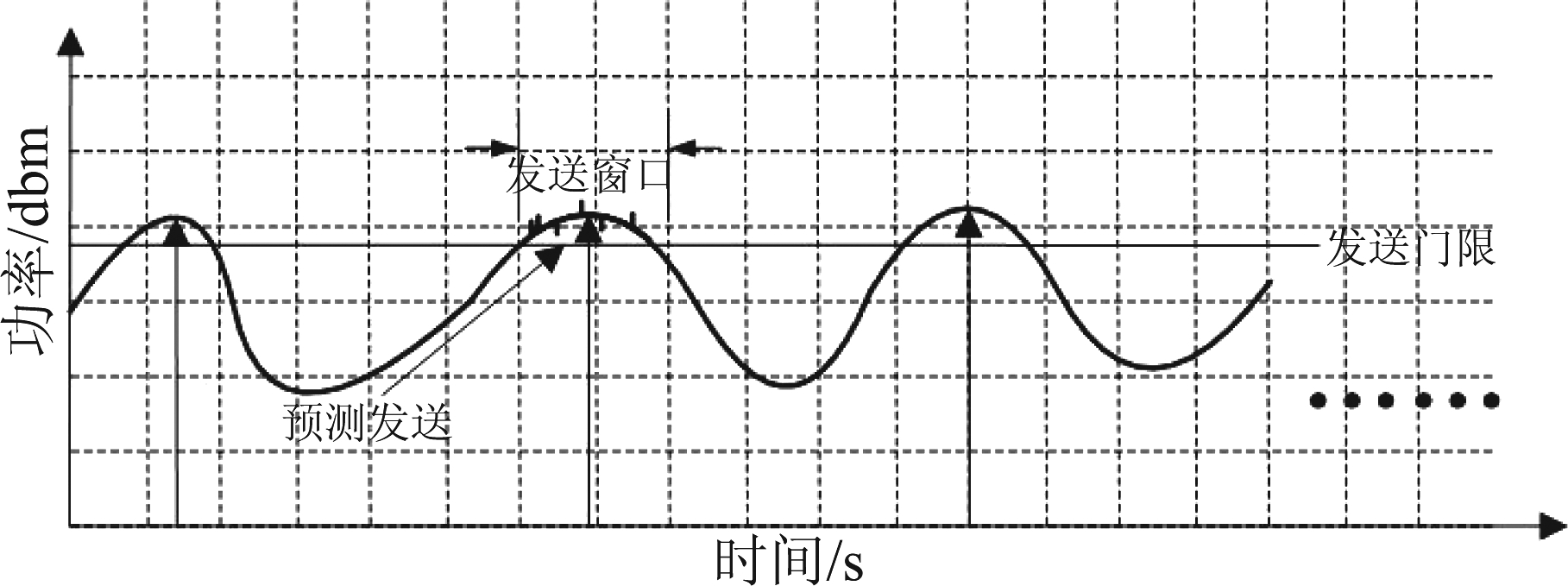
图3 发射功率与海况关联统计规律
Fig.3 Statistical law of correlation between transmitting power and sea conditions
为保证求救短报文发射成功率,理想状态下应在信号最强时产生发射操作,但实际环境情况复杂,信号受海浪以及人体姿态等因素的影响,受北斗卡频度以及自身电量的限制,按固定频率间隔发送短报文成功率很低,影响求救核心功能。通过上述观察及数据分析,发现在造浪池模拟3级海况场景下,发射功率信号具有一定规律性,因此设计找寻最优发射时机算法。在实际应用中应考虑发送门限窗口时间和功率变化趋势,以及变化中的毛刺现象。
试验数据主要来自于黄渤海海域数据积累,某试验场的试验数据。数据包含了位置信息、时间信息、部分气象信息、设备运动信息、星历信息等。数据集共包含10582条数据,其中正负样本数尽量接近(代表发射成功和失败,相差不超过2倍)。将这些数据随机分配到训练样本集和测试样本集,某试验场试验数据分配到测试样本集,其中10000条数据用于训练,582条数据用于测试评估效果,数据集中的部分结合其他情报数据经过手动标注以保证其准确性(表1)。
表1 样本分布
Tab.1 Sample distribution of data set

数据集正样本数负样本数样本总数训练集3820618010000测试集204378582合计4024655810582
共进行了不少于30万轮神经网络迭代训练,每5000轮进行一次评估。图4显示了训练及评估结果,Y轴平均准确率在本例中表示所有判断正确的样本占总样本数的比例,范围为[0, 1]。
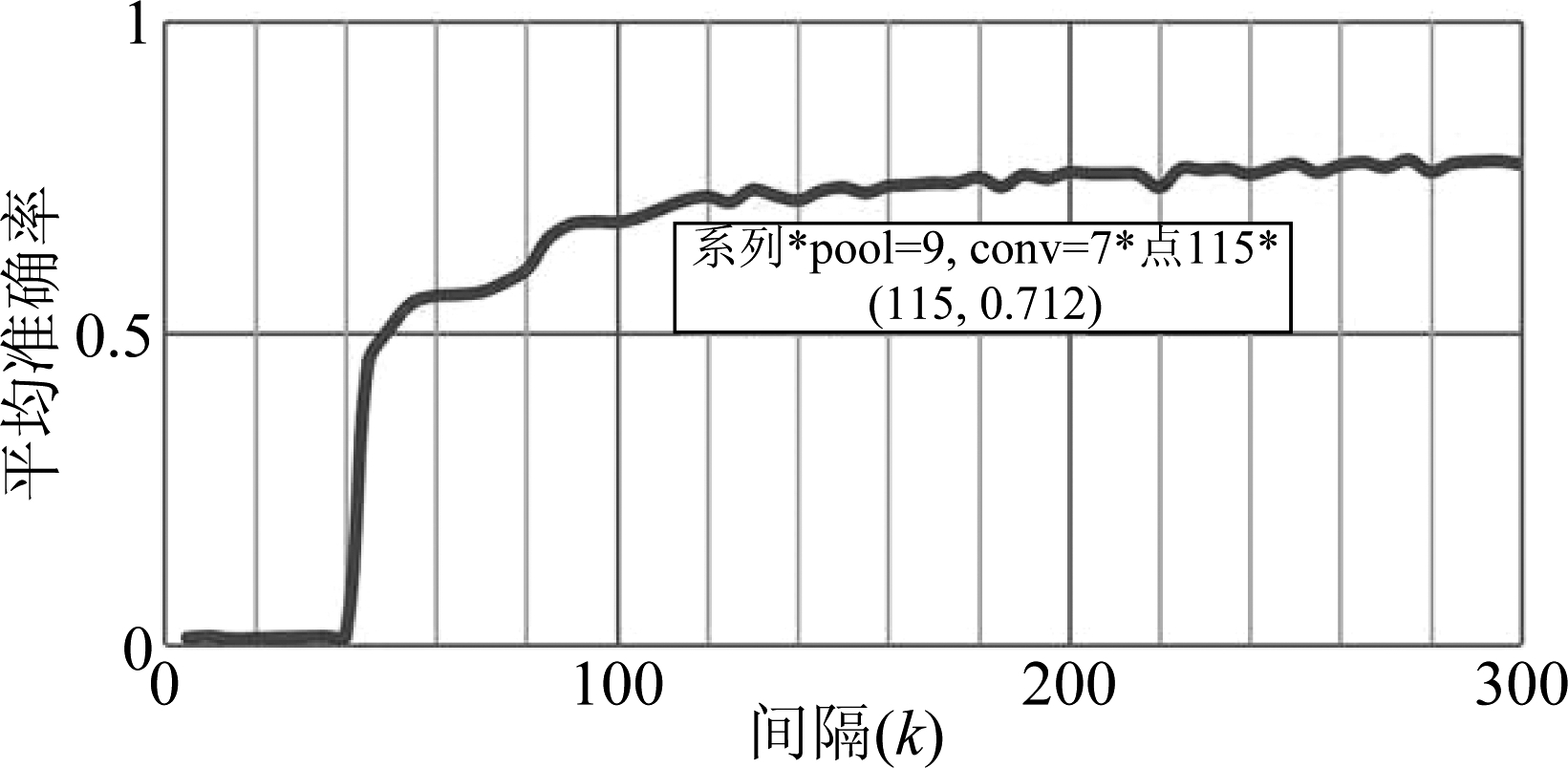
图4 训练评估结果
Fig.4 Results of training and evaluation
本文模型与固定周期发射模型比测条件和比测结果如表2所示。
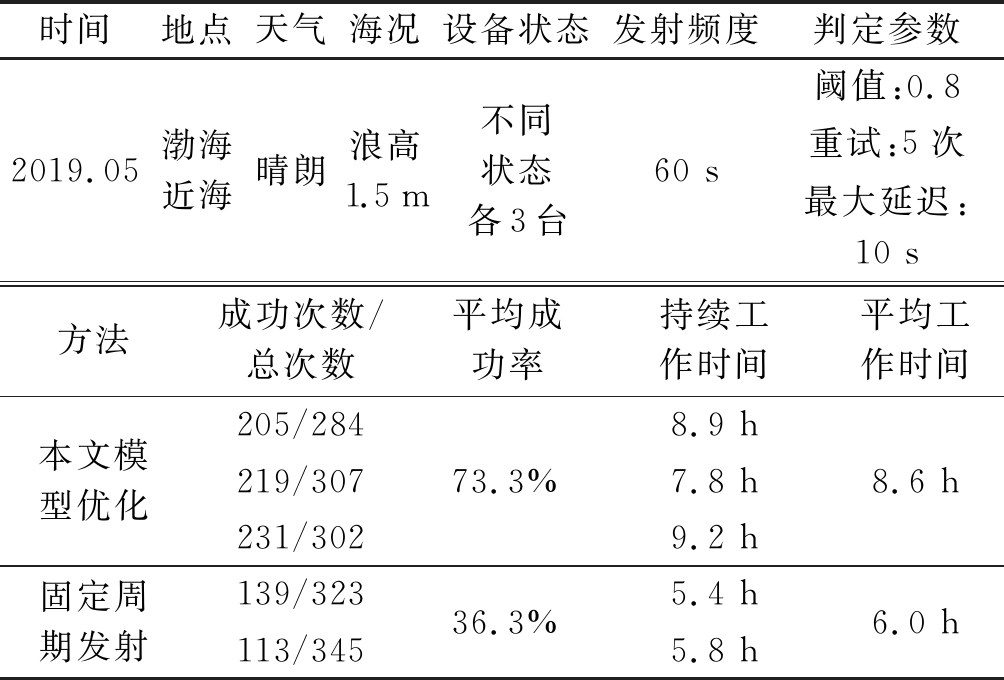
表2 比测条件和比测结果
Tab.2 Comparison test conditions and results
时间地点天气海况设备状态发射频度判定参数2019.05渤海近海晴朗浪高1.5 m不同状态各3台60 s阈值:0.8重试:5次最大延迟:10 s方法成功次数/总次数平均成功率持续工作时间平均工作时间本文模型优化205/284219/307231/30273.3%8.9 h7.8 h9.2 h8.6 h固定周期发射139/323113/34536.3%5.4 h5.8 h6.0 h
使用了本文报位策略后,RDSS发射成功率提高1倍以上,工作时长延长了2.6小时,提升了约43%。模型并没有增加发射总次数,反而使其略微减少。但同时有效发射次数(成功次数)相比固定周期大幅增加,从而使发射成功率得到大幅提升。由于发射总次数的减少节省了电池电量消耗,延长了设备工作时间。可见,模型在延长了设备工作时间的同时,增加了发射成功次数。

图5 一次发射散点图
Fig.5 Scatter plot of primary emission
图5是测试中一次发射数据散点图,这次测试在表2中标注出成功次数/总次数=205/284。图中横轴表示持续时间,30分钟为统计栅格,纵轴表示成功报位次数。从图中可以看到,前360分钟报位成功率呈现随机分布,大约第180分钟左右达到峰值,之后随着发射功率不足,报位成功率开始降低。
本文深入分析了影响海上RDSS发射成功率的多维度因素,利用深度学习技术实现了海上漂浮状态下的信号发射成功率及延时预测。受限于实验条件,测试仅基于北斗二号卫星的RDSS短报文通信设备进行。在该卫星系统的后续改进中,所需发射功率大幅降低,可在发射成功率预测网络的输出结果中设定多个发射功率等级,灵活调整发射功耗,进一步延长设备工作时间。
[1] Bruce R. Elbert. Introduction to Satellite Communication 3rd Edition[M]. London: Artech House Publishers, 2008.
[2] Madhavendra Richharia. Satellite Systems For Personal Applications-Concepts And Technology[M]. New Jersey: Wiley, 2010.
[3] LeCun Y, Bengio Y, Hinton G. Deep learning[J]. Nature, 2015, 521(7553): 436- 444.
[4] Huang Z, Xu J, Gong Z, et al. Source localization using deep neural networks in a shallow water environment[J]. J. Acoust. Soc. Am, 2018, 143(5): 2922-2932.
[5] 牛海强, 李整林, 王海斌, 等. 水声被动定位中的机器学习方法研究进展综述[J]. 信号处理, 2019, 35(9): 1450-1459.
Niu Haiqiang, Li Zhenglin, Wang Haibin, et al. Overview of machine learning methods in underwater source localization[J]. Journal of Signal Processing, 2019, 35(9): 1450-1459.(in Chinese)
[6] Hinton G E, Salakhutdinov R R. Reducing the dimensionality of data with neural networks[J]. Science, 2006, 313(5786): 504-507.
[7] 徐及, 黄兆琼, 李琛, 等. 深度学习在水下目标被动识别中的应用进展[J]. 信号处理, 2019, 35(9): 1460-1475.
Xu Ji, Huang Zhaoqiong, Li Chen, et al. Advances in Underwater Target Passive Recognition Using Deep Learning[J]. Journal of Signal Processing, 2019, 35(9): 1460-1475.(in Chinese)
[8] 刘世林. 船舶运动姿态短时高精度预测方法研究[D]. 哈尔滨: 哈尔滨工程大学, 2019.
Liu Shilin. A study of ship motion attitude short-time high-precision prediction method[D]. Harbin: Harbin University of Engineering, 2019.(in Chinese)
[9] Xu B, Wang N, Chen T, et al. Empirical evaluation of rectified activations in convolutional network. arXiv preprint arXiv: 2015: 1505.00853.
[10] Rubinstein R Y, Kroese D P. A Tutorial Introduction to the Cross-Entropy Method[M]. New York: Springer, 2004.
[11] Boer, Pieter Tjerk De, et al. A Tutorial on the Cross-Entropy Method[J]. Annals of Operations Research, 2005, 134.1: 19- 67.
[12] Zachary C. Liption, John Berkowitz, Charles Elkan. A Critical Review of Recurrent Neural Networks for Sequence Learning. arXiv preprint arXiv: 1506.00019, 2015.
[13] Alex Graves. Supervised Sequence Labelling with Recurrent Neural Networks[M]. Poland: Springer, 2008.
杨 航(通信作者) 男, 1978年生, 河南沁阳人。海军航空大学青岛校区讲师, 工学博士。主要研究方向为航空电子信息处理、航空应急救生通信。
E-mail: 390312268@qq.com
李洪烈 男, 1963年生, 山东滨州人。海军航空大学青岛校区教授, 主要研究方向为航空通信、航空搜救。
E-mail: lhlqd001@163.com
方 芳 女, 1984年生, 安徽贵池人。海军青岛特勤疗养中心工程师。主要研究方向为抗荷训练技术、计算机信息处理技术。
E-mail: bing_bang_yh@qq.com
程春华 男, 1986年生, 江西鹰潭人。海军航空大学青岛校区讲师, 工学博士。主要研究方向为航空仪表与控制。
E-mail: chch715@126.com