图1 纯方位交会定位示意图
Fig.1 Illustration for bearings-only localization
Reference format: Zhang Xu, Li Zhisheng. Distributed Accuracy Estimation for Bearings-Only Localization Based on Multi-Stations in the Large-Scale Sea Area[J]. Journal of Signal Processing, 2020, 36(12): 2052-2060. DOI: 10.16798/j.issn.1003- 0530.2020.12.011.
对于在空间尺度为数十千米的大范围深水域对海上无源目标进行水声定位测量的情况,测量系统设计时需要对基站数量、单站测量能力、布站几何等因素进行统筹考虑,整个测量海区精度性能及分布规律的估计和预测将作为重要的设计依据[1]。此类测量通常有两类体制[2]:一类是以到达方位角为测量要素的纯方位交会体制,另一类是以到达时延差为测量要素的时差交会体制。尽管在大范围测量条件下后者相对前者有一定的精度优势,但时差交会受到各基站时间同步、信号相关性、声速环境等诸多因素限制,特别是在深海垂向声速梯度显著的环境下,声信号沿多途路径以非均匀等效声速到达[3],时差等值线以非规则双曲线形式交会,造成了求解的复杂性和不确定性[4]。而纯方位交会虽有交会点不确定度随距离增加而增大的限制,但因受复杂水声信道约束小,仅通过基站位置和方位信息就可以直接定位,适用于实时性要求较高的目标快速定位问题[5]。
在工程应用中,测量系统通常采用多基站冗余设计[5- 6]。对于不考虑目标深度的二维水平定位问题,有2个可相交的方位测量信息即可解析唯一的定位结果,若有多个方位测量信息则可通过最优化方法进行估计。关于此类方法较常用的有重心法[7]、迭代法[8]以及最小二乘估计法[9-10],还有学者提出基于元启发算法的定位方法[11]。然而,求解方法不是论证设计中唯一要考虑的因素,还要求对测量海区的覆盖特性和精度水平进行有效估计[12-13],以支撑不同布站几何条件下的测量性能分析与比对,进而提出布站优化方案和量化指标。目前关于大范围海域精度分布特性的认识较为欠缺,在实际工程条件下通常只在单点做小样本验证实验,而大样本、全区域的估计则需要采用合理的数值方法加以实现。
本文针对大范围海域的多站纯方位定位测量设计问题,提出一种适用于全区域精度评估的数值分析方法,采用非线性最小二乘法实现定位求解,应用Monte-Carlo方法在每次测量模拟中迭加误差,通过大样本仿真计算实现误差稳定传递并建立全区域精度分布;在此基础上,通过一类典型场景验证该方法在布站几何优化中的有效性。
1)测量系统要求覆盖30 km×20 km的深海区域,针对在水面随机出现的声学目标进行无源定位测量,利用获取的方位信息确定其水平位置坐标的估计值;
2)测量基站以水面船为载体,搭载拖曳式声学系统,每个测量基站即为测量阵中的1个阵元,测量阵最多不超过5个阵元,以一定的几何分布构成;
3)每个阵元能够以充分的信噪比和有效的观测阵位检测到阵内出现的声学目标辐射信号,可获取的测向精度为2°～5°(主要包含方位估计误差和基站航向误差,其中方位估计误差与信噪比、收发条件等因素相关);
4)作为测量载体的水面船可利用卫星导航定位设备进行自定位,同时可利用航姿传感器和深度传感器对拖曳的声学系统进行实时标定,将等效水下接收深度设为150 m,典型水平方向的站址误差设为10 m,深度方向的站址误差设为1 m。
以测量海区在海面的几何中心为原点O建立测量直角坐标系,OX轴指向正东方向,OY轴垂直海面铅直向下,OZ轴指向正北方向,三轴构成右手坐标系。由于测量量为目标的二维位置坐标,可将目标、基站的位置投影至XOZ平面上进行平面交会求解(见图1)。理论上有2条不相交的方位线就可以直接解析计算目标位置;而在多站条件下,则可利用多条方位线的冗余信息进行最优化估计。
图1 纯方位交会定位示意图
Fig.1 Illustration for bearings-only localization
假设待测目标在XOZ平面的位置坐标为X=[x,z],根据目标到达声信号得出的方位角估计值为ψj(ψj∈(-π,π],沿X轴正向方向为0),各阵元位置坐标
(j=1,2,…,N,N为阵元数量)。根据目标与阵元的几何关系,目标参数与测量量之间满足以下关系:
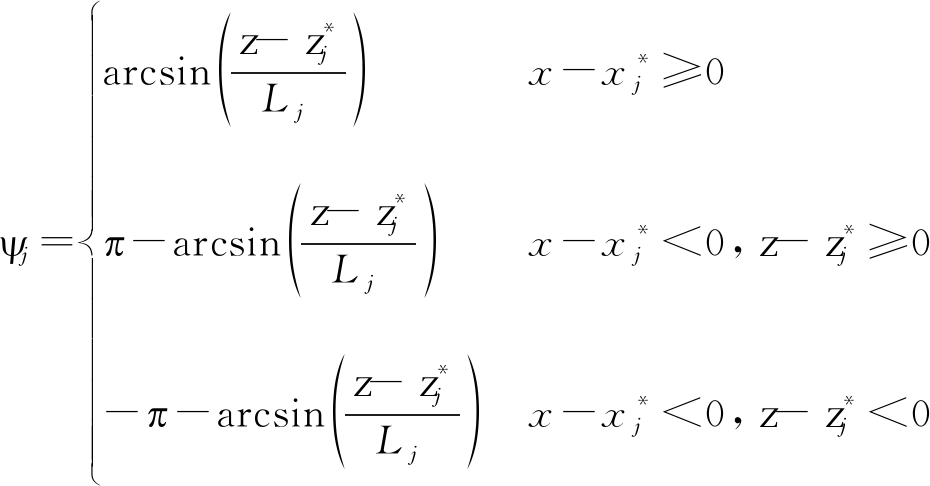
(1)
式中,
由于上式为非线性方程,直接求解较为困难,将其在初始位置X0=[x0,z0]处进行泰勒展开,并做一阶近似处理:
(2)
根据上式,可建立目标位置与初始位置的偏差量与两者相对于各基站的方位角变化量之间的函数关系,其矩阵形式表达式为:
ΔΨ=AΔX+ε
(3)
式中,ε为误差向量,其他项分别为:
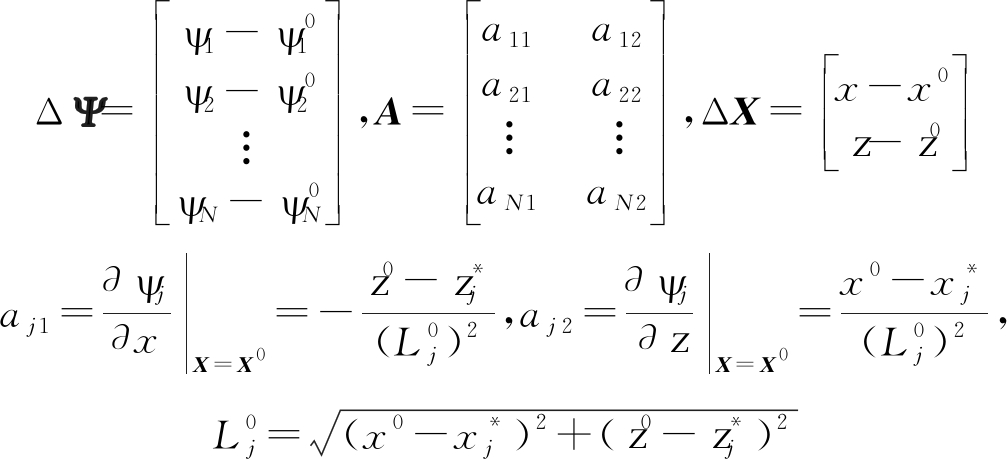
根据最小二乘原理,可利用方位角变化量对位置偏差量进行迭代修正,获取目标位置的最优估计值[8]:
(4)
在迭代求解过程中,可在各阵元测量方位线形成的包络区域内选取一个预估值,作为最初的初始位置X0,再由基于测量的方位角与基于初始位置的方位角做差得到ΔΨ,代入式(4)得到对初始位置X0的修正量
进而得到本次迭代的估计值
此后,将此估计值
更新为下次迭代的初始值X0,重新计算ΔΨ进而更新求解
和这样,通过多次迭代计算直到
收敛到预设精度(本文设为10-1m,‖·‖2表示向量的l2范数),此时的即为最终给出的目标位置估计参数。
上述解算基于XOZ平面上的水平方位角,但在实际情况下,信号到达声学接收器的位置在水下,因此根据到达目标声信号估计得到的实际是空间方位角,需将其转换为水平方位角再进行求解。假设待测水面目标到达声学基阵的等效位置为
该位置在水面的投影即为阵元位置
深度为Hj,到达斜距为
如图2(a)所示,则空间方位角
与水平方位角ψj的关系满足:
(5)
其中,
由于
均为可测量的量,可由上式将空间方位角修正到水平方位角:
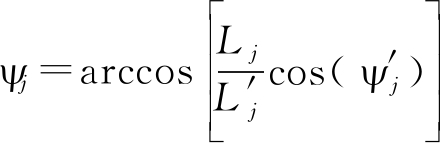
(6)
图2(b)显示了空间方位角分别15°、30°、45°、60°、75°时,由空间方位角修正的水平方位角随水平距离变化曲线,可以看出,两者在远场一致性较好,主要偏差出现在近场,特别是在距离基阵1 km以内的范围偏差显著,且空间方位角越小,偏差越明显。因此,在有近场阵元参与解算时,不能将空间方位角作为水平方位角代入求解,必须进行修正。
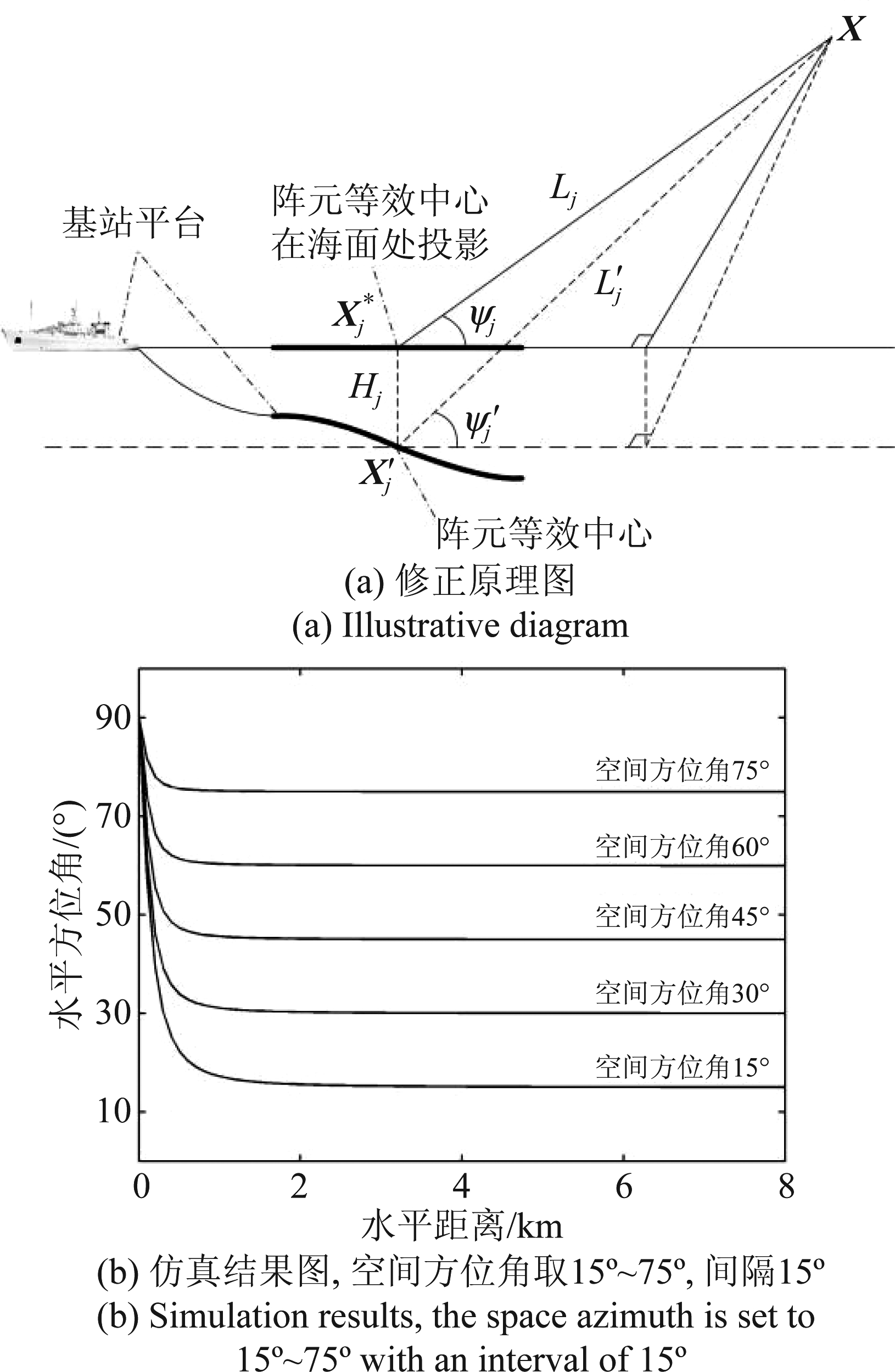
图2 水平方位角修正示意图
Fig.2 Illustration for horizontal azimuth revision
为对上述模型进行验证,并拓展为可用于评估全区域精度特性的仿真分析方法,参照文献[1]建立基于Monte-Carlo方法的仿真算法,将测量区域在XOZ平面划分为一定密度的网格,每一格点按以下步骤进行仿真计算:
a)建立目标与阵元的几何关系。设目标声源位置坐标真值为Xt=[xt,zt]T,第j个阵元位置坐标的真值为
分别按
生成该阵元位置坐标测量值,即
其中σx、σz分别为X、Z方向的站址误差标准差,根据前文假设取10 m;同时,按
生成阵元等效接收深度测量值Hmj,其中Htj为等效接收深度真值,σy为Y方向的站址误差标准差,根据前文假设取1 m。
b)迭加到达方位角估计误差。根据目标与基站的几何关系,由式(1)直接计算各阵元观测目标水平方位角的真值Ψt=[ψt1,ψt2,…,ψtN]T,并由式(5)计算其空间方位角的真值
按照
生成迭加方位角估计误差后的空间方位角测量值向量
其中σψ j为测向误差标准差;再根据式(6)将空间方位角测量值向量修正为水平方位角测量值向量Ψm,Ψm=[ψm1,ψm2,…,ψmN]T。上述过程中,测向误差标准差σψ j的确定方法为:假设在声源位于海面、等效接收器深度位于水下150 m的收-发条件下,传播损失随距离的变化曲线满足图3(a)的变化关系,根据声呐方程,SNR=SL-TL-NL,得到的接收信噪比曲线如图3(b)所示(经32点平滑),其中声源级SL取200 dB,背景噪声级NL取70 dB,TL为传播损失,上述各项均为谱级(@1 kHz);假设测向误差标准差随接收信噪比呈线性变化,根据前文假设,声学系统在全区域可获得2°～5°的测向精度,由此建立测向误差标准差随距离变化关系(图3(c)),σψ j可依据目标与阵元j的相对距离插值得到。
c)建立初始位置与阵元的几何关系。按
生成初始位置X0=[x0,z0]T,其中σx0、σz0分别为X、Z方向初值位置标准差,根据本文假设的工况条件,目标与最近的阵元斜距小于18.0 km,对应3°开角对应弧长为942.5 m,以此为参照将σx0和σz0设为1000 m;根据阵元位置与初始位置的几何关系计算到达方位角初始值
d)目标位置参数迭代求解。根据到达方位角的测量值和初始值建立方位差向量ΔΨm,ΔΨm=[Δψm1,Δψm2,…,ΔψmN]T,其中
根据式(3)、(4)求解位置修正量ΔX进而得到目标位置估计量
并在下一次迭代中代替X0作为初值,按上述步骤重复计算,直至
停止迭代,此时的即为该次抽样中的目标位置测量值Xm=[xm,zm]T。
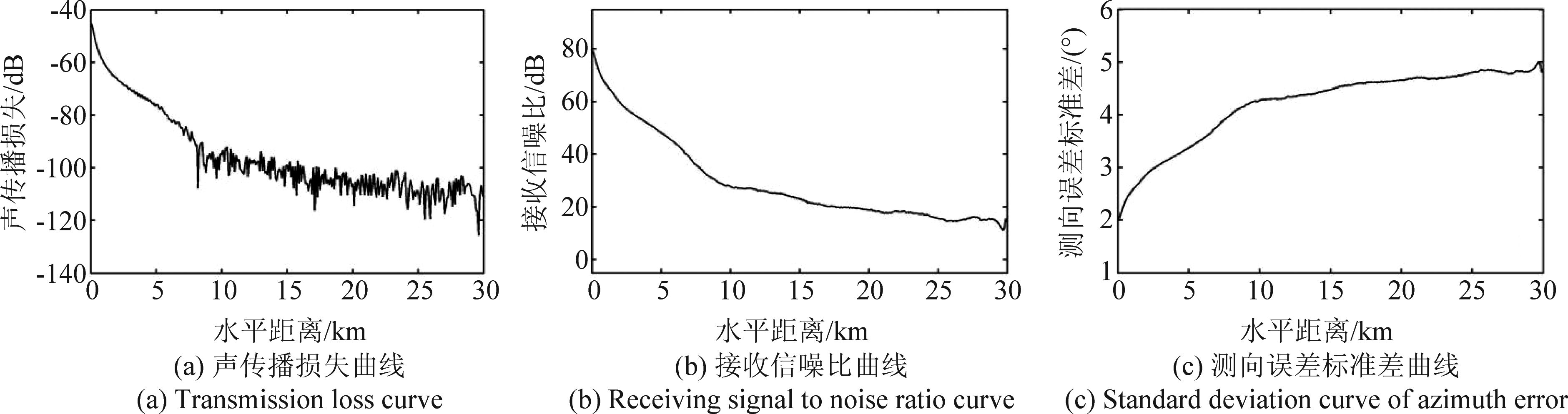
图3 测向误差设置示意图
Fig.3 Illustration for azimuth error setting
e)重复抽样与统计量计算。对于同一网格点,经过500次抽样后,形成目标位置测量值序列
(M为有效抽样数,若此次抽样中任意1个随机生成的阵元位置测量值与目标真值或测量值重合,则定义为此次抽样无效,有效抽样数为总抽样数减去无效抽样数),再计算该网格点测量序列的均方根误差
其中
为第i次抽样的目标测量值。
按照上述步骤历遍所有网格点后,就建立了关于精度区域分布的二维矩阵。
关于以方位估计量作为测量元素并应用最小二乘法进行最优化估计的收敛性问题,文献[9]中已有相关讨论。图4通过一个典型场景说明单次采样迭代求解过程中的收敛过程,图中5个基站以星形布站方式覆盖30 km×20 km的测量区域,目标真值位于(3, 1)处(单位为 km,下同),图中虚线表示基于真值的方位线,实线表示迭加测向误差和站址误差后的模拟测量结果,可见测量方位线相对于真方位线的偏差造成了多个交会点共存,并形成一定范围的包络区域,而由最小二乘法确定的某一最优估计位置即为各测量方位线相互“折中”的结果。
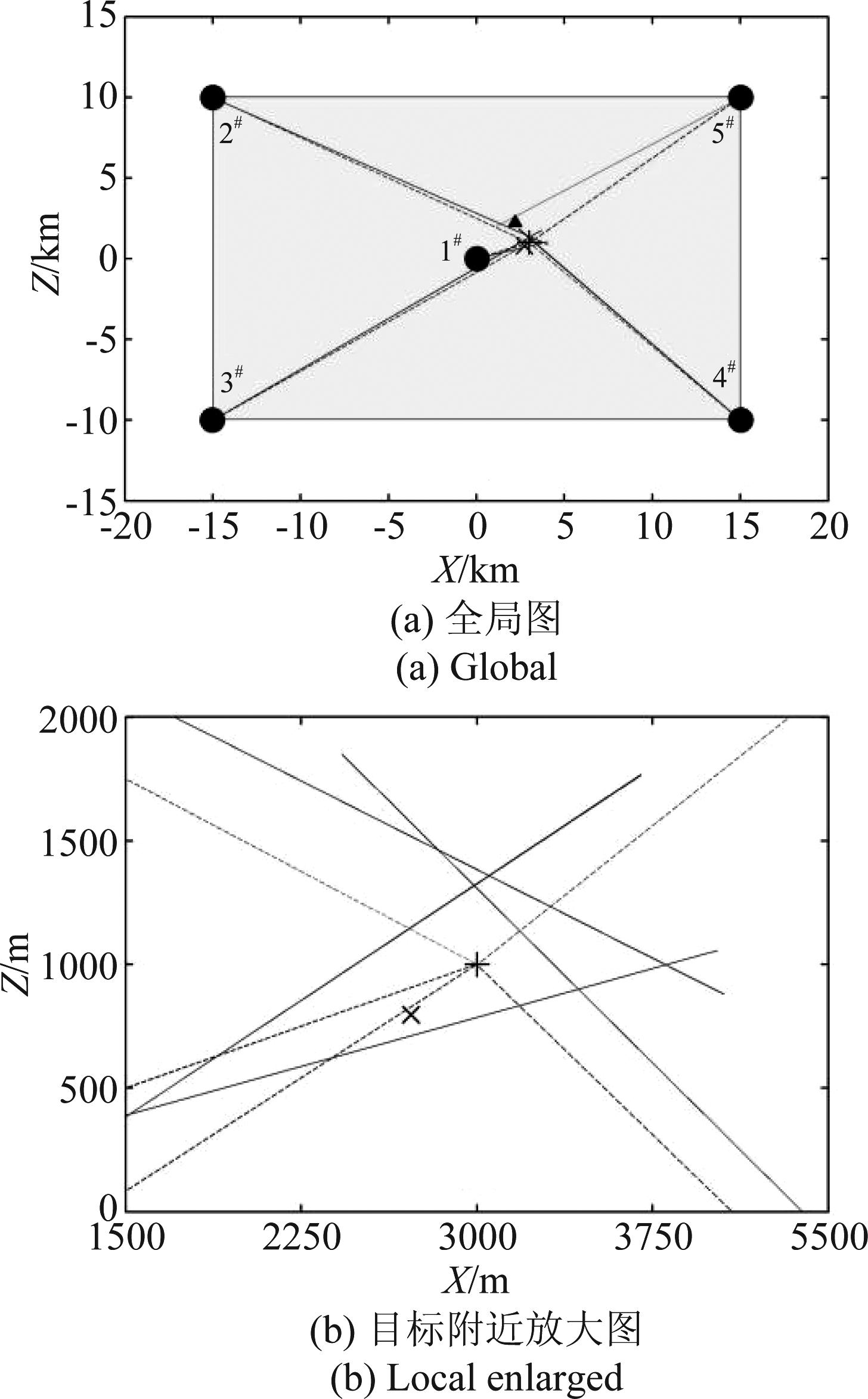
图4 方位线交会定位示意图
x=3 km, z=1 km; ×表示目标位置测量值,+表示目标位置真值,▲表示初始位置,●表示基阵阵元位置; 实线表示方位线测量值; 虚线表示方位线真值
Fig.4 Illustration for direction lines crossing
x=3 km, z=1 km; × denotes the measured target position, + the truth target position, ▲ the initial position, ● the array position; the full lines denote measured direction line, the dashed lines denote truth direction line
图5给出了根据上述仿真算法做500次抽样计算得到的定位偏差迭代箱型图(计算场景同图4),图中箱型中间线表示中值,箱型上沿为0.25分位数,下沿为0.75分位数。图5(a)为迭加测向误差和站址误差的结果,经过3次迭代后,定位偏差趋近于一个稳定值,反映了这两类误差源传播到定位结果的综合精度水平;图5(b)为未迭加任何误差的结果,方位角和阵元位置均代入真值,仅保留了初始位置的随机偏差,经过4次迭代后,定位偏差趋于零,说明即使初始位置有偏差,迭代后的目标位置估计值也会收敛于真值。
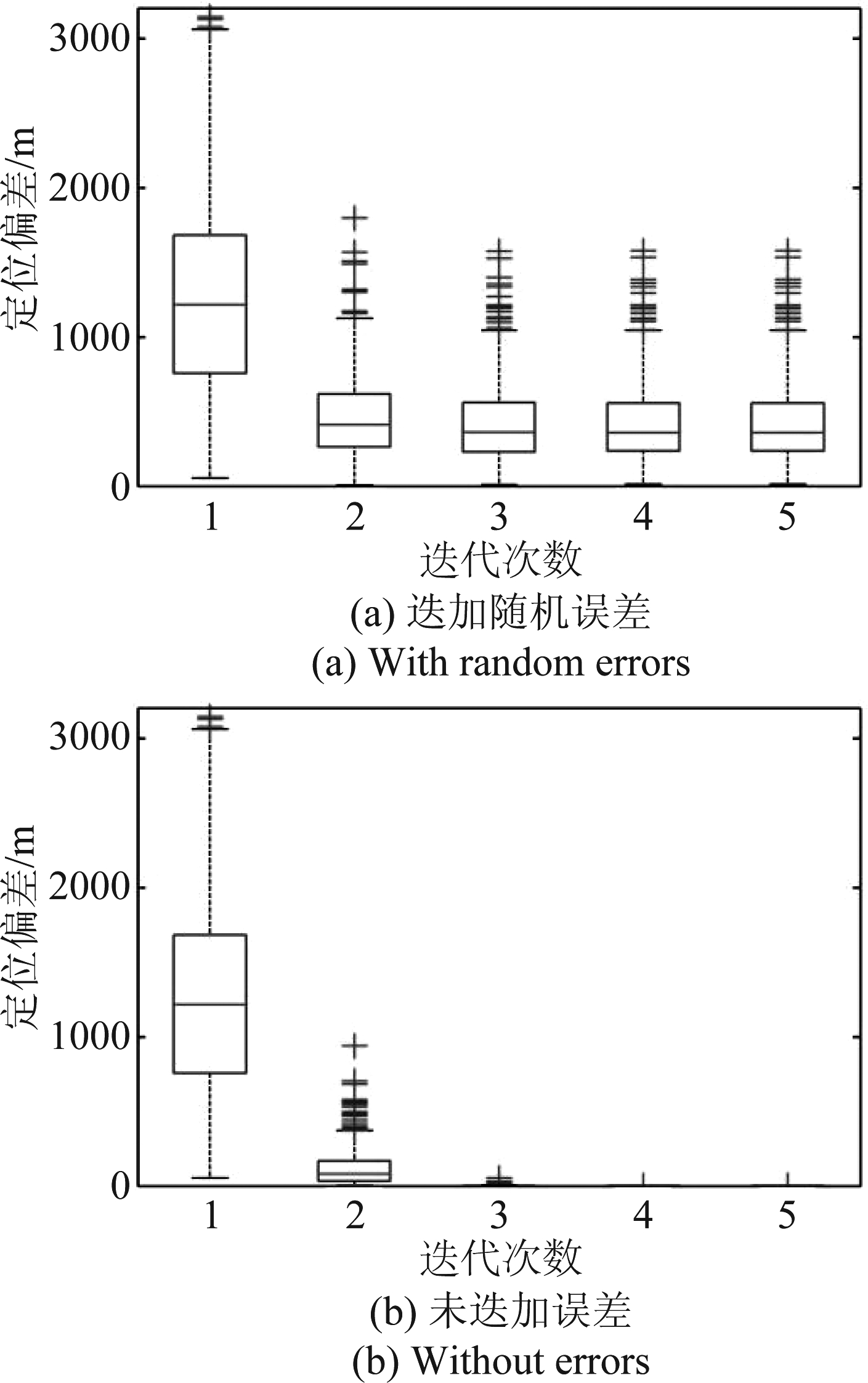
图5 定位偏差箱型图随迭代次数的变化
Fig.5 Box-plots of location bias in iteration
对于上述仿真算法,测向误差和站址误差是2类主要的误差源。但这2类误差源作为输入条件向定位结果进行传播的过程并不是简单迭加,而是与目标和阵元的相对位置有关,因此需要关注目标在测量海区不同位置时的精度分布特性。
将计算区域设为40 km×30 km(中心区域为要求覆盖的30 km×20 km测量海区),划分为201×151个格点,按照上述仿真算法进行逐一格点计算(每个格点抽样500次),得到海区二维平面的精度分布矩阵。图6显示了从2阵元到和5阵元典型拓扑设计条件下的RMSE水平分布,图中通过灰阶反映RMSE的量值差异, 虚线方框表示要求覆盖的测量区域。表1给出了对应的RMSE统计特性比较。
根据图6和表1,4种不同拓扑条件下精度分布的图样有明显差异。从2阵元到5阵元,随着阵元冗余度的增加,整体精度水平逐步提高,全区域RMSE中值从1.33 km降低到0.90 km;同时,相对高精度测量区的覆盖范围也越来越大,精度优于2 km的区域比例由76.8%提升到97.8%,5阵元测量优于1 km的区域比例达到45.4%。高精度测量区主要分布在阵元基线的两侧区域。比较这4类拓扑条件可以看出,仅有2阵元时覆盖能力极其有限;3阵元在区域相对收缩的条件下可达到与4阵元整体相近的精度水平,但中心附近高精度测量区重叠度更高,精度优于1 km所占比例比4阵元的情况高出11.8%;5阵元时基线缩短且精度测量区大面积重叠,大大提升了测量的冗余度,仅在对角线附近精度相对较低。
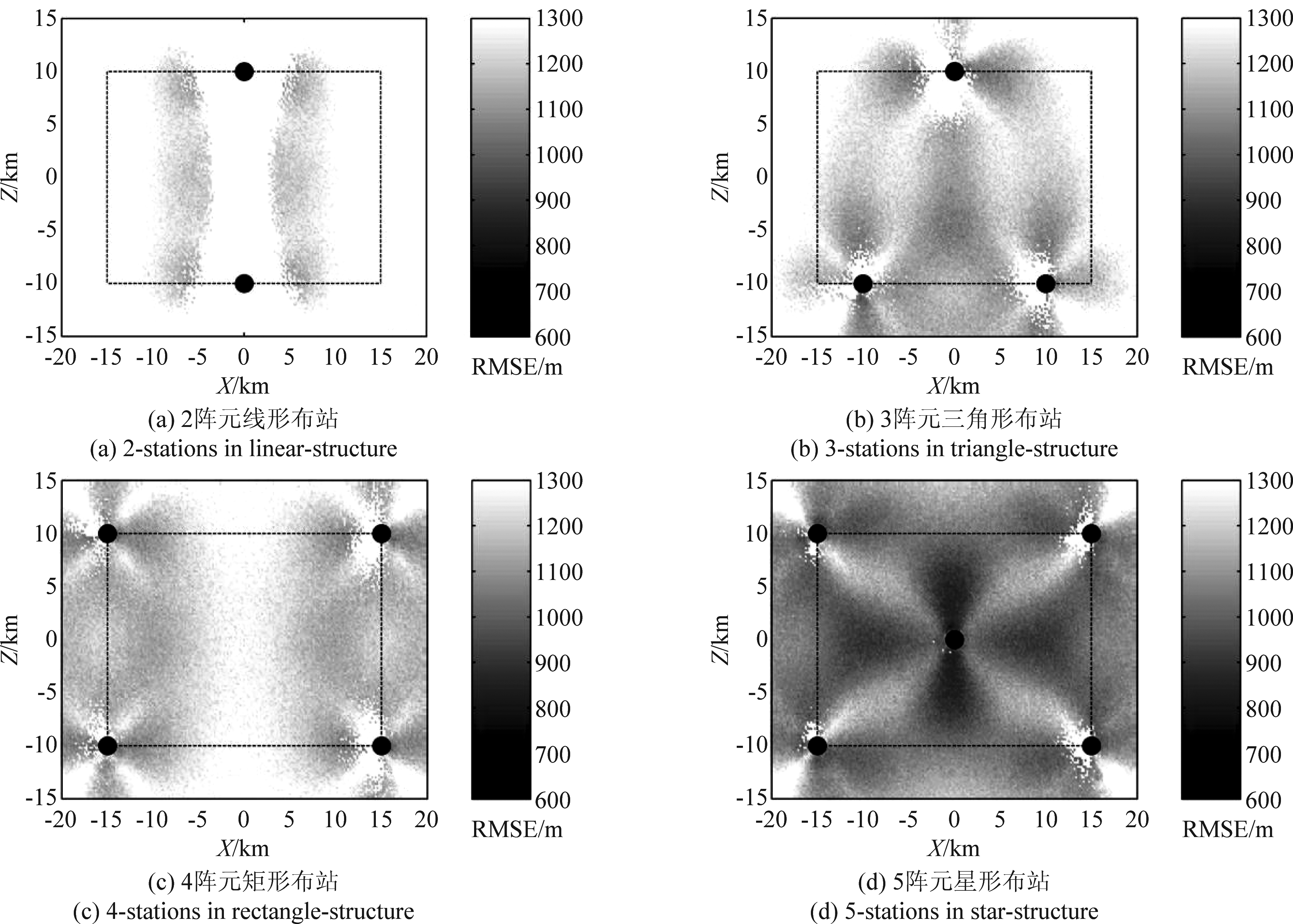
图6 不同拓扑条件下的RMSE水平分布图
●表示阵元位置, 虚线表示测量区域
Fig.6 RMSE distribution under different topology conditions
● denotes the array position, dashed line the surveying area
表1 不同拓扑设计条件下的RMSE统计特性比较
Tab.1 Comparison of RMSE statistics under different topology conditions
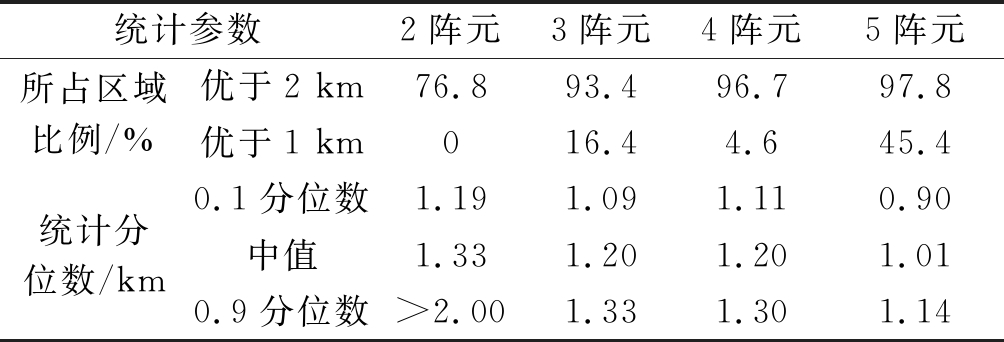
统计参数2阵元3阵元4阵元5阵元所占区域比例/%优于2 km76.893.496.797.8优于1 km016.44.645.4统计分位数/km0.1分位数1.191.091.110.90中值1.331.201.201.010.9分位数>2.001.331.301.14
为考察定位性能的边界性能,表2给出了4个有代表性的点位的RMSE中值比较。根据表2,2阵元条件下中心附近和边界附近的定位性能都差,特别是中心附近;3阵元条件下中心附近的定位特性相对较好,而边界附近的定位特性较差,两者RMSE中值相差0.32 km;4阵元条件下中心附近的定位特性不及边界附近,情况与3阵元相反,两者RMSE中值相差0.16 km;5阵元条件下中心附近和边界附近的定位性能都达到优于1 km的水平,只是对角线附近精度相对较差,与高精度测量区相约0.2 km。这些特性与图6中呈现的RMSE分布特性相一致。
表2 不同拓扑设计条件下典型位置的RMSE中值比较(km)
Tab.2 Comparison of RMSE median in the typical position under different topology conditions (Unit: km)
目标位置选取2阵元3阵元4阵元5阵元测量区中心附近(x=1, z=0)>2.001.111.290.98测量区内沿轴线(x=6, z=0)1.171.341.170.93测量区内沿对角线(x=6, z=6)1.251.271.201.17测量区边界附近(x=12, z=0)1.391.431.130.94
区域精度分布估计不仅提供了对海区定位性能的总体性认识,而且还预测了特定布站几何条件下的不同目标位置可能出现的精度结果,可支持测量系统论证阶段的布站优化设计。以下通过具体算例来考察在仅有5个阵元的限定下(对应前文假设),是否能够通过布站几何的变换提升整个测量区域的定位性能并最大限度地减小误差较大的覆盖区域。
图7给出了3类5阵元几何构型的RMSE水平分布图比较,即矩形布站、梯形布站和五边形布站,与前文中的星形布站进行比对,计算条件与图6中的设置相一致。表3中给出了对应的RMSE统计分位数比较。根据图7和表3,不同几何布站条件下的RMSE水平分布呈现出不同图样,高精度测量的覆盖区各不相同。矩形布站条件下,高精度区偏向于阵元密度大的一侧,区域内RMSE中值比星形布站(图6(d))增大了0.05 km,布站几何测量性能不及星形布站;梯形布站条件下,由于Z轴正向的两个阵元间基线长度缩短,在其附近也形成了一个相对高精度区,使得区域内RMSE中值比星形布站减小了0.05 km,体现出一定程度的优化;五边形布站条件下,阵元间的基线长度趋于均衡,高精度区向测量海区中心聚集,区域内RMSE中值比星形布站减小了0.09 km,体现出更加明显的优化效果。综上,从矩形布站、星形布站到梯形布站、五边形布站,变换阵型后呈现出不同程度的优化特征,表现为高精度区覆盖度的增加和总体精度水平的提升,而区域精度分布估计则是布站几何优化的重要依据。
图7 不同5阵元布站条件下的RMSE水平分布图
●表示阵元位置, 虚线表示测量区域
Fig.7 RMSE distribution under different 5-stations observation geometry conditions
● denotes the array position, dashed line the surveying area
表3 不同5阵元布站条件下的RMSE统计分位数比较(km)
Tab.3 Comparison of RMSE quantile statistics under different 5-stations observation geometry conditions (Unit: km)
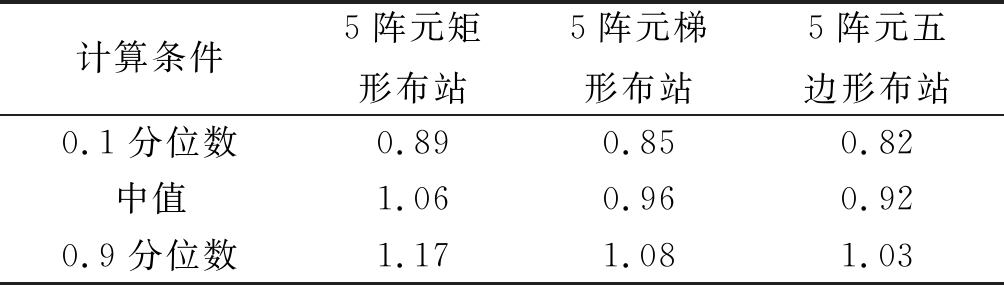
计算条件5阵元矩形布站5阵元梯形布站5阵元五边形布站0.1分位数0.890.850.82中值1.060.960.920.9分位数1.171.081.03
面向大范围海域的多站定位测量系统论证设计问题不仅涉及目标位置的求解或估计,而且还包括全区域的覆盖特性和精度分布特性的预测与估计,进而作为系统性能和布站使用设计的依据。解决此类问题需要将定位求解、精度分析与布站优化集成考虑,形成联合建模与仿真分析方法,从整体上、全局上认识定位性能与优化设计的关系。针对此问题,本文提出一种适用于全区域精度估计的多站方位交会定位仿真分析方法,并通过设置典型场景进行测试和验证。主要结论如下:
1)模型采用非线性最小二乘法对目标位置进行估计,应用Monte-Carlo方法在模拟测量过程中迭加误差,通过大样本抽样仿真给出误差传递的统计结果,并在全区域建立目标相对于不同阵元位置的精度分布图样。模型具有快速收敛特性,并且能够对测向误差、站址误差等主要误差源产生合理响应。
2)在大范围海区测量条件下,方位交会精度对于阵元的拓扑结构是敏感的,对于2°～5°的单站测向误差,在30 km×20 km测量区域内采用5阵元星形布站RMSE中值达到1 km的精度水平。
3)提出方法适用于布站优化设计,仿真算例表明,全区域精度分布图样随基站几何构型而变化。在5阵元条件下,采用五边形环形布站能够获取比星形布站、矩形布站和梯形布站更优的精度分布,区域内RMSE中值相对于星形布站降低0.1 km,同时高精度覆盖区明显增大。
在离岸支持的大范围海区对海上随机目标进行多站纯方位定位,需从系统性能和工程能力两个层面考虑符合实际应用的方法、技术,面临很多挑战。本文虽有针对性地提出了一种区域性定位性能分析方法,并结合算例进行了精度分析,但对于声系统的技术细节、环境影响的不确定性、不同空间位置的信噪比以及信号处理方法对测量元素的影响等方面未深入讨论,相关问题有待进一步开展研究。
[1] 张旭, 李智生, 邱仁贵, 等. 布站几何对深海时差定位精度分布特性的影响[J]. 水下无人系统学报, 2020, 28(2): 139-148.
Zhang Xu, Li Zhisheng, Qiu Rengui, et al. Effects of observation geometry on accuracy distributional characteristics using TDOA positioning system in deep sea[J]. Journal of Unmanned Undersea Systems, 2020, 28(2): 139-148.(in Chinese)
[2] 田中成, 刘聪锋. 无源定位技术[M]. 北京: 国防工业出版社, 2015.
Tian Zhongcheng, Liu Congfeng. Passive locating technology[M]. Beijing: National Defense Industry Press, 2015.(in Chinese)
[3] 王梦圆, 李整林, 秦继兴, 等. 深海直达声区水下声源距离深度联合估计[J]. 信号处理, 2019, 35(9): 1535-1543.
Wang Mengyuan, Li Zhenglin, Qin Jixing, et al. Combined estimation of range and depth for underwater source in the direct zone in deep water[J]. Journal of Signal Processing, 2019, 35(9): 1535-1543.(in Chinese)
[4] 张旭. 深海分层介质中的无源声定位时差交会特性[J]. 科学通报, 2019, 64(24): 2523-2536.
Zhang Xu. Time Difference Intersection Characteristics of Passive Underwater Acoustic Localization in the Stratified Deep Sea[J]. Chinese Science Bulletin, 2019, 64(24): 2523-2536.(in Chinese)
[5] 孙向前. 多冗余被动定位系统精度分析[J]. 声学技术, 2013, 32(3): 248-252.
Sun Xiangqian. Accuracy of Multi-Redundancy Passive Localization System[J]. Technical Acoustics, 2013, 32(3): 248-252.(in Chinese)
[6] Coraluppi S. Multistatic Sonar Localization[J]. IEEE Journal of Oceanic Engineering, 2006, 31(4): 964-974.
[7] 王志刚, 陈韶华, 王维. 分布式基阵联合定位算法仿真分析[J]. 水下无人系统学报, 2018, 26(5): 433- 438.
Wang Zhigang, Chen Shaohua, Wang Wei. Simulation Analysis of Joint Localization Algorithm Based on Distributed Arrays[J]. Journal of Unmanned Undersea Systems, 2018, 26(5): 433- 438.(in Chinese)
[8] Landau B V, West W. Estimation of the Source Location and the Determination of the 50% Probability Zone for an Acoustic Source Locating System(SLS) Using Multiple Systems of 3 Sensors[J]. Applied Acoustics, 1997, 52(1): 85-100.
[9] 刘利生, 吴斌, 吴正容, 等. 外弹道测量精度分析与评定[M]. 北京: 国防工业出版社, 2010: 123-188.
Liu Lisheng, Wu Bin, Wu Zhengrong, et al. Accuracy Analysis and Evaluation for Exterior Ballistic Measurement[M]. Beijing: National Defense Industry Press, 2010: 123-188.(in Chinese)
[10] 富森, 孔祥维, 李哲, 等. 多基纯方位目标交叉定位中的非线性最小二乘方法[J]. 火力与指挥控制, 2009, 34(8): 80- 83.
Fu Sen, Kong Xiangwei, Li Zhe, et al. Bearing-Only Target Cross Location of Multi-Station based on Nonlinear Least Squares[J]. Fire Control & Command Control, 2009, 34(8): 80- 83.(in Chinese)
[11] 赵伟康, 韩一娜, 杨益新, 等. 基于元启发算法的纯方位被动定位方法[J]. 水下无人系统学报, 2018, 26(6): 623- 627.
Zhao Weikang, Han Yina, Yang Yixin, et al. Bearing-Only Passive Location Based on Meta-Heuristic Algorithm[J]. Journal of Unmanned Undersea Systems, 2018, 26(6): 623- 627.(in Chinese)
[12] 周荣艳, 陈建峰, 闫青丽, 等. 海洋声场中分布式无源定位系统的节点配置方法[J]. 声学学报, 2020, 45(1): 29-37.
Zhou Rongyan, Chen Jianfeng, Yan Qingli, et al. A sensor configuration method for distributed passive localization system in ocean acoustic field[J]. Acta Acustica, 2020, 45(1): 29-37.(in Chinese)
[13] 闫青丽, 陈建峰. 分布式声源定位系统节点最优布局方法及性能研究[J]. 电子学报, 2018, 46(5): 1186-1193.
Yan Qingli, Chen Jianfeng. Node Placement Optimization for Distributed Acoustic Source Localization System and Performance Study[J]. Acta Electronica Sinica, 2018, 46(5): 1186-1193.(in Chinese)
张 旭 男, 1982年生, 黑龙江萝北县人。中国人民解放军91550部队, 高级工程师, 博士, 主要研究方向为海洋信息应用技术、水下测量技术等。
E-mail: x_zhang04@aliyun.com
李智生 男, 1975年生, 辽宁绥中县人。中国人民解放军91550部队, 高级工程师, 博士, 主要研究方向为水下测量技术。
E-mail: zhisheng_li@126.com