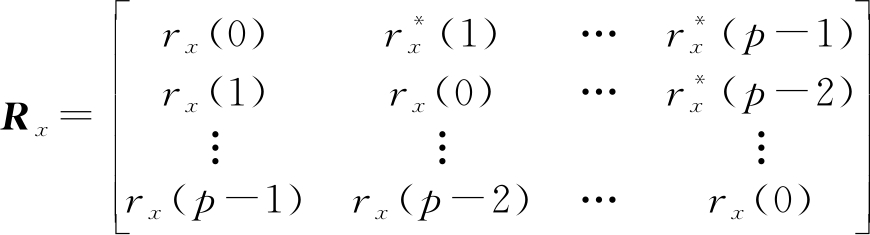
Reference format: Tang Xianhui, Li Dong, Su Jia, et al. An Adaptive Clutter Intelligent Suppression Method Based on AlexNet[J]. Journal of Signal Processing, 2020, 36(12): 2032-2042. DOI: 10.16798/j.issn.1003- 0530.2020.12.009.
雷达作为一种主动式微波目标观测设备,具有全天时、全天候和作用距离远等优势,在动目标监视及观测等领域应用广泛。复杂杂波背景下动目标观测一直以来都是世界性难题和挑战,也是当前研究的难点和热点问题[1-2],而杂波抑制是动目标检测的基础和前提;现有的海杂波抑制方法只有在特定的环境、空间才能够取得较好的效果,而且抑制效果的好坏很大程度上取决于对杂波的先验认知。然而,由于观测环境、雷达平台以及雷达参数(波段、极化方式、擦地角、分辨率)等因素的影响,往往导致杂波抑制性能不能满足后续动目标检测要求。因此,需要进一步研究鲁棒性更高、适应性更好的杂波抑制方法,以提升复杂杂波背景下雷达的海面目标检测性能。
近年来,国内外学者提出许多杂波抑制方法,这些方法主要包括时域对消法和子空间分解法两大类[2-3];时域对消法主要包括动目标显示(moving targets indication,MTI)[4-5]和动目标检测(moving target detection,MTD)[6-7]自适应方法[5,8]等。MTI方法利用雷达观测信号中目标和杂波多普勒频率的差异设计滤波器,使滤波器阻带凹口尽量对准杂波的中心频率,实现对杂波的滤除或削弱,该方法简单,易于工程实现,但是当检测目标为漂浮或慢速运动目标时,目标与杂波在多普勒域存在部分或完全重合,在抑制杂波的同时目标也会被抑制。MTD方法通过在MTI后串接一组相邻且部分重叠的滤波器组覆盖整个多普勒频率范围,从而实现对具有特定多普勒频移的动目标检测;然而当目标做非匀速运动时,雷达回波信号呈现出时变、非平稳等复杂特性,导致基于傅里叶变换的MTD方法不再有效。子空间分解法主要包括使用特征值分解(eigen value decomposition,EVD)[9]、奇异值分解(singular value decomposition,SVD)[4, 10]和高阶奇异值分解(high-order singular value decomposition,HOSVD)[3, 11]等分解法抑制海杂波。其中,SVD方法是该类方法的典型研究内容。SVD方法的基本思路是基于杂波窄带信号模型,通过雷达回波的时域信号构造Hankel矩阵,并利用将该矩阵中海杂波分量对应的奇异值归置为零,完成对海杂波的抑制;但实际回波序列中窄带信号数目不能直接获取,需要根据杂波先验信息实时调整Hankel矩阵的列数,导致难以达到理想的杂波抑制效果。随着神经网络技术的发展与应用,也有学者提出了基于浅层神经网络的杂波抑制方法,主要包括基于径向基函数(radial basis function,RBF)神经网络[12]和小波神经网络(wavelet neural network,WNN)[13-14]等。基于RBF神经网络的杂波抑制方法的主要思想是利用具有混沌特性的海杂波数据对RBF网络进行训练和优化,建立杂波预测模型,然后使用训练好的网络模型对未知杂波时间序列进行单步或多步预测,若预测误差大于给定门限值,则认为回波中存在目标,否则认为不存在目标;但是针对不同杂波数据,该方法需要根据先验信息手工调整网络结构和参数等,缺乏理论依据。基于WNN的杂波抑制方法通过小波神经网络重构海杂波混沌动态系统,学习海杂波内在动力学特性,实现对杂波信号的预测;当预测信号与实际信号的误差达到重构系统的指定精度时,幅度较强的杂波信号将转换为幅度较弱的随机噪声信号,从而能够检测出海杂波背景下的弱小目标。但是若该方法确定嵌入维和嵌入延迟的方法选取不当,使得重构的混沌系统不能很好地表征杂波特性,将严重影响杂波抑制效果。
在人工智能应用领域不断扩大的趋势下,利用深度学习方法进一步挖掘杂波数据的深层特征和精细信息,实现杂波的有效抑制已经成为可能[15-16]。本文提出一种基于AlexNet的自适应杂波智能抑制方法,首先,通过分析海杂波幅度特性,建立网络模型的训练和测试样本;然后,通过迁移AlexNet在ImageNet数据集上训练好的网络模型,并使用建立的杂波训练样本对该模型进行参数微调,实现对海杂波数据的准确分类,从而获取了服从独立同分布的杂波样本数据,使得自适应杂波抑制方法性能明显改善。相比于现有的海杂波抑制方法,提出的方法具有以下优点:(1)引入深度学习思想,准确获取了构造协方差矩阵需要的独立同分布杂波数据,提高了自适应杂波抑制性能;(2)利用迁移学习克服了有效标签样本数据不足的困难,实现了小样本条件下的杂波准确分类。最后,通过CSIR实测数据验证了该文所提方法的有效性。
相比于MTI、MTD等经典杂波抑制方法,自适应杂波抑制方法能够通过自适应估计杂波中心频率和谱宽自动调节滤波器凹口,实现对杂波自适应抑制[5]。假设某待检测距离单元l,其雷达观测信号xl(t)表示为
xl(n)=sl(n)+cl(n)+Nl(n)
(1)
其中,sl(n)和cl(n)分别为待检测单元的目标信号和杂波信号,Nl(n)是复高斯白噪声信号,{n=1,2,…,t},t为观测时间长度。杂波抑制就是在不损失目标信号sl(n)情况下,最大程度地抑制或削弱杂波信号cl(n)和噪声N(n),提高信杂噪比(signal-clutter-noise-ratios,SCNR);而自适应杂波抑制方法是挖掘利用目标信号和杂波信号的统计特性,自适应估计杂波中心频率和谱宽自动调节滤波器凹口,实现对杂波自适应抑制。
假设观测时间内待检测距离单元的相邻距离门回波信号为{xi, j},i=0,1,2,…,I-1, j=0,1,2,…,J,其中i是发射脉冲序号;j是距离单元数,且不同距离单元的回波数据满足独立同分布条件,则该时间内所有杂波数据构造的协方差矩阵Rx可以表示为
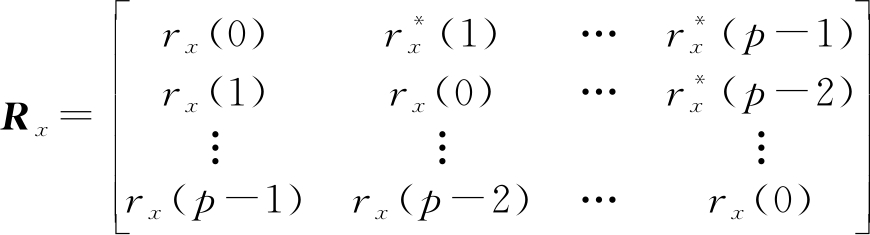
(2)
其中,p表示滤波器阶数,rx(·)是杂波自相关函数,其具体表达式为
(3)
由式(2)和(3)确定协方差矩阵Rx后,对其进行特征值分解,可得
RxWi=λiWi
(4)
其中,λi{i=0,1,2,…,p-1}是特征值,Wi表示与特征值λi对应的特征矢量;最小特征值λmin可表示为
λmin=min[λ0,λ1,...,λp-1]
(5)
对于确定的观测时间长度t,自适应滤波器的频率响应特性即为滤波器的权系数,因此滤波器权系数的确定是自适应方法的核心。已经证明[5],依据特征矢量法求解滤波器最佳权系数时,输入杂波的协方差矩阵的最小特征值λmin所对应的特征向量即为最佳权系数,记为Wopt;求得最佳权系数Wopt后,再对输入信号xl(n)进行滤波,滤波器的输出信号则可表示为:
yl(n)=Woptxl(n)
(6)
从而实现对待检测单元的杂波抑制,并且随着观测环境的变化最佳权系数Wopt能够自动更新,实现对杂波的自适应抑制。
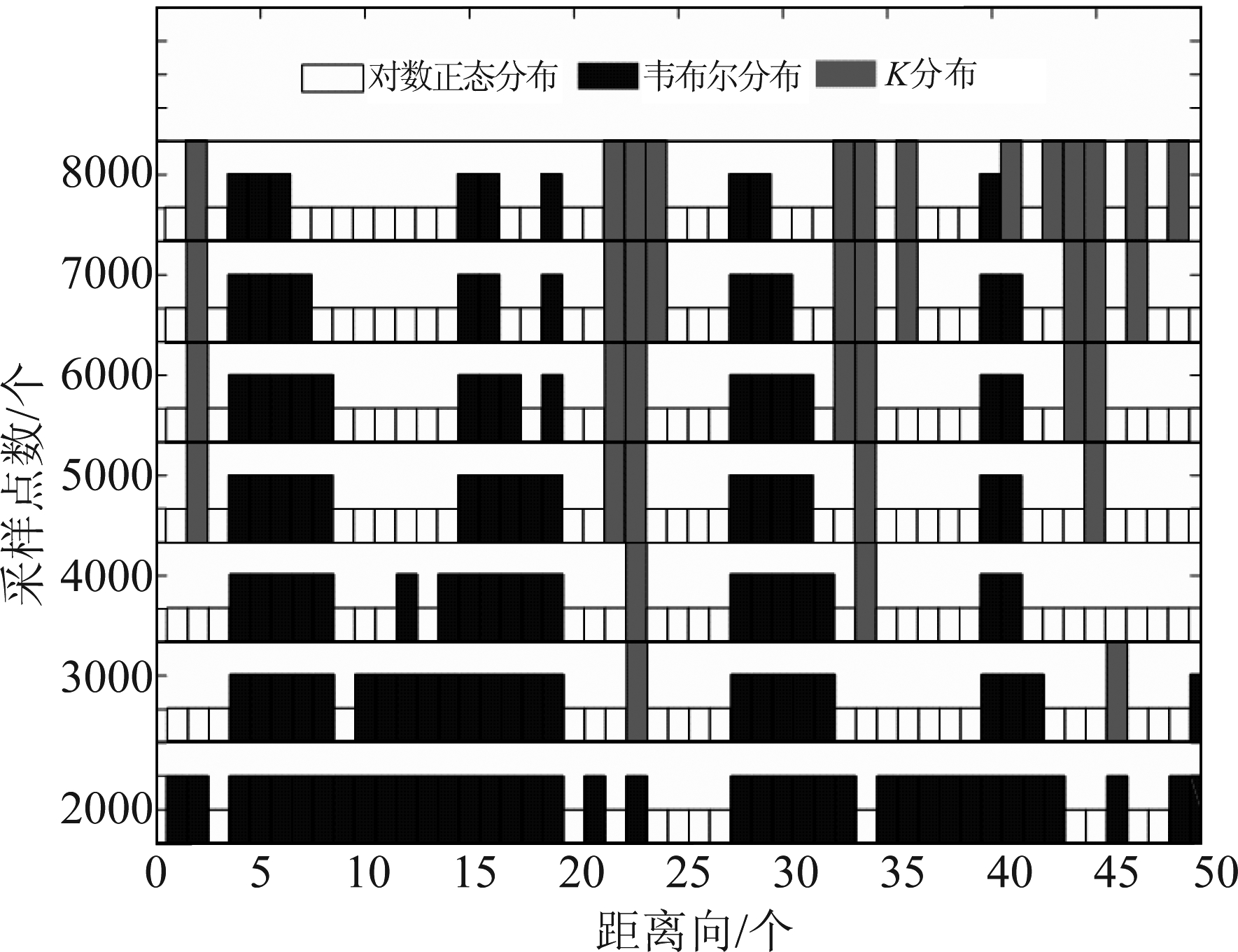
图1 实测数据不同距离单元分布情况
Fig.1 Distribution of measured data at different distances
根据上述分析可知,自适应杂波抑制方法是通过挖掘利用杂波的统计特性,并自适应调整滤波器参数从而达到理想的杂波抑制效果,但该方法要求构造协方差矩阵的杂波样本数据服从独立同分布;然而实际获取的杂波数据具有非平稳、非均匀和非高斯特性,导致构造协方差矩阵的相邻距离单元杂波样本数据难以满足独立同分布的要求。图1给出了某实测数据不同距离单元的杂波分布情况,由图1可知,不同距离单元的杂波不服从独立同分布,且随着方位采样点数的不同,分布的情况也越来越复杂,导致自适应杂波抑制方法性能不高。如何获取充足服从独立同分布的样本来精确估计协方差矩阵是自适应杂波抑制方法的关键。而深度学习可以有效挖掘杂波数据的深层特征和精细信息,为实现更为精准的杂波样本挑选,更为有效地杂波抑制带来了可能。
自适应方法杂波抑制性能取决于构造协方差矩阵的样本是否服从独立同分布;而杂波幅度特性作为一种判断杂波数据统计分布特征的重要手段,能够对海杂波统计特性进行很好的分析和描述。因此,本文利用幅度特征对实测海杂波数据进行统计分析。由于现代雷达系统主要工作在高分辨率、低入射余角、低擦地角状态,通过对不同雷达参数和海况环境下的海杂波幅度特性分析,以下3种[17]统计模型基本能够与实际海杂波幅度统计特性吻合:
(1)对数正态分布
在雷达面临擦地角较小或高海情的情况下,随机波动的海平面使得海杂波拖尾较长,此时海杂波幅度概率密度函数服从对数正态分布,其概率密度函数为
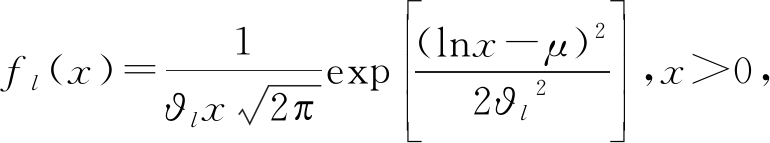ϑl>0,μ>0
(7)
其中,μ为尺度参数,表示对数正态分布的中值;ϑl为形状参数,是lnx2的标准差,表示对数正态的倾斜度,ϑl数值越大,表示杂波拖尾现象越严重,图2给出了μ和ϑl取不同值时对数正态分布的概率密度曲线。
图2 对数正态分布的概率密度曲线
Fig.2 Probability density curve of Log-Normal distribution
形状参数ϑl取决于实测数据,对数正态分布的均值和方差分别为
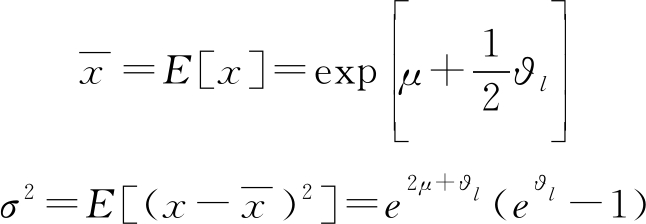
(8)
若采用最大似然估计法,μ和ϑl的参数估计结果可表示为
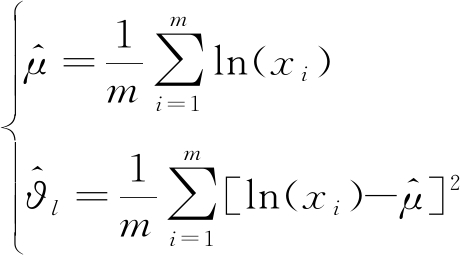
(9)
(2)韦布尔分布
在雷达近距离观测或杂波干扰严重的情况下,杂波分布范围较宽且起伏平稳,此时海杂波幅度概率密度函数服从韦布尔分布,其概率密度函数为
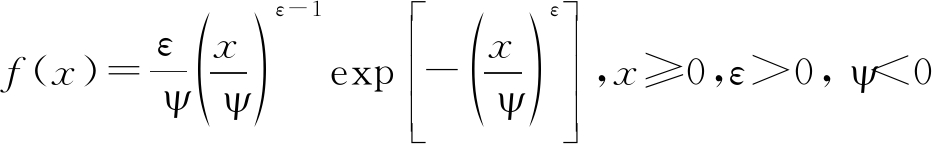
(10)
其中,ε表示杂波的形状参数,为韦布尔分布的倾斜度;ψ表示杂波尺度参数,表示韦布尔分布的中位数。图3给出了ε和ψ取不同值时韦布尔分布的概率密度曲线。
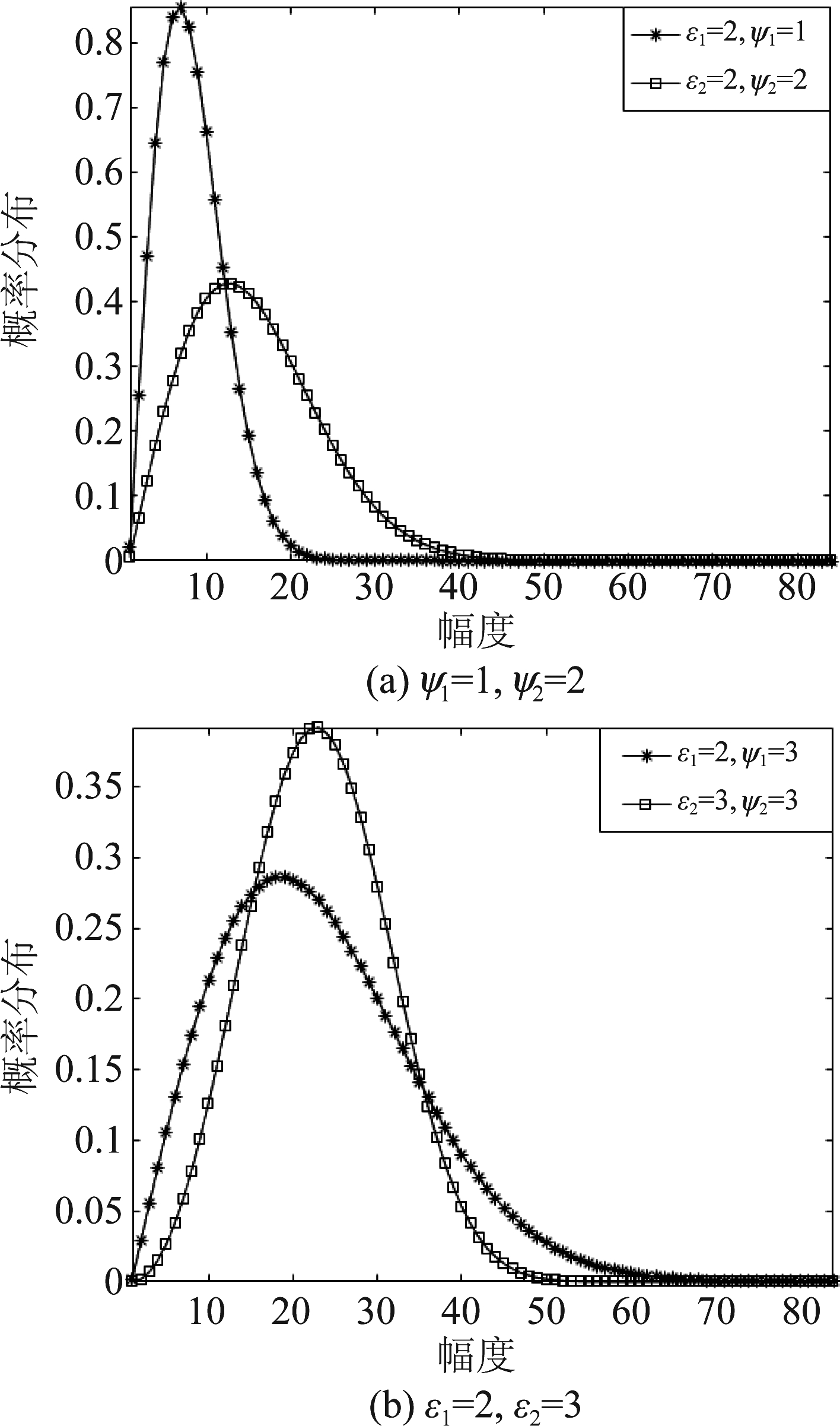
图3 韦布尔分布的概率密度曲线
Fig.3 Probability density curve of Weibull distribution
韦布尔分布的均值与方差分别为
μ=E(x)=ψ Γ[1+ε-1]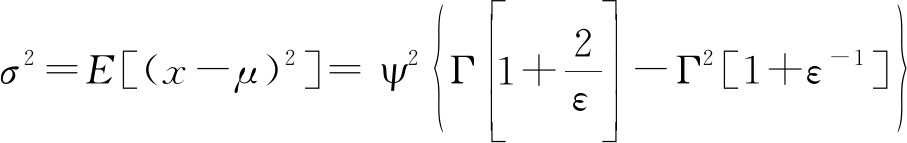
(11)
其中,Γ[·]表示伽马函数,由式(11)可知,当ε和ψ不同时,韦布尔分布的形状不同,因此可以通过调整ε和ψ的值来拟合实际海杂波幅度分布模型。
(3) K分布
与前述两种杂波模型不同,K分布考虑了杂波的时间和空间相关性。在雷达低入射角观测情况下,海杂波幅被描述为斑点分量(快变化分量)与基本幅度调制分量(慢变化分量)的乘积,此时海杂波幅度概率密度函数服从K分布,其概率密度函数为
(12)
其中,Iν[·]是修正ν阶贝塞尔函数;α表示尺度函数,与杂波均值有关;ν表示形状参数。图4是α和ν取不同值时K分布的概率密度曲线。
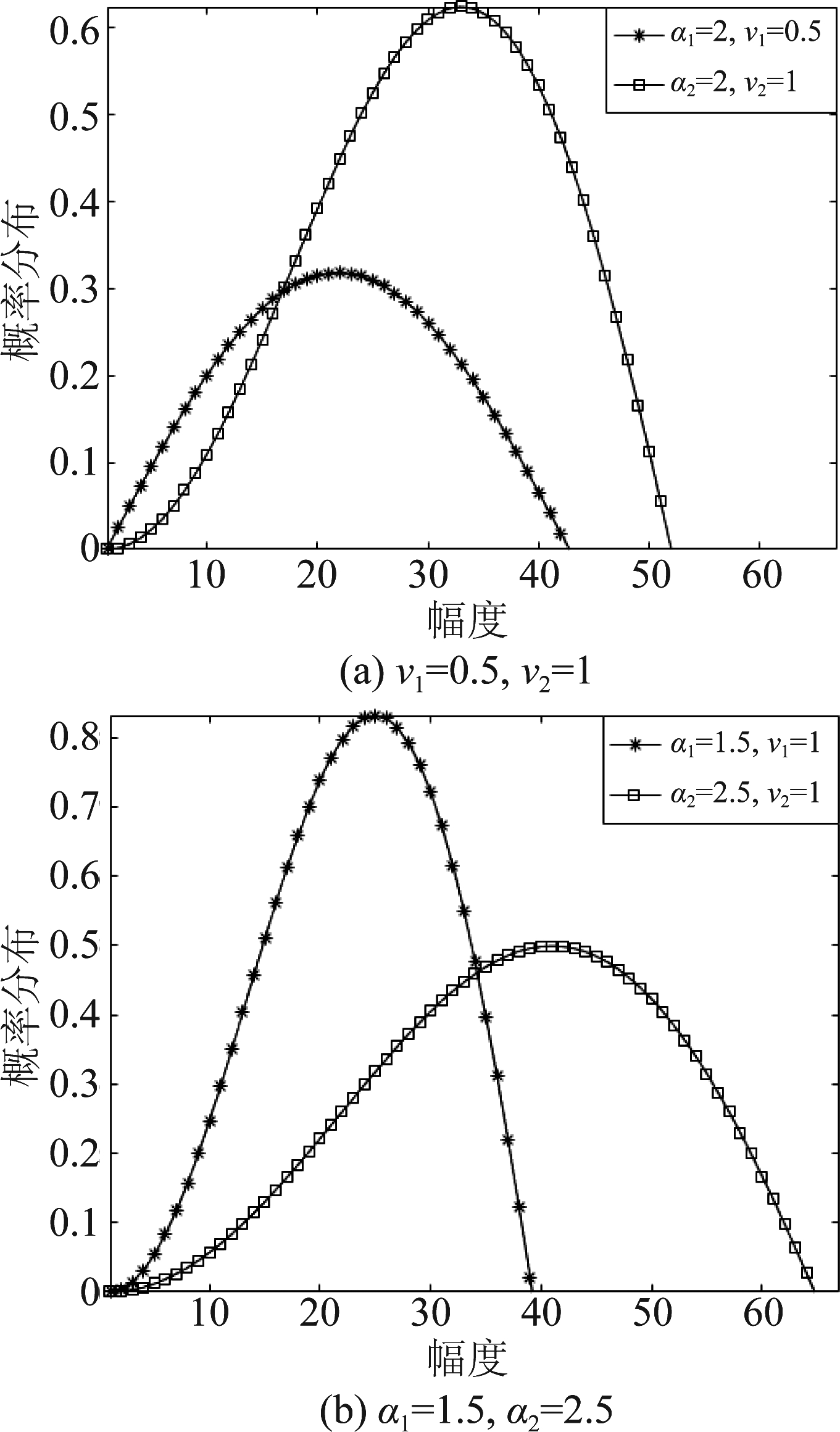
图4 K分布的概率密度曲线
Fig.4 Probability density curve of K distribution
K分布的均值与方差分别为
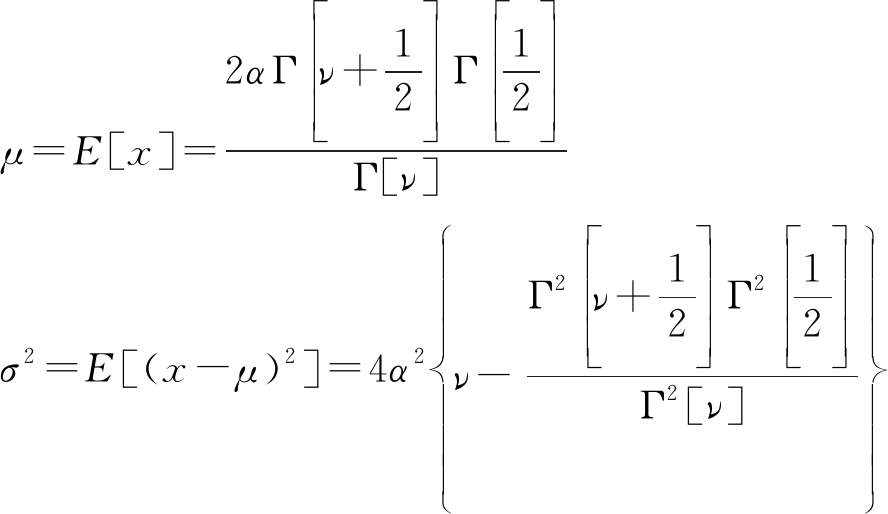
(13)
其中,Γ[·]表示伽马函数,α表示尺度函数,ν表示形状参数。
由以上分析可知,在不同的检测环境或雷达平台,杂波幅度呈现出不同的统计分布特性。因此,学习杂波幅度特性的变化规律和建立准确的统计模型,可为后续杂波样本库的建立提供理论支撑。
针对以上3种杂波概率密度分布模型,对实测海杂波数据进行幅度统计特性分析,并通过不同模型对其进行拟合,从而建立了海杂波样本库,为后续的自适应杂波智能抑制提供训练样本;本文使用的实验数据集来自南非科学和工业研究理事会(CSIR)于2006年在南非西南海岸线利用Fynmeet雷达获取的CSIR数据集;该数据集涵盖了多种参数组合,包括不同发射波形、方位角和作用距离等,同时,CSIR详细的试验方案和参数设计也为同类型试验的开展提供很好的参考与借鉴[18],其地理位置信息和海洋环境参数如表1所示。
表1 实验数据地理位置和环境参数[18]
Tab.1 Experimental data geographic location and environmental parameters[18]
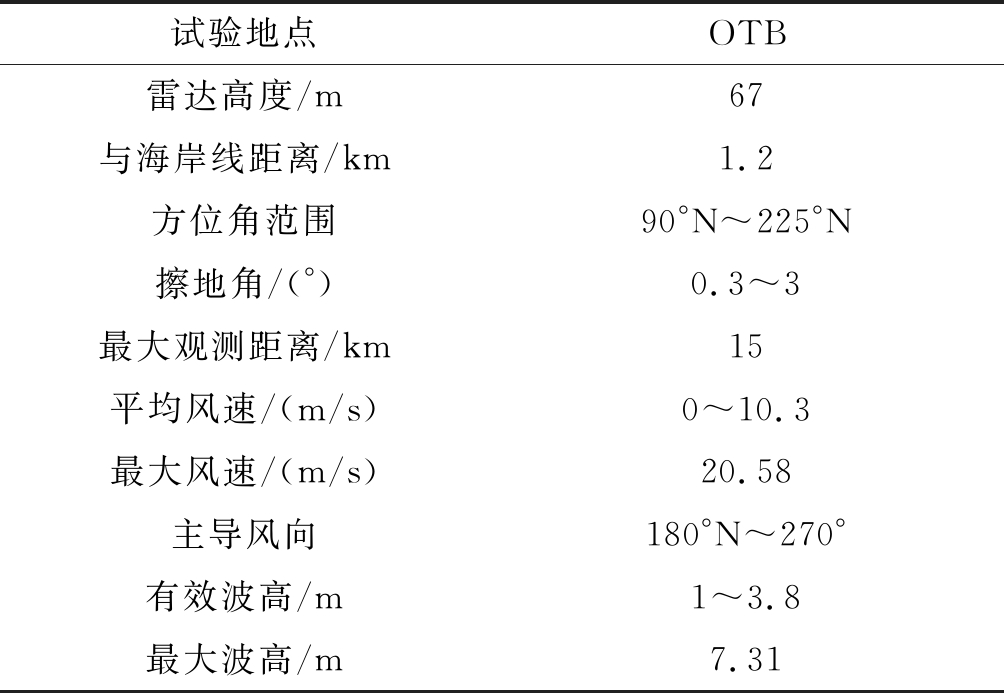
试验地点OTB雷达高度/m67与海岸线距离/km1.2方位角范围90°N～225°N擦地角/(°)0.3～3最大观测距离/km15平均风速/(m/s)0～10.3最大风速/(m/s)20.58主导风向180°N～270°有效波高/m1～3.8最大波高/m7.31
海杂波样本库的建立过程步骤如下:(1)随机选择脉冲压缩后的杂波数据进行幅度特性统计,并将其归一化0～10范围内;(2)使用非线性拟合函数inline对杂波幅度分布进行自适应拟合,并采用残差平方和(RSS)定量检验拟合效果,RSS值越小,拟合效果越好,杂波幅度就服从相应的分布;(3)将得到的幅度统计图进行分类保存,每个类别下300张,格式为.jpg,共900张图片;(4)将数据集划分为训练集和测试集,分别占总数据集的90%和10%。图5(a)、(b)、(c)分别给出了对数正态分布、韦布尔分布和K分布实测数据幅度统计特性图。
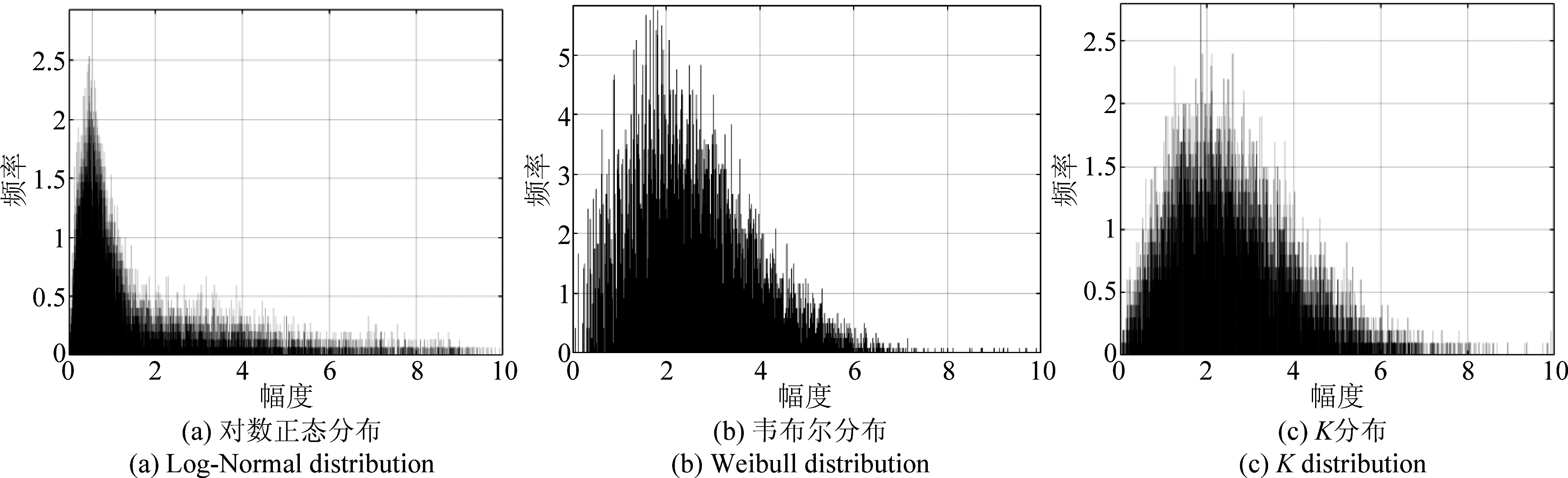
图5 实测杂波数据幅度统计特性
Fig.5 Statistical characteristics of measured clutter data amplitude
AlexNet作为经典的深度卷积神经网络之一,共有八层结构,其网络结构如图6所示。该网络作为2012年的图像识别大赛冠军[19],主要优点有:(1)采用线性整流函数(ReLU)激活函数替代Sigmoid函数,能更好的解决梯度弥散问题;(2)采用dropout随机丢弃部分神经元,避免了过拟合(overfitting)现象;(3)采用最大池化替代平均池化,丰富了数据特征;(4)采用局部响应归一化(LRN)操作,使得输出较大的神经元响应相对增大,而输出较小的神经元响应相对减小,增强了模型泛化能力;(5)采用具有强大并行能力的双GPU结构,提升了网络训练速度;因此,本文选取AlexNet作为杂波数据库的网络模型。
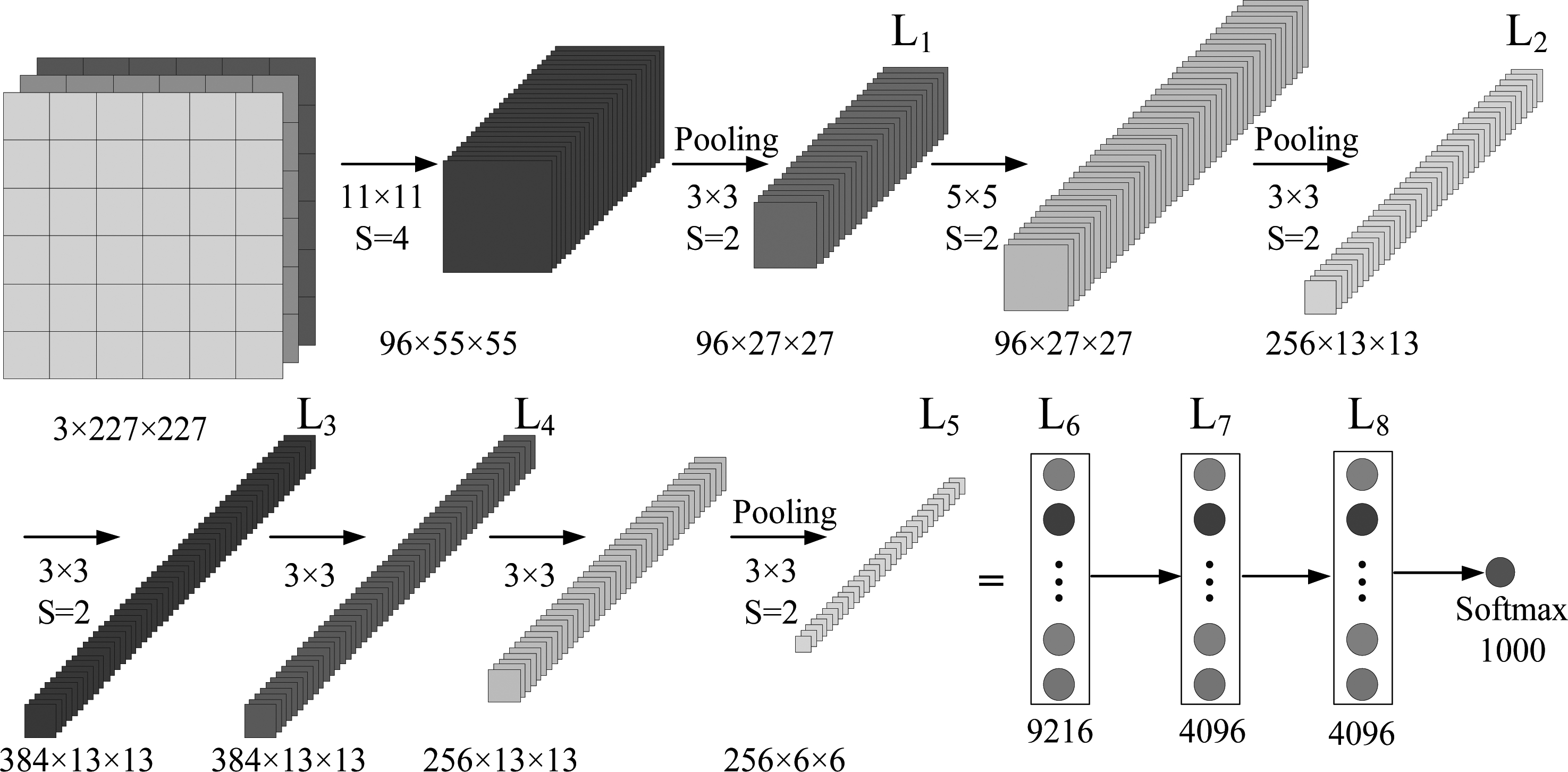
图6 AlexNet网络结构
Fig.6 Network structure of AlexNet
由于充足的杂波样本数据很难获取,因此在训练神经网络模型时,容易导致过拟合等问题。而基于模型的迁移学习(model based transfer learning,MTL)能够在目标域样本数据不足情况下,将已经训练好的模型和参数迁移到新的任务域,完成对新任务的模型训练;本文采用MTL方法训练杂波样本数据,缩短了AlexNet网络模型的训练周期。图7给出了网络训练过程中对Conv1的96张特征图、Conv3的384张特征图以及Conv5的256张特征图进行可视化的示意图,由图7(a)、(b)可知,Conv1和Conv3主要提取图像的边缘轮廓、形状、纹理等底层特征,图7(c)可知,Conv5主要提取的是一些肉眼不能识别的更高层特征。
图7 部分卷积层特征图可视化训练结果
Fig.7 Partial convolutional layer feature map visualization training results
在迁移AlexNet在ImageNet数据集分类模型的基础上,通过杂波训练样本对网络参数进行微调,其初始学习率η=0.001,总迭代次数Iters=9600,类别数Class=3。由于η过小会降低网络优化的速度,η过大可能导致网络不能收敛。所以为了兼顾训练效率和稳定性,本文将η设置为随迭代次数变化的分段函数。表2给出了几种训练效果较好的模型。
表2 不同模型参数情况
Tab.2 Different model parameters
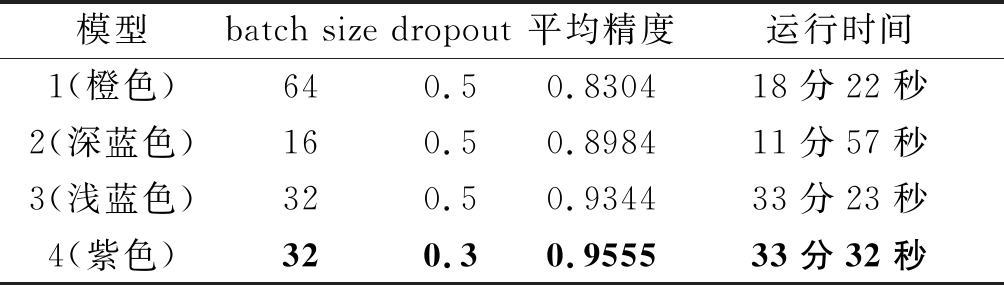
模型batch sizedropout平均精度运行时间1(橙色)640.50.830418分22秒2(深蓝色)160.50.898411分57秒3(浅蓝色)320.50.934433分23秒4(紫色)320.30.955533分32秒
由表2可知,批量大小(batch size)和dropout两个参数之间呈负相关,两者对训练精度和运行时间影响很大。图8给出了不同模型的训练曲线,由图8可知,通过网络参数的调整,模型训练精度从模型1的83.04%到模型4的95.55%,总体提升了12.51%。
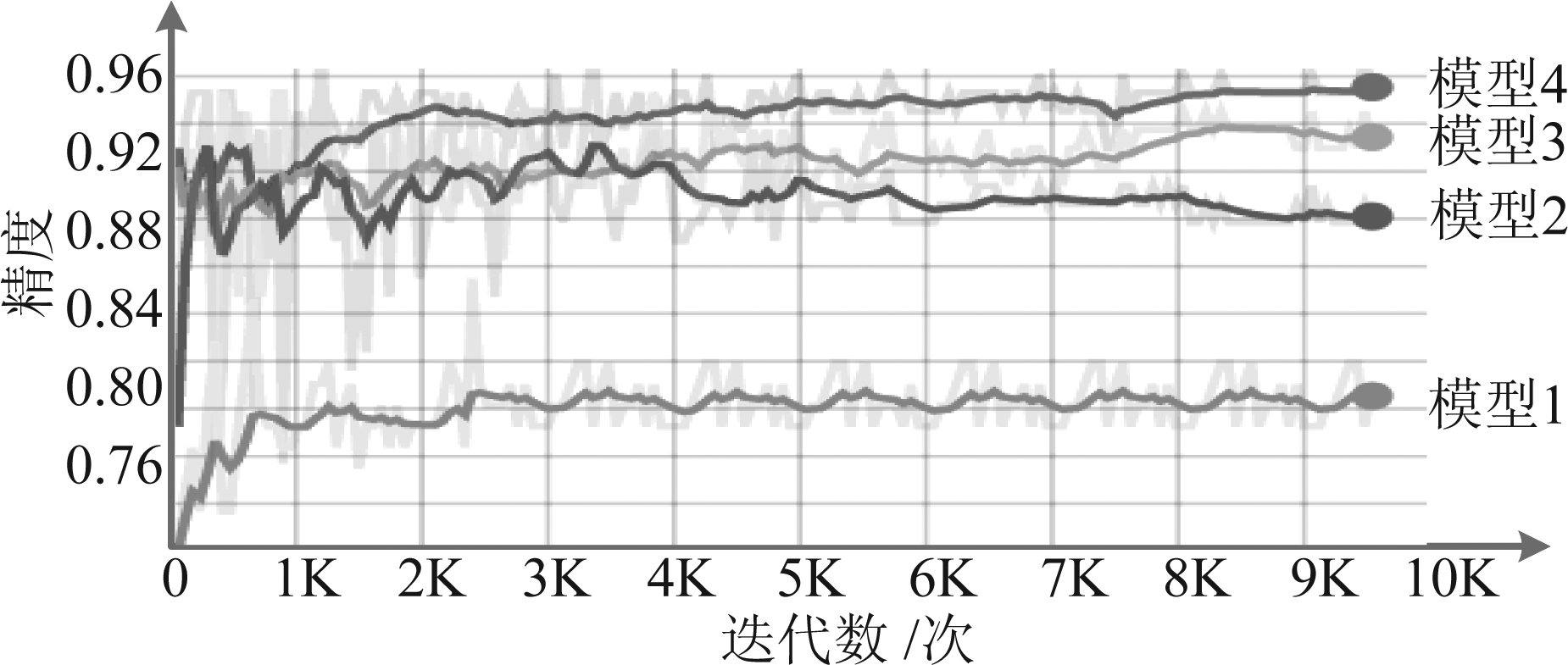
图8 不同模型训练曲线
Fig.8 Training curves of different models
通过上述分析可知,本文提出的方法首先利用AlexNet在ImageNet数据集上进行预训练,完成对ImageNet数据集的分类,建立网络分类模型;然后迁移该网络模型并使用杂波训练数据集微调网络参数,实现对杂波样本库的准确分类,再通过对不满足分布条件的样本数据进行替换,从而获得独立同分布杂波样本;最后通过计算杂波数据协方差矩阵和滤波器权系数,从而得到最佳权系数,实现自适应杂波智能抑制,提出方法的具体实现流程如图9所示。
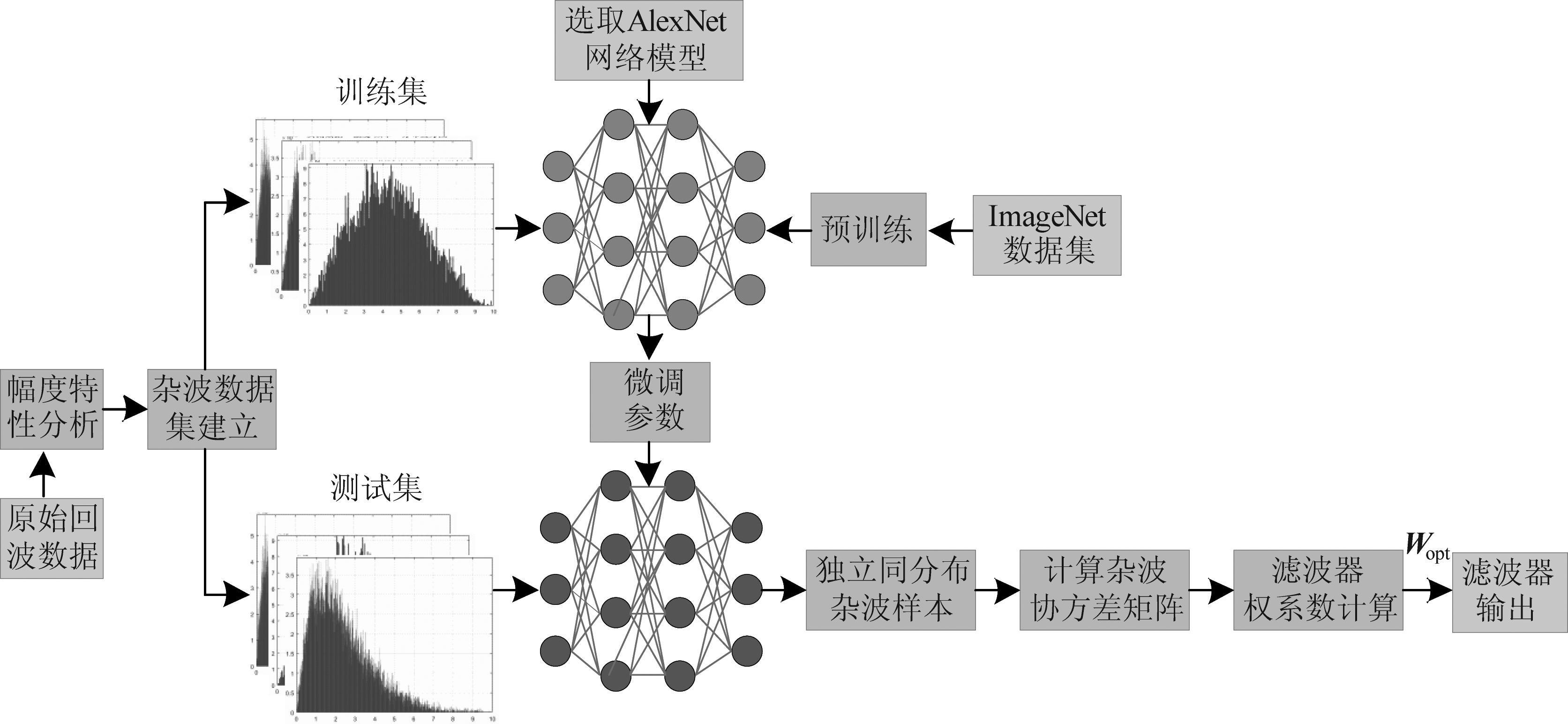
图9 基于AlexNet的自适应杂波智能抑制方法实现流程
Fig.9 Implementation process of adaptive clutter intelligent suppression method based on AlexNet
本节所用的数据文件是2006年7月28日CSIR在南非阿尼斯顿进行的海杂波测量试验中记录的数据集子集:雷达发射频率为9 GHz,脉冲重复频率(PRF)为2500 Hz;总共包含31个距离单元(1395 m),每个距离单元的采样点数为186180个(74.4716 s),每个实验使用全部距离单元的前8000个采样点(31*8000)。因为该实验数据本身是无目标的,因此事先加入3个仿真目标,目标参数信息如表3所示。加入目标后的距离-多普勒域图如图10(a)所示。
表3 实验中各目标的参数信息
Tab.3 Parameter information of each target in the experiment
目标所在距离单元多普勒频率/HzSCNRi/dB11050-821440-931851-15
通过上述数据对本文提出的自适应杂波智能抑制方法进行性能分析,并与MTI方法、SVD方法、自适应杂波抑制方法进行对比。4种算法的处理结果分别如图10(b)、(c)、(d)、(e)所示。由图10(b)可知,MTI方法严重损失了目标能量,且杂波抑制效果也很差;由图10(c)可知,SVD方法虽然目标信号的保持效果不错,但是杂波剩余仍然较强,不能准确地对海杂波和目标做出判断;图10(d)可知,自适应方法虽然对杂波抑制效果不错,但是目标信号的损失相对增加;图10(e)可知,自适应杂波智能抑制方法通过利用去除目标所在距离单元得到的独立同分布样本数据训练滤波器权值,使得杂波子空间构建更为精准,因此,对海杂波进行很好抑制的同时能够最大程度地保证目标能量不被削弱,有利于更好地从海杂波中检测目标,提高检测精度。
在方法性能分析中,使用SCNR的改善值(improvement of SCNR,ISCNR)[2]来衡量不同方法的性能,ISCNR的值越大,说明该方法的性能越好,其定义为
ISCNR=SCNRo-SCNRi
其中,SCNRo和SCNRi分别表示输出信杂噪比和输入信杂噪比。本文的SCNR定义为
SCNR=log(Ps)-log(Pc)
其中,Ps和Pc分别表示目标功率和杂波功率。值得指出的是,本文将多普勒域中目标所在距离单元中除了目标外的最大谱峰作为杂波功率。图11给出了不同方法在目标1所在距离单元处理前后归一化功率对比情况,表4给出了不同方法处理后各目标的SCNRo和ISCNR情况。由表4可知,相比于MTI方法、SVD方法、自适应杂波抑制方法,本文提出的自适应杂波智能抑制方法的ISCNR明显优于其他三种方法,进一步验证了提出方法的有效性。
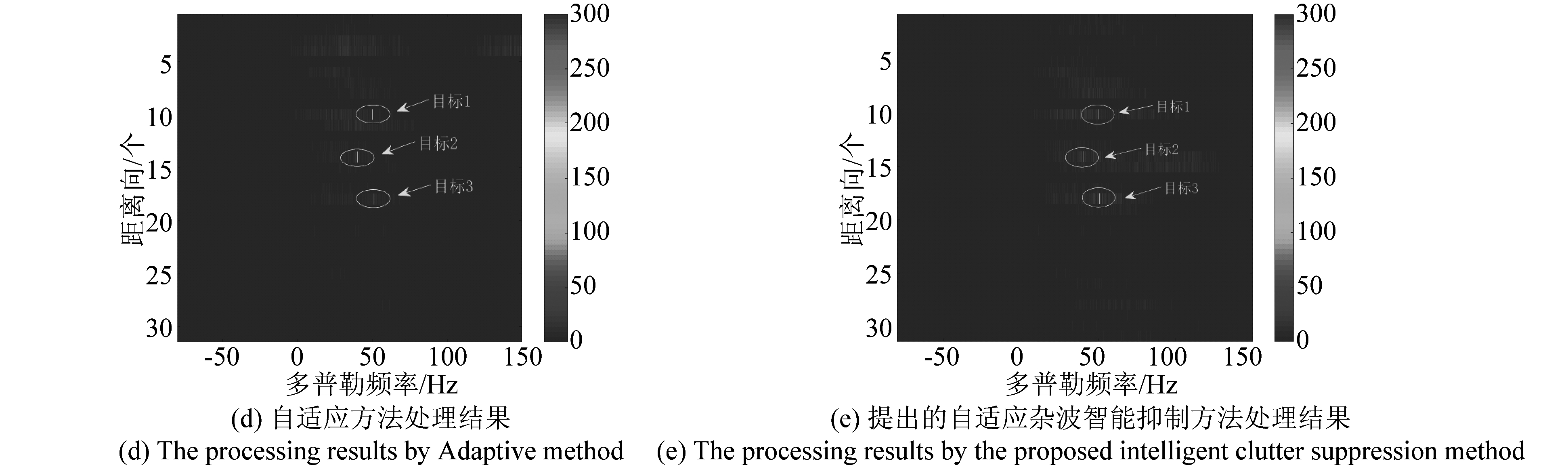
图10 不同方法的杂波抑制结果
Fig.10 Clutter suppression results of different methods
图11 不同方法在目标1所在距离单元处理前后归一化功率
Fig.11 Normalized power before and after processing in the distance range where is target 1 located
由于不同的样本挑选方法构造的协方差精准程度不同,因此,本文通过提出的基于AlexNet的自适应智能杂波抑制方法与传统的使用广义内积检测法[20](generalized inner products,GIP)和幅度-相位联合选法[21]进行样本挑选后,再用自适应方法进行杂波抑制。3种算法的处理结果分别如图12所示,由图12(a)可知,基于GIP样本挑选的自适应方法由于先假设所有初始化样本数据满足‘均匀’条件,导致实际的海杂波模型匹配失败,样本筛选不够合理,使得自适应方法的性能不够高;由图12(b)可知,基于幅度-相位联合法的自适应方法在进行样本估计时,相对较强的目标信号被保留了下来,然而,相对较弱的目标信号被剔除了。表5给出了不同方法处理后各目标的SCNRo和ISCNR情况,由表5可知,本文提出的基于AleNet杂波样本挑选方法能够明显改善自适应方法的杂波抑制性能。
表4 不同方法杂波抑制后各目标的SCNRo/dB和ISCNR/dB情况
Tab.4 SCNRo/dB and ISCNR/dB of each target after clutter suppression by different methods
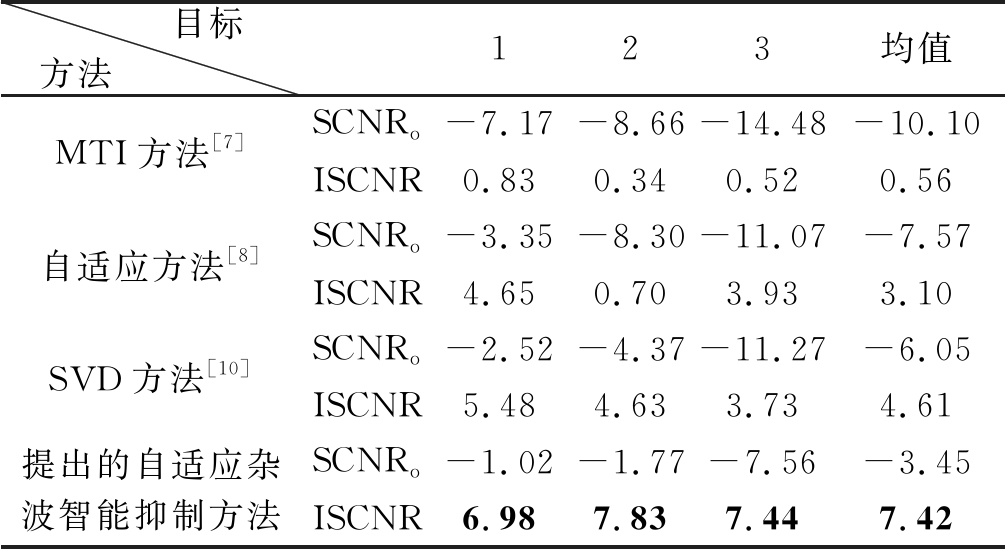
目标方法 123均值MTI方法[7]SCNRo-7.17-8.66-14.48-10.10ISCNR0.830.340.520.56自适应方法[8]SCNRo-3.35-8.30-11.07-7.57ISCNR4.650.703.933.10SVD方法[10]SCNRo-2.52-4.37-11.27-6.05ISCNR5.484.633.734.61提出的自适应杂波智能抑制方法SCNRo-1.02-1.77-7.56-3.45ISCNR6.987.837.447.42
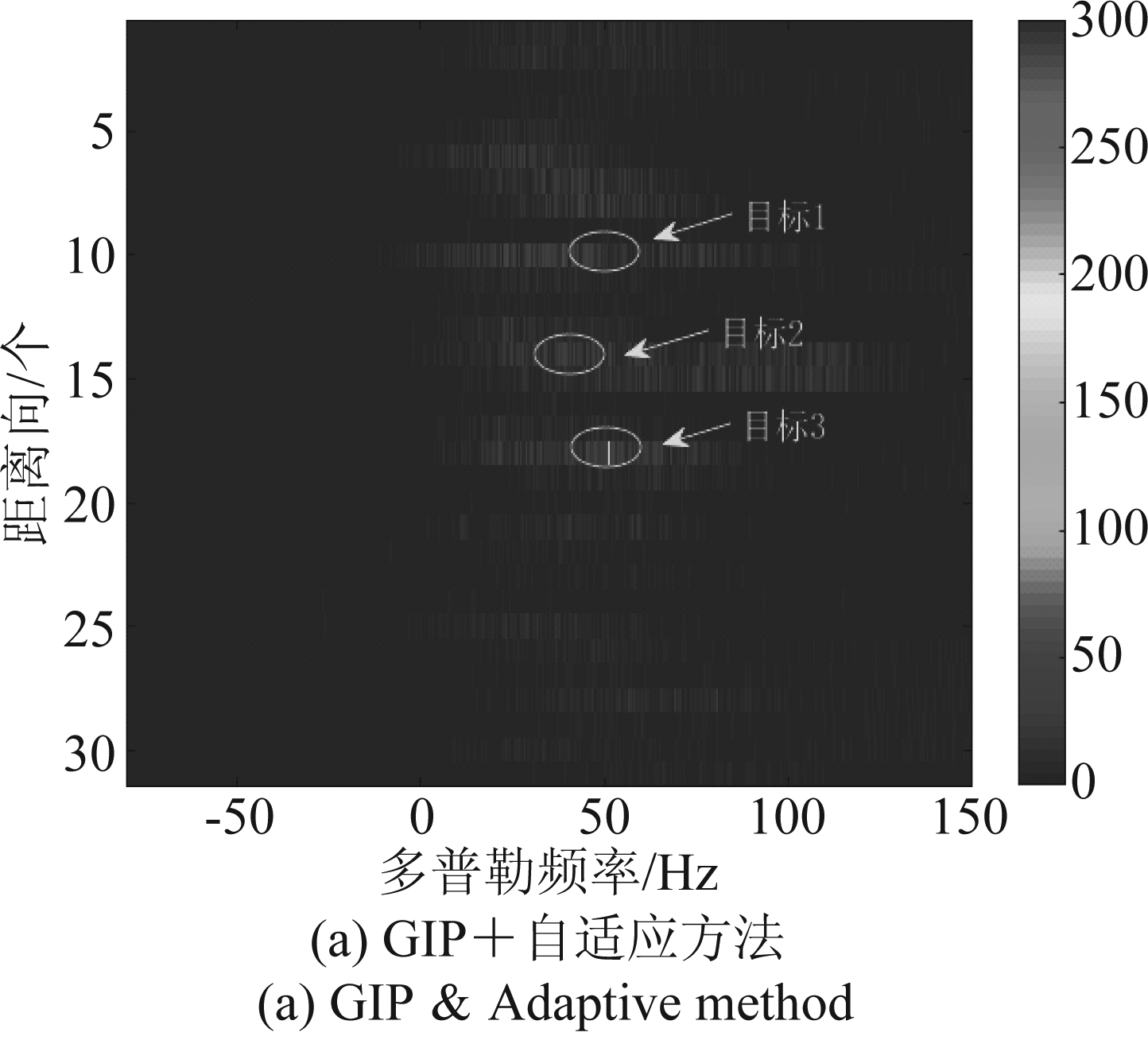
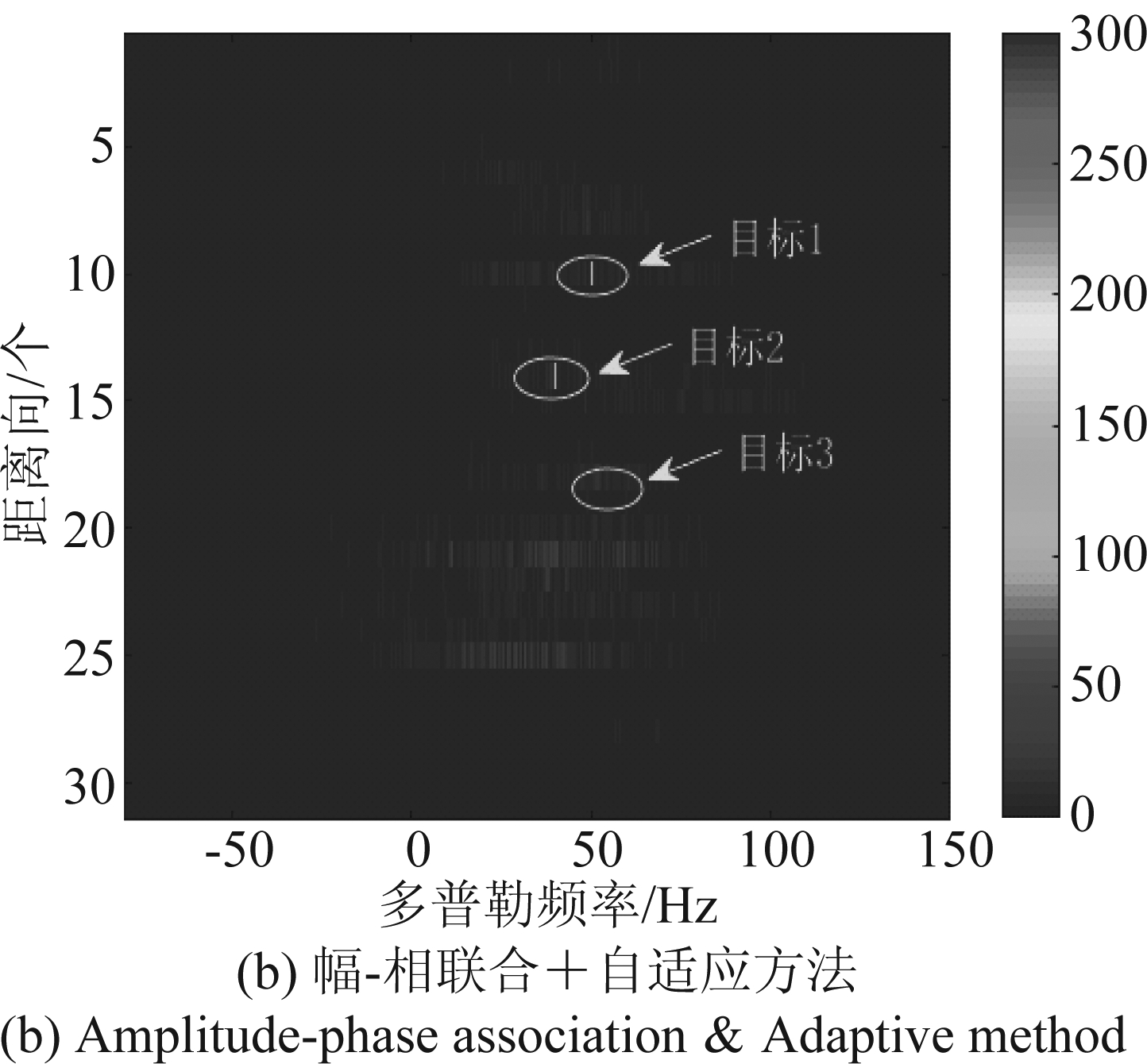
图12 不同样本挑选法+自适应方法的杂波抑制结果
Fig.12 Clutter suppression results of different sample selection methods & Adaptive method
表5 不同样本挑选法后各目标的SCNRo/dB和ISCNR/dB情况
Tab.5 SCNRo/dB and ISCNR/dB of each target by different sample selection methods
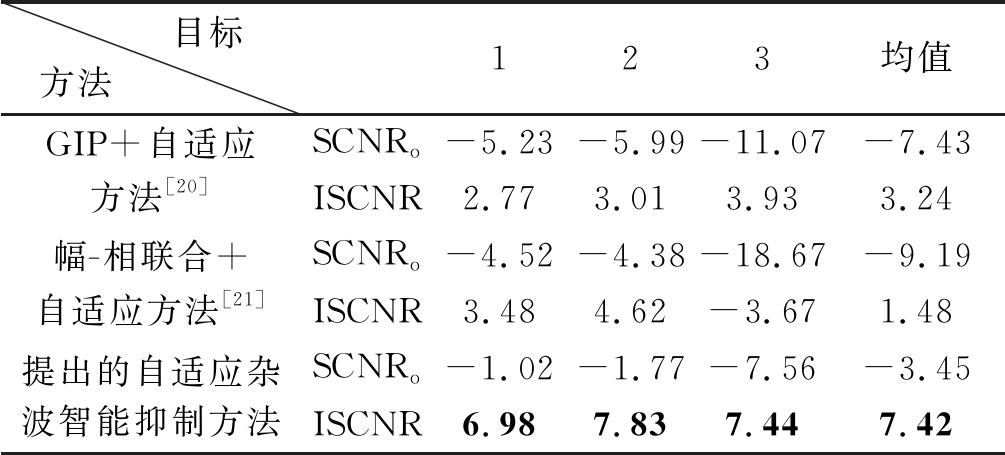
目标方法 123均值GIP+自适应方法[20]SCNRo-5.23-5.99-11.07-7.43ISCNR2.773.013.933.24幅-相联合+自适应方法[21]SCNRo-4.52-4.38-18.67-9.19ISCNR3.484.62-3.671.48提出的自适应杂波智能抑制方法SCNRo-1.02-1.77-7.56-3.45ISCNR6.987.837.447.42
针对由于观测环境、雷达平台以及雷达参数等因素的影响,往往导致获取的雷达回波数据不满足独立同分布条件,导致传统自适应杂波抑制方法性能恶化的问题,本文提出一种基于AlexNet的自适应杂波智能抑制方法。该方法通过深度卷积神经网络对杂波幅度分布进行分类识别,进而获取充足的服从独立同分布的杂波样本数据,提升了自适应杂波抑制方法性能;同时利用迁移学习,克服了有效标签样本不足的困难。实测数据的实验结果表明,与现有的杂波抑制方法以及基于不同样本挑选策略的自适应方法相比,本文提出的自适应杂波智能抑制方法具有明显的优势。
[1] 陈小龙, 关键, 黄勇, 等. 雷达低可观测目标观测技术[J]. 科技导报, 2017, 35(11): 30-38.
Chen Xiaolong, Guan Jian, Huang Yong, et al. The technology of radar low-observable target detection[J]. Science & Technology Review, 2017, 35(11): 30-38.(in Chinese)
[2] 关泽文, 陈建文, 鲍拯. 一种改进的基于峰值信噪比-高阶奇异值分解的天波超视距雷达自适应海杂波抑制算法[J]. 电子与信息学报, 2019, 41(7): 1743-1750.
Guan Zewen, Chen Jianwen, Bao Zheng. A modified adaptive sea clutter suppression algorithm based on PSNR-HOSVD for skywave OTHR[J]. Journal of Electronics & Information Technology, 2019, 41(7): 1743-1750.(in Chinese)
[3] Lv Mingjie, Zhou Chen. Study on sea clutter suppression methods based on a realistic radar dataset[J]. Remote Sensing, 2019, 11(23): 2721-2742.
[4] Schleher D C(美), 等. 动目标显示与脉冲多普勒雷达[M]. 北京: 国防工业出版社, 2016: 1- 468.
Schleher D C (USA), et al. Moving target display and pulse doppler radar[M]. Beijing: National Defense Industry Press, 2016: 1- 468.(in Chinese)
[5] 吴顺君, 梅晓春, 等. 雷达信号处理和数据处理技术[M]. 北京: 电子工业出版社, 2008: 1-512.
Wu Shunjun, Mei Xiaochun, et al. Radar signal processing and data processing technology[M]. Beijing: Electronics Industry Press, 2008: 1-512.(in Chinese)
[6] Candan C, Ispir M. On the design of staggered moving target indicator filters[J]. IET Radar Sonar & Navigation, 2016, 10(1): 205-215.
[7] Chen Peng, Zheng Le, Wang Xiaodong, et al. Moving target detection using colocated MIMO radar on multiple distributed moving platforms[J]. IEEE Transactions on Signal Processing, 2017, 65(17): 4670- 4683.
[8] 孙国政, 卞雷祥. 雷达杂波自适应抑制技术[J]. 雷达与对抗, 2011, 31(2): 11-13.
Sun Guozheng, Bian Leixiang. The technology of radar adaptive clutter suppression[J]. Radar and Confrontation, 2011, 31(2): 11-13.(in Chinese)
[9] 蔚娜, 李雪, 李铁成. 基于特征分解的多模杂波抑制方法[J]. 电波科学学报, 2016, 31(1): 85-90.
Wei Na, Li Xue, Li Tiecheng. An eigenvalue decomposition based method for suppressing multi-mode clutter[J]. Chinese Journal of Radio Science, 2016, 31(1): 85-90.(in Chinese)
[10] Chen Zezong, He Chao, Zhao Chen, et al. Using SVD-FRFT filtering to suppress first-order sea clutter in HFSWR[J]. IEEE Geoscience and Remote Sensing Letters, 2017, 14(7): 1076-1080.
[11] 薄超, 顾红, 苏卫民. 基于高阶奇异值分解的OTHR海杂波抑制算法[J]. 系统工程与电子技术, 2014, 36(5): 872- 878.
Bo Chao, Gu Hong, Su Weimin. OTHR sea clutter suppression algorithm based on higher order singular value decomposition[J]. Systems Engineering and Electronics, 2014, 36(5): 872- 878.(in Chinese)
[12] 陈瑛, 罗鹏飞, 曾勇虎. 基于RBF神经网络的海杂波建模[J]. 系统仿真学报, 2007, 19(3): 524-526.
Chen Ying, Luo Pengfei, Zeng Yonghu. The modeling of sea clutter based on RBF neural network[J]. Journal of System Simulation, 2007, 19(3): 524-526.(in Chinese)
[13] Qu Changwen, He You, Feng Su, et al. Detection of weak targets with wavelet and neural network[C]∥International Symposium on Advances in Neural Networks. Springer, Berlin, 2004: 886-891.
[14] Shen Yan, Liu Ming, Wang Jinbao, et al. A new image restoration algorithm based on mathematical morphology and wavelet neural network[C]∥Proceedings of the 2012 International Conference on Computer Application and System Modeling(ICCASM). IEEE, Atlantis, 2012: 1036-1039.
[15] Shi Sainan, Shui Penglang. Sea-surface floating small target detection by one-class classifier in time-frequency feature space[J]. IEEE Transactions on Geoscience and Remote Sensing, 2018, 56(11): 6395- 6411.
[16] Lopez R G, Grajal J, Diza O R. Target detection in sea clutter using convolutional neural networks[C]∥Proceedings of the 2003 IEEE Radar Conference. IEEE, Huntsville, USA, 2003: 321-328.
[17] Yang Yong, Xiao Shunping, Wang Xuesong, et al. Statistical distribution of polarization ratio for radar sea clutter[J]. Radio Science, 2017, 52(8): 981-987.
[18] 丁昊, 刘宁波, 董云龙, 等. 雷达海杂波测量试验回顾与展望[J]. 雷达学报, 2019, 8(3): 281-302.
Ding Hao, Liu Ningbo, Dong Yunlong, et al. Overview and prospects of radar sea clutter measurement experiments[J]. Journal of Radars, 2019, 8(3): 281-302.(in Chinese)
[19] Abdullah, Hasan M S. An application of pre-trained CNN for image classification[C]∥20th International Conference of Computer and Information Technology (ICCIT). Bangladesh, 2017: 22-24.
[20] 郭佳佳, 廖桂生, 杨志伟, 等. 利用广义内积值迭代加权的空时协方差矩阵估计方法[J]. 电子与信息学报, 2014, 36(2): 172-177.
Guo Jiajia, Liao Guisheng, Yang Zhiwei, et al. Iterative weighted covariance matrix estimation method for STAP based on generalized inner products[J]. Journal of Electronics & Information Technology, 2014, 36(2): 172-177.(in Chinese)
[21] 范西昆, 李俊, 赵雪岩, 等. 利用先验信息的幅度-相位联合STAP样本选取方法[J]. 数据采集与处理, 2011, 26(2): 140-145.
Fan Xikun, Li Jun, Zhao Xueyan, et al. Knowledge-aided amplitude and phase combined training strategy for space-time adaptive processing[J]. Journal of Data Acquisition & Processing, 2011, 26(2): 140-145.(in Chinese)
唐先慧 女, 1996年生, 四川巴中人。重庆大学微电子与通信工程学院研究生, 主要研究方向为雷达信号处理、目标智能检测与识别等。
E-mail: 201812021011@cqu.edu.cn
李 东 男, 1983年生, 内蒙古商都人。重庆大学微电子通信与测控中心副教授, 硕士生导师, 主要研究方向为SAR/ISAR成像算法设计、雷达信息处理、参数估计等。
E-mail: lidongcuit@126.com
粟 嘉 男, 1985年生, 广西桂林人。西北工业大学电子信息学院博士生, 主要研究方向为信号处理、时频分析、动目标检测等。
E-mail: Jiasu1011@126.com
程婉儒 女, 1996年生, 重庆綦江人。重庆大学微电子与通信工程学院研究生, 主要研究方向为雷达信号处理、目标智能检测与识别等。
E-mail: cwr304366383happy@163.com
任金芝 女, 1996年生, 湖北荆门人。重庆大学微电子与通信工程学院研究生, 主要研究方向为参数估计、SAR/ISAR成像算法设计等。
E-mail: renjz0224@163.com
李秀琴 女, 1997年生, 四川达州人。重庆大学微电子与通信工程学院研究生, 主要研究方向为人工智能、目标检测与识别等。
E-mail: l_xiuqin_123@163.com