Reference format: Xue Yonghua, Chen Xiaolong, Huang Yong, et al. Ionospheric Decontamination for Sky-wave Radars Based on General Parameterized Time-Frequency Transform[J]. Journal of Signal Processing, 2020, 36(12): 2024-2031. DOI: 10.16798/j.issn.1003- 0530.2020.12.008.
天波超视距雷达工作在短波波段(3～30 MHz),利用电离层对短波电磁波的反射效应,完成对数千公里外的空中或海/地面目标的超视距探测。由于其“下视”的工作方式,海/地面目标的探测时,海/地杂波干扰严重。海/地面目标运动速度较慢,要从强大的海/地杂波中检测目标,需要长的积累时间以获得足够的多普勒分辨力,在多普勒域中分离杂波和目标。对于海/地面目标的检测,典型的相干积累时间为10～40 s[1]。在该时间范围内,电离层信道是起伏的。电离层的起伏使得穿行其间的短波电波信号相位的起伏,破坏了脉冲之间的相干性,造成杂波和目标的多普勒频谱展宽,从而限制了天波雷达海/地面目标的检测。
虽然天波雷达在其自适应信道管理子系统的支持下可选择起伏相对较小的频率点工作,一定程度上可缓解电离层污染的问题,但污染仍不能完全避免。为保证目标检测的顺利进行,需进行电离层污染的校正。电离层污染的估计和校正最直接的方法是在观测区域内设置应答器,而实际应用中,受环境条件限制,无法在所有的观测区架设。为此,人们利用强的海/地杂波信息来估计和校正电离层污染。从多普勒域来看,地杂波主要集中在零多普勒附近,可用于电离层污染的校正,而海杂波则由一对一阶Bragg峰和多个二阶Bragg峰构成。海杂波Bragg峰的位置雷达发射频率、电离层状态、海面状态和收发站之间的几何关系等因素有关[2],且其一阶Bragg峰较强,可用于电离层污染的估计和校正。
天波雷达电离层相位污染在慢时间域表现为乗性干扰,且其变化是非线性的,无法采用常规的时频滤波器进行滤除,另外,电离层信道的多层性导致不同层污染不同,并在接收端叠加起来,使得污染更加复杂。为此人们提出了多种电离层污染校正方法,基本可分三个步骤:一、提取用于电离层污染校正的特征信号,一般在频域进行,多采用带通滤波滤出一个单频分量展宽后的多普勒谱峰;二、污染信号的提取;三、构造校正算子进行污染校正。目前的研究主要关注第二步,区别也主要体现在该步骤,按实现方式不同,主要有以下两类,一是利用频率和相位之间的关系,直接估计瞬时频率,积分得到污染相位序列,如相位梯度法、基于WVD的方法[3],基于修正S变换的方法[4],基于信号子空间分解的方法[5]等;二是将数据进行分段,对每个分段的瞬时频率或者相位进行估计,再合成相位污染序列,如最大熵谱法[6],基于奇异值分解的估计方法[7],分段多项式相位建模方法[8],基于优化准则的方法[9]等。
从各种污染校正方法的具体原理来看,相位梯度法、基于WVD的方法以及分段多项式相位建模方法需要提取一个单频分量展宽后的多普勒谱峰。相位梯度法是以信号序列的首个数据的相位为准,依次计算相位梯度的方式来估计污染信号,只有在单频信号时准确度较高。基于WVD的方法为二阶时频方法,当待分析信号为多分量时会出现交叉项,导致计算精度急剧下降,而分段多项式相位建模方法也是针对单分量信号,对其分段后的信号相位用多项式建模来估计多项式系数,多段联合起来完成污染的估计和校正。当提取的信号不是单分量信号时,上述几种算法性能会大打折扣。特征信号的提取一般在多普勒域进行,准确提取特征信号而不引入其他干扰,需谨慎选择杂波滤波器带宽,为较准确地提取特征信号,李雪[10]给出了一种基于最小熵的杂波滤波器带宽自适应选择算法,但前提是多个分量扩展后频谱不重叠,且需要配合污染校正算法进行搜索,运算量较大。故准确提取特征信号的困难导致了单分量分析类的污染算法校正效果难以保证。
对于最大熵谱法、基于奇异值分解的估计方法等可不用事先提取特征信号,最大熵谱法是将待污染信号进行分段后,用修正的Burg法对各段信号进行谱分析,提取最大分量的谱峰,将各段的谱峰点组合起来进行插值计算来估计和校正污染,但如何选择谱估计的AR模型阶数是一个需要解决的问题。基于奇异值分解的方法是利用短时间内污染频率的不变性,用提取出的特征信号构造Hankel矩阵进行奇异值分解,通过保留大奇异值进行降秩,抑制噪声分量,进而采用矩阵分块、特征分解等操作后实现污染信号的提取和校正,该方法的问题在于对噪声比较敏感。
另外,由于多模情形下接收信号的多普勒分量增多,目前的污染校正方法都针对于单模传播的情形,对多模情形下的污染并不适用。电离层污染校正的关键问题在于污染信号时频结构的分析,难点在于多分量信号使得污染信号时频结构的分析相互影响,难以精确分析。
为此,本文引入广义参数时频变换方法对天波雷达接收信号进行分析,给出了一种更有效的和稳健的天波雷达电离层污染估计和校正方法。广义参数化时频变换针对信号模型来构建匹配的核函数,选择核函数参数,能够精确地刻画非平稳信号的时频特性,可以有效地分离多分量信号[11]。用于电离层污染校正时,根据电离层污染的特点选取样条调频小波作为参数化时频变换的核函数,针对电离层污染后的信号估计核函数参数,利用核函数的时频特征量来估计污染序列,构造污染校正算子进行污染校正。对于多模传播条件下的电离层污染,采用校正后滤除的方式,多次迭代完成污染的校正。本文首先介绍天波雷达信号模型,给出电离层污染的表达式,然后给出了广义参数化时频变换方法电离层污染校正原理,最后进行了数值仿真验证。
考虑到电离层的多层性,在相干积累时间内,天波雷达慢时间域的回波信号可表示为:
(1)
其中t=1,…,N表示回波处理的慢时间序列,c(t)表示杂波回波,n(t)表示接收噪声,dm(t)=ejφm(t)表示第m(m=1,…,M)个电离层传播模式的污染信号,φm(t)表示对应传播模式的相位起伏,M表示电离层传播模式个数。
电离层污染带来的相位起伏φm(t)在短时间里可以看作线性变化的,此时仅会造成频谱的偏移,并不会影响到目标的检测,当相干积累时间较长时,如达到海面目标检测所需要的10～40 s时,相位污染非线性变化,脉冲间的相干性遭到破坏,目标和杂波多普勒谱扩展,有可能导致目标的检测无法进行。电离层污染的校正就是估计出相位起伏量,记为
构造相应的解污染序列
对应分量相乘即可完成污染的校正。
广义参数化时频变换定义如下[11]:
(2)
其中
表示变换核参数向量,
表示与核函数相关的频率旋转算子,
表示t0时刻附近时段由参数P定义的频率平移算子,kp(t)∈L2(R)表示可积核函数,wσ(t)表示由参数σ确定的窗函数。
对于非平稳信号而言,频率旋转算子的作用是在t0时刻附近的时间窗内将信号的时频脊进行旋转操作,即将信号的瞬时频率减去kp(t),频率频移算子是将该时间窗内对信号的进行频谱搬移,搬移的频率尺度为kp(t0)。从变换的定义来看,该变换是将原信号x(t)在t0时刻附近的一段经旋转、频移、加窗后进行傅里叶变换,变换后的频率分辨率由窗口宽度和核函数kp(t)决定,当核函数与原信号时频分布之差为一常数时,变换的频率分辨率仅由窗宽度决定,此时时频集中性最好。当kp(t)=0时,该变换退化为短时傅里叶变换。
从广义参数化时频变换的定义式(2)可以看出,变换核函数与信号的时频特征越相似,信号广义参数化时频变换后的时频分布越集中,对信号的时频特征刻画越准确。要使变换的时频集中性最好,就要根据信号的特点选择合适的核函数和核函数参数,使得核函数与原信号的时频分布之差为常数。核函数的选取及其参数的设定要使得其能够较好地逼近待分解信号的时频特征。
根据信号时频分布特点的不同,文献[11]分别给出了三种形式的核函数:多项式函数、样条函数和傅里叶级数,并给出了相应的核函数参数计算方法。对于电离层污染后的天波雷达接收信号,由于相位变化的随机性,接收信号的时频曲线变化较为复杂,若采用多项式函数则需要高次多项式,在拟合中高次多项式会出现“龙格”现象,导致数值不稳定,故应选用样条函数或傅里叶级数,而傅里叶级数要较好地逼近随机起伏的污染信号,需要较长的级数,待估计参数较多,故这里采用样条函数。
核函数参数需根据待变换信号的时频特征来估计,待变换信号时频特征刻画的准确性又与核函数参数的取值有关,取值越合适,变换后的时频分布越集中,时频特征的刻画越准确,进而估计的参数越合适,如此反复,形成一个循环逼近的过程,最终得到核函数参数。以单分量信号为例,核函数参数的估计可概括为:
(1)在第i(i=1,2,…,imax)次迭代中,采用广义参数化时频变换得到信号的时频分布,即
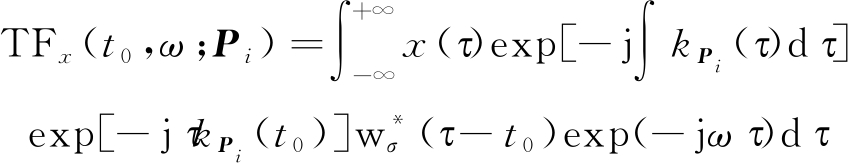
其中kPi(t)表示在第i次迭代中由参数Pi确定的变换核。初始变换时可令核函数kp(t)=0,即采用短时傅里叶变换来得到初始的时频分布;
(2)在时频分布中沿时间轴对频率进行峰值检测可得到信号的时频脊位置,将其作为信号的时频特征的估计值,即
(3)用样条函数对
进行曲线拟合,记拟合所得到的参数为
拟合所得到的曲线作为第i+1次变换的核函数kPi(t);
(4)判断迭代是否终止,判据为
或者i>imax,其中ζ为一小正数。当i=1时,
若判据不成立则转向(1),若成立则输出核函数参数。
分析上节核函数的参数计算过程可知,该过程实际上就是用核函数去拟合原信号时频特征的过程。从另一个角度看,计算所得的核函数可作为原信号时频曲线的一个估计。当天波雷达所接收的信号仅为单模传播的单分量信号(如仅有地杂波或目标信号)时,将核函数减去原信号的固定分量,对其进行积分就可得到污染相位序列的估计值。
当天波雷达接收信号为多分量(单模传播海杂波或者多模传播)信号时,对于单模传播的情形,各个分量的电离层污染相同,则估计出其中一个分量对应的核函数即可;对于多模传播的情形,有可能各传播模式中电离层函数不同,会造成不同传播模式对应分量的时频分布不同,需要逐一估计,逐一校正。
电离层污染校正可归纳如下:
(1)在第l(l=1,2,…)次校正中,记待校正的接收信号为xl(t),l=1时为初始信号x(t),如式(1)所示,采用3.2节中的方法估计xl(t)中最大分量(即时频脊提取时取峰值最大的时频脊)对应的变换核函数,作为其瞬时频率的估计IFl(t);
(2)根据杂波的先验信息,减去杂波的固定频率fB,并积分得到该模式下污染的估计
理想条件下,污染被准确估计,则
(3)解污染操作,解污染后信号为
(4)利用杂波的先验信息,将杂波的从解污染后的信号中滤除,滤除后再与
相乘以避免本次校正对下次污染校正的影响,将
作为下次校正的待校正信号,这里
表示利用先验信息得到的海杂波主要分量估计,为表示方便这里写成信号相减的形式,实际运算中采用滤波器实现;
(5)判断校正是否结束,判据为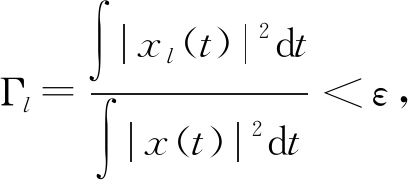
若不成立则转向(1)。
需说明的是,就电离层污染校正而言,在变换核函数参数的估计过程中,关心的并非核函数的参数,而是核函数的时间序列kPi(t),因此,在电离层污染校正的具体运算中,可采用对进行插值的方式得到kPi(t),省去曲线拟合和参数计算的步骤,简化计算流程。整个电离层污染校正流程如图1所示。
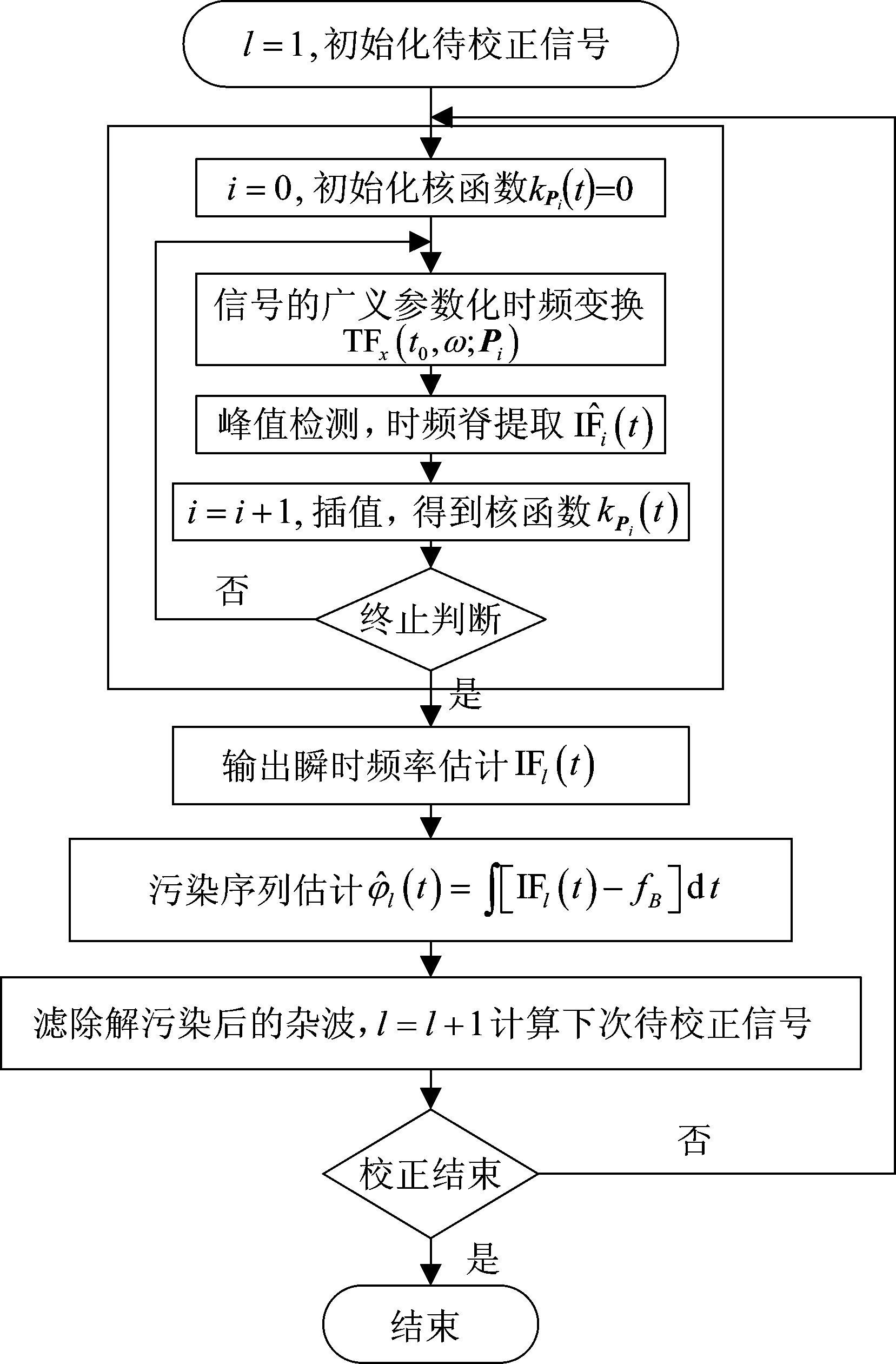
图1 电离层污染校正流程图
Fig.1 Flow chart of ionospheric decontamination
天波雷达电离层污染的校正可锐化接收信号的多普勒谱,以便在多普勒域抑制杂波后进行目标的检测及目标参数的估计。图1的电离层污染校正的过程也是海杂波抑制的过程,其中海杂波的抑制是根据校正后的杂波信号多普勒域特性实现的。回顾广义参数化时频变换的定义式(2),忽略频移因子和窗函数,表示如下:
(3)
从式(3)表达式来看,多模条件下的电离层污染校正中,杂波的滤除等效于在该变换后进行,即先根据估计的污染瞬时相位对信号进行解污染操作,后进行傅里叶变换。从变换的角度来看,解污染操作就等效于将污染后信号在时频域进行旋转,使得信号的瞬时频率平行于时间轴,即使其频率不随时间变化,最终使得信号可在频域达到最好的积累效果。
当待解污染的信号中包含目标信号,式(1)可重写如下:
(4)
其中s(t)表示目标信号。对天波雷达而言,相对杂波,目标信号一般较小,故不会影响到污染校正。由于目标先验信息一般未知,在多次校正后,杂波信号被滤除,仅剩目标和噪声信号。图1校正中,为使多个传播模式的污染不相互干扰,某次校正、滤除杂波后,又将污染因子乘回,这样会导致杂波滤除后的目标信号仍然是污染后的信号,理想情况下,杂波被完全滤除,表示如下:
(5)
进一步分析式(3)所示的变换可知,若核函数与电离层污染的瞬时频率不一致,则变换后的多普勒不会集中。故污染中信号的检测可以采用式(3)的变换,将污染校正中估计得到的各传播模式污染的瞬时频率作为核函数对其进行变换,即可有效的积累目标,提高信噪比。对多个传播模式变换后的信号进行联合检测,即可更可靠的检测目标。
为验证算法的有效性和稳健性设计以下数值仿真实验:
实验1
取天波雷达海面目标探测模式下的典型工作参数[1],脉冲间隔0.2 s,相干积累时间40 s。工作频率取18 MHz,海面入射余角为25°,收发准单基地配置,海杂波的一阶Bragg峰频率
其中g表示重力加速度,Ψ表示入射余角,λ表示波长。为验证算法的性能,假设海杂波仅由两个一阶Bragg峰和噪声组成,即x(t)=2exp(j 2πfB+t)+exp(j 2πfB-t)+n(t),其中fB+, fB-分别表示正负一阶Bragg峰频率,考虑单模传播的情形,加入的相位污染信号φ(t)=Bsin(2πfm1t+φ0),其中B为污染幅度,表征了污染起伏的大小, fm1为污染频率,表征了污染起伏的快慢,取信噪比为30 dB, fm1=0.08 Hz,φ0=0,小幅度污染(B=1)的污染相位估计和污染校正仿真结果如图2所示,为对比污染校正性能,同时给出了两种典型的电离层污染校正方法,最大熵谱法和基于奇异值分解的方法。图2(b)中原信号指的是未污染的信号频谱,其余为加入污染后采用相应校正后的信号频谱。从小幅度污染估计和校正的结果来看,本文方法和基于奇异值分解的方法均能够较好估计污染并校正之,最大熵谱法估计误差较大,校正性能也较差;大幅度污染(B=5)的污染相位估计和污染校正结果如图3所示,其中本文方法仍能以较高的精度估计污染,基于奇异值分解的方法几乎失效,最大熵谱法性能居中。 图2和图3的对比表明了本文方法对污染起伏大小的稳健性。为进一步分析本文方法的稳健性,图4给出了不同信噪比,污染幅度和频率条件下,污染估计绝对误差
的仿真结果。仿真中所取的标准参数组是:信噪比30 dB, fm1=0.08 Hz,B=1,不同条件下,其中一个参数变化。从图4(a)、(b)、(c)的总体变化趋势可以看出:(1)在小幅度污染,高信噪比条件下,基于奇异值分解的方法由于能够更精确地扑捉到污染变化的结构,性能稍优于本文方法,但其稳定性较差,更深入地仿真分析发现,基于奇异值分解的方法在进行信号分析时,需将待分析信号序列按一定规律排成矩阵,因此该分析方法严重依赖于待分析信号不同时间采样点之间的规律性和周期性,因此对频率分量较少、信噪比较高的信号能够较好地扑捉到其时频结构,但当信噪比降低,分析信号采样点之间的周期性被破坏,则该方法对信号时频结构的分析能力急剧下降;(2)最大熵谱法在大信噪比,中等污染频率下,性能稍优于本文方法,见图4(c),但同样稳定性较差,更多地仿真表明在此条件下最大熵谱法的优势并不总是存在,多数情况下与本文方法性能相当;(3)本文方法对污染幅度和频率变化均不敏感,表现出了良好的稳健性,只是在信噪比低于10 dB以下,误差明显增大,稳定性较差,但对于海杂波的情形,海杂波的二阶多普勒峰通常会比一阶Bragg峰值低20～30 dB,而这一区域本文方法性能较好,因此,该现象并不影响方法的适用性。
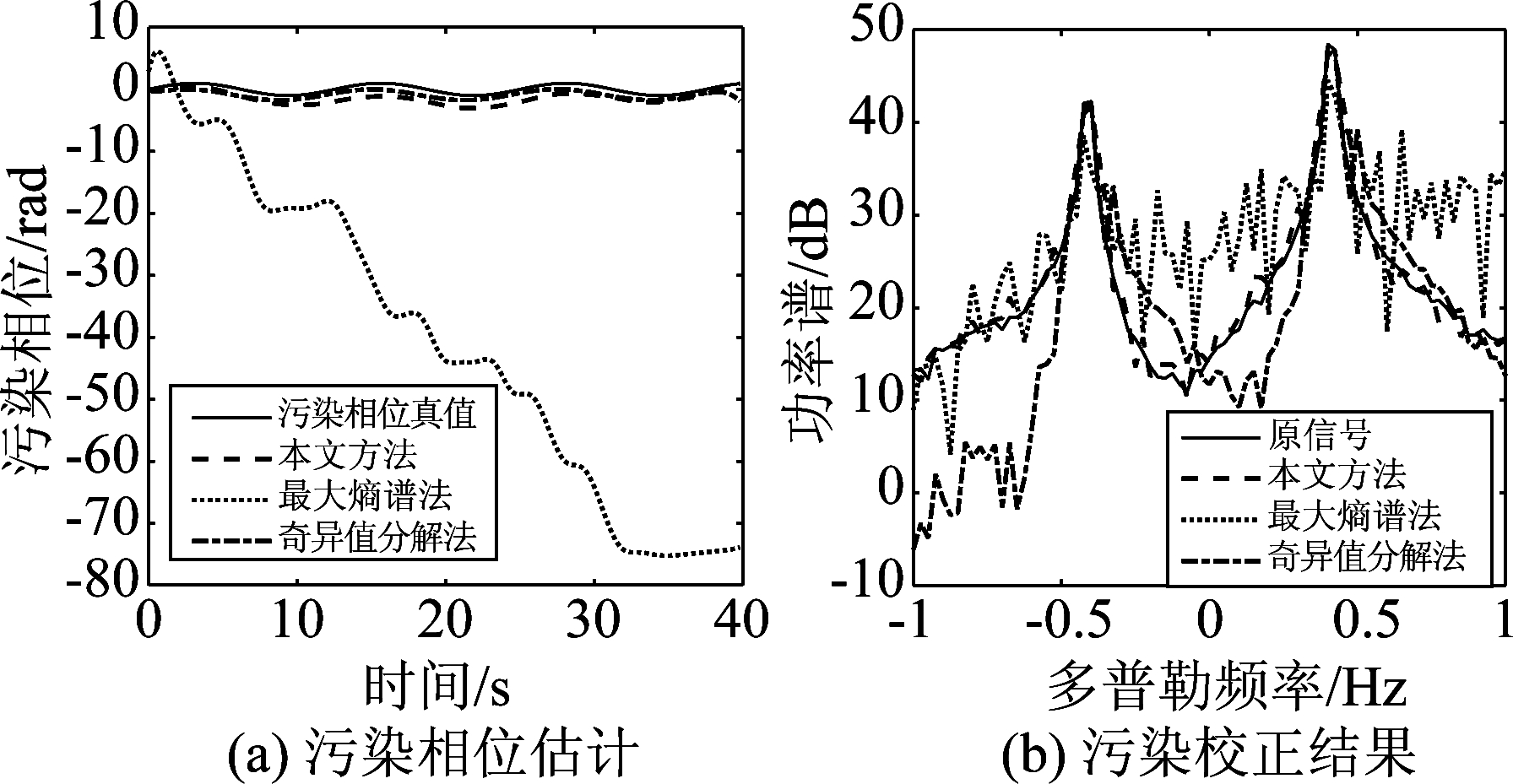
图2 小幅度污染(B=1)的情形下电离层污染估计和校正效果
Fig.2 Estimation and correction in the case of small scale contamination
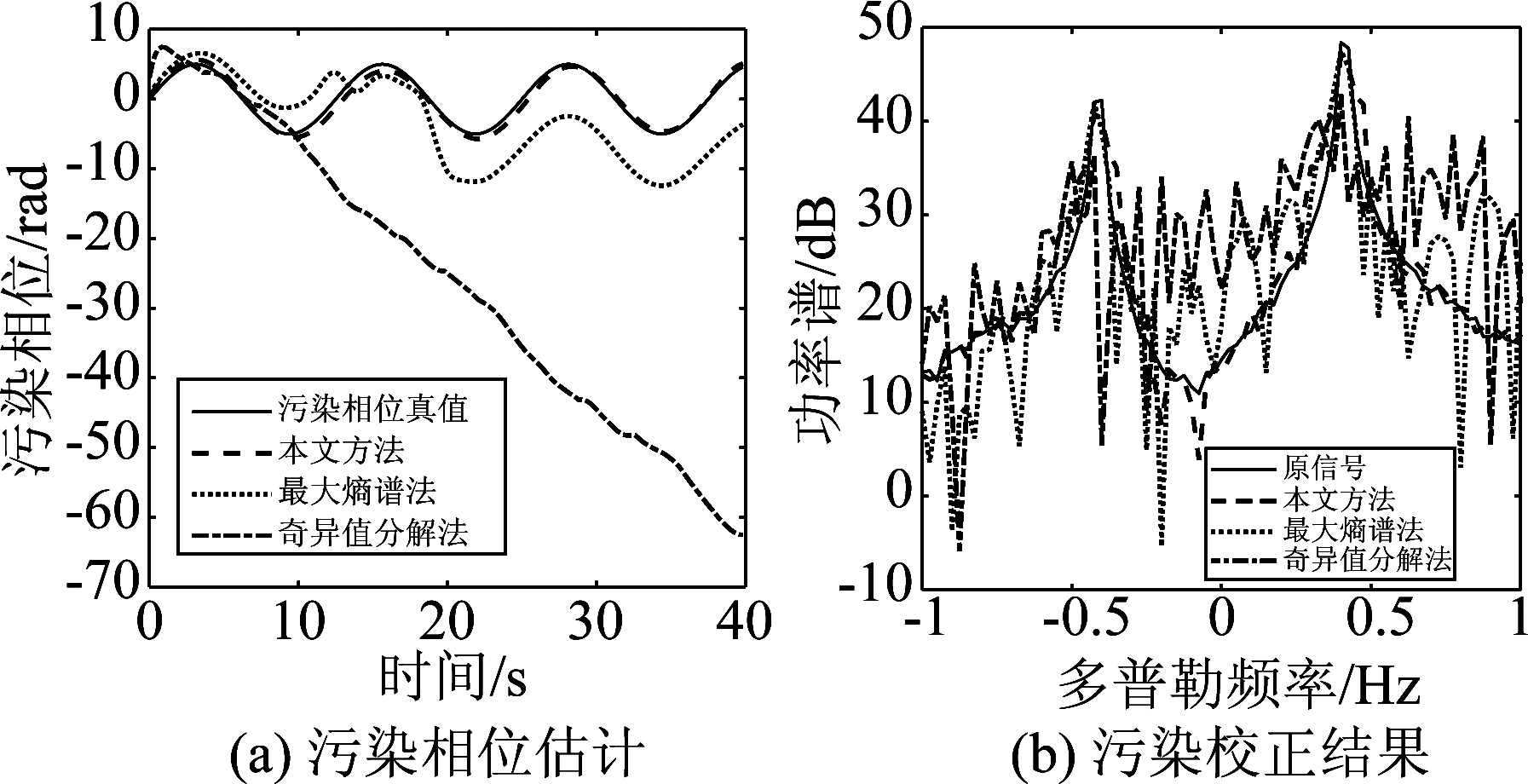
图3 大幅度污染(B=5)的情形下电离层污染估计和校正效果
Fig.3 Estimation and correction in the case of big scale contamination
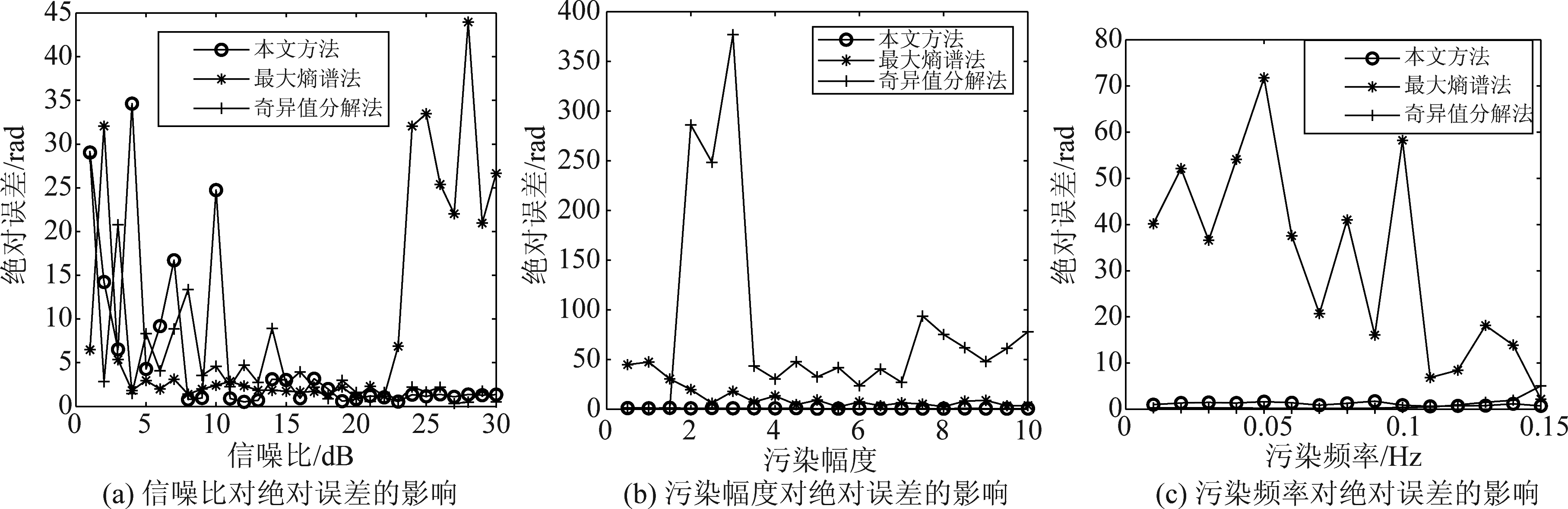
图4 不同信噪比,污染幅度和频率条件下污染估计的绝对误差
Fig.4 Absolute errors of contamination estimation under different SNR, contamination amplitude and frequency
实验2
为更逼真地仿真海杂波,进一步验证本文方法的电离层污染校正性能。这里采用文献[2]中的海杂波仿真方法,这里考虑了二阶及高阶谱峰的影响。仿真中,海面风速设为15 m/s,距离分辨率为7.5 km,半双基地角为0,即单基地的情形,脉冲间隔0.2 s,相干积累时间40 s。工作频率取18 MHz,海面入射余角为25°。杂噪比为30 dB, fm1=0.08 Hz,φ0=0,B=5条件下,电离层相位污染估计和校正结果如图5所示。从图中可以看出,受海杂波二阶和高阶谱的影响,相位污染的估计性能较图3有一定的下降,但本文方法仍能较好地估计和校正污染。图6中不同杂噪比,污染幅度和频率条件下污染估计绝对误差的变化趋势也进一步表明了本文方法的稳健性和性能优势。
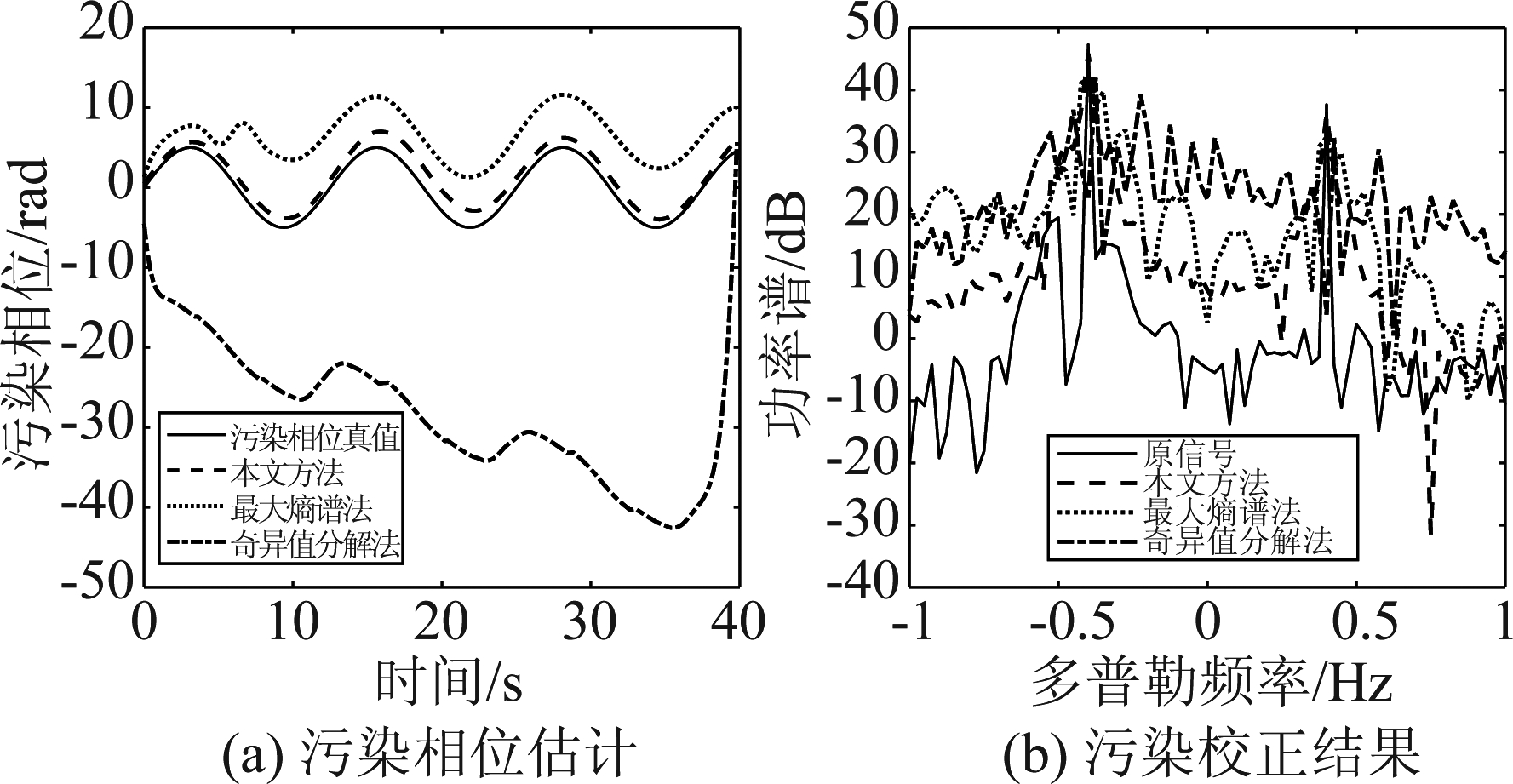
图5 仿真海杂波下电离层污染估计和校正效果
Fig.5 Estimation and correction in the case of simulated sea clutter
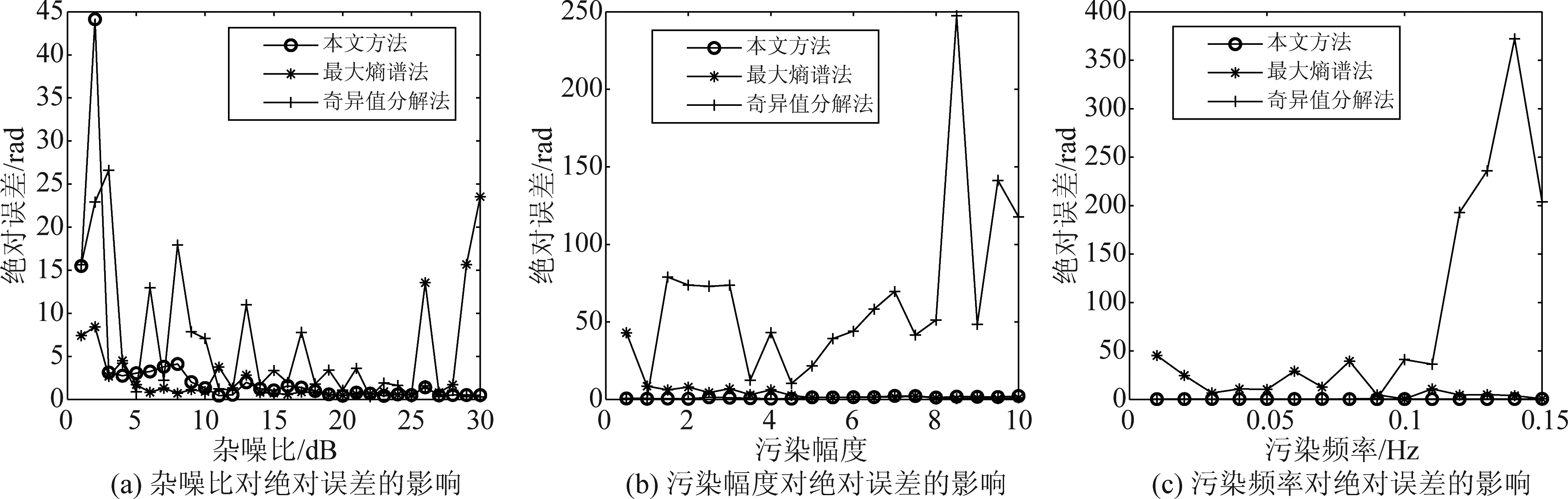
图6 不同杂噪比,污染幅度和频率条件下污染估计的绝对误差
Fig.6 Absolute errors of contamination estimation under different SNR, contamination amplitude and frequency
实验3
仍采用实验2中的海杂波仿真方法,考虑多模传播的情形,为方便起见,设有两个传播模式,两者之间的电离层带来的多普勒频移相差0.2 Hz。实验1和实验2中未考虑电离层带来的频移是因为,频移仅带来频谱的平移,并不会带来展宽效应,只需在展宽校正后,根据海杂波多普勒谱关于零频的对称性,进行搬移即可。仿真中,杂噪比为30 dB,传播模式1的污染参数为B=1, fm1=0.08 Hz,传播模式2的污染参数为B=1, fm1=0.08 Hz。仿真的原信号和污染信号如图7(a)所示,污染校正结果如图7(b)所示。从图中可以看出,按图1的步骤两种传播下的污染均可以被校正,表明了本文方法的有效性。但两者之间的相互影响使得校正的结果较原信号有一定程度的扩展。
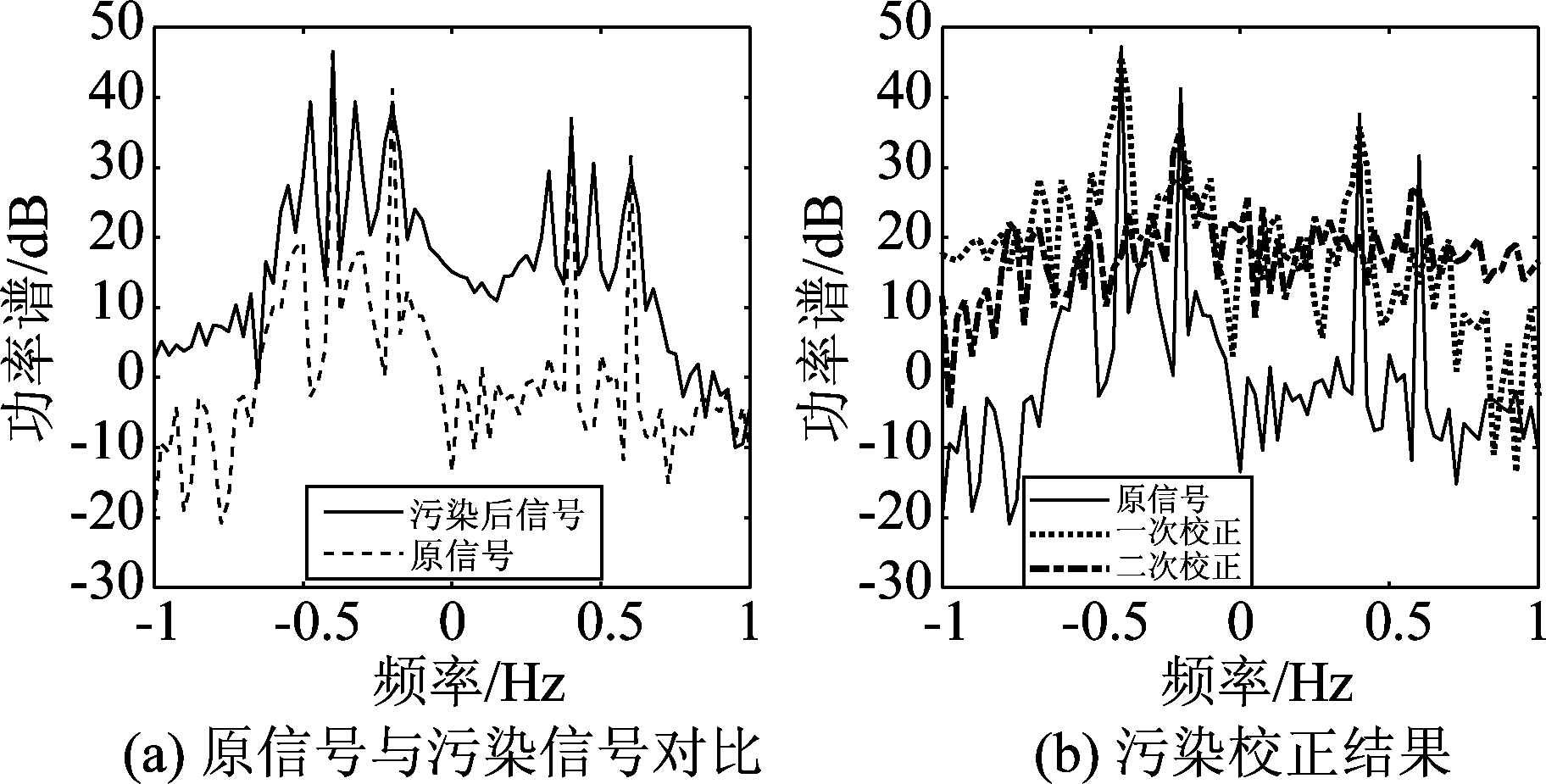
图7 多模条件下的电离层污染校正
Fig.7 Correction in the case of multi-mode contamination
广义参数化时频变换方法可对多分量信号的时频特性进行高精度地分析,且无交叉项等因素的影响,是一类优秀的时频分析方法。本文将其应用于天波雷达电离层污染估计和校正。根据电离层污染的特点选取样条调频小波作为参数化时频变换的核函数,针对电离层污染后的信号估计核函数参数,利用核函数的时频特征量来估计污染序列,构造污染校正算子进行污染校正。对于多模传播条件下的电离层污染,采用校正后滤除的方式,多次迭代完成污染的校正。
污染校正问题,本质上是多分量信号时频分析问题,单模传播条件下,多个分量(海杂波的情形,地杂波为单分量较为简单,兹不赘述)的时频结构具有相似性,且不同分量在时频平面的分布较开,比较容易分离和分别估计。多模传播条件下,多个分量的时频结构不具有相似性,且在时频平面分布较为密集,较难分离和估计,故污染校正性能较差,上节的仿真证明了这一点。关于如何识别多模传播,文献[10]给出了有效的方法,但本文方法通过迭代依次校正污染,是否为多模传播并不影响方法的实际执行。
事实上,本文在变换核参数估计时采用的方法是文献[12]中基于估计参数的多分量分解方法,该方法的分辨力取决于所采用的窗函数长度。更精确地多分量信号分析方法可采用文献[12]中的基于频谱集中性的方法,但该方法需要对核函数参数进行多峰搜索,运算量较大。更高精度的污染校正一方面可以采用该方法或者寻找更好的多分量信号时频分析方法,如同步压缩变换,多重同步压缩变换[13],高阶同步压缩变换[14]等,另一方面可以从分析电离层污染的形成机理出发,跳出时频分析污染校正的窠臼,寻找新的方法,如基于模型的深度学习信号分析和重构方法[15]等。这都将是后续研究的重点之一。
[1] Fabrizio G A. High Frequency Over-the-Horizon Radar: Fundamental Principles, Signal Processing, and Practical Applications[M]. New York: Mc Graw Hill Education, 2013.
[2] 薛永华, 安昕, 王国庆, 等. 分布式多输入多输出天波超视距雷达海杂波仿真[J]. 电波科学学报， 2015, 30(3): 576-582.
Xue Yonghua, An Xin, Wang Guoqing, et al. Distributed MIMO sky-wave over the horizon radar sea clutter simulation[J]. Chinese Journal of Radio Science, 2015, 30(3), 576-582.(in Chinese)
[3] 于文启, 陈建文, 李雪. 天波超视距雷达电离层相位污染时频校正方法综合性能评估[J]. 电子与信息学报， 2018, 40(4): 992-1001.
Yu Wenqi, Chen Jianwen, Li Xue. Comprehensive performance evaluation of ionosphere phase contamination time-frequency correction approaches in over the horizon radar[J]. Journal of Electronics & Information Technology， 2018, 40(4): 992-1001.(in Chinese)
[4] Zhou Qing, Yue Xianchang, Zhang Lan, et al. Correction of ionospheric distortion on HF hybrid sky-surface wave radar calibrated by direct wave[J]. Radio Science， 2019, 54(5): 380-396.
[5] 罗欢, 肖卉. 电离层回波谱展宽机理分析及频谱锐化方法[J]. 物理学报, 2019, 68(21): 308-316.
Luo Huan, Xiao Hui. Analysis of broadening mechanism of ionospheric echo spectrum and spectrum sharpening method[J]. Acta Phys. Sin.， 2019, 68(21): 308-316.(in Chinese)
[6] Bourdillon A, Gauthler F, Parent J. Use of maxmum entropy spectral analysis to improve ship detection by over-the-horizon radar[J]. Radio Sci.， 1987, 22(2): 313-320.
[7] Poon M W Y, Khan R H, Le-Ngoc S. A singular value decomposition (SVD) based method for suppressing ocean clutter in high frequency radar[J]. Signal Processing, IEEE Transactions on， 1993, 41(3): 1421-1425.
[8] Lu Kun, Liu Xingzhao, Liu Yongtan. Ionospheric decontamination and sea clutter suppression for HF skywave Radars[J]. IEEE Journal of Oceanic Engineering， 2005, 30(2): 455- 462.
[9] Luo Huan. Ionospheric Decontamination Method Based on Optimization Criteria in Over-the-Horizon Radar[J]. Journal of Communications Technology and Electronics， 2019, 64(11).
[10] 李雪. 电离层相位污染及多模传播抑制方法研究[D]. 哈尔滨： 哈尔滨工业大学, 2012.
Li Xue. Research on Ionospheric Phase pollution and multimode propagation suppression[D]. Harbin: Harbin Institute of Technology, 2012.(in Chinese)
[11] Yang Yang, Peng Zhike, Dong Xingjian, et al. General Parameterized Time-Frequency Transform[J]. Signal Processing, IEEE Transactions on, 2014, 62(11): 2751-2764.
[12] 杨扬. 参数化时频分析理论、方法及其在工程信号分析中的应用[D]. 上海: 上海交通大学, 2013.
Yang Yang. Theory, methodology of paramererized time-frequency analysis and its application in engineering signal processing[D]. Shanghai: Shanghai Jiaotong University, 2013.(in Chinese)
[13] Yu Gang, Wang Zhonghua, Zhao Ping. Multisynchrosqueezing Transform[J]. IEEE Transactions on Industrial Electronics, 2019, 66(7): 5441-5455.
[14] Liu Wei, Cao Siyuan, Wang Zhiming, et al. A Novel Approach for Seismic Time-Frequency Analysis Based on High-Order Synchrosqueezing Transform[J]. IEEE Geoscience and Remote Sensing Letters, 2018, 15(8): 1159-1163.
[15] Aggarwal H K, Jacob M. J-MoDL: Joint Model-Based Deep Learning for Optimized Sampling and Reconstruction[J]. IEEE Journal of Selected Topics in Signal Processing, 2020, 14(6): 1151-1162.
薛永华 男, 1985年生, 山西霍州人。海军航空大学讲师, 博士, 研究方向为天波超视距雷达信号仿真、雷达发射波形设计、海杂波中微弱目标检测。
E-mail: xueyhchina@163.com
陈小龙 男, 1985年生, 山东烟台人。海军航空大学副教授, 博士。研究领域包括雷达动目标检测、海杂波抑制、雷达信号精细化处理等。
E-mail: cxlcxl1209@163.com
黄 勇 男, 1979年生, 湖南汨罗人。海军航空大学副教授, 博士, 硕士生导师, 研究方向为雷达海上目标检测。
E-mail: huangyong_2003@163.com
张 林 男, 1986生, 山东烟台人。海军航空大学副教授, 博士, 研究方向为信号检测与估计。
E-mail: zhanglin4402@163.com