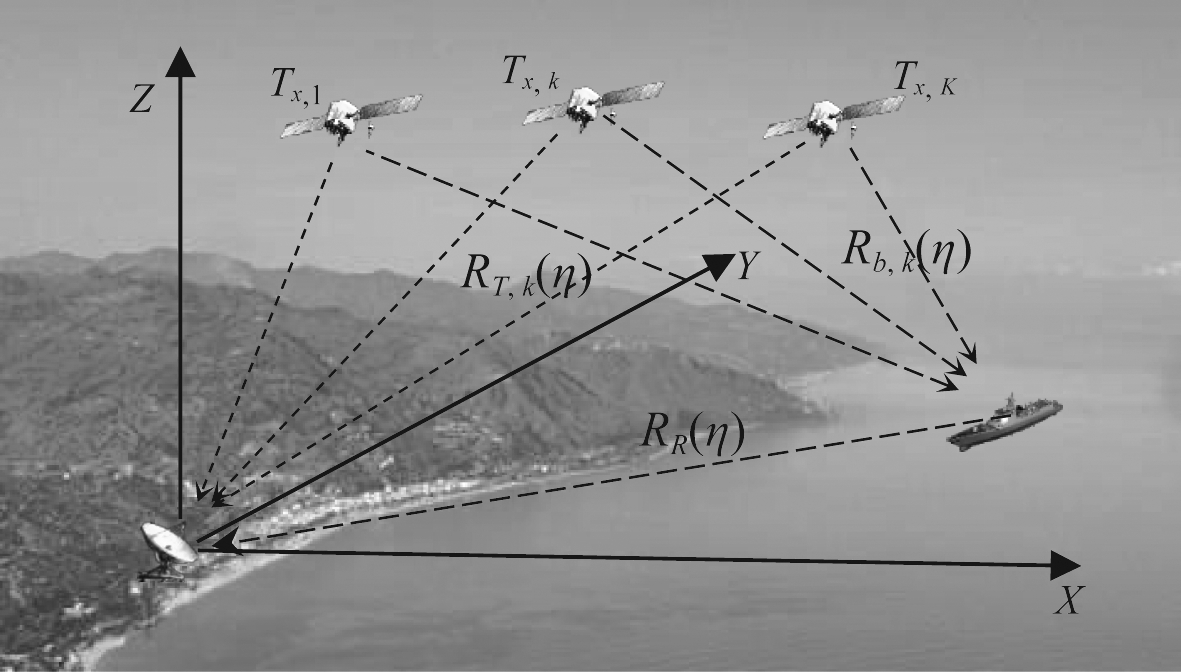
图1 基于北斗卫星的无源多基雷达几何配置
Fig.1 Beidou-based passive multistatic radar geometry
Reference format: Huang Chuan, Li Zhongyu, Zhang Lijun, et al. A Maritime Moving Target Detection and Localization Method for Passive Multistatic Radar[J]. Journal of Signal Processing, 2020, 36(12): 2016-2023. DOI: 10.16798/j.issn.1003- 0530.2020.12.007.
为实现对海洋资源的可靠保护与利用,可利用雷达这一有效探测手段,对海面区域进行有效监测,目前在该领域已有多方面研究[1- 4]。海面运动目标检测是其中的关键方向之一。为实现长时间、低成本、高隐蔽的运动目标检测,可利用无源雷达对海面监测区域进行持续照射。目前,无源雷达相关研究大多以FM信号、数字广播电视信号等地面信号作为辐射源[5- 6]。然而,由于其主要覆盖陆地区域,并不适用于远海区域监测。为突破这一限制,可利用卫星辐射源构成无源雷达,拓展辐射源覆盖范围。目前在轨的卫星中,北斗卫星导航系统由于其全球覆盖的特性,可为海面监测提供长时间、大范围、稳定可靠的信号来源。同时,由于地面任一点同时被北斗系统中的4~8颗卫星所覆盖,雷达接收机可同时接收来自不同卫星的辐射信号,构成无源多基雷达,通过多源回波信号处理,有效提升观测区域内目标检测性能,并提供更多目标信息[7]。
然而,北斗卫星播发信号在地球表面功率密度极低,其典型值为-135 dBW/m2[8],为以此为辐射源的无源雷达海面运动目标检测带来了困难。为提升目标回波信噪比,可对目标区域进行长时间观测并进行回波能量积累。然而,长时间目标回波存在非相干的特性[9],且卫星与目标的运动将在回波中引入不可忽略的距离徙动与多普勒徙动。对此,文献[10]提出了一种基于分数傅里叶变换(FrFT)的多帧积累方法,利用Keystone变换去除一阶距离徙动,在分帧处理后,利用FrFT实现帧内信号的相干积累,并在多普勒补偿后实现帧间信号的非相干积累。文献[11]同样将长时间目标回波分为多帧,忽略帧内信号的距离徙动与多普勒徙动,通过方位傅里叶变化在距离-多普勒域实现相干积累,并补偿帧间信号的峰值偏移,实现长时间能量积累。为进一步提升目标回波能量,可综合不同北斗卫星辐射下的多源回波,实现目标回波空间积累。然而,由于不同卫星位置与运动的差异,多源回波具有不同的距离历史,进而导致回波间存在不同的多普勒参数。对于无源多基雷达系统,文献[12]利用距离-多普勒域内长时间积累峰值获取不同卫星辐射源下的双基距离,并根据多点定位技术,结合已知卫星位置计算得到目标位置。文献[13]在文献[11]的基础上,将辐射源-目标-接收站表示的双基距离与多普勒变量转换为目标-接收站所表示的单基距离对应多普勒,在单基距离-多普勒域表示各目标回波长时间积累结果,并通过叠加多源回波积累结果,实现目标回波空间积累。
本文提出了一种无源多基雷达海面运动目标检测与定位方法,克服了以北斗卫星为辐射源时接收海面运动目标回波信号信噪比极低的问题。首先,利用距离反转-方位伸缩变换(RRAST)实现了距离徙动校正和多源回波多普勒质心均衡;然后,利用去调频积分变换(DcIT)去除多普勒徙动,实现单个回波的长时间有效积累;接着,非相干叠加多源回波积累结果,实现目标回波空间积累,进一步提高信噪比,实现海面运动目标的有效检测;最后,将来自不同北斗卫星的目标回波均映射到目标运动参数域,估计运动目标的位置和速度。仿真实验验证了本方法的有效性。
在海上背景中,基于北斗卫星辐射源的无源多基雷达几何配置如图1所示。考虑K颗北斗卫星作为辐射源,Tx,k是第k颗北斗卫星(k=1,2,3,…,K),Rx是位于海岸的静止雷达,Rb,k是Tx,k与Rx的基线,RR和RT,k分别是Rx和Tx,k到目标的距离。

图1 基于北斗卫星的无源多基雷达几何配置
Fig.1 Beidou-based passive multistatic radar geometry
北斗卫星发射信号将测距码和导航电文通过正交相移键控(QPSK)方式调制在载波上,表示为:
s(t)=A·C(t)·D(t)·exp(j 2πfct+φ0)
(1)
其中,A表示信号振幅;D表示导航电文;fc表示信号载频,φ0表示初始相位;C表示测距码,其为伪随机码。
接收站雷达配备有两个天线,即参考天线和监视天线,分别用于接收直达波和目标回波。接收到的直达波和目标回波为连续波,可根据测距码码长所对应时长为等效脉冲重复周期(PRI),对连续接收的回波进行时域二维划分。利用直达波生成参考信号[14],将该参考信号与目标回波进行互相关处理后,得到距离脉冲压缩信号为:
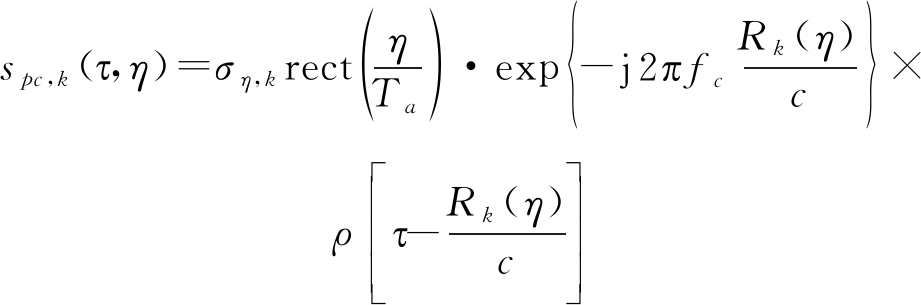
(2)
其中,τ和η分别表示距离向时间和方位向时间;ση,k为目标的复散射系数;Ta为目标观测时间;c为光速;fc为载波频率;ρ(·)为回波信号与参考信号的互相关函数,北斗信号对应互相关结果为三角波;Rk(η)=RR(η)+RT,k(η)-Rb,k(η)为双基距离历史,二阶泰勒展开为:
(3)
其中,R0,k是参考时刻的双基距离;λ是波长;![]() 分别表示多普勒质心和多普勒调频率。
分别表示多普勒质心和多普勒调频率。
将式(2)进行距离向傅里叶变换,得到:
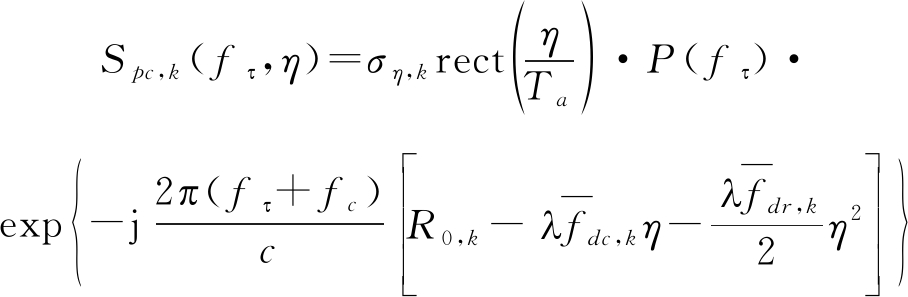
(4)
其中, fτ是距离向频率,P(·)是ρ(·)的傅里叶变换。
如图1所示建立接收站本地坐标系,以固定接收站为坐标原点,接收站视线方向为X轴正方向,Z轴与地球法线方向重合,向上为正,Y轴满足右手坐标系。在该坐标系下,设目标在参考时刻的位置矢量为RTg,速度矢量为vTg。第k颗北斗卫星的轨迹可由位置矢量为RT,k,速度矢量vT,k,加速度aT,k近似表示。则双基距离历史表示为:
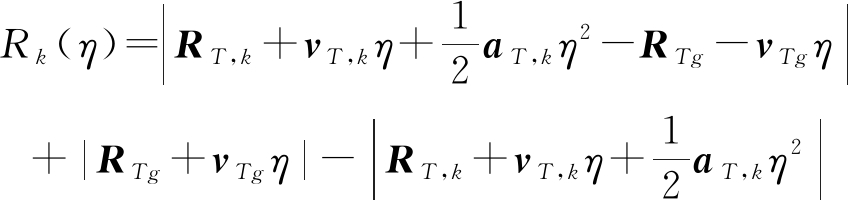
(5)
目标回波的多普勒参数表达式为:
![]()
![]()
|RTg|-1·RTgvTgT-|RT,k|-1·RT,kvT,kT}
(6)
![]()
![]()
|PT,k-PTg|-1·[|vT,k-vTg|2+(PT,k-PTg)aT,kT]+
|PT,k|-3·(PT,kvT,kT)2-|PT,k|-1·(|vT,k|2+PT,kaT,kT)-
|PTg|-3·(PTgvTgT)2+|PTg|-1·|vTg|2}
(7)
其中,|·|是向量取模,(·)T是向量转置。
由于卫星到接收站的距离远远大于目标到接收站的距离,且卫星速度远远大于目标速度,式(7)可近似表示为:
(8)
其中,![]() 是目标切向速度,θ是RTg和vTg的夹角。由式(8)可知,不同卫星辐射源对应的目标回波多普勒调频率
是目标切向速度,θ是RTg和vTg的夹角。由式(8)可知,不同卫星辐射源对应的目标回波多普勒调频率![]() 仅与目标位置和切向速度有关,而与作为辐射源的北斗卫星无关。故不同北斗卫星辐射下的同一目标回波具有相等的多普勒调频率值,即
仅与目标位置和切向速度有关,而与作为辐射源的北斗卫星无关。故不同北斗卫星辐射下的同一目标回波具有相等的多普勒调频率值,即![]()
由于海面运动目标与北斗卫星的运动,双基距离随方位向时间变化,造成距离徙动。由式(4)可知,距离徙动可解释为距离向频率与方位向时间的耦合。其中, fτ与η的耦合造成距离走动, fτ与η2的耦合造成距离弯曲。在典型卫星及目标运动参数条件下,仿真得到三颗北斗卫星辐射下的海面运动目标回波的双基距离历史如图2所示。可以发现,在长观测时间下,目标回波距离徙动不可忽略。同时,不同北斗辐射源对应的距离徙动存在差异。
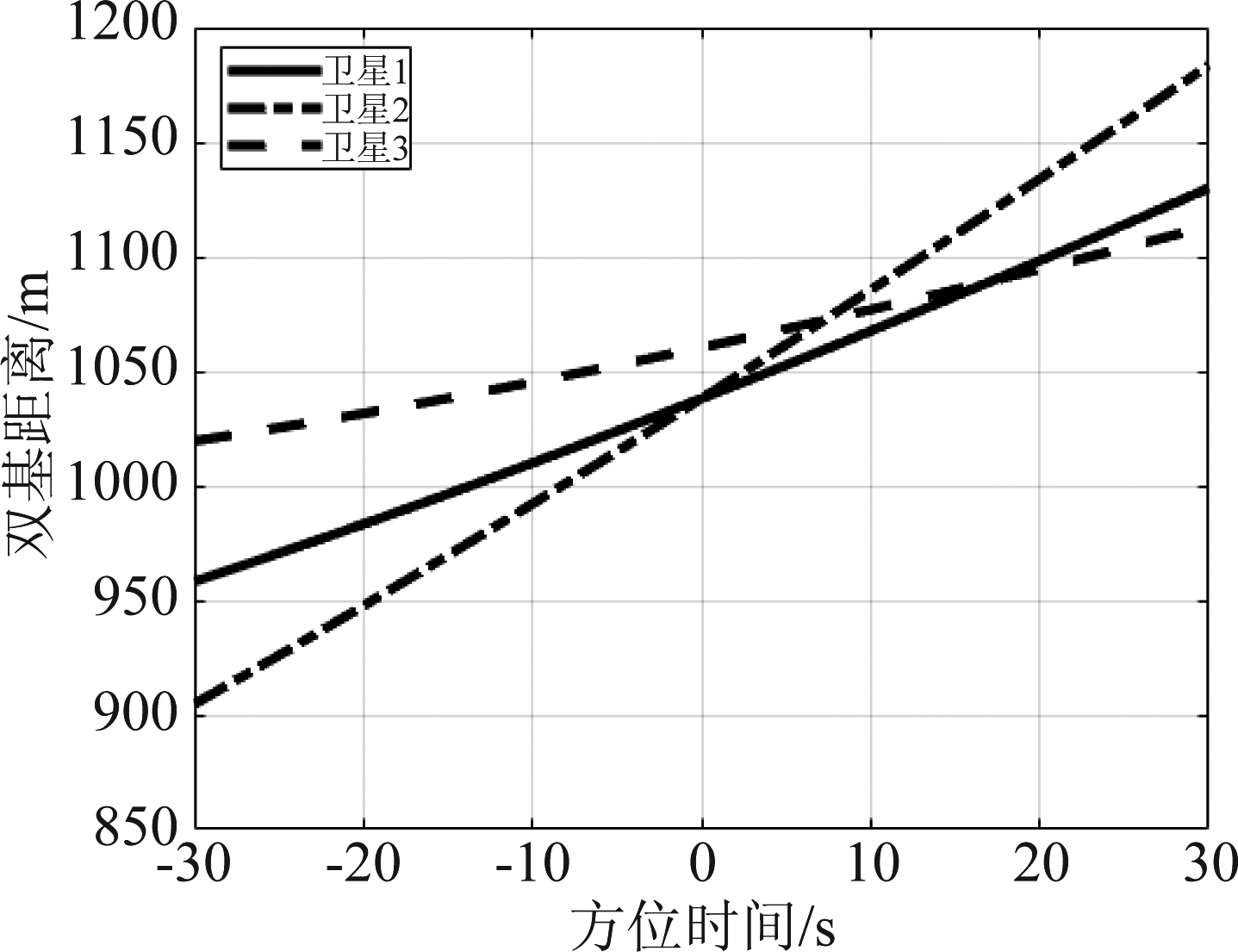
图2 多颗北斗卫星对应的距离徙动
Fig.2 Range migrations pertaining multiple Beidou satellites
在上述运动参数下,进一步可得到回波的多普勒历程,其结果如图3所示。可以发现,在长观测时间下,目标回波多普勒徙动远超其分辨单元。同样,不同北斗辐射源对应的多普勒徙动存在差异,即多源回波具有不同多普勒参数。
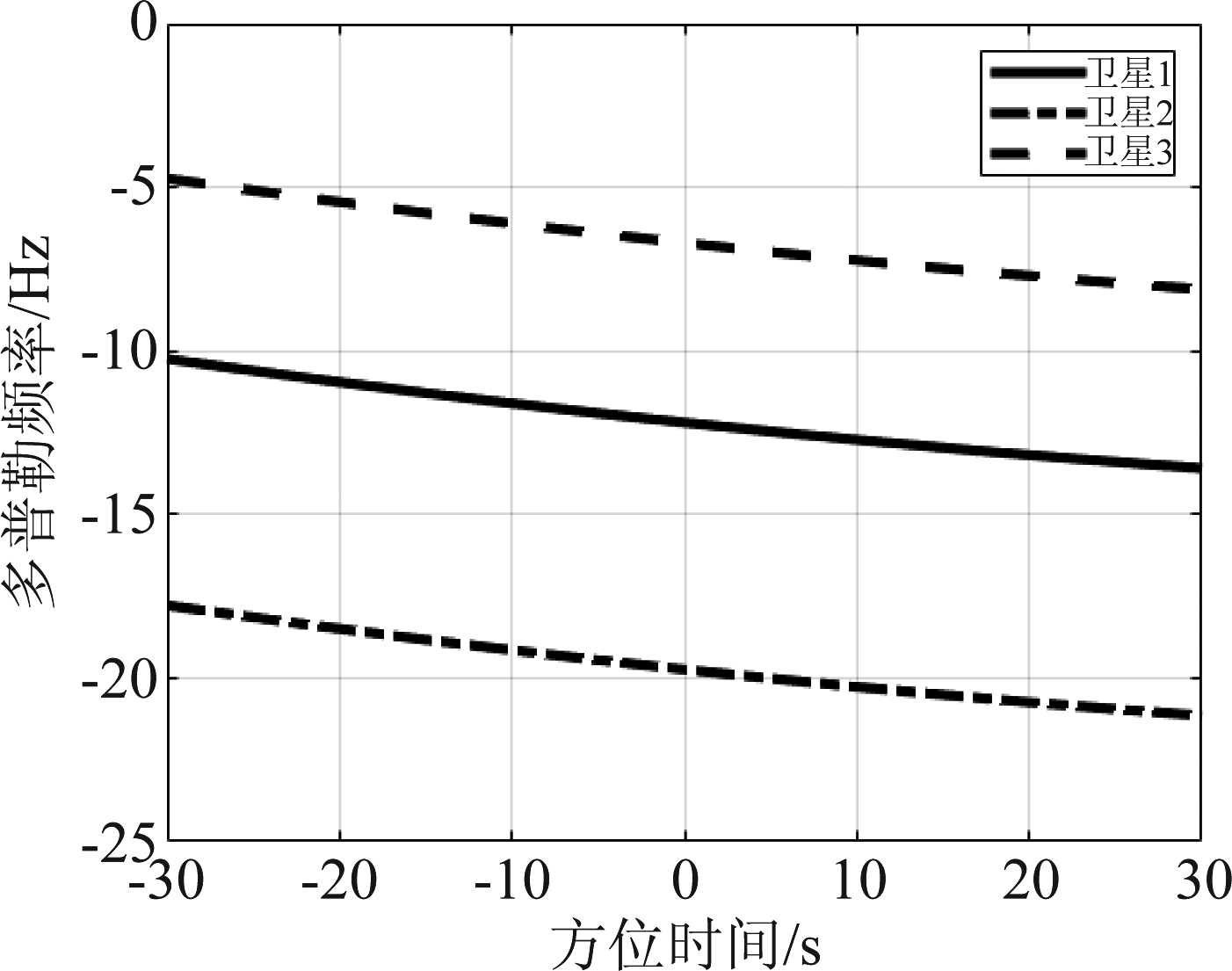
图3 多源回波对应的多普勒徙动
Fig.3 Doppler migrations pertaining multistatic echoes
为进一步展示回波间多普勒参数的差异,根据式(5)与式(6),计算上述多源回波所对应的多普勒质心和多普勒调频率值,结果如图4所示。由图4可知,不同北斗卫星辐射下的目标回波对应的多普勒质心不同,但其多普勒调频率几乎不变,这与式(8)得到的结果一致。
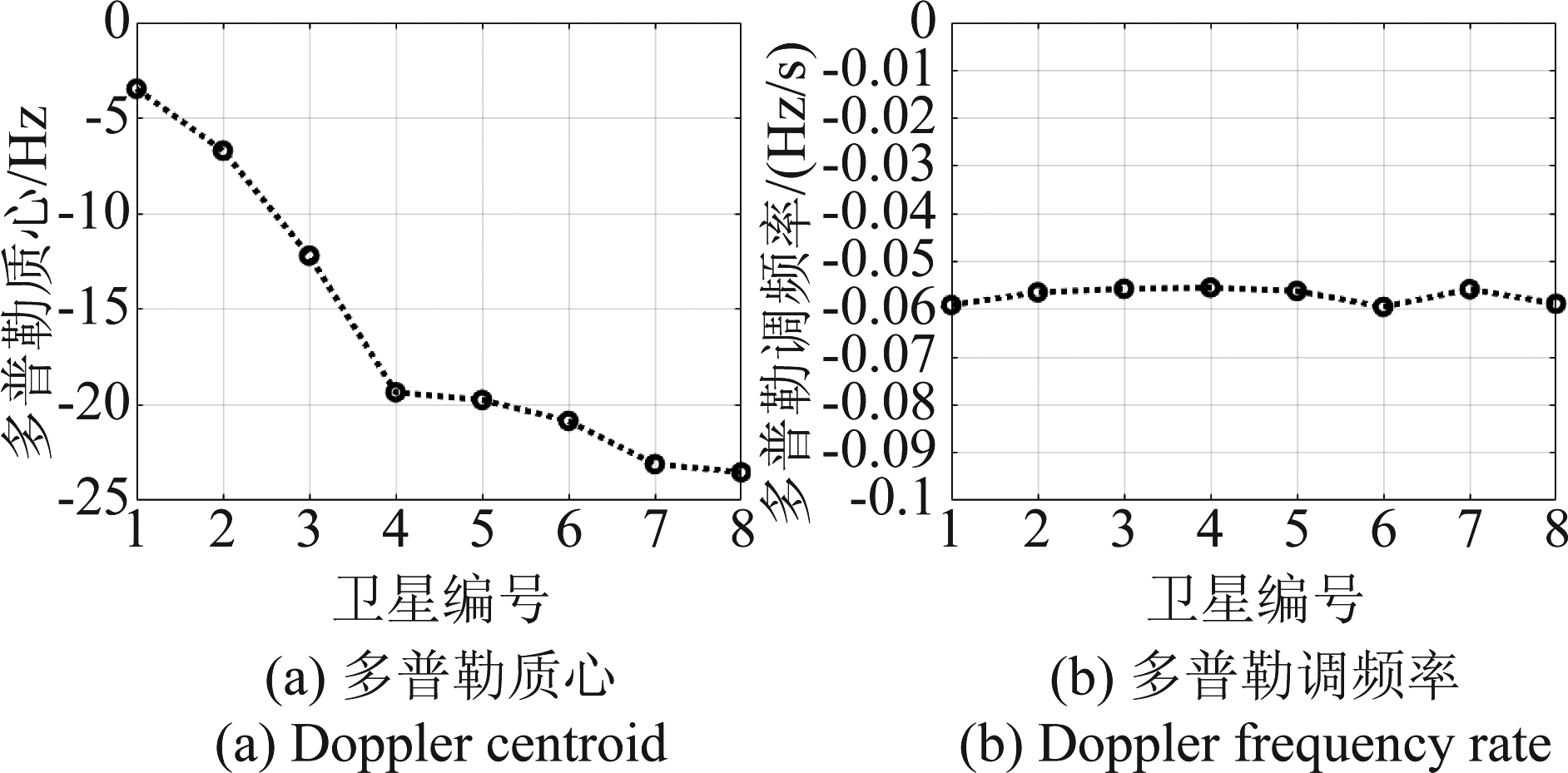
图4 多源回波多普勒参数
Fig.4 Doppler parameters of multistatic echoes
综合上述分析,在长观测时间条件下,目标回波存在不可忽略的距离徙动与多普勒徙动,将严重影响单个回波长时间积累效果;在多辐射源条件下,多源回波多普勒调频率近似相同,但多普勒质心存在较大差异,为多源回波空间积累带来困难。
本文首先提出RRAST,对不同北斗卫星辐射下的回波均进行该变换,实现各独立回波的距离徙动精确校正,并实现多源回波的多普勒质心均衡。RRAST在距离频率-方位时域进行,其表达式为:
(9)
将式(7)应用于式(4),可得到:
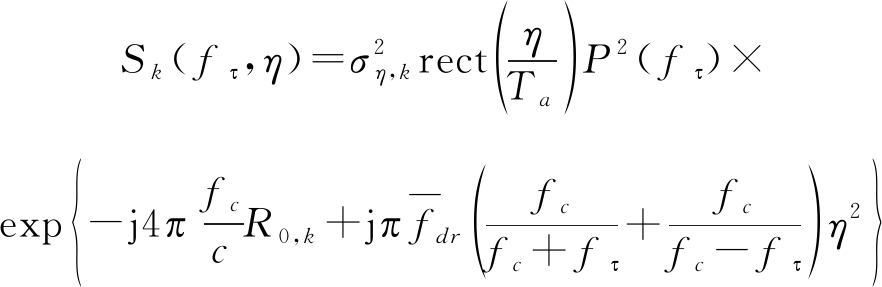
(10)
由于fc≫fτ,通过化简可得到:
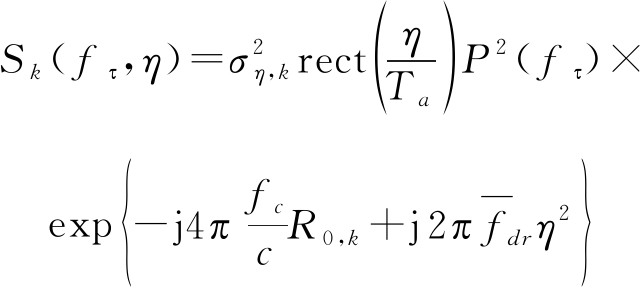
(11)
对式(11)进行距离向傅里叶反变换,可以得到二维时域信号:
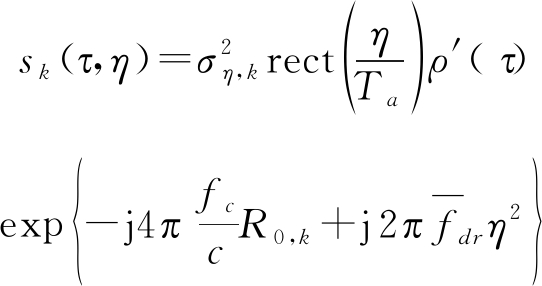
(12)
其中,ρ′(·)是P2(·)的傅里叶反变换结果。
由式(12)可知,通过RRAST完全去除了信号的距离徙动,使得信号的能量聚集于同一距离门,且该距离门已知,为τ=0。故可在该距离门沿方位向取出一维信号,将二维时域回波变换到一维。一维方位信号表示为:
(13)
根据式(13)可知,该方位信号的指数项中不含η的一次项,即通过RRAST同时将信号的多普勒质心置为零。
在长观测时间条件下,由于复散射系数的变化,不能直接对目标回波沿方位向进行相干积累。为保障足够的方位积累效果,可对取出的方位信号进行分帧处理。帧内信号可认为其复散射系数恒定,故可进行相干积累。若每帧信号时长为Tfra,故可将整个方位信号分为N帧(N=Ta/Tfra),其中第n帧(n=-(N-1)/2,...,(N-1)/2)信号表示为:
(14)
其中,σn,k为第n帧的复散射系数。
接着对帧内信号进行DcIT处理实现信号相干积累,该处理公式表示为:
Sn,k(fdr)=![]() sn,k(η)·exp{-j 2πfdrη2}dη
sn,k(η)·exp{-j 2πfdrη2}dη
(15)
将式(14)带入式(15),得到第n帧信号的相干积累处理结果为:
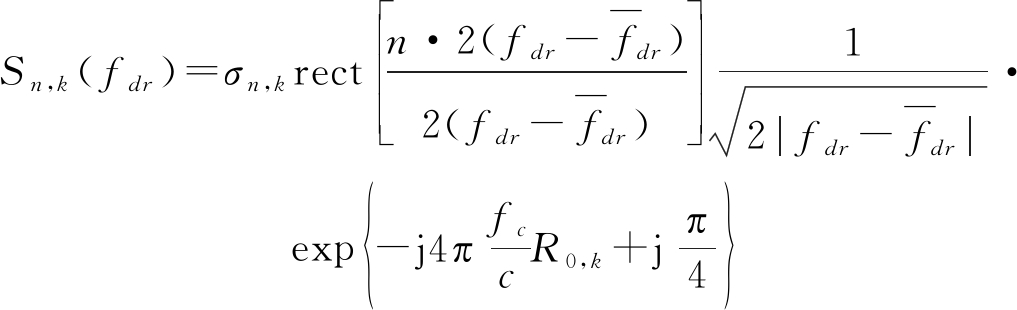
(16)
根据式(16)可知,通过DcIT处理可将帧内信号的能量在多普勒调频率域相干积累到![]() 处。同时,该相干积累峰值位置不随帧数变化,故不需要进行任何补偿操作,直接非相干叠加多帧信号积累结果即可完成目标回波长时间积累,即:
处。同时,该相干积累峰值位置不随帧数变化,故不需要进行任何补偿操作,直接非相干叠加多帧信号积累结果即可完成目标回波长时间积累,即:
(17)
最后,为进一步提高目标的检测性能,将来自多颗北斗卫星的独立回波均按上述处理进行长时间积累,并非相干叠加对应积累结果,完成目标回波空间积累。由于多源回波多普勒调频率值近似相等,故空间积累前无需进行补偿操作。空间积累公式表示为:
(18)
通过上述空时联合积累,提高了目标回波的信噪比,可实现海面运动目标的有效检测。同时,根据积累峰值位置,可提取目标回波的多普勒调频率值![]() 利于后续目标定位处理。
利于后续目标定位处理。
为进一步确定海面运动目标的位置,可将脉冲压缩后的多源回波投影至目标运动参数域(X-Y-VR)中。
可以认为海面运动目标位于图1所示坐标系中的X-O-Y平面内,将X-O-Y平面的观测区域划分为多个网格,每个网格的位置表示为(x,y,0)。进而可以得到网格到接收站的距离![]() 和观测角度θ=arctan(y/x)。根据检测结果所得多普勒调频率值
和观测角度θ=arctan(y/x)。根据检测结果所得多普勒调频率值![]() 从而可以计算得到不同空间位置对应的切向速度值νt,即
从而可以计算得到不同空间位置对应的切向速度值νt,即
(19)
接着,设置一组径向速度值νr,根据已得到的切向速度值νt和观测角度θ,可得到同一空间坐标系下的速度矢量(νx,νy,0),表示为:
(20)
根据位置矢量(x,y,0)和速度矢量(νx,νy,0),可以得到目标的运动轨迹,进而得到在当前位置(x,y,0)与速度νr条件下,不同卫星对应的双基距离历史![]() 在不同方位时刻,根据估计距离历史,即可从中的二维信号spc,k(τ,η)提取对应距离的回波,得到方位信号:
在不同方位时刻,根据估计距离历史,即可从中的二维信号spc,k(τ,η)提取对应距离的回波,得到方位信号:
(21)
然后,对所取出的方位信号进行能量积累。同样,将该方位信号分为N帧,第n帧信号表示为![]() 帧内信号根据所估计距离历史
帧内信号根据所估计距离历史![]() 进行相位补偿,完成相干积累,并对帧间信号进行非相干叠加,完成长时间信号能量在目标运动参数域的积累。其中,相干积累公式表示为:
进行相位补偿,完成相干积累,并对帧间信号进行非相干叠加,完成长时间信号能量在目标运动参数域的积累。其中,相干积累公式表示为:
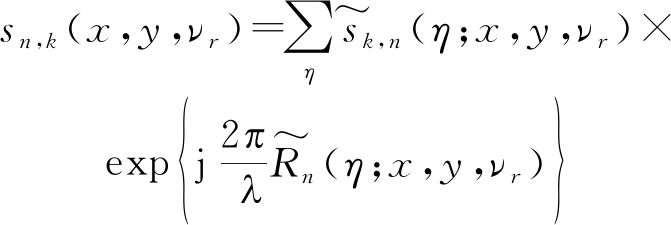
(22)
非相干积累公式表示为:
(23)
对X-Y-VR空间中的所有网格点进行上述处理,实现单个回波在X-Y-VR空间的映射,完整投影过程如图5所示。在X-O-Y平面内存在一组网格点对应于同一参考双基距离(即等距离线),在多普勒调频率确定的情况下,该等距离线上的点可找到对应的径向速度VR值恰满足二维时域中的回波轨迹,故在X-Y-VR空间中存在多个网格点对应于同一回波轨迹的情况。
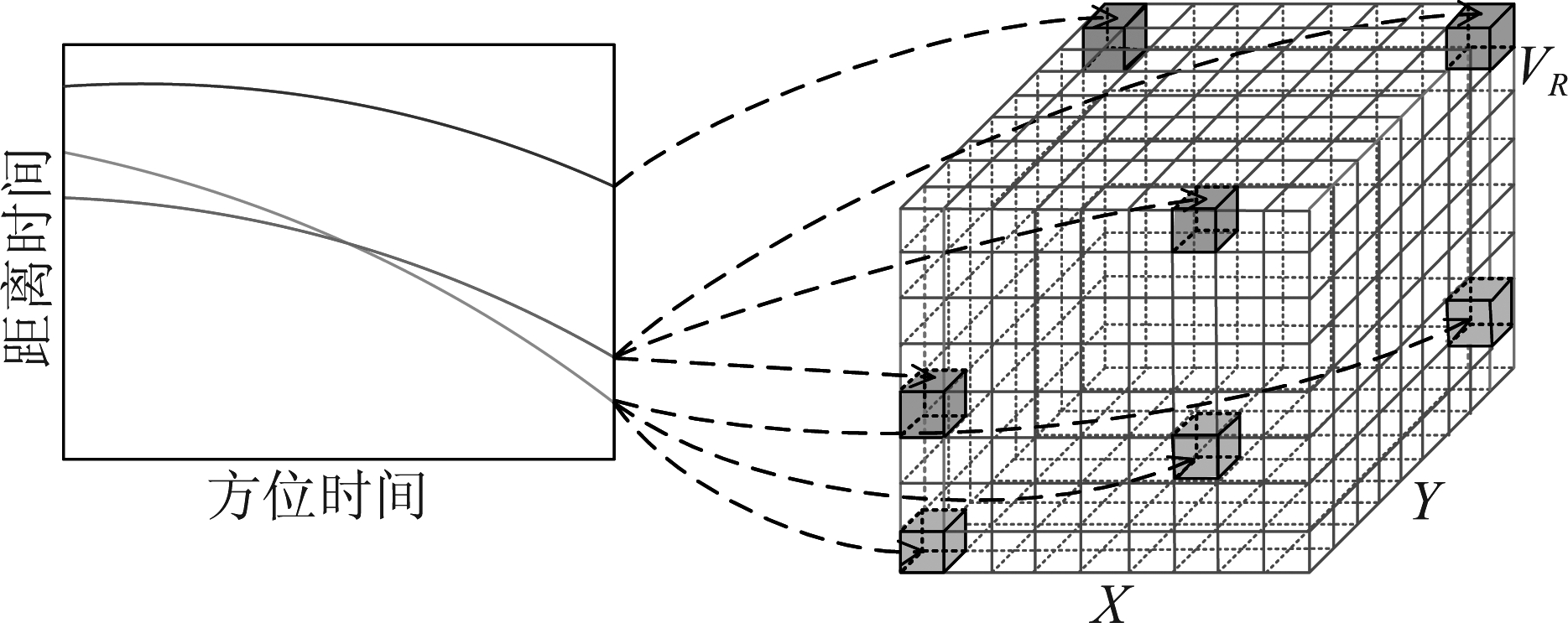
图5 单个回波X-Y-VR空间投影示意图
Fig.5 X-Y-VR domain projection of a single echo
最后,对多源信号的在目标参数域的投影结果进行非相干积累,表示为:
(24)
多源回波在X-Y-VR空间内的投影示意图如图6所示。由于不同北斗卫星对应X-O-Y平面内的等距离线方向存在差异,仅目标真实位置处始终经过不同卫星所对应等距离线,故可根据X-Y-VR空间中的峰值位置得到运动目标的位置矢量与速度矢量。
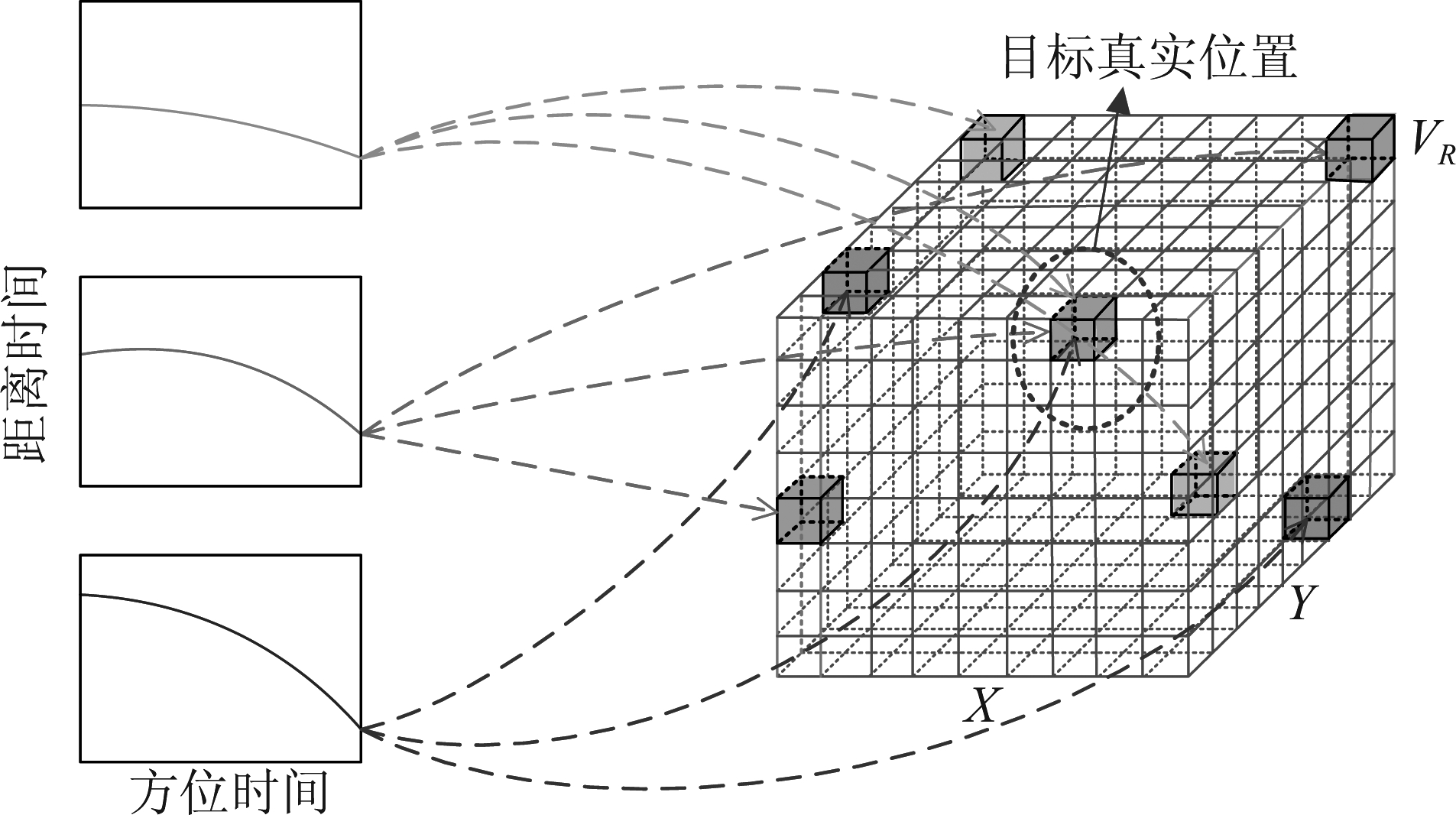
图6 多源回波X-Y-VR空间投影示意图
Fig.6 X-Y-VR domain projection of multistatic echoes
由上述分析可得,本文给出的基于多颗北斗卫星的海面运动目标检测与定位算法流程如图7。
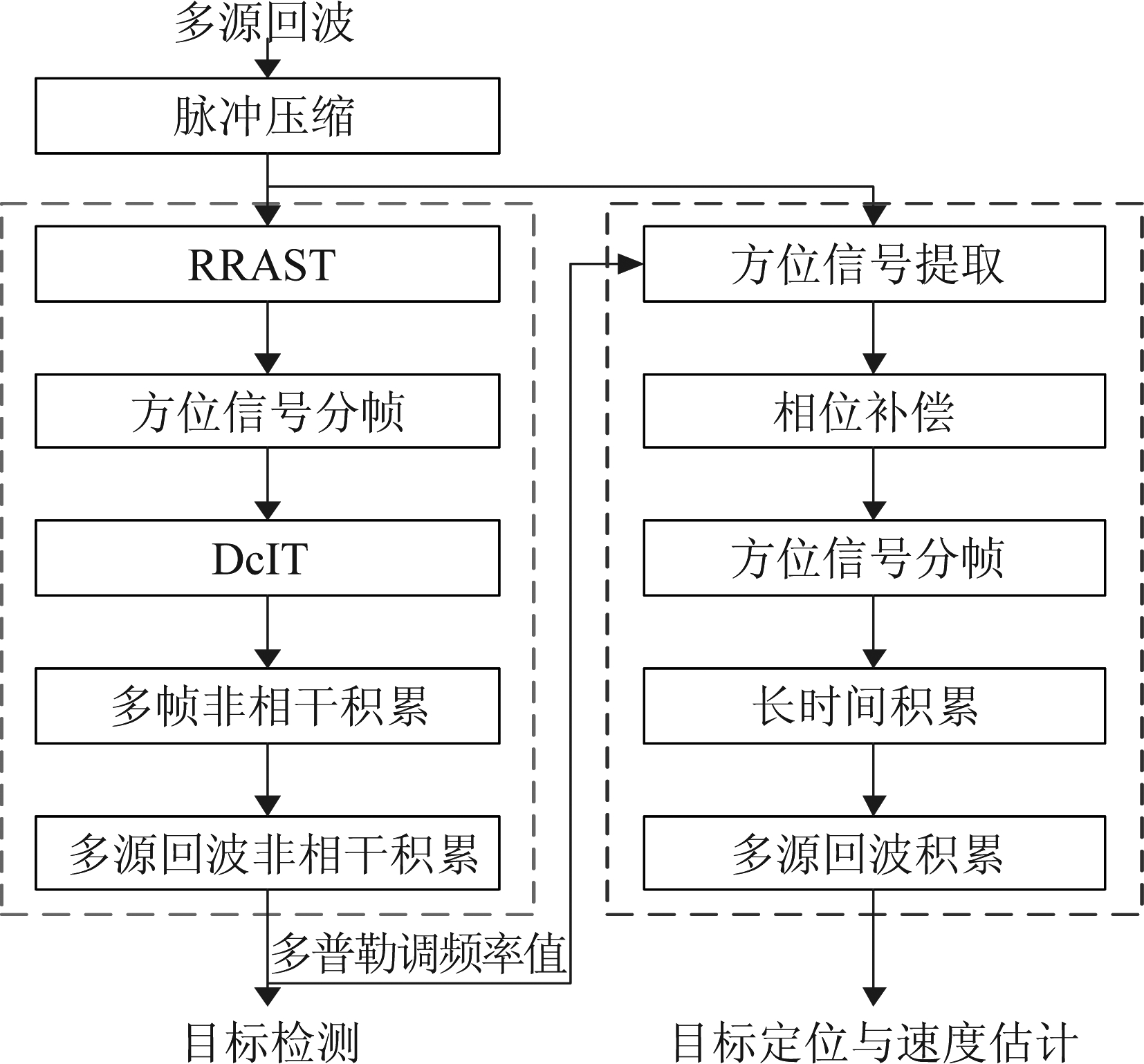
图7 海面运动目标检测与定位处理流程图
Fig.7 The flowchart of the proposed maritime moving target detection and localization method
仿真中选用5颗北斗卫星作为辐射源,其发射的B3I信号由地面静止接收站接收。仿真参数如表1所示。
表1 仿真参数
Tab.1 Simulation parameters
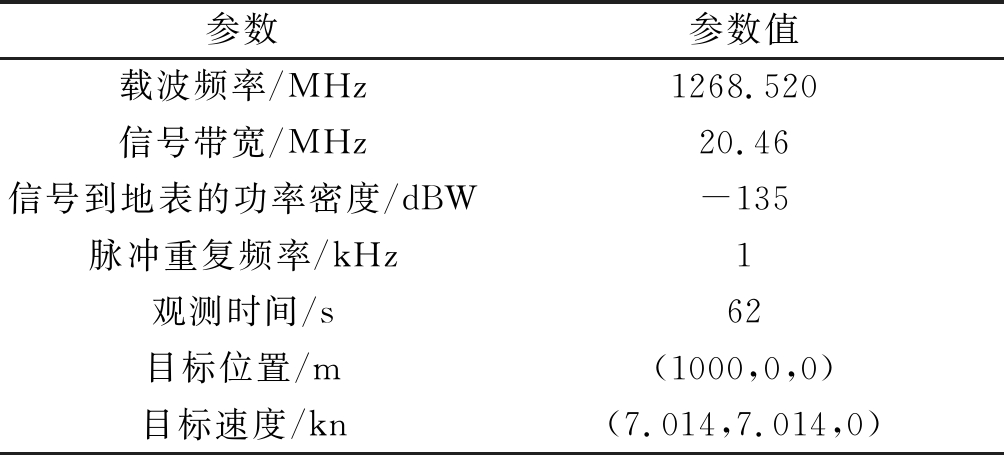
参数参数值载波频率/MHz1268.520信号带宽/MHz20.46信号到地表的功率密度/dBW-135脉冲重复频率/kHz1观测时间/s62目标位置/m(1000,0,0)目标速度/kn(7.014,7.014,0)
首先,在无噪声条件下验证RRAST的有效性。距离向脉冲压缩后的目标回波如图8(a)所示,其中明显存在不可忽视的距离徙动。对该目标回波进行RRAST,对应二维时域结果如图8(b)所示,距离徙动得到了精确校正,回波能量聚集于同一距离单元,且该距离单元已知。提取RRAST后目标回波的多普勒质心,并与原始回波进行比较,对应结果如图9所示。由该仿真结果可知,RRAST实现了多源回波多普勒质心的均衡。
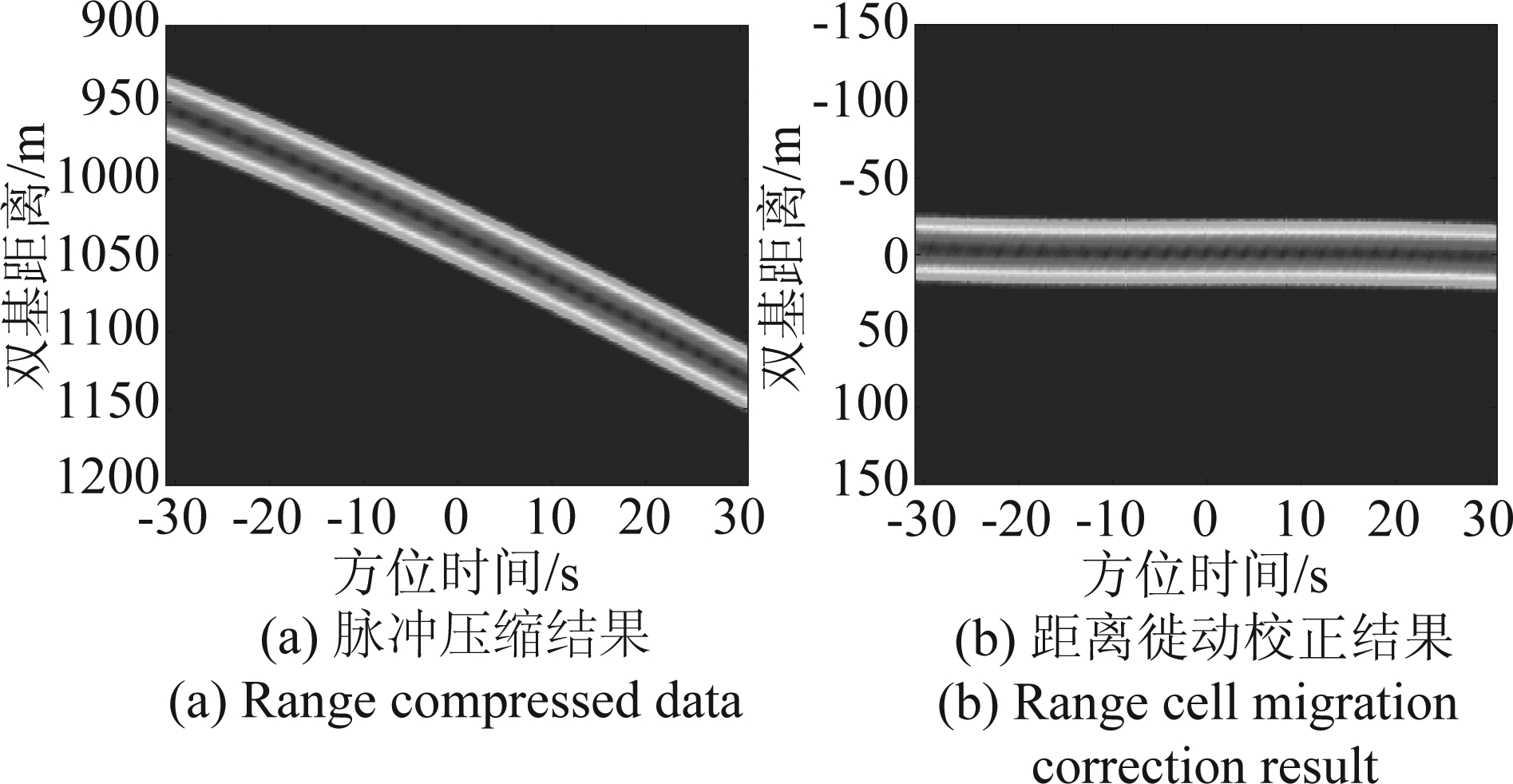
图8 RRAST变换的结果
Fig.8 Result of the RRAST
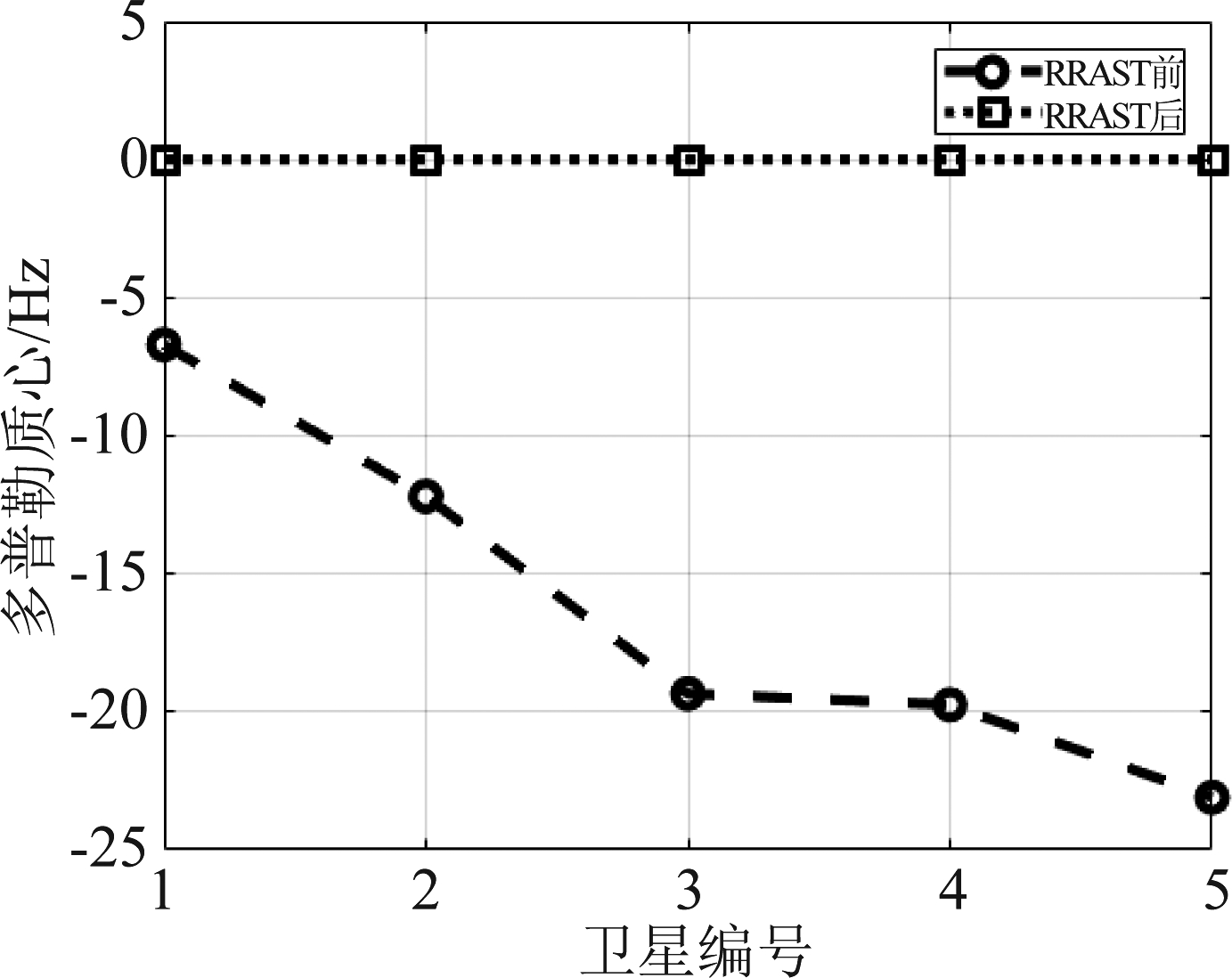
图9 RRAST变换前后多普勒质心比较
Fig.9 Doppler centroids before and after the RRAST
接着,为了验证本方法对海面运动目标检测的有效性,在仿真中加入噪声背景。将RRAST应用于每个回波,并将距离徙动校正后的回波按每帧时长2 s分为31帧。各帧信号通过DcIT处理,在多普勒调频率域实现相干积累,并通过非相干叠加实现各独立回波的长时间积累。如图10所示为其中两回波的积累结果,其中存在明显可见的峰值,验证了长时间积累的有效性。且该峰值位于同一位置,进一步通过非相干叠加多源回波的积累结果,完成目标回波的空间积累,对应结果如图11所示。显然,该结果中目标信噪比得到进一步提升,可有效实现海面运动目标的检测。
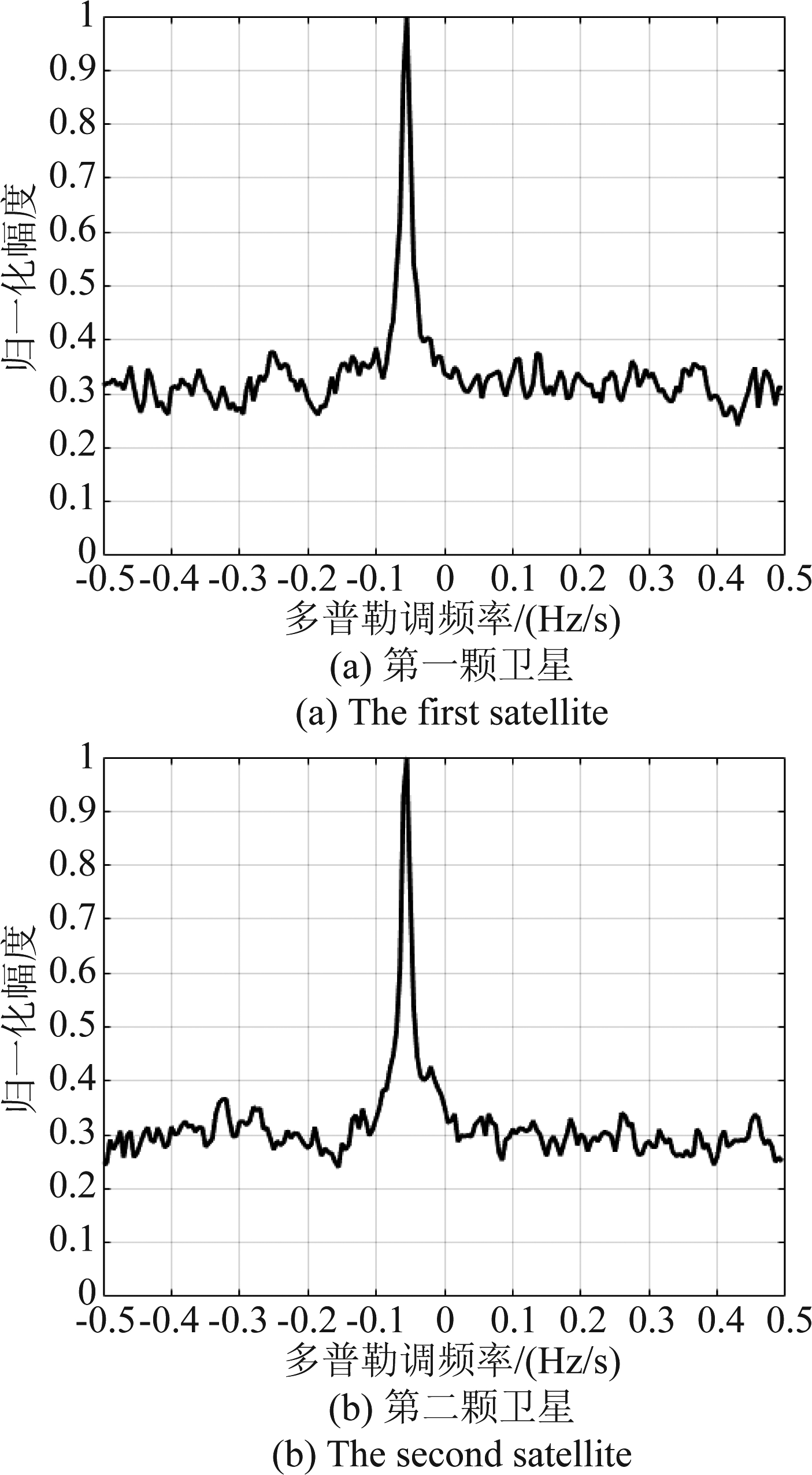
图10 单个目标回波长时间积累结果
Fig.10 Long-time integration result of a single echo
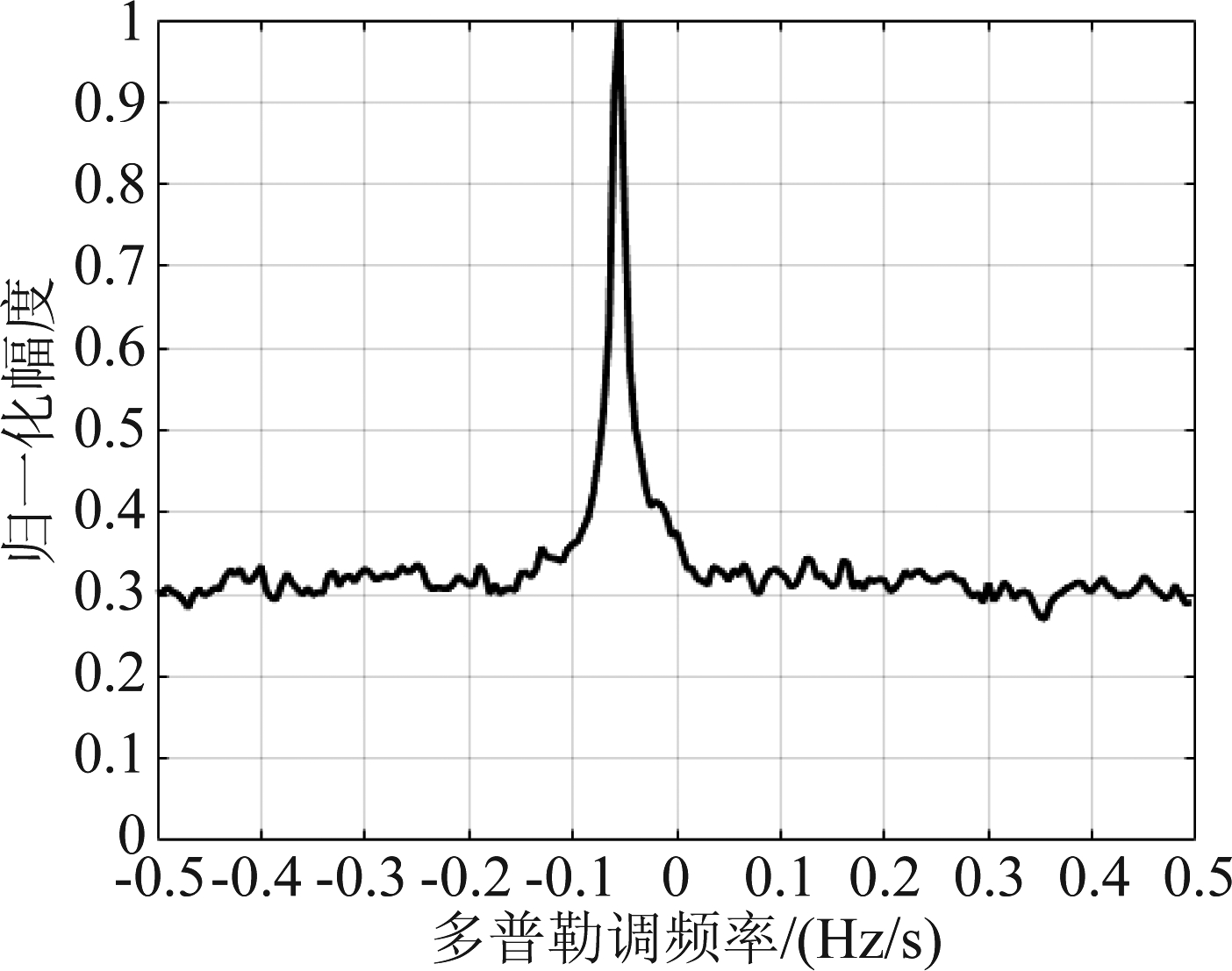
图11 多源回波积累结果
Fig.11 Integration result of multistatic echoes
根据上述检测结果,同时可得到目标回波的多普勒调频率值为-0.055 Hz/s。接着,为实现目标定位,建立接收站空间坐标系,并将X-O-Y平面上的监视区域划分网格。将来自5颗卫星的回波分别映射到X-Y-VR空间并完成能量积累。图12是其中两颗不同卫星的独立投影结果,可以观察到,在每个三维图中,目标都位于一组等距离线上,且等距离线方向不同。
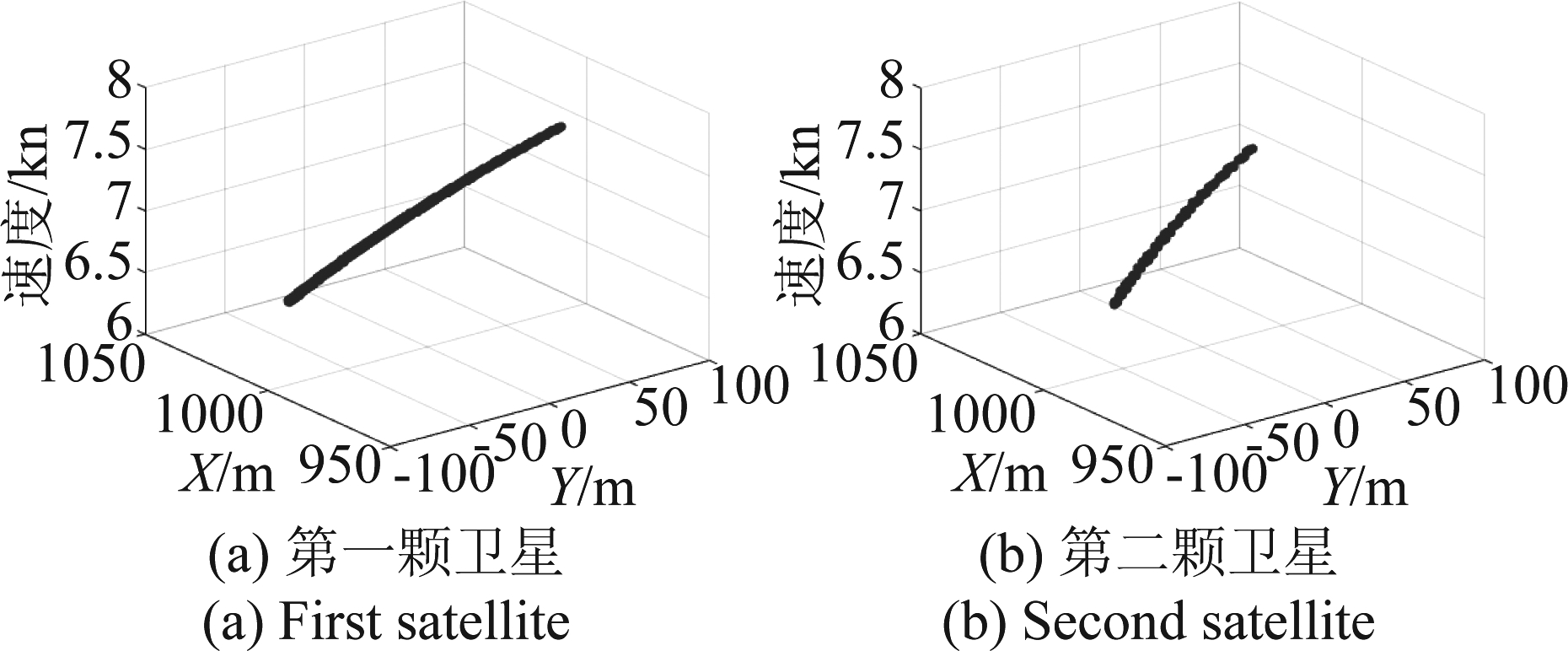
图12 单个回波X-Y-VR空间投影结果
Fig.12 Projection result in X-Y-VR domain of a single echo
最后,对5颗卫星的投影结果进行非相干积累,对应结果如图13所示。从最终的积累结果来看,目标回波信号能量很好地积累在X-Y-VR域中,出现了明显的峰值。图14为图13积累结果峰值处的X-O-Y剖面结果,可以得到目标在海面背景的位置为:(1002,-8,0)m。图15为速度剖面结果,可以得到对应切向速度为7 kn,进而得到目标速度为:(7.06,6.96,0)kn,实现了目标的准确定位与精确速度估计。

图13 多源回波在X-Y-VR空间映射结果
Fig.13 Final integration result in X-Y-VR domain
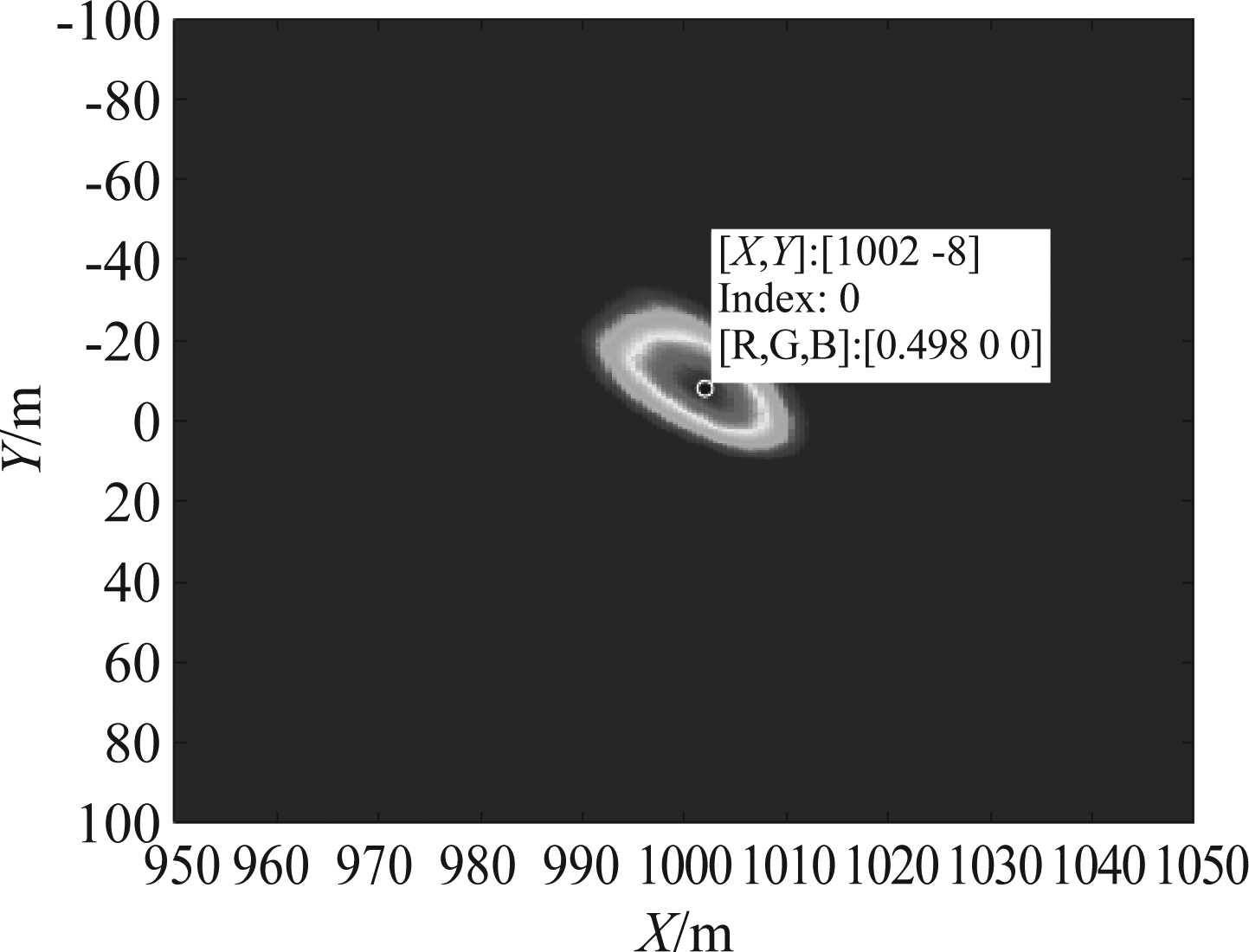
图14 X-O-Y剖面
Fig.14 X-O-Y profile
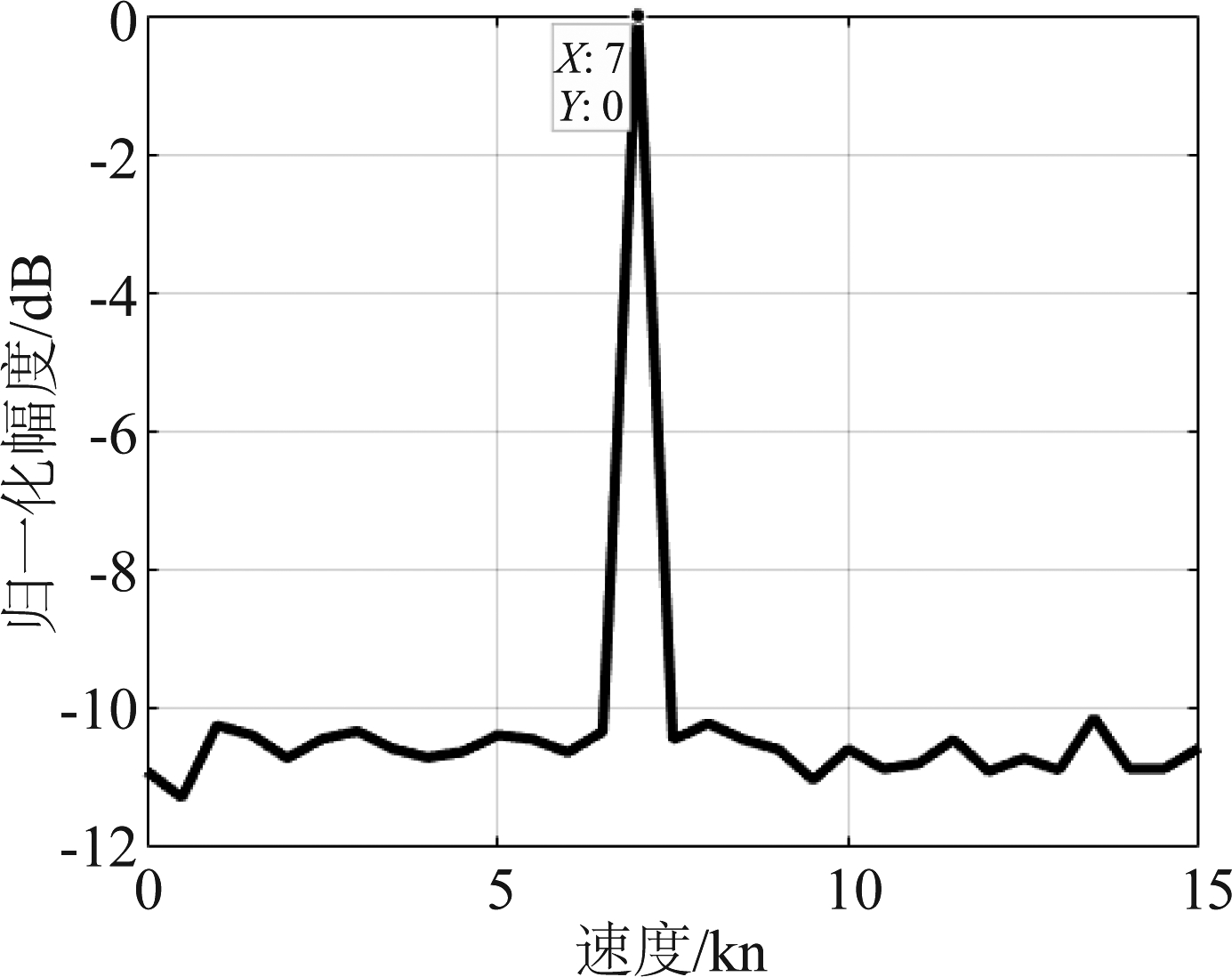
图15 速度剖面
Fig.15 Velocity profile
本文提出了一种基于无源多基雷达的海面运动目标检测与定位方法,解决了以卫星为辐射源目标回波信噪比极低的问题。该方法采用RRAST实现了对目标回波的距离徙动校正与多普勒质心置零,进而通过对方位信号的分帧DcIT处理,完成多个回波的长时间积累。通过多源回波空间积累,有效提高目标回波信噪比,实现海面运动目标检测,并估计多普勒调频率参数。相较于以单颗卫星为辐射源,以多颗卫星为辐射源的目标检测性能得到了提高。进一步,通过将各回波在已知条件下投影到X-Y-VR空间并积累,根据积累结果所在位置实现运动目标的定位与速度估计。
[1] Chen Xiaolong, Yu Xiaohan, Huang Yong, et al. Adaptive Clutter Suppression and Detection Algorithm for Radar Maneuvering Target With High-Order Motions Via Sparse Fractional Ambiguity Function[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2020, 13: 1515-1526.
[2] Mou Xiaoqian, Chen Xiaolong, Guan Jian, et al. Sea Clutter Suppression for Radar PPI Images Based on SCS-GAN[J]. IEEE Geoscience and Remote Sensing Letters, 2020.
[3] Yulian D, Hidayat R, Nugroho H A, et al. Automated ship detection with image enhancement and feature extraction in FMCW marine radars[C]∥2017 International Conference on Radar, Antenna, Microwave, Electronics, and Telecommunications, Jakarta, 2017: 58- 63.
[4] 苏宁远, 陈小龙, 关键, 等. 基于卷积神经网络的海上微动目标检测与分类方法[J]. 雷达学报, 2018, 7(5): 565-574.
Su Ningyuan, Chen Xiaolong, Guan Jian, et al. Detection and classification of maritime target with micro-motion based on CNNs[J]. Journal of Radars, 2018, 7(5): 565-574.(in Chinese)
[5] Zaimbashi A, Derakhtian M, Sheikhi A. Invariant Target Detection in Multiband FM-Based Passive Bistatic Radar[J]. IEEE Transactions on Aerospace and Electronic Systems, 2014, 50(1): 720-736.
[6] Choi S, Crouse D, Willett P, et al. Multistatic target tracking for passive radar in a DAB/DVB network: initiation[J]. IEEE Transactions on Aerospace and Electronic Systems, 2015, 51(3): 2460-2469.
[7] Ma Hui, Antoniou M, Cherniakov M, et al. Maritime target detection using GNSS-based radar: Experimental proof of concept[C]∥2017 IEEE Radar Conference, Seattle, 2017: 0464-0469.
[8] He X, Zeng Tao, Cherniakov M. Signal detectability in SS-BSAR with GNSS non-cooperative transmitter[J]. IEE Proceedings-Radar, Sonar and Navigation, 2005, 152(3): 124-132.
[9] Li Zhongyu, Santi F, Pastina D, et al. 2016 CIE International Conference on Radar[C]∥CIE International Conference on Radar. Guangzhou, 2016: 1- 4.
[10] Li Zhongyu, Santi F, Pastina D, et al. Multi-frame fractional Fourier transform technique for moving target detection with space-based passive radar[J]. Iet Radar Sonar & Navigation, 2017, 11(5): 822- 828.
[11] Pieralice F, Santi F, Pastina D, et al. GNSS-based passive radar for maritime surveillance: Long integration time MTI technique[C]∥2017 IEEE Radar Conference, Seattle, 2017: 0508-0513.
[12] Ma Hui, Antoniou M, Stove A G, et al. Maritime Moving Target Localization Using Passive GNSS-Based Multistatic Radar[J]. IEEE Transactions on Geoscience and Remote Sensing, 2018, 56(8): 4808- 4819.
[13] Pieralice F, Pastina D, Santi F, et al. Multi-transmitter ship target detection technique with GNSS-based passive radar[C]∥International Conference on Radar Systems, Belfast, 2017: 1- 6.
[14] Ma Hui, Antoniou M, Pastina D, et al. Maritime Moving Target Indication Using Passive GNSS-Based Bistatic Radar[J]. IEEE Transactions on Aerospace and Electronic Systems, 2018, 54(1): 115-130.
黄 川 男, 1994年生, 四川人。电子科技大学信息与通信工程学院博士研究生, 主要研究方向为无源雷达运动目标检测。
E-mail: huangchuan@std.uestc.edu.cn
李中余 男, 1988年生, 重庆人。电子科技大学信息与通信工程学院讲师, 博士, 主要研究方向为新体制雷达成像技术与运动目标检测技术等。
E-mail: zhongyu_li@uestc.edu.cn
张丽君 女, 1997年生, 四川人。电子科技大学信息与通信工程学院硕士研究生, 主要研究方向为无源雷达运动目标检测。
E-mail: 1770181037@qq.com
武俊杰 男, 1982年生, 河北人。电子科技大学信息与通信工程学院教授, 博士, 主要研究方向为前视SAR成像与目标检测技术。
E-mail: junjie_wu@uestc.edu.cn
杨建宇 男, 1963年生, 四川人。电子科技大学信息与通信工程学院教授, 博士, 主要研究方向为前视SAR成像技术。
E-mail: jyyang@uestc.edu.cn