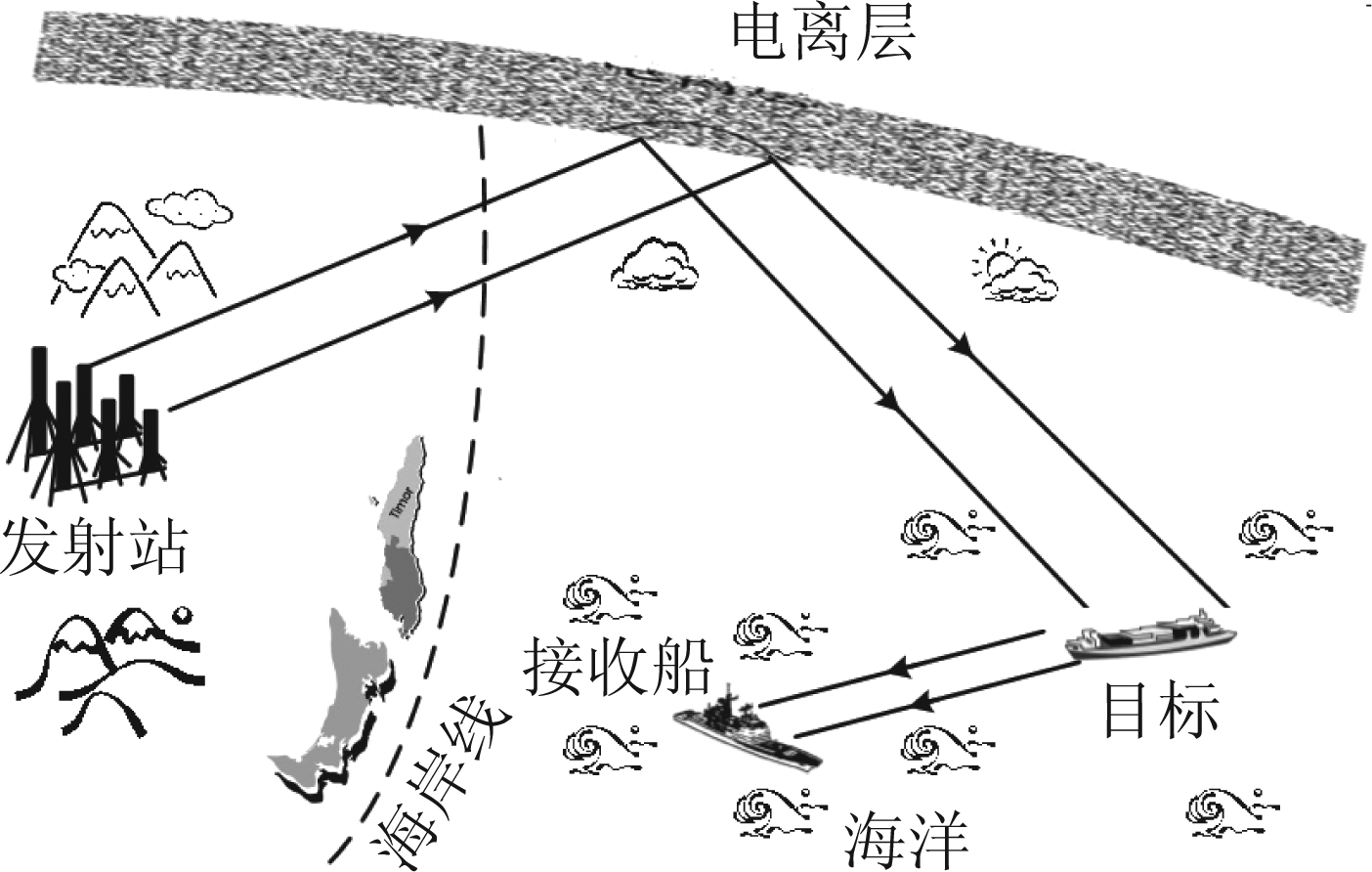
图1 天发船收高频雷达的系统探测示意图
Fig.1 Elementary detection principle for shipborne high frequency radar via hybrid sky-surface wave propagation
Reference format: Ding Mingkai, Tong Peng, Wei Yinsheng. Modeling of Target Echo for Shipborne High Frequency Hybrid Sky-surface Wave Radar[J]. Journal of Signal Processing, 2020, 36(12): 2007-2015. DOI: 10.16798/j.issn.1003- 0530.2020.12.006.
天波发射-地波接收混合传播模式下的高频雷达是一种新体制高频雷达,它以天波雷达和地波雷达技术为基础,其发射的电波信号经电离层反射后照射到目标,沿海面以地波绕射的传播模式到达接收站,兼具天波传播距离远、覆盖范围大和地波传播稳定、可相参积累时间长的双重优点[1-5]。天波发射-船载接收(以下简称天发船收)传播模式下,地波接收站由岸基平台转为船载运动平台,系统的超视距机动探测能力大大提高,探测防御区域进一步延伸,可有效提高舰队的早期预警能力[6]。
天发船收混合传播模式下,雷达目标回波不仅具有双基地系统动态空间几何关系引起的频谱偏移变化,还受到电离层不规则体导致的空时相位随机扰动,以及船体六维摆动引起的空时相位扰动调制,目标多普勒谱和空间谱发生展宽和畸变,严重影响杂波抑制等信号处理方法性能和参数估计精度[7]。因此,需要建立动态空间几何关系下的扰动目标回波模型,以描述天发船收高频雷达目标回波的空时特性变化。
传统的高频雷达系统模型中目标一般被假设为具有一定回波功率的理想点目标回波,将具有某个角度、多普勒频率和距离的目标导向矢量添加至距离-多普勒-方位三维数据块中。但该假设过于理想,没有考虑传播过程中的非理想因素对回波的作用。天发船收高频雷达目标回波主要受到电离层不规则体和接收船船体六维摆动扰动的影响,在电离层不规则体对高频天波信号影响研究方面,文献[8]给出了不规则体分布与回波多普勒展宽之间的理论关系,建立了高频天波雷达杂波模型,文献[9]在极区条件下基于几何光学方法分析了不规则体对回波空时相位随机调制的影响,建立了扰动相位的空时功率谱,在此基础上,文献[10]通过几何变换,建立了适应于中纬度的扰动相位空时功率谱模型;在船体六维摆动对高频雷达回波信号影响研究方面,现有研究集中于六维摆动下的高频雷达海杂波散射截面积建模,文献[11]建立了漂浮平台下的高频雷达一阶海杂波散射截面积模型,文献[12-14]分析了六维摆动对船载高频雷达一阶海杂波回波信号的影响。
上述研究成果均分别针对高频天波雷达和船载高频雷达进行讨论,而对于天发船收高频雷达在电离层不规则体和六维摆动扰动作用下的目标回波模型尚未有研究。针对天发船收高频雷达动态空间几何关系下的电离层不规则体和六维摆动非理想因素扰动影响,本文提出了多因素扰动作用下的天发船收高频雷达目标空时二维回波模型,结构安排如下。第2节介绍了天发船收高频雷达海面目标空时二维回波模型,包括动态系统空间几何关系下的目标频移模型、电离层不规则体空时相位扰动模型以及六维摆动空时相位扰动模型。第3节给出了该模型的仿真结果和利用测量数据的实验验证结果。在第4节中进行了总结。
在本部分内容中,我们对天发船收高频雷达海面船目标的空时二维回波进行了建模。首先给出了理想点目标空时二维回波数据模型,之后分别在2.1、2.2和2.3中给出了动态空间几何关系变化的目标频移模型、电离层随机空时扰动模型和接收船六维摆动扰动模型,最终获得了多扰动因素作用下的天发船收高频雷达目标空时二维回波模型。天发船收高频雷达的系统探测示意图如图1。
图1 天发船收高频雷达的系统探测示意图
Fig.1 Elementary detection principle for shipborne high frequency radar via hybrid sky-surface wave propagation
假设目标为一个远场源,可以被建模为一个点目标。对于距离R的目标,考虑一个给定的目标RCS σT,对应目标接收功率为PT[5],则目标回波的时域差频信号为[15]
(1)
其中fd为目标多普勒频率,Tr为频率调制周期,0≤t-nTr<Tr。对于具有M个阵元的均匀线性接收阵列,目标距离R处的二维阵元脉冲目标回波数据Xt可以表示为
(2)
式中
为目标方位与接收阵列法线夹角,d为阵元间距,aθ和sf分别为具有方位θt和多普勒频移fd的目标空间和时间导向矢量,λ为雷达波长。
基于式(2)中的理想点目标回波数据模型,假设电离层不规则体和六维摆动运动导致的空时相位扰动矩阵为Xc,则扰动目标回波数据可以表示为[9]
(3)
其中,⊙为Hadamard积。式(3)的扰动目标回波模型包括目标频移模型、电离层随机空时扰动模型和六维摆动模型,各模型之间的逻辑关系如图2,下面详细介绍这三个模型的具体建模过程。
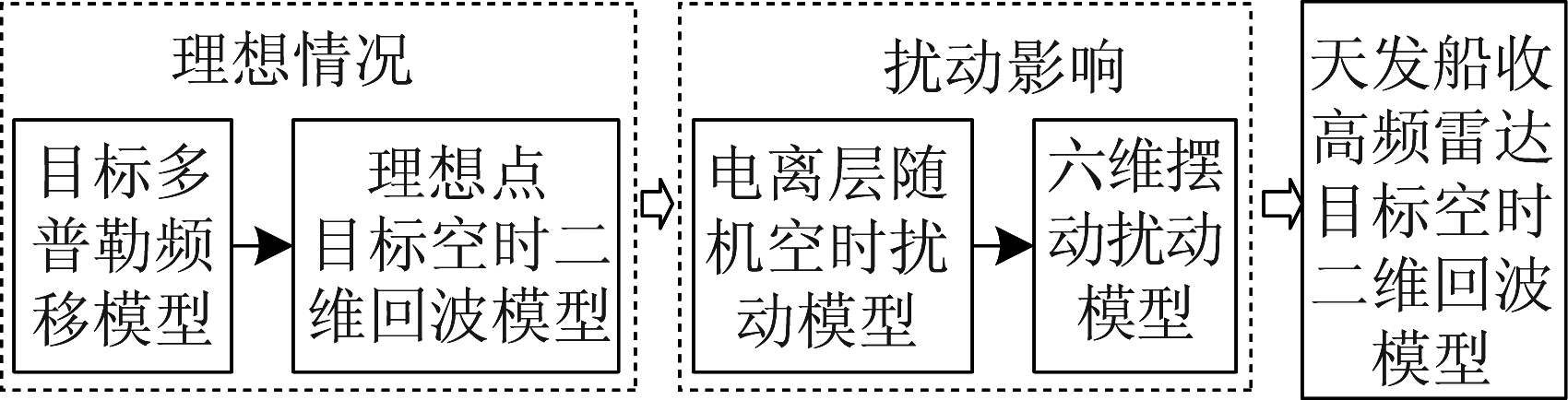
图2 天发船收高频雷达目标回波建模过程主要步骤
Fig.2 Main steps of modeling target echoes for shipborne high frequency hybrid sky-surface wave radar
天发船收高频雷达信号传播的动态空间几何关系如图3所示。本小节通过距离变化对时间的微分建立动态参数下的目标频移模型,给出系统几何参数、目标与接收船运动参数等对目标多普勒频移的定量影响。模型主要考虑目标和接收船做匀速直线运动时目标的多普勒频移特性,以及运动电离层对目标多普勒频移的影响。
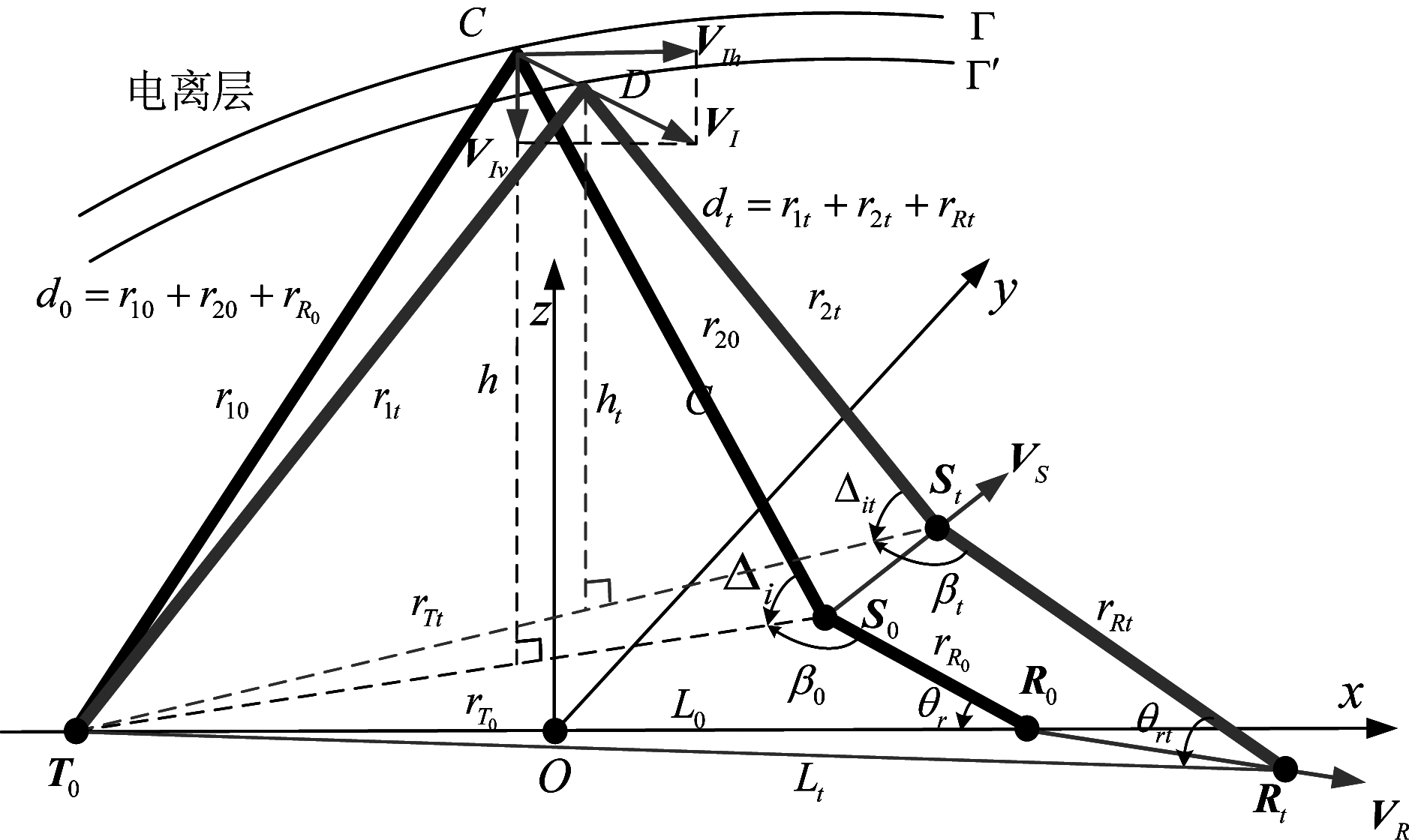
图3 信号传播过程中的动态空间几何关系示意图
Fig.3 Dynamic geometry spatial relationship for signal propagation
忽略地球曲率的影响,建立一个空间直角坐标系。在此坐标系内,雷达发射站、接收船与海面目标形成了一个立体的空间几何形状,如图3所示。发射站、接收站和海面目标的位置与运动参数定义如下。
T0——发射站的初始位置矢量;R0——接收船的初始位置矢量;VR——接收船的速度矢量;Rt——t时刻接收船的位置矢量,Rt=R0+VR·t;S0——海面目标的初始位置矢量;VS——海面目标的速度矢量;St——t时刻海面目标的位置矢量,St=S0+VS·t;L0——发射站、接收站的初始基线距离;Lt——t时刻发射站、接收站的基线距离;rT0——发射站与海面目标的初始地面距离;rTt——t时刻发射站与海面目标的地面距离;rR0——接收船与海面目标的初始斜距;rRt——t时刻接收船与海面目标的斜距;θr、θrt分别为初始时刻与t时刻目标方位角;Δi、Δit分别为初始时刻与t时刻擦地角;β0、βt分别为初始时刻与t时刻水平面双基地角;VI——电离层等效反射面的运动速度,可分解为垂直向速度矢量VIν与水平向速度矢量VIh。
在电离层反射为理想的镜面反射条件下,有r10=r20、r1t=r2t,分别为初始时刻与t时刻的天波路径,d0=r10+r20+rR0与dt=r1t+r2t+rRt分别为初始时刻与t时刻的总传播路径。根据空间几何关系,有
(4)
则混合传播路径总传播距离可以表示为
(5)
其中,t时刻发射站与海面目标的斜距可以表示为
rTt=|St-T0|=|S0-T0+VS·t|
(6)
将上式在t=0时刻进行二阶泰勒展开,近似表达式为
(7)
其中,cos θ=〈S0-T0,VS〉/(rT0·|VS|),〈A,B〉表示矢量A与B的内积。
同理,t时刻接收船与海面目标的斜距
rRt=|St-Rt|=|S0-R0+(VS-VR)·t|≈
(8)
其中,cos η=〈S0-R0,VS-VR〉/(rR0·|VS-VR|)。
由于电离层等效反射面的水平运动速度不会引起等效反射路径的变化,因此我们只考虑电离层等效反射面的垂直运动速度ν(t)(取向上运动为正)的影响,设t=0时刻反射面高度为h0,则t时刻高度为[16]
ht=h0+
ν(τ)dτ
(9)
双基地雷达多普勒频移fd定义为:波长λ归一化的散射信号的总路径长度随时间的变化率。参照远离雷达方向多普勒频率为负的定义,我们令总路径长度增加时的多普勒频率为负,则目标多普勒频移可以写为
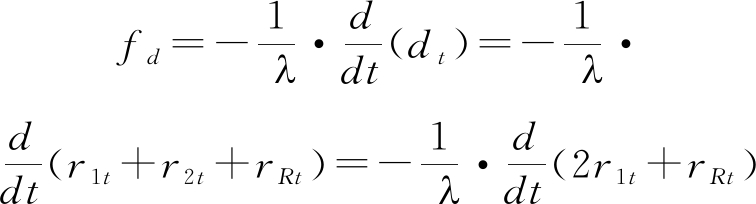
(10)
将式(5)、式(7)和式(8)代入到式(10)中,得到
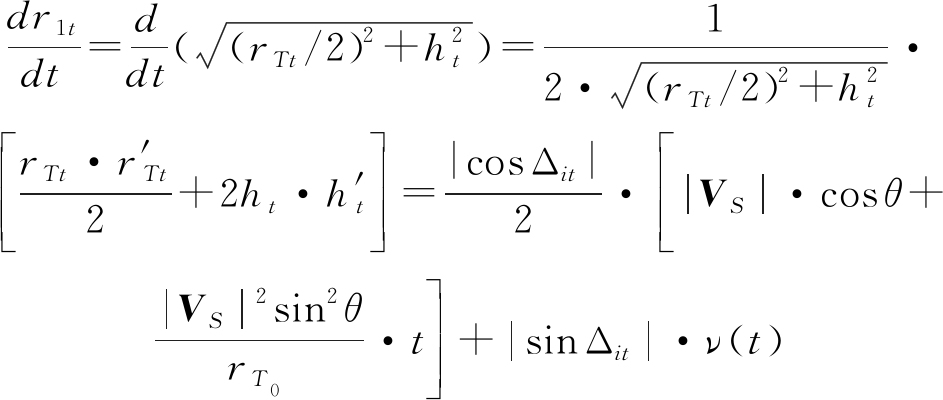
(11)
(12)
其中
由于Δit∈[0,π/2],所以|cos Δit|=cos Δit,|sin Δit|=sin Δit。假设观测时间内等效电离层反射面在垂直方向以速度ν1匀速运动,则目标多普勒频移fd可写作
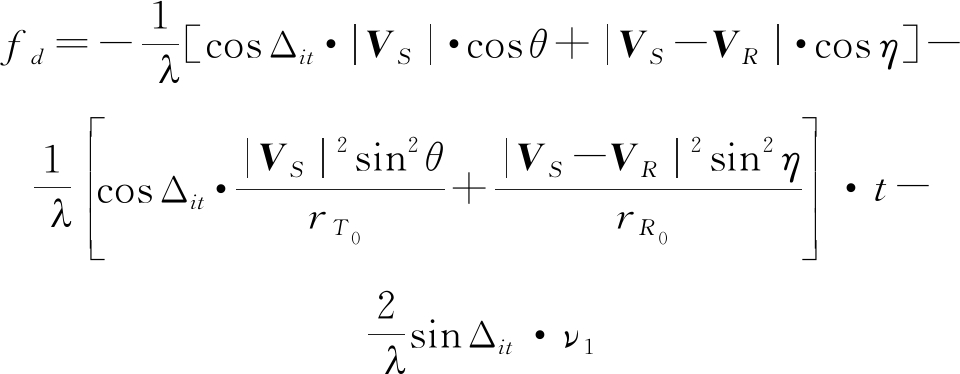
(13)
其中,cos θ=〈S0-T0,VS〉/(rT0·|VS|),cos η=〈S0-R0,VS-VR〉/(rR0·|VS-VR|)。
为简化cos θ和cos η计算,给出θ、η与系统几何参数的内在联系,设rT0=S0-T0,rR0=S0-R0,定义:
ηR——为rR0顺时针旋转至VR方向所转过的角度,ηR∈[0,2π];ηS——为rR0顺时针旋转至VS方向所转过的角度,ηS∈[0,2π]。
则式(13)各角度余弦值计算结果如下
cos θ=cos|ηS-β0|
(14)
(15)
其中
同时,由图3几何关系,有
本部分基于文献[10]得到的中纬度扰动相位空时功率谱,推导了高频天波信道的系统脉冲响应函数,建立了电离层不规则体引起的空时扰动相位模型。
扰动电离层引起的高频信号空时相位闪烁的功率谱[10,17]可以表示为
Sφ1(κx,κy,Ω)=8πL(reλcscθ)2Sn1(κx,κy,Ω)δ(κy)
(16)
L=z0[sin 2θsin αI(cos αD-sin αD)+cos2θcos αI]
(17)
其中,L是射线在电离层中传播的水平距离, z0是反射点距离电离层底部的高度,re=2.8×10-15 m为经典电子半径大小,λ是自由空间雷达波长,θ是射线仰角,αD和αI分别是磁偏角和磁倾角。Sn1(κx,κy,Ω)是不规则体的功率谱密度,我们采用文献[17]中式(42)的三阶场向不规则体功率谱
(18)
其中,κ0≈10-4m-1是电离层不规则体外尺度长度参数,
是反射高度处电子密度起伏的方差,κx是不规则体密度波数在垂直于射线方向的投影,κy是不规则体密度波数在平行于射线方向的投影,νdx和νdy分别是x和y方向的等离子体漂移速度。将式(18)代入式(16),则扰动相位功率谱函数可以表示为
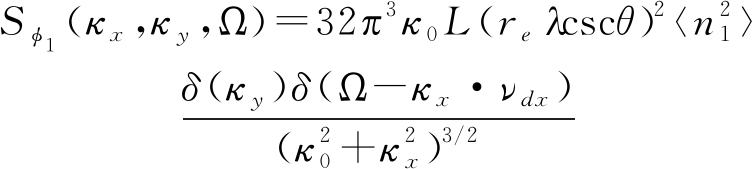
(19)
为了模拟不规则体空时相位扰动,我们对扰动相位功率谱函数的平方根进行逆傅里叶变换,得到高频电波传播通过扰动电离层的系统脉冲响应函数为
(20)
式中,
是电子密度起伏标准差,Kν(·)是阶数为ν的第二类修正贝塞尔函数,Γ(·)为伽马函数。令
则Hφ1(ρ,T)=Hφ1(X,Y,T)。
之后,将高斯白噪声信号与该系统脉冲响应函数做卷积运算,得到输出扰动相位
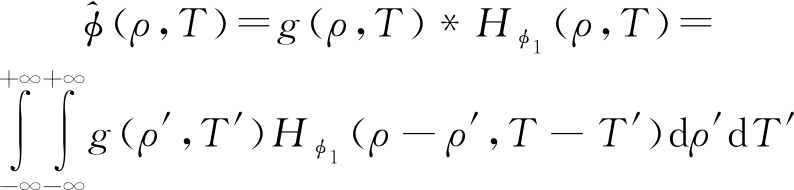
(21)
式中,g(ρ,T)为高斯白噪声信号。
将信号相位表示为信号复幅度,整个阵列和相参积累周期接收到的回波信号所附加的空时相位扰动矩阵可以表示为
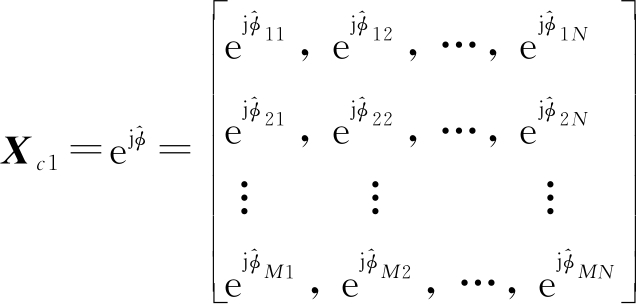
(22)
经过上述处理,我们便完成了电离层不规则体导致的空时扰动相位的模拟过程。
当接收船在海上航行时,船体与海浪的相互作用引起了船体的六自由度上的运动[6,18],包括振荡(纵荡u1、横荡u2、垂荡u3)运动和摇摆(纵摇u5、横摇u4、艏摇u6)运动,称作六维摆动,如图4所示。
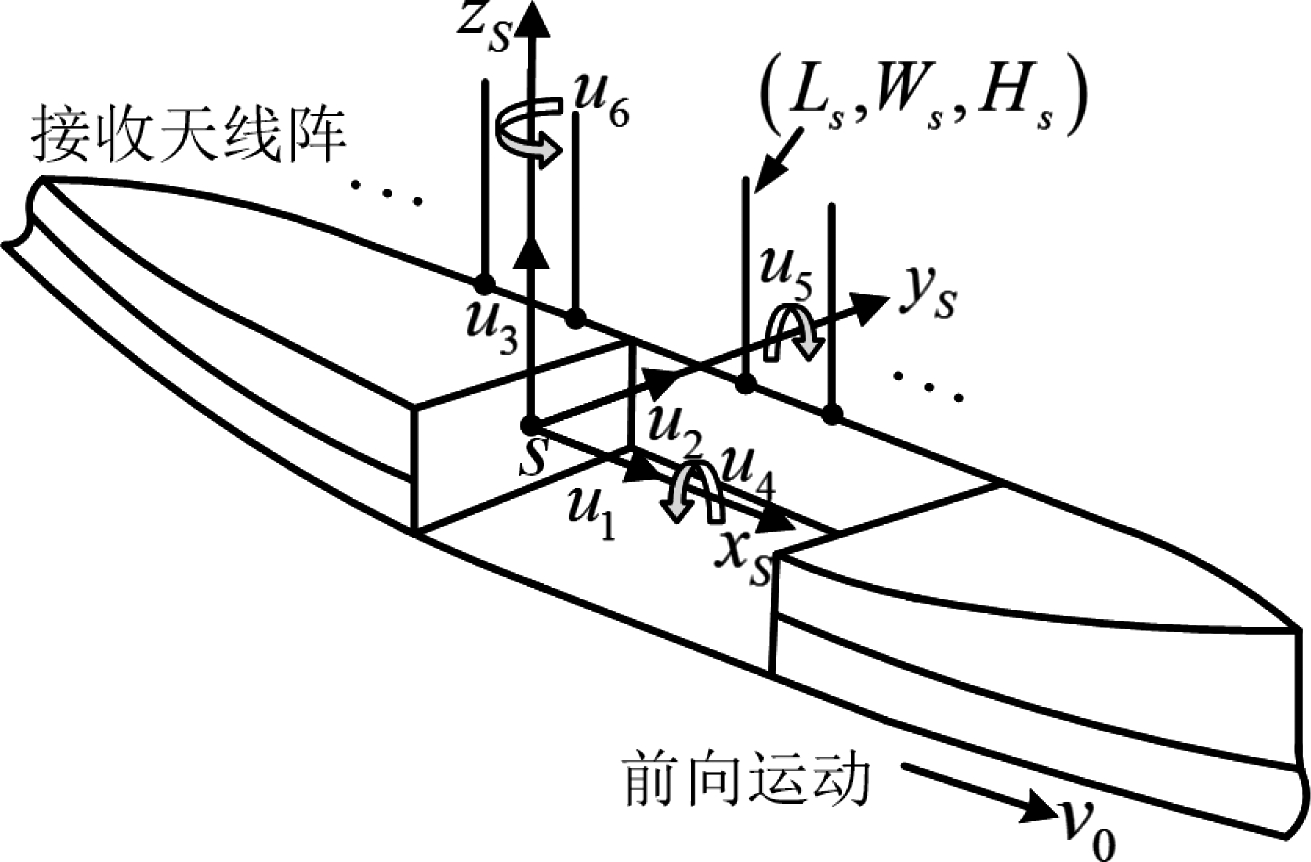
图4 船体六维摆动运动示意图
Fig.4 Six-degree-of-freedom (6-DOF) motion of the ship
船体的六维摆动引起了目标回波信号的空时相位变化,时间上的相位扰动使得目标回波的多普勒谱出现调制峰,进而引起多普勒展宽,空间上的相位扰动使得目标回波的空间谱发生形变,使得空间谱最大值方位估计出现偏差。研究表明,高海态条件下,船体六维摆动对一阶海杂波谱的空时调制作用非常明显,调制谱峰的贡献不可忽略[6]。为了定量描述六维摆动对目标回波导向矢量的空时相位扰动,本文采用文献[14]中的六维摆动模型,定义六维摆动引起的空时扰动向量为
(23)
式中
其中θt是目标方向与阵列法线夹角,t是时间,Ws是天线与平台中心线间的距离,Hs是船甲板与平台中心的垂直距离,ui,i=1,2,...,6为六维运动模型参数,可以表示为[6]
(24)
其中a和ω分别表示六维摆动运动幅度和角频率大小,下角标i∈(u,w,h,r,p,y)分别对应于六维摆动运动中的每一维分量。其中,垂荡运动u3既不会引入空间尺度上的相位频移,也不会引起探测距离的变化和多普勒谱的变化,因此本文中忽略垂荡运动的影响[6,14]。考虑一个相参积累周期(N个脉冲)时间内的回波数据,六维摆动空时扰动矩阵可以表示为
Xc2=[v(1),...,v(N)]
(25)
最终,受电离层扰动和六维摆动运动影响的目标空时回波数据可以表示为
(26)
基于上一节中给出的天发船收高频雷达扰动目标空时回波模型,在本节中,我们对目标回波的频移特性和空时特性进行仿真分析与部分实验验证。首先,利用实验数据获取的协作船目标位置和运动参数信息,根据目标频移模型计算理论多普勒频移,并与测量的频移值对比验证频移模型的有效性;之后,由于实验数据获取时海态等级较低,我们通过仿真分析不同海态下接收船六维摆动对目标空时分布的影响;最后,仿真分析典型电离层参数下的目标空时分布,并与实际目标回波进行对比。
本部分利用天发船收高频雷达海上目标探测试验协作船目标信息,验证目标频移模型的有效性。其中,协作船目标与接收船的位置、运动速度和方向等信息通过辅助设备获取,电离层反射点虚高通过斜测仪估计得到,利用这些参数可根据前述目标频移模型计算得到理论目标多普勒频移。作为对比的测量目标多普勒频移为目标回波多普勒谱最大值对应频率,实验中通过转发器信号的多普勒频率获取。目标船观测时间段为2020年8月7日8时51分至10时21分,每隔一个相参积累周期(41 s)进行一次目标多普勒频率测量,起始时间8时51分的几何参数如表1所示。
表1 系统几何参数
Tab.1 Geometry parameters of this system
参数值rT0/ km789.4rR0/ km112.3电离层虚高/ km257.6基线长度L0/ km694.4目标船速度/m-1s4.4 目标船速度方向(北偏东)/(°)4.3接收船速度/m-1s4.6接收船速度方向(北偏东)/(°)284.2
由表 1中的系统几何参数和前述目标频移模型,计算得到观测时间段起始第一个相参积累周期的理论目标多普勒频移为-0.0744 Hz,而测量值为-0.0981 Hz,二者相差0.0237 Hz,小于一个多普勒分辨单元的宽度(0.0244 Hz)。利用图5 (a)中观测时间段内的目标船与接收船位置和对应的系统几何参数,根据式(13)计算理论船目标多普勒频移,并与测量值作对比,观测时间段内对比结果如图5 (b)所示(假设等效电离层运动速度为零,9时22分至32分与9时44分至54分转发器关闭)。可以看到,在1小时左右的时间段内,由频移模型计算得到的理论多普勒移值与测量值具有较高的一致性,平均多普勒偏差为0.0169 Hz,小于一个多普勒分辨单元宽度,验证了本文建立目标频移模型的有效性。
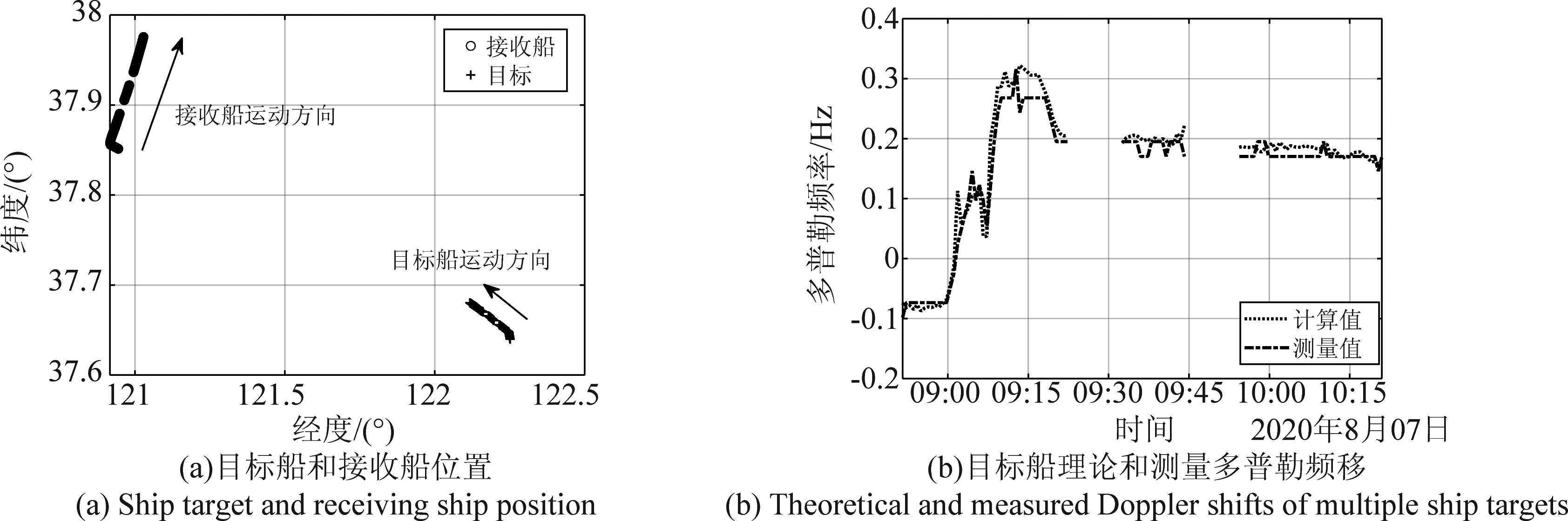
图5 目标船的多普勒频移模拟
Fig.5 Simulation of ship target Doppler shift
图6 六维摆动运动对目标多普勒谱和空间谱的影响
Fig.6 Effects of six-DOF motion on target Doppler spectrum and spatial spectrum
本文采用和文献[6]相同的六维摆动运动参数(见该文献表3-1和表3-2),分别仿真3级和5级海态下的六维摆动运动的扰动影响,对应中等程度的扰动和强扰动。
采用和实际目标回波相同的系统参数,根据式(23)和六维摆动模型参数,我们仿真了3级和5级海态下六维摆动影响后的目标回波数据,目标多普勒谱和空间谱如图6所示。其中,目标多普勒频率为-0.5127 Hz,方位为-13.5°。图6(a)多普勒谱结果表明,六维摆动运动会使得目标多普勒谱两侧出现调制谱,且海态等级越高,调制谱能量越高,调制谱峰多普勒频率向目标多普勒频率靠近。3级海态和5级海态下,目标与调制谱峰的功率分别相差23 dB和10 dB,这说明相比于目标多普勒谱,调制谱在较低的海态条件下贡献有限。图6(b)空间谱结果表明,六维摆动运动对空间谱影响结果较弱,可以忽略。六维摆动运动对目标回波谱的影响主要体现在对目标多普勒谱的调制作用,高海态下具有较高能量的调制谱恶化了目标回波的检测环境,需要研究相应的六维摆动补偿方法以校正目标回波的多普勒扩展。接收船上安装的惯导姿态测量设备可提供船体的姿态测量数据,通过模型参数拟合和基于模型的空时扰动补偿,为六维摆动运动校正提供了一种可行的途径。
本部分利用前述的电离层随机空时相位扰动模型,对电离层不规则体导致的回波信号多普勒谱和空间谱变化特性进行仿真分析,并将之与实际目标回波进行对比,以验证模型的有效性。由于天发船收高频雷达探测试验接收船工作在低海态条件下,根据上小节仿真结果,六维摆动对目标回波的影响可以忽略。
仿真采用的电离层不规则体参数如表 2所示,其中σn1/n0为电子密度随机起伏相对标准偏差,n0为背景电子密度,σn1=σn1/n0·n0, L是射线在电离层中传播的水平距离,通过测量目标的系统几何参数直接获取。根据式(20)和式(21),生成仿真的空时相位扰动矩阵,将之添加至目标回波模型,其中仿真的相位扰动矩阵是100次蒙特卡洛仿真输出的平均结果,得到时域、空域平均相位标准偏差均分别为0.70和0.72 rad。测量目标回波的多普勒频率为-0.5127 Hz,方位为-13.5°。图7给出了仿真结果和测量目标回波谱的对比图。从图7(a)中可以看出,扰动后的目标多普勒谱较理想目标回波发生了明显的展宽,其展宽程度和展宽谱形状与实际目标回波相近。图7(b)是仿真和实际目标的空间谱,可以看到扰动后的目标空间谱形状发生了展宽和畸变,旁瓣水平提高,空间谱峰值发生了偏移,目标测量空间谱也发生了类似的变化,但是拥有更高的旁瓣水平和谱展宽,这主要是由于不同接收机通道的不一致性加剧了空间谱的畸变。不规则体导致的目标多普勒谱和空间谱的展宽和畸变程度是由不规则体的起伏强度决定的,对于强不规则体电子密度起伏,其导致了较大的空时相位起伏进而导致了较大的空时谱展宽和形变,严重影响目标估值的准确性,需要研究相应的扰动校正方法以提高雷达系统性能。
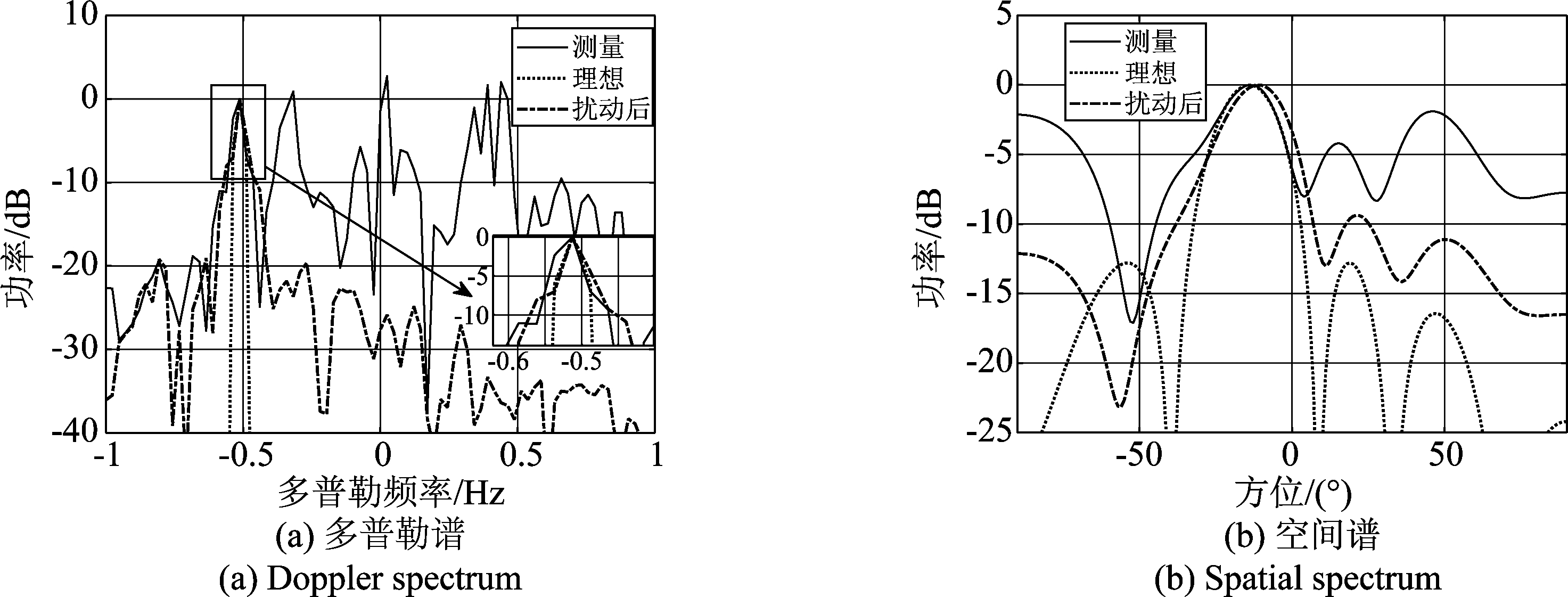
图7 不规则体空时扰动后的目标回波谱与测量目标回波谱对比
Fig.7 Comparison between the target echo spectrum after space-time perturbation by ionospheric irregularities and the measured target echo spectrum
表2 电离层不规则体空时扰动建模参数
Tab.2 List of space-time perturbation model parameters for ionospheric irregularities
本文建立了天发船收高频雷达扰动目标空时回波模型,该模型是对现有理想点目标回波模型和单一非理想因素作用下目标回波模型的汇聚和发展,综合考虑了动态空间几何、电离层不规则体扰动和六维摆动运动调制多因素作用对目标回波的空时扰动影响。首先,基于雷达信号传播距离对时间的微分建立了动态参数与目标多普勒频移的定量关系,多个相参积累周期船目标的频移计算结果与测量值基本一致,验证了频移模型的有效性;其次,应用随时间变化的六维摆动运动空间扰动向量模型,构建了六维摆动空时相位扰动矩阵,对应的扰动目标多普勒谱和空间谱仿真结果表明,六维摆动对目标空间谱影响有限,对目标多普勒谱影响主要体现为调制峰,调制峰谱强度与海态大小成正比,低海态下调制峰能量较低淹没于噪声中,可忽略其影响;之后,通过对电离层不规则体空时扰动相位功率谱的平方根进行逆傅里叶变换,构建了不规则体扰动相位仿真器,仿真的扰动目标回波谱表明,不规则体空时扰动相位导致了多普勒谱和空间谱的展宽、偏移以及旁瓣水平的提高,仿真目标回波与实际测量目标回波谱具有较好的一致性。
本文建立的天发船收高频雷达扰动目标回波模型定量描述了系统参数、电离层扰动参数和六维摆动运动参数与目标空时二维回波之间的关系,可为仿真研究信号处理算法性能,定量分析雷达系统性能提供依据。
[1] Yang Longquan, Fan Junmei, Guo Lixin, et al. Simulation Analysis and Experimental Study on the Echo Characteristics of High-Frequency Hybrid Sky-Surface Wave Propagation Mode[J]. IEEE Transactions on Antennas and Propagation, 2018, 66(9): 4821- 4831.
[2] Liu Tongxin, Hu Yaogai, Yang Guobin, et al. HF hybrid sky-SWR system based on MIMO technology[J]. IET Radar, Sonar & Navigation, 2018, 12(6): 626- 631.
[3] 童鹏. 天发地收高频雷达杂波抑制方法研究[D]. 哈尔滨: 哈尔滨工业大学, 2018.
Tong Peng. Research on clutter suppression in HF hybrid sky-surface wave radar[D]. Harbin: Harbin Institute of Technology, 2018.(in Chinese)
[4] Riddolls R J. Limits on the detection of low-Doppler targets by a High Frequency hybrid sky-surface wave radar system[C]∥2008 IEEE Radar Conference, Rome, 2008: 1-4.
[5] 焦培南, 杨龙泉, 凡俊梅. 短波天波反射/地波绕射组合新传播模式及其可能应用[J]. 电波科学学报, 2007, 22(5): 746-750+773.
Jiao Peinan, Yang Longquan, Fan Junmei. New propagation mode associating with HF sky-and-Surface wave and its application[J]. Chinese Research Institute of Radiowave Propagation, 2007, 22(5): 746-750+773.(in Chinese)
[6] 朱永鹏. 天发舰收高频雷达海杂波建模与抑制方法研究[D]. 哈尔滨: 哈尔滨工业大学, 2018.
Zhu Yongpeng. Modeling and suppression of sea clutter for shipborne HF hybrid sky-surface wave radar[D]. Harbin: Harbin Institute of Technology, 2018.(in Chinese)
[7] 李昕哲, 谢文冲, 王永良. 空时误差情况下的STAP方法性能分析[J]. 信号处理, 2020, 36(3): 439- 448.
Li Xinzhe, Xie Wenchong, Wang Yongliang. Performance Analysis of STAP Methods under Space-Time Errors[J]. Journal of Signal Processing, 2020, 36(3): 439- 448.(in Chinese)
[8] Coleman C J. A model of HF sky wave radar clutter[J]. Radio Science, 1996, 31(4): 869- 875.
[9] Ravan M, Adve R S. Modeling the received signal for the Canadian over-the-horizon-radar[C]∥2013 IEEE Radar Conference (RadarCon13), 2013: 1- 6.
[10] Yang Xuguang, Liu Aijun, Yu Changjun, et al. Ionospheric Clutter Model for HF Sky-Wave Path Propagation with an FMCW Source[J]. International Journal of Antennas and Propagation, 2019, 3(2019): 1-10.
[11] Walsh J, Huang W, Gill E. The First-Order High Frequency Radar Ocean Surface Cross Section for an Antenna on a Floating Platform[J]. IEEE Transactions on Antennas and Propagation, 2010, 58(9): 2994-3003.
[12] Yao Guowei, Xie Junhao, Huang Weimin. First-order Ocean Surface Cross Section for Bistatic HFSWR Incorporating a Horizontal Oscillation Motion Model[C]∥2019 IEEE Radar Conference (RadarConf), 2019: 1- 4.
[13] Yao Guowei, Xie Junhao, Huang Weimin, et al. Theoretical analysis of the first-order sea clutter in shipborne high-frequency surface wave radar[C]∥2018 IEEE Radar Conference (RadarConf18), 2018: 1255-1259.
[14] Chang Guanghong, Li Ming, Xie Junhao, et al. Ocean Surface Current Measurement Using Shipborne HF Radar: Model and Analysis[J]. IEEE Journal of Oceanic Engineering, 2016, 41(4): 970-981.
[15] Grosdidier S, Baussard A, Khenchaf A. HFSW Radar Model: Simulation and Measurement[J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(9): 3539-3549.
[16] 关泽文, 陈建文, 鲍拯. 天波超视距雷达海杂波模型修正与特性分析[J]. 电子与信息学报, 2017, 39(12): 2881-2888.
Guan Zewen, Chen Jianwen, Bao Zheng. Model Modifying and Characteristics Analyzing of Ocean Clutter in Skywave Over-the-horizon Radar[J]. Journal of Electronics & Information Technology, 2017, 39(12): 2881-2888.(in Chinese)
[17] Ravan M, Riddolls R J, Adve R S. Ionospheric and auroral clutter models for HF surface wave and over-the-horizon radar systems[J]. Radio Science, 2012, 47(3): 1-12.
[18] 陈小龙, 董云龙, 李秀友, 等. 海面刚体目标微动特征建模及特性分析[J]. 雷达学报, 2015, 4(6): 630- 638.
Chen Xiaolong, Dong Yunlong, Li Xiuyou, et al. Modeling of micromotion and analysis of properties of rigid marine targets[J]. Journal of Radars, 2015, 4(6): 630- 638.(in Chinese)
丁明凯 男, 1995年生, 黑龙江齐齐哈尔人。哈尔滨工业大学电子与信息工程学院博士研究生, 主要研究方向为高频雷达回波建模和信号处理。
E-mail: dingmingkaihit@126.com
童 鹏 男, 1987年生, 山东文登人。哈尔滨工业大学电子与信息工程学院助理研究员, 主要研究方向为雷达信号处理、雷达抗干扰、雷达回波建模等。
E-mail: tongpeng@hit.edu.cn
位寅生 男, 1974年生, 黑龙江伊春人。哈尔滨工业大学电子与信息工程学院教授, 博士生导师, 主要研究方向为雷达系统建模与分析、雷达信号处理、抗干扰与抗杂波雷达信号体制等。
E-mail: weiys@hit.edu.cn