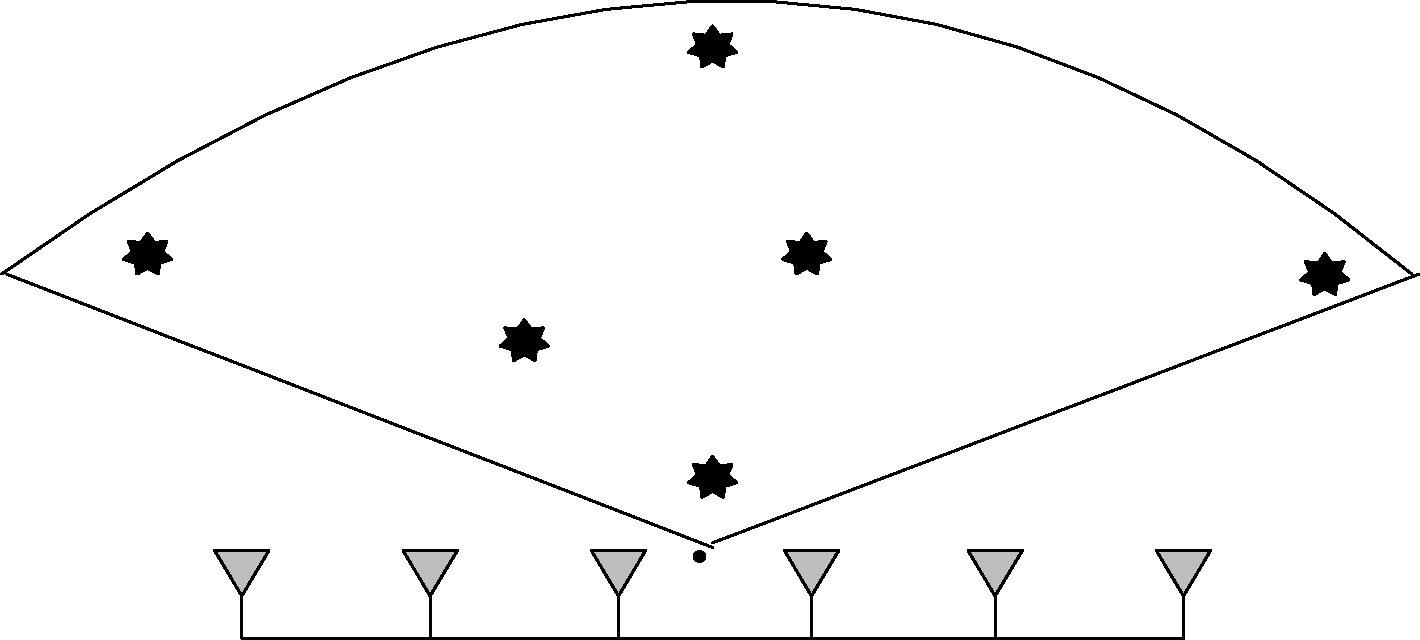
图1 发射正交波形的MIMO阵列雷达示意图
Fig.1 Schematic diagram of MIMO array radar transmitting orthogonal waveforms
Reference format: Chen Xiaolong, Huang Yong, Guan Jian, et al. Review of Long-time Integration Techniques for Weak Targets Using MIMO Radar[J]. Journal of Signal Processing, 2020, 36(12): 1947-1964. DOI: 10.16798/j.issn.1003- 0530.2020.12.001.
“微弱目标”的内涵随着科技水平的进步而不断发展,“微弱目标”指的是其回波淹没在杂波中的具有较低信杂噪比的目标[1-2]。归纳起来,“微弱目标”可分为如下几类[3- 4]:1)小尺寸目标,雷达反射回波微弱,例如旋翼无人机、飞鸟、渔船等;2)隐身目标,通过外形隐身、吸波涂层等技术使得目标雷达散射截面积低,缩短了雷达的有效探测距离和预警时间,从而增加了探测的难度，如隐身飞机等;3)远距离大目标,此类目标距离较远,目标占据所在分辨单元比重低,淹没在杂波或噪声背景;4)慢速目标,不仅在时域波形难以与背景区分,并且频谱淹没在杂波谱中,使得频域滤波方法失效;5)高速运动目标,在观测时间内,容易跨越多个距离和多普勒单元,能量发散。传统体制雷达以及信号处理方法难以实现目标能量的有效积累,目标分辨单元中的信杂噪比低,低可观测特性显著[5]。
长期以来,国内外对微弱目标的雷达探测技术开展了深入而有效的研究,在杂波特性分析与建模[6]、杂波抑制[7]、目标能量积累[8]、CFAR处理[9]以及目标跟踪[10-11]等方面都取得了大量的成果。常规雷达体制(脉冲多普勒体制、相控阵体制等)对微弱目标的探测还存在如下问题:1)从杂波中提取(发现)目标首先要寻找一个能够有效分离目标和杂波的观测空间。正是基于这一思想,信号处理所对应的观测空间从最初的时域逐渐扩展到频域、时频域、空时域、空时频域等。2)雷达探测面临着复杂多样的目标类型,这既加重了常规雷达信号处理与数据处理的复杂度,同时也严重影响了雷达探测的整体性能。例如,海上目标的强弱差异大,对于采用集中波束辐射能量的常规雷达来说,大的波束增益容易导致强目标(或强海杂波叠加的弱目标)回波饱和,影响目标航向航速的估计精度及跟踪性能,而小的波束增益又不利于弱目标的探测。目标的速度差异大,既有静止和慢速运动的目标,其多普勒极易淹没在展宽的杂波谱中,又有高速掠海飞行的反舰导弹等低空突防目标[12]。
长时间积累技术能够有效提高回波信噪比进而提高微弱目标的检测性能,得到了国内外学者的广泛关注,但传统体制雷达多为高增益窄波束模式,无法保证足够有效长的积累时间,限制了长时积累技术的发展。近年来,多输入多输出(Multiple Input Multiple Output, MIMO)雷达体制受到越来越多的关注,在波形设计、参数估计和目标检测等方面出现了大量的研究成果[13-15]。MIMO雷达体制在信号波形和阵元位置上的灵活性能够为复杂且动态的杂波背景下的信号处理提供更大的自由度;具有宽发窄收、泛探观测方式的正交波形MIMO雷达可有效延长目标驻留时间、实现时域、空域和频率的联合处理和高分辨估计[16-17],因此,对于强杂波背景下的雷达目标探测具有重要的应用潜力[18]。目标能量的长时间积累一般分为两种,长时间相参积累[8]和长时间非相参积累[19]。相比于长时间非相参积累,长时间相参积累(Long-time Coherent Integration, LTCI)同时利用信号的幅度和相位信息,实现快时间和慢时间的联合积累,可获得更高的积累增益,但在积累时间内,会出现复杂距离徙动和多普勒徙动现象,影响积累效果。
针对微弱目标检测的技术挑战,本文集中对近年来正交波形MIMO雷达长时积累技术的研究进展进行了归纳总结,并分析该技术领域存在的问题,指出其发展趋势。本文内容安排如下。第2节介绍MIMO雷达长时积累的概念与挑战。第3节分别从机动目标回波模型和特性分析、变换域相参积累、长时非相参积累、分段、分步、分级长时积累、基于参数搜索和非参数搜索的长时相参积累以及稀疏变换长时相参积累等几个方面,系统梳理了MIMO雷达动目标信号积累技术现状,并介绍了作者团队在此方面的工作。本文第4节针对现有研究存在的不足,提出今后的研究发展趋势。第5节对全文归纳总结。
在雷达信号处理中,通常可以通过延长积累时间达到增加目标能量、改善信杂噪比的目的。然而,对于机械扫描雷达,由于天线机械旋转的惯性,波束在每个指向的驻留时间有限,因此可供积累的回波脉冲数量有限。近年来,随着相控阵雷达、数字阵雷达、MIMO雷达、全息雷达等新体制的不断发展和应用,其宽发窄收模式、驻留模式以及凝视模式等工作模式为目标能量的长时间积累处理提供了可能[20-21]。
以发射正交波形的MIMO阵列雷达为例,如图1所示,由于各阵元发射波形正交,因此不能形成方向性波束,其能量基本均匀的分布在一个很宽的观测区域内,相当于发射波束一直照射在该区域内的每个目标上。只要信号能量积累方法得当,原则上目标能量的积累时间只取决于目标在该区域内的停留时间。
图1 发射正交波形的MIMO阵列雷达示意图
Fig.1 Schematic diagram of MIMO array radar transmitting orthogonal waveforms
设M个阵元,发射M个信号,s1(n),s2(n),…,sM(n),其中n表示各个阵元发射的第n个脉冲。假设在各个阵元上附加不同的相位,将这些相位项表示成矢量为,
然后将附加相位的信号从各个阵元上发射出去,即,第一个阵元发射的是a1(θ0)s1(n),……,第M个阵元发射的是aM(θ0)sM(n)。假设目标位于方位θ处,那么,第一个阵元发射的信号到达目标时的相移可记为a1(θ),依此类推,第M个阵元发射的信号到达目标时的相移记为aM(θ),那么,第一个阵元发射的信号到达目标时变为a1(θ0)s1(n)a1(θ),依此类推,第M个阵元发射的信号到达目标时变为aM(θ0)sM(n)aM(θ)。然后这些信号在目标处叠加在一起,记为xθ(n):
xθ(n)=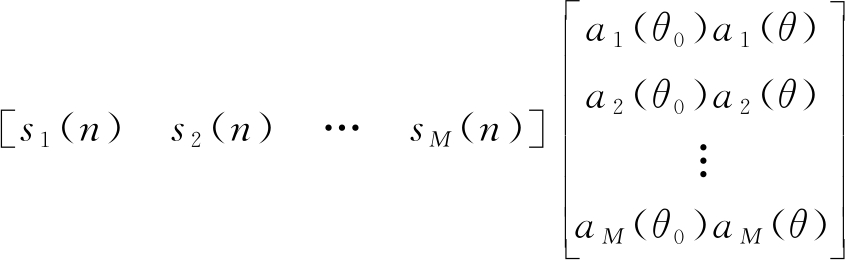
(1)
那么,目标处信号的功率为,
(2)
其中,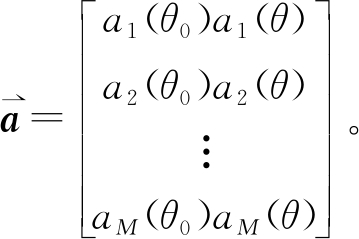
当各个阵元发射的信号相互正交时,那么,
NR=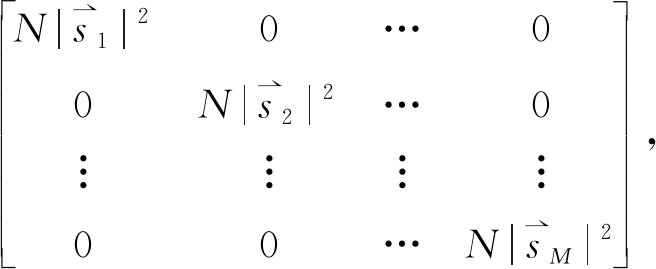
其中,
=p表示第m个阵元发射的脉冲串的功率。从而,上式可写为:
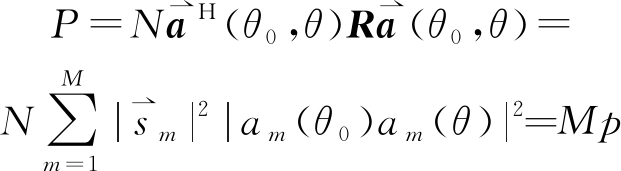
(3)
其中,导向矢量的模为1。
这表明,只要各个阵元各向同性发射的是正交信号,那么,无论各个阵元上附加什么样的相移,也无论目标处在那个方位角上,目标处的功率都是相同的,也就是说,此时发射功率密度是均匀的。以全向发射波束和数字波束形成接收多波束的探测体制被称为“泛探”工作模式,能够实现探测空域内连续和不间断的监视[13, 22-24]。因此该模式也是长时积累信号处理的基础,通过延长信号的积累时间,增加信号能量,从而对抗噪声和杂波背景,提高动目标雷达探测能力。
积累时间的长短是一个相对的概念,与最小相参积累增益、目标速度、天线波束驻留时间和回波采样频率密切相关,在海杂波背景下,还需要考虑海杂波和目标的去相关时间。针对不同的微动目标模型,其积累时间的选取也是不同的。相比于长时间非相参积累,长时间相参积累要求积累时间内目标RCS不能起伏,因此,相参积累时间通常要比非相参积累时间短,且相参积累时间内目标不宜跨越较大的角度范围,以免引起RCS起伏。鉴于两者的上述差别,一般在检测前跟踪(Track before detection, TBD)处理中采用长时间非相参积累,而在先检测后跟踪(Detection before track, DBT)处理中采用长时间相参积累。
在TBD方法中,长时间积累主要解决两方面问题,一是短时间相参积累达到TBD方法检测跟踪所需最低信噪比要求,二是长时间非相参积累过程中结合目标运动信息的目标航迹快速搜索。前一方面的问题可参照DBT方法中所述的内容。后一方面的问题已有多种解决方法,包括:1)三维匹配滤波器方法[25],该方法将运动点目标的检测转化为三维变换域中寻找匹配滤波器的问题。2)多级假设检验方法[26],该方法将大量可能的目标轨迹以树的形式组织起来,采用假设检验的方法对树形结构的每一层分支做出删减,具有同时检测出多个直线运动目标的能力,但在低信噪比条件下,算法所需计算量迅速增加,影响算法性能。3)动态规划方法[27],该方法实际上是将一个多变量联合优化问题通过分级处理转化为单变量优化问题,从而大大简化了求解过程。不过,该方法在信噪比很低时,继续增加帧数难以提高目标检测的性能。4)投影变换方法,该类方法分为二维投影和三维投影。作为其中的杰出代表,Hough变换方法[28]将位于距离-慢时间(帧时间)平面中的目标轨迹积累到参数空间中的一点,实现目标能量的积累。5)基于粒子滤波的TBD方法[10, 29]是递归贝叶斯滤波的一种实现方法,非常适合处理非线性、非高斯类的目标运动模型和传感器观测模型,完整地引入了跟踪的思想和算法,其实现过程简单,能对目标状态的后验概率进行较好地估计,是TBD技术实现方法中的研究热点。
在DBT方法研究中,长时间积累主要解决的是长时间相参积累问题。长时间相参积累(Long-time Coherent Integration, LTCI)技术同时利用了目标回波的幅度和相位信息,具有积累增益高,抗杂波性能好等优点,能对具有威胁的微弱动目标进行早期预警,非常适于复杂环境下微弱动目标的检测。然而,随着观测时间的延长,相参积累后的目标能量可能会在距离和多普勒平面上发生二维扩散,即所谓的距离和多普勒走动现象,从而限制了LTCI的性能。在未知目标运动参数的情况下,如何通过运动补偿来延长有效相参积累时间仍然是雷达信号长时间积累处理的一个重要研究方向[30]。
实际应用中,一方面由于雷达距离分辨力的不断提高和积累时间的增加,目标回波包络在不同脉冲周期当目标径向速度在观测时间里近似为匀速时,运动补偿主要是解决距离走动问题[31]。文献[32-34]分别采用距离拉伸联合时频分析方法、速度分段方法、频分包络移位补偿方法和时域包络插值补偿方法来校正目标的距离走动;文献[13]采用Keystone变换来校正距离走动,其优点是无需已知目标速度,但受多普勒模糊的影响,该方法不适用于重频较低的情况。文献[35]提出的Radon-Fourier变换方法在距离-慢时间二维平面中利用离散傅里叶变换沿目标运动参数给出的观测值轨迹进行积分,实现目标能量的LTCI。该方法本质上是一种多普勒滤波器,既避免了补偿类方法对目标距离走动的校正,又能将MTD、Hough变换和Radon变换等方法统一起来,是一种优秀的长时间积累方法。
在只考虑多普勒走动而不考虑距离走动的情况中,通常研究较多的是目标具有恒定径向加速度的情况。此时,目标回波在慢时间维是一个线性调频信号,可采用Radon-Wigner变换、Wigner-Hough变换、Radon-ambiguity变换、chirplet变换、分数阶傅里叶变换(FRFT)等时频分析方法对其进行能量积累[36]。当目标发生复杂机动而不能用简单的匀速和匀加速建模时,目标检测问题变得更加复杂,一般需要采用时频分布并联合其他方法对其进行检测,且难以实现目标能量的相参积累。
稳健和有效的杂波抑制及机动目标检测始终是雷达信号处理领域的难题,研究提高雷达对微弱动目标检测能力的信号处理方法具有重要意义。由于探测环境的复杂性以及目标运动形式的多样化,使得目标回波具有低可观测性,对雷达探测提出了严峻挑战。正交波形MIMO雷达长时积累的技术挑战具体表现为:1)机动目标,如快艇、舰船等,其运动形式表现为匀加速运动、变加速运动等高阶运动,其多普勒表现为明显的时变特性,传统相参积累检测方法难以有效对目标能量有效积累;2)由于目标机动,其回波相位表现为多项式相位信号,机动性越强,多项式阶数越高,对其检测和参数的高精度估计也越难;3)高速高机动使得目标容易跨越单个距离单元,可有效利用的脉冲数少,使得传统基于单一距离单元检测方法性能下降;4)受杂波影响,目标时域幅度和频谱均易被杂波覆盖,使得信杂比(Signal-to-Clutter Ratio, SCR)较低。因此,机动目标在距离和多普勒分辨单元中往往具有较低的SCR,提高了MIMO雷达探测的难度;5)在已有的LTCI方法中,很少研究同时补偿目标回波距离和多普勒走动的方法,另外,现有的大部分方法运算量较大,难以工程实现。
机动目标特性分析及其回波模型建模的准确性是检测的第一步,也是实现目标能量有效积累、提高目标检测性能的前提。在机动目标运动特征、电磁传播特性、目标散射特性的基础上,构建机动目标雷达回波模型,通过精确反映目标信号的幅度与相位的变换特点,进而得到目标的时变多普勒变化规律。对正交波形MIMO雷达各个阵元接收到的脉冲回波进行匹配滤波之后,形成了等效接收数字阵观测条件下的长时间多脉冲回波数据。以发射线性调频脉冲信号为例,脉内积累后的雷达回波数据sPC(t,tm),
sPC(t,tm)=
(4)
式中,APC为信号幅度,t为脉内快时间,tm为脉间慢时间,B为发射信号带宽,Rs(tm)为雷达与目标的径向距离,c0代表光速,2Rs(tm)/c为回波延迟,λ为信号波长。
假设目标朝向雷达运动,且仅考虑径向速度分量,则目标的距离走动为慢时间的N阶多项式函数。
(5)
式中,ai为多项式系数。
对于大多数机动目标,三阶多项式可描述大部分的机动目标的运动,即
(6)
式中,r0表示初始距离,ν0、as、gs为矢量,分别代表目标运动初速度、加速度和急动度。
对于以非匀速平动为主要运动方式的海面目标,如低空掠海飞行目标、快艇等,运动形式主要以加速或减速运动为主,同一距离单元脉间信号可建模为线性调频(Linear frequency modulated, LFM)信号,加速度与LFM信号的调频率相对应;而对于以变加速的高机动目标,如导弹等,其可建模为多分量二次调频(Quadratic Frequency Modulated, QFM)信号,具有二次调频的多普勒频率,与目标的加加速度(急动度)相对应;对于以旋转、进动为主要运动形式的目标,如直升机旋翼、导弹弹头等,其回波可建模为正余弦函数,周期频率对应目标的旋转转动速度。由于在一定的观测时间范围内,正余弦函数可近似为高阶多项式相位函数,因此,目前人们普遍将机动目标的回波信号函数建模为LFM或QFM信号,多项式阶次越高,后续的信号处理算法越复杂,也需要进行一定的折中考虑[37-38]。
机动目标是低可观测目标中很重要的目标类型之一,往往利用多普勒信息对其进行积累检测[3]。以滤波器为典型的处理手段的经典频域滤波方法为动目标显示MTI(Moving Target Indication, MTI)和动目标检测(Moving Target Detection, MTD),通过设计一定的低通或高通滤波器或窄带多普勒滤波器组来实现频域滤除杂波,保留动目标的目的。然而,对于具有复杂运动特性的机动目标回波,其回波信号具有时变、非平稳特性,难以在单一多普勒通道形成峰值,检测性能下降。为此,将一维频域处理扩展为时间-频率二维处理,即时频分析,适合分析时变信号,将其用于雷达动目标检测,能够反映多普勒随时间的变化[39]。从多分量信号变换后是否存在交叉项(变换是否为线性变换)将时频分析分为线性时频表示和非线性时频表示[40]。前者最为典型的是短时傅里叶变换(Short-time Fourier Transform, STFT)和小波变换(Wavelet Transform, WT)等;后者主要是Cohen类时频分布,其中典型的是WVD、伪WVD(Pseudo WVD, PWVD)以及平滑伪WVD(SPWVD)等[41]。表1比较了几种典型的变换域目标检测技术的优缺点。
傅里叶分析理论体系在分析与处理平稳信号时具有极大的优越性,然而在雷达高速高机动目标探测中,信号呈现出时变、非平稳等复杂特性。分数阶傅里叶变换(Fractional Fourier Transform, FRFT)以LFM作为基函数,介于时域和频域之间的任意分数域表征,能够反映多普勒的变化规律,适于处理时变的非平稳信号,且无交叉项的干扰。后续为了能够实现时变非平稳信号的时频谱表示,作者在短时FRFT(STFRFT)[42]理论的基础上,提出了STFRFT动目标检测方法[43],并用于低慢小目标的检测中,同时对于具有高阶相位的高机动目标,提出了分数阶模糊函数(Fractional Ambiguity Function, FRAF)以及线性正则模糊函数等[44],均在机动目标检测中得到了很好的应用。对具有急动度或高阶运动目标的多普勒徙动补偿方法则主要是以时频分析技术和高阶信号处理技术为主,包括对时频平面进行旋转处理的FRFT、对多项式相位信号进行降阶处理的高阶模糊函数(High-order Ambiguity Function, HAF)、对信号多项式系数进行参数搜索处理的多项式傅里叶变换(Polynomial FT, PFT)以及多项式相位变换(Polynomial Phase Transform, PPT)等方法[45- 46]。其中,FRFT仅适用于处理LFM信号,基于降阶的参数估计算法和高阶匹配相位变换参数估计法,算法复杂,并且高阶次的非线性变换会产生交叉项,影响参数估计和信号检测。此外,上述方法的补偿性能均受可利用信号长度的限制。
变换域和时频分析类目标检测方法极大推动了雷达目标检测理论和应用的发展,但在复杂探测环境下,性能仍有待改进,主要体现在:1)仅能利用同一距离单元的回波,积累增益低,对跨距离单元的机动目标检测效果差;2)检测方法通用性差,参数和影响因素多;3)应用到杂波背景中的动目标检测时,算法的积累增益往往受强杂波的影响。图2给出了几种变换域相参积累方法对海上目标的处理结果,可以发现STFT时频分辨率较差,WVD存在严重交叉项,海杂波在SPWVD和FRFT域也有一定的积累,谱峰影响动目标的正确检测。
表1 几种典型的变换域目标检测技术
Tab.1 Several typical target detection techniques in transform domain
方法技术原理优缺点STFT在FT的基础上加上一个长度恒定的窗函数,变换出窗内信号的时频信息。适用于匀速运动。时频聚集程度较低,没有交叉项。WVD对时域信号进行二次型变换。适合匀变速运动目标,存在交叉项,时频聚集程度较高。PWVD对WVD施加窗函数。适用于匀变速运动目标,一定程度上抑制了交叉项,但时频聚集程度降低。SPWVD对WVD施加窗函数和平滑函数。适合匀变速运动目标,运算量大,时频聚集程度下降,可有效抑制交叉项。WT采用可调时频窗。适用于慢速运动目标,较好解决了时间分辨率和频率分辨率的矛盾。FRFT时频平面旋转投影。适于匀加速运动目标,没有交叉项干扰;不能反映信号任意时刻频率变化。
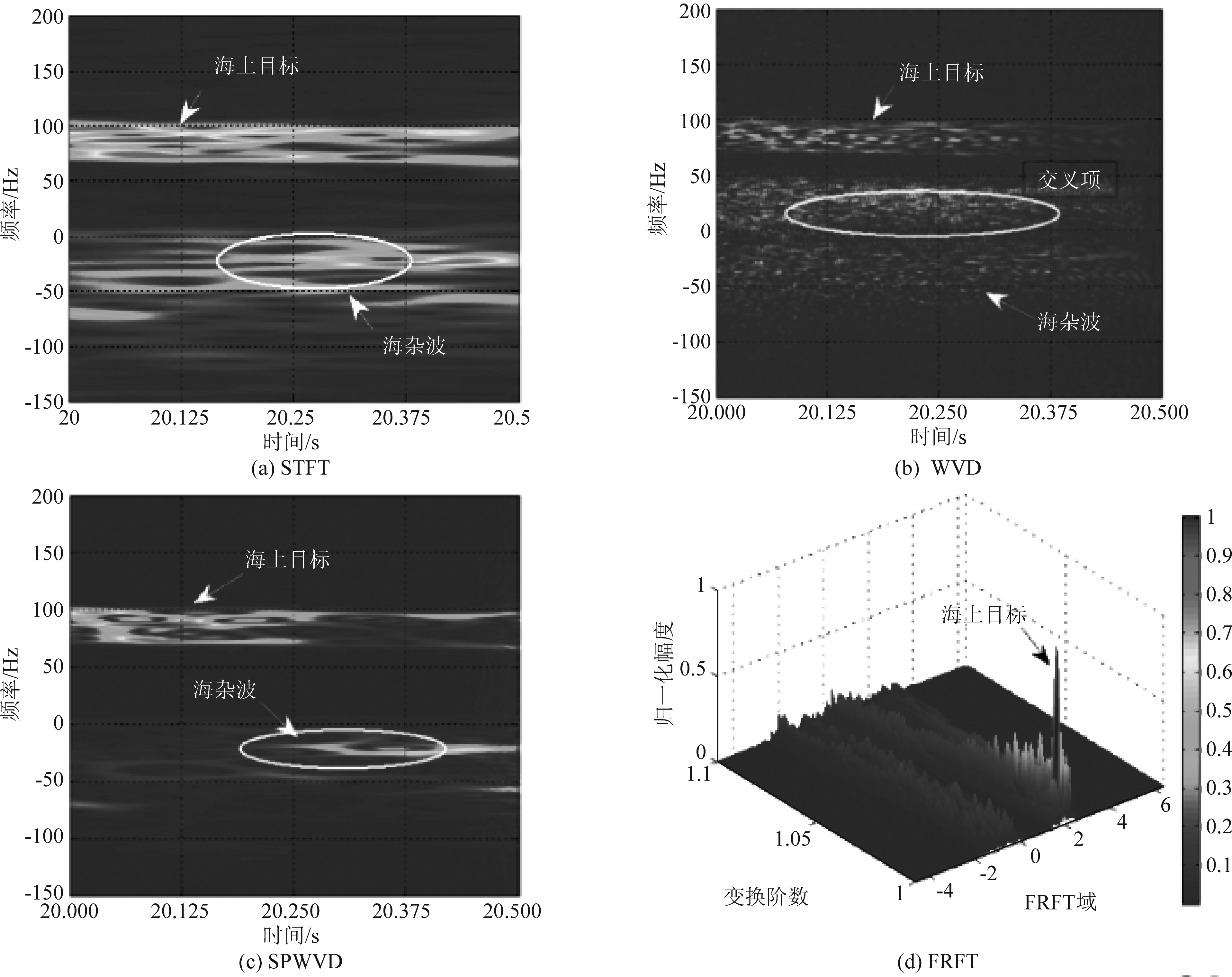
图2 海杂波背景下变换域相参积累结果比较[47]
Fig.2 Comparison of coherent integration results in transform domain under sea clutter background[47]
根据长时间脉冲积累是否利用目标信号的相位信息,可分为非相参积累、相参积累和混合积累三种。非相参积累方法包括包络插值移位补偿法、动态规划法、最大似然法和Hough变换(Hough Transform, HT)法等,对雷达系统硬件要求简单,但目标积累增益低,难以实现强杂波背景中的可靠检测。相参积累技术利用目标的运动特性和多普勒信息,可获得更高的积累增益[35, 48]。混合积累则是积累增益和算法复杂度介于非相参和相参积累之间。目前,对机动目标的长时间积累主要面临以下两个方面的问题:一方面由于雷达距离分辨力的不断提高和目标的高速运动,目标回波包络在不同脉冲周期之间走动和弯曲,产生距离徙动效应,使目标能量在距离向分散,例如由目标匀速运动产生的跨距离单元走动,称为一阶距离走动(First-order Range Migration, FRM);由目标加速或减速运动产生的跨距离单元走动,称为二阶距离走动(Second-order Range Migration, SRM);由目标高阶运动,如加速度变化,产生的跨距离单元走动称为三阶距离走动(Third-order Range Migration, TRM)[49-50]。另一方面,目标的加速、减速、高阶运动以及转动等会引起回波相位变化,使雷达回波信号具有时变特性并表现为高阶多项式相位形式,使得目标能量在频域分散,降低了相参积累增益。如式(4)可知,第一项sinc函数表示距离走动,第二个指数项表示多普勒信息,当距离和多普勒频率跨越多个多普勒单元时,便会产生距离和多普勒徙动效应。
目前,该领域的研究思路主要分为两类,第一类是根据目标的机动性和相应的运动状态来设计相应的长时积累方法,如匀速[35, 51]、匀加速或匀减速[52-55]、变加速或高阶运动目标[53, 56-57],来设计距离走动、距离弯曲和多普勒走动补偿方法,为了提高算法对目标机动特性的适应性,文献[30]提出了一种短时GRFT方法,通过准确估计目标运动模型的“转戾点”与模态变化的节点位置,随后通过判断和确定目标的具体运动模态,然后利用自适应处理,实现多模态间相参积累算法的自适应切换和匹配,从而对多种运动模态高机动目标动态相参处理。另一种研究思路主要是从处理的流程和算法运算量等角度来设计相应的长时积累方法,如分段处理、分步处理、分级处理、参数搜索LTCI、相位差分降阶LTCI、非参数搜索LTCI等,具体来说该部分的主要思路是:
1)基于运动轨迹搜索的长时间非相参积累方法
最为典型的是TBD技术,通HT等轨迹搜索方法,把可能是同一运动轨迹的回波能量进行幅值积累,也称长时间非相参积累[29, 58-59]。该类方法对系统没有严格的相参要求,在工程实现上比较简单,但其信号积累效率和SCR改善均明显低于相参积累方法,复杂环境下微弱动目标的检测性能难以保证。
2)分段长时间积累方法
即非相参和相参积累结合的混合积累方法,首先将距离分段,在段内完成脉冲间的相参积累,然后通过距离包络对齐或Keystone变换(Keystone Transform, KT)法实现回波的非相参积累。文献[60]通过将积累时间划分为若干个子孔径,在子孔径内同一个距离单元相参积累,在子孔径间实现高效的跨距离单元非相参积累,是一种混合积累方法。该方法是一种检测性能和运算量综合考虑的有效途径,但积累增益仍非常有限,无法应对强杂波背景和机动目标的复杂运动形式。
3)分步长时间积累方法
即先补偿距离走动,再采用变换域处理方法匹配时变的多普勒信号,如相位匹配法、FRFT、Chirplet变换等,最典型的距离走动补偿方法为KT法,这种方法能够通过插值对原有的坐标轴进行尺度变换,从而有效地校正距离徙动[61- 63]。但KT方法仅能补偿一阶距离走动,即匀速运动导致的距离走动,对于高阶机动目标信号,其距离走动体现为高阶多项式,难以有效补偿,需要研究二阶KT的补偿方法;并且后续多普勒走动补偿的效果受距离走动补偿结果影响,容易造成目标多普勒能量扩散,运动参数估计精度较差。
4)分级长时间积累方法
由于对机动目标的相参积累涉及多维参数的匹配滤波,运算量较大,但在雷达不同距离的雷达回波中,目标所占据的单元是有限的,因此,可对数据进行预处理,将有可能存在机动目标的单元筛选出来,后续再进行长时积累,是工程应用的一种有效途径。文献[64]综合利用MTD和FRFT、FRAF的优势,采用两级门限处理,即首先采用MTD处理通过较高的虚警概率条件下的门限(第一级门限),筛选出可能有机动目标的距离单元,然后将这些距离单元的回波并行经过FRFT和FRAF运算,通过最佳变换域输出SCR的比较,判断机动目标回波与哪种变换匹配最佳,从而在相应的距离-最佳变换域进行恒虚警检测(第二级门限),并进行运动参数估计,由于仅在超过第一级门限的少数几个距离单元内进行处理,从而在保证较高检测性能的同时降低运算量,并能准确估计出机动目标的多个运动参数,如速度、加速度和急动度等,实现机动目标的快速精细化处理。
5)基于参数搜索的LTCI方法
最典型的是Radon变换类方法,对距离徙动和多普勒徙动进行统一补偿,典型的方法为傅里叶变换(Radon-FT, RFT)[65],它在脉压后的距离-慢时间域通过搜索初始距离和旋转角度实现信号的相参积累,很好地将MTD、HT和RT统一起来,但RFT仅沿目标运动的直线轨迹进行相参积累,当遇到机动目标产生的距离弯曲和高阶非平稳相位时,RFT积累增益下降。为此,Radon-FRFT(RFRFT)[66]、Radon-FRAF(RFRAF)[67]、Radon-线性正则变换(RLCT)[53]、Radon-Lv分布(Radon Lv’s Distribution, RLVD)[56]、Radon-线性正则模糊函数(RLCAF)[68]、Radon多项式FT(Radon-Polynomial FT, RPFT)[69]等,方法根据预先设定的目标运动参数(初始距离、速度和加速度)搜索范围,提取位于距离-慢时间二维平面中的目标观测值,然后在相应的变换域选择合适的变换参数对该观测值进行匹配和积累,实现对动目标能量的LTCI,即通过在速度/加速度-距离域的多维联合搜索实现一阶/高阶距离徙动的校正同时获得目标的能量积累,该类方法的主要问题在于需要多维参数搜索,导致运算量较大,难以满足雷达实时信号处理的要求。
6)基于相位差分降阶的相参积累方法
由于机动目标脉压后回波相位可近似为多项式函数,目标机动性越强多项式相位越高,因此,先采用相关或相位差分方法将高阶多项式降阶为低阶多项式,再采用FRFT或FT进行积累,从而降低运算量[49],但该方法多为逐次降阶,每一次降阶均会产生交叉项,尤其是在多分量信号或低信噪比/信杂比条件下,杂波和多分量信号之间将产生交叉项,从而影响了积累效果和参数估计精度。
7)基于非参数搜索的LTCI方法
现有的LTCI处理方法多根据目标的机动参数在相应的快时间(距离)-慢时间(脉间)进的变换域进行匹配搜索,随着参数维度的增加,运算量也随之增加,这也限制了LTCI的应用。近年来,人们研究提出了基于非参数搜索的LTCI方法,通过快速降阶处理和多项式相位补偿等思路,提高算法运算效率[70]。文献[71]提出了一种基于非均匀采样降阶运算的非参数搜索LTCI,如图3所示。非均匀采样降阶运算不同于传统的相位差分运算,在不进行信号的延迟复共轭相乘逐次降阶的前提下,能够快速将N阶相位降阶至N/2或N/2+1阶,从而大大降低了运算量。
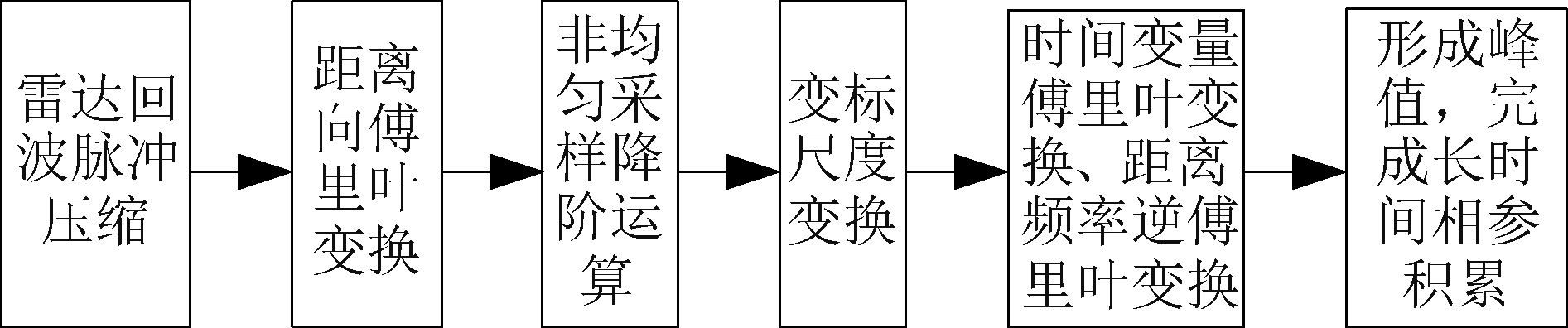
图3 基于非均匀采样降阶运算的非参数搜索LTCI处理流程[71]
Fig.3 Non-parametric search LTCI processing based on non-uniform sampling reduced order operation[71]
作者所在团队从目标加速度、急动度信息的利用及算法实时性角度出发,提出了3类12种高速高机动目标检测方法(图4),形成了较为完整的长时间相参积累理论框架。通过跨单元的多参数广义多普勒滤波器组、时间反转非均匀采样、变标处理等关键技术,实现距离和多普勒徙动同时补偿[64]。
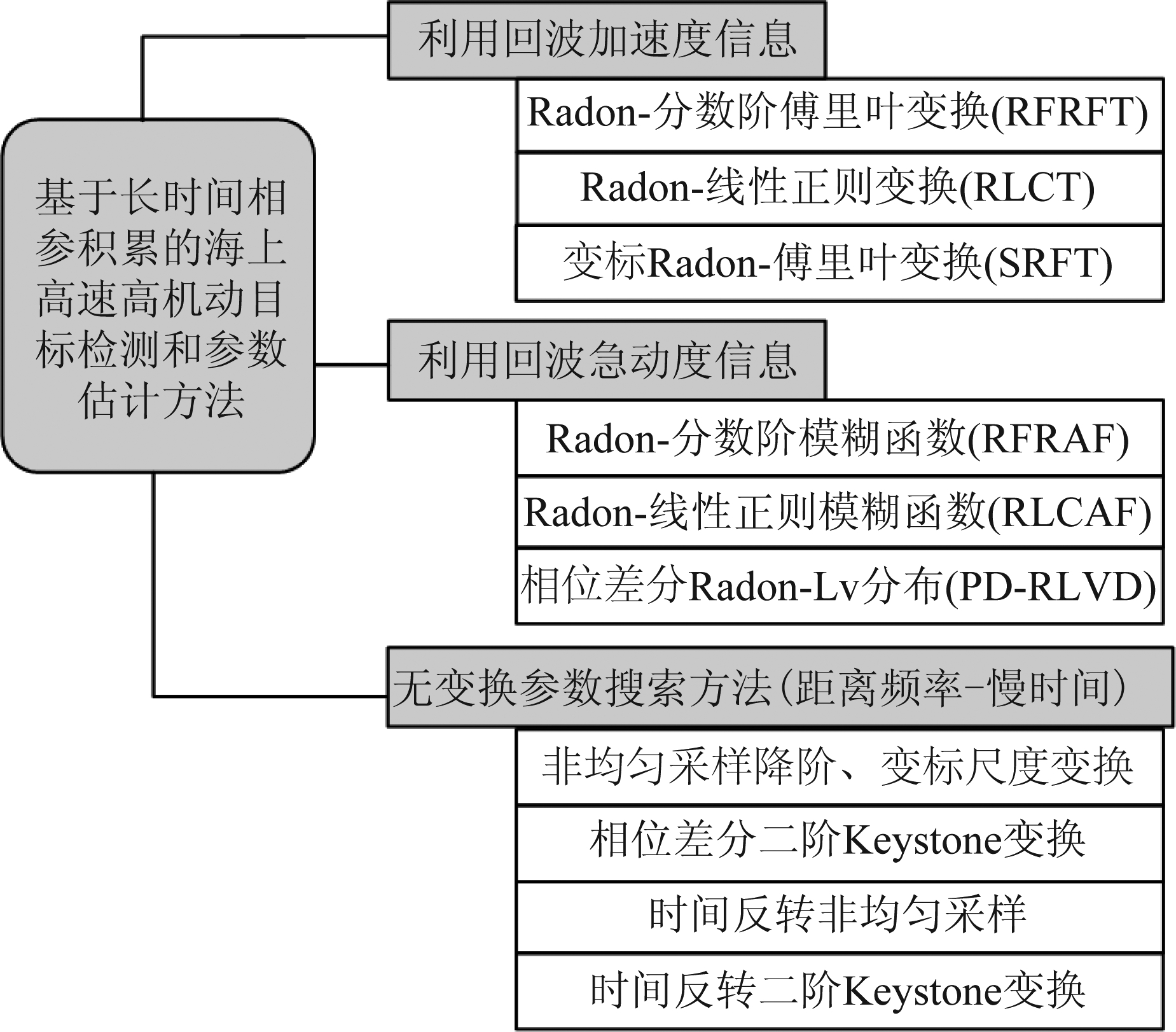
图4 基于长时间相参积累的海上机动目标检测理论框架
Fig.4 Theoretical framework for detection of maneuvering targets at sea based on long-time coherent integration
所提方法是MTD、FRFT、LCT、模糊函数、Lv分布等方法的广义形式,能够灵活匹配并积累杂波中的非匀速平动、转动以及高阶运动目标的回波信号,扩展信号利用的维度,解决了运动目标在长时间观测过程中的能量难积累、目标参数估计精度低、运算量大等问题。实测数据验证表明(图5),在三级海况、检测概率不低于80%条件下,相比频域处理方法,对SCR要求降低5 dB以上,显著提高了杂波背景中的机动目标检测性能。
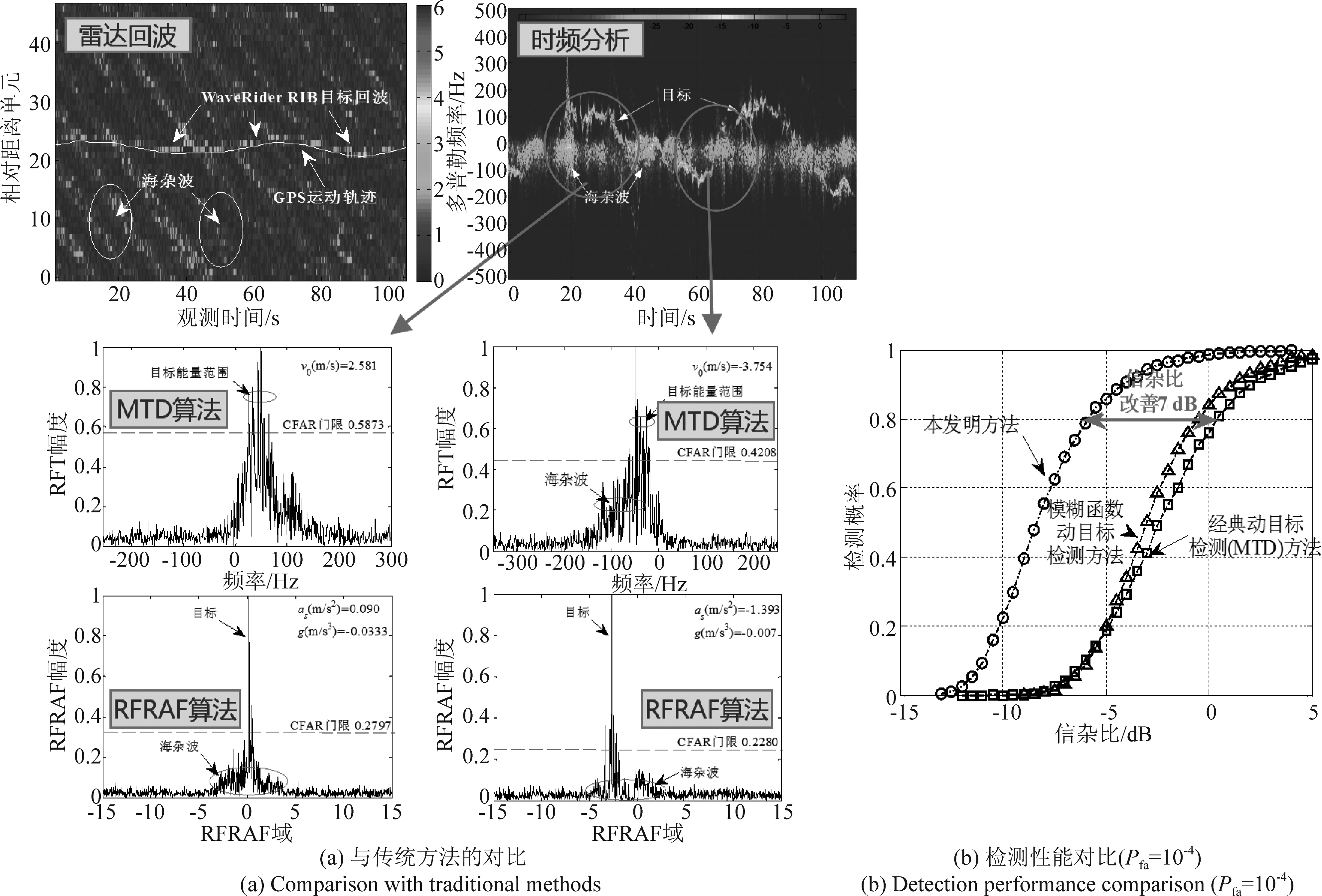
图5 海上高速高机动目标检测结果对比(实测雷达数据)[67]
Fig.5 Comparison of detection results of high speed and maneuvering targets at sea (real radar data)[67]
随着雷达观测时间的延长,回波脉冲采样点急剧增加,此时再采用参数搜索匹配的思路运算效率很低,如何高效利用大数据量回波脉冲,在长时观测条件下有效提取目标的特征并用于检测成为亟需研究的问题。利用动目标回波信号具有稀疏性的特点[72],将稀疏变换和稀疏时频分析的方法引入LTCI处理,能够有效提高算法运算效率、时频分辨率和参数估计性能,从而更有利于获得目标精细机动特征[73-74]。作者团队在SFT和SFRFT理论框架的基础上,结合时频分布(Time-frequency Distribution, TFD)类动目标检测和稀疏表示方法的优势,扩展了稀疏TFD(STFD)理论框架,提出短时稀疏TFD(ST-STFD)方法[44, 75-78],如短时稀疏傅里叶变换(ST-SFT)和短时稀疏分数阶傅里叶变换(ST-SFRFT)雷达动目标检测方法,并应用于海上机动目标特征提取及检测。因此,将稀疏变换以及STFD的思路与LTCI相结合,既可实现机动目标的跨距离和多普勒单元同时补偿,又能够降低运算量,实现快速积累和检测,同时,在机动目标稀疏域处理和检测,也能去除大部分的杂波信号,降低杂波虚警。
1)稀疏Radon变换LTCI
稀疏FRFT(SFRFT)算法主要包括时域Chirp乘法运算、SFT运算、频域Chirp乘法运算等三个过程,如图6所示,其中SFT运算主要包括以下几个步骤。
SFRFT算法对LFM信号具有良好的聚集性能,而且当数据长度N大于212时,能够明显降低FRFT的计算复杂度。根据Pei采样类离散分数阶Fourier变换(Discrete FRFT, DFRFT)方法,如果α≠Qπ(α表示旋转角度,Q为整数),离散FRFT可分解为一次FFT运算加两次Chirp乘法运算,因此SFRFT的基本思想是将离散FRFT的FFT阶段用SFT替换。
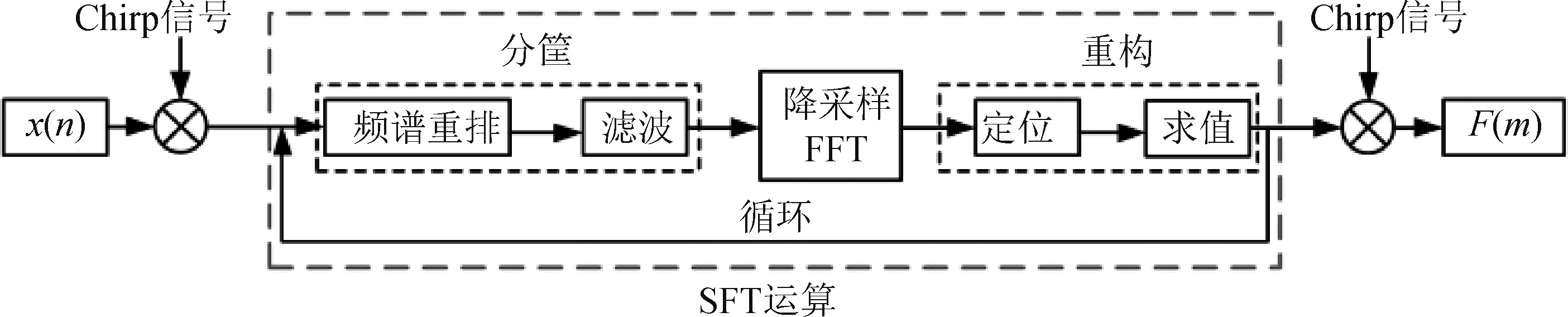
图6 SFRFT算法原理框图
Fig.6 Block diagram of SFRFT
稀疏FRAF算法(SFRAF)是在SFRFT的基础上,增加了信号的瞬时自相关函数(Instantaneous Auto Correlation Function, IACF)运算,
(7)
其中,
表示旋转角为α时信号的SFRAF,m∈[1,N]为SFRAF域离散变量,
和
分别表示Chirp乘法算子和SFT算子,Rs()为IACF,
Rs(t,τ)=s(t+τ/2)s*(t-τ/2)
(8)
将SFT和稀疏分数阶表示域处理方法与RFRFT、RFRAF和RLVD相结合,将高阶相位信号的变换域积累转变至稀疏变换域处理,设计稀疏Radon变换系列方法,如SRFRFT、SRFRAF和SRLVD,进一步提高长时间大数据量的运算效率和参数估计精度。SRFRFT、SRFRAF和SRLVD的研究方案流程图如图7所示,其中SLVD可通过二维SFT实现。
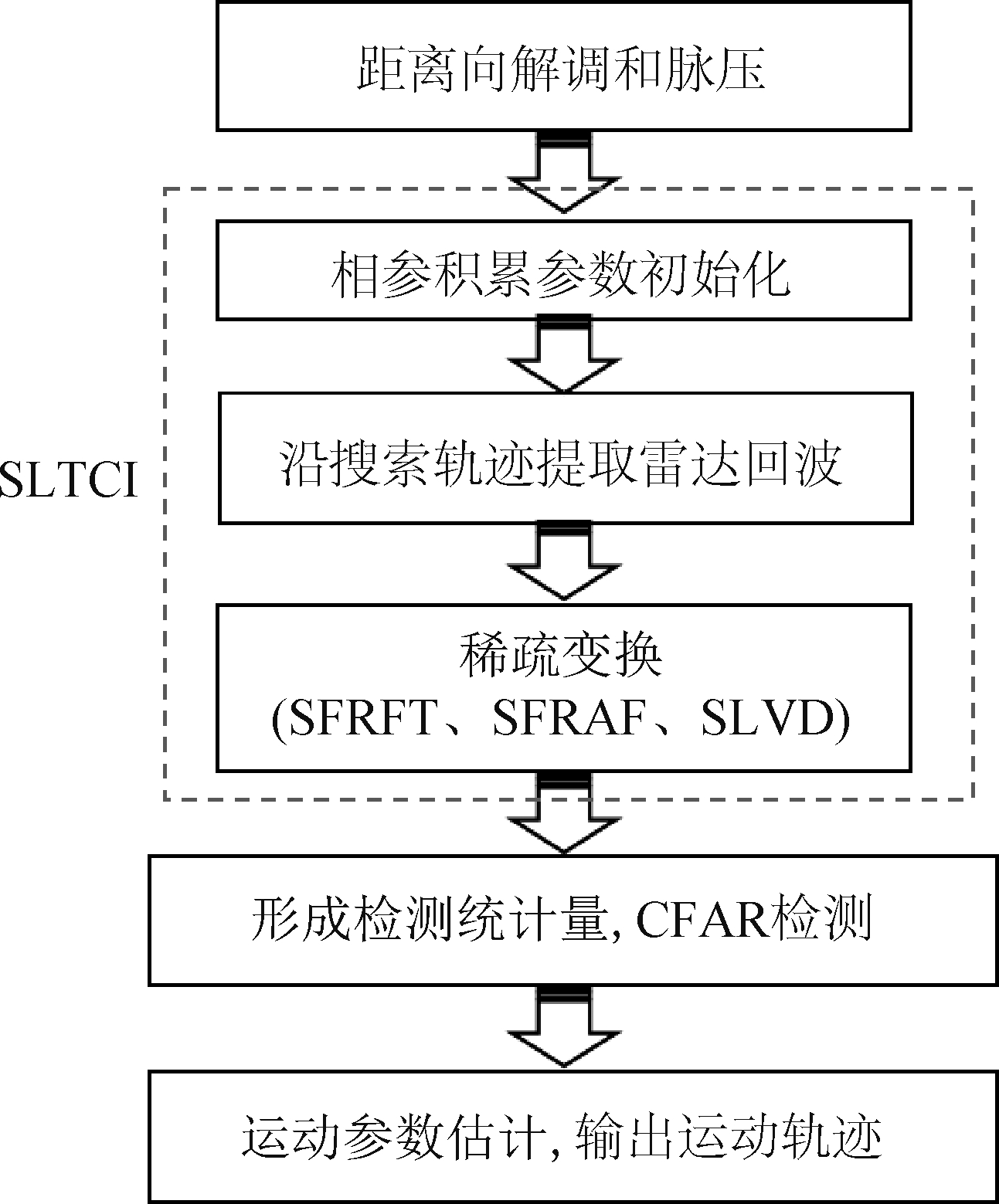
图7 稀疏变换LTCI的机动目标检测与参数估计算法原理框图
Fig.7 Block diagram of maneuvering target detection and parameter estimation algorithm based on sparse transform LTCI
2)稳健稀疏LTCI
SFT和SFRFT在降采样FFT后仅结合稀疏度和循环过程中频点出现的概率对大值系数进行估计,这在较低SCR的情况下难以保证重构信号的可靠性。此外,SFT和SFRFT方法需要预设稀疏度,而在实际应用中,信号的稀疏度往往是未知的或者可能发生改变的。针对上述问题,文献[77]提出一种稳健的稀疏变换积累检测方法,该方法主要是在图8所示的SFT理论框架中增加两级自适应的检测门限。一是改进降采样后频谱中目标频点的估计方式,二是基于重构后的疑似目标多普勒频率构造子空间检测器进行检测判决。降采样FFT形成的各个频率通道中引入标量CFAR检测,以抑制频域强杂波点对稀疏度及频点估值的影响,然后利用重构得到的疑似目标多普勒频率构造检测器,完成目标检测,以期满足复杂环境中的雷达动目标检测需求。
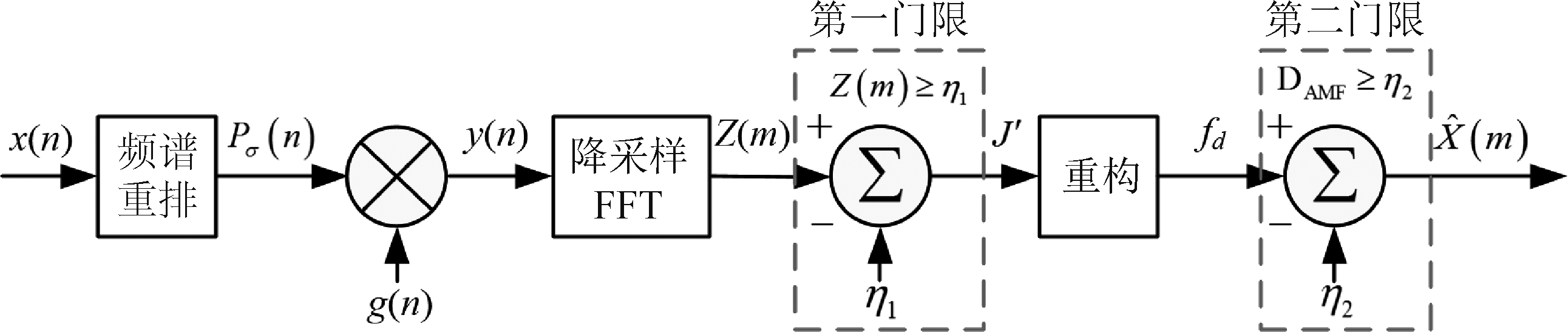
图8 自适应双门限稀疏傅里叶变换原理框图[77]
Fig.8 Functional block diagram of adaptive double threshold sparse Fourier transform (ADT-SFT)[77]
由图9给出了虚警概率Pfa=10- 4条件下,常规子空间检测算法、SFT算法、ADT-SFT算法、MTI-ADT-SFT算法的检测概率Pd与SCNR的关系曲线,图中K和H为无目标条件下,106次仿真得到的信号稀疏度估值和疑似目标多普勒频点数的平均值。可知:由于常规子空间检测算法通过逐个多普勒通道进行搜索并构造子空间检测器进行判决,因而在不考虑计算复杂度的情况下,相比于其他三种算法,它具有最佳的检测性能;常规子空间检测算法、ADT-SFT算法、MTI-ADT-SFT算法的检测性能均明显优于SFT算法至少10 dB以上,这表明,相比于SFT算法,ADT-SFT算法更适用于杂波背景,能够获得明显的检测性能改善;由于窗函数滤波造成的SCNR恶化问题,ADT-SFT算法的检测性能比常规子空间检测算法要差,但ADT-SFT只需对少量疑似目标多普勒频率构造子空间检测器,无需对多普勒通道进行逐一搜索,因而在计算复杂度方面具有较大优势;通过对原始数据进行MTI、AMTI等杂波抑制处理,能够进一步改善ADT-SFT算法的检测性能。
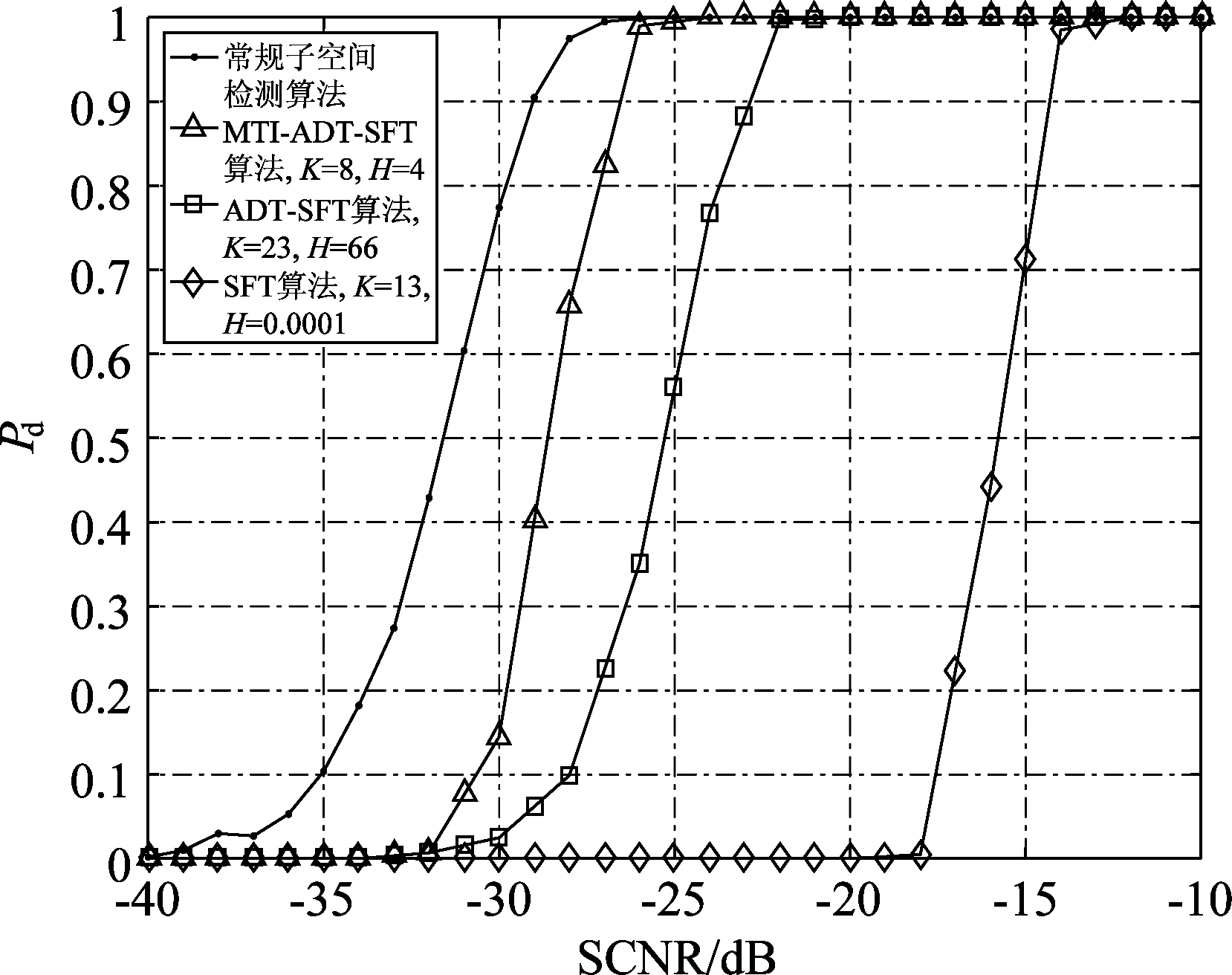
图9 ADT-SFT方法与SFT和常规子空间检测方法的检测性能比较[77]
Fig.9 Detection performance comparison of ADT-SFT, SFT, and subspace detector[77]
文献[79]将稳健的稀疏傅里叶变换方法推广到机动目标检测,在SFRFT的基础上增加两级检测门限,提出稳健SFRFT(Robust SFRFT, RSFRFT)的概念和基于RSFRFT的机动目标检测方法,如图10所示,以提高SFRFT算法的稳健性和低SCNR下机动目标信号重构的可靠性。为了进一步消除杂波虚警,文献[44]将自适应滤波方法引入SFRAF域,提出一种基于SFRAF的自适应杂波抑制和机动目标检测算法,不仅能够突破SFRAF对于稀疏度设置值的限制,而且在最大程度的保留信号能量的同时,能够较好的抑制杂波,在低信杂比情况下对高阶相位机动目标仍具有良好的检测性能。实测数据验证表明,相比经典稀疏成分分析(SCA)、MTD、SFT等方法,在大数据量条件下算法效率、杂波抑制和检测概率等方面有显著提高(图11)。将该思路应用于长时间相参积累,可有效改善算法运算效率。
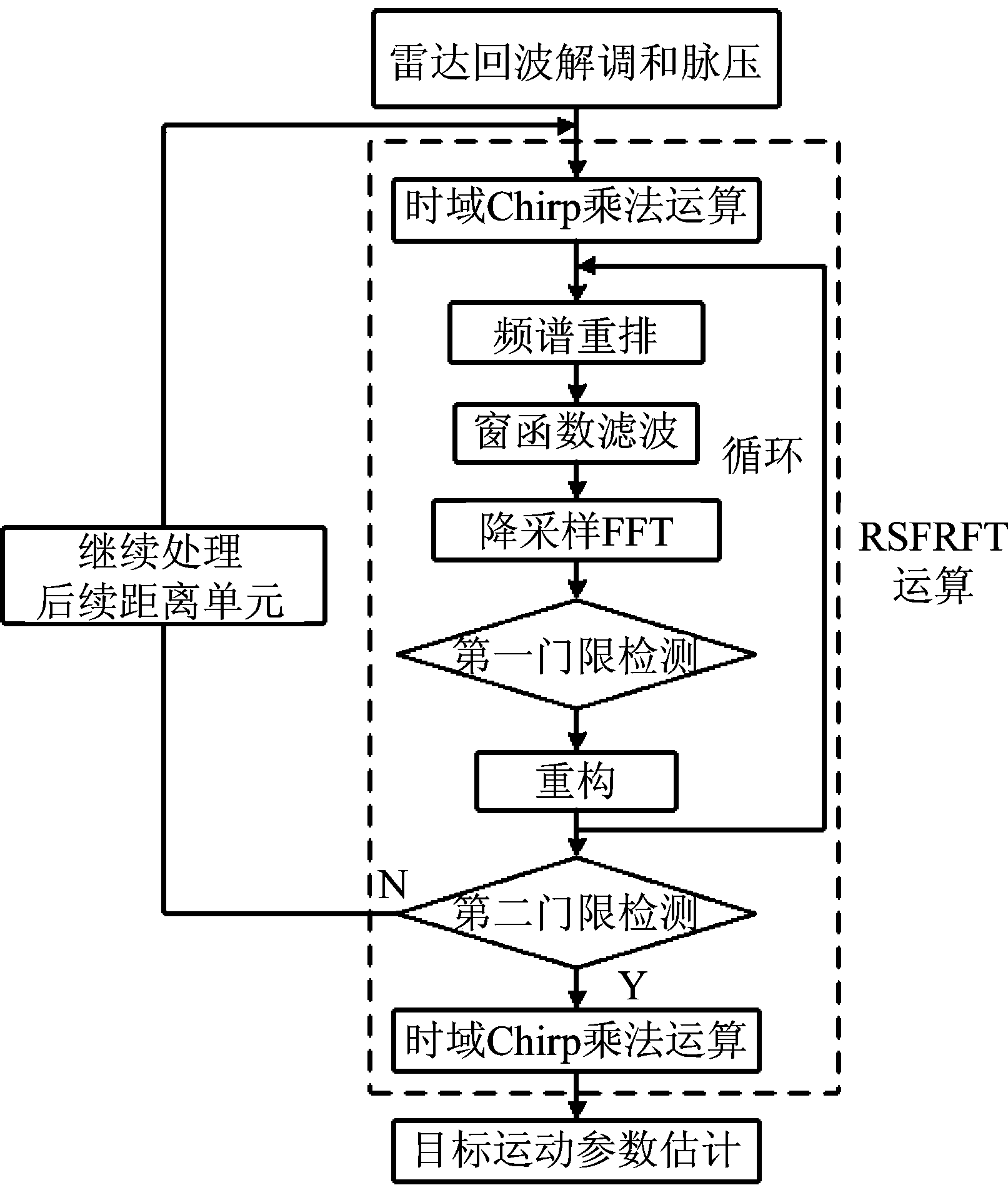
图10 基于RSFRFT的机动目标检测流程图[79]
Fig.10 Flow chart of maneuvering target detection based on RSFRFT[79]
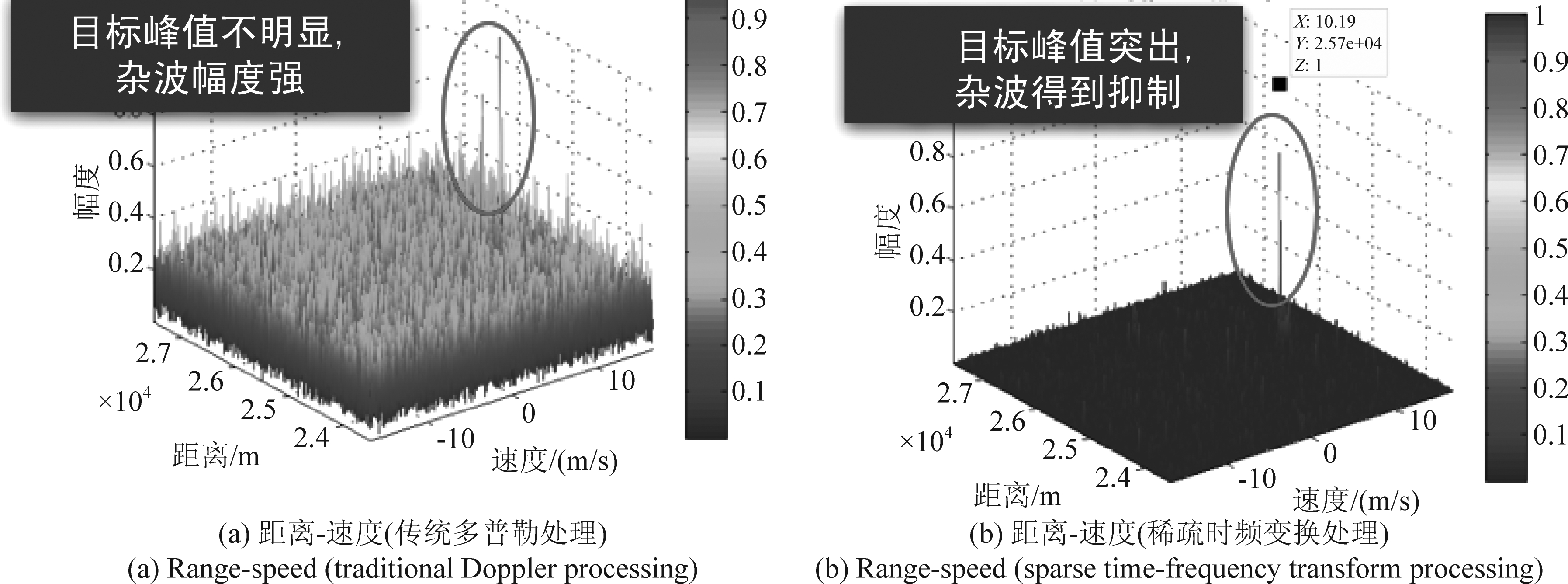
图11 基于STFD的海上低空飞行目标检测结果
Fig.11 STFD-based low-altitude flight target detection results
1)兼顾高积累增益性能和运算效率的非参数搜索LTCI
现有的Radon参数搜索类方法根据预先设定的目标运动参数(初始距离、速度和加速度)搜索范围,提取位于距离-慢时间二维平面中的目标观测值,然后在相应的变换域选择合适的变换参数对该观测值进行匹配和积累,实现对动目标能量的LTCI,但该类方法的主要问题在于需要多维参数搜索,导致运算量较大。相位差分逐次降阶的LTCI方法在处理机动目标高阶相位信号时,多次引入了交叉项,参数估计精度下降。通过快速降阶处理和多项式相位补偿等思路,提高算法运算效率。将非均匀采样降阶运算引入机动目标信号的多项式高阶相位的降阶处理,仅通过一次非均匀采样降阶运算,即可实现高阶相位信号降至低阶相位信号。利用时间反转及二阶KT对距离频率和高次项慢时间解耦,实现非参数搜索跨距离和多普勒单元的快速相参积累。
2)稀疏变换处理是LTCI工程化应用的有效手段
作为一种新兴的信号处理方法,信号稀疏表示在雷达信号处理方法具有很大的优势,能够突破采样定理的限制,利用目标信号在某个变换域中的稀疏性或稀疏分解下的稀疏性,对信号进行压缩,对频率具有超分辨能力,降低运算量,从而有利于机动目标的检测和获得精细的特征。自2012年美国麻省理工学院提出的SFT理论以来,已开发了多个版本的快速算法SFFT 1.0-3.0,克服了传统FFT算法运算量随采样点线性指数增加的不足,运算量近似保持线性增加,极大提高了大数据量条件下的运算效率[80],并应用于频谱感知、医学成像、图像检测和大数据处理等方面,因此非常适合LTCI的大数据量计算,并能够提高参数估计精度,成为LTCI工程化应用的有效手段。
3)长时积累虚警点剔除技术是强杂波背景下机动目标检测的重要保证
杂波具有非平稳、非线性特性,尤其是海面回波,即海杂波(海尖峰)与目标特性相似,尤其是相关性较低海况是明显增强,使得采用LTCI方法,将机动目标能量积累的同时也将海杂波的能量一并积累,导致SCR改善不明显,检测性能下降。因此,在LTCI的同时也应考虑该种处理方法对杂波的影响。在进行LTCI后,有部分杂波幅值超过检测门限,判为虚假目标,杂波在LTCI域的能量聚集性与机动目标有显著差异,可表现为峰值位置、谱聚集区域等特征差异[81],因此可基于杂波和机动目标的特性分析,进一步区分机动目标与杂波虚警,进而达到降低虚警的目的。
图12和图13比较了RFT、FRFT和RLCAF的相参积累结果,由图12的RFT谱和频域能量分布可知,经过RFT对距离的校正,目标能量能被积累至一个距离单元。海杂波能量也被积累起来,且某些距离单元的幅值高于目标幅值,因此容易产生虚警。虽然目标和海杂波的RFT谱分布有所差异,但由于RFT不能处理机动目标,机动目标谱与海杂波谱均发散,导致有部分重叠,因此,难以利用RFT谱能量聚集性差异性来区分杂波虚警和机动目标。采用RLCAF进行机动目标的LTCI,如图13所示,能够得到预期的两个峰值,由于海杂波相关时间较短,且失配于RLCAF,因此海杂波能量不集中,大部分幅值集中在较短的延迟时间范围内(τ∈[0, 0.1 s])。而机动目标峰值尖锐,且谱宽较窄,多信号分量间的交叉项的RLCAF谱峰较低,因此,通过海杂波和机动目标在LTCI域能量聚集性有明显差异,可用于机动目标和海杂波虚警分类和剔除。
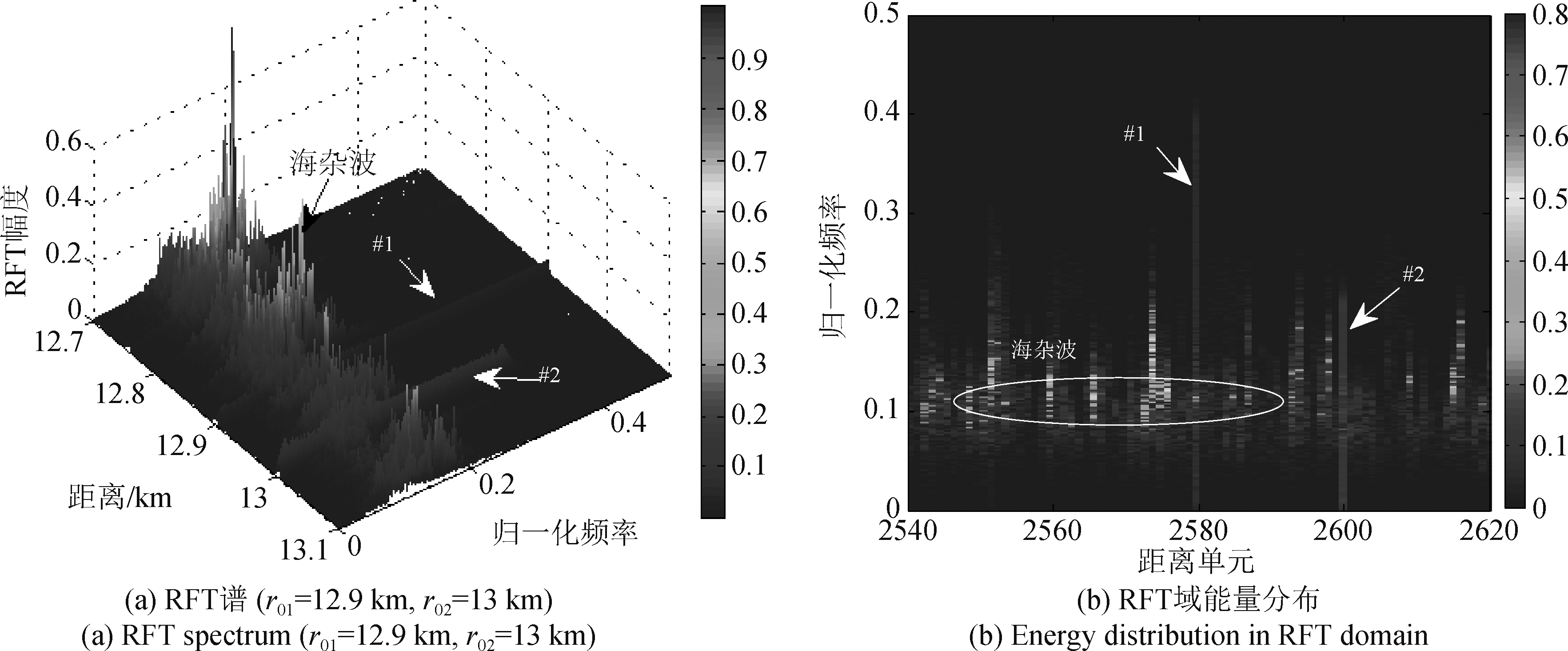
图12 RFT海面机动目标相参积累结果 (Tn=2 s)
Fig.12 Coherent integration results of marine maneuvering targets using RFT (Tn=2 s)
图13 RLCAF海面机动目标相参积累结果 (Tn=2 s)[53]
Fig.13 Coherent integration results of marine maneuvering targets using RLCAF (Tn=2 s)[53]
4)MIMO雷达空距频聚焦处理是实现“三跨”LTCI的有效途径
采用LTCI技术能够有效提高低可观测目标的探测性能,但对于常规体制雷达难以保证有效的长观测时间,例如,对于机械扫描雷达或窄波束高增益相控阵雷达,探测高速高机动目标时,波束难以覆盖目标,导致目标极易出现波束跨越现象,造成波束驻留时间减少,目标回波缺失,积累时间减少,出现除跨距离和多普勒单元以外的“跨波束”的“三跨”现象。MIMO雷达具备“泛探”工作模式,能够实现探测空域内连续和不间断的监视,能够获得空间(角度)、距离和频率(多普勒)的灵活自由度和能量聚集性,实现空距频联合处理。文献[82]基于频控阵MIMO雷达提出了空距频聚焦信号处理框架模型,是常规雷达信号处理的脉冲压缩、测角和多普勒滤波等多个级联处理环节整合,为解决“三跨”LTCI提供了新思路和新途径。
MIMO雷达给信号处理带来了维度的扩展,给雷达微弱目标检测这一世界性难题提供了新的途径,但也需要新的信号处理技术和手段。本文对正交波形MIMO雷达长时积累这一热点领域的主要技术手段和系统进行了梳理和总结,分析了各自的优缺点,并从提高运算效率、工程化应用手段、虚警点剔除等几个方面,对基于长时积累的动目标检测技术进行了展望。利用MIMO雷达的长时间凝视观测以及灵活的自由度,能够充分发挥信号长时间积累的优势,提高信号增益,是提高复杂环境下目标检测能力的有效途径。
[1] 杨建宇. 雷达技术发展规律和宏观趋势分析[J]. 雷达学报, 2012, 1(1): 19-27.
Yang Jianyu. Development Laws and Macro Trends Analysis of Radar Technology[J]. Journal of Radars, 2012, 1(1): 19-27.(in Chinese)
[2] 何友, 黄勇, 关键, 等. 海杂波中的雷达目标检测技术综述[J]. 现代雷达, 2014, 36(12): 1-9.
He You, Huang Yong, Guan Jian, et al. An overview on radar target detection in sea clutter[J]. Modern Radar, 2014, 36(12): 1-9.(in Chinese)
[3] 陈小龙, 关键, 黄勇, 等. 雷达低可观测动目标精细化处理及应用[J]. 科技导报, 2017, 35(20): 19-27.
Chen Xiaolong, Guan Jian, Huang Yong, et al. Radar refined processing and its applications for low-observable moving target[J]. Science & Technology Review, 2017, 35(20): 19-27.(in Chinese)
[4] 陈小龙, 关键, 黄勇, 等. 雷达低可观测目标探测技术[J]. 科技导报, 2017, 35(11): 30-38.
Chen Xiaolong, Guan Jian, Huang Yong, et al. Radar low-observable target detection[J]. Science & Technology Review, 2017, 35(11)：30-38.(in Chinese)
[5] 战立晓, 汤子跃, 朱振波. 雷达微弱目标检测前跟踪算法综述[J]. 现代雷达, 2013, 35(4):45-52.
Zhan Lixiao, Tang Ziyue, Zhu Zhenbo. An overview on track-before-detect algorithms for radar weak targets[J]. Modern Radar, 2013, 35(4): 45-52.(in Chinese)
[6] 丁昊, 董云龙, 刘宁波, 等. 海杂波特性认知研究进展与展望[J]. 雷达学报, 2016, 5(5): 499-516.
Ding Hao, Dong Yunlong, Liu Ningbo, et al. Overview and Prospects of Research on Sea Clutter Property Cognition[J]. Journal of Radars, 2016, 5(5): 499-516.(in Chinese)
[7] 行鸿彦, 龚平, 徐伟. 海杂波背景下小目标检测的分形方法[J]. 物理学报, 2012, 61(16): 70-79.
Xing Hongyan, Gong Ping, Xu Wei. Small target detection in the background of sea clutter using fractal method[J]. Acta Phys. Sin., 2012, 61(16): 70-79.(in Chinese)
[8] 许稼, 彭应宁, 夏香根, 等. 空时频检测前聚焦雷达信号处理方法[J]. 雷达学报, 2014, 3(2): 129-141.
Xu Jia, Peng Yingning, Xia Xianggen, et al. Radar Signal Processing Method of Space-Time-Frequency Focus-Before-Detects[J]. Journal of Radars, 2014, 3(2): 129-141.(in Chinese)
[9] 王永良, 刘维建, 谢文冲, 等. 机载雷达空时自适应检测方法研究进展[J]. 雷达学报, 2014, 3(2): 201-207.
Wang Yongliang, Liu Weijian, Xie Wenchong, et al. Research Progress of Space-Time Adaptive Detection for Airborne Radar[J]. Journal of Radars, 2014, 3(2): 201-207.(in Chinese)
[10] 裴家正, 黄勇, 董云龙, 等. 杂波背景下基于概率假设密度的辅助粒子滤波检测前跟踪改进算法[J]. 雷达学报, 2019, 8(3): 355-365.
Pei Jiazheng, Huang Yong, Dong Yunlong, et al. Track-before-detect algorithm based on improved auxiliary particle PHD filter under clutter background[J]. Journal of Radars, 2019, 8(3): 355-365.(in Chinese)
[11] Moyer L R, Spak J, Lamanna P. A Multi-Dimensional Hough Transform-Based Track-Before-Detect Technique for Detecting Weak Targets in Strong Clutter Backgrounds[J]. IEEE Transactions on Aerospace and Electronic Systems, 2011, 47(4): 3062-3068. DOI: 10.1109/TAES.2011.6034689.
[12] 陈小龙, 刘宁波, 王国庆, 等. 基于Radon-分数阶傅里叶变换的雷达动目标检测方法[J]. 电子学报, 2014, 42(6): 1074-1080.
Chen Xiaolong, Liu Ningbo, Wang Guoqing, et al. Radar Detection Method for Moving Target Based on Radon-Fourier Fractional Fourier Transform[J]. Acta Electronica Sinica, 2014, 42(6): 1074-1080.(in Chinese)
[13] 张月, 邹江威, 陈曾平. 泛探雷达长时间相参积累目标检测方法研究[J]. 国防科技大学学报, 2010, 32(6): 15-20.
Zhang Yue, Zou Jiangwei, Chen Zengping. Long-time coherent integration targets detection method for ubiquitous radar[J]. Journal of National University of Defense Technology, 2010, 32(6): 15-20.(in Chinese)
[14] Yi J, Wan X, Leung H, et al. MIMO Passive Radar Tracking Under a Single Frequency Network[J]. IEEE Journal of Selected Topics in Signal Processing, 2015, 9(8): 1661-1671. DOI: 10.1109/JSTSP.2015.2464188.
[15] Tang J, Li N, Wu Y, et al. On Detection Performance of MIMO Radar: A Relative Entropy-Based Study[J]. IEEE Signal Processing Letters, 2009, 16(3): 184-187. DOI: 10.1109/LSP.2008.2011704.
[16] 夏卓卿, 陆军, 陈伟建. 凝视动目标相参积累技术研究[J]. 中国电子科学研究院学报, 2009, 4(5): 498-502.
Xia Zhuoqing, Lu Jun, Chen Weijian. The research of long-time coherent integration for moving target[J]. Journal of CAEIT, 2009, 4(5): 498-502.(in Chinese)
[17] 张南, 陶然, 单涛, 等. 外辐射源雷达长时间积累目标探测性能分析[J]. 电子学报, 2008, 36(6): 1103-1107.
Zhang Nan, Tao Ran, Shan Tao, et al. Performance analysis of target detection using long-term integration in external illuminating radar[J]. Acta Electronica Sinica, 2008, 36(6): 1103-1107.(in Chinese)
[18] Chen X, Chen B, Guan J, et al. Space-Range-Doppler Focus-Based Low-observable Moving Target Detection Using Frequency Diverse Array MIMO Radar[J]. IEEE Access, 2018, 6: 43892- 43904. DOI: 10.1109/ACCESS.2018.2863745.
[19] Johnston L A, Krishnamurthy V. Performance analysis of a dynamic programming track before detect algorithm[J]. IEEE Transactions on Aerospace and Electronic Systems, 2002, 38(1): 228-242. DOI: 10.1109/7.993242.
[20] De Maio A, Lops M. Design Principles of MIMO Radar Detectors[J]. IEEE Transactions on Aerospace and Electronic Systems, 2007, 43(3): 886- 898. DOI: 10.1109/TAES.2007.4383581.
[21] Fishler E, Haimovich A, Blum R S, et al. Spatial Diversity in Radars—Models and Detection Performance[J]. IEEE Transactions on Signal Processing, 2006, 54(3): 823- 838. DOI: 10.1109/TSP.2005.862813.
[22] Rabideau D J, Parker P. Ubiquitous MIMO multifunction digital array radar[C]∥The Thrity-Seventh Asilomar Conference on Signals, Systems & Computers, 9-12 Nov.2003.
[23] Urzaiz F I, De Quevedo 
D, Ayuso A M, et al. Design, implementation and first experimental results of an X-band ubiquitous radar system[C]∥2018 IEEE Radar Conference (RadarConf18), 23-27 April 2018.
[24] Bao Q, Chen Z, Zhang Y, et al. Long term integration of radar signals with unknown Doppler shift for ubiquitous radar[J]. Journal of Systems Engineering and Electronics, 2011, 22(2): 219-227. DOI: 10.3969/j.issn.1004- 4132.2011.02.007.
[25] Reed I S, Gagliardi R M, Stotts L B. A recursive moving-target-indication algorithm for optical image sequences[J]. IEEE Transactions on Aerospace and Electronic Systems, 1990, 26(3): 434- 440. DOI: 10.1109/7.106120.
[26] De Feo M, Graziano A, Miglioli R, et al. IMMJPDA versus MHT and Kalman filter with NN correlation: performance comparison[J]. IEE Proceedings-Radar, Sonar and Navigation, 1997, 144(2): 49-56. DOI: 10.1049/ip-rsn: 19970976.
[27] 曲长文, 黄勇, 苏峰. 基于动态规划的多目标检测前跟踪算法[J]. 电子学报, 2006,34(12): 2138-2141.
Qu Changwen, Huang Yong, Su Feng. Radar Track-Before-Detect Algorithm of Multitarget Based on the Dynamic Programming[J]. Acta Electronica Sinica, 2006, 34(12): 2138-2141.(in Chinese)
[28] Carlson B D, Evans E D, Wilson S L. Search radar detection and track with the Hough transform. I. system concept[J]. IEEE Transactions on Aerospace and Electronic Systems, 1994, 30(1): 102-108. DOI: 10.1109/7.250410.
[29] 卢锦, 苏洪涛, 水鹏朗. 采用粒子滤波的非相干积累检测方法[J]. 信号处理, 2015, 31(6): 652- 659.
Lu Jin, Su Hongtao, Shui Penglang. Particle Filter based Non-coherent Integration Method for Detection[J]. Journal of Signal Processing, 2015, 31(6): 652- 659.(in Chinese)
[30] Li X, Sun Z, Yeo T S, et al. STGRFT for Detection of Maneuvering Weak Target With Multiple Motion Models[J]. IEEE Transactions on Signal Processing, 2019, 67(7): 1902-1917. DOI: 10.1109/TSP.2019.2899318.
[31] 关键, 陈小龙, 于晓涵. 雷达高速高机动目标长时间相参积累检测方法[J]. 信号处理, 2017, 33(3A): 1- 8.
Guan Jian, Chen Xiaolong, Yu Xiaohan. Long-time Coherent Integration-based Detection Method for High-speed and Highly Maneuvering Radar Target[J]. Journal of Signal Processing, 2017, 33(3A): 1- 8.(in Chinese)
[32] 王远模, 马君国, 付强, 等. 高速运动目标的积累检测研究[J]. 现代雷达, 2006(3): 24-27.
Wang Yuanmo, Ma Junguo, Fu Qiang, et al. Detection algorithm research for high velocity moving target[J]. Modern Radar, 2006(3): 24-27.(in Chinese)
[33] 陈远征, 朱永锋, 赵宏钟, 等. 基于包络插值移位补偿的高速运动目标的积累检测算法研究[J]. 信号处理, 2004, 20(4): 387-390.
Chen Yuanzheng, Zhu Yongfeng, Zhao Hongzhong, et al. Detection algorithm research of high velocity moving target based on the envelope interpolation[J]. Signal Processing, 2004, 20(4): 387-390.(in Chinese)
[34] 王俊, 张守宏. 微弱目标积累检测的包络移动补偿方法[J]. 电子学报, 2000, 28(12): 56-59.
Wang Jun, Zhang Shouhong. Study on the Motion Compensation of Range Migration for Weak Moving Target Detection[J]. Acta Electronica Sinica, 2000, 28(12): 56-59.(in Chinese)
[35] Xu J, Yu J, Peng Y, et al. Radon-Fourier Transform for Radar Target Detection, I: Generalized Doppler Filter Bank[J]. IEEE Transactions on Aerospace and Electronic Systems, 2011, 47(2): 1186-1202. DOI: 10.1109/TAES.2011.5751251.
[36] 陈小龙, 关键, 黄勇, 等. 分数阶Fourier变换在动目标检测和识别中的应用: 回顾和展望[J]. 信号处理, 2013, 29(1): 85-97.
Chen Xiaolong, Guan Jian, Huang Yong, et al. Application of Fractional Fourier Transform in Moving Target Detection and Recognition: Development and Prospect[J]. Journal of Signal Processing, 2013, 29(1): 85-97.(in Chinese)
[37] 陈小龙, 董云龙, 李秀友, 等. 海面刚体目标微动特征建模及特性分析[J]. 雷达学报, 2015, 4(6): 630- 638.
Chen Xiaolong, Dong Yunlong, Li Xiuyou, et al. Modeling of Micromotion and Analysis of Properties of Rigid Marine Targets[J]. Journal of Radars, 2015, 4(6): 630- 638.(in Chinese)
[38] 陈小龙, 关键, 何友. 微多普勒理论在海面目标检测中的应用及展望[J]. 雷达学报, 2013, 2(1): 123-134.
Chen Xiaolong, Guan Jian, He You. Applications and Prospect of Micro-motion Theory in the Detection of Sea Surface Target[J]. Journal of Radars, 2013, 2(1): 123-134.(in Chinese)
[39] 张南, 陶然, 王越. 基于变标处理和分数阶傅里叶变换的运动目标检测算法[J]. 电子学报, 2010, 38(3): 683- 688.
Zhang Nan, Tao Ran, Wang Yue. A Target Detection Algorithm Based on Scaling Processing and Fractional Fourier Transform[J]. Acta Electronica Sinica, 2010, 38(3): 683- 688.(in Chinese)
[40] 邹红星, 周小波, 李衍达. 时频分析: 回溯与前瞻[J]. 电子学报, 2000, 28(9): 78- 84.
Zou Hongxing, Zhou Xiaobo, Li Yanda. Which Time-frequency Analysis——A Survey[J]. Acta Electronica Sinica, 2000, 28(9): 78- 84.(in Chinese)
[41] 孙艳丽, 陈小龙, 柳叶. 雷达动目标变换域相参积累检测及性能分析[J]. 太赫兹科学与电子信息学报, 2019, 17(3): 457- 461.
Sun Yanli, Chen Xiaolong, Liu Ye. Detection and performance analysis of radar coherent integration for moving target in transform domain[J]. Journal of Terahertz Science and Electronic Information Technology, 2019, 17(3): 457- 461.(in Chinese)
[42] Tao R, Li Y, Wang Y. Short-Time Fractional Fourier Transform and Its Applications[J]. IEEE Transactions on Signal Processing, 2010, 58(5): 2568-2580. DOI: 10.1109/TSP.2009.2028095.
[43] Chen X, Guan J, Bao Z, et al. Detection and Extraction of Target With Micromotion in Spiky Sea Clutter Via Short-Time Fractional Fourier Transform[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(2): 1002-1018. DOI: 10.1109/TGRS.2013.2246574.
[44] Chen X, Yu X, Huang Y, et al. Adaptive Clutter Suppression and Detection Algorithm for Radar Maneuvering Target With High-Order Motions Via Sparse Fractional Ambiguity Function[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2020, 13:1515-1526. DOI: 10.1109/JSTARS.2020.2981046.
[45] Wang P, Djurovic I, Yang J. Generalized High-Order Phase Function for Parameter Estimation of Polynomial Phase Signal[J]. IEEE Transactions on Signal Processing, 2008, 56(7): 3023-3028. DOI: 10.1109/TSP.2007.916144.
[46] 李海, 周盟. 结合CPT的相控阵空中高机动目标参数估计[J]. 信号处理, 2015, 31(11): 1539-1546.
Li Hai, Zhou Meng. Parameter Estimation of Air Highly Maneuvering Targets under Phased Array System via CPT[J]. Journal of Signal Processing, 2015, 31(11): 1539-1546.(in Chinese)
[47] 陈小龙, 关键, 于晓涵, 等. 基于短时稀疏时频分布的雷达目标微动特征提取及检测方法[J]. 电子与信息学报, 2017, 39(5): 1017-1023. DOI: 10.11999/JEIT161040.
Chen Xiaolong, Guan Jian, Yu Xiaohan, et al. Radar Micro-Doppler Signature Extraction and Detection via Short-time Sparse Time-frequency Distribution[J]. Journal of Electronics and Information Technology, 2017, 39(5): 1017-1023. DOI: 10.11999/JEIT161040.(in Chinese)
[48] Huang P, Liao G, Yang Z, et al. Long-Time Coherent Integration for Weak Maneuvering Target Detection and High-Order Motion Parameter Estimation Based on Keystone Transform[J]. IEEE Transactions on Signal Processing, 2016, 64(15): 4013- 4026. DOI: 10.1109/TSP.2016.2558161.
[49] Li X, Cui G, Yi W, et al. A Fast Maneuvering Target Motion Parameters Estimation Algorithm Based on ACCF[J]. IEEE Signal Processing Letters, 2015, 22(3): 270-274. DOI: 10.1109/LSP.2014.2358230.
[50] Zheng J, Liu H, Liu Q H. Parameterized Centroid Frequency-Chirp Rate Distribution for LFM Signal Analysis and Mechanisms of Constant Delay Introduction[J]. IEEE Transactions on Signal Processing, 2017, 65(24): 6435- 6447. DOI: 10.1109/TSP.2017.2755604.
[51] Zheng J, Su T, Liu H, et al. Radar High-Speed Target Detection Based on the Frequency-Domain Deramp-Keystone Transform[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2016, 9(1): 285-294. DOI: 10.1109/JSTARS.2015.2453996.
[52] Huang X, Tang S, Zhang L, et al. Ground-Based Radar Detection for High-Speed Maneuvering Target via Fast Discrete Chirp-Fourier Transform[J]. IEEE Access, 2019, 7: 12097-12113.
[53] Chen X, Guan J, Liu N, et al. Detection of a Low Observable Sea-Surface Target With Micromotion via the Radon-Linear Canonical Transform[J]. IEEE Geoscience and Remote Sensing Letters, 2014, 11(7): 1225-1229. DOI: 10.1109/LGRS.2013.2290024.
[54] Li X, Cui G, Yi W, et al. Coherent Integration for Maneuvering Target Detection Based on Radon-Lv’s Distribution[J]. IEEE Signal Processing Letters, 2015, 22(9): 1467-1471. DOI: 10.1109/LSP.2015.2390777.
[55] Rao X, Tao H, Su J, et al. Detection of constant radial acceleration weak target via IAR-FRFT[J]. IEEE Transactions on Aerospace and Electronic Systems, 2015, 51(4): 3242-3253. DOI: 10.1109/TAES.2015.140739.
[56] Chen X, Guan J, Li X, et al. Effective coherent integration method for marine target with micromotion via phase differentiation and radon-Lv’s distribution[J]. IET Radar, Sonar & Navigation, 2015, 9(9): 1284-1295. DOI: 10.1049/iet-rsn.2015.0100.
[57] Li Xiaolong, Cui Guolong, Yi Wei, et al. Radar maneuvering target detection and motion parameter estimation based on TRT-SGRFT[J]. Signal Processing, 2017, 133: 107-116.
[58] 万洋, 王首勇, 吴卫华. 机动弱小目标动态规划检测前跟踪方法[J]. 信号处理, 2013, 29(5): 584-590.
Wan Yang, Wang Shouyong, Wu Weihua. Dynamic Programming Track Before Detect for Maneuvering Dim Targets[J]. Journal of Signal Processing, 2013, 29(5): 584-590.(in Chinese)
[59] Yi W, Fang Z, Li W, et al. Multi-Frame Track-Before-Detect Algorithm for Maneuvering Target Tracking[J]. IEEE Transactions on Vehicular Technology, 2020, 69(4): 4104- 4118. DOI: 10.1109/TVT.2020.2976095.
[60] 周煦, 许稼, 钱李昌, 等. 雷达高机动目标长时间混合积累快速算法[J]. 信号处理, 2015, 31(12): 1547-1553.
Zhou Xu, Xu Jia, Qian Lichang, et al. Fast Long-time Hybrid Integration for Highly Maneuvering Radar Target Detection[J]. Journal of Signal Processing, 2015, 31(12): 1547-1553.(in Chinese)
[61] 荣娟, 刘飞峰, 刘泉华, 等. 基于LTE信号的小目标回波相参积累: 目标散射建模与影响分析[J]. 信号处理, 2019, 35(6): 965-971.
Rong Juan, Liu Feifeng, Liu Quanhua, et al. Coherent Integration of Small Target Echoes Based on LTE Signals: Target Scattering Modeling and Impact Analysis[J]. Journal of Signal Processing, 2019, 35(6): 965-971.(in Chinese)
[62] Zeng C, Li D, Luo X, et al. Ground Maneuvering Targets Imaging for Synthetic Aperture Radar Based on Second-Order Keystone Transform and High-Order Motion Parameter Estimation[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2019, 12(11): 4486- 4501. DOI: 10.1109/JSTARS.2019.2951199.
[63] Wang H, Yi J, Wan X. Manoeuvring target detection based on keystone transforms and conjugates time reversing transform[J]. Electronics Letters, 2018, 54(21): 1237-1239. DOI: 10.1049/el.2018.5225.
[64] Chen X, Guan J, Wang G, et al. Fast and Refined Processing of Radar Maneuvering Target Based on Hierarchical Detection via Sparse Fractional Representation[J]. IEEE Access, 2019, 7: 149878-149889. DOI: 10.1109/ACCESS.2019.2947169.
[65] Xu J, Zhou X, Qian L, et al. Hybrid integration for highly maneuvering radar target detection based on generalized radon-fourier transform[J]. IEEE Transactions on Aerospace and Electronic Systems, 2016, 52(5): 2554-2561. DOI: 10.1109/TAES.2016.150076.
[66] Chen X, Guan J, Liu N, et al. Maneuvering Target Detection via Radon-Fractional Fourier Transform-Based Long-Time Coherent Integration[J]. IEEE Transactions on Signal Processing, 2014, 62(4): 939-953. DOI: 10.1109/TSP.2013.2297682.
[67] Chen X, Huang Y, Liu N, et al. Radon-fractional ambiguity function-based detection method of low-observable maneuvering target[J]. IEEE Transactions on Aerospace and Electronic Systems, 2015, 51(2): 815- 833. DOI: 10.1109/TAES.2014.130791.
[68] Chen X, Guan J, Huang Y, et al. Radon-Linear Canonical Ambiguity Function-Based Detection and Estimation Method for Marine Target With Micromotion[J]. IEEE Transactions on Geoscience and Remote Sensing, 2015, 53(4): 2225-2240. DOI: 10.1109/TGRS.2014.2358456.
[69] Wu W, Wang G H, Sun J P. Polynomial Radon-Polynomial Fourier Transform for Near Space Hypersonic Maneuvering Target Detection[J]. IEEE Transactions on Aerospace and Electronic Systems, 2018, 54(3): 1306-1322. DOI: 10.1109/TAES.2017.2780658.
[70] Li X, Cui G, Kong L, et al. Fast Non-Searching Method for Maneuvering Target Detection and Motion Parameters Estimation[J]. IEEE Transactions on Signal Processing, 2016, 64(9):2232- 2244.DOI:10.1109/TSP.2016.2515066.
[71] Chen X, Guan J, Chen W, et al. Sparse long-time coherent integration-based detection method for radar low-observable manoeuvring target[J]. IET Radar, Sonar & Navigation, 2020, 14(4): 538-546. DOI: 10.1049/iet-rsn.2019.0313.
[72] Varshney K R, Çetin M, Fisher J W, et al. Sparse Representation in Structured Dictionaries With Application to Synthetic Aperture Radar[J]. IEEE Transactions on Signal Processing, 2008, 56(8): 3548-3561. DOI: 10.1109/TSP.2008.919392.
[73] Yang B, Liu R, Chen X. Sparse Time-Frequency Representation for Incipient Fault Diagnosis of Wind Turbine Drive Train[J]. IEEE Transactions on Instrumentation and Measurement, 2018, 67(11): 2616-2627. DOI: 10.1109/TIM.2018.2828739.
[74] Zhao Z, Tao R, Li G, et al. Sparse Fractional Energy Distribution and its Application to Radar Detection of Marine Targets With Micro-Motion[J]. IEEE Sensors Journal, 2019, 19(24): 12165-12174. DOI: 10.1109/JSEN.2019.2937173.
[75] 陈小龙, 关键, 何友, 等. 高分辨稀疏表示及其在雷达动目标检测中的应用[J]. 雷达学报, 2017, 6(3): 239-251.
Chen Xiaolong, Guan Jian, He You, et al. High-resolution Sparse Representation and Its Applications in Radar Moving Target Detection[J]. Journal of Radars, 2017, 6(3): 239-251.(in Chinese)
[76] 陈小龙, 关键, 于晓涵, 等. 雷达动目标短时稀疏分数阶傅里叶变换域检测方法[J]. 电子学报, 2017, 45(12): 3030-3036.
Chen Xiaolong, Guan Jian, Yu Xiaohan, et al. Radar Detection for Moving Target in Short-Time Sparse Fractional Fourier Transform Domain[J]. Acta Electronica Sinica, 2017, 45(12): 3030-3036.(in Chinese)
[77] Yu X, Chen X, Huang Y, et al. Radar Moving Target Detection in Clutter Background via Adaptive Dual-Threshold Sparse Fourier Transform[J]. IEEE Access, 2019, 7: 58200-58211. DOI: 10.1109/ACCESS.2019.2914232.
[78] 陈小龙, 关键, 董云龙, 等. 稀疏域海杂波抑制与微动目标检测方法[J]. 电子学报, 2016, 44(4): 860- 867.
Chen Xiaolong, Guan Jian, Dong Yunlong, et al. Sea Clutter Suppression and Micromotion Target Detection in Sparse Domain[J]. Acta Electronica Sinica, 2016, 44(4): 860- 867.(in Chinese)
[79] Yu X, Chen X, Huang Y, et al. Fast Detection Method for Low-Observable Maneuvering Target via Robust Sparse Fractional Fourier Transform[J]. IEEE Geoscience and Remote Sensing Letters, 2020, 17(6): 978-982. DOI: 10.1109/LGRS.2019.2939264.
[80] Pawar S, Ramchandran K. FFAST: An Algorithm for Computing an Exactly 
k-Sparse DFT in O(k\log k) Time[J]. IEEE Transactions on Information Theory, 2018, 64(1): 429- 450. DOI: 10.1109/TIT.2017.2746568.
[81] Chen X, Guan J, He Y, et al. Detection of low observable moving target in sea clutter via fractal characteristics in fractional fourier transform domain[J]. IET Radar, Sonar & Navigation, 2013, 7(6): 635- 651. DOI: 10.1049/iet-rsn.2012.0116.
[82] 陈小龙, 陈宝欣, 黄勇, 等. 频控阵雷达空距频聚焦信号处理方法[J]. 雷达学报, 2018, 7(2): 183-193. DOI: 10.12000/JR18018.
Chen Xiaolong, Chen Baoxin, Huang Yong, et al. Frequency Diverse Array Radar Signal Processing via Space-Range-Doppler Focus (SRDF) Method[J]. Journal of Radars, 2018, 7(2): 183-193. DOI: 10.12000/JR18018.(in Chinese)
陈小龙 男, 1985年生, 山东烟台人。海军航空大学副教授，硕士生导师，博士。研究领域包括雷达动目标检测、海杂波抑制、雷达信号精细化处理等。入选中国科协“青年人才托举工程”，获中国电子学会优博，第十九届中国专利优秀奖，中国产学研促进会军民融合奖，军队科技进步一等奖等。
E-mail: cxlcxl1209@163.com
黄 勇 男, 1979年生, 湖南汨罗人。海军航空大学副教授, 硕士生导师, 研究方向为雷达目标检测、多维信号处理等。
E-mail: huangyong_2003@163.com
关 键 男, 1968年生, 辽宁锦州人。海军航空大学教授，博士生导师。主要研究方向包括雷达目标检测与跟踪、侦察图像处理和信息融合。获国家科技进步二等奖1项、军队科技进步一等奖2项，山东省技术发明一等奖1项；“百千万人才工程”国家级人选，入选教育部新世纪优秀人才支持计划。
E-mail: guanjian_68@163.com
宋伟健 男， 1982年生， 黑龙江哈尔滨人。海军航空大学助理研究员， 研究方向为军事装备学。
E-mail: 27537237@qq.com
薛永华 男, 1985年生, 山西霍州人。海军航空大学讲师, 主要研究方向为雷达发射波形设计和海上目标检测。
E-mail: xueyhchina@163.com