1 引言
21世纪以来,全球导航卫星系统(global navigation satellite systems,GNSS)[1]的广泛应用使得各国都在建立自己的卫星系统,这使得本就有限的频段资源变得更加紧张,而二进制偏移载波(Binary Offset Carrier,BOC)[2- 4]及其衍生信号[5-6]因为其频谱分裂的特性可以缓解该问题被提了出来。作为BOC的衍生信号,虽然高阶双二进制偏移载波(Double Binary Offset Carrier,DBOC)[7-8]信号在保密性和抗干扰方面有更加优异的性能。但是在通信过程中,DBOC信号的接收机不仅在高动态环境下工作,而且接收到的DBOC信号在传输的过程中可能会受到各种干扰,这会导致DBOC信号无法被精确捕获。所以研究干扰和高动态共存时DBOC信号的捕获方法具有一定的意义。
现阶段针对BOC及其衍生信号的捕获方法大致分为四类,第一类为无模糊捕获,如BPSK-Like[9],(Sub-Correlation Function,SCF)[10],(Pseudo-Correlation Function,PCF)算法[11]等,这类算法的实时性较低,不太适用于高动态环境下信号的捕获。第二类为基于部分匹配滤波加快速傅里叶变换(partial matching filter-fast Fourier transform,PMF-FFT)[12-16]的捕获算法,此算法的捕获速度快并且所需要的硬件复杂度较低,同时还能捕获大多普勒频率的信号。但是此类算法在抗干扰和抗高动态方面的效果不尽如人意。第三类为高动态环境下的捕获算法,如文献[17-20]通过分数阶傅里叶变换( fractional Fourier transform,FRFT)完成GNSS信号的捕获,但是此算法仅仅只针对高动态环境,对于干扰和高动态共存环境时其捕获性能并不理想。第四类为干扰环境下的捕获算法,如文献[21]提出采用全相位FIR滤波器和PMF-apFFT相结合的抗窄带干扰捕获算法,文献[22]提出基于FRFT的宽带线性调频干扰下的干扰抑制捕获算法,但是这一类算法大部分都是研究窄带或者宽带干扰,少有研究针对于干扰为正弦调频(sinusoidal frequency modulation, SFM)这一情况下的BOC及其衍生信号的捕获方法,并且此类算法对于干扰和高动态都存在时的情况下并不适用。
因此针对DBOC信号在SFM干扰和高动态共存环境下的捕获方法匮乏的问题,提出了一种基于正弦调频变换(discrete sinusoidal frequency modulation transform,DSFMT)结合离散多项式相位变换(discrete polynomial-phase transform, DPT),线性调频Z变换(CZT)的捕获方法。首先对接收到的信号做DSFMT,接着确定干扰位置并置零再做IDSFMT完成SFM干扰的抑制,然后利用定阶算法确定干扰抑制后信号的动态阶数再通过DPT去除其高阶动态项,最后利用CZT算法完成信号的捕获。实验结果表明,本文算法相比PMF-FFT和PMF-apFFT算法更加适合于SFM干扰和高动态共存环境下DBOC信号的捕获。
2 信号模型
复杂环境下接收到的含SFM干扰的高动态DBOC信号表示为:
(1)
其中,![]() 是动态DBOC信号,xSFM(t)是SFM干扰信号。ν0(t)是加性高斯白噪声,其均值是0、方差是σ2。
是动态DBOC信号,xSFM(t)是SFM干扰信号。ν0(t)是加性高斯白噪声,其均值是0、方差是σ2。
动态DBOC信号![]() 的表达式为:
的表达式为:
(2)
其中,A是信号幅度,d(t)是导航信息,c(t)是伪码信号,scDBOC(t)是副载波,φ(t)是载波。scDBOC(t)表示为:
![]()
δ(t-iTB1-kTB)
(3)
式中,pTB(·)表示矩形脉冲其幅度为1,NBOC1是第一次BOC信号的阶数,NBOC2是第二次BOC信号的阶数,TB1=Tc/NBOC1表示第一次调制的副载波码片间隔,TB=Tc/(NBOC1NBOC2)表示第二次调制的副载波码片间隔。
φ(t)表示为:
φ(t)=exp{j[(f0+fd)t+kdt2+kft3+φ0]}
(4)
其中, f0为载波频率, fd为多普勒频偏,kd为一阶多普勒变化率,kf为二阶多普勒变化率,φ0为初始相位。
xSFM(t)是SFM干扰信号;表示为:
xSFM(t)=A′exp{j[2πfct+mfsin(2πfmt)]}
(5)
其中A′为幅度; fc为载波频率; fm为调制频率;mf为调制系数。
3 算法原理
3.1 正弦调频变换
SFM序列x(n)的DSFMT变换XS( fm,l)为[23]:
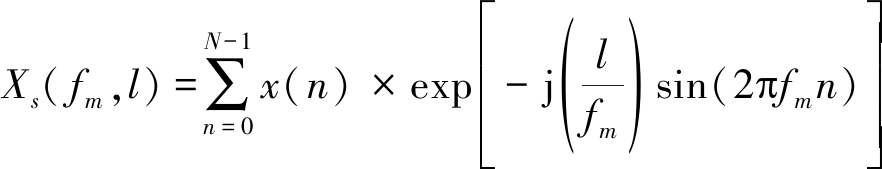
(6)
其中,l表示调制频偏;![]()
令SFM干扰x(n)表示为:
(7)
SFM干扰在DSFMT域表现为:
(1)当fm=fm0时
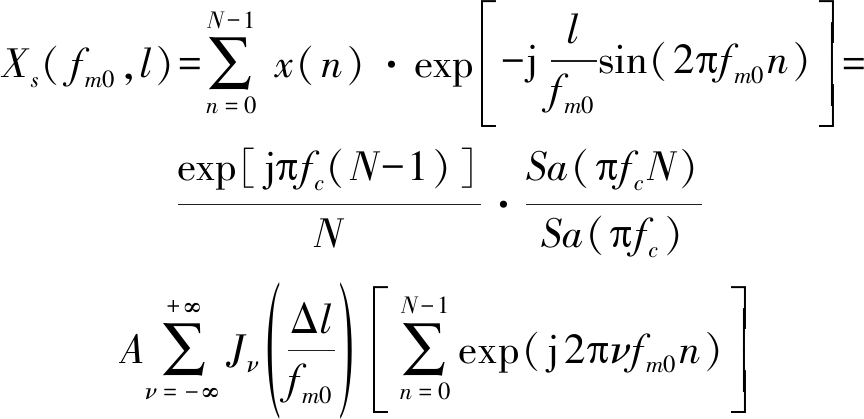
(8)
其中
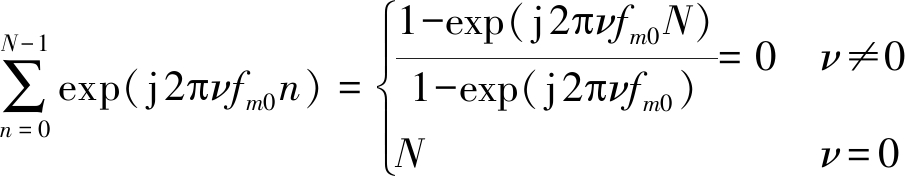
(9)
所以
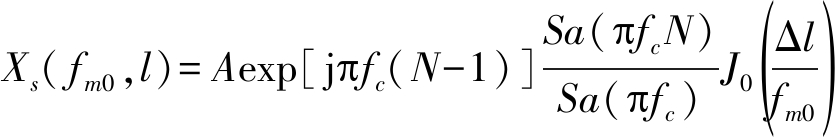
(10)
所以,当fm=fm0时,SFM干扰的DSFMT Xs( fm0,l)为:
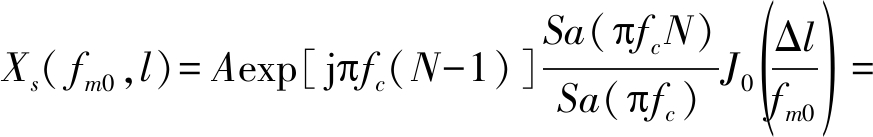
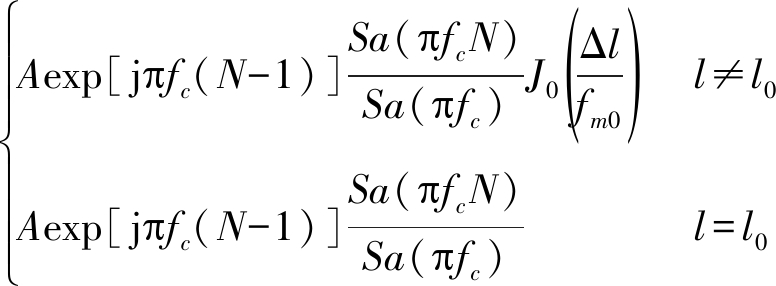
(11)
(2)当fm≠fm0时
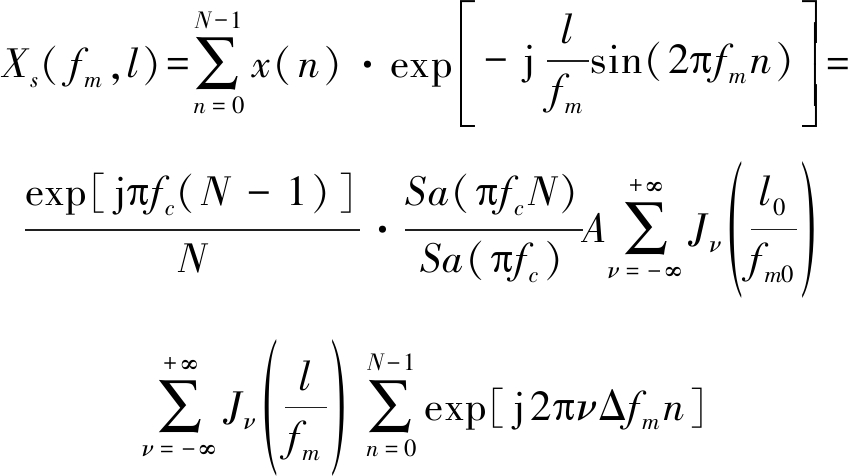
(12)
因为Δfm≠0,与式(9)同理
(13)
因此,若Δfm≠0
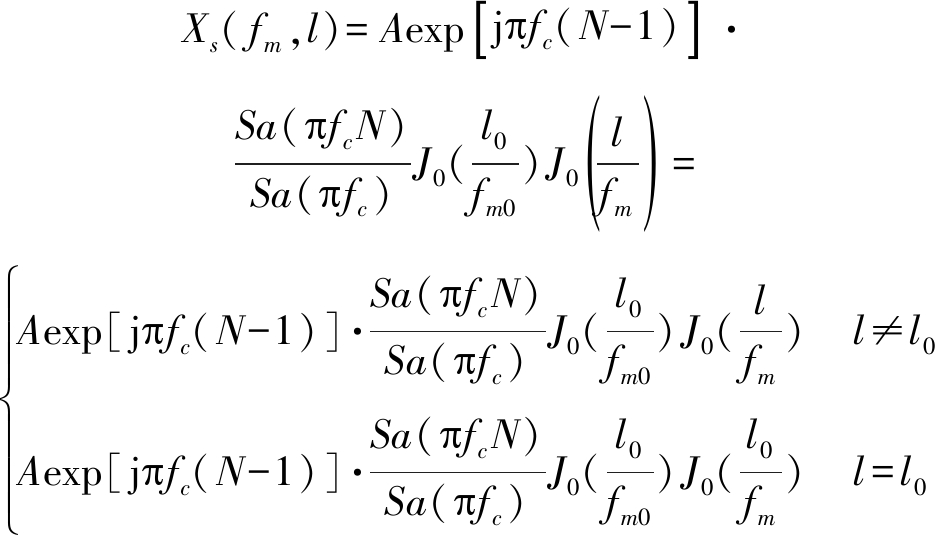
(14)
综上所述,SFM的DSFMT Xs( fm,l)为:
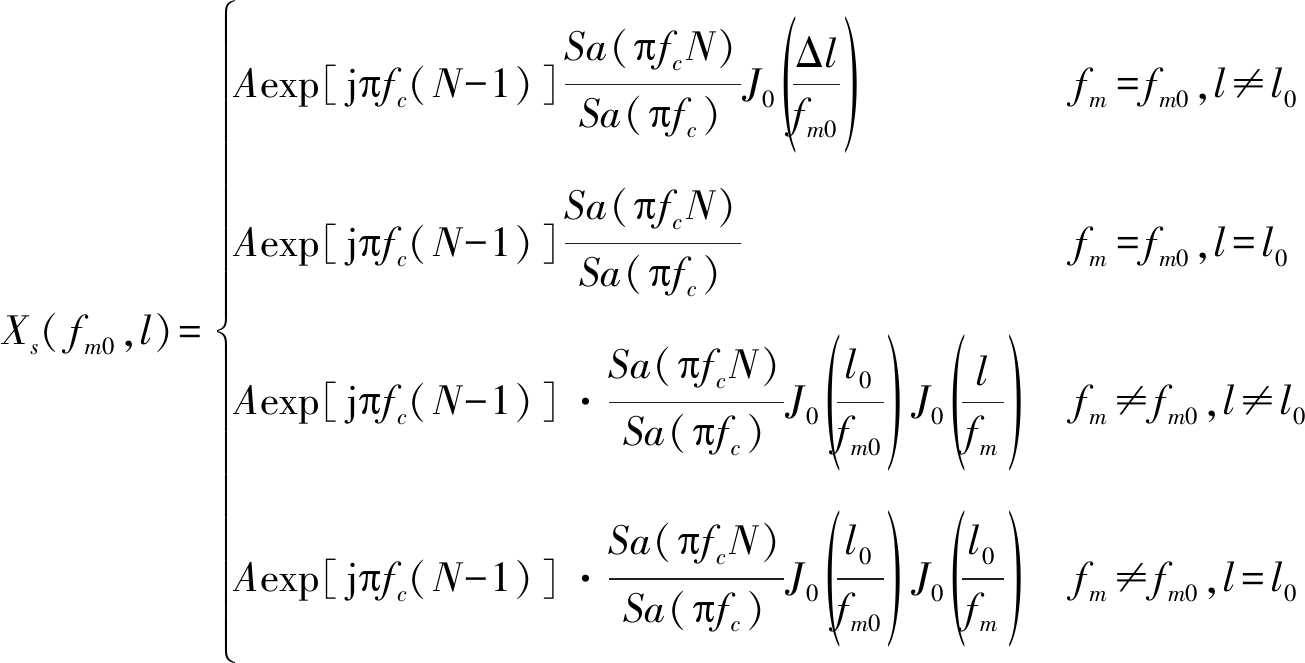
(15)
由式(15)可知,只有当fm=fm0且l=l0时,SFM信号在DSFMT域聚拢。其余情况时,SFM干扰信号的DSFMT都为幅度被![]() 加权的贝塞尔函数。所以通过SFM干扰在DSFMT域聚拢这一特征可以判断SFM干扰的位置并进行SFM干扰置零,从而达到去除SFM干扰的目的。
加权的贝塞尔函数。所以通过SFM干扰在DSFMT域聚拢这一特征可以判断SFM干扰的位置并进行SFM干扰置零,从而达到去除SFM干扰的目的。
为了验证DSFMT可以使SFM干扰在DSFMT域中聚拢,实验在信干比SIR=-25 dB,信噪比SNR=-10 dB时对含有SFM干扰的高动态DBOC信号做DSFMT,结果如图1。
由图1可知,对含SFM干扰的高动态DBOC信号做DSFMT时,高动态DBOC信号和噪声都平均分布在DSFMT域中,而SFM干扰呈现聚拢状态,所以,先确定聚拢的SFM干扰的位置,再做置零处理,就能完成高动态DBOC信号中的SFM干扰的抑制。
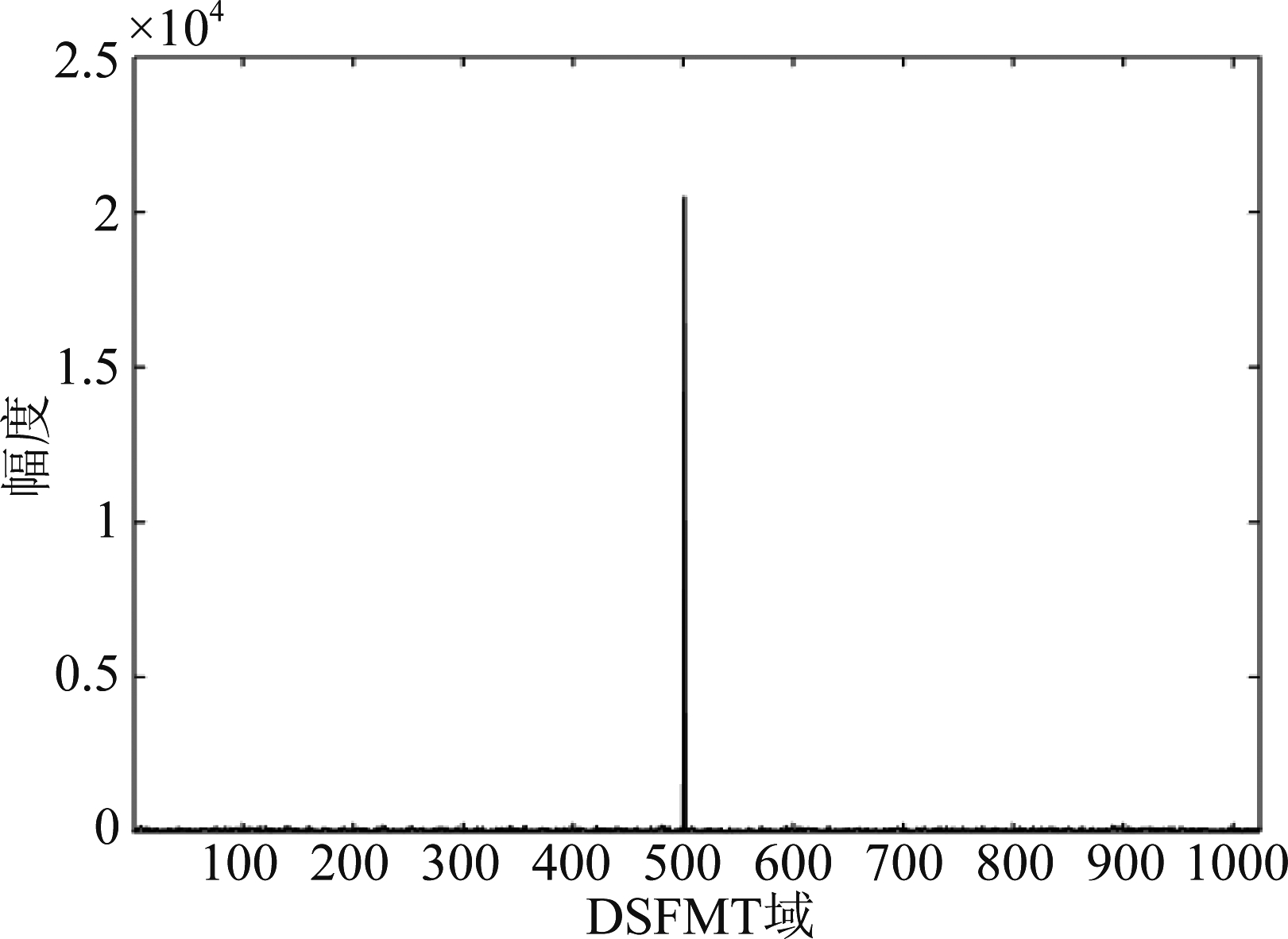
图1 含SFM干扰的高动态DBOC信号DSFMT域谱线
Fig.1 DSFMT domain spectral line of high dynamic DBOC signal with SFM interference
3.2 离散多项式相位变换
M阶相位多项式表示为:
(16)
其中,A0为幅度,M为阶数,ak为实相位系数,N′为采样长度,ΔT为采样间隔。
M阶瞬态矩DPM[s(n),τ]表示为[24]:
DPM[s(n),τ]=DP2{DPM-1[s(n),τ],τ}=![]()
(17)
其中,τ为延时长度,![]()
M阶离散多项式相位变换为:
DPTM[s(n),w,τ]=DFT{DPM[s(n),τ]}=![]()
(18)
因为DPT变换不改变导航信息,所以此处不考虑d(n)变换带来的影响,因此经过M阶瞬态矩处理后表达式可以表示为:
(19)
令![]() 可以被看作新的组合伪随机序列,所以,高动态DBOC信号被转换为:
可以被看作新的组合伪随机序列,所以,高动态DBOC信号被转换为:
(20)
其中,V0(n)是高斯白噪声。由式(20)可知,高动态DBOC信号被转化成带残余频偏的一阶信号和噪声之和。例如三阶信号s(n)的DP3[s(n),τ]:
DP3[s(n),τ]=DP2[s(n)s*(n-τ),τ]=
exp[fd(nTs)+kd(nTs)2+kf(nTs)3] · exp j[fd(nTs-2τ)+kd(nTs-2τ)2+kf(nTs-2τ)3] · exp{-j[fd(nTs-τ)+kd(nTs-τ)2+kf(nTs-τ)3]}=![]()
(21)
其中![]() 通过DP3[s(n),τ],三阶信号被转换成单频正弦信号,所以,经过DPT,高动态参数的三维搜索被简化为一维频率搜索,这使得系统的响应速度变得更快。
通过DP3[s(n),τ],三阶信号被转换成单频正弦信号,所以,经过DPT,高动态参数的三维搜索被简化为一维频率搜索,这使得系统的响应速度变得更快。
因为经过干扰抑制后的高动态DBOC信号的动态阶数未知,并且CZT方法无法处理高动态DBOC信号中一阶以上的动态项,所以需要对干扰抑制后的高动态DBOC信号先定阶再降阶,定阶的判断方法如下:
(1)m<M时频域表现为凌乱的谱线。
(2)m=M时频域表现为非0单线谱。
(3)m>M时频域表现为直流分量。
采用动态阶数为3的动态DBOC信号验证定阶算法。
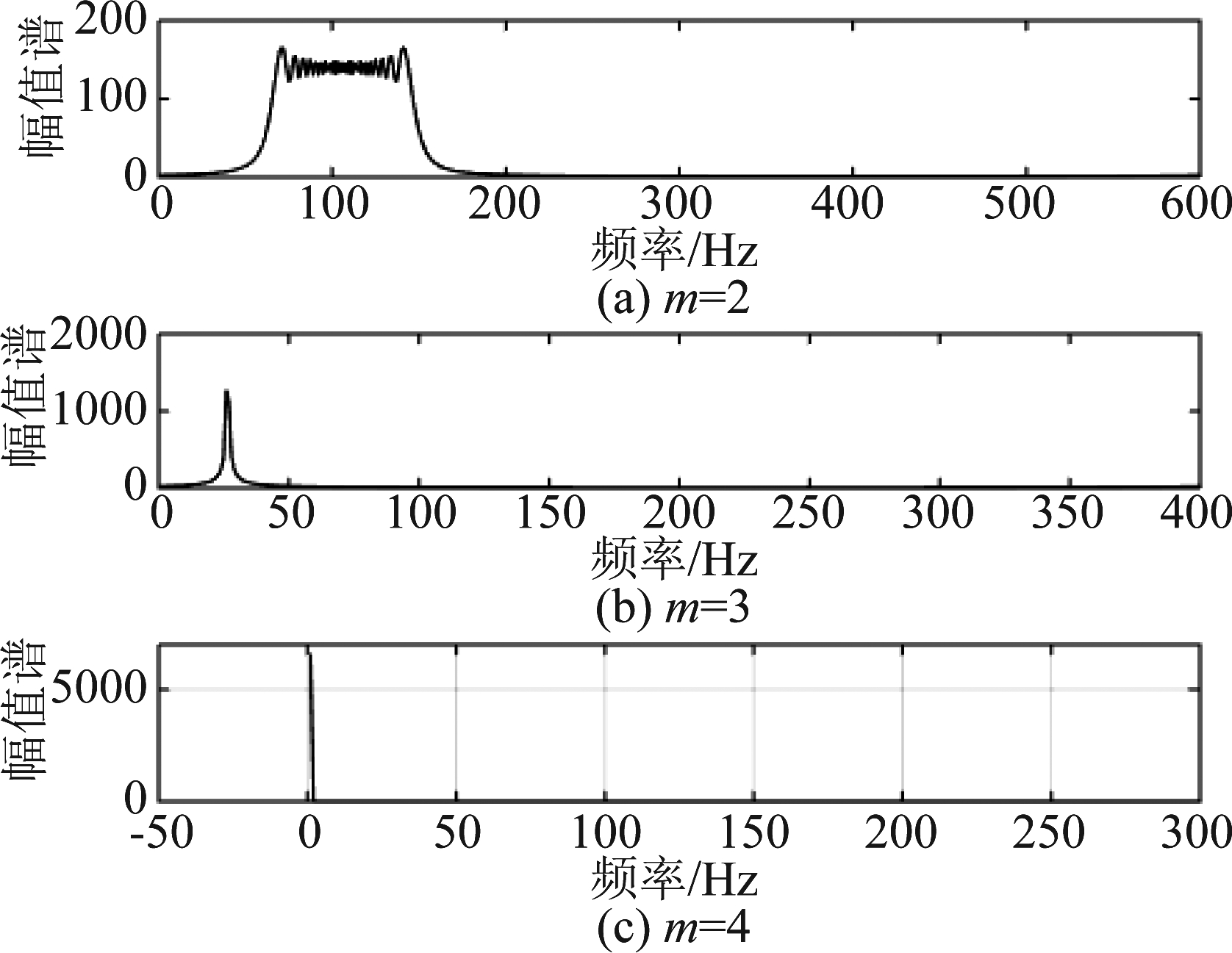
图2 DPT处理变化图
Fig.2 DPT process change diagram
由图2可知,当m=2时,频域表现为凌乱谱线,m=3时,频域表现为非0单线谱,m=4时,频域表现为直流分量。所以,此信号的动态阶数为3,这一实验说明此定阶算法可以有效判断高动态DBOC信号的动态阶数。
3.3 线性调频Z变换
长度为N的序列x(n)的z变换定义为:
(22)
令zk=AW-k,其中A,W为任意复数,MCZT为CZT采样点数,再令A=A0ejα表示采样轨迹的起点,W=W0e-jβ为相邻2个采样点之间的比例关系。
CZT是一种更灵活的频谱计算方法,可以看做z域上的沿螺旋曲线的Z变换。
CZT具体的实现步骤为[25]:
(1)选定实现CZT的总的点数NCZT,NCZT≥N+MCZT-1且NCZT=2m。
(2)定义NCZT点序列y(n):
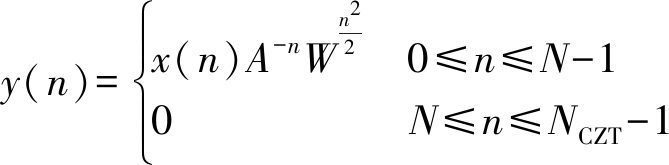
(23)
并求其FFT Y(k)。
(3)定义NCZT点序列h(n):
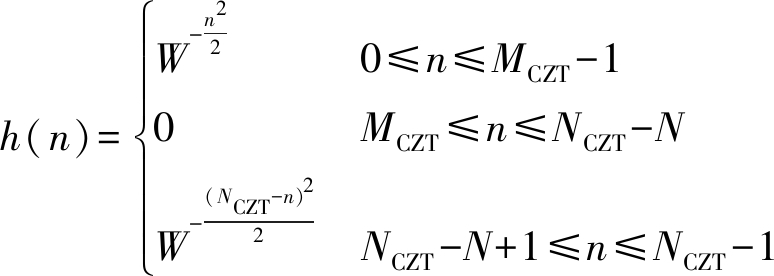
(24)
并求其FFT H(k)。
(4)求G(k)=Y(k)H(k),并求G(k)的IFFT g(n)。
(5)求抽样点Z变换:
(25)
以上即为CZT算法的过程,首先对接收到的信号分别利用DSFMT和DPT做干扰抑制和定阶降阶处理,然后再与本地DBOC信号进行相关,选定步长W以及起始点A,对相关过后的序列按照上述步骤进行CZT变换,通过CZT算法输出的谱峰值来确定PN码相位则能完成信号的捕获。
4 算法性能与算法流程
4.1 算法性能
进行瞬时互相关后输出的信噪比为:
(26)
由(26)可知,SNRout随着τ的增大而减小,对于τ的选择,较大的估计时延可以保证估计精度,但是也会造成SNRout的降低,所以在应用时需要根据系统的需求进行选择。
Z域的检测信噪比为:
(27)
其中,var为方差,S(α,U)和W(α,U)分别表示信号和噪声在Z域的幅值。
此算法的检测概率为:
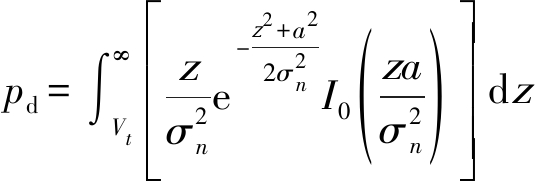
(28)
其中,I0是修正零阶贝塞尔函数,Vt是门限值,表示为:
(29)
其中,R(·)为DBOC信号的自相关函数,Δτ为码延时残差,Tcoh为相干积分时间。
此算法的平均捕获时间为:
(30)
其中,Pfa为虚警概率,K为惩罚因子,τd为积分时间。
4.2 算法流程
通过以上分析,本文所提捕获方法结构如图3。
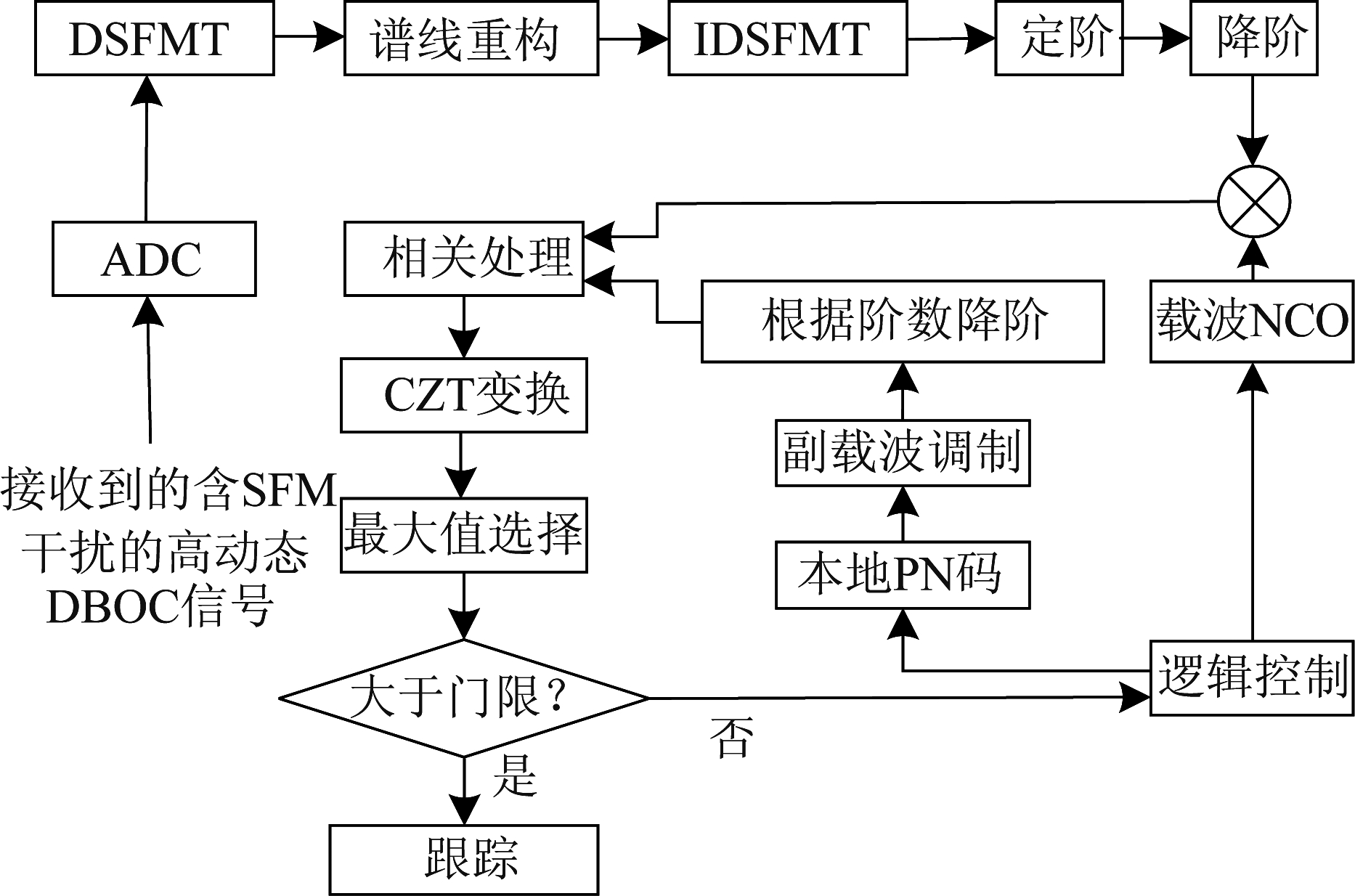
图3 所提算法捕获结构
Fig.3 Acquisition structure of the proposed algorithm
算法流程:
步骤1 对接收到的信号进行下变频、模数转换、离散采样处理。
步骤2 对处理后的信号做DSFMT。
步骤3 确定DSFMT域中SFM干扰谱线位置并对其置零,然后做IDSFMT。
步骤4 对干扰抑制后的信号先定阶,再降阶。所得信号记为s。
步骤5 先对本地产生的PN码序列做副载波调制,再根据阶数决定是否对其做降阶处理,接着与s做相关。
步骤6 对相关结果做CZT变换。
步骤7 将步骤6结果得到的最大值和预设门限V做对比,若超过预设门限V,说明PN码序列和接收到的DBOC信号伪码相位对齐,进入跟踪阶段;若没有超过,通过逻辑控制本地载波NCO,与此同时调整本地PN码相位。
步骤8 重复步骤4到7到伪码相位对齐为止。
5 实验仿真
实验采用MATLAB软件,信道为高斯白噪声信道。含SFM干扰的高动态DBOC信号r(t)=Ad(t)scDBOCc(t)·exp[j( fdt+kdt2+kft3)]+xSFM(t)+n0(t)。若无特别提示,实验参数设置为:fd=1000 Hz,kd=10 Hz/s,kf=1 Hz/s2。M为扩频码长度。延时τ=M/3。信号的采样频率为16.384 MHz,码速率为1.023 MHz,码片长度为1536,NBOC1=2,NBOC2=4。CZT的实验参数设置为,A0=1,W0=1,α=0,实验采用PMF-FFT和PMF-apFFT算法进行对比仿真。
实验1 干扰抑制前后频谱。
为了验证本文算法可以有效抑制DBOC信号中的SFM干扰,实验对SFM干扰抑制前后的频谱进行对比,实验结果如图4。
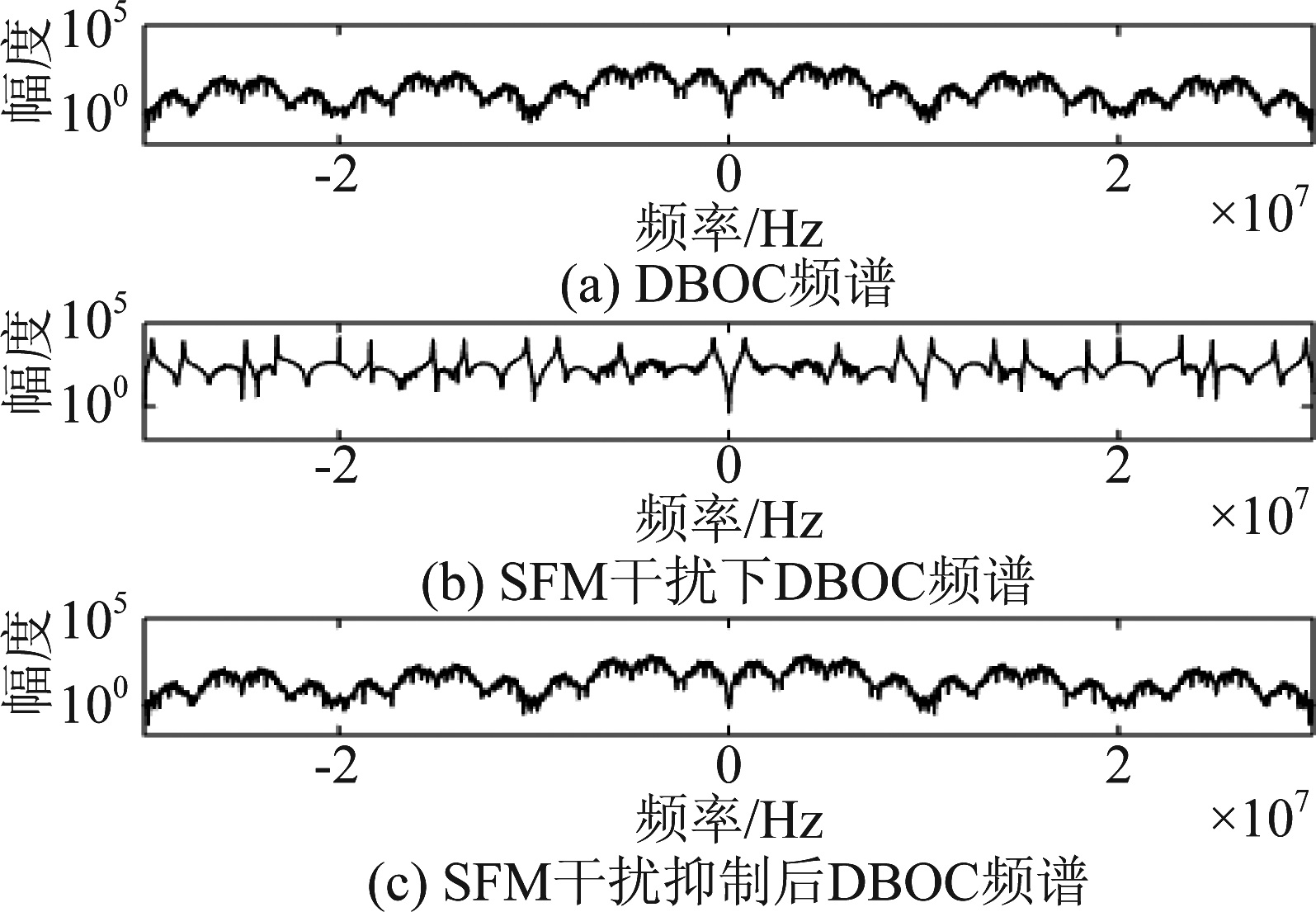
图4 DBOC信号频谱以及干扰抑制前后DBOC频谱
Fig.4 DBOC signal spectrum and DBOC spectrum before and after interference suppression
由图4可知,SFM干扰下的DBOC信号频谱发生失真现象,这显然不利于DBOC信号的捕获,而图4(a)和(c)中干扰抑制前后的DBOC信号频谱基本相同,这表明本文算法能有效抑制SFM干扰。
实验2 误码率。
为了验证算法的干扰抑制性能,实验分别在SIR=-15 dB,SIR=-30 dB,SIR=-60 dB时对系统误码的性能做了仿真分析。其中码片长度为4092, fc为300 Hz,mf为12.1, fm为120 Hz。仿真结果如图5。
由图5可知,当SNR一定时,干扰越强,误码率越大,因为干扰的强度决定了DBOC信号被污染的程度,当DBOC信号被污染的程度很高超过抗干扰容限时,算法的抑制性能会受到一定影响从而导致误码率增大。并且当SIR一定时,系统误码率随着SNR的增大而变小。当SNR到某一值时误码率将不变称为平底效应。

图5 不同条件下的系统误码率
Fig.5 Bit error performance under different conditions
实验3 捕获实现。
为了验证算法的捕获性能,实验在SIR=-25 dB时采用PMF-FFT、PMF-apFFT、本文方法对含有SFM干扰的高动态DBOC信号做捕获实验。通过100次Monte Carlo仿真实验。实验结果如图6。
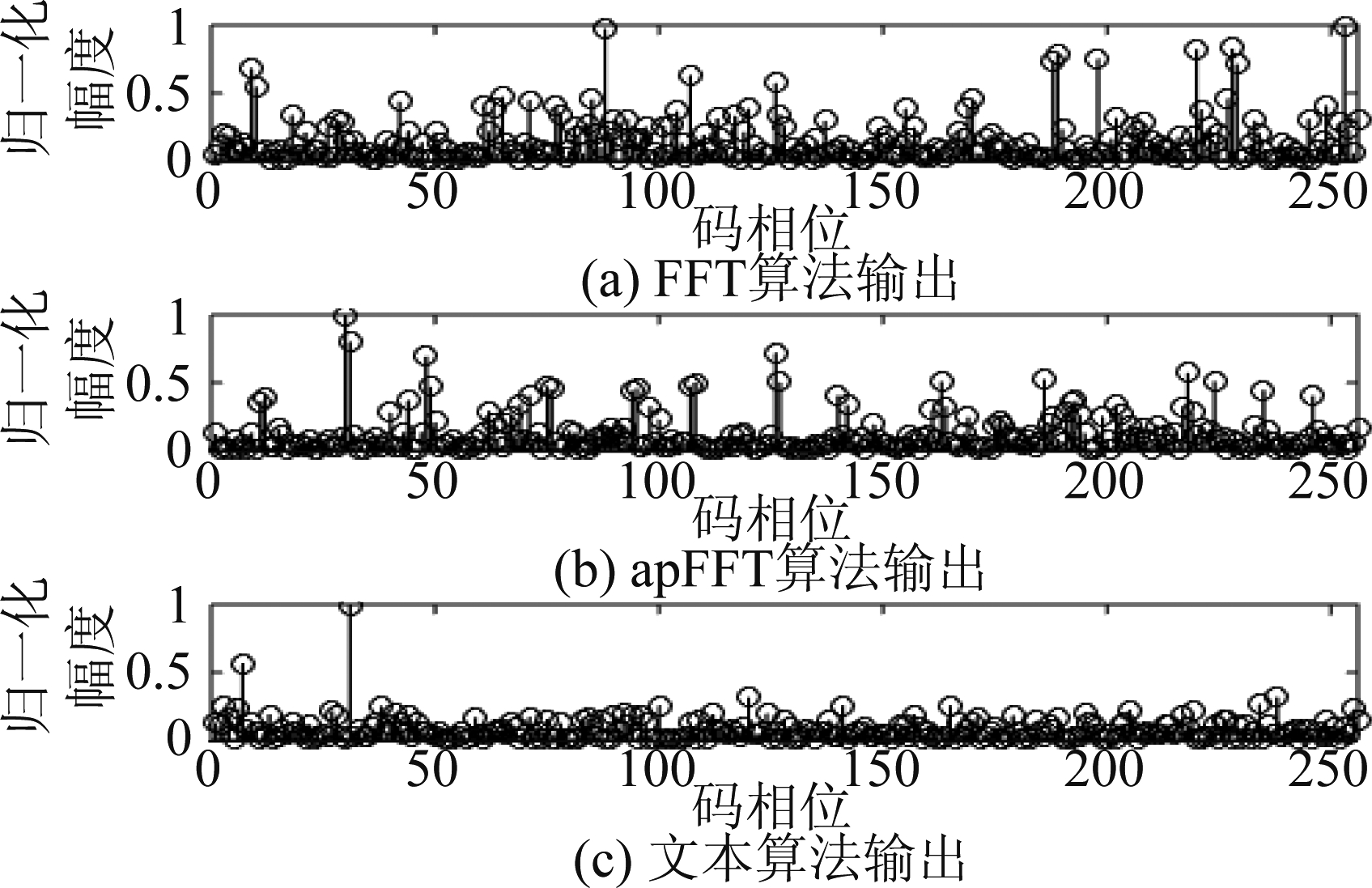
图6 不同算法的振幅输出
Fig.6 Amplitude output of different algorithms
由图6中(b)和(c)可知,PMF-apFFT和本文算法输出的主峰值都在码相位为31这一位置处,而图6(a)中PMF-FFT算法输出的主峰值所在码相位位置不正确,在图6(b)和(c)中,PMF-apFFT算法的次峰峰值相比于本文算法高出的很明显,这减小了判决器检测到主峰位置的概率,所以,通过上述的分析,本文算法能更加容易的使判决器检测到主峰的位置,从而有更加优异的性能。
实验4 不同算法的检测概率仿真。
实验在SIR=-25 dB时对PMF-FFT、PMF-apFFT、DSFMT-PMF-apFFT(以下简称DSFMT-apFFT)和本文算法的检测性能进行了仿真分析。通过500次Monte Carlo仿真实验,实验结果如图7。
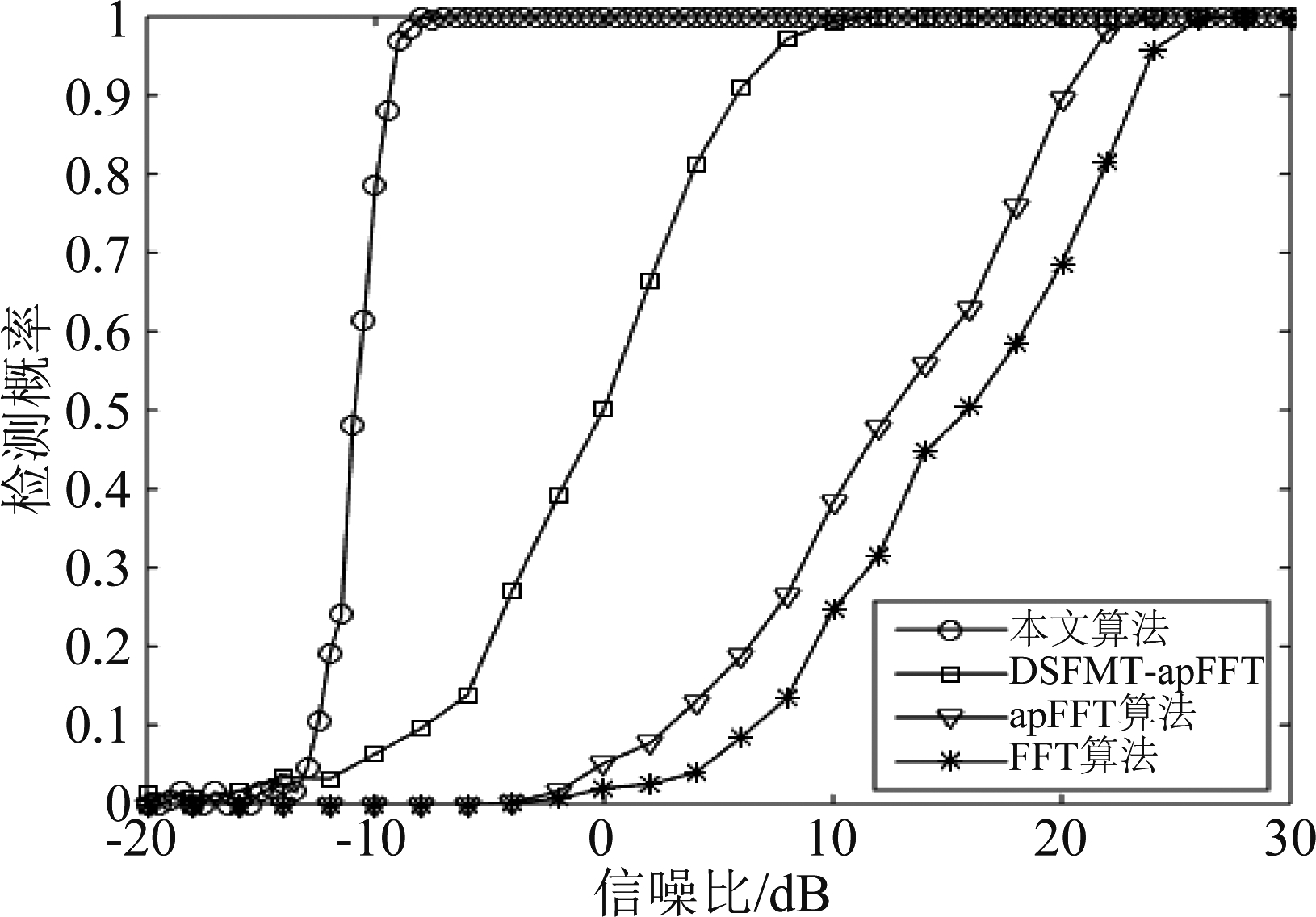
图7 不同算法对比
Fig.7 Comparison of different algorithms
由图7可知,本文算法的检测概率比DSFMT-apFFT高大约17 dB,比PMF-apFFT高大约30 dB,比PMF-FFT高大约34 dB。在0 dB之前,PMF-FFT和PMF-apFFT算法的检测概率很低,说明这两种算法基本无法在低信噪比下完成复杂环境中DBOC信号的捕获。而虽然DSFMT-apFFT相较于PMF-FFT和PMF-apFFT算法的检测性能有一定提升,但是由于动态阶数的影响,其性能还是和本文算法有一定的差距,这也表明相比于PMF-FFT、PMF-apFFT和DSFMT-apFFT算法,本文算法更加适合于SFM干扰和高动态共存环境下DBOC信号的捕获。
实验5 检测概率。
实验在SIR=0 dB,SIR=-15 dB,SIR=-25 dB,SIR=-40 dB时对算法的检测概率做了仿真分析。通过500次Monte Carlo仿真实验,实验结果如图8。
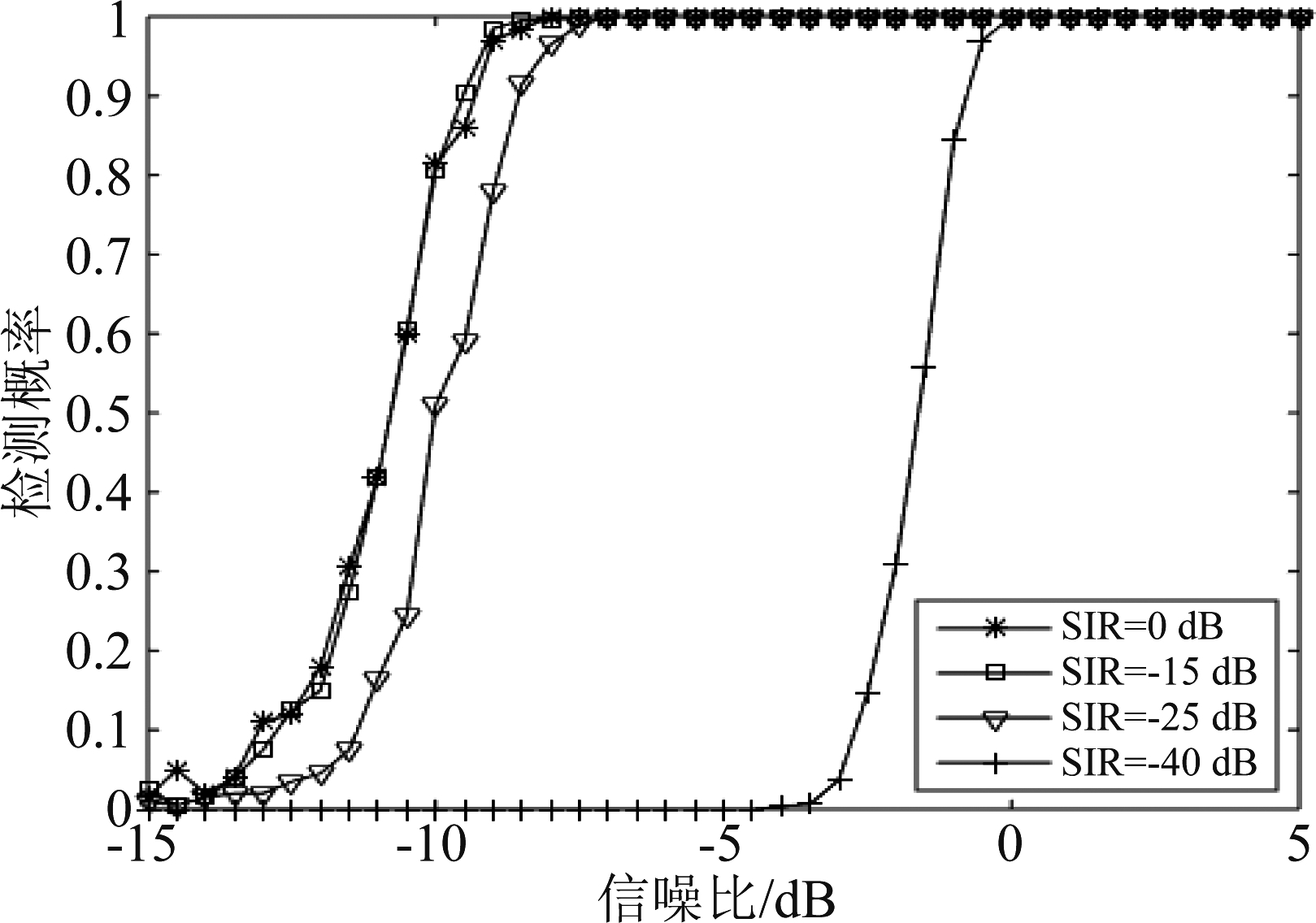
图8 不同条件下对应的检测性能
Fig.8 Detection performance corresponding to different conditions
由图8可知,当SIR=0 dB和SIR=-15 dB时,本文算法能在信噪比-8.5 dB时完成信号的捕获,这说明本文算法可以在干扰强度较低的情况下很好的实现干扰抑制,但是干扰强度为SIR=-25 dB和SIR=-40 dB时的检测性能较SIR=-15 dB时分别降低了1 dB和8 dB,这是因为在较高的干扰强度下,高动态DBOC信号被污染的强度就越大,算法的抑制效果会受到影响,使得检测性能下降。
实验6 不同CZT点数对检测性能的影响。
为了研究CZT点数对检测性能的影响,实验在点数分别为256,512,1024的情况下对本文算法的检测性能做了仿真分析,通过500次Monte Carlo仿真实验,实验结果如图9。
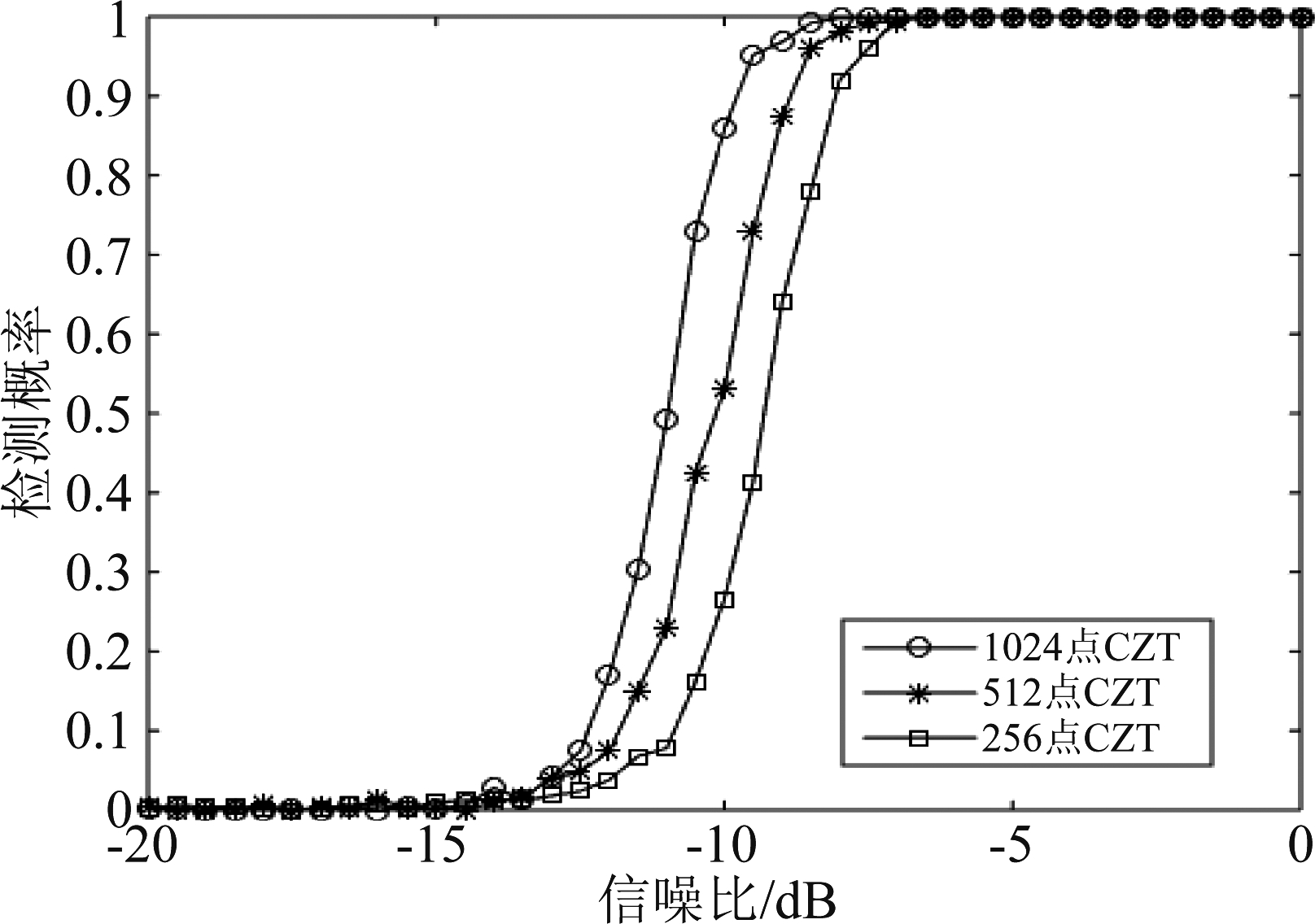
图9 不同CZT点数下算法的检测性能
Fig.9 Detection performance of algorithm under different CZT points
由图9可知,做CZT点数越大,算法的检测性能越好,例如做1024点CZT的检测性能比做512点CZT提高了0.5 dB,比做256点CZT提高了1.5 dB。这是因为所做CZT点数越大,频率分辨率也就越高,所以检测性能也会随之增高。
实验7 不同动态参数下算法的性能。
为了研究动态参数对本文算法的影响,实验在SIR=-25 dB,动态参数分别为fd=0 Hz,kd=0 Hz/s,kf=0 Hz/s2; fd=1500 Hz,kd=20 Hz/s,kf=2 Hz/s2和fd=3500 Hz,kd=30 Hz/s,kf=4 Hz/s2的情况下对本文的检测性能进行仿真。
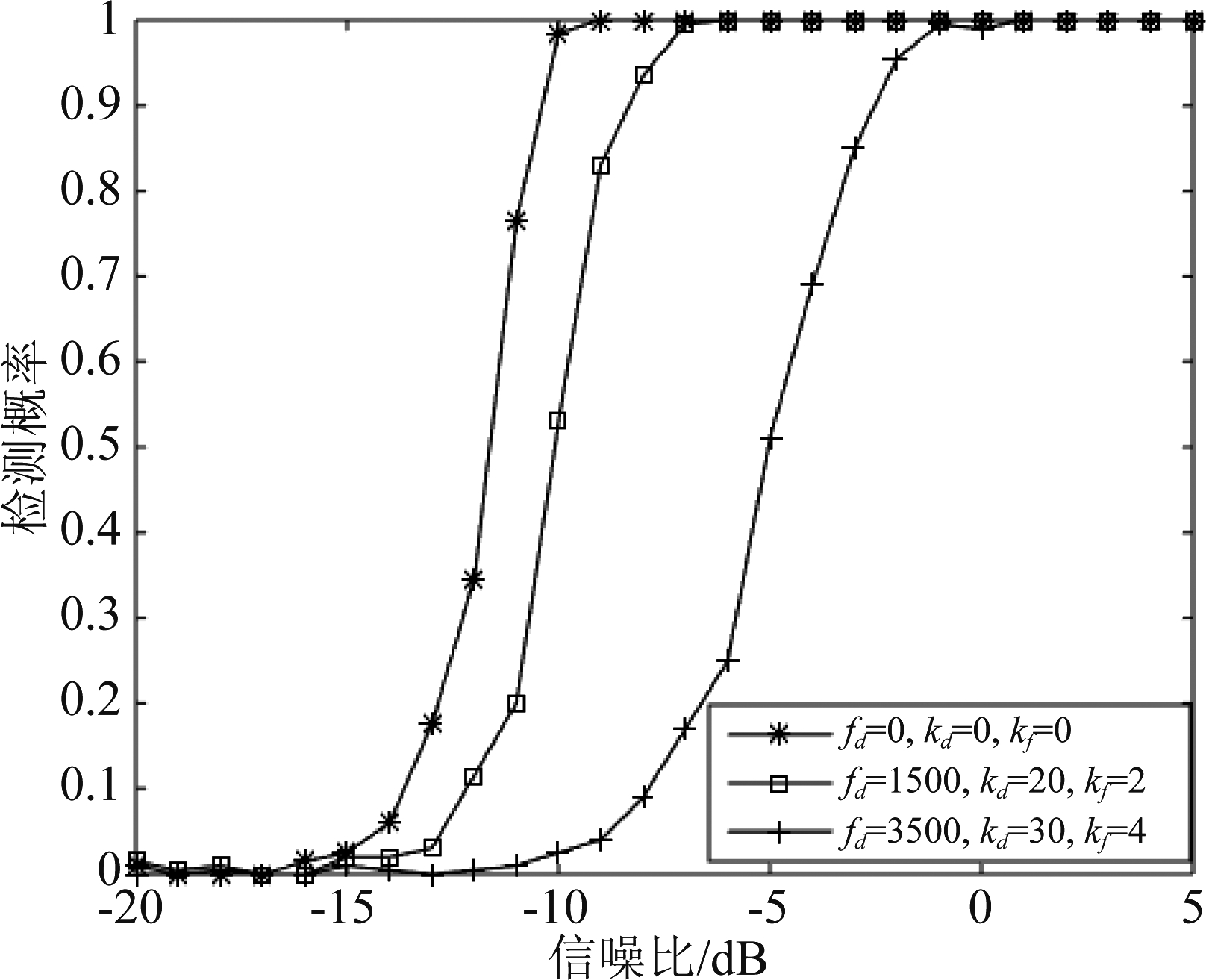
图10 不同动态参数下算法的检测性能
Fig.10 Detection performance of the algorithm under different dynamic parameters
由图10可知,本文算法在fd=1500 Hz,kd=20 Hz/s,kf=2 Hz/s2时的检测性能仅比fd=0 Hz,kd=0 Hz/s,kf=0 Hz/s2时低2 dB,说明本文算法在较低动态参数下可以比较好的补偿fd,kd和kf,但是随着动态参数增大,捕获性能会随之降低,这是因为在SFM干扰和高动态共存环境下大的动态参数不易被补偿从而导致捕获性能的降低。
实验8 计算复杂度。
在本文算法中,相比于乘法计算量,加法计算量的影响很小,所以本文只考虑乘法计算量。
对于本文算法:
DSFMT要对fm和l进行搜索,所以其计算量为:
CDSFMT=M1M2N
(31)
其中,M1为fm的搜索长度,M2为l的搜索长度。
做瞬时互相关的计算量为:
CDPT=(N-τ)log2(N-τ)
(32)
本文中![]() 时,做完瞬时互相关后序列长度变为
时,做完瞬时互相关后序列长度变为![]()
做CZT需要的计算量为:
CCZT=Llog2L
(33)
所以,本文算法总的计算量为:
(34)
对于PMF-FFT和PMF-apFFT算法:
因为PMF-apFFT是在PMF-FFT算法的基础上增加了全相位预处理,仅增加加法计算量,所以PMF-FFT和PMF-apFFT算法的计算量基本相同为:
C=Nlog2N
(35)
综上所述,相比于PMF-FFT和PMF-apFFT算法,本文算法的计算复杂度较高,虽然PMF-FFT和PMF-apFFT算法的计算复杂度较低,实时性也更好,但是其无法有效的补偿一、二阶多普勒变化率,使得此算法在SFM干扰和高动态共存环境中的捕获性能并不理想,但是本文提出的DSFMT可以有效的抑制高动态DBOC信号中的SFM干扰,并且本文所采用的DPT方法可以将带有二阶多普勒变化率的高动态DBOC信号转换成带残余频偏的一阶信号和噪声之和。这两个操作有效的处理了复杂环境中的不确定因素。使得本文算法的检测性能比PMF-apFFT高大约30 dB,比PMF-FFT高大约34 dB。而精确的捕获是跟踪的前提,如果仅仅只考虑计算复杂度而不考虑捕获的性能会使跟踪阶段出现较大问题,并且本文算法大幅度的提高了SFM干扰和高动态共存环境下DBOC信号的捕获性能,所以本文算法牺牲的计算量是值得的。
与此同时,通常情况下,当码片长度为1024,采样频率为16.3 MHz,码速率为1.023 MHz时,需要捕获算法在25 ms内完成捕获。本文算法在这一条件下完成一次捕获所需时间为13.13478 ms,小于25 ms,所以本文算法也同时满足捕获实时性的要求,综上所述,本文算法还是可取的。
6 结论
本文设计了SFM干扰和高动态共存环境下DBOC信号的捕获算法。该算法首先利用DSFMT对SFM干扰进行抑制,然后对处理后的信号做定阶降阶处理,最后利用CZT方法完成精确捕获。仿真情况表明,本文算法能很好的抑制SFM干扰,并且,在SFM干扰和高动态共存的环境下,本文算法相比于PMF-FFT和PMF-apFFT算法输出的谱峰值更加明显,对于检测性能,本文算法的检测概率相比于DSFMT-apFFT高大约17 dB,比PMF-apFFT高大约30 dB,比PMF-FFT高大约34 dB。说明本文算法相比于PMF-FFT,PMF-apFFT和DSFMT-apFFT算法更加适合于SFM干扰和高动态共存环境下DBOC信号的捕获。
[1] Liu E, Meng W, Han S. Research and development on satellite positioning and navigation in China[J]. IEICE Trans. on Communications, 2012, 95(11): 3385-3392.
[2] Betz J W. Binary offset carrier modulations for radio navigation[J]. Navigation, 2001, 48(4): 227-246.
[3] Martin N, Leblond V, Guillotel G, et al. BOC (x, y) signal acquisition techniques and performances[C]∥Proceedings of the 16th International Technical Meeting of the Satellite Division of the Institute of Navigation, 2003.
[4] Xiong H, Wang S, Gong S, et al. Improved synchronization algorithm based on reconstructed correlation function for BOC modulation in satellite navigation and positioning system[J]. IET Communications, 2018, 12(6): 743-750.
[5] Chae K, Yoo S, Kim S Y, et al. Unambiguous Tracking Technique Based on Sub-Carrier Pulse Grouping for TMBOC-Modulated Signals in GPS[J]. IEEE Access, 2016, 4: 7785-7794.
[6] Kim B, Kong S H. Two-dimensional compressed correlator for fast acquisition of CBOC-modulated signal in GNSS[C]∥IEEE/ION Position, Location & Navigation Symposium-plans. IEEE, 2014.
[7] Lohan E S, Lakhzouri A, Renfors M. Complex double-binary-offset-carrier modulation for a unitary characterisation of Galileo and GPS signals[J]. Radar Sonar & Navigation Iee Proceedings, 2006, 153(5): 403- 408.
[8] Lohan E S, Lakhzouri A, Renfors M. Binary-offset-carrier modulation techniques with applications in satellite navigation systems[J]. Wireless Communications and Mobile Computing, 2007, 7(6): 767-779.
[9] Elena Simona Lohan, Adina Burian, Markku Renfors. Low-complexity unambiguous acquisition methods for BOC-modulated CDMA signals[J]. International Journal of Satellite Communications & Networking, 2008, 26(6): 503-522.
[10] Sun X, Zhou Q, Ji Y, et al. An Unambiguous Acquisition Algorithm for BOC (n, n) Signal Based on Sub-correlation Combination[J]. Wireless Personal Communications, 2019, 106: 1609-1628.
[11] Chen H H, Wang R, Jia W M, et al. An Unambiguous Tracking Method Based on Pseudo Correlation Function for AltBOC(15,10) Signal[J]. Wireless Personal Communications, 2013, 69(4):1347-1364.
[12] Pan Y, Zhang T Q, Zhang G, et al. Analysis of an improved acquisition method for high-dynamic BOC signal[J]. Journal of Systems Engineering and Electronics, 2016, 27 (6): 1158-1167.
[13] Li M S, Cheng Y F, Wang X Z, et al. A synchronization acquisition algorithm for wireless communication system in high dynamic environment[C]∥IEEE 17th International Conference on Communication Technology, Chengdu, China, 2017: 1407-1411. doi: 10.1109 /ICCT.2017.8356864.
[14] Guo W F, Niu X J, Guo C, et al. A new FFT acquisition scheme based on partial matched filter in GNSS receivers for harsh environments[J]. Aerospace Science and Technology, 2016, 61: 66-72.
[15] Dong L, Ma Z X, Wang Y H. A hierarchical acquisition algorithm for high dynamic weak DSSS signals[J]. Telecommunication Engineering, 2015, 55(2): 182-186.
[16] Yang Q B, Wang Z L, Huang Q, et al. Folded PMF-FFT fast acquisition method for high dynamic scenarios[J]. Systems Engineering & Electronics, 2016, 38(8): 1723-1729.
[17] Luo Y, Yu C, Chen S, et al. A Novel Doppler Rate Estimator Based on Fractional Fourier Transform for High-Dynamic GNSS Signal[J]. IEEE Access, 2019, 7: 29575-29596.
[18] Luo Y, Zhang L, Ruan H. An Acquisition Algorithm Based on FRFT for Weak GNSS Signals in A Dynamic Environment[J]. IEEE Communications Letters, 2018, 22(6): 1212-1215.
[19] Xia X, Zhao J, Long H, et al. Fractional Fourier transform-based unassisted tracking method for Global Navigation Satellite System signal carrier with high dynamics[J]. Iet Radar Sonar & Navigation, 2016, 10(3): 506-515.
[20] Luo Y, Zhang L, El-Sheimy N. An improved DE-KFL for BOC signal tracking assisted by FRFT in a highly dynamic environment[C]∥IEEE Position, Location and Navigation Symposium (PLANS), 2018: 1525-1534.
[21] Pan Y, Zhang T, Zhang G, et al. A Narrowband Anti-jamming Acquisition Algorithm Based on All-phase Processing for BOC Signals[J]. IEEE Access, 2019, 7: 41416- 41425.
[22] 席闯, 常青, 李舸争, 等. 基于分数阶傅里叶变换的GNSS接收机抗线性调频干扰技术研究[J]. 导航定位与授时, 2018, 5(5): 54- 60.
Xi Chuang, Chang Qing, Li Gezheng, et al. Research on LFM interference suppression technology based on fractional fourier transform in GNSS receiver[J]. Navigation Positioning and Timing, 2018, 5(5): 54- 60.(in Chinese)
[23] 陈晶. 线性调频信号与正弦调频信号参数估计方法[D]. 哈尔滨: 哈尔滨工程大学, 2012.
Chen Jing. Parameters estimation methods of linear frequency signals and sinusoidal frequency signals[D]. Harbin: Harbin Engineering University, 2012.(in Chinese)
[24] Peleg S, Friedlander B. The discrete polynomial-phase transform[J]. IEEE Transactions on Signal Processing, 1995, 43(8): 1901-1914.
[25] 曾婵, 李卫民, 毕波. 高动态GPS信号粗捕和精捕算法仿真实现[J]. 北京航空航天大学学报, 2017, 43(4): 790-799.
Zeng Chan, Li Weimin, Bi Bo. Simulation realization of high dynamic GPS signal coarse acquisition and fine acquisition algorithm[J]. Journal of Beijing University of Aeronautics and Astronautics, 2017, 43(4): 790-799.(in Chinese)



