1 引言
当前,急剧增加的数据业务量对传统的蜂窝通信提出了巨大的挑战。设备到设备(Device To Device,D2D)通信允许移动终端之间直接进行通信,无需再通过基站(Base Station,BS),减少了基站的负担,成为传统蜂窝通信的重要补充。异构蜂窝网络中,D2D用户可以共享蜂窝用户的频谱资源[1],因此可以支持更多用户通信,不仅提高了整个系统的频谱利用率,还增加了系统的整体容量。目前,D2D 通信技术已被标准化组织3GPP纳入新一代移动通信系统的发展框架中[2-3],成为了 5G 通信的关键技术之一。
D2D对共享蜂窝频谱的方式主要有两种,分别是专用模式(overlay)和复用模式(underlay)[4]。前者将专用频谱分配给D2D链路,尽管频谱效率较低,但对蜂窝用户的干扰较少。后者允许D2D用户复用蜂窝用户的频谱资源,极大提高了频谱利用率,但是需要更复杂的干扰管理。未来无线通信的发展将会是海量设备接入和千倍流量增长,频谱资源将会更为紧张,因此,本文聚焦于D2D通信复用模式的研究。
解决异构蜂窝网络中的干扰管理问题,其中一个方法是控制用户的发送功率。文献[5]旨在保证蜂窝用户和D2D用户最大发射功率约束以及满足蜂窝链路的最小速率要求的条件下最大化全双工D2D链路的可实现总速率,制定最佳功率控制问题;文献[6]提出了一种基于距离和联合功率控制的通信模式选择方案,其中D2D用户和蜂窝用户与基站距离的比值决定了D2D用户是否采用 Underlay 模式进行通信,进而在约束蜂窝用户和D2D用户发射功率的条件下实现D2D链路和蜂窝链路的联合功率控制。集中式资源分配是由基站对各个通信链路统一进行调控,基站根据已知的信道状态信息做出最佳分配方案。针对D2D通信与蜂窝通信之间干扰问题,文献[7]开发了一种集中式资源分配算法,在蜂窝用户的服务质量(Quality of Service,QoS)约束下最大化D2D用户的数据传输速率;文献[8]为了保证蜂窝用户以及D2D用户的QoS,开发了集中式频谱分配方案来最大化整个系统的数据传输速率;文献[9]同样采用集中式资源分配方案,同时考虑具有异构QoS要求的频谱分配和功率控制方案来选择最佳的资源共享模式。
集中式资源分配需要大量的信道状态信息以及信令,不仅开销大,而且增加了基站的负担,相比之下,分布式资源分配不需要基站统一调度,只需要用户各自进行调控,减少了信令开销,极大的提高了效率。博弈论作为分布式资源分配设计的一个有利工具[10],能够将网络中各个用户的竞争行为以效用函数的形式表示出来,使得可以从数学分析的角度去探索激励机制对网络用户行为的影响。文献[11]制定了基于定价的非合作Stackelberg博弈模型,用于解决D2D和蜂窝网络频谱共享的干扰协调问题,其中基站是确定价格的领导者,D2D对是确定发射功率的跟随者;文献[12]采用合作博弈模型,提出一种重叠的联盟形成博弈,将共享同一资源块的用户设备(蜂窝用户和D2D用户)划分为一个联盟,形成初始的重叠联盟结构,再提出具有重叠联盟的合作博弈,目的是最大化所有D2D链路的和速率;文献[13]为提高系统中D2D通信性能将资源分配问题分解为信道分配和功率控制两个独立的子问题进行求解,其中信道分配问题表述为一个多对一匹配问题,功率控制问题建模为Stackelberg博弈求解;文献[14]研究蜂窝网络下的D2D通信的联合频谱共享和功率分配问题,BS作为Stackelberg中的领导者,通过对干扰定价来协调D2D传输到蜂窝用户的干扰,D2D对作为追随者以非合作方式竞争频谱;文献[15]提出两级博弈模型,内层应用Stackelberg博弈为小区边缘用户选择中继节点,外层应用联盟形成博弈为D2D链路分配适当的频谱资源;文献[16]提出了一种基于非合作博弈的分布式资源分配算法,以解决D2D通信和蜂窝用户之间的跨层干扰以及D2D通信之间的层内干扰的问题;文献[17]中应用混合博弈研究蜂窝和D2D用户的两个效用函数以增强系统频谱效率,将D2D用户和蜂窝用户分别建模为一个理性的参与者,再根据QoS最大化其各自的效用。
上述文献主要从系统和速率最大化角度研究资源分配问题,而在实际中,短距离D2D通信的一大优势是高能效(Energy Efficiency, EE),不仅可以节省电池电量以延长手机寿命,还可以绕过基站以节省发射功率[18]。文献[19]研究了在蜂窝网络用户QoS约束下使D2D通信能效达到最大化的问题,提出一种基于LambertW函数的功率控制算法,以此来最大化单个D2D对能效;文献[20]研究了蜂窝网络下D2D通信的联合资源分配和功率控制,利用分数规划的性质将分数形式的原始非凸优化问题转化为减法形式的等价优化问题;文献[21]提出了一种低复杂度的功率迭代算法,满足蜂窝通信QoS的同时最大化D2D对的能效。文献[22]研究了下行链路异构蜂窝网络中D2D的信道和功率分配问题,在保证其他层级用户的QoS要求的基础上使D2D对能效最大化,首先为D2D对分配合适的资源块,其次采用遗传方法优化D2D对和基站的功率;文献[23] 研究了具有底层D2D通信的分布式天线系统中的能效最大化问题,考虑了系统中信道状态信息不确定的情况,具有现实性和合理性。
针对异构蜂窝网络中D2D对的能效优化问题,本文引入Stackelberg博弈,对D2D通信的资源分配问题建立博弈模型,形成以BS作为领导者(leader),D2D对作为跟随者(follower)的一对多博弈模型,在最大化BS端蜂窝用户能效的基础上通过控制D2D对发送功率来最大化D2D对总能效。本文分别针对跨层干扰和层内干扰创新性地建立了干扰价格系数与D2D对发送功率之间的函数关系,并提出一种基于Stackelberg博弈的分布式功率控制算法。
2 系统模型与问题制定
2.1 系统模型
假设在一个单小区蜂窝网络中,D2D用户复用蜂窝网络上行链路频谱资源。系统模型如图1所示,假设该小区中有M个单天线蜂窝用户,任一蜂窝用户可用m(m∈M)表示;同时存在K个正交子信道,任一子信道可用k(k∈K)表示,预先为每个正交子信道分配一个蜂窝用户,每个蜂窝用户以固定的功率pc向BS发送信号。此外,系统中D2D对的数量为N(N>M),每个子信道最多可被nk(nk<N)个D2D对复用,而每个D2D对最多只能访问一个子信道,每组D2D对由一个单天线D2D发射机(D2D Transmitter,DT)和一个单天线D2D接收机(D2D Receiver,DR)组成。在该系统模型下,各个正交子信道之间不存在干扰,同一子信道中存在蜂窝用户和D2D用户之间的干扰以及D2D对之间的干扰。
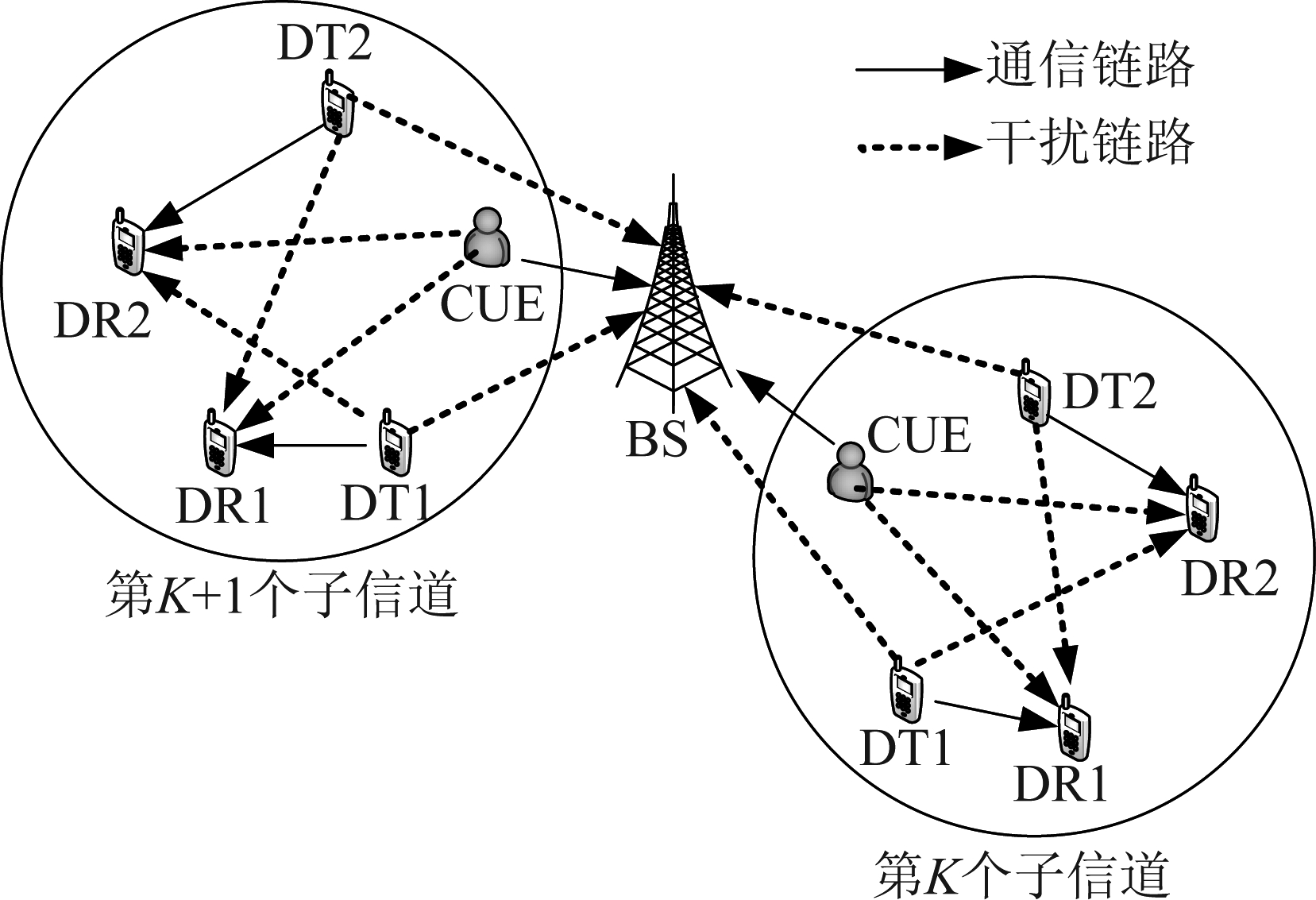
图1 系统模型
Fig.1 System model
2.2 问题制定
异构蜂窝网络中,蜂窝用户和D2D用户通过竞争或者合作的方式来最大化自身的利益,因此可以看作是一个分布式决策问题,需要制定出合适的分布式决策方案。首先要考虑多用户模型各个用户间的交互作用问题,其次各用户需要根据已知信息独立做出决策。博弈论提供了丰富的数学工具研究各个参与者之间复杂的相互作用,预测他们的策略选择。基于以上两方面的考量,本文引入博弈论中的Stackelberg博弈建模异构网络中蜂窝用户和D2D用户的能效优化问题。
上述系统模型,第k(k∈{1,2,3…K})个正交子信道中,令![]() 表示该子信道内蜂窝用户在BS端的信干噪比,即
表示该子信道内蜂窝用户在BS端的信干噪比,即
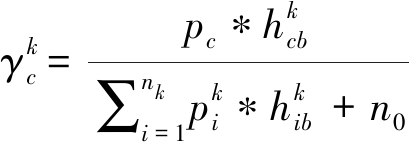
(1)
其中,pc表示该子信道中蜂窝用户到BS的发送功率,![]() 表示第i对D2D对的发送功率。
表示第i对D2D对的发送功率。![]() 分别表示蜂窝用户到BS的通信链路增益以及第i对DT到BS的干扰链路增益。n0表示加性高斯白噪声。
分别表示蜂窝用户到BS的通信链路增益以及第i对DT到BS的干扰链路增益。n0表示加性高斯白噪声。
同样在第k个正交子信道,令![]() 表示第i对DR端的信干噪比,即
表示第i对DR端的信干噪比,即
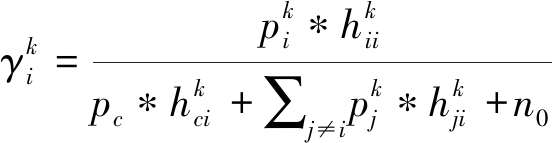
(2)
其中![]() 为该子信道中除了第i对D2D对以外其他D2D对的发送功率。
为该子信道中除了第i对D2D对以外其他D2D对的发送功率。![]() 和
和![]() 分别表示第i对D2D发送端到接收端的通信链路增益,蜂窝用户到第i对D2D接收端的干扰链路增益以及同一子信道中其他D2D对发送端到第i对D2D接收端的干扰链路增益。n0表示加性高斯白噪声。
分别表示第i对D2D发送端到接收端的通信链路增益,蜂窝用户到第i对D2D接收端的干扰链路增益以及同一子信道中其他D2D对发送端到第i对D2D接收端的干扰链路增益。n0表示加性高斯白噪声。
本文采用时分双工模式,根据信道互易性,第i对D2D对接收端可以获得![]() 同样地,BS也可以获得DT到BS和蜂窝用户到BS的信道信息。
同样地,BS也可以获得DT到BS和蜂窝用户到BS的信道信息。
在第k个正交子信道,当信干噪比较高时,![]() 表示除去第i对D2D对以外其他所有D2D对的能效,
表示除去第i对D2D对以外其他所有D2D对的能效,![]() 表示蜂窝链路的能效。定义:
表示蜂窝链路的能效。定义:
(3)
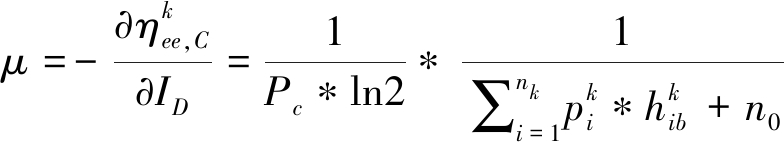
(4)
式(3)中,![]() 表示DR端接收到的来自蜂窝用户和其他D2D用户的干扰,πj始终是一个非负数,表示随着接收到的干扰信号的减少用户j∈Nk\{i}可获得的能效的边际增量,可以表示为同一子信道中不同D2D对之间的干扰,即层内干扰价格系数。式(4)中,
表示DR端接收到的来自蜂窝用户和其他D2D用户的干扰,πj始终是一个非负数,表示随着接收到的干扰信号的减少用户j∈Nk\{i}可获得的能效的边际增量,可以表示为同一子信道中不同D2D对之间的干扰,即层内干扰价格系数。式(4)中,![]() 则表示BS端接收到的来自子信道内所有D2D对的干扰,μ同样是一个非负数,表示D2D对与蜂窝用户之间的干扰,即跨层干扰价格系数。
则表示BS端接收到的来自子信道内所有D2D对的干扰,μ同样是一个非负数,表示D2D对与蜂窝用户之间的干扰,即跨层干扰价格系数。
本文的系统模型中,各个子信道之间不存在干扰,因此每个子信道的能效最大化问题是独立的,可以单独进行求解。令蜂窝小区中的BS作为领导者,D2D对作为跟随者,形成一个单领导者多跟随者的分布式博弈方案。基站作为领导者,其博弈论收益优化问题可表示为
(5)
(6)
领导者效用可以表示蜂窝通信在D2D用户发送功率约束条件下通过将频谱资源出售给D2D对所获得的收益。当提高价格系数μ时,跟随者复用频谱资源的成本增加,为降低成本而减小DT端发送功率,使得对领导者的干扰减少,从而使领导者从跟随者处获得的收益也减少,因此,价格系数μ与DT端发送功率之间存在博弈。
D2D用户作为跟随者,其能效优化问题可转化为如下的博弈论收益优化问题
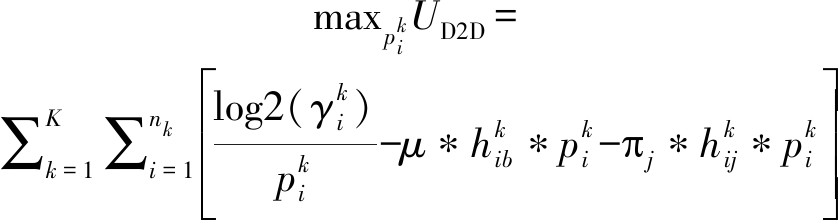
(7)
(8)
跟随者的效用函数共分为三部分:第一部分是其本身的能效收益,第二部分是复用蜂窝频谱资源对蜂窝用户产生干扰而损失的收益,第三部分是由于D2D对之间的干扰而损失的收益。一方面,较高的发送功率意味着较高的效用;另一方面,过高的发送功率会导致D2D对与蜂窝之间的干扰和D2D对之间的干扰增加,进而使跟随者效用降低。
令P (P1,P2,P3…PK)为所有子信道中D2D发送功率的集合,
(P1,P2,P3…PK)为所有子信道中D2D发送功率的集合,![]() 为第k个子信道中D2D发送功率的集合。博弈的最终目的是获得博弈均衡点,使得领导者与跟随者均不能为了自身利益的最大化而自私的偏离该点。因此本文的Stackelberg博弈均衡定义如下:
为第k个子信道中D2D发送功率的集合。博弈的最终目的是获得博弈均衡点,使得领导者与跟随者均不能为了自身利益的最大化而自私的偏离该点。因此本文的Stackelberg博弈均衡定义如下:
定义1(Stackelberg均衡) μ为跨层干扰系数,Pk为D2D对的发送功率集合,S(μ,Pk)为策略集。当且仅当策略集满足以下条件时,策略![]() 达到Stackelberg均衡。
达到Stackelberg均衡。
(9)
(10)
本文Stackelberg博弈中,BS具有先行性,D2D用户根据观察到的BS的价格系数计算最佳发送功率,然后BS根据D2D用户最佳发送功率调整自己的价格系数,通过发送功率和价格系数迭代优化,最终达到均衡。当价格系数确定时,跟随者之间的博弈可以看作Stackelberg的一个子博弈![]() 即各D2D对发送功率的博弈。因此为达到Stackelberg均衡点,首先要获得子博弈的纳什均衡解。
即各D2D对发送功率的博弈。因此为达到Stackelberg均衡点,首先要获得子博弈的纳什均衡解。
3 算法设计
3.1 分布式功率控制算法
令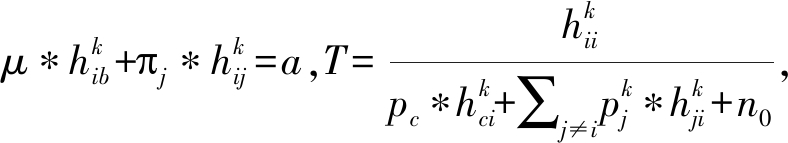 则式(7)可改写为
则式(7)可改写为
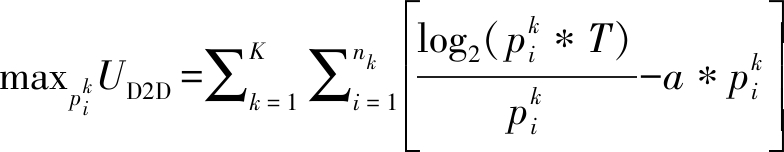
(11)
对![]() 求偏导,可得
求偏导,可得
(12)
上式等号右侧的分母始终大于0,若考虑该偏导式是否为0,只需考虑分子即可。
令分子为f
(13)
对式(13)中的![]() 求导,即
求导,即
(14)
![]() 表示同一正交子信道中第i对D2D对的发送功率,由于
表示同一正交子信道中第i对D2D对的发送功率,由于![]() 恒正,所以f ′<0恒成立, f是减函数。当
恒正,所以f ′<0恒成立, f是减函数。当![]() 趋近于0时, f的函数值是正值;当
趋近于0时, f的函数值是正值;当![]() 趋近于正无穷时, f的函数值为负值。因此必存在
趋近于正无穷时, f的函数值为负值。因此必存在![]() 使得f=0成立,即
使得f=0成立,即![]() 因此效用函数UD2Di是一个凸函数,所以存在
因此效用函数UD2Di是一个凸函数,所以存在![]() 可以使D2D效用函数取得极大值。
可以使D2D效用函数取得极大值。
为求解上述![]() 的闭合表达式,可先将式(13)改写为
的闭合表达式,可先将式(13)改写为
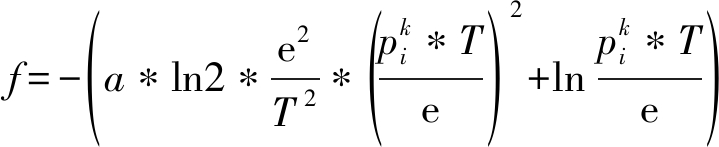
(15)
令f=0,可得
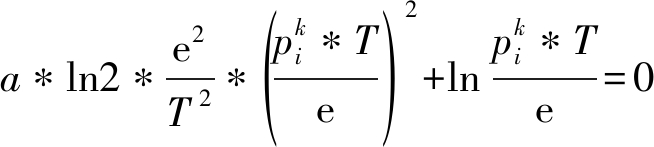
(16)
再令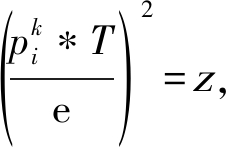 即
即![]() 则式(16)可以写成
则式(16)可以写成
(17)
最后令lnz=x,z=ex,可解出
(18)
进而可得
(19)
再由DT端最大最小发送功率的限制,D2D对最佳发送功率的闭合表达式为
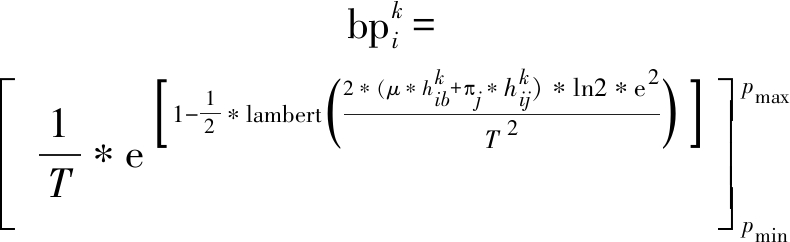
(20)
其中![]() 表示第i对D2D对的最佳发送功率,
表示第i对D2D对的最佳发送功率,![]()
纳什均衡为博弈过程提供了一个稳定的状态,各个参与者通过竞争达到自身利益最大化,但并不希望偏离纳什均衡点。接下来证明D2D用户间基于能效的子博弈纳什均衡的存在性和唯一性。
定理1(纳什均衡) 若功率策略集是欧氏空间中非空、封闭、有界的凸集,且效用函数是关于发送功率的连续凸函数,则存在纳什均衡。
根据上一小节可知功率策略集Pk是一个非空、封闭且有界的凸集,效用函数UD2D是![]() 的连续函数,并且式(12)~式(14)表明效用函数存在唯一的极大值,因此UD2D是关于
的连续函数,并且式(12)~式(14)表明效用函数存在唯一的极大值,因此UD2D是关于![]() 的凸函数,该博弈存在纳什均衡。又由于每次功率迭代的值是唯一的,因此子博弈纳什均衡点也是唯一的。
的凸函数,该博弈存在纳什均衡。又由于每次功率迭代的值是唯一的,因此子博弈纳什均衡点也是唯一的。
本文通过控制发送功率![]() 最大化子博弈G的收益,πj表示层内干扰价格系数,每次发送功率更新完毕后更新πj,具体功率控制算法如表1所示。
最大化子博弈G的收益,πj表示层内干扰价格系数,每次发送功率更新完毕后更新πj,具体功率控制算法如表1所示。
表1 给定干扰价格系数下D2D发送功率的迭代优化算法
Tab.1 Iterative optimization algorithm for D2D transmission power under given interference price coefficient

3.2 跨层干扰价格系数更新
在给定干扰价格系数μ下,通过上节的分布式功率控制算法可以获得博弈关于D2D功率![]() 的纳什均衡解,即可以满足Stackelberg均衡的式(9)。为了让BS端蜂窝用户的收益最大化,即为了满足Stackelberg均衡的式(10),需要让干扰价格系数与发送功率迭代更新,具体算法如表2所示。
的纳什均衡解,即可以满足Stackelberg均衡的式(9)。为了让BS端蜂窝用户的收益最大化,即为了满足Stackelberg均衡的式(10),需要让干扰价格系数与发送功率迭代更新,具体算法如表2所示。
表2 D2D发送功率与干扰价格系数的迭代更新算法
Tab.2 Iterative update algorithm for D2D transmission power and interference price coefficient

主要算法流程:1.初始化:根据pint计算初始跨层干扰系数μ0,设置迭代次数n=0;2.计算U0BS;3.n=n+1;4.根据算法1更新功率,计算Un+1BS;5.IfUn+1BS
4 仿真分析
本文仿真参数如表3所示。
表3 仿真参数设置
Tab.3 Simulation parameter settings
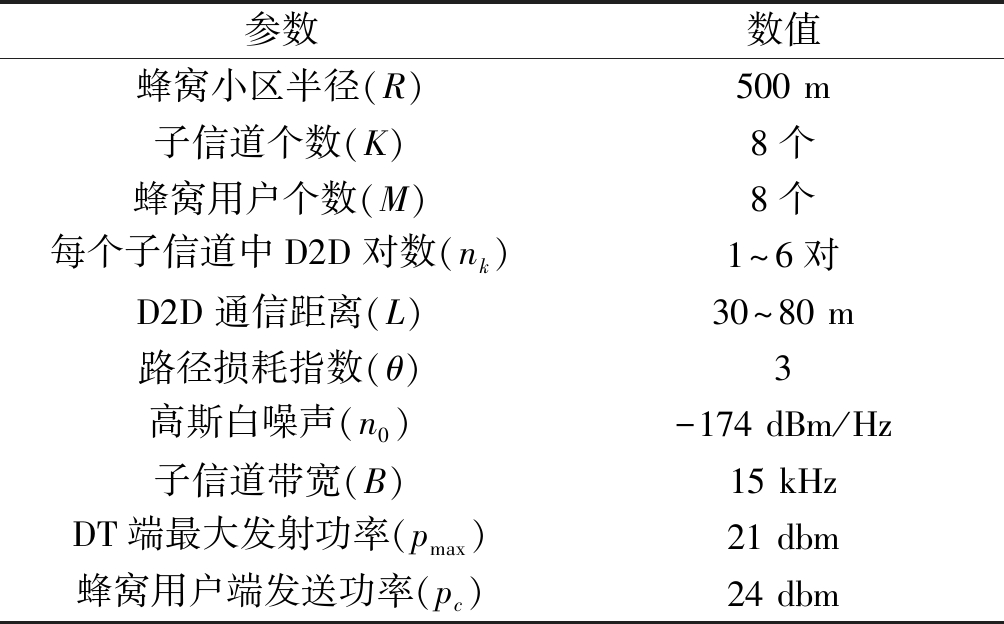
参数数值蜂窝小区半径(R)500 m子信道个数(K)8个蜂窝用户个数(M)8个每个子信道中D2D对数(nk)1~6对D2D通信距离(L)30~80 m路径损耗指数(θ)3高斯白噪声(n0)-174 dBm/Hz子信道带宽(B)15 kHzDT端最大发射功率(pmax)21 dbm蜂窝用户端发送功率(pc)24 dbm
本文考虑多径衰落和阴影衰落的影响,使用文献[13]中的路径损耗模型,不同链路的路径增益可以表示为
h=ξ*L-θ
(21)
其中,ξ表示呈指数分布的快衰落模型,L表示各通信链路发送端到接收端的距离,θ为路径损耗常数。
仿真中蜂窝用户和D2D用户的位置是随机产生的,规定每对D2D链路的距离不超过70 m,为提高频谱效率并减小层内干扰,足够远的D2D对可以复用同一子信道,但干扰链路的距离最远不超过140 m。
Stackelberg博弈属于动态非合作博弈,领导者与跟随者是竞争关系,二者目的都是实现自身利益的最大化,文献[14]效用函数的建立仅考虑领导者与跟随者之间的干扰,没有考虑跟随者之间的干扰,为单纯的非合作博弈。本文算法则在此基础上考虑跨层干扰和层内干扰同时存在的情况,层内干扰主要是为了限制了某一D2D对自私的最大化其自身能效。此外,本文将文献[11]中速率为优化目标的算法拓展到能效问题,该算法中跨层干扰价格系数是由迭代的方法逐步寻找到最优解,本文则建立了干扰价格系数与![]() 的函数关系,可以有效提高算法的收敛性能。以下仿真将本文算法分别与文献[14]中的非合作算法以及文献[11]中的价格迭代算法进行比较。
的函数关系,可以有效提高算法的收敛性能。以下仿真将本文算法分别与文献[14]中的非合作算法以及文献[11]中的价格迭代算法进行比较。
图2为每个子信道中D2D个数与D2D对总能效关系图,分别为本文算法、价格迭代算法与非合作算法的能效对比。如图所示,随着子信道中复用D2D对数的增加,三种算法的能效均先呈上升趋势后趋于平稳,表明子信道内复用多个D2D对可以有效提高D2D总能效,但超过某一定值时,干扰也随之增多致使能效不再增加。子信道中只有一个D2D对时,不存在层内干扰,因此本文算法与非合作算法能效相等,价格迭代算法略低于本文算法。随着子信道中D2D对数的增加,层内干扰也随之增加,由于本文算法可以有效地限制非合作算法中D2D对的自私性,能效高于非合作算法,价格迭代算法依旧低于本文算法。相比于价格迭代算法与非合作算法,本文所提出的分布式功率控制算法可以获得更高的能效。
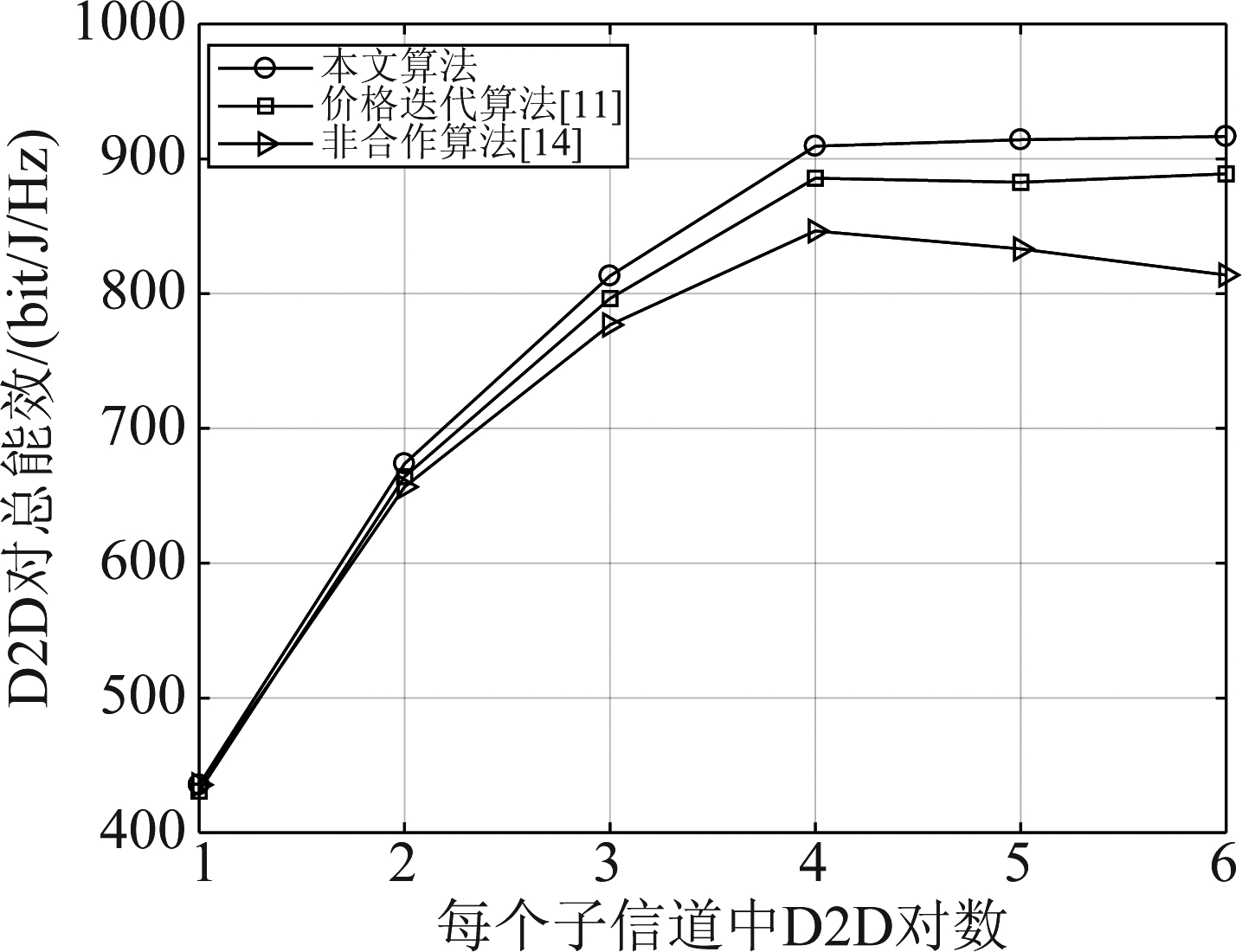
图2 子信道中不同D2D对数下的能效(其中L=40 m)
Fig.2 Energy efficiency under different D2D numbers in sub-channels (where L=40 m)
图3为D2D收发两端距离与D2D对总能效的关系图。如图所示,三种算法的能效均随着D2D收发两端距离的增加而降低,即D2D对两端距离越近,能效越高,随着通信距离增加,能效逐渐降低。此外,系统内子信道数越多,D2D总能效也就越高。随着D2D对收发两端距离增大,信道增益和数据传输速率势必也会随之降低,如果此时通过增大D2D发送功率来获得更高的数据传输速率,则干扰和功耗同样也会增加。因此三种算法的能效都会随着通信距离的增加而降低。从图中可以看出本文算法相比另外两种算法D2D对总能效更高。
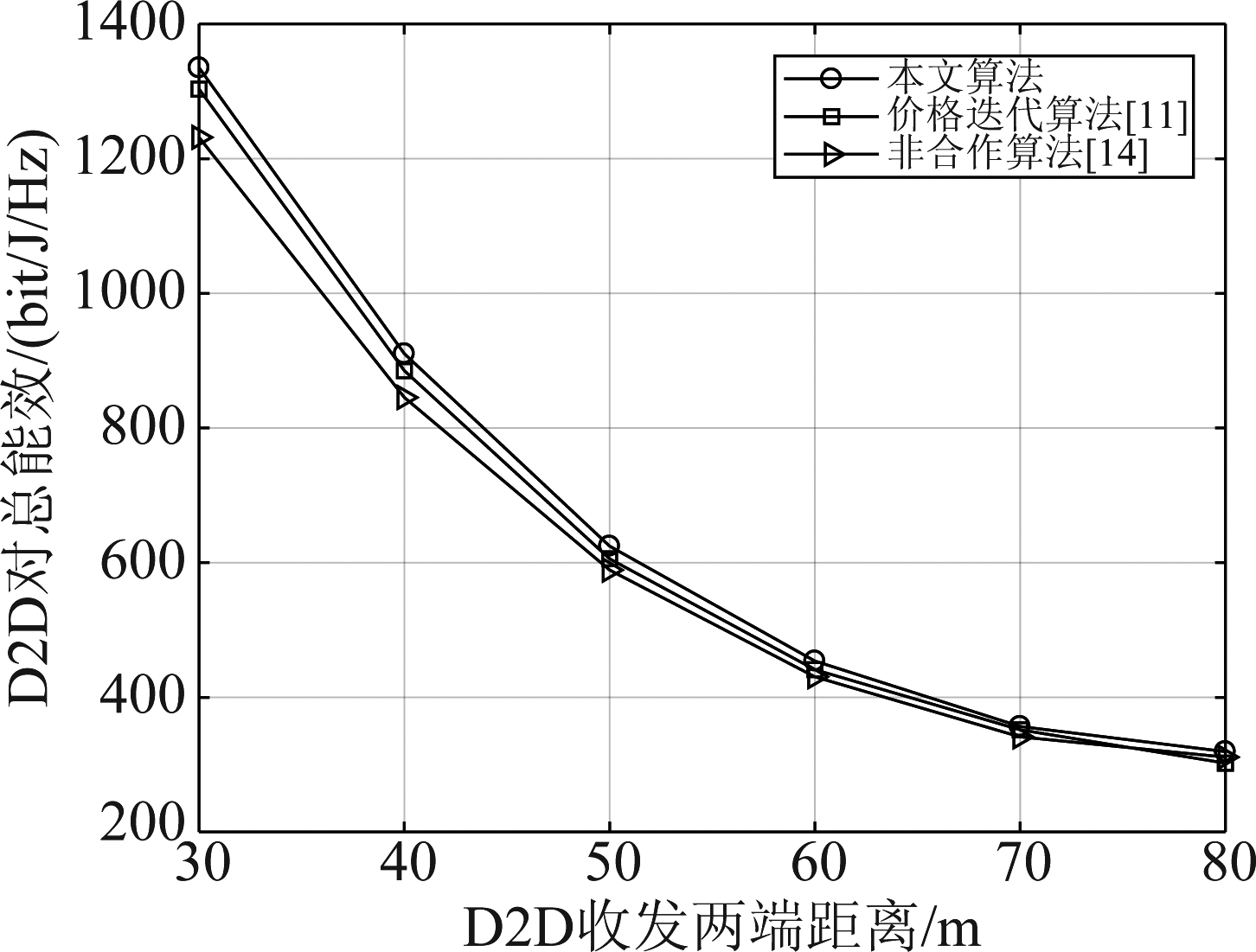
图3 不同D2D收发两端距离下的能效(其中nk=4)
Fig.3 Energy efficiency at different distances between D2D transceivers (where nk=4)
图4为本文算法与价格迭代算法关于D2D对总能效的收敛性能比较。如图所示,两种算法经过有限次迭代均能收敛到最佳能效,而本文算法达到收敛时的能效明显高于价格迭代算法收敛时的能效。由于本文算法中的价格系数与发送功率存在函数关系,根据发送功率的值能快速计算出价格系数,相比之下,二者的迭代速度基本一致,但本文算法达到收敛时的能效更高。
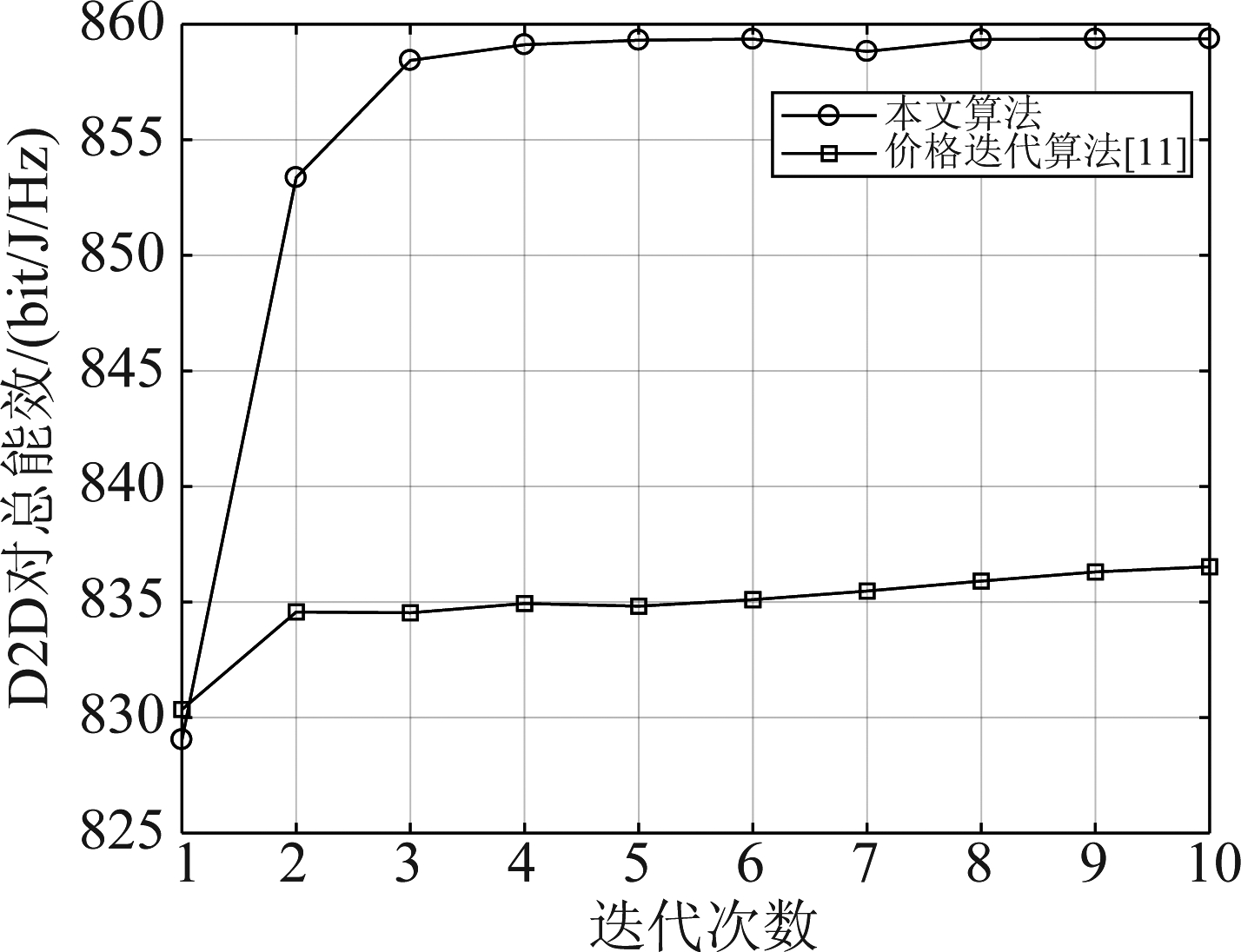
图4 收敛性比较(其中nk=4)
Fig.4 Convergence comparison (where nk=4)
5 结论
本文在异构蜂窝网络下提出了一种基于Stackelberg博弈的分布式功率控制算法,用于蜂窝用户与D2D用户和D2D对之间的干扰管理,目的是保证蜂窝用户收益的前提下最大化D2D对总能效。首先,本文系统模型中一个子信道中可以被一个蜂窝用户和多个D2D对同时复用,针对同一子信道中存在的干扰,功率控制问题被建模为Stackelberg博弈,其中基站作为领导者,用于协调D2D对复用频谱的情况,并对其复用频谱收取一定的费用;D2D对作为跟随者,根据基站收取价格的变化调整发送功率,二者的目标都是实现自身利益的最大化。其次,本文建立了基站端收取的价格系数与D2D端发送功率的函数关系,使得其从数学角度分析更具有合理性。此外,本文还证明了分布式功率控制算法中纳什均衡的存在性和唯一性,进一步证明了算法的可行性。最后,仿真结果表明本文算法相比价格迭代算法和非合作算法,能够显著提高D2D对的总能效。本文采用随机的方式为蜂窝用户与D2D用户分配频谱资源,后续工作将进一步考虑基于最佳子信道分配的能效优化问题。
[1] Hossain E, Rasti M, Tabassum H. Evolution toward 5G multi-tier cellular wireless networks: An interference management perspective[J]. IEEE Wireless Communications, 2014, 21(3): 118-127.
[2] Malandrino F, Casetti C, Chiasserini C F. Toward D2D-Enhanced Heterogeneous Networks[J]. IEEE Communications Magazine, 2014, 52(11): 94-100.
[3] Qiao J, Shen X S, Mark J W, et al. Enabling Device-to-Device Communications in Millimeter-Wave 5G Cellular Networks[J]. IEEE Communications Magazine, 2015, 53(1): 209-215.
[4] Asadi A, Wang Q, Mancuso V. A Survey on Device-to-Device Communication in Cellular Networks[J]. IEEE Communications Surveys & Tutorials, 2014, 16(4): 1801-1819.
[5] Han L, Zhang Y, Zhang X, et al. Power Control for Full-Duplex D2D Communications Underlaying Cellular Networks[J]. IEEE Access, 2019, 7: 111858-111865.
[6] 姜鸿强, 张晶. D2D/蜂窝通信模式切换与联合功率控制方案[J]. 信号处理, 2020, 36(2): 233-239.
Jiang Hongqiang, Zhang Jing. D2D/cellular communication mode switching and joint power control scheme[J]. Journal of Signal Processing, 2020, 36(2): 233-239.(in Chinese)
[7] Lyu J, Chew Y H, Wong W. A Stackelberg Game Model for Overlay D2D Transmission with Heterogeneous Rate Requirements[J]. IEEE Transactions on Vehicular Technology, 2016, 65(10): 8461- 8475.
[8] Kai C, Li H, Xu L, et al. Energy-Efficient Device-to-Device Communications for Green Smart Cities[J]. IEEE Transactions on Industrial Informatics, 2018, 14(4): 1542-1551.
[9] Ma X, Liu J, Jiang H. Resource Allocation for Heterogeneous Applications with Device-to-Device Communication Underlaying Cellular Networks[J]. IEEE Journal on Selected Areas in Communications, 2016, 34(1): 15-26.
[10] Song L, Niyato D, Zhu Han, et al. Game-theoretic resource allocation methods for device-to-device communication[J]. IEEE Wireless Communication, 2014, 21(3): 136-144.
[11] Zhang G, Hu J, Heng W, et al. Distributed Power Control for D2D Communications Underlaying Cellular Network Using Stackelberg Game[C]∥2017 IEEE Wireless Communications and Networking Conference, 2017: 1- 6.
[12] Hu J, Heng W, Zhu Y, et al. Overlapping Coalition Formation Games for Joint Interference Management and Resource Allocation in D2D Communications[J]. IEEE Access, 2018, 6: 6341- 6349.
[13] Yuan Y, Yang T, Feng H, et al. An Iterative Matching-Stackelberg Game Model for Channel Power Allocation in D2D Underlaid Cellular Networks[J]. IEEE Transactions on Wireless Communications, 2018, 17(11): 7456-7471.
[14] Yin R, Zhong C, Yu G, et al. Joint Spectrum and Power Allocation for D2D Communications Underlaying Cellular Networks[J]. IEEE Transactions on Vehicular Technology, 2016, 65(4): 2182-2195.
[15] Zhao J, Chai K K, Chen Y, et al. Two-level game for relay-based throughput enhancement via D2D communications in LTE networks[C]∥2016 IEEE International Conference on Communications, 2016: 1- 6.
[16] Dun H, Ye F, Jiao S, et al. The Distributed Resource Allocation for D2D Communication with Game Theory[C]∥2019 IEEE-APS Topical Conference on Antennas and Propagation in Wireless Communications, 2019: 104-108.
[17] Najeh S, Bouallegue A. Distributed Interference and Power Control based-Game Theory for D2D Communication[C]∥2019 15th International Wireless Communications & Mobile Computing Conference, Morocco, 2019: 991-996.
[18] Feng D, Jiang C, Lim G, et al. A survey of energy-efficient wireless communications[J]. IEEE Communications Surveys & Tutorials, 2013, 15(1): 167-178.
[19] Liu S, Wu Y, Li L, et al. A Two-Stage Energy-Efficient Approach for Joint Power Control and Channel Allocation in D2D Communication[J]. IEEE Access, 2019, 7: 16940-16951.
[20] Jiang Y, Liu Q, Zheng F, et al. Energy Efficient Joint Resource Allocation and Power Control for D2D Communications[J]. IEEE Transactions on Vehicular Technology, 2017, 65(8): 6119- 6127.
[21] Pei L, Yang Z, Pan C, et al. Energy-Efficient D2D Communications Underlaying NOMA Based Networks with Energy Harvesting[J]. IEEE Communications Letters, 2018, 22(5): 914-917.
[22] Algedir A, Refai H H. Energy-Efficient D2D Communication under Downlink HetNets[C]∥2019 IEEE Wireless Communications and Networking Conference, Morocco, 2019: 1- 6.
[23] He C, Tian C, Zhang C, et al. Energy Efficiency Optimization for Distributed Antenna Systems With D2D Communications Under Channel Uncertainty[J]. IEEE Transactions on Green Communications and Networking, 2020,4(4): 1037-1047.


