1 引言
机载预警雷达在现代战争中发挥着重要作用,因其工作在万米左右的高空,受地杂波影响较大,普遍采用了拥有强大的抗干扰能力和杂波抑制能力的空时自适应处理(Space-Time Adaptive Processing, STAP)技术[1-2]。对敌方机载预警雷达进行干扰的一个重要途径就是降低其STAP处理效能,唐孝国等人通过分析STAP的局限性提出了几种可能的干扰方式和作用机理,但并没有建立相应干扰数学模型[3]。薛冰心等人研究了频移假目标干扰[4],沈佳琪等人研究了间歇采样转发干扰[5],张嘉曦研究了延迟转发干扰[6],洪成洋研究了前沿复制循环转发干扰[7],这些研究均从理论和仿真的角度说明了干扰的有效性,但干扰维度单一,形成的假目标与真实目标具有相同的方位。谌诗娃等人研究了投散射式伪杂波干扰,通过运动平台上的干扰机向地面投射干扰信号,利用地物散射特性和雷达、干扰机、地面运动特性产生类似杂波的与STAP处理器信号空时二维矢量特性一致的干扰信号,克服了传统干扰信号的单维性[8-10],具有较大的研究价值,但文献[8]中采用干扰机发射天线参数简化近似计算伪杂波散射块面积,对功率可行性研究影响不大,但要精细评估干扰效果应该用雷达的接收天线参数来计算伪杂波地面分辨单元面积。文献[9]和[10]在进行伪杂波仿真时基于给定JNR,利用伪杂波的空时导向矢量生成伪杂波信号,不能准确反映干扰信号的功率分布,由于伪杂波干扰信号在方位和多普勒频率上不具有对称性,功率分布的不准确使伪杂波谱与实际不符。为了更好地对伪杂波进行仿真,有必要准确计算伪杂波地面分辨单元面积。由于伪杂波类似于空基双基地雷达地面杂波,其等距离环为椭圆,并不能像杂波的圆形等距离环那样直观地给出分辨单元面积的解析表达式。文献[11]给出了一种空基双基地雷达地面杂波分辨单元计算的精确解析式,但简化地把空基雷达地面投影点作为其杂波地面等距离椭圆环的焦点,在实际中较难满足该条件。本文根据投散射式伪杂波干扰几何布局模型,通过建立合适的坐标系,用坐标变换的方法给出了伪杂波地面等距离椭圆环的解析表达式,区分了高、低掠射角的情形并给出了判断条件,给出了伪杂波地面分辨单元面积的计算方法和积分表达式。据此计算伪杂波块散射的功率,实现对伪杂波的仿真。最后,通过仿真对比了两种方法产生的伪杂波,证实了基于分辨单元面积计算产生的伪杂波更符合实际,能更准确地评估干扰效果。
2 投散射式伪杂波干扰基本原理
投散射式伪杂波干扰信号具有空时二维特性,经STAP处理器处理后产生一条与杂波凹口类似的伪杂波凹口,通过控制频移和延时等参数可以改变伪杂波凹口的位置,当伪杂波凹口覆盖目标时,目标信号被STAP处理器滤除而不被雷达准确检测。
2.1 干扰信号模型
机载预警雷达A、目标T和干扰机J的几何配置如图1所示,雷达以速度νA沿x轴方向飞行,距地面高度为HA,与干扰机的距离为RJ,与目标的距离为RT,与地面散射点P的距离为R1。干扰机以速度νJ飞行,飞行方向与x轴夹角为δj,距地面高度为HJ,与地面散射点P的距离为R2。RJ、RT、R1和R2在地面的投影距离分别为rj、rt、r1和r2。
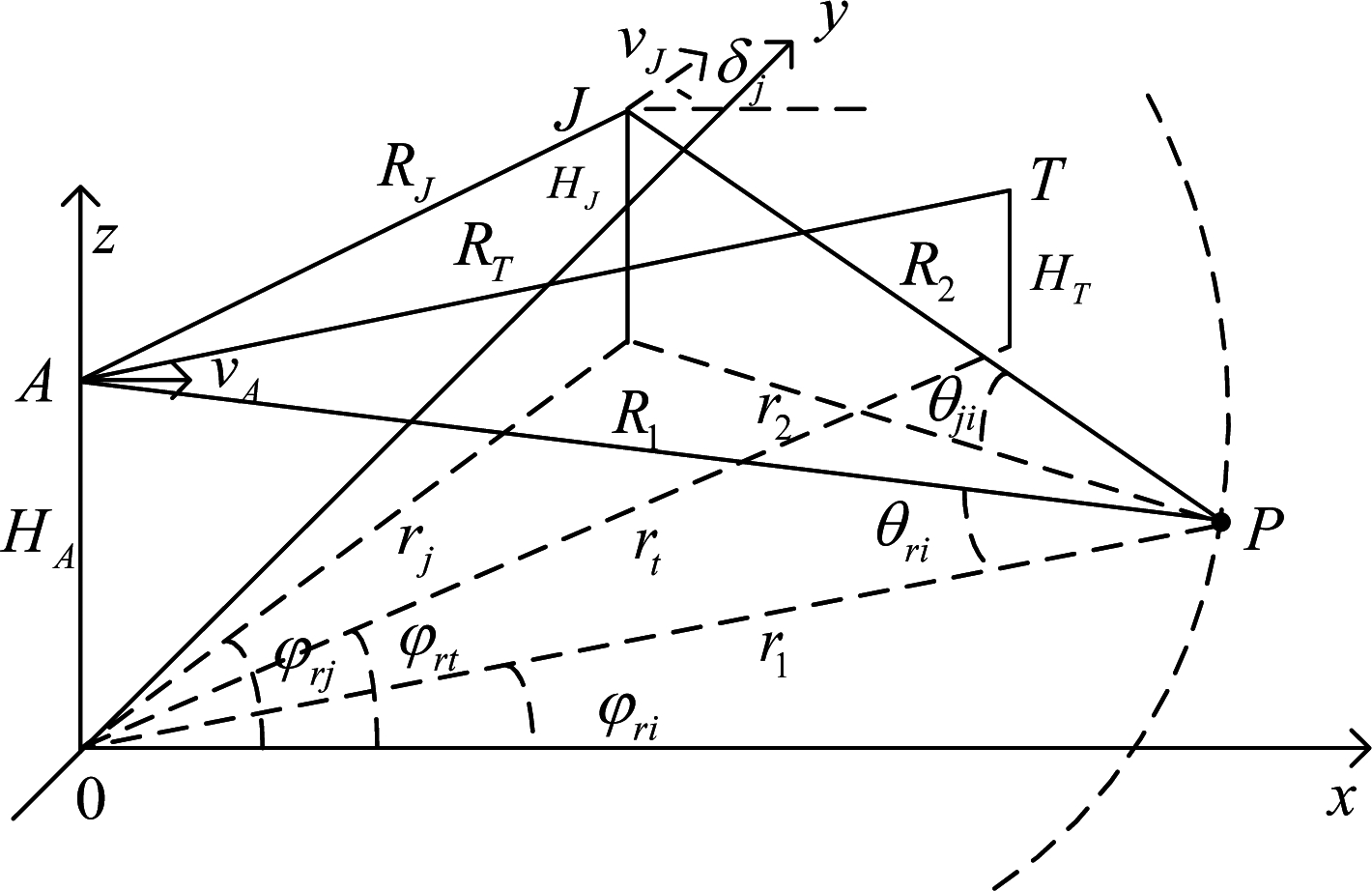
图1 雷达、目标和干扰机几何配置图
Fig.1 Geometric configuration of the radar, the target and the jammer
假设雷达发射信号为R[AtE(t)ej2πfct],其中![]() 为发射功率,E(t)为发射波形包络, fc为载波频率。根据雷达和干扰机的相对运动关系,干扰机的相对径向速度为
为发射功率,E(t)为发射波形包络, fc为载波频率。根据雷达和干扰机的相对运动关系,干扰机的相对径向速度为
νr1=νAcos θrjcos φrj-νJcos θrj(cos φrj-δJ)
(1)
干扰机接收信号为R[AjE(t-τ(t))ej2πfc(t-τ(t))],其中τ(t)=(RJ-νr1t)/c,由相对运动产生的多普勒频移为
(2)
干扰机将接收到的雷达信号调制和延时后向地面投射,经地面散射后形成干扰信号。干扰机调制产生的多普勒频移为fj。散射点P到雷达、干扰机的距离和R1+R2是随时间变化的,由此产生的多普勒频移为
(3)
其中
νr2=νAcos θricos φri-νJcos θjicos(φrj-δj)
(4)
经散射点P散射产生的干扰信号总的多普勒频移为
fdi=fd1+fd2+fj
(5)
雷达采用线性侧视阵列,N个阵元沿x轴分布,脉冲积累数为M,则干扰机产生的单一伪杂波块的时间相位项和空间相位项分别为:
Φjm(νA,νJ,φri)=exp[j2πfdimT] m=1,…,M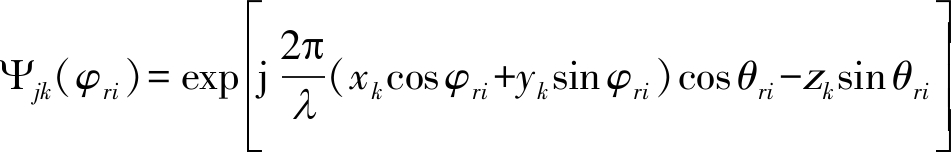
k=1,…,N
(6)
2.2 干扰效果分析
由式(5)可知伪杂波块的多普勒频移fdi由三部分组成。fd1由干扰机接收雷达信号时与雷达的相对位置和速度决定。fd2与散射点P的位置有关,由式(3)、(4)可知fd2具有方位依从性。fj由干扰机调制产生,通过改变fj大小可以控制fdi。由于fd2的方位依从性,伪杂波干扰的功率谱与杂波的功率谱类似,具有空时二维性质,如图2所示。伪杂波谱分裂为两部分是由于雷达脉冲重复频率不够大而产生的模糊响应。由图2(b)可以更清楚地看到,与杂波谱类似,这两部分伪杂波谱覆盖了所有角度和多普勒频率,在单一维度上无法滤除。STAP处理器像处理杂波一样处理伪杂波,不仅产生杂波凹口以滤除杂波,还产生伪杂波凹口以滤除伪杂波。通过调整fj可以使伪杂波谱在空时二维平面上平移,进而使STAP产生的伪杂波凹口平移。fdi是φri和fj的函数, fdi=F(φri, fj)。当调整fj使目标的多普勒频率fdt和方位角φrt满足fdt=F(φrt, fj)时,伪杂波凹口覆盖目标,目标也被滤除。干扰前、后的最优响应如图3所示,目标多普勒频率为-210.15 Hz,方位余弦为0.6428,图3(a)是干扰前STAP处理器最优响应,可以看到目标处获得最大响应,目标被准确的检测到。图3(b)是干扰后STAP处理器最优响应,此时伪杂波凹口覆盖了目标,STAP处理器不能准确检测目标。目标所在方位上的改善因子如图4所示,可以看到干扰后不仅在杂波所在多普勒频率上形成了杂波凹口滤除杂波,还在目标所在多普勒频率上形成了伪杂波凹口,滤除伪杂波的同时也滤除了目标。
由以上分析可知要实现伪杂波凹口覆盖目标需要知道目标的多普勒频率、方位、所在距离单元等先验信息,由于转发的滞后性,干扰信号最快只能从第2个脉冲开始与目标信号处于同一距离单元,因此还需要知道雷达的脉冲重复频率。对先验信息的高要求是这种干扰方式的最大短板,需要强大的侦察体系来支撑。如果先验信息不足则很难使伪杂波凹口精确覆盖目标,但因为具有空时二维特性,仍然可以占据比传统转发式干扰更大的自由度,并造成非均匀杂波环境,使得STAP雷达对杂波协方差矩阵估计不准确而性能下降,达到一定的干扰效果。另外,通过多部干扰机进行分布式投散射干扰,将各干扰机产生的伪杂波凹口合成为一个覆盖更多多普勒频率和方位的凹口,可以降低对先验信息的要求,更容易覆盖目标。
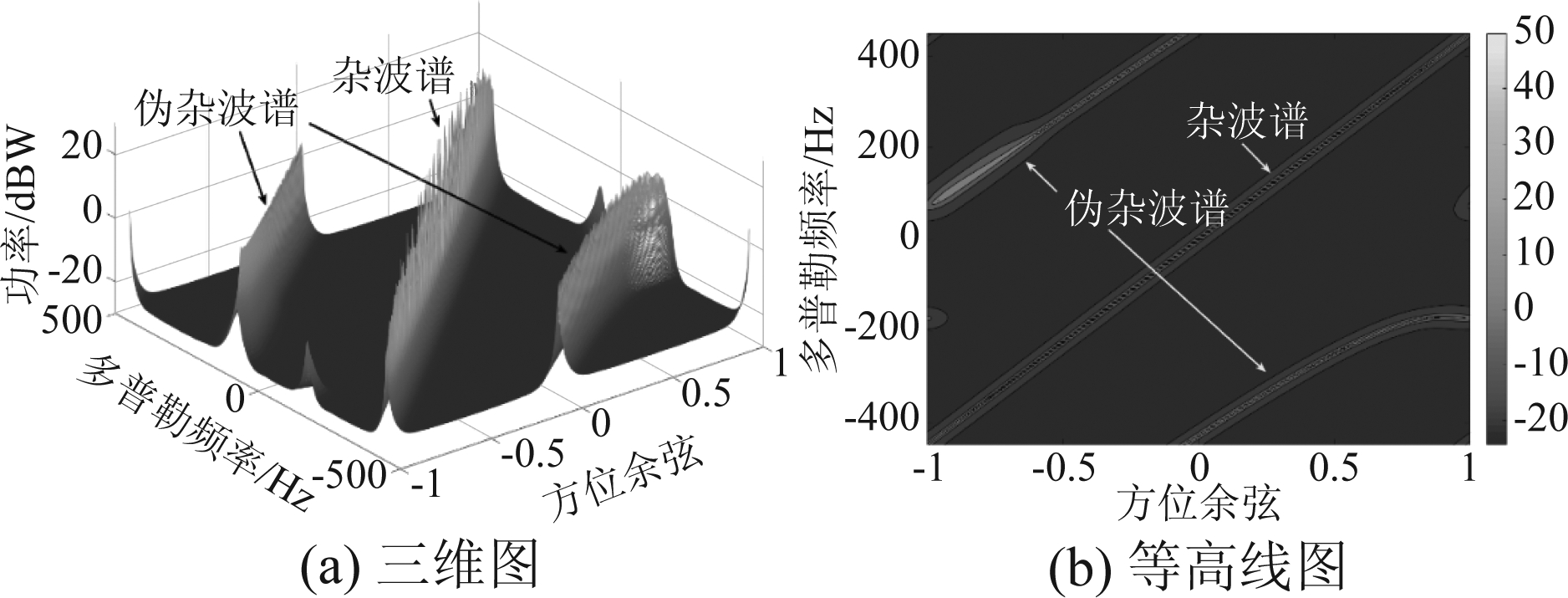
图2 投散射干扰条件下的功率谱
Fig.2 The spectrum under scattered jamming
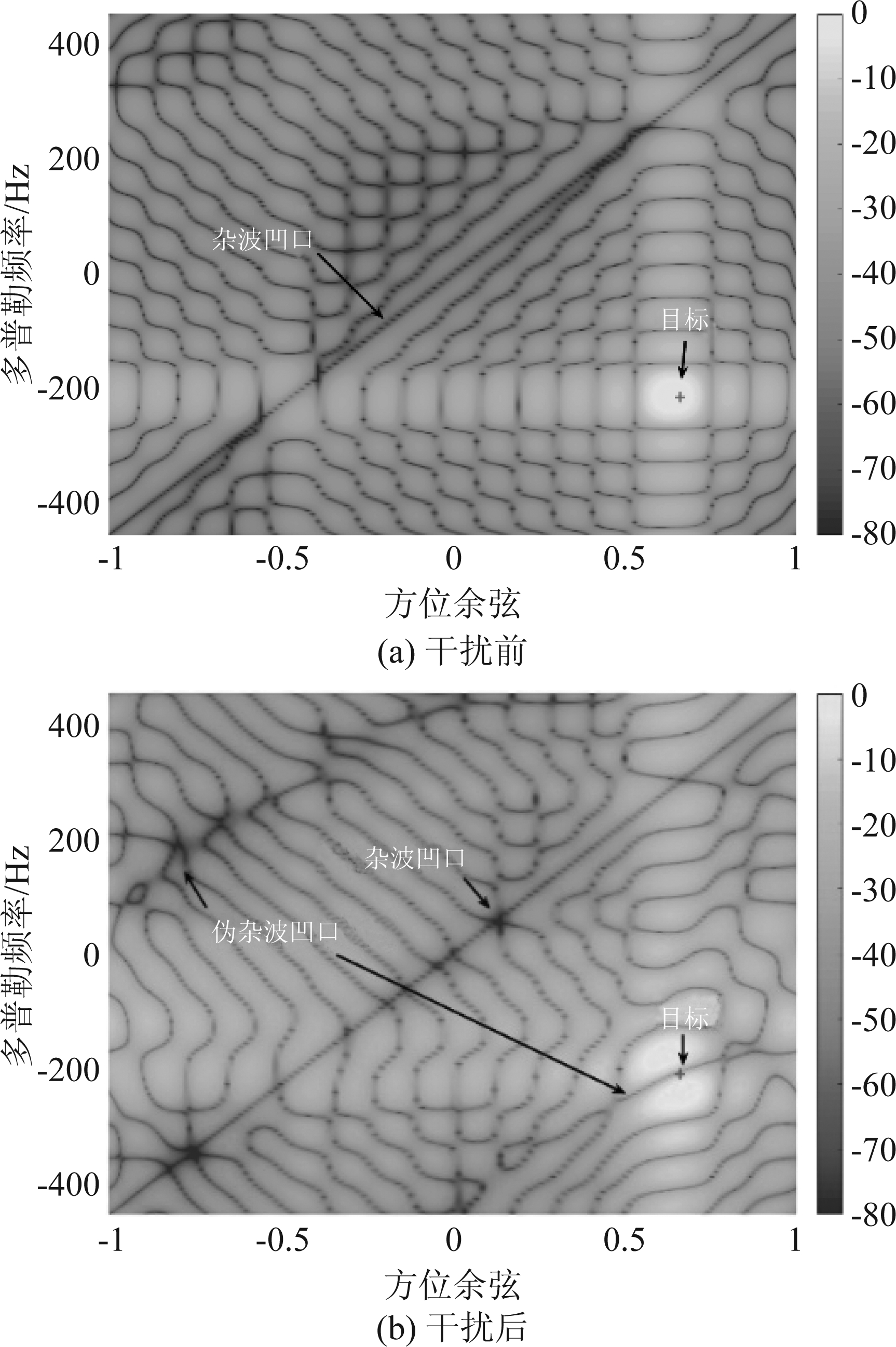
图3 干扰前、后STAP最优响应
Fig.3 STAP optimal response before and after jamming
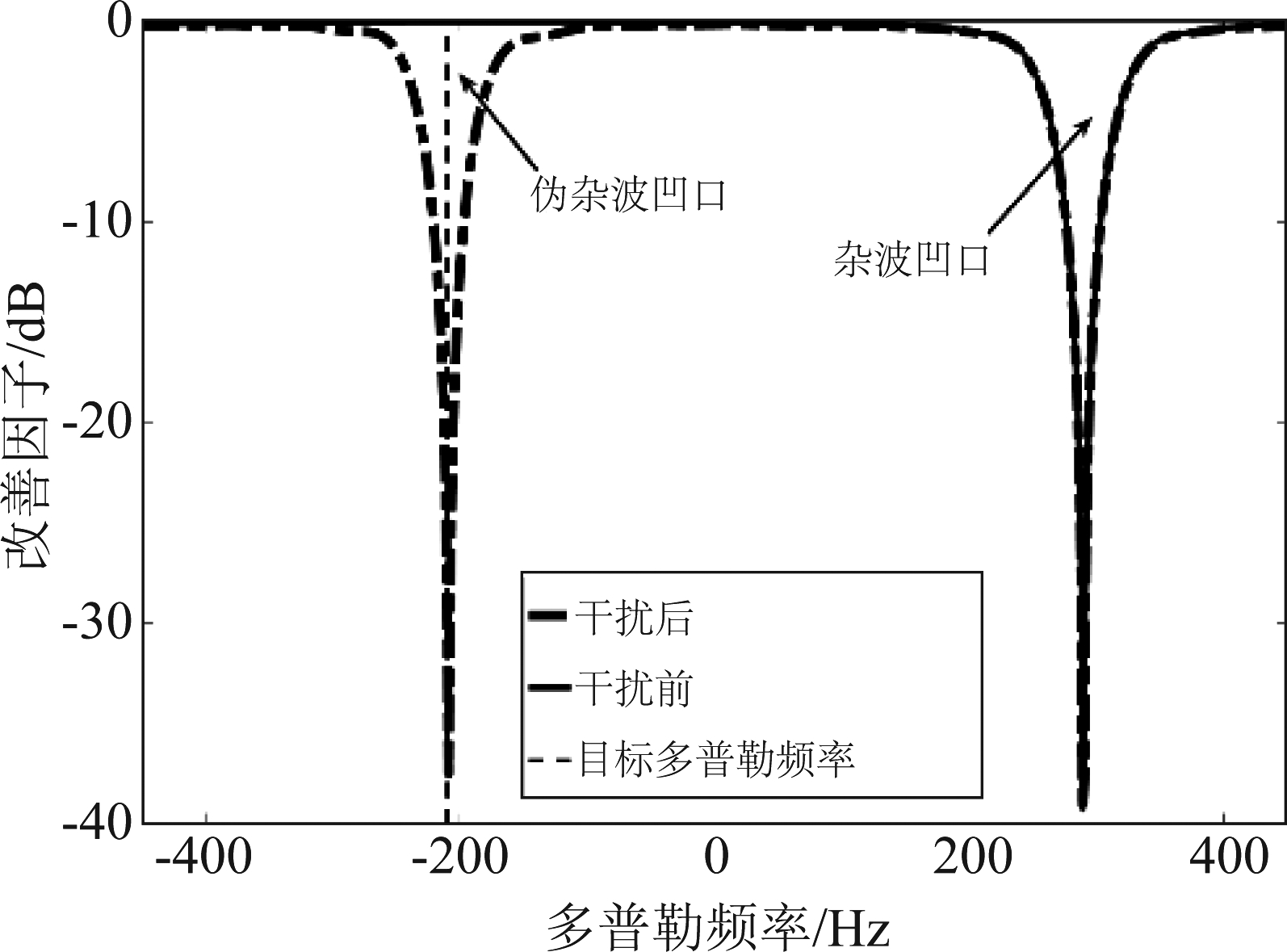
图4 干扰前、后改善因子对比
Fig.4 Comparison of improvement factors before and after jamming
3 投散射式伪杂波干扰分辨单元面积计算
3.1 投散射式伪杂波等距离环数学模型
雷达、干扰机和目标的几何配置如图1所示,假设雷达的最大不模糊距离为Run。要使伪杂波凹口准确覆盖目标,需要使伪杂波干扰信号与目标回波信号在同一个距离单元内,即伪杂波干扰信号和目标回波信号同时(或时间间隔对应的距离差为最大不模糊距离的整数倍)到达雷达接收机。从雷达发射信号开始计时,伪杂波干扰信号到达雷达接收机所用时间对应的距离RFC应满足:
RFC=2RRT+nRun=R2w+Rdelay
(7)
其中n为大于1的整数,RFC由两部分构成,一是实际的空间路径距离和R2w,即图1中的R1+R2,二是由延时产生的附加距离Rdelay。文献[9]中论证了伪杂波干扰的可控性,可以通过调整Rdelay使RFC满足式(7)以使干扰与目标在同一距离单元内。本文在伪杂波干扰信号与目标回波在同一距离单元的前提下仅考虑实际空间路径距离R2w。
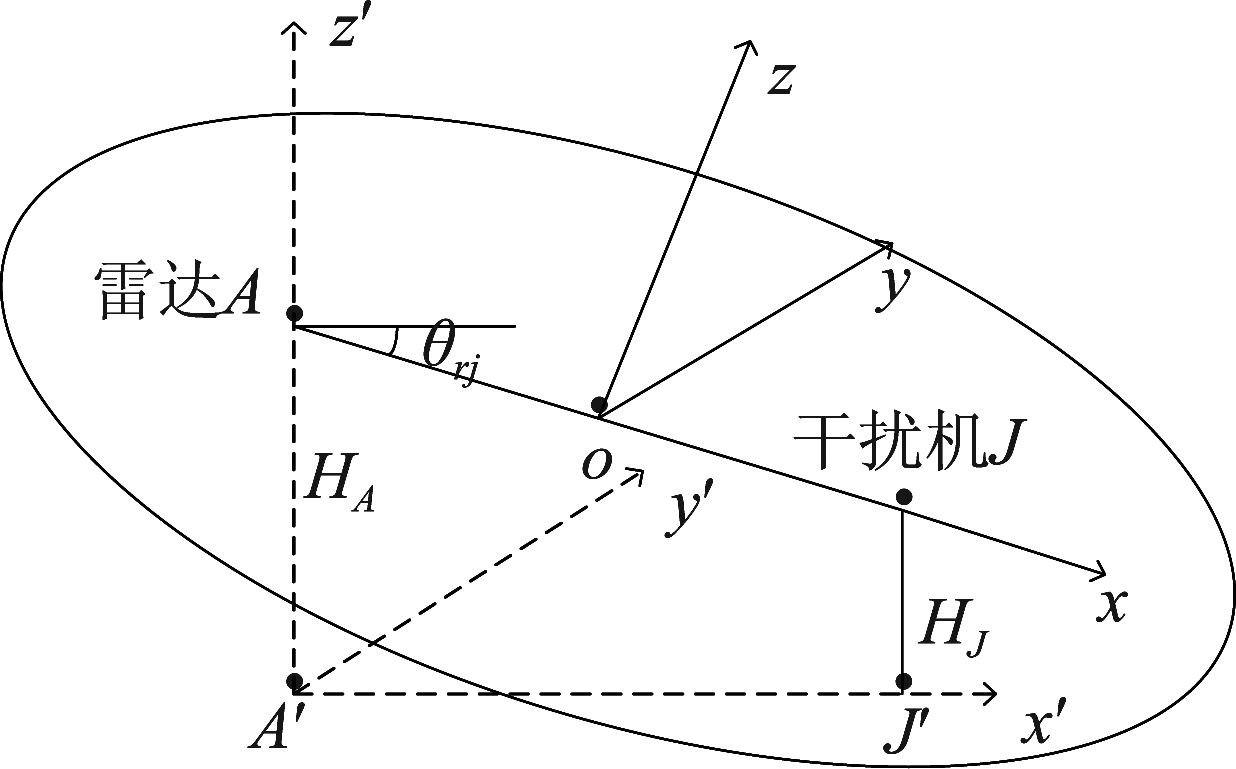
图5 伪杂波干扰信号坐标系
Fig.5 The coordinate system of fake clutter jamming signal
如图5所示,以雷达在地面投影点A′为原点,雷达和干扰机连线投影方向为x′轴,雷达与其投影点连线为z′轴,垂直z′和JJ′所在平面作y′轴建立坐标系x′y′z′。以雷达和干扰机连线为x轴,连线中点为原点o,在z′轴和JJ′所在平面内作x轴垂线为z轴,平行于y′轴作y轴建立坐标系xyz,则在坐标系xyz中椭球为标准椭球,其长轴为R2w,焦距为RJ,其方程为:
(8)
坐标系xyz可由坐标系x′y′z′经一次旋转两次平移变换而来,其关系可表示为:
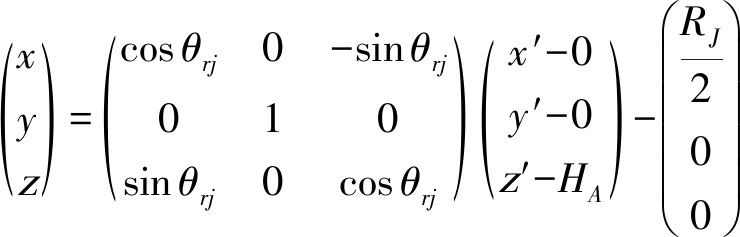
(9)
即:
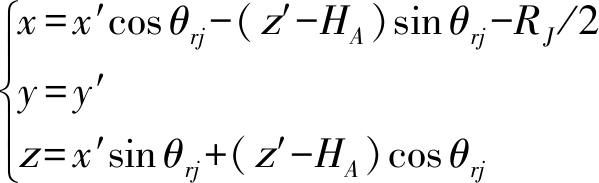
(10)
对于地面某伪杂波散射点P,其在坐标系x′y′z′中坐标为(xi,yi,0),代入式(10)并将结果代入式(8)有:
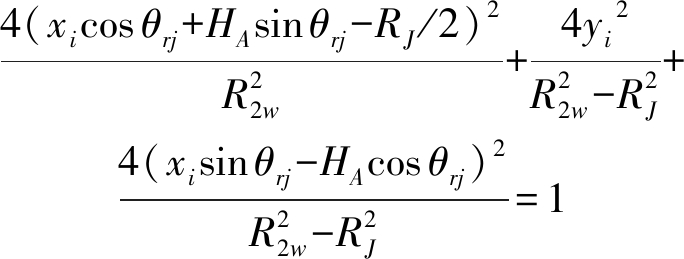
(11)
为了化成标准椭圆形式,先给出二元二次方程形式:
(12)
其中
![]()
![]()
![]()
![]()
(13)
当![]() 时,即
时,即![]() 时地面等距离环为椭圆,否则椭球与地面没有交点或仅有1个交点,不符合干扰场景。地面投影如图6内侧椭圆所示,该椭圆可化为标准形式:
时地面等距离环为椭圆,否则椭球与地面没有交点或仅有1个交点,不符合干扰场景。地面投影如图6内侧椭圆所示,该椭圆可化为标准形式:
(14)
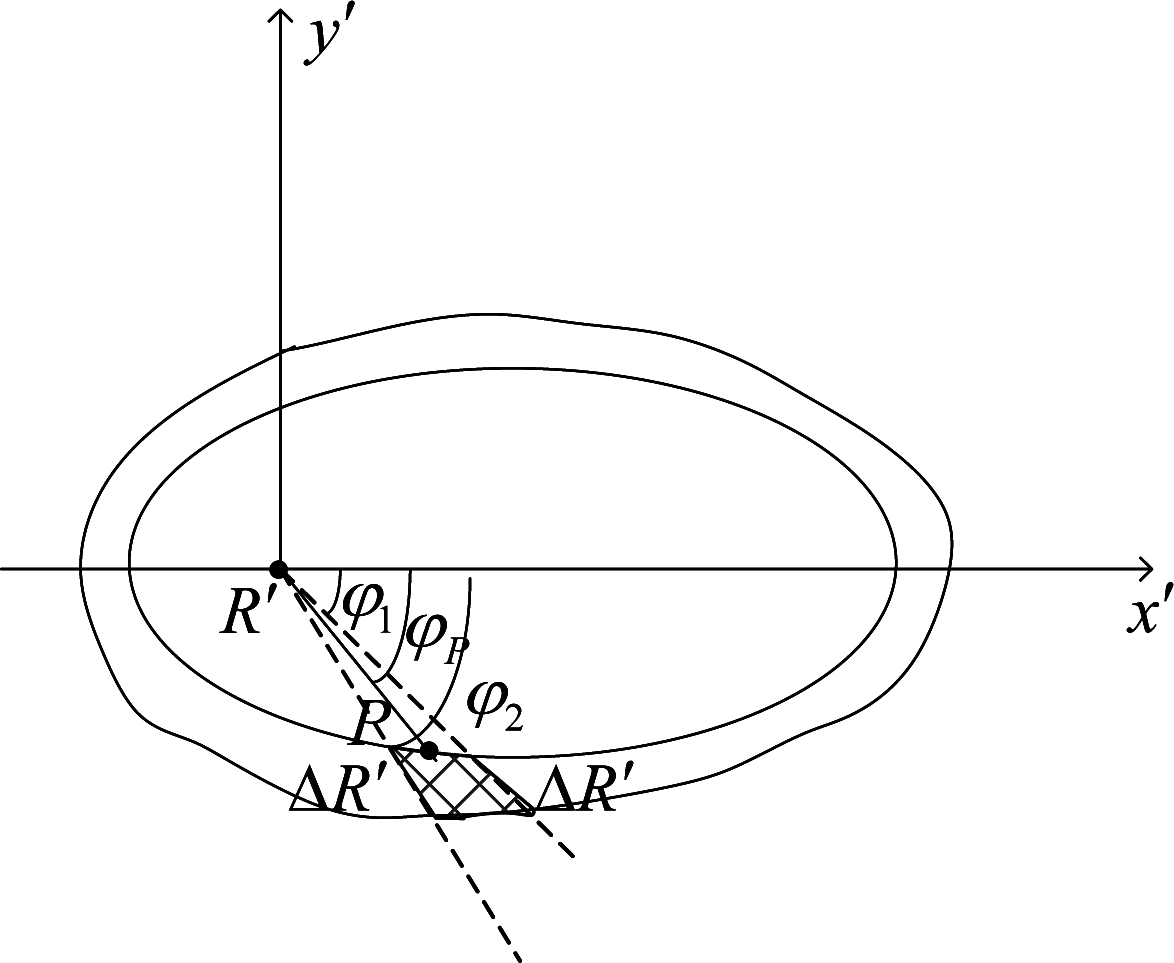
图6 伪杂波等距离环地面投影图
Fig.6 Ground projection of fake clutter equidistant ring
由式(13)可知d0>a0,故椭圆焦点在x′轴上,且其半长轴a、半短轴b长度分别为:
(15)
为了后续计算散射点坐标,给出椭圆轨迹的函数形式:
(16)
可解出xi取值范围为:
(17)
易知c0≤0时原点在其取值范围内,即雷达地面投影点A′在椭圆内。要使c0≤0,由其表达式可以推出:
(18)
在干扰场景中预警机雷达高度大于两倍干扰机高度,故式(18)右边
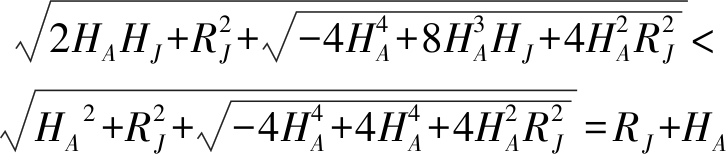
(19)
故当R2w>RJ+HA时雷达地面投影点A′在椭圆内,因为干扰场景中干扰机到雷达距离RJ远大于雷达飞行高度HA,且由三角不等式可知伪杂波空间路径R2w大于RJ,可以认为在干扰场景中总是满足雷达地面投影点A′在椭圆内的条件。
3.2 投散射式伪杂波距离分辨单元面积计算方法
为计算伪杂波距离分辨单元面积,令坐标平移量b0/2a0=l。图6内侧椭圆可用极坐标形式表示为:
(20)
为仿真需要,将其变换为函数形式:
(21)
其中:
由图6可知r(φ)的取值范围为(a-|l|,a+|l|),文献[12]给出了计算表面杂波的方法,雷达飞行高度HA不变,区分两种情形。
一是当r(φ)较大时的低掠射角情形,假设雷达接收波束方位向波束宽度为φB,雷达接收距离分辨单元为ΔR=cτ/2,式中c为光速,τ为雷达脉冲宽度,ΔR在地面投影ΔR′=ΔRsecθP,θP为雷达对伪杂波块的俯角,可将等距离环看成如图6所示的不规则环,内侧为椭圆,外侧为沿A′与椭圆上各点连线延长相应的ΔR′所形成的不规则曲线,φP方向上的伪杂波块面积如图中阴影部分所示。图6中的角度关系为(φ1+φ2)/2=φP,φ2-φ1=φB,解得:
(22)
伪杂波块面积可用积分方式获得:
![]()
![]() (r(φ)ΔR′+ΔR′2/2)dφ
(r(φ)ΔR′+ΔR′2/2)dφ
(23)
将![]() 代入可得:
代入可得:
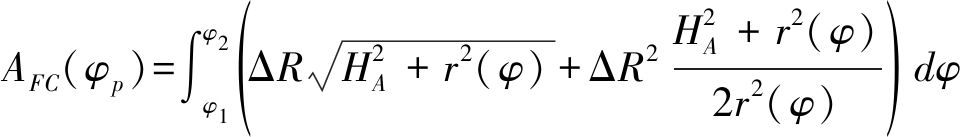
(24)
二是r(φ)较小时的高掠射角情形,θP很大而使ΔR′超过了俯仰方向波束宽度θB在地面的投影,即ΔR′>RθBcscθP,其中R为雷达到伪杂波块的距离。根据几何关系可以解出:
(25)
当满足式(25)时,伪杂波分辨单元是由两个主平面的波束宽度θB和φB决定,与第一种情形类似,伪杂波分辨单元面积仍可由式(23)表示,只是此时![]() 代入可得:
代入可得:
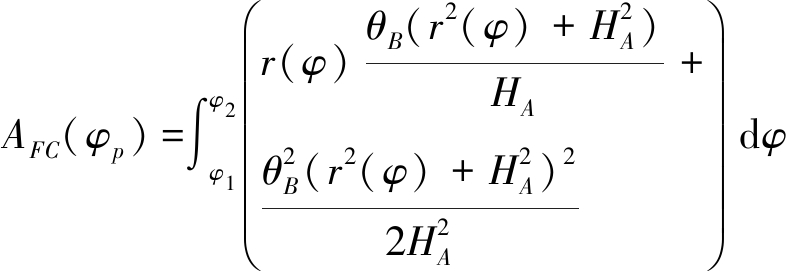
(26)
综上,在计算伪杂波分辨单元面积时,首先根据式(21)和式(25)判断是否存在交集,直观表示如图7所示,以A′为圆心,式(25)右侧数值为半径做圆C,当R2w较小时伪杂波等距离椭圆环E1和圆C有交点,即式(21)和式(25)存在交集,此时可由交点处r(φ)和式(17)求解出φ的取值范围。当φP在该范围内时,为高掠射角情形,使用式(26),否则为低掠射角情形,使用式(24)。而当R2w较大时, 伪杂波等距离椭圆环E2和圆C没有交点,即式(21)和式(25)没有交集,任意方位对应的r(φ)都属于低掠射角情形,此时伪杂波分辨单元面积只使用式(24)计算。
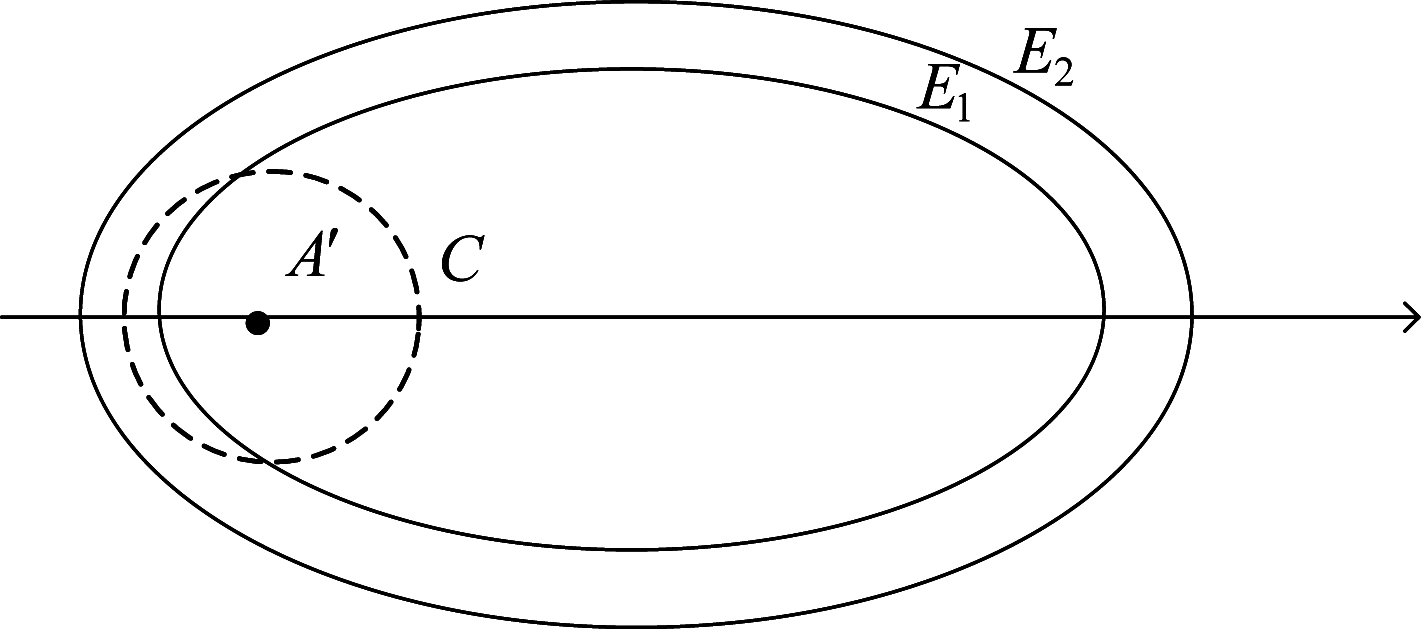
图7 高、低掠射角情形判断示意图
Fig.7 Schematic diagram for judging high and low grazing Angle
需要注意的是,当R2w很小而使式(18)等号成立时,A′恰好落在椭圆上,此时φP的取值范围为[-90°,90°]。
3.3 伪杂波功率计算
按照分辨单元或更小角度分割将伪杂波等距离环分为若干块,第i块的功率为
(27)
其中Pjt为干扰机发射功率,Gjt为干扰机发射增益,Grr为雷达接收增益,φri、φji分别为第i块伪杂波块中心对雷达和干扰机的方位角,AFC(i)为根据上节计算得到的第i块伪杂波块面积,R1(i)、R2(i)分别为第i块伪杂波块中心至雷达和干扰机的距离。
4 仿真实验
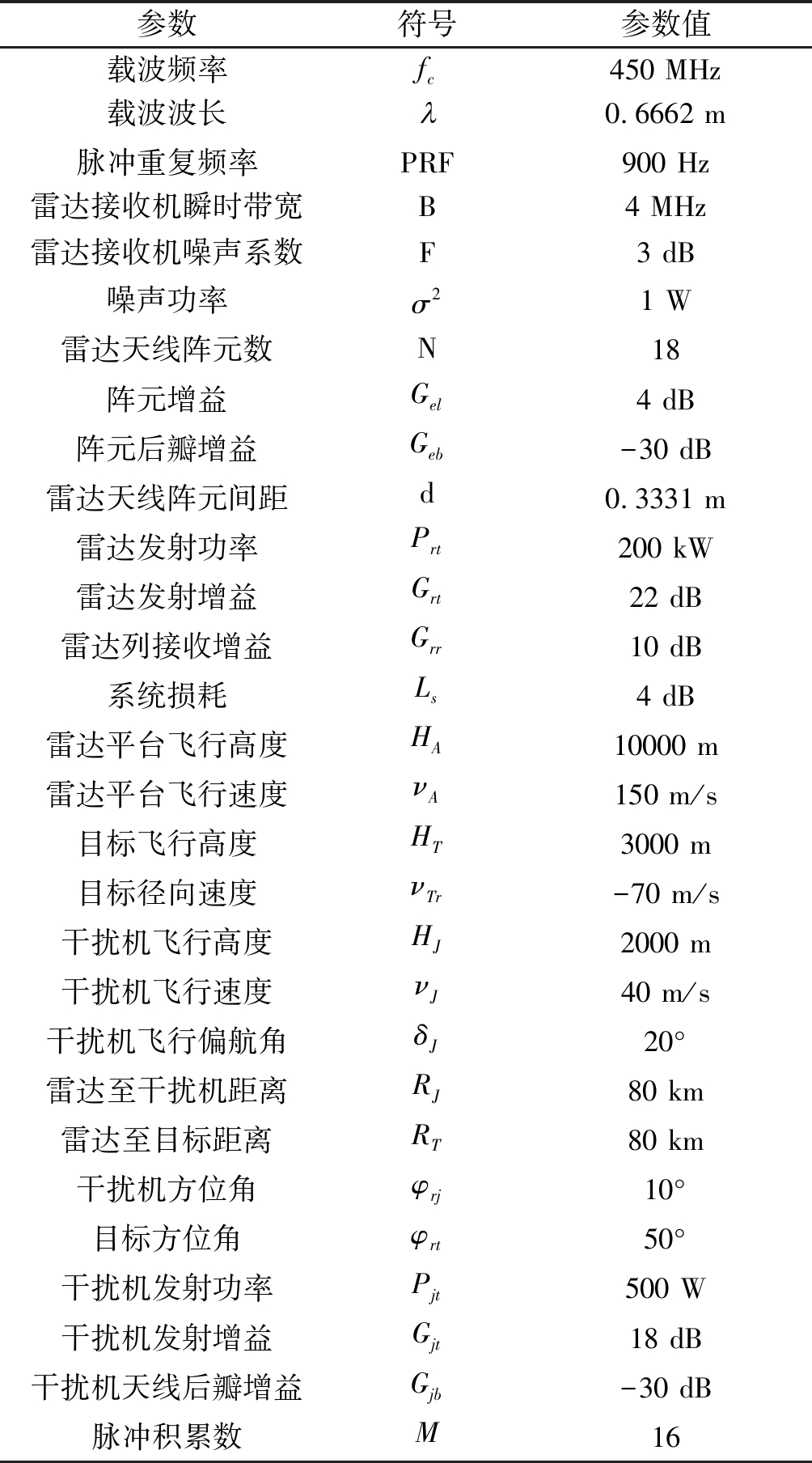
本节主要对基于第3节所述的分辨单元面积通过计算伪杂波块实际功率仿真生成的伪杂波和基于干噪比(JNR)用复高斯随机分布仿真生成的伪杂波进行对比。伪杂波等距离环方位角范围为[-180°,179°],均匀分为60块。雷达天线阵元和干扰机天线均采用余弦方向图,雷达天线阵元合成的波束指向目标,干扰机天线指向目标所在方位上的伪杂波块,目标多普勒频率为-210.15 Hz,方位余弦为0.6428。仿真参数见表1。
表1 仿真参数
Tab.1 Simulation parameters
4.1 伪杂波块功率对比
图8对比了用分辨单元面积计算得出的伪杂波块功率和基于JNR用复高斯随机分布生成的伪杂波块功率。R2w选取为160 km,JNR由第一种方法中伪杂波块平均功率计算得到,使得两种方法得到的伪杂波总功率相同。目标方位角为50°,该方位角上的伪杂波块序号为38。可以看到基于分辨单元面积计算得到伪杂波块功率反映了功率的真实分布,在干扰机天线主瓣指向上(即目标方位上的伪杂波块)取得最大值,而干扰机天线尾瓣对应的伪杂波块功率极小。基于JNR生成的伪杂波则将功率更均匀地分配到每个伪杂波块上,不能反映功率的实际分布。
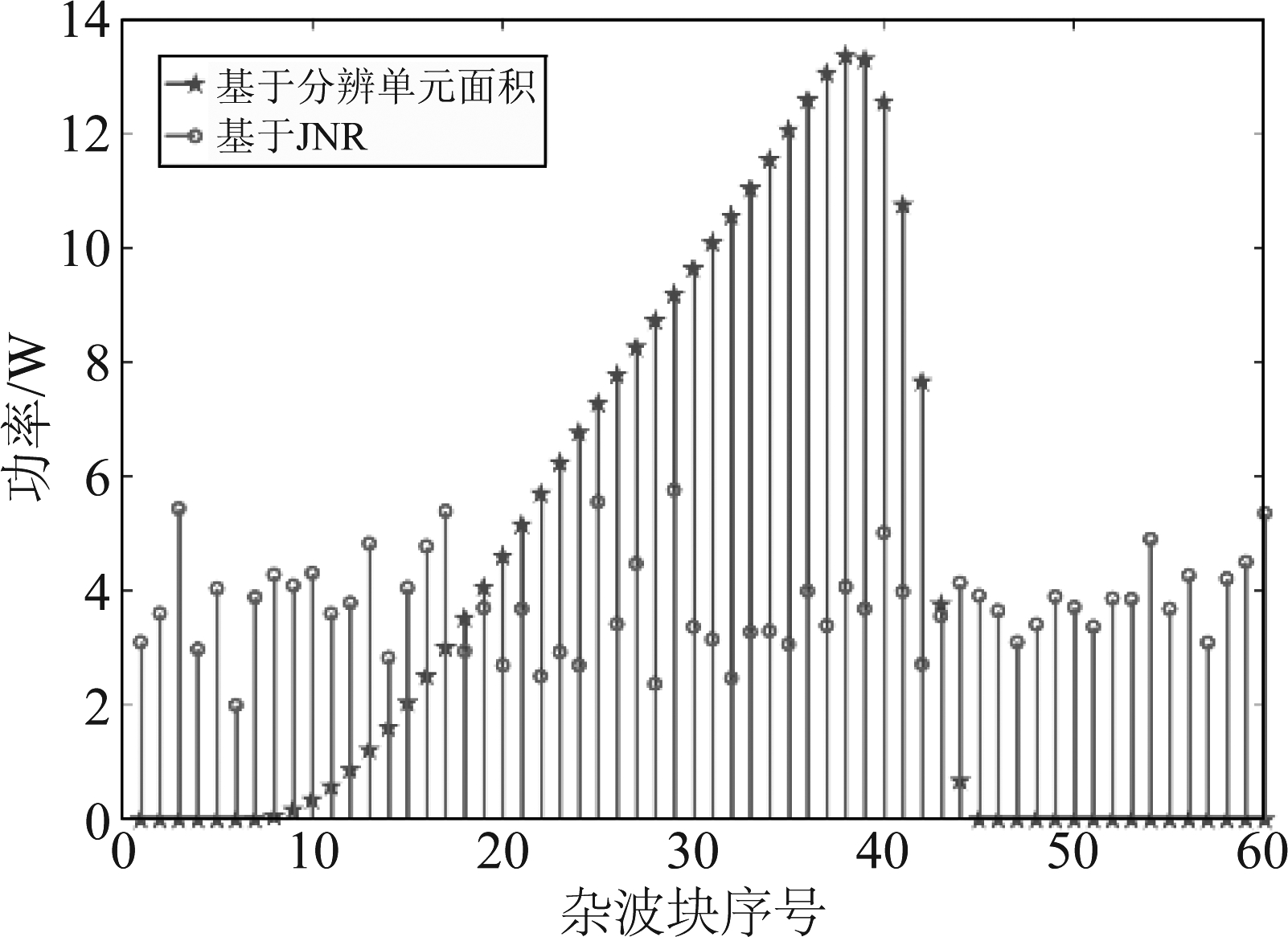
图8 伪杂波块功率比较
Fig.8 Power comparison of the fake clutter patches
4.2 伪杂波谱对比
图9和图10分别是两种仿真方法产生的伪杂波谱。图9中基于JNR产生的伪杂波谱反映了类似双基地杂波谱的结构,这是因为投散射干扰空时特性并不存在方位或多普勒的对称性,而通过JNR仿真产生的伪杂波块功率都大于噪声功率,因此完整地反映了这一结构,但并不能区分出前瓣和尾瓣。图10中基于分辨单元面积计算而产生的伪杂波谱则没有反映出投散射干扰空时特性的真实结构,这是因为干扰机功率有限且尾瓣增益很小,尾瓣对应的伪杂波块功率小于噪声功率,这些伪杂波块的方位多普勒性质被噪声掩盖而不在伪杂波谱中体现。若将噪声基底去掉,则两种方法得到的伪杂波谱具有相同结构,如图11所示。从图11(b)中可以看到基于分辨单元面积产生的伪杂波谱清晰地反映了天线方向图的前瓣和尾瓣。
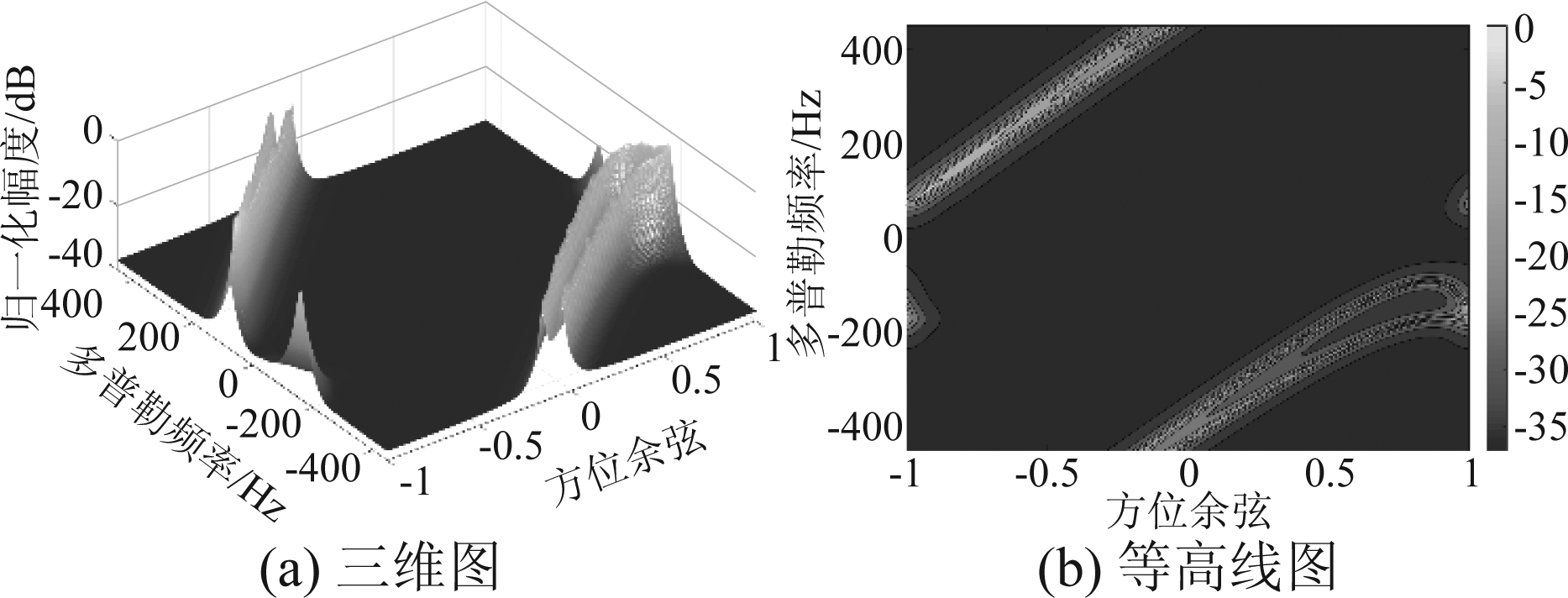
图9 基于JNR的伪杂波谱
Fig.9 Fake clutter spectrum based on JNR
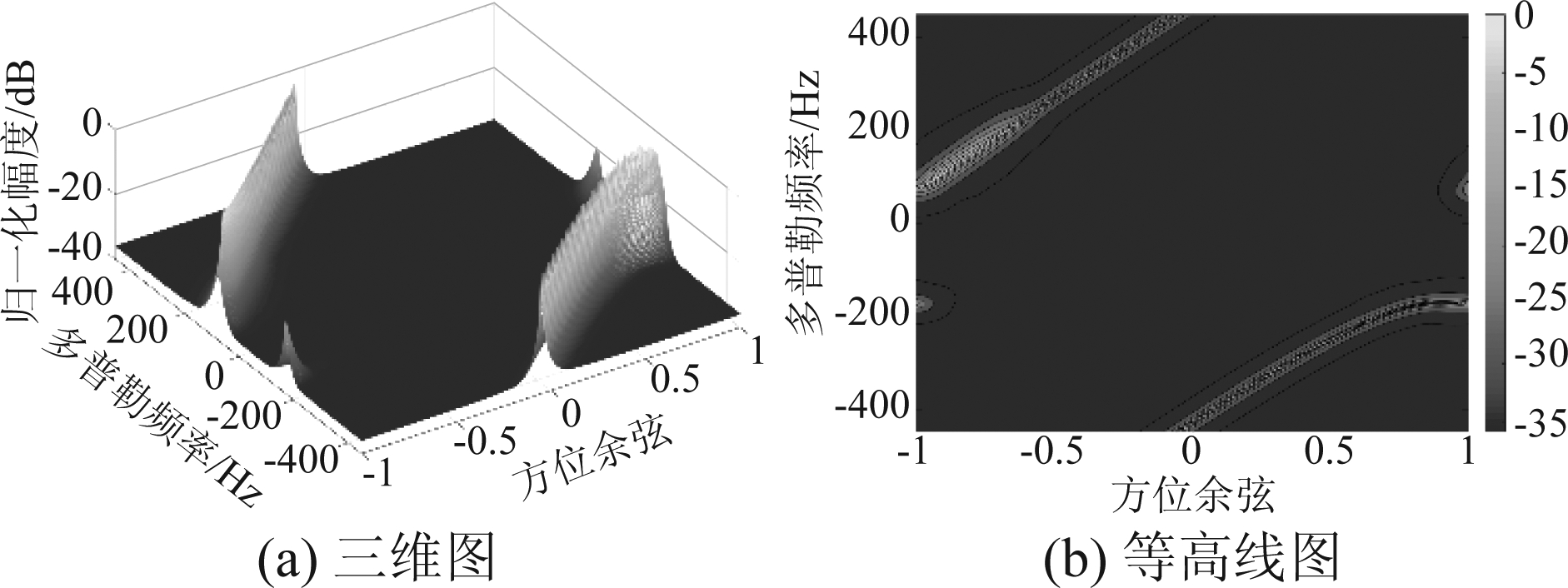
图10 基于分辨单元面积的伪杂波谱
Fig.10 Fake clutter spectrum based on resolution cell area
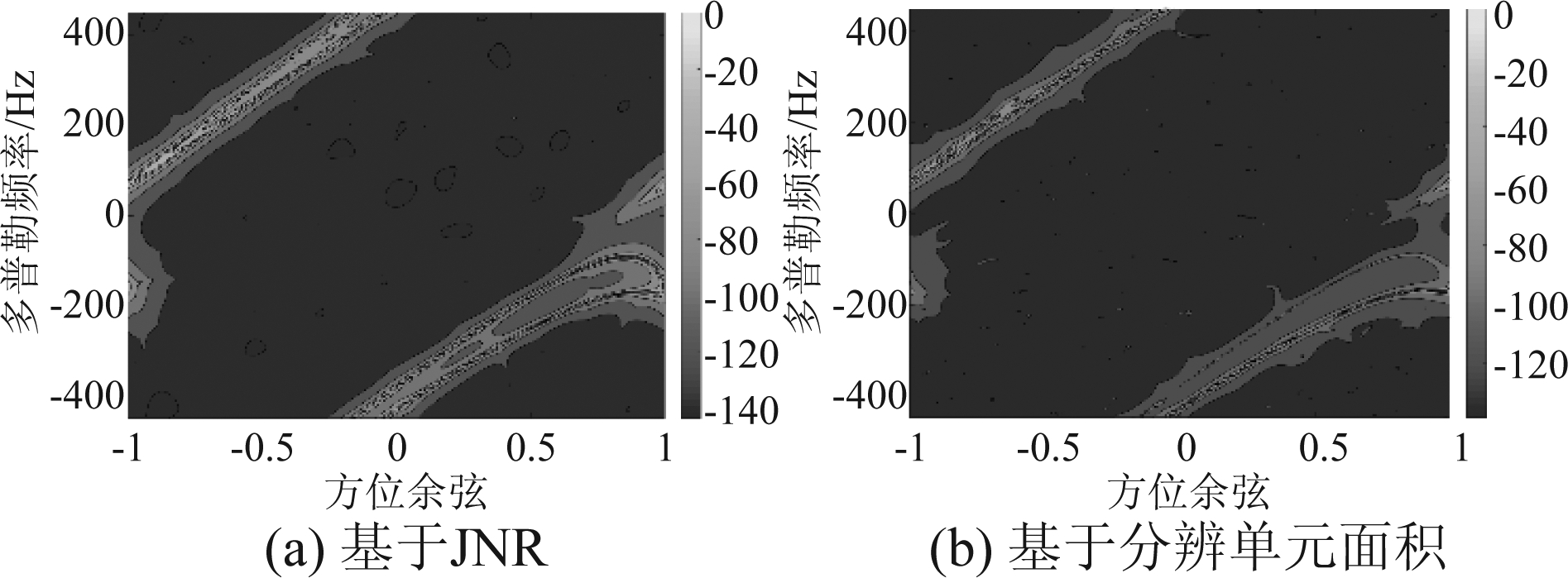
图11 无噪声情况下伪杂波谱对比
Fig.11 Comparison of fake clutter spectrum without noise
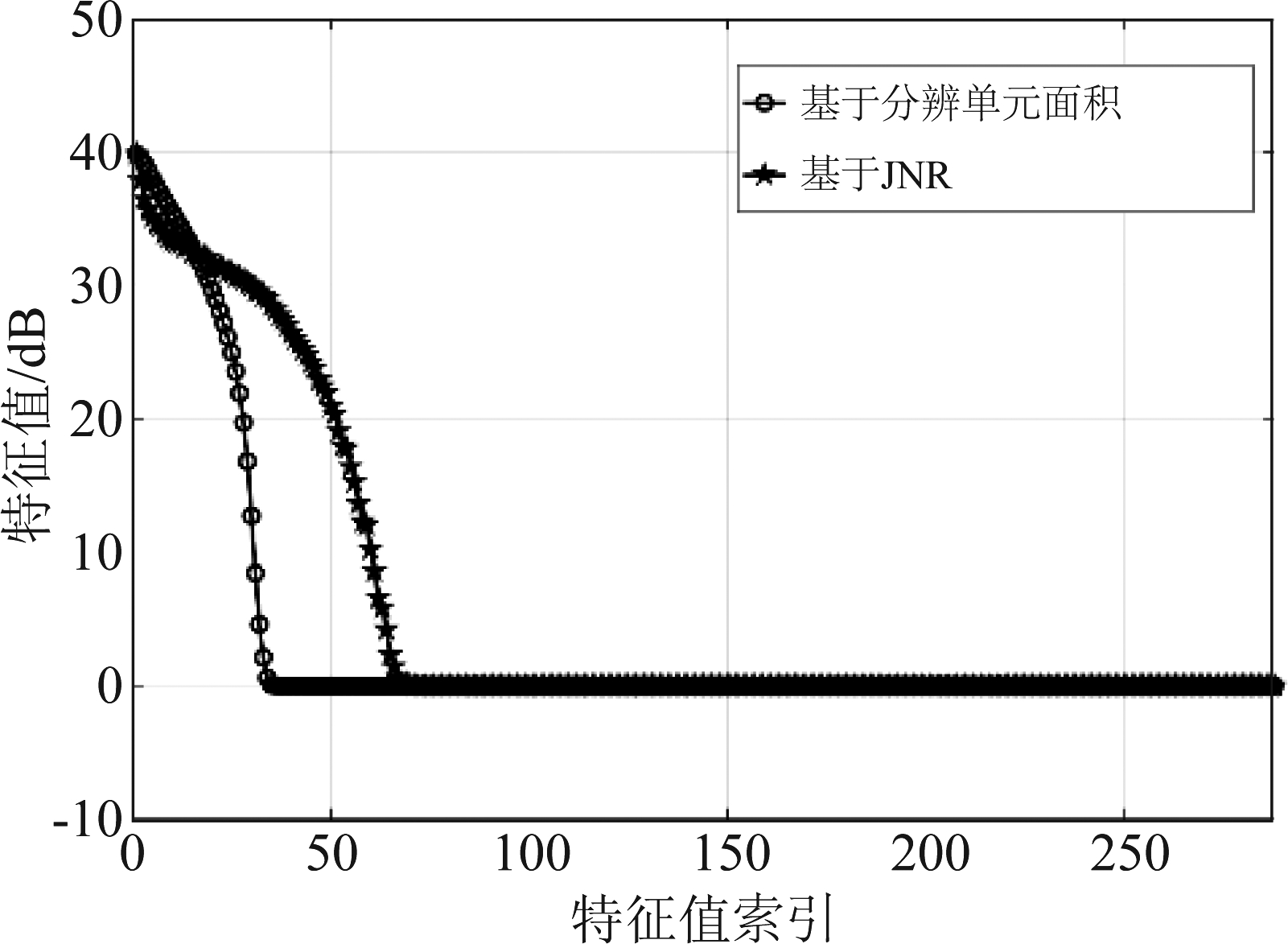
图12 特征值数对比
Fig.12 Comparison of the number of eigenvalues
该现象也可以从特征值的角度解释,两种仿真方法的伪杂波+噪声的特征值分布如图12所示,可以看到基于JNR产生的伪杂波特征值数大于基于分辨单元面积计算得到的伪杂波特征值数,前者的特征值分布较为均匀,而后者的特征值则集中在数值较大的位置,这也反映了4.1节所述两者功率的分布。特征值数反映在伪杂波谱上则是占据方位和多普勒区域的大小,基于JNR产生的伪杂波具有更大特征值数,因此比基于分辨单元面积计算得到的伪杂波占据了更多方位和多普勒区域。
4.3 干扰效果对比
图13是STAP处理器在伪杂波干扰下的最优响应。由于最优权矢量本质上可以看成是对杂波和伪杂波的白化和对目标的匹配滤波,在响应图中可以看到杂波和伪杂波方位多普勒性质。与图9和图10反映出的方位多普勒性质相同,图13(a)中仅能看到滤除前瓣伪杂波的凹口,而图13(b)中还有滤除尾瓣伪杂波的凹口。目标被前瓣伪杂波凹口覆盖而不能获得最大响应。图14是目标所在方位改善因子的比较,可以看到基于JNR产生的伪杂波经STAP处理后形成了两个伪杂波凹口,而基于分辨单元面积产生的伪杂波经STAP处理后只有一个伪杂波凹口。目标所在多普勒频率被伪杂波凹口覆盖。从凹口深度来看,基于分辨单元面积产生的伪杂波经STAP处理后形成的伪杂波凹口更深,这反映了图8所示的功率对比,因为伪杂波凹口本质是伪杂波谱的逆,实际干扰实施中,干扰功率集中在干扰机主瓣,在对应方位上伪杂波谱的幅度更大因而处理后得到的凹口更深。
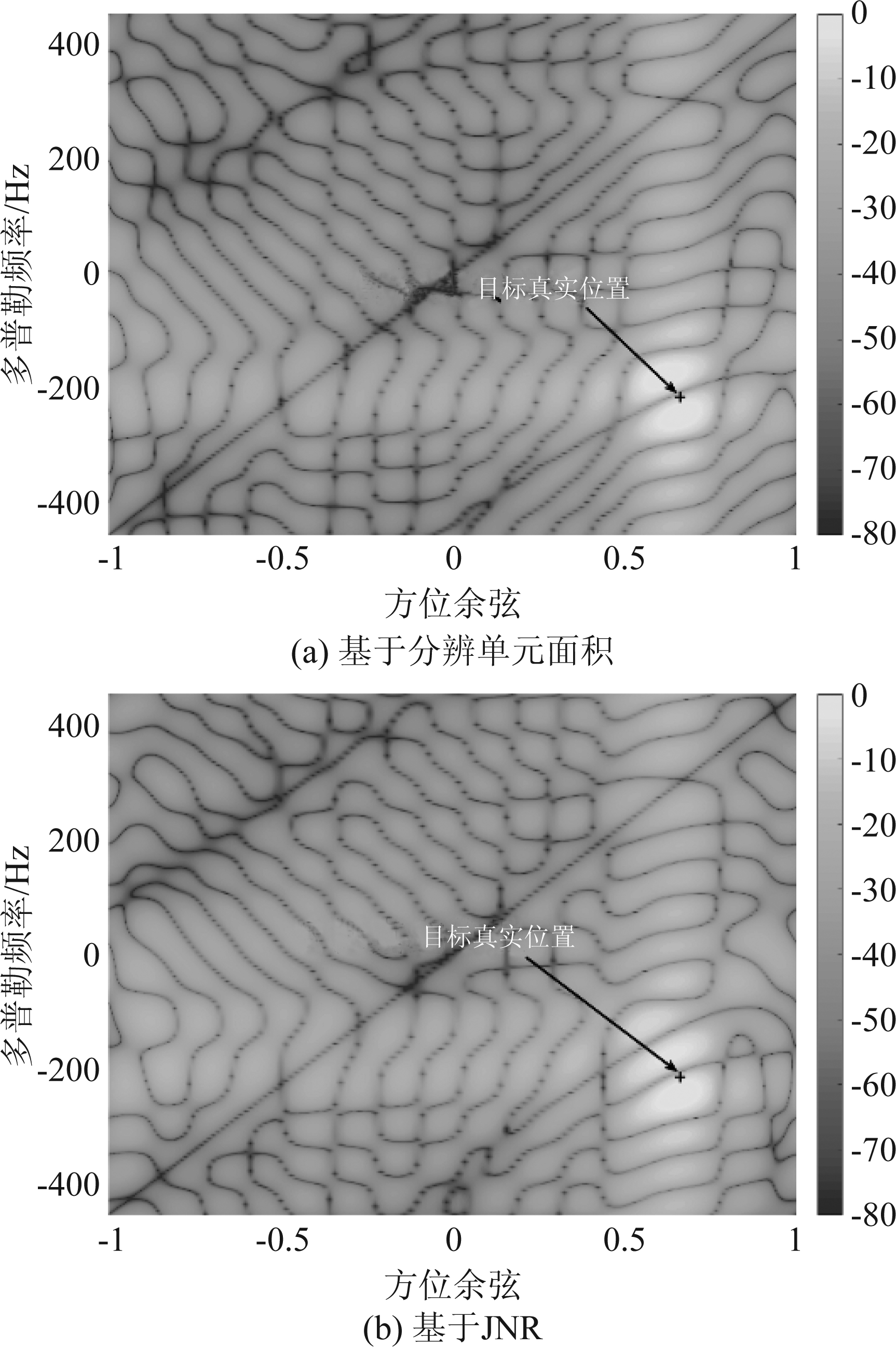
图13 伪杂波干扰下的STAP最优响应
Fig.13 STAP optimal response under fake clutter jamming
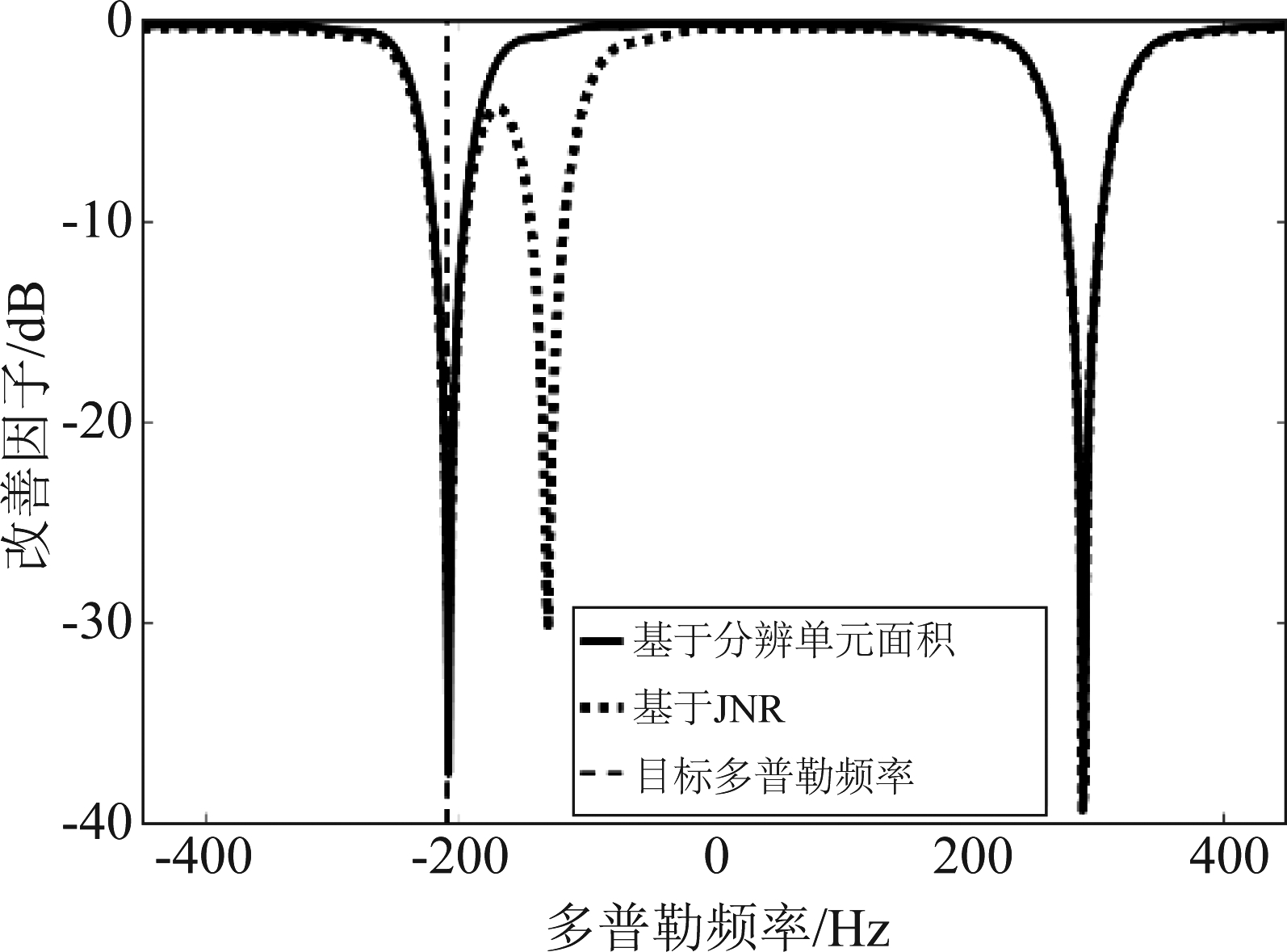
图14 改善因子对比
Fig.14 Comparison of improvement factors
综上所述,基于JNR仿真产生的伪杂波虽然反映了投散射式干扰的空时特性,但由于不能准确反映干扰功率的实际分布,没有区分开尾瓣和前瓣,使本该被噪声压制的尾瓣凸显出来而使对干扰效果的仿真不准确。基于分辨单元面积计算得到的伪杂波则能区分尾瓣和前瓣,正确反映了干扰功率分布,因而对干扰效果的仿真更准确。
5 结论
本文研究了投散射式伪杂波地面分辨单元面积的计算方法。通过坐标变换给出了伪杂波地面等距离环的解析表达式,根据空间几何关系,分析推导得出伪杂波地面分辨单元面积是由雷达接收波束宽度、雷达高度和所选取的伪杂波干扰信号空间路径距离所决定的不规则区域,区分高、低掠射角情形,给出了分辨单元面积的积分表达式和伪杂波块功率计算公式,基于此可以对伪杂波进行仿真。通过仿真实验从功率分布、功率谱和干扰效果三个方面对比了基于JNR仿真的伪杂波和基于分辨单元面积仿真的伪杂波。仿真结果表明基于分辨单元面积生成的伪杂波更符合实际,能更准确地评估伪杂波干扰效果。
[1] Klemm R. Principle of Space-Time Adaptive Processing[M]. 3rd Edition. London: The Institution of Electrical Engineer, 2002: 11-13.
[2] Melvin W L. A STAP Overview[J]. IEEE A&E Systems Magazine, 2004, 19(1): 19-35.
[3] 唐孝国, 张剑云. 机载相控阵雷达STAP原理及其干扰方法研究[J]. 电子设计工程, 2012, 20(15): 71-77.
Tang Xiaoguo, Zhang Jianyun. Study on the principle of STAP and jamming methods for airborne phased array radar[J]. Electronic Design Engineering, 2012, 20(15): 71-77.(in Chinese)
[4] 薛冰心, 张友益. 基于频移假目标对机载雷达STAP技术干扰效果的研究[J]. 舰船电子对抗, 2012, 35(1): 11-13, 59.
Xue Bingxin, Zhang Youyi. Research into the effect of false target jamming based on shift-frequency on airborne radar STAP technology[J]. Shipboard Electronic Counter-measure, 2012, 35(1): 11-13, 59.(in Chinese)
[5] 沈佳琪, 蒋东旭. 对预警雷达STAP的间歇采样转发干扰研究[J]. 舰船电子对抗, 2017, 40(3): 21-25.
Shen Jiaqi, Jiang Dongxu. Research into Intermittent Sampling Repeater Jamming to Early-warning Radar STAP[J]. Shipboard Electronic Counter-measure, 2017, 40(3): 21-25.(in Chinese)
[6] 张嘉曦. 对机载雷达STAP的干扰方法研究[D]. 西安: 西安电子科技大学, 2018.
Zhang Jiaxi. Research on Jamming Method to Airborne Radar STAP[D]. Xi’an: XiDian University, 2018.(in Chinese)
[7] 洪成洋. 对应用STAP技术的预警机的干扰研究[D]. 镇江: 江苏科技大学, 2016.
Hong Chengyang. Study on interference of early warning aircraft using STAP technology[D]. Zhenjiang: Jiangsu University of Science and Technology, 2016.(in Chinese)
[8] 谌诗娃, 张剑云, 周青松, 等. 对STAP雷达的投散射式干扰可行性研究分析[J]. 信号处理, 2016, 32(10): 1252-1259.
Chen Shiwa, Zhang Jianyun, Zhou Qingsong, et al. Feasibility Analysis for STAP Radar Scatter Wave Jamming[J]. Journal of Signal Processing, 2016, 32(10): 1252-1259.(in Chinese)
[9] 谌诗娃, 周青松, 张剑云, 等. 对STAP处理器的投散射式伪杂波干扰技术[J]. 现代雷达, 2016, 38(10): 83- 87.
Chen Shiwa, Zhou Qingsong, Zhang Jianyun, et al. A Study on the Scatter Wave Fake Clutter Jamming Method for Space-time Adaptive Processing[J]. Modern Radar, 2016, 38(10): 83- 87.(in Chinese)
[10] 谌诗娃, 周青松, 张剑云, 等. 对空时自适应处理雷达的投散射式伪杂波干扰方法信号特性分析[J]. 电子学报, 2018, 46(2): 401- 409.
Chen Shiwa, Zhou Qingsong, Zhang Jianyun, et al. Siganl Characteristic Analysis of Scattered-Wave Fake Clutter Jamming Method for STAP Radar[J]. Acta Electronica Sinica, 2018, 46(2): 401- 409.(in Chinese)
[11] 曲卫, 贾鑫, 裴世兵. 空基双基地雷达地面杂波分辨单元面积计算方法[J]. 装备指挥技术学院学报, 2007, 18(2): 81- 84.
Qu Wei, Jia Xin, Pei Shibing. Computation Method of Airborne Bistatic Radar Ground Clutter Resolution Cell Area[J]. Journal of the Academy of Equipment Command & Technology, 2007, 18(2): 81- 84.(in Chinese)
[12] 斯克尼克. 雷达系统导论[M]. 第三版. 电子工业出版社, 2010: 304-306.
Merrill I. Skolnik. Introduction to Radar Systems[M]. Third Edition. Publishing House of Electronics Industry, 2010: 304-306.(in Chinese)



