1 引言
高频信号绕射能力差、覆盖面有限,双向中继网络凭借其优越的通信可靠性和良好的通信覆盖能力得到广泛关注和应用[1-3]。然而,中继节点由于有限的电池容量无法满足网络的长期运转[4]。为此,无线信息和能量协同传输(Simultaneous Wireless Information and Power Transfer, SWIPT)技术应用于中继网络以延长能量受限的中继节点的工作寿命[5-9]。通过功率切割策略或时隙切换策略,中继节点采集射频(Radio Frequency, RF)信号能量并服务于下一步通信[10]。目前能量采集双向中继网络主要存在两种传输模式,即多址广播和时分广播[11]。多址广播需要两个时隙来完成网络的通信[12-15]。然而,当节点配备单天线且处于半双工模式时,这种传输模式不能有效地利用网络中的直达链路。时分广播需要三个时隙来完成网络的信息交互[16-21]。与多址广播不同,时分广播凭借其时隙特点能够充分地利用网络中的直达链路。故采用时分广播模式的能量采集双向中继网络可以实现更高的分集增益。
已知的大多数研究和文献均是在理想的硬件条件下进行分析[12-21]。然而,在实际通信中收发机遭受着来自不同方面的影响,例如I/Q支路不平衡、射频电路噪声及高功率放大非线性等[22-24]。尽管不少学者提出的算法缓解了这些影响,但残余的硬件损伤仍会影响网络的性能。特别地,在中、高数据传输速率下对网络的性能影响极大[25]。对于时隙切换策略下的能量采集双向中继网络,文献[26]考虑了收发机的硬件损伤,并分别研究了该网络在多址广播和时分广播下的端到端中断性能。对于功率切割策略下的能量采集双向中继网络,文献[27]研究了硬件损伤下网络的端到端中断性能。文献[26-27]表明,硬件损伤降低了网络的端到端中断性能。文献[28]分析了硬件损伤下能量采集双向中继网络的端到端中断性能,并且验证了具有硬件损伤的网络存在一个数据传输速率的上界。
通过上述工作回顾可知,现有相关工作均是从端到端中断概率角度评估硬件损伤对能量采集双向中继网络的影响,但还未有研究成果报道存在硬件损伤时能量采集双向中继网络的系统中断性能及硬件损伤对系统中断性能的影响。端到端中断概率在于评估一个终端节点能否将信息成功传输至另外一个终端节点,然而系统中断概率侧重评估两个终端节点能否通过双向中继方式相互成功传递信息。需要指出的是,推导系统中断概率需要考虑两条中继链路的相关性,故刻画硬件损伤下能量采集双向中继网络的系统中断性能和研究硬件损伤对系统中断性能的影响极具挑战性。
受上述因素的启发,本文面向能量采集双向放大转发中继网络,分别研究该网络在SC方案和MRC方案下的系统中断性能。在所考虑的网络中,各节点的收发机均遭受硬件损伤,中继节点通过功率切割策略采集RF信号能量。
本文的主要技术贡献总结如下：
(1)推导了网络在SC方案下的系统中断概率。在此基础上,得到了网络因硬件损伤而引起的两种效应,即中继协作效应和系统协作效应。具体来讲,在给定硬件损伤程度下,当数据传输速率超过中继协作门限时中继链路中断,即中继协作效应。在此情况下,网络仅通过直达链路实现终端的信息交互。当数据传输速率进一步提高且超过系统协作门限时直达链路中断,即系统协作效应。在此情况下,无论终端的发射功率取何值,整个网络均处于中断状态。
(2)推导了网络在MRC方案下的系统中断概率。结合仿真,明确了网络因硬件损伤仅产生系统协作效应。具体来讲,当数据传输速率低于系统协作门限时中继链路与直达链路共同协助网络的通信。然而,当数据传输速率超过系统协作门限时网络中断。
(3)通过实验仿真验证了理论分析的准确性并得到了如下结论。在给定硬件损伤程度下,MRC方案对应的最优功率分割因子大于SC方案对应的最优功率分割因子;相比于MRC方案,SC方案对硬件损伤更加敏感;在给定硬件损伤程度下,SC方案和MRC方案中使能量效率最大化的输入信噪比相同。当数据传输速率低于系统协作门限时,采用MRC方案可以实现更好的系统中断性能。
本文其他部分组织如下：第2节介绍了系统与信道模型;第3节推导了网络在SC方案下的系统中断概率;第4节推导了网络在MRC方案下的系统中断概率;第5节进行了仿真验证;最后给出了结论。
2 系统与信道模型
网络模型如图1所示,在硬件损伤条件下考虑了一个能量采集双向放大转发中继网络。中继节点R采用功率分割策略收集RF信号能量并利用收集-转发协议辅助网络的通信。所有节点均配有单发射天线且采用半双工模式。假设终端Sa、Sb之间存在直达链路。该网络采用时分广播传输模式,故每个传输块(持续时间为T)分为三个子时隙,各占T/3。如图2所示,在第一子时隙,终端Sa将信号xa广播到中继节点R和终端Sb。类似地,在第二子时隙,终端Sb将信号xb广播到中继节点R和终端Sa。接收到信号xa和xb后,中继节点R将接收信号分为两部分：一部分用于能量采集,另一部分用于信息处理。在第三子时隙,中继节点R放大用于信息处理的信号并利用采集的能量将其转发到终端Sa、Sb。
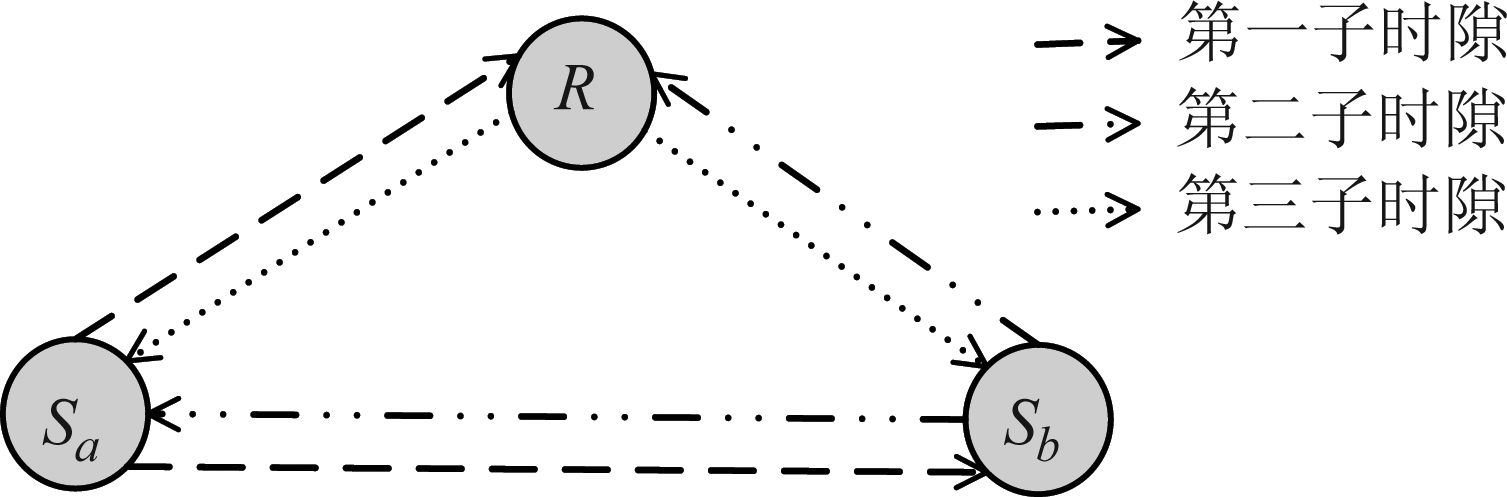
图1 能量采集双向中继网络模型
Fig.1 System model of energy harvesting enable two way relay network
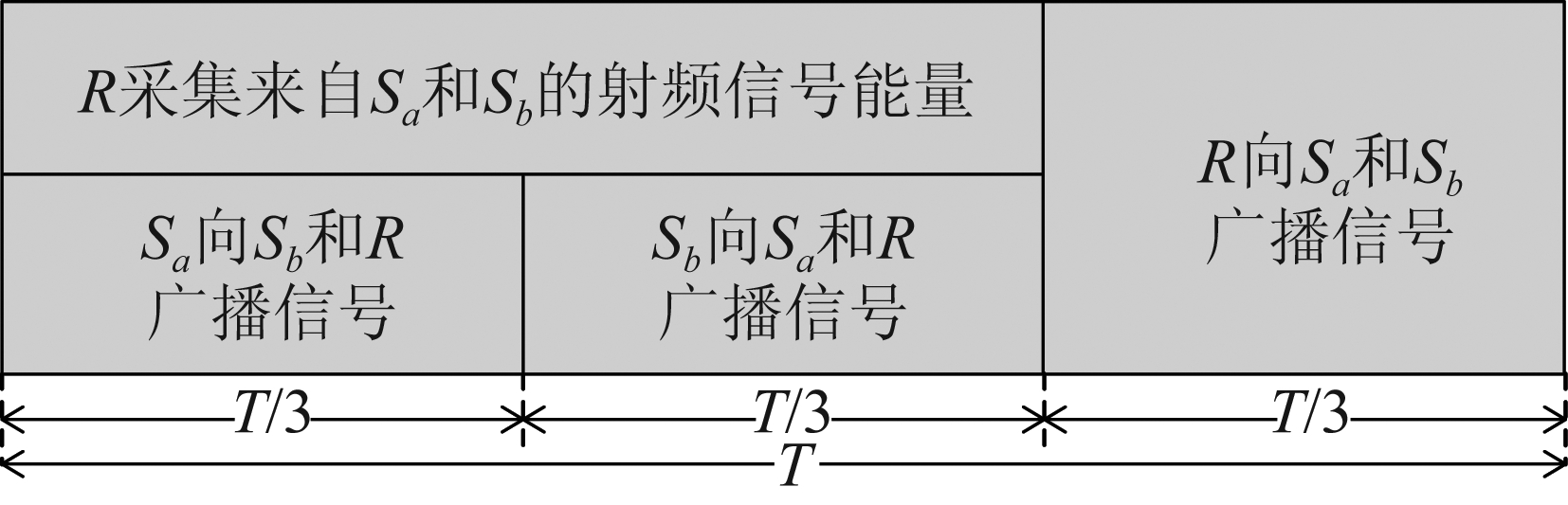
图2 时分广播传输模式的时隙结构
Fig.2 Transmission block structure for time division broadcast
假设在数据传输过程中各信道为瑞利衰落信道,信道衰落系数在各传输块内保持不变且在不同传输块之间相互独立。hir表示Si-R链路的信道衰落系数且服从均值为0方差为
的高斯分布,其中α1为Si-R链路的路径损耗,dir为Si-R链路的距离,i∈{a,b}。hij表示Si-Sj链路的信道衰落系数且服从均值为0方差为
的高斯分布,其中α2为Si-Sj链路的路径损耗,dij为Si-Sj链路的距离,i、 j∈{a,b}且i ≠ j。
如上所述,在第一、二子时隙,终端Sa和Sb分别广播信号xa和xb。由文献[28]可知,在硬件损伤条件下,终端Sj通过直达链路接收到的信号可以表示为
(1)
其中,P表示终端Si的发射功率,τti表示终端Si的发射机由于硬件损伤引起的失真噪声且服从均值为0方差为
的高斯分布,τrj表示终端Sj的接收机由于硬件损伤引起的失真噪声且服从均值为0方差为
的高斯分布,nij表示加性高斯白噪声(Additive White Gaussian Noise, AWGN)且服从均值为0方差为σ2的高斯分布,i、 j∈{a,b}且i ≠ j。k1和k2分别表示发射机和接收机硬件损伤程度的参数,在3GPP LTE中k1、k2∈[0.08,0.175][28]。由式(1)可知,终端Sj通过直达链路接收到的信损噪比(Signal-to-Noise-plus-Distortion Ratios, SNDR)为
(2)
其中,ρ=P/σ2表示输入信噪比。
对于中继链路而言,在硬件损伤条件下,中继R接收到的来自终端Si的信号可以表示为
(3)
其中,nir1表示天线噪声,τti表示终端Si的发射机由于硬件损伤引起的失真噪声且服从均值为0方差为的高斯分布,i∈{a,b}。中继R通过功率分割策略采集能量,故接收到的信号被分为两部分：
用于能量采集,
用于信息处理。因此,中继R采集到的总能量为
(4)
其中,0<η<1表示能量转换效率,0<β<1表示功率分割因子。根据收集-转发协议,中继R的转发功率可以表示为
(5)
此外,中继R用于信息处理的信号可以表示为
(6)
其中,τrr表示中继R的接收机由于硬件损伤引起的失真噪声且服从均值为0方差为
的高斯分布,nir表示AWGN且服从均值为0方差为σ2的高斯分布,i∈{a,b}。
在第三子时隙,中继R放大
并将其转发到终端Sa和Sb。根据文献[28],在硬件损伤条件下,终端Si通过中继链路接收到的信号可以表示为
(7)
其中,
表示放大系数,τtr表示中继R的发射机由于硬件损伤引起的失真噪声且服从均值为0方差为的高斯分布,τri表示终端Si的接收机由于硬件损伤引起的失真噪声且服从均值为0方差为
的高斯分布,nri表示AWGN且服从均值为0方差为σ2的高斯分布,i∈{a,b}。由式(7)可知,终端Si通过中继链路接收到的SNDR为
(8)
其中,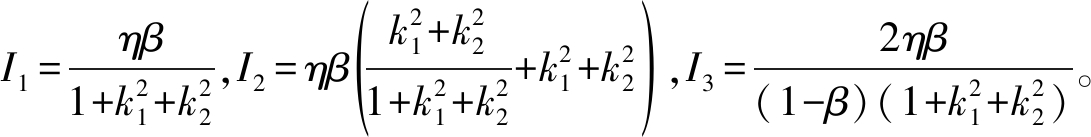
3 网络在SC方案下的系统中断性能分析
3.1 端到端SNDR
网络采用SC方案,根据文献[28],可得相应情况下终端Sa和Sb的端到端SNDR,即：
(9)
(10)
其中,γba=γab。
3.2 系统中断概率
由文献[20]可知,系统中断概率表示至少存在一个终端的数据传输速率低于特定门限Rth的概率。结合式(9)和式(10),网络在SC方案下的系统中断概率可以表示为
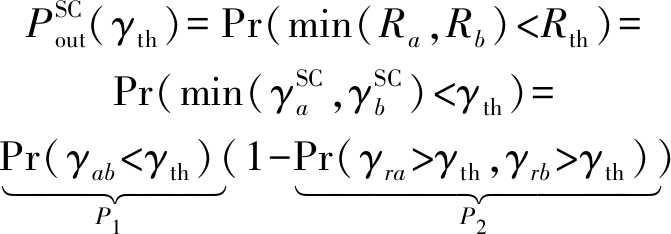
(11)
其中,γth=23Rth-1表示SNDR门限,Ra和Rb分别表示终端Sa和Sb的数据传输速率。接下来,通过讨论P1和P2得到式(11)的闭式解。
假设|har|2=X,|hbr|2=Y,|hab|2=Z。将式(2)代入式(11),可得P1的表达式为
(12)
由式(12)可以看出,根据SNDR门限的取值,P1的求解可分为如下两种情况。
当SNDR门限满足
时,无论Z(Z>0)取何值,式(12)中的不等式恒成立,故P1=1。
当SNDR门限满足
时,P1可转化为
即
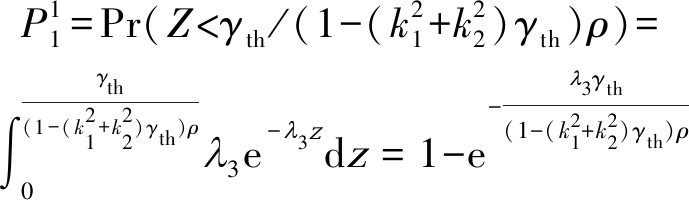
(13)
基于上述讨论,P1的闭式解为
(14)
将式(8)代入式(11),可得P2的表达式为
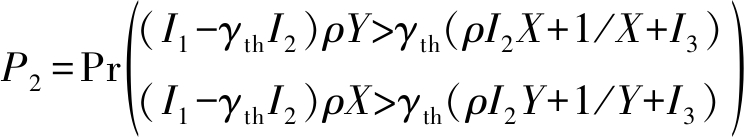
(15)
类似地,根据SNDR门限的取值,P2的求解也可分为如下两种情况。
1)γth≥I1/I2
当SNDR门限满足γth≥I1/I2时,无论X(X>0)和Y(Y>0)取何值,式(15)中的不等式恒不成立,故P2=0。
2)γth<I1/I2
当SNDR门限满足γth<I1/I2时,P2可转化为
P2=Pr(Y>I4γth(ρI2X+1/X+I3),
X>I4γth(ρI2Y+1/Y+I3))
(16)
其中,I4=1/ρ(I1-γthI2)。鉴于式(16)中的两个不等式之间存在相关性,故很难直接对其求解。为了得到P2的闭式解,首先讨论式(16)中不等式所包含的积分区域。然后,在此基础上通过求解定积分得到P2的闭式解。由式(16)可以看出,积分区域由两条曲线构成,即l1(x): y=I4γth(ρI2x+1/x+I3)和l2(y): x=I4γth(ρI2y+1/y+I3)。此外,定义曲线l3(x): y=x。针对曲线l1、l2和l3,通过观察及相关的数学推导,可得到如下结论：
(1)l1(x)和l2(y)关于l3(x)对称;
(2)l1(x)和l2(y)在区间
单调递减,在区间
)单调递增;
和
分别为l1(x)和l2(y)的唯一极小值点;
,
;
(5)当γth满足I1/(2I2)≤γth<I1/I2时,l1(x)和l3(x)在第一象限内无交点;
(6)当γth满足γth<I1/(2I2)时,l1(x)和l3(x)在第一象限内有且仅有一个交点xin,xin=
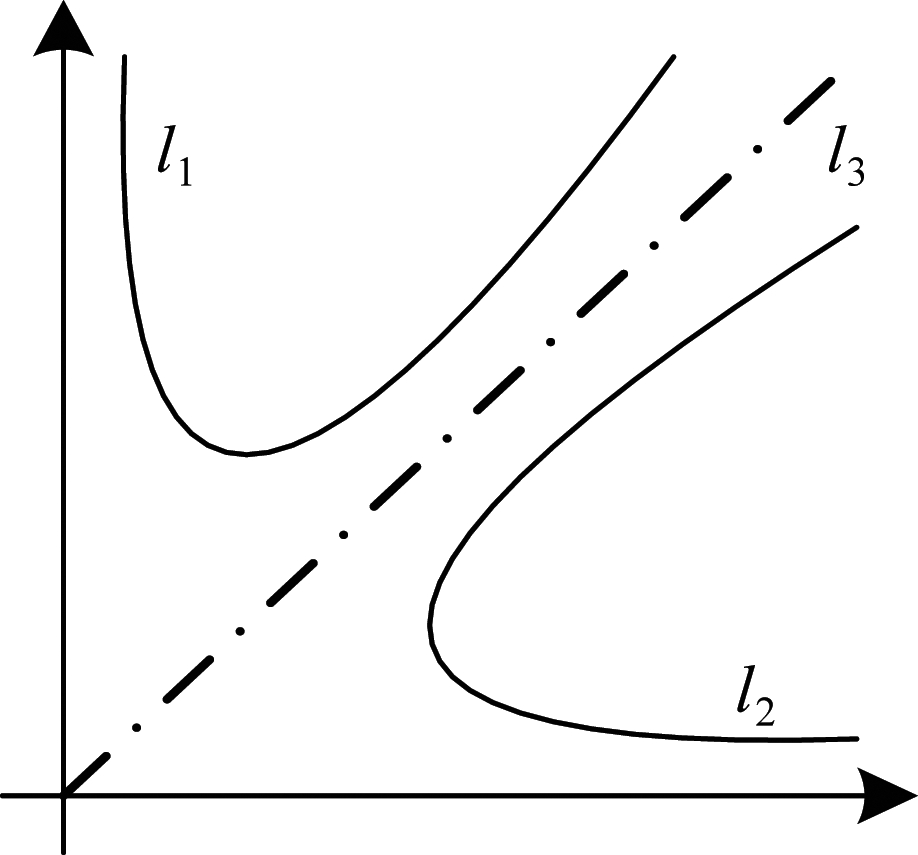
图3 l1和l2无交点
Fig.3 l1 and l2 have no intersection point
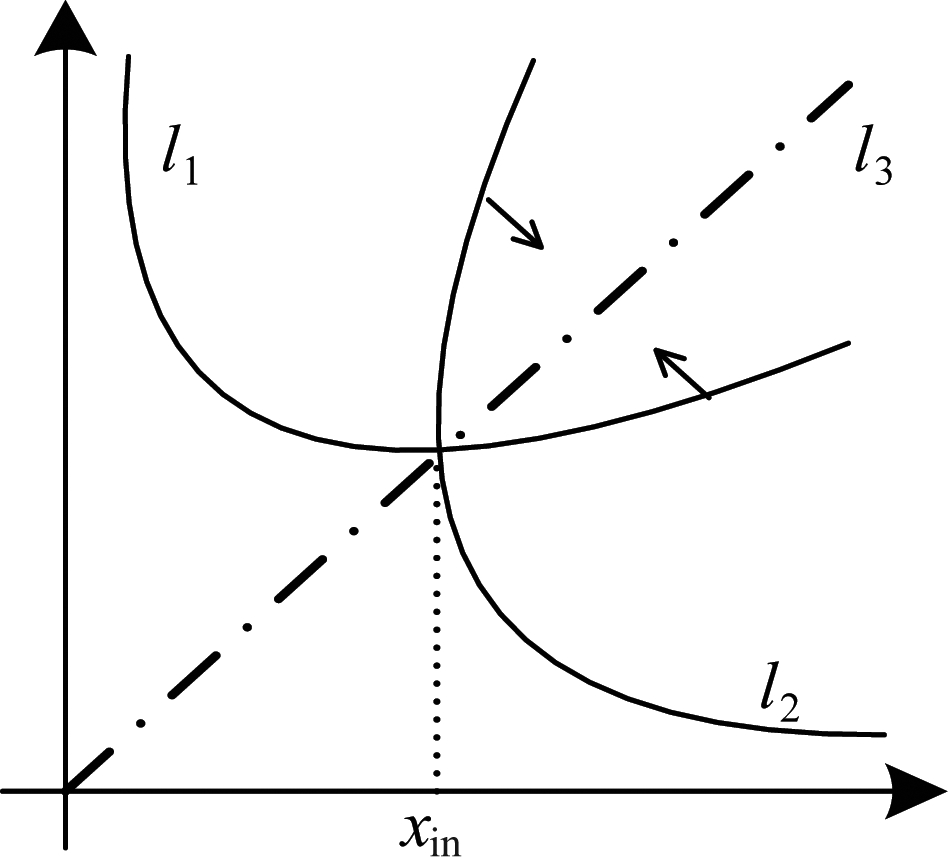
图4 l1和l2存在一个交点
Fig.4 l1 and l2 have only one intersection point
当SNDR门限满足γth<I1/I2时,根据l1和l2的交点个数,可进一步将P2分为如下两种情况。
(1)当l1与l3在第一象限内无交点时,即I1/(2I2)≤γth<I1/I2,l1与l2在第一象限内无交点,如图3所示。显然,在此情况下式(16)中不等式包含的积分区域为0,故P2=0。
图5 l1和l2存在三个交点
Fig.5 l1 and l2 have three intersection points
(2)当l1与l3在第一象限内有交点时,即γth<I1/(2I2),l1与l2在第一象限内存在交点。联立l1和l2,可得到如下方程组
(17)
通过初步运算,式(17)可转化为如下的一元四次方程
c4x4+c3x3+c2x2+c1x+c0=0
(18)
其中,
结合上述关于曲线的结论,可知式(18)中解的情况为：存在一个正实根xin或存在三个不同的正实根x1、x2和xin。也就是说,曲线l1与l2在第一象限内存在一个交点或三个不同交点。由文献[30],可以确定式(18)中根的情况并且可以得到正实根的值。当SNDR门限满足γth<I1/(2I2)时,根据式(18)中正实根的个数,P2又可进一步分为如下两种情况。
a)式(18)仅有一个正实根xin,如图4所示。在此情况下式(16)中不等式包含的积分区域如图4的箭头所示,故P2可表示为
即
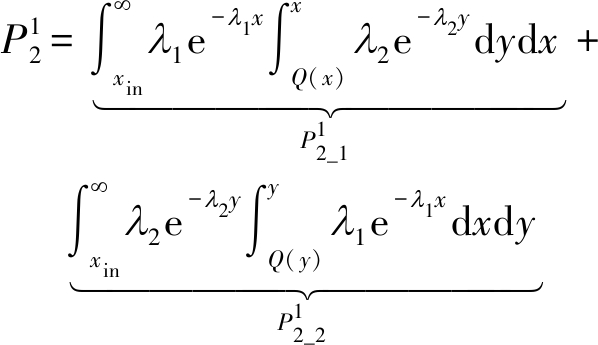
(19)
其中,Q(x)=I4γth(ρI2x+1/x+I3),Q(y)=I4γth(ρI2y+1/y+I3)。通过初步的数学推导,
可表示为
λ1e-λ2I3I4γth
e-(λ1+λ2I2I4ργth)(x+xin)-λ2I4γth/(x+xin)dx
(20)
考虑到式(20)中的积分无法直接求出,利用高斯切比雪夫积分得到
的近似解为
(21)
其中,w=π/N,νn=cos((2n-1)π/2N),θn=π(νn+1)/4,N表示复杂度与精确度的平衡参数。同理,可得
的近似解为
(22)
b)式(18)有三个不同的正实根x1、x2和xin,如图5所示。在此情况下式(16)中不等式包含的积分区域如图5的箭头所示,故P2可表示为
即
(23)
其中,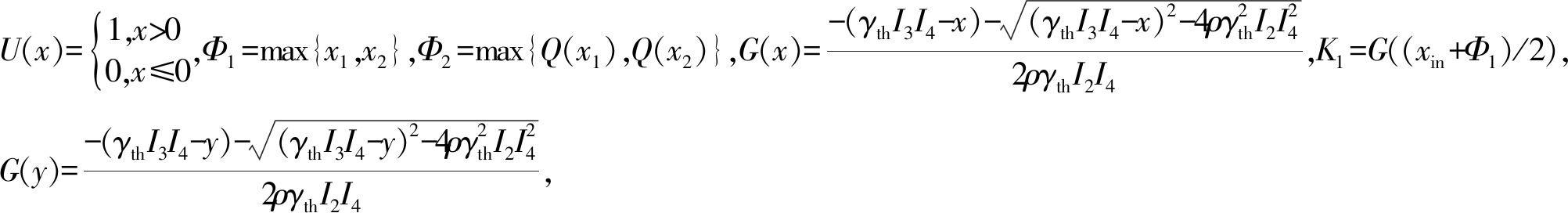
K2=Q((xin+Φ1)/2)。通过初步的数学推导,
可表示为
λ1e-λ1x-λ2G(x)dx+
λ1e-λ1x-λ2Q(x)dx
(24)
利用高斯切比雪夫积分,可得
的近似解为
(25)
其中,
同理,可得
的近似解为
(26)
其中,
基于上述讨论,P2的闭式解为
(27)
根据式(11)、式(14)和式(27),该网络在SC方案下的系统中断概率可表示为如下：
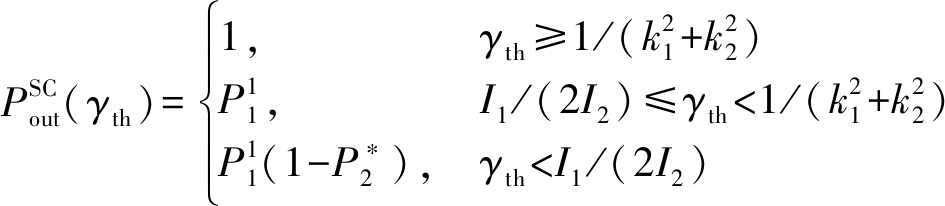
(28)
其中,当式(18)仅有一个正实根时
当式(18)有三个不同的正实根时
由式(28)可以看出,硬件损伤限制了网络的数据传输速率。当SNDR门限满足γth<I1/(2I2)时中继链路与直达链路共同协助网络的通信。当SNDR门限满足
时中继链路中断,这种现象被称为中继协作效应。特别地,
为中继协作门限。中继协作效应发生后,网络仅依靠直达链路完成终端之间的通信。当SNDR门限进一步增加且满足时直达链路中断,这种现象被称为系统协作效应。特别地,
为系统协作门限。系统协作效应发生后,无论输入信噪比取何值,整个网络均处于中断状态。
4 网络在MRC方案下的系统中断性能分析
4.1 端到端SNDR
网络采用MRC方案,根据文献[29],可得相应情况下终端Sa和Sb的端到端SNDR,即：
(29)
(30)
其中,γba=γab。
4.2 系统中断概率
根据3.2节中关于系统中断概率的定义,网络在MRC方案下的系统中断概率可以表示为
fγA(γ)FγB(γth-γ)dγ
(31)
其中,fγA(γ)表示变量γA的概率密度函数(Probability Density Function),FγB(γ)表示变量γB的累积分布函数(Cumulative Distribution Function)。
引理1 γA的概率密度函数为
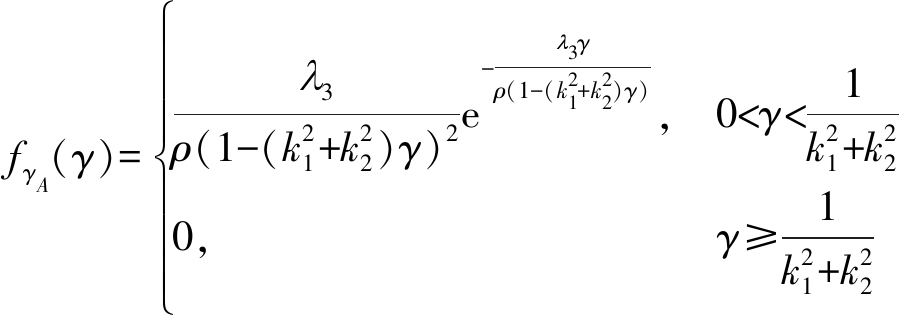
(32)
证明 见附录。
根据式(31)中γB的表达式,γB的累积分布函数可表示为
FγB(γ)=Pr(min(γra,γrb)<γ)=1-Pr(γra>γ,γrb>γ)
(33)
根据第3节中关于P2的讨论,可得到γB的累积分布函数,如引理2所示。
引理2 γB的累积分布函数为
(34)
其中,当式(18)仅有一个正实根时
当式(18)有三个不同的正实根时
结合引理1和引理2,根据SNDR门限的取值,式(31)可分为如下两种情况。
当SNDR门限满足时,
可以表示为P3,即
P3=
fγA(γ)dγ+
fγA(γ)FγB(γth-γ)dγ=
(35)
其中,Φ3=max{0,γth-I1/(2I2)}。利用高斯切比雪夫积分,可得P3的近似解为
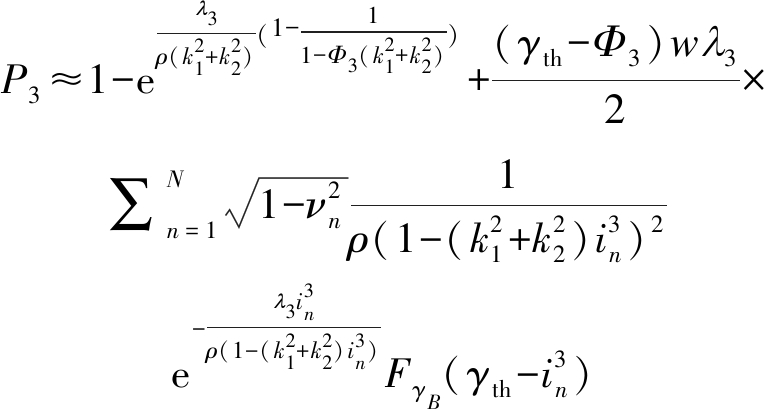
(36)
其中,
当SNDR门限满足时,可以表示为P4,即
P4=
fγA(γ)dγ+
fγA(γ)FγB(γth-γ)dγ=
(37)
其中,
利用高斯切比雪夫积分,可得P4的近似解为
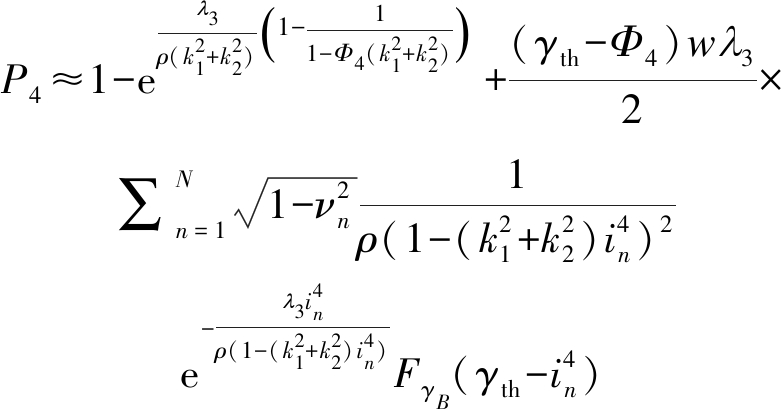
(38)
其中,
综上所述,网络在MRC方案下的系统中断概率可表示为如下：
(39)
5 仿真结果与分析
本节提供仿真来验证上述的理论分析并探究硬件损伤及系统参数对系统中断性能的影响。本文的仿真参数参照文献[20]和文献[28]设置,假设能量转换效率η=0.6,传输块的持续时间T=1 s,复杂度与精确度的平衡参数N=30,Sa-R链路的距离dar =5 m,Sb-R链路的距离dbr =5 m,Sa-Sb链路的距离dab =10 m,中继链路的路径损耗α1=2.7,直达链路的路径损耗α2=3,k1=k2=kave。
图6验证了SC方案和MRC方案下系统中断概率的推导。假设功率分割因子β=0.8,kave=0.1。根据式(28)和式(39),选取三种数据传输速率来验证推导的准确性,即1 bit/Hz、1.5 bit/Hz和2 bit/Hz(对应的SNDR门限分别为7 dB、22 dB和63 dB)。SC方案和MRC方案的系统中断概率与SNDR门限的对应关系分别如下所示：
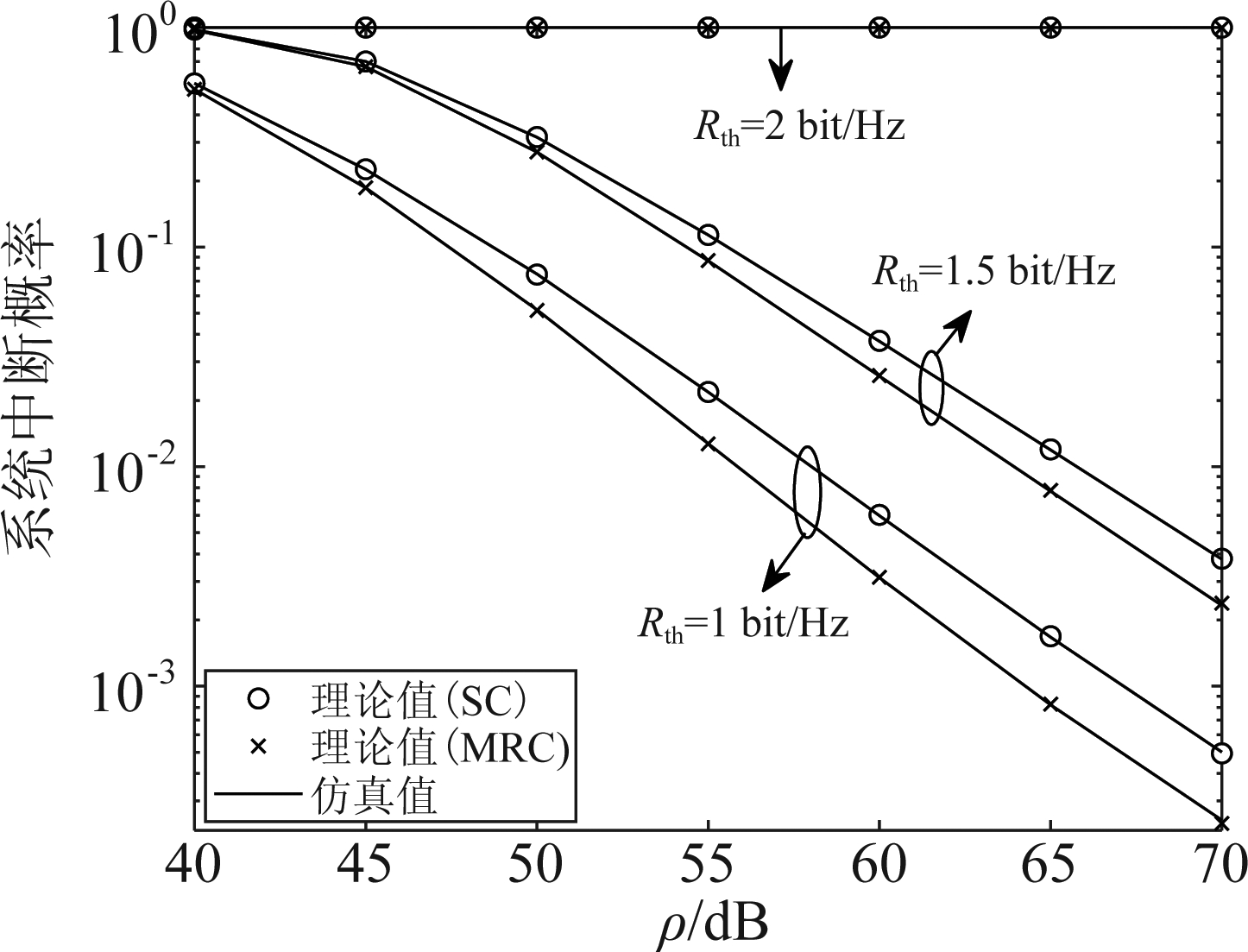
图6 不同数据传输速率的系统中断概率
Fig.6 System outage probability for different data transmission rates
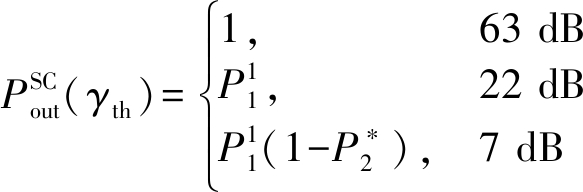
从图6可以看出,理论曲线与仿真曲线在不同数据传输速率下均较为贴合,验证了SC方案和MRC方案下系统中断概率推导的准确性。
图7对比了不同传输网络的系统中断概率,即直传网络、基于多址广播的双向中继网络和基于时分广播的双向中继网络。假设功率分割因子β=0.8,数据传输速率Rth=0.5 bit/Hz。从图中可以看出,在给定硬件损伤程度(kave=0.1)下,所研究网络实现了最低的系统中断概率,而基于多址广播的双向中继网络的系统中断概率最高。这是因为所研究网络充分利用了中继链路和直达链路,而基于多址广播的双向中继网络仅依靠中继链路实现通信。此外,从图7可以看出,所研究网络在硬件损伤下的系统中断性能对比于理想硬件下有明显下降。这表明硬件损伤对于系统设计有不可忽略的影响。最后,从图7也可以看出,相对于SC方案,所研究网络在MRC方案下可以实现更好的系统中断性能。
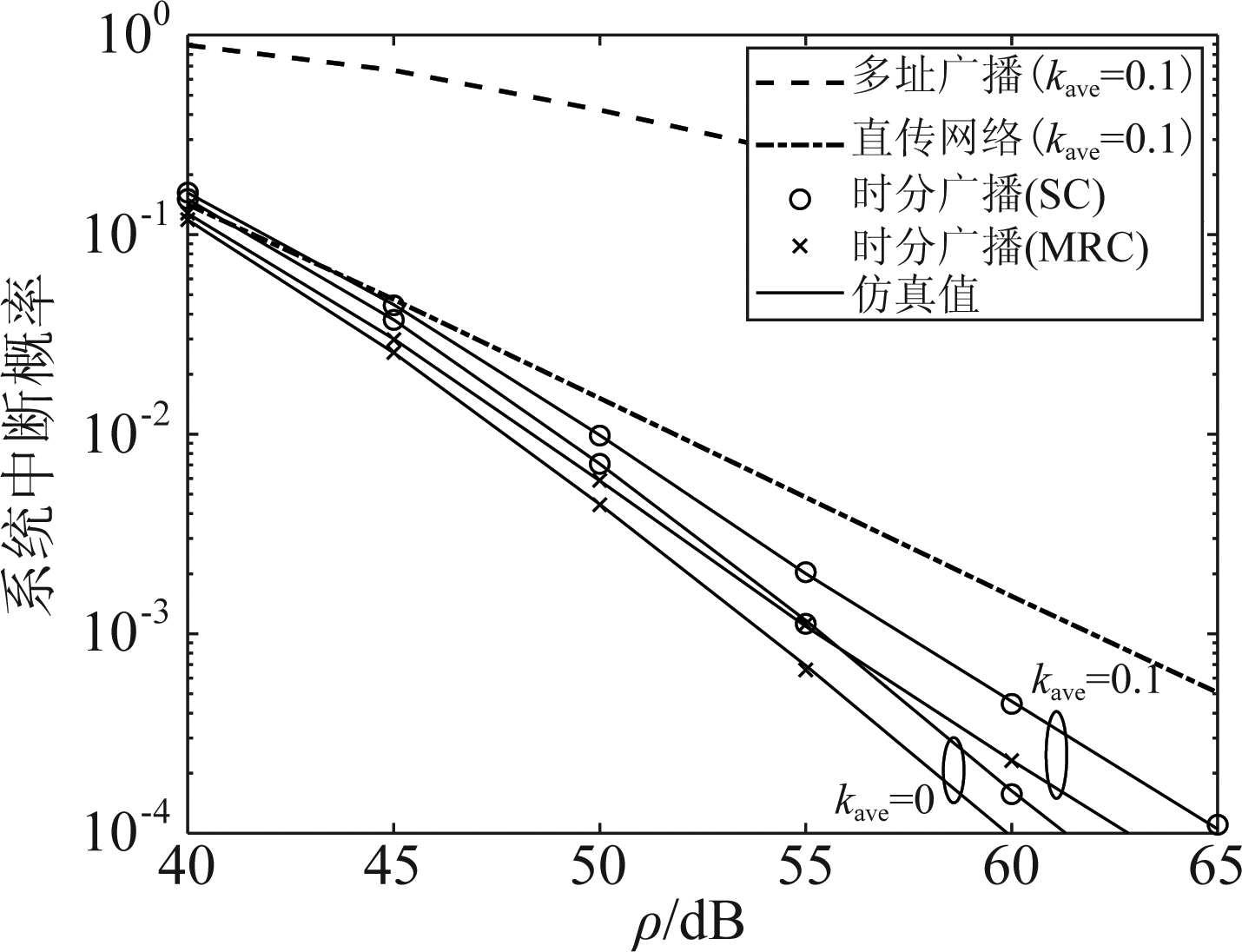
图 7 不同传输网络的系统中断概率
Fig.7 System outage probability for different transmission networks
图8给出了理想硬件和硬件损伤下系统中断概率随功率分割因子变化的曲线。假设输入信噪比ρ=45 dB,数据传输速率Rth=0.5 bit/Hz。从图8可以看出,所有曲线随着功率分割因子的增加呈现先减小后增大的趋势。这表明存在最优的功率分割因子使SC/MRC方案的系统中断概率达到最小。这种变化趋势可以做如下解释。当功率分割因子小于最优的功率分割因子时,中继节点因采集的能量较少导致用于信号转发的功率较小,进而造成系统中断概率较大。当功率分割因子大于最优的功率分割因子时,中继节点将接收的信号大多用于能量采集,而较少的部分用于信号转发。因此,较弱的信号强度以及被放大的噪声使终端接收的SNDR较低,导致系统中断概率较大。此外,在同一合并方案下,最优的功率分割因子不随硬件损伤程度的变化而变化。在给定硬件损伤程度下,MRC方案对应的最优功率分割因子大于SC方案对应的最优功率分割因子。最后,从图中也可以看出,在给定功率分割因子和硬件损伤程度下,MRC方案能够实现更好的系统中断性能。
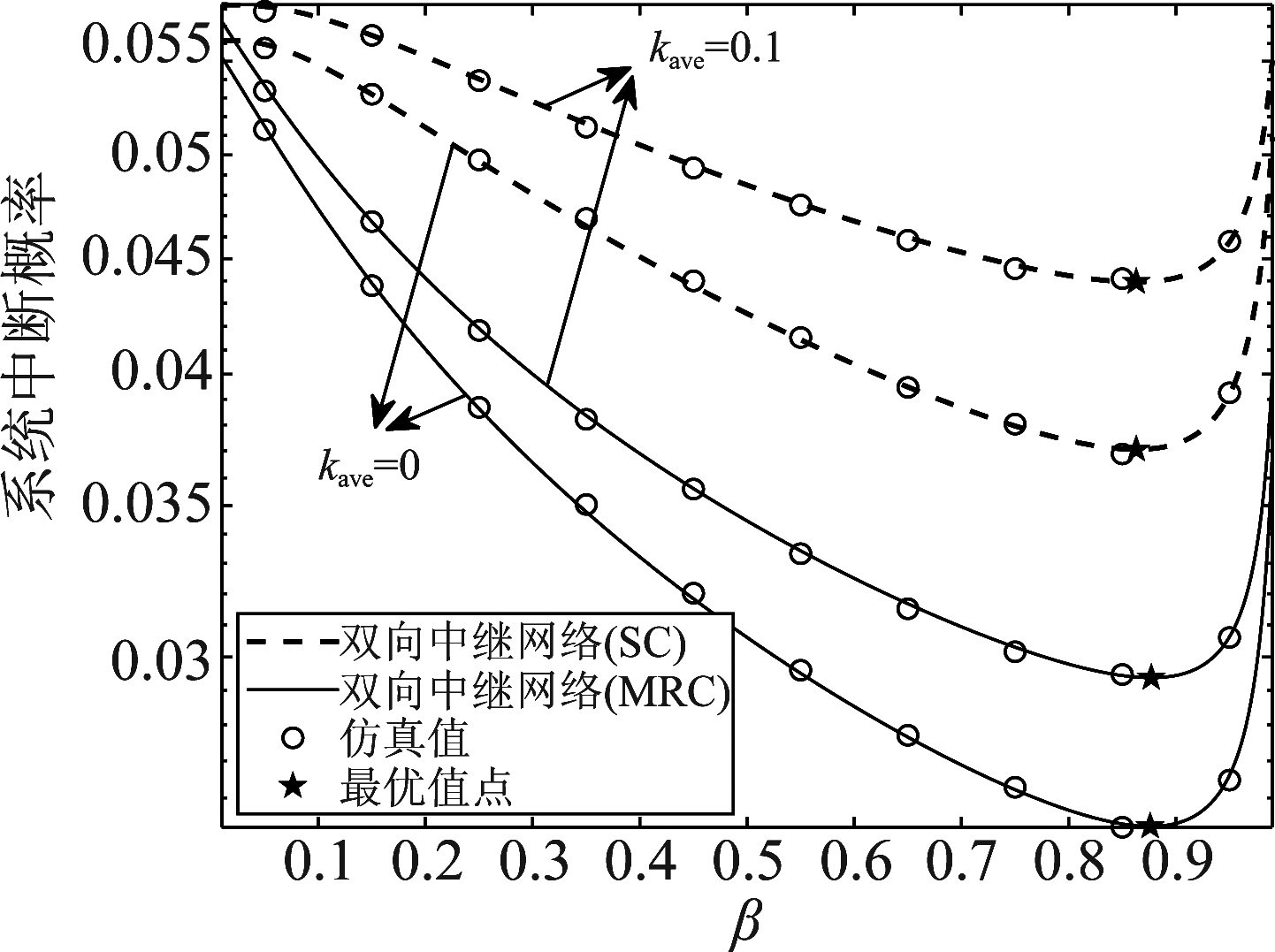
图 8 不同功率分割因子的系统中断概率
Fig.8 System outage probability versus power splitting ratio
图9给出了系统中断概率随硬件损伤程度变化的曲线,其中kave∈[0,0.18]。假设功率分割因子β=0.8,数据传输速率Rth=1.5 bit/Hz。从图9可以看出,随着硬件损伤参数的增加,SC方案和MRC方案的系统中断概率均先逐渐增加后保持不变。结合图9和式(28),可以将SC方案下的硬件损伤程度分为如下三类：
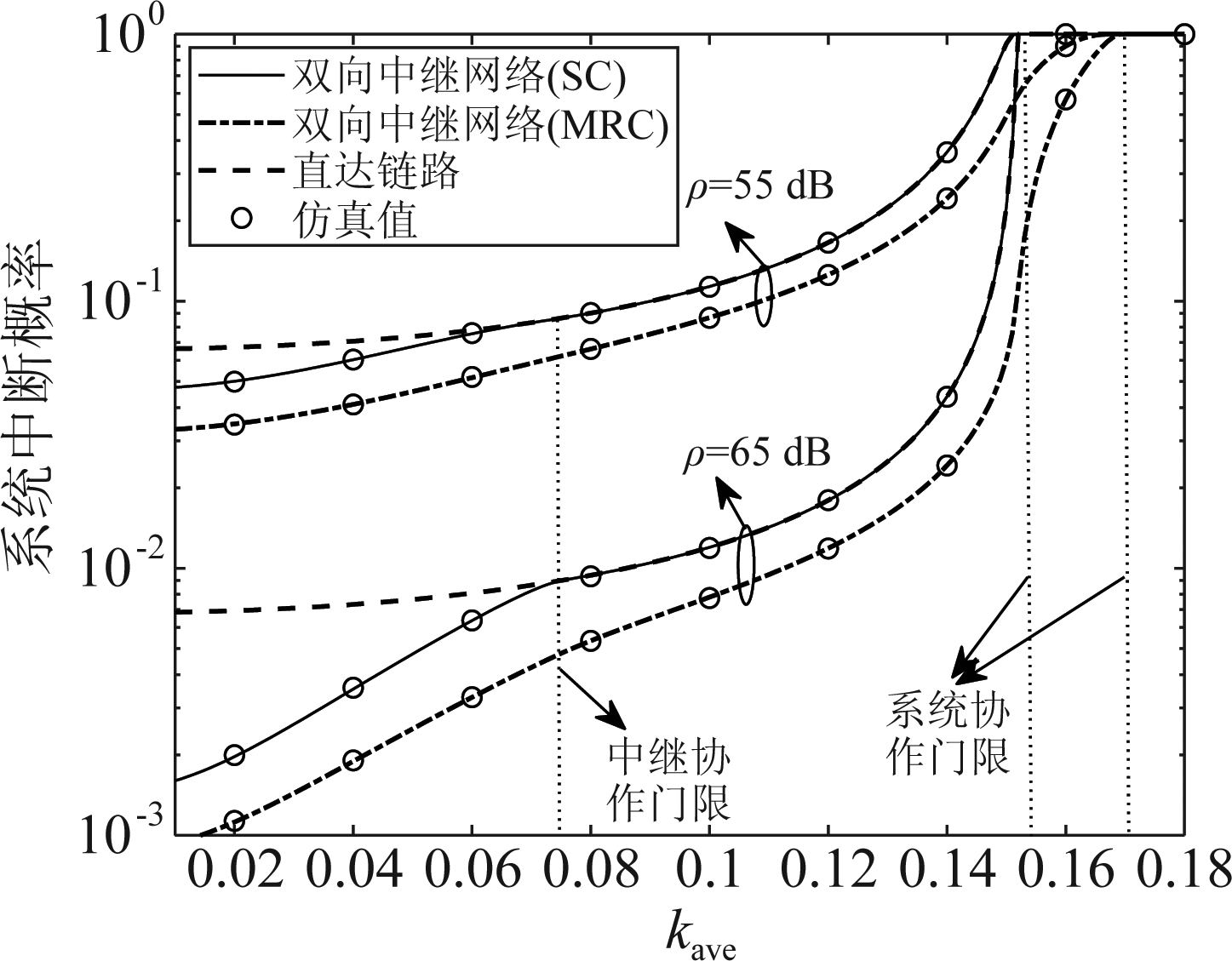
图9 不同硬件损伤程度的系统中断概率
Fig.9 System outage probability versus hardware impairments levels
1)当硬件损伤参数kave满足kave∈[0,0.0758)时,凭借直达链路与中继链路共同协助通信的优势,网络能够实现最好的系统中断性能。
2)当硬件损伤参数kave满足kave∈[0.0758,0.152)时,中继链路中断,即中继协作效应。特别地,kave=0.0758为中继协作门限。这表明中继链路相比于直达链路对硬件损伤更敏感。
3)当硬件损伤参数kave满足kave∈[0.152,0.18]时,直达链路中断,即系统协作效应。特别地,kave=0.152为系统协作门限。在此情况下,无论输入信噪比取何值,系统中断概率始终为1。
从图9也可以看出,MRC方案在硬件损伤条件下仅引起系统协作效应,其中系统协作门限kave≈0.17。这表明当数据传输速率低于系统协作门限时直达链路与中继链路共同协助网络的通信。此外,MRC方案的系统协作门限大于SC方案的系统协作门限,故SC方案对硬件损伤更加敏感。
图10给出了理想硬件和硬件损伤下系统中断概率随SNDR门限变化的曲线。假设功率分割因子β=0.8,输入信噪比ρ=50 dB。从图10可以看出,在硬件损伤条件下,当SNDR门限超过某个特定值之后SC/MRC方案的系统中断概率恒为1。在理想硬件条件下,SC/MRC方案的系统中断概率随着SNDR门限的增加而逐渐增大,但不存在SNDR门限上界。从图中也可以看出,硬件损伤在低SNDR门限下对系统中断性能影响较小,但在中、高SNDR门限下对系统中断性能影响很大。此外,无论硬件是否存在硬件损伤,MRC方案均可以实现更好的系统中断性能。
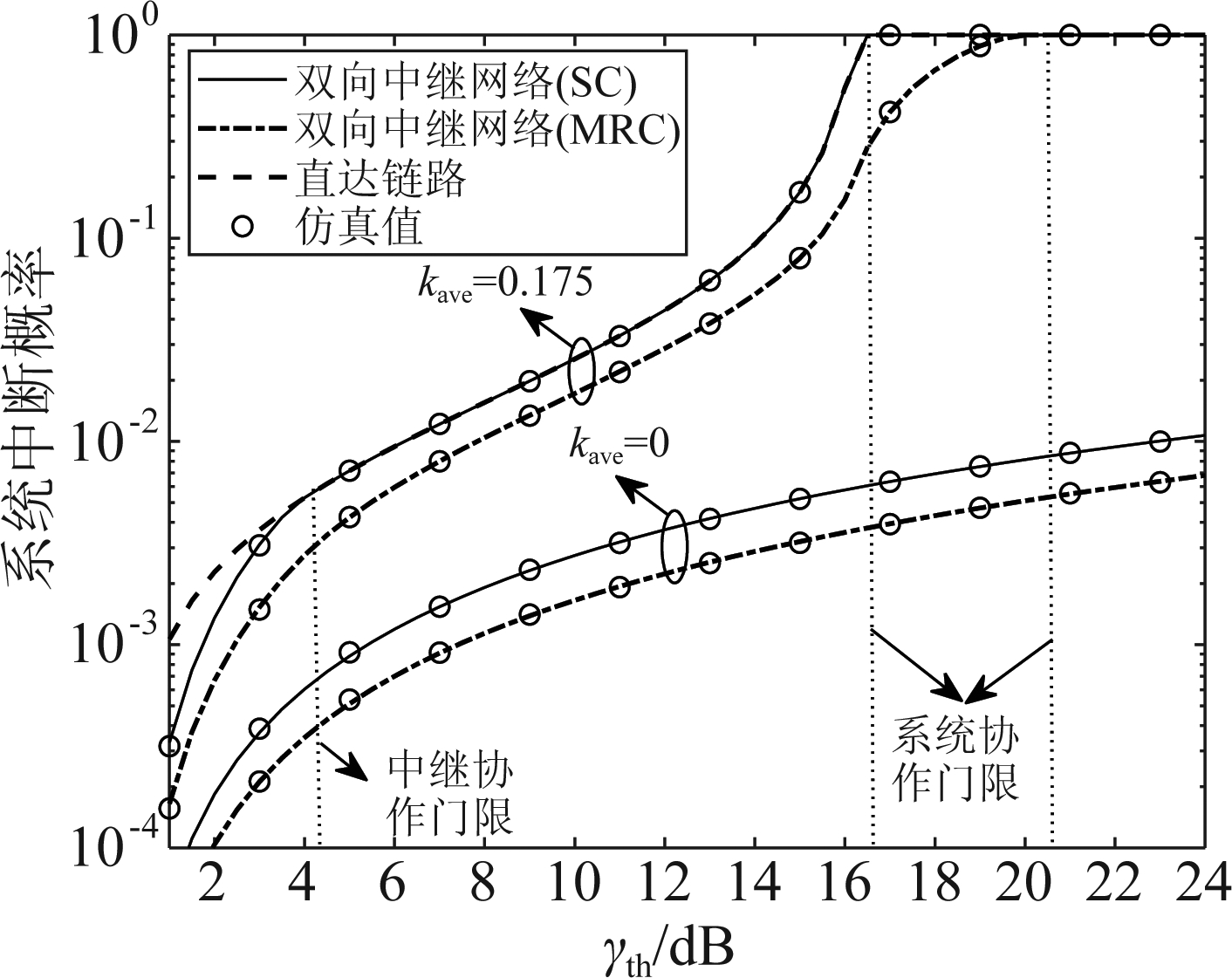
图10 不同SNDR门限的系统中断概率
Fig.10 System outage probability versus SNDR threshold
图11给出了理想硬件和硬件损伤下能量效率随输入信噪比变化的曲线。根据文献[28],SC方案和MRC方案的能量效率可分别定义为
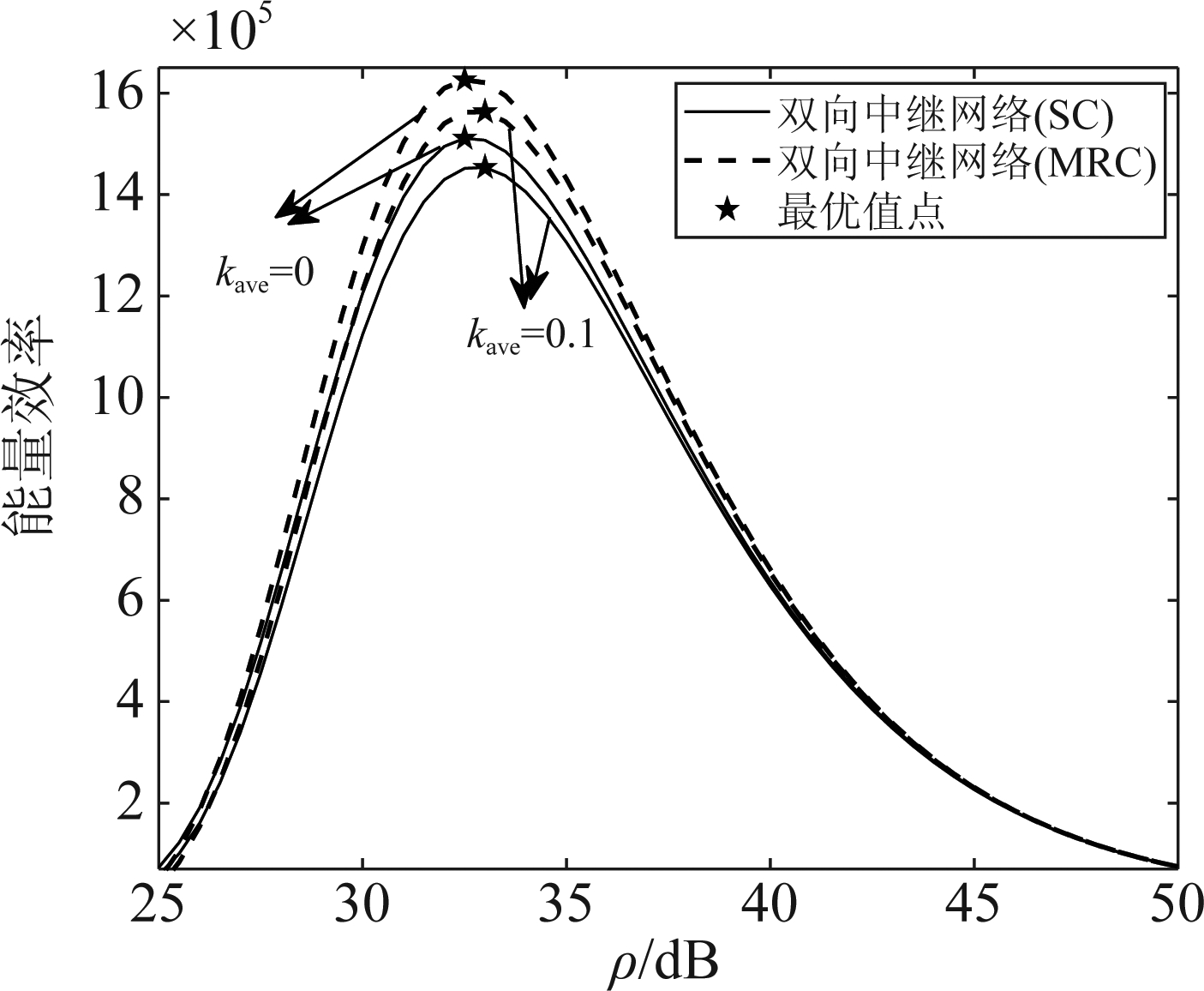
图11 不同输入信噪比的能量效率
Fig.11 Energy efficiency versus input signal to noise ratios
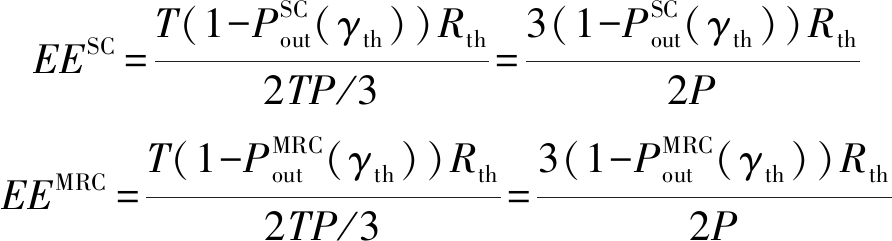
从图11可以看出,随着输入信噪比的增加,所有曲线呈现先增大后减小的趋势。这表明无论在理想硬件还是硬件损伤下网络均存在最优的输入信噪比使能量效率达到最大。因此,终端发射功率的选择对于平衡频谱利用和能量消耗起着至关重要的作用。从图11也可以看出,在同一合并方案下,最优的输入信噪比随着硬件损伤参数的增加而增加。
6 结论
对于硬件损伤条件下的能量采集双向放大转发中继网络,本文分别分析了该网络在SC和MRC方案下的系统中断性能。首先,推导了SC方案下的系统中断概率,并进一步得到了由硬件损伤而引起的两种效应,即中继协作效应和系统协作效应。具体来讲,当数据传输速率超过中继协作门限时,中继链路中断。当数据传输速率进一步增加且超过系统协作门限时,直达链路中断。其次,推导了MRC方案的系统中断概率,并结合仿真得到了由硬件损伤而引起的系统协作效应。具体来讲,当数据传输速率低于MRC方案下的系统协作门限时,中继链路和直达链路共同辅助网络的通信。当数据传输速率超过系统协作门限时,整个网络处于中断状态。最后,通过实验仿真分析了硬件损伤及系统参数对系统中断性能的影响,并比较了SC和MRC方案的性能差异。具体结论如下：在给定硬件损伤程度下,MRC方案对应的最优功率分割因子大于SC方案对应的最优功率分割因子;相比于MRC方案,SC方案对硬件损伤更加敏感;当数据传输速率低于系统协作门限时,MRC方案可以实现更好的系统中断性能。
附录
由式(2)和式(31)可知,变量γA和Z满足
(40)
根据γA的取值,其概率密度函数可分为如下两种情况。
当γA满足
时,γA的概率密度函数恒为0,即fγA(γ)=0。
当γA满足
时,式(40)可以转为
由概率论的相关理论可知,γA的概率密度函数可表示为
fγA(γ)=fZ(z)|Z′|
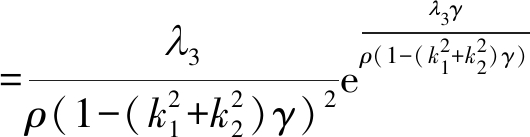
(41)
其中,fZ(z)表示变量Z的概率密度函数,Z′表示式(40)关于γA的导数。
综上,引理1得证。
[1] Zhang C, Ge J, Li J, et al. A Unified Approach for Calculating the Outage Performance of Two-Way AF Relaying Over Fading Channels[J]. IEEE Transactions on Vehicular Technology, 2015, 64(3): 1218-1229.
[2] Zhang C, Hu Y, Li J, et al. Performance Evaluation for Asymmetric Two-Way AF Relaying in Rician Fading[J]. IEEE Wireless Communications Letters, 2013, 2(3): 307-310.
[3] 仇艮祥, 杨洁, 曹雪虹. 译码转发中继网络的能量效率分析[J]. 信号处理, 2016, 32(7): 872- 880.
Qiu Genxiang, Yang Jie, Cao Xuehong. Energy Efficiency Analysis in Decode-and-Forward Cooperative Networks[J]. Journal of Signal Processing, 2016, 32(7): 872- 880.(in Chinese)
[4] Chen Z, Dong Y, Fan P, et al. Optimal Throughput for Two-Way Relaying: Energy Harvesting and Energy Co-Operation[J]. IEEE Journal on Selected Areas in Communications, 2016, 34(5): 1448-1462.
[5] Liu K, Lin P. Toward self-sustainable cooperative relays: state of the art and the future[J]. IEEE Communications Magazine, 2015, 53(6): 56- 62.
[6] 洪鑫龙, 许晓荣, 石振波. 无线携能网络中一种基于时隙切换的中继辅助信能同传协议[J]. 信号处理, 2018, 34(12): 1467-1473.
Hong Xinlong, Xu Xiaorong, Shi Zhenbo. A Relay-aided Information and Power Transfer Protocol Based on Time Switching Structure in SWIPT[J]. Journal of Signal Processing, 2018, 34(12): 1467-1473.(in Chinese)
[7] 聂志巧, 赵睿, 方嘉佳, 等. 基于功率分配能量采集的全双工放大转发中继系统[J]. 信号处理, 2017, 33(4): 641- 648.
Nie Zhiqiao, Zhao Rui, Fang Jiajia. Amplify-and-Forward Full-Duplex Relay with Power Splitting-Based Energy Harvesting[J]. Journal of Signal Processing, 2017, 33(4): 641- 648.(in Chinese)
[8] Ponnimbaduge Perera T D, Jayakody D N K, Sharma S K, et al. Simultaneous Wireless Information and Power Transfer (SWIPT): Recent Advances and Future Challenges[J]. IEEE Communications Surveys & Tutorials, 2018, 22(1): 264-302.
[9] Liu Y. Joint Resource Allocation in SWIPT-Based Multiantenna Decode-and-Forward Relay Networks[J]. IEEE Transactions on Vehicular Technology, 2017, 66(10): 9192-9200.
[10] Nasir A A, Zhou X, Durrani S, et al. Relaying Protocols for Wireless Energy Harvesting and Information Processing[J]. IEEE Transactions on Wireless Communications, 2013, 12(7): 3622-3636.
[11] Liu Y, Wang L, Elkashlan M, et al. Two-way relay networks with wireless power transfer: design and performance analysis[J]. IET Communications, 2016, 10(14): 1810-1819.
[12] Quoc Bao V N, Van Toan H, Le K N. Performance of two-way AF relaying with energy harvesting over Nakagami-m fading channels[J]. IET Communications, 2018, 12(20): 2592-2599.
[13] Modem S, Prakriya S. Performance of Analog Network Coding Based Two-Way EH Relay With Beamforming[J]. IEEE Transactions on Communications, 2017, 65(4): 1518-1535.
[14] Do T P, Song I, Kim Y H. Simultaneous Wireless Transfer of Power and Information in a Decode-and-Forward Two-Way Relaying Network[J]. IEEE Transactions on Wireless Communications, 2017, 16(3): 1579-1592.
[15] Alsharoa A, Ghazzai H, Kamal A E, et al. Optimization of a Power Splitting Protocol for Two-Way Multiple Energy Harvesting Relay System[J]. IEEE Transactions on Green Communications and Networking, 2017, 1(4): 444- 457.
[16] Ju M, Kim I. Relay Selection with ANC and TDBC Protocols in Bidirectional Relay Networks[J]. IEEE Transactions on Communications, 2010, 58(12): 3500-3511.
[17] Liu Y, Wang L, Elkashlan M, et al. Two-way relaying networks with wireless power transfer: Policies design and throughput analysis[C]∥2014 IEEE Global Communications Conference. Piscataway: IEEE Press, 2014: 4030- 4035.
[18] Gurjar D S, Singh U, Upadhyay P K. Energy harvesting in hybrid two-way relaying with direct link under Nakagami-m fading[C]∥2018 IEEE Wireless Communications and Networking Conference. Piscataway: IEEE Press, 2018: 1- 6.
[19] Ye Y, Shi L, Chu X, et al. On the Outage Performance of SWIPT-Based Three-Step Two-Way DF Relay Networks[J]. IEEE Transactions on Vehicular Technology, 2019, 68(3): 3016-3021.
[20] Shi L, Ye Y, Hu R Q, et al. System Outage Performance for Three-Step Two-Way Energy Harvesting DF Relaying[J]. IEEE Transactions on Vehicular Technology, 2019, 68(4): 3600-3612.
[21] Shi L, Ye Y, Chu X, et al. Optimal Combining and Performance Analysis for Two-Way EH Relay Systems With TDBC Protocol[J]. IEEE Wireless Communications Letters, 2019, 8(3): 713-716.
[22] Qi J, Aissa S, Alouini M. Analysis and compensation of I/Q imbalance in amplify-and-forward cooperative systems[C]∥2012 IEEE Wireless Communications and Networking Conference. Piscataway: IEEE Press, 2012: 215-220.
[23] Costa E, Pupolin S. M-QAM-OFDM system performance in the presence of a nonlinear amplifier and phase noise[J]. IEEE Transactions on Communications, 2002, 50(3): 462- 472.
[24] Dardari D, Tralli V, Vaccari A. A theoretical characterization of nonlinear distortion effects in OFDM systems[J]. IEEE Transactions on Communications, 2000, 48(10): 1755-1764.
[25] Bjornson E, Matthaiou M, Debbah M. A New Look at Dual-Hop Relaying: Performance Limits with Hardware Impairments[J]. IEEE Transactions on Communications, 2013, 61(11): 4512- 4525.
[26] Nguyen D K, Matthaiou M, Duong T Q, et al. RF energy harvesting two-way cognitive DF relaying with transceiver impairments[C]∥2015 IEEE International Conference on Communications Workshop. Piscataway: IEEE Press, 2015: 1970-1975.
[27] Nguyen D K, Jayakody D N K, Chatzinotas S, et al. Wireless Energy Harvesting Assisted Two-Way Cognitive Relay Networks: Protocol Design and Performance Analysis[J]. IEEE Access, 2017, 5: 21447-21460.
[28] Solanki S, Singh V, Upadhyay P K. RF Energy Harvesting in Hybrid Two-Way Relaying Systems With Hardware Impairments[J]. IEEE Transactions on Vehicular Technology, 2019, 68(12): 11792-11805.
[29] Katiyar H, Jana R, Bhattacharjee R. Performance analysis of two-hop regenerative relay network with generalized selection combining at multi-antenna relay[J]. IEEE India Conference. IEEE, 2010: 1- 4.
[30] Marseken S F, Surhone L M, Timpledon M T, et al. Quartic function[OL]. https:∥www.morebooks.de/store/es/book/quarticfunction/isbn/978- 613- 0-34265- 4, 2010.
