1 引言
盲信道均衡或盲语音去混响都是从非理想传输信道的输出信号恢复源信号的过程,其本质是信号的盲解卷积。在语音去混响应用中,盲解卷积仍然是一个尚未完全解决的问题[1- 6]。盲解卷积的理想方案是直接由观测信号估计解卷积信号。通常情况下,盲解卷积过程是盲系统辨识过程后跟一个解卷积过程,不是一个理想方案。如果盲系统辨识过程和解卷积过程能够同步进行,则将更接近理想方案。本文就是出于这种考虑,提出一种基于卡尔曼滤波的同步盲多信道系统辨识和解卷积方法。
众所周知,基于二阶矩的单信道系统辨识是不可能的,但基于二阶矩的多信道系统辨识是可行的。本文讨论的内容是建立在卡尔曼滤波理论基础上的多信道系统辨识和解卷积问题。
传统上,通信系统中需要利用训练信号来进行系统辨识,并对接收信号进行均衡处理,以便消除码间干扰,但这是以牺牲通信系统效率为代价的[7]。在语音去混响应用中是不存在用来辨识信道的训练语音的,只能依靠盲系统辨识技术。
盲解卷积方法大体上可以分为三类。(Ⅰ)盲信道辨识与逆滤波相结合:通过盲系统辨识获得信道参数,在此基础上对观测信号进行解卷积而获得源信号[8];(Ⅱ)盲逆系统辨识与滤波:在一定条件下可以直接估计多信道系统的逆系统,然后对观测信号滤波而得到源信号,但这种方法不适用于语音这种非白信号[9];(Ⅲ)直接解卷积:解卷积与信道(或信道的逆)估计同步进行[1,10]。文献[1]中,在短时傅里叶变换域内提出基于卡尔曼滤波和最大似然估计的EM算法:在E步利用卡尔曼滤波估计声源信号,在M步利用最大似然法估计冲激响应及噪声方差等参数。
大多数盲解卷积算法都属于第一类,因此盲信道辨识是该类方法要解决的关键问题。盲信道辨识方法大体上可分为基于二阶矩和高阶矩的方法。高阶矩方法直接或间接利用高阶统计量的性质,而二阶矩算法利用源信号的循环平稳特性或多信道系统(单输入多输出系统:SIMO)[11-12]。盲语音去混响系统是典型的SIMO系统[8];生物医学工程上,通过外周动脉压力波形重建中心动脉压力波形问题也是SIMO系统的典型例子[13]。
对于非最小相位系统来说,已经证明,如果输入信号不满足某些特殊条件(如循环平稳性),二阶统计量是不足以盲辨识该系统的。但是对于SIMO系统,情况完全不同。对于SIMO系统,可以利用多信道输出信号间的交叉关联关系(Cross Relation: CR条件)通过子空间分解[12,14]或优化算法[15-21]实现多信道盲辨识。
基于CR条件的盲辨识算法可以分为自适应算法[15-21]和非自适应算法[12,14,18]。自适应算法由于其内在的时间跟随性而更受关注。
在这些基于CR条件的自适应盲辨识算法中,多信道最小均方算法(MCLMS)[16,19]和归一化频域最小均方算法(NMCFLMS)[17]由于其原理简单、直观而受到更多关注,但是其收敛速度和噪声稳定性不理想。为了提高盲辨识算法噪声稳定性,又有若干改进算法,如DP-NMCFLMS算法[20]、功率约束的 DP-NMCFLMS算法[21]和lp-RNMCFLMS算法[22]。
为了提高基于CR条件的多信道盲辨识算法的收敛速度和噪声稳定性,有人提出基于卡尔曼滤波的盲辨识算法[8,23]。这些算法具有更好的收敛速度和噪声稳定性。
在文献[23]中给出一种基于卡尔曼滤波盲系统辨识算法与基于卡尔曼滤波的解卷积算法级联的语音去混响系统。在这种级联结构中,盲系统辨识过程和信号解卷积过程是分开的,是两个独立的卡尔曼滤波系统。在本文中将证明,这两个独立的卡尔曼滤波系统可以统一到一个卡尔曼滤波系统中。
2 单输入多输出系统与CR条件
对于SIMO系统,设房间中有N个传声器,第i个传声器接收到的数字化混响语音信号(即观测信号)为xi(n) (i=1, 2, …, N; n为时间),则观测信号与声源信号s(n)之间的关系为:
(1)
其中,hi(k)是第i个传声器与声源之间的房间冲激响应(Room Impulse Response: RIR),长度为L;vi(n)为第i个观测信号的观测噪声,为零均值、方差为
的白噪声。同时假设各路观测噪声之间互不相关,且与声源信号也不相关。
不管多信道系统的冲激响应如何,在没有噪声的情况下,系统的各输出信号之间存在如下的交叉关联关系(CR):
xi(n)*hj(n)=xj(n)*hi(n)
(2)
其中i,j=1,2,...,N(i≠j);‘*’为卷积运算符。只要各个冲激响应之间不存在公共零点,就可以通过这一关系在二阶矩上辨识系统[7]。在有噪声时可以修正为如下关系:
xi(n)*hj(n)=xj(n)*hi(n)-εij(n)
(3)
其中εij(n)=vj(n)*hi(n)-vi(n)*hj(n)。这时可以通过优化来辨识系统。
同步盲系统辨识与解卷积就是利用SIMO系统的输入输出关系(1)和交叉关联关系式(2)或(3)构造卡尔曼滤波问题。
3 同步盲系统辨识与解卷积算法
就卡尔曼滤波问题而言,最重要的是把所研究问题在状态空间用过程方程和测量方程表示出来。同步盲系统辨识与解卷积过程就是同时估计多信道系统冲激响应hi(n)(i=1,2,...,N)和源信号s(n),因此状态矢量必须包含hi(n)(i=1,2,...,N)和s(n)。
在下面的讨论中,首先来建立卡尔曼滤波问题的测量方程,然后给出相应的过程方程。
首先,令n时刻源信号矢量为
s(n)=[s(n),s(n-1),...,s(n-Ls+1)]T(Ls≥L)
(4)
同时令Bs=Ls-L+1和卷积矩阵(Bs×Ls):
Hi=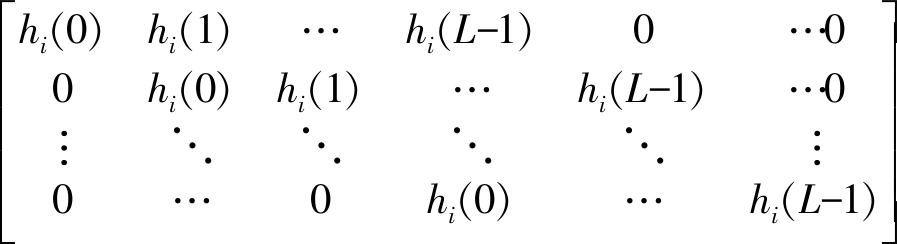
(5)
此外,令n 时刻多信道卷积矩阵:
则多信道系统的输入输出关系方程(1)可写成如下形式:
(6)
其中
x(n)=[x1(n),x1(n-1),…,x1(n-Bs+1),…,
xN(n),xN(n-1),…,xN(n-Bs+1)]T
是(NBs×1)维观测信号矢量;
为相应的观测噪声矢量。此外,需要说明的是,当取Ls>L(即Bs>1)时,是为了增加算法的噪声稳定性。
其次,定义n时刻多信道冲激响应矢量:
其中hi=[hi(0),hi(1),hi(L-1)]T。同时,出于算法噪声稳定性和块运算考虑,由观测信号定义(B+1)×L阶汉克尔矩阵:
xi(n)=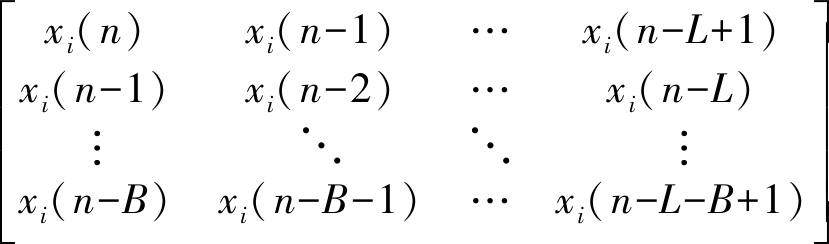
并在此基础上定义[(B+1)N(N-1)/2]×NL阶矩阵Cx(n)如下:
Cx(n)=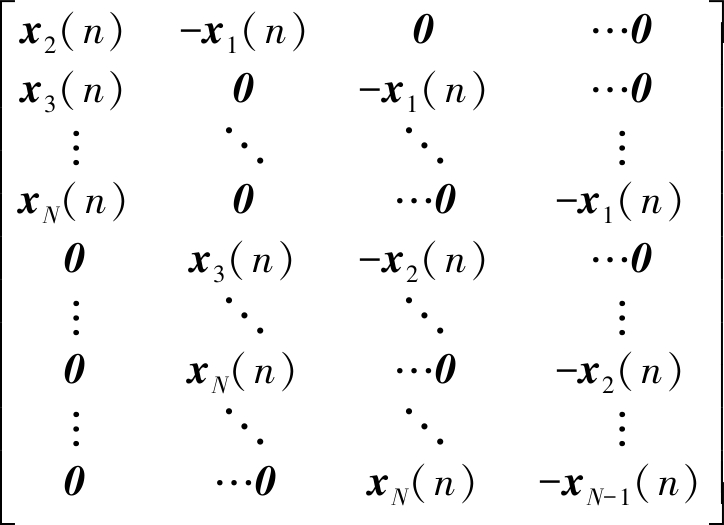
(7)
其中,每个0元素都是一个与xi(n)同阶的零矩阵。则式(3)所给出的交叉关系式可以用矩阵表示如下:
(8)
其中,符号0p×q表示p×q维零矩阵或列矢;噪声矢量
定义如下:
ε1N(n-B),ε23(n),…,ε23(n-B),…,
ε(N-1)N(n),…,ε(N-1)N(n-B)]T
联合式(6)和式(8),得到如下的卡尔曼滤波问题的测量方程:
y(n)=C(n)hs(n)+v2(n)
(9)
其中,
观测矢量:
它不仅包含实际观测信号矢量x(n),而且包含由CR条件隐含的零矢量0[(B+1)N(N-1)/2]×1;
状态矢量:hs(n)=[hT(n),sT(n)]T;
测量噪声:
并且假设它具有如下性质:
(10)
测量矩阵:
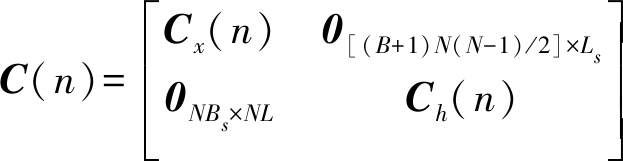
(11)
根据式(9)中定义的状态矢量,可以给出如下的过程方程:
hs(n+1)=F(n+1,n)hs(n)+sν(n)+vα(n)
(12)
其中:sν(n)=[01×NL,s(n),01×(Ls-1)]T,是状态矢量hs(n)的s(n)部分的转移增量;vα(n)是状态矢量的h(n)部分的状态转移噪声。状态转移矩阵定义如下:
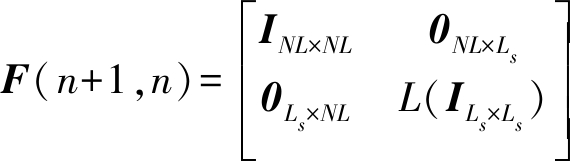
(13)
并且F(n,n+1)=FT(n+1,n),其中
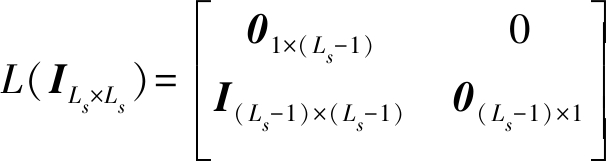
(14)
令v1(n)=sν(n)+vα(n),视其为过程噪声,并假设满足如下条件:
(15)
其中Q1(n)是对角阵,它的第(NL+1)个对角元素对应矢量sν(n),所以在实际计算时,该元素的值要远大于其他对角元素。
至此,方程(9)和(12)构成一个标准卡尔曼滤波问题。状态矢量hs(n)的最后一个分量作为解卷积信号
输出。标准卡尔曼滤波算法如下:
表1 同步盲多信道辨识与解卷积算法
Tab.1 The algorithm of synchronic blind multichannel identification and deconvolution
开始:输入观测信号xi(n)(i=1,2,...,N);初始化:给定盲多信道系统冲激响应的长度L;源信号矢量s(n)的长度Ls≥L;Bs≥1;B≥0;状态转移矩阵:F(n+1,n)及F(n,n+1);状态矢量初值h^s(0)=[1,0,...,0];过程噪声的自相关矩阵Q1(n)=10-8diag([1,...,1,108,1,...,1]) (diag(.)表示对角阵,108对应第NL+1个对角元素);测量噪声自相关矩阵Q2(n)=10-8Ip×p (p=NBs+(B+1)N(N-1)/2);预测的状态矢量误差自相关矩阵K(n,n-1)n=1=105I(NL+Ls)×(NL+Ls)。迭代计算:n=1,2,3,...(1)生成观测矢量y(n)和测量矩阵C(n);(2)卡尔曼增益计算:G(n)=F(n+1,n)K(n,n-1)CT(n)[C(n)K(n,n-1)CT(n)+Q2(n)]-1(3)新息计算:α(n)=y(n)-C(n)h^s(n);(4)h^s(n)=F(n+1,n)h^s(n-1)+G(n)α(n);(5)s^(n)=h^s(n)的最后一个分量(6)K(n)=K(n,n-1)-F(n,n+1)G(n)C(n)K(n,n-1)(7)K(n+1,n)=F(n+1,n)K(n)FT(n+1,n)+Q1(n)结束迭代。
4 有关算法实现方面的考虑
在表1所给出的算法中,无论参数Bs和B取何值,观测矢量y(n)和测量矩阵C(n)都是按点更新:即每一个采样周期更新一次,迭代一次。因此,Bs和B取值越大,算法计算量越大。适当增大Bs和B可以提高算法的噪声稳定性。
很明显,当多信道系统冲激响应很长时,如在房间语音去混响的应用中,或者信道数过多,都会导致上面给出的算法计算量过大,这在实际应用中是必须要考虑的问题。通过分析发现,在整个算法流程中,信道冲激响应矢量h(n)与源信号矢量s(n)之间是完全解耦的,可以分别构成两个标准卡尔曼滤波算法。其一(对应系统辨识):
(16)
其中
其二(对应解卷积):
(17)
其中,
通过解耦,原来的一个标准卡尔曼滤波问题变成两个阶次低的标准卡尔曼滤波问题,仍在同一个迭代周期内同步进行。所谓同步性是指两个卡尔曼滤波问题可以并行实现,无主从之分,这样有利于算法的优化。初步分析可以发现,当状态矢量维数(假设为a=b+c)远大于观测矢量维数时,一个标准卡尔曼滤波的计算量约正比于a3,如果把它拆分成两个状态矢量维数分别为b和c(仍远大于观测矢量维数)的卡尔曼滤波问题,总的计算量正比于(b3+c3),远小于未拆分之前的计算量,这是降维在计算量方面所带来的优势。算法优化问题不是本文的中心内容,在此不进行更深入讨论。
此外,解耦之后,盲辨识过程可以按块更新:即每B个采样周期更新一次,迭代一次。但是解卷积过程仍然按点更新。可以大幅减少计算量。
在仿真、实验阶段,为了定量衡量算法性能,定义信号-估计误差比(Signal-to-Error Ratio: SER):
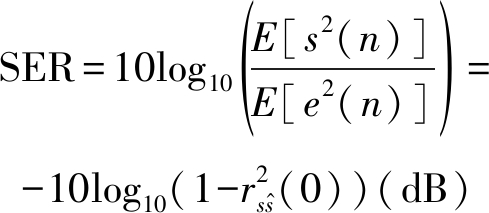
(18)
其中:
为解卷积信号的估计误差序列;
是
间零时延互相关系数(首先时间对齐！)。在仿真阶段,递归估计源信号均方值:E[s2(n)]≈αE[s2(n-1)]+(1-α)s2(n) (α=0.9);E[e2(n)]的估计与前式同。
在比较原系统冲激响应与估计的系统冲激响应之间的关系时,采用通用的归一化投影失调NPM(Normalized projection misalignment)值:
(19)
其中,
是
间互相关系数。
5 算法仿真、实验与讨论
为了验证本算法的可行性和有效性,除了进行大量仿真实验外,还用一段房间内实录语音信号来验证。
在一个相对封闭且安静的会议室(约10 m×6 m×3 m)中用扬声器播放一段语音(该语音已知,这里称之为声源信号,声源信号时长3.98 s,连续重复播放8次),用四个与扬声器距离分别为1 m、2 m、3 m、4 m的传声器进行录音,得到四路实测的混响语音信号(分别对应声道1～4),录音时间长度31.9 s,采样率为8 kHz。
首先,利用已知声源和LMS(Least mean squares)算法估计4路房间冲激响应(长度1300点),并把它作为新算法的标准。LMS算法估计的四路房间冲激响应如图1所示。
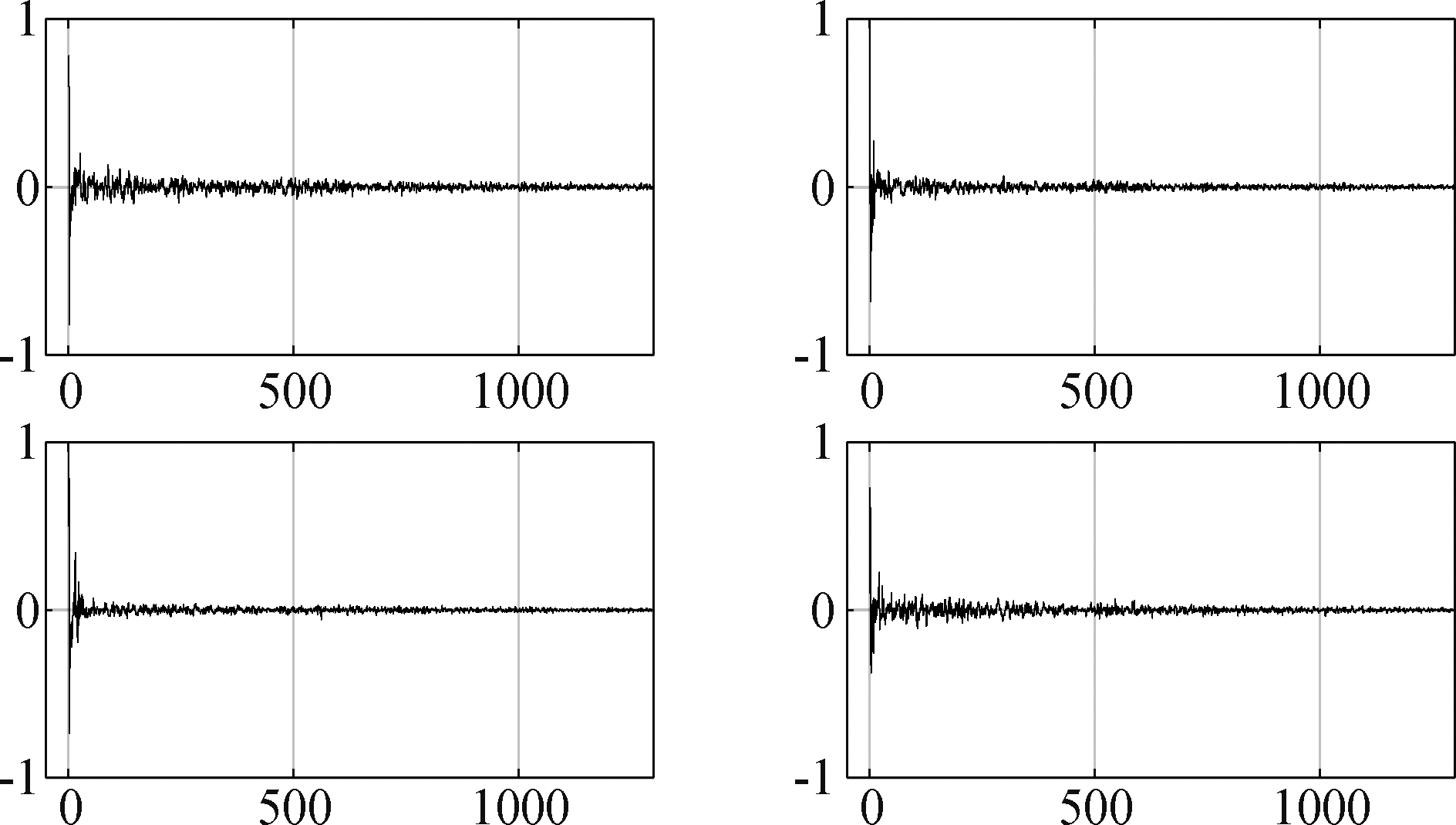
图1 四路实测房间冲激响应(LMS算法:1300点)
Fig.1 The four RIRs measured in a Room (1300 samples)
5.1 仿真实验
为了验证本算法的理论正确性,首先建立一个小规模的理想信号模型:随机产生4路长度为35点的系统冲激响应,它们与已知语音信号卷积而得到四路卷积信号作为理想观测信号,无背景噪声。总采样点数1.5×106。对理想模型信号进行同步盲系统辨识和解卷积,结果如图2所示。图2的上图中给出了算法迭代过程中NPM曲线随采样点数的变化,当采样点数达到106左右(甚至更早,直到1.5×106)时,NPM值开始出现下溢出现象了(这时Matlab给出的NPM=-Inf,即负无穷大,已经不是数值了,所以图中画不出！),说明系统辨识精度极高。在图2的下图中也可以看出,同步解卷积结果的信号-误差比(SER)超过100 dB。说明新算法的理论基础是可靠的。
值得一提的是,无论是表1给出的同步盲辨识与解卷积算法,还是由式(16)、(17)给出的并行盲系统辨识和解卷积算法,在盲辨识和解卷积精度及稳定性方面是完全一致的,没有区别。但两种实现方式的计算量差别极大:解耦之后的并行算法计算量显著降低。此外,当考虑实时SIMO系统解卷积,所有计算必须在一个采样周期内完成,那么传统级联结构的盲系统辨识/解卷积系统就可能胜任不了计算任务,而由式(16)、(17)给出的并行盲系统辨识/解卷积算法则可以通过空间换取时间,从而实现有限时间内完成复杂计算任务。
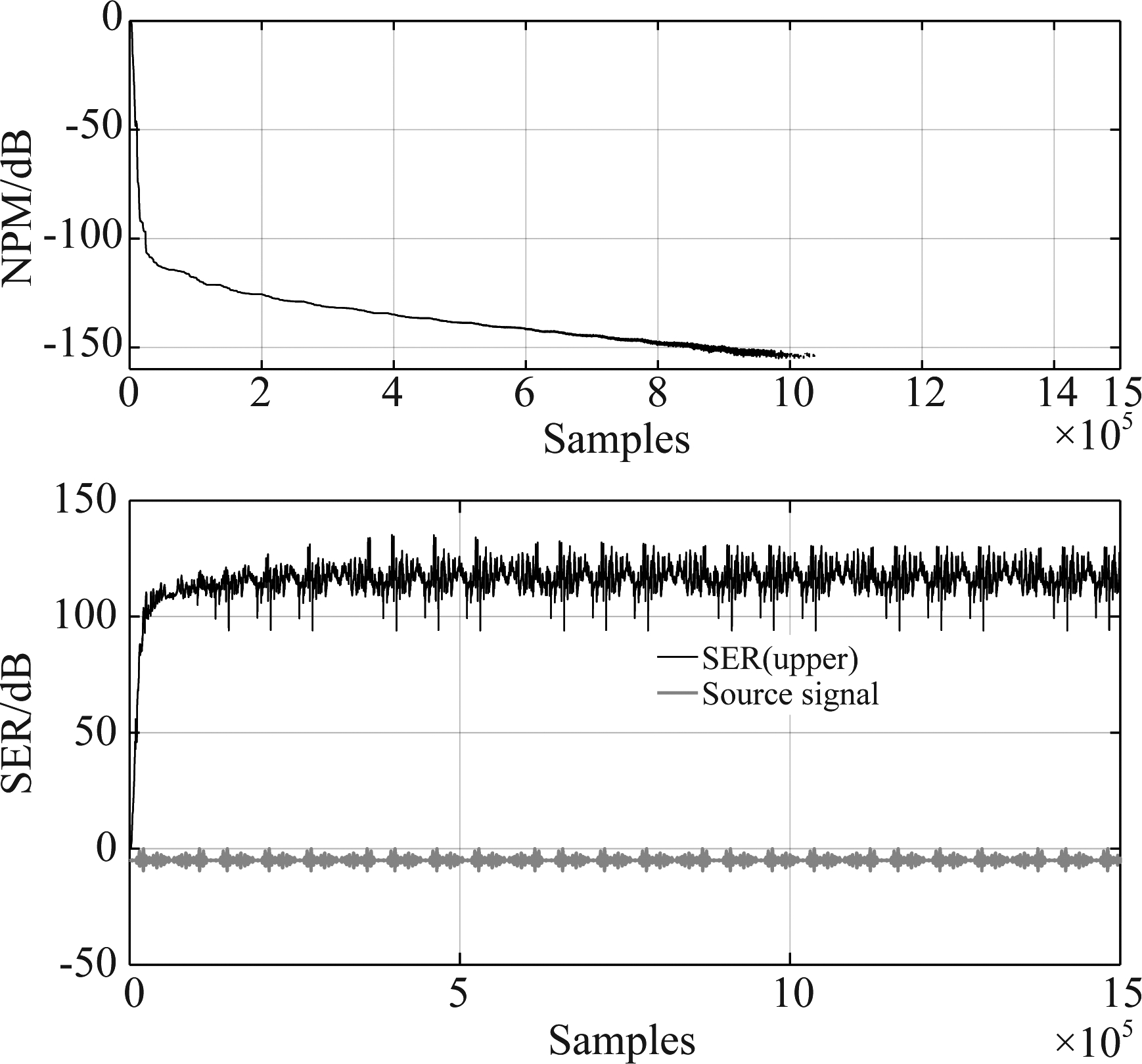
图2 理想卷积信号模型的同步盲系统辨识和解卷积结果(上图:同步盲系统辨识的NPM曲线;下图:同步解卷积结果的SER曲线)
Fig.2 The results of synchronic blind multichannel identification and deconvolution of an ideal convolutive signal model
其次,在仿真实验中,建立一个接近理想模型的低背景噪声、高阶系统(1300阶)的卷积信号模型:即声源信号与图1中的四路房间冲激响应进行卷积,并加入少量白噪声(信噪比(Signal-to-Noise Ratio)SNR=100 dB)来仿真混响信号。利用新算法对这组仿真信号进行同步盲系统辨识和解卷积。盲辨识得到的四路房间冲激响应相对图1中的冲激响应之间(收敛后波形差别及其细微！)的NPM曲线如图3所示;同时盲解卷积得到的解卷积信号与源信号之间(同样,收敛后波形差别及其细微！)的SER曲线如图4(a)所示。为了了解SER的波动情况,在图4(a)中把源信号也展示在同一时间轴上。图4(b)是图4(a)在横轴方向上的局部放大图(为了便于观察,对语音信号波形进行了幅度放大并在垂直方向向上平移,水平方向与SER曲线保持同步！),可以发现,SER的波动情况与源信号的幅度波动(有音/无音)、清音/浊音变化情况是一致的,即在无音段SER会明显下降,对应局部极小值区间(横轴7.15×105附近),这是由于信号能量突然变小所致;而在清音段(接近白噪声)SER会出现局部极大值区间(横轴[7.16,7.18]×105、[7.17,7.19]×105区间附近),这可能是由于宽带信号区段对应的系统冲激响应辨识精度更高造成的,说明解卷积算法对宽带信号效果更好。这也从另一侧面说明算法的稳定性是没有问题的。以上结果说明,本文所给出的基于卡尔曼滤波的同步盲系统辨识与解卷积方法是可行的。
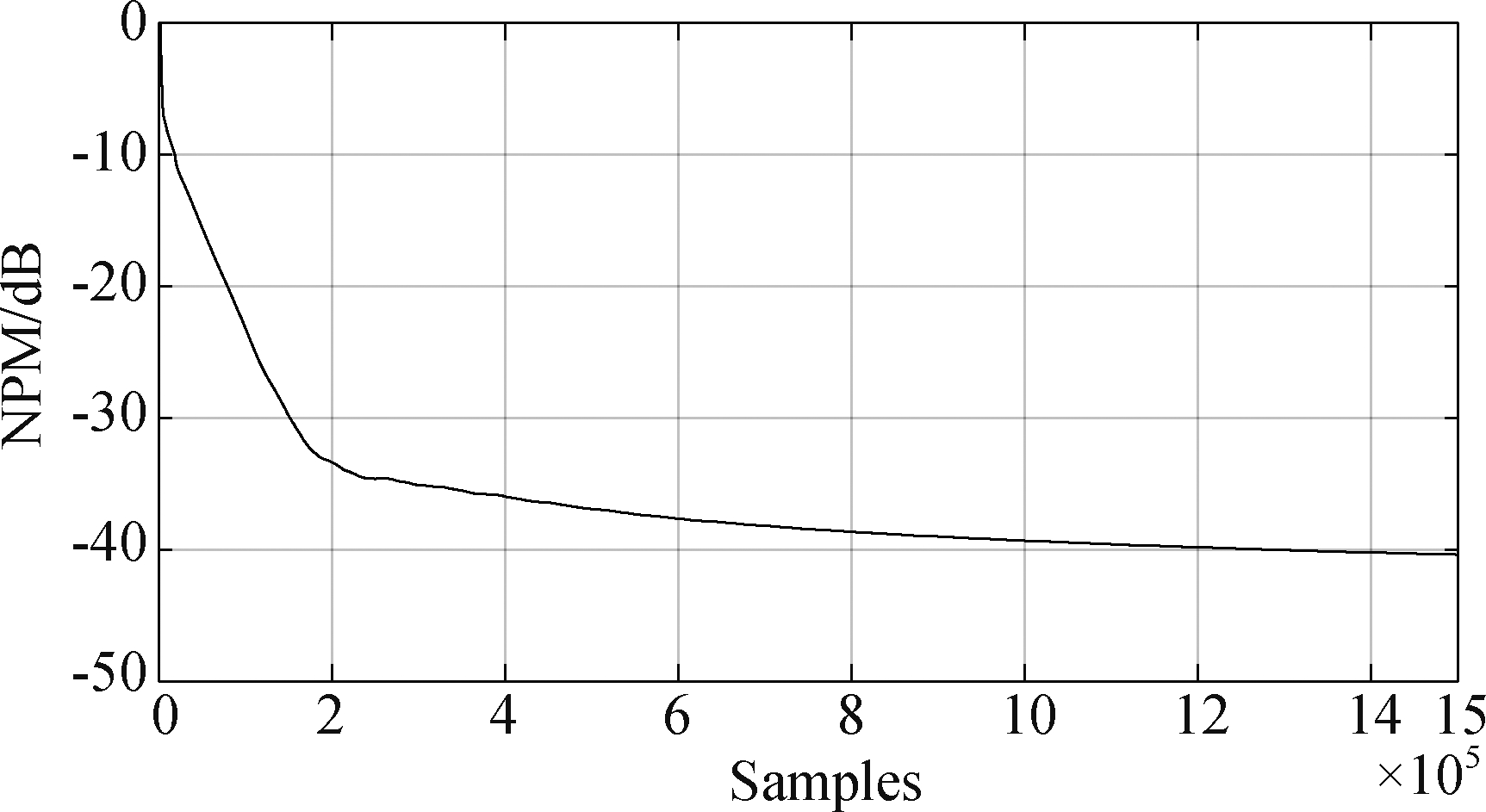
图3 新算法得到的房间冲激响应相对实际房间冲激响应(图1)的动态NPM曲线
Fig.3 The dynamic NPM of the RIRs with the proposed algorithm
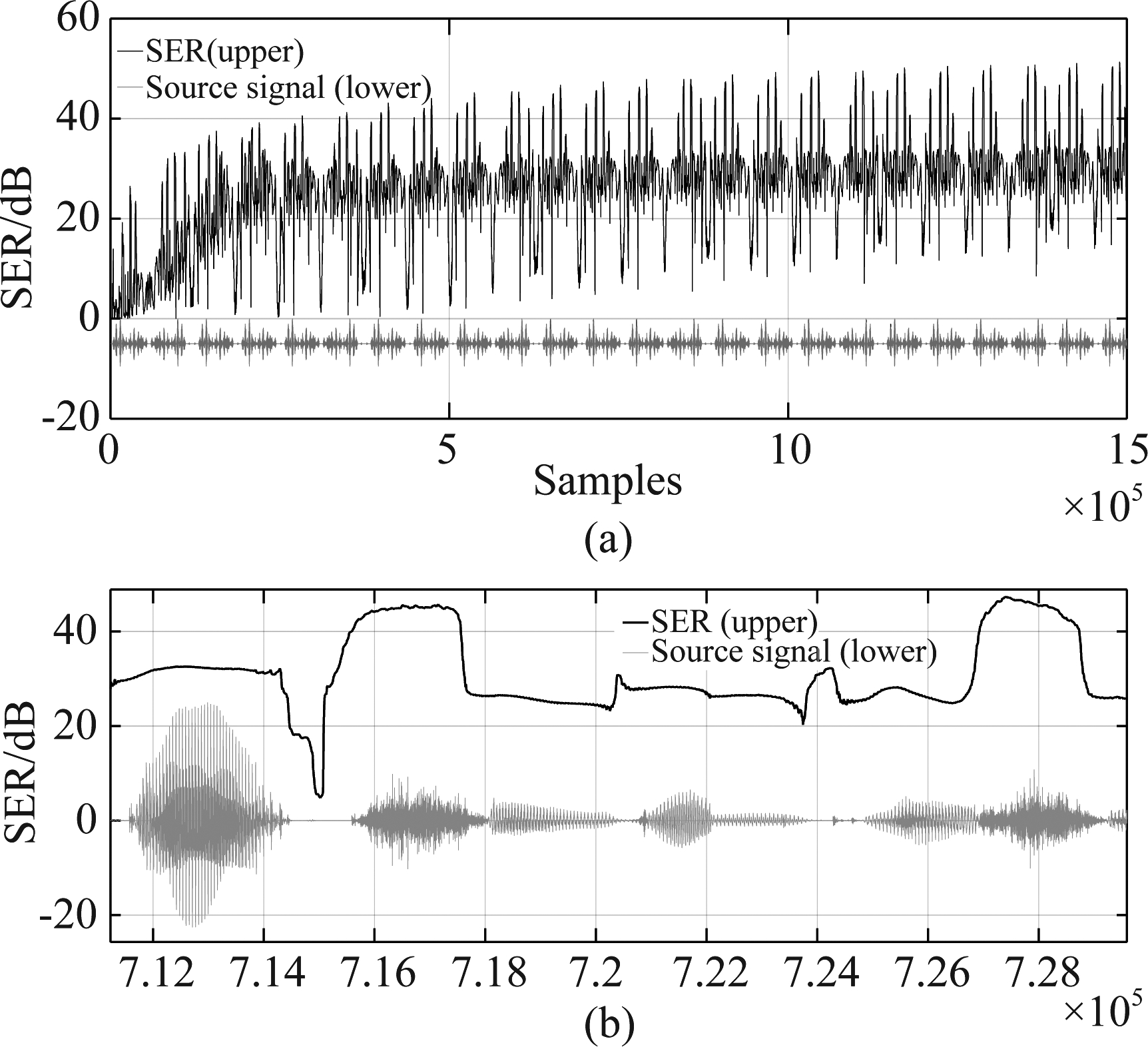
图4 (a)新算法得到的解卷积信号相对源信号的动态SER曲线(上曲线);(b)图(a)的局部放大图
Fig.4 (a) The dynamic SER (upper) of the deconvolved signal with the proposed algorithm; (b) Locally zooming-in picture of (a)
5.2 真实实验
在真实实验中,直接把新算法应用于实测的四路混响信号,同时得到四路房间冲激响应和源信号的盲估计结果。新算法得到的四路房间冲激响应如图5所示,它相对于由LMS算法得到的房间冲激响应的NPM曲线如图6所示。算法收敛后,去混响信号(需经过带通后处理[8])与声源信号之间的互相关系数为0.88,明显高于实测混响信号与声源信号之间的平均相关系数0.74,说明在一定程度上实现了源信号波形恢复。
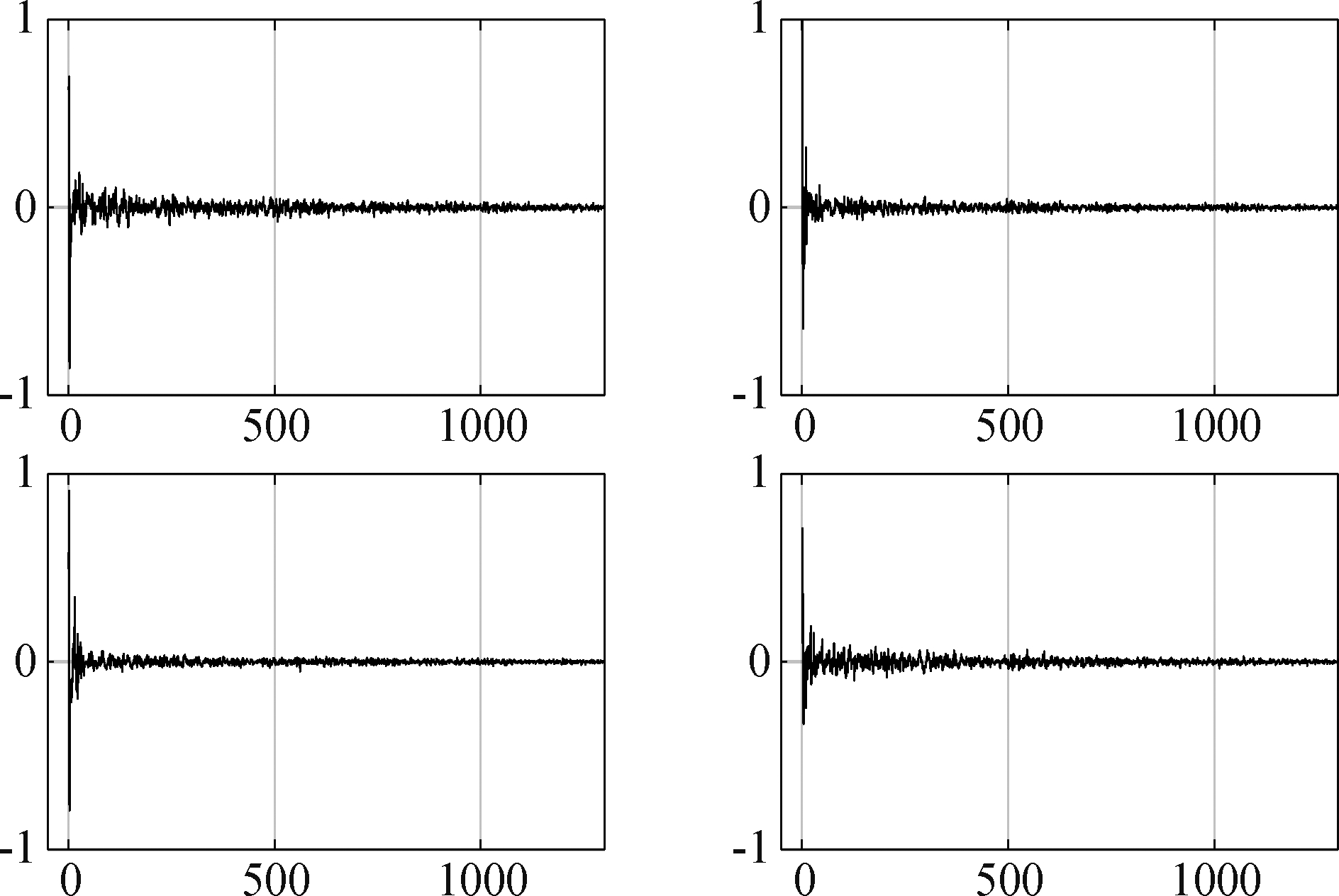
图5 新算法得到的四路房间冲激响应(L=1300点)
Fig.5 The estimated RIRs with the proposed algorithm
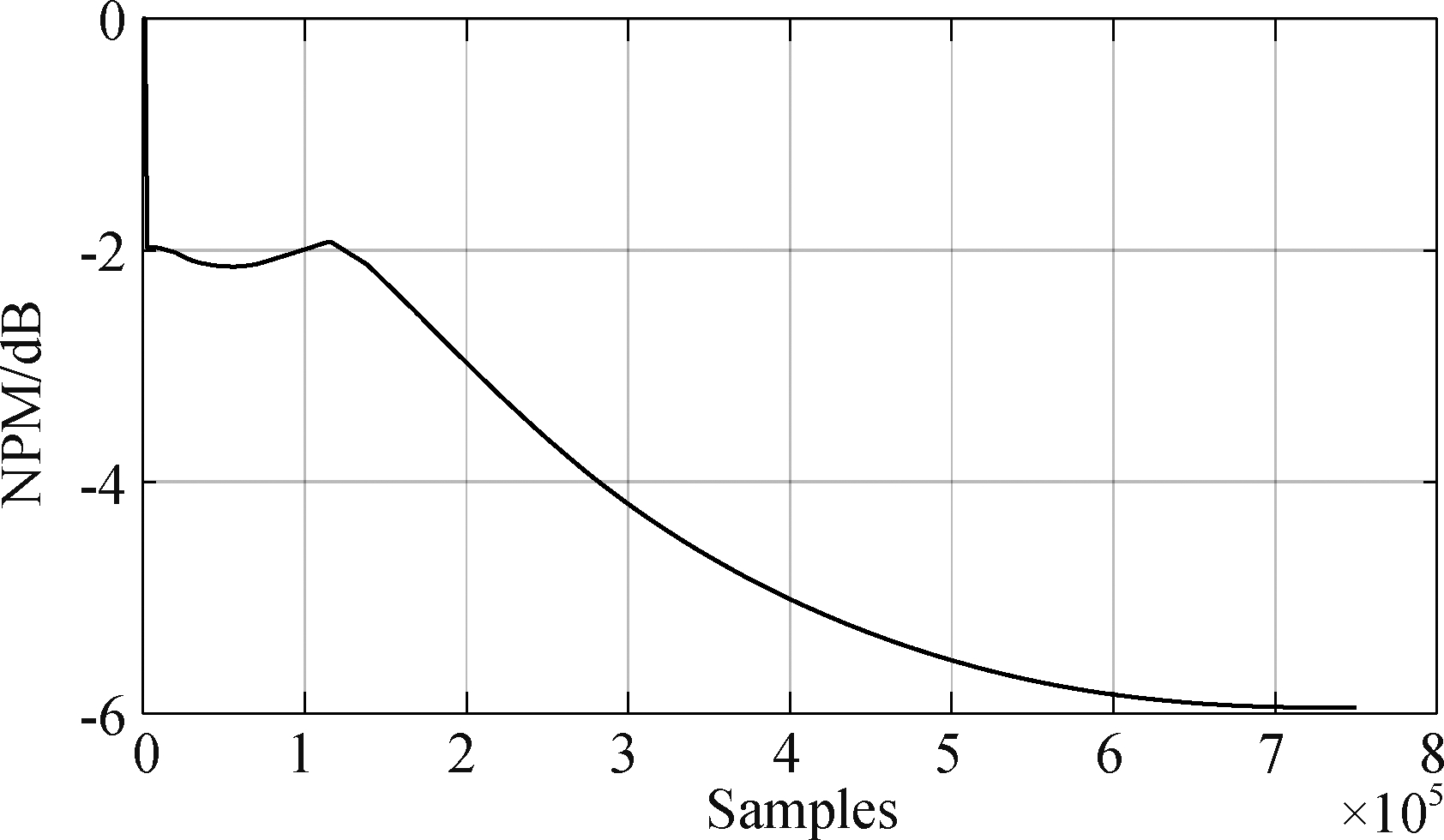
图6 用新算法估计的房间冲激响应(图5)相对于LMS算法估计结果(图1)的NPM曲线
Fig.6 The dynamic NPM of the four RIRs estimated with the proposed algorithm
6 结论
通过理论分析,建立起基于卡尔曼滤波的同步盲多信道系统辨识与解卷积算法,仿真实验验证了它的可行性。此外,盲多信道系统辨识部分与解卷积部分是可以解耦的,产生两个看似独立的卡尔曼滤波问题。同步性在于两个卡尔曼滤波问题的计算过程可以并行实现,无主从之分。与级联结构相比,并联结构一方面有利于算法的总体优化,另一方面更适合实时信号处理。
[1] Schwartz B, Gannot S, Habets E A P. Online speech dereverberation using Kalman filter and EM algorithm[J]. IEEE Transactions on Audio Speech and Language Processing, 2015, 23(2): 394- 406.
[2] Braun S, Habets E A P. Online dereverberation for dynamic scenarios using a Kalman filter with an autoregressive model[J]. IEEE Signal Processing Letters, 2016, 23(12): 1741-1745.
[3] Williamson D S, Wang D. Speech dereverberation and denoising using complex ration masks[C]∥Proceedings of IEEE International Conference on Acoustics, Speech and Signal Processing, 2017: 5590-5594.
[4] 齐园蕾, 杨飞然, 杨军. 基于卡尔曼滤波的低复杂度去混响算法[J]. 应用声学, 2018, 37(4): 560-566.
Qi Y L, Yang F R, Yang J. Kalman filter based low-complexity dereverberation algorithm[J]. Journal of Applied Acoustics, 2018, 37(4): 560-566.(in Chinese)
[5] Braun S, Kuklasinski A, Schwartz O, et al. Evaluation and comparison of late reverberation power spectral density estimators[J]. IEEE Transactions on Audio, Speech, and Language Processing, 2018, 26(6): 1056-1071.
[6] 郭颖, 彭任华, 郑成诗, 等. 偏度最大化多通道逆滤波语声去混响研究[J]. 应用声学, 2019, 38(1): 58- 67.
Guo Y, Peng R H, Zheng C S, et al. Maximum skewness-based multichannel inverse filtering for speech dereverberation[J]. Journal of Applied Acoustics, 2019, 38(1): 58- 67.(in Chinese)
[7] Tong L, Perreau S. Multichannel blind identification: from subspace to maximum likelihood methods[C]∥Proceedings of the IEEE, 1998, 86(10): 1951-1968.
[8] 梅铁民. 基于反幂法和卡尔曼滤波的自适应语音去混响方法[J]. 信号处理, 2018, 34(7): 776-786.
Mei T M. Adaptive speech dereverberation based on inverse power method and Kalman filter[J]. Journal of Signal Processing, 2018, 34(7): 776-786.(in Chinese)
[9] Furuya K, Sakauchi S, Kataoka A. Speech dereverberation by combining MINT-based blind deconvolution and modified sepctral subtraction[C]∥Proceedings of IEEE International Conference on Acoustics, Speech and Signal Processing, 2006, I: 813- 816.
[10] Godard D N. Self-recovering equalization and carrier tracking in two-dimensional data communication systems[J]. IEEE Transaction on Communications, 1980, 28(11): 1867-1875.
[11] Haykin S. Adaptive Filter Theory (Third edition)[M]. Prentice-Hall, 1996.
[12] Tong L, Xu G, Kailath T. Blind identification and equalization based on second-order statistics: a time domain approach[J]. IEEE Transactions on Information Theory, 1994, 40(2): 340-348.
[13] Patel A M, Li J K, Finegan B, et al. Aortic pressure estimation using blind identification approach on single input multiple output nonlinear Wiener systems[J]. IEEE Transactions on Biomedical Engineering, 2018, 65(6): 1193-1200.
[14] Mayyala Q, Abed-Meraim K, Zerguine A. Structure-based subspace method for multichannel blind system identification[J]. IEEE Signal Processing Letters, 2017, 24(8): 1183-1187.
[15] Xu G, Liu H, Tong L, et al. A least-square approach to blind channel identification[J]. IEEE Transactions on Signal Processing, 1995, 43(12): 2982-2992.
[16] Huang Y, Benesty J. Adaptive blind channel identification: Multi-channel and least mean square and Newton algorithms[C]∥Proceedings of IEEE International Conference on Acoustics, Speech and Signal Processing, 2002, II: 1637-1640.
[17] Huang Y, Benesty J. A class of frequency-domain adaptive approaches to blind multichannel identification[J]. IEEE Transactions on Signal Processing, 2003, 51(1): 11-24.
[18] Moulines E, Duhamel P, Cardoso J F, et al. Subspace methods for the blind identification of multichannel FIR filters[J]. IEEE Transactions on Signal Processing, 1995, 43(2): 516-525.
[19] Huang Y, Benesty J. Adaptive multi-channel least mean square and Newton algorithms for blind channel identification[J]. Signal Processing, 2002, 82(8): 1127-1138.
[20] Hasan M K, Benesty J, Naylor P A, et al. Improving robustness of blind adaptive multichannel identification algorithms using constraints[C]∥Proceedings of European Signal Processing, 2005: 1- 4.
[21] Liao L, Khong A W H. A noise robust multichannel algorithm for blind estimation of room impulse responses[C]∥Proceedings of the 12th International Workshop on Acoustic Echo and Noise Control (IWAENC), 2010.
[22] He H, Chen J, Benesty J, et al. Noise robust frequency domain adaptive blind multichannel identification with lp constraint[J]. IEEE Transactions on Audio Speech and Language Processing, 2018, 26(9): 1608-1619.
[23] Mei T. Blind multichannel identification based on Kalman filter and eigenvalue decomposition[J]. International Journal of Speech Technology, 2019, 22(1): 1-11.
