1 引言
单通道语音增强通过降低或抑制混合语音中的噪声成分,实现人声与噪声的分离,提升增强语音的可懂度和整体质量。近年来,单通道语音增强算法的一个研究重点是从输入语音信号中估计出各个声源的幅度谱。目前,在多种噪声条件下的语音增强任务通过基于幅度谱的语音增强算法得到了有效解决[1- 4]。基于幅度谱的语音增强算法现多采用机器学习算法,如稀疏编码[1]、非负矩阵分解(non-negative matrix factorization, NMF)[2-3]和深度神经网络(Deep Neural Network, DNN)[4]等。然而,这些方法在重构目标语音时,直接使用输入混合信号的相位谱,没有利用目标语音的相位谱[2- 4]。这是由于早期在语音处理领域大家存在一种共识,短时相位谱是可以忽略的,因为它包含的信息量可能很小。
但是最近研究发现,相位实际上是会提供重要信息的,这些信息与语音可懂度密切相关,因此应该在信号重构之前估计相位谱[5-7]。在此基础上,研究人员提出了多种基于迭代信号重构[8]、群延迟几何[9]和相位谱补偿(PSC)[10-11]的相位估计方法。
基于深度学习的单通道语音增强方法,如基于波形网络(wavenet-based)[12]和生成对抗网络(generative adversarial network, GAN)[13]的语音增强算法。这两种网络具有端到端的网络结构,采用时域波形样本作为模型的输入和输出,尝试在时域中直接将目标语音与混合语音分开。它们可以隐式地估计目标语音的幅度谱和相位,在处理语音增强任务时的性能优于传统的维纳滤波法[12-13]。然而这些方法包含许多参数,需要大量的计算复杂度和内存来实现,在资源受限的设备中的适用性有限。
传统相位谱补偿(PSC)算法可以代替基于深度学习的时域方法,因为它在一定程度上提高了大部分基于幅度谱的语音增强算法的性能,并且具有较低的计算复杂度[10]。PSC算法只利用噪声的幅度谱,通过控制输入混合信号的共轭对称性来增强目标信号。然而,除非提供理想的噪声幅度谱,否则PSC算法的性能可能会受到限制,这对于低信噪比条件下的大多数语音增强算法都是困难的。换句话讲,由于频谱时间重叠,估计的目标语音和噪声的幅度谱可能会在一定程度上恶化[2- 4]。另外,PSC函数中的补偿因子是一个固定值,无法随带噪语音信噪比的变化进行调整。
为改进传统PSC算法,本文提出一种基于稀疏性的相位谱补偿(SPSC)函数,通过考虑目标语音和噪声的幅度谱,来控制每个局部时频单元的频谱补偿水平。首先,由噪声估计算法[14]得到噪声幅度谱,由基于幅度谱的语音增强算法,如SNMF[15]和DNN[16],得到目标语音幅度谱;接着,估计当前时频单元的谱时间稀疏性[17-18],确定目标语音和噪声幅度谱估计值之间的重叠部分;然后,利用sigmoid函数改进PSC算法中的相位补偿因子,使其随着带噪语音信噪比的变化进行实时调整;最后,构造补偿相位谱的SPSC函数,利用SPSC函数和目标语音幅度谱估计值重构语音信号。
2 传统相位谱补偿(PSC)语音增强算法
假设x(t)表示纯净语音,d(t)表示加性噪声,且x(t)与d(t)相互独立,则带噪语音y(t)的时域表达式为:
y(t)=x(t)+d(t)
(1)
对y(t)做短时傅里叶变换, 其频域可表示为:
(2)
其中,k为频率索引,n为帧索引,N为离散傅里叶变换(discrete Fourier transform, DFT)帧大小,ω(n)为窗函数。带噪语音复频谱Yn(k)的极坐标形式为:
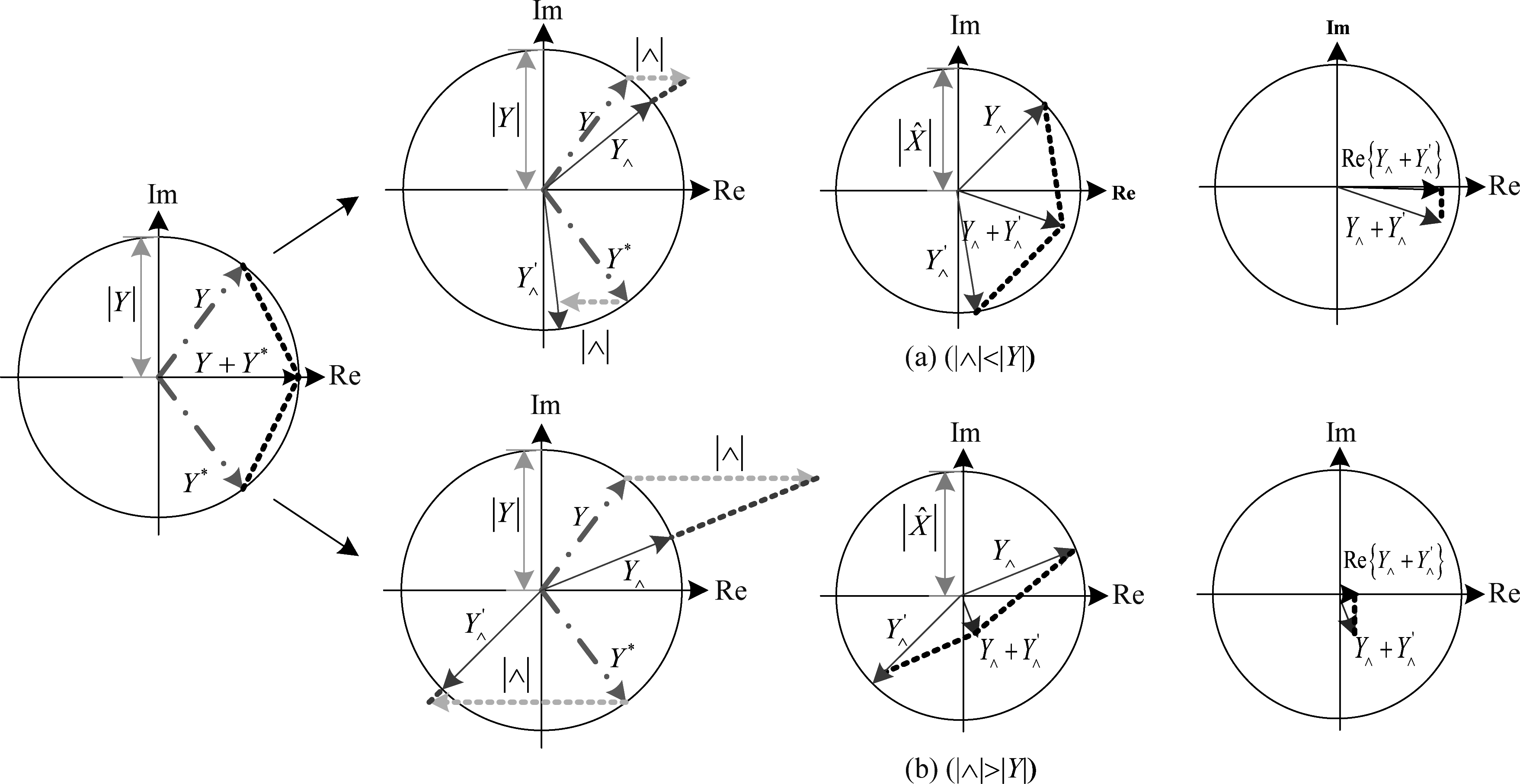
图1 相位谱补偿语音增强算法矢量原理图
Fig.1 The vector schematic diagram of phase spectrum compensation speech enhancement algorithm
Yn(k)=|Yn(k)|exp(j∠Yn(k))
(3)
其中,|Yn(k)|和∠Yn(k)分别为时间帧为n、频率为k的时频单元内,带噪语音的幅度谱和相位谱。由于带噪语音信号是实信号,所以其短时傅里叶变换满足共轭对称,最终重构得到的时域信号需要依赖两个共轭向量的和向量。传统的PSC函数定义为:
(4)
其中,λ是用于控制相位补偿强度的补偿因子,![]() 是估算出的第n帧第k个频率点的噪声幅度谱,ψ(k)是一个时不变反对称函数,定义为:
是估算出的第n帧第k个频率点的噪声幅度谱,ψ(k)是一个时不变反对称函数,定义为:

(5)
在信号重构阶段,利用PSC函数![]() n(k)改变Yn(k)的相位,结合补偿后的相位谱与语音增强算法估计的纯净语音幅度谱
n(k)改变Yn(k)的相位,结合补偿后的相位谱与语音增强算法估计的纯净语音幅度谱![]() 增强语音的频谱可表示为:
增强语音的频谱可表示为:
X![]()
![]()
![]() n(k)))
n(k)))
(6)
图1为两种不同信噪比场景下,传统PSC算法的矢量原理图。
图1(a)对应高信噪比场景,此时噪声幅度谱![]() 远小于纯净语音幅度谱
远小于纯净语音幅度谱![]() 那么PSC函数的绝对值应小于带噪语音幅度谱,即|
那么PSC函数的绝对值应小于带噪语音幅度谱,即|![]() n(k)|<|Yn(k)|。图1(b)对应低信噪比场景,此时|
n(k)|<|Yn(k)|。图1(b)对应低信噪比场景,此时|![]() n(k)|>|Yn(k)|。
n(k)|>|Yn(k)|。
从图1可以看出,不同的![]() n(k)作用于相同的信号段时,产生的补偿程度不同。观察图1(a)可以发现,当信噪比较高时,
n(k)作用于相同的信号段时,产生的补偿程度不同。观察图1(a)可以发现,当信噪比较高时,![]() n(k)不会对信号产生明显的衰减;只有|
n(k)不会对信号产生明显的衰减;只有|![]() n(k)|大于带噪语音幅度谱|Yn(k)|,信号才会有明显的改变。
n(k)|大于带噪语音幅度谱|Yn(k)|,信号才会有明显的改变。
![]() n(k)取值的关键在于相位补偿因子λ的值,λ取值过大,对信号的压缩程度会变大,可能造成信号失真严重;λ取值过小,对噪声的压缩程度较小,噪声抑制效果差。传统的PSC算法采用固定的λ值,实验证明,虽然λ值保持不变能取得较好的去噪效果,但在信噪比较小的信号段,如非语音段,噪声抑制效果比较差,仍有噪声残留。对纯净语音信号加5 dB的NOISEX-92数据集[19]中的White噪声,图2分别为纯净语音、带噪语音和采用传统的PSC算法进行语音增强的时域波形图。从图2(c)可以看出,带噪语音中的噪声得到了一定程度的抑制,但是增强语音的非语音段仍残留部分噪声,会影响语音的听感。
n(k)取值的关键在于相位补偿因子λ的值,λ取值过大,对信号的压缩程度会变大,可能造成信号失真严重;λ取值过小,对噪声的压缩程度较小,噪声抑制效果差。传统的PSC算法采用固定的λ值,实验证明,虽然λ值保持不变能取得较好的去噪效果,但在信噪比较小的信号段,如非语音段,噪声抑制效果比较差,仍有噪声残留。对纯净语音信号加5 dB的NOISEX-92数据集[19]中的White噪声,图2分别为纯净语音、带噪语音和采用传统的PSC算法进行语音增强的时域波形图。从图2(c)可以看出,带噪语音中的噪声得到了一定程度的抑制,但是增强语音的非语音段仍残留部分噪声,会影响语音的听感。
另外,由式(4)可以看出,![]() n(k)的取值还依赖噪声幅度谱
n(k)的取值还依赖噪声幅度谱![]() 的准确性。然而,除非提供理想的噪声幅度谱,否则PSC算法的性能可能会降低。
的准确性。然而,除非提供理想的噪声幅度谱,否则PSC算法的性能可能会降低。
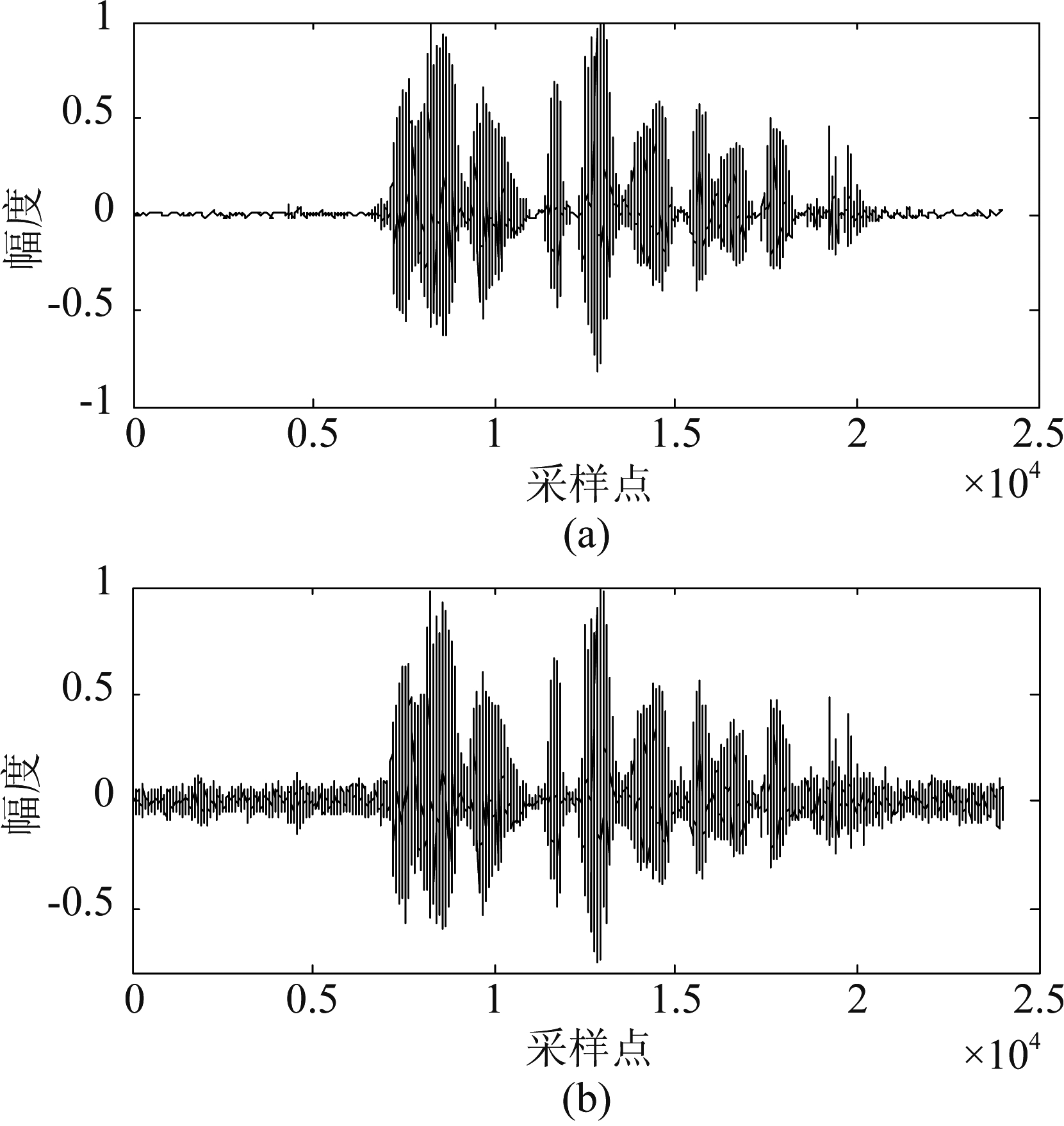
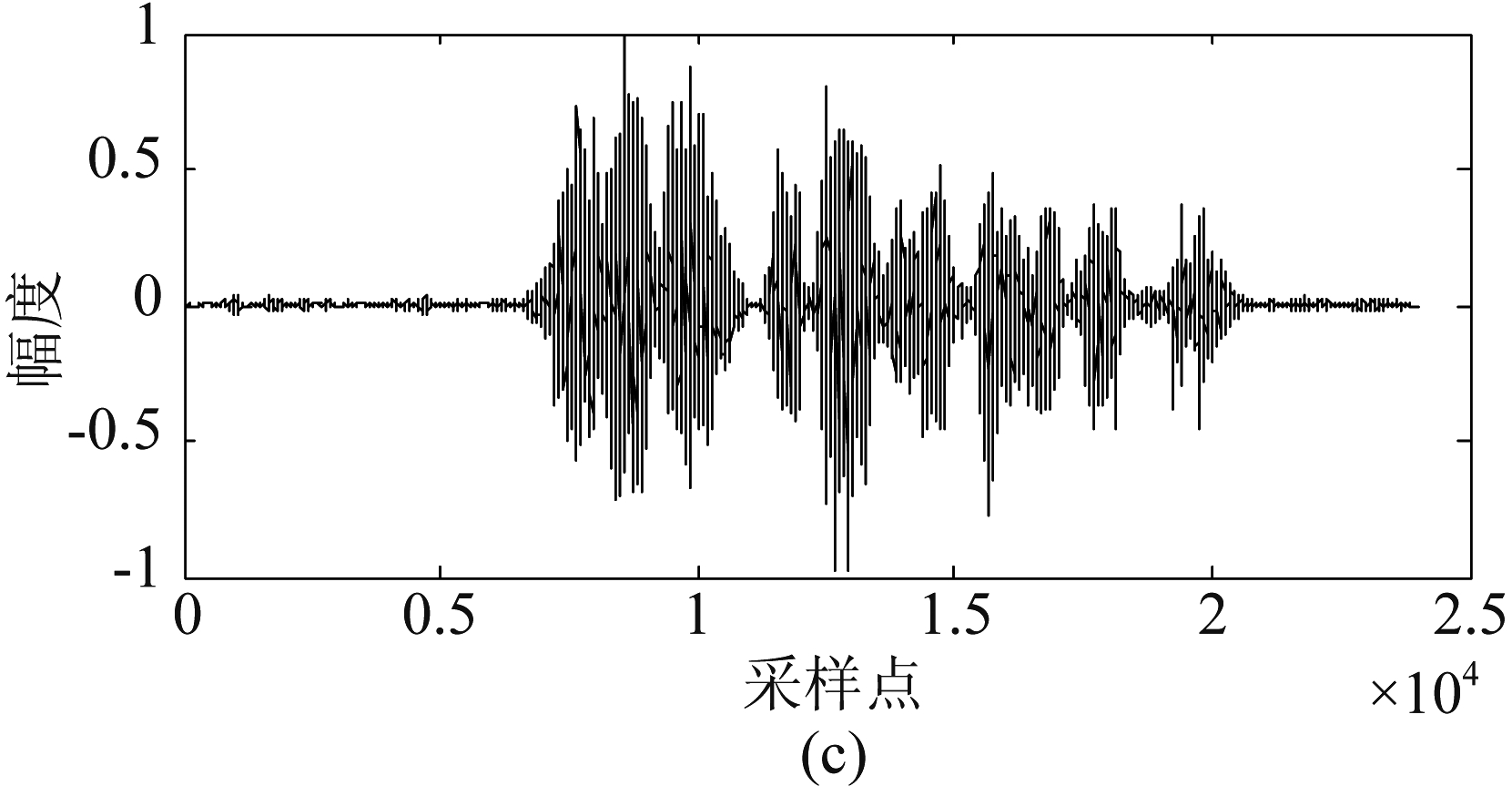
图2 纯净语音、带噪语音和采用传统的PSC语音增强算法增强后的语音波形图
Fig.2 Waveforms of clean speech, noisy speech and enhanced speech with the traditional PSC speech enhancement algorithm
3 基于稀疏性的相位谱补偿语音增强算法
为解决传统的PSC函数存在的两个问题,本文通过估计谱时间稀疏性和改进相位补偿因子得到一种新的PSC函数,称为基于稀疏性的相位谱补偿(SPSC)函数。稀疏性估计已经在一些盲源分离算法中得到了应用,如退化分解估计技术(degenerate unmixing estimations technique, DUET)[20]和稀疏分量分析(sparse component analysis, SCA)[21]等算法。但是,如果稀疏性很低,例如在混合信号中一个声源与另一个声源重叠,则不适合DUET算法中使用的W-不相交正交性和SCA算法中使用的L1范数来估计稀疏性。
本文利用语音和噪声的幅度谱来估计谱时间稀疏性,图3给出了本文提出的SPSC语音增强算法结构图。如图所示,首先,分别利用噪声估计算法[14]和基于幅度谱的语音增强算法得到噪声幅度谱![]() 和增强语音幅度谱
和增强语音幅度谱![]() 接着,使用两者的幅度谱估计局部信噪比(SNR)rn(k)及谱时间稀疏性qn(k);然后,利用sigmoid函数改进相位补偿因子,联合新的补偿因子λnew和谱时间稀疏性,在每个时频单元计算SPSC函数
接着,使用两者的幅度谱估计局部信噪比(SNR)rn(k)及谱时间稀疏性qn(k);然后,利用sigmoid函数改进相位补偿因子,联合新的补偿因子λnew和谱时间稀疏性,在每个时频单元计算SPSC函数![]() 最后,对相位谱中的谱分量进行补偿,利用短时傅里叶逆变换得到最终增强后的时域信号。
最后,对相位谱中的谱分量进行补偿,利用短时傅里叶逆变换得到最终增强后的时域信号。
3.1 谱时间稀疏性估计
对于第n帧第k个频率的局部SNR,rn(k)被定义为:
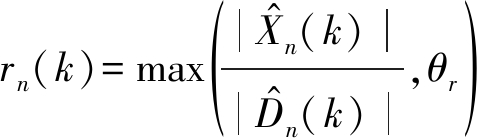
(7)
其中,max(x,y)表示取x和y之间的较大值。当目标语音幅度谱小于噪声幅度谱时,为避免以噪声为主的频带参与稀疏性计算,利用θr来限制局部SNR的大小,最终只有目标语音的主要谱成分参与谱时间稀疏性的计算[17-18]。

图3 改进相位谱补偿算法结构图
Fig.3 The structure diagram of improved phase spectrum compensation algorithm
局部SNR确定后,按照Hoyer的稀疏性估计方法[22]来估计谱时间稀疏性,因为该方法提供了对稀疏性的聚合值,而不考虑用于估计稀疏性的数据的顺序。通过计算第n帧第k个频率点及之前的Iq帧Kq个相邻频带的局部SNR,当前时频点的谱时间稀疏性可表示为:
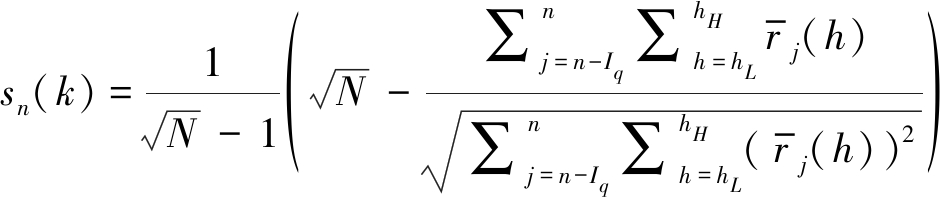
(8)
其中,⎣x」表示小于或等于x的最大整数,![]() 如果以第n帧和第k个频率点为中心的局部SNR稀疏分布,sn(k)趋于1;当局部SNR密集分布时,sn(k)趋于0。即sn(k)的值随着
如果以第n帧和第k个频率点为中心的局部SNR稀疏分布,sn(k)趋于1;当局部SNR密集分布时,sn(k)趋于0。即sn(k)的值随着![]() 和
和![]() 的进一步分离而增大,语音和噪声之间的相互干扰减小。
的进一步分离而增大,语音和噪声之间的相互干扰减小。
接着,通过一个sigmoid函数使sn(k)获得掩蔽形式,表示为:
(9)
其中,qn(k)∈[0,1],γ用于控制稀疏性。
3.2 基于稀疏性的相位谱补偿
根据qn(k)确定噪声与语音重叠部分的幅度谱,即:
(10)
其中,rect[x]表示如果x<0,则返回0的半整流器。根据0≤qn(k)≤1,In(k)从![]() 到0变化,可用于控制相位补偿的程度。
到0变化,可用于控制相位补偿的程度。
另外,传统PSC算法中,用于控制相位补偿强度的比例因子λ是一个固定经验值,无法随噪声强度的变化进行调整。现将λ设为一个随带噪语音信噪比的变化而变化的sigmoid函数,表达式为:
(11)
其中,κ为固定经验值[11]。
联合式(5)、(10)和(11),SPSC函数的定义如下:

(12)
基于幅度谱的语音增强算法的性能与目标语音和噪声的重叠程度有关,在式(12)中添加语音幅度谱与噪声幅度谱的重叠部分In(k),可以有效提升噪声估计的准确性,进而更好地控制相位补偿程度。
为评估本文结合稀疏性的噪声估计算法,将其与文献[11]进行比较。文献[11]利用DD算法计算先验信噪比,对文献[14]中的噪声估计算法的先验信噪比(固定值)进行了改进。但是DD算法依赖前一帧的先验信噪比,可能造成单帧时延,影响信号质量。对纯净语音信号加0 dB的NOISEX-92数据集中的Factory噪声,下图分别为采用文献[11]和本文算法得到的噪声功率谱估计值曲线,如图4所示。
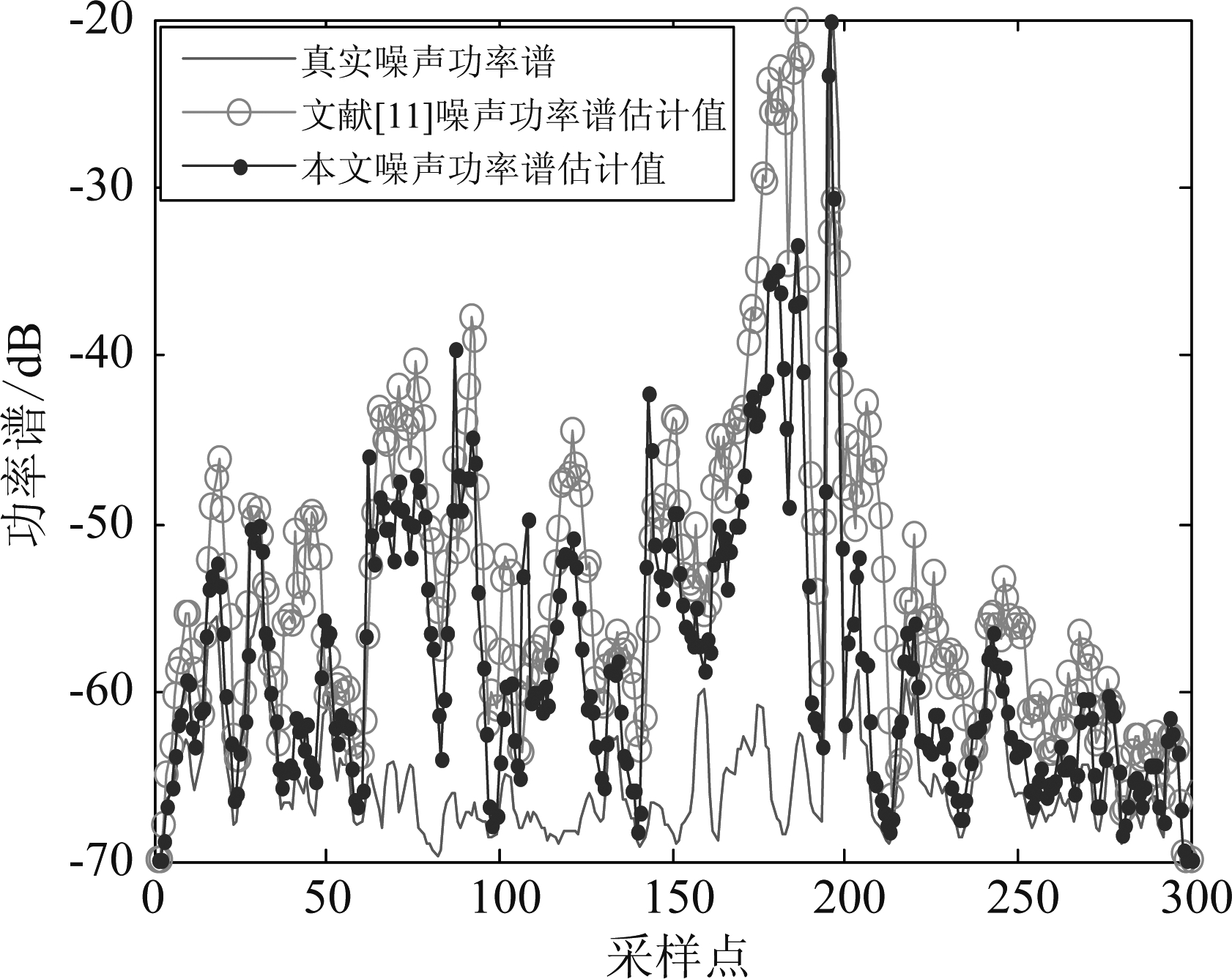
图4 噪声功率谱真实值与估计值比较
Fig.4 Comparison of real and estimated values of noise power spectrum
由图4可知,相比文献[11],本文噪声功率谱估计值更接近真实噪声。即结合稀疏性的噪声估计算法要优于改进先验信噪比,估计的噪声更准确。
最后,将本文提出的SPSC函数与纯净语音幅度谱![]() 相结合,得到增强语音时域表达式:
相结合,得到增强语音时域表达式:
(13)
4 实验仿真与结果分析
4.1 数据集及参数设置
为了进行性能评估,提取TIMIT数据库[23]中的20段不同说话人的语音作为实验数据,其中男女声语音各一半。将所有语音信号下采样8 kHz,16 bit采样。噪声样本选取NOISEX-92数据集[19]中的四种噪声:Babble噪声、F16噪声、Pink噪声和Factory噪声。将20条纯净语音同4种噪声按4种不同信噪比进行混合,信噪比以5 dB为间隔从-5到10选取。最终得到320条带噪语音作为测试样本。窗函数为窗长32 ms、帧移16 ms的汉宁窗。
基于SNMF的语音增强算法,选取200段男声、200段女声,共400条语音进行训练。通过训练得到模型的语音字典和噪声字典。基向量个数设为100。
基于DNN的语音增强算法,语音数据来自TIMIT数据库中的1600条语音,其中1500条用于训练,100条用于验证,所有数据中男女声语音各占一半。输入层设置128个神经元,以带噪语音能量谱作为DNN模型的输入特征,由于语音信号具有时间相关性,将连续的5帧信号(前两帧、当前帧、后两帧)合并作为输入特征,维度为5f×t(5×128×300),即640×300。隐层层数设为3,每层设置1024个神经元,输出层设置128个神经元。隐层采用修正线性单元(Rectified Linear Units, ReLU)函数,输出层激活函数为sigmoid函数。优化器采用Adam(Adam Optimization Algorithm),学习率设为0.001。
参数设置:式(4)中λ=3.14,式(7)中θr=0.25,式(8)中Iq=6,Kq=8,式(9)中γ=0.3,式(11)中κ值参考文献[11],取κ=3.5。
4.2 对比算法及评价指标
本文使用文献[14]算法对时域的噪声信号进行估计。在做对比实验时,选取两种基线算法:基于稀疏非负矩阵分解(SNMF)的语音增强算法和联合DNN和凸优化的语音增强算法(简记为“DNN”)。将式(4)中定义的传统相位谱补偿(PSC)函数及式(12)本文提出的基于稀疏度的相位谱补偿(SPSC)函数分别应用于这两种基线算法,得到六种语音增强算法:SNMF、SNMF+PSC、SNMF+SPSC(本文算法)、DNN、DNN+PSC和DNN+SPSC(本文算法)。
选取了3种评价指标,客观语音质量(Perceptual Evaluation of Speech Quality, PESQ)[24]用于衡量增强语音的听感;分段信噪比(segmental Signal to Noise Ratio, segSNR)用于评价算法对噪声的抑制效果;对数谱距离(Log Spectral Distance, LSD)是用来测量纯净语音和增强语音的对数谱距离的评价指标,数值越小说明两者之间的对数距离越小,增强语音的质量越好,越接近纯净语音。其他两个评价指标数值越大表明算法增强效果越好。
4.3 结果分析
表1、表2、表3和表4分别为各算法在Babble噪声、Pink噪声、F16噪声和Factory噪声的4种信噪比下的平均LSD、PESQ和segSNR值。表中最佳结果均用黑体标出。
表1 各算法在Babble噪声下得到的LSD、PESQ和segSNR结果
Tab.1 Results of LSD, PESQ and segSNR obtained by each algorithm under Babble noise

评价指标SNR/dBLSD-50510PESQ-50510SegSNR-50510SNMF2.962.732.562.340.730.771.071.28-6.16-5.34-4.16-3.41SNMF+PSC2.882.662.512.300.770.761.161.36-6.14-5.21-4.01-3.82SNMF+SPSC2.782.322.212.010.820.851.241.54-5.58-4.74-3.92-3.25DNN2.762.632.522.221.311.411.661.78-1.95-2.28-0.92-0.04DNN+PSC2.532.602.442.181.361.441.701.83-1.94-2.20-0.750.07DNN+SPSC2.222.252.041.821.381.461.761.89-0.81-1.561.252.50
由表中数据可以看出,本文算法(“SNMF+SPSC”和“DNN+SPSC”)在不同信噪比下的三项指标都要优于传统PSC算法及基线算法。信噪比为0 dB时,LSD值提升了约0.3~0.8 dB,PESQ得分提升了约0.1~0.4,segSNR值提升了0.6~1.4 dB左右。说明本文算法可以有效恢复带噪语音中的语音成分,对噪声抑制效果明显,增强语音的质量有一定提升。除在信噪比为-5和0 dB的Pink噪声及信噪比为-5 dB的Factory噪声条件下,本文算法(“DNN+SPSC”和“SNMF+SPSC”)的PESQ值略低或等于相应的传统PSC算法,即“DNN+PSC”和“SNMF+PSC”算法。说明本文算法在低信噪比下的听感还有待改进。在信噪比为10 dB的Factory噪声条件下,本文算法(“SNMF+SPSC”)的segSNR值略低于相应的传统PSC算法(“SNMF+PSC”)。
表2 各算法在Pink噪声下得到的LSD、PESQ和segSNR结果
Tab.2 Results of LSD, PESQ and segSNR obtained by each algorithm under Pink noise
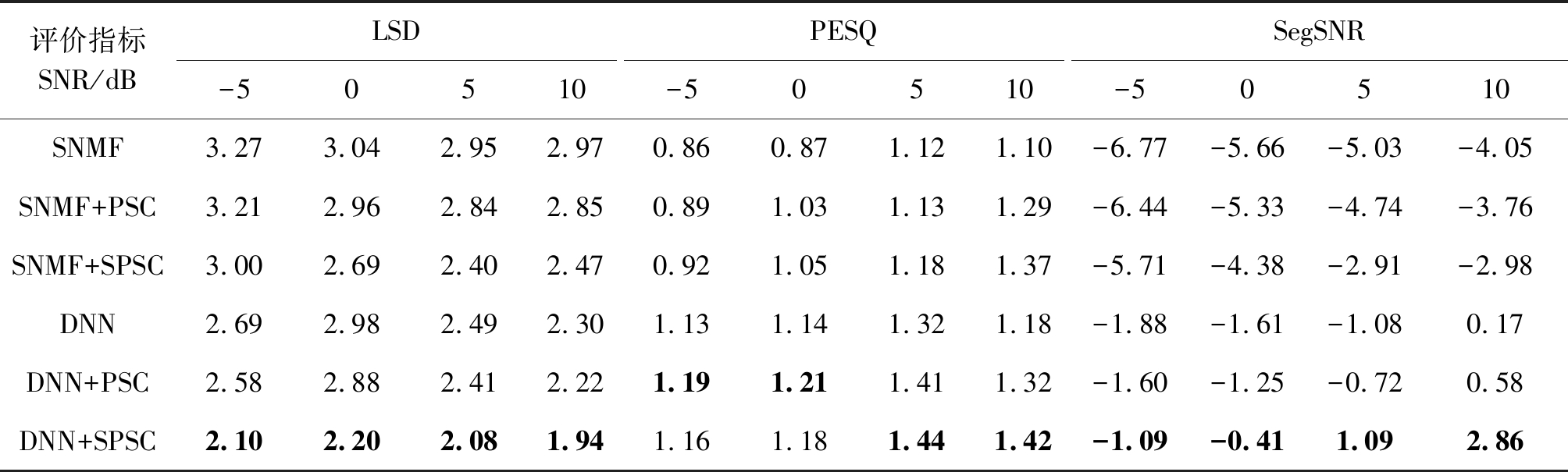
评价指标SNR/dBLSD-50510PESQ-50510SegSNR-50510SNMF3.273.042.952.970.860.871.121.10-6.77-5.66-5.03-4.05SNMF+PSC3.212.962.842.850.891.031.131.29-6.44-5.33-4.74-3.76SNMF+SPSC3.002.692.402.470.921.051.181.37-5.71-4.38-2.91-2.98DNN2.692.982.492.301.131.141.321.18-1.88-1.61-1.080.17DNN+PSC2.582.882.412.221.191.211.411.32-1.60-1.25-0.720.58DNN+SPSC2.102.202.081.941.161.181.441.42-1.09-0.411.092.86
表3 各算法在F16噪声下得到的LSD、PESQ和segSNR结果
Tab.3 Results of LSD, PESQ and segSNR obtained by each algorithm under F16 noise
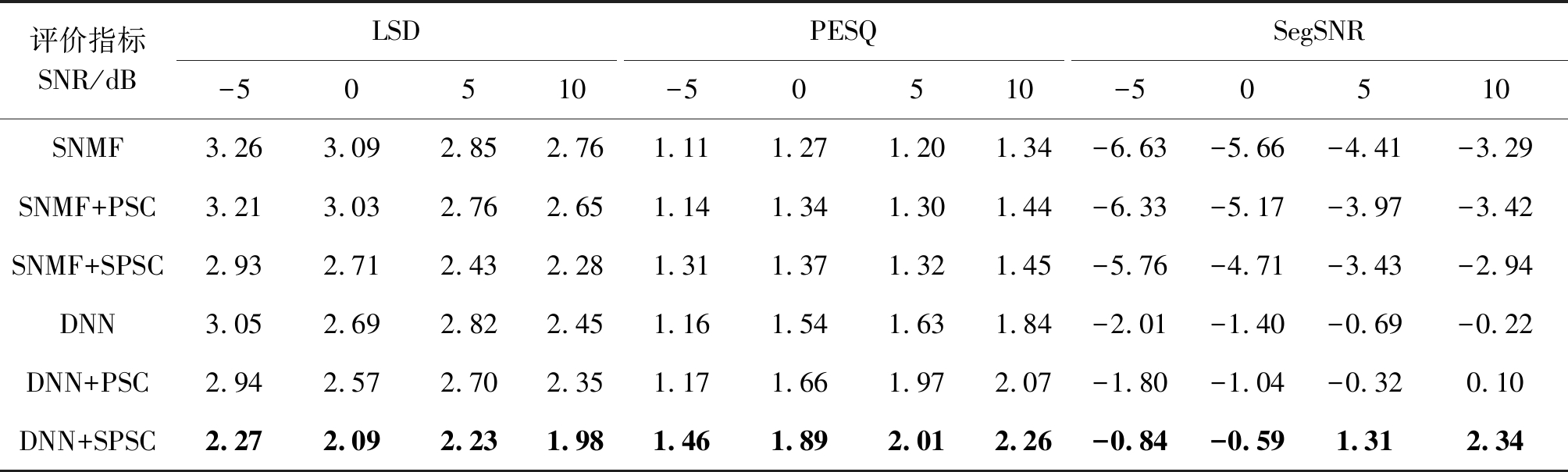
评价指标SNR/dBLSD-50510PESQ-50510SegSNR-50510SNMF3.263.092.852.761.111.271.201.34-6.63-5.66-4.41-3.29SNMF+PSC3.213.032.762.651.141.341.301.44-6.33-5.17-3.97-3.42SNMF+SPSC2.932.712.432.281.311.371.321.45-5.76-4.71-3.43-2.94DNN3.052.692.822.451.161.541.631.84-2.01-1.40-0.69-0.22DNN+PSC2.942.572.702.351.171.661.972.07-1.80-1.04-0.320.10DNN+SPSC2.272.092.231.981.461.892.012.26-0.84-0.591.312.34
表4 各算法在Factory噪声下得到的LSD、PESQ和segSNR结果
Tab.4 Results of LSD, PESQ and segSNR obtained by each algorithm under Factory noise
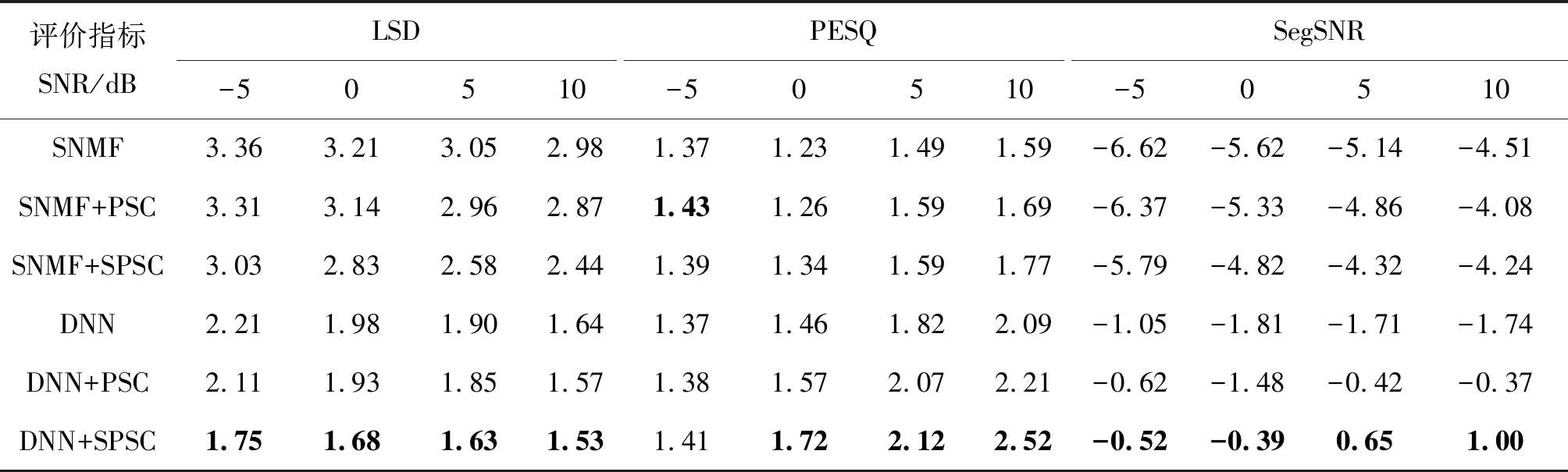
评价指标SNR/dBLSD-50510PESQ-50510SegSNR-50510SNMF3.363.213.052.981.371.231.491.59-6.62-5.62-5.14-4.51SNMF+PSC3.313.142.962.871.431.261.591.69-6.37-5.33-4.86-4.08SNMF+SPSC3.032.832.582.441.391.341.591.77-5.79-4.82-4.32-4.24DNN2.211.981.901.641.371.461.822.09-1.05-1.81-1.71-1.74DNN+PSC2.111.931.851.571.381.572.072.21-0.62-1.48-0.42-0.37DNN+SPSC1.751.681.631.531.411.722.122.52-0.52-0.390.651.00
另外,从整体上来看,基于DNN的语音增强算法的各项指标要优于基于SNMF的语音增强算法,其中segSNR提升明显。在F16和Factory噪声下,基于SNMF的语音增强算法的PESQ得分要比该算法在Babble噪声和Pink噪声下高。分析原因,可能是F16噪声和Factory噪声这种非平稳噪声的结构特征比较鲜明,易于用噪声字典来表示,所以基于SNMF的语音增强算法对这类结构化噪声的建模能力较好,语音的听感得到了一定的提升。
对纯净语音信号加0 dB的NOISEX-92数据集中的Babble噪声,下图分别为“NMF”、“NMF+PSC”、“NMF+SPSC”、“DNN”、“DNN+PSC”和“DNN+SPSC”进行语音增强的频谱图,如图5所示。
从图5可以看出,与图5(a)纯净语音及图5(b)带噪语音的频谱图相比,图5(c)~(e)由“NMF”、“NMF+PSC”和“NMF+SPSC”算法得到的频谱图语音恢复程度比较差。这三种算法的语音段和非语音段均有大量的噪声残留,噪声抑制效果较差,只有低频段(语音能量主要集中区域)能恢复部分语音。观察频谱图的高频段可发现,图5(e)的语音恢复程度要稍好于图5(c)和图5(d),即本文提出的SPSC函数可有效提升增强语音的性能。
相比较,图5(f)~(h)由“DNN”、“DNN+PSC”和“DNN+SPSC”算法得到的增强语音频谱图明显要好于图5(d)~(e),即相较基于NMF的语音增强算法,基于DNN的语音增强算法不仅能有效恢复低频段增强语音,还能恢复高频段的部分语音,增强语音的质量得到了提高。两种基线算法的性能相差较大,基于NMF的算法的频谱图缺失严重,说明传统的PSC算法和本文的SPSC算法的性能还需依赖基线语音增强算法。
另外,相较图5(f)和图5(g),图5(h)的频谱图低频段语音能量成分比较清晰,并且非语音段噪声去除明显。不过受限于目前语音声学特征的提取方法和语音主要集中于低频部分,其高频段语音恢复度不是很高。但从整体上来看,图5(h)的频谱图恢复程度要高于图5(f)和图5(g)。
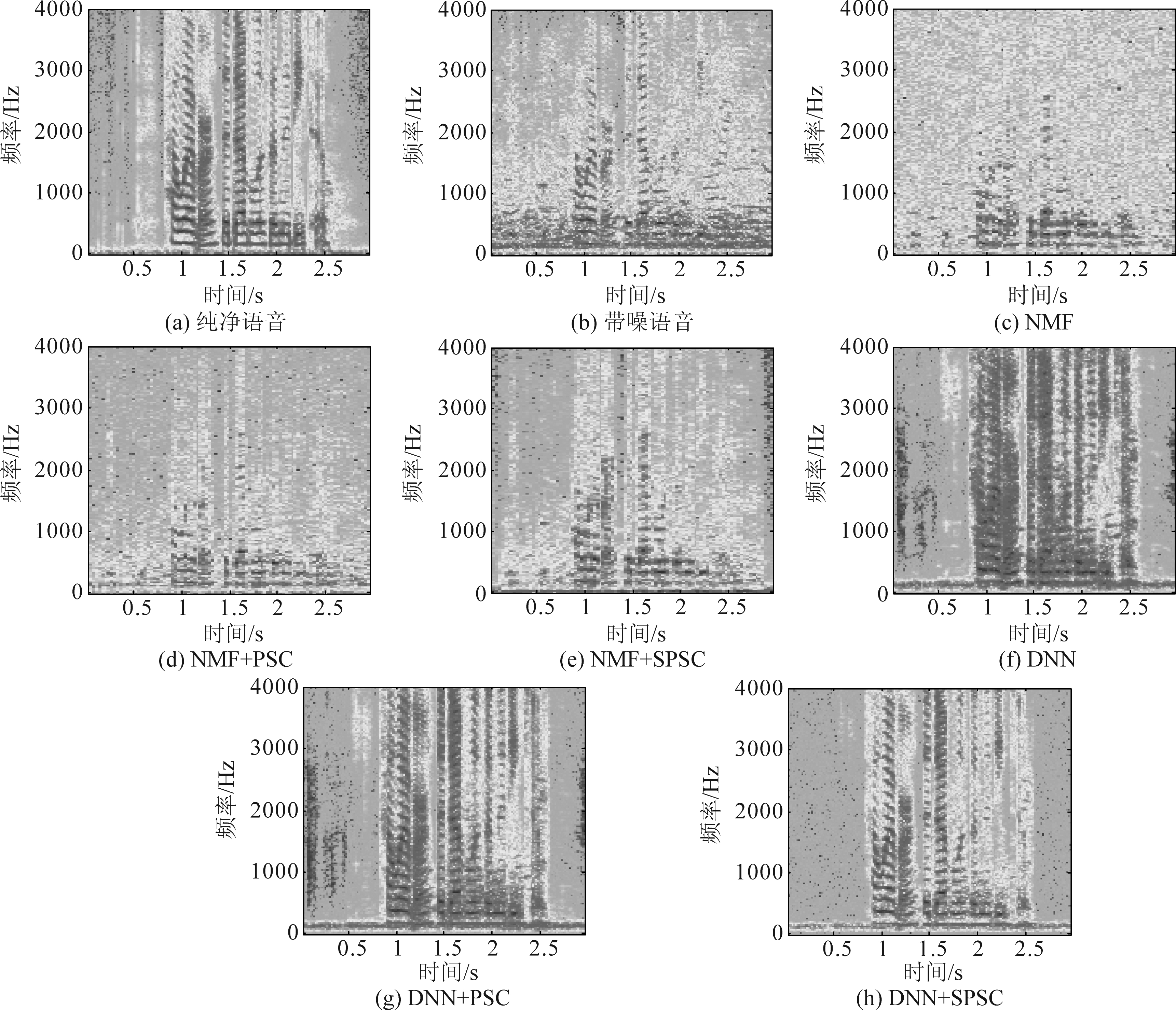
图5 增强语音信号频谱图比较
Fig.5 The comparison of spectrograms of enhanced speech signal
综上,本文提出的SPSC算法要优于传统的PSC算法,可以有效恢复语音且抑制噪声。
5 结论
本文提出一种基于稀疏度的相位谱补偿算法,用于提升传统相位谱语音增强算法的性能。首先,考虑到在基于幅度的语音增强算法中,目标语音和背景噪声幅度谱存在重叠,通过噪声和语音幅度谱之间的局部SNR估计谱时间稀疏性;然后,将传统相位谱补偿算法中的补偿因子进行改进,使其可随输入信号不同的信噪比条件灵活调整;最后,联合谱时间稀疏性和补偿因子得到SPSC函数,对相位谱进行补偿。仿真结果表明,本文提出的SPSC算法的3项评价指标都要优于传统PSC算法及基线算法。信噪比为0 dB时,LSD值提升了约0.3~0.8 dB,PESQ值提升了约0.1~0.4,增强语音的质量和听感有一定提高。segSNR指标提升了0.6~1.4 dB左右,说明本文算法在低信噪比下,可有效恢复带噪语音中的语音成分,对噪声抑制效果明显。
[1] Xu Y, Bao G, Xu X, et al. Single-channel speech separation using sequential discriminative dictionary learning[J]. Signal Processing, 2015, 106(1): 134-140.
[2] Virtanen T. Monaural Sound Source Separation by Nonnegative Matrix Factorization With Temporal Continuity and Sparseness Criteria[J]. IEEE Transactions on Audio Speech & Language Processing, 2007, 15(3): 1066-1074.
[3] 时文华, 倪永婧, 张雄伟, 等. 联合稀疏非负矩阵分解和神经网络的语音增强[J]. 计算机研究与发展, 2018, 55(11): 2430-2438.
Shi Wenhua, Ni Yongjing, Zhang Xiongwei, et al. Deep Neural Network Based Monaural Speech Enhancement with Sparse Non-Negative Matrix Factorization[J]. Journal of Computer Research and Development, 2018, 55(11): 2430-2438.(in Chinese)
[4] Po-Sen Huang, Minje Kim, Mark Hasegawa-Johnson, et al. Joint optimization of masks and deep recurrent neural networks for monaural speech source separation[J]. IEEE/ACM Transactions on Audio Speech & Language Processing, 2015, 23(12): 1-12.
[5] Paliwal K K, Wojcicki K, Shannon B, et al. The importance of phase in speech enhancement[J]. Speech Communication, 2011, 53(4): 465- 494.
[6] Mowlaee P, Saeidi R, Stylianou Y, et al. Advances in phase-aware signal processing in speech communication[J]. Speech Communication, 2016, 81(1): 1-29.
[7] 王栋, 贾海蓉. 改进相位谱补偿的语音增强算法[J]. 西安电子科技大学学报, 2017, 44(3): 83- 88.
Wang Dong, Jia Hairong. Speech enhancement using improved phase spectrum compensation[J]. Journal of Xidian University, 2017, 44(3): 83- 88.(in Chinese)
[8] 闵刚, 张雄伟, 杨吉斌, 等. 应用于非负稀疏信号重构的交替方向乘子法[J]. 信号处理, 2015, 31(11): 1411-1417.
Min Gang, Zhang Xiongwei, Yang Jibin, et al. Nonnegative Sparse Signal Recovery via Alternating Direction Method of Multipliers[J]. Journal of Signal Processing, 2015, 31(11): 1411-1417.(in Chinese)
[9] Pejman Mowlaee, Rahim Saeidi. Iterative closed-loop phase-aware single-channel speech enhancement[J]. IEEE Signal Processing Letters, 2013, 20(12): 1235-1239.
[10] Kamil Wojcicki, Mitar Milacic, Anthony Stark, et al. Exploiting conjugate symmetry of the short-time Fourier spectrum for speech enhancement[J]. IEEE Signal Processing Letters, 2008, 15(1): 461- 464.
[11] 吉慧芳, 贾海蓉, 王雁. 改进相位谱补偿的语音增强方法[J]. 计算机工程与应用, 2019, 55(8): 48-52.
Ji Huifang, Jia Hairong, Wang Yan. Speech Enhancement Method for Improving Phase Spectrum Compensation[J]. Computer Engineering and Applications, 2019, 55(8): 48-52.(in Chinese)
[12] Rethage D, Pons J, Serra X. A wavenet for speech denoising[C]∥International Conference on Acoustics Speech and Signal Processing (ICASSP). Calgary, Canada: IEEE, 2018: 5069-5073.
[13] 许春冬, 许瑞龙, 周静. 基于自动编码生成对抗网络的语音增强算法[J]. 计算机工程与设计, 2019, 40(9): 2578-2583.
Xu Chundong, Xu Ruilong, Zhou Jing. Speech enhancement based on auto-encoders and generative adversarial network[J]. Computer Engineering and Design, 2019, 40(9): 2578-2583.(in Chinese)
[14] Gerkmann T, Hendriks R C. Unbiased MMSE-Based Noise Power Estimation With Low Complexity and Low Tracking Delay[J]. IEEE Transactions on Audio Speech & Language Processing, 2012, 20(4): 1383-1393.
[15] Schmidt M, Larsen J, Hsiao F. Wind noise reduction using non-negative sparse coding[C]∥International Workshop on Machine Learning for Signal Processing. Thessaloniki, Greece: IEEE, 2007: 431- 436.
[16] 李煦, 王子腾, 王晓飞, 等. 采用性别相关的深度神经网络及非负矩阵分解模型用于单通道语音增强[J]. 声学学报, 2019, 44(2): 221-230.
Li Xu, Wang Ziteng, Wang Xiaofei, et al. Single-channel speech enhancement based on gender-related deep neural networks and non-negative matrix factorization models[J]. Acta Acustica, 2019, 44(2): 221-230.(in Chinese)
[17] Kwang Myung Jeon, Hong Kook Kim. Audio enhancement using local SNR-based sparse binary mask estimation and spectral imputation[J]. Digital Signal Processing, 2017, 68(1): 138-151.
[18] Kwang Myung Jeon, Hong Kook Kim. Sparsity-based phase spectrum compensation for single-channel speech source separation[J]. Digital Signal Processing, 2020, 97: 102632.
[19] Varga A, Steeneken H J. Assessment for automatic speech recognition II: NOISEX-92: a database and an experiment to study the effect of additive noise on speech recognition systems[J]. Speech Communication, 1993, 12(3): 247-251.
[20] Abdulla S M, Jayakumari J. DUET using automatic peak detection and histogram thresholding[C]∥International Conference on Circuits and Systems (ICCS). Thiruvananthapuram, India: IEEE, 2017: 291-296.
[21] Li Y, Cichocki A, Amari S. Sparse component analysis for blind source separation with less sensors than sources[C]∥International Symposium on Independent Component Analysis and Blind Signal Separation. Nara, Japan: IEEE, 2003: 89-94.
[22] Hoyer P O. Non-negative matrix factorization with sparseness constraints[J]. Journal of Machine Learning Research, 2004, 5(1): 1457-1469.
[23] Garofolo J S, Lamel L F, Fisher W M, et al. Darpa Timit Acoustic-Phonetic Continuous Speech Corpus CD-ROM {TIMIT}[J]. Web Download. Phila-delphia: Linguistic Data Consortium, 1993.
[24] ITU-T, Perceptual Evaluation of Speech Quality (PESQ), an Objective Method for End-to-End Speech Quality Assessment of Narrow-band Telephone Networks and Speech Codecs, International Telecommunications Union (ITU-T) Recommendation, 2001: 862.



