1 引言
跑道容量的定义有两种:实际容量和最大容量。实际容量是指对应于一个可接受的延误水平,单位时间内跑道可服务的飞机架数。最大容量是指在持续服务请求,不违反空中交通管理规定,不考虑延误水平的情况下,单位时间跑道系统可服务的最大航空器架次[1-2]。本文基于ADS-B历史解析数据评估得到的跑道容量为实际容量,实际容量能够反映跑道历史高峰服务能力。客观、科学且准确地评估跑道容量对于应对空中交通流量的迅猛增长,减少航班延误、缓解机场拥堵具有十分重要的作用。
跑道容量评估的主流方法有三种,一是建立跑道数学模型评估容量,二是用仿真软件(SIMMOD、Arena)模拟评估,三是基于航班历史运行数据分析评估。构建数学模型分析跑道容量是将机场的运作过程用数学公式表示,通过模拟它们的运作流程来确定容量。一般来说,这些数学模型是抽象的、简化的,因此这些方法只适合对机场进行宏观理论分析[3]。基于仿真软件评估是用软件详细模拟飞行区运行的各个方面,精确仿真跑道、滑行道以及空域系统。这种方法得到的容量最接近实际情况,但是评估耗时较长且软件昂贵[4]。基于航班历史运行数据评估跑道容量的思想是指,在基于过去的一段时间内,所观察到的高峰抵港和离港架次能够反映在或接近机场的容量水平值。其中,根据对航班历史数据操作的不同又分成两类,一是由单位时间内的起降架次数据获得容量包络曲线求解跑道容量[5- 8],二是由统计学的办法分析跑道容量[9-10]。其中,基于统计学的方法评估容量具有简便快捷适用性强的优点,文献[9]统计得到小时航班架次数据的频率密度直方图,计算了分布的参数并用不同的评估策略(保守、正常和积极)评估容量;文献[10]通过构造机场小时进离港架次的欧几里得距离,引入正态分布单侧置信区间的概念来确定容量(原文指高峰服务能力)。但是,文献[10]把选取的样本范围扩大到一年后,发现小时进离港架次和构造的欧几里得距离都不符合正态分布;文献[9]统计得到的频率密度直方图也存在不符合正态分布的情况,文章并未给出明确的处理方法。
在以上三种方法当中,基于历史运行数据构建容量包络曲线评估的方法最容易实施,因此在欧洲和美国的一些主要机场中,该方法得到了广泛的应用[8]。但是该方法所得到的包络线与所选取的数据集高度相关,当样本数据不同时,包络线的鲁棒性受到了挑战[6]。为了解决容量评估结果易受样本数据差异影响的问题,基于文献[9-11]的工作,提出了基于ADS-B数据的跑道容量评估新方法。该方法通过分析ADS-B原始信号解码处理后的数据,统计得到跑道小时抵港离港架次,然后应用K-S检验[12]对样本数据的分布进行假设检验,Box-Cox变换转换非正态分布数据,区间估计评估正态分布数据。通过给出不同置信水平的跑道容量区间,有效降低了样本数据的差异对评估结果的影响,容量评估结果更加准确可靠。空管人员可根据实际需要,依据适当的容量估计区间合理安排抵港离港航班,降低航班延误,优化跑道容量。
2 基于ADS-B数据评估跑道容量
ADS-B是一种利用全球卫星定位系统实现精确定位,将飞机位置、速度、身份和飞行状态信息向地面站和其他航空器进行周期性广播的新监视技术[13]。ADS-B与雷达相比具有成本低、易安装;数据精度高、获取容易和报文信息丰富等优势。根据国际民航组织与中国民航局的部署要求,中国将在2020年实现广播式自动相关监视技术的全面覆盖。作者所在实验室位于天津滨海国际机场附近,实验室的ADS-B接收机能够实时接收并记录机场每条跑道上每架飞机发出的ADS-B信号。通过对接收到的ADS-B信号解码处理,可得到解析后的飞机ID、经纬度信息、运动状况以及朝向/航迹等信息,根据这些信息设计SQL程序可以统计每条跑道上小时抵港离港架次。
(1)K-S假设检验。在对ADS-B原始信号解码处理后,由K-S检验对由ADS-B解析数据统计得到的小时抵港离港架次样本数据进行假设检验。记一系列小时抵港离港架次样本数据为x1,x2,…,xn,它们的累积分布函数为F1(x),假设分布函数为F0(x)。假设小时抵港离港架次样本数据服从正态分布,如果在一定的误差范围内有F1(x)=F0(x),这时说明原假设成立,可以认为小时抵港离港架次样本数据服从正态分布;否则,应该认为小时抵港离港架次样本数据不服从正态分布。故记原假设H0:F0(x)=F1(x),备择假设H1:F0(x)≠F1(x)。
其中,累积分布函数F1(x)定义为:
(1)
式中I(·)为示性函数,当输入条件满足时,取1;否则,取0。
假设分布函数,即正态分布函数F0(x)为:
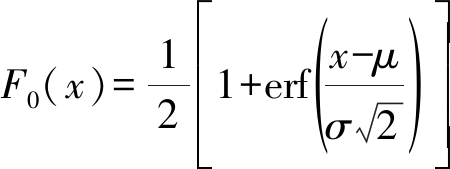
(2)
将F1(x)与F0(x)之间差异的最大值作为分布拟合检验的统计量,即
D sup|F1(x)-F0(x)|
sup|F1(x)-F0(x)|
(3)
在实际容量评估的过程中,可由式(4)对D进行估计
(4)
计算假设检验判决指标P值:
(5)
其中,
(2)给定K-S检验判决显著性水平β,若P≥β,则接受H0,即认为小时抵港离港架次样本数据服从正态分布。这时由区间估计给出总体均值和方差的估计区间。区间估计是统计学中常用的参数估计方法,它能够根据样本数据指标给出总体指标的上下限,并给出一定的概率保证。记样本均值为![]() 样本方差记为S2,设总体X~N(μ,σ2),有:
样本方差记为S2,设总体X~N(μ,σ2),有:
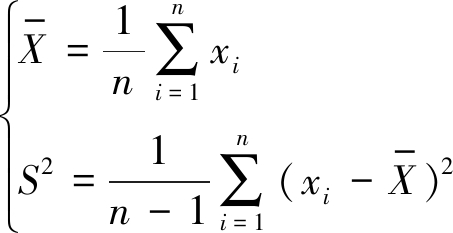
(6)
总体均值μ的置信水平为1-α的置信区间为:
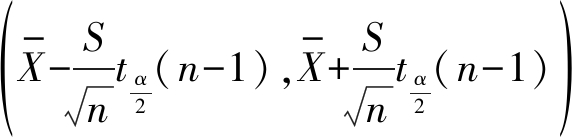
(7)
总体方差σ2的置信水平为1-α的置信区间为:

(8)
其中,α为区间估计显著性水平。跑道容量的估计式由Y=μ+mσ给出,Y是容量值,在本文中指容量区间,μ是总体均值,σ是总体标准差,m称为标准差系数,跑道的容量区间为(θ1,θ2),其中

(9)
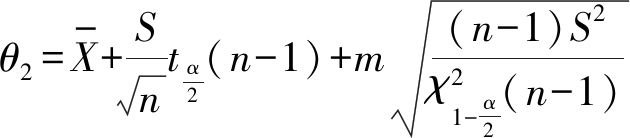
(10)
(3)当P<β时,则拒绝H0,即认为小时抵港离港架次样本数据不服从正态分布,需用Box-Cox变换将数据转换为正态分布再做分析。Box-Cox变换是一种能够将非正态数据转换为正态数据的常用的幂变换族,式中变换参数λ决定了具体的Box-Cox变换式的形式。λ的计算有最大似然估计和贝叶斯估计两种方法,本文给出了最大似然估计计算λ的步骤。首先,在(-2,2)之间均匀地取11~21个值,对选取的每个λ计算极大似然函数:
(11)
式中,
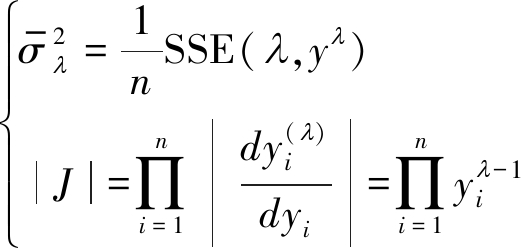
(12)
令![]() 对极大似然函数取对数,并略去与λ无关的常数项,可得
对极大似然函数取对数,并略去与λ无关的常数项,可得
(13)
其中,SSE(Sum of Squares due to Error)表示误差平方和。根据最大似然估计求解的方法,使得SSE最小的λ便是最终需要的λ。另外一种求解λ的方法可以参考文献[14],对所有λ对应转换之后的数据求偏度,偏度最接近0的λ便是我们需要的。偏度(skewness)是对分布对称性的度量,正态分布的偏度为零,样本数据的偏度越接近零说明正态性越好。偏度的计算公式如下。
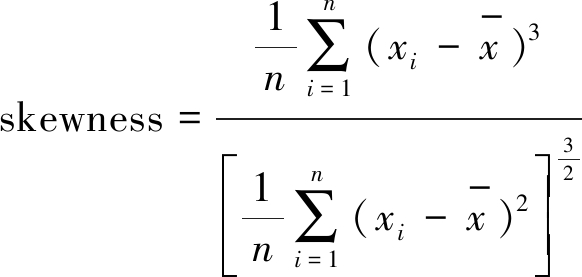
(14)
最后,将求得的λ代入式(15)
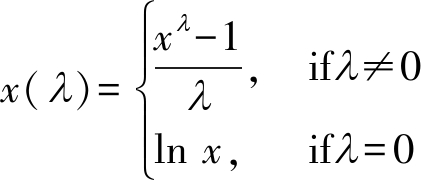
(15)
并对小时抵港离港架次样本数据做Box-Cox变换,得到一系列转换之后的样本数据,记为xi(λ)(i=1,…,n)。
xi(λ)(i=1,…,n)的总体均值μ′的置信水平为1-α的置信区间为
(16)
xi(λ)(i=1,…,n)的总体方差(σ2)′的置信水平为1-α的置信区间为:
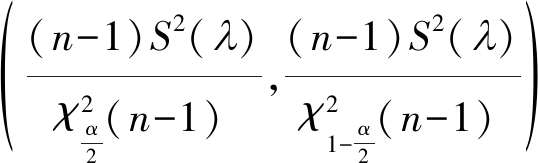
(17)
其中,样本均值为
样本方差为
xi(λ)(i=1,…,n)的容量区间为![]() 其中
其中
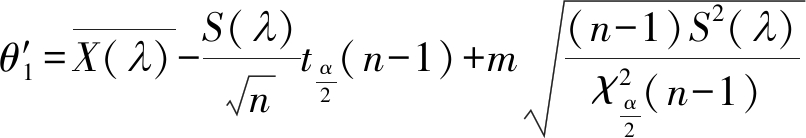
(18)
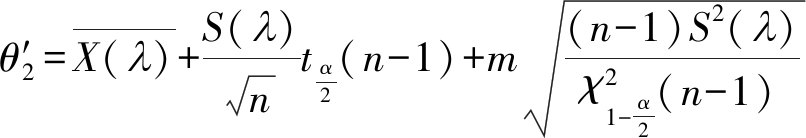
(19)
最后,对![]() 逆Box-Cox变换,可得原样本数据x1,x2,…,xn的跑道容量区间为
逆Box-Cox变换,可得原样本数据x1,x2,…,xn的跑道容量区间为
(20)
3 仿真验证
为了验证本文提出方法的有效性,通过分析天津滨海国际机场ADS-B实际解析数据,以小时为单位统计抵港离港架次,统计时间从2019年8月1号至8月10号、8月12号至8月31号,剔除小时抵港离港架次为0的时段,共574条样本数据集。天津滨海国际机场拥有两条平行跑道,间距2100 m,实行隔离平行运行,16L/34R跑道为抵港跑道,16R/34L跑道为离港跑道。在隔离平行运行模式下,以小时抵港架次为依据评估的是16L/34R跑道容量,以小时离港架次为依据评估的是16R/34L跑道容量。
3.1 单跑道容量
通过分析小时抵港离港架次样本数据分别得到抵港离港频数分布直方图,如图1所示。
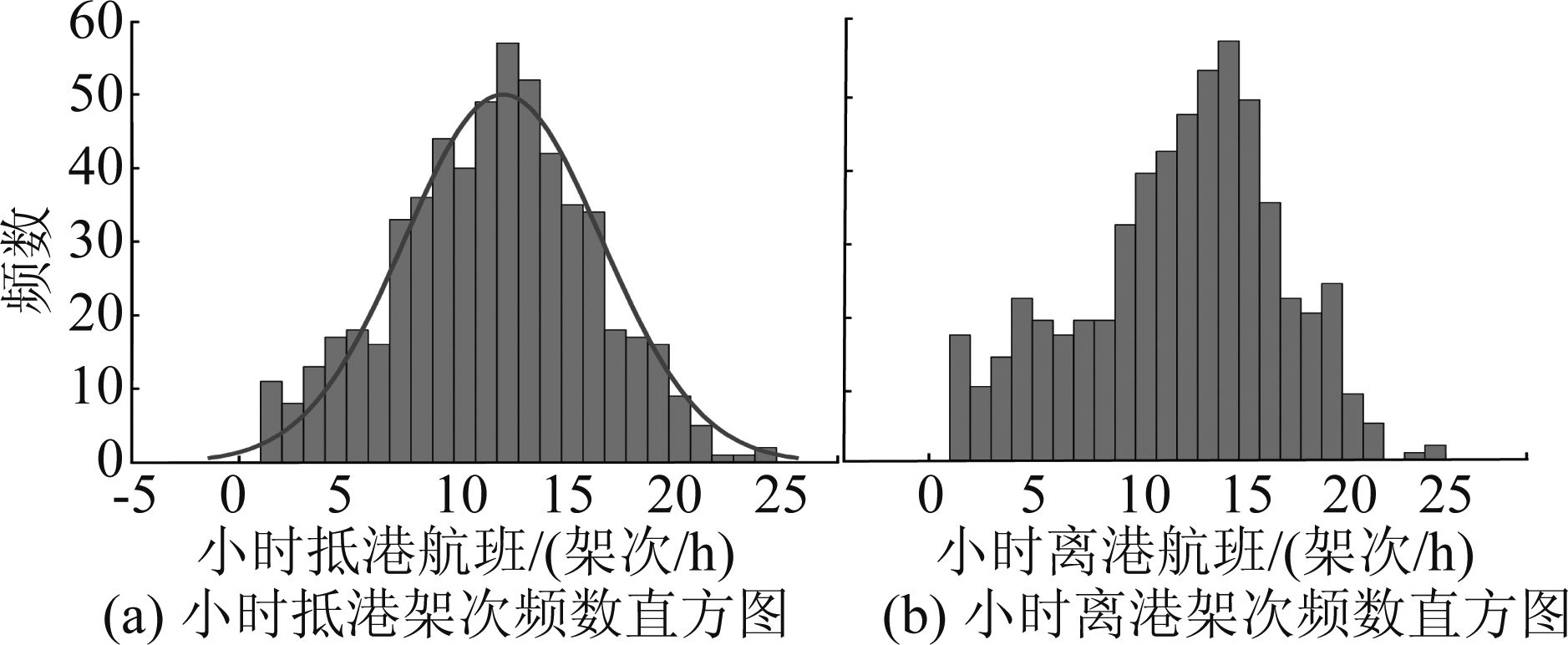
图1 小时抵港离港架次频数分布直方图
Fig.1 Histogram of frequency distribution of hourly arrivals and departures
为了直观的查看样本数据是否服从正态分布,在应用K-S检验之前先采用Q-Q图进行分析检验。Q-Q图(分位数-分位数图)是可专门用于评估正态性检验的图形。它采用样本数据的分位数与所指定分布的分位数之间的关系曲线来检验数据是否服从正态分布。若关系曲线为直线,则待验证的数据服从正态分布;反之,则不服从正态分布。经检验,小时抵港离港架次样本数据的Q-Q图如图2所示。
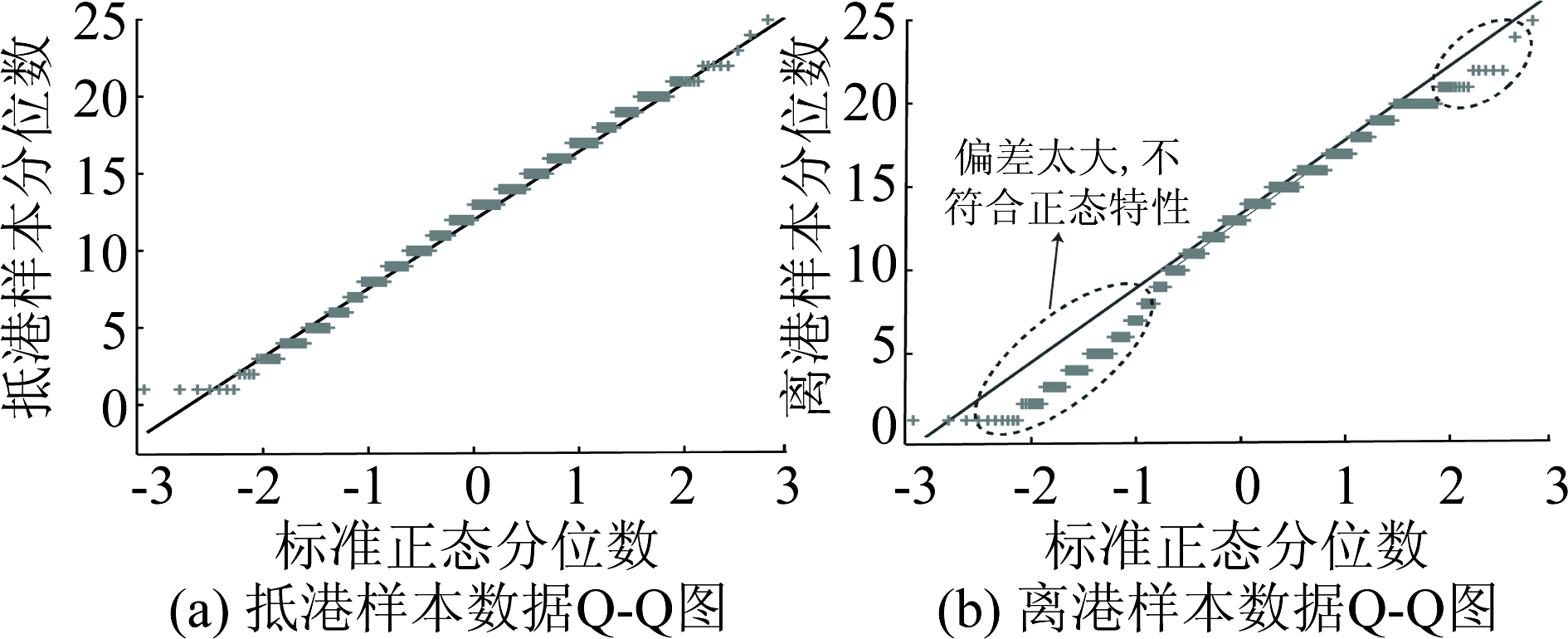
图2 小时抵港离港架次Q-Q图
Fig.2 Q-Q chart of hourly arrivals and departures
(1)16L/34R跑道容量。由图2(a)可知,小时抵港架次样本数据基本吻合正态分布。给定K-S检验显著性水平β(一般取β=0.05),计算K-S检验的P值为0.062,0.062>0.05,说明在一定的误差范围内,小时抵港架次样本数据符合正态分布的特性。利用式子(7)、(8)对总体指标进行区间估计,结果如表1所示。
表1 总体指标的置信区间
Tab.1 Confidence interval for the overall indicator
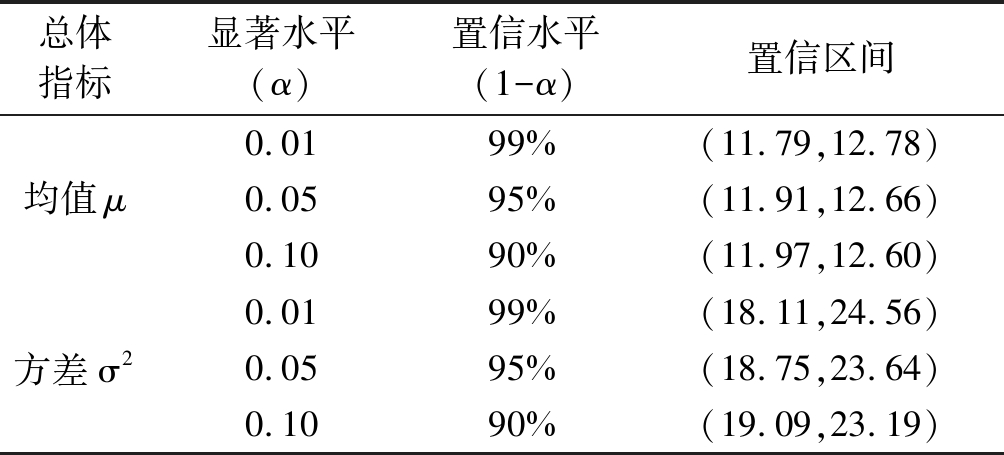
总体指标显著水平(α)置信水平(1-α)置信区间均值μ0.0199%(11.79,12.78)0.0595%(11.91,12.66)0.1090%(11.97,12.60)方差σ20.0199%(18.11,24.56)0.0595%(18.75,23.64)0.1090%(19.09,23.19)
表1给出了不同置信水平的置信区间,置信水平反映了由样本估计总体的可靠程度,置信区间则反映了总体指标所在的区间范围。标准差系数m的大小与样本量的多少以及机场的历史运行情况有关。本文给出了覆盖范围较为典型的几种情况,对应标准差系数分别取 1.29, 1.65, 2.33,如表2所示。
表2 不同m值的覆盖占比
Tab.2 The coverage ratio of different m values

标准差系数覆盖占比/%1.2990.151.6595.052.3399.01
表2中,标准差系数的不同取值代表着样本数据的取舍程度,标准差系数取值越大,容量评估覆盖的样本数据越多,评估越积极,舍弃的离群数据越少。经公式(9)、(10)计算得到的不同置信水平的16L/34R跑道运行容量如表3所示。
表3 16L/34R跑道容量
Tab.3 The runway capacity of 16L/34R
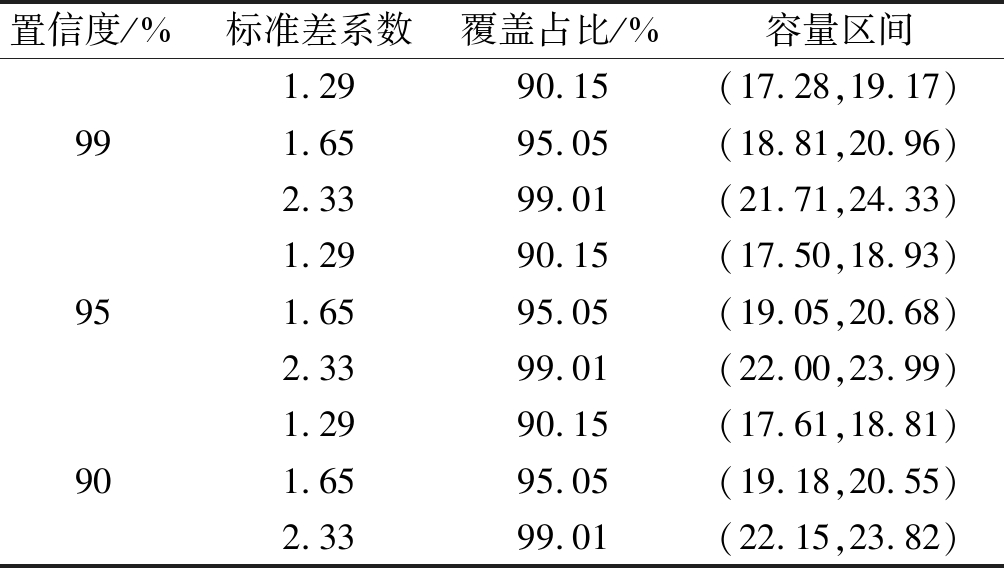
置信度/%标准差系数覆盖占比/%容量区间991.2990.15(17.28,19.17)1.6595.05(18.81,20.96)2.3399.01(21.71,24.33)951.2990.15(17.50,18.93)1.6595.05(19.05,20.68)2.3399.01(22.00,23.99)901.2990.15(17.61,18.81)1.6595.05(19.18,20.55)2.3399.01(22.15,23.82)
(2)16R/34L跑道容量。从图2(b)可以看出,顶部和底部的标识偏离直线较大,说明小时离港架次数据不吻合正态分布的特性。经计算,K-S检验的P值为0.001,0.001<0.05,说明小时离港架次样本数据的确不符合正态分布。需用Box-Cox变换进行正态转换。根据第2节的分析,计算每个λ及其对应的偏度值,如图3所示。
从图3可以看出,当λ=1.4时,对应偏度为0.025,非常接近最优偏度。将λ=1.4代入公式(15),便是最终求解的Box-Cox变换式。Box-Cox变换前后样本数据的Q-Q图尾部部分如图4所示。
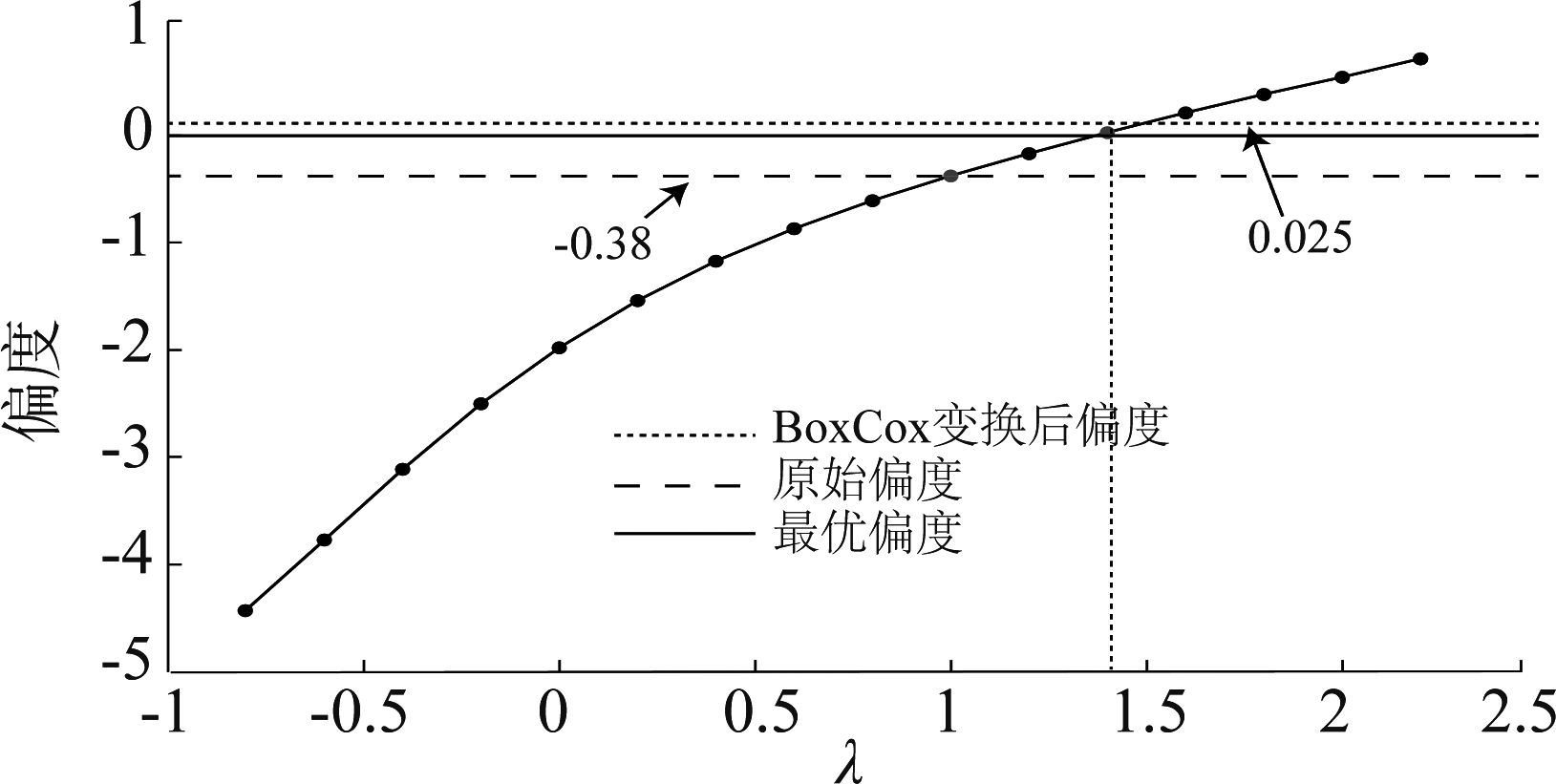
图3 λ与对应偏度值的关系曲线
Fig.3 Relation curve between λ and corresponding skewness
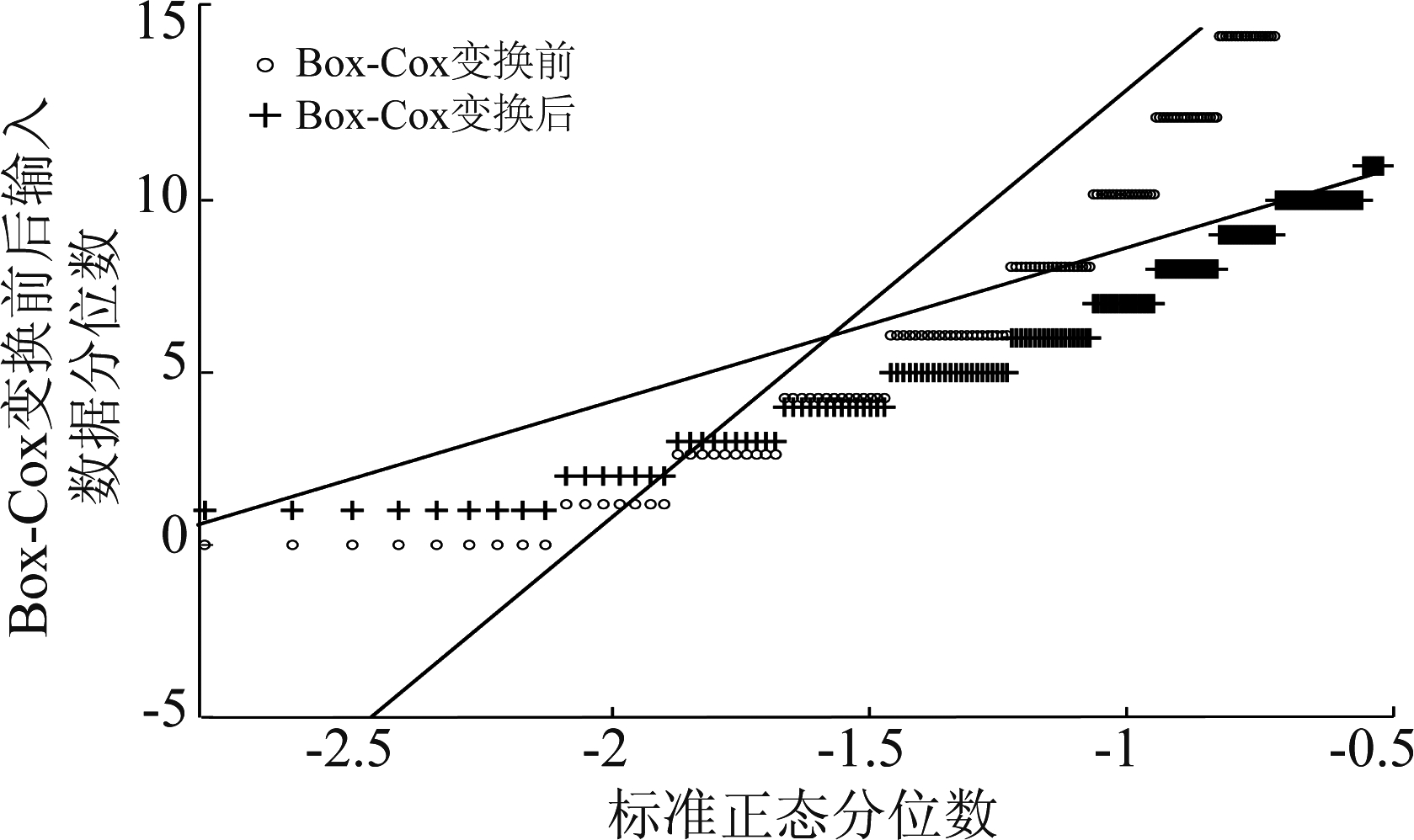
图4 Box-Cox变换前后Q-Q图尾部
Fig.4 The tail of the Q-Q diagram before and after the Box-Cox transformation
从图4可以看出,变换后的标识比变换前的标识更加接近对应的直线,说明经Box-Cox变换之后,正态性更好。计算变换之后的P值为0.186,0.186>0.05,故认为变换之后的小时离港样本数据符合正态分布。之后,同正态分布的样本数据分析一致,先用区间估计给出总体指标的置信区间,再用公式(18)、(19)给出区间上下限,最后借助公式(20)求解跑道容量区间。经计算,16R/34L跑道的运行容量如表4所示。
3.2 双跑道容量
计算双跑道容量不是两条跑道容量的简单求和,而是先将ADS-B实际解析数据统计得到的每时段抵港离港架次求和,再根据本文第2节分析评估。根据公式(14)计算得到不同的λ与其对应的偏度值如图5所示。
表4 16R/34L跑道容量
Tab.4 The runway capacity of 16R/34L
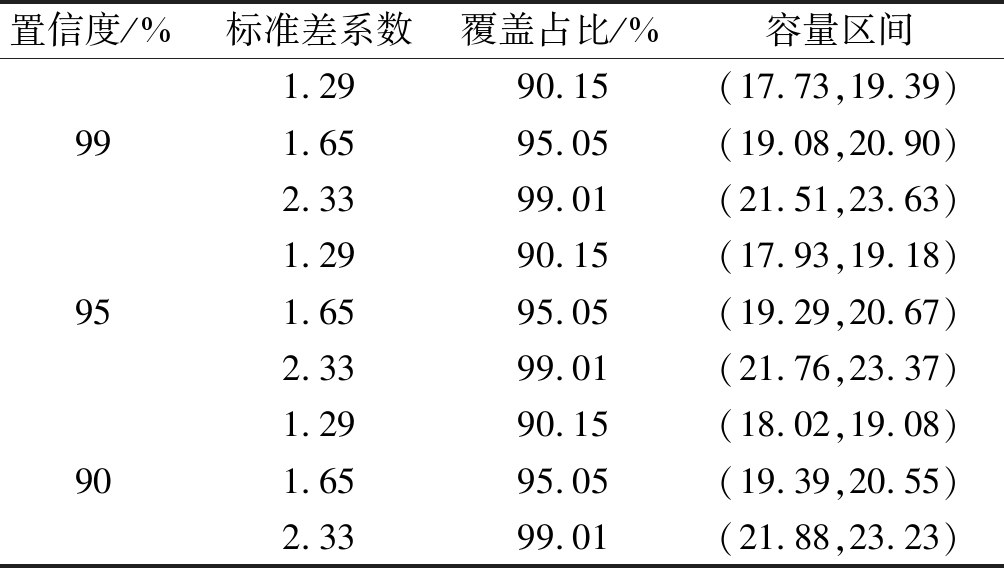
置信度/%标准差系数覆盖占比/%容量区间991.2990.15(17.73,19.39)1.6595.05(19.08,20.90)2.3399.01(21.51,23.63)951.2990.15(17.93,19.18)1.6595.05(19.29,20.67)2.3399.01(21.76,23.37)901.2990.15(18.02,19.08)1.6595.05(19.39,20.55)2.3399.01(21.88,23.23)
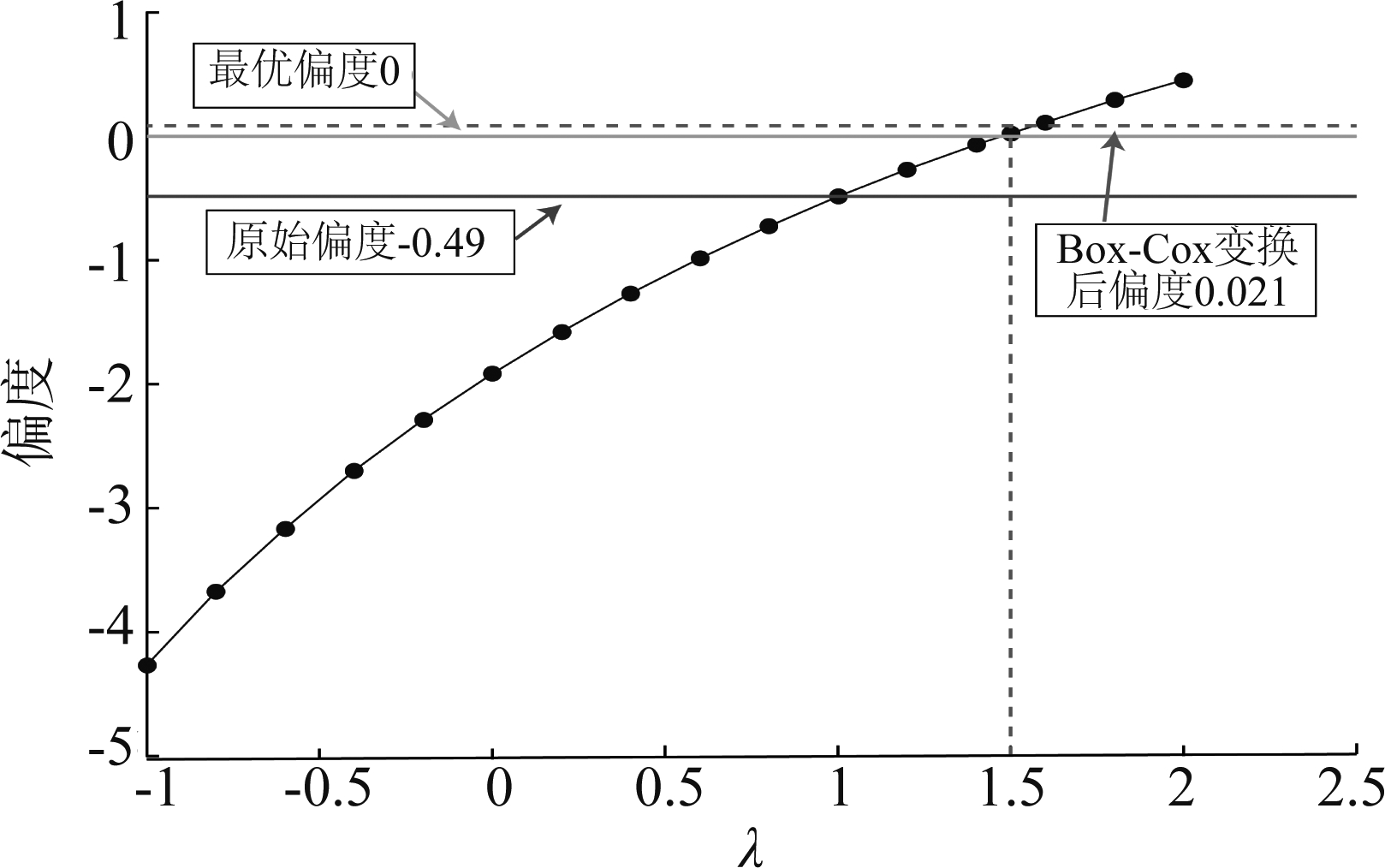
图5 λ与对应偏度值的关系曲线
Fig.5 Relation curve between λ and corresponding skewness
由图5可知,小时抵离港架次求和后数据的原始偏度为-0.49,当λ=1.5时,偏度为0.021,接近最优偏度。故将λ=1.5代入公式(15),此式即为Box-Cox变换式,经Box-Cox变换前后Q-Q图的尾部如图6所示。
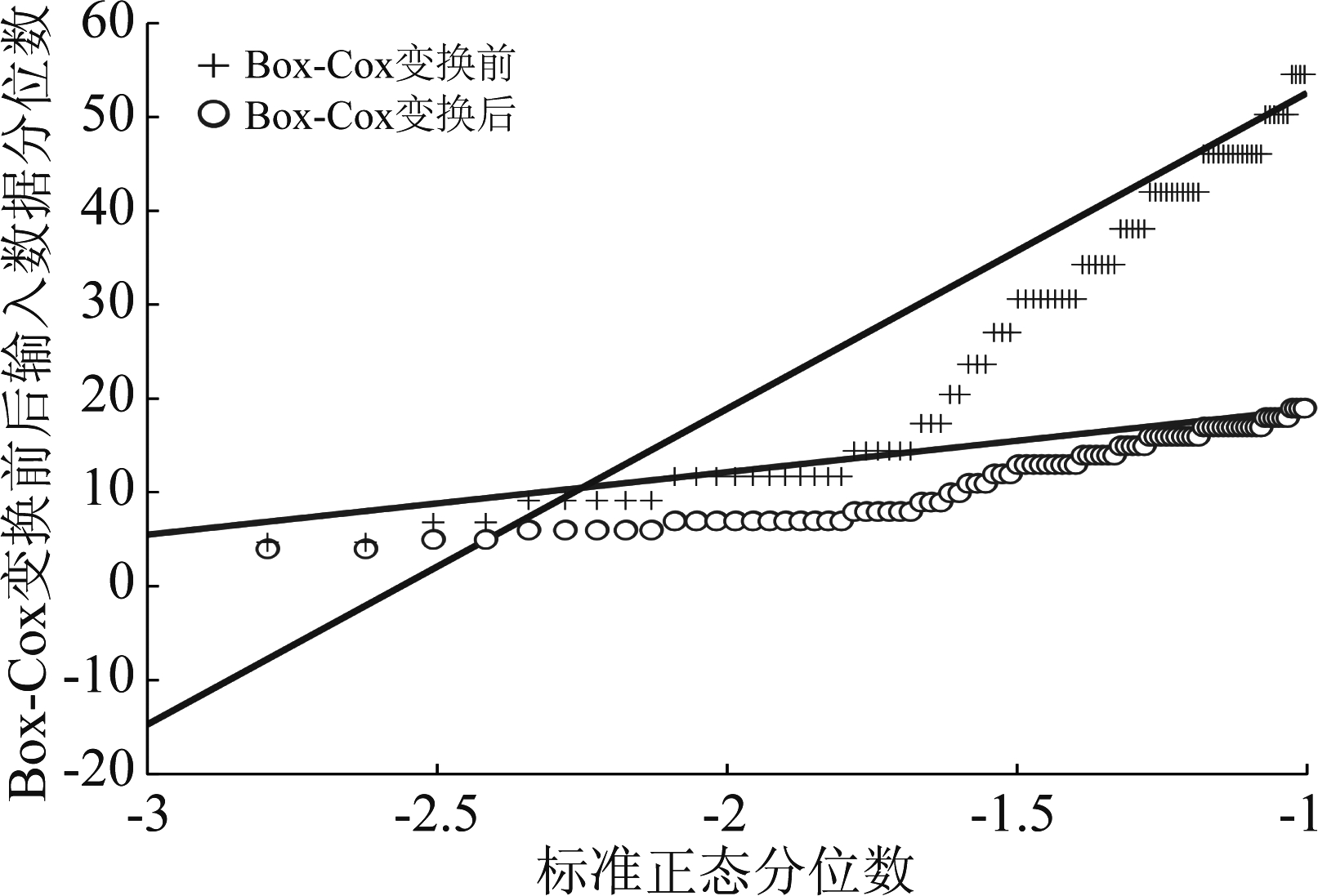
图6 Box-Cox变换前后Q-Q图尾部
Fig.6 The tail of the Q-Q diagram before and after the Box-Cox transformation
从图6可以看出,变换后的标识更接近对应的直线,说明经Box-Cox变换后样本数据正态性更好。对经过Box-Cox变换后的样本数据先用区间估计给出总体指标的置信区间,再用公式(18)(19)给出区间上下限,最后借助公式(20)求解跑道容量区间,最终计算结果如表5所示。双跑道容量在本文中视为机场容量,考虑到本文用了1个月的样本数据,且天津滨海机场多数时段处于容量未饱和状态的实际情况,本文取置信度为95%,m=2.33情形下对应的容量区间作为后续与其他方法比较的依据。
表5 机场双跑道容量
Tab.5 Airport dual runway capacity
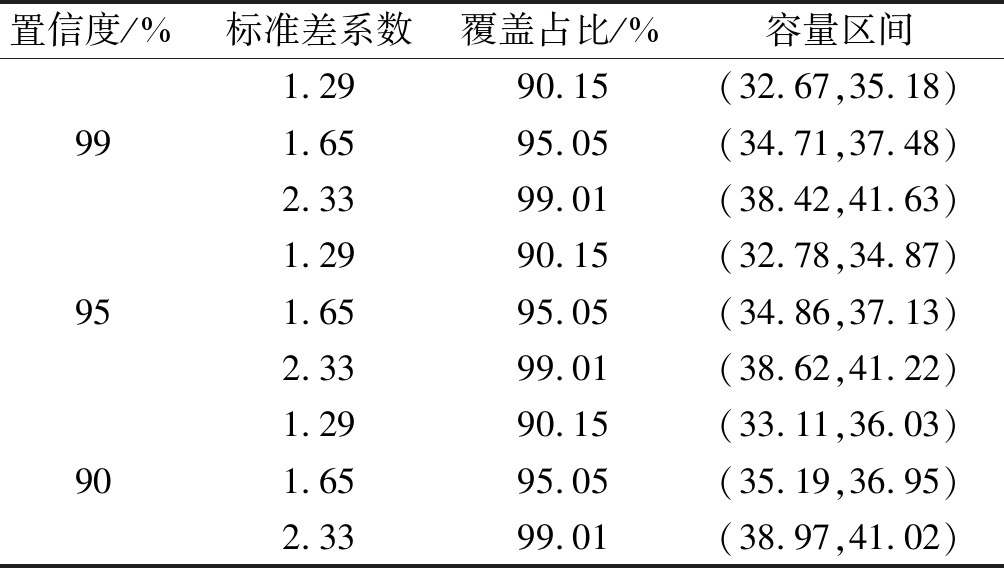
置信度/%标准差系数覆盖占比/%容量区间991.2990.15(32.67,35.18)1.6595.05(34.71,37.48)2.3399.01(38.42,41.63)951.2990.15(32.78,34.87)1.6595.05(34.86,37.13)2.3399.01(38.62,41.22)901.2990.15(33.11,36.03)1.6595.05(35.19,36.95)2.3399.01(38.97,41.02)
为了直观的反映评估容量值的变化情况,绘制表3、表4和表5的跑道容量评估结果,如图7所示。

图7 容量评估准确性与可靠性的关系
Fig.7 Relationship between accuracy and reliability of capacity assessment
图7给出了当m=2.33情形下不同显著水平α对应的跑道容量。从中可以看出不同置信度(1-α)下容量区间的变化情况,要想提高估计的准确性,即缩小容量区间的范围,就必然会降低估计的可靠性(估计的置信度降低)。要想提高估计的可靠性,即提高置信度,就必然会降低估计的准确性(容量区间范围变大)。这两者相互矛盾,不可兼得的。在实际的容量评估工作中,我们要根据自己的需要提出其中的一个条件,然后推导另一个条件的变动情况,如果所推出的另一个条件不能满足实际要求,就应该考虑增加样本数据、改善抽样组织,直至符合实际需要。
4 与基于包络曲线评估容量对比分析
机场的抵港容量和离港容量是相互联系的,在不同的抵港离港比率下,容量的完整信息可由确定的函数关系来表示,反映在几何图形上是一条凸状的连续的包络线[5]。基于包络曲线评估容量的关键是对离群值的处理,离群值包括记录错误的数据以及超出运行容量的数据。文献[5]中的基于频率阈值筛选是按照样本数据出现的频率来处理离群数据,低于设定阈值的数据将作为离群值排除在外,文献[6]中的分位数回归法则将超出设定分位数的样本数据视为离群值。本文用频率阈值筛选的方法给出了频数为1次和2次的包络线,如图8所示。

图8 频率阈值筛选绘制的包络曲线
Fig.8 The envelope curve drawn by frequency threshold filtering
图8两条包络线是在剔除最外层4个离群值后得到的,99.3%和98.8%分别是指对应容量包络线包含的数据占总数据量的比值。其中,99.3%包络线涵盖了频数为2次和1次的样本数据,以1次居多,评估比较积极;98.8%包络线只包含频数为1次的样本数据,评估较为保守。文献[6]提出将小时离港架次表示成小时抵港架次的分位数函数,通过线性规划求解分位数函数的参数来获得包络曲线。本文将包络线分成4段进行分析,分别给出了分位数为99%,98%,97%的容量包络线,如图9所示。
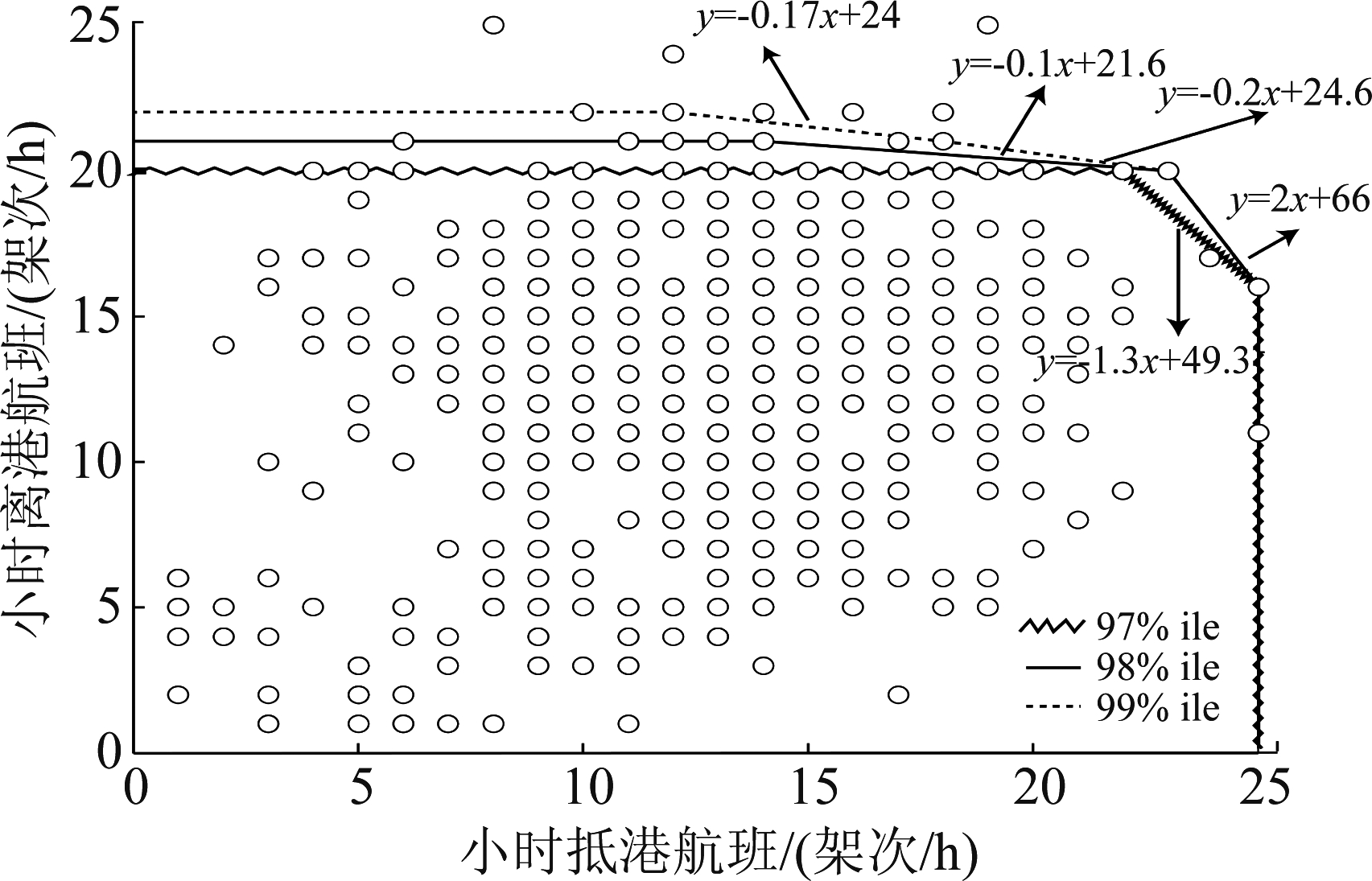
图9 不同分位数对应的包络曲线
Fig.9 Envelope curves corresponding to different quantiles
图9中的99%分位数对应的包络线在最外层,97%分位数对应的包络线在最内层,从图可以看出分位数设置越大,评估越积极,评估结果越大。该方法计算的容量值在42~43之间,同频率阈值筛选法计算得到的容量值一致。将全年的小时吞吐量从大到小排序后,第30个小时便是典型高峰小时,典型高峰小时对应的吞吐量即为机场参考容量(Reference Capacity)[15]。参考容量具有重要意义,它是机场规划设计和运行管理的重要指标。将评估结果与参考容量作比较具有实际意义,比较结果如图10所示。
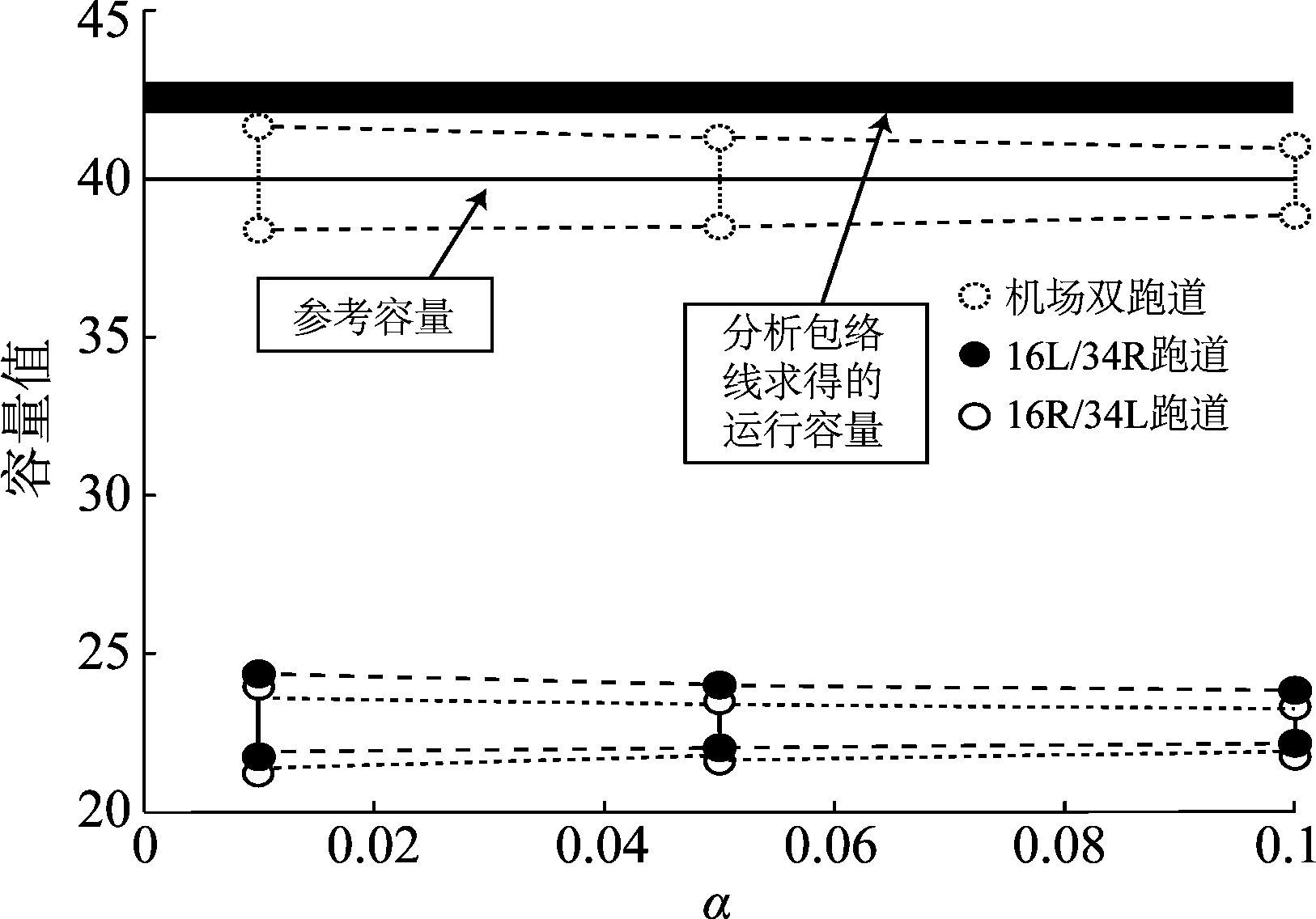
图10 评估结果比较
Fig.10 Comparison of assessment results
从图10可知,与参考容量相比,本文的计算方法给出的容量区间(38.42,41.63)涵盖参考容量值,而通过包络线分析得到的评估结果超出参考容量值的5%~7.5%。这是由于包络分析评估的方法过分依赖样本数据的缘故,在低样本数量的情况下,基于包络曲线评估无法对某些数据做出相信还是舍弃的判断。而本文所提出的基于ADS-B数据的跑道容量评估通过区间估计的方法给出不同置信水平的跑道容量区间,有效地降低了样本数据差异对评估结果的影响,容量评估结果更加准确可靠。
5 结论
本文对ADS-B原始信号经过解码处理后的信息进行了深入分析,统计得到跑道小时抵港离港架次,作为容量评估的样本数据。针对基于历史数据构建包络曲线评估容量的不足,提出基于ADS-B数据的跑道容量评估新方法,该方法能有效降低评估结果对样本数据的依赖,评估结果更加稳健可靠。与参考容量作比较,表明评估方法能够应用于民航空管部门,未来可以通过该方法评估特定数据集(IFR、MVFR、LIFR)的跑道容量,建立不同运行条件的跑道容量区间,为空管人员实施跑道流量规划、合理安排抵港离港航班提供参考依据。
[1] Zou X, Cheng P, Cheng N. A Simulation Model for Airport Runway Capacity Estimation[C]∥IEEE 17th International Conference on Intelligent Transportation Systems (ITSC). Qingdao China, 2014: 2669-2674.
[2] 张静. 天气影响的机场容量与延误评估研究[D]. 南京: 南京航空航天大学, 2011.
Zhang Jing. Airport capacity and delay assessment study on weather impact[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2011.(in Chinese)
[3] Wang F, Zhao L G. Capacity Evaluation Method for Parallel Runway Based on Monte Carlo Simulation[C]∥The 30th Chinese Control and Decision Conference (2018 CCDC). Hefei China, 2018: 1259-1263.
[4] Kicinger R, Chen J T, Steiner M, et al. Airport Capacity Prediction with Explicit Consideration of Weather Forecast Uncertainty[J]. Journal of Air Transportation, 2016, 24(1): 18-28.
[5] Gilbo E P. Airport capacity: Representation, Estimation, Optimization[J]. IEEE Transactions on Control Systems Technology, 1993, 1(3): 144-154.
[6] Ramanujam V, Balakrishnan H. Estimation of arrival-departure capacity tradeoffs in multi-airport systems[C]∥48th IEEE Conference on Decision and Control(CDC) and 28th Chinese Control Conference(CCC). Shanghai China, 2009: 2534-2540.
[7] Ju F, Cai K, Yang Y, et al. A Scenario-based Optimization Approach to Robust Estimation of Airport Capacity[C]∥IEEE 18th International Conference on Intelligent Transportation Systems. Beijing China, 2015: 2066-2071.
[8] Sebastian Kellner. Airport capacity benchmarking by density plots[C]∥GARS Seminar. Flughafenwesen Germany, 2009: 1- 4.
[9] Wang S, Zhang Y, Yu H, et al. A Fast Method to Evaluate the Runway Capacity at the Airport Based on Arrival/Departure Capacity Curve[C]∥2011 IEEE International Conference on Automation and Logistics(ICAL). Chongqing China, 2011: 271-274.
[10] 许辰澄, 胡明华, 赵征. 基于置信区间的机场高峰服务能力评估研究[J]. 航空计算技术, 2018, 48(4): 28-32.
Xu Chencheng, Hu Minghua, Zhao Zheng. Research on evaluation of airport peak service capacity based on confidence interval[J]. Aeronautical Computing Technique, 2018, 48(4): 28-32.(in Chinese)
[11] 赵征. 空域容量评估与预测技术研究[D]. 南京: 南京航空航天大学, 2015.
Zhao Zheng. Research on airspace capacity evaluation and prediction technology[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2015.(in Chinese)
[12] Wang F, Wang X. Fast and Robust Modulation Classification via Kolmogorov-Smirnov Test[J]. IEEE Transactions on Communications, 2010, 58(8): 2324-2332.
[13] 陈蕾, 吴仁彪, 卢丹. 利用多普勒效应的ADS-B欺骗式干扰检测方法[J]. 信号处理, 2018, 34(6): 722-728.
Chen Lei, Wu Renbiao, Lu Dan. ADS-B Spoofing Detection Method Using Doppler Effect[J]. Journal of Signal Processing, 2018, 34(6): 722-728.(in Chinese)
[14] Osborne J W. Improving your data transformations: Applying the Box-Cox transformation[J]. Practical Assessment, Research& Evaluation, 2010, 15(12): 1-9.
[15] Schinwald C, Hornung M. Methodical Approach to Determining the Capacity Utilisation of Airports: the Development of the European Air Traffic System between 2008 and 2012[C]∥Deutscher Luftund Raumfahrtkongress. Munich Germany, 2014: 1-10.


