1 引言
作为各种学科中最重要的技术之一,聚类分析已成为发现数据中隐藏模式/特征的强大工具。由于数据的显著差异(从社会科学到生物学,从数值数据集到时间序列数据集,从小样本数据到超大规模数据库),诸多学者开发了诸多聚类算法来解决特定数据集的聚类问题,如基于密度的聚类[5-6],分层聚类[7]和k-means[8]等。尽管提出了诸多聚类算法,但是仍然没有通用的聚类算法来解决所有的聚类问题。
由于在许多预处理过程中缺乏先验统计信息,聚类分析通常被视为无监督学习。然而,对于包括本文在内要解决的聚类问题中,可以通过其他数据特征[9-10]获得部分先验信息,这些特征可用于获得更好的聚类结果,即半监督聚类。在聚类算法研究中,簇的数量和聚类中心初始化对收敛速度和聚类结果有很大影响。对簇的数目的研究主要集中在以不同的k值多次运行聚类算法,并且根据特定的准则(如贝叶斯信息准则[15],速率失真理论[16],Akaike信息准则[17])来估计簇的数目k;对聚类中心初始化的研究,主要集中在通过统计信息来最小化初始聚类中心的距离,如k-means++[18]。
约束聚类是当前聚类研究的热点问题。在约束聚类中,“必须链接”约束(must link,ML)和“不能链接”约束(cannot link,CL)是两个基本规则。ML约束用于指定两个数据点应归属于同一个标签/簇,而CL约束用于指定两个数据点不能属于同一个标签/簇,用户可以根据具体的需求来运用不同的约束规则来解决特定的问题。典型的约束聚类算法包括约束k-means聚类[11],成对约束k均值[12],完整链接[13],约束分层聚类算法[14]等。
过去,MOTD问题的主流解决方法是基于模型的方法[22-23]。在军事对抗或环境噪声较大的场景中,敌对双方会采用诸多干扰/隐身技术,干扰对方雷达。在这种情况下,目标的运动模型通常有较大的误差,基于模型的方法在迭代计算过程中会因为运动模型的误差而有较大的估计误差。
近年来,许多学者开始通过基于聚类的方法来解决MOTD问题。西北工业大学李天成教授在多源聚类算法上面做了很多开创性的工作,他在文献[24]中提出了clustering for filtering(C4F)聚类算法,C4F算法相对于基于模型的算法,运行时间和聚类精度都有较大的优势,但仅适用于观测噪声已知的场景,其聚类精度易受传感器目标检测概率和选定传感器量测顺序的影响;在文献[25]中提出了multi-source n-points算法,该算法解决了目标观测噪声未知情况下多源聚类问题,运算速度快,但其聚类精度受传感器漏检率和选定传感器量测顺序的影响;在文献[26]中提出了用flooding then clustering (FTC)聚类算法来解决分布式多传感器的多目标状态估计问题,运算量较大,但其聚类精度受传感器目标检测概率的影响较小;在文献[27]中用FTC算法得到的目标的均值和方差反馈给分布式probability hypothesis density (PHD)多传感器,得到了更加鲁棒的跟踪性能。文献[30]提出的multi-source density peak clustering (MSDPC)算法,通过筛选局部密度较大的数据点,再按照有无重叠簇两种情况分别进行聚类,聚类精度较高,可以有效解决传感器目标检测概率较低时的多源聚类问题,但运算耗时大;电子科技大学张天贤老师对将C4F算法检测得到的目标进行数据关联[28],相对于传统的数据关联方法,其运行时间大大减少,但其跟踪精度易受传感器目标检测概率和选定传感器量测顺序的影响。
综上所述,传感器量测的顺序对多源聚类的性能至关重要,对选定传感器量测的顺序重新筛选排序成为衡量多源聚类算法性能的关键。本文在multi-source n-points算法的基础上,分析了传感器量测的不同顺序对该算法的影响,详见本文3.1节,并提出了improved multi-source n-points(IMSNP)算法,详见3.2节。
本文的其余部分安排如下。问题模型将在第2节中讨论。第3节分析Multi-source n-points算法的不足之处并介绍了提出的改进算法的详细信息。第4节讨论了实验仿真结果,第5节对此进行了总结。
2 多传感器目标融合
2.1 问题假设
MOTD问题涉及在观测噪声的情况下,根据传感器的量测数据估计未知数量和状态的多个目标。MOTD问题在遥感图像融合,海洋学和军事领域具有广阔的应用空间。可以通过以下假设对一般MOTD问题建模:
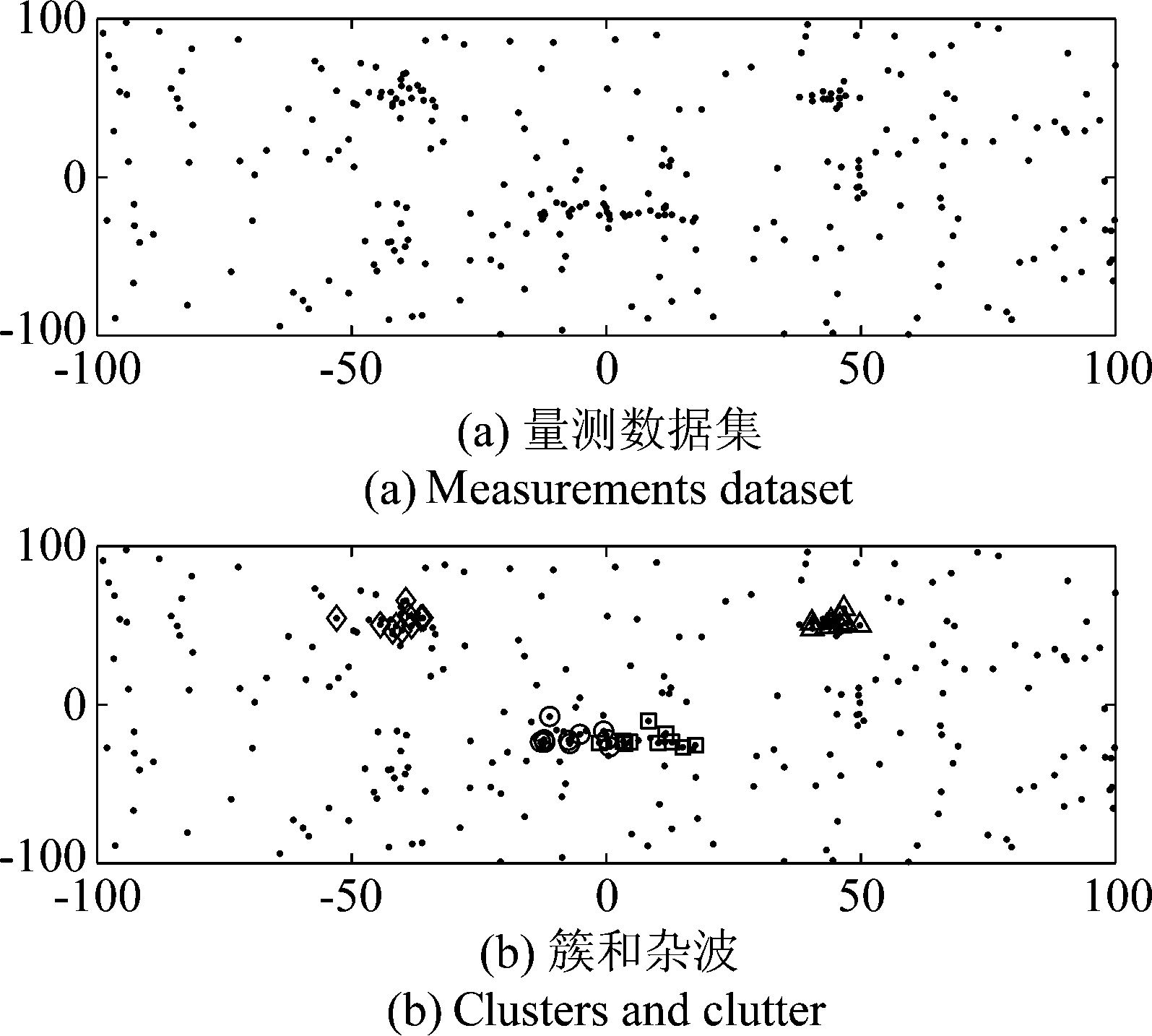
图1 二维平面的多传感器的数据点
Fig.1 Multi-sensor data points in a two-dimensional plane
假设1 每个目标的观测/测量结果彼此独立;
假设2 传感器的量测数据包含目标的观测和杂波,杂波通常为零均值高斯噪声;
假设3 一个目标在每次扫描中最多只能产生一个量测。
假设4 杂波的分布密度远低于目标观测的密度。
为了说明问题,图1给出了10个独立同分布的传感器量测数据的二维平面的结果,目标的量测数据点(“△”“◇”“□”“○”),杂波(“·”)。我们的目的是滤除杂波,将各个目标的观测数据分别区分开,并求得各个簇的聚类中心。
2.2 问题描述
上述的MOTD问题可以用公式描述为CL约束聚类问题。考虑一个包含多个传感器量测数据的数据集Z,zi是数据集Z中的数据点。
zi∈P,i=1,…,N
(1)
其中N是数据点的目标数,P是参数空间。在本文中,我们定义zi为二维笛卡尔坐标系中的一个点。
数据集Z可以表示为多个传感器的量测集的并集的形式。定义传感器s的量测集为
其中ms是传感器s中的数据点的数目,数据集Z可以表示为:
(2)
其中n是传感器的数目。MOTD聚类问题要求数据集Z必须分成k个簇,即:C1,C2,…,Ck。我们定义数据集Z中的杂波为C0,目标的观测集为CT,数据集Z可以定义为:
Z=C0∪C1∪…∪Ck=C0∪CT,k∈T
(3)
CL约束规定任意一个传感器的两个量测数据点与簇Ce、杂波C0的关系为:
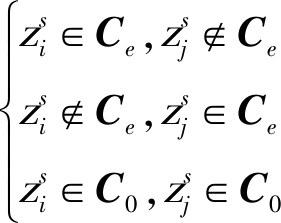
(4)
其中,i, j∈{1,2,…,ms},s∈{1,2,…,n},e∈{1,2,…,k},i≠j。公式(4)是指,传感器s的任意两个量测
和
不能同时属于同一个目标量测形成的簇,但是可以同为杂波。
同时,任意一个簇和其他簇的交集为空集
Ci∩Cj=Φ,∀i, j∈{1,2,…,k,0}
(5)
如上所述,MOTD约束聚类问题可以描述为:将多个传感器的量测数据集Z聚类成k个簇,聚类的过程需满足公式(4)的CL约束和公式(5)的无交集约束。
2.3 CL约束以及簇的大小
公式(4)的CL约束,将限制每个簇的大小(簇中数据点的数目)为小于或等于传感器的数目n
(6)
其中|Ci|是簇Ci的数据点的数目,
是指小于或者等于。
更具体的,我们可以估计每个簇的期望大小,也就是每个目标i的量测形成的簇的数据点的数量。簇的大小与目标视场覆盖的传感器的数量及每个传感器的目标检测概率有关,将覆盖目标i的传感器的数量表示为ni,假定传感器s对目标i的目标检测概率为
为了简化计算,我们将
视为一个常数pD,簇Ci的期望大小可以定义为:
(7)
在给定pD和传感器数目n的情况下,E[|Ci|]是一个常数。
E[|Ci|]=r
(8)
任意一个簇Ci中的目标/子簇的个数可以计算为
(9)
其中,[·]为四舍五入计算符号。
3 IMSNP算法
3.1 Multi-source n-points算法的不足
Multi-source n-points算法通过计算数据集中传感器s的量测数据点
与其他传感器e,e∈{1,2,…,n}的量测数据点
之间的高斯核函数距离
如公式(10)所示。
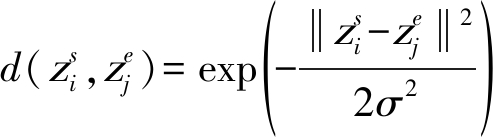
(10)
其中,σ为观测噪声。如果
小于截断距离εi,则认定和
相互关联,挑选和其他传感器距离最小的点,聚类为簇Ci。当|Ci|>l×r时,则判定Ci为目标的量测形成的簇,聚类得到的簇Ci的中心即估计的目标的位置,l=0.8为参考值,可以根据传感器检测概率来调整。如果簇Ci的目标数目ki≥2,则判定Ci为重叠簇,需要将该重叠簇划分为满足CL约束的多个子簇。
Multi-source n-points算法通过高斯核函数来计算距离,一方面可以有效减少观测噪声带来的误差,另一方面也有负面影响:同一个传感器s中的多个量测数据点
的顺序不同,聚类结果不同。其原因是:在距离计算步骤,如果选定Ci附近的杂波数据点作为
来计算距离高斯核函数较强的映射能力会将部分Ci的数据点和部分C0的数据点聚类为簇Cj,且同时满足公式(4)和(5),在这种情况下其聚类结果就会有较大的误差。图2给出了用不同的数据点
和
通过multi-source n-points算法聚类得到的不同的聚类结果,可以看到用数据点聚类得到的簇和真实的目标的量测形成的簇几乎重合,而用数据点聚类得到的簇中的数据点杂波的比重更大,其聚类结果有较大的误差。
图2 数据点
和
进行聚类的结果
Fig.2 Clustering results of data points and
在multi-source n-points算法的程序设计中,为了减少误差,用对数据集Z聚类得到的簇Ci,在求得簇Ci及其聚类中心
后需将Ci数据点从数据集Z中删除。以图2为例,如果先用数据点
进行距离计算,在求得簇Ci及其聚类中心后删除簇Ci的数据点,会导致后续再用数据点
进行聚类会因为不满足|Cj|>l×r而导致聚类失败,数据点
和
位置如图3所示。因此,距离计算步骤传感器s中数据点的顺序对聚类的精度至关重要。
3.2 IMSNP算法
基于以上分析,IMSNP算法的主要创新点是:筛选传感器s中的量测数据点,将疑似目标的量测数据点筛选出来,优先进行聚类。筛选疑似目标的量测,依赖一个先验规律:传感器s产生的目标i的量测数据点在不考虑漏检的情况下,其附近应该有n-1个其他传感器产生的量测(考虑到杂波,我们可以用n代替),这导致和数据集Z的欧氏距离矩阵中,前n个最小距离的平均值应该小于3倍的观测噪声[24],即:
(11)
其中,
(12)
(13)
(14)
其中,L是量测数据点最多的传感器
是数据点
与量测集Z的第T个最小距离,
是数据点与量测集Z前n个最小距离的平均值。当传感器有漏检的情况时,每个目标产生的量测形成的簇的期望数目为r,公式(12)可以变更为:
(15)
筛选量测数据点最多的传感器L,是考虑到同样的杂波率和传感器目标检测概率情况下,一方面量测数据点最多的传感器其目标漏检率可能更低,另一方面量测数据点最多意味着更多的杂波落入CT附近的概率更大(远离CT的杂波可以被有效被排除),假如传感器s漏检目标i,同时有传感器s中的杂波落入目标i的量测形成的簇附近,这种情况会导致聚类的精度更高。满足公式(11)的传感器s中的数据点为目标的量测数据点。
当数据集Z的观测噪声方差已知的时候,可以直接用公式(11)来筛选满足条件的量测数据点;反之观测噪声方差未知的时候,可以用文献[25]来计算参数截断距离εi的方法,将公式(11)替换为
(16)
经过公式(11)筛选后的传感器L的量测数据点为
(17)
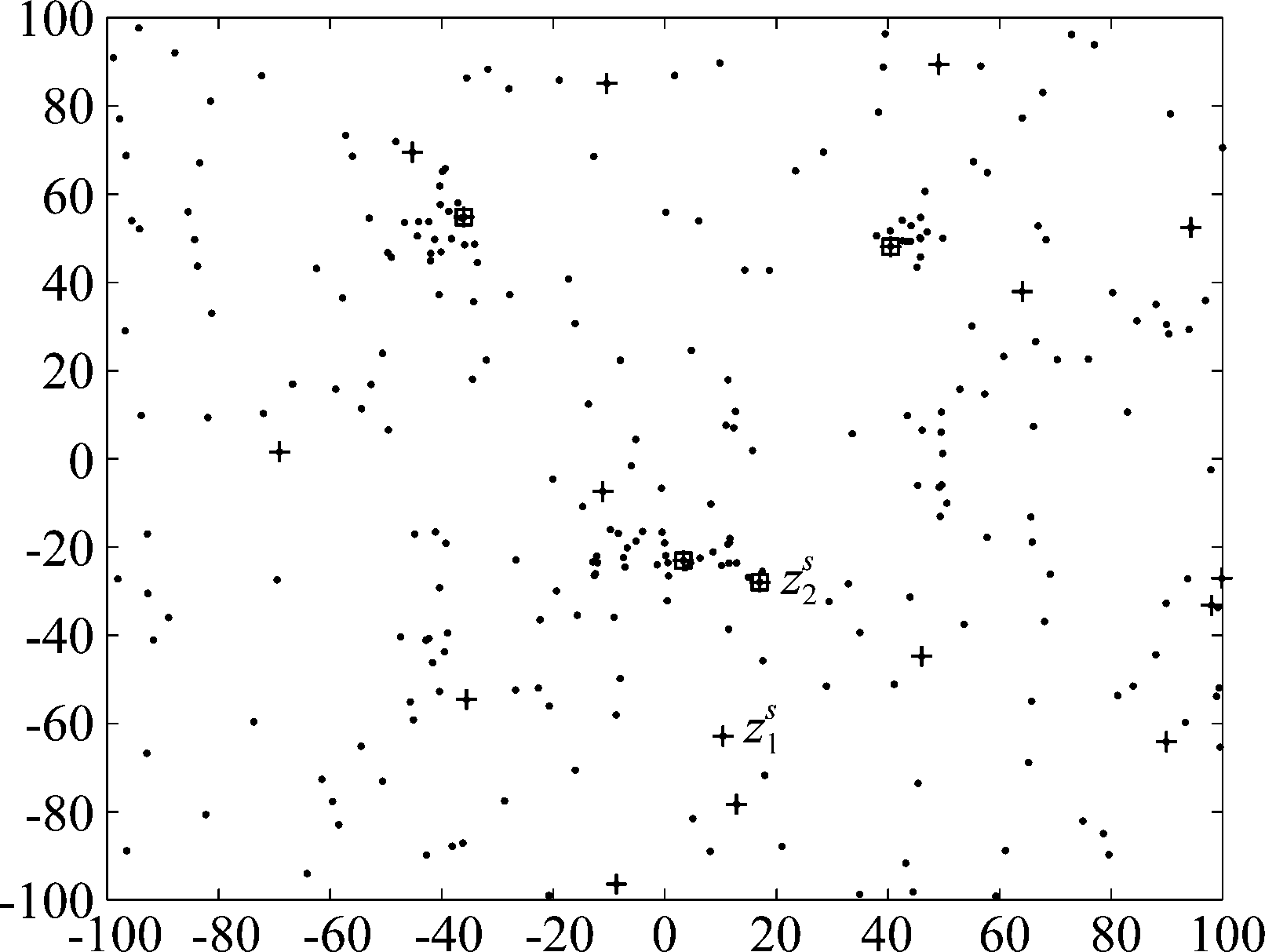
图3 筛选后的数据集
Fig.3 The filtered dataset
筛选后的量测数据集如图3所示,其中数据集Z(“·”),数据集
数据集SL(“+”),数据点和
和“□+ ”)。经过筛选后,数据集SL(19个数据点)变为
(4个数据点)。可以看到,虽然对选定传感器的量测筛选增加了计算量,但是在后续的聚类过程中,减少了计算量。
IMSNP聚类算法:
输入:SL和Z。
输出:簇Ci及其聚类中心
1.计算SL中的数据点
与Z中数据点的欧氏距离,得到距离矩阵MmL×|Z|,对MmL×|Z|每一行由小到大排序,并计算前n个最小值的平均值
2.筛选满足公式(16)数据点,得到数据集
计算中的每一个数据点与其他传感器量测的高斯核距离
返回距离最小的点
当和距离小于截断距离时,判定两个点关联。遍历所有传感器,当关联的数据点数量大于l×r时,判定其为目标量测形成的簇。
3.当ki≥2时,簇Ci为重叠簇,Ci将被进一步分解为满足公式(5)和公式(7)的ki个子簇,遍历中所有的数据点,生成k个簇。
4.检查每一个簇,确保每一个数据点都遵守CL约束,并计算每一个簇的聚类中心
4 实验
本节,我们将IMSNP算法、multi-source n-points算法、MSDPC算法在两种场景中进行对比,第一个场景对应于传感器漏检造成部分目标缺失,同时考虑目标靠近和交叉等情况对多源聚类算法的影响;第二个场景对应于传感器目标检测概率较高,有多种运动模型的线性和非线性运动目标,同时目标的出现和消失随机的场景。在两个实验中,目标的观测噪声均值为0,方差为[16 0;0 16]T(m2)。需要注意的是,虽然提供了噪声的参数,但是三种聚类算法并不需要该参数,而是通过截断距离的计算方法[5,25]从传感器的量测集中学习而得到。
我们使用optimal sub-pattern assignment (OSPA)算法[29]来衡量各个算法的性能,该算法需要两个参数,其中顺序参数p=2确定对异常值的敏感度,截断参数c=100确定分配给基数和定位误差的惩罚相对权重。
4.1 量测缺失条件下多目标聚类
在本实验中,我们构造了4个运动目标,用来测试IMSNP、multi-source n-points算法和MSDPC算法在目标邻近、交叉,以及传感器有漏检情况下的性能,目标的运动区域为[-100,100]×[-100,100](m),4个目标的生存周期均为t∈[1,30],目标的幸存概率为PS=0.98,目标状态转移模型和观测模型为
(18)
其中,Ft-1和Ht分别为状态转移矩阵和观测矩阵,xt为目标的状态,ut-1和μt为均值为0,方差分别为Qt-1和Rt的过程噪声、观测噪声,Ft-1,Ht,Qt-1和Rt分别为:
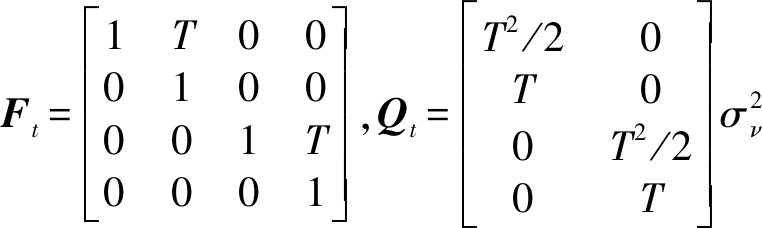
T=1 s,σν=0.1 m/s2。各个目标的初始状态如下:
x(1)=[-60(m),5(m/s),-57(m),4(m/s)]T
x(2)=[-57(m),5(m/s),-72(m),4(m/s)]T
x(3)=[-70(m),5(m/s),80(m),-4(m/s)]T
x(4)=[0(m),0(m/s),80(m),-5(m/s)]T
目标的运动轨迹如图4所示,目标的起始位置标记为“△”,结束位置标记为“□”。
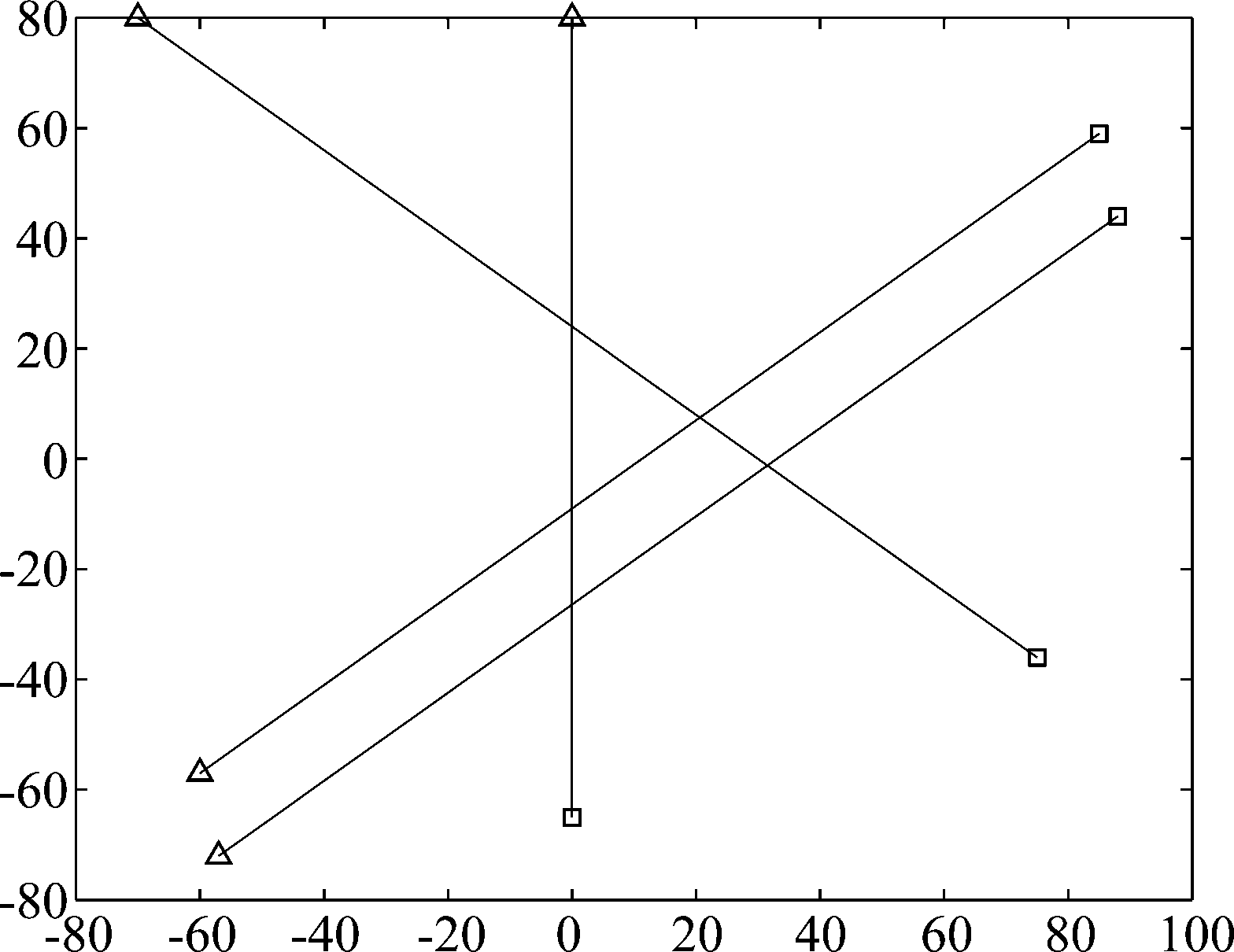
图4 多个相互交叉临近的目标的运动轨迹
Fig.4 The trajectories of multiple targets that cross and close to each other
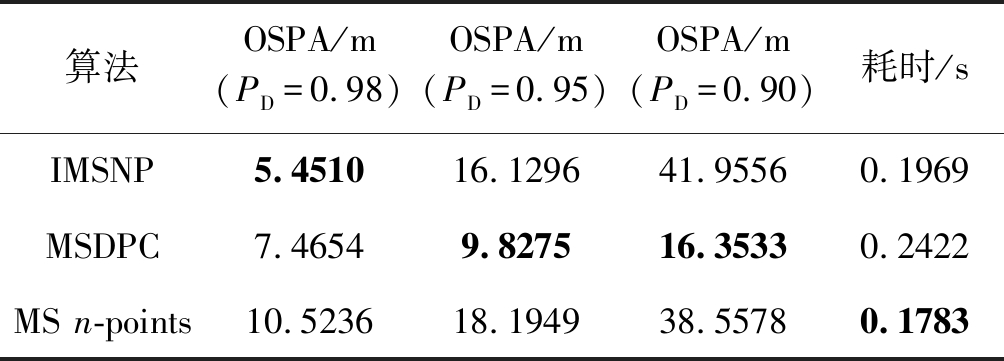
在不同的传感器目标检测概率(PD=0.98,PD=0.95,PD=0.90)条件下,20个独立同分布的传感器100次Monte Carlo实验的不同算法平均OSPA如表1所示。可以看到随着传感器目标检测概率的下降,IMSNP算法和multi-source n-points算法的目标跟踪性能迅速下降,MSDPC的多源聚类算法的目标跟踪性能也相应随之下降,但好于另外两种算法。运行时间方面,multi-source n-points算法耗时最低,MSDPC算法最耗时,IMSNP算法耗时比multi-source n-points算法稍高。综合跟踪精度和平均耗时,在传感器目标检测概率较高的情况下,IMSNP算法是最优的选择;在传感器目标检测概率较低的时候,MSDPC算法是最优的选择。
表1 三种算法的平均OSPA对比
Tab.1 The average OSPA of three algorithms
算法OSPA/m(PD=0.98)OSPA/m(PD=0.95)OSPA/m(PD=0.90)耗时/sIMSNP5.451016.129641.95560.1969MSDPC7.46549.827516.35330.2422MS n-points10.523618.194938.55780.1783
4.2 无先验信息的多目标聚类
在本实验中,我们考虑一个有多个运动模型的场景,各个目标随机出现和消失,目标的运动区域为[-100,100]×[-100,100](m),目标轨迹等参考文献[26]提供的MATLAB代码。在多目标运动场景中,关于杂波和目标动态模型的信息是未知的,唯一已知的信息是多个传感器的量测数据集(二维笛卡尔坐标系中的数据点),每个目标的开始/结束时间、初始位置(“□”)和结束位置(“△”)在目标运动轨迹附近进行了标记,如图5所示。每次扫描杂波的泊松率为10,传感器的目标检测概率为0.98。
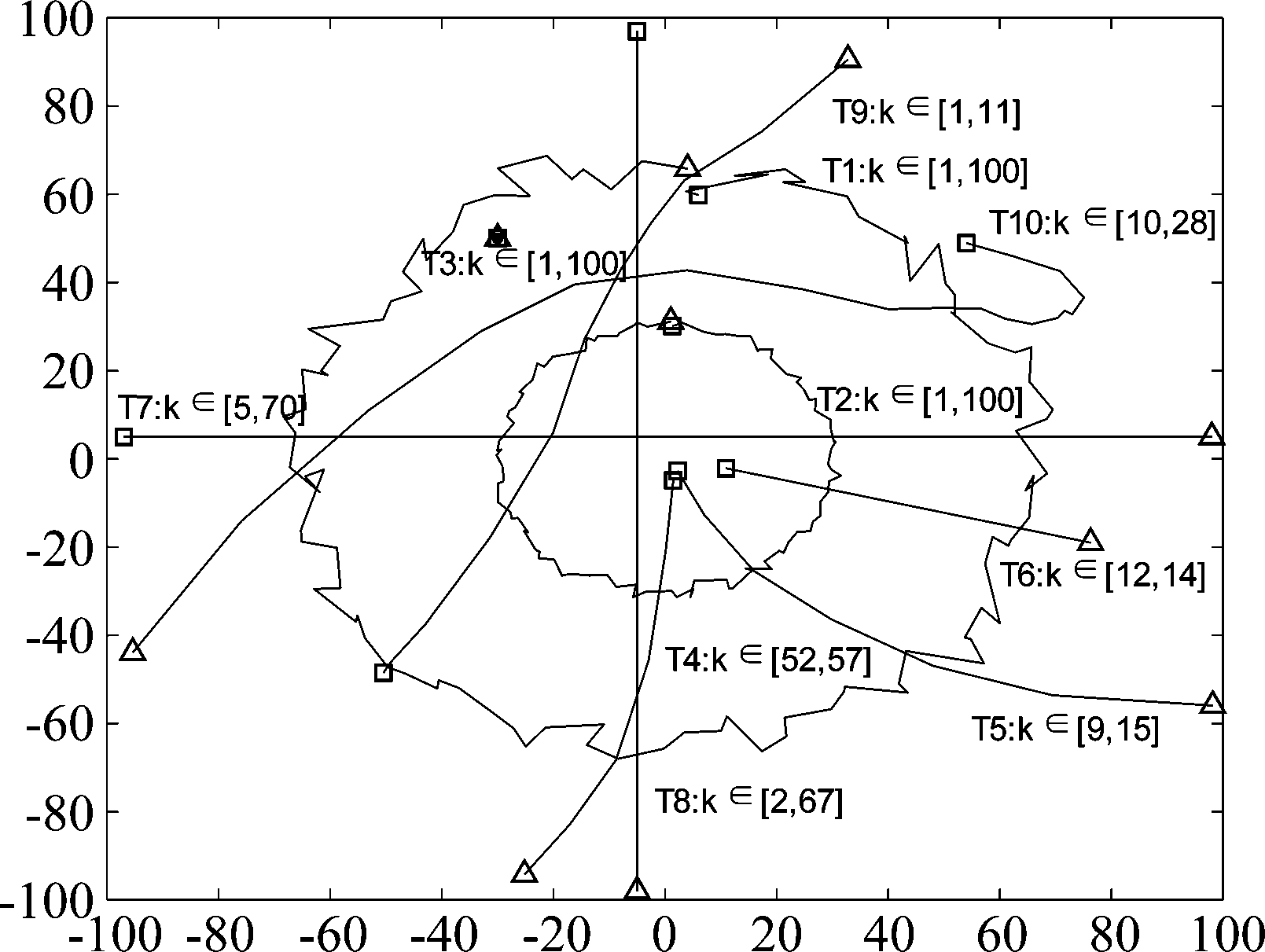
图5 多个目标的运动轨迹
Fig.5 Trajectories of targets
图6给出了50个独立同分布的传感器三种算法经过100次Monte Carlo实验的平均目标个数和平均OSPA距离的对比图,为了更清楚展示效果,截取时间t∈[1,50]的效果图。从图中可以看到:IMSNP算法和MSDPC算法的平均目标数基本和真实目标数重合,multi-source n-points算法的平均目标数在部分时刻有一些波动;平均OSPA距离方面,IMSNP算法(4.4985 m)优于multi-source n-points算法(8.9248 m)和MSDPC算法(5.4018 m);在运算时间方面,IMSNP算法(1.4261 s),优于multi-source n-points算法(1.5096 s),MSDPC算法(4.4406 s)最耗时。
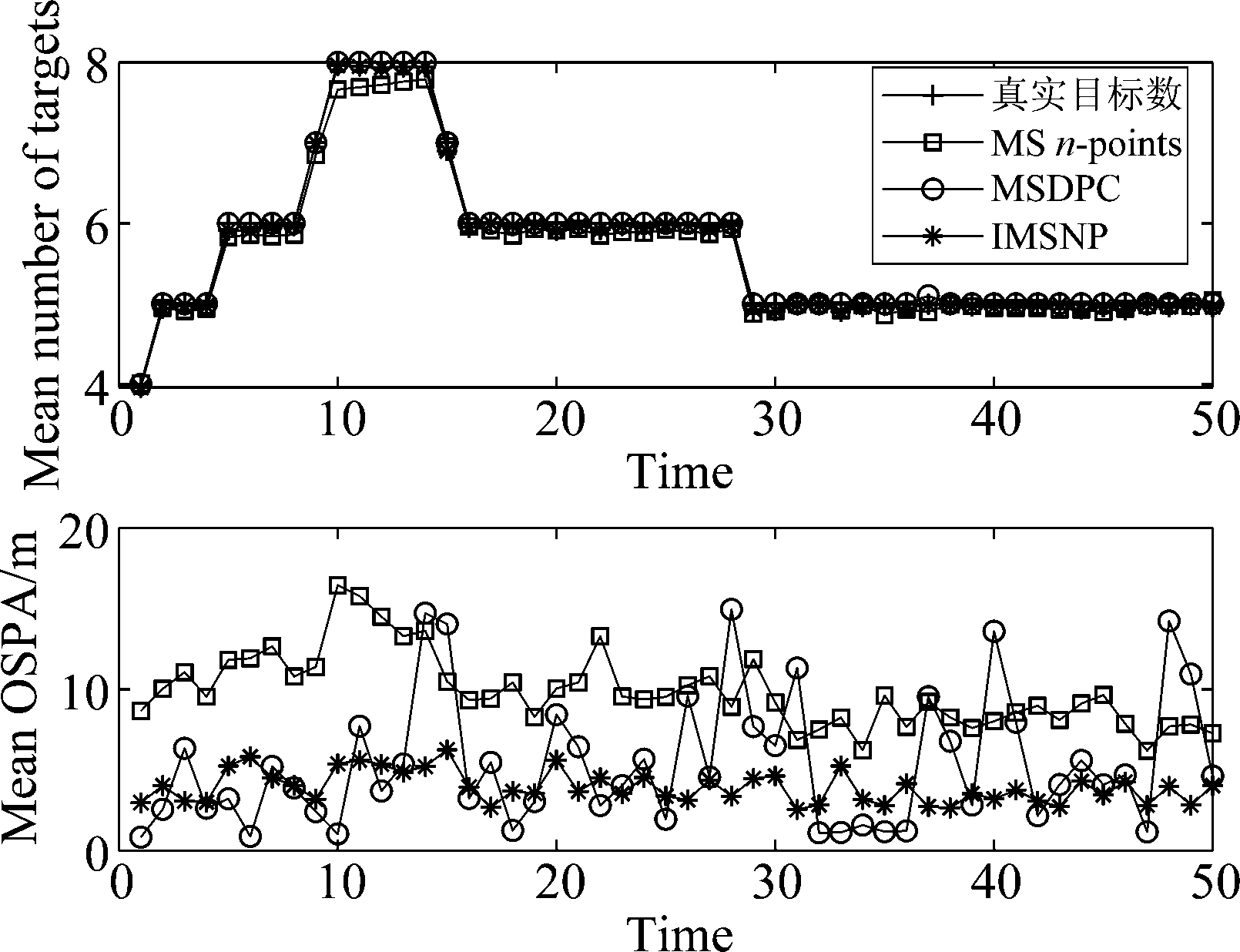
图6 平均目标数和平均OSPA距离对比
Fig.6 Comparison of mean estimated number of targets and mean OSPA
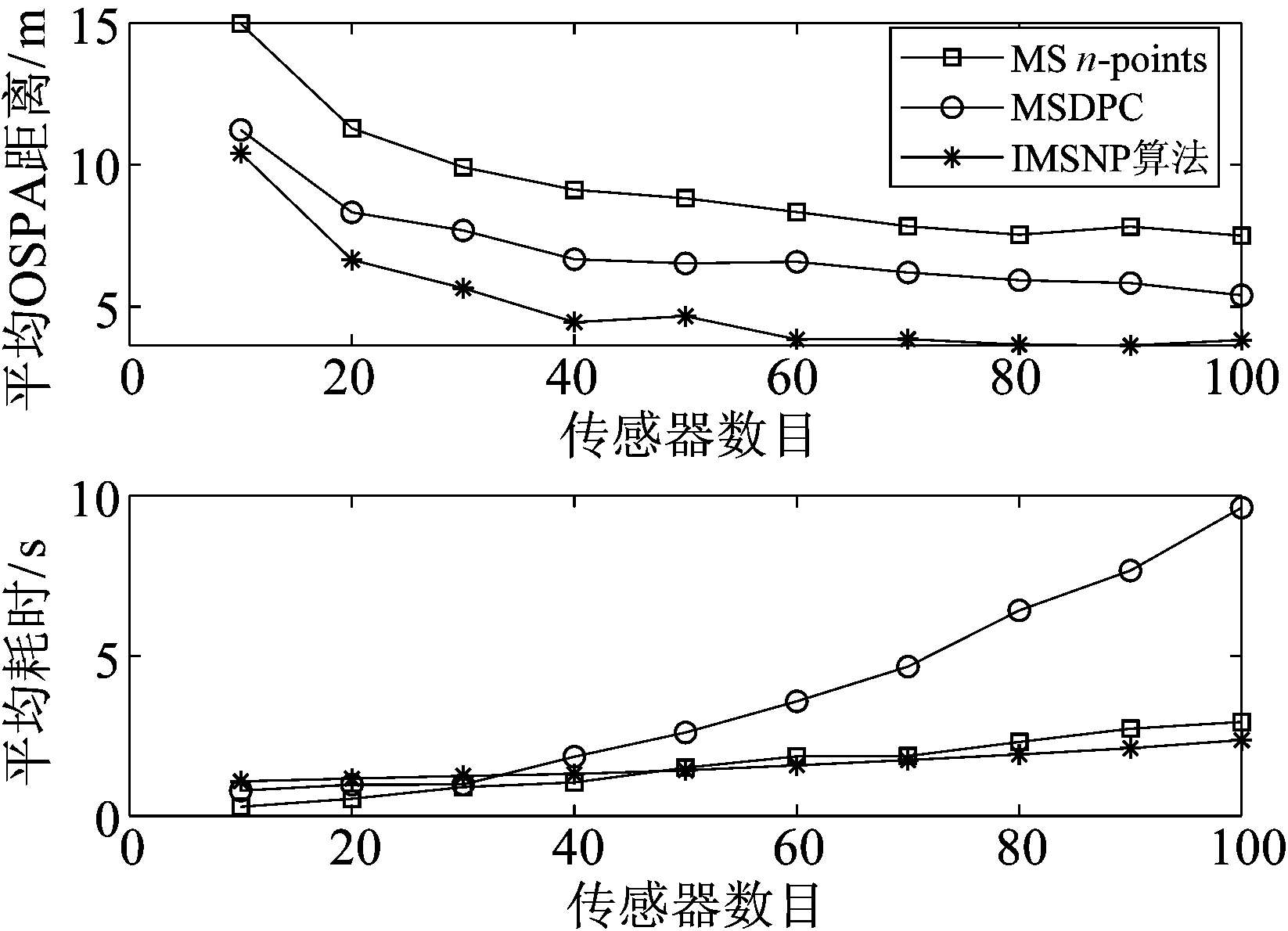
图7 不同数目的传感器的平均OSPA距离和平均耗时对比
Fig.7 Comparison of mean OSPA and mean processing time vs different number of sensors
图7给出了不同数量的传感器100次Monte Carlo实验的平均耗时和平均OSPA效果对比,可以看到IMSNP算法在平均OSPA距离方面优于multi-source n-points算法和MSDPC算法,证明了IMSNP算法的有效性和可靠性。平均耗时方面,MSDPC算法要计算所有的点与点的距离,导致计算量最大,耗时最多;当传感器数量n≤40时,IMSNP算法平均耗时多于multi-source n-points算法,当传感器数量n>50时,IMSNP算法平均耗时少于multi-source n-points算法,说明IMSNP算法通过筛选疑似目标的量测,减少了运算量,在传感器数量较多的时候更有优势。
5 结论
在本文中,我们提出了一种改进的约束聚类算法用来解决多传感器多目标跟踪问题。多传感器的量测数据可能受未知的观测噪声和漏检概率影响,簇/目标的数目未知。改进的方法可以有效筛选出疑似目标的量测数据,并优先对该类数据进行聚类,在传感器目标检测概率较高的场景中,与同类算法相比,聚类精度大大提升,且随着传感器数量的增加,运算时间也有所降低。
[1] Belkin M, Niyogi P. Laplacian Eigenmaps for dimensionality reduction and data representation[J]. Neural Computation, 2003, 15(6): 1373-1396.
[2] Felzenszwalb P F, Huttenlocher D P. Efficient Graph-Based Image Segmentation[J]. International Journal of Computer Vision, 2004, 59(2): 167-181.
[3] Li J, Wang J Z. Real-Time Computerized Annotation of Pictures[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2008, 30(6): 985-1002.
[4] Liu H, Yu L. Toward integrating feature selection algorithms for classification and clustering[J]. IEEE Transactions on Knowledge and Data Engineering, 2005, 17(4): 491-502.
[5] Rodriguez A, Laio A. Clustering by fast search and find of density peaks[J]. Science, 2014, 344(6191): 1492-1496.
[6] Ester M, Kriegel H, Sander J. A density-based algorithm for discovering clusters in large spatial Databases with Noise[C]∥Knowledge Discovery and Data Mining, 1996: 96(34): 226-231.
[7] Jain A K, Murty M N, Flynn P J. Data clustering: a review[J]. ACM Computing Surveys, 1999, 31(3): 264-323.
[8] Wong J A H A. Algorithm AS 136: A K-Means Clustering Algorithm[J]. Journal of the Royal Statistical Society. Series C (Applied Statistics), 1979, 28(1): 100-108.
[9] Shi J, Malik J. Normalized cuts and image segmentation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2000, 22(8): 888-905.
[10] Navarro J F, Frenk C S, White S D. A Universal density profile from hierarchical clustering[J]. The Astrophysical Journal, 1997, 490(2): 493-508.
[11] Wagstaff K, Cardie C, Rogers S, et al. Constrained k-means clustering with background knowledge[C]∥International Conference on Machine Learning, 2001, 1: 577-584.
[12] Han L, Luo S, Wang H. An Intelligible Risk Stratification Model Based on Pairwise and Size Constrained Kmeans[J]. IEEE Journal of Biomedical and Health Informatics, 2017, 21(5): 1288-1296.
[13] Hansen P, Delattre M. Complete-Link Cluster Analysis by Graph Coloring[J]. Journal of the American Statistical Association, 1978, 73(362): 397- 403.
[14] Miyamoto S, Terami A. Constrained agglomerative hierarchical clustering algorithms with penalties[C]∥2011 IEEE International Conference on Fuzzy Systems (FUZZ-IEEE 2011). IEEE, 2011: 422- 427.
[15] Pelleg D, Moore A W. X-means: Extending k-means with efficient estimation of the number of clusters[C]∥International Conference on Machine Learning, 2000, 1: 727-734.
[16] Akaike H T. A New Look at the Statistical Model Identification[J]. IEEE Transactions on Automatic Control, 1974, 19(6): 716-723.
[17] Davisson L. Rate Distortion Theory: A Mathematical Basis for Data Compression[J]. IEEE Transactions on Communications, 2003, 20(6): 1202-1202.
[18] Arthur D, Vassilvitskii S. k-Means++: The advantages of carefull seeding[J]. Proceedings of the Eighteenth Annual ACM-SIAM Symposiumon Discrete algorithms, Society for Industrial and Applied Mathematics, 2007, 11(6): 1027-1035.
[19] Coué C, Fraichard T, Bessiere P, et al. Using Bayesian programming for multi-sensor multi-target tracking in automotive applications[C]∥2003 IEEE International Conference on Robotics and Automation, 2003, 2: 2104-2109.
[20] Qiao D, Liang Y, Jiao L. Boundary detection-based density peaks clustering[J]. IEEE Access, 2019, 7: 152755-152765.
[21] Jiang J, Chen Y, Meng X, et al. A novel density peaks clustering algorithm based on k nearest neighbors for improving assignment process[J]. Physica A: Statistical Mechanics and its Applications, 2019, 523: 702-713.
[22] Li T, Corchado J M, Sun S. Partial consensus and conservative fusion of Gaussian mixtures for distributed PHD fusion[J]. IEEE Transactions on Aerospace and Electronic Systems, 2018, 55(5): 2150-2163.
[23] Vo B, See C M, Ma N. Multi-Sensor Joint Detection and Tracking with the Bernoulli Filter[J]. IEEE Transactions on Aerospace and Electronic Systems, 2012, 48(2): 1385-1402.
[24] Li T, Corchado J M, Sun S, et al. Clustering for filtering: Multi-object detection and estimation using multiple/massive sensors[J]. Information Sciences, 2017, 388-389: 172-190.
[25] Li T, Pintado F D L P, Corchado J M, et al. Multi-source Homogeneous Data Clustering for Multi-target Detection from Cluttered Background with Misdetection[J]. Applied Soft Computing, 2017, 60: 436- 446.
[26] Li T, Corchado J M, Chen H. Distributed Flooding-then-Clustering: A Lazy Networking Approach for Distributed Multiple Target Tracking[C]∥International Conference on Information Fusion, 2018: 2415-2422.
[27] Li T, Prieto J, Fan H. A Robust Multi-Sensor PHD Filter Based on Multi-Sensor Measurement Clustering[J]. IEEE Communications Letters, 2018, 22(10): 2064-2067.
[28] Fan J, Xie W, Du H, et al. A Robust Multi-Sensor Data Fusion Clustering Algorithm Based on Density Peaks[J]. Sensors, 2019, 20(1).
[29] Shi Q, Zhang T, Cui G, et al. Multi-target Tracking Algorithm Based on Multi-source Clustering in Distributed Radar Network[C]∥2019 22th International Conference on Information Fusion (FUSION). IEEE, 2019: 1- 6.
[30] Schuhmacher D, Vo B T, Vo B N. A consistent metric for performance evaluation of multi-object filters[J]. IEEE Transactions on Signal Processing, 2008, 56(8): 3447-3457.
