1 引言
随着手持设备的发展与普及,人们可以利用手机、数码相机等设备进行简单的视频拍摄。与专业摄像机相比,手持设备拍摄出的视频在视觉上常常会存在不希望出现的抖动情况。因此,如何消除视频序列中的随机抖动,成为了近年来研究学者们的研究热点。
视频稳像算法包括二维稳像方法、三维稳像方法和基于深度学习的稳像方法。相比于三维稳像方法和基于深度学习的稳像方法,二维稳像方法具有处理速度快的优点,容易做到实时稳像,近年来受到关注。二维视频稳像算法包括以下三个步骤:(1)估计原始摄像机路径(即全局运动);(2)对摄像机路径进行平滑或者拟合;(3)对原始路径进行运动补偿,生成稳定的视频。其中摄像机路径估计是关键环节。
目前常用的全局路径估计方法包括Liu等人[1]和Yu等人[17]的基于网格的图像局部的全局运动估计和Grundmann等人[2]的基于特征点跟踪的全局运动估计,其中Bundled Paths算法[1]虽然精度高但是计算复杂度高,耗时长,而L1范数优化算法[2]利用单一的运动模型,计算复杂度小,更容易做到实时稳像。但是由于原始路径存在高频抖动噪声,导致L1范数优化算法[2]路径拟合结果产生误差,从而使得稳定后的视频存在残余抖动,稳像效果不佳。如果能通过路径平滑将原始视频路径中的高频抖动噪声去除,使路径拟合结果更准确,则有望彻底去除抖动。另外,L1范数优化算法中未考虑视频缩放尺度的路径拟合问题,导致稳定后的视频在缩放层面的平滑度不够。
针对以上问题,本文受[22-23]启发,提出了路径平滑步骤:通过Savitzky-Golay滤波(简称S-G滤波)算法去除相机原始路径的高频抖动噪声。经过处理后的相机运动路径去除了高频噪声,使得后续的路径拟合结果更准确。S-G滤波算法[15,22]是一种信号处理领域常见的平滑算法,可以滤除信号中的高频分量,实现降噪,同时保留原信号形状,而且算法计算速度很快,适用于实时处理应用。
本文提出了一种S-G滤波和L1范数优化相结合的数字稳像方法。首先对原始视频图像序列进行基于特征点跟踪的全局运动估计;其次通过S-G滤波算法对提取的全局运动路径进行平滑处理,去除相机全局运动高频噪声;最后采用优化的L1范数优化算法进行稳定路径的拟合。通过对不稳定视频帧进行运动补偿,合成了摄像机的稳定视频序列。在视频稳定效果上,超过了原有的L1范数优化算法和Wang等人[20]的深度学习方法,略低于Bundled Paths算法,算法运行时间接近于Bundled Paths算法的1/5。
2 相关工作
目前,已经有很多视频稳像的方法,包括二维、三维和基于深度学习的视频稳像方法都对视频有一定的稳像效果。
二维稳像方法的模型简单,计算复杂度低。首先估计相机的运动,提取运动轨迹。全局运动估计的方法包括下列方法:Chen等人[3]利用块匹配运动估计得到参数运动模型;Erturk[4]使用相位相关算法进行全局运动估计;Xu等人[22]使用Horn-Schunck算法进行全局运功估计。Lucas与Kanade[5]的金字塔光流为很多稳像算法的全局运动估计提供了基础;基于Harris算法[6]、FAST算法[7]、KLT算法[8]等的特征点法构建变换矩阵描述相机的运动。其次,对相机的运动路径进行运动补偿,总体上有两种处理方式,运动路径平滑和运动路径拟合。运动路径平滑方法是对抖动相机的运动路径进行噪声的平滑,以消除高频和低频抖动。Yasuyuki等人[9]使用高斯滤波器进行平滑;Erturk等人[10]使用卡尔曼滤波器进行运动平滑,实现稳像;Xu等人[22]和Tsoligkas等人[23]对相机路径进行基于S-G滤波器的路径平滑实现视频稳像。Jiang等人[24]将利用原始视频序列生成广角视图,通过抽取视频帧合成稳定视频。Yang等人将粒子滤波器首先引入视频稳像领域进行路径平滑。运动路径拟合方法模仿专业电影摄像技巧,将相机路径由静止、直线和抛物线组合而成,不仅能够去除抖动视频的高低频抖动,更可以使稳定后的视频更符合人观看视频的主观习惯。Chen等人[11]将相机路径拟合成折线路径。Grundmann等人[12]利用L1范数优化处理算法将相机路径用静止、直线、抛物线三种线条拟合,并分配不同的权重,取得了不错的效果。新兴的二维算法如Liu等人[1]将视频帧图像分为大小相等的网格进行基于“as-similar-as-possible”思想的多路径稳像算法等方法取得了优越的效果,但是算法复杂性较高,处理速度慢于传统二维算法。
三维稳像方法和二维方法具有同样的处理步骤,估计相机的三位运动模型,进行运动路径平滑和生成稳定视频。Liu等人[12]利用SFM算法进行相机路径估计,并进行运动平滑。最后利用3D场景点云和参考帧图像进行稳定视频的生成。三维稳像的运动路径平滑基于非线性滤波,Lee等人[13]将运动数据投射到向量空间进行滤波,最后将数据投射回运动空间。
基于深度学习的方法:随着卷积神经网络(CNN)的发展,近年来一些人利用预训练好的网络进行视频稳像工作。Wang等人[20]提出了Stabnet模型,首次将卷积神经网络引入视频稳像任务,通过历史帧直接计算当前帧的单应性矩阵。Huang等人[18]利用Siamese网络和之前的帧序列预测当前帧的运动矩阵。Yu等人[19]直接将帧间的外观变化建模为连续帧的密集光流场。Lin等人[21]提出了基于变形网格的算法,提高了相邻帧的连续性。端到端的算法无需设计复杂的平滑算法和拟合算法,只需通过对网络进行训练实现稳像,但是模型训练要求大量的稳定-不稳定配对的数据集。而且算法计算速度较慢,很难应用于实时计算。
3 本文方法
3.1 方法概述
本文的方法主要分为四个部分,分别是运动估计、S-G平滑滤波、 L1范数优化和运动补偿,如图1所示:首先对输入的视频进行全局运动估计,分别检测出视频每帧图像的角点,每两帧之间检测出的角点进行配对,根据配对成功的角点计算每两帧之间的仿射变换矩阵。从仿射变换矩阵中提取出后一帧相对于前一帧的全局运动变量,即水平方向位移量、垂直方向位移量、倾斜角度、缩放尺度。将视频图形帧序列所有帧之间的全局运动变量分别叠加后,得到摄像机的全局运动路径。
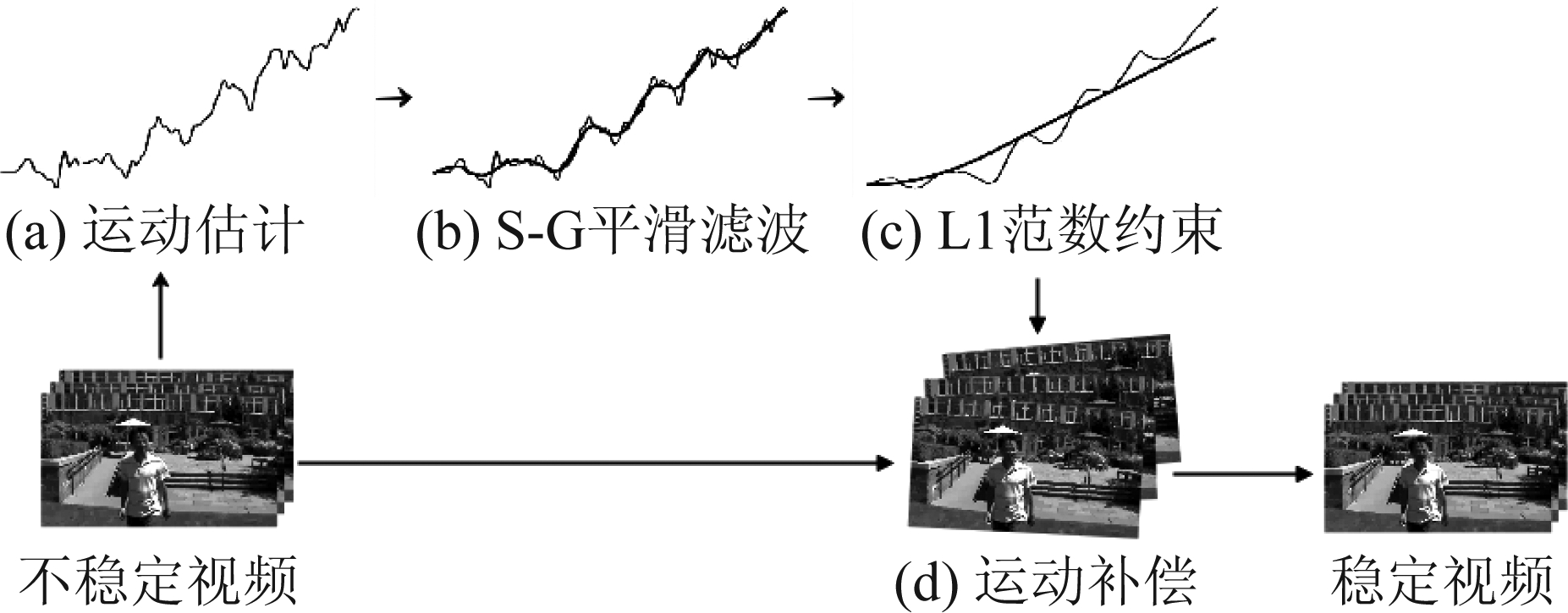
图1 算法流程图
Fig.1 Algorithm flow chart
其次,对全局运动路径进行基于S-G滤波算法的平滑处理,去除全局运动路径中的高频分量,消除高频抖动对后续运动路径拟合的影响。
进一步,对经过平滑的运动路径进行基于L1范数优化算法的路径拟合。本文对原算法进行了优化,在Grundmann等人[2]的基础上加入了缩放尺度的路径拟合,并改变了权重。得到了平滑的运动路径。
最后,计算稳定后每一帧的运动路径相对于原始运动路径的补偿量,对每一帧的图像进行运动补偿,得到稳定的视频。
3.2 全局运动估计
首先,对输入的视频进行全局运动估计,计算相机的运动路径。两帧图像在二维空间内存在平移、倾斜、缩放等变换。本文采用了四参数仿射变换模型进行全局运动的估计。仿射变换矩阵模型如下所示:
(1)
x和y分别代表后一帧图像相对于前一帧图像的水平和垂直位移量,s代表缩放尺度,θ代表倾斜角度。利用两帧之间匹配的角点计算仿射变换矩阵,本文采用Shi-Tomasi算法[8]进行角点检测。

图2 视频中第t帧和第t+1帧之间的匹配角点
Fig.2 Matched corner in video frame t and video frame t+1
角点是图像中的极值点。在同一场景内,角点具有稳定的性质。Shi-Tomasi算法[8]利用固定尺寸的滑动窗口在帧图像的灰度图上移动,对于窗口在任意方向的移动都有明显灰度变换的情况,定义该位置为角点。每帧图像检测100个角点,得到第t帧的角点序列ft。
其次,利用Lucas-Kanade稀疏光流法跟踪角点ft,得到角点在t+1帧的位置ft+1。
Lucas-Kanade稀疏光流法计算两帧之间的稀疏光流,并基于亮度恒定假设跟踪两帧之间相匹配的角点。两帧之间的角点跟踪结果如图2所示,匹配角点用黑色直线相连。为方便观察,图中仅展示部分角点的跟踪结果。
对匹配的角点利用RANSAC算法[14]进行随机抽样和多次迭代,每次抽取10对匹配角点并迭代20次计算两帧之间的最优仿射变换矩阵A。
3.3 基于S-G滤波算法的运动路径平滑3.3.1 S-G滤波算法
S-G滤波器(也称卷积平滑)被广泛地应用于数据流平滑去噪处理,是一种在时域内基于区域性多项式最小二乘法拟合的滤波方法。最大的特点是去除信号噪声的同时保持信号的形状、宽度不变。
定义一个宽度为n=2m+1的窗口,对原始曲线进行自左至右的测量。考虑一组以数据点yt为中心的2m+1个数据,对这组数据点进行基于k-1次多项式的拟合,如式(2)所示。
y=a0+a1·x+a2·x2+...+ak-1·xk-1
(2)
为使方程有解,一般令n大于k。对于2m+1个数据,分别有2m+1个方程,因此可以将拟合方程表示为矩阵形式。设数据值向量为Y,系数矩阵为A,自变量矩阵为X,残差为ε。方程可写为如下形式。
Y=X·A+ε
(3)
经过最小二乘法解得的稀疏矩阵为A^,其值如式(4)所示。拟合后的数据预测值为Y^,其值如式(5)所示。
A^=(XT·X)-1·XT·Y
(4)
Y^=X·A=X·(XT·X)-1·XT·Y
(5)
窗口自左至右滑动,直至拟合完所有数据点。拟合后的曲线即被去除了原有的高频分量。
3.3.2 运动路径平滑
原始路径中存在大量低高频分量,其中大部分来源于拍摄者手部的快速抖动造成的摄像机镜头抖动。本文对相机的原始路径进行拟合,从而生成稳定的相机路径。而原始运动路径中的高频分量噪声对于路径拟合是无益的,因此需要首先将其去除。对高频分量的平滑操作可以选取上述S-G滤波算法,具体过程如下。
将每两帧之间的运动分量分别累加,得到原始视频的运动路径,如式(6)所示,t为帧数,k是视频帧数。同理可求出Cy、Cθ、Cs,分别代表四个维度的相机运动轨迹。
(6)
将得到的运动轨迹分别进行平滑。通过实验发现,缩放维度的运动路径不存在高频分量,经过滤波处理后会增大误差。因此将路径的值Cx、Cy、Cθ分别通过S-G滤波器进行平滑处理。平滑效果如图3所示。图中细曲线为相机原始的水平维度运动路径Cx,粗曲线为平滑后的运动路径,横坐标为时间(帧),纵坐标为运动路径(像素)。经过平滑后,原始运动路径的高频分量被成功去除,同时保留了包含有效信息的低频分量,更有利于后续的路径拟合处理。
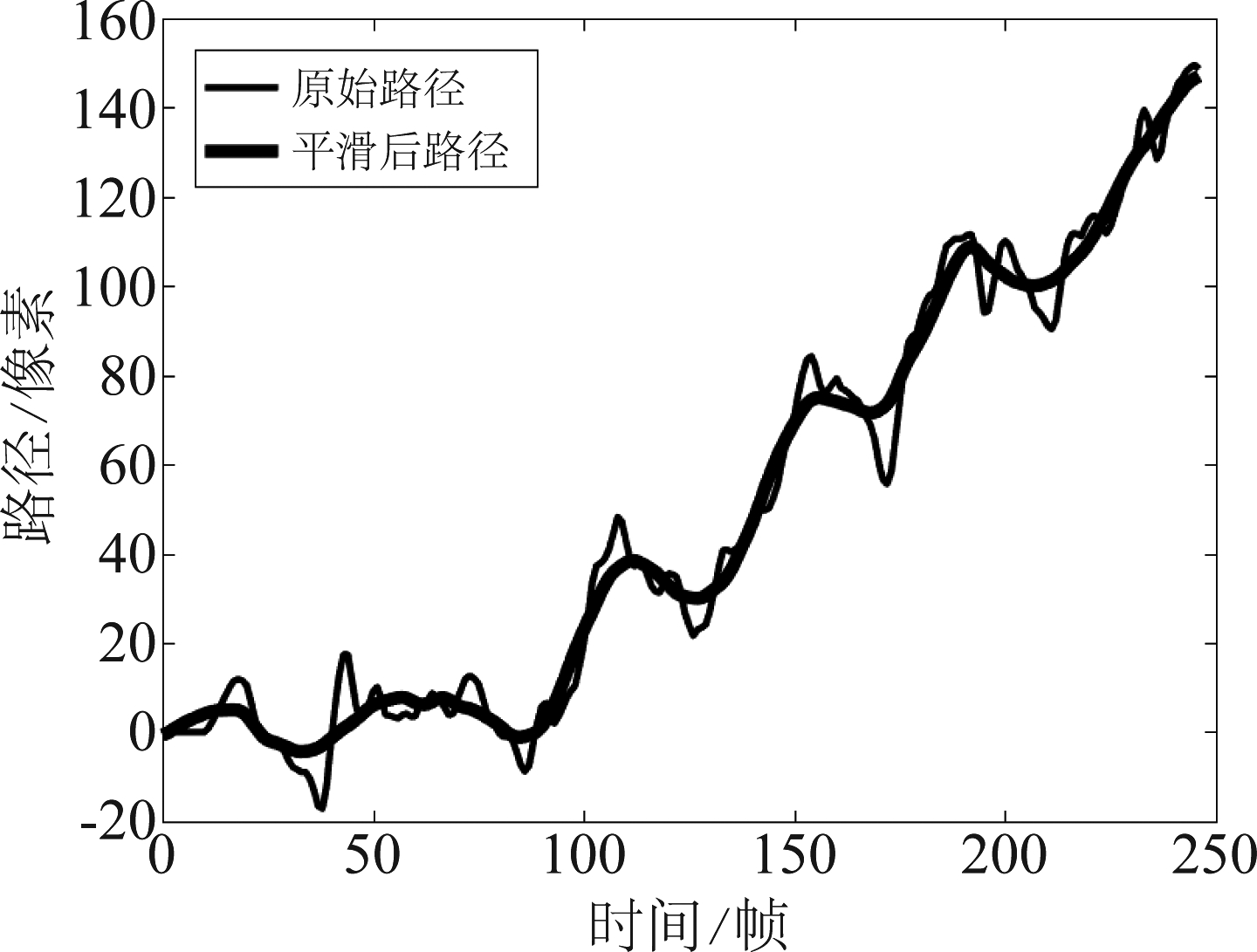
图3 S-G平滑效果图
Fig.3 S-G smooth renderings
3.4 基于优化的L1范数优化的路径拟合
为了得到稳定的相机运动路径,同时让相机路径更符合专业相机的拍摄风格,本文采用了Grundmann等人[2]的L1范数优化算法,并对算法进行了优化,增加了稳像的效果。
将经过平滑后的相机运动路径定义为![]() 每两帧之间的全局运动变量定义为运动矢量为
每两帧之间的全局运动变量定义为运动矢量为![]() 可以如式(7)所示化简。
可以如式(7)所示化简。
(7)
为了得到稳定的视频帧序列,需要分别对每帧图像进行运动补偿,定义补偿量为![]() 中包含水平、垂直、倾斜角度、缩放尺度四个维度的补偿值。定义稳定后的相机运动路径为Pt,那么Pt可以表示为
中包含水平、垂直、倾斜角度、缩放尺度四个维度的补偿值。定义稳定后的相机运动路径为Pt,那么Pt可以表示为
(8)
稳定后的相机路径由下面三种线条进行拟合:
(1)相机静止,即相机运动路径的一阶导数D(P)为零。使用前向差分公式计算D(P),并将式(7)、(8)代入公式并化简,即
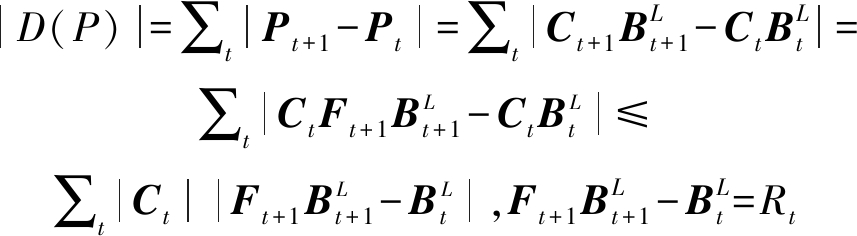
(9)
因此,最小化D(P)即最小化残差Rt。
(2)相机匀速移动,即相机运动路径的二阶导数D2(P)为零,即
|D2(P)|=∑t|DPt+2-DPt+1|=
∑t|Pt+2-2Pt+1+Pt|≤|Rt+1-Rt|
(10)
最小化D2(P)即最小化残差差分Rt+1-Rt。
(3)相机匀加速,即相机运动路径的三阶导数D3(P)为零,即
|D3(P)|≤|Rt+2-2Rt+1+Rt|
(11)
最小化D3(P)即最小化Rt+2-2Rt+1+Rt。
因此,路径拟合的目标函数为:
O(P)=ω1|D(P)|+ω2|D2(P)|+ω3|D3(P)|
(12)
其中,ω1、ω2、ω3是三种线条的权重,代表拟合后曲线中相应线条所占的比例。原始算法对相机水平、垂直、倾斜角度进行了基于公式(12)的路径拟合,本文在此基础上将缩放尺度考虑在内,对缩放尺度的路径同样进行了拟合,并基于本文的任务设置了稳像效果更好的权重。最小化目标函数后,便可得到补偿量![]() 的最优解。
的最优解。
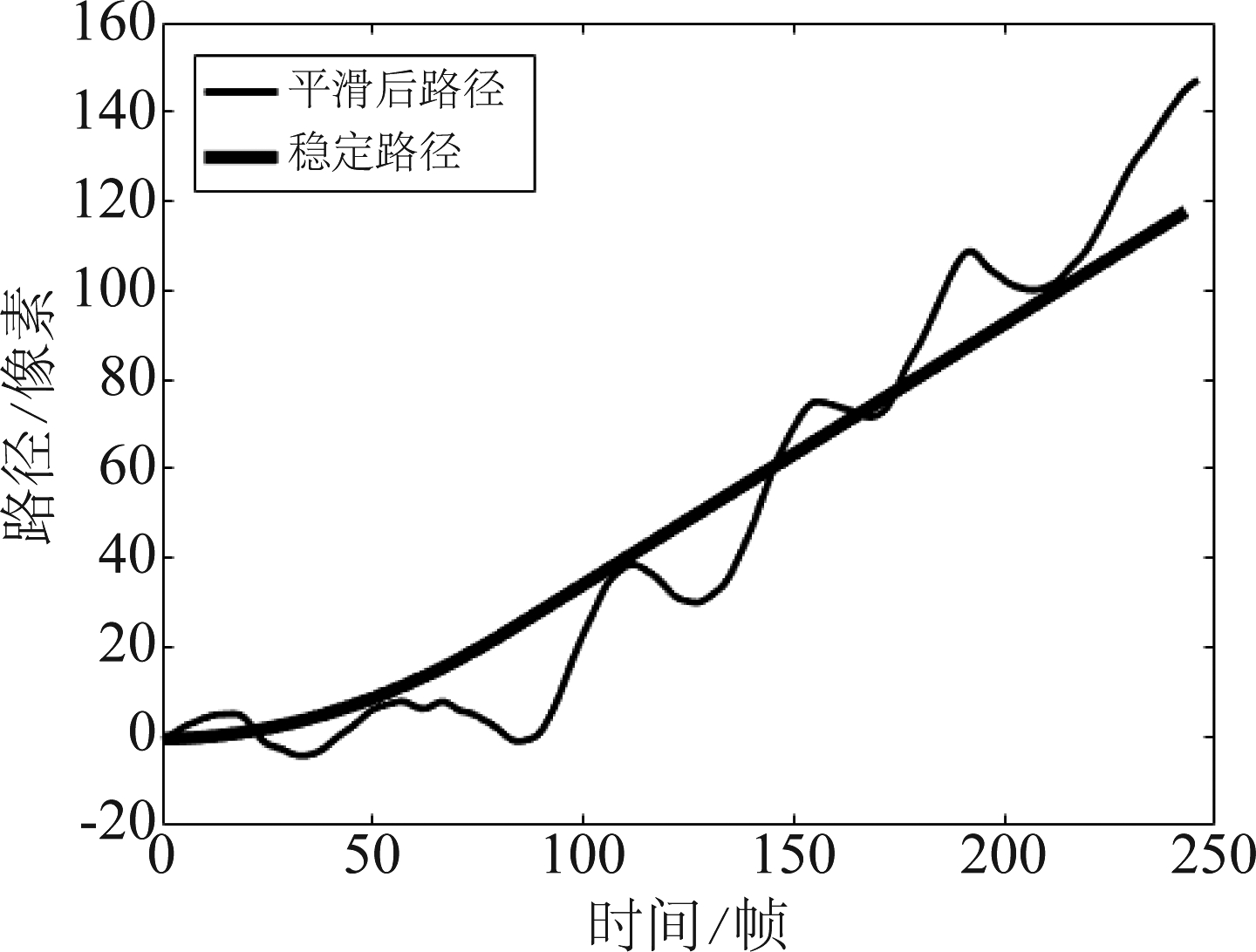
图4 路径拟合效果图
Fig.4 Path fitting renderings
拟合效果如图4所示。图中细曲线是平滑后的相机水平方向路径![]() 粗曲线是利用
粗曲线是利用![]() 拟合的水平方向稳定路径。
拟合的水平方向稳定路径。
3.5 运动补偿
经过路径平滑和路径拟合步骤后得到了稳定的相机运动路径Pt。需要根据稳定的相机运动路径Pt和原始相机运动路径Ct之间的关系(即补偿量Bt)得到稳定视频的图像帧序列,生成稳定的视频。由于原始相机路径一共经过了两次处理(路径平滑和路径拟合),因此补偿量由两部分组成,定义如下:

图5 裁剪范围示例
Fig.5 Clipping range example
![]()
(13)
![]() 已经通过3.4节中介绍的路径拟合算法求得,还需要求解
已经通过3.4节中介绍的路径拟合算法求得,还需要求解![]() 可以由平滑后的路径和原始路径求解,数学表示为:
可以由平滑后的路径和原始路径求解,数学表示为:
(14)
原始相机运动路径Ct经过运动补偿量Bt 进行补偿后得到稳定视频路径Pt,如公式(15)所示。
Pt=CtBt
(15)
将公式(14)代入到公式(15),得到最终的运动补偿公式:
(16)
对公式(16)的求解即可得到稳定后的视频帧图像序列。
进行运动补偿后,图像的位置和姿态发生了改变,会在视频边界处产生空白区域,影响视觉效果。因此需要对图像进行裁剪。裁剪值为运动补偿量Bt中的水平和垂直方向的最大补偿值Bx(max)和By(max)。将经过裁剪的图像序列恢复成视频后,即可得到稳定视频。
4 实验
4.1 实验细节
借鉴文献[16]的方法,视频的稳定效果可以通过峰值信噪比(PSNR)评估。
一段绝对稳定的视频图像序列的运动轨迹十分平滑,每两个连续帧之间的像素误差很小。因此,一段视频图像序列的每两个连续帧之间的PSNR值越大,序列就越稳定。本文测量了每段视频的平均PSNR值作为评估指标。
(17)
在S-G滤波平滑部分,进行了对比实验,对窗口宽度n和拟合多项式的阶次k两个参数进行了不同的取值,观察同一段视频的稳像结果,如图6所示。纵坐标是多项式的阶次k,横坐标是窗口宽度n,图中颜色越深表示PSNR值越大。从图中看出,k取7、9、13时出现了稳像失败的情况,随着n值的升高,PSNR值越大。同时观察n在高取值范围的稳像视频效果,发现某些视频的裁剪率过大,导致视频不完整。因此,为了保持稳像效果、视频完整性以及算法实时性之间的平衡,本文将窗口宽度n设置为63,将多项式阶次k设置为3。

图6 S-G滤波对比实验结果
Fig.6 Contrast experiment result of S-G filter
本文用python实现本文的方法。实验数据集来自于文献[1]提供的稳像数据集,包含6种场景共144段视频(5~20秒),分别是:(1)Crowd,(2)parallax,(3)Quick Rotation,(4)Regular,(5)Zooming,(6)Running。
本文选择了近年来在二维稳像方法中稳像效果较好的Liu等人[1]的Bundled Paths方法、本文的基准模型Grundmann等人[2]的L1范数优化算法和当前结果较好的Wang等人[20]的Deep Learning方法进行对比实验。
4.2 结果分析4.2.1 运行时间的比较
本文测量了几种方法处理同样分辨率的一帧图像所需要的时间。结果如表1所示。处理同样分辨率的视频,L1范数优化算法的75 ms/帧比本文方法的82 ms/帧稍快,而二者均明显快于Bundled Paths方法的392 ms/帧。而Yu等人[19]的基于深度学习算法处理速度明显慢于其他方法,不利于稳像的实时性。Wang等人[20]的Deep Learning方法处理速度快,可以做到实时稳像。但同时具有网络模型复杂,参数量大的缺点,需要21.3 Mb内存和GPU运算,而本文方法模型仅有35 Kb大小和CPU运算,更适合轻量级的设备。
表1 运行时间的比较
Tab.1 Run time comparison

视频稳像方法分辨率/像素时间/msBundled Paths1280×720392L1范数优化1280×72075Yu等人-6000本文方法1280×72082Deep Learning640×3603
4.2.2 稳像效果对比
视频的稳像效果由PSNR值评估。不同方法的稳像视频PSNR值如图7所示。
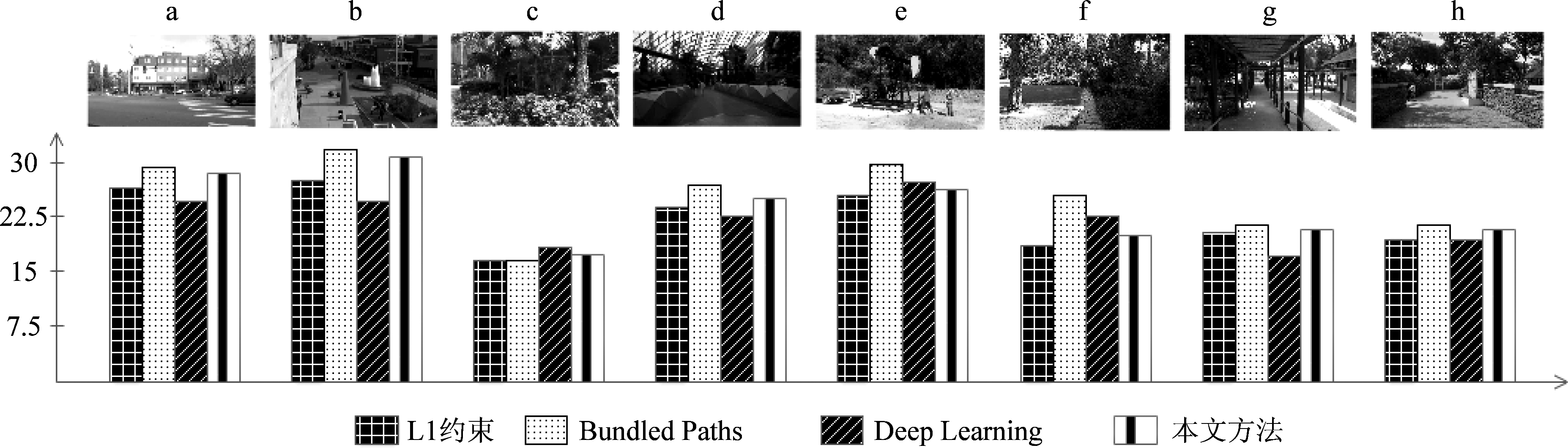
图7 稳像实验结果
Fig.7 Video stabilization experiment results
通过实验结果可以看出,大部分情况下Bundled Paths方法比本文方法略好,从第(c)段视频的实验结果可以看出,本文方法的结果在某些情况下好于Bundled Paths方法。从整体来看,本文的方法优于L1范数优化算法结果和Deep Learning方法。
本文方法优于L1范数优化算法和Deep Learning方法的原因是引入了基于S-G滤波的路径平滑算法。本文进行了路径平滑实验,以图7第(a)段视频为例进行分析,实验结果如图8所示。(a)(c)中曲线为相机在垂直方向的原始路径;(b)为Deep Learning方法对垂直运动路径的稳像效果,实线为稳像结果。(d)为利用L1范数优化算法对相机垂直方向路径直接进行路径拟合的结果,实线为拟合后的结果;(e)为本文方法中的S-G滤波平滑结果,对原始路径进行去噪处理,去除原始路径中的高频分量,平滑后的结果为图中实线;对平滑后的曲线进行基于优化的L1范数优化算法的路径拟合,结果如( f )所示,实线为稳像后的输出结果。
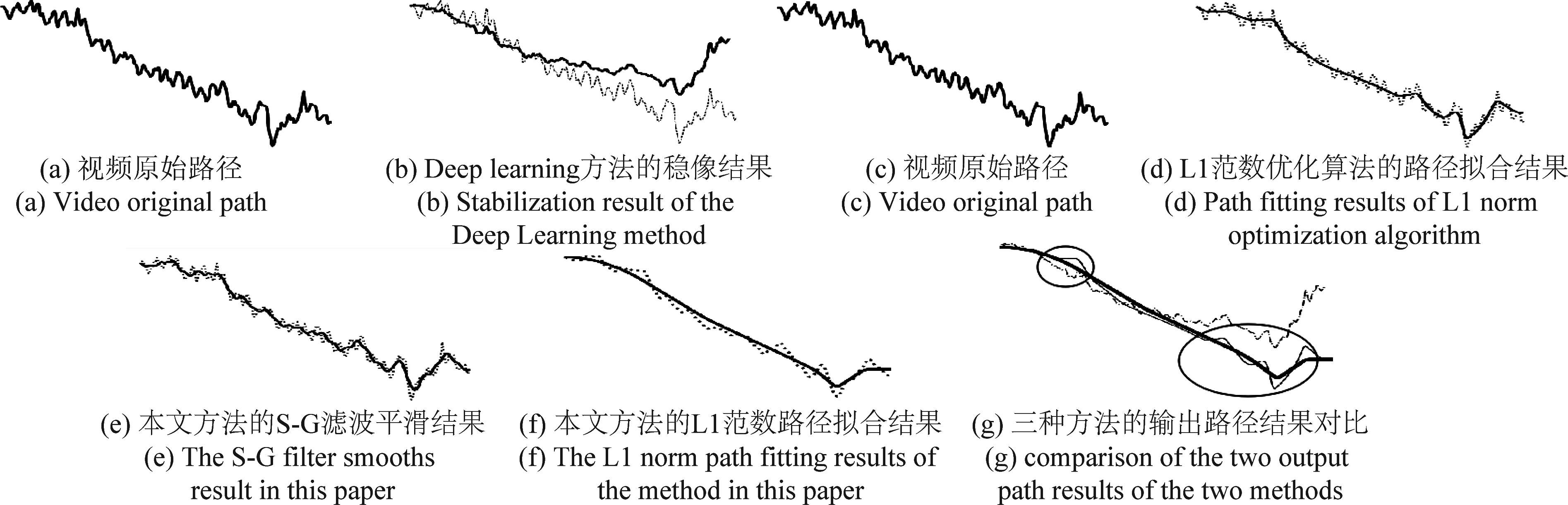
图8 路径平滑对比实验
Fig.8 Path smoothing contrast experiment
对比三种方法合成的稳定路径,如(g)所示。虚线为Deep Learning方法的结果,细实线为L1范数优化算法的结果,粗实线为本文方法得到的结果。可以看出,虚线存在较多低频与高频噪声,稳像效果不佳,稳像后的路径相对于原始路径产生了明显偏移;细实线在圆圈标记处出现了抖动情况,粗实线相对于细实线更平滑。由此得出结论,通过S-G滤波平滑算法去除原始路径的高频分量,得到的有效路径信息能够拟合生成更加稳定的路径。

图9 本文方法与Deep Learning方法及L1范数优化方法的稳像效果对比.
(a)~(c),(d)~( f ),(g)~(i)为三种方法对不同视频的稳像结果对比
Fig.9 Comparison of stabilization results by the proposed method,Deep Learning method and L1 norm optimization algorithm.
(a)~(c),(d)~( f ),(g)~(i) are the comparison of the results of three methods for different videos
稳定的路径在视频上体现为画面的稳定。如图9(a)~(c)所示,分别代表三种方法对图7第(a)段视频的稳像结果,从左至右分别为时间上连续的视频帧。由于Deep Learning方法的稳像效果不佳,稳像后的视频垂直路径明显偏移于原始视频,(a)中雕塑头部被裁剪掉,丢失了原始视频的信息。(b)画面中的雕塑随时间的变化在垂直方向出现了抖动,而(c)中雕塑在垂直方向上没有出现明显的抖情况。图9(d)~( f )为三种方法对图7第(h)段视频的稳像效果对比。可以看出,图中(d)行Deep Learning方法的稳像视频随时间的变化在水平方向产生了较大的位移和抖动,而( f )行本文方法的稳像视频在水平方向移动更为平滑,没有产生明显抖动。同时,相对于(e)行L1范数优化算法稳像视频,本文方法的稳像视频保留了更多地原始频频信息。图9(g)~(i)为三种方法对图7第(d)段视频的稳像效果对比。第(i)行本文方法的稳像结果相对于第(g)行Deep Learning方法的稳像结果保留了更多的原始视频信息,同时在水平方向、垂直方向和倾斜角度三个维度保持了更好的稳定性和平滑度。
实验结果表明,本文方法的稳像效果超越了原始L1范数优化算法和Wang等人[20]的Deep Learning方法,在计算时间上快于其他二维稳像算法,在模型复杂度上优于深度学习方法。
5 结论
本文提出了一种S-G滤波算法和L1范数优化相结合的稳像方法,利用帧间对应特征点进行运动估计,有效去除了原始路径中的高频噪声,利用原始路径中的有效信息通过优化的L1范数优化算法生成效果更好的稳定路径。实验证明,相对于其他二维稳像算法,本文提出的方法耗时更少,相对于原始L1范数优化算法和基于深度学习的稳像算法,本文更彻底地去除了原始视频路径的不稳定抖动。
[1] Liu S, Yuan L, Tan P, et al. Bundled camera paths for video stabilization[J]. ACM Transactions on Graphics (TOG), 2013, 32(4): 1-10.
[2] Grundmann M, Kwatra V, Essa I. Auto-directed video stabilization with robust l1 optimal camera paths[C]∥CVPR 2011. IEEE, 2011: 225-232.
[3] Chen T. Video stabilization algorithm using a block-based parametric motion model[J]. Information System Laboratory, Department of Electrical Engineering, Stanford University, 2000.
[4] Erturk S. Digital image stabilization with sub-image phase correlation based global motion estimation[J]. IEEE Transactions on Consumer Electronics, 2003, 49(4): 1320-1325.
[5] Lucas B, Kanade T. An iterative image registration technique with an application to stereo vision[C]∥Proc of Int Joint Conf on Artificial Intelligence. Menlo Park, CA: AAAI, 1981: 674- 679.
[6] Harris C G, Stephens M. A combined corner and edge detector[C]∥Alvey vision conference. 1988, 15(50): 147-151.
[7] Rosten E, Porter R, Drummond T. Faster and better: A machine learning approach to corner detection[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2008, 32(1): 105-119.
[8] Shi Jiaobo, Tomasi C. Good features to track[C]∥Proc of IEEE Computer Society Conf on Computer Vision and Patern Recognition Los Alamitos, CA: IEEE Computer Society, 1994: 593- 600.
[9] Matsushita Y, Ofek E, Ge W, et al. Full-frame video stabilization with motion inpainting[J]. IEEE Transactions on pattern analysis and Machine Intelligence, 2006, 28(7): 1150-1163.
[10] Erturk S. Real-time digital image stabilization using Kalman lilters[J].Real-Time Imaging, 2002, 8(4): 317-328.
[11] Chen B Y, Lee K Y, Huang W T, et al. Capturing Intention-based Full-Frame Video Stabilization[J]. Computer Graphics Forum, 2008, 27(7): 1805-1814.
[12] Liu F, Gleicher M, Jin H, et al. Content-preserving warps for 3D video stabilization[M]. ACM Transactions on Graphics (TOG). ACM, 2009.
[13] Lee J, Shin S Y. General construction of time-domain filters for orientation data[J]. IEEE Transactions on Visualization and Computer Graphics, 2002, 8(2): 119-128.
[14] Fischler M A, Bolles R C. Random sample consensus: a paradigm for model fitting with applications to image analysis and automated cartography[J]. Communications of the ACM, 1981, 24(6): 381-395.
[15] Schafer R W. What is a Savitzky-Golay filter?[lecture notes][J]. IEEE Signal Processing Magazine, 2011, 28(4): 111-117.
[16] Liu S, Tan P, Yuan L, et al. Meshflow: Minimum latency online video stabilization[C]∥European Conference on Computer Vision. Springer, Cham, 2016: 800- 815.
[17] Yu J, Ramamoorthi R. Selfie video stabilization[C]∥Proceedings of the European Conference on Computer Vision (ECCV), 2018: 551-566.
[18] Huang C H, Yin H, Tai Y W, et al. StableNet: Semi-Online, Multi-Scale Deep Video Stabilization[J]. arXiv preprint arXiv: 1907.10283, 2019.
[19] Yu J, Ramamoorthi R. Robust video stabilization by optimization in cnn weight space[C]∥Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2019: 3800-3808.
[20] Wang M, Yang G Y, Lin J K, et al. Deep online video stabilization with multi-grid warping transformation learning[J]. IEEE Transactions on Image Processing, 2018, 28(5): 2283-2292.
[21] Lin K, Jiang N, Liu S, et al. Direct photometric alignment by mesh deformation[C]∥Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2017: 2405-2413.
[22] Xu W, Lai X, Xu D, et al. An integrated new scheme for digital video stabilization[J]. Advances in Multimedia, 2013, 2013.
[23] Tsoligkas N A, Xu D, French I, et al. A motion model based video stabilisation algorithm[C]∥2006 World Automation Congress. IEEE, 2006: 1- 6.
[24] 蒋双霜, 朱振峰, 常冬霞. 利用全景图的视频稳像算法[J]. 信号处理, 2018, 34(7): 852- 859.
Jiang Shuangshuang, Zhu Zhenfeng, Chang Dongxia. Video Stabilization Algorithm Using Generated Panorama[J]. Journal of Signal Processing, 2018, 34(7): 852- 859.(in Chinese)




