1 引言
雷达信号分选是现代电子侦察系统的重要组成部分之一[1-2],其目的是从互相交错的脉冲序列中筛选出分属各部雷达的脉冲。信号分选结果的好坏直接影响后续辐射源个体识别、辐射源威胁等级判断等一系列工作。信号分选水平的高低在一定程度上反映着电子战作战能力的强弱。
传统的信号分选算法主要可分为两大部分:一类是基于信号的全脉冲参数中的载频(Radio Frequency,RF)、脉宽(Pulse Width,PW)、到达角(Direction of Arrival,DOA)的分选算法,典型算法为模板匹配法;一类是利用信号到达时间信息提取脉冲重复周期(Pulse Recurrence Interval,PRI)的分选算法,典型算法包括累计差值直方图法(Cumulative Difference Histogram,CDIF)、序列差值直方图法(Sequence Difference Histogram,SDIF)以及PRI变换法。然而随着军事科技的飞速发展,战场电磁信号日益密集,每秒脉冲数已达百万级别[3-5]。同时,新体制雷达的使用,使得雷达信号的PRI调制、脉内调制形式多样、变化迅速。这最终不仅导致单部雷达信号的全脉冲参数日益复杂,也导致不同雷达之间的全脉冲参数交叠严重。脉间参数复杂度的提升使得传统信号分选算法的分选正确率急剧下降。
与越来越不稳定的脉间参数相比,雷达信号的脉内特征具有更强的稳定性[6]。为提高信号分选正确率,近年来领域内学者将多种雷达信号脉内特征引入到信号分选中来。文献[6-13]分别将信号的相像系数、高阶累积量、奇异谱熵、小波包特征等脉内特征成功应用到雷达信号分选中来,有效提高了信号分选的准确率。其中,文献[12]利用相像系数法提取信号模糊函数二维特征图的特征作为分选参数之一。相像系数作为一种比较两信号之间相似程度的方法,在雷达信号脉内特征提取领域广泛使用。文献[14]从Holder不等式受到启发,提出了提取信号脉内特征的Holder系数法,同时证明了Holder系数法是相像系数法的推广。文献[15]又对Holder系数法做出了改进,提出了对称Holder系数法。对称Holder系数法也包括相像系数法。凡是可以转化为二维谱线形式的脉内信息,均可以使用相像系数法、Holder系数法或对称Holder系数法对脉内特征进行提取。文献[6-7,11]对信号的频谱使用相像系数法提取脉内信息,而文献[8,10]使用相像系数法对信号的高次频谱提取脉内信息。信号的高次频谱可以更好地反映信号的细微特征[8],使用相像系数法可以对这些特征进行提取,但对称Holder系数法由于可以更灵活地改变参数,从而比相像系数有更大的寻优空间。于是,本文在前人研究的基础上,提出一种对信号的高次频谱提取对称Holder系数作为脉内参数的信号分选算法。对4种不同调制类型信号的仿真实验结果表明,通过将这一稳定的脉内参数与全脉冲参数中的[RF,DOA,PW]组合成新的特征向量,并运用K-means算法进行聚类分选,能够有效提高雷达信号的分选正确率。
2 高次频谱对称Holder系数
2.1 对称Holder系数的定义
对称Holder系数由Holder不等式演变而来,可以用来描述两信号之间的相似程度[16]。文献[15]给出了对称Holder系数的定义:对于两个非负离散序列{S1(i)≥0,i=1,2,…,N}、{S2(j)≥0, j=1,2,…,N},若p、q>1,且满足1/p+1/q=1,则序列S1、S2的对称Holder系数定义为:
Hs=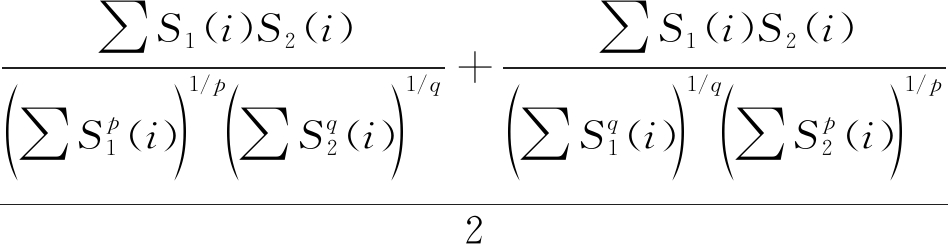
(1)
由Holder不等式可知,Hs取值介于[0,1]之间。
相像系数可看作对称Holder系数的特殊情况。对于两个非负离散序列S1、S2,其相像系数定义式为:

(2)
对比公式(1)与公式(2)可发现,当公式(1)中p=q=2时,公式(1)与公式(2)等价,即此时对称Holder系数与相像系数等价。因此,对称Holder系数可看作相像系数的推广。这两个参数都可以用来描述两个信号形状之间的相似程度,但对称Holder系数的优势在于它比相像系数具有更大的寻优空间,即可以取多组不同的p、q值,从中选取效果最优的一组。而相像系数的p、q值固定为2,不够灵活,不一定能够达到最优的描述效果。
2.2 基准信号
对称Holder系数量化的是信号之间的相似程度,在提取雷达脉冲信号的对称Holder系数时,我们引入两个第三方信号序列作为基准信号:
矩形信号序列:
(3)
三角形信号序列:
(4)
矩形信号序列能量分布较为均匀,三角形信号序列能量分布较为集中,因而比较适合作为基准信号[6]。
2.3 高次频谱对称Holder系数的提取
信号的频谱包含着信号的能量分布、频率等信息[17],不同脉内调制类型雷达脉冲的频谱之间存在着差异。通过提取脉冲频谱之间的差异信息,可以更好地区分交错在一起的脉冲。高次频谱是指对信号频谱进行k次方计算,信号的高次频谱可以更好地反映信号在频谱上的细节[8]。
在计算信号高次频谱对称Holder系数时,首先对信号做傅里叶变换(Fast Fourier Transform,FFT)得到一次频谱,然后对一次频谱做能量归一化后再求信号的高次频谱,最后计算每个雷达信号的高次频谱与两个基准信号的对称Holder系数,得到的二维特征向量即为反映雷达信号频谱形状的脉内参数。
3 信号分选流程
信号分选流程如下:
Step1 对信号做FFT与能量归一化处理后,计算信号的高次频谱。
Step2 提取信号高次频谱的对称Holder系数。
Step3 将对称Holder系数与脉冲描述字(Pulse Description Word,PDW)中的[RF,DOA,PW]组成新的特征向量。
在雷达信号的PDW中,脉幅(Pulse Amplitude,PA)在接收过程中极易受影响,因此一般不采用PA作为分选参数[18]。同时,对于单个脉冲来讲,到达时间(Time of Arrival,TOA)也是无意义的。因此选择RF、DOA以及PW与信号的高次频谱对称Holder系数组成新的特征向量作为聚类参数。
Step4 对新的特征向量做归一化处理。
特征向量各个维度参数之间的量纲不同,因而在数值上存在较大差异。若直接进行聚类,则数值较大的特征向量会在聚类中起决定性作用,使得聚类结果不能正确反映数据样本之间的关系。因此,聚类之前要先对特征向量做归一化处理,归一化的目的是消除特征向量各维度参数之间量纲不同的影响。本文采用最大-最小归一化方法:
(5)
式中,x为特征向量,x*为归一化后的特征向量,归一化后,特征向量各维度参数的值均在[0,1]之间。
Step5 使用K-means聚类算法对归一化后的特征向量进行聚类分选。
本文提出的信号分选流程总结如图1。

图1 信号分选流程框图
Fig.1 Block diagram of signal sorting process
4 仿真实验分析
4.1 高次频谱对称Holder系数参数的确定
高次频谱对称Holder系数的提取需要确定两个参数:高次频谱的次数k以及对称Holder系数公式中的参数p。为确定这两个参数,首先在信噪比0 dB条件下,按照表1参数设置生成常规雷达信号(Continuous Wave,CW)、线性调频(Linear Frequency Modulated,LFM)、频率编码(Frequency Shift Keying,FSK)、相位编码(Phase Shift Keying,PSK)等四种信号。
表1 四种雷达信号参数设置
Tab.1 Four kinds of radar signal parameter settings

信号类型PW/μsRF/MHz脉内参数CW10250无LFM10250带宽BW:10 MHzFSK102502FSK,子脉冲频率:350 MHz、450 MHPSK10250BPSK,编码方式:7位巴克码采样率:1000 MHz
分别以矩形信号、三角形信号为基准,绘制上述四种信号1~4次频谱的对称Holder系数随p值变化的曲线,如图2与图3所示。
由图2(a)、图3(a)可以看出,在一次频谱条件下,LFM信号的对称Holder系数曲线与其他三种信号曲线的间隔较大,但图2(a)中的CW、2FSK、BPSK三种信号的曲线相邻很近、图3(a)中的CW、2FSK曲线相邻很近;从图2(b)与图2(a)、图3(b)与图3(a)的比较可以发现,与一次频谱相比,二次频谱条件下各条曲线之间的间隔变大;同时,由图2(b)~图2(d)与图3(b)~图3(d)可以看出2次频谱的各条曲线相较于3次频谱、4次频谱,各条曲线之间间隔变化不再明显,但2次频谱的计算复杂度要低于3次频谱和4次频谱。因此可以判断,计算信号高次频谱时的参数k应取值为2。
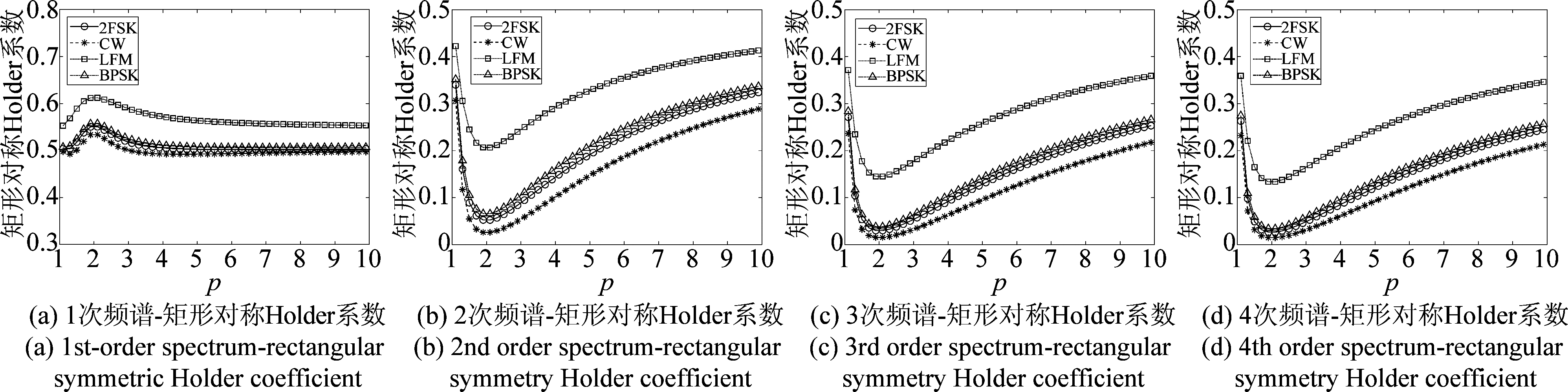
图2 k次频谱-矩形对称Holder系数
Fig.2 k-th order spectrum-rectangular symmetric Holder coefficient
此外,图2(b)显示,从p=5往后,各条曲线之间的间隔开始缓慢变小;图3(b)显示,从p=5往后,LFM曲线与BPSK曲线之间的间隔同样开始缓慢变小,BPSK曲线与CW曲线间隔无明显变化,CW曲线与2FSK曲线间隔逐步变大。若仅为追求CW曲线与2FSK曲线之间大的间隔而取一个较大的p值,将会导致算法的计算复杂度大幅度提升。因此,根据上述分析并考虑到算法的复杂度,选定k=2,p=5作为提取信号高次频谱对称Holder系数的参数。
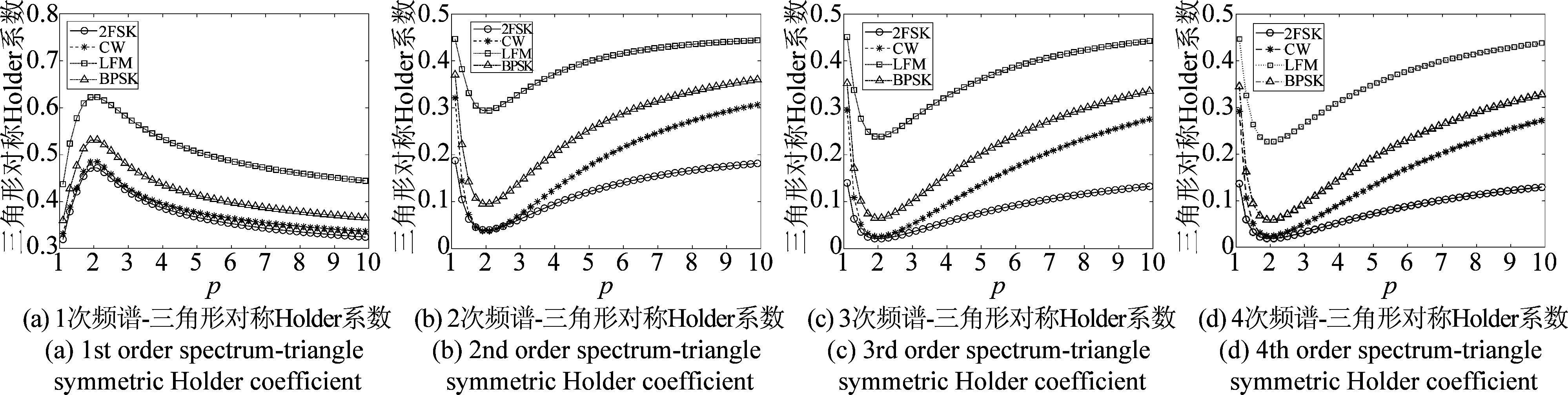
图3 k次频谱-三角形对称Holder系数
Fig.3 k-th order spectrum-triangle symmetric Holder coefficient
4.2 脉内调制参数对高次频谱对称Holder系数的影响
同种调制类型的信号可以有不同的调制参数,调制参数的变化可能会导致信号频谱的形状也发生变化从而影响信号高次频谱对称Holder系数的取值。表1中给出的4种信号,除CW信号无脉内调制参数外,其余三种信号的脉内调制参数均有多种选择。为研究信号脉内参数对高次频谱对称Holder系数的影响,首先在信噪比0 dB的条件下,按照表2、表3、表4生成测试信号。
表2 LFM信号脉内参数设置
Tab.2 LFM signal in-pulse parameter setting

信号编号信号类型脉间参数脉内参数LFM10LFM20LFM30LFM40LFMPW:10 μsRF:250 MHz带宽BW:10 MHz带宽BW:20 MHz带宽BW:30 MHz带宽BW:40 MHz采样率:1000 MHz
表3 FSK信号脉内参数设置
Tab.3 FSK signal in-pulse parameter setting
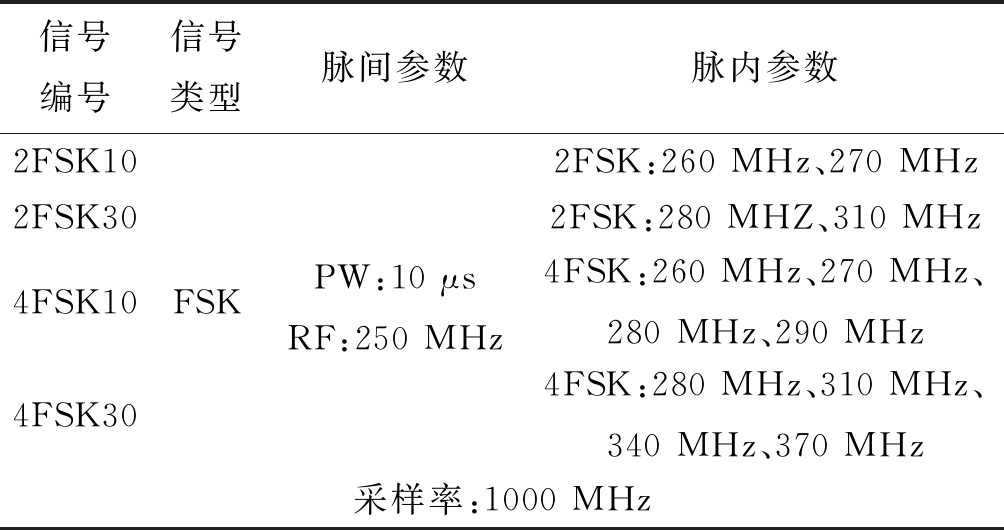
信号编号信号类型脉间参数脉内参数2FSK102FSK304FSK104FSK30FSKPW:10 μsRF:250 MHz2FSK:260 MHz、270 MHz2FSK:280 MHZ、310 MHz4FSK:260 MHz、270 MHz、280 MHz、290 MHz4FSK:280 MHz、310 MHz、340 MHz、370 MHz采样率:1000 MHz
表4 PSK信号脉内参数设置
Tab.4 PSK signal in-pulse parameter setting

信号编号信号类型脉间参数脉内参数BPSK5BPSK13QPSK FrankQPSK P1PSKPW:10 μsRF:250 MHzBPSK:5位巴克码BPSK:13位巴克码QPSK:Frank编码QPSK:P1编码采样率:1000 MHz
分别计算上述12种信号的高次频谱对称Holder系数(k=2,p=5),并绘制矩形对称Holder系数和三角形对称Holder系数的条状图,如图4、图5所示。
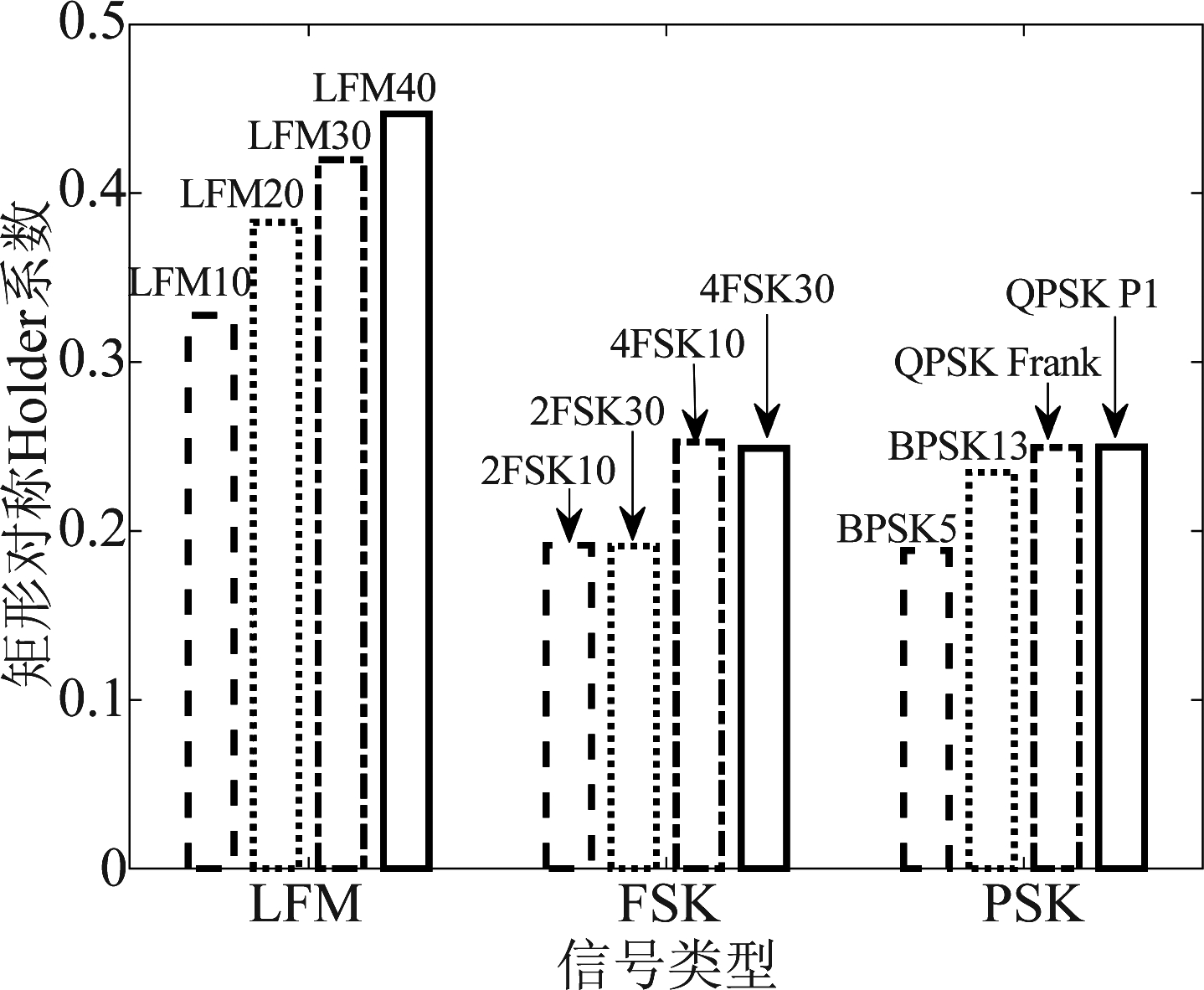
图4 12种信号的矩形对称Holder系数
Fig.4 Rectangular symmetry Holder coefficient of 12 kinds of signals
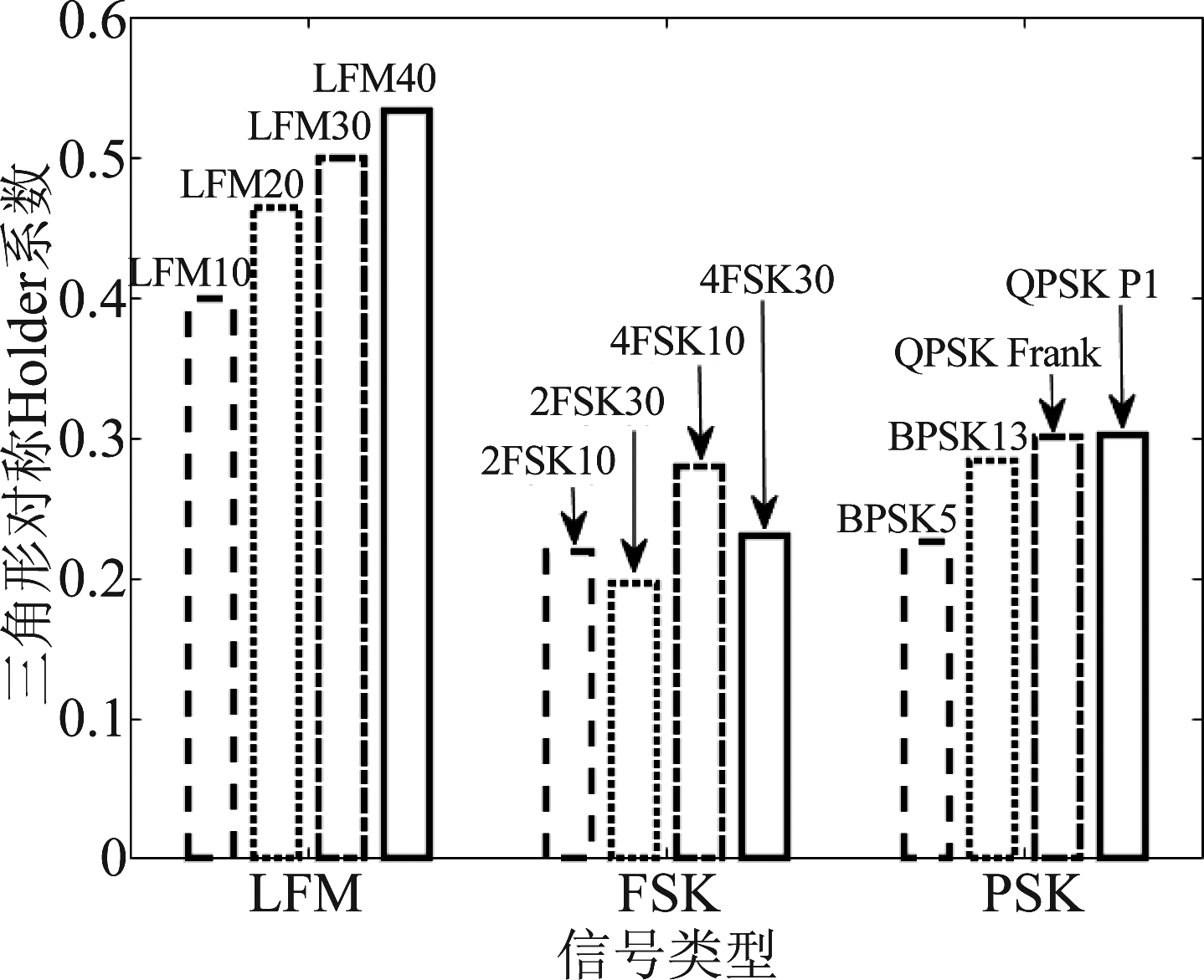
图5 12种信号的三角形对称Holder系数
Fig.5 Triangular Symmetric Holder Coefficients of 12 Signals
由图4可知:
(1)对于LFM信号,不同的调频带宽使得信号的矩形对称Holder系数有明显差异,这是因为它们的信号频谱有着明显的差异;
(2)对于FSK信号,信号子脉冲数相同的条件下,矩形对称Holder系数几乎无差异,这是由于子脉冲数相同导致信号的频谱十分相像,同时矩形信号能量分布又较为均匀;子脉冲数不同的FSK信号的矩形对称Holder系数有较为明显差异,这是因为不同的子脉冲数使得它们的频谱分别具有不同数量的子频点,从而有较大差异;
(3)对于PSK信号,BPSK5和BPSK13有明显差异的原因是其子脉冲的脉宽差异较大,从而导致频谱差异也较大;QPSK Frank和QPSK P1信号几乎无差异,这是因为这两种信号只在信号的相位上有较大差异,在信号的频谱上差异较小;BPSK5与QPSK Frank、QPSK P1信号的矩形对称Holder系数有明显差异,是因为它们的子脉冲脉宽不同导致信号频谱出现明显不同造成的;BPSK13与QPSK Frank、QPSK P1信号的矩形对称Holder系数差异较小是因为它们的子脉冲宽度较为接近,从而使得频谱形状也较为相近,因此矩形对称Holder系数也较为相近。
由图5可知:
(1)对于LFM信号,其三角形对称Holder系数存在差异的情况与原因与矩形对称Holder系数的一致;
(2)对于FSK信号,4种信号的三角形对称Holder系数的分布规律之所以与图4的不同,是因为三角形信号的能量分布与矩形信号不同;
(3)对于PSK信号,其三角形对称Holder系数的分布规律与图4相同,这是因为PSK信号的频谱只有一个频点,受三角形信号能量不均匀的影响较微弱。
由上述分析可知,脉内调制参数对信号高次频谱对称Holder系数的影响主要是通过影响其频谱形状而实现的,频谱差异越大,高次频谱对称Holder系数的差异也越大。
4.3 信号分选实验及结果分析
4.3.1 仿真条件
按照表5设置生成雷达信号。
实验设置的4部雷达分别具有不同的脉内调制类型(雷达1无调制),雷达2与雷达3在RF、DOA、PW上都有交叠;雷达3与雷达4在RF、DOA、PW三个维度同样也有交叠;雷达1与雷达4在RF、DOA上有交叠。聚类前各部雷达样本点分布如图6所示。

图6 各部雷达聚类前分布情况
Fig.6 Distribution of radars before clustering
使用本文所提算法提取信号脉内特征(高次频谱参数k=2,对称Holder系数参数p=5),然后联合[RF,DOA,PW]组成新的特征向量进行聚类分选。为量化算法分选效果,对正确率定义如下:
η=![]()
(6)
4.3.2 实验结果及分析
在-3 dB到5 dB信噪比条件下分别进行100次实验,对分选正确率求平均值。各部雷达分选正确率随信噪比变化的曲线如图7所示。
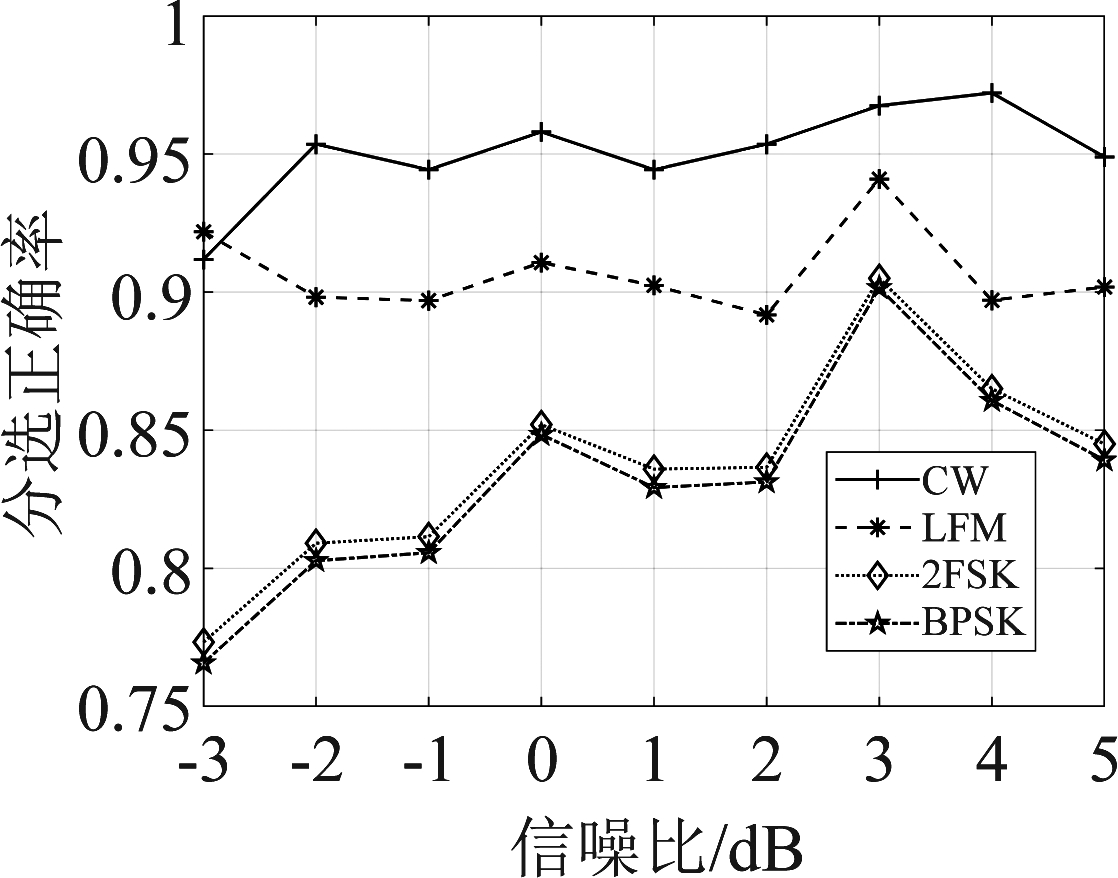
图7 各部雷达分选正确率随信噪比变化曲线
Fig.7 Variation curves of the accuracy of the sorting with signal-to-noise ratio
由图7可知,信噪比优于-1 dB时,四部雷达在不同信噪比下的分选正确率均在80%以上。其中雷达1(CW)的分选正确率较高,这是因为雷达1(CW)样本点在特征空间中分布较为孤立,因此更容易被聚类到同一簇;各条分选正确率曲线均有起伏,这是受信号噪声以及K-means聚类算法初始聚类中心不确定共同影响的结果。
4.4 对比实验
为检验本文所提算法的性能,设置2个对比实验,分别对信号分选正确率和算法计算复杂度进行对比,实验信号参数设置同表5,实验条件同4.3.2节。2个对比实验的设置如下:
表5 分选实验信号参数设置
Tab.5 Sorting experiment signal parameter setting

雷达编号PW/μsRF/MHzDOA/(°) 信号类型调制参数脉冲数雷达110脉间捷变:230,捷变率为10%42~45CW无500雷达211脉间捷变:270,捷变率为10%33~38LFM带宽BW:10 MHz500雷达311脉间捷变:250,捷变率为10%37~42FSK2FSK:350 MHz、450 MHz500雷达411脉间捷变:240,捷变率为10%39~44PSKBPSK:7位巴克码500采样率:1000 MHz;PW误差范围:±1%;RF误差范围:±1%
对比实验1:使用相像系数提取信号脉内特征,然后联合[RF,DOA,PW]组成新的特征向量进行聚类分选,称之为相像系数法;
对比实验2:不使用信号的脉内参数,仅使用常规三参数即[RF,DOA,PW]作为特征向量进行聚类分选,称之为脉间参数法。
4.4.1 分选正确率对比
经过仿真实验得到4部雷达平均分选正确率随信噪比变化曲线,如图8所示。
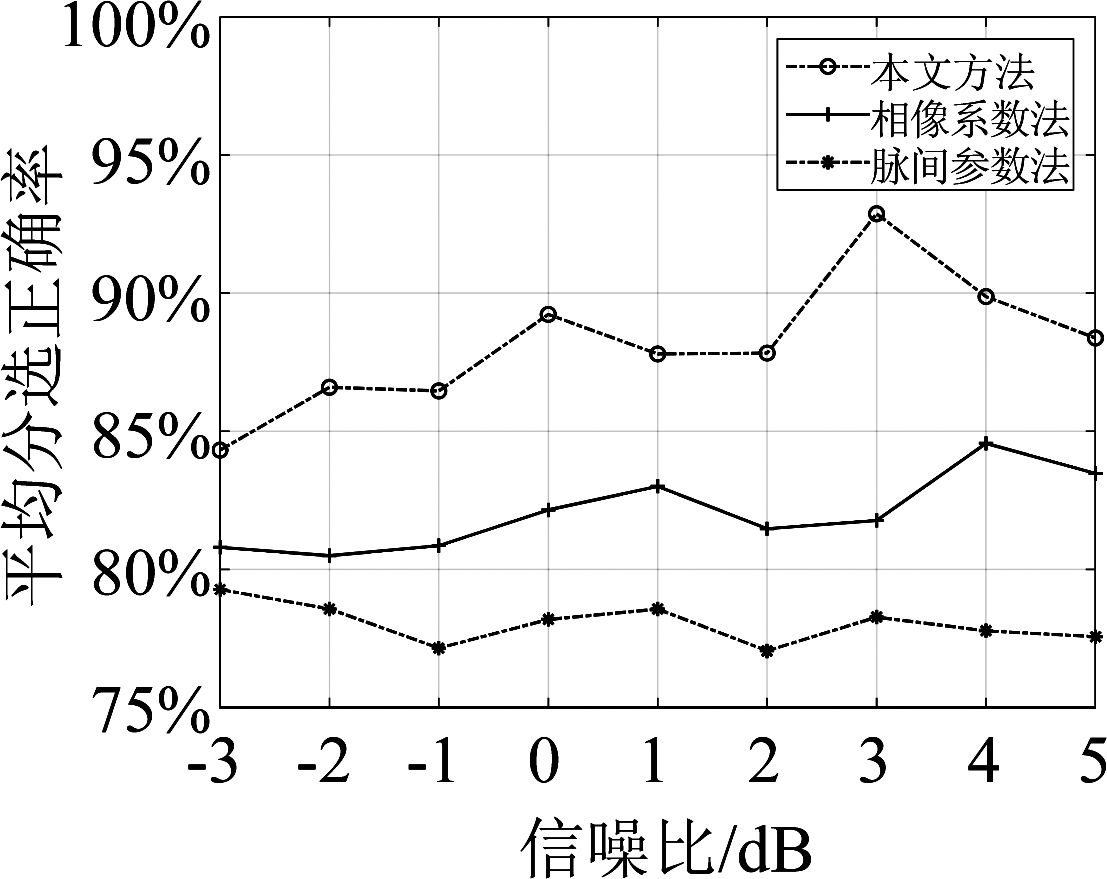
图8 平均分选正确率对比图
Fig.8 Comparison chart of the average sorting accuracies
由图8可以看出,本文提出的方法明显优于相像系数法,而相像系数法又明显优于脉间参数法,由此可知本文方法能有效提高信号分选正确率。
4.4.2 计算复杂度对比
计算复杂度是衡量一个算法性能的重要指标之一,上述三种方法的计算复杂度主要在特征提取和聚类分选这两个步骤上存在较大差异。在特征提取方面,从公式(1)与公式(2)的对比容易发现,本文方法的计算复杂度要明显高于相像系数法,而脉间参数法没有使用到脉内特征;在聚类分选方面,本文方法与相像系数法使用的特征向量均为5维,而脉间参数法使用的特征向量为3维,但聚类分选步骤的计算复杂度不仅取决于特征向量维数还与聚类算法的迭代次数有关。
为了量化比较上述三种方法的计算复杂度,在信噪比0 dB的条件下,对按照表5参数设置生成的4种调制类型的2000个脉冲,分别使用本文方法和相像系数法进行100次特征提取实验并计算对一个脉冲进行特征提取的平均耗时。获得上述三种方法所需的信号特征向量后,使用K-means算法对这三种特征向量分别进行100次聚类分选实验并计算进行一次聚类分选的平均耗时。算法运行环境设置如表6所示,实验结果如图9、图10所示。
表6 算法运行环境
Tab.6 Algorithm operating environment

项目版本/型号CPUI5-7400@3.00GHz四核内存8GB DDR4@2400MHzMATLABR2020a
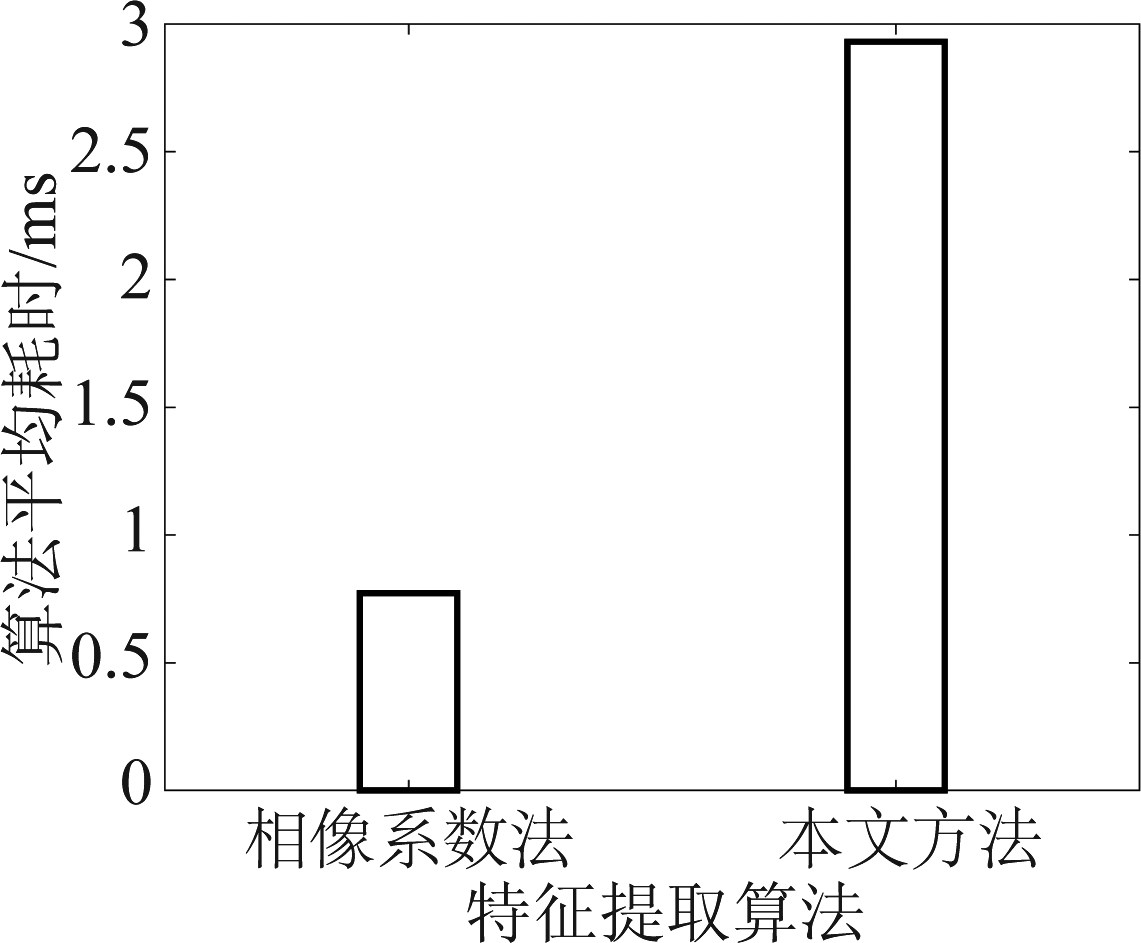
图9 特征提取平均运行时间对比
Fig.9 Feature extraction average running time comparison
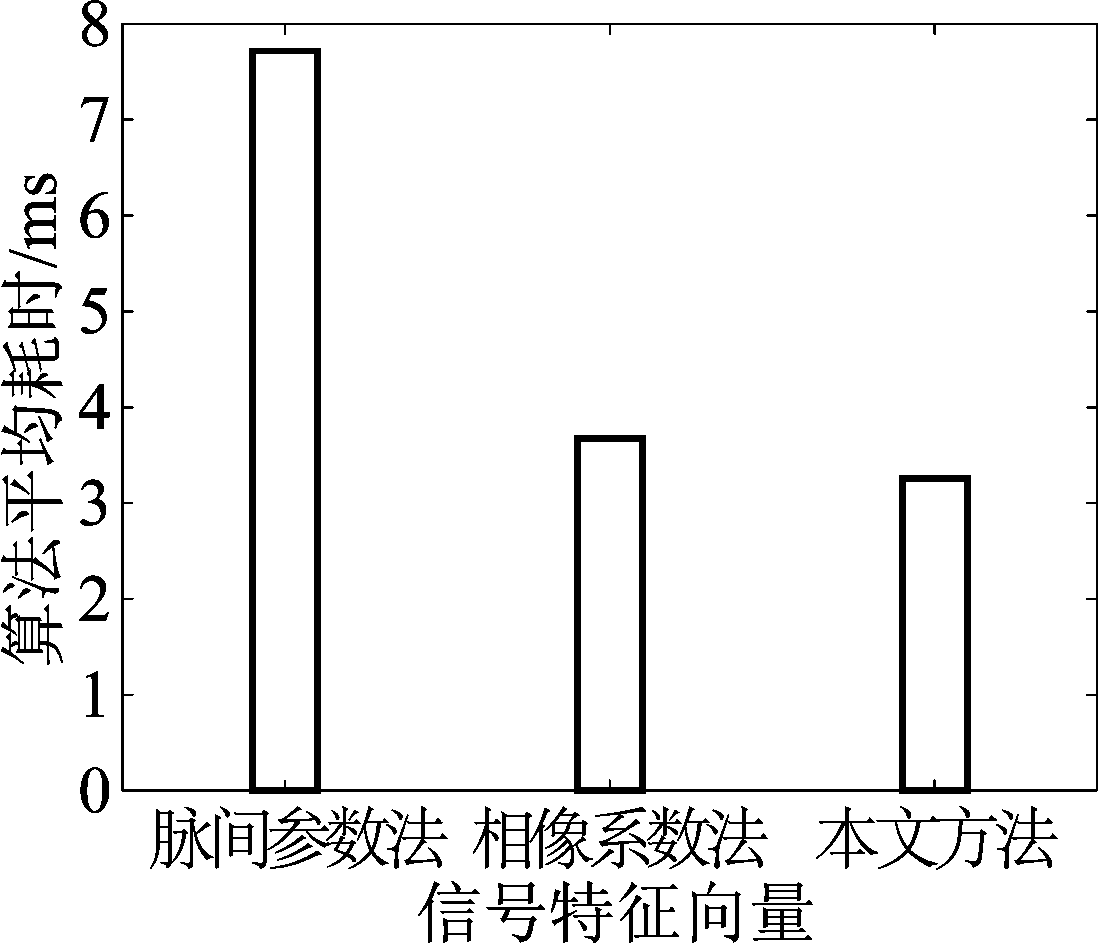
图10 聚类分选平均运行时间对比
Fig.10 Comparison of average running time of cluster sorting
由图9可知,使用本文方法对信号进行特征提取的平均耗时要明显高于相像系数法,这是因为与相像系数法相比,本文方法在提取信号特征时首先要对信号频谱做平方运算,在提取二次频谱对称Holder系数时还要多次进行高次幂运算,而相像系数法无需进行频谱平方以及高次幂运算。此外,由于本文使用的是对称Holder系数,计算过程可分为对称的两部分,每一部分与相像系数比较都具有较高的计算复杂度,因而对称的两个部分的计算复杂度加起来要远高于相像系数法。
由图10可知,聚类分选平均耗时由高到低依次为:脉间参数法、相像系数法、本文方法。其中,脉间参数法的信号特征向量维度为3维,在三种方法中最低,但其聚类分选的平均耗时在三种方法中反而最高。这是因为其特征向量的可分性较差,使得K-means算法达到收敛所需的迭代次数也较多,这最终导致脉间参数法聚类分选的平均耗时较高。相像系数法和本文方法使用的信号特征向量均为5维,但本文方法在聚类分选时平均耗时更低。这是因为与相像系数法相比,使用本文方法获得的特征向量的可分性更强,在使用K-means算法进行聚类时通过较少次数的迭代即可达到收敛。
通过上述分析可知,本文方法在获得较高分选正确率的同时也提高了特征提取算法的计算复杂度,这也是本文方法的一个缺点。为提高特征提取算法的运算速度,可使用GPU或FPGA对算法进行硬件加速,这也是笔者下一步研究的重点方向。
5 结论
针对基于全脉冲参数的雷达信号分选算法的准确率下降这一问题,本文提出一种基于信号高次频谱对称Holder系数的信号分选方法。该方法首先提取信号高次频谱对称Holder系数作为脉内特征参数,然后将此脉内特征参数与稳定的脉间参数组合形成新的特征向量并运用K-means算法进行聚类分选。本文方法通过引入高次频谱对称Holder系数这一稳定的脉内参数,有效提高了新特征向量的可分性。对不同种调制类型信号的仿真实验结果表明,本文方法能有效提高信号分选正确率。但本文方法在提高信号分选正确率的同时也提高了特征提取算法的计算复杂度。如何在保持较高的信号分选正确率的情况下提高特征提取算法的运行速度将是笔者下一步研究的重点方向。
[1] 郜丽鹏, 纪风有. 基于联合概率关联的雷达信号分选方法[J]. 应用科技, 2019, 46(1): 69-75.
Gao Lipeng, Ji Fengyou. Radar signal sorting method based on joint probabilistic association[J]. Applied Science and Technology, 2019, 46(1): 69-75.(in Chinese)
[2] 孟祥豪, 罗景青, 马贤同. 新体制雷达信号PRI样本子图周期搜索提取方法[J]. 信号处理, 2015, 31(4): 399- 406.
Meng Xianghao, Luo Jingqing, Ma Xiantong. A New System Radar Signal Extraction Method by Searching PRI Pulse Sequence Subpattern Cycle[J]. Journal of Signal Processing, 2015, 31(4): 399- 406.(in Chinese)
[3] 郜丽鹏, 沙作金. 一种改进的数据场聚类算法[J]. 应用科技, 2019, 46(6): 30-34.
Gao Lipeng, Sha Zuojin. An improved data field clustering algorithm[J]. Applied Science and Technology, 2019, 46(6): 30-34.(in Chinese)
[4] 刘智鑫, 赵拥军. 约束准则下扩展时差直方图脉冲分选配对方法[J]. 西安电子科技大学学报(自然科学版), 2019, 46(6): 102-111.
Liu Zhixin, Zhao Yongjun. Pulse sorting and pairing based on the constrained extended TDOA histogram [J]. Journal of Xidian University, 2019, 46(6): 102-111.(in Chinese)
[5] 郭仕剑, 唐鹏飞, 宿绍莹, 等. 实时频谱态势图的生成和伪彩色显示编码方法[J]. 信号处理, 2011, 27(9): 1375-1379.
Guo Shijian, Tang Pengfei, Su Shaoying, et al. Build of Image for Real-time Spectrum’s State and Display of Pseudo coloring Coding[J]. Signal Processing, 2011, 27(9): 1375-1379.(in Chinese)
[6] 袁泽恒, 田润澜, 袁如月, 等. 一种新的雷达信号脉内分选方法[J]. 航天电子对抗, 2018, 34(5): 24-28.
Yuan Zeheng, Tian Runlan, Yuan Ruyue, et al. A new intra pulse sorting method for radar signals[J]. Aerospace Electronic Warfare, 2018, 34(5): 24-28.(in Chinese)
[7] 袁泽恒, 田润澜, 王晓峰. 复杂体制雷达信号预分选的方法[J]. 电信科学, 2018, 34(9): 97-104.
Yuan Zeheng, Tian Runlan, Wang Xiaofeng. Pre-sorting method of complex system radar signals [J]. Telecommunications Science, 2018, 34(9): 97-104.(in Chinese)
[8] 关欣, 朱杭平, 张玉虎. 基于FRFT的雷达辐射源信号特征分析及提取[J]. 探测与控制学报, 2018, 40(2): 71-76.
Guan Xin, Zhu Hangping, Zhang Yuhu. Analysis and Extraction of Radar Emitter Signal Feature Based on Fractional Fourier Transform[J]. Journal of Detection & Control, 2018, 40(2): 71-76.(in Chinese)
[9] 陈恒, 张友益, 王玉梅. 基于常规参数和脉内特征参数的雷达信号分选[J]. 舰船电子工程, 2018, 38(6): 58- 61.
Chen Heng, Zhang Youyi, Wang Yumei. Radar Signal Sorting Based on Conventional and Intravenous Characteristic Parameters[J]. Ship Electronic Engineering, 2018, 38(6): 58- 61.(in Chinese)
[10] 刘凯, 韩嘉宾, 黄青华. 基于改进相像系数和奇异谱熵的雷达信号分选[J]. 现代雷达, 2015, 37(9): 80- 85.
Liu Kai, Han Jabin, Huang Qinghua. Sorting Radar Signal Based on the Improved Resemblance Coefficient and Singular Spectrum Entropy [J]. Modern Radar, 2015, 37(9): 80- 85.(in Chinese)
[11] 刘江波. 基于相像系数与SVM的雷达辐射信号分选技术[J]. 电子对抗, 2014(2): 25-28.
Liu Jiangbo. Sorting Radar Emitter Signal Based on Resemblance Coefficient and SVM [J]. Electronic Warfare, 2014(2): 25-28.(in Chinese)
[12] 陈昌孝, 何明浩, 徐璟, 等. 基于模糊函数相像系数的雷达辐射源信号分选[J]. 电波科学学报, 2014, 29(2): 260-264.
Chen Changxiao, He Minghao, Xu Jing, et al. Radar emitter signal sorting based on resemblance coefficient of ambiguity function[J]. Chinese Journal of Radio Science, 2014, 29(2): 260-264.(in Chinese)
[13] 冯明月, 何明浩, 王冰切, 等. 基于改进相似熵的参数交叠雷达信号分选[J]. 电子信息对抗技术, 2013, 28(4): 1- 4.
Feng Mingyue, He Minghao, Wang Bingqie, et al. Radar Signal Sorting of Parameters Overlapping Based on Improved Similitude Entropy[J]. Electronic Information Warfare Technology, 2013, 28(4): 1- 4.(in Chinese)
[14] 王海华, 沈晓峰. 一种新的雷达辐射源信号脉内特征提取方法[J]. 系统工程与电子技术, 2009, 31(4): 809- 811.
Wang Haihua, Shen Xiaofeng. New intra-pulse feature extraction approach of radar emitter signals [J]. Systems Engineering and Electronic, 2009, 31(4): 809- 811.(in Chinese)
[15] 王海华, 沈晓峰. 基于对称Holder系数的雷达辐射源信号特征分析[J]. 空间电子技术, 2010, 7(3): 55-59.
Wang Haihua, Shen Xiaofeng. Signal Characteristic Analysis of Radar Radiation Source Based on Symmetric Holder Coefficients[J]. Space Electronic Technology, 2010, 7(3): 55-59.(in Chinese)
[16] 楼康威. 基于脉内特征的雷达信号分选技术研究[D]. 长沙:国防科学技术大学, 2016.
Lou Kangwei. Research on Radar Signal Sorting Technology Based on Intra-pulse Features [D]. Changsha: National University of Defense Technology, 2016.(in Chinese)
[17] 李强. 雷达辐射源信号分选技术研究[D]. 西安: 西安电子科技大学, 2019.
Li Qiang. Research on Radar Emitter Signal Sorting Technology[D]. Xi’an: Xidian University, 2019.(in Chinese)
[18] 彭刚, 袁晓, 刘闻. 雷达辐射源信号聚类分选算法综述[J]. 雷达科学与技术, 2019, 17(5): 485- 492.
Peng Gang, Yuan Xiao, Liu Wen. A Survey of Clustering and Sorting Algorithms for Radar Source Signals[J]. Radar Science and Technology, 2019, 17(5): 485- 492.(in Chinese)



