1 引言
目标定位作为阵列信号处理研究的重要内容之一,在雷达领域有着广泛的应用。雷达系统中的目标定位可以通过计算目标在空间中的位置信息来完成,即目标角度与距离的估计问题[1]。传统的相控阵雷达已经被广泛应用于目标角度,即波达方向(DOA)估计。MUSIC算法[2]是传统DOA估计技术中最具代表性的方法,利用噪声子空间与信号子空间的正交特性构建谱峰函数,通过谱峰搜索完成DOA估计。但算法对快拍数与信噪比要求较高,计算量大,对相关信源的估计性能较差[3]。随着基于稀疏信号重构(SSR)与压缩感知(CS)[4-5]方法的研究,DOA估计取得了新的成果。其中,具有代表性的是文献[6]提出的L1-SVD算法,该算法采用L1范数构造SSR模型,通过奇异值分解(SVD)降低算法复杂度与噪声敏感性。并且该算法对相关信源也具有较高的估计精度。稀疏贝叶斯学习(SBL)[7-11]是压缩感知中稀疏信号重构的另一种代表性方法。该算法从贝叶斯理论出发,利用稀疏先验假设对感兴趣的信号进行稀疏处理。SBL的一个优点是它在建模稀疏信号方面的灵活性,这可以提高解的稀疏性。因此近年来基于稀疏贝叶斯学习(SBL)与贝叶斯压缩感知(BCS)的DOA估计研究工作不断取得发展[12-20]。然而,上述算法实现高性能的DOA估计都有一个假设,即真实的DOA位于空间离散采样网格点上。但是,在实际情况下,这种假设通常是不成立的,即目标真实DOA偏离空间离散采样网格点。真实的DOA与其最近的网格点之间的间格称为离网间距。为了解决这种离网模型下的DOA估计问题,文献[21]提出了基于稀疏贝叶斯学习的离网DOA估计方法,通过一阶泰勒近似目标真实方向矢量,完成了离网模型下的DOA估计问题。随后,文献[22]研究了离网稀疏贝叶斯模型下的窄带与宽带DOA估计。文献[23]采用压缩感知理论研究了离网模型下目标方位角与俯仰角的估计,即二维离网DOA估计问题。
尽管这些方法显示了其相对于传统算法的优势,但是,传统的相控阵雷达波束指向在所有距离内都固定在一个角度,因此由于固有的距离模糊性,无法直接从其波束形成输出中估计目标的距离信息[24]。为克服相控阵的这一缺陷性,Antonik和Wicks等人提出了一种更灵活的阵列雷达,称为频率分集阵列(FDA)雷达[25],并经由文献[26]正式译为频控阵雷达。与传统的相控阵雷达不同, FDA发射的信号载频在相邻阵元间存在一个较小的频率偏移量,使得FDA波束图具有角度距离依赖特性[27-28],这一特性使得FDA一经提出便引起国内外学者广泛关注。文献[29]通过研究FDA雷达与传统相控阵雷达在空间波束扫描上的区别,从理论上分析了FDA发射方向图随时间、角度和距离的周期性变化关系。文献[30]分析了FDA波束合成中的角度-距离耦合问题,随后文献[31]研究了FDA雷达的自适应波束形成方法以及角度-距离解耦合方法,文献[32]通过对FDA添加非均匀对数频偏也得到了角度-距离解耦合的波束方向图。文献[33]介绍了三种FDA信号接收处理方法并对其方向图特性进行了分析。在此基础上,文献[34]重点研究了FDA的第三种全频带信号接收处理方式,并对其进行了自适应与非自适应波束扫描,均得到了角度-距离解耦合的波束图。同时,为了实现FDA对目标的定位,许多优秀学者不断进行研究。文献[35]提出了一种以非均匀FDA作为发射端,以均匀传统相控阵作为接收端的信号处理模型,这种模型具有目标角度-距离解耦合的能力,直接从发射-接收方向图中提取出距离和角度信息实现FDA雷达目标二维成像;文献[36]提出了一种发射子阵方法,将FDA划分成若干个子阵,每个子阵发射互不相同的信号,再利用MUSIC算法对目标空间角度与距离进行了联合估计;与之相似,文献[37]也提出了一种发射子阵方法,将FDA划分为两个频偏不同的FDA子阵,通过角度-距离解耦的波束方向图,实现了FDA目标定位;文献[38]针对FDA信号单频接收处理方法,通过对发射阵元采取正负两次频偏的方式,利用MUSIC算法,实现了对目标的角度距离估计。
目前,结合FDA特性进行目标定位的方法需要对整个二维空间进行扫描,计算复杂度高,并且无法对离网模型下的目标进行有效定位。本文在研究FDA雷达特性的基础上,结合稀疏贝叶斯理论,提出一种基于稀疏贝叶斯学习的双脉冲频控阵雷达离网目标定位方法(FDA-OGSBL),解决FDA雷达中目标角度与距离的离网估计问题。最后仿真验证本文所提方法的有效性与可靠性。
2 频控阵发射接收信号模型
与传统的相控阵雷达不同, FDA发射的信号载频在相邻阵元间存在一个较小的频率偏移量Δf。考虑如图1所示的单基地FDA信号发射-接收模型:
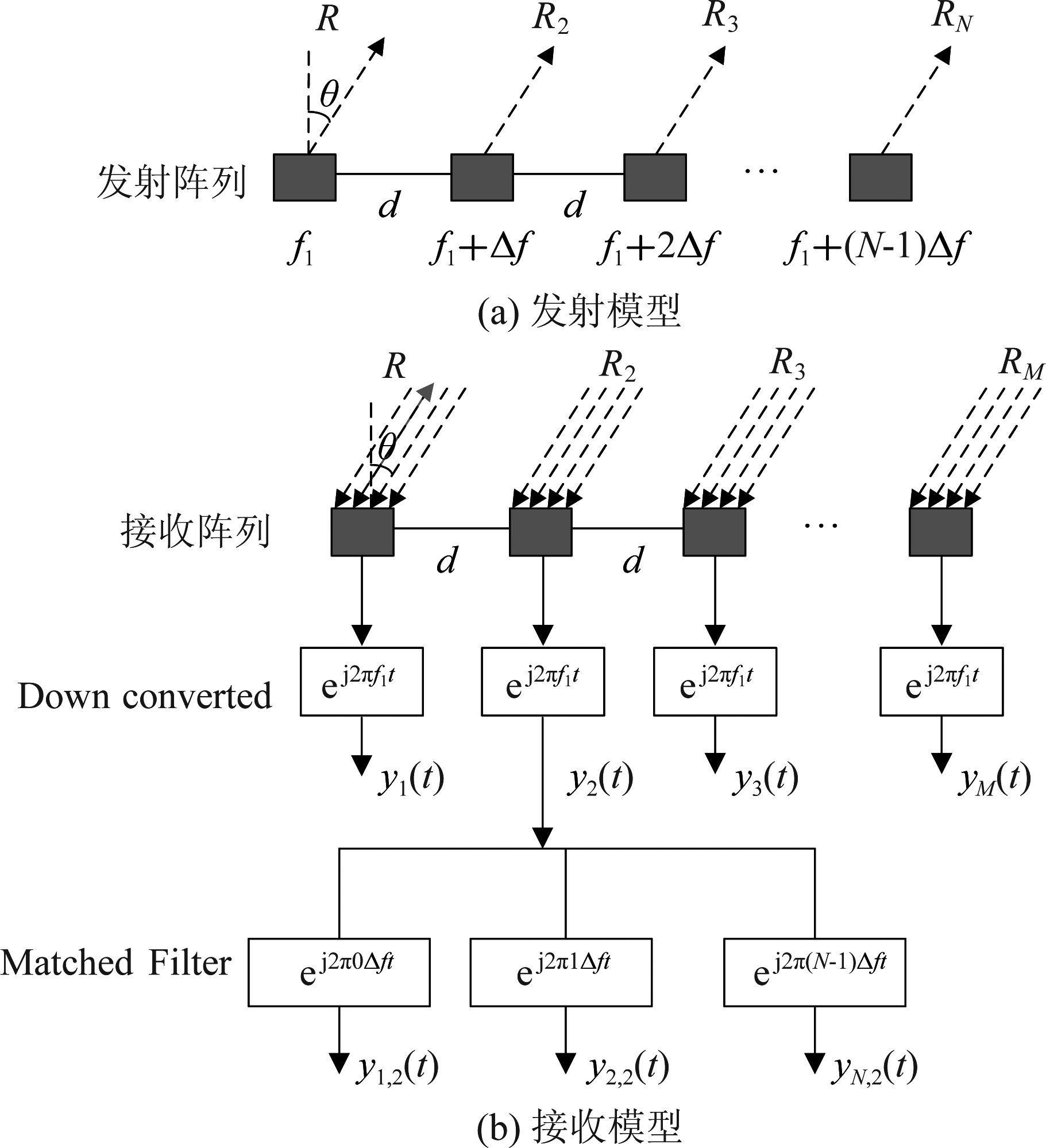
图1 FDA发射接收模型
Fig.1 FDA transmitted and received model
假设发射阵列与接收阵列是分别具有N个阵元与M个阵元的均匀线阵,且发射阵元与接收阵元间距均为d,发射阵列第n个阵元的信号载频为:
fn=f1+(n-1)Δf, n=1,2,…,N
(1)
式中, f1为发射阵列参考阵元载频,Δf为发射阵列相邻阵元间的频率偏移量,并且满足f1≫Δf。在本文中假设各阵元发射的信号均满足窄带条件,发射端第n个阵元发射信号的形式可以表示为:
sn(t)=a(t)exp{j 2πfnt}, n=1,2,…,N
(2)
式中,a(t)为信号复包络。假设在远场存在K个目标点,相对于参考阵元的位置分别为(θk,Rk),k=1,2,…,K。则接收端第m个阵元接收到的信号为:
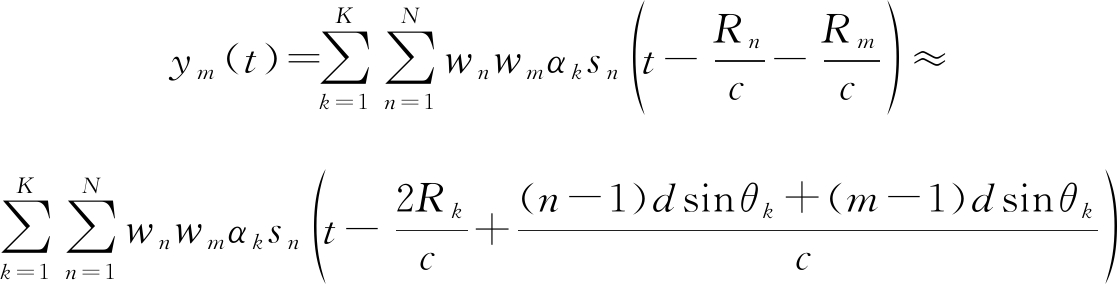
(3)
式中,wn为第n个发射阵元的权值,wm为第m个接收阵元的权值,c为电磁波传输速度,αk第k个目标的反射系数。信号到达接收阵元后,先以ej2πf1t做下变频变换到基带:
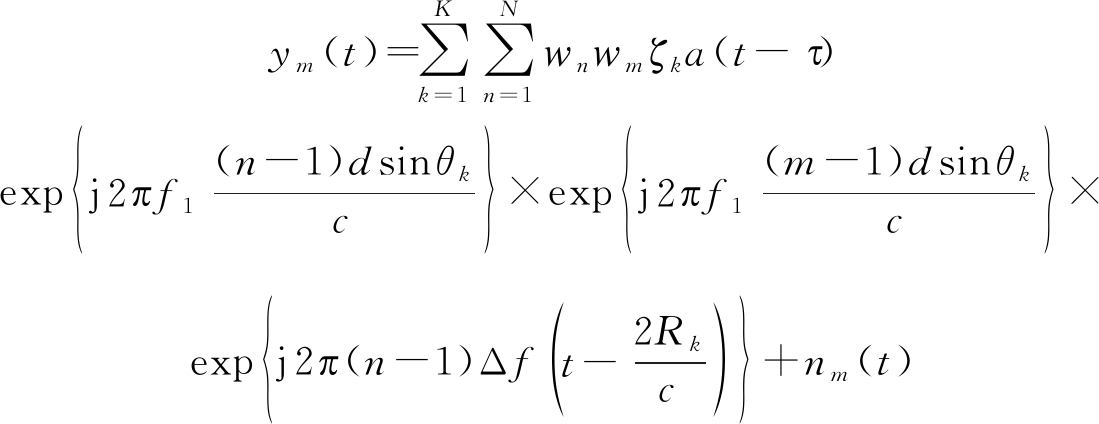
(4)
式中τ=2Rk/c为公共时延,ζk=αkexp{-j4πf1Rk/c}为公共相位项与目标反射系数的乘积,不失一般性,将其重新定义为第k个目标的反射系数并且令ζk=1,nm(t)为阵元的加性复高斯白噪声。对于目标点(θk,Rk),FDA发射-接收阵列因子定义为:
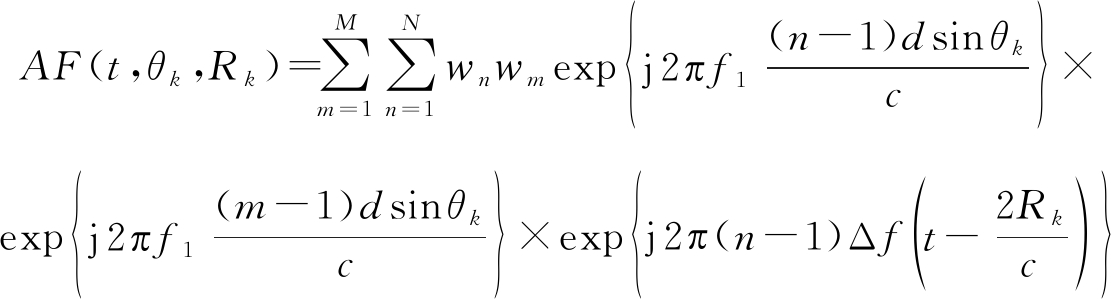
(5)
其幅度平方,称为FDA发射-接收波束图:
BF(t,θk,Rk)=![]()
![]()
![]()
(6)
为使得FDA波束图在目标位置(θ0,R0)处取得最大值,定义阵列发射端与接收端权值分别为:
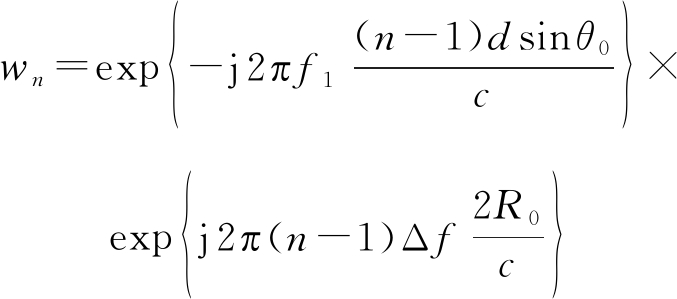
(7a)
(7b)
此时,FDA发射-接收波束图为:
BF(t,θk,Rk)=![]()
![]()
![]()
(8)
令f1=10 GHz,Δf=200 kHz,d=c/2fmax,N=M=21,图2为目标位置(θ0,R0)设置为(10°,9300 m)与(10°,9500 m)时FDA发射-接收波束图。

图2 FDA发射-接收波束图
Fig.2 FDA transmit-receive beampattern
与传统相控阵不同,FDA波束图依赖于目标角度与距离,且与时间参数t相关。FDA的时间依赖性使得波束可以在全空间扫描且不需要使用移相器。但是,时变的全空间扫描难以控制且不适用于目标定位的需求。因此,在目标定位中,合理的处理FDA波束方向图的时变性具有重要意义。考虑文献[39]提出的针对FDA的匹配滤波器设计,在接收端,每个接收阵元都连接一个由N个匹配滤波器构成的匹配滤波器组,信号经过下变频处理后,由滤波器组对信号进行分离并进行相位补偿,其中第n个匹配滤波器表示为ej2π(n-1)Δft。并且为便于分析,在接下来假设wn=wm=1。则第m个阵元接收到的信号经匹配滤波后可得到由第n个阵元发出的信号,此时回波信号为:
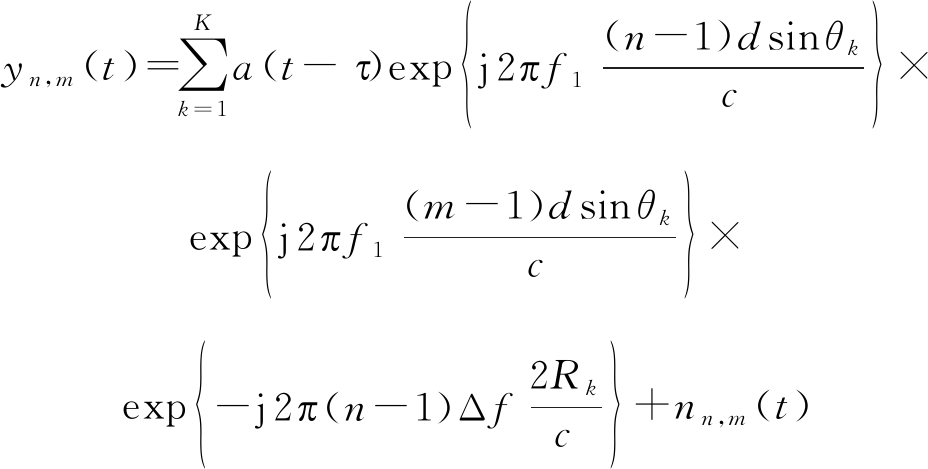
(9)
将第m个接收阵元中分离出的N个目标回波信号按发射阵元顺序进行排列,并将M个接收阵元中的目标回波信号按接收阵元顺序进行排列,重新排列后的信号大小为NM×1,将信号通过矢量形式表示。
y(t)=[y1,1(t),…,yN,1(t),y1,2(t),…yN,M(t)]T
(10a)
n(t)=[n1,1(t),…,nN,1(t),n1,2(t),…nN,M(t)]T
(10b)
并且,令
x(t)=[x1(t),x2(t),…,xK(t)]T
(11)
A(θk,Rk)=[a(θ1,R1),a(θ2,R2),…,a(θK,RK)]
(12)
式中,xk(t)=a(t-2Rk/c)。A(θ,R)为NM×K阶阵列流型矩阵,矩阵中任意一列矢量a(θk,Rk)是远场目标点(θk,Rk)的NM×1维方向矢量,即:
a(θk,Rk)=[a1,1(θk,Rk),…,aN,1(θk,Rk),
a1,2(θk,Rk),…,aN,M(θk,Rk)]T
(13)
其中

(14)
因此,信号模型可以通过矢量形式表示为:
y(t)=A(θ,R)x(t)+n(t)
(15)
在实际处理中,数据是对y(t)进行时域采样所取得的,用矩阵形式表示为:
Y=A(θ,R)X+N
(16)
式中Y=[y(1),y(2),…,y(T)],X=[x(1),x(2),…,x(T)],N=[n(1),n(2),…,n(T)],T为快拍数。
3 角度距离二维离网模型
为了将角度与距离的联合估计问题转化为稀疏表示问题,令![]() 为角度范围[-90°,90°]上的P个采样网格点,
为角度范围[-90°,90°]上的P个采样网格点,![]() 为感兴趣的距离范围上的L个采样网格点,其中,P≫K,L≫K。如果采样网格足够精细,则目标的角度和距离都在采样网格上,由此,观测矩阵Y的稀疏在网模型为:
为感兴趣的距离范围上的L个采样网格点,其中,P≫K,L≫K。如果采样网格足够精细,则目标的角度和距离都在采样网格上,由此,观测矩阵Y的稀疏在网模型为:
Y=AS+N
(17)
式中![]() 为X的零扩展矩阵,S的每一列中只有K个非零元素对应于目标位置。然而,在实际情况下,目标位置在空间中是随机分布的,因此在预定义的空间采样网格上对真实目标位置的假设通常是无效的。为了解决目标偏离采样网格下的定位问题,考虑文献[21]提出的线性近似离网模型来处理网格失配问题。
为X的零扩展矩阵,S的每一列中只有K个非零元素对应于目标位置。然而,在实际情况下,目标位置在空间中是随机分布的,因此在预定义的空间采样网格上对真实目标位置的假设通常是无效的。为了解决目标偏离采样网格下的定位问题,考虑文献[21]提出的线性近似离网模型来处理网格失配问题。
假设![]() 是与空间中第k个目标位置(θk,Rk),k∈1,2,…,K距离最近的采样网格点。则目标点(θk,Rk)的方向矢量可以通过一阶泰勒近似:
是与空间中第k个目标位置(θk,Rk),k∈1,2,…,K距离最近的采样网格点。则目标点(θk,Rk)的方向矢量可以通过一阶泰勒近似:
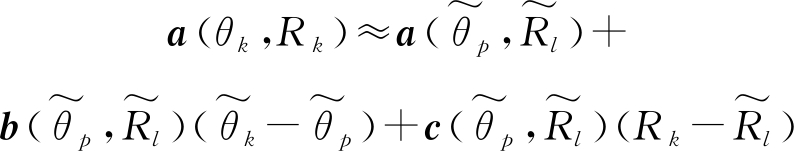
(18)
式中
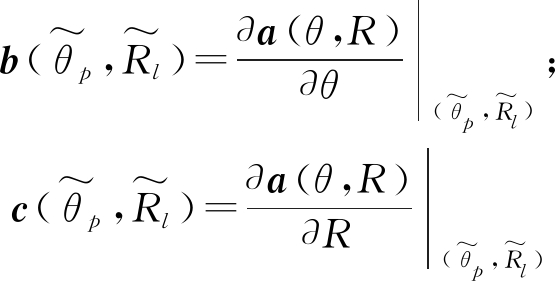
(19)
令
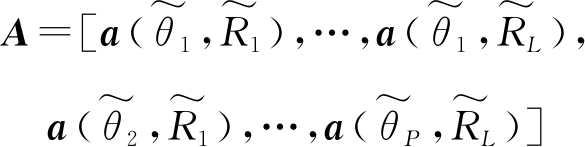
(20)
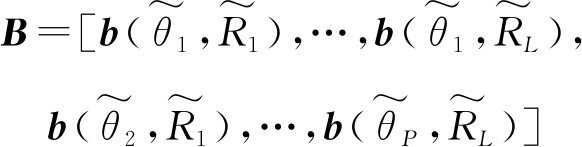
(21)
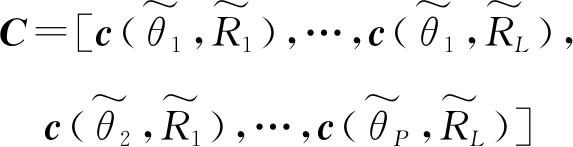
(22)
定义角度与距离的离网参数如下:
(23)
(24)
将近似误差考虑到噪声矢量中,则离网稀疏信号角度距离联合估计模型可以表示为:
Y=Φ(β,ζ)S+N
(25)
式中![]()
4 二维离网模型难点分析
将SBL方法与角度距离二维离网模型结合非常直接。然而,SBL在二维离网模型的应用仍然存在一些困难使得目前尚无基于SBL的二维角度距离联合估计算法提出。
4.1 计算的复杂度
当采样网格从一维扩展到二维时,二维采样网格需要大量的采样网格点才能保持与一维相同的估计精度。如图3(a)所示,在角度域范围[-5°,5°],以1°为采样网格间距,只需要11个采样网格点,距离域范围[9900 m,10000 m],以10 m为采样网格间距,也仅仅只需要11个采样网格点;而从一维扩展到二维时,则需要121个采样网格点。大量的采样网格点会导致算法复杂度呈几何增长。
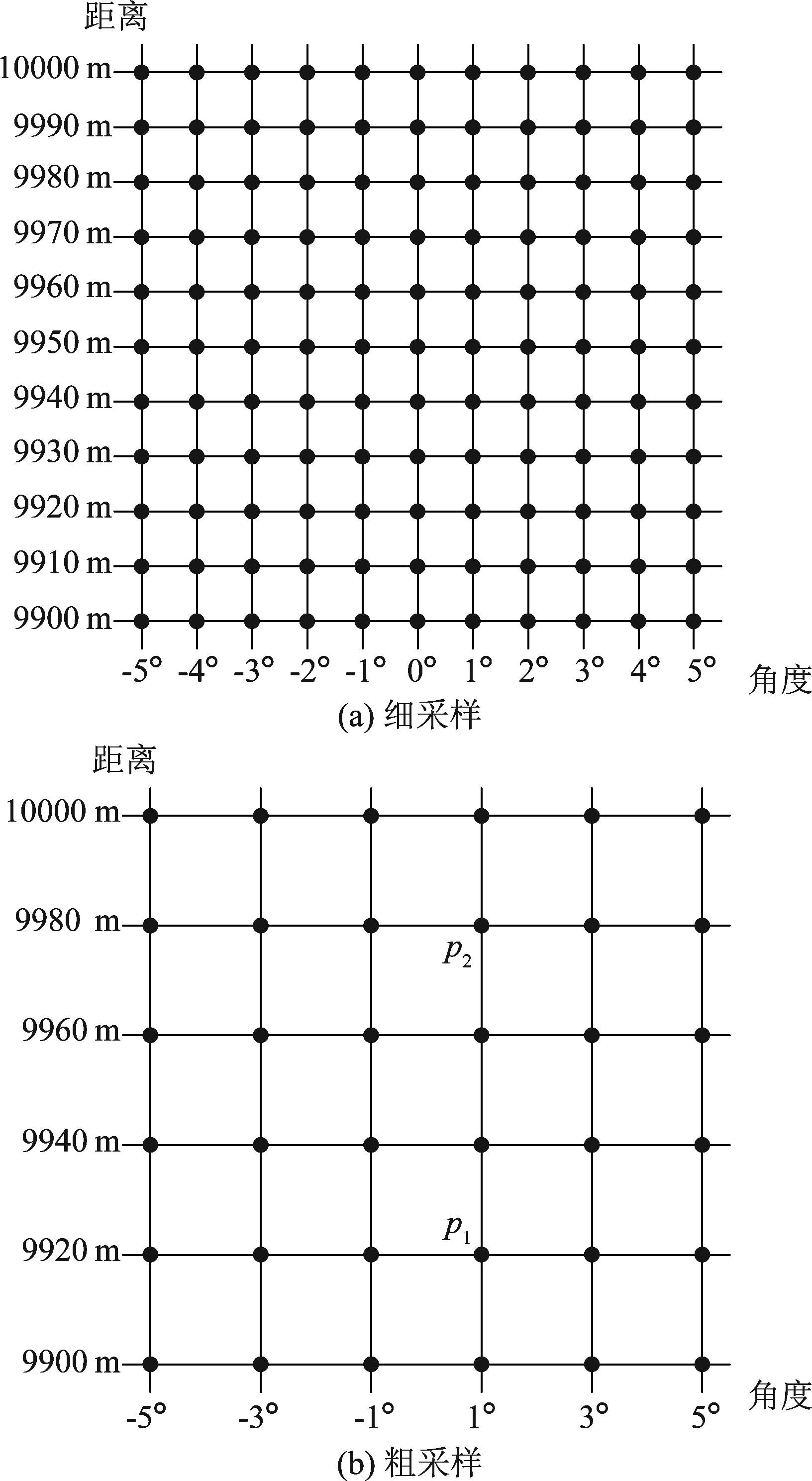
图3 空间二维均匀采样网格
Fig.3 Uniformly sampled 2D grid
4.2 网格点间的相关性
为克服3.1节所述算法的复杂度,最简单的办法是在进行二维估计时采用较粗糙的采样网格,即增大采样网格间距。如图3(b)所示,显然,可以有效减小算法复杂度。但是,此时仍存在第二个难点。如图3(b)目标p1和p2的位置分别为[0°,9940 m]与[0°,9960 m],它们具有相同的角度值,因此在稀疏矩阵S中两个目标具有相关性。此时一维SBL方法中,假设信源之间相互独立的特性在二维角度距离估计中并不成立。此时SBL方法将遭受严重的虚假谱峰问题,导致估计精度明显降低。
为了解决上述SBL模型在二维角度距离估计中存在的难点,本文提出一种FDA双脉冲角度距离二维离网目标定位方法。该方法具有复杂度低,定位精度高的优点。该方法包括两个信号处理步骤,首先,FDA雷达发射零频率偏移量的相干脉冲(Δf=0 Hz,在这种情况下,它作为相控阵雷达使用),之后FDA雷达以非零频率偏移量(Δf≠0 Hz)发射相同的脉冲。在Δf=0 Hz的条件下,即在传统相控阵雷达下检测每个角度单元中是否存在目标点。如果存在,则通过调整非零的频率偏移量Δf在距离域中定位目标。因此,这种距离-角度定位方法可以理解为先在角度域中检测目标,然后在在距离域中定位目标。
5 离网角度估计
5.1 信号模型
设置发射阵元频率偏移量(Δf=0 Hz),由式(14)可得此时阵列方向矢量只与目标角度θk相关。回波信号式(9)重新表示为:
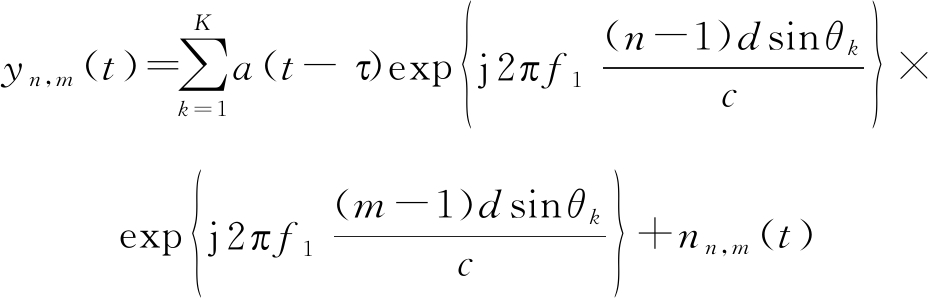
(26)
此时,信号模型重新表示为:
Y=A(θ)X+N
(27)
如图4所示,假设![]() 是在角度范围[-90°,90°]内的固定采样网格,其中P为网格数并且满足P≫K。不失一般性,令
是在角度范围[-90°,90°]内的固定采样网格,其中P为网格数并且满足P≫K。不失一般性,令![]() 为网格间距是
为网格间距是![]() 的均匀网格。假设目标真实角度
的均匀网格。假设目标真实角度![]() 且
且![]() 是最接近θk的网格点,满足
是最接近θk的网格点,满足![]()
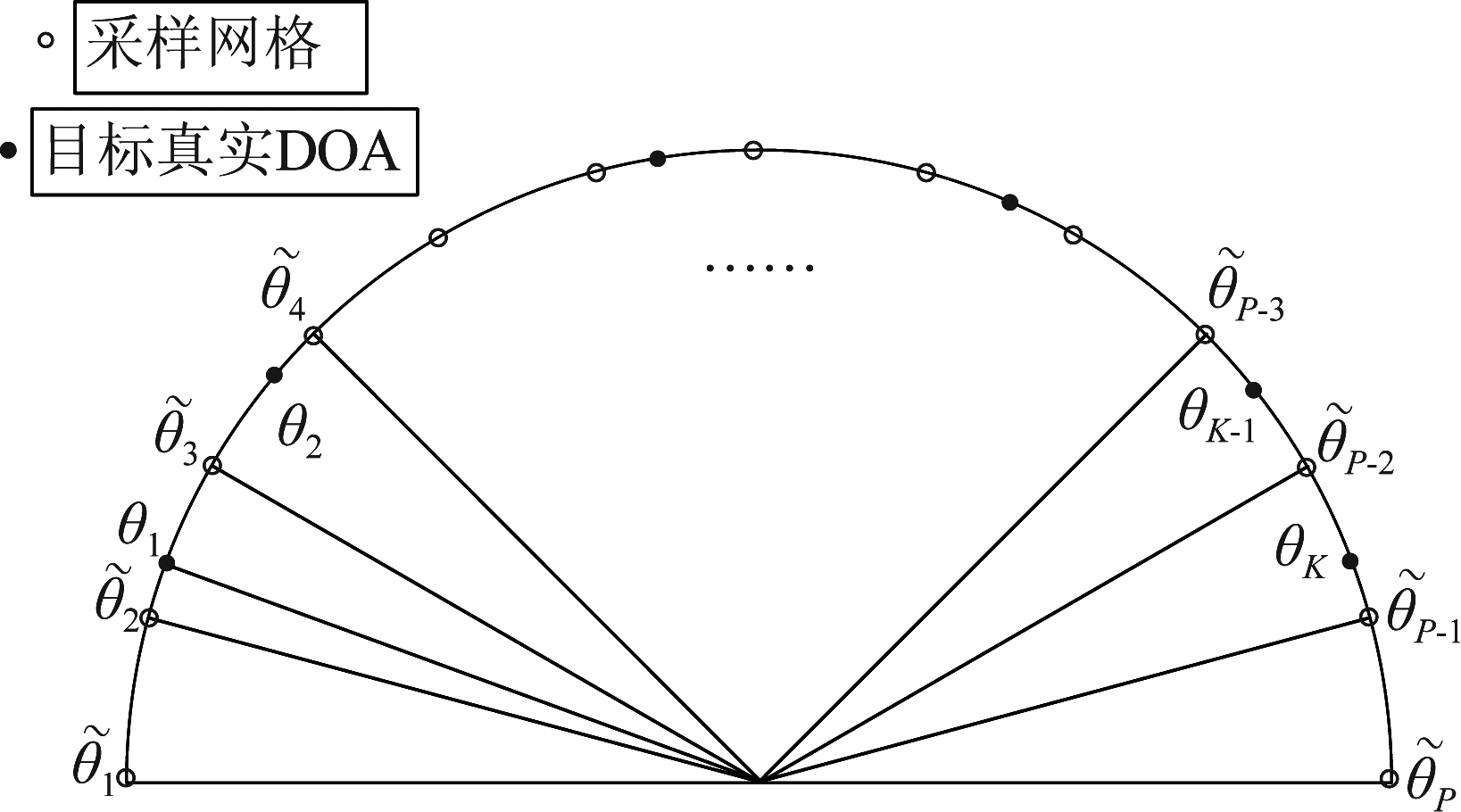
图4 离网角度估计模型
Fig.4 Off-grid DOA estimation model
阵列方向矢量线性近似为:
(28)
式中![]() 表示
表示![]() 对
对![]() 的一阶导数。令
的一阶导数。令
(29)
(30)
β=[β1,β2,…,βP]T∈[-r/2,r/2]P
(31)
将近似误差考虑到噪声矢量中,则离网稀疏角度估计模型可以表示为:
Y=Φ(β)S+N
(32)
式中Φ(β)=A+Bdiag(β)并在下文中将其简写为Φ,Y=[y(1),y(2),…,y(T)],S=[s(1),s(2),…,s(T)],N=[n(1),n(2),…,n(T)],T为快拍数。
5.2 离网稀疏贝叶斯推断
对于稀疏表示下的离网角度估计模型
Y=ΦS+N
(33)
假设不同快拍不同阵元下的噪声相互独立且服从相同的复高斯分布,则

(34)
式中τ≡σ-2表示噪声精度,σ2为噪声方差,I表示单位矩阵。复高斯分布的概率密度为[40]:
CN(u|μ,![]()
![]()
![]() -1(u-μ)}
-1(u-μ)}
(35)
式中μ为u的均值,![]() 为u的协方差矩阵,则:
为u的协方差矩阵,则:
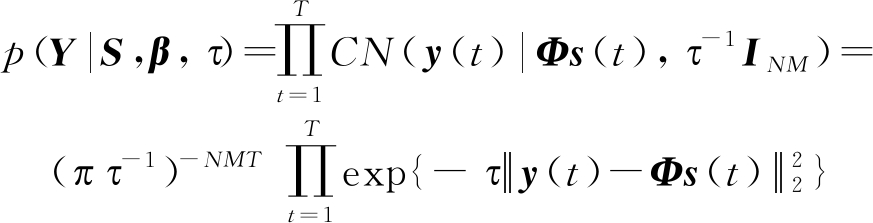
(36)
式中||·||2表示向量的2范数。信源矩阵S与噪声精度τ为待估计参数,在Bayesian框架下,待估计的参数可以通过极大似然估计获得,但为避免过学习现象,需要对待估计的量指定先验分布。假设sp(t)(p=1,2,…,P;t=1,2,…,T)相互独立,依据相关向量机(RVM)理论[7],为sp(t)指定均值为0,方差为![]() 的复高斯先验:
的复高斯先验:
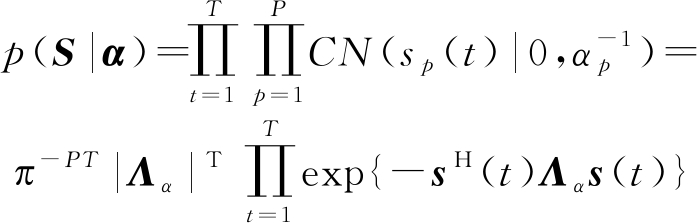
(37)
式中α=(α1,α2,…,αP)为超参数,控制sp(t)的估计精度,Λα=diag(α)。由于高斯分布的方差的倒数的共轭先验是Gamma分布[41],因此为超参数αp与噪声参数τ指定Gamma先验:
(38)
p(τ)=Γ(τ|c,d)
(39)
Gamma分布的定义为:
(40)
上述为每一个待估计参数设置相互独立的超参数是稀疏贝叶斯学习模型中最显著的特点,也是模型最终具有稀疏性的根本原因[7]。假设离网距离模型β服从均匀分布,其先验为:
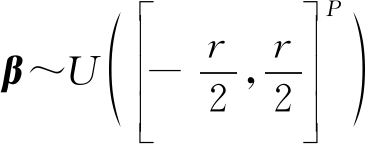
(41)
上述各参数之间关系如图5所示。

图5 SBL离网角度估计参数模型
Fig.5 SBL Off-grid DOA estimation parameter model
由此可得模型的联合概率分布为
p(Y,S,α,β,τ)=
p(Y|S,β,τ)p(S|α)p(α)p(β)p(τ)
(42)
根据贝叶斯理论,可以得到待估计量的后验分布为
p(τ,β,α,S|Y)=![]()
(43)
然而,由于p(Y)难以求解使得精确后验p(τ,β,α,S|Y)并不能以闭式形式给出[42]。在稀疏贝叶斯模型下是通过对p(τ,β,α,S|Y)进行分解,进而求解待估计量的后验分布:
p(τ,β,α,S|Y)=p(S|Y,α,β,τ)p(τ,β,α|Y)
(44)
式中
![]()
![]() s)
s)
(45)
即s(t)服从均值为μs(t),协方差矩阵为![]() s的多维复高斯分布,其中:
s的多维复高斯分布,其中:
μs(t)=τ![]() sΦHy(t), t=1,2,…,T
sΦHy(t), t=1,2,…,T
(46)
![]() s=(τΦHΦ+Λα)-1
s=(τΦHΦ+Λα)-1
(47)
因此,μs(t)与![]() s的计算需要估计参数α、β与τ。在稀疏贝叶斯模型中,是使用最大后验估计进行参数求解,即最大化p(τ,β,α|Y),由于p(Y)与参数无关,因此最大化p(τ,β,α|Y)等价于最大化p(τ,β,α,Y):
s的计算需要估计参数α、β与τ。在稀疏贝叶斯模型中,是使用最大后验估计进行参数求解,即最大化p(τ,β,α|Y),由于p(Y)与参数无关,因此最大化p(τ,β,α|Y)等价于最大化p(τ,β,α,Y):
![]()
![]()
(48)
使用最大期望算法(EM),将S视为隐变量并最大化Ep(S|Y,α,β,τ)[lnp(Y,S,α,β,τ)],其中Ep(S|Y,α,β,τ)[·]表示使用参数的当前估计值对隐变量S的后验概率式求期望,并在下文中简写为E[·]。对于α,忽略与之无关的对数项:
(49)
同理,对于τ:
(50)
由此可得参数α与τ的更新为:
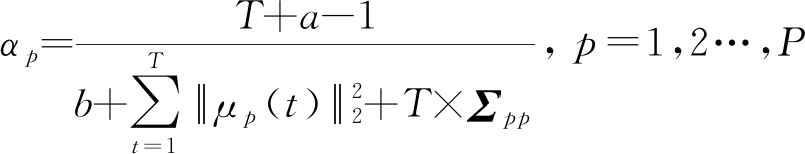
(51)
(52)
式中US=[μs(1),μs(2),…,μs(T)],||·||F表示矩阵的F范数。tr(·)表示矩阵的迹。网格偏移矢量β的推断是离网稀疏贝叶斯的核心,由式(36)、(41)、(42)、(48)最大化E[lnp(Y|S,β,τ)+lnp(β)]等价于最小化E[||Y-ΦS![]() ]:
]:
![]()
βTPβ+2vTβ+C
(53)
式中,C为与β无关的常数项,P为半正定矩阵,且:
(54)
v=Re{T×diag(BHA![]() s)}-
s)}-![]()
(55)
式中(·)*表示共轭,⊙表示Hadamard积,Re(·)表示取实部。因此,β的优化问题为:
(56)
这是一个带有边界约束的线性最小二乘问题。令其关于β的偏导数为零:
![]() βTPβ+2vTβ=2(Pβ+v)=0
βTPβ+2vTβ=2(Pβ+v)=0
(57)
因此,当P可逆时,存在唯一解:
(58)
当![]() 则
则![]() 当上述两个条件之一不满足时,则需要对β进行逐元素更新。更新βp时,固定其他元素,求解使偏导数为零的第p个方程:
当上述两个条件之一不满足时,则需要对β进行逐元素更新。更新βp时,固定其他元素,求解使偏导数为零的第p个方程:
(59)
式中(·)-p表示向量去除第p个元素,Pp表示矩阵P的第p列。若![]() 则
则![]() 否则取离
否则取离![]() 最近的网格值。综上,得到β的更新方程为:
最近的网格值。综上,得到β的更新方程为:

(60)
实验证明,当超参数α迭代更新完成后,大部分的αp会趋向于无穷大,这就表示与该αp相关的sp(t)服从均值为零,方差为零的高斯分布,即sp(t)=0。假设其余Q(Q≤K)个较小的αp对应的网格坐标为![]() 则最终的角度估计可以通过下式得到:
则最终的角度估计可以通过下式得到:
(61)
式中,![]() 为与
为与![]() 相对应的角度离网参数。
相对应的角度离网参数。
6 离网距离估计
6.1 信号模型
当FDA发射阵列以非零频率偏移量(Δf≠0 kHz)发射脉冲时,由式(14)可得,阵列方向矢量同时依赖于目标角度θk与距离Rk。由于在零频率偏移量(Δf=0 kHz)的条件下已经实现了对目标角度的检测,因此方向矢量中只有目标距离信息是未知的。假设在目标角度![]() 上存在J(J≤K)个相对于参考阵元的距离分别为Rj(j=1,2,…,J)的目标点。
上存在J(J≤K)个相对于参考阵元的距离分别为Rj(j=1,2,…,J)的目标点。![]() 上的回波信号表示为:
上的回波信号表示为:
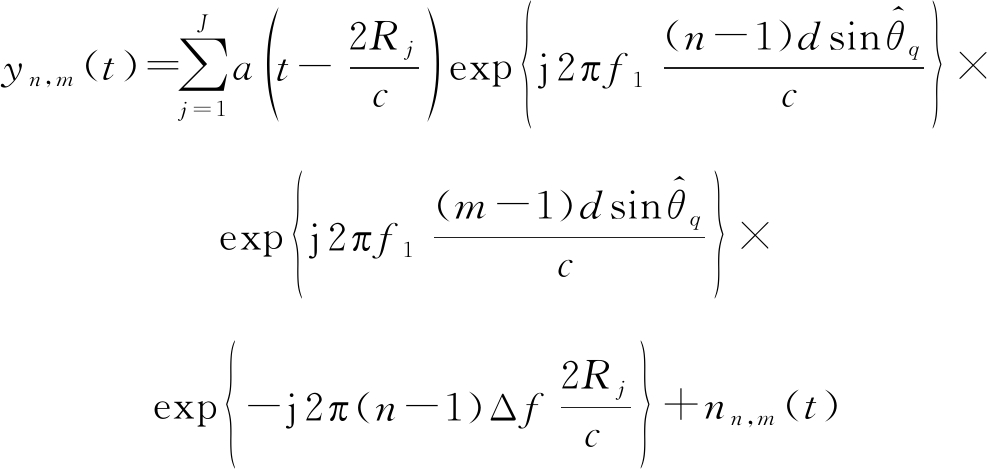
(62)
此时,信号模型重新表示为:
(63)
如图6所示,令![]() 是在目标角度
是在目标角度![]() 上感兴趣的距离范围内的网格间距是
上感兴趣的距离范围内的网格间距是![]() 的均匀采样网格。假设目标真实距离
的均匀采样网格。假设目标真实距离![]() 且
且![]() 是最接近Rj的网格点,满足
是最接近Rj的网格点,满足![]()
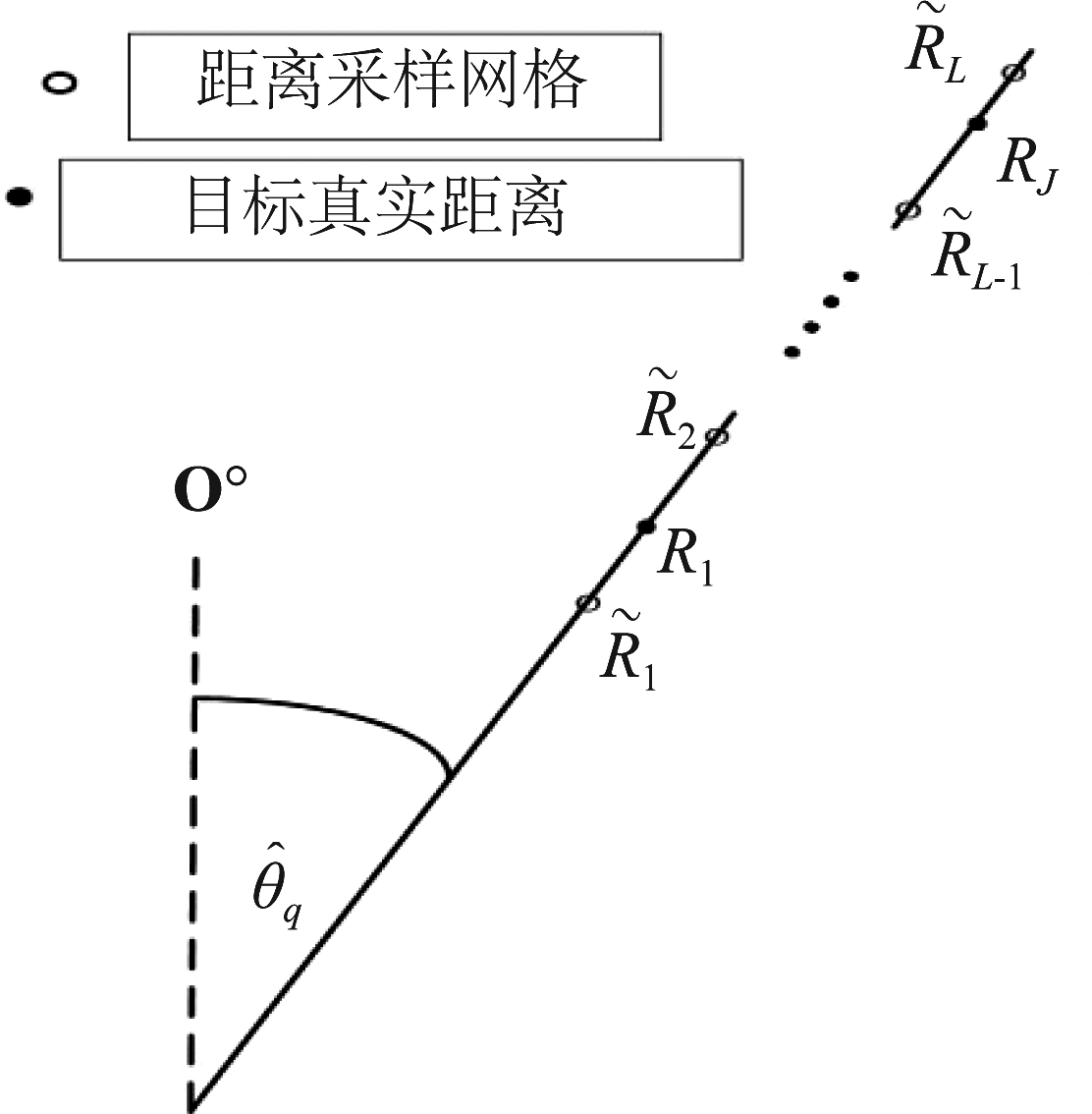
图6 离网距离估计模型
Fig.6 Off-grid range estimation model
阵列方向矢量线性近似为:
(64)
式中![]() 表示
表示![]() 对
对![]() 的一阶导数。令:
的一阶导数。令:
(65)
(66)
ζ=[ζ1,ζ2,…,ζL]T∈[-g/2,g/2]L
(67)
将近似误差考虑到噪声矢量中,则离网稀疏距离估计模型可以表示为:
Y1=Φ1(ζ)H+N1
(68)
6.2 离网稀疏贝叶斯推断
依据离网稀疏贝叶斯角度估计中对参数的处理,可得h服从均值为μh,协方差矩阵为![]() h的多维复高斯分布:
h的多维复高斯分布:
μh=τ![]() hΦ1Hy1(t), t=1,2,…,T
hΦ1Hy1(t), t=1,2,…,T
(69)
![]() h =(τ Φ1HΦ1+Λρ )-1
h =(τ Φ1HΦ1+Λρ )-1
(70)
式中τ为噪声精度参数,ρ=[ρ1,ρ2,…,ρL]为距离域上的超参数,Λρ=diag(ρ)且:
(71)
p(τ)=Γ(τ|c,d)
(72)
由EM算法可得ρ与τ的更新公式为:
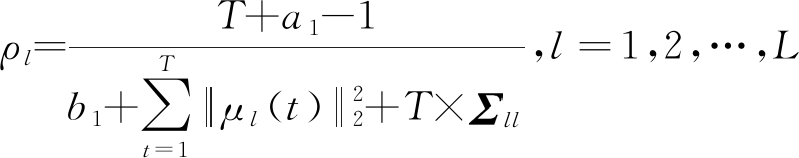
(73)
(74)
距离域上的离网参数ζ采取与角度离网参数β一致的处理方式,可得ζ的更新公式为:

(75)
式中
(76)
(77)
(78)
v1=Re{T×diag(B1HA1![]() h)}-
h)}-![]()
(79)
因此,最终的距离估计可以通过下式得到:
(80)
式中![]() 为ρl中J个较小的值对应的网格坐标,
为ρl中J个较小的值对应的网格坐标,![]() 为与之相对应的距离离网参数。
为与之相对应的距离离网参数。
在此步骤之后,即完成了目标的角度和距离二维定位。即目标定位在角度-距离域中![]() 由上述分析给出目标偏离初始采样网格点情况下的离网稀疏贝叶斯学习目标定位算法如表1所示。
由上述分析给出目标偏离初始采样网格点情况下的离网稀疏贝叶斯学习目标定位算法如表1所示。
表1 离网稀疏贝叶斯学习目标定位算法
Tab.1 Off-Grid Targets Localization algorithm based on SBL

7 仿真结果
本节对本文所提FDA-OGSBL算法的有效性进行验证,按照图1所示的FDA信号模型建立仿真,假设均匀线性FDA具有N=M=21个阵元用于发射信号与接收回波信号,发射阵列与接收阵列阵元间距均为d=c/2fmax,并且发射阵列参考阵元载频f1=10 GHz,距离估计中非零频率偏移量Δf=150 kHz。角度估计与距离估计中均设置快拍数T=100,信噪比SNR=0 dB。
7.1 单目标
考虑一个位于(0.5°,9533 m)的目标。设置a=c=1,b=d=0以获得信源超参数αp与噪声参数τ上的均匀分布,即假设p(α)∝1,p(τ)∝1,初始化αp=1,σ2=10-SNR/10||Yo![]() /MNT,其中Y°为无噪情况下的信号接收矩阵,初始化离网参数β=0。设置最大迭代次数max_iter=500,收敛阈值为ε=10-4,设置角度估计上的网格间距r=1°。将感兴趣的距离范围设置为9000 m至10000 m,设置距离估计上的网格间距g=10 m,对于参数的设置与迭代收敛条件采取与角度估计中相同的设置。图7(a)与(b)分别为目标角度域与距离域的仿真结果。
/MNT,其中Y°为无噪情况下的信号接收矩阵,初始化离网参数β=0。设置最大迭代次数max_iter=500,收敛阈值为ε=10-4,设置角度估计上的网格间距r=1°。将感兴趣的距离范围设置为9000 m至10000 m,设置距离估计上的网格间距g=10 m,对于参数的设置与迭代收敛条件采取与角度估计中相同的设置。图7(a)与(b)分别为目标角度域与距离域的仿真结果。
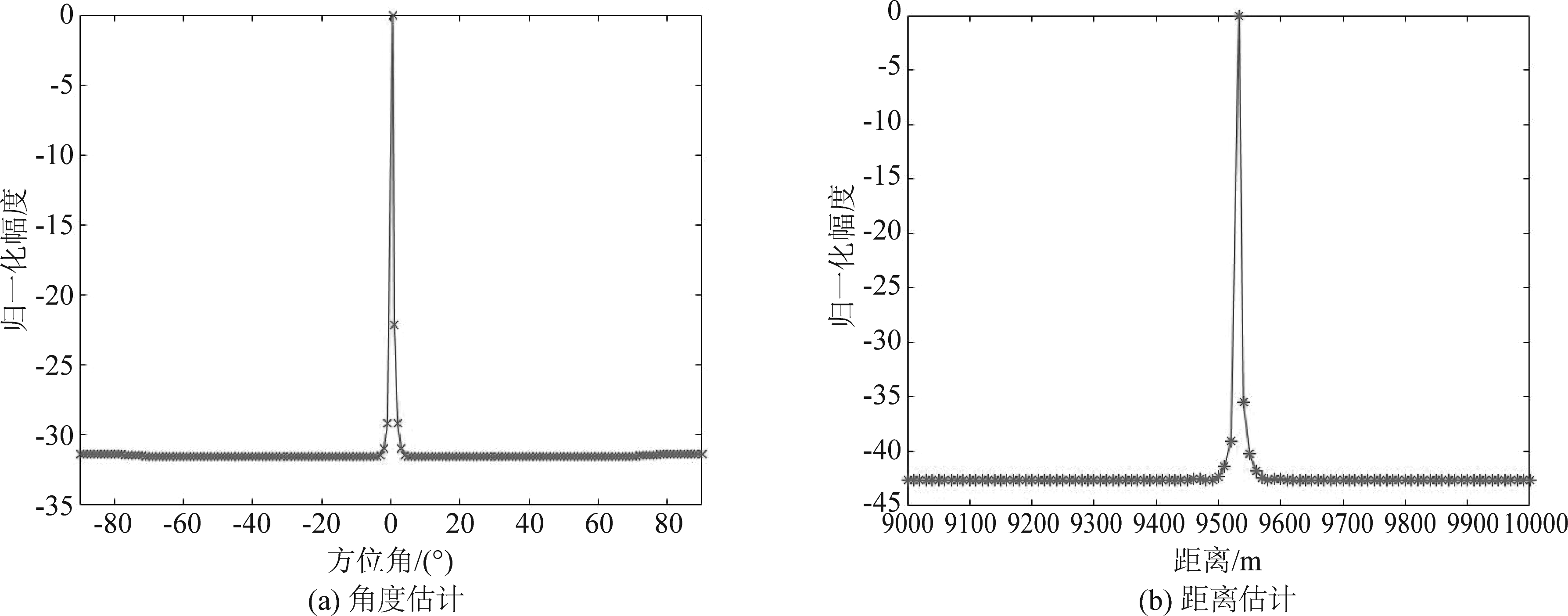
图7 单目标定位
Fig.7 Localization of one target
7.2 相同角度不同距离多目标
设置目标位置分别为(0.5°,9576 m)、(0.5°,9492 m)、(0.5°,9533 m)。参数设置与7.1节相同。图8(a)与(b)分别为目标角度域与距离域的仿真结果。

图8 同角度不同距离多目标定位
Fig.8 Localization of multi-targets with the same angle
对比图7与图8仿真结果可以看出,双脉冲方法的第一步(Δf=0 kHz,在这种情况下,它作为相控阵使用)只能在角度域中对目标进行检测,而无法对目标进行有效区分;但是在第二步通过对阵元添加适合的频偏后,在距离域完成了对目标的有效区分。
7.3 不同角度不同距离多目标
设置目标位置分别为(-2.4°,9576 m)、(0.5°,9492 m)、(3.6°,9533 m)。参数采取与7.1节相同的设置。图9(a)与(b)分别为目标角度域与距离域的仿真结果。
其中7.3估计的目标位置结果如表2所示。
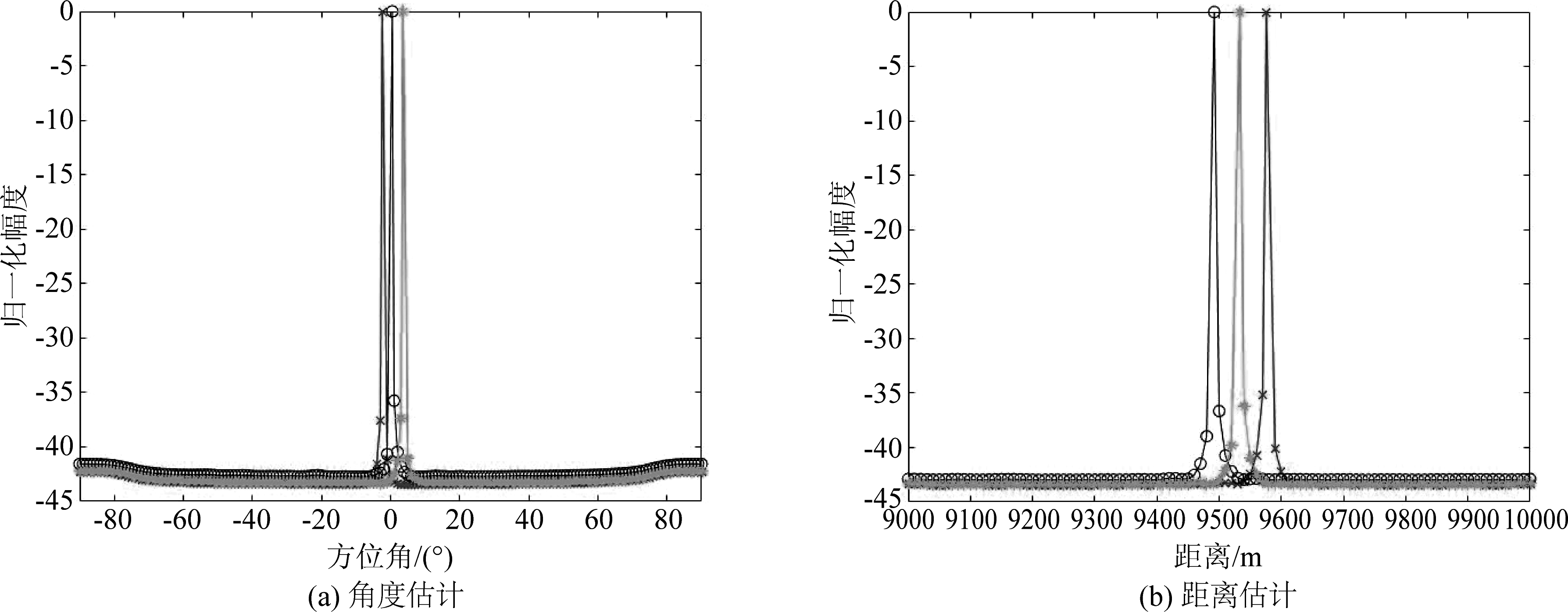
图9 不同角度不同距离多目标定位
Fig.9 Localization of multi-targets with the different angle and different range
表2 不同角度不同距离多目标估计结果
Tab.2 Localization of multi-targets with the different angle and different range
估计结果(-2.4025°,9575.7643 m)(0.5000°,9482.0388 m)(3.5982°,9533.0201 m)
由仿真结果可得,本文将FDA特性结合离网稀疏贝叶斯模型所提FDA-OGSBL目标定位算法能高精度的完成对目标的角度距离二维离网模型的定位,并且通过双脉冲方法将目标的二维信息估计转化为两次一维估计,分别得到目标的角度与距离,减少了计算量,提高了算法效率。
7.4 性能对比
本节主要将本文所提的FDA-OGSBL算法与传统MUSIC算法、L1-SVD算法进行性能对比,对比结果将显示本文所提的基于稀疏贝叶斯学习的离网目标定位算法具有更高精度,并通过仿真结果分析MUSIC算法与L1-SVD算法无法对离网模型下的目标进行精确估计。角度域与距离域的均方根误差以dB形式由式(81)、(82)给出:
(81)
(82)
式中,K为目标总个数,P为实验次数,![]() 与
与![]() 分别为第p次实验下第k个目标的角度与距离的估计值。目标位置采取与7.3中相同的设置,设置角度域上的采样网络间隔为1°,距离域上的采样网络间隔为10 m,实验次数P=100次。图10为发射阵元个数与接收阵元个数N=M=21,快拍数T=100的条件下角度域与距离域上的均方根误差随信噪比变化的性能对比图,图11为信噪比SNR=0 dB,快拍数T=100的条件下角度域与距离域上的均方根误差随阵元数变化的性能对比图,图12为信噪比SNR=0 dB,发射阵元个数与接收阵元个数N=M=21的条件下角度域与距离域上的均方根误差随快拍数变化的性能对比图。
分别为第p次实验下第k个目标的角度与距离的估计值。目标位置采取与7.3中相同的设置,设置角度域上的采样网络间隔为1°,距离域上的采样网络间隔为10 m,实验次数P=100次。图10为发射阵元个数与接收阵元个数N=M=21,快拍数T=100的条件下角度域与距离域上的均方根误差随信噪比变化的性能对比图,图11为信噪比SNR=0 dB,快拍数T=100的条件下角度域与距离域上的均方根误差随阵元数变化的性能对比图,图12为信噪比SNR=0 dB,发射阵元个数与接收阵元个数N=M=21的条件下角度域与距离域上的均方根误差随快拍数变化的性能对比图。
从仿真结果可以分析出FDA-OGSBL算法在低信噪比下也能实现高精度的估计性能并且估计性能随信噪比的增大而提高。而MUSIC算法与L1-SVD算法无论在角度域还是距离域上,当信噪比达到一定时,均方根误差均呈一条直线。以角度估计为例进行分析,3个目标点的角度分别为-2.4°,0.5°与3.6°,MUSIC算法与L1-SVD算法的估计精度分别为-2°,0°或1°,4°。因此角度域上均方根误差根据式(81)可得:
![]()
-3.6062 dB
(83)
为对不同算法的估计精度进行验证,表3与表4在信噪比SNR=0 dB的条件下,通过四次在角度域与距离域上的不同采样网格设置进行均方根误差求解,验证了不同算法所能达到的估计精度。
对比表3与表4可得,本文将FDA特性结合稀疏贝叶斯理论提出的FDA-OGSBL算法的均方根误差会随着采样网格间距的增大而增大,并且即使在较为粗糙的采样网格下均方根误差也较小,说明即使采样网格较为粗糙,FDA-OGSBL算法也能保持较好的估计性能,而MUSIC算法与L1-SVD算法的估计精度只能达到与目标位置最近的采样网格,而无法对偏离采样网格的离网参数进行有效估计,这是传统算法的不足之处。
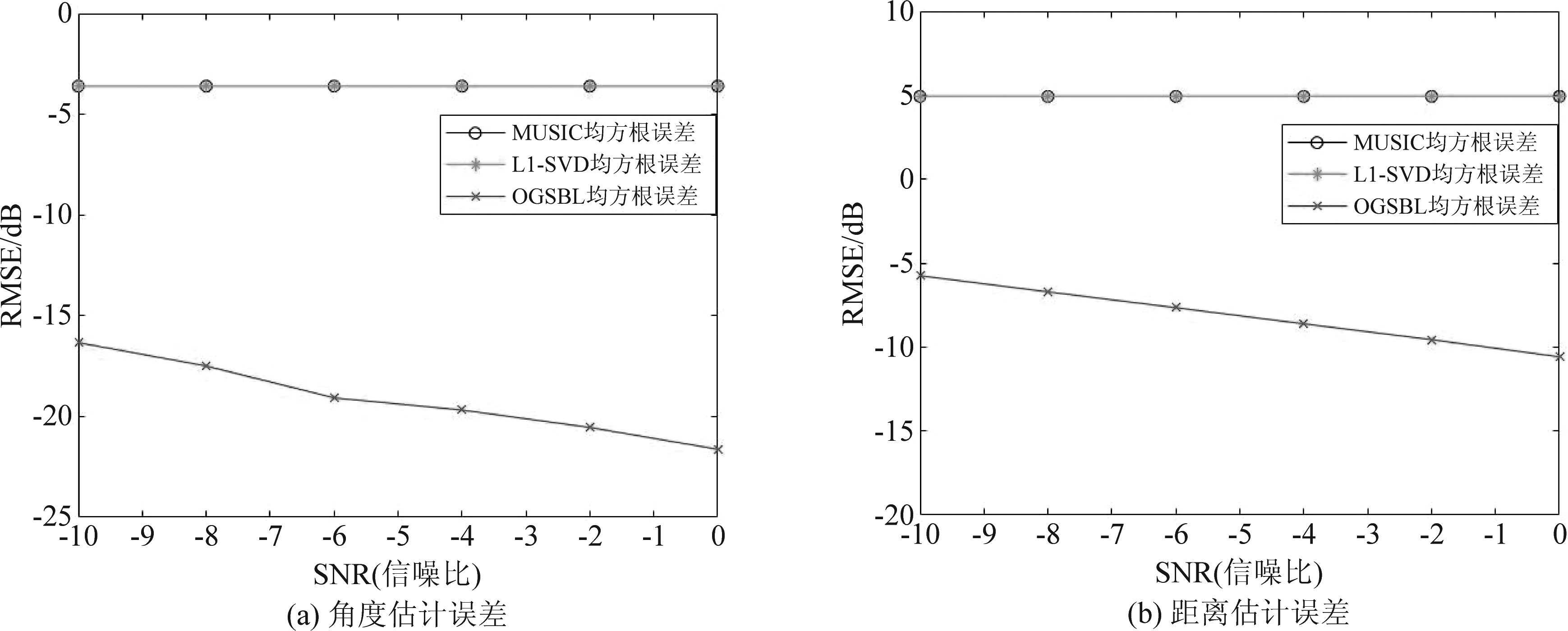
图10 不同信噪比下均方根误差
Fig.10 RMSE with different SNR
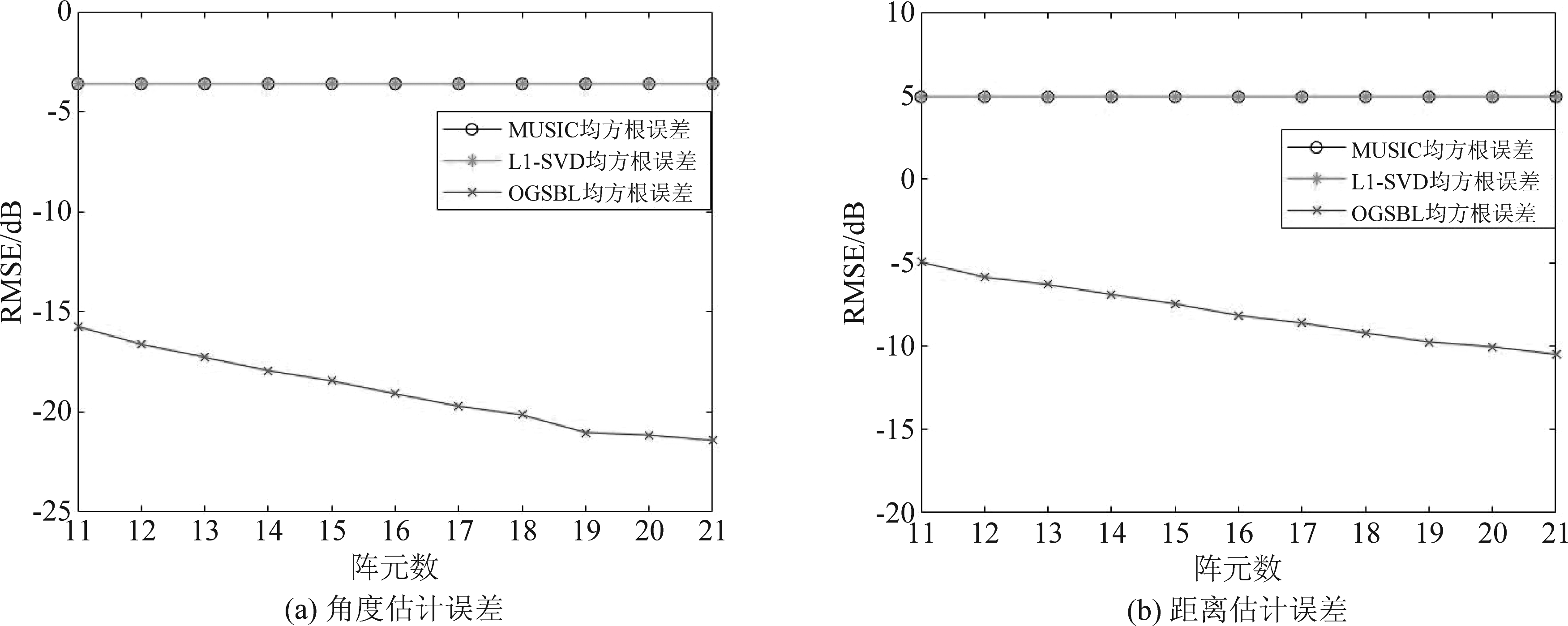
图11 不同阵元数下均方根误差
Fig.11 RMSE with different elements
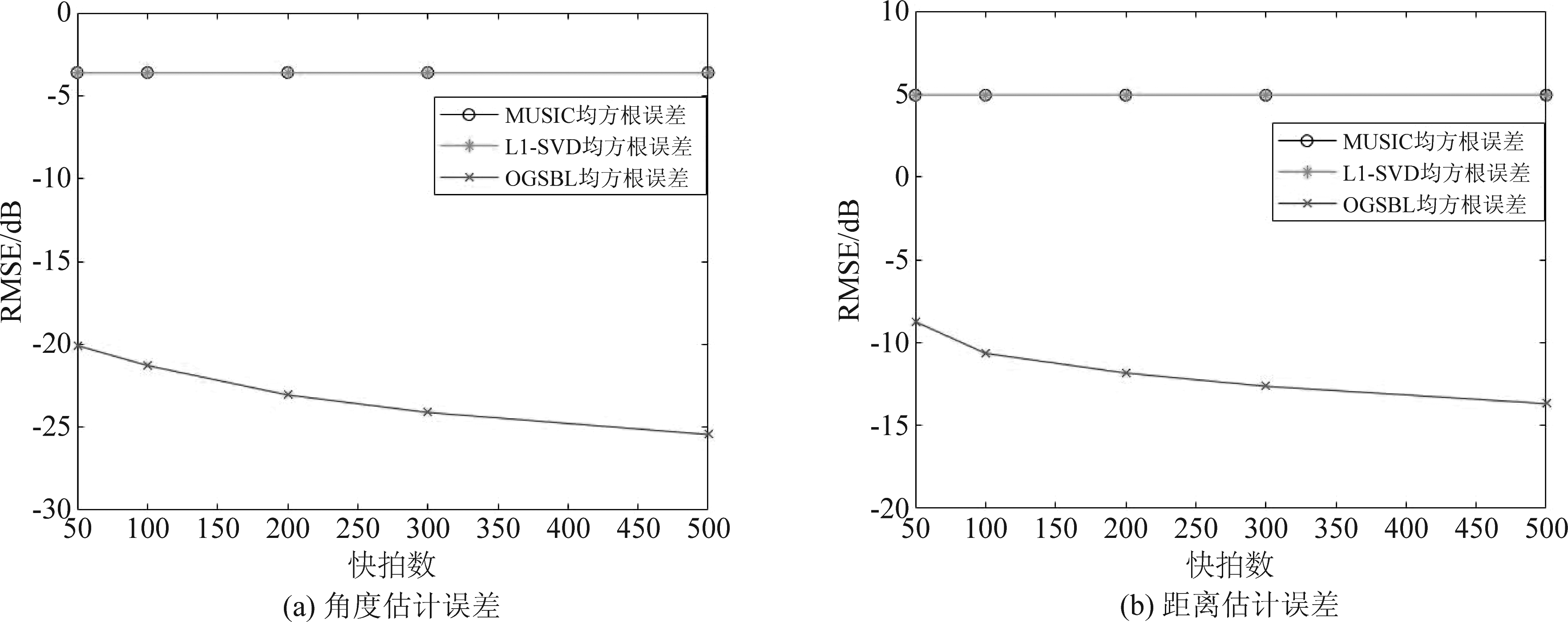
图12 不同快拍数下均方根误差
Fig.12 RMSE with different snapshots
表3 不同网格间距下角度域的RMSE
Tab.3 RMSE of angle with different grid interval

SNR=0 dBRMSE/dBr=0.5°r=1°r=2°r=5°MUSIC-10.8805-3.6062-3.60622.1217L1-SVD-10.8805-3.6062-3.60622.1217FDA-OGSBL-27.9396-21.9926-19.6244-11.8920
表4 不同网格间距下距离域的RMSE
Tab.4 RMSE of range with different grid interval
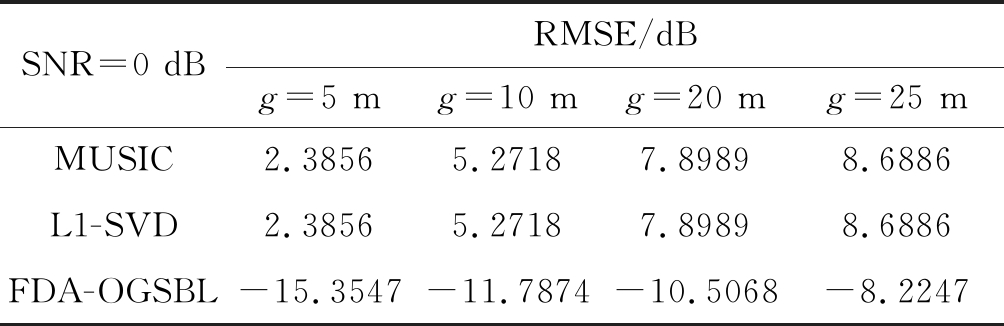
SNR=0 dBRMSE/dBg=5 mg=10 mg=20 mg=25 mMUSIC2.38565.27187.89898.6886L1-SVD2.38565.27187.89898.6886FDA-OGSBL-15.3547-11.7874-10.5068-8.2247
8 结论
本文针对频控阵(FDA)雷达传统的目标定位算法计算量大以及无法对离网模型下的目标进行有效定位而导致的精度不足问题,通过将FDA雷达特性结合稀疏贝叶斯模型,提出一种基于稀疏贝叶斯学习的双脉冲FDA雷达离网目标定位方法,该方法适用于单快拍与多快拍场景,克服了传统算法对快拍数要求较高的不足。通过实验仿真分析,本文算法能对离网目标实现高精度的定位估计,克服了FDA雷达传统目标定位方法无法对离网目标进行有效估计的缺陷。存在的不足之处在于,本文的方法是一种基于贝叶斯循环迭代的过程,在采样网格较小的情况下算法运行速度较慢,尽管可以采用较大的采样网格提升算法速度,但会损失一定精度,另外本文方法的提出是在信号为窄带信号的前提下对远场目标进行定位估计,对于近场条件下的目标定位,还未对其算法性能进行评估,上述问题将会在接下来的研究中继续展开。
[1] Bandiera F, Mancino M, Ricci G. Localization Strategies for Multiple Point-Like Radar Targets[J]. IEEE Transactions on Signal Processing, 2012, 60(12): 6708- 6712.
[2] Schmidt R O. Multiple emitter location and signal parameter estimation[J]. IEEE Transactions on Antennas & Propagation, 1986, 34(3): 276-280.
[3] Krim H, Viberg M. Two decades of array signal processing research: the parametric approach[J]. IEEE Signal Processing Magazine, 1996, 13(4): 67-94.
[4] Candès E J, Romberg J, Tao T. Robust Uncertainty Principles: Exact Signal Frequency Information[J]. IEEE Transactions on Information Theory, 2006, 52(2): 489-509.
[5] Donoho D L. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289-1306.
[6] Malioutov D, Cetin M, Willsky A S. A sparse signal reconstruction perspective for source localization with sensor arrays[J]. IEEE Transactions on Signal Process, 2005, 53(8): 3010-3022.
[7] Tipping M E. Sparse Bayesian Learning and the Relevance Vector Machine[J]. Journal of Machine Learning Research, 2001, 1(3): 211-244.
[8] Wipf D P, Rao B D. Sparse Bayesian learning for basis selection[J]. IEEE Transactions on Signal Processing, 2004, 52(8): 2153-2164.
[9] Wipf D, Palmer J, Rao B. Perspectives on sparse Bayesian learning[C]∥Proceedings of the 16th International Conference on Neural Information Processing Systems. MIT Press, 2003.
[10] Ji S, Xue Y, Carin L. Bayesian Compressive Sensing[J]. IEEE Transactions on Signal Processing, 2008, 56(6):2346-2356.
[11] Babacan S D, Molina R, Katsaggelos A K. Bayesian Compressive Sensing Using Laplace Priors[J]. IEEE Transactions on Image Processing, 2010, 19(1): 53- 63.
[12] Liu Zhangmeng, Huang Zhitao, Zhou Yiyu. An Efficient Maximum Likelihood Method for Direction-of-Arrival Estimation via Sparse Bayesian Learning[J]. IEEE Transactions on Wireless Communications, 2012, 11(10): 1-11.
[13] Nannuru S, Gerstoft P, Koochakzadeh A, et al. Sparse Bayesian Learning for DOA Estimation Using Co-Prime and Nested Arrays[C]∥2018 IEEE 10th Sensor Array and Multichannel Signal Processing Workshop (SAM). IEEE, 2018.
[14] Groll H, Mecklenbrauker C, Gerstoft P. Sparse Bayesian Learning for Directions of Arrival on an FPGA[C]∥2018 IEEE Statistical Signal Processing Workshop (SSP). IEEE, 2018.
[15] Mecklenbriiuker C F, Gerstoft P, Leus G. Sparse Bayesian Learning for DOA Estimation of Correlated Sources[C]∥2018 IEEE 10th Sensor Array and Multichannel Signal Processing Workshop (SAM). IEEE, 2018.
[16] Nannuru S, Gerstoft P. 2D Beamforming on Sparse Arrays with Sparse Bayesian Learning[C]∥ICASSP 2019-2019 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP). IEEE, 2019.
[17] Alibrahim F, Inggs M. Sparse Bayesian Learning for Spinning Antenna DOA Super-Resolution[J]. Electronics Letters, 2018, 54(6): 389-391.
[18] Bai Hua, Duarte M F, Janaswamy R. Direction of Arrival Estimation for Complex Sources Through  1 Norm Sparse Bayesian Learning[J]. IEEE Signal Processing Letters, 2019, 26(5): 765-769.
1 Norm Sparse Bayesian Learning[J]. IEEE Signal Processing Letters, 2019, 26(5): 765-769.
[19] Hannan M A, Rocca P. Directions-of-Arrival Estimation in Linear Sub-Arrayed Array Through Compressive Sensing[C]∥2019 IEEE International Symposium on Antennas and Propagation and USNC-URSI Radio Science Meeting. IEEE, 2019.
[20] Wang Shixin, Zhao Yuan, Ibrahim L, et al. Joint 2D DOA and Doppler frequency estimation for L-shaped array using compressive sensing[J]. Journal of Systems Engineering and Electronics, 2020, 31(1): 28-36.
[21] Yang Zai, Xie Lihua, Zhang Cishen. Off-Grid Direction of Arrival Estimation Using Sparse Bayesian Inference[J]. IEEE Transactions on Signal Processing, 2013, 61(1): 38- 43.
[22] Das A, Sejnowski T J. Narrowband and Wideband Off-Grid Direction-of-Arrival Estimation via Sparse Bayesian Learning[J]. IEEE Journal of Oceanic Engineering, 2018, 43(1): 108-118.
[23] Park Y, Gerstoft P. Compressive 2-d Off-grid DOA Estimation for Propeller Cavitation Localization[C]∥ICASSP 2020-2020 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP). IEEE, 2019.
[24] Bai Yanying, Xiao Shaoqiu, Tang Mingchun, et al. Wide-Angle Scanning Phased Array With Pattern Reconfigurable Elements[J]. IEEE Transactions on Antennas & Propagation, 2011, 59(11): 4071- 4076.
[25] Antonik P, Wicks M C, Griffiths H D, et al. Frequency diverse array radars[C]∥IEEE Conference on Radar. IEEE, 2006.
[26] 王文钦, 邵怀宗, 陈慧. 频控阵雷达: 概念, 原理与应用[J]. 电子与信息学报, 2016, 38(4): 1000-1011.
Wang Wenqin, Shao Huaizong, Chen Hui. Frequency Diverse Array Radar: Concept, Principle and Application[J]. Journal of Electronics & Information Technology, 2016, 38(4): 1000-1011.(in Chinese)
[27] Antonik P. An investigation of a frequency diverse array[D]. [Ph.D.dissertation], University College London, 2009.
[28] Wicks M C, Antonik P. Frequency diverse array with independent modulation of frequency, amplitude, and phase[P]. USA, 7319427, 2008.
[29] Secmen M, Demir S, Hizal A, et al. Frequency Diverse Array Antenna with Periodic Time Modulated Pattern in Range and Angle[C]∥IEEE Radar Conference. IEEE, 2007.
[30] Higgins T, Blunt S D. Analysis of range-angle coupled beamforming with frequency-diverse chirps[C]∥International Waveform Diversity & Design Conference. IEEE, 2009.
[31] Higgins T, Blunt S D, Shackelford A K. Space-Range Adaptive Processing for Waveform-Diverse Radar Imaging[C]∥IEEE Radar Conference. IEEE, 2010.
[32] Mobeen M, Hasan M. Frequency Diverse Array Beamforming Using Nonuniform Logarithmic Frequency Increments[J]. IEEE Antennas and Wireless Propagation Letters, 2018, 17(10): 1817-1821.
[33] Jones A M, Rigling B D. Frequency diverse array radar receiver architectures[C]∥International Waveform Diversity & Design Conference, 2012.
[34] Xu Jingwei, Liao Guisheng, Zhu Shengqi. Receive beamforming of frequency diverse array radar systems[C]∥2014 XXXIth URSI General Assembly and Scientific Symposium (URSI GASS). IEEE, 2014.
[35] Wang Wenqin, So H C, Shao Huaizong. Nonuniform Frequency Diverse Array for Range-Angle Imaging of Targets[J]. Sensors Journal IEEE, 2014, 14(8): 2469-2476.
[36] Wang Wenqin, So H C. Transmit Subaperturing for Range and Angle Estimation in Frequency Diverse Array Radar[J]. IEEE Transactions on Signal Processing, 2014, 62(8): 2000-2011.
[37] Wang Luo Shengbin, Xu Zhenhai, Liu Xinghua, et al. Subarray-Based Frequency Diverse Array for Target Range-Angle Localization With Monopulse Processing[J]. IEEE Sensors Journal, 2018, 18(14): 5937-5947.
[38] 顾坤良, 欧阳缮, 李晶晶, 等. 基于MUSIC算法的频率分集阵列雷达目标定位方法[J]. 桂林电子科技大学学报, 2017, 37(2): 87-91.
Gu Kunliang, Ouyang Shan, Li Jingjing, et al. An algorithm of targets localization for frequency diverse array radar[J]. Journal of Guilin University of Electronic Technology, 2017, 37(2): 87-91.(in Chinese)
[39] Xu Jingwei, Lan Lan, Liao Guisheng, et al. Range-angle matched receiver for coherent FDA radars[C]∥2017 IEEE Radar Conference (RadarConf17). IEEE, 2017.
[40] Goodman N R. Statistical analysis based on a certain multivariate complex Gaussian distribution (an introduction)[J]. Ann. Math. Statist., 1963, 34(1): 152-177.
[41] Bishop C M. Pattern Recognition and Machine Learning (Information Science and Statistics)[M]. Springer-Verlag New York, Inc. 2006.
[42] MacKay David J C. Bayesian Interpolation[J]. Neural Computation, 1992, 4(3): 415- 447.




