1 引言
随着通信技术的发展,无线通信平台从扁平化向立体化延伸,信号传输环境也愈发复杂多变。从电磁波辐射的角度看,在无线传输过程中,信号遇到障碍物会发生折射、反射和散射,导致信号将从不同路径先后到达接收端,带来非零延迟分量,引起信号时域波形拖尾展宽[1]。当符号周期大于信道最大传输时延时,信道表现为平坦衰落,不会引起码间串扰,此时可采取分集技术将平坦衰落信道改善为加性高斯白噪声(Additive White Gaussian Noise, AWGN)信道[2]。当符号周期小于信道最大传输时延时,历史符号将会影响当前符号判决,带来码间串扰(Inter Symbol Interference, ISI),导致系统误码率升高,且难以通过增大发射功率的方式来降低误码率[3],此时信道表现为频率选择性衰落。
为消除码间串扰,提升系统可靠性,有许多学者投入了研究[4-14],主要分为三种思路:一种思路是将频率选择性衰落转化为平坦衰落,从源头上避免码间串扰。广泛应用在4G和5G通信的正交频分复用(Orthogonal Frequency Division Multiplexing, OFDM)技术便采用增大了符号周期的方法,将一个高速比特流通过串并转换变为多个低速比特流,再通过多载波调制的方式将信号发射出去。但是OFDM系统存在两个缺点:一是高峰均比导致信号失真[7],二是系统对频偏敏感,对多个子载波之间的正交性要求高[8]。
另一种思路是,对于有记忆接收信号,若能得到信道参数,求出条件概率密度,就可以通过最大似然序列检测(Maximum Likelihood Sequence Estimation, MLSE)的方法从理论上消除码间干扰。但是MLSE计算量大,假设信道长度为Lh+1,对于数据长度为N的M进制符号,需要计算MN次全局欧式距离,即使采用Andrew提出的Viterbi算法实现MLSE的递推搜索,也需要计算NMLh+1次欧式距离,难以实际应用[9-10]。
第三种思路是在接收端采用均衡技术来消除多径信道影响,即设计一种均衡器,使得信道响应和均衡器的卷积等效为理想AWGN信道[11-14]。根据不同的优化准则,均衡器主要可以分为迫零均衡器和MMSE均衡器。两种均衡器存在稳定性上的差异,但都起到了信道匹配滤波的作用,文献[1]证明了信道匹配滤波器具有最大比同相合并作用,在信道系数归一化的条件下,能完全利用信号能量,获得最大信噪比,对于低莱斯因子的信道环境有很强的应用价值。但是信道匹配滤波同时会引入双向ISI和有色噪声,不利于符号的独立判决。
本文主要针对低莱斯因子的慢衰落时变多径信道环境下,接收信号经过MMSE均衡后存在双向码间串扰的问题,提出了一种新的MMSE均衡算法:即对硬判决信号进行改判,获得频域重构信号,再根据时域误差进行时频联合判决的均衡算法,仿真结果表明本方案不仅能很好地达成消除双向ISI的目的,且在低莱斯因子条件下对于多径信号的能量具有良好的搜集作用。
2 低莱斯因子多径信道模型
理想AWGN信道的单位冲激响应为δ函数,具有无穷大的带宽,是一种无记忆信道。针对无记忆调制信号,在接收端根据最大后验概率准则即可实现符号独立判决,不会出现码间串扰现象。在实际传输中,当符号周期小于信道最大传输时延,即信号带宽大于相干带宽时,产生频率选择性衰落,此时的多径信道显然不是理想AWGN信道,而是一种有记忆AWGN信道,可以将其建模为具有离散抽头延迟线结构的有限长单位冲激响应(Finite Impulse Response, FIR)滤波器,以便为每个可解析的延迟路径生成时变抽头来模拟信道。即:
(1)
其中,ai(t)ej(2πfit+φi)表示第i条路径的抽头系数,根据中心极限定理,ai(t)ej(2πfit+φi)服从复高斯分布,其模值服从瑞利分布, fi表示第i条路径的频偏,φi表示第i条路径的相偏,τi表示第i条路径的传输时延,Nd表示散射径数目。在无线电信号的传播过程中,多径往往由一条直射径和多条散射径组成,因此总的抽头数为Nd+1。
一般来说直射径能量最大,可以看做非零均值的随机变量,在某些情况下可以看做常数[19]。当信道中存在直射径这样的静态分量时,抽头模值不再服从瑞利分布,转而服从莱斯分布。定义直射径和散射径的能量比为莱斯因子:
K=10log10(A2/σ2)
(2)
其中,A2为直射径的功率,σ2为所有散射径的总功率。对于高莱斯因子的信道,可以忽略散射径,只利用直射径能量,使得信道近似为AWGN信道,对于低莱斯因子信道只能通过搜集多条延迟路径上的能量才能使得发射端能量得到有效利用。一般来说,莱斯因子越小,信道越恶劣,通信系统的误码率越高。
3 MMSE均衡器与信道匹配滤波
3.1 MMSE均衡器
MMSE均衡器是指根据最小均方误差准则来调整均衡器抽头系数,使得发送符号和均衡输出符号的均方误差最小的均衡器。MMSE均衡器的系统函数表达式为:
(3)
其中,H(z)为信道的z域表达式,H*(z-1)为信道匹配滤波器的z域表达式,其时域表达式为
是信道hn的共轭时域翻转,N0为噪声谱密度。式(4)给出了迫零均衡器的系统函数:
(4)
比较式(3)和式(4)发现,MMSE均衡器的系统函数在分母处多了一项噪声谱密度N0,系统在单位圆上及附近不存在极点,因此不存在不稳定的情况。
MMSE均衡器系统函数的极点在单位圆内外成对出现,而这种高阶多项式的时域分解是很麻烦的。实际上在频域可以同时实现双向滤波,并且可以基于FFT快速实现,效率高,复杂度低。基于MMSE准则的均衡处理方法一般采用块传输的方式在频域进行均衡,即单载波频域均衡(Single Carrier Frequency Domain Equalization, SC-FDE),既可以减少组与组之间的码间串扰,还可以利用FFT和IFFT实现快速计算,同时避免了OFDM系统的缺点[15-17]。SC-FDE系统的框图如图1所示。
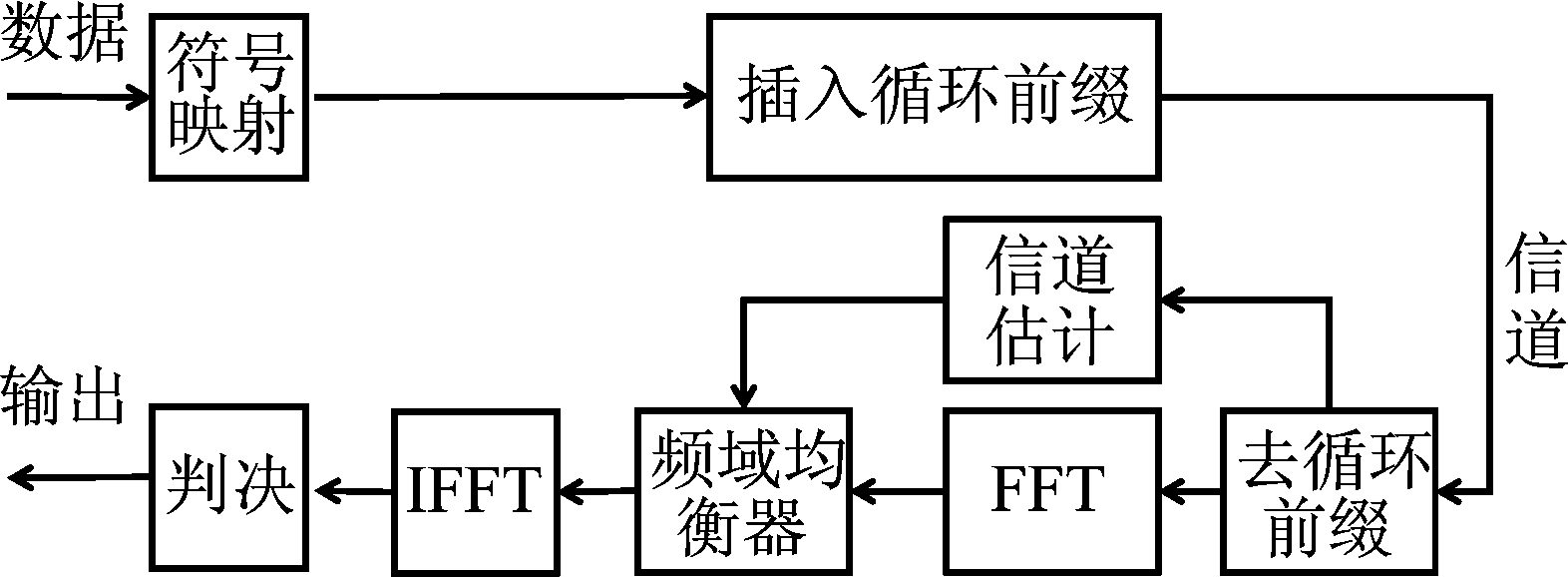
图1 单载波频域均衡(SC-FDE)系统框图
Fig.1 SC-FDE System
SC-FDE系统接收部分的具体信号处理流程如下:假设接收端已经完成载波解调并消除频偏,同时完成信号的同步和信道估计,在对估计出的信道单位冲激响应{he(τ)}插零后得到N点的{h(τ)},以对齐接收信号长度,对{h(τ)}进行N点FFT得到H(k),进而求出其自相关函数的频域表达式。同时,将接收信号
也进行N点FFT变换到频域得到
完成接收信号的均衡,再通过IFFT变换到时域得到
最后硬判决输出均衡信号的星座序列
3.2 信道匹配滤波
假设信道抽头系数已知,在接收端采用信道匹配滤波的方法来提高信噪比:
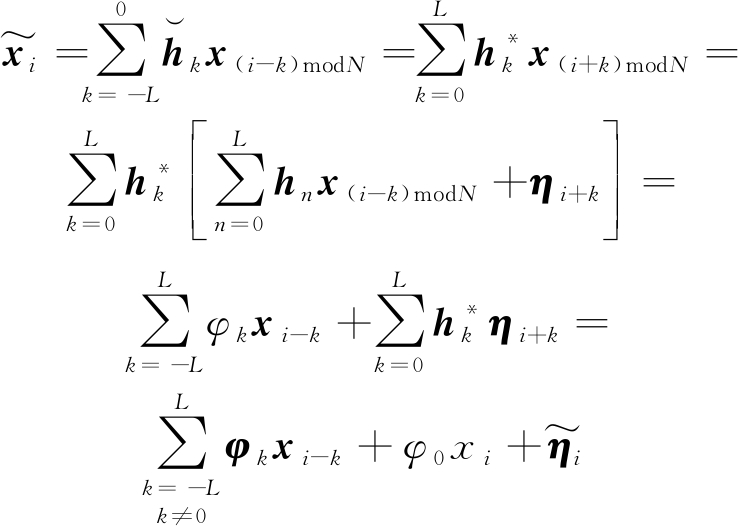
(5)
式(5)推导结果的第一项为双向ISI,第二项为当前符号的最大比同相合并结果,最后一项
为高斯白噪声经过匹配滤波器之后的有色噪声序列。
假设信道系数是归一化的,则匹配滤波器的系数也是归一化的,则有
式中每个符号矢量的能量为φ0|xi|2=Es,噪声能量为
信噪比为Es/N0,相当于将所有有用信号延迟分量的能量加到一条功率谱密度为N0的AWGN信道后进行符号检测。
基于上面的讨论,如果能采取一定措施消除双向ISI,就可以得到类似AWGN信道输出判决,并且完全利用信号能量,没有信噪比损失:
(6)
观察式(3)的分母可知,MMSE均衡已经包含了信道匹配滤波的过程。
4 信号重构和时频联合判决
由上面的分析可以得到,信道匹配滤波使得信号完成最大比同相合并,完全利用了多径能量,但是同时带来了双向的码间串扰。因此考虑对信号进行改判以降低误码率,改判的方法是:首先对信道做进一步的修正处理,让硬判决符号通过修正信道后得到重构信号,再比较一个信道长度内,重构信号和接收信号之间的误差,重构信号误差总能量最小的即为最佳判决。
4.1 信号重构
考虑最简单的线性修正:
(7)
其中,r为实数,
为修正后信道的频域表达式。修正的准则是使得接收符号的频域序列和重构信号的频域序列的均方误差最小。即:
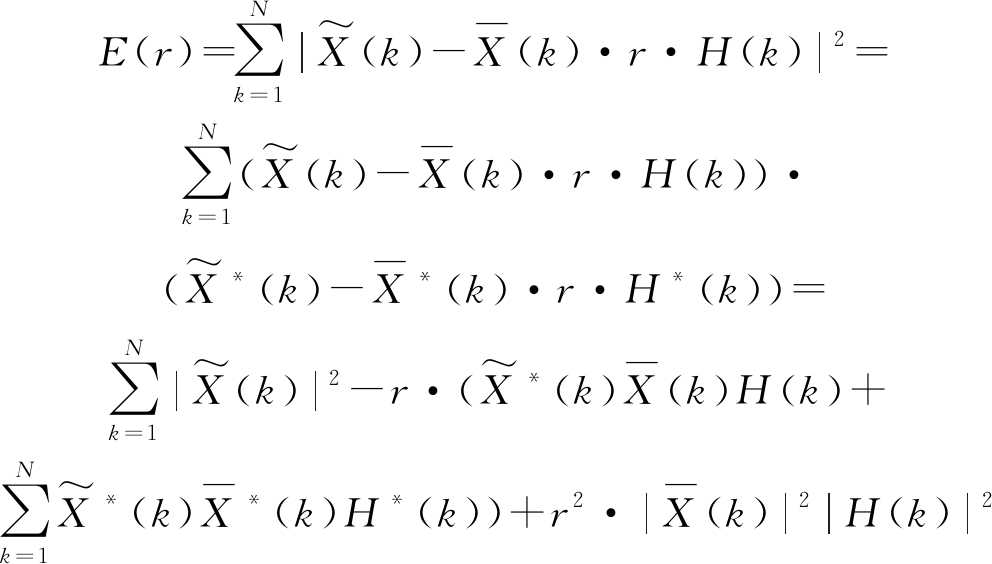
(8)
E(r)是r的函数,关于r求导,使导数等于零:
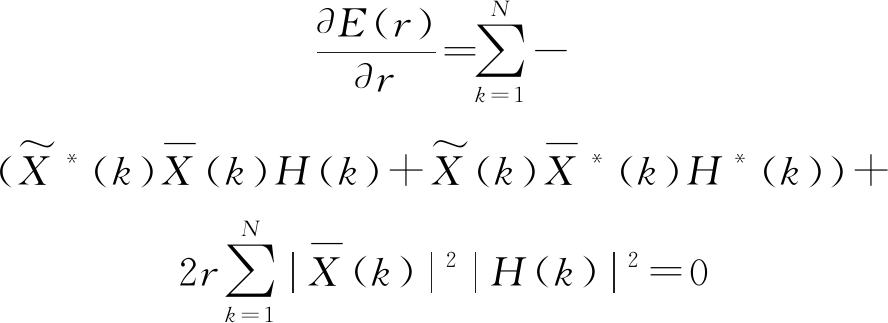
(9)
得到r的表达式:
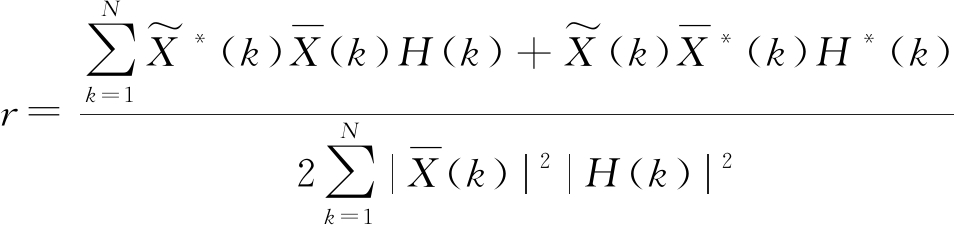
(10)
为得到实数r,对分子取其实部:
r=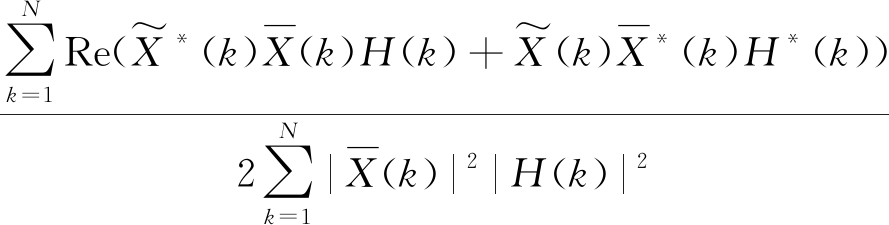
(11)
即为重构信号的频域输出
(12)
4.2 时频联合判决
当前符号的码间串扰影响范围为两个信道长度,因此考虑两个信道长度内误差能量最小的即为最佳判决。时频联合判决的含义是:遍历N个硬判决输出,将频域误差变换到时域,以当前硬判决符号为起点,只进行当前符号的改判,计算左边和右边各一个信道长度的总误差能量,得到对应的原始误差能量和改判误差能量,其中误差能量最小对应的判决即为最佳判决。由于卷积运算在频域处理更加简便,信号重构部分也是在频域完成,因此首先计算得到频域误差能量,而变换到时域是为了更好地比较不同改判结果的码间串扰引起的误差能量。
以QPSK信号为例,若硬判决输出
为{1+1i},对其分别改判为{1-1i}、{-1+1i}和{-1-1i},并且分别将改判后的星座序列进行FFT,得到改判后的频域表达式,并通过修正信道得到改判的重构信号
其中m={1,2,3,4}为重构信号下标。
定义重构信号的频域误差:
(13)
计算与接收信号的频域误差Errm(k),将频域误差通过IFFT变换到时域得到errm(n),计算两个信道长度的误差能量:
(14)
其中,em最小所对应判决即为四种判决中的最佳判决,此时即可判决输出。信号处理流程如图2所示。
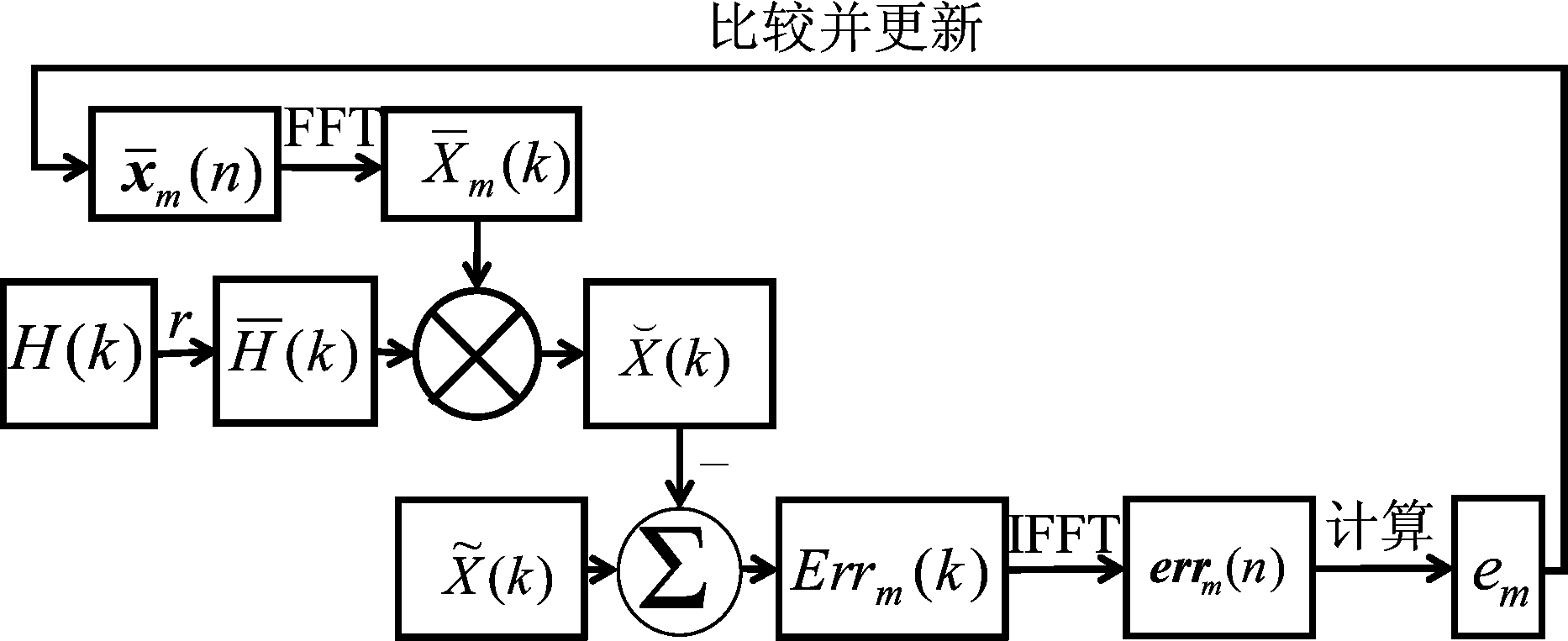
图2 时频联合判决MMSE均衡信号处理流程图
Fig.2 Time-frequency Joint Decision MMSE Equalization
4.3 算法性能分析
4.3.1 误码性能分析
由于MMSE均衡后存在残留ISI,无法直接推导错误概率公式,但可将残留ISI与有色噪声的和近似看作加性高斯白噪声,进行错误概率计算。设{qn}表示均衡器{cn}与等效信道冲激响应{fn}的卷积:
(15)
文献[1]推导了PAM信号的平均错误概率:
(16)
其中,DJ为残留ISI,M表示PAM对应的星座点种类,P(vJ)为对应的星座点vJ出现的概率,ση为有色噪声的方差:
(17)
当所有序列等概率出现时,平均错误的上边界为:
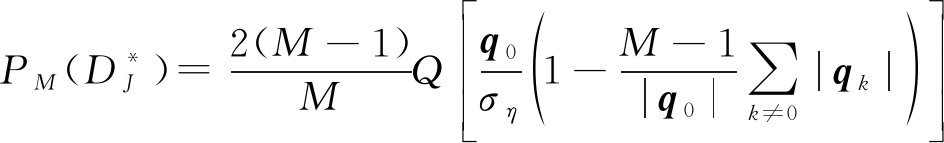
(18)
M=2即为BPSK的平均错误概率,而QPSK和BPSK的误码性能一致,因此QPSK的平均错误概率同样为式(17),本文算法的误码性能优于直接MMSE,但也可将式(18)作为平均错误的上边界。
4.3.2 复杂度分析
设符号长度为N,需要进行N次遍历改判,每次改判需要涉及M种符号。每帧数据仅需要计算一次r,每次计算r需要8N+1次乘法和2N次加法,计算重构信号需要N+1次乘法和N-1次加法,FFT运算和IFFT运算的复杂度均为o(N2)。每一轮改判和能量误差计算需要大量的FFT和IFFT运算,由于FFT运算和IFFT运算占了运算量的绝大部分,因此总体上来看,算法的复杂度为o(MN2)。
5 数据仿真与讨论
为验证算法在低莱斯因子下的性能,首先需要对多径信道进行设计,以得到不同莱斯因子的信道,其次需要根据信道的先验信息,设计SC-FDE系统的帧结构以求得到最优的系统性能。
5.1 信道设计
时变多径衰落信道的特征是延迟功率谱和多普勒谱。简单起见,假设延迟按照采样频率均匀分布。下面主要讨论多普勒功率谱,以往文献中建模最多的两种多普勒谱分别是高斯谱和Jakes谱[19]。
文献[20]提出一种可以利用一定数量正弦波合成离散瑞利信道的蒙特卡罗建模方式,其中多普勒频谱的形状由等效的多普勒概率密度函数确定。直接蒙特卡罗模拟方法将时间变化表示为延迟不能分辨的回波的离散和,如图3所示。
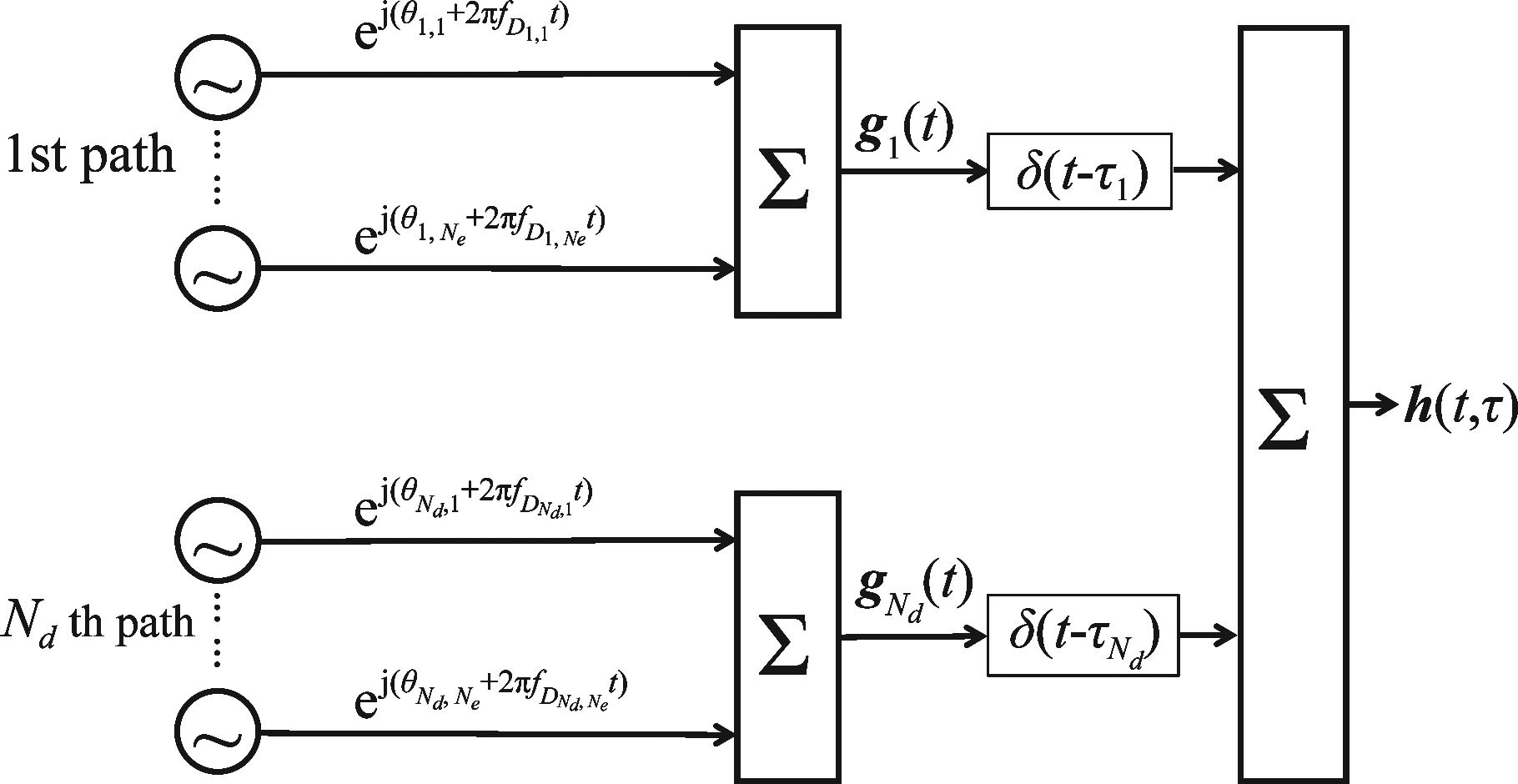
图3 正弦波合成离散瑞利信道
Fig.3 Sine wave synthesis discrete Rayleigh channel
每个回波都是具有随机相位和多普勒的正弦信号:
(19)
其中,Ne为正弦波个数, fDi,n和θi,n分别为第i个抽头中第n个正弦波的多普勒频率和初始相位。
文献[20]指出高斯频谱通常用来模拟高频无线电信道上存在的大气传播条件,而Jakes谱通常用来模拟移动性非常强的收发信机的地面传播。且高斯谱在分布尾部有能量扩散,比Jakes多普勒频谱更易变。因次,我们设计时变多径信道多普勒频谱为高斯谱的莱斯信道。
对于多普勒频谱为高斯谱的信道:
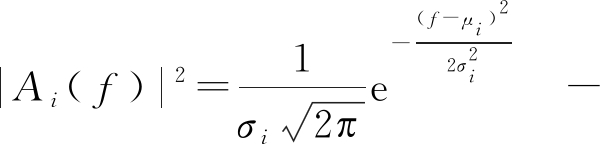
<f<
(20)
其中, f～N(μi,σi)。
信道长度Lh+1取13,包括1条零延迟路径分量和12条非零延迟路径分量,取Ne=200,即每条非零延迟路径由200个正弦波叠加而成。图4为时变多径信道的单位冲激响应的一个归一化样本值,从信道的单位冲激响应可以看出,零延迟分量相较其他多径分量的幅度是最大的,莱斯因子K约等于0 dB。
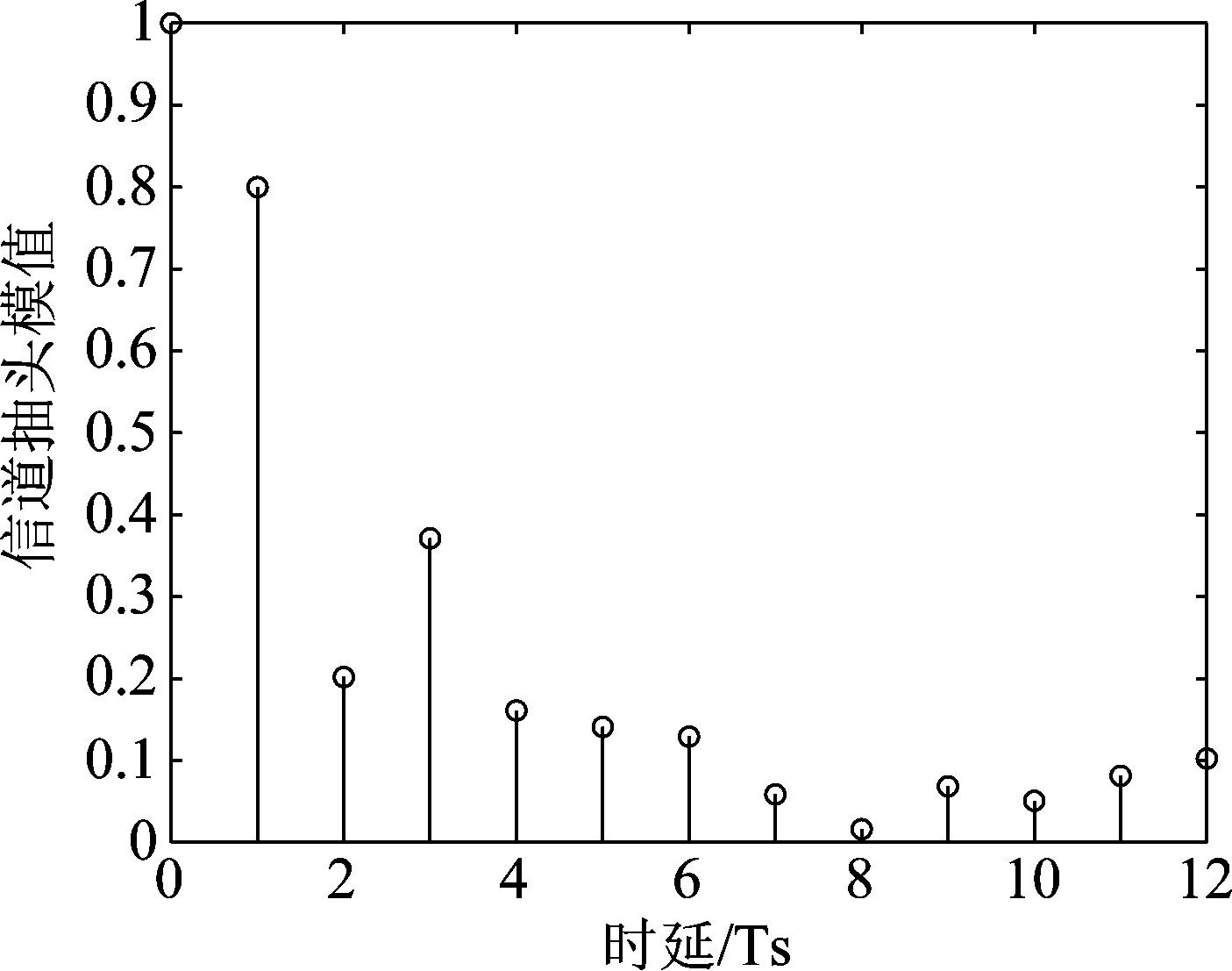
图4 某一时刻多径信道单位冲激响应
Fig.4 Unit Impulse response of Multipath Channel at a Certain Time
5.2 帧结构
数据帧设计:实验部分产生76800 bit数据,共分为200帧,每帧384 bit数据,采用16进制产生96个符号,每帧数据采用RS(8,6)编码,监督位为2符号,可纠错4符号。采用QPSK的数字调制方式,符号的传输速率为2.178 Msps,进行3倍上采样的根升余弦成形方式,滚降因子为0.333,载波频率为2.45 GHz。
帧头设计:反馈系数为{1 1 0 1 1 0 1}的移位寄存器可产生长度为63的m序列记为m63。由于成型滤波器的对称性,输出往往存在超前分量和滞后分量,考虑有2个超前分量,1个直达分量和10个滞后分量,m63-Head设计为{m63的后10个码片、m63、m63的前2个码片}的组合。
图5 数据帧结构
Fig.5 Frame Structure
表1总结了帧结构参数设置。
表1 帧结构参数
Tab.1 Frame parameters
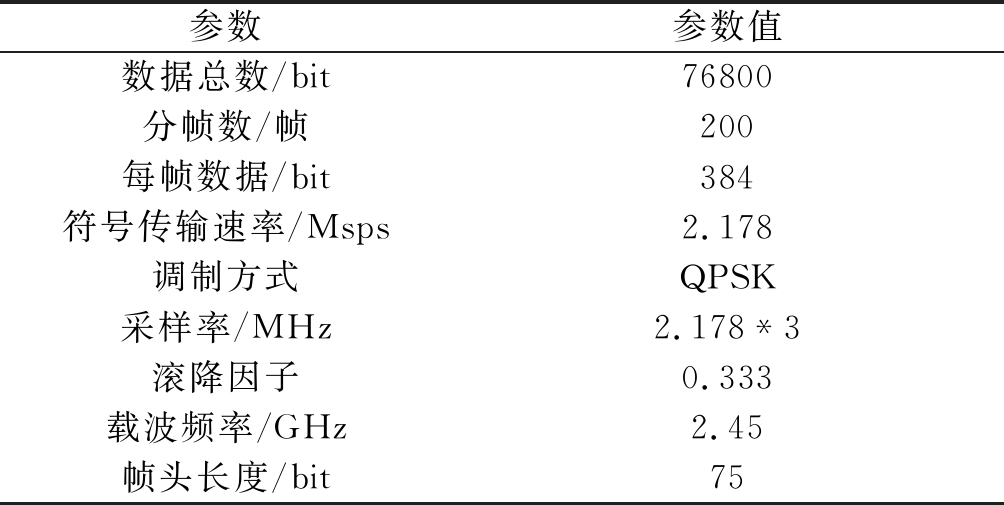
参数参数值数据总数/bit76800分帧数/帧200每帧数据/bit384符号传输速率/Msps2.178调制方式QPSK采样率/MHz2.178*3滚降因子0.333载波频率/GHz2.45帧头长度/bit75
5.3 仿真结果与分析
本文所提出算法只涉及均衡的处理部分,算法以接收端已经完成符号同步,载波同步以及信道估计为前提。为了验证算法具有消除双向ISI、利用多径分量信号的性能,设置三个仿真实验,并引入AWGN信道以模拟信号在自由空间传播,信噪比变化范围为0～20 dB。信噪比为20 dB的条件下,得到图6所示信道的信道输出星座图,即均衡器输入星座图和一般MMSE算法直接硬判决的MMSE均衡的软判决输出星座图7。可以看出即使在信噪比为20 dB的条件下,多径信道输出仍然很差,难以分辨星座,经过MMSE均衡处理,使得星座分布更加集中,起到了一定的均衡效果。
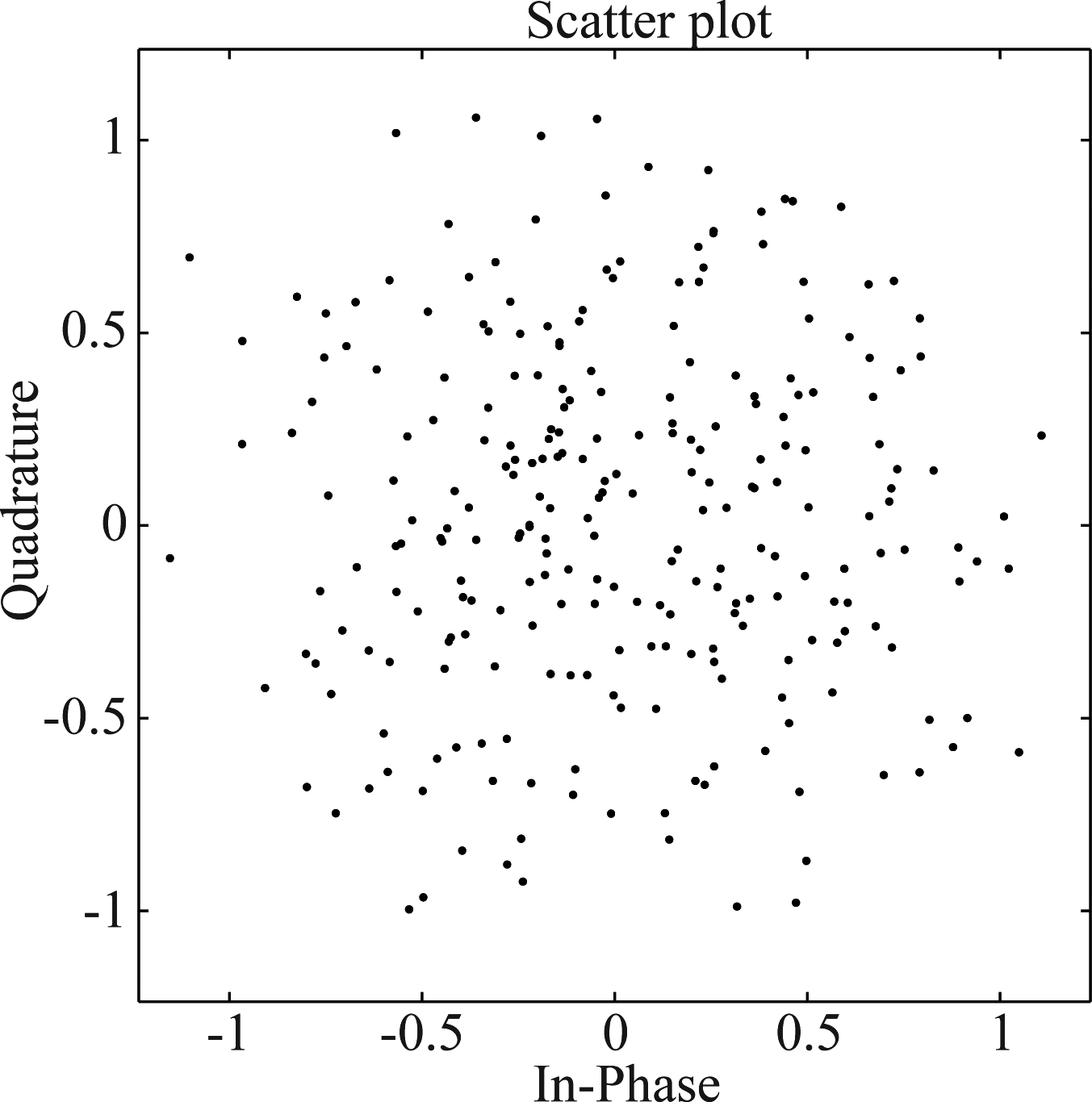
图6 均衡器输入
Fig.6 Input of Equalizer
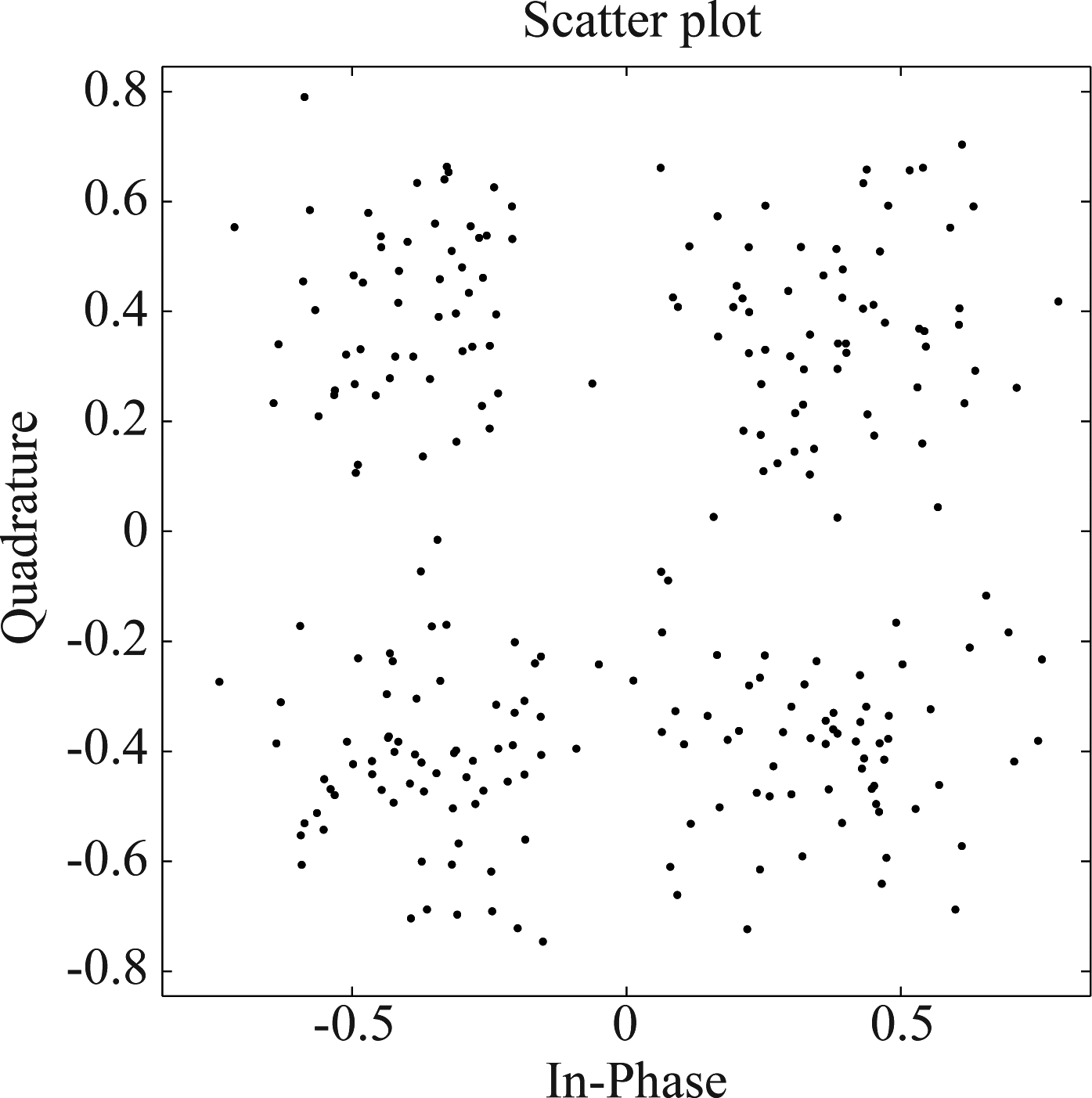
图7 MMSE均衡器软判决输出
Fig.7 Soft Output of MMSE Equalizer
仿真1 莱斯因子取值对系统误码率的影响
仿真1以SC-FDE系统的误码率作为性能指标,讨论莱斯因子分别取0 dB、5 dB和10 dB时,对一般MMSE均衡的影响。
从图8可以看出,当莱斯因子为0 dB时,系统的误码率在1%以上,当增大直射分量,莱斯因子分别取5 dB和10 dB时,系统误码性能分别在0.005和0.001以上,此时的误码性能略有提升但还是不能达到实际可靠通信的要求。综上可知,当莱斯因子很小时,MMSE均衡算法不能有效地降低系统误码率,即不能有效消除双向的ISI。对比QPSK信号通过瑞利信道的理论误码率可知,MMSE均衡系统仍有较大的提升空间。
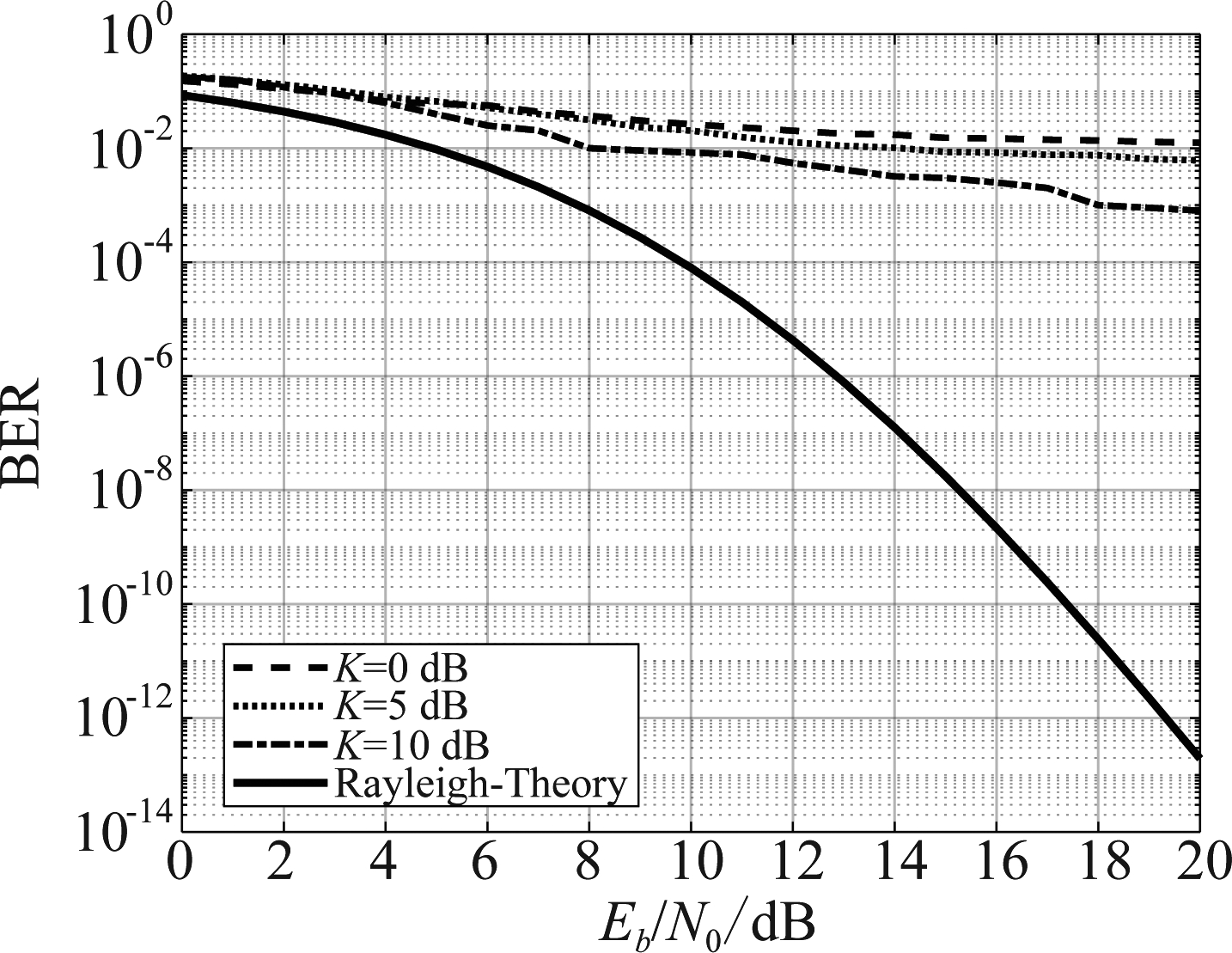
图8 不同莱斯因子下的系统误码率曲线
Fig.8 Different Rice Factor, Bit Error Rate Curve of System
仿真2 莱斯因子取0 dB下的算法性能
仿真2同样以系统误码率作为性能指标,讨论在莱斯因子等于0 dB的条件下,即直射信号功率与散射信号功率一样的条件下,本文算法和一般MMSE均衡算法的性能差别。仿真参数设置与前面一致。
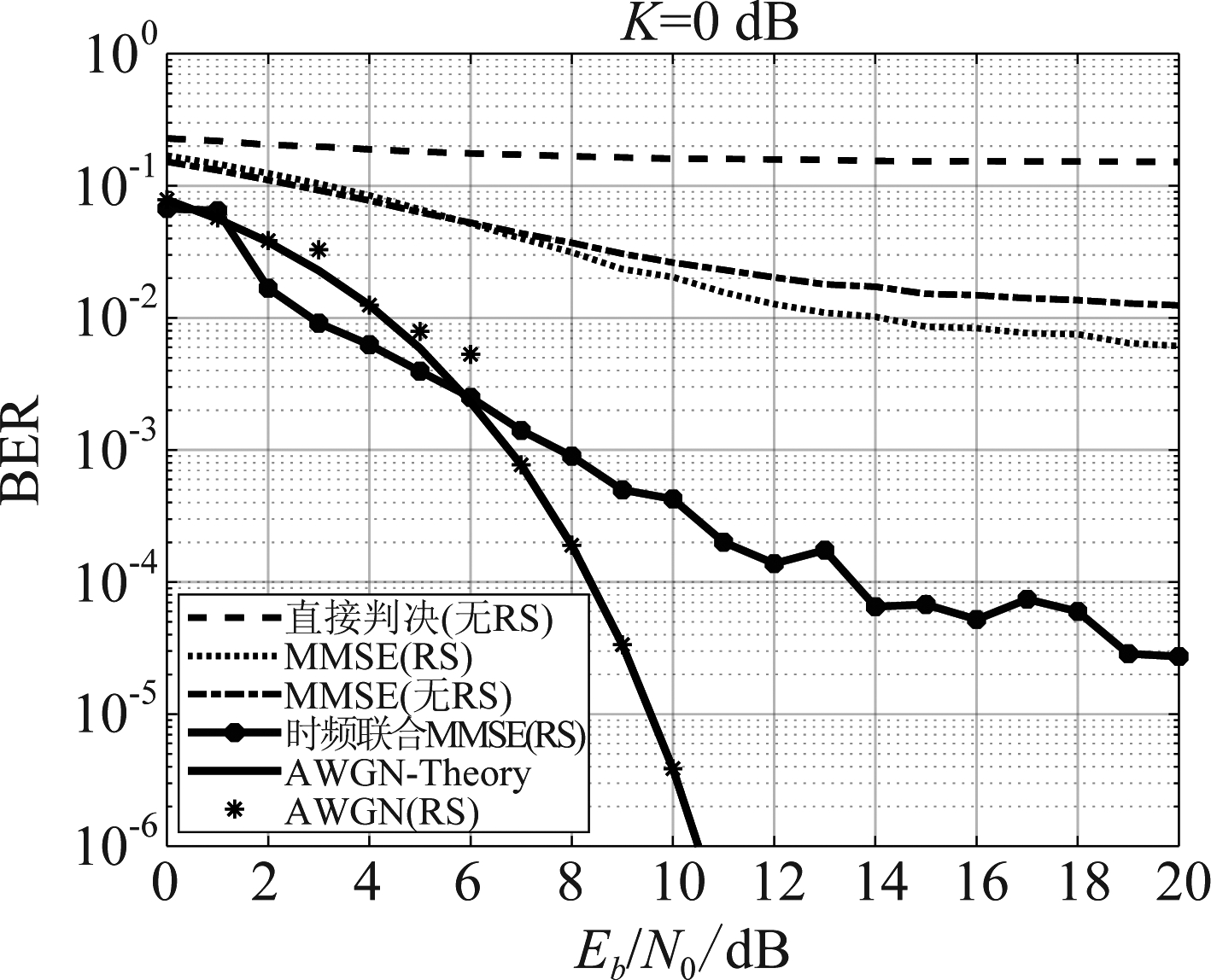
图9 K=0 dB时,系统误码率曲线
Fig.9 K=0 dB, Bit Error Rate Curve of System
从图9可以看出,QPSK信号经过莱斯因子为0 dB的多径信道后,在接收端不做任何处理的情况下,增大信噪比无法解决其误码问题,且误码率几乎不变保持在0.15,产生平台效应,此时无法满足正常通信要求。而当信号采用RS编码,以及接收端进行MMSE均衡处理后能使误码率降低到0.01,且误码率会随着信噪比发生变化。而在一般MMSE均衡的基础上,加上本文提出的信号重构和时频联合判决的后续处理就可以使得误码率在20 dB时降低至10-4以下,而且在信噪比为2～6 dB的条件下,联合判决输出的误码率要低于QPSK信号在自由空间传播的误码率。原因在于MMSE均衡使得多条路径的能量叠加,但是噪声功率却无法进行叠加,功率谱密度被平均,使得整体的信噪比增大,系统获得了信噪比增益,误码性能优于AWGN信道。经过MMSE均衡处理后,随着信噪比增大,影响系统误码率性能的主要因素由式(5)中的有色噪声转为双向码间串扰。而时频联合判决没有实现双向码间串扰的完全消除,均衡器输出残留有码间串扰,因此信噪比增大使得残留码间串扰对系统的影响增大,此时的系统误码率低于QPSK在AWGN信道下传播的误码率。
仿真3 不同莱斯因子下的算法性能
仿真3主要验证算法在不同莱斯因子下的性能表现,仿真条件与前面一致,更改信道的莱斯因子值大小分别取-5 dB、0 dB、5 dB和10 dB,得到系统的误码率曲线。
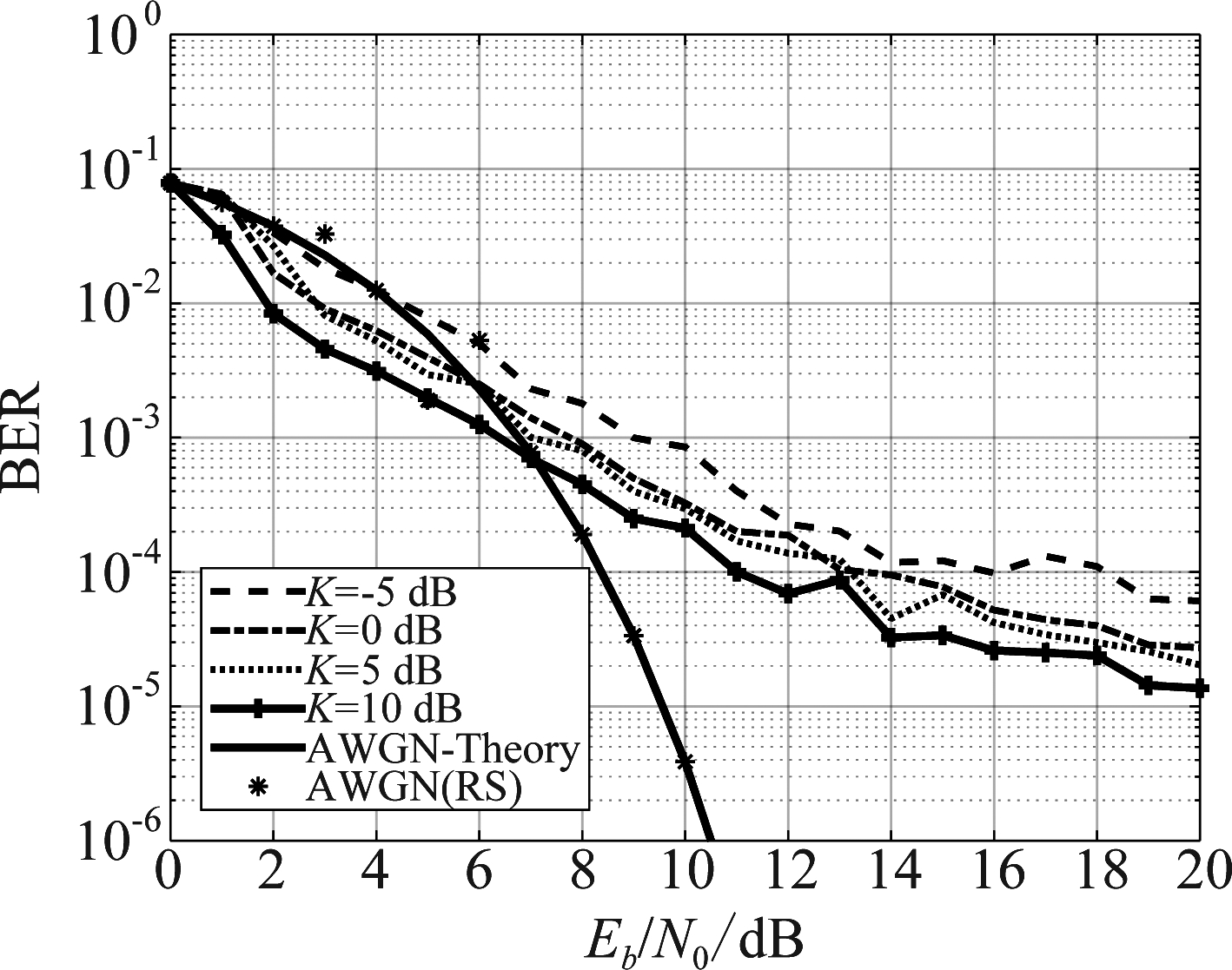
图10 K取不同值时的系统误码率曲线
Fig.10 Bit Error Rate Curve of System with Different K
从图10可以看出,经过本文算法处理后,低莱斯因子信道的误码率特性接近高莱斯因子的误码率特性,主要原因在于:MMSE均衡的信道匹配滤波起到了很好的能量搜集作用,使得低莱斯因子信道的符号能量利用接近高莱斯因子信道,虽然能量搜集对高莱斯因子的作用效果一般,但是改判对于信道的误码性能改善是不以莱斯因子的高低为条件的。因此本文算法对于高莱斯因子多径信道的误码特性也有一定的提升。
6 结论
慢衰落时变多径信道对于信号的传输的影响是非常严重的,尤其在低莱斯因子条件下,信号能量难以全部利用,存在信噪比损失,单纯的MMSE均衡不一定能够获得很好地接收效果。本文基于MMSE均衡提出了一种新的时频联合判决方法,即利用硬判决信号实现信号的重构,得到改判信号,比较改判信号的误差能量,误差能量最小的判决即为均衡器输出相比直接判决,仿真结果表明时频联合判决改善了系统的双向ISI,使得系统获得信噪比增益,降低了误码率,提高了系统性能。
[1] 易克初, 孙永军. 数字通信理论与系统[M]. 电子工业出版社, 2013: 228-229.
Yi Kechu, Sun Yongjun. Digital Communication: Theory and Systems[M]. Publishing House of Electronics Industry, 2013: 228-229.(in Chinese)
[2] 李东武, 裴昌幸. 莱斯衰落信道下协作通信的分集接收算法[J]. 华南理工大学学报(自然科学版), 2015(3): 84- 89.
Li Dongwu, Pei Changxing. Diversity Reception Algorithm for Cooperative Communications in Rice Fading Channels[J]. Journal of South China University of Technology (Natural Science Edition), 2015(3): 84- 89.(in Chinese)
[3] Dong Shuli, Zhang Taotao, Wang Yan. A real-time simulation design of multi-path fading channel based on SOS method[C]∥2019 IEEE 4th Advanced Information Technology, Electronic and Automation Control Conference (IAEAC), Chengdu, China, 2019: 2550-2554, doi: 10.1109/IAEAC47372.2019.8997884.
[4] Hwang T, Yang C, Wu G, et al. OFDM and Its Wireless Applications: A Survey[J]. in IEEE Transactions on Vehicular Technology, 2009, 58(4): 1673-1694. doi: 10.1109/TVT.2008.2004555.
[5] Rubsamen M, Gene J M, Winzer P J, et al. ISI Mitigation Capability of MLSE Direct-Detection Receivers[J]. in IEEE Photonics Technology Letters, 2008, 20(8): 656- 658.
[6] Ahmed T, Ali M M, Sarkar M Z I. BER performance analysis of M-ary modulation techniques in an outdoor environment with MLSE equalizer over fading channels[C]∥2012 15th International Conference on Computer and Information Technology (ICCIT), Chittagong, 2012: 279-283, doi: 10.1109/ICCITechn.2012.6509742.
[7] Jiang T, Wu Y. An Overview: Peak-to-Average Power Ratio Reduction Techniques for OFDM Signals[J]. in IEEE Transactions on Broadcasting, 2008, 54(2): 257-268. doi: 10.1109/TBC.2008.915770.
[8] 余海, 汪晓宁. OFDM系统中抗频偏的改进方案[J]. 系统工程与电子技术, 2015, 37(6): 1405-1410.
Yu Hai, Wang Xiaoning. Improved scheme of resistance frequency offset in OFDM system[J]. Journal of Systems Engineering and Electronics, 2015, 37(6): 1405-1410.(in Chinese)
[9] Li Lifu, Li Haiwen, Li Hongliang, et al. Research and implementation of Viterbi decoding in TD-LTE system[C]∥2017 IEEE 2nd Advanced Information Technology, Electronic and Automation Control Conference (IAEAC), Chongqing, 2017: 890- 894, doi: 10.1109/IAEAC.2017.8054142.
[10] Mishra S, Tripathi R R. VDHL Implementation of Viterbi Algorithm for Decoding of Convolutional Code[C]∥2015 International Conference on Computational Intelligence and Communication Networks (CICN), Jabalpur, 2015: 1367-1370.
[11] Simon Haykin. Adaptive Filter Theory [M]. 4th Edition. Kluwer Academic Publishers, 2003: 238-240.
[12] 李文艳, 朱婷婷, 王琪. 稀疏多径信道自适应均衡算法研究[J]. 声学技术, 2019(6): 698-704.
Li Wenyan, Zhu Tingting, Wang Qi. Research on adaptive equalization algorithm for sparse multipath channel[J]. Technical Acoustics, 2019(6): 698-704.(in Chinese)
[13] 李彬, 陈凯, 喻俊浔, 等. 一种适用于强脉冲噪声下的对数型恒模盲均衡算法[J]. 电讯技术, 2019, 59(2): 218-222.
Li Bin, Chen Kai, Yu Junxun, et al. A Logarithmic-type Constant Modulus Blind Equalization Algorithm for Strong Impulsive Noise[J]. Telecommunication Engineering, 2019, 59(2): 218-222.(in Chinese)
[14] 周孟琳, 陈阳, 马正华. 一种适用于稀疏多径信道的自适应均衡算法[J]. 电讯技术, 2019, 59(3): 266-270.
Zhou Menglin, Chen Yang, Ma Zhenghua. An Adaptive Equalization Algorithm for Sparse Multipath Channel[J]. Telecommunication Engineering, 2019, 59(3): 266-270.(in Chinese)
[15] 何礼, 何培宇, 张晓枫, 等. 一种适合于低空无线信道的改进SC-FDE技术[J]. 四川大学学报(自然科学版), 2015, 52(2): 306-310.
He Li, He Peiyu, Zhang Xiaofeng, et al. An improved SC-FDE technique for low-altitude wireless channel[J]. Journal of Sichuan University (Natural Science Edition), 2015, 52(2): 306-310.(in Chinese)
[16] Li B, Shi Y, Yu F, et al. Frame Design of SC-FDE System for Noise Suppression Used in UAV Data Link[C]∥2012 Second International Conference on Instrumentation, Measurement, Computer, Communication and Control, Harbin, 2012: 785-788.
[17] Florea A A, Gacanin H, Adachi F. Performance comparison of cooperative OFDM and SC-FDE relay networks in a frequency-selective fading channel[C]∥2010 IEEE International Conference on Communication Systems, Singapore, 2010: 371-375.
[18] Zhang H, Wu H, Wu Y. Robust pilot-detection technique for channel estimation in single-carrier frequency-domain equalization systems[C]∥2015 IEEE International Symposium on Broadband Multimedia Systems and Broadcasting, Ghent, 2015: 1- 4.
[19] Fayziyev A, Pätzold M. The design of sum-of-sinusoids channel simulators using the iterative nonlinear least square approximation method[C]∥SoftCOM 2012, 20th International Conference on Software, Telecommunications and Computer Networks, Split, 2012: 1-5.
[20] Hirschausen P, Davis L M, Haley D, et al. Identifying key design parameters for Monte Carlo simulation of Doppler spread channels[C]∥2014 Australian Communications Theory Workshop (AusCTW), Sydney, NSW, 2014: 33-38.
