1 引言
传统星载SAR都运行在500～1500公里高度的近地轨道上[1]。随着SAR应用技术的发展,地球同步轨道SAR (GEO SAR)即高轨SAR开始受到科研工作者的关注。因为高轨SAR在军事和民用方面具有良好的应用前景,特别是随着对地球表面运动目标进行更全面监测的需求的增加[2],使得在不久的将来将高轨SAR卫星送入轨道成为可能。
超高轨道为GEO SAR提供了许多优点,如覆盖范围广、重复访问周期短等。但是也带来了传播时间长、合成孔径轨迹弯曲等问题,这意味着“走停走”假设在GEO SAR中也将失效[3]。因此,高轨SAR和地面动目标的距离历史模型不再是普通的线性关系,需要考虑到二阶及更高阶距离历史变化。而慢时间和快时间的高阶耦合会产生严重的距离走动,传统Keystone变换方法已经不再适用。而广义Keystone变换[4-5]可以针对高轨SAR模式下较快速运动目标带来的更高阶相位项进行补偿和矫正。
现有的单发双收系统利用相位中心偏置天线(DPCA: Displaced Phase Center Antenna)方法可以实现低信噪比条件下的运动目标检测。但快速目标距离走动一般较大,同时存在多普勒中心频率模糊,这些都对运动目标的成像和参数估计带来困难。本文提出双载频、双通道的思想为系统提供更多的自由度。DPCA技术可以很好解决通道之间静止杂波的问题,但是双通道的体制可能无法准确估计目标运动参数[6]。文献[7- 8]通过设置双星或者放置不等间距天线的方法来解决速度模糊的问题,但是硬件成本较高,不容易实现。广义Keystone可以很好的解决运动目标距离走动和距离弯曲问题,离散调频傅里叶变换[9](DCFT: Discrete Chirp-Fourier Transform)结合牛顿迭代法搜索完成多普勒参数估计。最后,提出一种运动目标参数搜索的方法,利用不同载频条件下对应多普勒模糊次数不同来求取运动目标不模糊速度。
2 GEO SAR运动目标回波模型与杂波对消
高轨SAR双通道双载频的几何模型如图1所示,首先沿高轨SAR航迹方向放置两个间隔为d的通道,通道S1和通道S2分别发射载频为fc1和fc2的线性调频信号,然后S1和S2分别同时接收回波信号,通过带通滤波器将载频为fc1和fc2的信号分开,这样就一个构成双发双收的高轨SAR系统。雷达卫星高度为h,并沿航迹向做匀速运动且速度均为V,对应初始坐标分别为(0,0,h)和(d,0,h)。地面运动目标P(X,Y,0)具有恒定的径向速度νr和方位向速度νx。其中,由通道Si发射并且由S1和S2接收的双程回波距离历史记为Ri(t),Ri=Ri1+Ri2。由于高轨SAR轨道高度比低轨卫星高出两个数量级,所以可将上述双程距离Ri(t)等效为一虚拟单程距离Ri1(t)的两倍,即令Ri=2Ri1。假设发射雷达归一化调频信号如下:
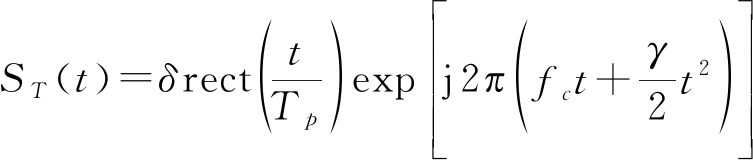
(1)
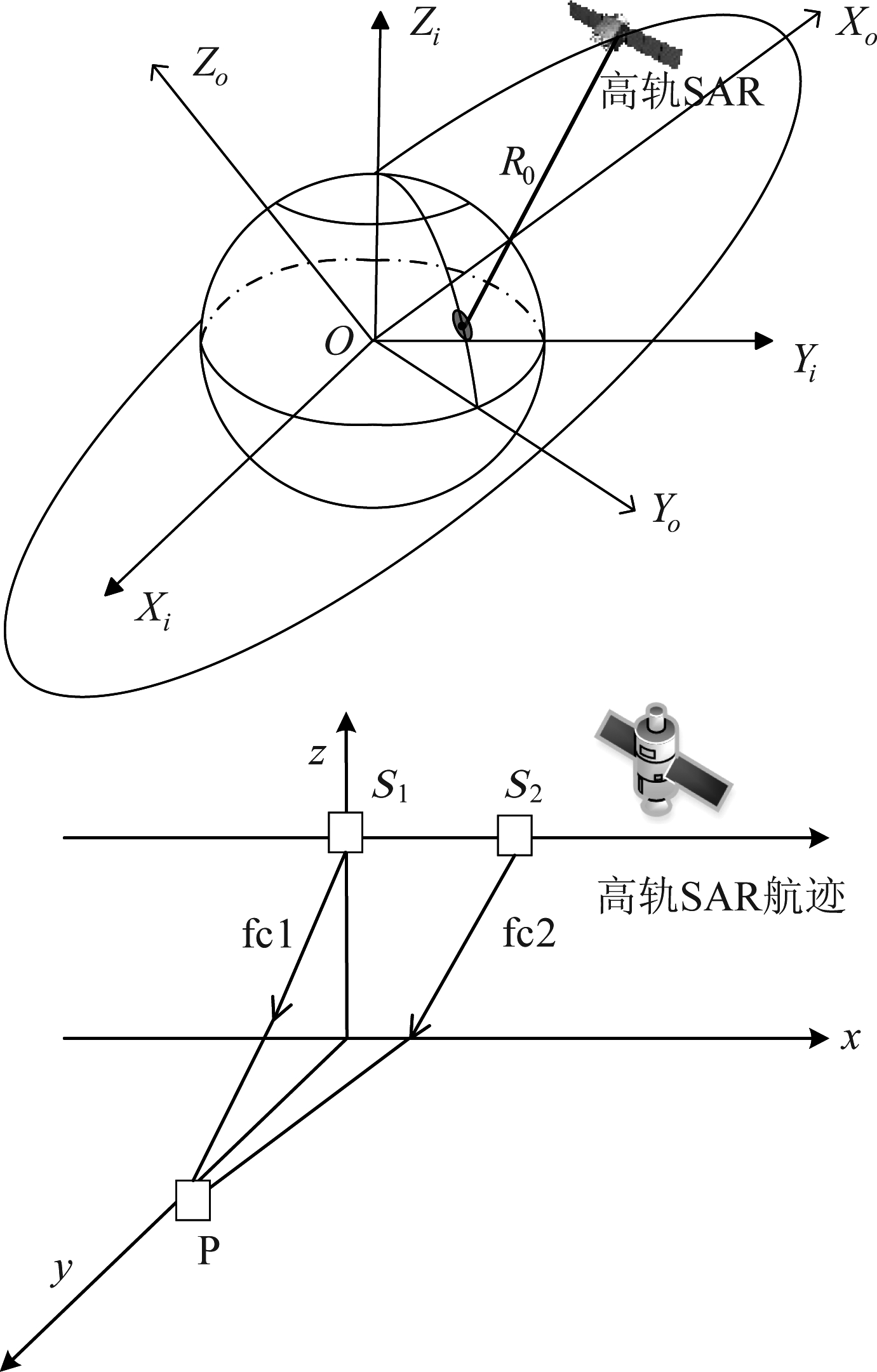
图1 GEO SAR几何模型和双频双通道检测系统
Fig.1 GEO SAR geometric model and dual-frequency dual-channel detection system
接收的反射信号距离压缩后可以表示为:
(2)
式中δ是散射系数,B是信号带宽,
表示快时间,tm表示慢时间,λi为第i个通道发射信号的波长,c为光速,
的下标i∈{1,2}代表的是不同的通道发射中心频率为fi的信号,k∈{1,2}代表的是不同的接收通道。由于距离历史Ri1是一个非线性的变化,通过相关文献[10]可以得到一个近似值,经过泰勒展开可以简化写为:
(3)
是雷达平台与目标的初始斜距。这样双频双通道系统一共会产生四路回波信号,将四路信号中频率相同的信号在时间补偿后进行DPCA两两对消后只保留动目标信息。为了提高静止目标的抑制效果,通过补偿函数
来补偿掉通道之间的间距带来的相位差。在距离压缩后的信号进行两两对消后得到的运动目标信息为:
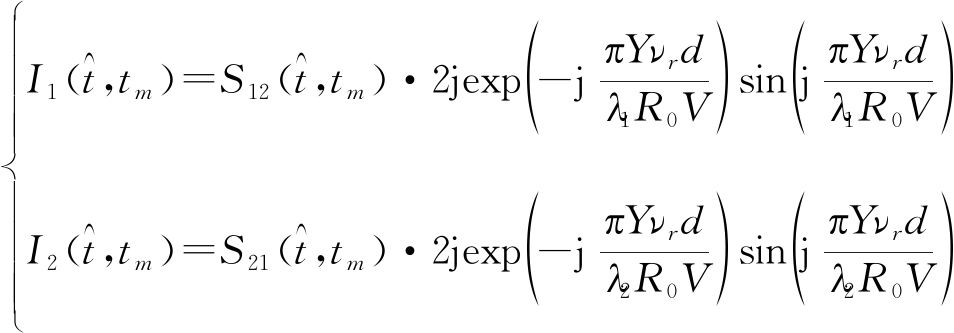
(4)
取第一路对消信号结果为例进行分析,将式带入到距离频域方位时域的动目标信号为:
(5)
对式(5)加以分析,第一个指数项为初始斜距带来的常数相位项,第二、第三、第四个指数项为非线性距离历史带来的距离走动项。与低轨SAR对动目标检测和成像不同,当使用高轨SAR系统检测时会出现非常严重的距离走动和距离弯曲。第五个指数项为目标运动引起的相位,最后一项决定了目标的盲速点分布。
3 广义Keystone变换聚焦成像
经过脉冲压缩和DPCA处理后的信号静止杂波已经得到抑制,接下来取式(5)中存在距离和方位耦合相位加以分析处理。令ε=fr/fc1,则我们可以得到:
Q( fr,tm)=
(6)
由式(6)可知慢时间的三次、二次和一次相位项都和距离频域存在耦合。此时的运动目标回波存在一阶、二阶、三阶距离偏移,信号的能量无法被集中到同一个距离门里,影响运动目标信号积累的效果,严重情况下甚至会丢失目标。
首先对回波进行三阶距离走动矫正,对式(6)中的回波做三阶Keystone变换,令
做变量代换可得:
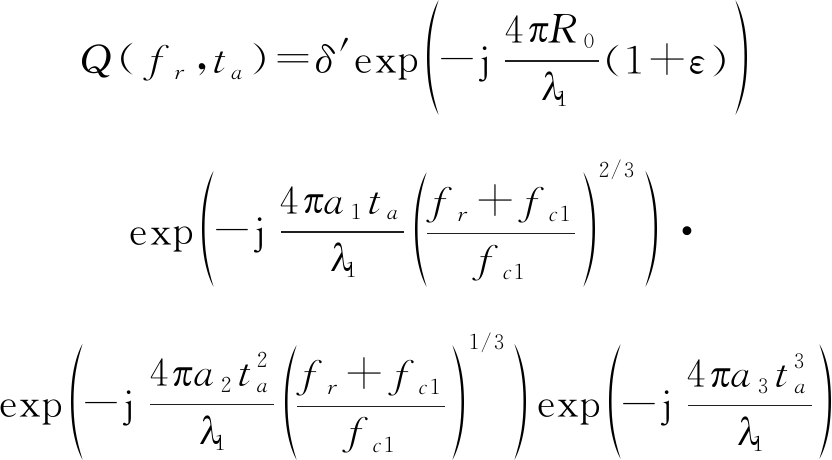
(7)
由式(7)可以看出三阶相位项已经不再有慢时间和距离频域耦合。再乘以估计的三阶构造相位函数
可以得到:
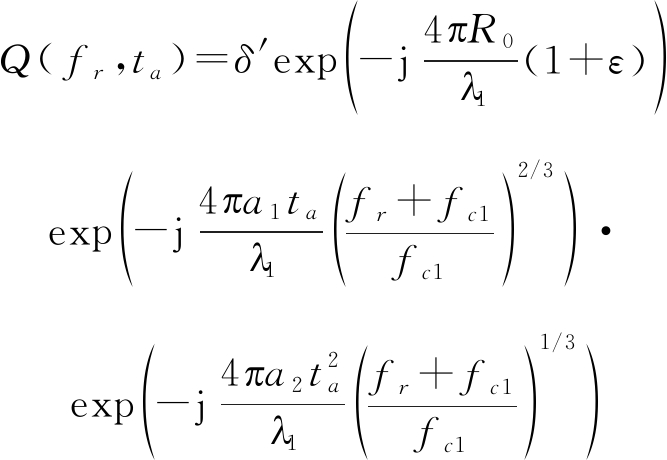
(8)
然后为了矫正剩下二阶相位项耦合,对式(8)做六阶Keystone变换,令
做变量代换可得:
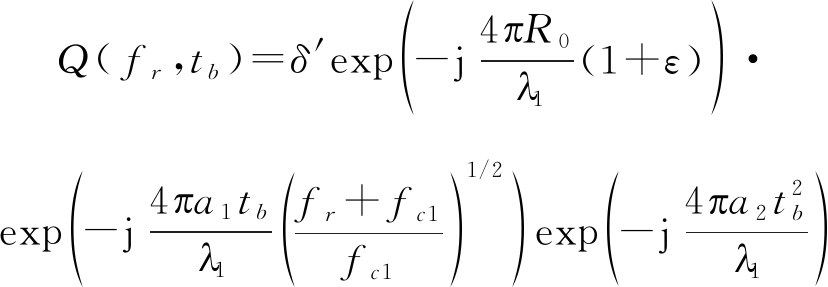
(9)
由式(9)可以看出,二阶相位项不再有慢时间和距离频域耦合。再乘以估计的二阶构造相位函数
可得:
Q( fr,tb)=
(10)
此时回波只剩下一阶相位项耦合,对式(10)做二阶Keystone变换,令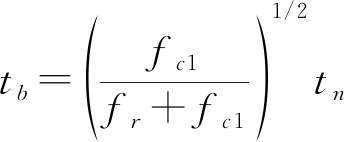
做变量代换可得:
(11)
这样二阶和三阶相位中的快时间和距离频域的耦合就被全部消除了。将式(11)带入到式(5)中进行距离向IFFT变换和方位向FFT变换,在方位向进行FFT变换之前需要进行一阶相位项和常数相位项补偿,矫正函数为
完成上述这些处理后,可以得到在抑制了静止杂波和距离徙动矫正后的动目标成像结果为:
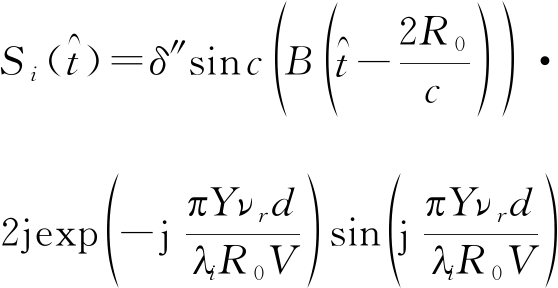
(12)
其中δ″是信号幅度,由上式可知此时运动目标所有信号能量聚集在
处,如果设置一个参考门限,只要峰值大于该门限就可以检测到动目标信息。
4 动目标参数估计与解速度模糊
经过DPCA处理和广义Keystone处理后的回波信号在方位向依然是一个线性调频信号,可以将第一路回波信号的表达式写为:
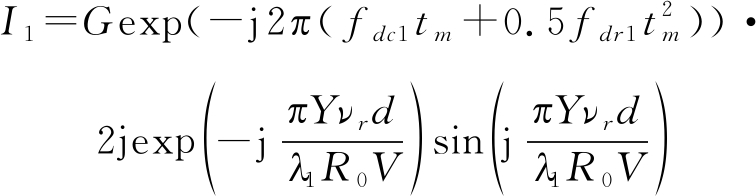
(13)
其中G为信号幅度, fdc1和fdr1分别为第一路动目标信号多普勒中心频率和多普勒调频率,式(13)中的第二指数项只和距离向速度有关,不影响多普勒参数估计。
离散调频傅里叶变换是估计线性调频信号的常用且有效手段,假设一个长度为N的离散化线性调频信号
则其对应的DCFT形式为:
0≤k,l≤N-1
(14)
其中WN=e-j 2π/N,离散化线性调频信号
则它的DCFT值Sc(k,l)应该在(a,b)处取得最大值。现在有线性调频信号s(t)=exp(-j 2π( fdc1t+0.5fdr1t2))通过上述离散化处理的步骤,就可以使用牛顿迭代法搜索其多普勒参数。那么线性调频信号s(t)离散调频傅里叶变换后的信号形式为:
0≤m<M,0≤n<M
(15)
其中f0和k0分别代表搜索的起始值,Δf和Δk分别代表每次搜索多普勒频率和调频率的步长,m和n分别代表每次多普勒频率和调频率的搜索进度。
这里将整个DCFT估计多普勒参数的搜索过程分为两步,一次粗搜索和一次精搜索。根据系统的先验条件可以求出信号的多普勒频率和调频率的初始范围。假定多普勒调频率的粗搜索范围是(k0-β,k0+β),第一次粗搜索的步长为Δk1,在经过第一次搜索后估计得到多普勒调频率为
接下来进一步估计精搜索范围是
定义精搜索步长为Δk2。最后通过搜索
里的最大值来确定多普勒调频率。根据DCFT原理,多普勒频率和调频率可以同时估计得到。
由DCFT结合牛顿迭代法估计得到的多普勒频率只是位于主值区间的一个范围值,当距离向速度νr∈(νrmin,νrmax)时,νrmax和νrmin分别为最大可检测速度和最小可检测速度,此时多普勒频谱没有发生折叠。但当目标速度较快时,频谱偏移量超过了半个脉冲重复周期(PRF),将会产生速度模糊的问题。首先可以得到不同工作频率系统下最大不模糊速度为νrmax=λiPRF/4。下面通过设置两个不同载频工作模式得到两个速度区间,增加了系统自由度,然后求取两个速度区间的交集来获得目标真实的径向速度。对两路动目标回波数据估计得到中心频率估计值为fdci,那么两个不同载频工作模式下的目标径向速度估计值可以表示为:
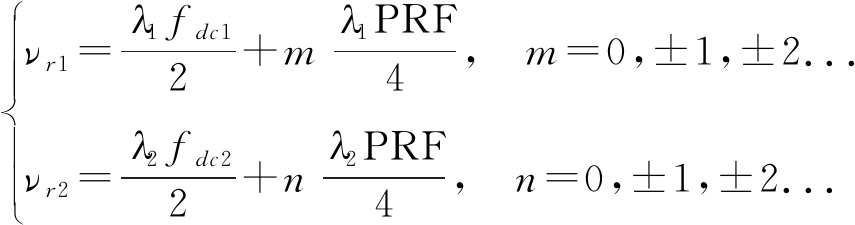
(16)
m和n分别为对应频率下的模糊次数。虽然是两路信号,但是检测的都是同一个目标的径向速度,只是在不同的工作频率下模糊次数不同而已。搜索两路信号对应的速度集合,这两个集合中应该只有一个交集,即为目标的实际速度,通过下面的公式可以较快的提高计算效率:
νreal=(νr1+νr2)/2, abs(νr1-νr2)≤2%νr1
(17)
得到准确的径向速度之后,可以根据目标径向速度νreal和多普勒调频率fdr求出目标对应的方位向速度,即:
(18)
整个算法的流程图为图2所示。
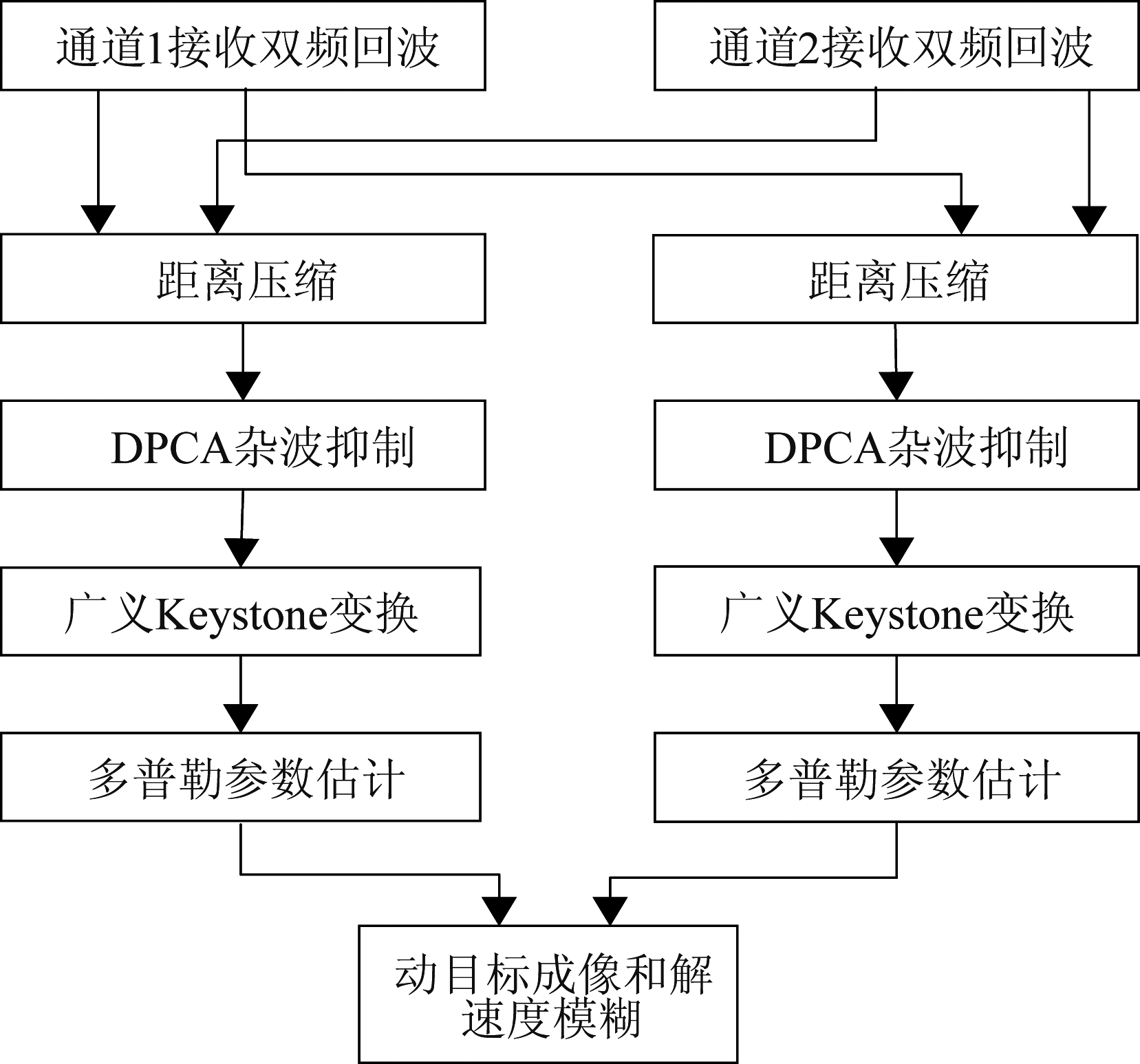
图2 算法实现流程
Fig.2 Algorithm implementation flow
5 仿真实验
下面以第一路仿真实验为例,分析多通道DPCA对杂波抑制和广义Keystone变换对距离单元徙动矫正的有效性,仿真参数:卫星轨道高度35768 km,飞行速度3091.6 m/s,雷达发射信号带宽5 MHz,脉冲宽度10 μs,波长0.2 m,采样频率20 MHz,脉冲重复频率200 Hz。首先通过在杂波场景中设置一个动目标进行仿真成像来验证DPCA杂波抑制技术的有效性。图3(a)为通道一成像结果,根据高轨SAR系统的工作参数,我们可以设置输入信噪比为-27 dB,计算得到系统的输出信噪比为23.1 dB。场景中运动目标被淹没在杂波中难以检测出来,此时计算目标图像信杂比结果为3.5 dB。将通道均衡后的两个通道复图像数据做DPCA对消处理得到结果如图3(b)所示,此时运动目标比周围剩余杂波高出29.1 dB以上,很容易被检测出来。由以上分析可以看出,本文提出的DPCA结合广义Keystone方法可以有效实现快速检测和成像,大幅提高信杂噪比。
图3 双通道DPCA对消
Fig.3 Dual-channel DPCA cancellation
由于DPCA是在距离压缩后进行的,此时的动目标因为速度矢量的影响信号在距离向上有严重的距离走动和距离弯曲,需要通过广义Keystone变换进行矫正。假设场景中运动目标坐标为(1000 km,3600 km,0)对应动目标径向速度为νr=25 m/s,方位向速度νx=15 m/s。由图4(a)可以看到距离压缩后的回波包络能量没有聚集在一个距离门里,有较大的偏移,这对后续的参数估计带来影响,必须加以处理。图4(b)为距离走动和距离弯曲矫正后的结果,此时回波包络集中在一个距离门里。
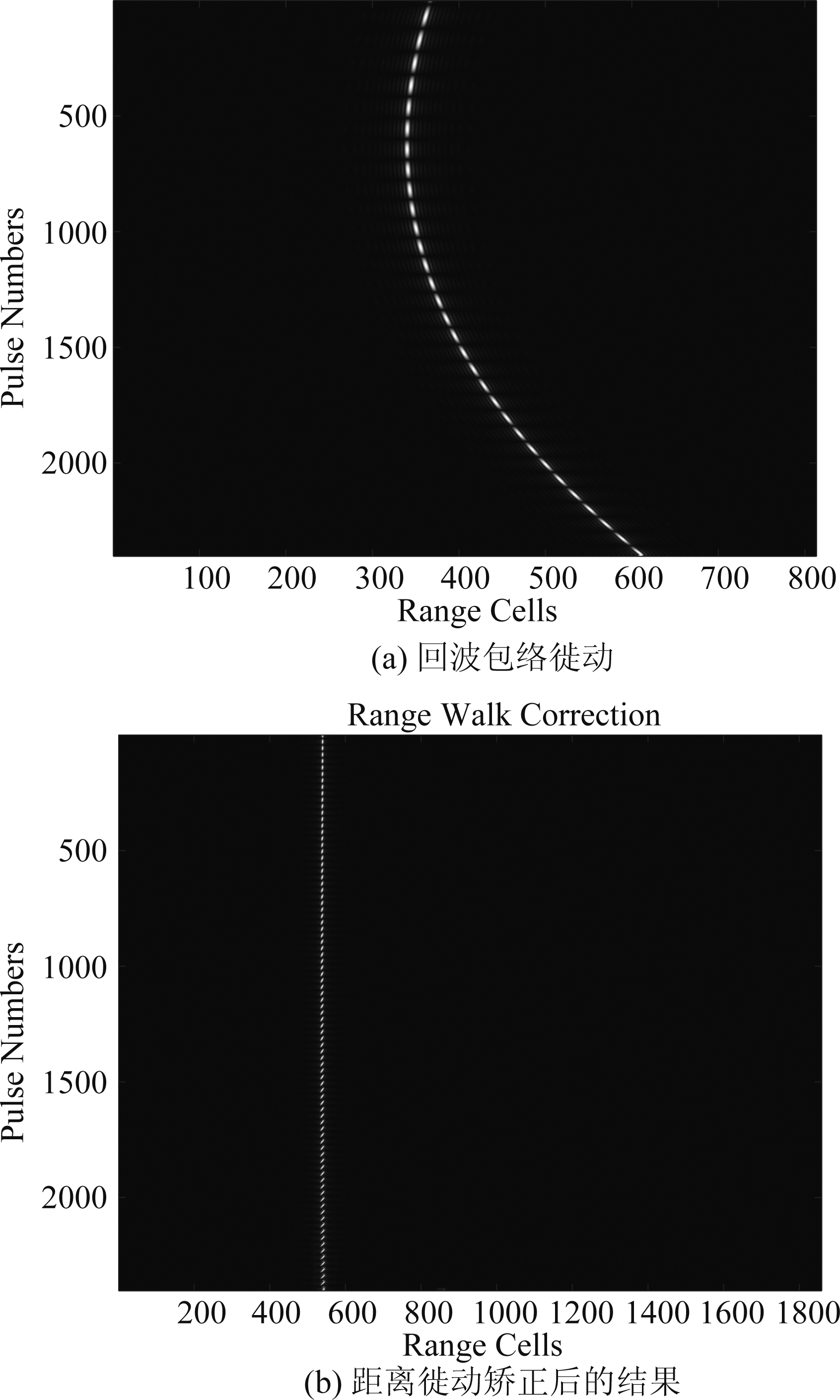
图4 回波包络矫正
Fig.4 Echo envelop correction
接下来就可以使用DCFT结合牛顿迭代法来估计信号的目标多普勒参数,忽略目标速度所带来的常数相位和自身幅度后的信号可以表示为I=exp(-j 2π( fdct+0.5fdrt2))。采用牛顿迭代法对离散调频傅里叶变换后的信号进行两次搜索,第一次粗搜索步长取Δf1=1,第二次精搜索步长取Δf2=0.1,估计得到的多普勒中心频率为
由于目标速度超过了最大可检测速度的上限,此时的多普勒中心频率是模糊的,无法求出准确的速度。
下面取两个工作频率分别为2.0 GHz和1.5 GHz的系统进行实验,如果想要达到解速度模糊的效果,两个载频需要满足互质的条件[11]。两路动目标信号多普勒中心频率估计值分别为
和
多普勒调频率估计值分别为
和
将两路信号估计的多普勒中心频率带入到公式(16)中,通过公式(17)提供的方法不断搜索两个速度集合的值,如果得到的结果小于一定的阈值则认为是真实的目标速度。求得在频率一工作模式下的模糊次数m=3,得到的速度为νr1=24.7103 m/s,频率二工作模式下的模糊次数n=2,得到的速度为νr2=25.165 m/s,且满足条件abs(νr1-νr2)≤2%νr1,那么经过上述分析处理,得到目标的真实速度值为
m/s,相对误差为0.25%。针对方位向速度,取任意频率工作模式下估计的多普勒调频率和真实的径向速度代入到公式(18)求得νx=14.744 m/s,相对误差1.71%。
6 结论
基于GEO SAR的快速运动目标检测技术已经成为动目标检测新的发展方向。本文在分析了多通道杂波对消的基础下,利用广义Keystone变换来修正运动目标回波包络偏移,离散调频傅里叶变换结合牛顿迭代搜索估计目标多普勒参数。同时针对快速运动目标估计多普勒中心频率模糊的问题,通过不同载频条件下模糊次数不同获得两个速度集合的交集来确定真实的目标速度。最后,仿真实验验证该方法的有效性。
[1] Melzi M, Hu C, Dong X, et al. New moving target Doppler centroid expression in geosynchronous SAR[J]. The Journal of Engineering, 2019, 2019(19): 5797-5800.
[2] An H, Wu J, He Z, et al. Geosynchronous Spaceborne-Airborne Multichannel Bistatic SAR Imaging Using Weighted Fast Factorized Backprojection Method[J]. IEEE Geoscience and Remote Sensing Letters, 2019, 16(10): 1-5.
[3] Bao M, Xing D M, et al. Chirp scaling algorithm for GEO SAR based on fourth-order range equation[J]. Electronics Letters, 2012, 48(1): 41- 42.
[4] Zhou F, Wu R, Xing M, et al. Approach for single channel SAR ground moving target imaging and motion parameter estimation[J]. IET Radar, Sonar & Navigation, 2007, 1(1): 59- 66.
[5] Kong L, Li X, Cui G, et al. Coherent Integration Algorithm for a Maneuvering Target With High-Order Range Migration[J]. Signal Processing, IEEE Transactions on, 2015, 63(17): 4474- 4486.
[6] 夏猛. 多通道SAR系统地面运动目标信息获取方法研究[D]. 西安: 西安电子科技大学, 2012.
Xia Meng. Reserch on the method of obtaining ground moving target information in Multi-channel SAR system[D]. Xi’an: Xidian University, 2012.(in Chinese)
[7] Kang Xueyan, Yang Jiefang, Zhai Wenshuai, et al. Radial velocity ambiguity mitigation of moving target by dual-subband ATI approach with a two-channel SAR[C]∥2014 International Radar Conference, Lille, 2014: 1- 6.
[8] Zhu S, Liao G, Qu Y, et al. A New Slant-Range Velocity Ambiguity Resolving Approach of Fast Moving Targets for SAR System[J]. IEEE Transactions on Geoscience & Remote Sensing, 2010, 48(1): 432- 451.
[9] Xia X G. Discrete chirp-Fourier transform and its application to chirp rate estimation[J]. IEEE Transactions on Signal Processing, 2000, 48(11): 3122-3133.
[10] Hu C, Long T, Zeng T, et al. The Accurate Focusing and Resolution Analysis Method in Geosynchronous SAR[J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(10): 3548-3563.
[11] 武其松, 邢孟道, 保铮. 双通道MIMO-SAR运动目标成像[J]. 系统工程与电子技术, 2010, 32(5): 921-926.
Wu Qisong, Xing Mengdao, Bao Zheng. Imaging of moving targets of dual-channel MIMO-SAR[J]. Systems Engineering and Electronics, 2010, 32(5): 921-926.(in Chinese)
