1 引言
分辨问题是雷达系统的基本问题。传统上距离分辨限是利用波形模糊函数衡量,将模糊函数的响应下降到3 dB时对应的距离间隔,称为距离维的瑞利限。同样,雷达在测量目标方位时存在由于波束宽度引起的分辨瓶颈,将波束响应的峰值下降到3 dB对应的波束宽度定义为方位上的瑞利限。在一些高分辨场合,如波达方向角估计、空间谱估计中,很多超分辨算法[1-5]能够分辨位方位瑞利限内的目标,因此出现超分辨的定义和衡量标准。
最早的超分辨定义是观察所得到的谱函数在待分辨参数(如空间频率)响应是否存在“凹陷”,如果存在即可分辨。在数学上通常计算两待分辨参数的响应均值是否大于均值的响应[1]。实际中由于系统的采样点数总是有限的,导致估计的频点相对真实频点会发生偏移,导致该方法失效,因此文献[2]提出了基于谱函数二阶导数的零点判断法。该方法认为:对不可分辨的目标,信号频谱仅出现一个峰值,否则在频谱中间值两边存在两对称峰值。由于频谱函数是连续的,当存在两个峰值时,此时频谱函数在中间值的二阶导数必然大于零。我们将上述两种方法称为观察法。采用观察法定义分辨性能虽然直观,但难以定量描述正确分辨概率和错误分辨概率(这里称为虚判概率),因此有学者提出统计分辨限的概念。所谓统计分辨限,指的是考虑目标分辨过程的随机性,将分辨问题看作统计问题,研究给定正确分辨概率和虚判概率前提下,研究能够达到的分辨极限;或给定分辨极限下,研究正确分辨概率和虚判概率的大小。正确分辨概率指的是存在两个目标条件下而正确判断的概率,虚判概率指的是存在两个目标而判断只有一个目标的概率。文献[1]研究了MUSIC算法分辨概率的统计表达,采用“凹陷法”的定义,得到分辨概率与波形、信噪比和相关系数等参数的关系;文献[3]和[4]对上述结论做了进一步推广。以上研究可以对分辨概率进行量化分析,但是并没有考虑虚判概率的大小。文献[6]得到了距离-多普勒二维匹配滤波统计分辨限表达式,给出了分辨限和虚判概率、分辨概率和信噪比等的关系,但该研究针对一般分辨问题,不能用于瑞利限以内的超分辨情形。
近年来不少学者利用假设检验理论研究统计分辨限[7-13]。这些研究主要集中在频率维和方位维,在距离维上的研究较少。距离是雷达分辨的重要参数维度,因此有必要开展距离维的统计分辨研究。文献[14]推导了距离维统计分辨限表达式,并分析了影响分辨性能的因素。该研究假定目标的幅度响应为确定未知,实际中雷达观测的快起伏目标为随机分布情况,此时分辨统计量的分布会发生变化,因此有必要开展目标回波幅度在随机分布假设下的统计分辨研究。
本文假定目标回波为随机高斯分布,推导了统计分辨限的表达式,得到分辨性能的影响因素,研究可丰富统计分辨理论,为高分辨系统设计提供借鉴思路。与确定未知条件下的结果相类似,此时统计分辨性能与目标的信噪比、两目标的幅度相关系数等均有关。通过与应用于延迟超分辨的MUSIC空间谱估计算法比对,本文方法表现出良好的超分辨性能。需要指出的是,MUSIC算法用于延迟超分辨的研究和空间谱估计的原理相类似,具体方法可见文献[15-16]。
本文中,(·)T和 (·)H分别表示向量或矩阵的转置和共轭转置,(·)*表示取共轭操作,E{·}表示对随机量取期望。L×1维向量s构成的子空间对应的正交投影矩阵为
表示维度为L×L的单位阵。⎣·」代表不超过该值的最大整数。
代表复数集合。后续内容组织如下:第2节简单回顾了基于二元假设检验的距离分辨模型;第3节推导了分辨统计量的表达式,讨论了其分辨性能;第4节分别针对分辨正确性和与MUSIC算法分辨能力对比设计了仿真;第5节对算法在雷达信号处理中的位置进行了说明;最后第6节对论文内容进行了总结。
2 基于二元假设检验理论的距离分辨模型
记作两目标回波幅度为α1和α2,假定服从相关系数为c的零均值正态分布,方差分别为
发射复数基带信号记为s(t),长度为τ,则延迟分别为t1和t2的两目标回波可表示为x(t)=α1s(t-t1)+α2s(t-t2)+n(t),n(t)为加性白噪声。假定两信号到达时间间隔小于瑞利分辨单元,即满足δt=t2-t1<1/Bmax,Bmax为信号带宽。两目标回波中心时刻t0=(t1+t2)/2假定已知,则上述目标分辨问题可以建模为二元假设检验模型:
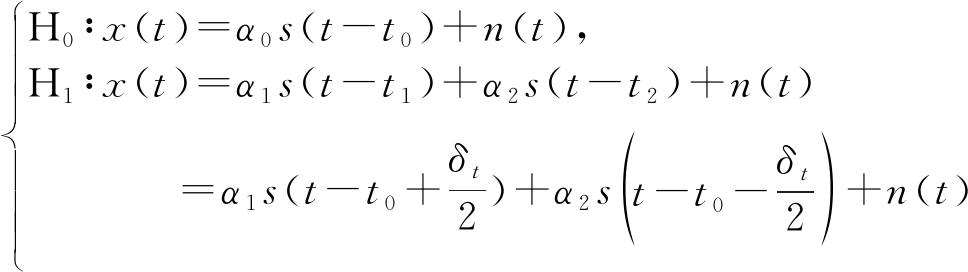
(1)
H0假设代表不能分辨,H1假设代表能够分辨。设s(t)在t处n(n≥2)阶可导,由于δt足够小,则将两目标回波信号在t′=t-t0处进行泰勒展开并保留二阶项近似,得到关于待检验参数δt的多项式模型:
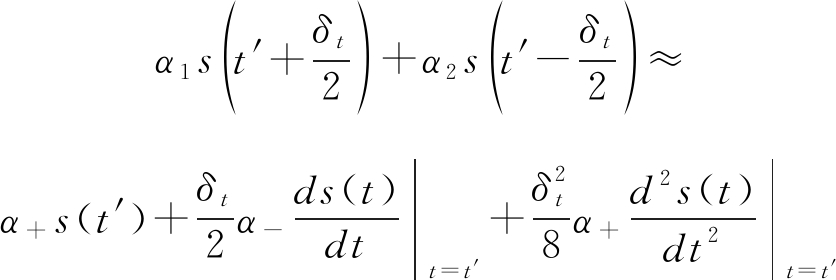
(2)
其中α-=α1-α2,α+=α1+α2。
将式(2)代入式(1)中,并对(1)回波进行采样,采样频率fs>Bmax,取采样时长为信号长度,则采样点数为L=⎣τ×fs」。记信号及其1阶、2阶导数的采样分别为
则式(1)转化为离散模型:
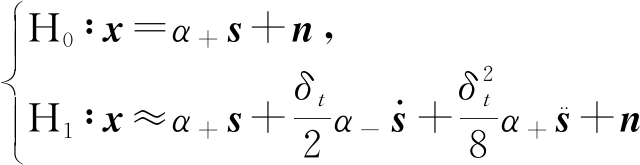
(3)
其中n=[n(1) n(2) … n(L)]T,这里假定n为零均值协方差矩阵为
的复加性高斯白噪声。
进一步,将式(3)中两方程分别在信号正交补空间上进行投影,投影矩阵
满足
并令y=UHx和w=UHn,由于UHs=0,得到关于待检验参数
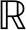2×1的线性模型:
(4)
其中
假设检验的目标是判断θ是否为零向量,由于存在未知参数α-,α+,该模型为复合假设检验模型。由于噪声向量满足E{wwH}=E{UHnnHU}=IL-1,与数据协方差矩阵无关,因此w为加性白噪声,满足恒虚警特性。对于更为复杂的信号检测模型,读者可以参考文献[17]。
3 分辨统计量及性能
根据假设检验的知识,当幅度参数为随机分布时,分辨统计量为估计-相关器,需先求其最小均方误差(Minimized Mean Square Estimator——MMSE)估计。式(2)中等价的未知目标信号可定义为Hθ
t,则目标的自相关矩阵(由于均值为0,所以这里的自相关矩阵等价于协方差矩阵)可以写为:
Rt=HRθHH
(5)
其中
为未知参数,根据假设,两随机变量的相关系数为c=E{α1*α2}/(σ1σ2)=cR+jcI,其中cR和cI分别代表相关系数的实部和虚部。
根据公式(4)中未知向量表达式,可求得未知参数的自相关矩阵为:
(6)
则两种假设下回波分布分别为:
(7)
这里的
为H1假设下信号的MMSE估计[18],则最优估计-相关器表示为:
(8)
γ为检测门限,由给定的虚警概率确定。
根据式(5)可知,目标协方差矩阵的秩为 rank{Rt}=rank{HRθHH}=2,设特征分解为Rt=VΛVH, 则特征矩阵和特征值可以分别表示为V=[v0 v1 …]和Λ=diag([λ0 λ1 0 … 0]T),其中非零特征值为λ0,λ1,v0,v1为其对应的特征向量。不失一般性,假定λ0>λ1,可以得到:
(9)
其中
代表对角矩阵。
设
为标准高斯分布随机向量,根据式(7),则H1条件下协方差矩阵为
令
则此时检测统计量为:
uHVΠ1/2VHVΛVHVΠ-1/2VHu=
uHVΛVHu=λ0z2[0]+λ1z2[1]
(10)
上式利用了特征矩阵满足的关系VHV=IL-1。由于z[k]=uHvk,k=1,2是高斯过程的线性变换,故仍旧服从零均值复高斯分布,则平方和z2[k]服从自由度等于2的卡方分布(因为复数包括实部和虚部,因此这里的自由度为2),则上述检测统计量服从卡方分布的加权和。
同理,在H0条件下回波数据也服从高斯分布,满足
则检测统计量为:
(11)
其中
(12)
满足关系μ0>μ1。和式(10)相类似,上式也服从两自由度为2的卡方分布加权和。
综合式(10)和式(11)可得检测统计量的表达式为:
(13)
其中,X1,X2均为自由度为2的中心卡方分布随机变量。该统计量的性能可通过特征函数[19]来求解(具体过程见附录),其虚判概率和分辨概率分别为:
(14)
和
(15)
式中γ为检测门限。给定虚判概率Pf,则根据式(14)可以求得门限γ,进而根据式(15)可以求得分辨概率Pd。
由于λ0,λ1为矩阵的特征值,难以分析影响分辨性能的因素。为了方便分析,我们对式(3)保留泰勒展开的一阶项近似。根据附录2的推导,此时统计量服从自由度为2的中心卡方分布:
(16)
(17)
自由度为2的卡方分布为指数分布,统计量的概率密度函数为:
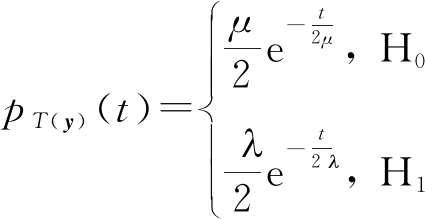
(18)
根据定义,得到分辨概率和虚判概率为:
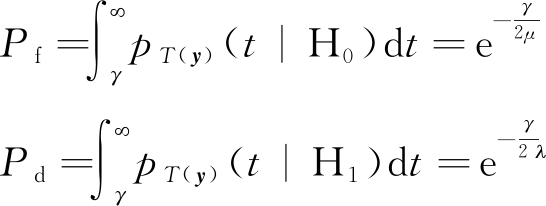
(19)
消去门限γ,得到如下表达式:
(20)
定义信噪比为
得到统计分辨限δt和Pd、Pf的近似关系式:
(21)
从上式可以看出,在Pd、Pf给定后,
可以确定,
越大则能够达到的统计分辨下限越小,因此有:
1)当两信号的相关系数满足cR=0时,则信噪比的和ρ1+ρ2越大,能够达到的δt越小;
2)当两信号的信噪比ρ1,ρ2一定时,则cR越小,则能够达到的δt越小;
3)ρ1,ρ2和cR一定时,δt还与波形有关;
越大,则能够达到的δt越小。
另一方面,给定Pf和
越大则分辨概率越大,因此有:
1)当两信号的相关系数满足cR=0时,则信噪比和ρ1+ρ2越大,则分辨概率越大;
2)当两信号的信噪比ρ1,ρ2一定时,则cR越小,则分辨概率越大;
3)ρ1,ρ2和cR一定时,越大,则分辨概率越大。
4 算法实现的考虑
实际系统中利用二元假设检验进行目标分辨,通常是在完成MIMO雷达常规信号检测基础上,对怀疑存在多个目标的距离单元进行假设检验,如图1所示。
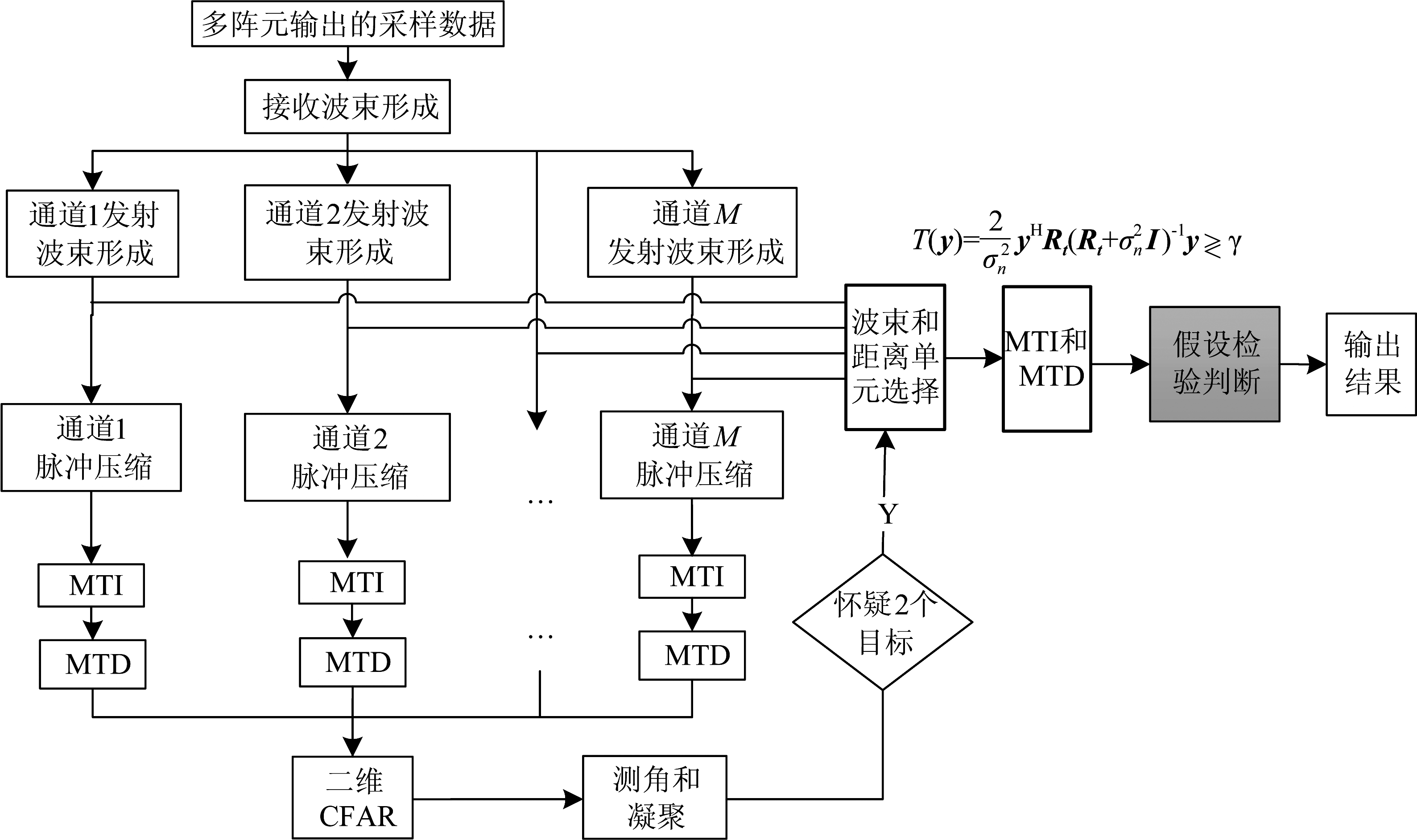
图1 MIMO雷达假设检验超分辨处理流程图
Fig.1 Flow of MIMO radar signal processing with hypothesis test super-resolution
如图1所示,系统首先对多个接收阵元的数据进行多波束形成,然后逐个波束通道进行脉冲压缩、MTI和MTD处理,最后CFAR检测和测角凝聚。如怀疑某个通道的某距离单元存在2个以上目标,则取出该接收波束和相应距离单元数据,在MTI滤波和MTD积累基础上开展二元假设检验判决,当分辨统计量大于分辨门限时,则判断存在2个目标,否则认为只有1个目标。
5 算法仿真
5.1 算法正确性和分辨性能影响因素
假定发射信号采用线性调频信号波形s(t)=rect(t/τ)ejπKt2,-τ/2≤t≤τ/2,K=B/τ为信号的调频率,带宽B=106Hz和时宽τ=10 μs。采样频率取fs=10 B,考虑匹配滤波增益,这里定义信噪比为
其中L=⎣τ×fs」为采样点数,回波幅度的相关系数定义为c=E{α1*α2}/(σ1σ2),注意这里的相关系数与文献[13]的定义不同。为了仿真超分辨性能,这里设两个目标时间/距离间隔小于瑞利限。
仿真1 仿真理论与蒙特卡洛的结果,以及分辨性能随信噪比变化。假定两信号幅度不相关(c=0),设计两信号的间隔分别为0.2,0.4和0.5倍瑞利限。保持一信噪比不变(13 dB),另一信噪比从3到23 dB变化。设计多次随机实验,对每种信噪比进行1000次蒙特卡洛仿真,根据式(8)计算统计量,然后统计超过门限γ的次数(γ由式(14)计算得到,取虚判概率Pf=0.001),除以总次数得到分辨概率的数值解。理论解可以通过(14)和(15)进行仿真得到。绘制理论和数值结果如图2(a)所示,图中不同曲线对应不同的分辨间隔,实线代表理论结果,符号代表数值解。另一方面,固定分辨概率和虚判概率,仿真系统所能达到的最小分辨限与信噪比的关系,如图2(b)所示。这里给出的是理论结果,根据式(21)得到。
图2 分辨性能与信噪比的关系
Fig.2 Relationship of the resolution performance and SNR
从图(a)可以看出,在两个信号相距不同间隔下,理论值和数值解基本一致,分辨概率均随着信噪比增加而提高,间隔越大则分辨性能越好。而从图(b)可以看出,随着信噪比增加,所能达到的统计分辨限的下限降低;从不同曲线可以看出,要求的分辨概率越小,则能够达到的分辨下限也越小。
仿真2 从前文分析可以看出,分辨性能还与两信号相关系数有关。设SNR1=SNR2=10 dB,其他参数同仿真1,仿真与相关系数幅度和相位的三维关系如图3(a)所示;给定相关系数模值,仿真与相关系数相位的关系如图3(b)所示。
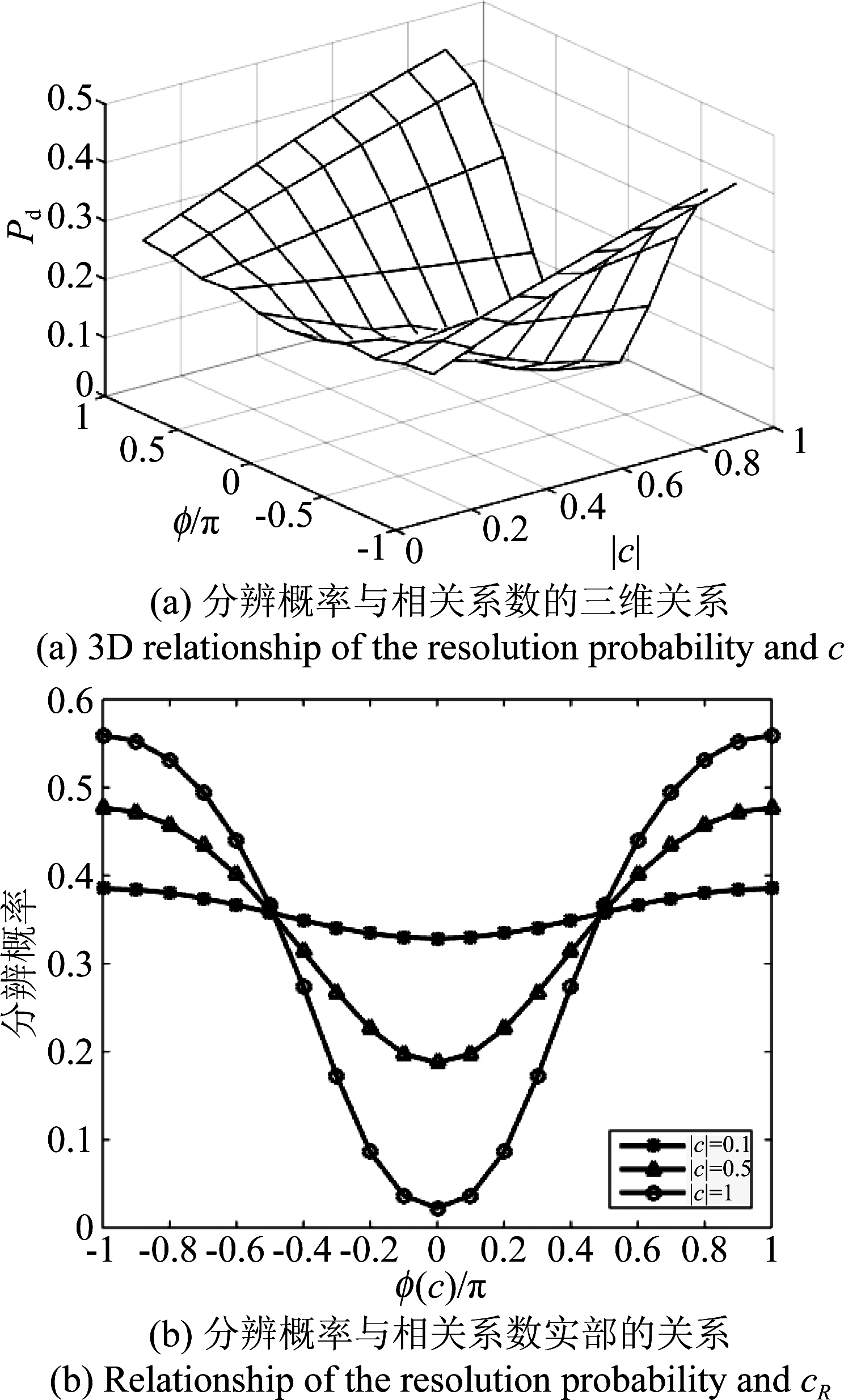
图3 分辨概率与相关系数的关系
Fig.3 Relationship of the resolution probability and c
从图(a)可以看出,当相关系数模不同时,分辨概率受相关系数相位的影响呈现出不同的曲线,当模值比较小时,分辨概率曲线比较平缓,当模值较大时,分辨概率曲线波动较大。从图(b)可以看出,固定相关系数模值,当相关系数的相位为0(两幅度同相,信号相似度最大)时,分辨概率最小;而当相关系数的相位为-π和π时(两幅度反相,相似度最小),分辨概率则达到最大。
5.2 与MUSIC算法对比
这一节,我们对比应用于时延超分辨估计的MUSIC超分辨算法。对于存在P个回波信号的时延估计模型表示为:
(22)
式中τp为第p个信号延迟,αp为该信号的幅度,w(t)为高斯白噪声。Ts代表采样时间间隔,采样点为n=1,…np,np=⎣τp/Ts」,则采样后得到的矢量模型
次快拍的回波数据矩阵为:
(23)
该模型与高分辨谱估计的数据模型一致,等价性见表1。这里时间采样相当于谱估计的阵列空间阵元采样,而多次快拍为多次的时间采样。
表1 空间谱估计与时延分辨问题的等价性
Tab.1 Equivalence of space spectrum estimation and time delay resolution
信号采样协方差矩阵的估计为
对其进行特征分解,得到噪声特征向量v3,…,vL构成的矩阵,EN=[v3,…,vL],考虑到两个目标分辨,则MUSIC算法估计延迟为:
(24)
在延迟参数可能所在的区间进行谱峰搜索,可以得到两延迟的估计
然后采用“凹陷法”来判断是否分辨成功。关于MUSIC算法的理论性能分析可参考文献[4],下面采用蒙特卡洛仿真分辨结果。
仿真2 对间隔为0.4倍瑞利限的两不相关目标,分别采用MUSIC算法和本文的假设检验方法进行分辨,设置不同的快拍数。假设检验方法采用的回波为不同快拍数据的直接迭加,虚警概率设置为0.001。MUSIC算法搜索范围为-0.8:0.8,步长0.01。两目标信噪比见图中所示,对每种信噪比进行1000次蒙特卡洛仿真,统计分辨成功概率,结果如图4所示。
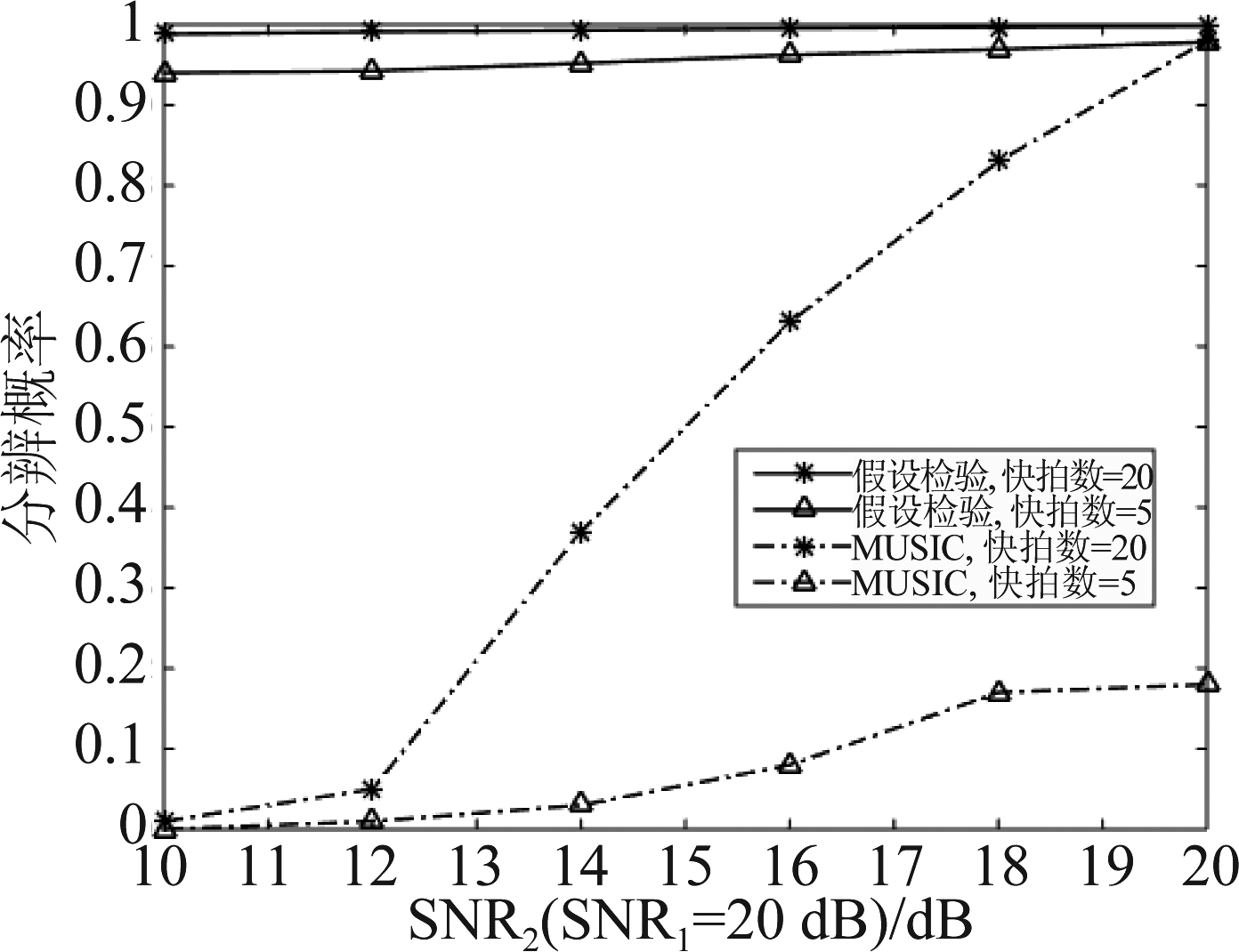
图4 与MUSIC算法分辨比较(两信号距离间隔为0.4倍瑞利限)
Fig.4 Comparison with the MUSIC algorithm (the separation is 0.4 times of the Rayleigh limit for two signals)
从图中可以看出,对于瑞利限以内的两目标,本文的假设检验方法的分辨能力远高于MUSIC算法。另外,MUSIC算法受到快拍数影响较大,而假设检验方法对于快拍数的变化更为鲁棒。
6 结论
本文假定两个目标回波的幅度信号服从随机高斯分布,利用二元假设检验理论研究了距离近邻目标的统计分辨性能。我们采用正交投影将分辨问题转化为检测问题,从而得到距离统计分辨限的解析表示。理论和仿真均表明,统计分辨性能和发射信号波形、信噪比和幅度相关系数有关。仿真结果表明,假设检验方法比MUSIC算法具有更好的分辨性能。需要指出的是,假设检验方法只能得到该分辨单元目标个数估计,而MUSIC算法可以估计目标的具体位置。
附录1:公式(14)和(15)的证明
根据式(13),统计量在H0下的分布为:
T(y)=μ0x0+μ1x1
(25)
其中
为自由度为2的卡方分布。
根据特征函数的定义[19],概率密度为pT(t)的随机变量T的特征函数为:
ΦT(w)=E{ejwT}=
ejwtpT(t)dt
(26)
考虑到变量x0和x1之间独立,则有:
ΦT(w)=E{ejwT}=E{ejw(μ0x0+μ1x1)}=
(27)
由于
为指数分布,其矩母函数为:
(28)
则有下式成立:
(29)
则式(27)可以进一步写为:
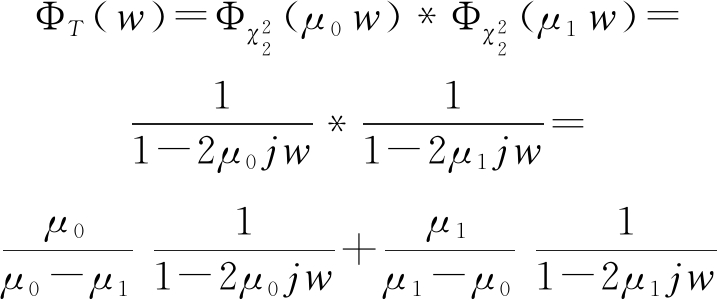
(30)
由于变量T的概率密度函数为特征函数的逆傅里叶变换,考虑到随机变量T≥0,t<0时概率密度函数为0,于是得到其分布为:
t≥0
(31)
设检测门限为γ,根据虚判概率定义,有:
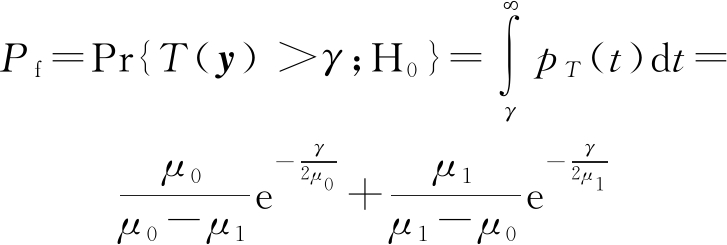
(32)
同理,可以获得检测概率的表达式为:
(33)
证毕。
附录2:公式(16)和(17)的证明
当保留一阶近似项时,式(4)变为关于待检验参数θ=α-δt/2的线性模型:
(34)
其中
可以看出,该模型为未知参数的线性模型,可以把hθt看作等价信号,于是可以求得等价信号的自相关矩阵:
(35)
式(8)给出了检测统计量,经过和公式(9)-(12)类似处理,得到两种假设下的分布为:
(36)
其中
(37)
(38)
可以验证λ为矩阵Ct的特征值,对应的特征向量为
因此得证。
[1] Kaveh M, Barabell A J. The statistical performance of MUSIC and the minimum-norm algorithms in resolving plane waves in noise[J]. IEEE Transactions on Acoustics., Speech, Signal Processing, 1986, 34(3): 331-341.
[2] Sherman K C, Durrani T S. Resolving Power of Signal Subspace Methods for Finite Data Lengths[J]. International Conference on Acoustics, Speech and Signal Processing, 1985: 1501-1504.
[3] Lee H, Wengrovitz M S. Statistical Characterization of the MUSIC Null Spectrum[J]. IEEE Transactions on Signal Processing, 1991, 39(4): 1333-1347.
[4] Zhang Q. Probability of Resolution of the MUSIC Algorithm[J]. IEEE Transactions on Signal Processing, 1995, 43(4): 978-987.
[5] 郑恩明, 孙长瑜, 陈新华, 等. 改善高分辨逆波束形成检测性能方法研究[J]. 信号处理, 2013, 29(5): 570-576.
Zheng Enming, Sun Changyu, Chen Xinhua, et al. The research of detection performance improving method for high-resolution inverse beam-forming[J]. Journal of Signal Processing, 2013, 29(5): 570-576.(in Chinese)
[6] Mir H, Wilkinson J. Radar target resolution probability in a noise-limited environment[J]. IEEE Transactions on Signal Processing, 2018, 44(3): 1234-1239.
[7] Shahram M, Milanfar P. On the resolvability of sinusoids with nearby frequencies in the presence of noise[J]. IEEE Transactions on Signal Processing, 2005, 53(7): 2579-2588.
[8] Korso EL MN, Boyer R, Renaux A, et al. On the asymptotic resolvability of two point sources in known subspace interference using a GLRT-based framework[J]. Signal Processing, 2012, 92(10): 2471-2483.
[9] Zhu W, Tang J, Wan S. Angular Resolution Limit Of Two Closely-spaced Point Sources Based on Information Theoretic Criteria[C]∥International Conference on Acoustics, Speech and Signal Processing, 2014: 86-90.
[10] Sun M, Jiang D, Song H, et al. Statistical resolution limit analysis of two closely spaced signal sources using Rao test[J]. IEEE Access, 2017, 2017(5): 22013-22022.
[11] Thamwei M, Abed M K, Foroozan F, et al. On the statistical resolution limit for time-reversal based MIMO radar[J]. Signal Processing, 2018, 144(MAR): 373-383.
[12] Zhang Y, Zhu W, Tang B, et al. Angular statistical resolution limit of two closely-spaced point targets: A GLRT-Based Study[J]. IEEE Access, 2018, 2018(6): 75924-75936.
[13] Zhang Y, Wang L, Wang J, et al. Colocated MIMO radar waveform design for angular SRL in the context of hypothesis testing[J]. SCIENCE CHINA Information Sciences, 2019, 62(4): 1-3.
[14] 张云雷, 汤俊, 王力. 基于假设检验理论的雷达近邻目标距离统计分辨限[J].雷达学报, 2019, 8(1): 17-24.
Zhang Yunlei, Tang Jun, Wang Li. Hypothesis-testing-based range statistical resolution limit of radar[J]. Journal of Radars, 2019, 8(1): 17-24.(in Chinese)
[15] Bruckstein A M, Shan T J, Kailath T. The Resolution of Overlapping Echoes[J]. IEEE Transactions on Acoustics, Speech, and Signal Processing, 2003, 33(6): 1357-1367.
[16] Pallas M-A, Jourdian G. Active high resolution time delay estimation for large BT signals[J]. IEEE Transactions on Signal Processing, 1991, 39(4): 781-788.
[17] Liu W, Xie W, Liu J, et al. Adaptive double subspace signal detection in Gaussian background—Part I: homogeneous environments[J]. IEEE Transactions on Signal Processing, 2014, 62(9): 2345-2357.
[18] Kay S M. Fundamentals of Statistical Signal Processing-Detection Theory[M], NJ, vol.2: Prentice Hall, 1998: 486.
[19] 陆大. 随机过程及其应用[M]. 北京: 清华大学出版社, 1986: 668.
Lu Dajin. Stochastic Process and Its Application[M]. Beijing: Tsinghua University Press,1986:668.(in Chinese)
