1 引言
随着信息化程度的不断加深,无论是在军用还是民用领域,雷达和通信系统作为最重要的电子系统,都得到了广泛的应用[1]。在一些特定应用中,需要将两个功能结合起来,形成雷达通信一体化系统,用于降低系统冗余、体积、重量、能耗、操作复杂度等。
雷达、通信收发装置主要由控制与显示、处理、孔径、通道、信号部分组成。围绕这五个部分的共享设计,雷达通信一体化系统发展分为四个阶段。第一个阶段是独立式结构,是一体化系统发展的萌芽阶段,雷达、通信等电子系统各自实现独立的功能,只将设备集中于一个平台之上;第二个阶段是联合式结构,是一体化发展的初级阶段,雷达、通信等电子系统共享控制与显示终端;第三个阶段是综合式电子系统,实现了雷达、通信等对控制与显示终端和信号处理机等功能的共享;第四个阶段是第三阶段的延伸,进一步实现了对通道和孔径等资源的共享。目前,部分欧美国家已初步实现了雷达和通信对控制与显示、数据处理、通道和射频前端等资源的共享,并进一步将其研究重点延伸至一体化共享信号设计,旨在通过一个处理机、一个显示终端、一个射频通道、一个天线、一个信号对雷达和通信信息的统一承载、处理和显示[2]。
从雷达和通信的理论模型和系统构型来看,两者的信号一体化是核心难点。雷达和通信在信号设计方面存在许多固有的、不可调和的矛盾[3]。这主要是因为,雷达的基本任务是探测天线波束内的目标,获得有关目标的距离、方向、速度等状态信息。为了最大化、不失真探知目标状态信息,雷达对信号点扩展函数的旁瓣提出了较高要求。相比之下,通信的目的在于实现信源和信宿之间的信息传输。为了消除多径、多普勒对通信的影响,往往需要在通信信号中嵌入导频、同步、循环前缀等信号[4]。然而,依据模糊函数定义可知,周期性导频、同步和循环前缀信号势必会在雷达匹配滤波的点扩展函数中产生伪峰。另外,高随机的通信信息也会抬高点扩展函数旁瓣。在过多伪峰和过高旁瓣的影响下,雷达探测性能严重下降。因此,基于匹配滤波理论可知,雷达对信道信息的探测与通信对信源信息的探测是相互矛盾的。
为了突破上述矛盾约束,本文以正交频分复用(Orthogonal Frequency Division Multiplexing, OFDM)通信信号为基础,从模糊函数的角度分析了OFDM通信信号用于雷达探测的本质限制,从失配滤波的角度提出了将OFDM通信信号点扩展函数旁瓣和伪峰外推至雷达观测窗口外的处理算法,进而实现了雷达和通信功能对OFDM信号的一体化共享,在保证高速无线通信的同时,使之具备良好的雷达探测性能。
2 OFDM一体化共享信号模型
2.1 基于OFDM一体化共享信号的系统框架与帧结构
OFDM信号是一种由多载波组成的扩频传输技术,具有频谱利用率高,抗符号间干扰(ISI)和子载波间干扰(ICI)、低误码率等优点,已被广泛的应用于4G、5G通信[5]。与此同时, OFDM信号具有独立的距离和多普勒处理能力,已被同样广泛应用到雷达探测方面。基于OFDM一体化共享信号,可兼备高速无线通信和低截获雷达探测性能。
假设子载波数为Nc,符号数为Ns,OFDM符号的有效时间为Ts,循环前缀的时间长度为Tg,则完整的OFDM符号持续时间为T=Ts+Tg,子载波频率间隔为![]() 信号带宽为B=NcΔf,发射的OFDM基带信号的实部表达式为
信号带宽为B=NcΔf,发射的OFDM基带信号的实部表达式为
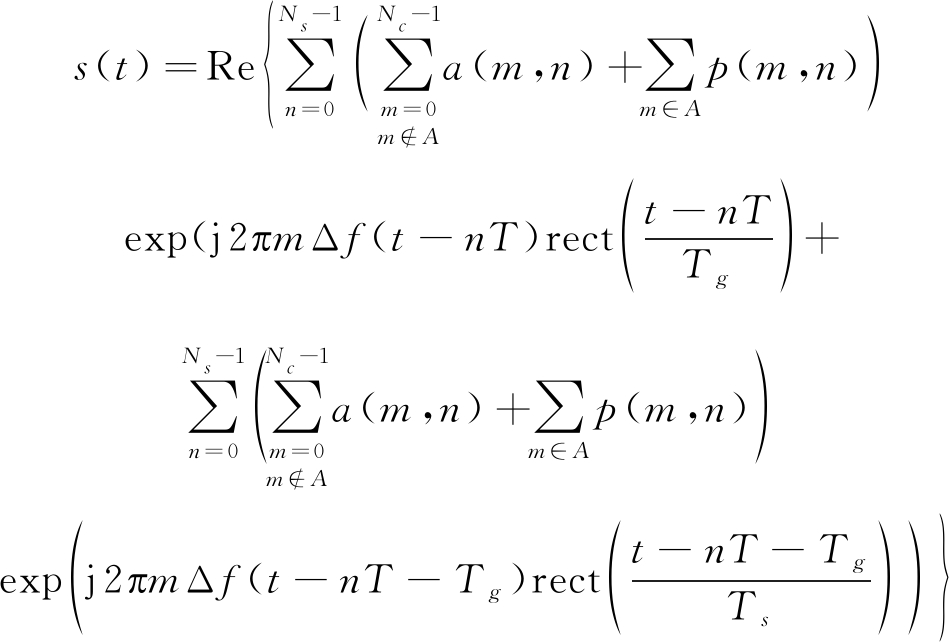
(1)
其中,a(m,n)和p(m,n)分别为第n个符号、第m个子载波上调制的复加权系数和导频序列,A⊂[0,Nc-1]代表导频占用的子载波位置集。
基于OFDM一体化共享信号的系统框架如图1所示[6]。在发送端,通信二进制数据先经过MQAM或MPSK数字调制方式完成星座映射,得到的复调制序列am通过串并转换器将串行数据转换成N路并行数据,再经过IFFT变换完成OFDM调制。调制好的符号数据经过D/A转换成模拟信号,并经天线辐射。
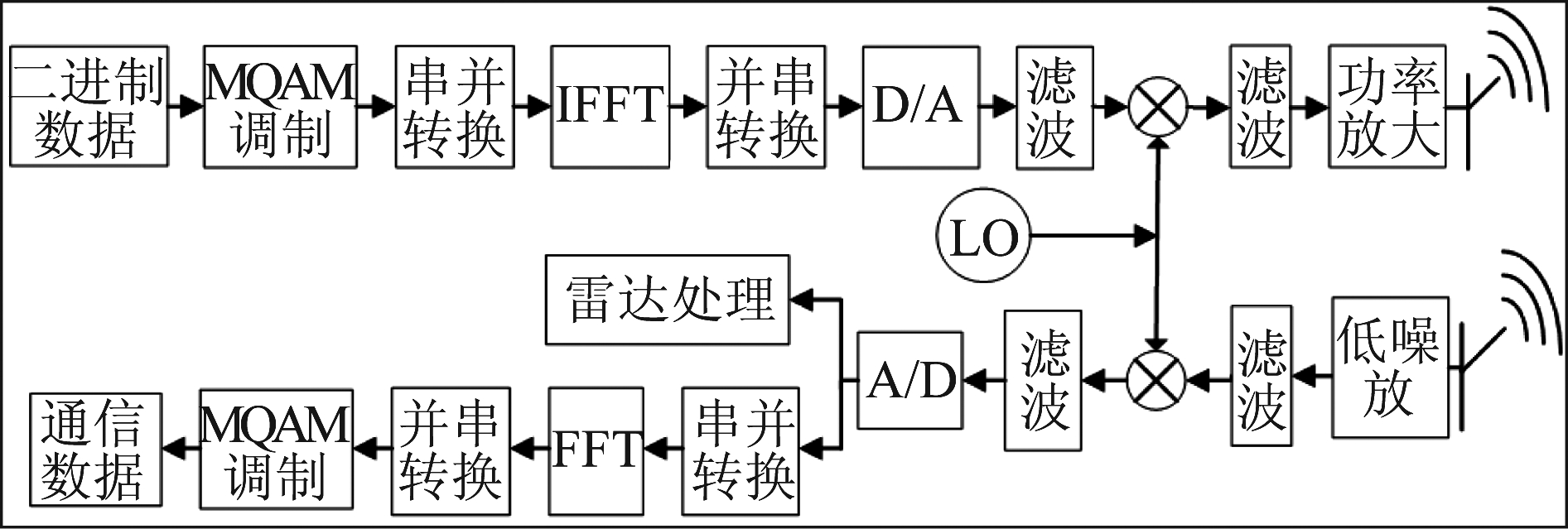
图1 OFDM一体化系统框架图
Fig.1 The diagram of the OFDM-based joint system
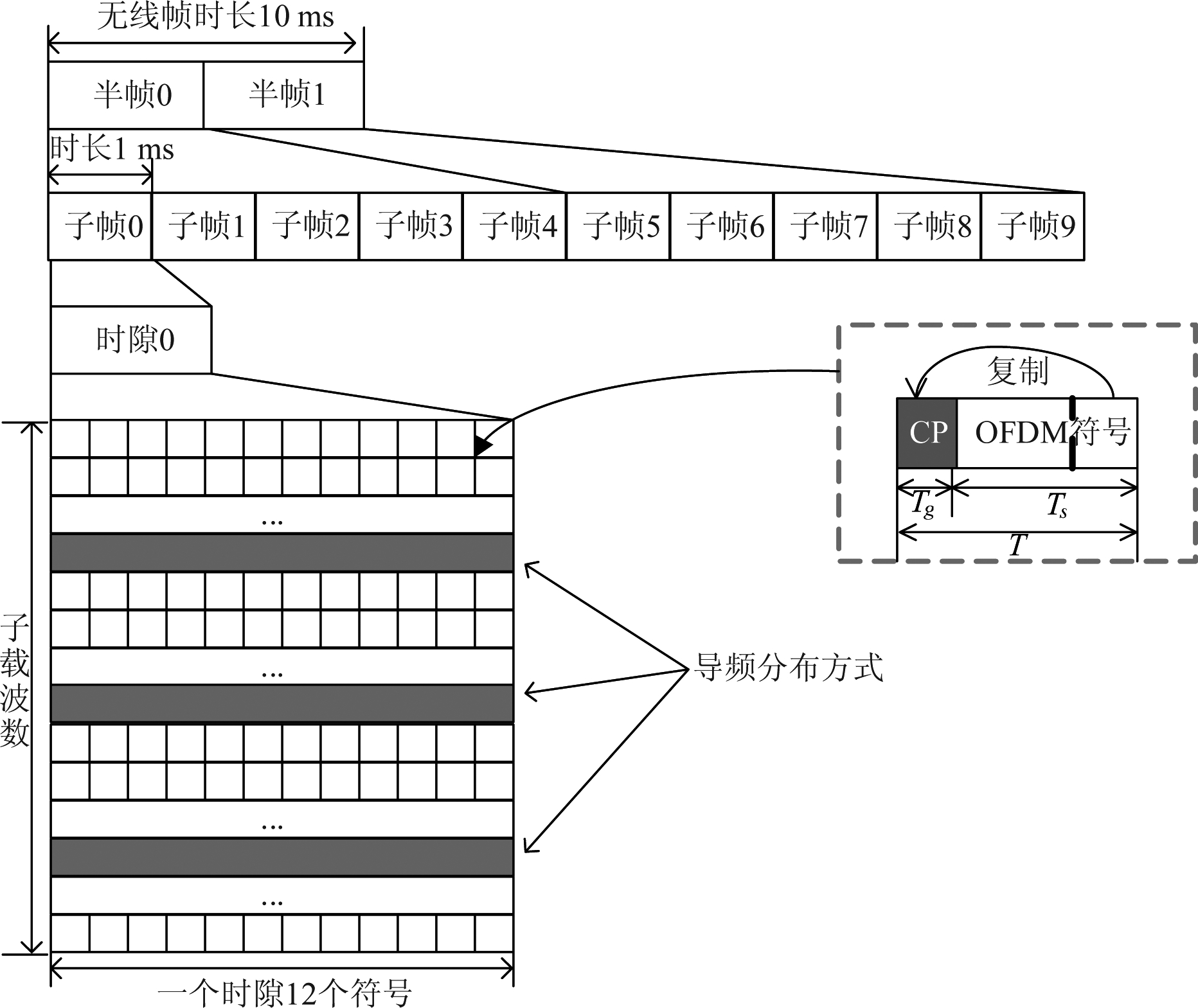
图2 完整的通信帧结构
Fig.2 The structure of the communication frame
OFDM一体化共享信号的帧结构为图2所示。一个完整的帧长度为10 ms,包含10个子帧,每个子帧的长度为1 ms。根据5G通信协议的标准[7],将每个子帧定义为一个时隙,且每个时隙含有12个完整的OFDM符号。每个完整的OFDM符号由循环前缀和符号组成。循环前缀位于OFDM符号的前端,是OFDM符号尾部数据的重复。循环前缀可以有效解决由多径效应引起的符号间干扰(ISI)和载波间干扰(ICI)。导频序列采用梳状导频形式[8],即导频信号均匀地分布于每个OFDM符号内并且每个符号具有相同的导频信息。在每个符号中,相邻导频的子载波位置间隔36个子载波。
基于OFDM一体化共享信号的数据处理主要包括雷达信号处理和通信信息解调。通信数据处理主要包括对接收的回波信号进行FFT变换完成OFDM解调和对复调制序列am进行数字通信解调步骤。对于雷达信号处理而言,传统的匹配滤波势必会引入高旁瓣和伪峰问题。本文中将采用失配处理,下面首先分析该信号的模糊函数特性。
2.2 OFDM一体化共享信号的模糊函数分析
模糊函数是对雷达信号进行分析研究和波形设计的有效工具。它可以定量的分析系统的分辨力、模糊度和抑制杂波的能力。模糊函数定义如下[9]:
(2)
将公式(1)中的OFDM雷达通信一体化信号复数形式带入到公式(2)中,可得雷达通信一体化信号的模糊函数。
为简化分析,令![]() 为向下取整函数,则有:
为向下取整函数,则有:
(1)当|τ|>NsT,χ(τ,0)=0;
(2)当0<|τ|<NsTs,OFDM通信帧的模糊函数计算过程如图3所示。在任意时延τ下,模糊函数计算过程可拆解为两部分,如图3中的黑色框和绿色框。
图3 OFDM通信帧的模糊函数计算示意图
Fig.3 The diagram of the ambiguity function calculation for the OFDM frame
χ(τ,0)=G1+G2
(3)
其中,G1和G2分别表示黑色框和绿色框的计算结果,黑色框表示在时延τ下,第n个OFDM符号和第n+k个OFDM符号之间的互模糊函数(n=0,1,2,…,Ns-1-k),绿色框表示第n个OFDM符号与第n+k+1个OFDM符号之间的互模糊函数(n=0,1,2,…,Ns-2-k)。且有
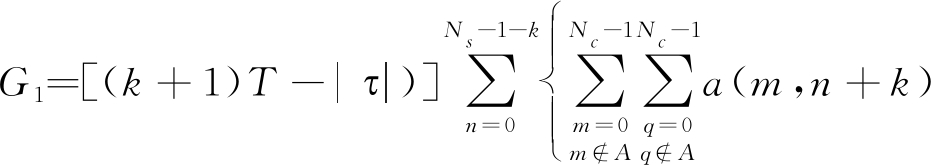
a*(q,n) exp{jπ(m+q)Δf|τ|}*
exp{jπΔf[(m-q)-(m+q)k]T}
sinc{π(m-q)Δf((k+1)T-|τ|)}+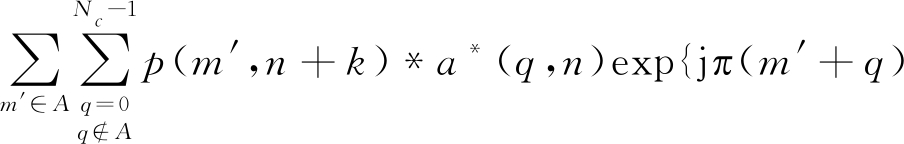
Δf|τ|}exp{jπΔf[(m′-q)-(m′+q)k]T}*
sinc{π(m′-q)Δf((k+1)T-|τ|)}+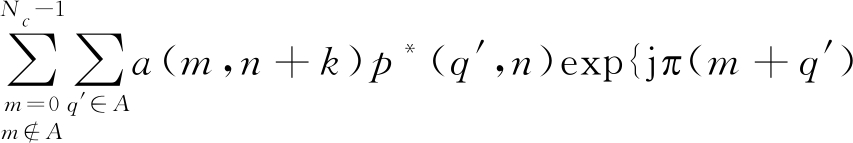
Δf|τ|}*exp{jπΔf[(m-q′)-(m+q′)k]T}
sinc{π(m-q′)Δf((k+1)T-|τ|)}+![]()
Δf|τ|}exp{jπΔf[(m′-q′)-(m′+q′)k]T}*
sinc{π(m′-q′)Δf((k+1)T-|τ|)}
(4)
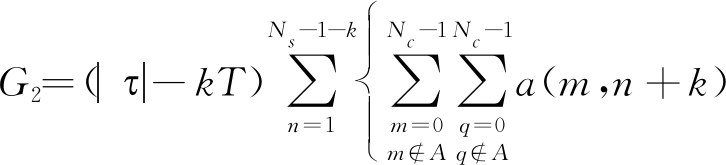
a*(q,n-1)exp(jπ(m+q)Δf|τ|)![]() sinc(π(m-q)
sinc(π(m-q)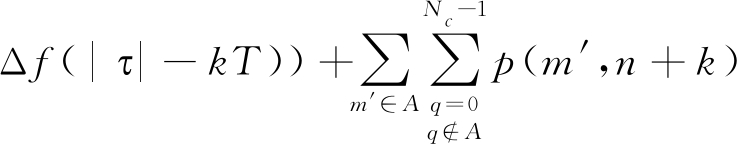
a*(q,n-1)exp(jπ(m′+q)Δf|τ|)*
![]()
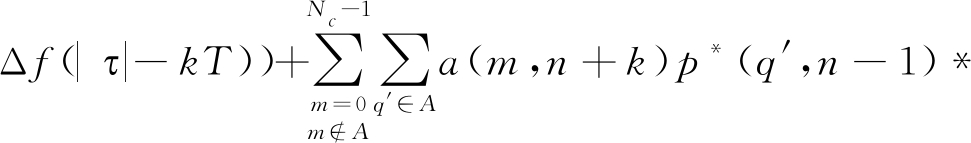
![]()
![]()
p*(q′,n-1)exp(jπ(m′+q′)Δf|τ|)![]()
sinc(π(m′-q′)Δf(|τ|-kT))
(5)
依据(4)和(5)可知,G1,G2表现形式类似,都包含三个子项。每个子项的具体形式都由与数据项a(m,n)有关的自相关/互相关决定。将与数据项a(m,n)有关的公式单独列出,可得
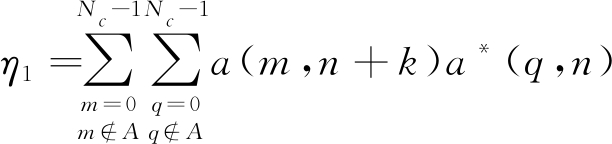
(6)

(7)
(8)
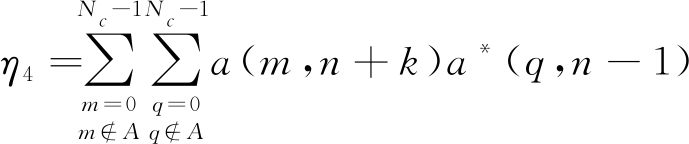
(9)
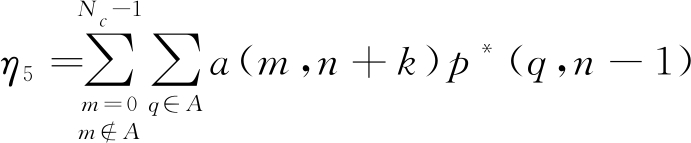
(10)
(11)
其中,η4、η5、η6分别表示G2中通信数据互相关,通信与导频互相关,导频自相关。若k=0,η1、η2、η3分别表示通信数据自相关,通信与导频互相关,导频自相关,若k≠0,η1、η2、η3分别表示通信数据互相关,通信与导频互相关,导频自相关。
对于η1,η4而言,为了获得较低的自相关和互相关函数旁瓣,需要对通信数据项a(m,n)进行优化。然而a(m,n)代表需要传输的通信数据,不能被改变。因此,当通信信息确定后,a(m,n)也就随之确定且不能被优化,其相关函数往往具备较高的旁瓣。同理,若给定信道,导频序列也随之确定,而η2和η5表示未经优化的通信数据与导频互相关。因此,η2和η5往往具有较高的旁瓣。最后,对于η3和η6而言,其具体形式为导频信号的自相关,会在OFDM模糊函数中产生伪峰。需要说明的是,伪峰不仅与导频有关,还与循环前缀CP密切相关。为了进一步分析伪峰,本文将k=0,|τ|=Ts的情况单独列出。
如图4所示,若k=0且|τ|=Ts,则对每个符号而言,原始信号的CP和参考信号的后段数据重叠。由于CP与后端数据一致(如图2所示),则此时出现峰值。然而,该峰值并不代表原始信号与参考信号完全匹配,而是表示原始信号中每个符号的CP与对应符号的后端数据的匹配。因此,该峰值是一种由OFDM CP结构引入的伪峰。

图4 循环前缀对模糊函数影响的图示
Fig.4 The impact of the cyclic prefix on ambiguity function
综上所述,从模糊函数的角度来看,对于OFDM雷达通信一体化共享信号而言,其点扩展函数往往具有过多的伪峰和过高的旁瓣,通常会导致雷达探测性能严重下降。为了降低或消除OFDM一体化共享信号经过脉冲压缩处理后的高旁瓣和伪峰,本文将在下一节提出基于失配滤波的处理算法。
3 OFDM一体化共享信号的失配处理
依据模糊函数的模糊体积恒定特性可知,原始信号与参考信号的互相关必然存在旁瓣,且这种旁瓣在模糊平面的分布是可以通过原始信号设计或参考信号设计来控制的[10]。本文提出的失配处理算法思想是[11-12]通过设计参考信号,将脉压处理后的OFDM一体化共享信号旁瓣和伪峰能量移至模糊平面远端。而对于模糊平面近端的主瓣临近区域,旁瓣和伪峰近似为零。因此,若给定了原始OFDM一体化共享信号形式,可依据旁瓣和伪峰能量位于距离远端的点扩展函数形式来计算参考信号形式。依据卷积定理可知,为了尽可能地将旁瓣和伪峰远离主瓣,需要使参考信号长度大于原始信号,且参考信号越长,旁瓣和伪峰离主瓣越远。在相同的采样率条件下,若原始信号的采样点数为N,采用的参考信号采样点数为3N,则可将旁瓣和伪峰推离主瓣N个采样点的距离,雷达的不模糊测绘带采样点数为N/2。
假设接收机接收到的OFDM雷达通信一体化波形的离散采样信号可以表示为
S={s(0),s(1),...,s(N-1)}
(12)
接收信号的霍尔维茨多项式表示为
Fs(x)=s(N-1)xN-1+s(N-2)xN-2+...+s(1)x+s(0)
(13)
数字相关滤波器的脉冲特性表示为
H={h(0),h(1),...,h(N-1)}
(14)
对应的霍尔维茨多项式表示为
Fh(x-1)=h*(N-1)x-(N-1)+
h*(N-2)x-(N-2)+...+h*(1)x-1+h*(0)
(15)
因此,相关处理后的霍尔维茨多项式可以表示为[13-15]
(16)
=(s(N-1)xN-1+s(N-2)xN-2+...+s(1)x+s(0))×
(h*(N-1)x-(N-1)+h*(N-2)x-(N-2)+...+h*(1)x-1+h*(0))
(17)
将公式(17)展开化简为
Qsh(x)=q(N-1)xN-1+q(N-2)xN-2+...+q(1)x+
q(0)+q(-1)x-1+...+q(-N+1)x-(N-1)
(18)
(19)
(20)
q(0)和q(-N+1),…,q(-1),q(1),q(2),…,q(N-1)分别是互相关函数的主瓣和旁瓣。
如果相关处理滤波器采用匹配滤波器,其脉冲特性表示为
HM={s*(0),s*(1),...,s*(N-1)}
(21)
匹配滤波器输出信号的信噪比最大,但是输出信号的自相关函数较高。为了解决强信号的副瓣遮盖弱信号的主瓣的问题,可采用失配滤波器的方法,将旁瓣能量推离远端,使近端旁瓣能量为零。
假设设计的失配滤波器的脉冲特性表示为
HMMF={h(0),h(1),...,h(N-1),...,h(M-1)}
M>N
(22)
则相关处理后输出信号的互相关函数的霍尔多项式表示为
Qsh(x)=q(-M+1)x-(M-1)+q(-M+2)x-(M-2)+...+
q(-1)x-1+q(0)+q(1)x+...+q(N-1)xN-1
(23)
根据前述的点扩展函数形式,则公式(23)改写为
Qsh(x)=q(-M+1)x-(M-1)+...+q(-M+N-1)x-(M-N+1)+
0x-(M-N)+...+x-N+0x-(N-1)+...+q(1)+...+q(N-1)xN-1
(24)
因此,构建约束条件如下
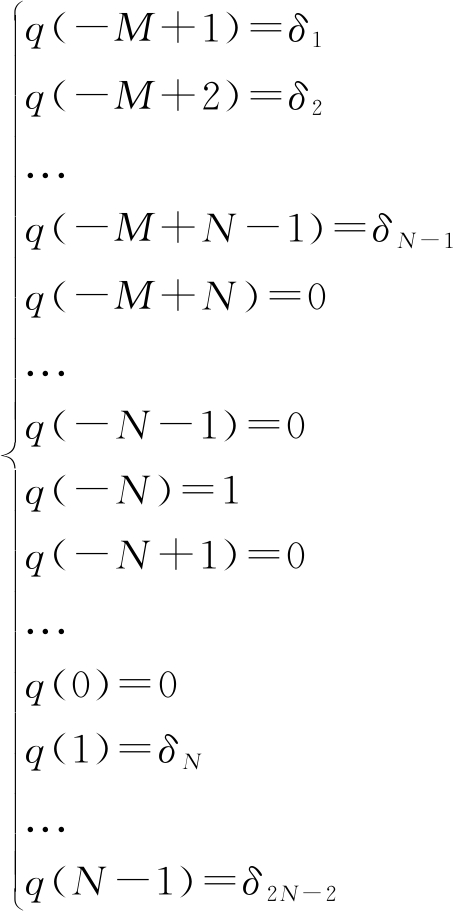
(25)
其中,δ1,δ2,...,δ2N-2为近似零的值,再根据公式(19)和(20)可得
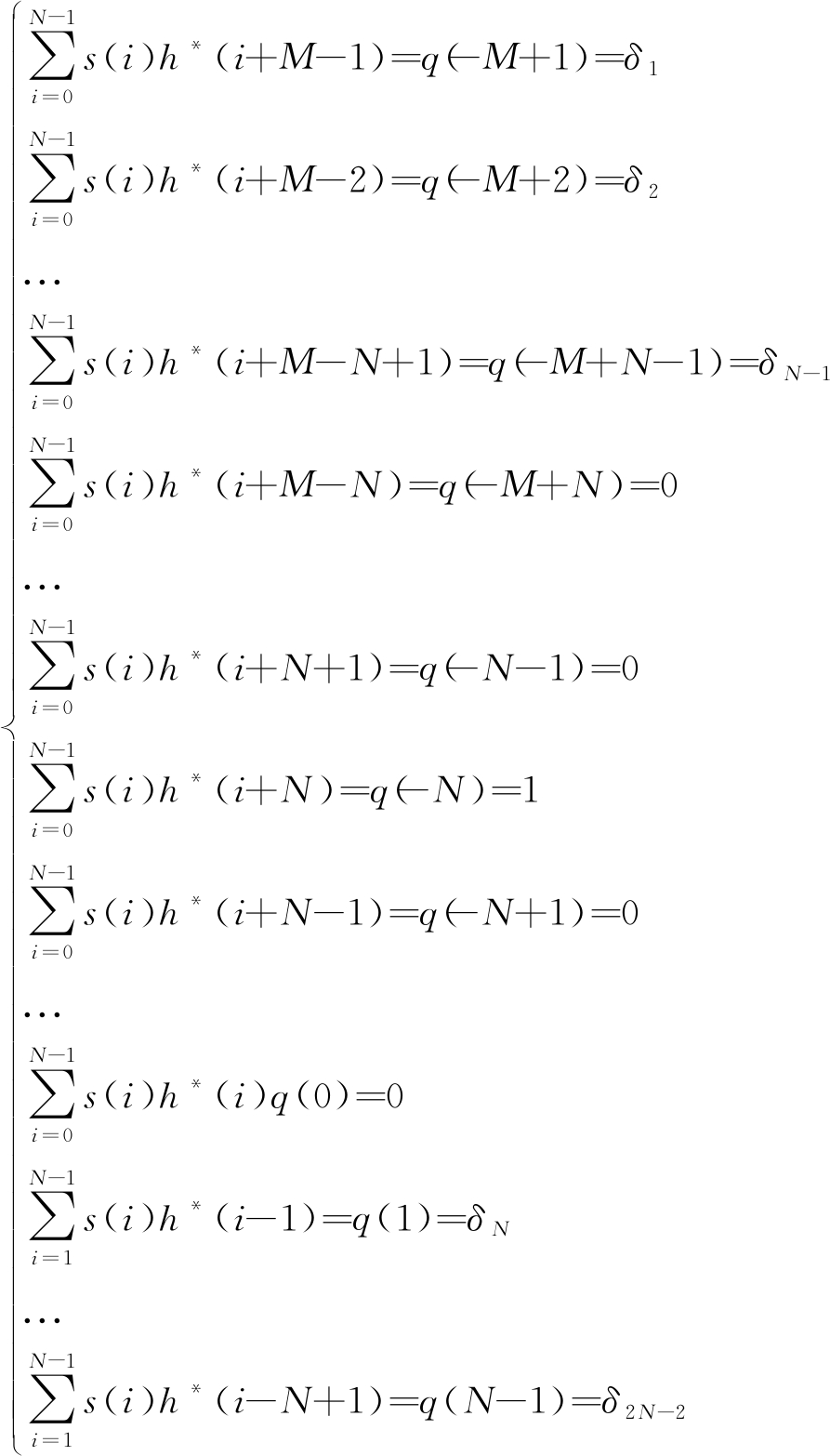
(26)
由于公式(26)中S已知,则可得到H的脉冲特性。
下面通过一个例子对本文失配滤波算法进行补充说明。设长度N=3的接收信号(12)与长度M=3N的失配滤波器相关处理后的输出信号(17)
(s(0)+s(1)x+s(2)x2)(h*(0)+h*(1)x-1+h*(2)x-2+
h*(3)x-3+h*(4)x-4+h*(5)x-5+h*(6)x-6+
h*(7)x-7+h*(8)x-8=q(-8)x-8+q(-7)x-7+
q(-6)x-6+q(-5)x-5+q(-4)x-4+q(-3)x-3+
q(-2)x-2+q(-1)x-1+q(0)+q(1)x+q(2)x2
(27)
将公式(27)左右两边式子展开,可得到等式
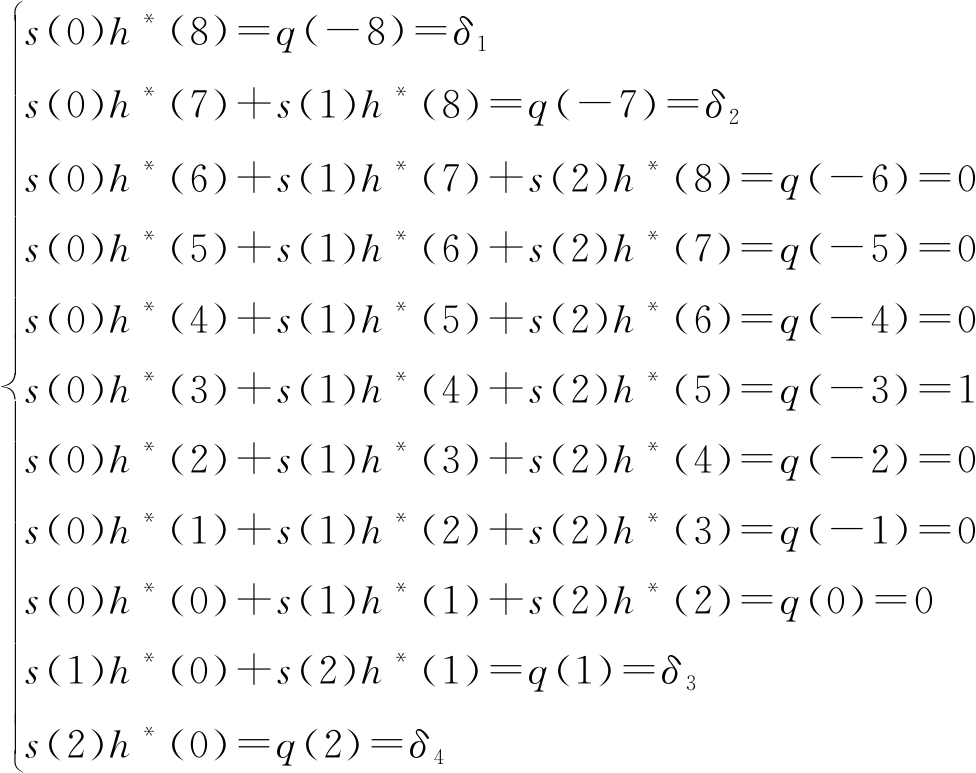
(28)
根据公式(16),若给定Fs(x)和Qsh,则可计算出失配滤波器的霍尔多项式![]() 从等式(28)可以看出,方程组的数目为M+N-1,而失配滤波器脉冲特性的系数数目为M,所以方程组有且只有唯一解,可以根据携带任何通信信息的OFDM信号设计对应的失配滤波器的表现形式。
从等式(28)可以看出,方程组的数目为M+N-1,而失配滤波器脉冲特性的系数数目为M,所以方程组有且只有唯一解,可以根据携带任何通信信息的OFDM信号设计对应的失配滤波器的表现形式。
4 仿真实验
4.1 仿真模型
基于OFDM的雷达通信一体化共享信号仿真场景如图5所示。雷达通信一体化系统在与通信接收机高速通信时,可对波束内的雷达目标进行探测。
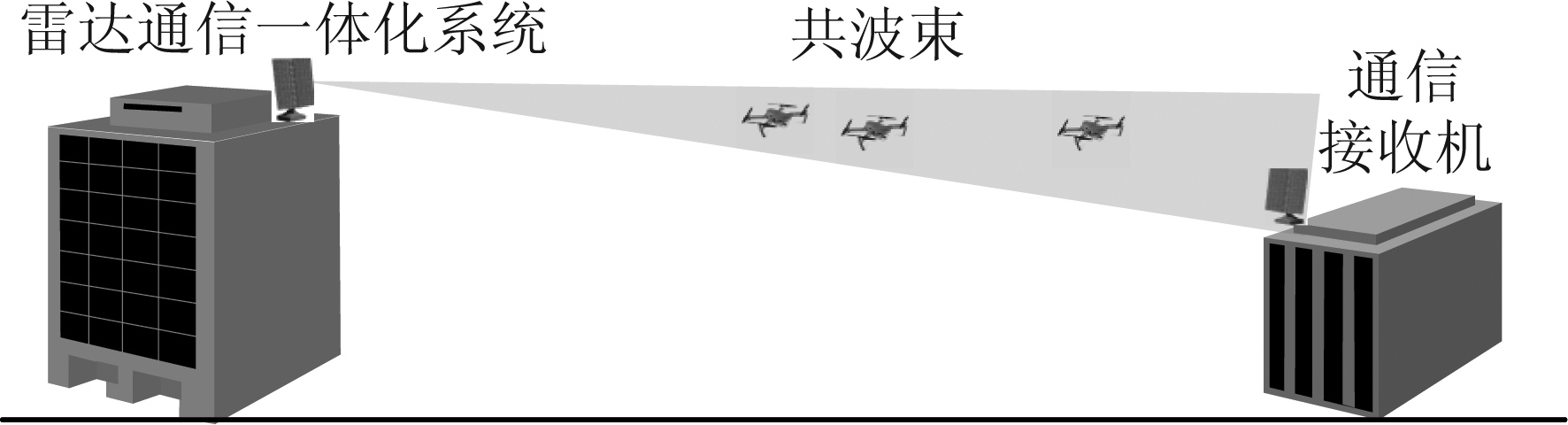
图5 仿真场景
Fig.5 The simulation scene
假设通信链路存在点目标m1、m2和m3。其中,m1和m2的RCS相同且较强,m3的RCS较弱。这三个目标与一体化系统的距离分别为R1=3000 m, R2=5000 m,R3=9000 m。一体化系统工作于连续波体制,发射信号帧结构与5G通信协议的帧结构一致(见图2),雷达重复周期为1 ms子帧的持续时间。基于OFDM的雷达通信一体化共享信号仿真参数如表1所示。
表1 仿真参数
Tab.1 Simulation parameters
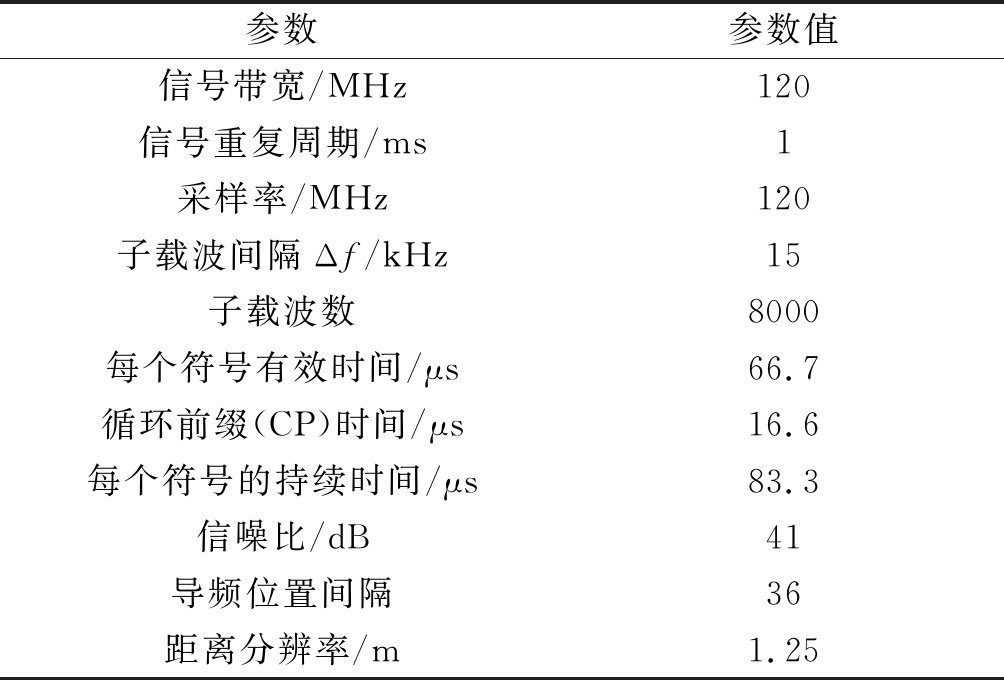
参数参数值信号带宽/MHz120信号重复周期/ms1采样率/MHz120子载波间隔Δf/kHz15子载波数8000每个符号有效时间/μs66.7循环前缀(CP)时间/μs16.6每个符号的持续时间/μs83.3信噪比/dB41导频位置间隔36距离分辨率/m1.25
4.2 仿真结果
基于图1所示系统框架,发送的通信信息为随机的二进制数据,采用256QAM调制,形成的OFDM雷达通信一体化发射信号实部如图6所示。
图6 发射的OFDM雷达通信一体化离散信号实部
Fig.6 The real part of transmitted joint radar and communication signal
对于接收信号,可通过经典的OFDM处理算法解调出信源信息。在表1所示参数下和图5所示场景下,通信误码率与信噪比的关系如图7所示。依图7可知,随着信噪比增加,通信误码率逐渐降低。为了满足通信系统的可靠性,本文以10-5的通信误码率为要求,选取41 dB的 SNR开展雷达通信一体化仿真实验。
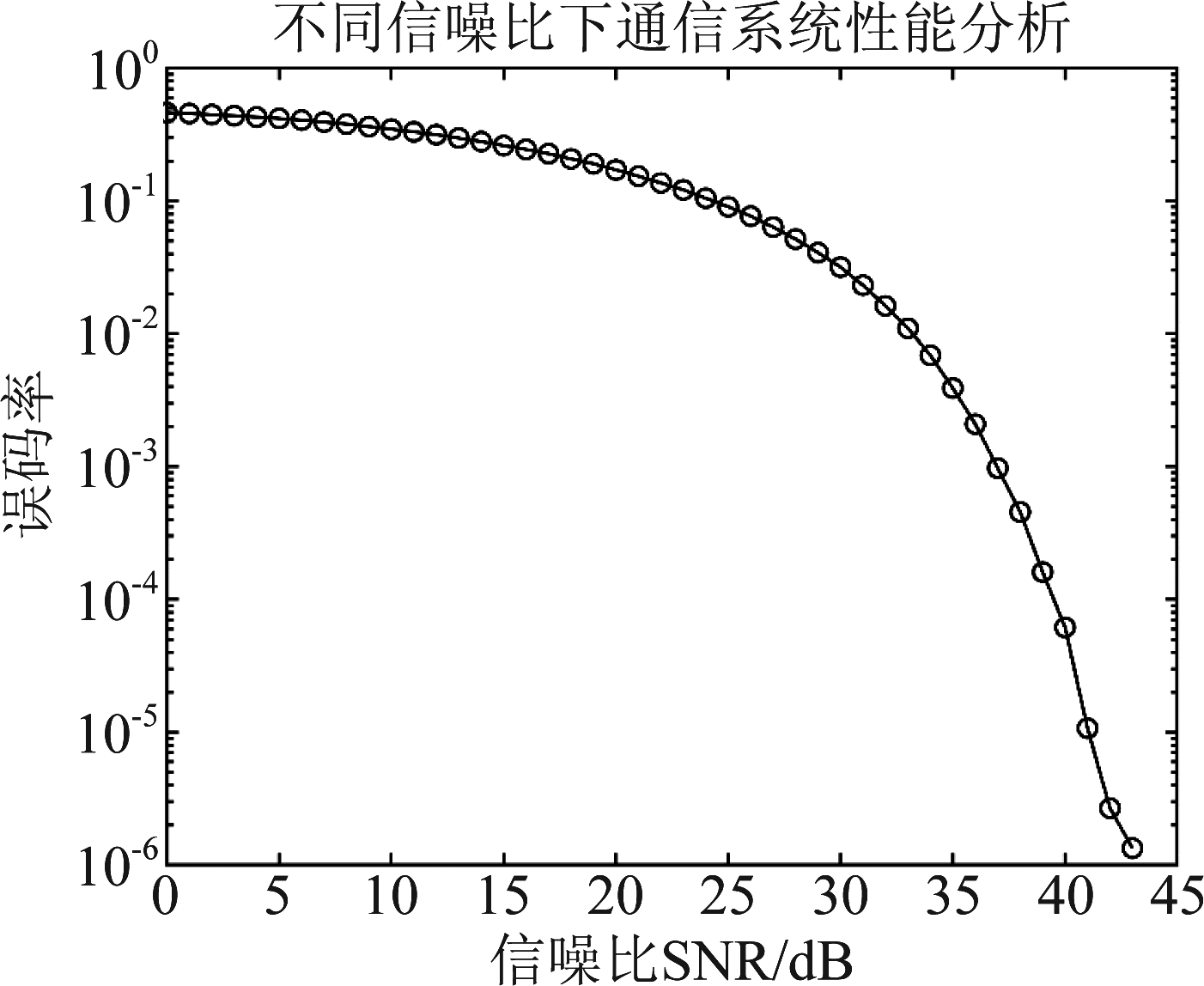
图7 在不同信噪比下通信误码率分析
Fig.7 The analysis of the bit error rate under the various SNR
在SNR=41 dB情况下,对含有三个点目标的接收信号分别经过匹配滤波和失配处理,可得图8所示处理结果。依图8可知,受通信信息的高随机性和通信帧结构的周期性影响,匹配滤波结果出现了高旁瓣和伪峰现象。这不仅会淹没小目标,还会产生虚假目标。但是,通过本文提出的失配处理,可将旁瓣和伪峰能量推离距第一个目标150 km处,旁瓣和伪峰都完全推离出雷达观测区域,进而去除虚假目标,并使淹没的小目标“浮现出来”。
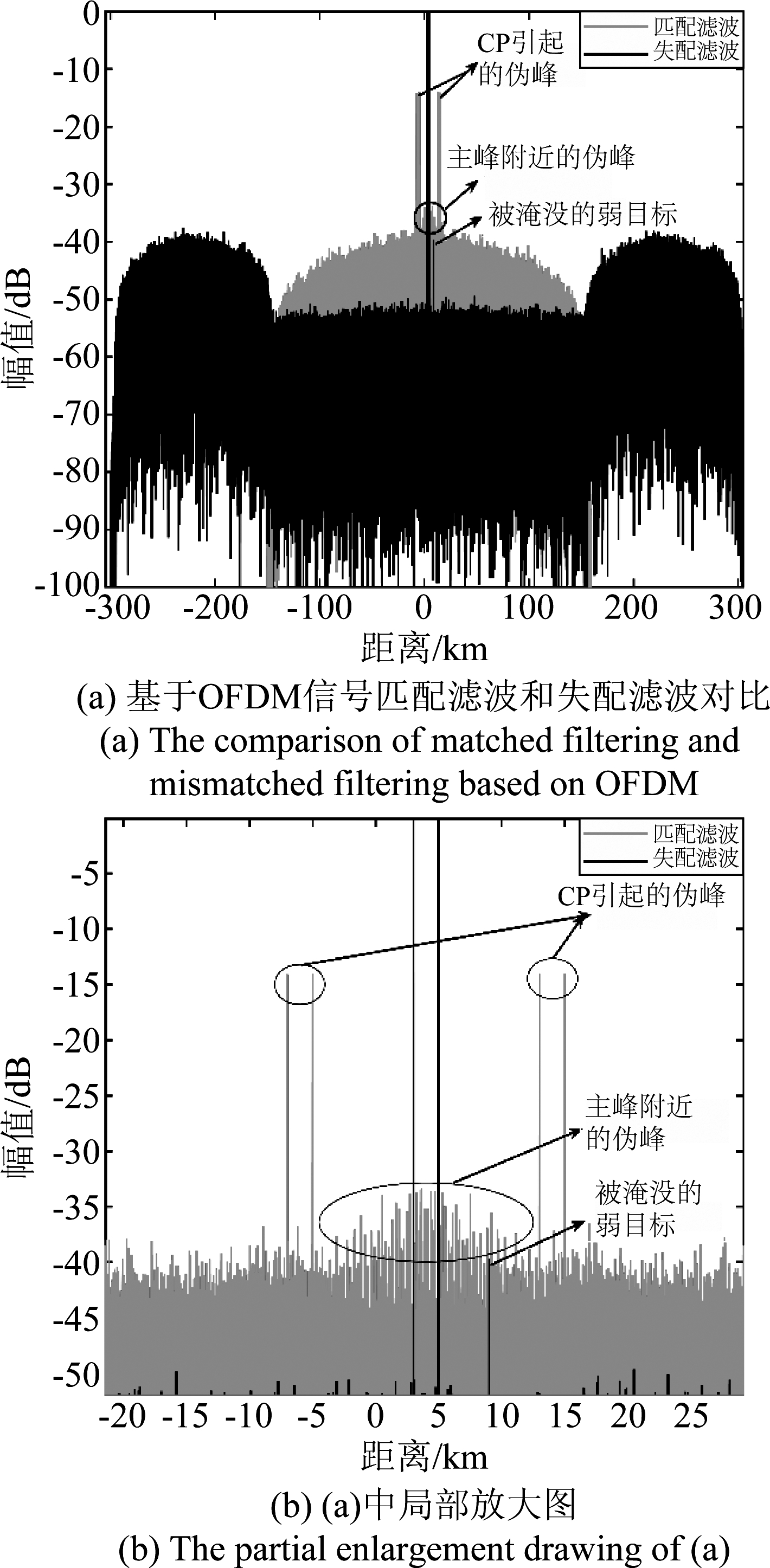
图8 SNR=41 dB时匹配滤波和失配滤波处理的对比
Fig.8 The comparison of matched filtering and mismatched filtering under the 41dB SNR
因此,从点扩展函数的角度来看,本文提出的失配处理算法明显优于传统的匹配滤波。通过失配滤波处理,可以去除匹配滤波中循环前缀引起的高伪峰和主峰附近的伪峰。在三个目标的雷达观测区内,除了有加入系统的噪底,并没有其他信号干扰。从雷达探测理论来看,雷达性能的衡量标准不仅与点扩展函数形状有关,还与信噪比有关[16]。为了进一步衡量失配滤波的性能,需要进一步分析信噪比损失。
对于输入信号s(t)经过滤波器h(t)后,输出为
(29)
而噪声n(t)经过滤波器h(t)的输出为
(30)
一般地,n(t)为高斯白噪声,设单边的功率谱密度为![]() 于是,任意时刻的条件下输出的噪声的平均功率为
于是,任意时刻的条件下输出的噪声的平均功率为
(31)
其中,E(·)代表求数学期望。假定滤波器输出的有用信号成分在t=t0时形成一个峰值,于是y(t)的峰值功率与噪声平均功率的比为
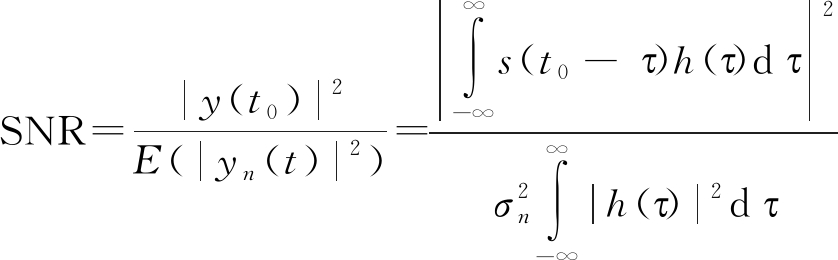
(32)
于是可得滤波器的信噪比损失LSNR为
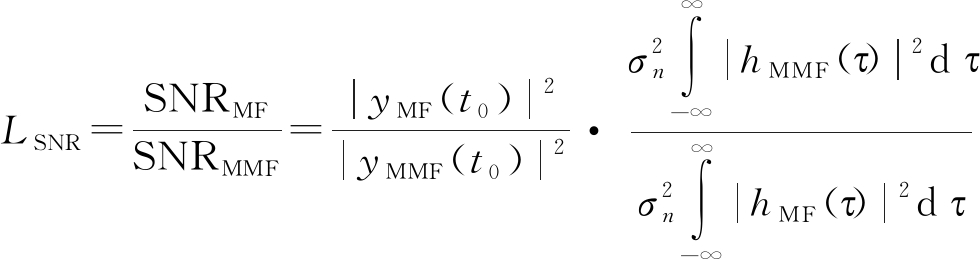
(33)
如果设计的失配滤波器和匹配滤波器的功率相同,则信噪比损失LSNR为
(34)
信噪比损失系数只与匹配滤波器在t=t0时输出的峰值和失配滤波器在t=t0时输出的峰值有关。图9为点目标m4的回波信号经过匹配滤波和失配滤波的信噪比损失对比,且m4相距雷达通信一体化系统为3000 m。

图9 滤波器功率相同时,匹配滤波和失配滤波信噪比损失对比
Fig.9 The comparison of loss of signal-noise ratio when the power of matched filter and mismatched filter are same
依图9和公式(34)可知,失配滤波器相对于匹配滤波器处理,信噪比损失了9.8 dB,旁瓣也降低了9.8 dB。虽然信号的旁瓣有所降低,但是主瓣的峰值也降低了,这对于雷达信号检测是不利的。
如果保证匹配滤波器和失配滤波器输出的点扩展函数的主瓣峰值相等,则信噪比损失LSNR为
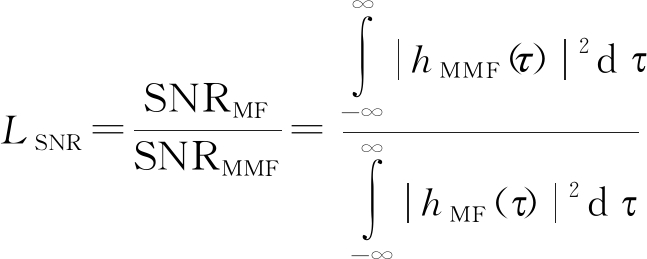
(35)
信噪比损失系数和两个滤波器的功率有关。在本文失配滤波器的长度是匹配滤波器长度的三倍且保证两者的滤波器输出主瓣峰值相同的条件下,信噪比损失系数为9.8 dB。由图10可知,失配滤波器和匹配滤波器在点扩展函数主瓣峰值相同的条件下,失配滤波器输出的旁瓣相对于匹配滤波器输出的旁瓣幅值没有变化,由于信号的旁瓣是远离目标的观测区,对雷达检测性能并没有影响。
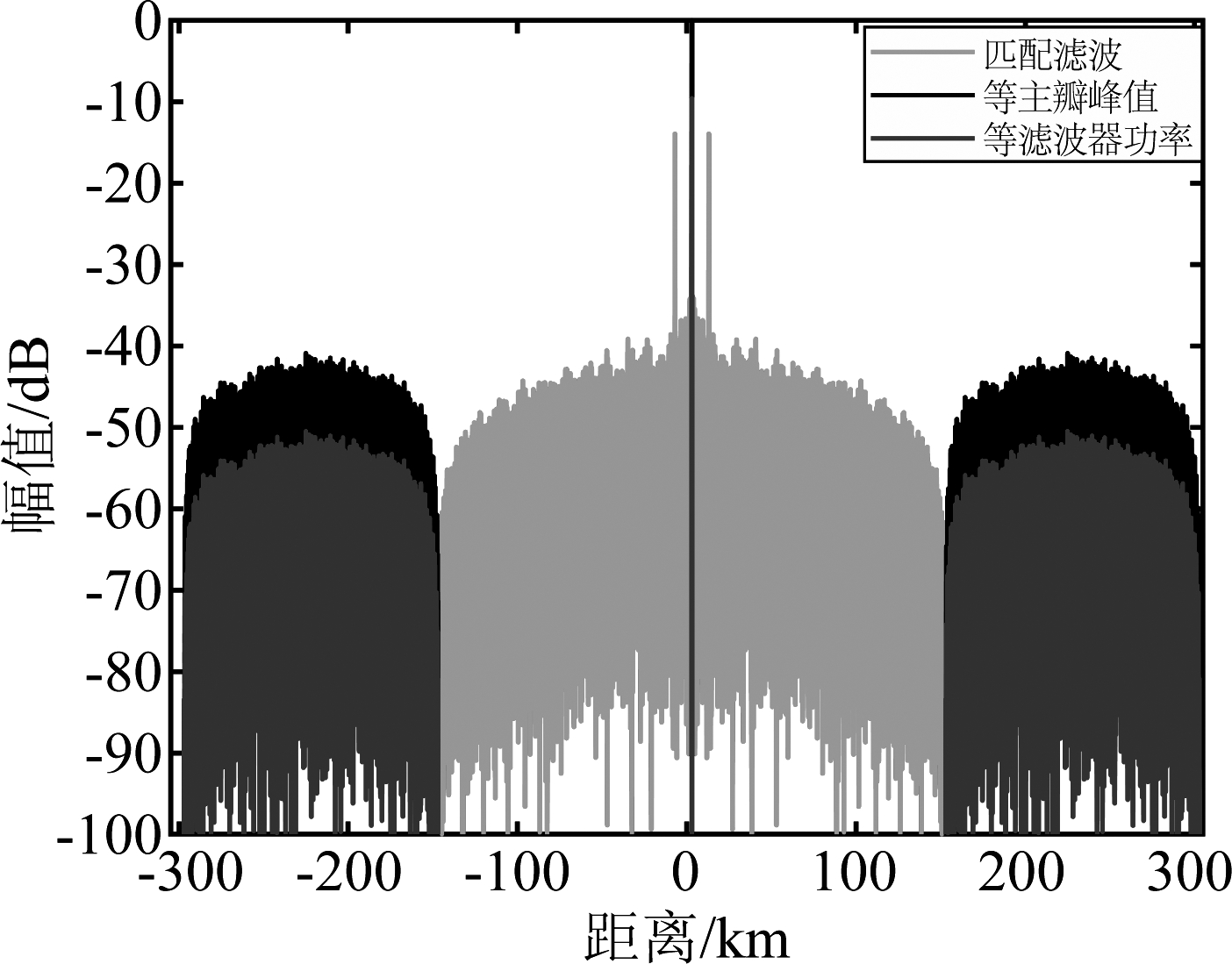
图10 不同条件下失配滤波与匹配滤波的对比
Fig.10 The comparison of matched filter and mismatched filter under different conditions
因此,在雷达观测窗口内,与匹配滤波相比,失配处理会引入信噪比损失。然而,这种损失本质上是雷达观测窗口内的旁瓣能量损失,与目标的峰值、噪底无关。因此,失配处理损失是有害的旁瓣能量,并没有损失目标能量,也没有抬高噪底。
综上所述,本文提出的失配处理算法不仅能获得理想的点扩展函数形状,还能够不损失目标的能量噪声比,可在实现高速无线通信的同时,满足高精度雷达探测要求。
5 结论
随着应用需求的不断增长,通信、探测等设备对频谱资源的需求也日益迫切,各系统对频谱资源的竞争也日益剧烈,给现有的频谱分配与优化方案带来了巨大的挑战。在此背景下,国内外学者提出了通过一体化共享信号实现雷达、通信对频谱资源的共享利用。然而,依据传统的匹配滤波理论可知,雷达对信道信息的探测与通信对信源信息的探测是相互矛盾的。具体而言,周期性的通信导频、同步和循环前缀信号势必会在雷达匹配滤波的点扩展函数中产生伪峰。高随机的通信信息也会抬高点扩展函数旁瓣。鉴于此,本文提出利用失配滤波将旁瓣和伪峰外推至雷达观测窗口外的处理算法,可有效突破传统匹配滤波理论引入的约束。依据理论分析和仿真实验可知,失配处理不仅能去除通信信号脉压伪峰引入的虚假目标,还能检测被通信信号脉压旁瓣淹没的小目标,在不损失目标的能量噪声比的条件下,实现OFDM雷达通信一体化共享信号的旁瓣和伪峰抑制。
[1] Feng Z, Fang Z, Wei Z, et al. Joint radar and communication: A survey[J]. in China Communications, Jan. 2020, 17(1): 1-27.
[2] 杨熙, 戎华, 王君可. 雷达-电子战-通信一体化系统雷达侦察作战效能模型研究[J]. 科技信息, 2014(13): 220-221.
Yang Xi, Rong Hua, Wang Junke. Integration of radio-warfare-communication radar reconnaissance system operational effectiveness model research[J]. Science & Technology Information, 2014(13): 220-221.(in Chinese)
[3] Wang J, Liang X D, Chen L Y, et al. First Demonstration of Joint Wireless Communication and High-Resolution SAR Imaging Using Airborne MIMO Radar System[J]. IEEE Trans. Geosci. Remote Sens, Sep. 2019, 57(9): 6619-6632.
[4] 张辉, 曹丽娜. 现代通信原理与技术[M]. 第二版. 西安: 西安电子科技大学出版社, 2008.
Zhang Hui, Cao Lina. Modern Communication Theory and Technology[M]. 2nd edition. Xi’an: Xidian University Press, 2008.(in Chinese)
[5] 张翼. 基于OFDM的雷达通信一体化波形设计[D]. 成都: 电子科技大学, 2018.
Zhang Yi. Design of Radar Communication Integrated Waveform Based on OFDM[D]. Chengdu:University of Electronic Science and Technology of China, 2018.(in Chinese)
[6] Sturm C, Wiesbeck W. Waveform Design and Signal Processing Aspects for Fusion of Wireless Communications and Radar Sensing[J]. in Proceedings of the IEEE, 2011, 99(7): 1236-1259.
[7] 张长青. 5G系统定义的帧结构分析[J]. 邮电设计技术, 2019(6): 42- 46.
Zhang Changqing. Frame Structure Analysis of 5G System Definition[J]. Post and Telecommunications Design Technology, 2019(6): 42- 46.(in Chinese)
[8] 林海生. OFDM信道参数估计与自适应导频图案的研究[D]. 广州: 华南理工大学, 2014.
Lin Haisheng. Research on Parameter Estimation and Adaptive Pilot Pattern in OFDM Channel[D]. Guangzhou:South China University of Technology, 2014.(in Chinese)
[9] 林茂庸, 柯有安. 雷达信号理论[M]. 北京: 国防工业出版社, 1984.
Lin Maoyong, Ke Youan. Radar signal Theory[M]. Beijing: National Defense Industry Press, 1984.(in Chinese)
[10] 刘永军. 基于OFDM的雷达通信一体化设计方法研究[D]. 西安: 西安电子科技大学, 2019.
Liu Yongjun. Study on Integrated Radar and Communications Design Method Based on OFDM[D]. Xi’an:Xidian University, 2019.(in Chinese)
[11] Rossler, Carl W. Adaptive Radar with Application to Joint Communication and Synthetic Aperture Radar (CoSAR)[J]. Dissertations & Theses Gradworks, 2013.
[12] Iliev M, Bedzhev B, Bedzheva M, et al. An Algorithm for Synthesis of Mismatched Filters for Processing of Aperiodic Phase Manipulated Signals[C]∥2019 16th Conference on Electrical Machines, Drives and Power Systems (ELMA), Varna, Bulgaria, 2019.
[13] Bedzhev, Borislav, Velikova, et al. Analysis of The Conditions for Synthesis of Efficient Side-lobes Suppression Filters for Phase Manipulated Signals[J]. Journal Scientific & Applied Research, 2014.
[14] Tsankov T, Trifonov T, Staneva L. An Algorithm for Synthesis of Phase Manipulated Signals with High Structural Complexity[J]. Journal Scientific & Applied Research, 2013.
[15] Mihail Iliev, Borislav Bedzhev. Necessary Conditions for Synthesis of Side_Lobe Suppression Filters for Phase Manipulated Signals[J]. 2015 IEEE International Black Sea Conference on Communications and Networking (BlackSeaCom), Constanta, 2015: 201-205.
[16] 丁鹭飞, 陈建春. 雷达原理[M]. 第四版. 北京: 电子工业出版社, 2009.
Ding Lufei, Chen Jianchun. Principles of Radar[M]. Fourth edition. Beijing: Electronics Industry Press, 2009.(in Chinese)


