1 引言
随着电子技术的不断发展和军事作战需求的不断提升,作战平台装载的电子设备也不断增多,多功能多任务的电子系统已成为发展趋势。将多种电子系统简单集成虽然可实现该系统,但也会增大作战平台雷达截面积(Radar Cross Section, RCS),引发电磁兼容、调度困难、系统性能下降等问题。因此,对不同功能设备实现更高程度的集成、整合[1-2],构建多功能综合射频系统[3],将是未来多功能电子系统的主要研究方向之一,同时也有助于上述问题的有效解决,缩减系统的体积、重量,降低能源消耗,增强系统的可靠性。目前,雷达和通信系统广泛应用于同一作战平台,是现代电子装备必不可少的功能系统。因此,实现雷达和通信的一体化对推动军事装备的发展具有重要意义。
实现雷达通信一体化的技术有多种,其中基于信号共用的一体化波形设计方式可使系统的集成度最高[4-5]。该方式在发射端只使用一套射频链路,发射一种信号,同时实现通信和探测两种功能。目前,基于信号共用的一体化信号设计主要有两种方式:一种是利用已有的或改进的通信信号实现探测功能;另一种是对已有的雷达波形的参数或波形本身进行通信信息调制,以实现通信功能。针对第一种方案,正交频分复用(orthogonal frequency division multiplexing, OFDM)信号[6- 8]的研究较多。OFDM信号具有高的频谱利用率,抗多径衰落,便于同步和均衡,子载波调制灵活等优点,但应用于雷达探测时存在峰均功率比过高、多普勒敏感等问题。在另一种一体化信号设计方式中,通常将传统的线性调频(linear frequency modulation, LFM)信号作为载波,在一个LFM脉冲内通过不同的调频或调相方式进行通信信息调制[9-16]。LFM信号带宽大、易生成,便于一体化信号设计,是一种较为理想的一体化信号载体。
基于LFM的雷达通信一体化信号的研究主要聚焦于理想情况下雷达和通信性能,如文献[9,13-15]研究了该类一体化信号的模糊函数,文献[10-13]研究了该类一体化信号的误码率和通信速率。在一体化系统实现通信功能时,会遇到频谱展宽、通信能量降低、通信速率受限等问题,其中同步是通信功能实现所需解决的关键问题之一。源于传统通信系统的设计方案,目前相关研究主要考虑在一体化信号中添加额外设计的相关性较好的同步前导信号,用以实现时间同步[14]。由于LFM信号具有良好的自相关性质,可直接将未经调制的LFM信号作为同步前导信号,在接收端通过匹配滤波或脉冲压缩获取信号的时间同步信息[17]。在文献[18]中,OFDM通信系统的发送端将LFM构成的同步信号叠加在数据信号上作为发射信号,接收端对信号进行分数阶傅里叶变换(fractional Fourier transform, FRFT),并在分数阶傅里叶域中搜索变换结果的峰值,利用峰值的位置信息实现时间和载波的联合同步。文献[19-20]也采用了类似的同步方法。在基于LFM的雷达通信一体化系统中,可在一体化信号前加入未调制的LFM载波作为同步前导单元,接收端通过匹配滤波以实现同步[21]。这种在一体化信号前面添加同步前导信号的方案存在着以下问题:若同步信号过长,则会大幅损失通信数据率;若同步信号过短,将会因相关检测时积累能量较小而造成信号漏检。此外,当设计的同步信号不适合雷达探测时,无疑将进一步降低一体化系统的集成度。
针对上述问题,结合LFM信号良好的自相关性质和探测性能,本文设计了一种同时包含正负斜率的LFM雷达通信一体化信号,通信信息通过多阶相移键控(multiple phase shift keying, MPSK)调制加载在LFM载波之上。基于所设计的LFM-MPSK一体化信号,提出了一种基于Costas环结构的时频同步方案,通过Costas环消除调制符号后,利用上下调频两种载波实现时间和载波的联合同步。理论分析和仿真结果表明,通过改变LFM-MPSK一体化信号的调制参数,所提时频联合同步方案在不额外占用信号的时间和带宽情况下,能够高效实现一体化信号的时频同步,完成一体化系统的通信功能。
2 LFM-MPSK一体化信号模型
为实现时频联合同步,所设计的一体化信号需在同一周期同一频带内包含两种不同时频关系的LFM载波[22],可表达为
st(t)=sLFMU-MPSK(t)+sLFMD(t)
(1)
其中sLFMU(t)和sLFMD(t)分别表示正、负调频斜率的LFM载波。在正调频斜率的LFM载波上,采用MPSK调制加载通信信息,相应信号为sLFMU-MPSK(t)。 文献[22]中虽采用同样的一体化信号设计方案,但其下调频部分主要用于雷达探测,且未涉及通信功能具体实现步骤。本文利用下调频信号辅助解决通信中的同步问题。
正负调频斜率的LFM载波分别表示为
(2)
(3)
其中AU、AD为信号幅度, f0为基带起始频率,μ为调频斜率,T为一个周期LFM信号的持续时间。矩形窗函数rect(t)为
(4)
加载通信信息的一体化信号sLFMU-MPSK(t)为
sLFMU-MPSK(t)=sLFMU(t)exp(jθ(t))
(5)
其中θ(t)为调制相角,对于MPSK,式(5)可写为
(6)
其中N为时间T内的通信调制符号数目,M为调制阶数,di∈{0,1,…,M-1}为符号数据,Ts为符号时宽,则T=NTs。
所设计的LFM-MPSK一体化信号表现出以下三点特征:
1)相比于以单个LFM周期作为一个通信码元的一体化信号设计方案,LFM-MPSK一体化信号中通信信息改变的是LFM信号的附加相位,在硬件条件允许的情况下(一体化信号的频谱扩展),其具有更高的通信速率。
2)sLFMU-MPSK(t)是一个恒包络信号,但正负调频信号合在一起的一体化信号st(t)并非恒包络。由于只有两个载波,LFM-MPSK一体化信号的峰均功率比小于2,在通过功率放大器时也不易产生畸变。
3)所设计的LFM-MPSK一体化信号中sLFMD(t)主要用于辅助通信同步,sLFMU-MPSK(t)则用于通信信息传输,这两部分信号皆适宜于雷达探测。而无论是雷达探测威力,还是通信误码率和同步概率,都与信号的信噪比直接相关。因此,为权衡雷达和通信两方面的性能,不同的信号周期中两部分信号的幅度AU、AD可变,根据需求可合理设计一体化信号的发射时序,如图1所示。

图1 所设计一体化信号的发射时序
Fig.1 The transmission timing of designed integrated signal
图1中,通信初始阶段,AD≠0,即加入用于辅助时频同步的下调频载波信号,此时上调频部分可加载调制的系统信息,用于辅助后续的信息解调。由于系统信息的数据率不高,该阶段可采用低阶相移键控调制,如BPSK调制。在发射通信数据主体阶段,此时已获得同步信息,该阶段无需进行额外的同步步骤,故可设置AD=0,相应的信息调制方式可采用高阶相移键控调制。这两个阶段在时序上是交替进行的,可根据应用需求设计合理的通信协议,包括两阶段的持续时间及周期数、每一阶段信号的强度及调制数据个数等。
3 时频联合同步
雷达通信一体化系统的接收端中频信号为
sr(t)=Arst(t-τ)exp(j 2πfd(t-τ))+n(t)
(7)
其中Ar为接收信号幅度,n(t)为高斯白噪声,τ为信号发射端到接收端的延时, fd为多普勒频移,其产生原因包括发射端与接收端之间的晶振频率偏差、平台相对运动。通信同步过程需要利用已知信息和接收信号,估计信号到达时延τ和载波频偏fd,并根据估计值对接收信号进行补偿,以完成解调过程,实现通信功能。
由于时延及载波频偏直接影响接收信号的相位,鉴于传统的Costas环(也称同相正交环)具有载波跟踪的功能,本文根据LFM-MPSK一体化信号的特征,设计了基于LFM载波的Costas环,用于消除调制信息的影响,实时提取一体化信号载波,便于同步参数估计。所设计的Costas环与传统通信系统中Costas环有两个不同点。其一,所采用参考载波与所设计的一体化信号相关,即需要上下调频两类LFM信号对接收信号进行混频。其二,输出信号包含的信息不同,对于LFM信号,混频步骤将使信号时延信息包含于差频信号中,因此所设计的Costas环的输出信号中同时包含时延和载波频偏信息,需进行后续处理提取这两类信息。
当调制模式为BPSK(binary phase shift keying)时,所设计的Costas环如图2所示。在图2中,sri(t)、srq(t)分别是sr(t)的实部和虚部,波形控制生成器输出的参考信号与一体化信号的载波具有相同的形式,两类参考信号分别为
(8)
其中th为参考信号起始时间,Th为参考信号持续时间,通过改变th与Th可以改变参考信号窗的位置与时长。
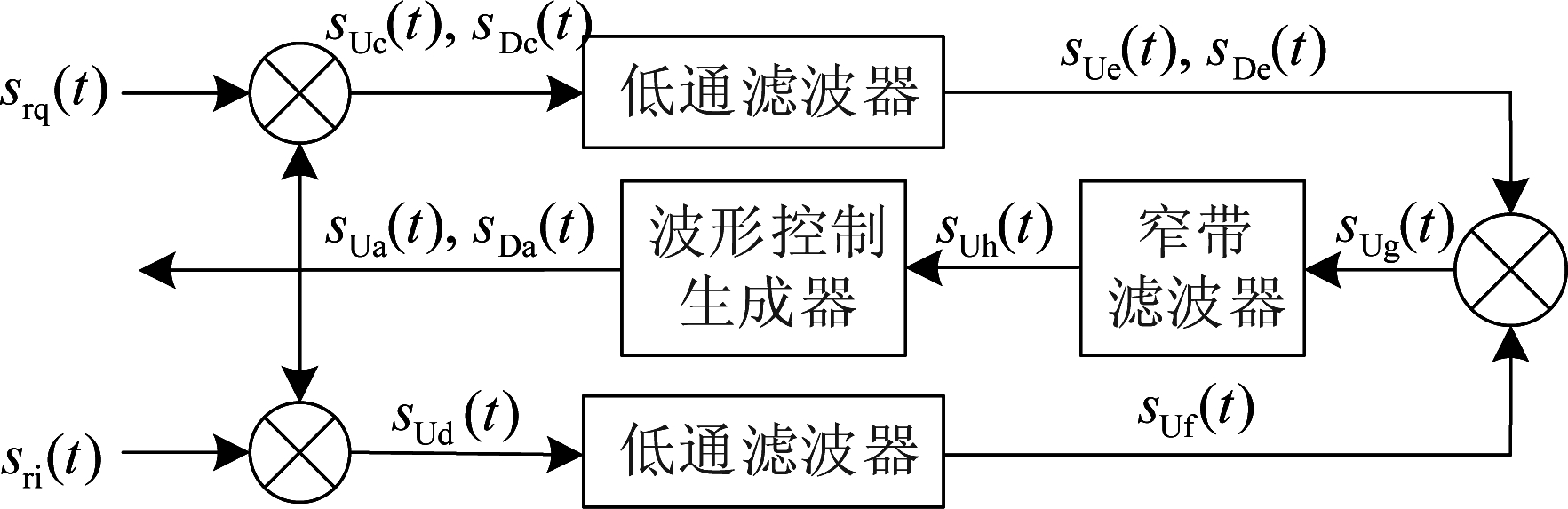
图2 基于LFM-BPSK一体化信号的Costas环结构
Fig.2 The structure of Costas loop based on the LFM-BPSK integrated signal
当参考信号为sUa时,上下两路混频信号分别为
sUc(t)=![]()
![]()
sUd(t)=![]()
![]()
(9)
其中φi是与时间无关的相位量,AUr和ADr分别为接收信号上、下调频部分的信号幅度, fm为中频信号的起始频率。
低通滤波后,将这两路信号混频,可得
(10)
其中![]() 为多个噪声项之和。
为多个噪声项之和。
当参考信号为sDa(t)时,经推导可得
(11)
其中![]()
在利用Costas环实时跟踪获得上下调频载波差频信号后,分别对sUg(t)以及sDe(t)进行快速傅里叶变换(fast Fourier transform, FFT),可估计出信号频率成分为
(12)
求解方程组(12)即可估计出接收信号的到达时延![]() 和载波频偏
和载波频偏![]() 需要注意的是,sUg(t)是针对接收信号中上调频载波的处理结果,其中nUsum(t)包含了来自下调频载波的干扰。同理,下调频载波的处理结果sDe(t)的噪声项nDsum(t)也会包含来自上调频载波的干扰。
需要注意的是,sUg(t)是针对接收信号中上调频载波的处理结果,其中nUsum(t)包含了来自下调频载波的干扰。同理,下调频载波的处理结果sDe(t)的噪声项nDsum(t)也会包含来自上调频载波的干扰。
综上,LFM-MPSK雷达通信一体化系统的通信同步流程如图3所示。需要说明的是,在所设计的Costas环中,参考信号起始时间th及持续时间Th可合理设计,它直接关系到式(12)中频率值及其能量值。若参考信号窗过短,则sUg(t)及sDe(t)中单频信号的能量值过低,影响峰值检测;若参考信号窗过长,发射信号为连续波时,则可能混叠其他频率信号。一般地,可设置Th=T/2。另一方面,可设置不同的th(相当于参考信号滑窗)以获得不同的频率值fUg和fDe,利用拟合或者平均的方法处理这些频率值,可进一步提高同步参数估计精度。
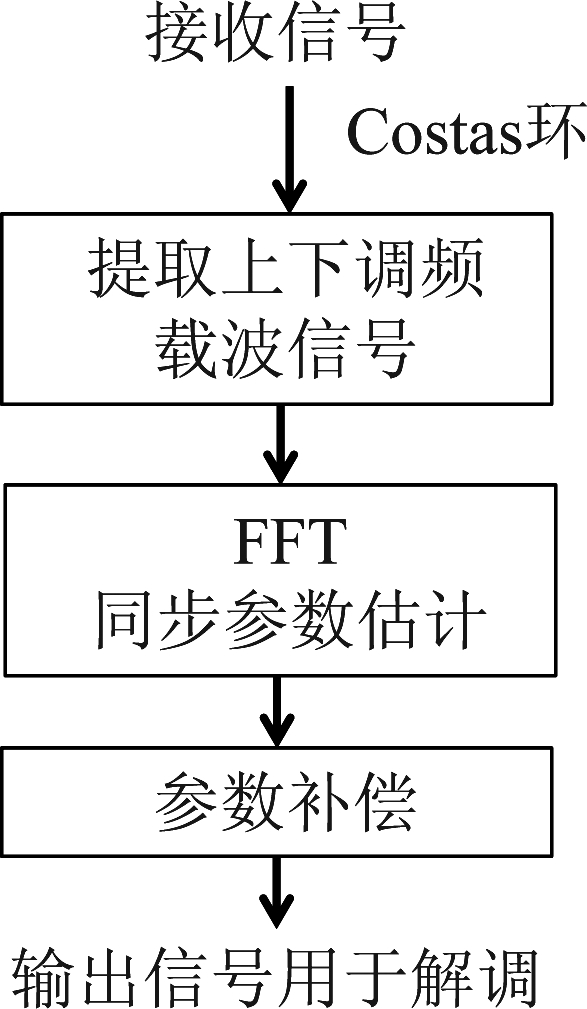
图3 LFM-MPSK一体化信号的通信同步流程
Fig.3 The synchronization procedure of the LFM-BPSK integrated signal
当调制阶数出现变化时,需要调整同步处理流程中的Costas环。当调制模式为QPSK (quadrature phase shift keying)时,所设计的Costas环结构如图4所示。其中sUa(t)、sDa(t)与式(8)一致,sUb(t)为
sUb(t)=sin(2πf0t+πμt2+φUa(t,th)+π/4)
(13)
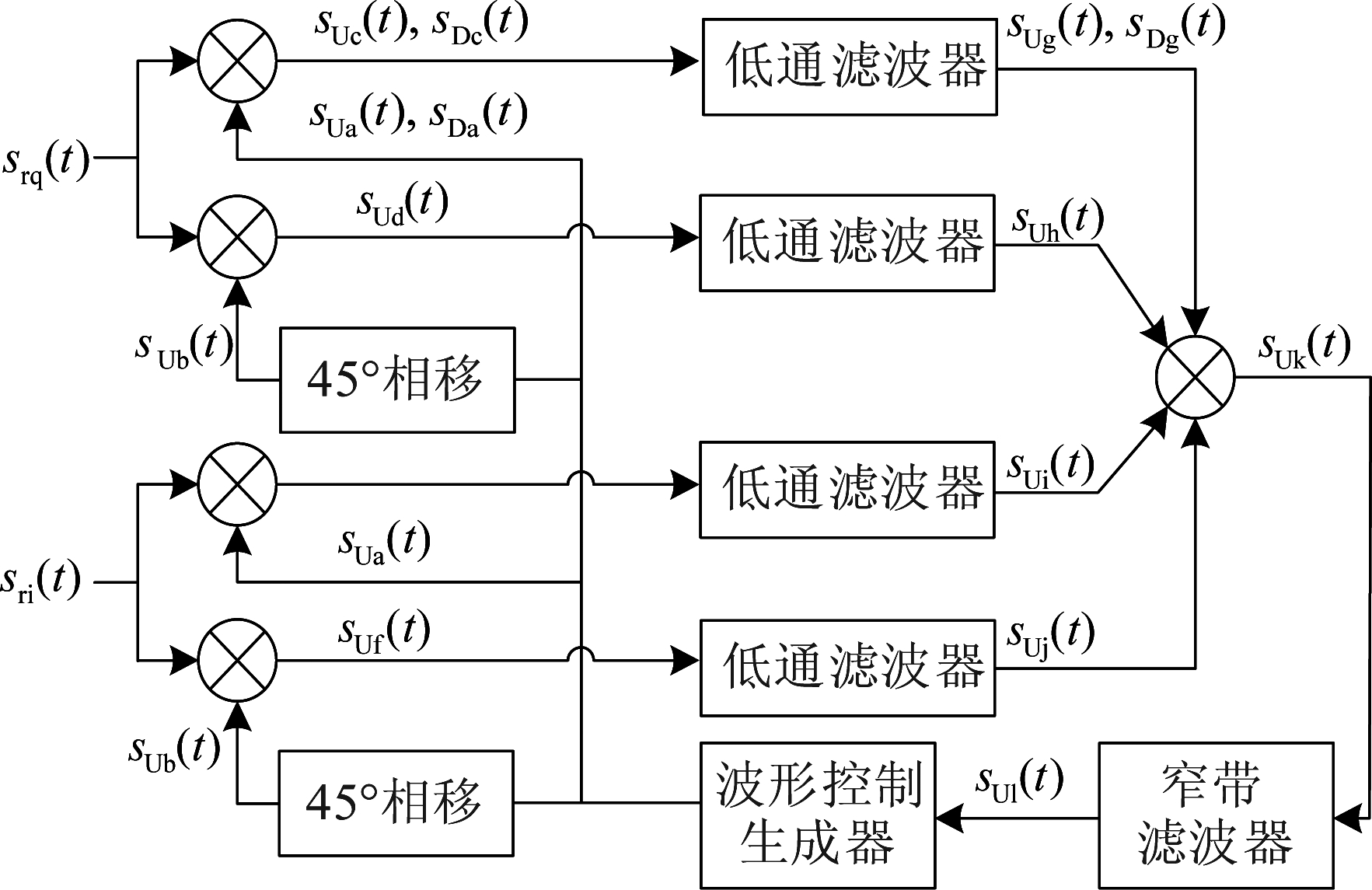
图4 基于LFM-QPSK一体化信号的Costas环结构
Fig.4 The structure of Costas loop based on the LFM-QPSK integrated signal
当波形控制生成器输出为sUa(t)时,最终输出结果为
(14)
其中![]()
当波形控制器输出为sDa(t)时,图4中第一路输出结果为
(15)
其中![]()
对输出信号sUk(t)、sDg(t)进行FFT,可得频率成分为
(16)
求解方程组(16)可估计出接收信号的到达时延![]() 和载波频偏
和载波频偏![]()
当调制模式为8PSK时,所设计的Costas环结构如图5所示,其推导过程和处理方法和上述类似。
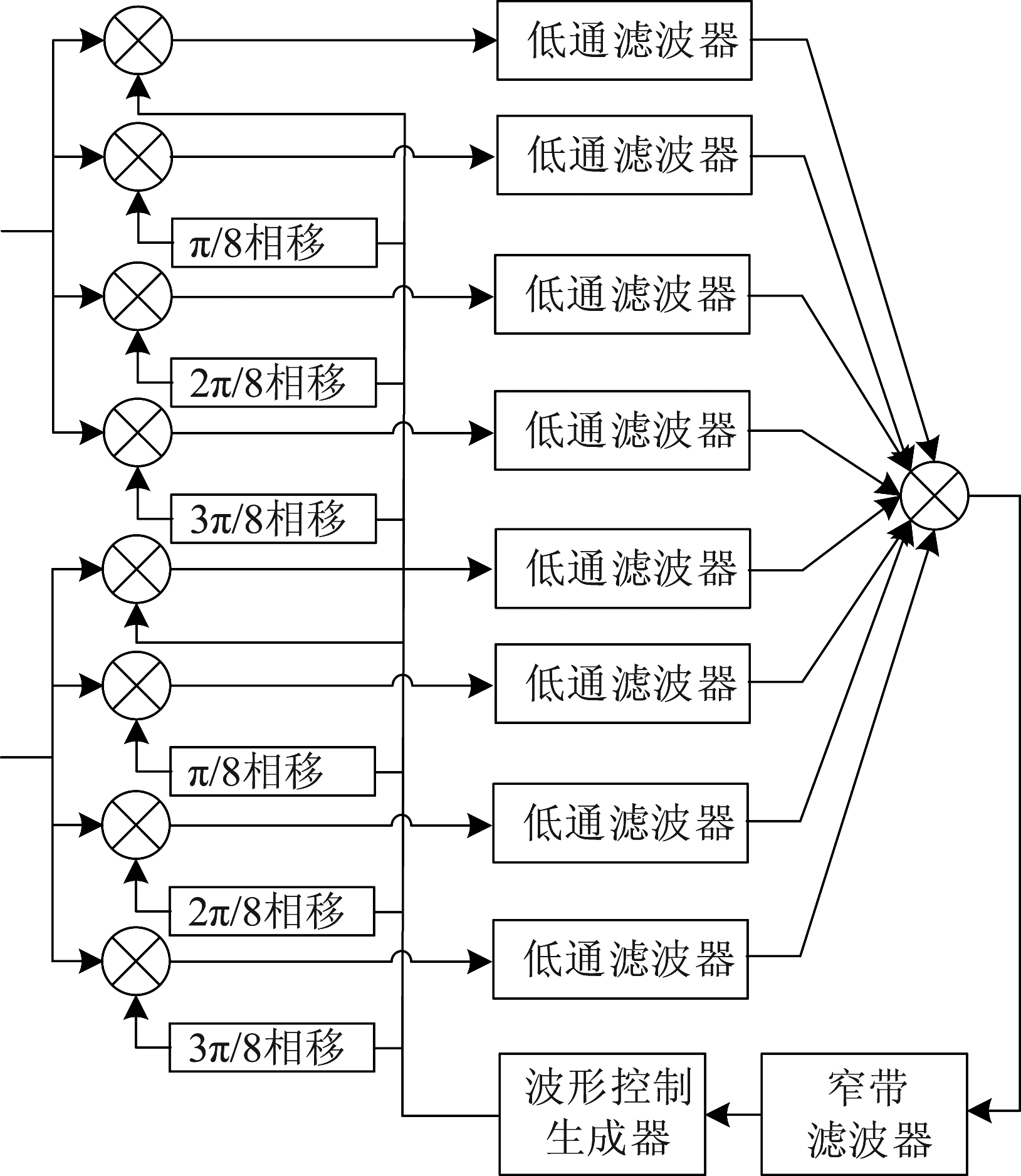
图5 基于LFM- 8PSK一体化信号的Costas环结构
Fig.5 The structure of Costas loop based on the LFM- 8PSK integrated signal
比较上述三种调制下的Costas环结构,可知符号调制阶数越高,同步处理流程就越复杂,运算开销越大。此外,对于式(10)以及(14)中上调频信号输出中的噪声集合项nUsum(t),当调制阶数越高时,同步过程中信号的混频次数越多,导致nUsum(t)所包含的噪声项增加。因此对于高阶符号调制而言,上调频部分的混频输出信噪比会降低,导致同步性能有所下降。
比较图2、图4及图5,可知调制阶数越高,Costas环的结构越复杂。因此,基于Costas环的时频联合同步技术的计算复杂度与调制阶数成正比。对于上路混频部分,共需进行M次混频和低通滤波;对于下路混频部分,需进行1次混频和低通滤波。然后将上路混频部分所得的M路信号相乘,相当于进行了M-1次混频。而每次混频需进行Nh=fsTh次乘法,其中fs为采样率;每次低通滤波需进行NhNFIR次乘法,其中NFIR为低通滤波器的阶数。综合可得,所提同步技术的计算复杂度为Ο(Nh(2M+MNFIR+NFIR))。
4 仿真结果
4.1 同步结果
仿真参数设定如表1所示。
表1 仿真参数
Tab.1 Simulation parameters

参数参数值采样率/MHz100LFM载波带宽/MHz50LFM周期/ms1符号速率/sps106信号时延/ms0.1信号频偏/kHz6参考信号起始时间/ms0.2参考信号时长/ms0.5
首先给出同步处理结果,分析实现同步的可行性。发射信号包含两种载波,以整体信号功率和噪声功率之比作为信噪比(signal-to-noise ratio, SNR)。当SNR为5 dB,且上下调频载波幅度相等时,FFT输出结果如图6所示。根据设定参数,FFT峰值理论位置分别为M(fd-μτ+μth)=M×5006 kHz和fd+μ(T-Th+τ-th)=20006 kHz,仿真结果中峰值频点和理论相符。仿真结果中,第一列上调频部分对应的峰值频率值随调制阶数的升高而增大,而噪声基底随之抬高。这是因为在上调频部分的处理流程中,混频次数随调制阶数上升而增加,导致频率值变大。而噪声干扰项的功率随混频次数的上升而升高,导致噪声基底抬升。图6中,8PSK调制下FFT峰值被噪声掩盖,而下调频部分对应的第二列结果则没有明显变化,因为下调频部分的处理流程并不受调制信息的影响。
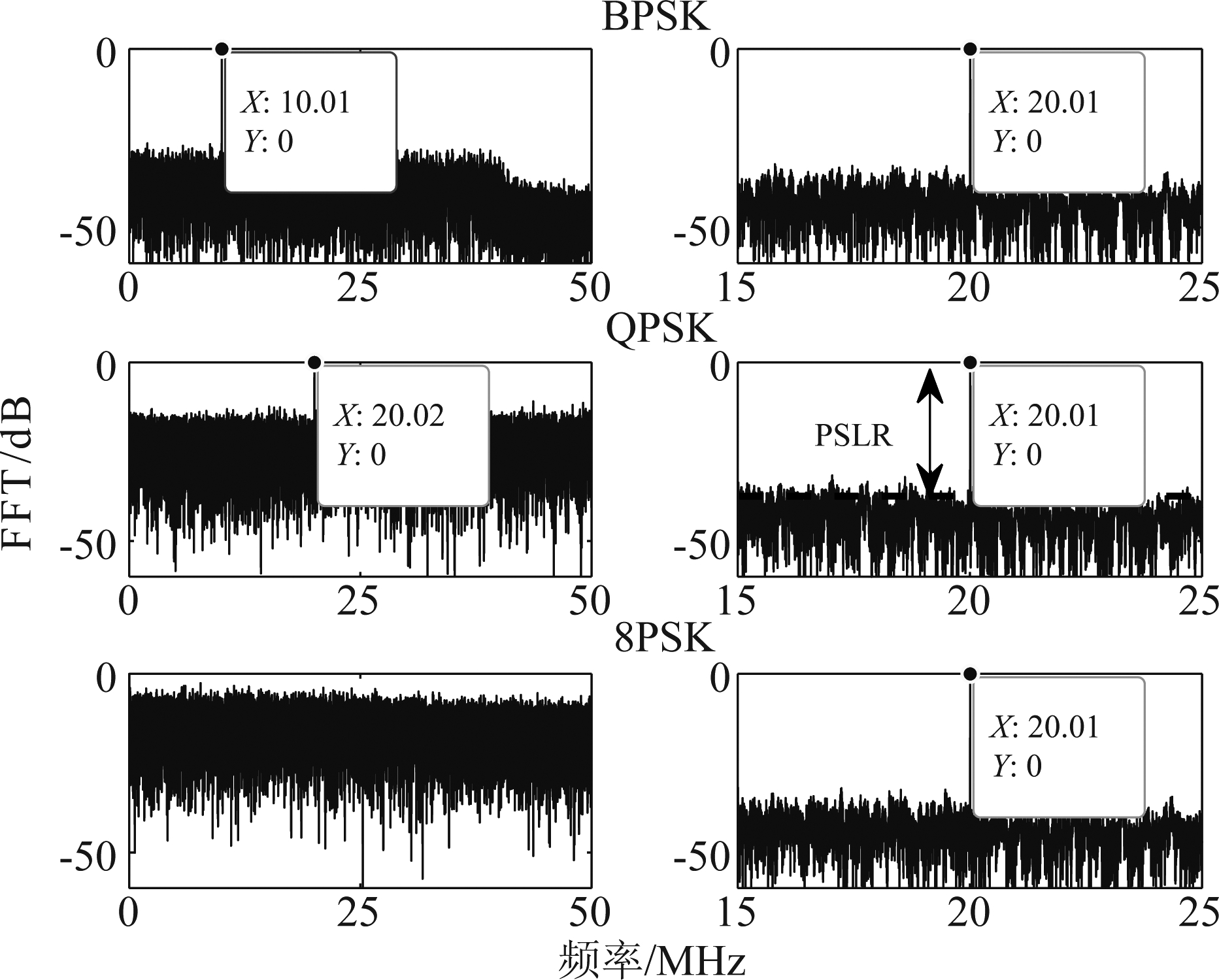
图6 同步处理的FFT输出
Fig.6 The FFT output of synchronization
4.2 同步性能
进一步仿真分析所提同步方案的性能。同步性能的评价指标采用峰值旁瓣比(peak-to-sidelobe ratio, PSLR),定义为主峰值功率与次峰值功率的比值。PSLR值越大,表明FFT峰值越容易被检测,系统同步正确的概率越高。BPSK、QPSK及8PSK三种调制下上下调频载波的同步输出如图7所示。上调频部分的输出PSLR随调制阶数的上升而下降,对于8PSK而言PSLR一直接近于零;下调频部分的输出PSLR则不受调制阶数影响,并且一直高于上调频曲线。
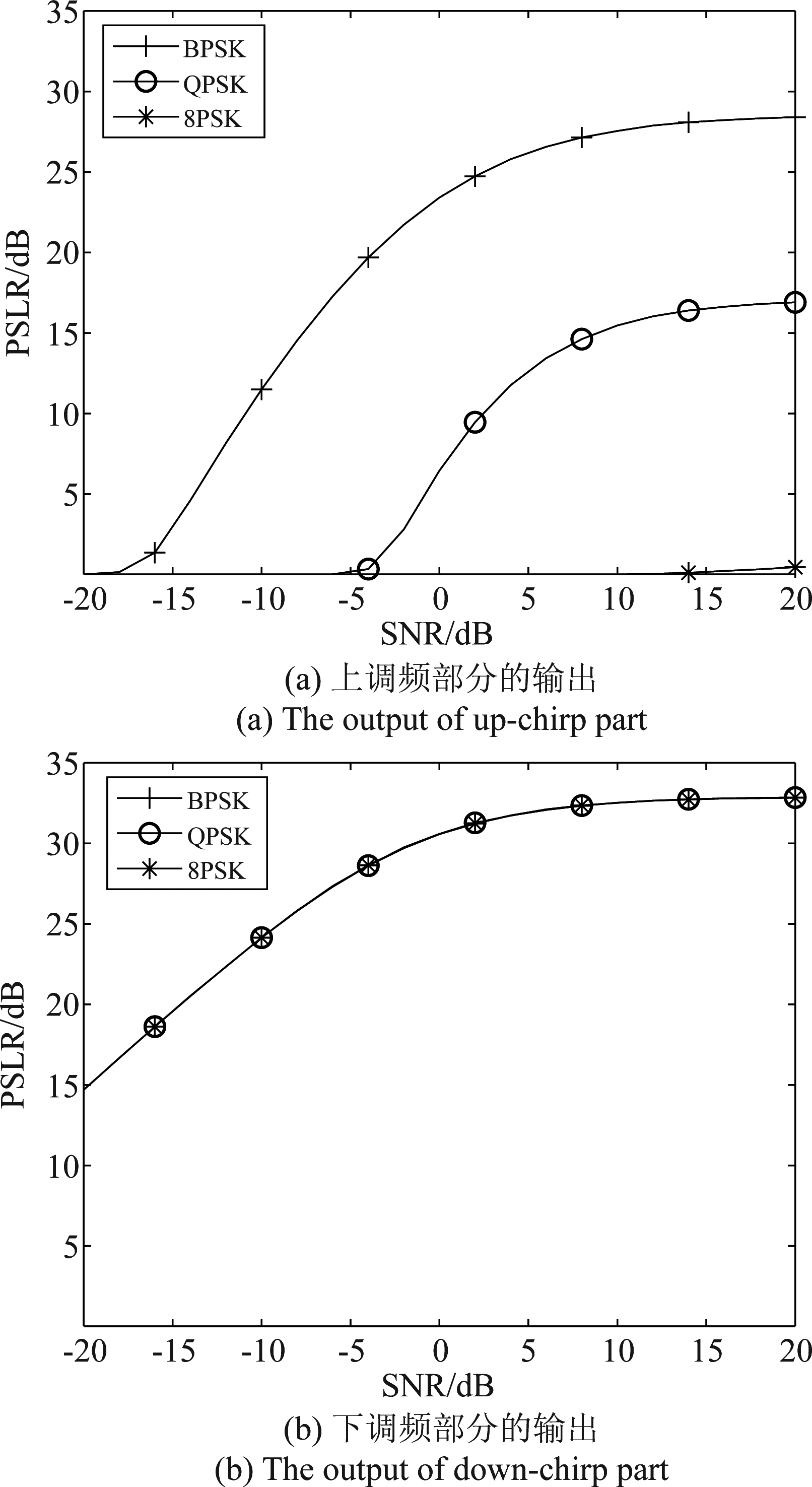
图7 同步输出的PSLR曲线
Fig.7 The PSLR curve of synchronization output
另一方面,当SNR较高时,PSLR几乎保持不变,原因在于同一个LFM周期内,利用上、下调频载波进行时频同步过程中,载波之间存在相互干扰。当噪声功率较小时,相互干扰会更加明显。故综合表现为PSLR无法随SNR的增加而升高。
可以通过调整上下调频载波的功率占比来改善上调频参考信号PSLR较低的情况。以8PSK为例,适当降低发射信号的下调频载波幅度,结果如图8所示。图8中的前三条曲线为上调频部分对应的输出,后三条为下调频部分的输出,且依次对应上下调频载波幅度比为1、5和10。可见调整载波功率占比可有效提升上调频载波输出的PSLR,但下调频载波对应的PSLR则会下降。此外,当SNR接近或小于零时,上调频的输出依然不理想。

图8 不同载波幅度比下PSLR曲线
Fig.8 The PSLR curve with different ratio of carrier amplitude
分析估计时延、载波频偏的均方误差 (mean squared error, MSE),如图9所示。假设FFT输出的峰值位置恰好位于仿真FFT的采样点上,即只考虑FFT输出结果中分辨率1/Th整数倍的误差。设置上下调频载波幅度相等,且只针对BPSK和QPSK调制进行分析。为表明MSE和PSLR的联系,将两种曲线置于同一图中,PSLR1,PSLR2分别对应图7中上下调频输出,图中箭头指向出现误差的位置为失步点。由于时延和载波频偏是一同计算得出的,二者的失步点位置相同。当其中一路输出的PSLR接近零时,必然会导致时延和载波频偏估计产生误差。在设定的载波幅度下,SNR降低时PSLR1会先接近零,使得PSLR1的零点决定了失步点的位置。因此,为提升同步性能,需要升高上调频载波的功率占比,保证PSLR1、PSLR2的零点相近。经分析测试,将上下调频载波的幅度比调整为5∶1可以较为显著地提升同步性能。
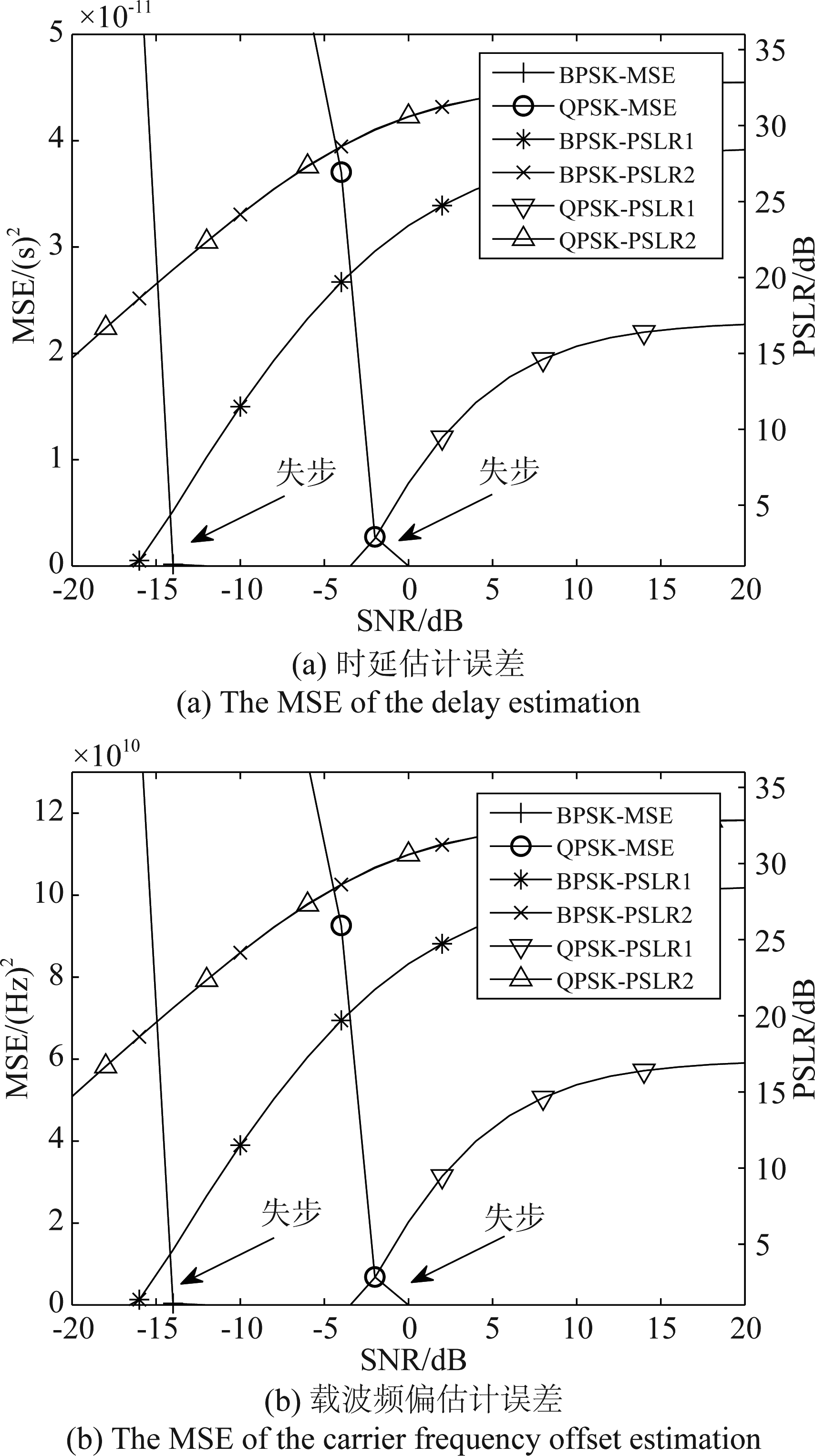
图9 同步参数估计的MSE曲线
Fig.9 The MSE of the synchronization parameter estimation
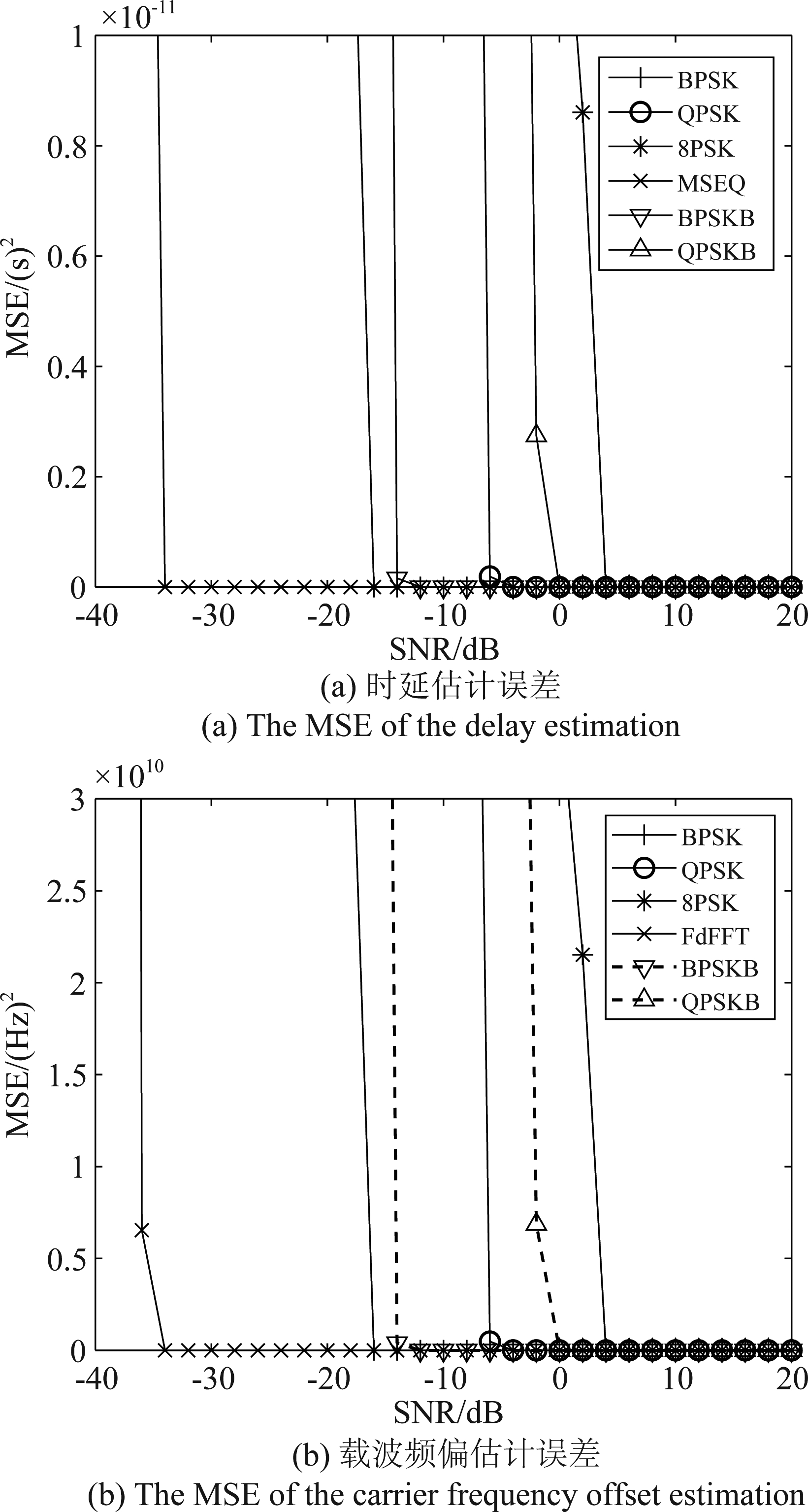
图10 载波幅度比5∶1时的MSE曲线
Fig.10 The MSE with 5 to 1 ratio of carrier amplitude
比较不同上下调频载波的幅度比的同步性能,结果如图10所示。图中虚线为调整载波幅度比之前的MSE曲线,实线为调整后的MSE曲线,对比可见同步性能有一定的提升。此外,时延估计误差图中列出了只存在时延时,用同步前导序列实现时间同步的误差曲线MSEQ。具体方法是将一段已知的m序列调制信号作为同步前导信号,接收端使用参考信号与接收信号进行自相关,仿真设定前导信号时长和带宽与LFM载波的时长和带宽一致。在载波频偏估计误差图中列出了只存在载波频偏时,用插入导频法实现载波频率同步的误差曲线FdFFT。具体方法是发射端在信号前额外添加一段时长和LFM周期相等的恒频载波,并在接收端通过FFT计算载波频偏。相比传统通信中的同步技术,所提时频联合同步方法的性能略差,原因在于利用Costas环跟踪载波信息时,调制信息相关项与噪声相混叠,进而抬高噪声基底。然而,所提同步方案优势在于可以同时实现时间和载波同步,并且无需额外发射前导序列或导频,这样保证了信息传输速率,因此部分同步性能的损失是可承受的。
4.3 通信解调性能
实现同步的目的是解调数据,进一步仿真分析通信误码率。针对LFM-MPSK一体化信号,其具体解调流程如图11所示。
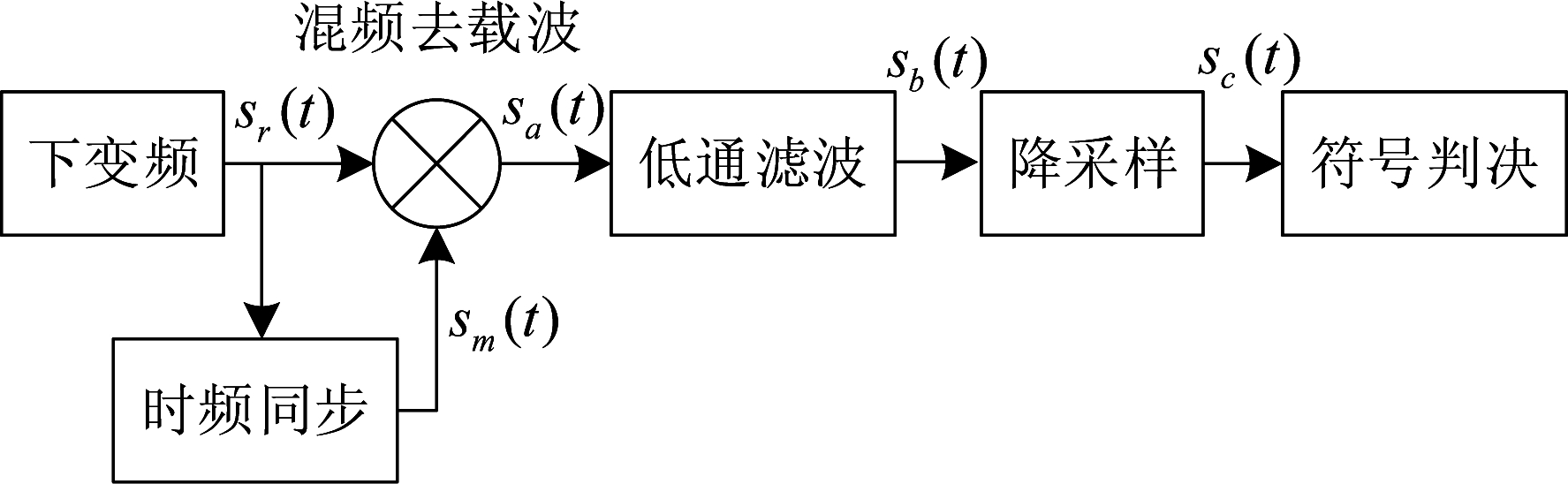
图11 LFM-MPSK一体化信号的解调流程
Fig.11 The demodulation procedure of the LFM-MPSK integrated signal
需要注意的是,应用于此解调流程时,发射端需要对下调频载波进行改动,具体原因如图12所示。通过时频图可以看出,sa(t)包含两种信号成分:基带数据信号sMPSK(t)、下调频载波和上调频载波混频后的LFM信号sD(t)。经过低通滤波后,sb(t)在保留基带数据信号的同时,在箭头指向的虚线框内还残留了sD(t)的部分信号,这会干扰数据解调。因此,发射端应对残留信号的这段时间区域内的下调频载波进行消除,以避免对通信解调造成干扰。如图12(b)所示,根据数据信号占据的带宽,这段时间区间应为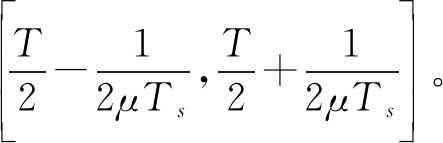
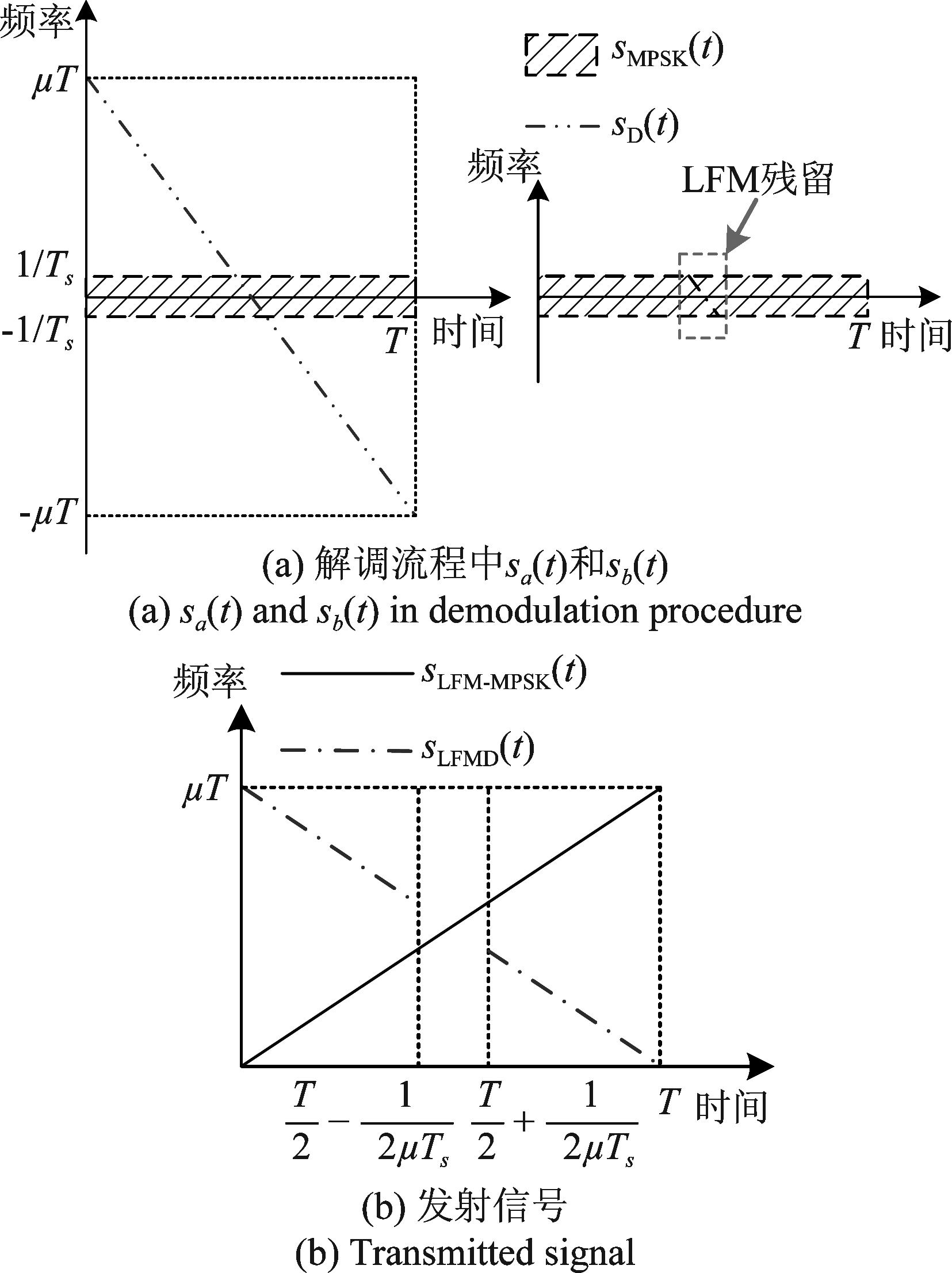
图12 信号时频示意图
Fig.12 The time-frequency diagram of signal
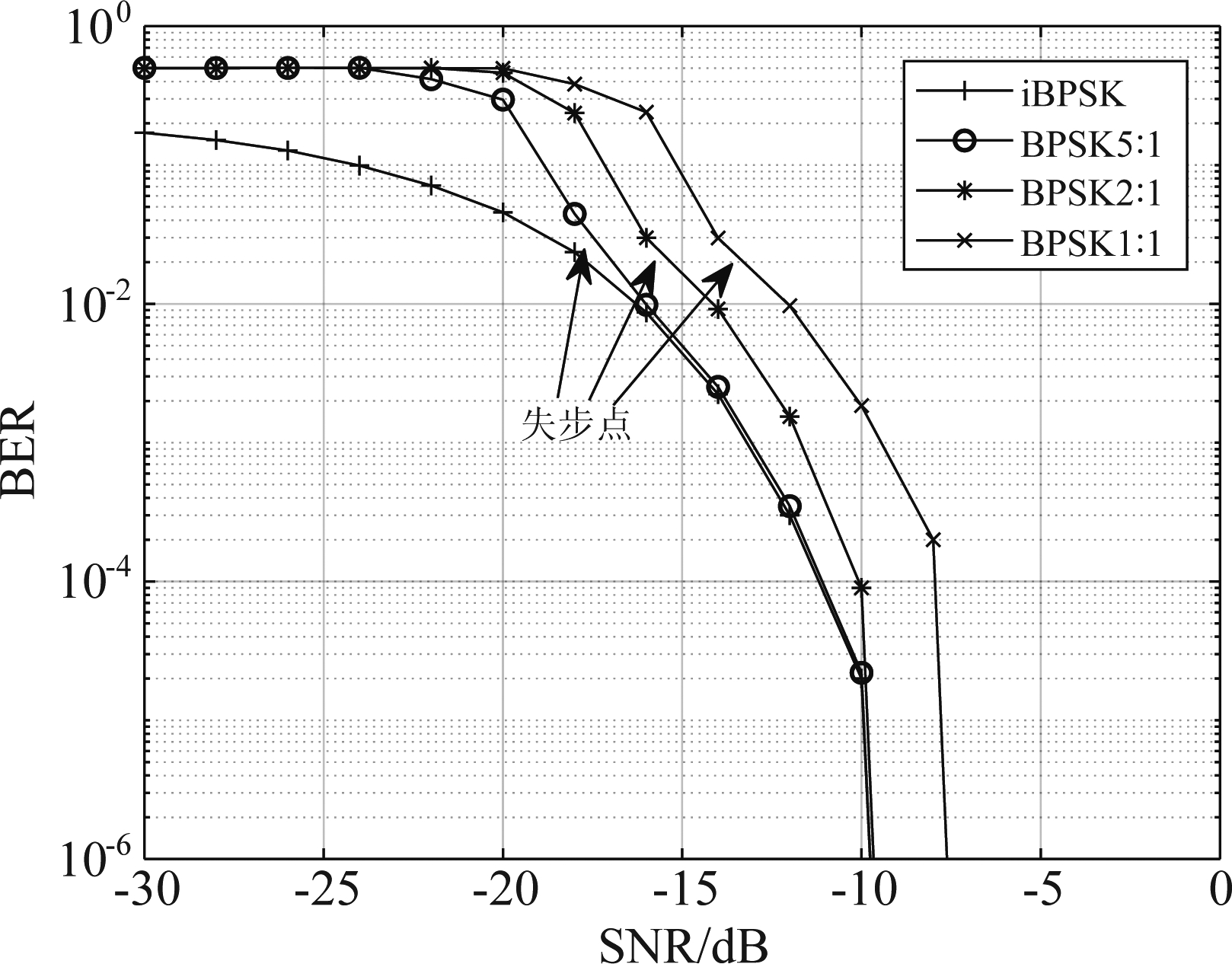
图13 解调误码率随SNR变化曲线
Fig.13 The BER changing with SNR
将发射信号上下调频载波幅度分别设定为5∶1,2∶1以及1∶1,BPSK调制下误码率随信噪比的变化曲线如图13所示。图中的第一条曲线为已经实现同步后不包含副载波的单一LFM-BPSK信号解调误码率,对应的SNR为该信号和噪声功率比;后三条曲线为采用所提方案进行同步再进行解调的误码率,对应的SNR为整体信号和噪声功率比。对比第一条曲线和传统BPSK通信系统的误码率性能曲线,可知LFM-MPSK通信系统的误码率性能更优。LFM-MPSK通信系统可认为是一个扩频通信系统,经图11中混频去载波和低通滤波后,MPSK信号带内噪声能量降低,存在扩频处理增益[23],因此,LFM-MPSK通信系统误码率性能更优。对比后三条曲线,同步-解调曲线在箭头指向的位置出现明显的抬升,说明随SNR降低,信号已经失步。随着信息载波功率占比的提升,失步点对应的SNR有所下降,并且同步区间内的BER更接近理想BER曲线。因此,适当提升信息载波功率占比不仅能增强同步性能,还能保证更理想的误码率性能。
4.4 LFM-MPSK一体化信号的雷达性能
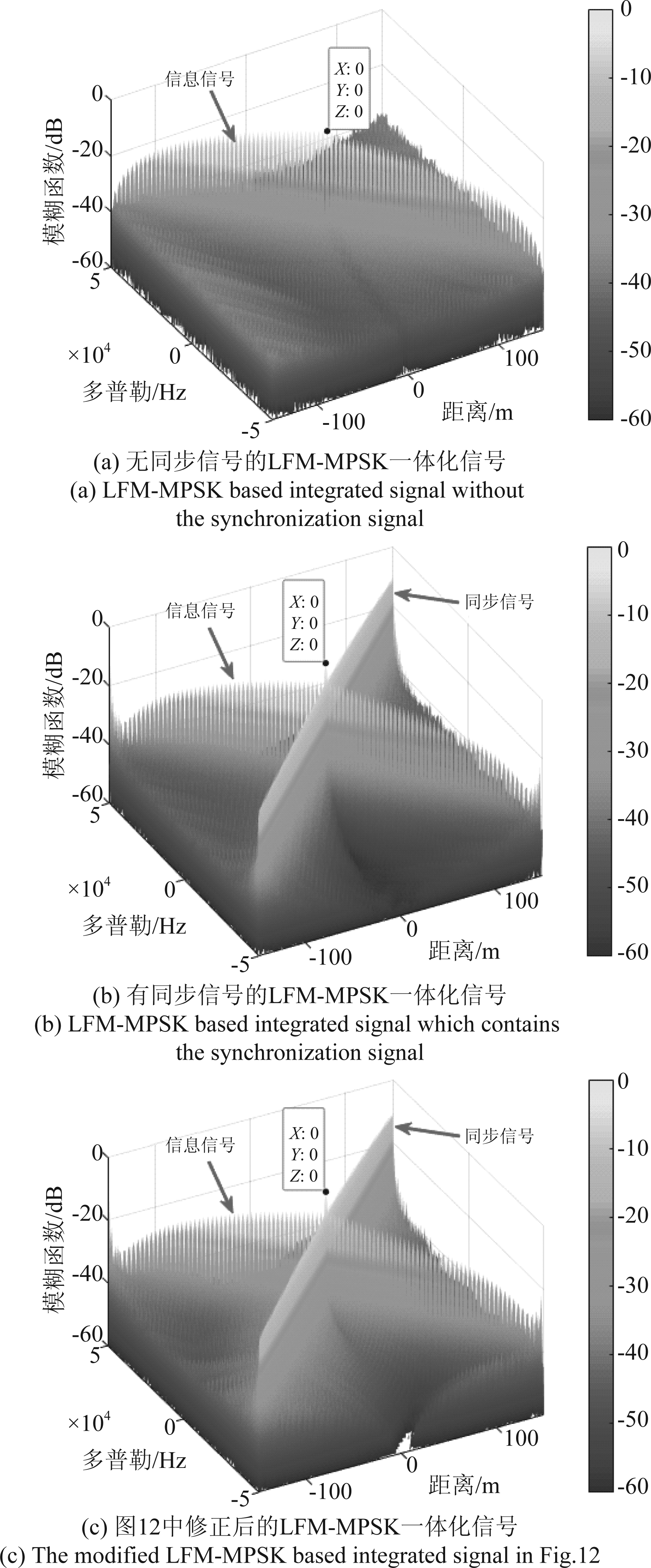
图14 一体化信号模糊函数图
Fig.14 The ambiguity function of the integrated signal
最后验证所设计的一体化信号的雷达性能,以表明满足一体化系统的功能需求。比较三种一体化信号的模糊函数:无同步信号的LFM-MPSK、含有同步信号的LFM-MPSK及图12(b)中修正同步信号后的LFM-MPSK,设定上下调频载波幅度比为1∶1,结果如图14所示。图12(b)中去除了部分下调频载波,其对信号的模糊函数影响不大。此外,发射信号的上调频信息信号和下调频同步信号会形成不同的模糊函数主峰。当调制数据带宽远小于LFM带宽时,信息信号仍具备LFM模糊函数的特性,即主峰在一定范围内为三角峰。具体范围在距离维度上由数据符号宽度决定,当距离超出Tsc/2=150 m时,由于符号之间不相关,模糊函数不存在距离多普勒耦合。总之,这三种信号都能满足雷达探测需求,差异在于多普勒容忍范围不同,故图1中所设计的一体化信号也能实现雷达功能。
5 结论
本文基于LFM-MPSK雷达通信一体化信号提出了一种基于Costas环的时频联合同步技术。首先给出了一种基于LFM-MPSK的一体化信号设计方案,然后根据所设计一体化信号的特征,设计了一种基于LFM信号的Costas环结构。分析了该Costas环的输出信号与通信时延、载波频偏之间的理论关系,提出相应的同步参数估计方案。仿真结果表明,所提时频联合同步技术在不影响通信频谱效率和保障雷达性能的前提下,可有效地完成一体化系统的通信功能。此外,仿真分析表明,通过适当提升信息载波功率占比可提升同步性能,并使通信误码率接近理想情况。因此,所设计的LFM-MPSK一体化信号能够同时实现雷达探测和信息传输,是一种可行的雷达通信一体化信号形式。
[1] Tavik G C, Hilterbrick C L, Evins J B, et al. The advanced multifunction RF concept[J]. IEEE Transactions on Microwave Theory and Techniques, 2005, 53(3): 1009-1020.
[2] Russell M E. Future of RF technology and radars[C]∥IEEE Radar Conference. Boston: IEEE, 2007: 11-16.
[3] Van Rossum W L, De Wit J J M, Otten M P G, et al. SMRF architecture concepts[J]. IEEE Aerospace and Electronic Systems Magazine, 2011, 26(5): 12-17.
[4] Xu Cuichun, Chen Tianqi. Conception of "signal sharing" in integrated radar and jammer system and the integrated signal design[C]∥IEEE International Conference on Communications, Circuits and Systems and West Sino Expositions. Chengdu: IEEE, 2002: 502-505.
[5] Piet van G. A communication waveform for radar[C]∥8th International Conference on Communications. Bucharest: IEEE, 2010: 289-292.
[6] Sturm C, Pancera E, Zwick T, et al. A novel approach to OFDM radar processing[C]∥IEEE Radar Conference. Pasadena: IEEE, 2009: 1- 4.
[7] Wang Wenqing, Zheng Zhi, Zhang Shunsheng. OFDM chirp waveform diversity for co-designed radar-communication system[C]∥18th International Radar Symposium. Prague: IEEE, 2017: 1-9.
[8] Wei Cao, Zhu Jiahua, Li Xiaotian, et al. Feasibility of multi-carrier modulation signals as new illuminators of opportunity for passive radar: orthogonal frequency division multiplexing versus filter-bank multi-carrier[J]. IET Radar, Sonar & Navigation, 2016, 10(6): 1080-1087.
[9] Chen Xingbo, Wang Xiaomo, Xu Shanfeng, et al. A novel radar waveform compatible with communication[C]∥International Conference on Computational Problem-Solving, Chengdu: IEEE, 2011: 177-181.
[10] Roberton M, Brown E. Integrated radar and communications based on chirped spread-spectrum techniques[C]∥IEEE MTT-S International Microwave Symposium Digest. Philadelphia: IEEE, 2003: 611- 614.
[11] Werner S, Reinhard F, Andreas H, et al. In-chirp FSK communication between cooperative 77-GHz radar stations integrating variable power distribution between ranging and communication system[J]. International Journal of Microwave and Wireless Technologies, 2016, 8(4-5): 825- 832.
[12] Liu Zhipeng, Chen Xingbo, Wang Xiaomo, et al. Communication analysis of integrated waveform based on LFM and MSK[C]∥IET International Radar Conference. Hangzhou: IET, 2015: 1-5.
[13] Nowak M, Wicks M, Zhang Z, et al. Co-designed radar-communication using linear frequency modulation waveform[J]. IEEE Aerospace and Electronic Systems Magazine, 2016, 31(10): 28-35.
[14] Liu Zhipeng, Zhang Wenkang, Xu Shanfeng. Implementation on the integrated waveform of radar and communication[C]∥International Conference on Communications, Circuits and Systems. Chengdu: IEEE, 2013: 200-204.
[15] Zhang Chaozhu, Chen Qiang. Design of signal-sharing for radar and communication[C]∥International Conference on Mechatronic Sciences, Electric Engineering and Computer. Shengyang: IEEE, 2013: 1250-1253.
[16] Nowak M, Zhang Z, LoMonte L, et al. Mixed-modulated linear frequency modulated radar-communications[J]. IET Radar, Sonar & Navigation, 2017, 11(2): 313-320.
[17] 万磊. Chirp超宽带系统的同步技术研究与实现[D]. 郑州: 解放军信息工程大学, 2010.
Wan Lei. Research on Acquisition technology and Implementation of Chirp-UWB System[D]. Zhengzhou: PLA Information Engineering University, 2010.(in Chinese)
[18] 刘琦. OFDM系统中基于线性调频信号的同步及信道估计与均衡[D]. 上海: 复旦大学, 2008.
Liu Qi. Synchronization, channel estimation and equalization based on LFM signal in OFDM systems[D]. Shanghai: Fudan University, 2008.(in Chinese)
[19] 申勇, 达新宇, 曾武. FRFT-OFDM系统联合同步算法[J]. 中国科学院研究生院学报, 2012, 29(5): 714-719.
Shen Yong, Da Xinyu, Zeng Wu. Joint synchronization algorithm for FRFT-OFDM system[J]. Journal of Graduate University of Chinese Academy of Sciences, 2012, 29(5): 714-719.(in Chinese)
[20] Tang Xun, Sha Xuejun. Joint timing and frequency synchronization for OFDM based on fractional Fourier transform[J]. China Communications, 2010, 7(5): 93-102.
[21] 杨云飞, 杨瑞娟, 古秦弋. CPM-LFM雷达通信一体化共享信号解调处理与仿真[J]. 空军预警学院学报, 2017, 31(4): 243-247.
Yang Yunfei, Yang Ruijuan, Gu Qinyi. The demodulation processing and simulation of CPM-LFM radar communication integrated Shared signal[J]. Journal of Air Force Early Warning Academy, 2017, 31(4): 243-247.(in Chinese)
[22] Roberton M, Brown E R. Integrated radar and communications based on chirped spread-spectrum techniques[C]∥IEEE MTT-S International Microwave Symposium Digest, Philadelphia: IEEE, 2013: 611- 614.
[23] 田日才, 迟永钢. 扩频通信[M]. 第二版. 北京: 清华大学出版社, 2014: 30- 41.
Tian Ricai, Chi Yonggang. Spread spectrum communication[M]. 2nd Ed. Beijing: Tsinghua University Press, 2014: 30- 41.(in Chinese)



