1 引言
由于综合电子一体化系统具有通用化、小型化和多功能化等优点,近年来受到了越来越多研究者的关注[1]。其中,雷达通信一体化系统不仅可以极大地提高系统的作战能力,还能克服传统方式情报传递速度慢、保密性差和误报率高等方面的不足,是多功能一体化电子系统的重要研究方向[2-3]。近年来,许多研究者对雷达通信一体化系统进行了研究[4-12]。文献[4]提出了基于正交频分复用(Orthogonal Frequency Division Multiplexing,OFDM)雷达信号的解多普勒模糊方法,通过利用OFDM的多载波结构和随机相位调制来消除多普勒模糊。文献[5]提出了一种虚拟波形设计方案,与传统方法相比,该方法的性能提升效果较为明显。文献[6]研究了OFDM雷达通信一体化波形在相参积累中的特性。文献[7]针对多基地雷达和点对点通信系统存在的频谱复用限制问题,提出了一种新颖的自适应雷达接收机配置机制,该机制不仅能明显地提高通信发射机和雷达接收通道的信噪比,还能降低几何稀释精度。文献[8]通过波束形成与波形分集技术,允许雷达与单个或多个非主瓣方向的基站通信,实现了雷达通信一体化。文献[9]针对雷达通信频谱复用中存在的相互干扰问题,提出了一种干扰信道选择算法,通过将雷达信号投射到干扰信道的零空间以减轻雷达对通信系统的干扰。文献[10]探究了强化学习在雷达和通信协同共存中的应用,通过强化学习训练并形成雷达通信一体化系统的频谱分配策略。文献[11]从博弈论的角度研究了多输入多输出雷达与目标之间的相互作用,并将其建模为零和博弈,研究了单边博弈、层次博弈和对称博弈模型,推导了各模型的均衡解。文献[12]提出了衡量目标跟踪性能的评价指标,推导了不同频谱管控方案下雷达通信一体化系统的性能内界。
信息论理论早在1953年就被用于设计雷达后验接收机[13]。互信息是信息论中一种有用信息的度量,由于其可以表征一个随机变量包含另一个随机变量的信息量,被广泛用于雷达探测领域[14-16]。文献[14]利用目标频谱方差、噪声功率谱和杂波功率谱等先验信息,根据最大互信息准则设计发射波形,有效地提升了探测性能。文献[15]研究了多输入多输出雷达在频谱拥挤环境中的波形设计问题,以目标回波和目标响应之间的互信息作为度量,提出了一种基于一阶泰勒级数近似和最小最大化算法的频谱约束波形设计方法,使得雷达可以更有效地与其他通信系统实现频谱复用。文献[16]提出了一种自适应正交频分多路复用的雷达通信一体化波形设计方法,有效提高了系统频谱资源利用率。然而,上述文献均是利用互信息进行波形设计,缺乏基于互信息的雷达通信一体化的理论分析及性能分析,且目前尚未有公开文献进行相关研究。
本文基于信息论,将雷达获取目标信息的过程看作是雷达与目标之间的非合作通信问题,通过联合信息论与检测估计等典型理论,提出基于互信息的雷达通信频谱复用方法,为雷达通信一体化系统提供统一的理论基础,从而可更为系统地分析雷达通信一体化系统的性能。首先,建立了雷达通信一体化系统的信号模型;然后,构建了基于信息论的雷达性能评价指标,并以通信率作为通信性能指标建立了基于信息论相关理论基础的雷达通信一体化系统性能评价模型;接着,根据接收到的雷达信号与通信信号的频带复用程度将频谱分配模式分为传统频谱非复用、通信为主频谱复用和雷达为主频谱复用三种模式,推导了雷达通信一体化系统在三种模式下的性能内界;最后,通过仿真验证了该方法的有效性。
2 信号建模
如图1所示,雷达通信一体化系统既可以对目标进行探测,又可以与通信基站进行通信。
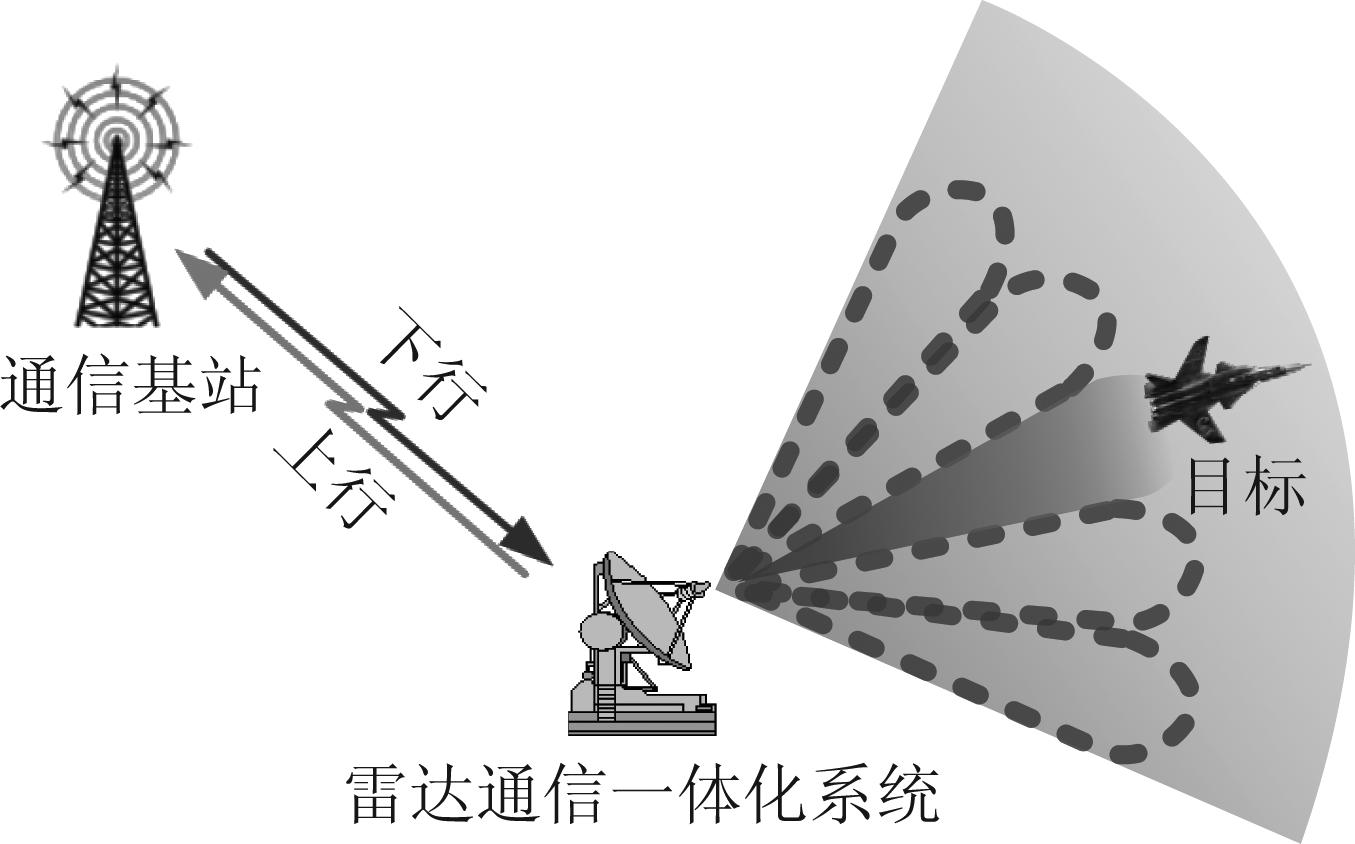
图1 雷达通信一体化系统应用场景示意图
Fig.1 Application scene graph of the radar and communication integration system
雷达通信一体化联合接收机可以同时接收雷达信号zr(t)和通信信号zc(t),进而提取目标信息,并对观测到的通信信号进行解码。复合信号的表达式为:
z(t)=zr(t)+zc(t)
(1)
假设雷达信号发射功率为Pr,信号带宽为Br,雷达接收信号zr(t)可表示为:
ξrxr(t-τ)ej2πfrt+n(t)
(2)
式中ξr、τ分别表示雷达信号的传播损耗和传播时延,xr,b(t)为雷达基带信号,
为雷达信号载频。n(t)指均值为0、方差为σ2=κBrT0的加性高斯白噪声,κ表示玻耳兹曼常数,T0表示系统噪声温度。同样的,定义通信带宽为Bc,通信信号发射功率为Pc,可以得到接收到的通信信号为:
ξcxc(t)ej2πfct+n(t)
(3)
式中ξc表示通信信号的传播损耗,xc,b(t)表示通信基带信号,
表示通信信号载频。
3 雷达通信一体化系统性能评价模型
雷达通信一体化系统性能表征方法是雷达通信一体化研究的难题。本节结合信息论,将雷达探测目标看成非合作通信问题,提出了衡量雷达获取目标信息能力的性能指标——互信息。进而以通信率为通信性能评价指标,建立了基于信息论相关理论基础的雷达通信一体化系统性能评价模型。下文将对互信息进行推导并给出通信率的数学表达式。
雷达对目标的探测可以看作是目标在不情愿地向雷达传递其参数信息,目标脉冲响应g(t)和接收到的雷达信号zr(t)中均包含目标信息。g(t)和zr(t)之间的互信息I(g(t);zr(t))可以表征雷达获取的目标信息量。互信息I(g(t);zr(t))越大,测量后先验不确定性的降低幅度越大,雷达获取的目标信息越多,对表征目标特性参数的估计就越准确。
将雷达探测目标的过程建模成一个非合作通信问题,其信道模型如图2所示,y(t)是被目标散射的雷达信号,它是一个能量有限的随机过程。
y(t)=
g(m)xr(t-m)dm
(4)
图2 雷达探测目标的信道模型
Fig.2 The channel mode of target detection
设目标响应为高斯随机过程,相应的傅里叶变换为G( f ),xr(t)的傅里叶变换为Xr( f )。由傅里叶变换的卷积定理可知y(t)的傅里叶变换为Xr( f )G( f ),其幅度谱为|Y( f )|2=|Xr( f )|2|G( f )|2。对该幅度谱取期望可得:
E(|Y( f )|2)=|Xr( f )|2E(|G( f )|2)
(5)
其中,
是G( f )的均值,
是G( f )的方差。
鉴于xr(t)已知,μG( f )可以通过对Y( f )求均值进行求解,从信息论的角度分析,μG( f )不能提供任何关于目标的信息。而
是不确定的,即其包含目标信息,故我们只对感兴趣。不妨设μG( f )=0,因为目标在空间中的位置是随机的,雷达回波中存在一个随机延迟τ,由傅里叶变换的时移性质可知该随机时延对应于频域一个随机相位因子exp(-j 2πfτ)。随机相位因子不会影响的值,故随机延迟τ不会影响雷达回波与目标之间的互信息。综上,设被观察的目标能量有限,其高斯脉冲响应的谱方差满足
其中H和ε是常数,H为幅度的峰值,ε=10-13 s2。
由于雷达发射信号是已知的,所以zr(t)与g(t)之间的互信息等效为zr(t)与y(t)之间的互信息。令n(t)的单边功率谱为Pnn( f ),设
当
足够小时,对于
有Y( f )≈Y(fk)、Zr( f )≈Zr(fk)、Pnn( f )≈Pnn(fk)。令
表示y(t)对应频率的信号分量,
表示zr(t)对应频率的信号分量。给定时间
为脉冲宽度,和之间的互信息可以表示为[17]:
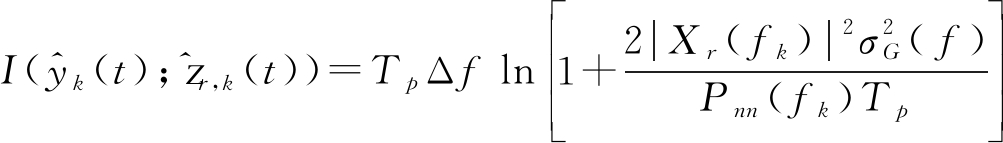
(6)
考虑一个与不相交的频率间隔
表示y(t)对应频率
的信号分量,
表示zr(t)对应频率的信号分量,
表示xr(t)对应频率的信号分量,
表示xr(t)对应频率的信号分量。令nk(t)、nj(t)分别表示n(t)对应频率
的信号分量。我们注意到,两个功率谱密度不相交的高斯随机过程在统计上是相互独立的[18],因此与相互独立,
与
相互独立,nj(t)与nk(t)相互独立。进而可知
与
之间的互信息等于与之间的互信息
与之间的互信息的线性叠加。
(7)
对于雷达带宽Br=[f0, f0+fr],将其划分为许多个间隔为Δf的不相交的子带宽,使得Δf→0,从而可以得到g(t)与z(t)之间的互信息的表达式为[13]:
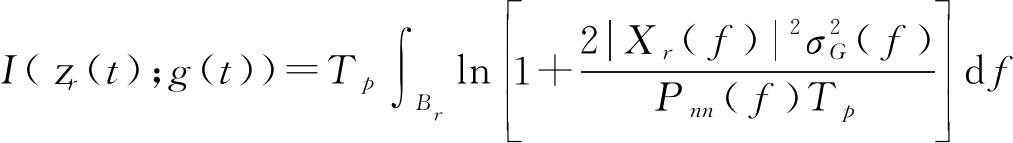
(8)
通信率Rcom可表征通信链路的性能,通信率越大表示单位时间内信道所能传输的最大比特数越大,性能越好。根据香农第二定理可得[19]:
(9)
4 雷达通信一体化系统性能分析
根据雷达与通信是否进行频谱复用,本节将频谱分配模式分为传统频谱非复用、雷达为主频谱复用及通信为主频谱复用三种模式。进而,本节分别以互信息、通信率表征雷达性能和通信性能,分析推导了不同频谱分配模式下雷达通信一体化系统的性能。下文将对三种频谱分配模式下的系统性能进行详细分析。
4.1 传统频谱非复用模式
如图3所示,在传统频谱非复用模式下总带宽B被分为两部分,一部分用于通信,称为通信带宽Bc,另一部分用来执行探测任务,称为雷达带宽Br。雷达和通信在分配给它们的带宽上执行各自的任务,二者之间没有相互干扰。设带宽调节因子为α(0≤α≤1),两个子带宽可表示为:
Bc=αB,Br=(1-α)B
(10)
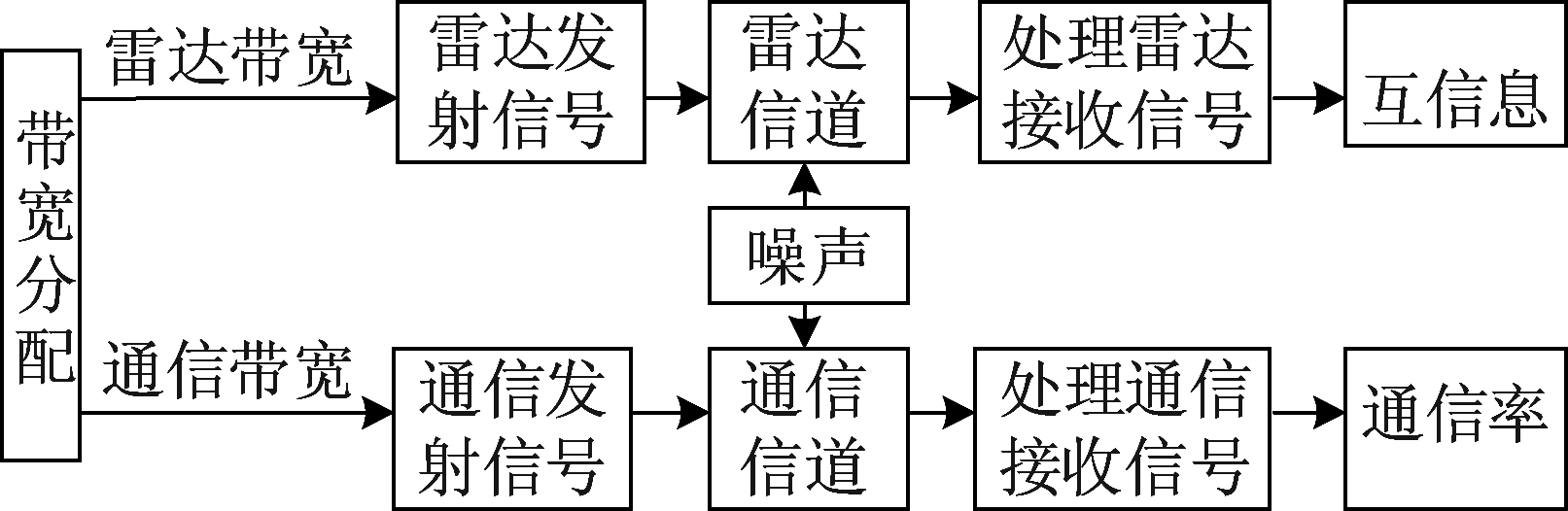
图3 传统频谱非复用模式结构框图
Fig.3 The structure block diagram of traditional non-sharing mode
根据式(8)及式(9),传统频谱非复用模式下的通信率及互信息可分别表示为:
(11)
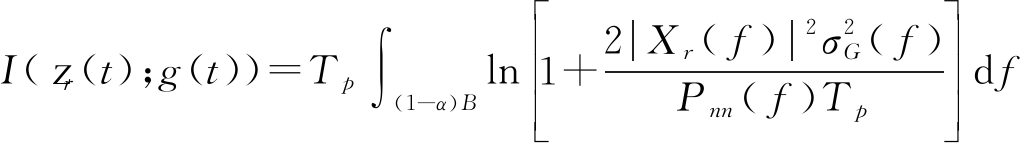
(12)
4.2 通信为主频谱复用模式
如图4所示,在通信为主频谱复用模式下系统总带宽被分为两部分,一部分仅用于通信,称为通信独立带宽Bc,另一部分同时用于探测和通信,称为复用带宽Bs,给定带宽调节因子α(0≤α≤1),两个子带宽的数学表达式为:
Bc=αB,Bs=(1-α)B
(13)
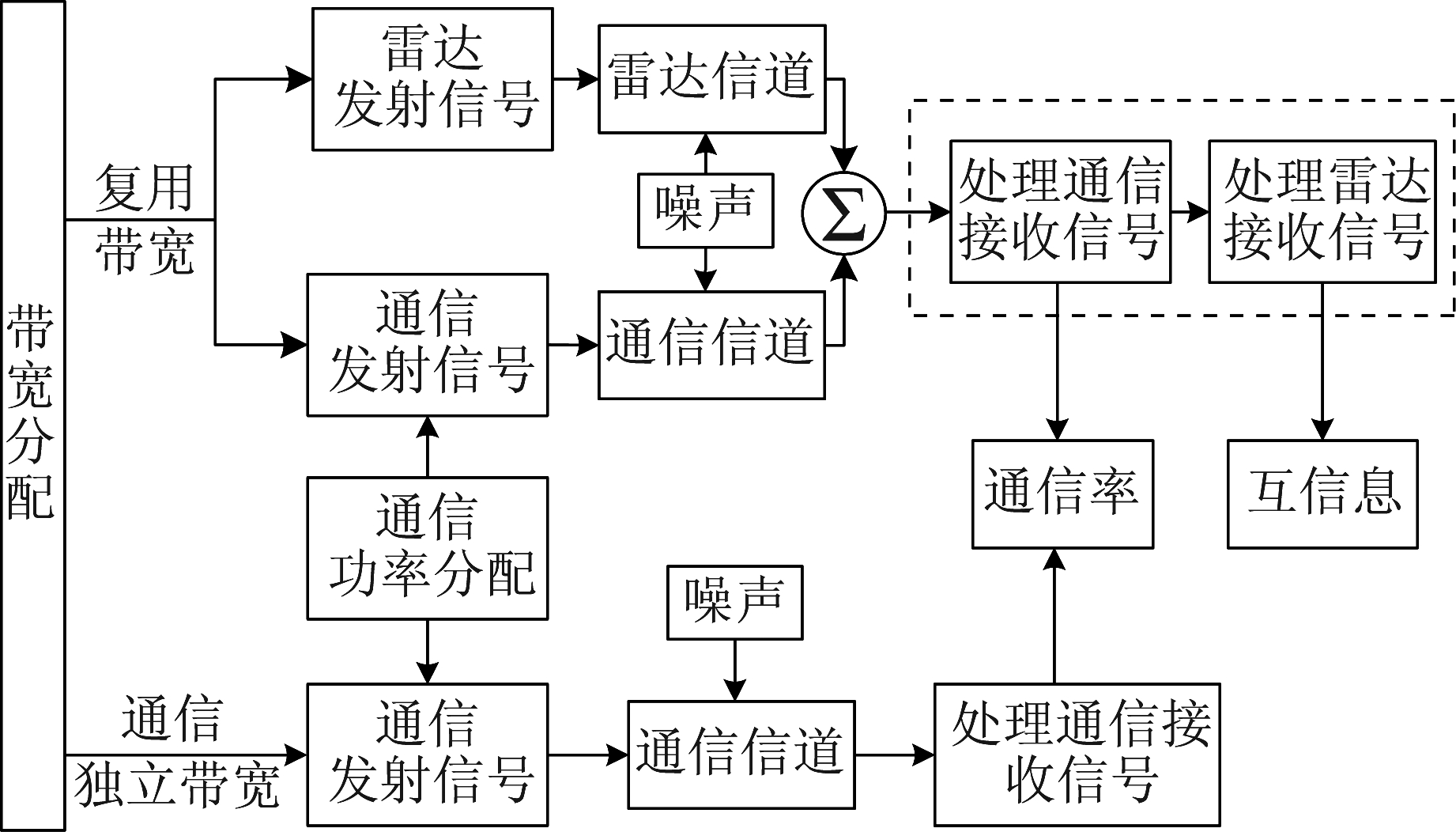
图4 通信为主频谱复用模式结构框图
Fig.4 The structure block diagram of communication as the primary user of spectrum sharing mode
设Pc,o表示分配给通信独立带宽的通信功率。由于通信独立带宽的通信信号不受雷达信号的干扰,故相应的通信率Rcom,o可表示为:
(14)
设Pc,s表示分配给复用带宽的通信功率,复用带宽中雷达信号和通信信号之间存在相互干扰,故复用带宽通信信号的信干噪比为:
(15)
进而可得复用带宽的通信率Rcom,s为:
Rcom,s=(1-α)Blog2(1+SINRc,s)
(16)
将式(14)、式(16)相加可得通信为主频谱复用模式下系统的总通信率。针对复用带宽中通信信号与雷达信号之间的相互干扰,本文采用串行干扰消除(Successive Interference Cancellation,SIC)对复用带宽中的信号进行处理,文献[20-21]对该方法的合理性问题进行了研究,因其不是本文的研究重点,在此不多加讨论。
接收机先对通信信号进行解码,再将其从观测波形中移除。故复用带宽雷达信号的信干噪比为:
(17)
式中λ(0≤λ≤1)为消除因子[21],当λ=0时为理想消除情况,即干扰信号可被完全消除,当λ=1时干扰无法被消除。通信为主频谱复用模式下的互信息可表示为:
I(zr(t);g(t))=
(18)
由于功率的优化管控不在本文的讨论范围,本文仅采用经典的注水算法[22]来解决具体的分配情形。令通信功率按照功率分配因子β分配给两个子带宽。
Pc,o=βPc,Pc,s=(1-β)Pc
(19)
式中,ν为拉格朗日乘子,μc,o、μc,s分别表示通信独立带宽和复用带宽的功率分配系数,(x)+=max(x,0)。
当α=1时,全部带宽用于通信,有:
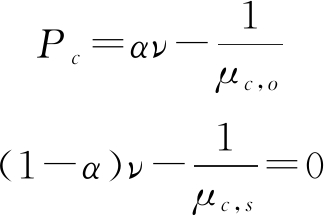
(20)
当0≤α<1时,有:
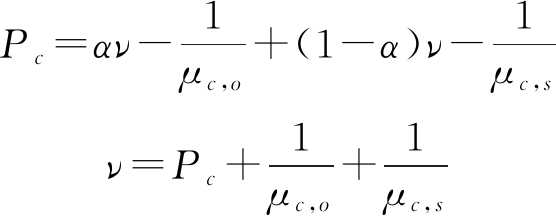
(21)
综上可得通信功率分配因子β满足以下条件:
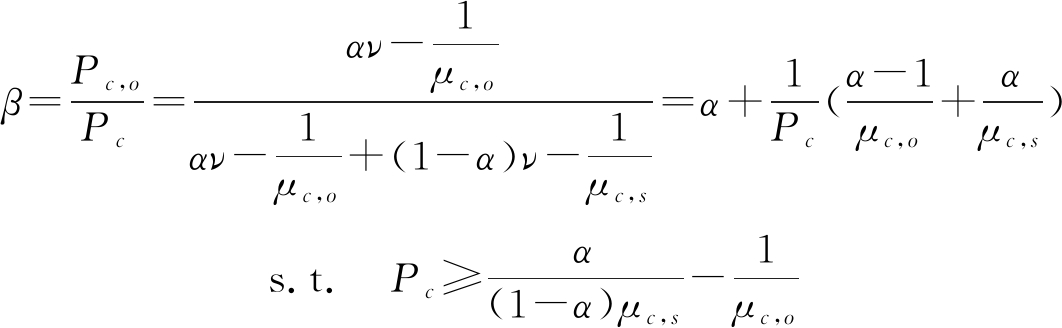
(22)
4.3 雷达为主频谱复用模式
如图5所示,在雷达为主频谱复用模式下,总带宽被分为两部分,一部分仅用于探测,称为雷达独立带宽Br,另一部分同时用于探测和通信,称为复用带宽Bs。给定带宽调节因子α(0≤α≤1),两个子带宽可表示为:
Br=αB,Bs=(1-α)B
(23)
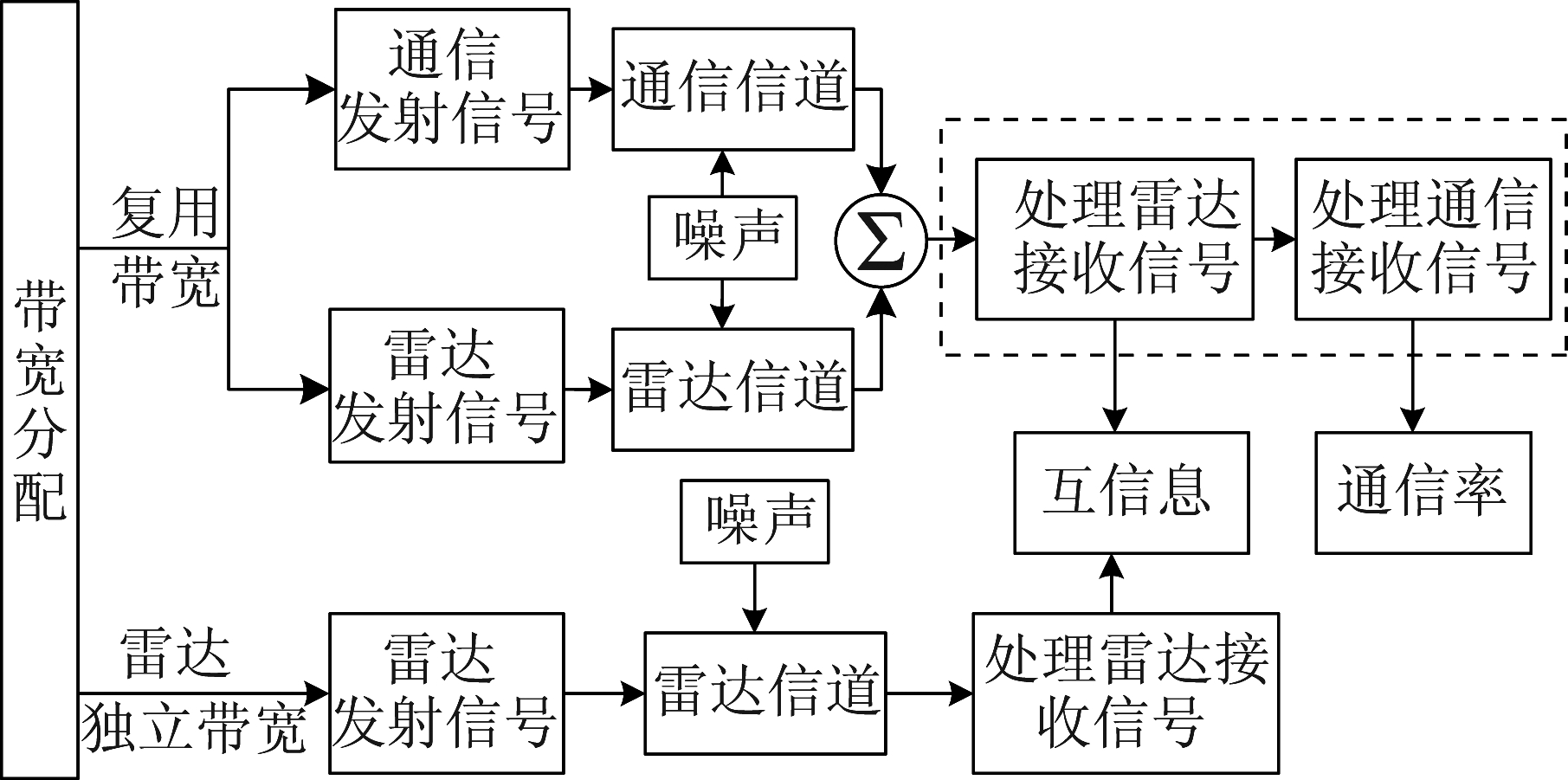
图5 雷达为主频谱复用模式结构框图
Fig.5 The structure block diagram of radar as the primary user of spectrum sharing manner
雷达独立带宽中的雷达信号不受通信信号的干扰,相应的互信息可表示为Io(zr(t);g(t)):
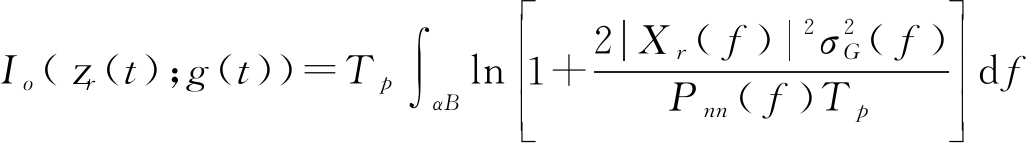
(24)
由于复用带宽中既存在雷达信号,又存在通信信号,通信信号会对雷达信号造成干扰,故复用带宽中的互信息为:
Is(zr(t);g(t))=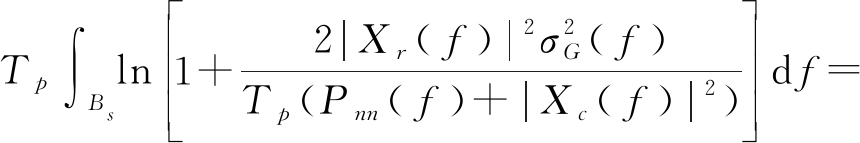
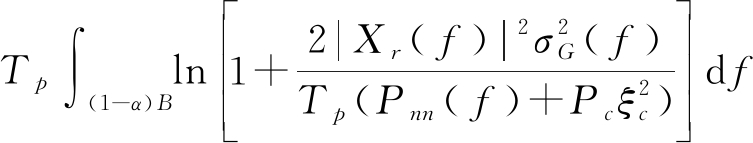
(25)
将式(24)、式(25)相加可以得到雷达为主频谱复用模式下系统的总互信息。为了缓解雷达信号对通信信号的干扰,在此我们采用SIC[20-21]对复用带宽的信号进行处理。先对雷达信号进行解码,再将雷达信号从观测波形中移除。雷达为主频谱复用模式下的通信率可以表示为:
(26)
式中λ(0≤λ≤1)为消除因子。
5 仿真分析
本小节给出了三种频谱分配模式下雷达通信一体化系统性能的仿真结果。假设接收功率遵循典型的路径损耗模型,即功率衰减与Ln成正比,其中L是目标探测距离或通信传输距离,n为路径损耗指数。具体仿真参数如表1所示。
表1 仿真参数
Tab.1 Simulation parameters
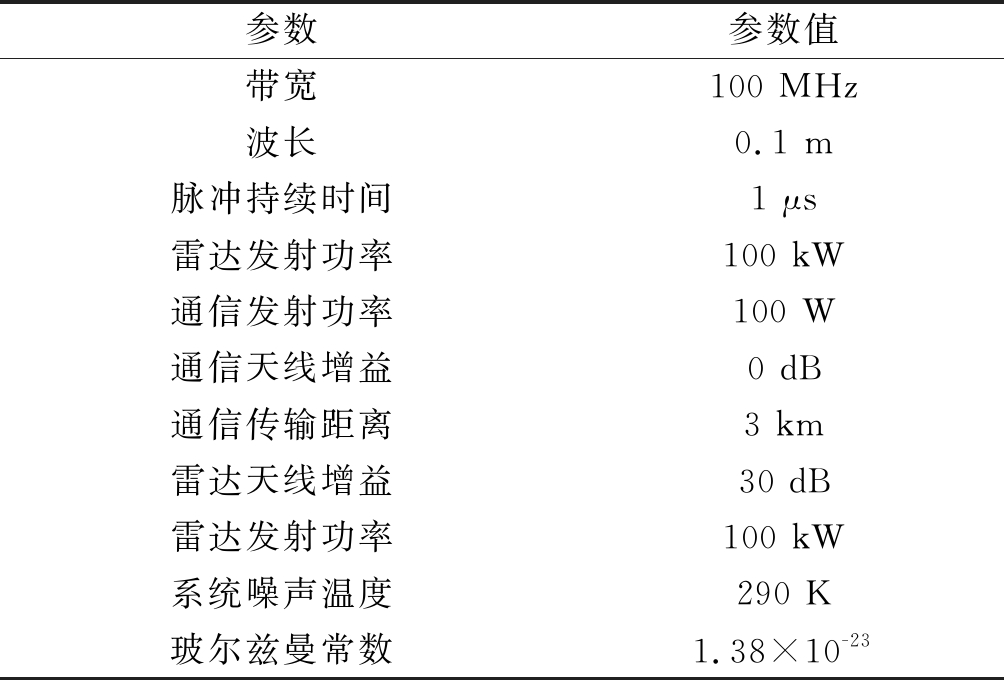
参数参数值带宽100 MHz波长0.1 m脉冲持续时间1 μs雷达发射功率100 kW通信发射功率100 W通信天线增益0 dB通信传输距离3 km雷达天线增益30 dB雷达发射功率100 kW系统噪声温度290 K玻尔兹曼常数1.38×10-23
图6示出了SIC消除性能对系统性能的影响。图6(a)描绘了通信为主频谱复用模式下SIC消除性能对互信息性能的影响,图6(b)描绘了雷达为主频谱复用模式下SIC消除性能对通信率性能的影响,图中实线、虚线及点线分别表示λ等于0.001、0.1及0.3情况下互信息(通信率)的性能。由图可知,随着λ的增大,即SIC消除性能的下降,通信率和互信息的性能均下降。这是因为随着SIC消除性能的下降,干扰信号的残留就会增加,进而导致有用信号的信干噪比下降。因此,雷达通信频谱复用性能的关键在于如何消除雷达通信的相互干扰。为了便于仿真分析,下文对理想消除情况下(λ=0)的系统性能进行了分析,但本文所提方法及相关理论分析适用于λ≠0的情形,并也具有优势。
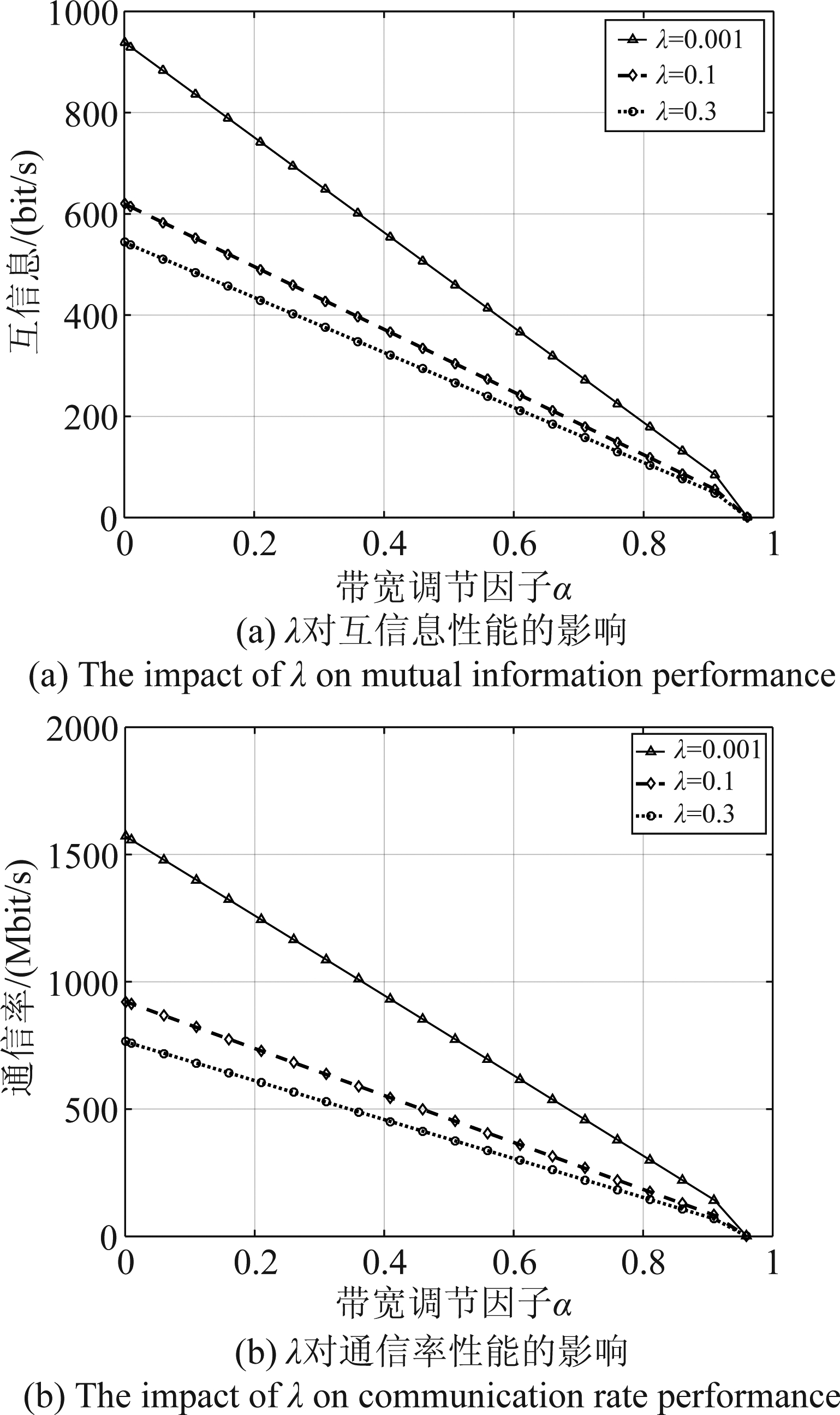
图6 λ对系统性能的影响
Fig.6 The impact of λ on system performance
图7中给出了理想消除情况下三种频谱分配模式下的互信息-通信率性能内界,图中黑色实线代表的是传统频谱非复用模式,黑色虚线代表的是通信为主的频谱复用模式,黑色点线代表的是雷达为主的频谱复用模式。对于传统频谱非复用模式,横轴最大值为雷达占用所有带宽时的互信息,相应的,纵轴最大值为通信占用所有带宽时的通信率。点A表示雷达为主频谱复用模式实现最大通信率时对应的互信息。点B表示通信为主的频谱复用模式实现最大互信息时对应的通信率。从图中可以看出两种频谱复用模式下的互信息-通信率容量区域均大于传统频谱非复用模式,即传统频谱非复用模式的通信率、互信息性能均低于其他两种频谱复用模式。两种频谱复用模式下的通信率增益和互信息增益如图8所示。
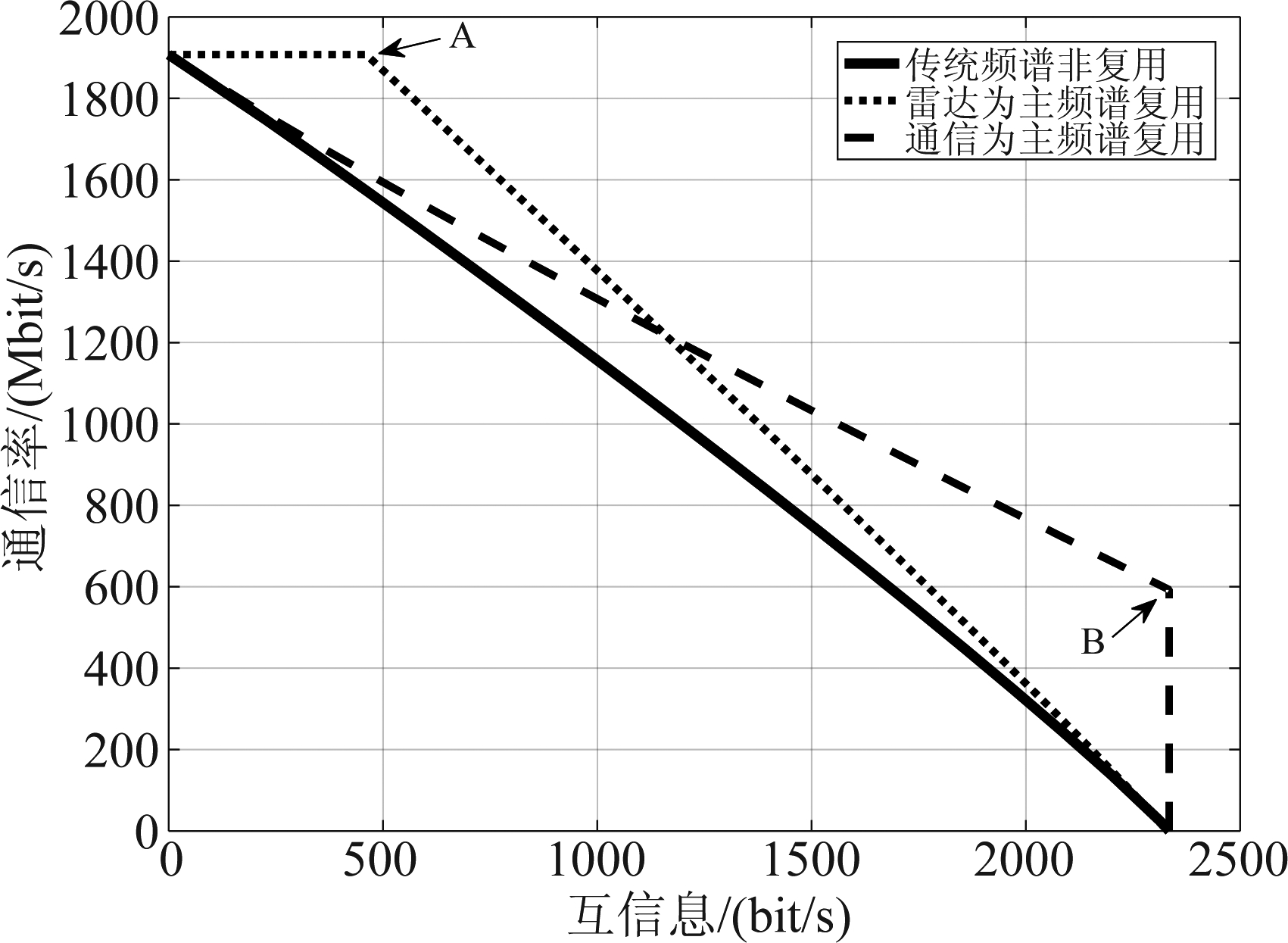
图7 λ=0时互信息-通信率性能内界
Fig.7 The inner bounds of performance of mutual information-communication rate when λ=0
图8中,(a)、(b)两图分别描绘了理想消除情况下,两种频谱复用模式相对于传统频谱非复用模式的通信率增益和互信息增益曲线。图8(a)中,当互信息较小时,即雷达所占带宽较小时,雷达为主频谱复用模式下的通信率增益大于通信为主频谱复用模式,并在互信息为466 bit/s时达到最大,具体数值为330 Mbit/s;随着互信息的增加,雷达为主频谱复用模式下的通信率增益逐渐减小,直至为0,而通信为主频谱复用模式下的通信率增益则在互信息最大时达到最大,具体数值为592.8 Mbit/s。
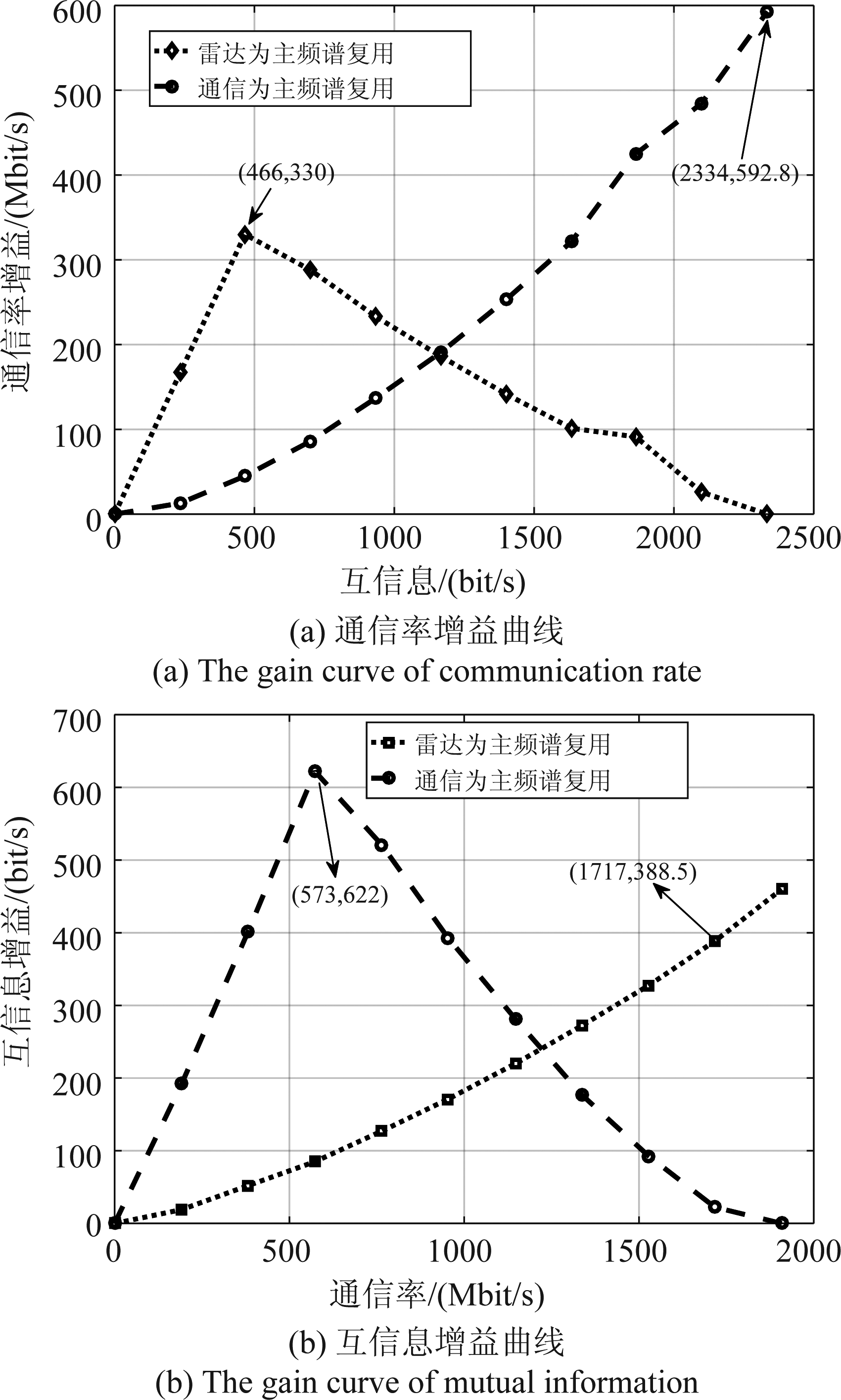
图8 λ=0时频谱复用模式相对非复用模式的通信率增益和互信息增益曲线
Fig.8 The gain curve of communication rate and mutual information in spectrum sharing mode compared with non-sharing mode when λ=0
这是由于雷达为主频谱复用是以雷达为主导的模式(雷达占用部分独立带宽),通信为主频谱复用是以通信为主导的模式(通信占用部分独立带宽)。当互信息达到最大值时,传统频谱非复用模式及雷达为主频谱复用模式下雷达占用所有带宽,通信带宽为0,二者通信率均为0;而通信为主频谱复用模式下雷达、通信共用所有带宽,故通信率增益仍然可观。
同理,如图8(b)所示,当通信率达到最大值时,通信为主频谱复用模式下通信占用所有带宽,其互信息增益为0,而雷达为主频谱复用模式下雷达、通信共用所有带宽,互信息增益达到最大。
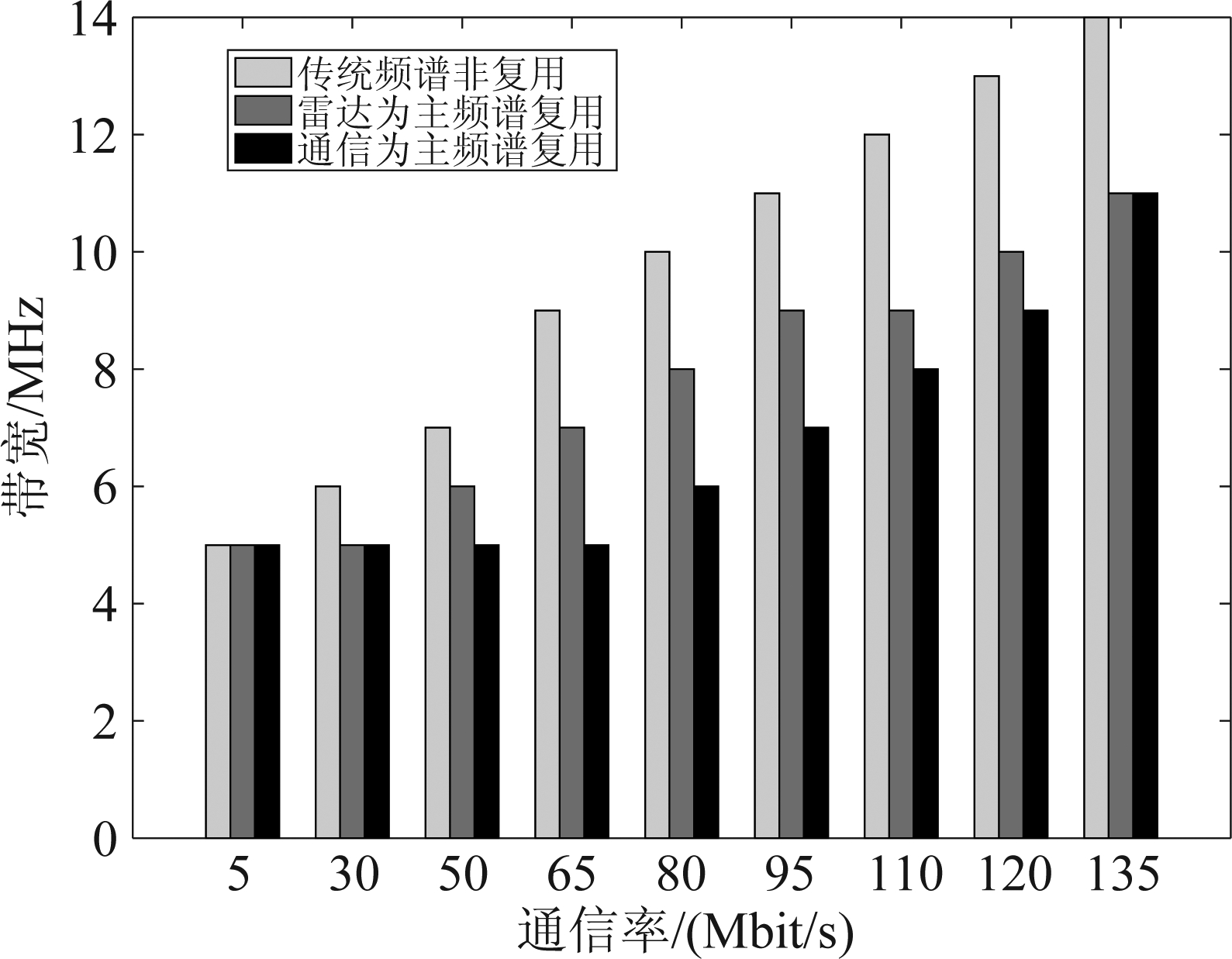
图9 λ=0时各频谱分配模式的频谱资源需求量
Fig.9 Spectrum resource required of different spectrum allocation modes when λ=0
图9示出理想消除情况下,当互信息等于10.4 bit/s时,随着通信率的增加,不同频谱分配模式频谱资源需求量的柱状图。其中,颜色由浅至深依次表示传统频谱非复用、雷达为主频谱复用以及通信为主频谱复用模式。从图9可以看出,随着通信率的增加,三种频谱分配模式的频谱资源需求量不断递增,但两种频谱复用模式的频谱资源需求量均少于传统频谱非复用模式。而通信为主频谱复用模式下的频谱资源需求量少于雷达为主频谱复用模式(这是因为通信为主频谱复用模式下的通信率增益更加明显的缘故);随着通信率的逐渐增加,两种频谱复用模式的频谱资源需求量趋于一致。所以,在实现相同系统效能的条件下,与传统频谱非复用模式相比,两种频谱复用模式的频谱资源需求量更少,频谱利用率更高。
6 结论
雷达通信一体化系统的综合效能评估可以为雷达通信一体化系统的相关研究提供理论支撑。本文面向雷达通信一体化的应用需求,提出了基于信息论的雷达通信频谱复用方法。首先,建立了雷达通信一体化信号模型;然后,构建了基于信息论的雷达性能评价指标,在此基础上以通信率为通信性能评价指标,建立了基于信息论相关理论基础的雷达通信一体化性能评价模型;接着,根据雷达接收信号与通信接收信号的频带复用程度将频谱分配模式分为传统频谱非复用、雷达为主频谱复用及通信为主频谱复用三种模式,分析了雷达通信一体化系统在三种模式下的性能。仿真表明,与传统频谱非复用模式相比,在同等频谱资源条件下,两种频谱复用模式可有效提升探测性能和通信性能;在实现相同系统效能的前提下,两种频谱复用模式下的频谱资源需求量均少于传统频谱非复用模式。
[1] 马定坤, 匡银, 杨新权. 侦干探通一体化现状与关键技术研究[J]. 中国电子科学研究院学报, 2016, 11(5): 457- 462.
Ma Dingkun, Kuang Yin, Yang Xinquan. Key Issues and Status Research of Integrated Reconnaissance, Interference, Detection and Communications[J]. Journal of CAEIT, 2016, 11(5): 457- 462.(in Chinese)
[2] 卢俊, 张群飞, 史文涛, 等. 探测通信一体化研究现状与发展趋势[J]. 信号处理, 2019, 35(9): 1484-1495.
Lu Jun, Zhang Qunfei, Shi Wentao, et al. Development and Prospect of Detection and Communication Integration[J]. Journal of Signal Processing, 2019, 35(9): 1484-1495.(in Chinese)
[3] Zhou Shenghua, Liang Xueling, Liu Hongwei, et al. Dual-function radar-communication using GPS gold codes[C]∥International Conference on Radar Systems, Belfast, 2017: 1- 4.
[4] Tigrek R F, De Heij W J A, van Genderen P. OFDM Signals as the Radar Waveform to Solve Doppler Ambiguity[J]. IEEE Transactions on Aerospace and Electronic Systems, 2012, 48(1): 130-143.
[5] Kumari P, Vorobyov S A, Heath R W. Adaptive Virtual Waveform Design for Millimeter-Wave Joint Communication-Radar[J]. IEEE Transactions on Signal Processing, 2020, 68: 715-730.
[6] 刘永军, 廖桂生, 杨志伟. OFDM雷达通信一体化波形相参积累研究[J]. 信号处理, 2017, 33(3): 253-259.
Liu Yongjun, Liao Guisheng, Yang Zhiwei. A Study for the Coherent Integration with Integrated Radar and Communication Waveform Based on OFDM[J]. Journal of Signal Processing, 2017, 33(3): 253-259.(in Chinese)
[7] Ben Kilani M, Gagnon G, Gagnon F. Multistatic Radar Placement Optimization for Cooperative Radar-Communication Systems[J]. IEEE Communications Letters, 2018, 22(8): 1576-1579.
[8] Hassanien A, Amin M G, Zhang Y D, et al. Dual-Function Radar-Communications: Information Embedding Using Sidelobe Control and Waveform Diversity[J]. IEEE Transactions on Signal Processing, 2016, 64(8): 2168-2181.
[9] Khawar A, Abdelhadi A, Clancy C. Target Detection Performance of Spectrum Sharing MIMO Radars[J]. IEEE Sensors Journal, 2015, 5(9): 4928- 4940.
[10] Ma O, Chiriyath A R, Herschfelt A, et al. Cooperative Radar and Communications Coexistence Using Reinforcement Learning[C]∥Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 2018: 947-951.
[11] Song Xuefeng, Willett P, Zhou Shengli, et al. The MIMO Radar and Jammer Games[J]. IEEE Transactions on Signal Processing, 2012, 60(2): 687- 699.
[12] Chiriyath A R, Paul B, Jacyna G M, et al. Inner Bounds on Performance of Radar and Communications Co-Existence[J]. IEEE Transactions on Signal Processing, 2016, 64(2): 464- 474.
[13] Bell M R. Information theory and radar waveform design[J]. IEEE Transactions on Information Theory, 1993, 39(5): 1578-1597.
[14] Wang Lei, Wang Huabing, Chen Mingyan. Cognitive radar waveform design for multiple targets based on information theory[C]∥2016 CIE International Conference on Radar (RADAR), Guangzhou, 2016: 1-5.
[15] Tang Bo, Li Jian. Spectrally Constrained MIMO Radar Waveform Design Based on Mutual Information[J]. IEEE Transactions on Signal Processing, 2019, 67(3): 821- 834.
[16] Liu Yongjun, Liao Guisheng, Xu Jingwei, et al. Adaptive OFDM Integrated Radar and Communications Waveform Design Based on Information Theory[J]. IEEE Communications Letters, 2017, 21(10): 2174-2177.
[17] Bell M R. Information theory and radar: Mutual information and the design and analysis of radar waveforms and systems[D]. Pasadena: California Inst Technol, 1988.
[18] Papoulis A. Probability, Random Variables, and Stochastic Processes[M]. New York: McGraw-Hill, 1965: 353-353.
[19] Shannon C E. A mathematical theory of communication[J]. The Bell System Technical Journal, 1948, 27(4): 623- 656.
[20] 赵旦峰, 王杨, 钱晋希. MIMO系统中一种改进的迭代串行干扰消除算法[J]. 信号处理, 2012, 28(10): 1423-1426.
Zhao Danfeng, Wang Yang, Qian Jinxi. An Improved Iterative SIC Algorithm for MIMO Systems[J]. Signal Processing, 2012, 28(10): 1423-1426.(in Chinese)
[21] Liu Ming, Mao Yuming, Leng Supeng, et al. Successive interference cancellation in full duplex cellular networks[C]∥2017 IEEE International Conference on Communications, Paris, 2017: 1- 6.
[22] He Peter, Zhao Lian, Zhou Shen, et al. Water-Filling: A Geometric Approach and its Application to Solve Generalized Radio Resource Allocation Problems[J]. IEEE Transactions on Wireless Communications, 2013, 12(7): 3637-3647.
