1 引言
随着信息技术的飞速发展,电磁频谱资源已呈现出日渐稀缺的演化态势[1]。大量用频设备的部署致使多类电磁信号在时域、频域、空域密集交叠,电磁环境日趋阻塞。在现有频谱资源规划下,基于S波段、C波段等的陆基、舰载、航空雷达,其工作频率毗邻大量通信设备的工作频段,可能会造成雷达设备与通信设备间严重的互相互扰[2-3]。为提升频谱利用效率,同时减缓设备间互扰,亟需研究跨设备频谱共享的雷达-通信一体网络,探索雷达与通信设备的频谱协作机制,以动态适应复杂多变的电磁环境,实现对雷达与通信设备频谱资源的协同管理。
现有雷达通信一体化技术体制大体可分为以下三类[4]:雷达通信脉冲参数一体化设计体制[5]、雷达通信波形一体化设计体制[6]以及雷达与通信系统一体化设计体制[7]。其中雷达与通信系统一体化利用频谱协作、频谱共享等技术消除系统中雷达设备与通信设备间干扰,泛用性强,因而受到学界持续关注。文献[8-9]分别基于计算机仿真和实物验证的方式检验了雷达设备与LTE(Long Term Evolution)通信设备在3.5 GHz频段共用频谱的可能性,研究结果显示在雷达的隔离区(Exclusion Zone)外,LTE设备凭借其自身的动态频谱接入技术,可有效减缓雷达对通信设备的临近信道干扰。文献[10]研究了市民宽频无线电服务(Citizen Broadband Radio Service,CBRS)中同频带下舰载雷达与无线通信设备的互扰模型,同时提出一种新的通信设备发射功率调控算法,该算法能大幅减小雷达隔离区半径。文献[11]针对多输入多输出(Multi-Input-Multi-Output, MIMO)S波段雷达与LTE-Advanced设备共存的场景,利用载波聚合技术,提出一种基于空间域的无线资源分配算法。该算法通过对用户端配置不同的资源接入优先级从而实现雷达与LTE-Advanced设备间的频谱共享。文献[12]考虑了信道状态信息不完全情况下多用户下行MIMO通信系统与MIMO雷达间的频谱共享问题,并将其构建为一个半正定规划问题。近年来,基于博弈论的雷达-通信一体化设计方案也成为学界研究热点[13-16]。然而上述工作重点关注一体化系统中雷达设备的服务质量,忽略对通信设备端服务质量的研究;同时,这些工作主要研究设备间的功率分配问题,缺乏对设备间频谱资源的统一协同管理。此外,也有一些工作利用机器学习进行雷达通信一体化设计[17-19],然而此类研究需要大量数据集做支撑。由于雷达-通信网络周围电磁频谱环境快速变化,很难提前获取准确的大样本数据集,此外经验性数据可能并不与实时变化的环境匹配,因而此类方法在实际中很难适用。总体来说,现阶段关于雷达-通信一体化方案的研究[8-19]仅聚焦于当前时刻下瞬时网络效用的最优性,并未考虑前若干时刻决策信息对当前时刻的影响。而雷达-通信一体网络涉及雷达与通信设备在时域、频域、空域上多类无线资源的长期复杂调度,其各个时刻间的决策信息可能具有时间关联性。因此,面向最优瞬时网络效用的资源分配策略很有可能因忽略决策信息的关联性而难以取得长期网络效用的最优化。根据作者调研的研究现状,在雷达-通信网络频谱共享的研究中尚不存在面向长期网络效用的动态协同算法的研究。
本论文研究由一个地面雷达、一个地面控制站及多个通信用频设备组成的雷达-通信一体网络,并对该网络中上行通信链路的频率选择及功率分配进行联合动态优化,在保障用户服务质量(Quality of Service,QoS)需求的条件下最小化用频设备的长期平均发射功率。本论文通过分析雷达-通信一体网络的特点,构建前后时刻网络状态及决策信息的关联性,将所述的频率选择与功率分配动态优化问题建模为以最小化长期平均损耗为目标的马尔可夫决策过程[20]问题。该问题不依赖系统模型,即信道状态分布及用户移动特性可不作为先验信息。以长期平均损耗为优化目标的马尔可夫决策过程问题通常可利用相对值迭代方法(Relative Value Iteration,RVI)[21]求解。然而,由于本问题中的状态维度随用户数量呈指数型增长,传统的相对值迭代方法在用户数量较大时易陷入“维度诅咒”(Curse of Dimensionality)[21]而难以甚至无法收敛。为避免“维度诅咒”,本论文提出一种分布式相对值迭代算法,将原有的马尔可夫决策过程问题解耦为多个可并行求解的低维度马尔可夫决策过程子问题。每个解耦后子问题的状态维度较原马尔可夫决策问题均大幅下降至可接收范围,因而直接利用相对值迭代方法便可在较低复杂度下对每个解耦后子问题进行求解。本文研究主要包含以下贡献和创新:
本论文构建了包含一个地面雷达、一个地面控制站及多个用频设备组成的雷达-通信一体网络,旨在解决该网络上行通信链路中的频率选择及功率分配联合优化问题。与以往侧重于网络在某一时刻的网络效用最大化的研究不同,本文考虑了前后时刻网络状态及决策信息的时间关联性,并将雷达-通信一体网络下的频率选择及功率分配优化问题建模为一个以最小化长期平均损耗为目标的马尔可夫决策过程问题。针对上述马尔可夫决策过程问题易陷入“维度诅咒”的缺陷,本论文提出了一种分布式相对值迭代算法对该问题进行求解。分布式相对值迭代算法首先对网络频谱资源进行预分配处理,从而将原马尔可夫决策过程问题解耦为若干个低维度马尔可夫决策过程子问题;随后对于每个解耦后子问题,先利用拉格朗日乘子法推导功率分配最优解的闭式解形式,再利用基于相对值迭代方法的迭代架构求解资源分配策略。仿真结果显示,基于分布式相对值迭代算法的长期效用策略较瞬时效用策略可获得到更低的长期平均发射功率损耗。
本论文其余部分主要内容如下:第2节进行系统建模;第3节提出分布式相对值迭代算法;第4节评估网络性能;第5节对本论文做出总结。
2 系统模型
本文考虑包含一个地面雷达、一个地面控制站及K个用频通信设备的雷达-通信一体网络中用频设备的上行通信链路,如图1所示。用频设备、地面控制站均假设为单天线。网络的各个时隙表示为t=0, 1, 2, …。网络的工作频带内共包含N个频谱资源块。在每个时隙,每个用频设备需占用一个频谱资源块进行上行传输,而雷达则需占用N0(N0 ≥ 1)个频谱资源块以进行目标探测。假定N ≥ K,即网络中频谱资源块总数大于通信设备对频谱资源块的总需求数。
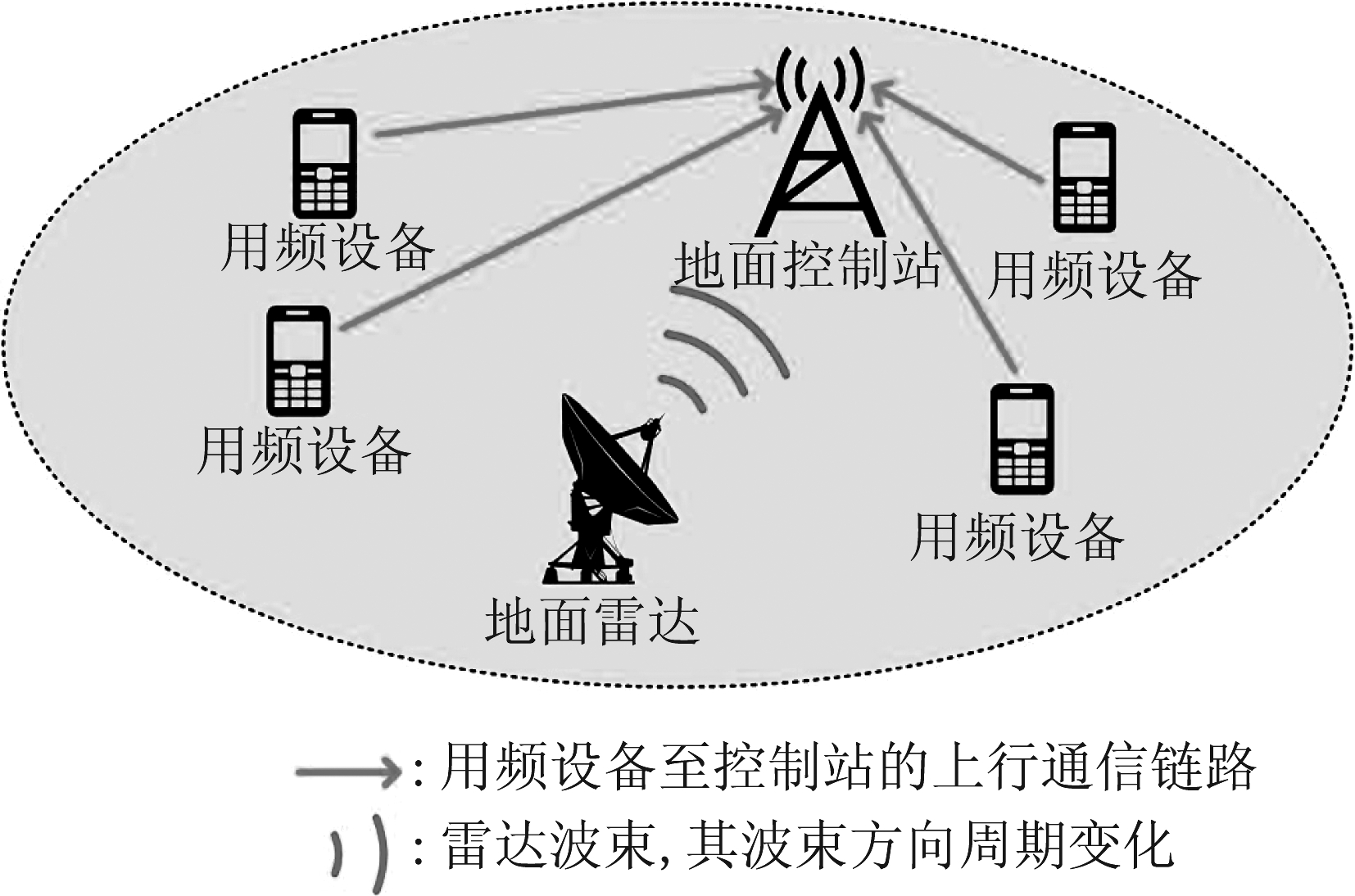
图1 雷达-通信一体网络中通信设备的上行通信链路
Fig.1 Uplink transmission of communication equipment in radar-communication integrated networks
对于网络中的通信设备,其工作频率和发射功率依据电磁环境变化规律进行动态决策。在第t个时隙开始时,每个用频设备需在N个频谱资源块中选择一个用于上行传输。令布尔型变量αt,k,n表示第k个用频设备在第t个时隙内是否占用第n个频谱资源块:如果αt,k,n取值为1,则第k个设备占用第n个频谱资源块;否则,第k个设备不占用第n个频谱资源块。每台设备在一个时隙内所能占用的频谱资源块个数有且仅有1个。第k个用频设备在第t个时隙内的发射功率表示为pt,k。
对于网络中的雷达设备,其在每个时隙内需从N个频谱资源块中占用N0个用于目标探测。由于雷达的工作频率通常固定或按某种已知规律规则变化,因此本论文假设在第t个时隙内雷达对频谱资源块的占用状况为已知信息。令P0表示雷达设备的发射功率,Gt,k表示在第t个时隙内雷达与用频设备k间的天线增益。本论文假设雷达的发射功率固定。由于地面雷达的发射功率通常较大,会对临近信道造成比较严重的干扰。为描述雷达对频谱资源块的占用情况和度量雷达-通信一体网络中雷达在各个频谱资源块的干扰程度,定义雷达占用因子βt,n。对于雷达本身占用的N0个频谱资源块,βt,n=1/N0;对于其余频谱资源块,βt,n表示雷达发射功率在该资源块上的邻信道泄露比(Adjacent Channel Leakage Power Ratio, ACLR)。
用频设备k在第n个频谱资源块上相对于地面控制站的信道功率增益记为gt,k,n。网络中的背景噪声假定为均值为0,方差为σ2的高斯白噪声。同时,受未知干扰源、设备间互调干扰等因素影响,雷达-通信网络中可能存在其他各类随机干扰。令δt,k表示地面控制站接收到的各类随机干扰信号的总功率。按照实际情况,δt,k的统计特性假定为未知。由于周围电磁环境的复杂多变性,该随机干扰项δt,k可能在一个时隙内变化若干次。不失一般性,假定一个时隙可等效视为M个等间隔时间段,δt,n(m)表示在时隙t下第m个时间段内在频谱资源块n上的随机干扰。在实际中,用频设备频繁切换工作频率可能导致严重的系统时延[22],因而本论文假定频谱选择变量αt,k,n、雷达占用因子βt,n及信道功率增益gt,k,n在同一时隙下各个时间段内需维持恒定;另一方面,在第t个时隙下第m个时间段内的功率调控变量pt,k(m)和天线增益Gt,k(m)则会随时间段的不同而动态变化。频谱选择变量αt,k,n与功率调控变量pt,k(m)的相对变化关系如图2所示。综上所述,在第t个时隙内的第m个时间段,地面控制站所接收的用频设备k在频谱资源块n上信号的传输速率为
(1)
其中gt,0,n表示雷达在第n个频谱资源块上相对于地面控制站的信道功率增益。根据上述建模,在第t个时隙中的第m个时间段,所有用频设备在第n个频谱资源块上的和速率可表示为∑kRt,k,n(m)。
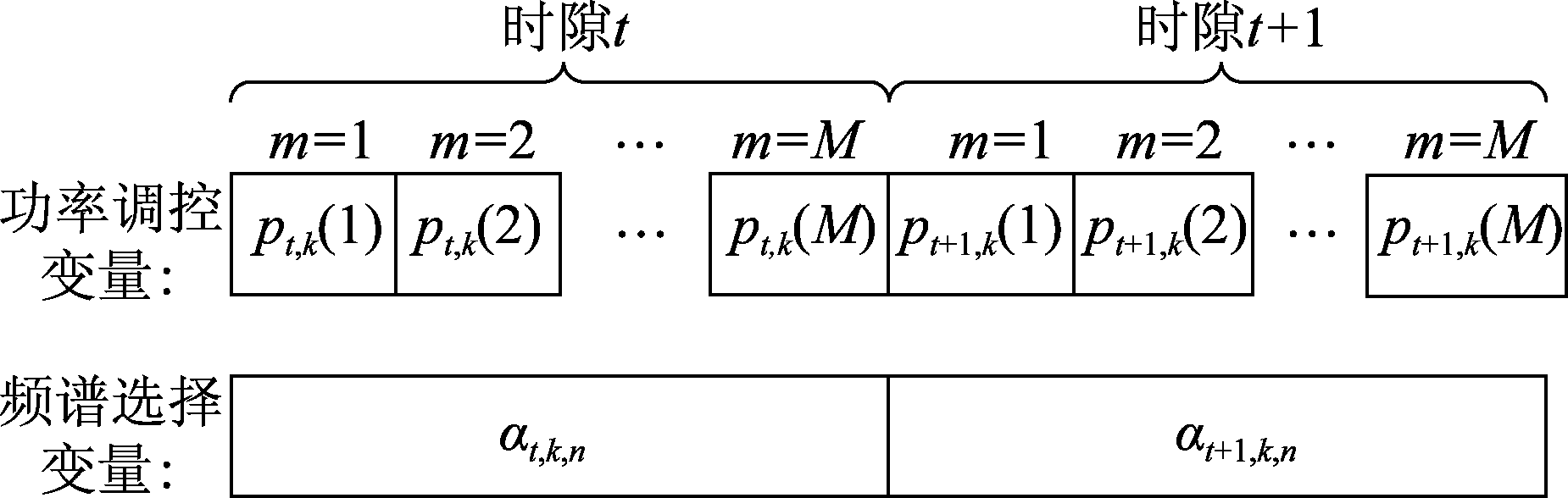
图2 频谱选择变量与功率调控变量相对变化关系
Fig.2 Relationship between the frequency selection variable and the power control variable
本论文通过对雷达-通信一体网络中用频设备的频率选择及功率分配进行联合优化,在满足各用频设备QoS需求的条件下,实现网络中各用频设备长期平均发射功率的最小化。上述优化问题可建模为以下形式:
s.t. ∑nαt,k,n=1, ∀t,k,
αt,k,n∈{0,1}, ∀t,k,n
pt,k(m)≥0, ∀t,k,m 
(2)
其中
表示用频设备k的传输速率阈值。优化问题(2)共包含以下四类约束条件:1)同一用频设备在同一时隙内能且仅能占用一个频谱资源块;2)频率选择优化变量αt,k,n为布尔型整数变量;3)功率调控变量pt,k(m)为非负实数;4)每个用频设备的QoS需求存在下限
上述的频率选择与功率分配联合优化问题本质上是一个以长期平均损耗为优化目标的马尔可夫决策过程问题,其状态空间、动作空间、瞬时损耗等属性定义如下:
1)状态:雷达-通信一体网络在第t个时隙内的状态为一向量St,其第k个元素St,k定义为第k个用频设备在第t个时隙内占用频谱资源块在频谱资源块集合中所对应的序号nk。
2)动作与策略:在第t个时隙开始时,每个用频设备需选择其占用频谱资源块,并决定该时隙下各个时间段内所对应的发射功率。因此,第k个用频设备在第t个时隙内的动作空间可以表示为at,k={(αt,k,n, pt,k(m))|
n,m}。网络中所有用频设备在第t个时隙内的动作空间则可表示为at={at,1, at,2, …, at,K}T。网络的策略π则定义为从状态空间至动作空间的映射,即at=Aπ(St)。
3)瞬时损耗:瞬时损耗Ct可定义为在第t个时隙内所有用频设备发射功率之和,即
3 分布式相对值迭代算法
本节提出一种分布式相对值迭代算法对优化问题(2)进行求解。该问题为以长期平均损耗为目标的马尔可夫决策过程问题,其在第t个时隙的贝尔曼最优性方程(Bellman Optimality Equation,BOE)可以写作
(3)
其中V(St)为状态St的相对值函数;S0为一任意但固定的相对状态;At代表在第t个时隙的状态空间。对于以长期平均损耗为目标的马尔可夫决策过程问题,通常可利用相对值迭代方法求解,即通过反复求解贝尔曼方程求得状态St与相对值函数V(St)的更新序列,直到当前状态的相对值函数V(St)与初始状态下的相对值函数V(S0)间差值收敛[21]。然而,相对值迭代方法通常只能解决状态及动作空间维度有限的问题。对于雷达-通信一体网络下的频谱选择与功率分配联合优化问题(2),其状态维度随用频设备数的增加而急剧增长,其动作空间中更是包含发射功率这一连续优化变量。因而对于问题(2)直接利用传统的相对值迭代方法容易陷入“维度诅咒”问题而导致难以甚至无法收敛。基于此,本论文提出一种高效的分布式相对值迭代算法求解上述马尔可夫决策过程问题。
为降低原优化问题的维度,分布式相对值迭代算法首先对频谱资源块进行预分配处理,将原有的以长期平均损耗为目标的马尔可夫决策过程问题解耦为多个小规模、低维度马尔可夫决策过程子问题。为对优化问题(2)进行解耦,首先注意到问题(2)中的瞬时损耗Ct可分解为与St,k和at,k相关的K个子项,即
其中
此外,可以观察到除约束条件∑nαt,k,n=1外,问题(2)中的其余约束条件同瞬时损耗Ct一样,均可分解为与at,k相关的K个子约束集。因此,对约束条件∑nαt,k,n=1进行解耦,即可将原优化问题分解为K个可并行求解的子问题。本论文假设网络中各个信道具备遍历特性。对于网络中频谱资源,首先进行预分配处理,使可用的(N-N0)个频谱资源块分解为K个频谱资源块子集,并分别对应K台用频装备。具体来说,本论文将(N-N0)个频谱资源块平均分配至K个用频设备,保障每个用频设备至少具备⎣ (N-N0)/K」个可用频谱资源块,其中⎣·」表示向下取整。对于N能被K整除的情况,则频谱资源块恰好可平均分配至K台用频设备;对于N不能被K整除的情况,则将余下频谱资源块随机分配至各台装备。对于用频设备k,令Nk表示其对应频谱资源块子集中的资源块数目,令nk∈{1, 2, …, Nk}表示第k个频谱资源块子集中频谱资源块的序号。至此,上述以长期平均损耗为优化目标的马尔可夫决策过程问题(2)可解耦为K个低维度马尔可夫决策过程子问题。具体来说,在第t个时隙内关于第k个用频设备的以长期平均损耗为优化目标的低维度马尔可夫决策过程子问题可以表示为
s.t. ∑nkαt,k,nk=1, ∀t,
αt,k,nk∈{0,1}, ∀t,nk, pt,k(m)≥0, ∀t,m
(4)
其中πk表示第k个用频设备的策略。令At,k表示动作at,k的动作空间,则关于子优化问题(4)的贝尔曼方程可以写作
(5)
其中St,k可看作第k个用频设备在第t个时隙内的状态;Vk(St,k)表示状态St,k对应的相对值函数。值得注意的是,对于解耦后第k台用频设备所对应的低维度马尔可夫决策过程子问题,其状态St,k的维数仅为其对应频谱资源块子集内的资源块数目,即Nk。因此,求解K个马尔可夫决策过程子问题较直接求解马尔可夫决策过程问题(2)可大大减少所涉及状态维度。此外,解耦后的马尔可夫决策过程子问题具有分布式结构,可并行独立求解,从而进一步降低运算复杂度,提升运行时间。求解子优化问题(4)其本质在于迭代求解对应的贝尔曼方程(5)。面对频率选择与功率分配两组决策变量,可将贝尔曼方程(5)进一步解耦为分别关于频率选择和功率分配的两个子问题:(a)频率选择已知条件下的功率分配问题;(b)功率分配最优解形式已知条件下的频率选择问题。
3.1 频率选择已知条件下的功率分配
注意到本论文中的频率选择在一个时隙中只进行一次,而功率分配在一个时隙内总共进行M次。因此,在该时隙下第一个时间段内,优化问题(4)包含对频率选择与功率分配的联合优化;而在该时隙下其余 (M-1)个时间段内,优化问题(4)仅包含对功率分配的优化。本部分内容首先考虑仅包含功率分配时间段下的优化问题,即问题(4)中的频率选择优化变量αt,k,nk为已知的常数。不失一般性,令n*表示该时隙下用频设备所选择频率。在上述前提下,优化问题(4)所对应的贝尔曼方程(5)退化为在时隙t内的第m个时间段(m>1)对第k个用频设备的最优功率分配问题:
s.t. pt,k(m)≥0 , 
(6)
其中gt,k,n*表示第k个用频设备在其已选择频率n*上与地面控制站间的信道功率增益;gt,0,n*表示雷达在其频率n*上与地面控制站间的信道功率增益。可以看出,功率分配优化问题(6)是一个凸优化问题。为求解问题(6),通过引入拉格朗日乘子,可得到原优化问题的拉格朗日对偶项:
L(pt,k(m),λt,k(m))=pt,k(m)-
s.t. pt,k(m)≥0
(7)
接下来,对问题(7)中的目标函数关于变量pt,k(m)求偏导,并令偏导数等于零,从而得到关于pt,k(m)最优性条件:
pt,kL(pt,k(m),λt,k(m))=
(8)
同时,根据K.K.T条件(Karush-Kuhn-Tucker condition)[23]理论,优化问题(6)中对传输速率约束的互补松弛条件(complementary slackness condition)可以写为
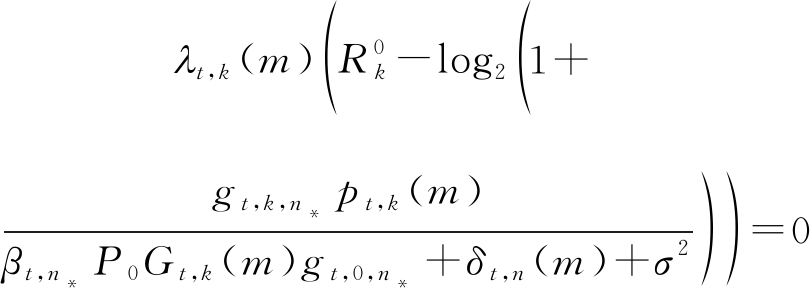
(9)
结合等式(8)与等式(9),在所选择频率n*已知且固定的条件下,第k个用频设备在时隙t下第m个时间段内(m > 1)的最优功率分配及对应的最优拉格朗日乘子可以表示为
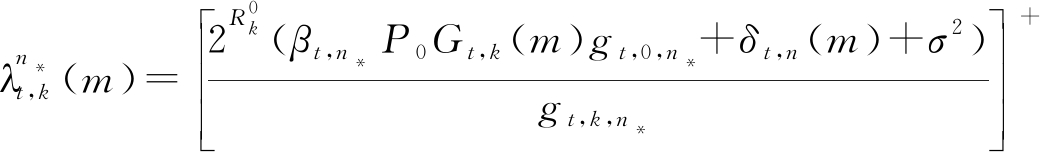
(10)
其中非负运算[·]+由非负约束条件pt,k ≥ 0及λt,k ≥ 0得到。换言之,对于网络中的每台用频设备,若其频率选择情况已知,便可由等式(10)计算出功率分配最优解的闭式解形式。
3.2 功率分配最优解形式已知条件下的频率选择问题
上述的频率选择已知条件下的功率分配问题适用于任一时隙下后(M-1)个时间段。对于每个时隙下的第一个时间段,优化变量不仅包含每台设备的功率分配,还涉及每台设备的频率选择。注意到最优功率分配的闭式解形式(10)适用于任意时间段下任一被选择频率。换言之,被选择频率一旦确定,其对应的最优分配功率便可由等式(10)唯一确定。基于此,各时隙下第一个时间段内的频率选择与功率分配联合优化问题本质上可归结为一个功率分配最优解形式已知条件下的频率选择问题:
s.t. ∑nkαt,k,nk=1,
αt,k,nk∈{0,1}, ∀nk, 
(11)
其中
表示在t时隙下第一个时间段内,用频设备k的所选频率为nk时对应的功率分配最优解形式,可由等式(10)在n*=nk时计算得到。注意到在问题(11)中优化变量αt,k,nk为布尔型变量,且其对应的动作空间复杂度较低,因此对于功率分配最优解形式已知条件下的频率选择问题(11),其频率选择最优解αt,k,n*可利用枚举法快速求解。在得到频率最优解αt,k,n*与功率最优解
后,分布式相对值迭代算法利用传统的相对值迭代方法对价值函数Vk(St,k)进行更新,其中更新策略为ε-贪婪规则[24]。综上所述,分布式相对值迭代算法的伪代码如表1所示。
表1 分布式相对值迭代算法
Tab.1 Distributed relative value iteration algorithm
分布式相对值迭代算法初始化。对于V0,k和St,k赋初值;令t=0,m=0;对频谱资源集进行预分配处理;迭代:1. 重复:2. 对于k从1到K:3. m=m+1;4. 对于频率nk从1到Nk,按等式(10)更新pnkt,k(m)(令n*=nk);5. 如果m=1:6. 利用枚举法求解问题(11),得到频率选择最优解αt,k,n*;7. 在频率选择αt,k,n*已知的条件下,按等式(10)获取最优功率分配pn*t,k(m);8. 如果m=M:9. 采用ε-贪婪规则,利用相对值迭代方法更新Vt+1,k(St,k)及Vt+1,k(S0,k);10. t=t+1,m=0;11. 直到满足终止条件。
4 仿真结果
本节内容对所提算法进行性能评估与仿真验证。本论文提出的分布式相对值迭代算法旨在解决面向频率选择与功率分配联合动态优化的马尔可夫决策过程问题。与以往的研究相比,本论文所提方法针对长期网络效用,关注前后时刻网络状态变化的关联性。而以往研究大多采用面向瞬时网络效用,不考虑当前时刻决策对前后状态的影响。在下文中,将应用分布式相对值迭代算法求解动态优化问题(2)形成的策略称为长期效用策略。作为对比,将最小化每个时刻瞬时损耗Ct的策略称为瞬时效用策略。通过观察可以看出,长期效用策略与瞬时效用策略的区别在于长期效用策略除考虑瞬时效用Ct外,也考虑未来效用
而瞬时效用策略仅考虑瞬时效用Ct。在下文的仿真中,长期效用策略与瞬时效用策略的起始点与终止条件均相同。
仿真场景设置为一长宽均为2000 m的城区范围。城区内共有一个机械扫描式雷达与一个地面控制站。其中地面指挥站在城区的中心位置,其坐标设为(0, 0)。机械扫描站悬停于空中的固定位置,其坐标表示为(-500, 500, 1000)。用频设备的信道模型采用3GPP TR 36942中的宏小区模型[26]。雷达的天线方向图采用ITU-R M.1581中的均匀场分布模型[27]。用频设备在地面的移动满足随机游走模型(Random Walk Model)[28]。随机干扰项δt,n假定满足瑞利分布。其余的系统参数如表2所示。仿真实验中雷达占用因子βt,n的取值规则如下:若在第t个时隙内第n个频谱资源块被雷达设备所占用,则依据雷达占用因子的定义βt,n=1/N0;若第n个频谱资源块没有被雷达设备所占用,则βt,n=α|n-m|,其中m为与第n个频谱资源块相邻最为接近的雷达设备所占用频谱资源块;α为衰减比例,在本仿真实验中取值为0.001。
表2 仿真参数[25]
Tab.2 Simulation parameters[25]
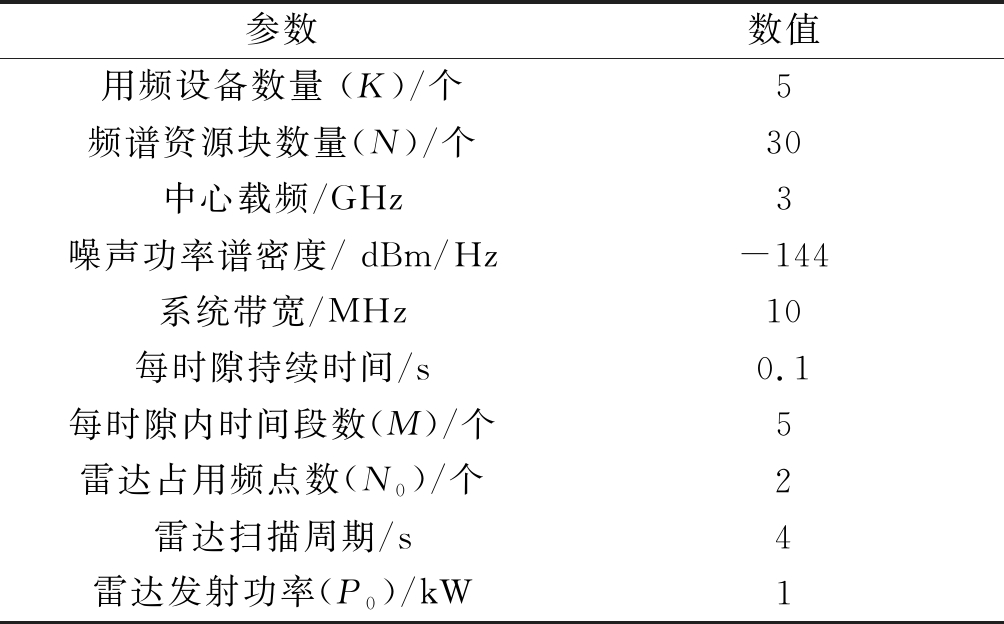
参数数值用频设备数量 (K)/个5频谱资源块数量(N)/个30中心载频/GHz3噪声功率谱密度/ dBm/Hz-144 系统带宽/MHz10每时隙持续时间/s0.1每时隙内时间段数(M)/个5雷达占用频点数(N0)/个2雷达扫描周期/s4雷达发射功率(P0)/kW1
图3研究在长期效用策略与瞬时效用策略下网络中所有用频设备合计的长期平均发射功率与算法迭代次数间的关系。可以看出,随着迭代次数增加,长期效用策略与瞬时效用策略均可达到收敛。相对于瞬时网络策略,长期网络策略在可获得更低的长期平均功耗,其原因在于长期效用策略考虑了前后时刻网络状态及决策信息的关联性,而瞬时效用策略仅关注当前时刻下的网络效用,忽略了前后时刻决策信息对当前时刻网络状态的影响。
由第3节内容可以看出,长期效用策略中的分布式相对值迭代算法利用ε-贪婪规则防止算法陷入局部最优解。为研究ε-贪婪规则中ε取值变化对算法性能的影响,图4研究了当ε取值分别为0.1、0.2及0.3时,网络中所有用频设备合计的长期平均发射功率与算法迭代次数的变化关系。由图4仿真结果可以看出,随着ε取值的增大,长期效用策略所决策出的长期平均发射功率损耗逐渐降低。这是因为在算法运行初期,由于网络动态特性未知,长期效用策略所选择的行为(对应于本论文中的频率选择与功率分配)很有可能并非当前时刻下的最优决策。因此需利用ε-贪婪规则跳出局部解,以寻求全局最优决策。而ε的值越大则意味着算法越有可能提早跳出局部最优解。
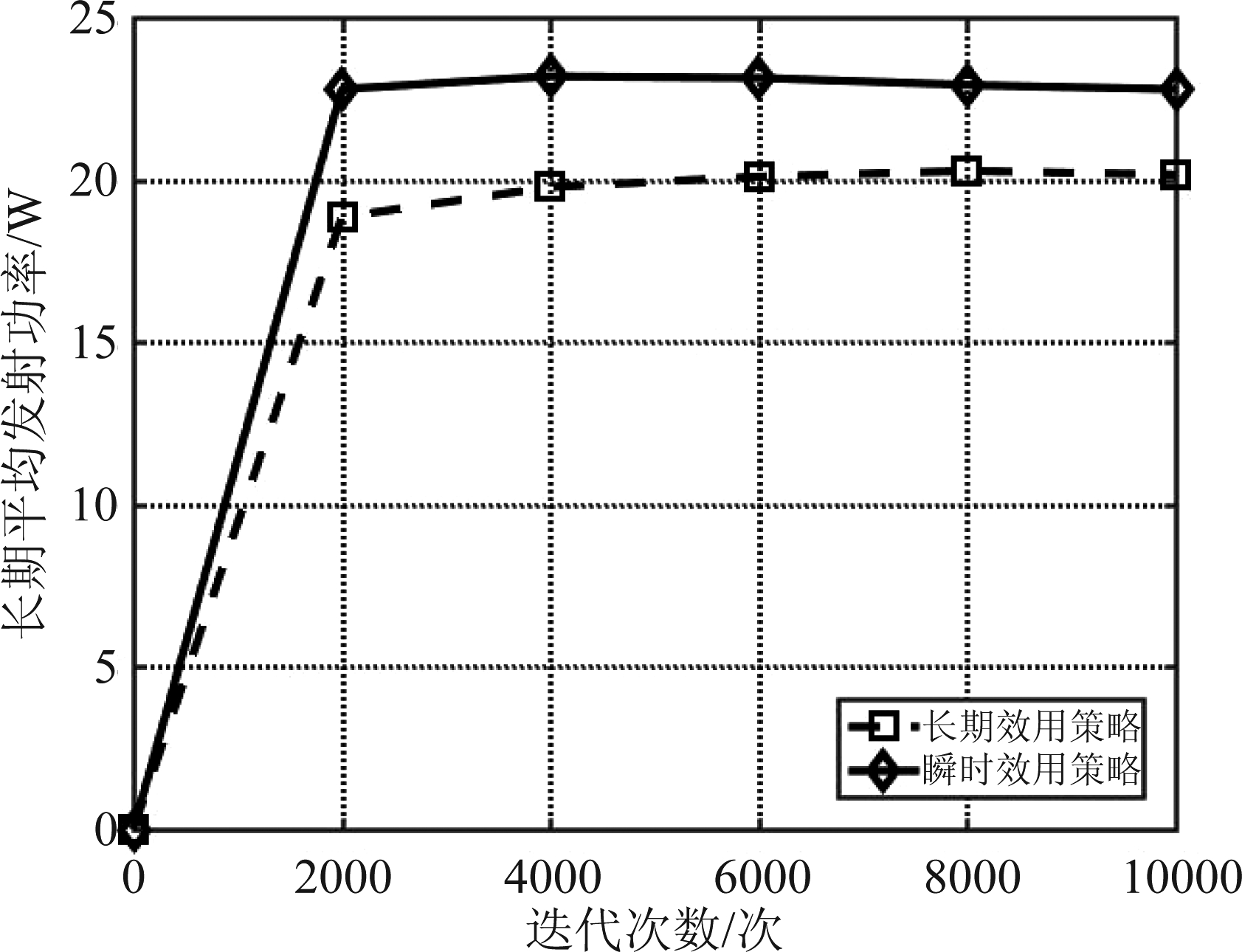
图3 长期平均发射功率与迭代次数的变化关系
Fig.3 Long-term average transmit power vs. the number of iterations
图5研究了网络中用频设备的信干噪比(Signal-to-Interference-plus-Noise Ratio,SINR)阈值取值分别为10 dB、5 dB及0 dB时,网络中所有用频设备合计的长期平均发射功率与算法迭代次数的变化关系。由图5仿真结果可以看出,长期效用策略的长期平均发射功率损耗随着信干噪比阈值的降低逐渐降低。其原因在于对于每一台用频设备,由等式(10)可以看出其功率分配的最优解随传输速率阈值
的提升而提升,而则与信干噪比阈值正相关。
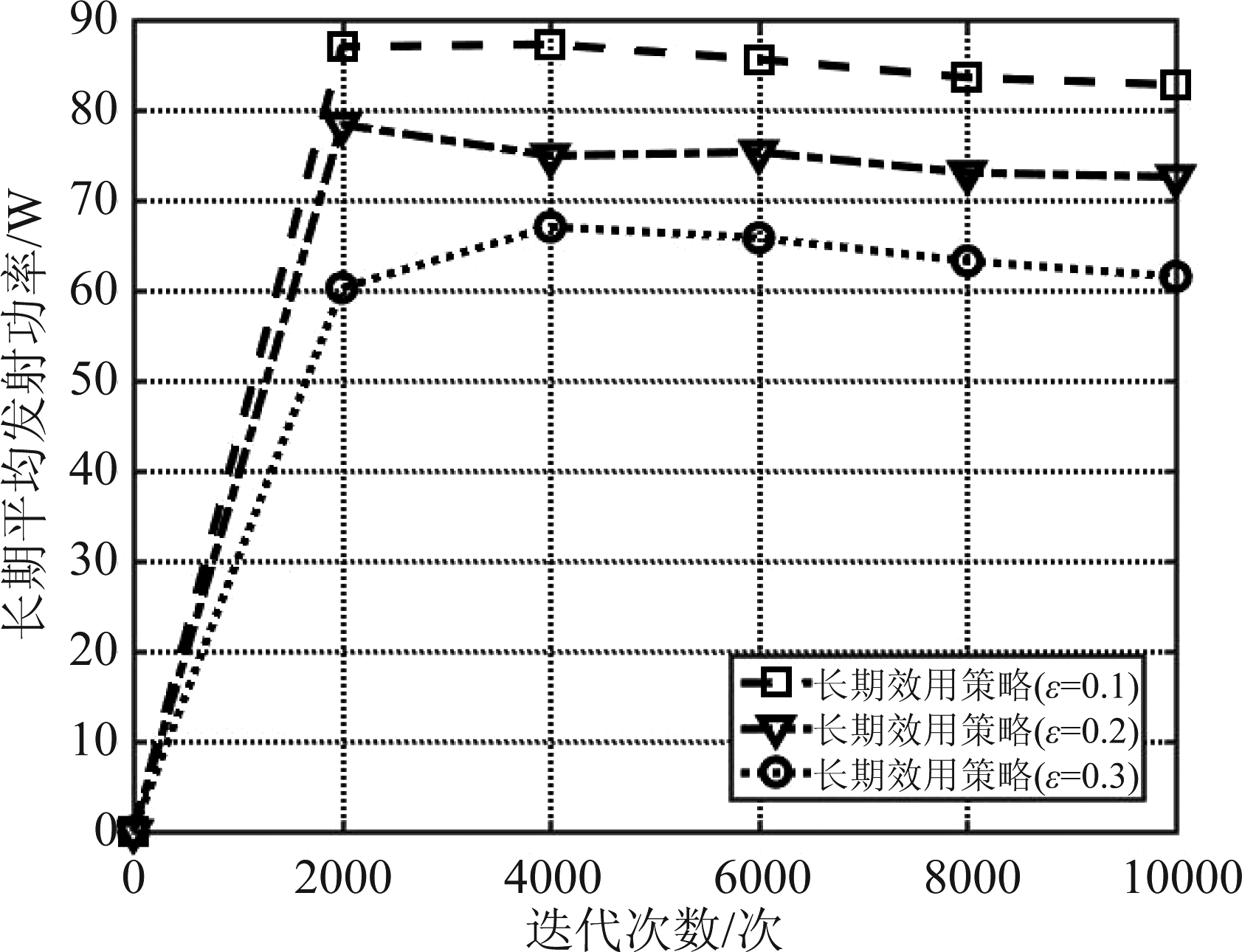
图4 不同ε值下长期平均发射功率与迭代次数的变化关系
Fig.4 Long-term average transmit power vs. the number of iterations under different value of ε
图5 不同信干噪比阈值下长期平均发射功率与
迭代次数的变化关系
Fig.5 Long-term average transmit power vs. the number of iterations under different value of SINR
5 结论
本论文研究了雷达-通信一体网络中的频率选择与功率分配动态优化问题。该优化问题可以构建为一个以长期平均损耗为目标的马尔可夫决策过程问题。为避免陷入“维度诅咒”,本论文提出了一种分布式相对值迭代算法。该算法基于对频带的预分配处理将原高维马尔可夫决策过程问题解耦为多个低维度的马尔可夫决策过程子问题,随后利用传统的相对值迭代方法并行求解每个子问题,并推导出最优功率分配的闭式解形式,极大减少问题复杂度。本论文提出的分布式相对值迭代算法除应用于雷达-通信一体网络外,其将高维度复杂问题分解为多个低维度子问题的机理也可拓展至其他基于长期网络效用的动态资源分配问题。
[1] 吴启晖, 任敬. 电磁频谱空间认知新范式: 频谱态势[J]. 南京航空航天大学学报, 2016, 48(5): 625- 632.
Wu Qihui, Ren Jing. New paradigm of electromagnetic spectrum space: Spectrum situation[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2016, 48(5): 625- 632.(in Chinese)
[2] Naik G, Liu Jinshan, Park J M. Coexistence of wireless technologies in the 5 GHz bands: A survey of existing solutions and a roadmap for future Research[J]. IEEE Communications Surveys & Tutorials, 2018, 20(3): 1777-1798.
[3] Labib M, Reed J H, Martone A F, et al. Coexistence between radar and LTE-U systems: Survey on the 5 GHz band[C]∥2016 United States National Committee of URSI National Radio Science Meeting (USNC-URSI NRSM). IEEE, 2016: 1-2.
[4] 曾瑞琪, 刘方正, 姜秋喜, 等. 雷达通信一体化的六种主要技术体制[J]. 现代雷达, 2019, 41(2): 10-14.
Zeng Ruiqi, Liu Fangzheng, Jiang Qiuxi, et al. Six major technological systems of radar communication integration[J]. Modern Radar, 2019, 41(2): 10-14.(in Chinese)
[5] Lou Hao, Wu Yong, Ma Zhiqiang, et al. A novel signal model for integration of radar and communication[C]∥2016 IEEE International Conference on Computational Electromagnetics (ICCEM). IEEE, 2016: 14-16.
[6] 张令浩, 张剑云, 周青松. 雷达与通信共享频谱波形优化算法研究[J]. 信号处理, 2019, 35(11): 1861-1870.
Zhang Linghao, Zhang Jianyun, Zhou Qingsong. Research on waveform optimization algorithm of radar and communication spectrum sharing[J]. Journal of Signal Processing, 2019, 35(11): 1861-1870.(in Chinese)
[7] 邢文革. 探测通信一体的自组织泛在无线网络体系架构探讨[J]. 现代雷达, 2019, 41(6): 1-7.
Xing Wenge. A study on self-organizing ubiquitous wireless network architecture of radar communication[J]. Modern Radar, 2019, 41(6): 1-7.(in Chinese)
[8] Reed J H, Clegg A W, Padaki A V, et al. On the co-existence of TD-LTE and radar over 3.5 GHz band: An experimental study[J]. IEEE Wireless Communication Letters, 2016, 5(4): 368-371.
[9] Ghorbanzadeh M, Visotsky E, Moorut P, et al. Radar inband and out-of-band interference into LTE macro and small cell uplinks in the 3.5 GHz band[C]∥2015 IEEE Wireless Communications and Networking Conference (WCNC). IEEE, 2015: 1829-1834.
[10] Krishnan N N, Kumbhkar R, Mandayam N B, et al. Coexistence of radar and communication systems in CBRS bands through downlink power control[C]∥MILCOM 2017-2017 IEEE Military Communications Conference (MILCOM). IEEE, 2017: 713-718.
[11] Shajaiah H, Khawar A, Abdel-Hadi A, et al. Resource allocation with carrier aggregation in LTE Advanced cellular system sharing spectrum with S-band radar[C]∥2014 IEEE International Symposium on Dynamic Spectrum Access Networks (DYSPAN). IEEE, 2014: 34-37.
[12] Liu Fan, Masouros C, Li Ang, et al. Robust MIMO beamforming for cellular and radar coexistence[J]. IEEE Wireless Communications Letters, 2017, 6(3): 374-377.
[13] Shi Chenguang, Wang Fei, Sellathurai M, et al. Non-cooperative game theoretic power allocation strategy for distributed multiple-radar architecture in a spectrum sharing environment[J]. IEEE Access, 2018, 6: 17787-17800.
[14] Shi Chenguang, Wang Fei, Salous S, et al. Nash bargaining game-theoretic framework for power control in distributed multiple-radar architecture underlying wireless communication system[J]. Entropy, 2018, 20(4): 267.
[15] Shi Chenguang, Qiu Wei, Wang Fei, et al. Power control scheme for spectral coexisting multistatic radar and massive MIMO communication systems under uncertainties: A robust Stackelberg game model[J]. Digital Signal Processing, 2019, 94: 146-155.
[16] Garnaev A, Trappe W. An OFDM-based dual radar/communication system facing uncertain jamming power[C]∥2017 IEEE Conference on Communications & Network Security (CNS). IEEE, 2017: 1-9.
[17] Kozy M, Yu Jianyuan, Buehrer R M, et al. Applying deep-Q networks to target tracking to improve cognitive Radar[C]∥2019 IEEE Radar Conference (RadarConf). IEEE, 2019: 1- 6.
[18] Wang Qing, Du Panfei, Dou Tongdong, et al. Cognitive passive radar system: software defined radio and deep learning approach[J]. The Journal of Engineering, 2019, 21: 7326-7330.
[19] Alberge F. Deep learning constellation design for the AWGN channel with additive radar interference[J]. IEEE Transactions on Communications, 2018, 67(2): 1413-1423.
[20] Puterman M L. Markov decision processes: discrete stochastic dynamic programming[M]. John Wiley & Sons, 2014.
[21] Powell W B. Approximate Dynamic Programming: Solving the curses of dimensionality[M]. John Wiley & Sons, 2007.
[22] Li Mingyan, Guan Xinping, Hua Cunqing, et al. Predictive pre-allocation for low-latency uplink access in industrial wireless networks[C]∥IEEE INFOCOM 2018-IEEE Conference on Computer Communications. IEEE, 2018, 306-314.
[23] Boyd S, Vandenberghe L. Convex optimization[M]. Cambridge University Press, 2004.
[24] Watkins C J C H, Dayan P. Q-learning[J]. Machine Learning, 1992, 8(3- 4): 279-292.
[25] Al-Hourani A, Kandeepan S, Jamalipour A. Modeling air-to-ground path loss for low altitude platforms in urban environments[C]∥2014 IEEE Global Communications Conference. IEEE, 2014: 2898-2904.
[26] Equipment U. Evolved universal terrestrial radio access (e-utra); radio frequency (rf) system scenarios, 3rd generation partnership project (3GPP)[J]. TR 36.9422010, 2010.
[27] International Telecommunication Union Radiocommunications Sector. ITU-R Recommendation M.185--2018, Mathematical Models for Radiodetermination Radar Systems Antenna Patterns for use in Interference Analysis[S]. Geneva: International Telecommunication Union, 2018.
[28] Camp T, Boleng J, Davies V. A survey of mobility models for ad hoc network research[J]. Wireless Communications and Mobile Computing, 2002, 2(5): 483-502.
