1 引言
雷达通信一体化共享信号(RadCom)技术，即使用一种信号同时实现雷达与通信两种功能，不但能够有效降低平台的负重、能耗以及电磁干扰等问题，而且能大大提高对能量与频谱资源的利用率，近年来受到了军事与民用领域的广泛关注[1-2]。
OFDM是通信系统中一种成熟的多载波数据传输技术，具有频谱利用率高、抗多径干扰能力强等优点，同时由于其波形设计灵活，也逐渐应用于雷达领域，因此成为一种合适的共享信号体制。然而由于通信信息的调制，OFDM共享信号的自相关性能通常较差，经过匹配滤波处理后将出现较高的距离旁瓣，在雷达目标检测中容易形成假目标，在多目标环境下还将产生严重的遮蔽现象。因此，抑制OFDM共享信号的距离旁瓣成为一个急需解决的问题。
Sebt采用最小二乘法合成OFDM信号的模糊函数，使其具有图钉型的模糊函数以及较低的峰均功率比(PAPR)，但该方法只适用于OFDM雷达信号[3]。Ellinger优选自相关性能好的多载波相位编码信号(MCPC)[4]，将其映射比特信息实现共享信号传输，但频谱效率仅有0.2bit/Hz/s左右[5]。Li对通信数据进行格雷编码，然后在子载波上循环移位，产生具有低PAPR和高主旁瓣比(Peak to Side Lobe Ratio, PSLR)的OFDM共享信号[6]。但该方法的频谱利用率与PSLR成反比，这导致通信速率严重降低，相同的矛盾出现在采用m序列[7]、完全互补码[8]、混沌序列[9]编码的类似方法中。刘永军采用相位编码预调制降低传输相同数据时的旁瓣恶化问题，但该方法在传输随机信息时没有旁瓣抑制作用[10]。Sturm提出了一种基于调制符号域(Modulation Symbol-Domain based, MSD)的信号处理方法，通过OFDM接收符号与发射符号的除法，消除发射信号随机性带来的距离旁瓣波动[2]。
可以看到，当前通过波形设计抑制OFDM共享信号距离旁瓣的方法都存在频谱利用率不足的问题，对于高速率OFDM共享信号，须在雷达接收处理过程中抑制距离旁瓣。而MSD方法更多适用于矩形频谱信号，当发射时采用QAM调制或自适应调制技术[11-15]时，OFDM共享信号就具有非矩形且不断变化的幅度谱，这导致MSD方法的信噪比损失巨大。尤其当出现深度零谱时，该方法将完全失去旁瓣抑制效果。
针对该问题，本文提出一种低信噪比损失的OFDM距离旁瓣抑制方法，在MSD方法的基础上，根据发射信号功率谱自适应设计频域加权函数。文章首先建立了加权函数的优化模型，在给定峰值旁瓣电平(Peak Side lobe Level, PSL)约束条件下，最小化信噪比损失，然后采用序列二次规划(SQP)方法，对问题进行求解。仿真结果表明，该方法在发射信号频谱变化甚至断续的条件下，都能有效抑制OFDM共享信号的距离旁瓣，且信噪比损失远小于常规方法。
2 OFDM共享信号模型
雷达通信共享信号采用脉冲体制，假设每个共享信号脉冲由N个OFDM符号组成，每个OFDM符号包含M个子载波。则OFDM共享信号脉冲的复包络可表示为
(1)
式(1)中T为一个OFDM符号的持续时间，Δf为子载波频率间隔，为保持子载波正交有
是矩形窗函数。dn,m=An,mejφn,m表示第n个OFDM符号的第m个子载波上传输的星座图上的点，An,m与φn,m分别表示该点的幅度与相位。dn,m通过QAM调制产生，且假设在不同位置上的调制数据dn,m相互独立。设第m个子载波上传输的平均功率为Pm，即对任意n，有Pm=E[|dn,m|2]，E[·]表示数学期望。
3 加权函数优化
3.1 峰值旁瓣电平
接收机频域匹配滤波及幅度加权处理原理框图如图1所示。假设输入到该滤波器的信号为式(1)表示的OFDM共享信号，其傅里叶变换为S(f)，则该滤波器的输出响应为
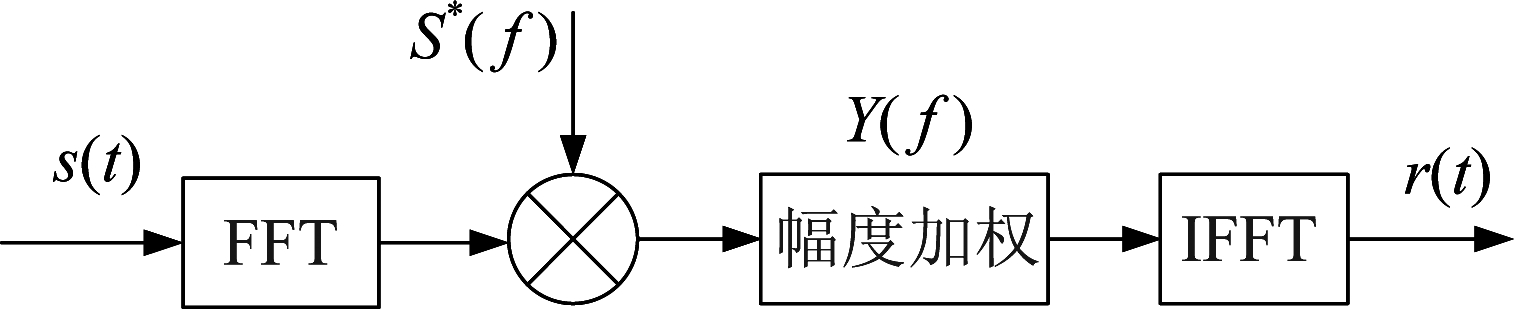
图1 频域匹配滤波及幅度加权处理
Fig.1 Matched filtering and amplitude weighted processing in frequency domain
r(τ)=
S(f)S*(f)Y(f)ej2πftdf
(2)
其中Y(f)表示幅度加权函数，对于传统的矩形幅度谱信号如线性调频信号，Y(f)通常采用具有低旁瓣的窗函数。而在MSD方法中，针对频谱受通信信息调制的OFDM雷达通信共享信号，还需要补偿发射信号的能量谱，从而保持滤波器输出的信号旁瓣不受通信信息影响[2]。因此，加权函数Y(f)可表示为
(3)
在MSD方法中，式(3)中W(f)采用低旁瓣的窗函数，而在本方法中，W(f)需要根据发射信号的频谱进行自适应设计。将式(3)代入式(2)可得
r(τ)=W(f)ej2πfτdf
(4)
式(4)表明，采用该方法处理后的滤波器输出响应只与W(f)有关，因此可以消除通信信息对距离旁瓣的影响。进一步将式(4)离散化，令
得
(5)
式(5)中rk表示不同时刻的滤波器输出。则接收信号的峰值旁瓣电平可表示为
(6)
式(6)中k0表示旁瓣区域的起始采样点。
3.2 信噪比损失
频域幅度加权作为一种失配处理，将损失脉压信噪比，根据文献[16]，信噪比损失L与加权函数Y(f)有如下关系
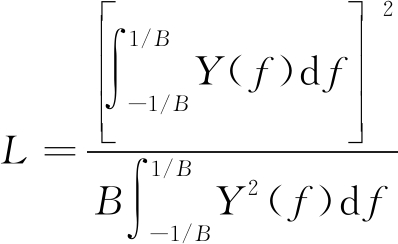
(7)
当OFDM子载波数足够多时，式(7)可近似表示为
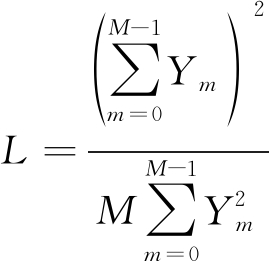
(8)
(9)
对于式(1)表示的OFDM共享信号，根据傅里叶变换，可求得|S(f)|2为
sinc[π(f-fm)T]sinc[π(f-fm′)T]
(10)
由于dn,m携带通信信息，因此|S(f)|2可看作随通信信息变化的随机过程。根据模型假设，OFDM不同位置的调制数据相互独立，因此在不同位置的调制数据dn,m与
的互相关函数
只有当m=m′,n=n′时不为零，即
(11)
因此，对|S(f)|2求期望并将式(11)代入可得
(12)
当子载波数足够大时(大于100)，近似有|S(f)|2≈E[|S(f)|2][15]，因此
(13)
根据辛格函数的性质有
|S(fm)|2=NTPm
(14)
将式(14)、(9)代入(8)有
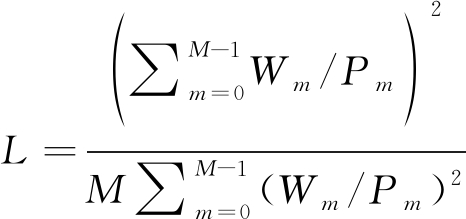
(15)
特别地，当Pm=0时，为了避免出现无效值，令该子载波上Wm/Pm=0。
3.3 优化模型
为了保证雷达目标检测性能，信号的旁瓣电平需要保持在一定数值以下，而信噪比损失越小越好。因此，我们建立如下优化模型，在给定的峰值旁瓣电平条件下，最小化信噪比损失，结合式(5)、(15)可得
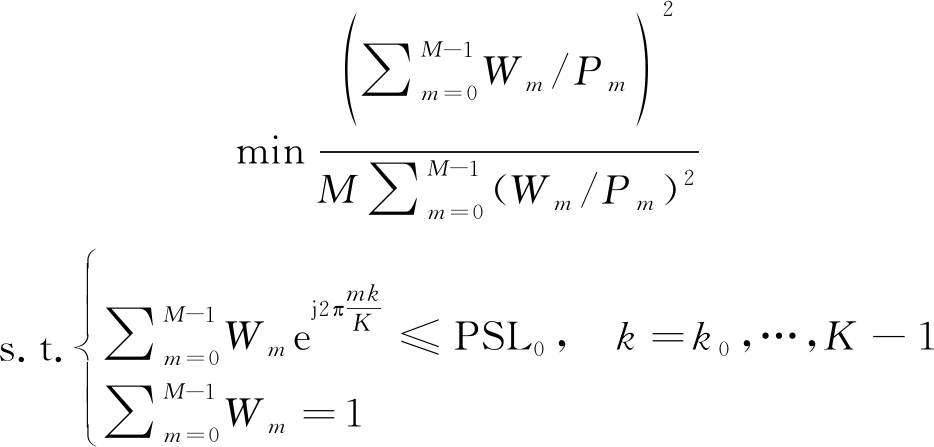
(16)
式(16)中
表示将主瓣输出归一化，PSL0表示给定的峰值旁瓣电平。对于这个非线性约束的优化问题，可采用序列二次优化(SQP)算法求解。SQP算法的核心思想是：在每一次迭代中，使用拟牛顿法逼近由目标函数和约束函数增广而成的拉格朗日函数的海森矩阵；然后通过海森矩阵产生一个二次规划子问题，并求解得到变量的搜索方向；然后通过线性搜索确定步长；最后用搜索方向和步长来更新当前的变量。
4 仿真与分析
实验方法：采用MATLAB优化工具包中的fmincon函数求解式(16)，在该函数中调用SQP算法，得到优化的加权函数。然后随机产生时宽带宽积为BT的OFDM共享信号，加入0 dB的高斯白噪声，通过匹配滤波器与幅度加权网络后，统计输出的主瓣信噪比SNRmain，计算得到信噪比损失，计算公式为L=10lg(BT)- SNRmain。为了验证所提算法的有效性，将优化加权函数与多尔夫—切比雪夫(Dolph-Chebyshev)加权函数作为对比，Chebyshev函数是天线旁瓣抑制理论中提出的一种最佳加权函数，在给定的PSL下具有最窄的主瓣宽度。仿真信号参数：OFDM信号子载波数128，符号数4，带宽20 MHz。
4.1 算法仿真
对于四种具有不同功率谱的信号，分别采用PSL0=-30 dB的优化加权函数与30 dB的Chebyshev函数加权，对处理后的自相关函数进行比较，仿真结果如图2所示，在每种情形中，下图表示信号的功率谱，上图为信号的自相关函数。优化加权仿真中旁瓣起始采样点k0为12，两种方法得到主瓣宽度几乎一致。
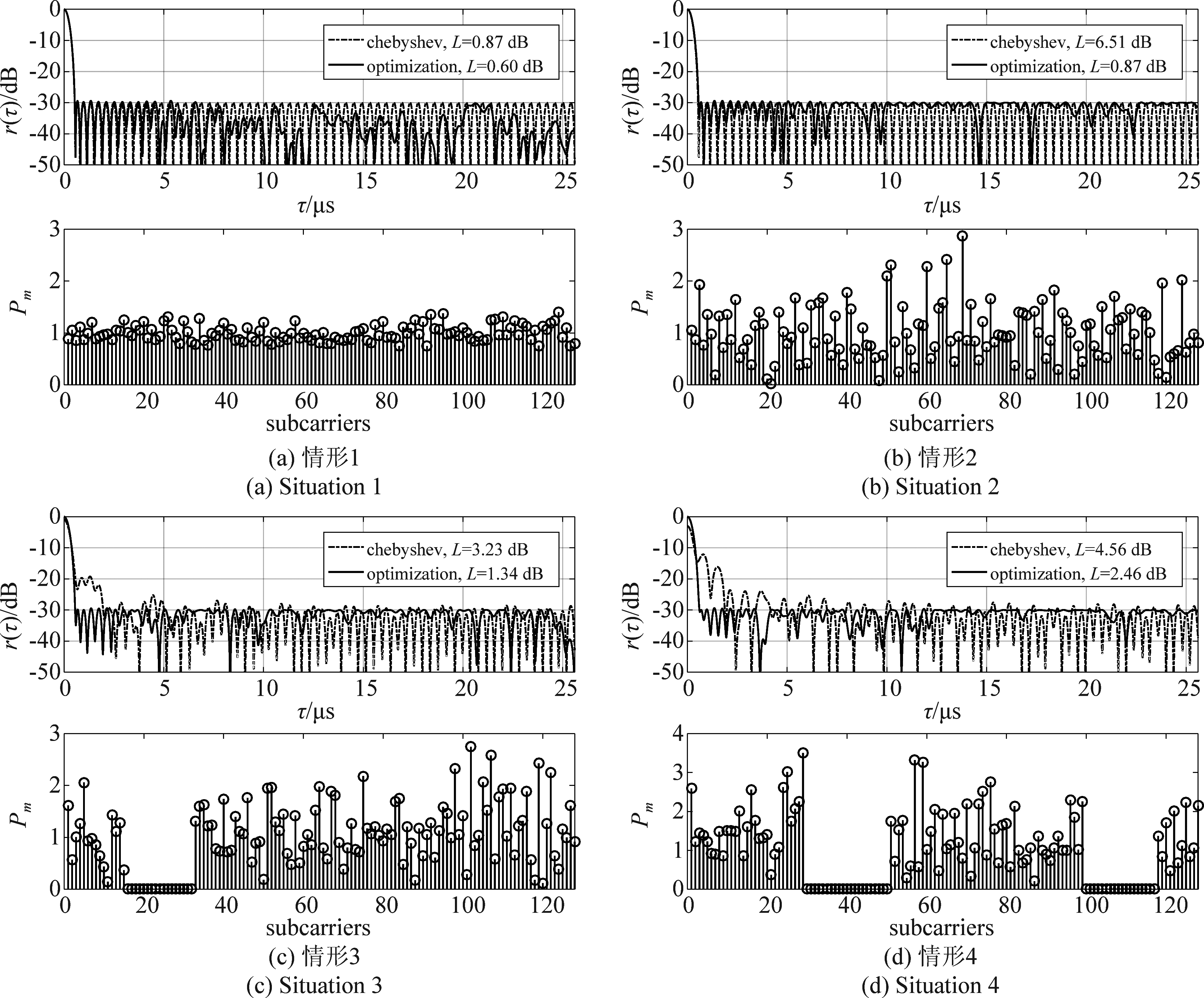
图2 四种不同功率谱信号的自相关函数
Fig.2 Autocorrelation function of four signals with different power spectrum
四种情形分别是：第一种(图2(a))，各个子载波功率分配比较均匀，出现在雷达和通信信道都较为平坦的情况。第二种(图2(b))，各个子载波功率分配相差较大，对应于通信的频率选择性衰落信道或者雷达存在杂波或色噪声干扰的情况，该情形较为常见。第三种(图2(c))，各个子载波功率分配差别较大，并且在信号频谱存在断续。这种情况通常出现于通信子信道深度衰落，或者杂波、干扰功率较大的情况。第四种(图2(d))，各个子载波功率分配差别较大，并且在多段频带上功率分配为零，这种情况出现在衰落或干扰更为严重的情况。
从图2可以看到，旁瓣抑制方面，Chebyshev加权在第一、二种情况中表现正常，而在第三、四种情况下旁瓣抑制失效，PSL仅为-20 dB、-10 dB，这是缺失了部分子载波所导致的。而优化加权函数在全部四种情况下，都很好地达到了-30 dB的旁瓣抑制效果。
信噪比损失方面，在第一种情况中，Chebyshev加权与优化加权的信噪比损失均在1 dB以内，而随着子载波功率分配差异的增加，Chebyshev加权的信噪比损失明显加大，在第二种情况中损失最大，达到了6.51 dB，这将严重影响雷达的目标检测性能。相比之下，优化加权函数的信噪比损失保持较低水平，分别为0.60 dB、0.87 dB、1.34 dB、2.46 dB，体现出优化算法的有效性。
4.2 性能分析
当PSL从-30 dB变化到-45 dB时，统计了优化加权与Chebyshev加权的信噪比损失与-3 dB展宽系数[16]，如表1所示。通过多次试验调整，优化加权仿真中旁瓣起始采样点k0分别取12、14、16、18，可使信噪比损失与-3 dB展宽系数达到较好平衡。从表1可以看出，随着PSL的降低，优化加权的信噪比损失逐渐增大，从0.87增加到3.34，仍然远小于Chebyshev函数的信噪比损失。随着PSL的降低，两种加权函数的主瓣也逐渐展宽，优化加权的展宽程度略高于Chebyshev加权，这说明，只需要稍微牺牲主瓣的宽度(距离分辨率)，就能达到有效降低信噪比损失的目的。
表1 加权函数性能表
Tab.1 Performance of weighting function
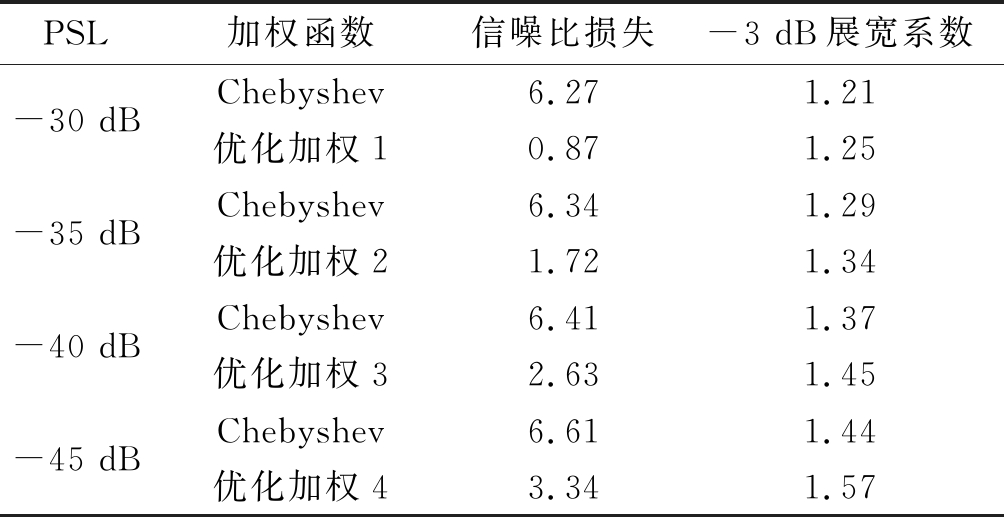
PSL加权函数信噪比损失-3 dB展宽系数-30 dBChebyshev6.271.21优化加权10.871.25-35 dBChebyshev6.341.29优化加权21.721.34-40 dBChebyshev6.411.37优化加权32.631.45-45 dBChebyshev6.611.44优化加权43.341.57
5 结论
本文提出了一种新的OFDM雷达通信共享信号旁瓣抑制方法，该方法在MSD方法的基础上，建立了频域幅度加权函数的优化模型，在给定PSL约束条件下，最小化信噪比损失，然后采用SQP算法求解该优化问题。仿真结果表明，该方法在发射信号频谱变化甚至断续的条件下，都能有效抑制OFDM共享信号的距离旁瓣，且信噪比损失远小于常规方法。
[1] Liu Fan, Masouros C, Petropulu A, et al. Joint radar and communication design: Applications, state-of-the-art, and the road ahead[J]. IEEE Transactions on Communications, 2020, 68(6): 3834-3862.
[2] Sturm C, Wiesbeck W. Waveform Design and Signal Processing Aspects for Fusion of Wireless Communications and Radar Sensing[J]. Proceedings of the IEEE, 2011, 99(7): 1236-1259.
[3] Sebt M A, Sheikhi A, Nayebi M M. Orthogonal frequency-division multiplexing radar signal design with optimized ambiguity function and low peak-to-average power ratio[J]. IET Radar Sonar & Navigation, 2009, 3(2): 122-132.
[4] Levanon N. Multifrequency complementary phase-coded radar signal[J]. IEE Proceedings-Radar, Sonar and Navigation, 2000, 147(6): 276-284.
[5] Ellinger J, Zhang Z, Wicks M, et al. Multi-carrier radar waveforms for communications and detection[J]. IET Radar, Sonar & Navigation, 2017, 11(3): 444- 452.
[6] Li Cong, Bao Weimin, Xu Luping, et al. Radar communication integrated waveform design based on OFDM and circular shift sequence[J]. Mathematical Problems in Engineering, 2017, 2017: 1-10.
[7] Tian Xuanxuan, Song Zhaohui. On radar and communication integrated system using OFDM signal[C]∥2017 IEEE Radar Conference (RadarConf). Seattle, WA, USA: IEEE, 2017: 0318-0323.
[8] Takase H, Shinriki M. A dual-use system for radar and communication with complete complementary codes[C]∥11th International Radar Symposium. Vilnius, Lithuania: IEEE, 2010: 1- 4.
[9] Zhao Jingjing, Huo Kai, Li Xiang. A chaos-based phase-coded OFDM signal for joint radar-communication systems[C] ∥12th International Conference on Signal Processing (ICSP). Hangzhou, China: IEEE, 2014: 1997-2002.
[10] 刘永军, 廖桂生, 杨志伟. 基于OFDM的雷达通信一体化波形模糊函数分析[J]. 系统工程与电子技术, 2016(9): 2008-2018.
Liu Yongjun, Liao Guisheng, Yang Zhiwei. Ambiguity function analysis of integrated radar and communication waveform based on OFDM[J]. Systems Engineering and Electronics, 2016(9): 2008-2018.(in Chinese)
[11] Zhou Yifan, Zhou Huilin, Zhou Fuhui, et al. Resource allocation for a wireless powered integrated radar and communication system[J]. IEEE Wireless Communications Letters, 2018, 8(1): 253-256.
[12] Liu Yongjun, Liao Guisheng, Yang Zhiwei, et al. Multi-objective optimal waveform design for OFDM integrated radar and communication systems[J]. Signal Processing, 2017, 141: 331-342.
[13] Liu Yongjun, Liao Guisheng, Yang Zhiwei, et al. Adaptive OFDM integrated radar and communications waveform design based on information theory[J]. IEEE Communications Letters, 2017, 21(10): 2174-2177.
[14] Kumari P, Vorobyov S A, Heath Jr R W. Adaptive virtual waveform design for millimeter-wave joint communication-radar[J]. IEEE Transactions on Signal Processing, 2019, 68: 715-730.
[15] Liu Yongjun, Liao Guisheng, Yang Zhiwei. Robust OFDM integrated radar and communications waveform design based on information theory[J]. Signal Processing, 2019, 162: 317-329.
[16] 林茂庸, 柯有安. 雷达信号理论[M]. 北京: 国防工业出版社, 1981: 139-141.
Lin Maoyong, Ke Youan. Radar signal theory[M]. Beijing: National Defense Industry Press, 1981: 139-141.(in Chinese)
