1 引言
随着电子技术的发展,不论在军事领域还是民用领域,雷达通信一体化都将是一个必然的趋势[1-3]。比如军用领域的无人战斗机不仅需要完成空中侦察以及战场环境的监视等任务,还需要将获得的数据及时地传回地面。在民用领域的智能交通系统中,智能车辆在感知周围交通环境的同时还需与其他车辆或者融合中心进行通信,这些都需要设备同时具备雷达和通信的功能。在一体化系统中,因为需要监控的环境比较复杂且通信任务较重等原因,单天线已经很难满足需求。多输入多输出技术(Multiple-input multiple-output, MIMO)在雷达系统和通信系统中都已体现出明显的优势,在一体化的研究中也受到研究者的关注[4-9]。本文研究MIMO雷达和MIMO通信一体化系统的性能。
雷达和通信系统共存作为一体化研究的重要任务,得到了学者们的广泛关注[4-20]。从现有的研究情况来看,共存一体化系统的研究大致可分为三类。第一类是在发射端通过合理设计发射波形等手段来减小两个系统间的相互干扰[4,5,7-11]。第二类是在接收端利用连续干扰消除等技术去掉两个系统间的干扰[6,12-14]。第三类是两个系统通过合作,利用另外一个系统来辅助完成本系统的任务,例如文献[15-17]考虑了单天线雷达系统利用通信信号来提升目标检测性能和参数估计性能。本文研究合作式的共存一体化系统,MIMO雷达系统和MIMO通信系统不再视另一方信号为干扰,而是通过合作加以利用,从而使双方的性能都获得增益。
两个系统的合作主要是指信息共享[18-19],例如两个系统的天线位置都与另外一个系统共享,雷达发射信号与通信系统共享,利用通信系统共享的信息,雷达接收端可较准确地译码和重构通信信号[22]。合作式一体化系统不仅可以利用传统雷达的目标回波,还可以利用通信信号携带的目标回波来完成雷达任务。因此,得益于信息共享,合作式一体化系统可等效为一个主动MIMO雷达和被动MIMO雷达混合式的系统,简称主被动混合式MIMO雷达系统。另一方面,由于合作一体化系统雷达端的发射信号和天线位置是与通信端共享的,利用共享的信息,通信接收端可以较准确地获得雷达目标参数,进而在传统通信信息提取的基础上,利用经雷达目标反射后的通信信号来进一步提高通信质量。
本文在雷达任务中考虑目标检测问题[6,15,21-22],且推导合作式MIMO一体化系统的雷达目标检测概率作为衡量性能的准则。将互信息作为衡量通信性能的准则[7,9,18-19,22],推导合作式MIMO一体化系统的通信互信息表达式。分析表明,通过雷达端与通信端的合作,一体化系统的雷达目标检测概率和通信互信息都可以得到提升。鉴于总功率限制是一体化系统不得不考虑的问题,文末简要分析总功率受限情况下合作式MIMO一体化系统的功率分配问题,给出了最优功率分配的方法和结果。
2 信号模型
考虑一个合作式MIMO雷达通信一体化系统,假设雷达端有MR个发射机和NR个接收机,通信端有MC个发射机和NC个接收机,所有的发射机和接收机都是分置的单天线。第m(m=1,…,MR)个雷达发射机和m′(m′=1,…,MC)个通信发射机的发射信号分别为
和
其中ER,m和EC,m′代表发射功率,Ts为采样周期,k(k=1,...,K)表示时间序号,K=「T/Ts⎤,「·⎤代表向上取整,T是观测时间。判定目标是否存在的检测单元位于二维笛卡尔坐标中的(x,y)处。合作式MIMO雷达通信一体化系统的示意图如图1所示。
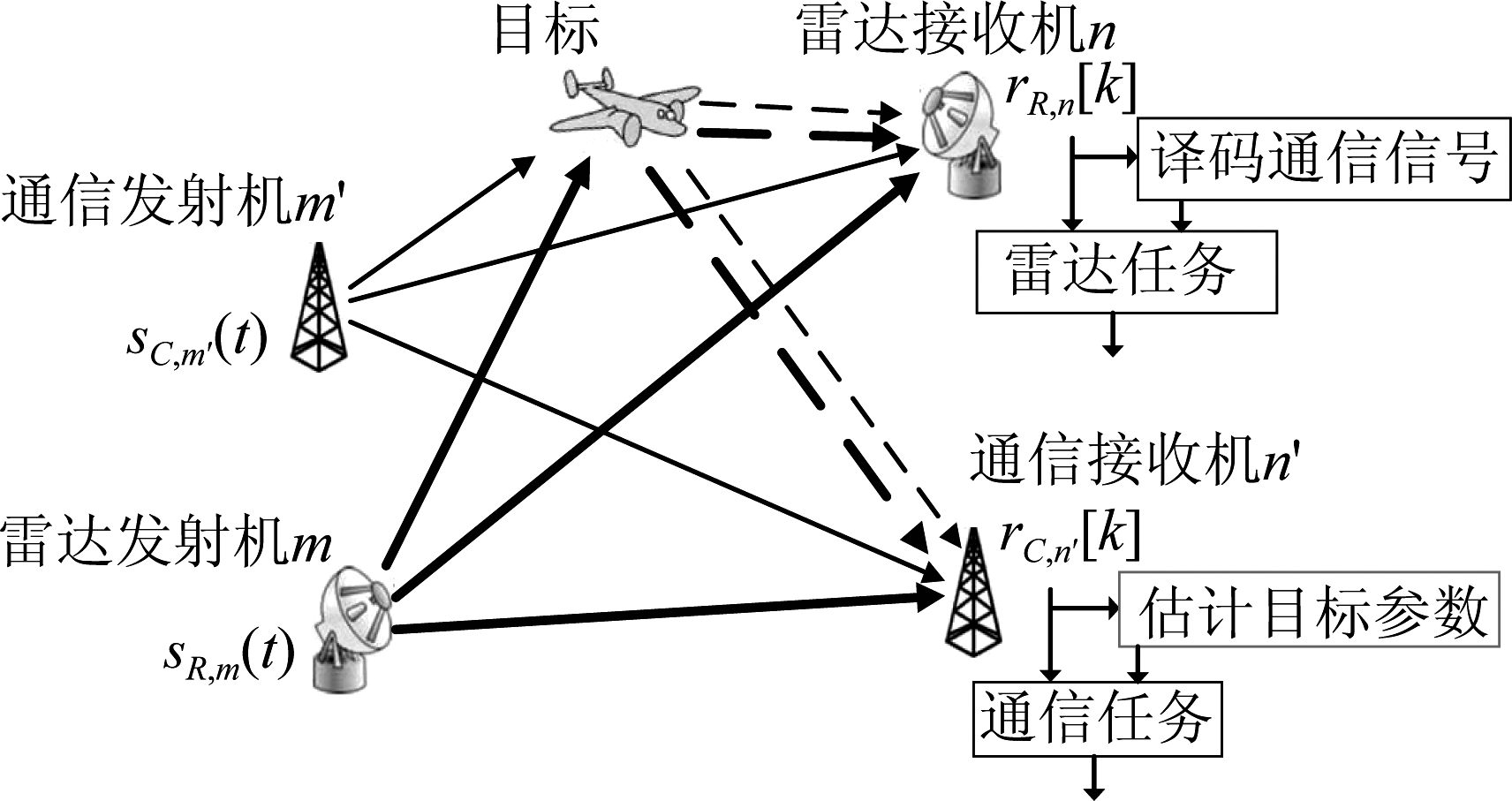
图1 合作式MIMO雷达通信一体化系统示意图
Fig.1 Cooperative MIMO radar and MIMO communication systems
2.1 雷达端接收信号模型
将第n(n=1,…,NR)个雷达接收机处在kTs时刻的接收信号建模为
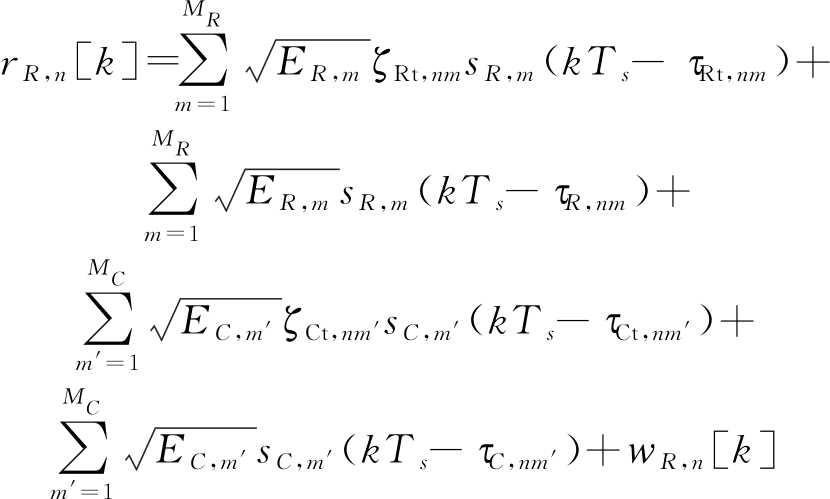
(1)
其中前四项分别表示雷达发射信号对应的目标反射路径和直达路径、通信发射信号对应的目标反射路径和直达路径,τRt,nm,τR,nm,τCt,nm′和τC,nm′则表示相应路径的时延,ζRt,nm和ζCt,nm′为相应的目标反射系数,wR,n[k]代表k时刻的杂波加噪声分量。定义第n个雷达接收机的观测矢量为rR,n=(rR,n[1],…,rR,n[K])T,其中(·)T表示转置,则总的雷达接收信号矢量可以写为
(2)
式中
表示块对角化算子,且
uRt,n[k]=(uRt,n1[k],…,uRt,nMR[k])T,
(3)
公式(2)中的矢量UR,UCt,UC采用与URt类似的定义方式。信号矢量
sRt=(sRt,1[1]T,sRt,1[2]T,…,sRt,NR[K]T)T
(4)
其中sRt,n[k]=[sR,1(kTs-τRt,n1),…,sR,MR(kTs-τRt,nMR)]T。公式(2)中其他信号矢量sR,sCt,sC的定义方式与sRt类似。杂波加噪声向量为
上式中wR,n=(wR,n[1],…,wR,n[K])T,且假设wR服从零均值协方差矩阵为QR的高斯分布。
2.2 通信端接收信号模型
与雷达端的接收信号模型(1)类似,将第n′(n′=1,…,NC)个通信接收机处在kTs时刻的接收信号建模为
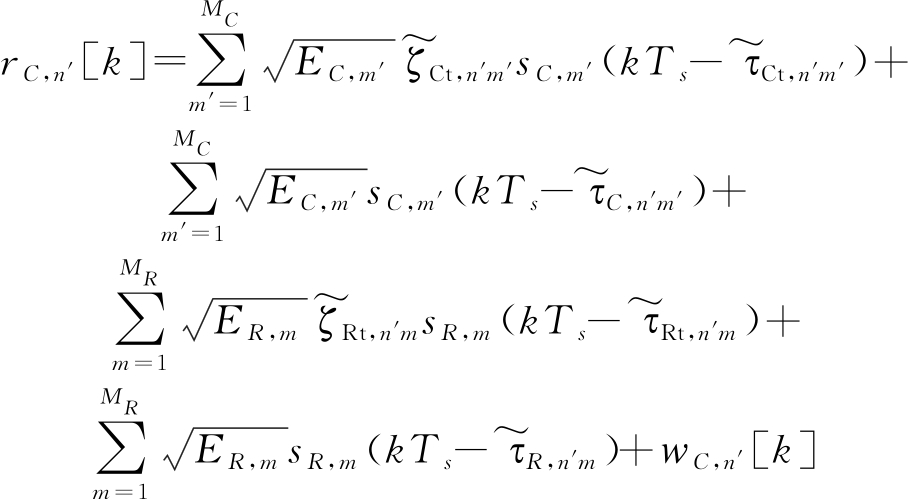
(5)
其中前四项分别表示通信发射信号对应的目标反射路径和直达路径、雷达发射信号对应的目标反射路径和直达路径,
和
则表示相应路径的时延,
和
为相应的目标反射系数,wC,n′[k]代表k时刻的杂波加噪声分量。令rC,n′=(rC,n′[1],…,rC,n′[K])T,则总的通信接收信号矢量可以写为
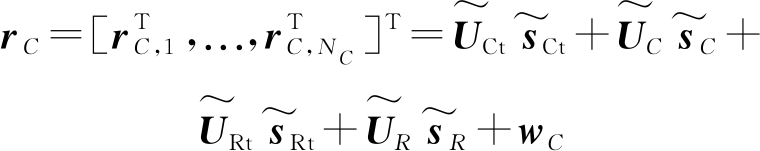
(6)
其中
其对角元素为
(7)
公式(6)中的矢量
采用与
类似的定义方式。式(6)中的信号矢量
(8)
其中
公式(6)中其他信号矢量
的定义方式与
类似。假设通信端的杂波加噪声向量
服从零均值协方差矩阵为QC的高斯分布,其中wC,n′=(wC,n′[1],…,wC,n′[K])T。
前面分别讨论了合作式MIMO雷达通信一体化系统雷达端和通信端的接收信号模型,接下来分析一体化系统的雷达目标检测和通信互信息。
3 合作式MIMO一体化系统中雷达目标检测
本节考虑合作式MIMO雷达通信一体化系统雷达任务中的目标检测问题。利用通信系统共享的信息,假设雷达接收端可较准确地译码和重构通信信号[22]。通过合作,雷达系统不再将通信信号视为干扰,而是将源自通信端的目标回波用来完成雷达目标检测。因此,合作式一体化系统不仅可以利用传统雷达的目标回波,还可以利用通信信号携带的目标回波来完成雷达任务,其中雷达发射信号被目标反射后传到雷达接收端是一个常规主动式雷达的传播过程,而通信信号经目标反射后到达雷达接收端形成的回波被用以完成雷达任务,而不是被当成干扰加以抑制,则相当于一个被动雷达系统。得益于信息共享,合作式一体化系统可等效为一个主被动混合式MIMO雷达系统。
假设雷达任务是在感兴趣的检测单元中探测目标是否存在,根据公式(2)的雷达接收信号模型,记检测单元中目标存在的假设为H1、目标不存在的假设为H0,则检测问题可以描述为
H0∶rR=URsR+UCsC+wR
H1∶rR=URtsRt+URsR+UCtsCt+UCsC+wR
(9)
为了简化分析,考虑通信信号已被译码和重构[22]的情况,且假设可通过预处理等方式使目标反射系数ζRt,nm和ζCt,nm′已知[18,23],则在式(9)中除了噪声wR项其他项都是确知的,因而两种假设下接收信号rR均为高斯分布,概率密度函数分别为
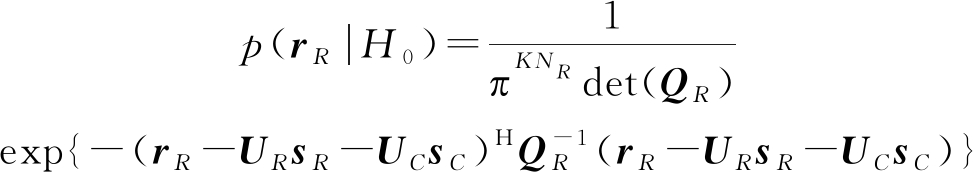
(10)
和
exp{-(rR-URsR-URtsRt-UCsC-UCtsCt)H×
(11)
其中det(·)表示行列式算子。推导可得对数似然比函数为
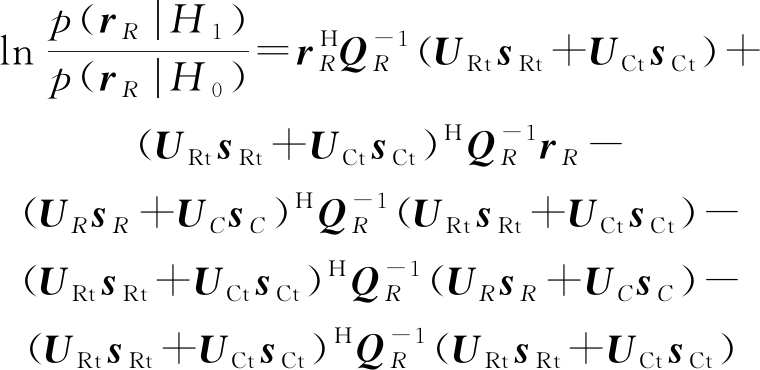
(12)
在式(12)等式右端,除前两项外的其他项都是与rR无关的量,忽略这些项的影响,可以得到检测统计量为
(13)
由上式可见检测统计量TR是接收信号rR的线性组合,因为在H0假设和H1假设下rR均为高斯分布,不难得知两种假设下TR的分布分别为
(14)
其中
μ1=2Re{(URsR+UCsC+URtsRt+
(15)
式中Re{·}表示取一个复数的实部。
根据虚警概率PFA的定义
(16)
可以得到检测门限β为
β=σQ-1(PFA)+μ0
(17)
上式中Q(·)表示标准高斯分布的互补分布函数,其表达式为
(18)
一体化MIMO系统的雷达目标检测概率可以计算如下
(19)
4 合作式MIMO一体化系统中通信互信息
合作式一体化系统中雷达端的发射信号和天线位置是与通信端共享的,利用共享的信息,通信接收端不仅可以消除雷达直达波的干扰,还可以估计雷达未知目标位置θ=(x,y)。根据目标位置的估计结果可进一步去掉通信接收端的雷达目标回波信号的干扰,且可消除经雷达目标反射的通信回波中的未知目标信息。因此,通过合作,一体化系统的通信端不但能消除雷达信号的干扰,还可以使通信端除了利用常规的通信直达波之外,还可利用经雷达目标反射的通信回波来提取有用的通信信息。
假设通信发射信号是已知分布的高斯信号[22],根据通信接收信号模型(6)可得rC的概率密度函数
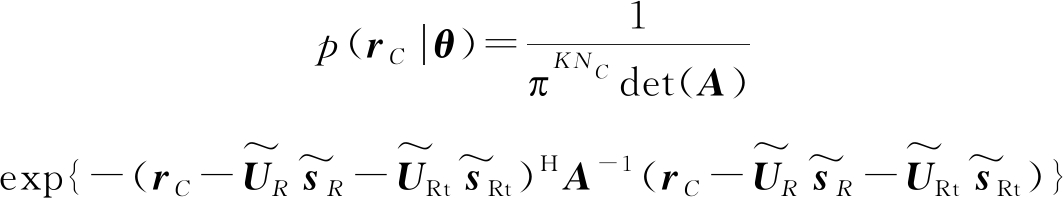
(20)
其中rC的协方差矩阵为
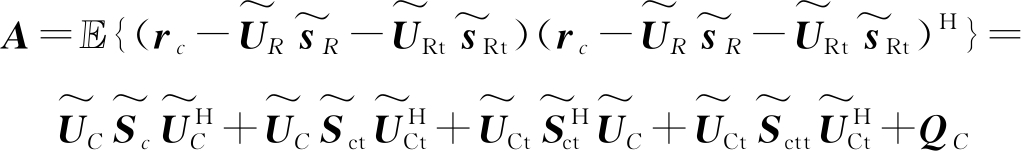
(21)
上式中
表示求数学期望。于是目标位置的最大似然估计结果为
(22)
利用目标位置的估计值,可将目标反射的通信信号的时延估计值和雷达信号的时延估计值分别表示为
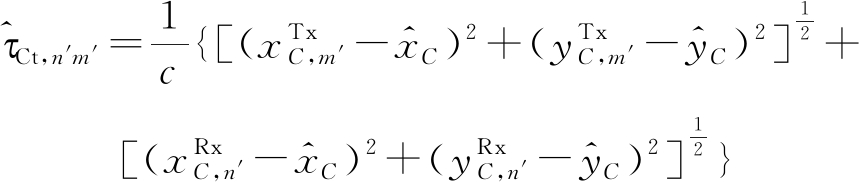
(23)
和
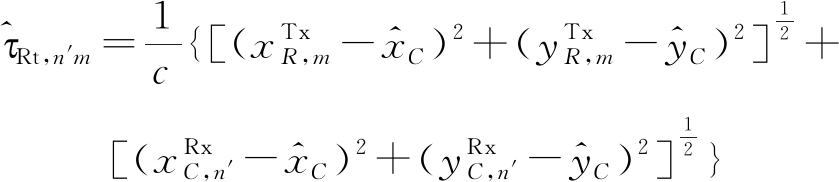
(24)
其中
和
分别表示第m′个通信发射站,第m个雷达发射站和第n′个通信接收站的位置,c表示光速。时延估计结果可以被进一步写为
(25)
其中nCt,n′m′和nRt,n′m表示估计误差,可假设其服从高斯分布[7]。
将式(6)的雷达回波信号
中包含的
替换为估计值
可以得到的估计值,将其表示为
则可以利用这个估计值消除来自雷达发射信号的目标回波。由于合作系统的雷达信号和天线位置是共享给通信系统的,则通信接收端的来自雷达发射的直达信号
也可以被消除。在消除雷达信号之前,先利用文献[12]中的方法得到下面的近似
(26)
其中
表示sR,m(t)关于t的导数。因此,根据公式(26),消除式(6)中雷达信号的干扰后,可得通信接收信号向量为
(27)
其中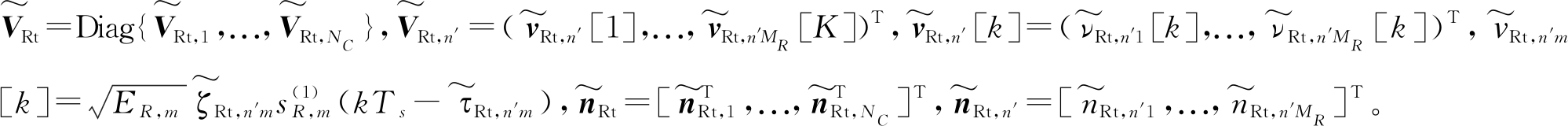
类似地,式(27)中
包含的未知时延
用估计值
替换,为简化分析假设估计误差nCt,n′m′足够小,则此替换的影响可以被忽略[17]。
从式(27)中可以发现观测向量
中
和
都包含通信信号的有用信息,则一体化系统的通信互信息可以计算为[24]
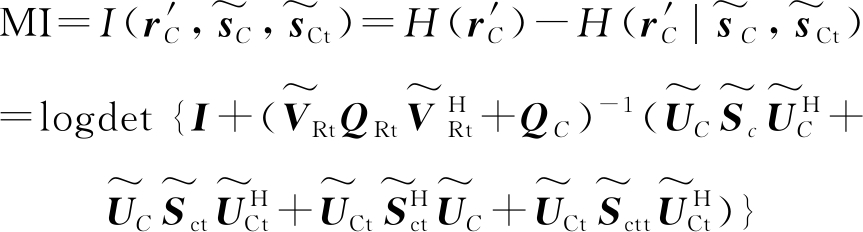
(28)
其中H(·)表示微分熵,
5 性能分析
本节通过数值仿真来对合作式MIMO一体化系统的雷达目标检测和通信互信息进行分析。为便于分析,假设通信系统有MC=2个发射天线和NC=3个接收天线,发射站位置为(70,0)km和(-70,0)km,接收站位置分别为(65,24)km,(-54,50)km和(-12,-69)km,MIMO雷达系统的发射天线数目和接收天线数目分别为MR=2和NR=3,其发射站位置为(0,70)km和(0,-70)km,接收站位置分别为(-41,57)km,(-28,-64)km和(69,7)km。假设雷达目标检测单元位于(0.5,0.3)km。通信系统发射的OFDM信号可表示为
(29)
其中am′[n]表示数据符号,pT′(t)为单位幅度且宽度为T′的矩形脉冲,Δf是两个子载波之间的频率间隔,Nf表示子载波的数目,脉宽为T′。令Δf=125 Hz,Nf=6,T′=0.01 s。假设每个通信发射信号的发射功率相同,即EC,1=...=EC,MC=EC。通信端的杂波加噪声为白高斯分布,协方差矩阵表示为
雷达系统发射频率扩展高斯单脉冲信号,其表示为
sm(t)=(2/T2)(1/4)exp(-πt2/T2)ej2πmfΔt
(30)
其中fΔ表示雷达发射信号之间的频率间隔,T为脉宽。令fΔ=125 Hz和T=0.01。每个雷达发射信号的发射功率相同,即ER,1=...=ER,MR=ER。雷达端的杂波加噪声为白高斯分布,协方差矩阵表示为
将合作式MIMO雷达通信一体化系统的总发射功率表示为E,分配给雷达端的比例设为α,则MRER=Eα、MCEC=E(1-α)。定义信号与杂波加噪声的比为
令E=104、SCNR=5 dB。
5.1 合作式MIMO一体化系统中雷达目标检测性能增益
图2给出了两种场景下雷达目标检测概率随着α变化的曲线。第一种场景(合作)考虑了雷达与通信系统合作的情况,即采用式(2)描述的接收信号模型rR。第二种场景(非合作)考虑一体化MIMO系统中的雷达用传统方式进行目标检测而没有与通信系统合作的情况,也即采用的接收信号模型为rR=URtsRt+URsR+wR。从图中可以看出,合作式一体化系统的目标检测概率PD总是比非合作式一体化系统的PD更大,说明合作的确有助于提升雷达的目标检测性能。从图中还可以看出,随着α的增加,两种一体化系统的检测概率PD均会增加,但合作带来的检测性能增益则越来越小,这说明检测概率和性能增益之间存在一个折中。
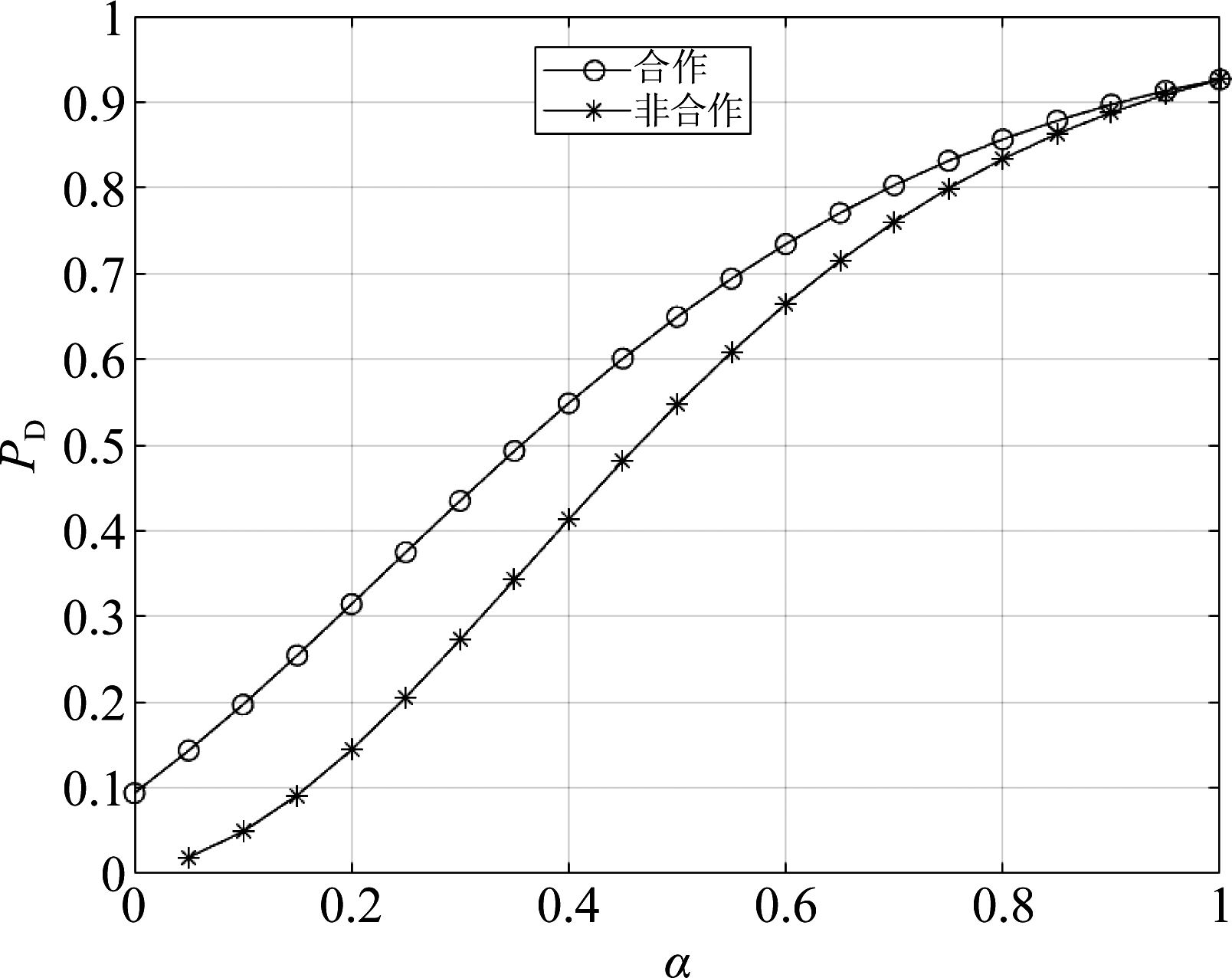
图2 合作式MIMO雷达通信一体化系统的雷达检测概率随α变化曲线
Fig.2 Target detection probability PD versus α for cooperative MIMO radar-communication systems
5.2 合作式MIMO一体化系统中通信互信息增益
考虑前述一体化MIMO系统,参数设置与前例保持一致,此外假设通信信号是相关矩阵为
的白高斯分布[25]。图3画出两种场景下通信互信息随着α变化的曲线。第一种场景(合作)考虑一体化系统中MIMO通信与MIMO雷达系统合作的情况,通信系统估计出目标参数并对通信目标回波加以利用,即采用式(6)描述的接收信号模型rC。第二种场景(非合作)考虑一体化系统中MIMO通信系统未与MIMO雷达合作而用传统方式进行通信,也即采用接收信号模型
从图中可以看出,合作情况的互信息总是比非合作场景的大,说明与雷达系统合作有助于提升通信互信息。同时从图中看出,随着α的增加互信息和性能增益都逐渐变小。
综合分析图2和图3,一体化MIMO系统中雷达端和通信端的合作可以使雷达、通信两方面都获得性能增益,但雷达性能增益和通信性能增益之间存在一个折中。
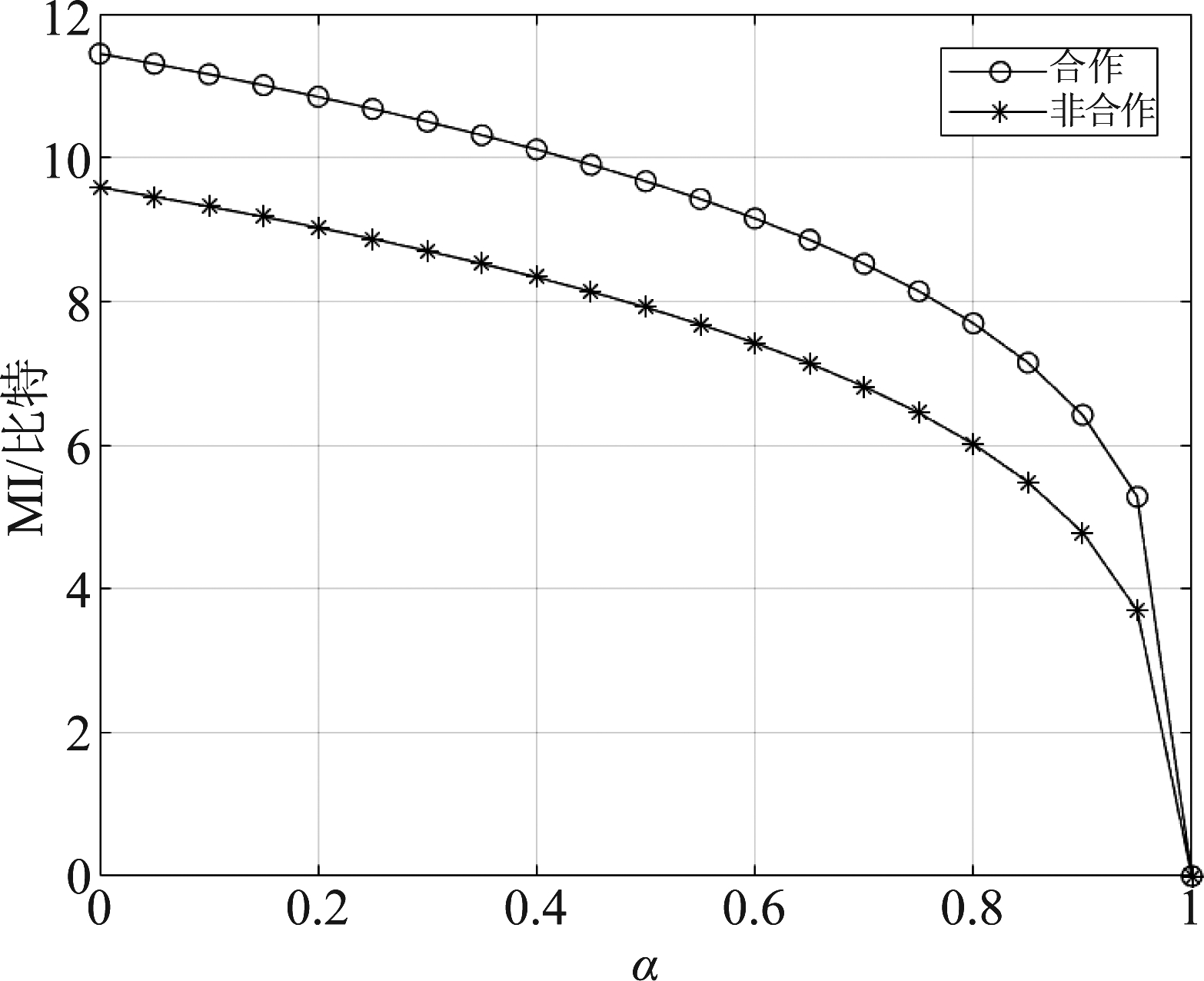
图3 合作式MIMO雷达通信一体化系统的通信互信息随α变化曲线
Fig.3 MI versus α for cooperative MIMO radar-communication systems
5.3 合作式MIMO一体化系统中的功率分配
根据式(19)和式(28)推得的一体化系统中雷达检测概率和通信互信息可以看出,发射波形、收发天线数目、杂波加噪声水平以及信号功率等参数都会影响检测概率和互信息的性能。前文分析了合作式MIMO一体化系统中雷达检测性能和通信互信息的增益。从仿真结果可以看出随着雷达端与通信端功率分配比例的不同,一体化系统的雷达检测性能和通信互信息之间存在折中。接下来,基于检测概率和互信息,简要分析一体化MIMO系统的功率分配问题。
为了体现合作式MIMO雷达通信一体化系统的综合性能,一个简单的准则就是把雷达性能和通信性能进行线性加权,不失一般性,考虑下式作为雷达与通信任务的综合性能指标
Pco=PD+βCMI
(31)
其中系数βC表示通信任务相对雷达任务的重要性,可根据具体应用场景对其进行调整。在功率受限的一体化系统中,优化问题可以描述为
s.t. 0≤α≤1
(32)
假设雷达任务和通信任务在一体化系统中的重要性一样,即将雷达检测概率和通信互信息的归一化结果之和作为衡量合作系统总性能的指标,令权重系数为βC=PD,max/MImax,其中PD,max是检测概率的最大值,MImax为互信息的最大值。图4画出了随着α变化的合作系统综合性能Pco的变化曲线。从图中可以看出,随着α的增加合作系统的性能先升后降,在α=0.725处得到最大值。可见,在对合作式MIMO雷达通信一体化系统进行设计时,若想兼顾雷达和通信的性能,可根据具体的应用场景调整比重参数βC,再通过求解式(32)中的优化问题,得到使综合性能最优的功率分配方式。
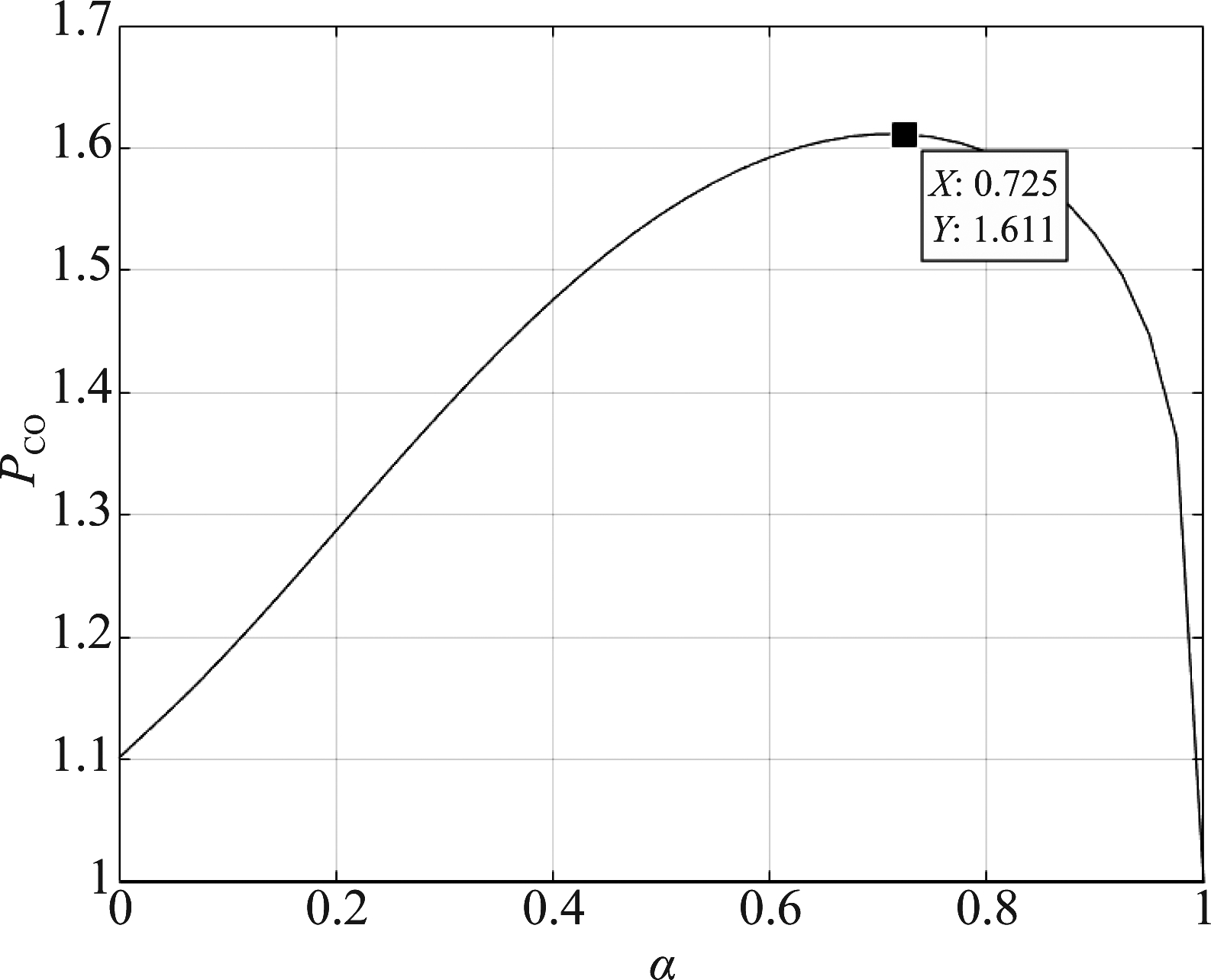
图4 合作式MIMO雷达通信一体化系统的联合性能随α变化曲线
Fig.4 Joint performance versus α for cooperative MIMO radar-communication systems
6 结论
本文给出了合作式MIMO雷达通信一体化系统的信号模型,即在接收端同时考虑了源自雷达发射和通信发射的目标回波和直达波。在雷达端,合作式一体化系统等价为一个主被动混合式MIMO雷达,文中分析了混合式MIMO雷达的目标检测概率。在通信端,利用共享的雷达信息,通信回波也可以被用来提取有用通信信息,论文对互信息进行了推导以衡量通信的有效性。在数值分析中,考虑OFDM通信信号和频率扩展高斯单脉冲雷达信号,仿真验证了一体化系统中雷达和通信的合作能显著提升雷达和通信的性能,且分析表明,合作式一体化系统中雷达和通信性能之间存在折中。进一步通过仿真,分析了合作式一体化MIMO系统的功率分配问题。
[1] Han Liang, Wu Ke. Joint wireless communication and radar sensing systems-state of the art and future prospects[J]. IET Microwaves, Antennas Propagation, 2013, 7(11): 876- 885.
[2] 肖博, 霍凯, 刘永祥. 雷达通信一体化研究现状与发展[J]. 电子与信息学报, 2019, 41(8): 739-750.
Xiao Bo, Huo Kai, Liu Yongxiang. Development and prospect of radar and communication Integration[J]. Journal of Electronics & Information Technology, 2019, 41(8): 739-750.(in Chinese)
[3] 卢俊, 张群飞, 史文涛, 等. 探测通信一体化研究现状与发展趋势[J]. 信号处理, 2019, 35(9): 1484-1495.
Lu Jun, Zhang Qunfei, Shi Wentao, et al. Development and Prospect of Detection and Communication Integration[J]. Journal of Signal Processing, 2019, 35(9): 1484-1495.(in Chinese)
[4] Deligiannis A, Daniyan A, Lambotharan S, et al. Secrecy rate optimizations for MIMO communication radar[J]. IEEE Transactions on Aerospace and Electronic Systems, 2018, 54(5): 2481-2492.
[5] Dokhanchi S H, Bhavani Shankar M R, Mishra K V, et al. Multi-constraint spectral co-design for colocated MIMO radar and MIMO communications[C]∥2020 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), 2020: 4567- 4571.
[6] Hong Bingqing, Wang Wenqin, Liu Congcong. Ergodic interference alignment for spectrum sharing radar-communication systems[J]. IEEE Transactions on Vehicular Technology, 2019, 68(10): 9785-9796.
[7] Qian Junhui, Lops M, Zheng Le, et al. Joint system design for coexistence of MIMO radar and MIMO communication[J]. IEEE Transactions on Signal Processing, 2018, 66 (13): 3504-3519.
[8] Rihan M, Huang Lei. Optimum co-design of spectrum sharing between MIMO radar and MIMO communication systems: An Interference Alignment Approach[J]. IEEE Transactions on Vehicular Technology, 2018, 67 (12): 11667-11680.
[9] Liu Jiawei, Saquib M. Transmission design for a joint MIMO radar and MU-MIMO downlink communication system[C]∥2018 IEEE Global Conference on Signal and Information Processing (GlobalSIP), 2018: 196-200.
[10] 张令浩, 张剑云, 周青松. 雷达与通信共享频谱波形优化算法研究[J]. 信号处理, 2019, 35(11): 1861-1870.
Zhang Linghao, Zhang Jianyun, Zhou Qingsong. Research on waveform optimization algorithm of radar and communication spectrum sharing[J]. Journal of Signal Processing, 2019, 35(11): 1861-1870.(in Chinese)
[11] Zhou Yifan, Zhou Huilin, Zhou Fuhui, et al. Resource allocation for a wireless powered integrated radar and communication system[J]. IEEE Wireless Communications Letters, 2019, 8(1): 253-256.
[12] Chiriyath A R, Paul B, Jacyna G M, et al. Inner bounds on performance of radar and communications co-existence[J]. IEEE Transactions on Signal Processing, 2016, 64(2): 464- 474.
[13] Chiriyath A R, Paul B, Bliss D W. Radar-communications convergence: coexistence, cooperation, and co-design[J]. IEEE Transactions on Cognitive Communications and Networking , 2017, 3(1): 1-12.
[14] Bică M, Koivunen V. Radar waveform optimization for target parameter estimation in cooperative radar-communications systems[J]. IEEE Transactions on Aerospace and Electronic Systems, 2019, 55(5): 2314-2326.
[15] Bica M, Huang Kuanwen, Mitra U, et al. Opportunistic radar waveform design in joint radar and cellular communication systems[C]∥2015 IEEE Global Communications Conference(GLOBECOM), 2015: 1-7.
[16] Bica M, Koivunen V. Delay estimation method for coexisting radar and wireless communication systems[C]∥2017 IEEE Radar Conference (RadarConf), 2017: 1557-1561.
[17] Shi Chenguang, Wang Yijie, Wang Fei, et al. Low probability of intercept-based OFDM radar waveform design for target time delay estimation in a cooperative radar-communications system[J]. IET Radar, Sonar & Navigation, 2019, 13(10): 1697-1704.
[18] He Qian, Wang Zhen, Hu Jianbin, et al. Performance gains from cooperative MIMO radar and MIMO communication systems[J]. IEEE Signal Processing Letters, 2019, 26(1): 194-198.
[19] Wang Zhen, He Qian, Blum R S. Target localization and mutual information improvement for cooperative MIMO radar and MIMO communication systems[C]∥2019 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), 2019: 4315- 4319.
[20] 刘永军, 廖桂生, 杨志伟. OFDM雷达通信一体化波形相参积累研究[J]. 信号处理, 2017, 33(3): 253-259.
Liu Yongjun, Liao Guisheng, Yang Zhiwei. A study for the coherent integration with integrated radar and communication waveform based on OFDM[J]. Journal of Signal Processing, 2017, 33(3): 253-259.(in Chinese)
[21] Wang Pu, Li Hongbin, Himed B. A parametric moving target detector for distributed MIMO radar in non-homogeneous environment[J]. IEEE Transactions on Signal Processing, 2013, 61(9): 2282-2294.
[22] Richmond C D, Basu P, Learned R E, et al. Performance bounds on cooperative radar and communication systems operation[C]∥2016 IEEE Radar Conference (RadarConf), 2016: 1- 6.
[23] Godrich H, Petropulu A P, Poor H V. Sensor selection in distributed multiple-radar architectures for localization: a knapsack problem formulation[J]. IEEE Transactions on Signal Processing, 2012, 60(1): 247-260.
[24] Cover T M, Thomas J A. Elements of Information Theory[M]. John Wiley & Sons, New York, 1991.
[25] Zhang Xin, Li Hongbin, Liu Jun, et al. Joint delay and doppler estimation for passive sensing with direct-path interference[J]. IEEE Transactions on Signal Processing, 2016, 64(3): 630- 640.
