1 引言
传统的电子系统中,雷达设备和通信设备一般是分立存在,但很多情况下均要求同时工作,其中涉及频率资源的浪费、射频前端的加倍开销以及系统间的电磁兼容等诸多问题。随着人们对多平台集成的需求越来越高,同时无线信道的频谱资源也愈发紧张,雷达通信一体化受到了越来越多的关注[1]。现阶段已有多种方式实现雷达和通信集成化设计,概括来说可以分为以下几类:基于时分、频分、空分体制的雷达通信一体化技术以及基于波形共用体制的雷达通信一体化技术。基于时分[2-3]和频分[4]的一体化技术,分别是在时域和频域上对雷达和通信信号进行区分。基于波形共用体制的一体化技术,对一体化波形进行设计,使其同时具有雷达探测与通信的功能,二者共享相同的时间和频谱资源。如,基于扩频(spread spectrum, SS)的雷达通信一体化技术[5],和基于正交频分复用(orthogonal frequency division multiplexing, OFDM)的雷达通信一体化技术[6-7]等。
本文的研究重点为基于空分体制的雷达通信一体化技术。Euziere等人在文献[8]首次提出利用时间调制阵列实现雷达通信一体化双功能天线阵列,在主瓣区域进行雷达探测,同时在旁瓣区域利用不同旁瓣电平实现调幅(amplitude modulation,AM)通信。文献[8]所提控制方案,在保证主瓣区域恒定不变的同时,在通信方向可控制实现两种旁瓣电平,分别对应通信0和1两个比特。文献[9]在此基础之上增加了通信方向旁瓣控制的自由度,将可控旁瓣电平数量由2增加至4,这使得一个旁瓣电平可以表示2个比特的通信数据,意味着通信速率的提升。更进一步,文献[10]增加了约束条件,对通信部分功能进行优化,实现了4-QAM(quadrature amplitude modulation)的通信方式,即通过控制可在通信方向实现恒定的幅度大小和4种不同的相位,即0、90、180和270度。4种符号区分度良好且可被接收端正确探测。Hassanien等人采用波束赋形算法[11-12],设计了两组加权向量,保证主瓣不变的同时,使通信方向分别产生两个旁瓣电平,以幅移键控(amplitude shift keying,ASK)的方式进行通信,误码率性能较之前有所提升。Ahmed等人利用波束赋形算法控制天线方向图[13],同样利用主瓣实现雷达功能,而利用旁瓣实现QAM方式的通信功能,且通信速率得到改善。然而上述方案具有一定的局限性,即雷达波束与通信波束均为固定波束,可通信方向受限,通信方向与天线阵元数目、排布等参数关系密切且复杂,难以随意更改,无法进行实时独立的自由扫描。此外通信只能采用特定的AM等低可靠度的调制方式。Shan等人在文献[14]针对以上问题,提出了基于时间调制阵列的雷达通信一体化方式,利用基波分量进行雷达探测,利用正一次谐波分量进行通信,二者波束可自由扫描控制,且雷达波形与通信调制方式不受严格限制。文献[15]进一步针对时间调制阵列固有的谐波能量泄露问题进行改进。但上述两个方案都只实现了双波束的雷达通信一体化,即一个雷达用户与一个通信用户的集成。
针对上述存在的问题与不足,本文提出多波束雷达通信一体化算法与结构,在文献[14]和[15]的基础上,结合多波束赋形算法,实现单个雷达扫描波束与两个通信扫描波束的自由控制,或单个雷达扫描波束与多个通信固定波束的控制。通信扫描波束适用于动态通信用户跟踪等场景,通信固定波束适用于多基站通信等场景。此外还实现了非对称的雷达与通信发射功率,使一体化结构应用场景更加广泛。仿真结果验证了所提结构与算法的正确性和可行性,雷达与通信能够同时完成各自的功能,且不会受到相互影响。
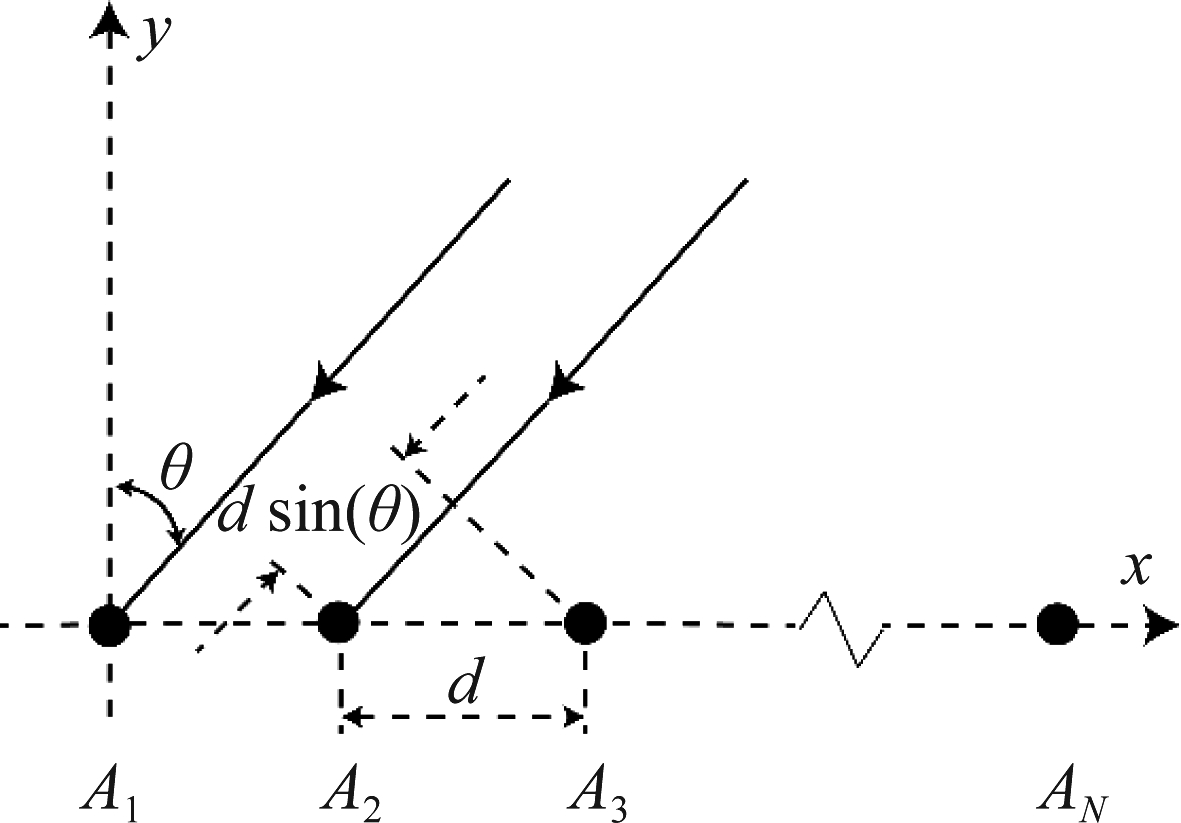
图1 n元均匀线阵
Fig.1 The n-element uniform linear array
2 系统模型
2.1 时间调制阵列
考虑一个N元均匀直线阵列(uniform linear array, ULA),阵元间距d,如图1所示。其阵列因子可以表示为:
(1)
其中,An=anejφn是第n个阵元的静态激励的幅度和相位,β=2π/λ,λ是波长,θ为信号入射方向。ULA可以通过周期性调制转变为TMA。相对于传统的天线阵列,时间调制阵列在阵列的每个射频前端上增加了一个周期性调制的射频开关。从数学意义上讲,即是用一个周期函数去调制该通道上接收或发射的信号。假设Un(t)为调制第n个阵元的周期性函数,表示为:
(2)
其中,Tp是调制周期。gn(t)是门函数,可以写成:
(3)
其中,
和
分别代表第n个阵元的开启时刻和关闭时刻。图2是Un(t)和gn(t)的示意图。
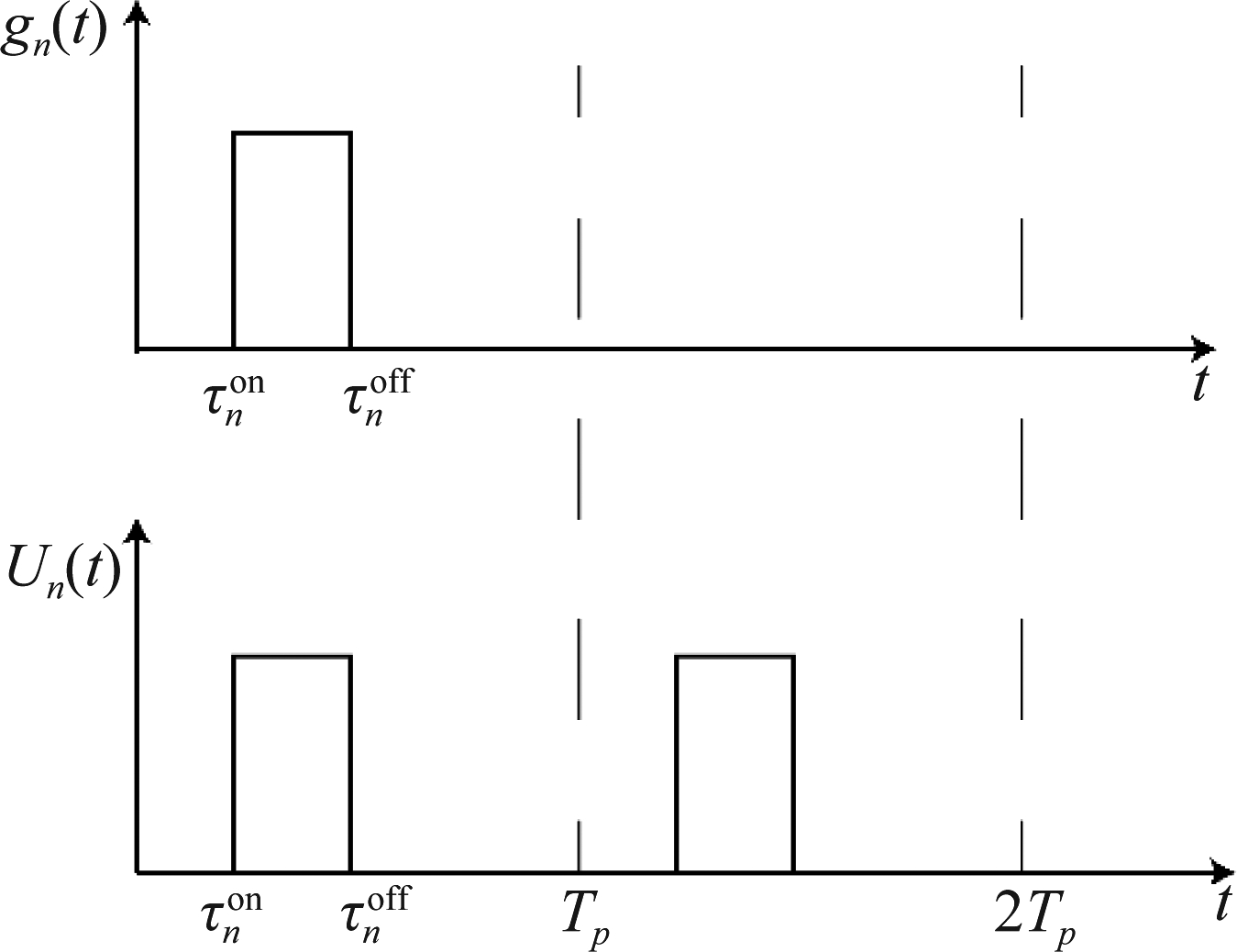
图2 门函数和周期性调制函数
Fig.2 Gate functions and periodic modulation functions
周期性函数Un(t)可以被傅里叶级数展开为:
(4)
其中Fp=1/Tp是调制频率,αnk是第k阶谐波系数,可以由下式计算:
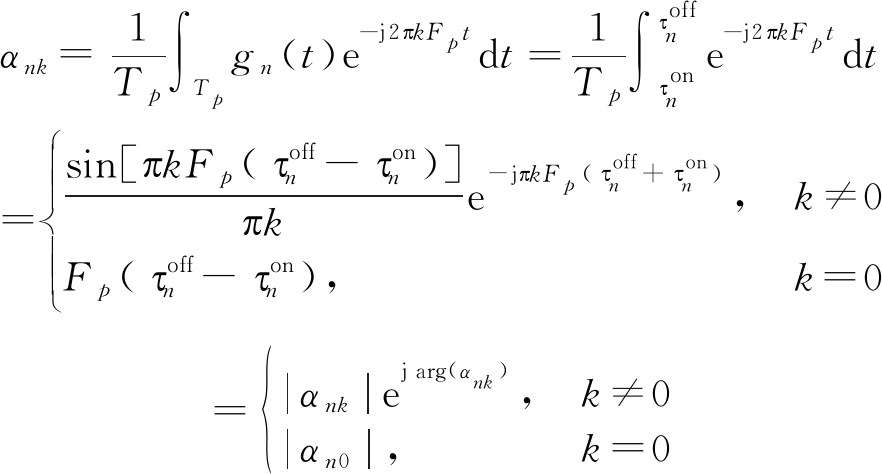
(5)
观察式(5)可以得出以下结论。首先,第n个信道的基波分量αn0是实数,其幅度与开启时间的占空比
相关。其次,谐波分量αnk的幅度是一个自变量为k的sin c(·)函数,其相位与开关时刻的中心位置有关,即
在TMA中,式(1)可以重新写成:
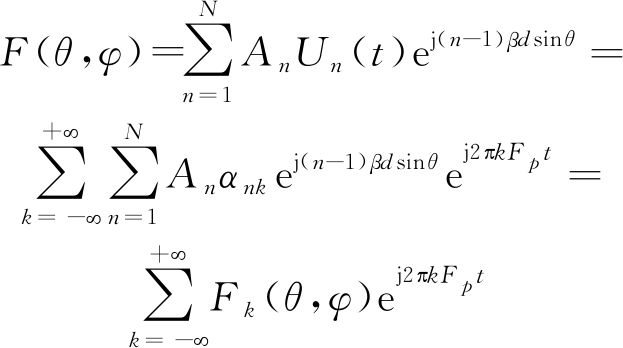
(6)
TMA的阵列因子变成基波分量和各次谐波分量的和,可以分别表示为:
(7)
(8)
如式(7)和(8)所示,对于基波分量而言,因为其系数αn0为实数,主瓣指向与具有相同配置的ULA相同。对于谐波分量而言,由于其系数αnk是复数,它们的主瓣分别指向不同的方向。如式(5)所示,谐波系数的幅度和相位是由开启时间
以及关闭时间
所决定的。综上,阵列的基波方向图类似ULA,可以由静态系数An所控制。通过选取合适的开启时刻及关闭时刻,可以控制各次谐波的辐射方向图。
2.2 多波束赋形
图3(a)是多波束赋形算法接收系统框图。假设天线阵列为N元线阵,每个阵元都与一个加权网络相连接。一个天线阵元所接收到的信号先分为M个部分(M为用户数量)。然后他们分别被N个加权单元加权。最后这些被加权的信号组合起来输出到接收端。图3(b)是多波束赋形算法发射系统框图。与接收的情况相类似,只是信号传输方向相反。
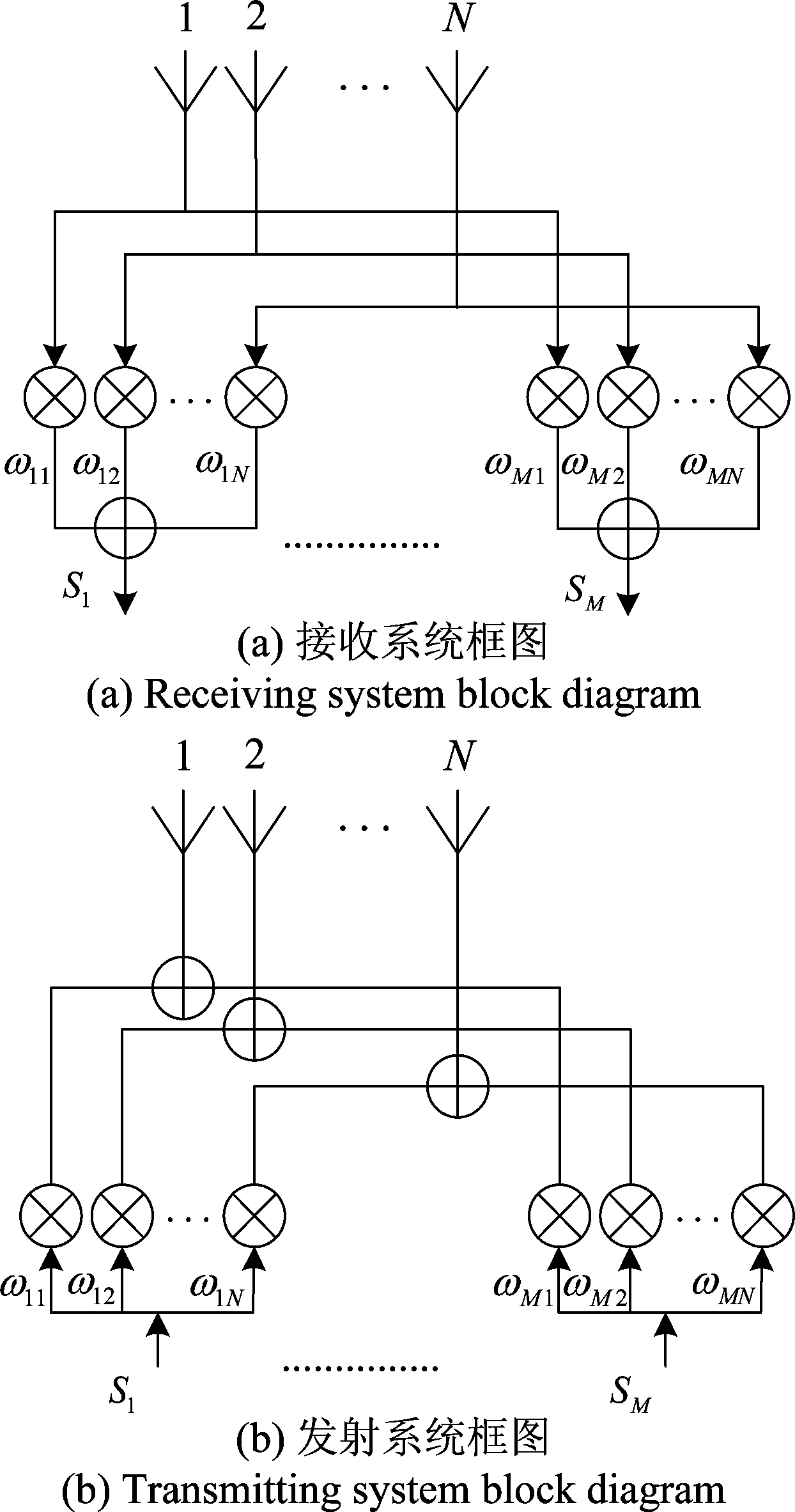
图3 多波束赋形接收与发射系统框图
Fig.3 Multi-beamforming receiving and transmitting system block diagram
假设存在两个用户。如果只有用户1,则相对应的信道方向图可以通过加权矢量ω11,ω12,…,ω1N获得,设其天线方向图函数为F1(θ),则
(9)
其中,β=2π/λ,λ是波长,θ为信号入射方向,其定义方式与图1相同。同样,对于用户2,可以选择加权矢量ω21,ω22,…,ω2N来获得相应的信道方向图,设其天线方向图函数为F2(θ),则
(10)
如果两个用户同时工作,则能量方向图为前两者的和,两个波束分别分配给用户1和用户2。用F(θ)表示总的天线方向图函数,则
F1(θ)+F2(θ)
(11)
在这种情况下,两个用户可以共享传统的信道(如相同的频谱资源)。在一个智能天线系统中,不同的信道方向图是独立的。它们可以分别跟踪自己的用户,除非有两个用户位于相同的空间方向。上述分析结果表明,信道方向图的数量与天线阵元的数量N无关,只取决于加权向量集的数量M。
3 空分多波束雷达通信一体化技术
3.1 雷达通信一体化架构
本部分利用时间调制阵列及多波束赋形技术,实现空分多波束雷达通信一体化功能。图4(a)和图4(b)分别给出了其发射与接收结构。利用多波束成形网络的第一组加权值,对雷达波束进行控制,假设加权值为A11,A12,…,A1N,则雷达子波束为:
(12)
多波束成形网络的第二组加权值,结合周期性时间调制,用于控制通信波束。假设加权值为A21,A22,…,A2N,通信子波束为:
(13)
其中Un(t)是第n个阵元上的周期性调制函数,由式(2)给出,式(5)给出了第k阶谐波系数αnk的值。可以发现通信子波束变成无穷阶谐波分量的和,类似式(7)和式(8),基波分量和第k阶谐波分量分别为:
(14)
(15)
根据图4(a)的发射结构,假设同时发射载频为Fc的雷达信号srad(t),载频为Fc的通信用户1信号scom1(t)和载频为Fc-Fp的通信用户2信号scom2(t)。则总的发射信号可以表示为:
sTX(t)=Frad(θ)srad(t)+Fcom,0(θ)scom1(t)+
Fcom,1(θ)scom2(t)e-j 2πFptej2πFpt=Frad(θ)srad(t)+
Fcom,0(θ)scom1(t)+Fcom,1(θ)scom2(t)
(16)
其中Frad(θ)srad(t)为雷达信号分量,载波为Fc,发射方向为Frad(θ)主瓣方向;Fcom,0(θ)scom1(t)和Fcom,1(θ)scom2(t)分别为通信用户1和通信用户2信号分量,载波均为Fc,发射方向分别为Fcom,0(θ)和Fcom,1(θ)的主瓣方向。其中由于用户2使用TMA的正一次谐波分量,需要提前调制到负一次谐波分量后再传输至TMA发射,预调制频率e-j 2πFpt与正一次谐波附加频率ej2πFpt相抵消,具体原理可参阅文献[14]。综上,该多波束成形雷达通信一体化发射架构(双通信用户)能够同时将雷达信号和两个通信用户信号发射至三个不同的方向,且占用相同的频带资源。
根据天线互异性原理,接收过程与发射过程是互逆的。根据图4(b)的发射结构假设雷达回波信号
与两个通信信号
分别同时从三个方向θrad,θcom,0和θcom,1入射(θrad,θcom,0和θcom,1分别为天线方向图Frad(θ),Fcom,0(θ)和Fcom,1(θ)的主瓣方向),与多波束成形接收分析方法类似,雷达输出信号为:
图4 多波束雷达通信一体化发射与接收结构
Fig.4 Multi-beam radar-communication integrated transmission and receiving structure
(17)
通信用户1和2的输出信号分别为:
(18)
(19)
加权向量组A11,A12,…,A1N将雷达回波信号提取出来,分别经过下变频,ADC和带通滤波器后,做雷达相关接收处理,实现雷达探测功能。加权向量组A21,A22,…,A2N结合周期性开关调制,将两个方向的通信信号分别调制到基波分量和正一次谐波分量上,信号经过下变频,ADC之后,分别由不同的带通滤波器取出,两个用户各自完成基带解调。
上述雷达通信一体化架构,采用多波束赋形的第一组加权网络实现雷达探测功能,第二组加权网络结合时间调制阵列实现通信功能。其中,通信部分只采用了基波分量和+1次谐波分量,其波束指向可通过静态激励和射频开关开启与关闭时刻自由控制,具体控制算法由后文给出。进一步,若同时采用时间调制阵列的多个谐波分量进行通信,则可实现多个方向的用户同时通信,具体发射与接收结构如图5所示。
由于图5采用了时间调制阵列的多个谐波分量,多波束成形网络的第一组加权值用于对雷达波束的控制,第二组加权值结合周期性时间调制,用于控制通信波束。这里假设存在2M+1个通信用户,分别利用了基波分量至±M次谐波分量。通信用户信号在送至TMA之前,需要分别调制到各次对偶的谐波频率上。如,使用第M次谐波分量(载频为Fc+MFp)进行通信,需要提前调制到载频Fc-MFp上。
对于多通信用户的一体化发射和接收结构,各个谐波分量的指向具有一定的约束关系,因而只适用于通信方向固定的场景,如基站之间的通信。多波束指向之间的约束关系由后文给出。
3.2 雷达及通信波束控制算法
本部分首先给出图4所示结构的波束控制算法。假设我们要控制雷达波束指向θrad方向,基波分量通信波束指向θcom,0方向,+1次谐波分量通信波束指向θcom,1方向。
对于第一组(雷达部分)加权网络,各个静态激励的幅值|A11|,|A12|,…,|A1N|由Dolph-Chebyshev方法确定,其相位arg(A11),arg(A12),…,arg(A1N)由雷达波束指向θrad所确定,具体为:
arg(A1n)+(n-1)βdsin θrad=2Kπ,K∈Z
(20)
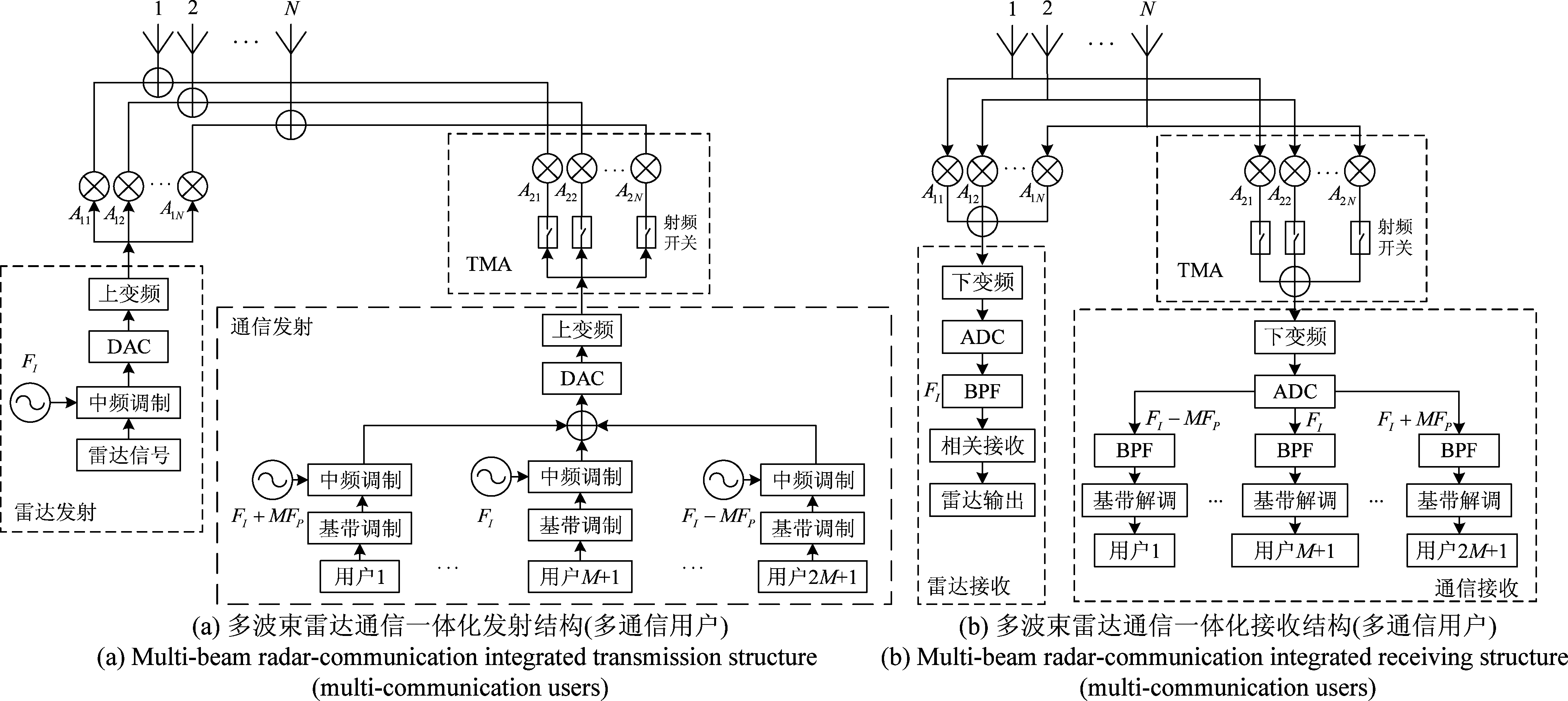
图5 多波束雷达通信一体化发射与接收结构(多通信用户)
Fig.5 Multi-beam radar-communication integrated transmission and receiving structure (multi-communication users)
上式的物理解释为,各个天线单元之间,由加权相位造成的相位差arg(A1n),以及由阵列分布所造成的相位差(n-1)βdsin θrad相互抵消,当各个矢量的相位相同时,其求和能够达到最大值,在空间上这个最大和值对应于天线辐射方向图的主瓣。
对于第二组(通信部分)加权网络,首先给出其基波分量和+1次谐波分量的天线方向图表达式,令
代表第n个阵元射频开关归一化开启与关闭时刻,根据(14)和(15)有:
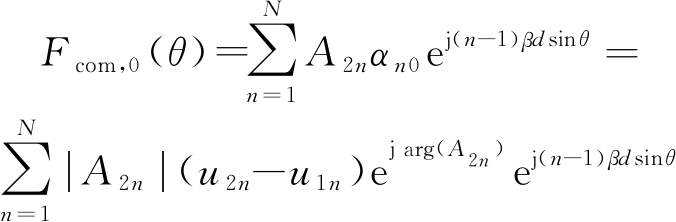
(21)
e-jπ(u2n+u1n)ej(n-1)βdsin θ
(22)
与第一组加权网络类似,各个静态激励的幅值|A21|,|A22|,…,|A2N|由Dolph-Chebyshev方法确定,其相位arg(A21),arg(A22),…,arg(A2N)由基波分量通信波束指向θcom,0所确定,具体为:
arg(A2n)+(n-1)βdsin θcom,0=2Kπ,K∈Z
(23)
根据+1次谐波分量通信波束指向θcom,1来确定各个射频开关的归一化开启与关闭时刻u1n, u2n。首先令ωn=sin[π(u2n-u1n)]=1,然后根据相位关系可得:
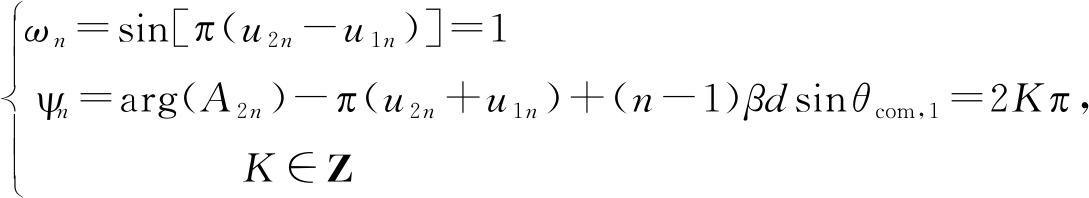
(24)
于是:
(25)
进一步化简可得:
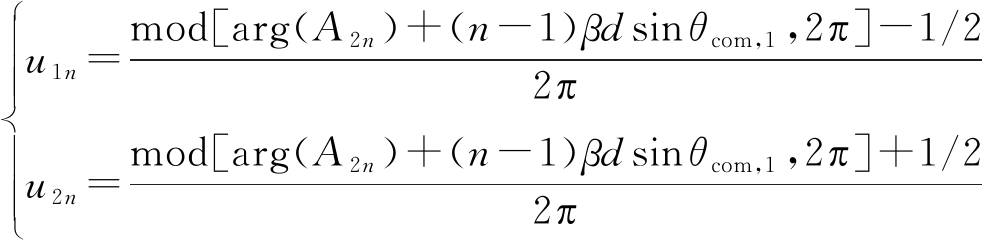
(26)
对于图5所示的多通信用户结构,雷达部分控制方法同上。通信部分其基波分量和某一次(k次)谐波分量波束指向可自由控制(分别用θ0和θk表示),剩下谐波分量的指向由约束关系所决定,这里进行详细推导。根据(5)和(15)可得:
(27)
若θk为其主瓣方向,则:
arg(A2n)-πk(u2n+u1n)+(n-1)βdsin θk=2Kπ,K∈Z
(28)
求解得到:
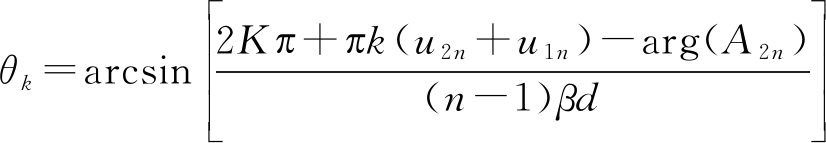
(29)
即,当加权向量的相位φn和开关时间u2n+u1n确定之后,各次谐波主瓣方向θk方向仅与谐波次数k有关,而且它们是相互制约的,大体规律为,随着谐波次数k的增加,其谐波主瓣方向越来越偏离阵列的基波主瓣方向。(由于较高次谐波分量幅度较低,能量不足以为通信用户使用,故仅考虑较低的几次谐波分量。)计算第-k次谐波分量谐波系数:
(30)
假设第-k次谐波分量主瓣指向为θ-k,则:
arg(A2n)+πk(u2n+u1n)+(n-1)βdsin θ-k=2Kπ,K∈Z
(31)
将(28)和(31)相加可得:
2arg(A2n)+(n-1)βd(sin θk+sin θ-k)=2Kπ,K∈Z
(32)
又因为基波分量主瓣指向θ0满足:
arg(A2n)+(n-1)βdsin θ0=2Kπ,K∈Z
(33)
由(32)和(33)可得约束关系(为便于分析取K=0):
sin θk+sin θ-k=2sin θ0
(34)
约束关系可分析如下:当基波分量主瓣指向0°方向(法向)时,正k次谐波分量与负k次谐波分量的天线方向图关于阵列的法向对称;当基波分量主瓣不在法向时,正k次谐波分量与负k次谐波分量的方向关于阵列主瓣指向对称。因此当调整TMA阵列的基波分量主瓣指向时,各次谐波分量的主瓣指向会随之移动。
类似图4和图5的结构,在理论上如果增加加权网络(或被时间调制的加权网络),即可增加独立控制的雷达波束(或独立控制的一组通信波束)。这里涉及到的是可控波束数目与硬件复杂度之间的一个权衡问题,当波束增多,为避免多个波束在空域重叠相互影响,对波束宽度等指标要求更严格。
3.3 雷达通信一体化结构复杂度分析
本文给出了几种空分多波束雷达通信一体化设计方案,这里对各个雷达通信一体化结构复杂度进行分析。
结构1——单雷达波束与双通信波束:该一体化结构采用了两组加权网络,分别对应于雷达子系统和通信子系统,两组加权网络意味着需要两组射频通道。通信子系统由于采用时间调制阵列,需要一组高速射频开关,然而其多谐波特性,使得双通信用户可以共用一个射频通道。
结构2——单雷达波束与多通信波束:该一体化结构同样采用两组加权网络,与结构1的区别在于,通信子系统不仅仅采用基波分量与+1次谐波分量,而是同时采用多次谐波分量,以支持更多的通信用户。然而受限于多个谐波分量之间的约束关系,多通信用户的指向无法独立控制,因而只适用于固定通信的场景。结构2与结构1的系统硬件复杂度相同,两者在波束控制自由度与支持用户数量之间进行取舍。
结构3——多雷达波束与双/多通信波束:如3.2节最后所述,通过增加加权网络的数目,可以增加独立控制的雷达波束和/或通信波束,这种结构无疑增加了硬件复杂度。与结构1和2相比,属于硬件复杂度和可控波束数目之间的权衡问题。
4 仿真分析
在本部分,我们给出基于以上算法的仿真结果。仿真中采用图5的发射与接收结构,天线阵为32元线阵,阵元为全向天线,间距半波长。第一组加权网络用于雷达探测,波束指向为θrad=-30°,旁瓣电平设置为-50 dB,第二组加权网络采用时间调制的方式,利用其基波和±1次谐波分量,分别指向θcom,0=0°,θcom,+1=50°,θcom,-1=-50°三个方向,旁瓣电平设置为-30 dB。时间调制的频率为Fp=50 MHz,载波频率为Fc=1 GHz。雷达采用脉冲chirp信号,脉冲宽度T=20 μs,脉冲重复频率prf=10 kHz,发射功率1000 W。通信采用QPSK调制方式,发射功率1 W,通信与雷达信号带宽均为22 MHz。
图6为多波束雷达通信一体化系统天线方向图。图中给出了4个分量,包括第一组加权网络产生的雷达波束,以及由第二组加权网络结合时间调制产生的3个通信波束,分别为基波分量和±1次谐波分量。该方案与文献[14]相比,有以下改进:1.通信用户数目增多,不局限于一个雷达波束和一个通信波束;2.两个加权网络的旁瓣电平可分别设置,如图6所示雷达波束的旁瓣电平更低(-50 dB)。第二条改进表明,在不对通信性能有明显影响的前提下,雷达可采用更高的发射功率。
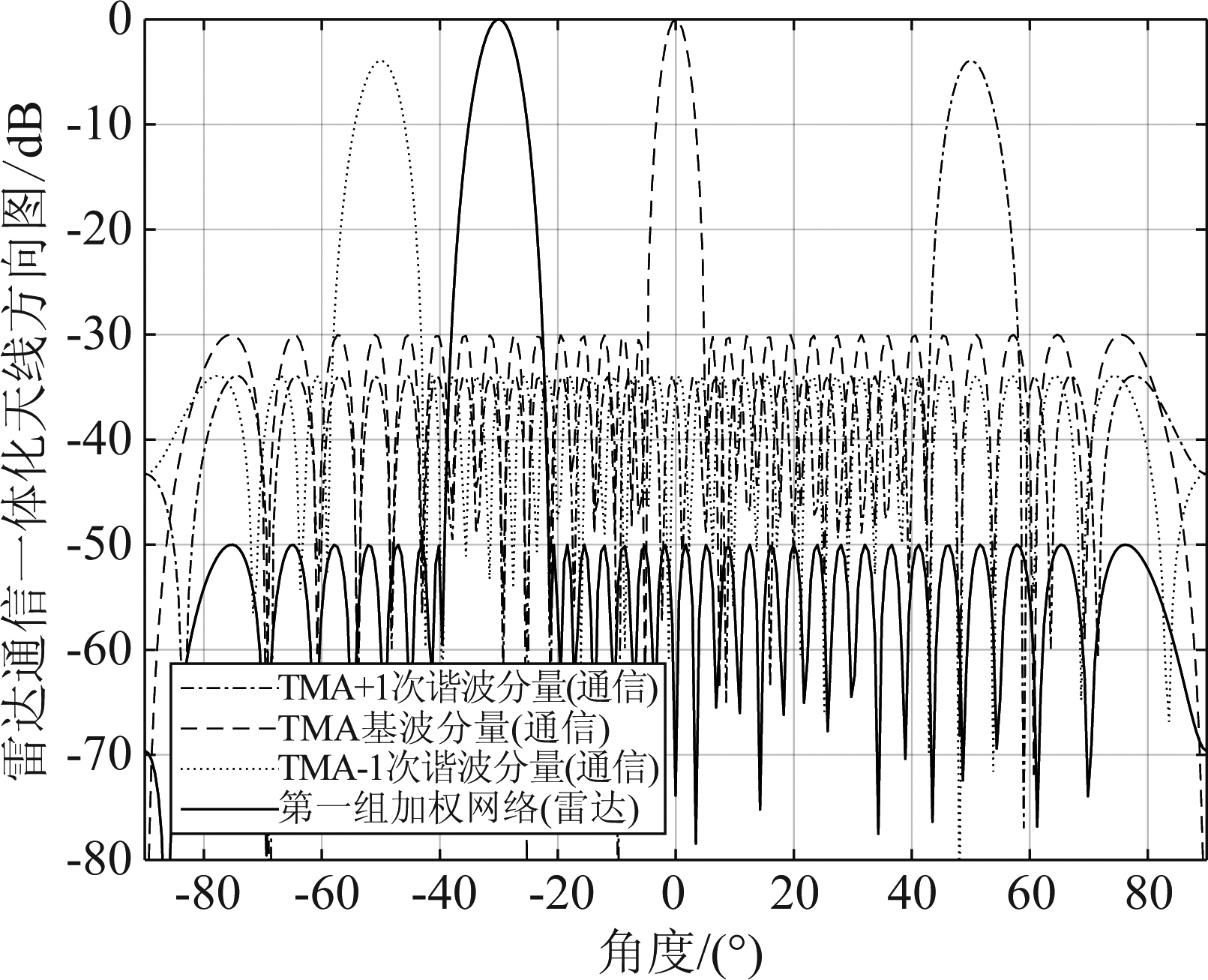
图6 多波束雷达通信一体化系统天线方向图
Fig.6 Antenna pattern of multi-beam radar-
communications integration system
图7～图9旨在说明所提一体化结构的通信性能。以1个雷达波束和2个通信波束的情况为例,对所提一体化系统通信性能进行仿真分析。仿真采用图6中的雷达波束及通信波束中的基波分量(通信用户1)和+1次谐波分量(通信用户2)。通信用户1采用相干解调方式下的误码率性能曲线如图7所示。图中最下方三条曲线分别对应单用户QPSK通信误码率曲线理论结果,单用户QPSK通信误码率曲线仿真结果,多通信用户(通信用户1和2)和雷达分量同时工作情况下的通信误码率曲线仿真结果。这三条曲线几乎重合,证明雷达以及其他通信用户的信号没有对所考察的通信用户的通信性能造成影响。主要原因如下:1)对于雷达分量,即使雷达发射功率远高于通信发射功率,但雷达波束的旁瓣电平被控制得足够低(-50 dB),经过如此大的衰落之后,残余能量与高斯白噪声带来的影响相比,已经微乎其微;2)对于通信用户2分量,由于旁瓣电平控制得足够低(-30 dB),与原因1)类似,残余能量与高斯白噪声带来的影响相比,已经微乎其微;3)三个波束没有重叠,主要能量各自分开,没有造成主瓣干扰。
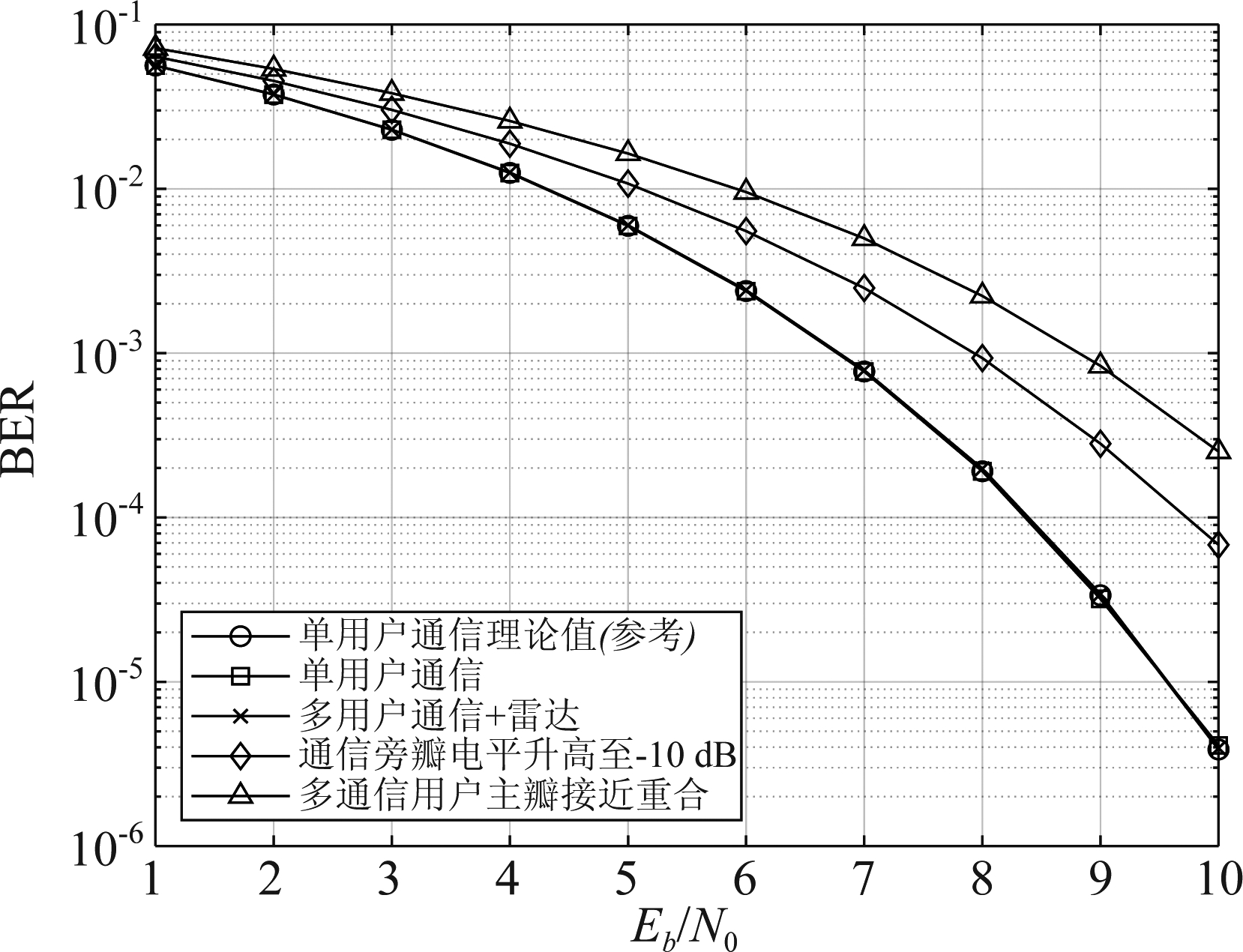
图7 通信BER随SNR变化曲线
Fig.7 BER versus SNR for communications
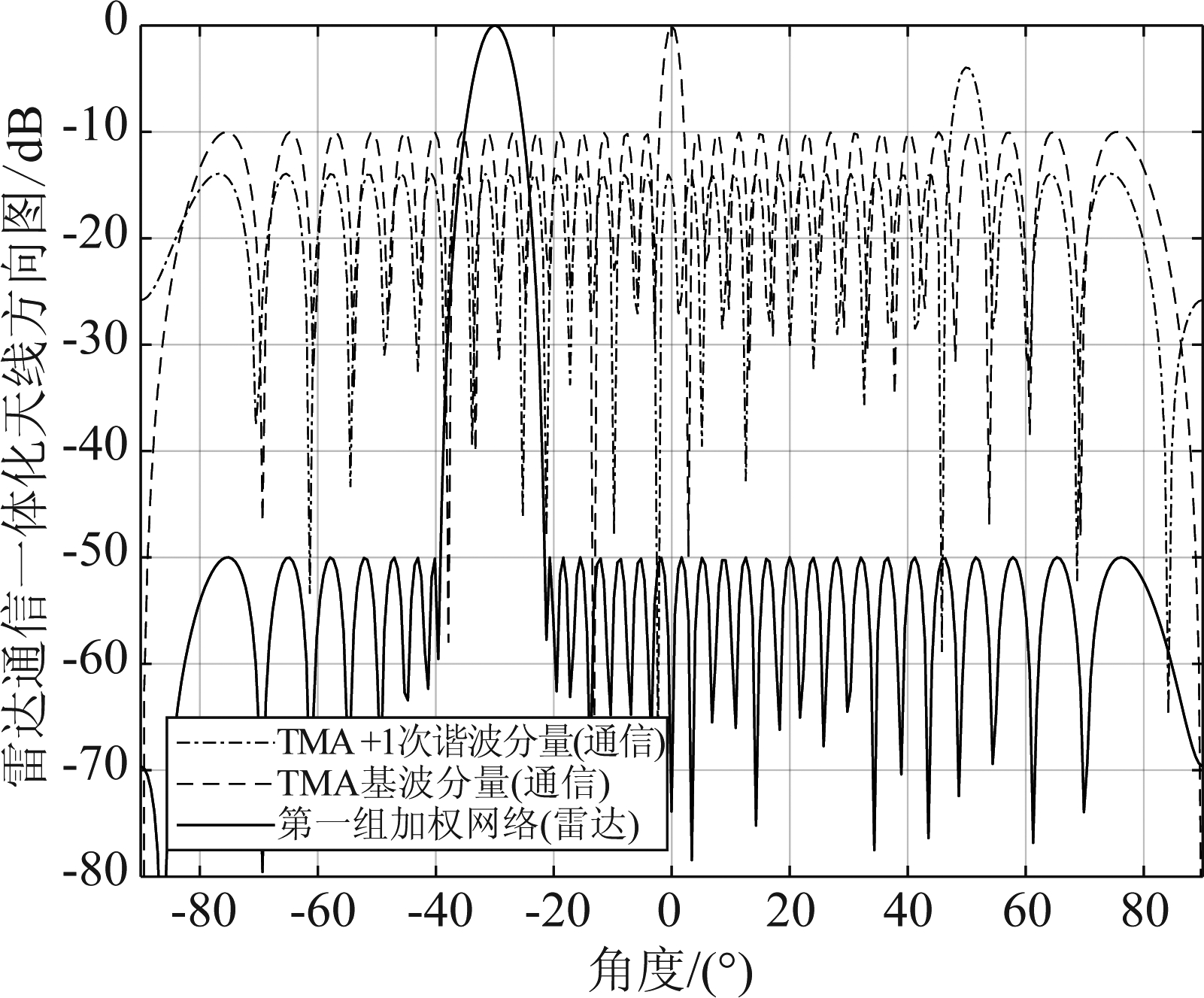
图8 通信子波束旁瓣电平SLL=-10 dB情况下天线方向图
Fig.8 Antenna patterns when communications sub-beam sidelobe level SLL=-10 dB
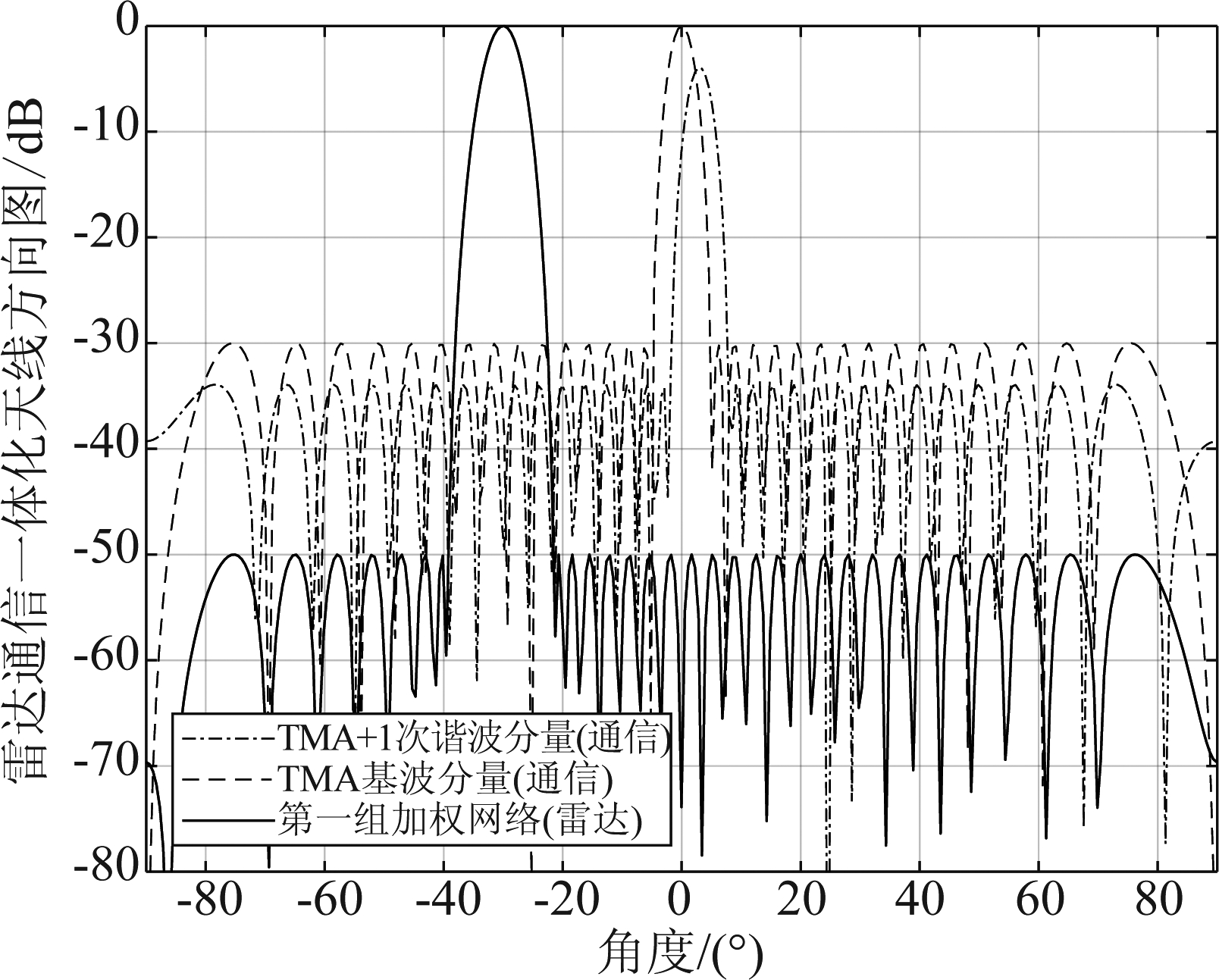
图9 通信子波束主瓣几乎重叠情况下天线方向图
Fig.9 Antenna patterns with the mainlobes of the communications sub-beams almost overlapping
为了进一步说明旁瓣电平和主瓣重叠所带来的影响,图8给出通信子波束旁瓣电平SLL=-10 dB情况下的天线方向图,图9给出通信用户1和通信用户2主瓣几乎重合情况下的天线方向图(θcom,0=0°,θcom,+1=3°)。图7中菱形和上三角形标记的两条误码率曲线分别对应以上两种恶化情况,仿真结果证实了旁瓣电平的控制以及主瓣指向的合理分配,对多通信用户通信性能至关重要。
图10～图12旨在说明所提一体化结构的雷达性能。仿真中假设雷达方向存在3个目标,分别位于4 km,5 km和8 km处,速度分别为50 m/s,100 m/s和350 m/s。图10给出雷达和两个通信用户都在工作的情况下,雷达回波经过匹配滤波器的处理结果,积累脉冲60个。仿真结果可以看到,根据距离和速度的不同,三个目标清晰可辨。图11进一步给出雷达距离探测结果。其中图11(a)和图11(b)分别为无通信信号和存在通信信号情况下的处理结果;为了便于观察两者的区别,把两个仿真结果在8 km处进行局部放大,分别对应于图11(c)和图11(d)。通过对比仿真结果可以发现,通信信号对雷达探测结果几乎没有任何影响。理论上可以从以下两点进行解释:1)雷达发射功率本身比通信高很多;2)通信子波束旁瓣电平控制得很低。综合以上两点,通信信号与高斯白噪声相比,影响微乎其微。类似地,图12分别给出无通信信号和存在通信信号情况下速度测量结果,同样证明通信信号对雷达几乎没有任何影响。
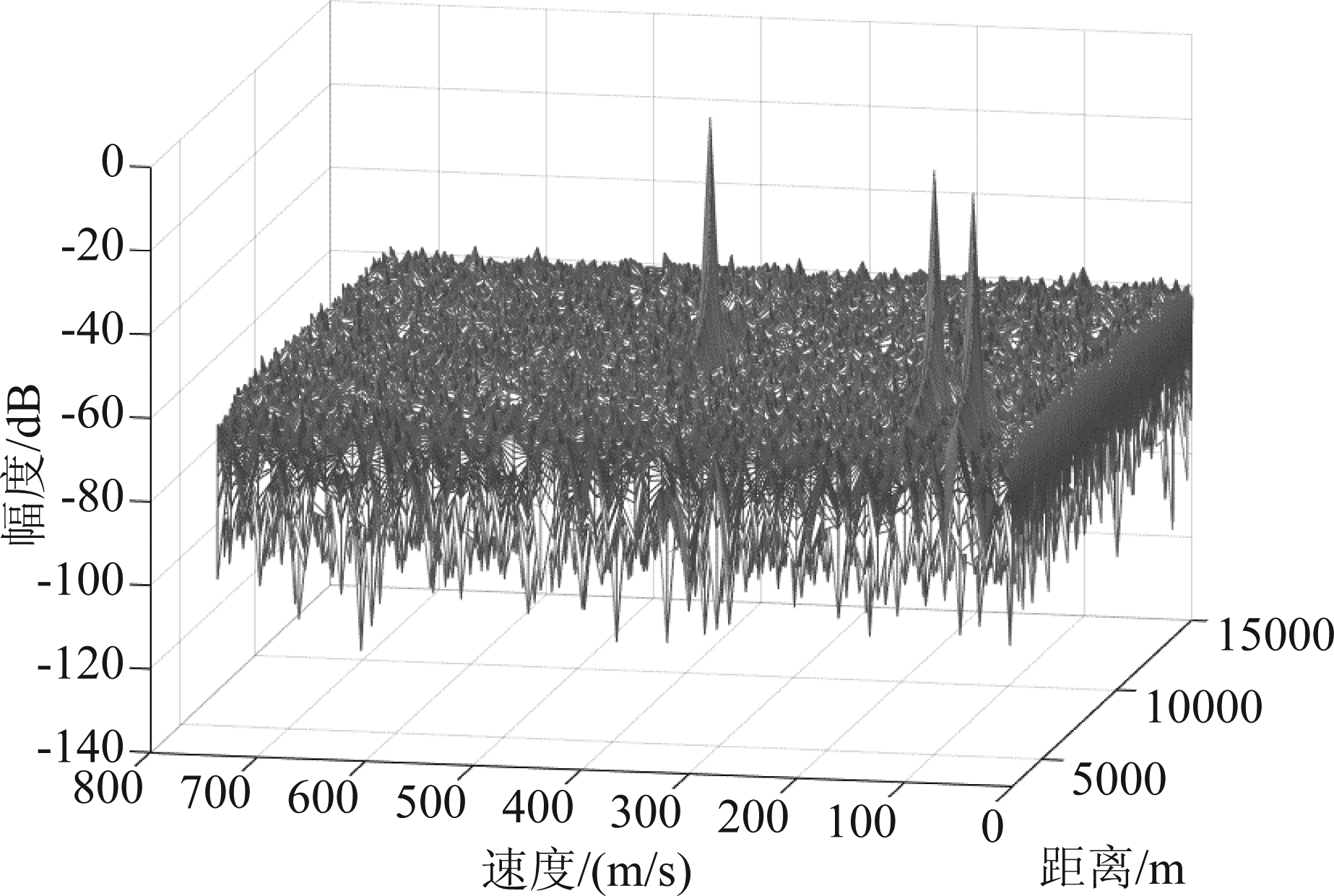
图10 雷达回波经处理后的距离-速度三维图
Fig.10 Three-dimensional range-velocity diagram of radar echo after processing
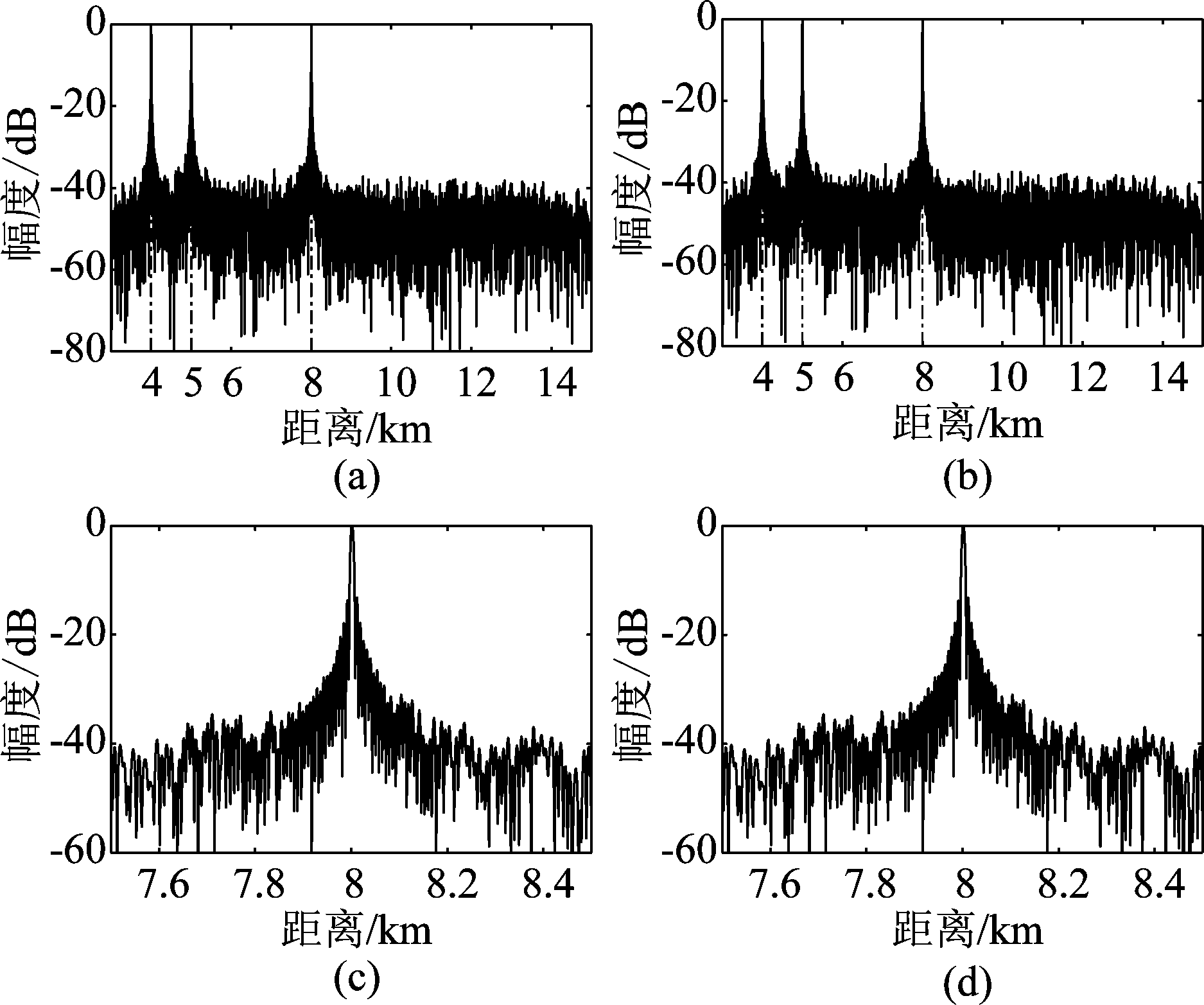
图11 脉冲压缩后的雷达回波:(a)无通信信号和(b)有通信信号时的距离探测结果;(c)无通信信号和(d)有通信信号时8 km处局部放大图
Fig.11 Radar echoes after compression: distance detection result of (a) no communications signals and (b) with communications signals; partial enlarged view at 8 km of (c) no communications signals and (d) with communications signals
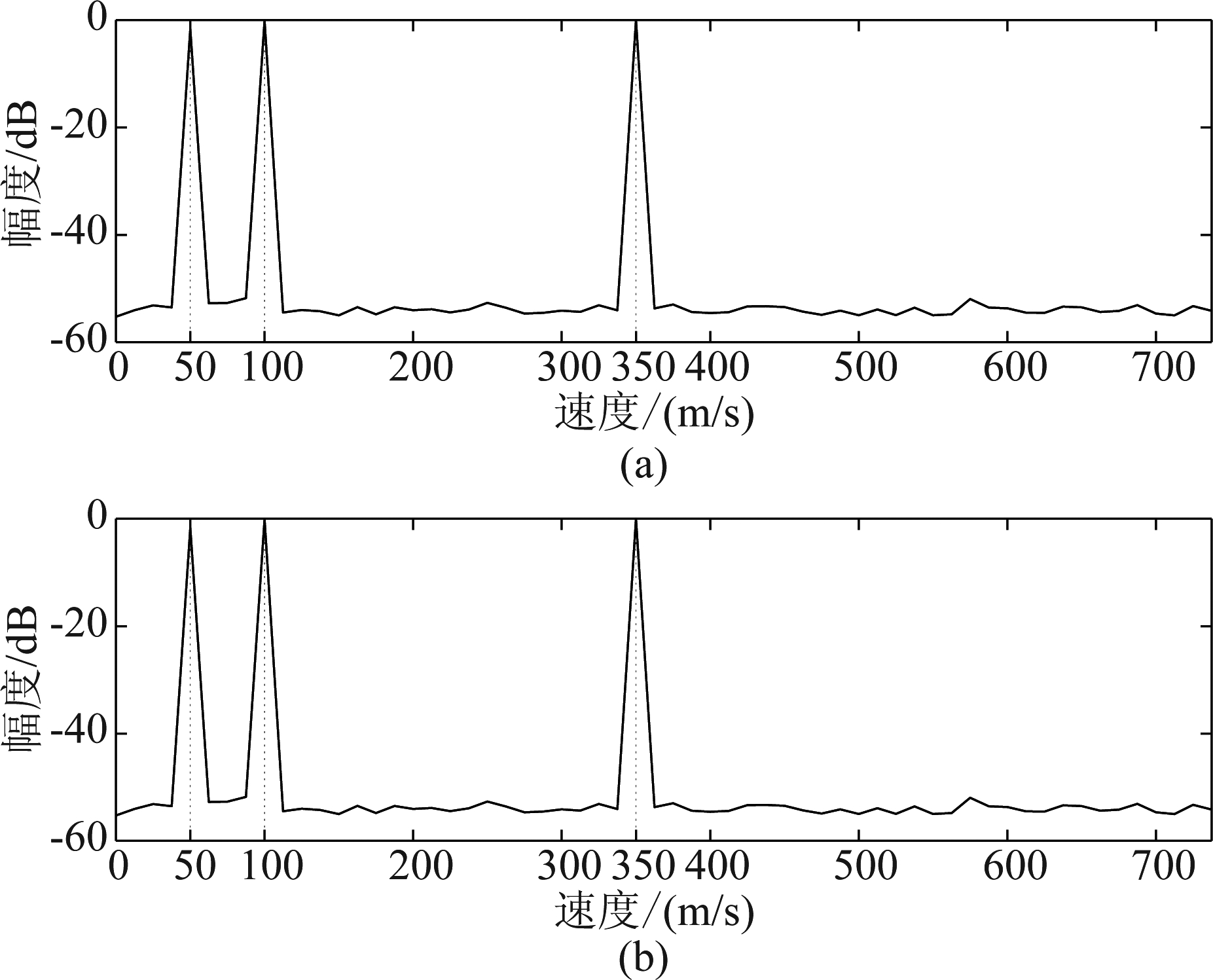
图12 速度测量结果:(a)无通信信号和(b)有通信信号
Fig.12 Velocity measurement results: (a) without communication signal and (b) with communication signal
与传统的空分雷达通信一体化结构[8-13]相比,所提方案具有如下优势。首先,所提方案雷达和多通信用户波束主瓣指向可独立随意调整,而文献[8-13]中方案雷达波束与通信方向是固定的,改变指向需要进行天线阵列的重新设计。第二,所提方案雷达和多通信用户在系统内部是独立的子系统,即雷达波形以及通信调制方式等没有严格的限制,而文献[8-13]中通信只能采用AM、ASK、QAM等固定且通信能力受限的调制方式。
5 结论
本文研究雷达与通信一体化的方案,提出一种多波束雷达通信一体化结构。结合多波束赋形技术和时间调制阵列技术,通过在硬件上增加加权网络数目来增加可控波束,同时各组加权网络的旁瓣电平也得到了独立的控制。所提方案在波束数量和旁瓣控制上得到了改进,能够实现单个雷达扫描波束与两个通信扫描波束的自由控制,或单个雷达扫描波束与多个通信固定波束的控制。实现非对称的雷达与通信发射功率,使一体化结构应用场景更加广泛。仿真结果表明,一体化系统能够同时实现雷达与通信功能,且不会受到相互影响。
[1] 卢俊, 张群飞, 史文涛, 等. 探测通信一体化研究现状与发展趋势[J]. 信号处理, 2019, 35(9): 1484-1495.
Lu Jun, Zhang Qunfei, Shi Wentao, et al. Development and Prospect of Detection and Communication Integration[J]. Journal of Signal Processing, 2019, 35(9): 1484-1495.(in Chinese)
[2] 刘光明, 李延军, 陈建勇, 等. 雷达通信机的设计[C]∥第九届全国雷达学术年会论文集, 2004: 986-989.
Liu Guangming, Li Yanjun, Chen Jianyong, et al. Design of radar communications machine[C]∥Proceedings of the Ninth National Radar Academic Annual Conference, 2004: 986-989.(in Chinese)
[3] 尚飞, 范鹏. 基于雷达传感器的公共数据链构想[J]. 中国电子科学研究院学报, 2007, 2(4): 344-348.
Shang Fei, Fan Peng. Conception of Public Data Link Based on Radar Sensor[J]. Journal of China Academy of Electronics, 2007, 2(4): 344-348.(in Chinese)
[4] Surender S C, Narayanan R M. UWB Noise-OFDM Netted Radar: Physical Layer Design and Analysis[J]. IEEE Transactions on Aerospace and Electronic Systems, 2011, 47(2): 1380-1400.
[5] Xu Shaojian, Chen Bing, Zhang Ping. Radar-Communication Integration Based on DSSS Techniques[C]∥International Conference on Signal Processing, IEEE, 2007.
[6] Sit Y L, Sturm C, Reichardt L, et al. The OFDM joint radar-communication system: An overview[C]∥Advances in Satellite and Space Communications, 2011: 69-74.
[7] 刘永军, 廖桂生, 杨志伟. OFDM雷达通信一体化波形相参积累研究[J]. 信号处理, 2017, 33(3): 253-259.
Liu Yongjun, Liao Guisheng, Yang Zhiwei. Research on Coherent Accumulation of OFDM Radar Communication Integrated Waveform[J]. Journal of Signal Processing, 2017, 33(3): 253-259.(in Chinese)
[8] Euziere J, Guinvarc H R, Uguen B, et al. Dual function Radar Communication Time-Modulated Array[C]∥IEEE Radar Conference, 2014.
[9] Euziere J, Guinvarc H R, Hinostroza I, et al. Time Modulated Array for dual function radar and communication[C]∥IEEE International Symposium on Antennas & Propagation & Usnc/ursi National Radio Science Meeting, 2015.
[10] Euziere J, Guinvarc H R, Hinostroza I, et al. Optimizing communication in TMA for radar[C]∥2016 IEEE International Symposium on Antennas and Propagation & USNC/URSI National Radio Science Meeting, 2016.
[11] Hassanien A, Amin M G, Zhang Y D, et al. A dual function radar-communications system using sidelobe control and waveform diversity[C]∥IEEE Radar Conference, 2015: 1260-1263.
[12] Hassanien A, Amin M G, Zhang Y D, et al. Dual-function radar-communications: information embedding using sidelobe control and waveform diversity[J]. IEEE Transactions on Signal Processing, 2016, 64(8): 2168-2181.
[13] Ahmed A, Zhang Y, Gu Y J. Dual-Function Radar-Communications Using QAM-based Sidelobe Modulation[J]. Digital Signal Processing, 2018, 82: 166-174.
[14] Shan C Z, Ma Y K, Zhao H L, et al. Joint radar-communications design based on time modulated array[J]. Digital Signal Processing, 2018, 82: 43-53.
[15] Shan C Z, Ma Y K, Zhao H L, et al. Time modulated array sideband suppression for joint radar-communications system based on the differential evolution algorithm[J]. Digital Signal Processing, 2020, 97.
