1 引言
随着人类向信息时代的迈进,在未来6G、空天地海一体化等信息网络的覆盖下,信息通信容量将持续呈爆炸式几何增长,为了保证信息网络的安全高效运行,信息感知和处理技术也不断向前演进,测量、感知、通信、计算等信息处理技术在信息时代分别发挥着巨大的作用[1]。复杂多样的信息感知和处理技术也不可避免地给信息网络带来了高成本和高复杂度,多功能一体化的信息感知处理技术正成为科研者追求的目标。此外,在国防领域,面对复杂多变的战场环境,研制多功能一体化的小型信息感知处理装备也愈发重要。多模光纤因其大量的空间模式和低损耗特性,在信息感知、传输和处理方面具有独特作用。
多模光纤被发明早期主要用于光通信领域,其低连接损耗和低制造难度等特性使其广泛用于早期短距离光通信组网中。但由于模式色散的存在,多模光纤的传输带宽受到极大限制,难以将其应用于长距离光通信,近而逐渐被单模光纤所取代。但近年来,随着研究人员对多模光纤所具有的包括模间干涉、模式耦合、空间频率映射等复杂物理特性研究的深入,多模光纤在光谱分析、射频感知及成像领域的应用越来越广泛,其信息传输的高密度、微型化的特点也为未来实现多种信息感知和处理的一体化提供了可能性。
光谱仪是一种应用广泛的光谱分析精密仪器。诸如物质成分测量和鉴定,化学分析等场合,就可以根据光谱信息来解决问题。传统的基于光栅的光谱仪,尽管可以实现高分辨率光谱测量,但重量、体积、功耗和成本无法保证。利用多模光纤的频率空间映射关系,可以通过测量光纤输出模斑求解光谱信息,这使多模光纤和波导成为一种新型的光谱测量器件[2- 4]。其优势在于制造成本低廉,可实现光谱仪的微型化,同时保证高分辨率的光谱测量。如果能够降低机械振动,环境因素的影响,或者加强校准方法与重建算法,可穿戴式的光纤光谱仪有可能走上实用。在未来,多模光纤有潜力用于可穿戴式的光纤光谱仪的制造,在灾情救险,军事探测等场合,将发挥出巨大的作用。
宽带射频谱感知作为无线电识别与电子战领域的关键技术,在未来广频谱、宽频带的非线性电子战场将发挥重要作用[5- 6]。传统射频接收设备需要高精度、高稳定性的接收前端,采集的射频信号被模数转换器(ADC)采集后进行存储。而大带宽、高信息量等要求对传统ADC采集方式在重量、功耗和成本等方面提出了严峻的挑战。近年来,在压缩感知理论的指导下,基于压缩采样的射频感知系统被广泛研究与应用,从而成倍减小射频信号采集和存储的压力。系统的关键在于对信号的高速稳定的编码,而传统的高速信号发生装置仍然受限于其体积、重量、功耗和成本。多模光纤的频率空间映射为光信息的随机编码开辟了新的思路,其被动式的编码方式和固有的低损耗、大带宽特性,可使其在基于压缩采样的射频感知系统发挥巨大价值。
单根多模光纤内窥成像系统是一种通过微创方式对人体或组织内部进行成像的工具,用于给医生提供组织检测的必要信息[7]。传统单光纤成像器使用包含数万根芯的光纤束进行成像,其优点是抗弯曲和环境影响,但其分辨率收到光纤芯径限制。近年来,利用多模光纤模式传播特性的多模光纤成像系统被广泛研究,结合先进的图像重构算法,可恢复出高质量、高分辨率的内窥图像。多模光纤传导空间信息,大大提升了设备的微型化程度,是未来医用和军用内窥镜领域有前景的发展方向。
本文将通过基于多模光纤的光谱分析、射频谱感知和成像技术三个方面的研究进行梳理,以阐述多模光纤面向这些特殊领域及一体化应用所面临的挑战及未来发展的趋势。
2 基于多模光纤的光谱分析技术
2.1 多模光纤光谱仪背景
在光学测量领域,光谱仪被广泛应用于化学、生物、材料分析和通信测量等领域。传统的基于光栅的光谱仪通过色散实现光谱到空间的一对一映射,可实现高分辨率的光谱测量。而光栅式光谱仪的分辨率与其传播光程长度是成正比,这导致了测量分辨率与仪器尺寸的矛盾。近年来,人们对微型光谱仪的研究逐渐增多,基于小型光栅、微腔、调制变换的微型光谱仪已经被报道[2- 4]。然而,光谱仪的小型化势必会导致分辨率的降低或可操作带宽的减小。
为了克服以上的挑战,耶鲁大学Redding B.等人于2012年提出了基于多模光纤的高分辨率光谱仪[8-9]。 其系统硬件复杂度非常低,仅仅包含单根多模光纤和一个相机,如图1所示。
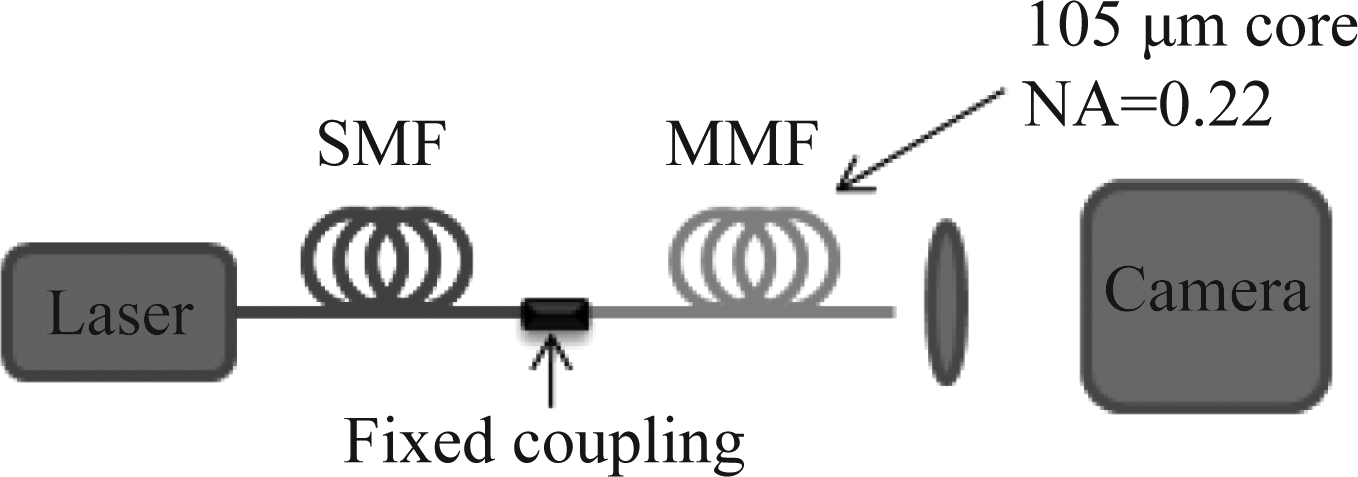
图1 多模光纤光谱仪系统框图[9]
Fig.1 A schematic of the fiber spectrometer setup[9]
该系统利用了多模光纤的频率空间映射特性,通过入射光在多模光纤中传播在输出段产生的模斑来重构输入的光谱信息。 这种频率空间映射关系可以定义为输入多模光纤的不同光波长所产生的输出模斑之间的非相关性。这种非相关性源于多模光纤的模间干涉(Model interference),不同模式的相位延迟随光线传播不断增加,理论上,当最高阶模式与最低阶模式之间的相位差为π时,输出模斑将表现出非相关性[9]。由于不同波长的光信号在传播过程中是相互独立的,所以待测光谱所产生的模斑是每一个波长分量所产生的模斑的线性组合。多模光纤光谱仪正是通过这一关系测量输入光谱的。数学上来说,这种映射关系可以被抽象为一个传输矩阵T,该传输矩阵作用于入射光信号S,在光纤输出端的空间模斑即是观测向量I。进而系统模型可以写成
I=TS
(1)
在求解这个问题之前,需要对传输矩阵进行校准。通过一个可调谐激光器产生不同频谱信道所对应的单色光,分别记录它们所激发的空间模斑作为传输矩阵T的每一列,形成观测矩阵。最终测量输入光谱的问题变为已知传输矩阵T和所观测向量I,求解输入光谱S。目前,截断的SVD分解、模拟退火算法[9]、优化迭代算法[10]和压缩感知[11]等重构算法已被用于解决该问题。
多模光纤光谱仪的光谱分辨率δλ取决于光纤频谱相关函数[9]:
C(Δλ,x)=〈I(λ,x)I(λ+Δλ,x)〉/
[〈I(λ,x)〉〈I(λ+Δλ,x〉]-1
(2)
其中I(λ,x)代表在波长λ处输出模斑空间位置x的强度,〈…〉代表在波长上的平均。光谱分辨率δλ等于频谱相关宽度C(δλ/2)=C(0)/2。也就是说,当输入波长改变δλ时,输出模斑改变后与原来近似不相关。物理上,光谱分辨率由光纤的参数决定,光纤的数值孔径越大、长度越长,分辨率越高。多模光纤光谱仪的带宽由光纤所支持的模式数量决定,模式数量越多,支持的信息量越多。
2.2 多模光纤光谱仪研究现状
基于多模光纤光谱仪原型[8],Redding B.等人使用100 m和4 cm的多模光纤分别在红外和可见光波段实现了分辨率1 pm 和带宽250 nm的光谱仪[12]。基于长距离的光纤可以提高光谱仪的分辨率,但其重构带宽受到限制。除此之外,光纤过长会减少系统稳定性,稳定、位置等环境变化会使多模光纤的传输矩阵发生改变,需要重新校准。短光纤更稳定同时支持大带宽的重构,但其光谱分辨率会相应降低。
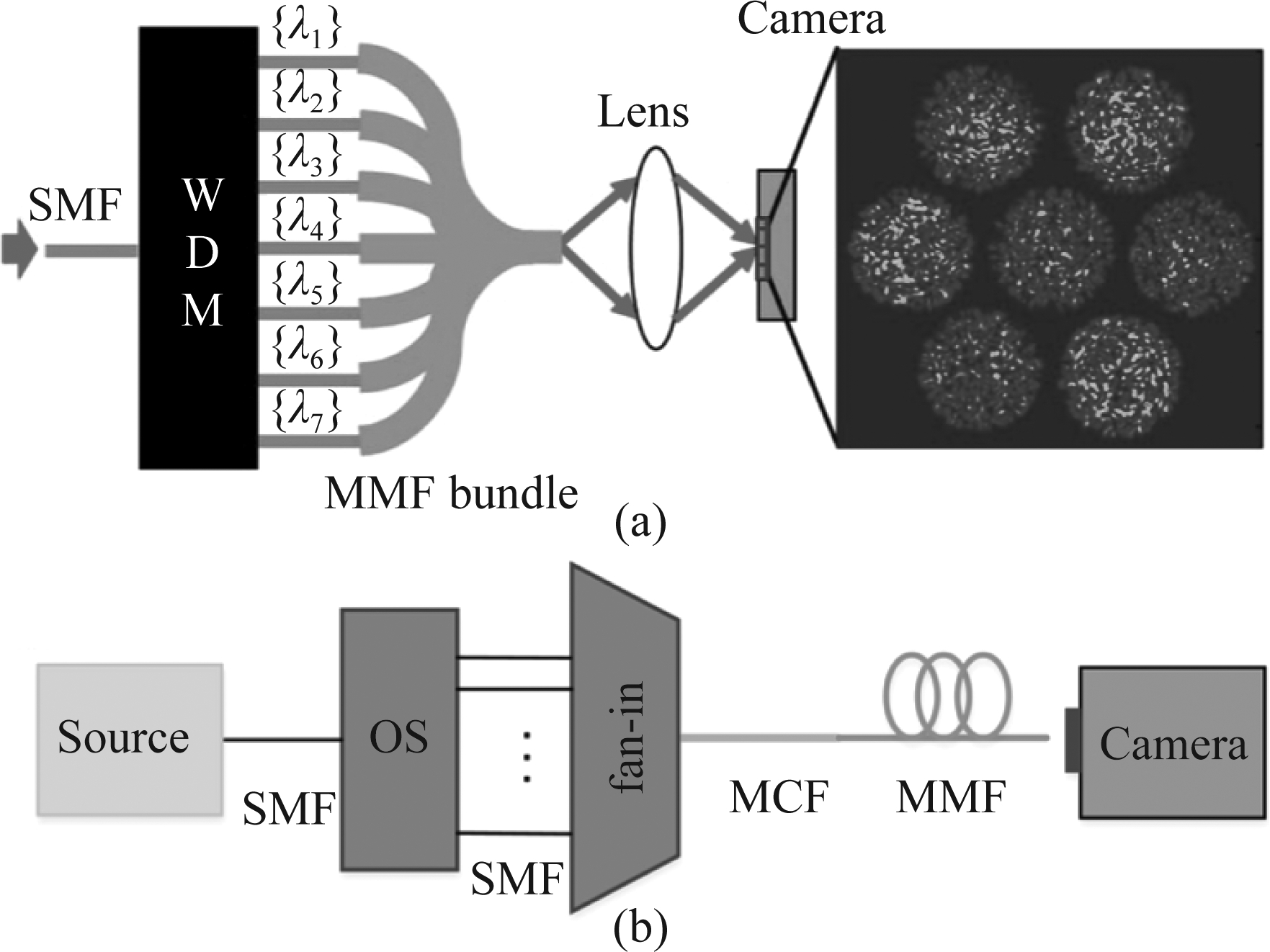
图2 (a) 波分复用MMF光谱仪结构图[13] ; (b)空分复用MMF光谱仪结构图[10]
Fig.2 (a) Setup of WDM-based MMF spectrometer[13]; (b) Setup of SDM-based MMF spectrometer[10]
针对以上问题,耶鲁大学和北京邮电大学分别通过频分复用[13]和空分复用[10]技术在不牺牲光谱分辨率的情况下成倍提高了光谱仪带宽。如图2(a)所示,在基于频分复用的方法中,一个波分复用器将输入宽带光信号按波长分成了多路,每一路分别输入不同的多模光纤,最后用一个相机采集所有模斑,每一路相互独立。这种方法成倍地扩展了光谱仪的操作带宽,其操作波段可以灵活选择。使用基于频分复用的方法,实现了1500 nm处的0.03 nm的解析度和100 nm的带宽[13]。图2(b)展示了基于空分复用的多模光纤光谱仪系统,这种方案利用多模光纤不同空间激发位置产生独立模斑的特性,将一根多芯光纤与多模光纤耦合形成多种输入状态,从而实现复用,仅用单根多模光纤实现了光谱仪带宽的灵活扩展。该实验使用一根多模光纤和七芯光纤中的3条芯,实现了1550 nm处的0.02 nm的解析度和30 nm的带宽[10]。
麻省理工学院Wan N. H.等提出一种基于拉锥光纤的光谱仪方案[14]。该方案不同于之前对输出端面模斑检测的方案,而是设计了一种拉锥结构的多模光纤,对光纤拉锥锥面模斑进行检测,这种方式可以使输出模斑对波长的变化更加敏感,仅使用一根长度较短的光纤就可以提供较高的光谱分辨率。研究人员实验实现了在可见光波段40 pm和红外波段10 pm的光谱分辨率。更重要的是,这种方法因使用较短光纤从而提高了光谱仪的环境稳定性。
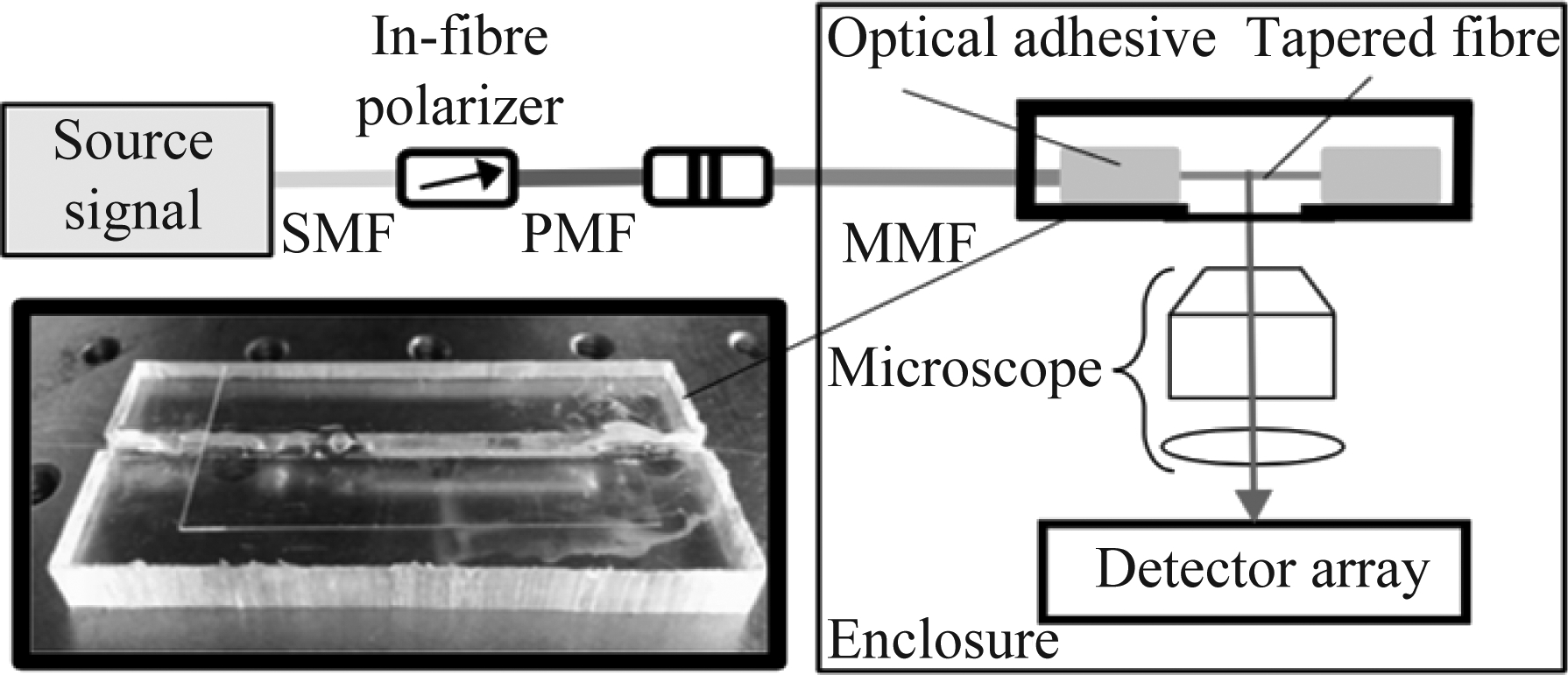
图3 拉锥式MMF光谱仪的结构图[14]
Fig.3 Structure diagram of fused-tapered MMF spectrometer[14]
为了使基于模斑的光谱仪实现芯片级的小型化,Redding B.等人分别在2013年和2016年提出了基于无序光子芯片[15]和多模螺旋波导[11]的片上光谱仪结构。如图4(a)所示,无序光子芯片由绝缘硅晶片制成,包含半圆空洞和脊型空洞二维散射结构。入射光由波导传入半圆无序散射介质后向周围传播,在通过多个脊型散射介质的传导后由探测器探测,实现输出信道化。与多模光纤光谱仪类似,通过得到的模斑对输入光谱进行重构。实验中,研究人员在100×50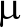 
m的面积上,1500 nm波长处,实现了分辨率为0.75 nm且带宽为25 nm的光谱仪。图4(b)展示了基于多模螺旋波导的光谱示意图,研究人员设计了一种螺旋结构的多模波导,其核心是利用相邻波导间倏逝场耦合使光场在波导内不断旋转,这使得不同导模之间的相位差变大,减小了频谱相关宽度,从而提高了光谱分辨率。该实验使用一个半径250 μm的螺旋结构,在1520 nm处获得了0.01 nm的分辨率。
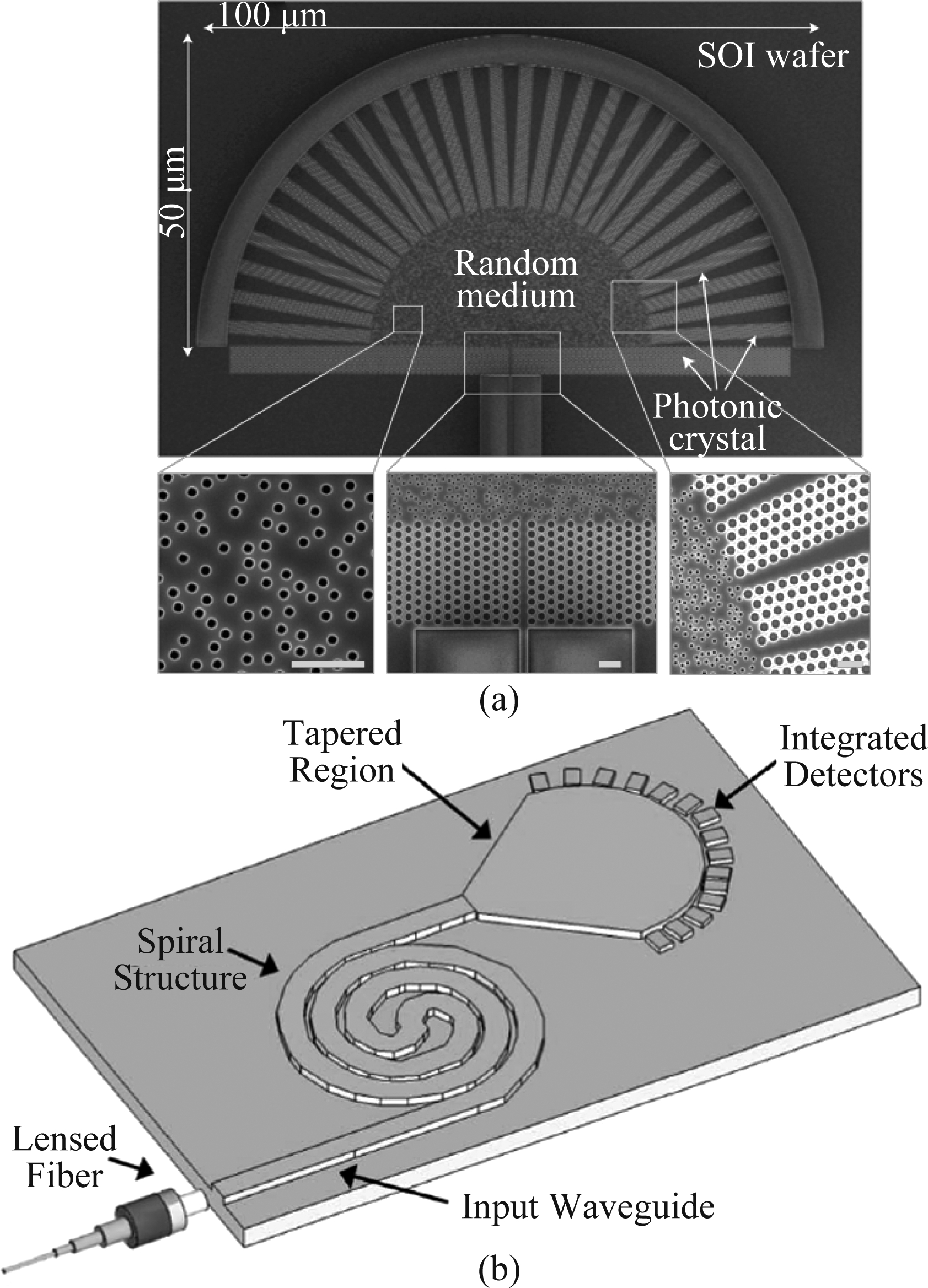
图4 (a) 无序光子芯片光谱仪结构图[15]; (b) 螺旋多模波导光谱仪结构图[11]
Fig.4 (a) Spectrometer based on a disordered photonic chip[15]; (b) Evanescently coupled multimode spiral spectrometer[11]
理论上,任何可以通过光的散射、干涉和衍射产生随机模斑的物理器件都可以用于制造基于模斑的光谱仪[16-17]。多模光纤的优势在于其易于制造、低成本和可制成全光纤光谱仪,但它同样面临着以上提到的在带宽、分辨率和环境稳定性上的挑战。为了克服多模光纤光谱仪的以上问题,研究人员分别从硬件和算法等多个角度上改进原有系统,并提出一些衍生方案。在硬件设计上,包括集成了光开关的多模波导[18]、散射介质[19]和集成球腔[20]等方案已经被提出用于提升光谱仪带宽与分辨率。在重构算法设计上,主成分分析克服了模斑相关将多模光纤光谱的分辨率提高到阿米(am)量级[21],深度学习算法提高了光谱仪的重构准确度与动态范围[22]。
2.3 多模光纤光谱仪的发展趋势
随着多模光纤光谱仪的发展,它所面临的技术和性能要求也在逐步提高,频谱分辨率与测量带宽是两个重要的性能指标。提升这两个指标可以简单地通过增加光纤长度和光纤芯径的方式实现。然而,这会导致光纤对环境扰动更加敏感,降低系统稳定性和光谱重构精度。针对这一挑战,目前有如下几个潜在解决方案:一是模块化传输矩阵校准系统,即通过集成可调谐激光器与校准控制系统,实现对多模光纤传输矩阵的快速或实时校准,在使用光谱仪前进行当下环境的系统校准即可获得准确测量。这种方法的缺陷在于实现复杂和成本高。二是特种多模光纤设计,即通过特殊材料、参杂和物理结构[17],在保证光纤尺寸的情况下,提高光纤模式色散和输出光场模斑信息量。三是片上光谱仪[11,18],即通过多模波导结构集成光谱仪到芯片尺寸,使环境干扰对光谱仪的影响降到最低。但目前该方向受限于系统分辨率和带宽,模斑探测难度高,很难实现大规模集成。
探测器噪声是影响光谱重构精度的重要因素。目前对于稀疏光谱的重构,传统优化算法可以在一定噪声的情况下获得与商用光谱仪性能相近的结果,然而对于宽带光谱,其输出模斑对比度下降、噪声累加等问题将导致重构难度增加。对于该问题,目前可以从硬件设计和算法两个方面进行探索,例如基于波分复用[13]和空分复用[10]的多模光纤光谱仪系统,利用不同自由度提高模斑信息量,减小宽带信号重构难度。算法方面,目前大部分工作仅采用了简单的优化算法,还有很多发展空间。随着深度学习在各个领域的广泛应用,基于深度神经网络的算法有潜力用于从二维模斑到一维光谱信息的重构,并得到高鲁棒性的结果。
多模光纤光谱仪的另一个局限在于输入至多模光纤的光必须具有固定的空间模式和偏振态,这样才能确保某一频率的光在多模光纤输出端产生不变的模斑,也就是说,如果光的空间输入条件变化,会影响多模光纤的传输矩阵。固定的输入条件往往通过一个保偏单模光纤与多模固定光纤耦合来实现。这样系统在测量一个具有很大空间模式的发散光源时,会出现测量灵敏度降低等问题。目前多模光纤光谱仪适用于具有光纤耦合的光源光谱测量需求的应用,比如通信信道监控,光学相干层析等。
多模光纤光谱仪的另一个重要发展趋势是集成化,进一步的小型化乃至芯片化不仅可以提高光谱仪的稳定性,更有利于其完成商业化应用。然而集成化对空间的压缩势必会带来对光谱仪分辨率与带宽的限制。与传统光栅光谱仪类似,多模光纤光谱仪频谱分辨率取决于光纤长度,测量带宽取决于模斑信息量,即横向尺寸。空间尺寸的减小将限制光谱仪的性能。目前主要的解决思路基本上是在不牺牲尺寸的情况下,通过对多模光纤和波导的特殊设计,提高其模式色散能力,通过复用技术提高光谱仪带宽。
3 基于多模光纤的射频感知技术
3.1 射频感知背景
宽带射频谱感知是无线电识别与电子战领域的关键技术。在具体的电磁环境中,接收机接受的信号往往具宽带和稀疏的特性,即在较宽的频谱范围分布着多个频带的信号。奈奎斯特采样定理要求以大于信号最高频率分量两倍的采样率(奈奎斯特速率)对模拟信号进行采样,可以不需要考虑任何信号先验信息的情况下保证信号中的信息不丢失。传统的电子接收机依赖于使用超高速ADC采集信号的时域信息。但随着带宽需求的越来越高,其问题也凸显出来。首先,高速ADC采样的时间抖动会降低信号采集的精度与准确性。其次,其体积、重量、功耗与采样率近似成正比。另一方面,对高速信号的采样产生的海量数据将给后端的数据存储、传输、处理带来巨大压力。
压缩感知技术把信号的稀疏性(大部分自然信号在某种变换域上呈现稀疏分布特性)作为先验信息,通过随机采样突破了奈奎斯特采样速率,结合非线性重构算法精确恢复信号[23-25]。将该理论应用于模拟信息转换,将大大降低对信号采样速率的需求,减小信息传输和存储的压力。基于压缩感知的电子接收机已经被广泛研究[26-27],但由于电子器件的带宽与抖动限制,在宽带信号的盲估计与多频带信号感知上仍存在巨大挑战。
光子辅助的射频系统得益于光子器件的巨大带宽、低延时、抗电磁干扰和良好的频率一致性等优势,在射频通信、雷达和电子对抗上有着重要应用[5- 6]。为了克服电子器件带宽与稳定性的限制,光子辅助的压缩射频感知系统引起了越来越多的研究[28-37]。其中,研究人员提出了多种基于光子时域拉伸的射频感知系统[28,33,36]。基于色散傅里叶变换原理[38],利用锁模激光器产生的超窄脉冲与色散光纤产生的二阶色散实现了光信号的时频映射关系,并通过高速伪随机信号的调制产生时域拉伸的高速结构光。得益于锁模激光器极高的时间频率稳定性,该结构光可用于对调制到光场上的射频信号进行编码,通过脉冲的压缩或拉伸技术实现压缩采样。B. T. Bosworth等人基于上述原理提出了基于高速超宽带光压缩感知稀疏射频信号的方案[35-36],实现了高压缩比的同时,对带宽为10 GHz以上的多个射频谱线的测量。对于这类光子辅助压缩采样系统,通常观测矩阵的产生都是通过在光上调制高速的伪随机信号实现的,其速率要高于对射频信号的奈奎斯特采样速率才能保证信号的恢复,这使得要求大带宽的系统的复杂度与成本大大增加。大带宽要求下,高速伪随机信号的时间抖动也将对信号重构造成严重影响。
2016年,Valley G. C.等人第一次提出了基于多模光纤的宽带稀疏射频感知方案[39]。利用多模光纤的频率空间映射关系,将时域信号映射至空间并产生观测矩阵。这种方法采用光纤无源的处理结构,避免了高速伪随机码的使用,以无源编码方式和多模光纤固有的低损耗、大带宽特性,将大大降低系统的体积、重量和成本。
3.2 基于多模光纤的射频感知
(1)压缩采样数学模型
射频信号x可看成是一个长度为N的一维向量,它在某些变换域下呈现稀疏特性,即
x=Ψ -1s
(3)
其中s是一个与x维度相同稀疏向量。压缩采样的过程是用一个维度为M×N的观测矩阵Φ对信号x进行观测,得到一个M维的观测向量,这里M≪N。前向模型如式(4)所示:
y=Φx+g=ΦΨ -1s+g
(4)
其中,g是测量噪声。压缩感知理论表明,当测量矩阵Φ满足有限等距性质时,则可以由M维信号y,恢复出x信号[23-25]。通常来说观测矩阵可以是一个随机高斯矩阵。对于宽带射频信号压缩感知系统的设计,关键在于在硬件上实现观测矩阵,以及矩阵与输入射频信号的相乘操作。光子辅助射频感知系统通常采用伪随机序列调制产生观测矩阵,而这种方法需要高速信号产生,面临时间抖动、成本功耗等问题。
(2)多模光纤产生观测矩阵
Valley G. C.等人在2016年利用多模光纤的频率空间映射产生压缩感知观测矩阵[39]。曾提出光啁啾信号通过多模光纤或平面波导的传输实现了压缩感知测量矩阵的功能。图5展示了该系统的理论实验装置图。
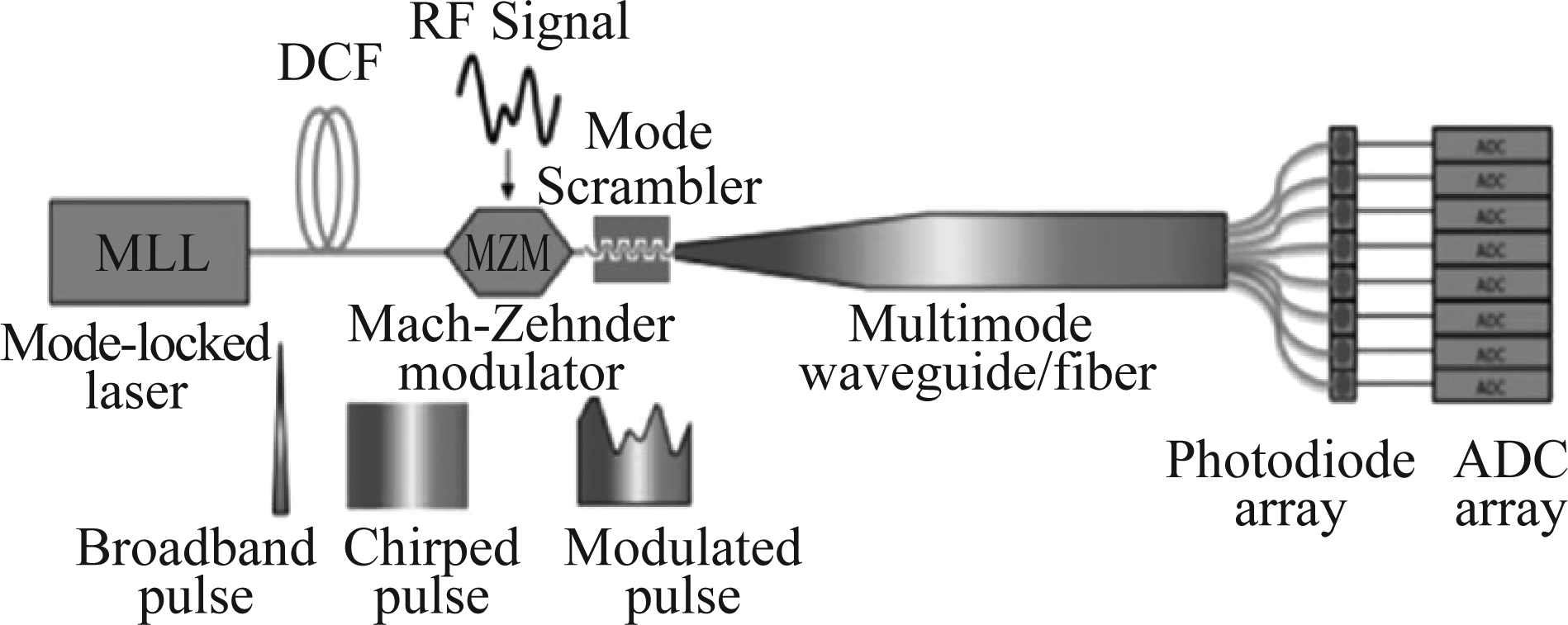
图5 基于多模波导的光子压缩感知系统[39]
Fig.5 Photonic compressive sensing system using a multimode waveguide[39]
首先,飞秒锁模激光器发出的脉冲经过色散补偿光纤(DCF)进行时域拉伸,实现信号的时频映射。通过马赫曾德尔调制器(MZM),将射频信号进行强度调制,随后进入多模光纤,在输出端产生空间模斑。该方案利用多模光纤的空间频率映射,对输入脉冲的光谱编码至空间,即输出模斑是不同频率所产生模斑的线性组合。最后,在多模光纤输出端通过光探测器阵列对模斑进行采集。总的来说,通过色散光纤实现信号时频映射,再通过多模光纤实现频空映射。该方案的优点在于使用无源光器件产生压缩感知观测矩阵,功耗、成本和系统复杂度低。
2018该团队基于上述研究,演示了一个完整的基于多模光纤的压缩感知系统[40],实验装置如图6所示。其中,一个32芯的光纤束将多模光纤所产生的模斑进行空间分割,再通过一个光探测器阵列进行探测。研究人员采用差分探测的方法实现了16个通道压缩感知系统,差分探测有利于提高系统的动态范围,减小噪声干扰。最终系统实现了2～19 GHz的可探测范围,仅用单个脉冲(4.5 ns)实现系统分辨率100 MHz,在2.8 μs的时间窗口下利用100个脉冲周期,可实现20 kHz的频谱分辨率。
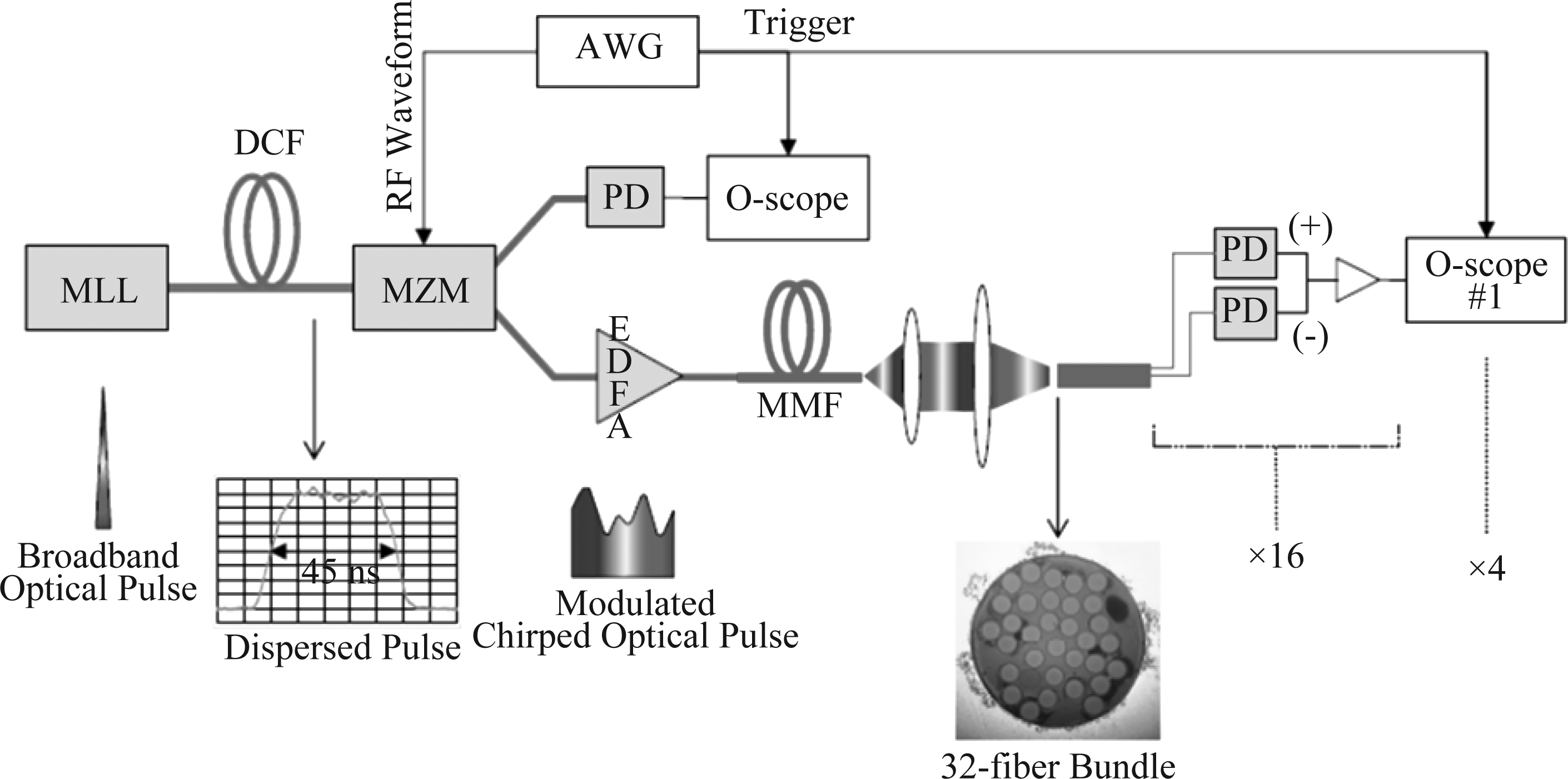
图6 射频光子辅助检测射频信号的压缩感知系统[40]
Fig.6 Compressed sensing system for RF photon assisted detection of RF signals[40]
3.3 基于多模光纤的射频感知的发展趋势
目前,针对基于多模光纤的射频感知系统,研究趋势主要集中在高稳定性、高精确度和高压缩比三个方面。利用多模光纤产生观测矩阵的方法可以最大程度减小系统复杂度,避免高速伪随机序列产生所带来的时间抖动,减小系统功耗和成本。然而由于多模光纤对环境扰动十分敏感,温度和应变等条件都会影响多模光纤传输特性,即改变系统观测矩阵,这将严重恶化信号重构精度。而对系统观测矩阵的校准不具备实时性,观测矩阵一旦改变,就需要重新进行校准。提高压缩比可以大大降低对高速ADC的需求并减轻后端的存储压力,但受到压缩感知理论限制,恢复算法需要足够的观测才能对信号进行良好重构。除此之外,受系统噪声影响,带有误差的观测会进一步恶化重构效果。
以上问题主要有两种解决途径供研究人员探索。一是系统集成化和芯片化,通过将关键器件如多模波导、探测器阵列和电光调制器芯片化,可大大减少环境对系统的干扰,其难度在于光子芯片的设计与制造。针对多模光纤系统,产生有足频谱够分辨率的频率空间映射需要足够的模式色散与模式耦合,通常需要一段较长多模光纤来实现,但其环境敏感特性将降低系统的稳定性,长光纤系统将需要大量外围器件维持恒稳,这将限制系统的集成化。一种思路是研制具有高数值孔径的特种多模光纤或采用特殊物理结构,在保证足够模式色散的前提下减小光纤长度,从而提高稳定性易于集成。二是发展更强大的信号重构算法,提高系统对噪声和校准误差的鲁棒性。传统恢复算法采用迭代优化策略。这种方式的重构表现受噪声影响大,很难实现大压缩比重构,每次采集的数据需要重新计算,速度慢效率较低,不利于实时的应用。随着深度学习的广泛应用,基于深度神经网络的重构算法也是一个研究趋势,针对于某个系统,采集大量训练数据后,通过训练神经网络可以学习到系统的传输特性,对于一个已经训练好的网络,可以快速高效的恢复原始信号。除此之外,深度神经网络有能力学习不同噪声环境下的系统传输矩阵,从而提高系统对噪声和校准误差的鲁棒性。基于深度学习的算法有潜力提高了系统的精确度,解决了高压缩比下恢复困难的问题。
4 基于多模光纤的成像技术
4.1 多模光纤成像背景
光纤成像技术是一种用于对人体天然管道内部成像的医用内窥和深层组织成像显微技术。相比于传统使用透镜的光学成像系统,光纤成像的任务更加具体,其优势在于其直径小、损耗低、成本低等,是一种理想的侵入式导光介质。在生物医学和临床应用中,实时细胞活动、形态学和整体组织结构的可视化对于基础研究和医学诊断越来越重要,因此光纤成像系统需要能够深入到器官和组织内部以微创的方式进行实时的活体成像[7]。
光纤成像的一个关键问题就是如何并行地传输图像信息。早期的研究是采用光纤束的结构实现多个并行空间信道,每一个光纤核作为一个“像素”来收集图像信息,即使用多芯光纤(MCFs)进行成像[41- 42]。光纤束直径越大,包含的光纤核越多,则分辨率越高。此外,这种方法要求光纤核之间空间分离,避免光纤在核与核之间的耦合。受制备工艺的影响,目前光纤核可达到的最小直径约为4 μm,最小间隙为1 μm,即每增加一个像素点的成像至少需要增加光纤束5 μm的直径。这一方面限制了成像分辨率与微型化的程度,并使图像像素化严重,另一方面降低了成像系统的光子收集效率[43]。
为了解决多芯光纤成像系统中芯径大、分辨率低的问题,多模光纤芯径小、模式多的性质使得单根多模光纤成像成为可能[44]。在成像光纤的直径上,使用多模光纤相比于光纤束具有显著的优势。多模光纤用于成像的像素密度ρ(即每个单位面积上的模式数)约为:
(5)
其中NA为光纤的数值孔径,λ为光源的波长。在数值孔径NA=0.5的情况下,每个像素占用约为λ2大小的区域。相比光纤束成像,单根多模光纤成像的成像密度可以大1～2个数量级[45]。与使用单模光纤的光纤束不同,多模光纤可以传输成百上千种导波模式,在输出端形成不同的空间散斑分布。光纤中每一种导波模式都有不同的相速度,这会使不同的图像信息间失去原有的相位关系,最终会在输出端产生看似随机的散斑。虽然多模光纤使原有的图像发生了畸变,但这个过程并没有损失图像信息,而是将其进行了复杂的编码,如果光在光纤中的传播过程可以被得知,那么就有可能恢复原始的图像信息。
利用多模光纤进行成像最早要追溯到研究者们对散射介质的研究。20世纪60年代,Oliver等[46]发现当激光束透过带有尘土的空气或胶质溶液等介质后会出现明显的“散斑图案”,这源于是光在这些介质表面和内部的随机散射,而光在传播过程中因受到介质中微观粒子的作用而改变其光强空间分布的现象被定义为散射现象。2007年,Vellekoop I. M.等人第一次利用波前整形实现了激光通过散射介质聚焦[47]。如图7所示,平面波通过散射介质输出散斑,而波前被整形后的光波通过散射介质可实现在输出端聚焦的特性,这表明散射介质可以像透镜一样成像。
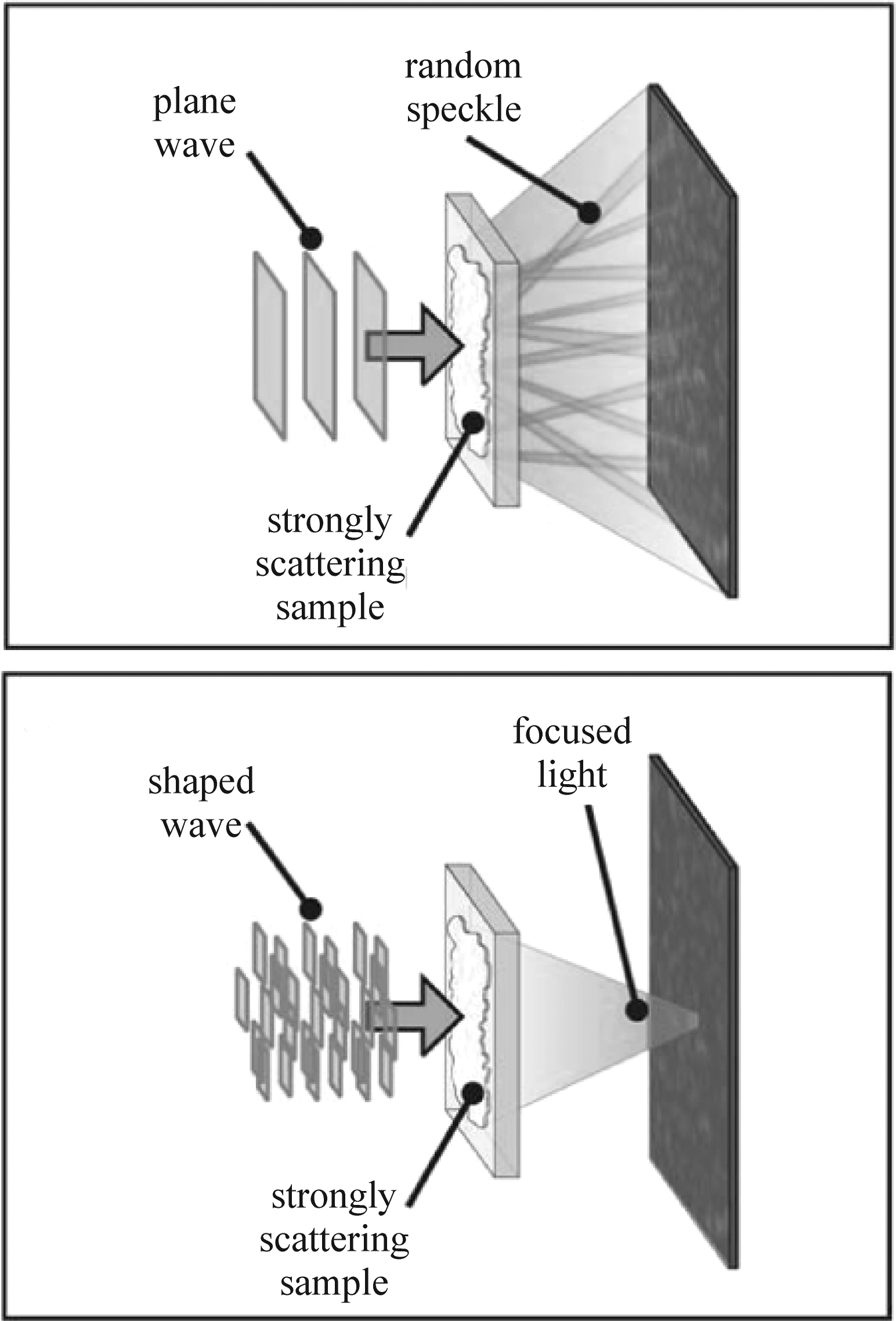
图7 波前整形后的激光通过散射介质聚焦[47]
Fig.7 The wavefront of the laser shaped so that scattering makes the light focus at a predefined target[47]
多模光纤的物理特性与散射介质类似,光纤的导波模式之间的干涉与耦合会在输出端产生散斑。而多模光纤成像技术也是在散射介质成像技术的基础之上逐步发展出来的[48- 49]。光纤可以被看作一种特殊的散射介质,而多模光纤成像可以看作是散射介质成像技术的一个特例。
4.2 传统多模光纤成像技术
(1)相位共轭法
最早使用多模光纤传输图像是通过相位共轭补偿法实现的,通过全息板或非线性晶体构造时间反演波来补偿光纤对图像造成的畸变[50-51]。在理想光学系统中,利用任意可以对光场进行正交变换的光学元件(包括散射介质和多模光纤)对光场进行一次正交变换,然后计算其逆变换,便可以消除输出光场的畸变进而准确恢复原始图像。1976年,加州理工大学的Yariv等[52]使用两段完全相同的光纤,利用第二段光纤中产生与第一段光纤中的光束相位互为共轭的相位,以此来消除相位畸变。然而在实际条件中很难生产出这种光纤,因此这种方法应用较少。
虽然光相位共轭法在克服多模光纤散射特性方面的应用奠定了基础,但受制于光折变晶体的特性,这种方法也有波长特异性、响应时间缓慢和系统在多路复用情况下过于复杂等缺点。为了解决这些缺点,柏林夏里特大学的Papadopoulos等引入了数字相位共轭技术用于多模光纤成像[53]。数字相位共轭是光学相位共轭的一种实现方式,它不是利用晶体的非线性特性来产生共轭光场,而是利用数字全息记录的方法来计算畸变波前的实际相位,然后将计算出的相位投影到空间光调制器(SLM)上,并将此信息分配给未调制的光束,最后形成相位共轭光场。当共轭光束通过多模光纤介质前向传播时,畸变消除,原始图像在输入平面CCD相机上生成。使用数字全息技术的数字相位共轭法在记录和存储大量通过多模光纤传输的光的全息图方面提供了前所未有的灵活性,使我们能够建立输入输出数据对的数据库,从而对多模光纤进行表征和控制。
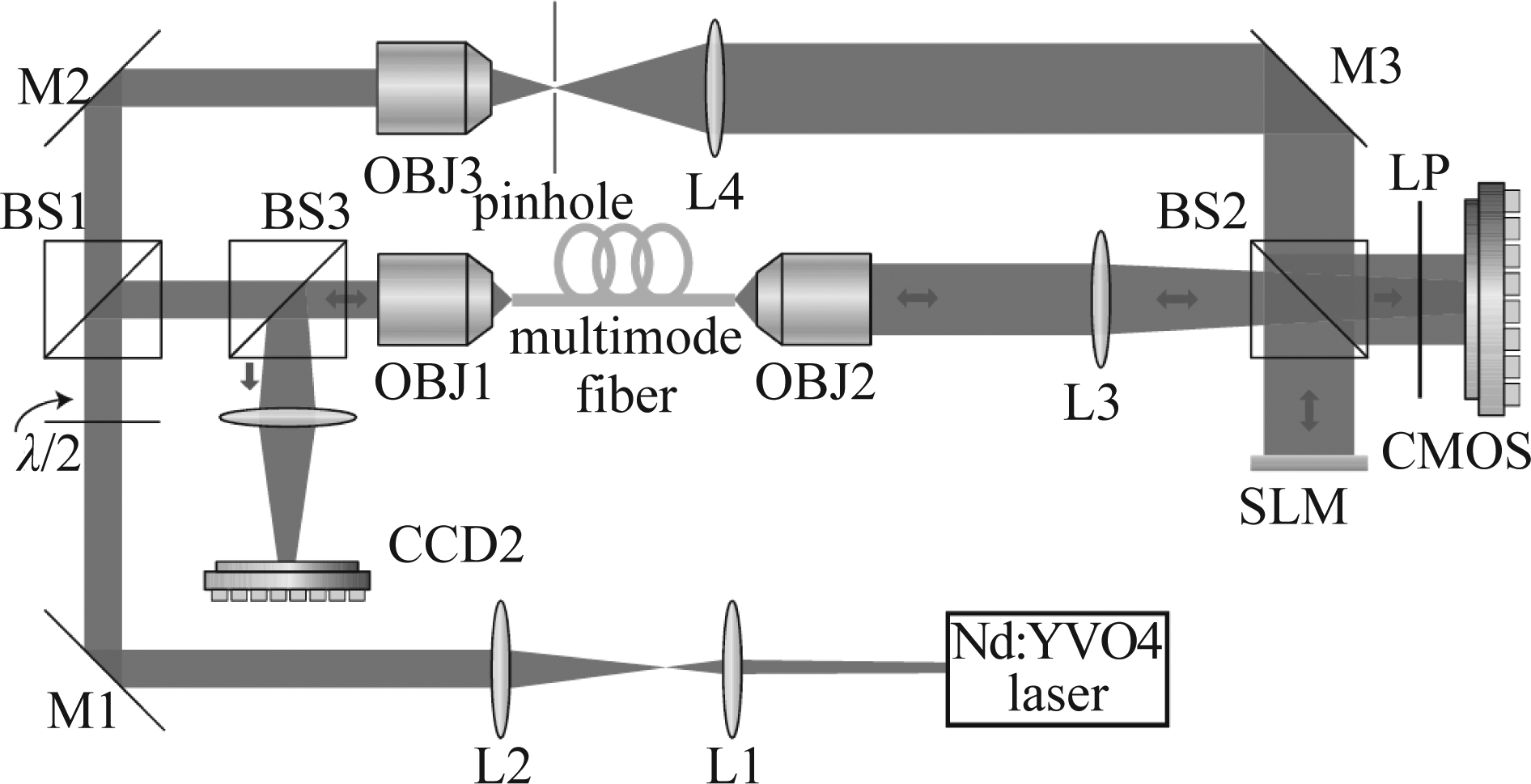
图8 数字相位共轭技术[53]
Fig.8 Digital phase conjugation technique[53]
(2)波前整形法
在光通过混浊介质的传输领域,使用波前整形技术[47,54]是另外一种有效的方法。波前整形法将多模光纤对输入光的作用看作是一种调制作用,将散射介质输出的调制光输入到空间光调制器中,利用空间光调制器对该调制作用进行解调,并应用于输入光对其整形。格勒诺布尔大学的Tzang等在多模光纤成像中引入波前整形法(WFS),在光纤和光谱信息的输入耦合处使用空间光调制器作为反馈,来控制多模光纤中的非线性相互作用[55]。并且通过遗传算法来优化和调控折射率渐变多模光纤中的受激拉曼散射和级联四波混频等高阶非线性效应的产生。
图9 波前整形法[55]
Fig.9 Wavefront shaping system[55]
(3)传输矩阵法
在光学系统中,当光场与光学元件不产生非线性作用时,光学系统输入信号和输出信号之间的关系可以用一个系统函数来描述。可以将多模光纤看作一个线性时不变系统,如果可以预先测定出光纤的传输特性便可以根据实测的输出光场计算得到输入光场。由于散射介质与光场作用的随机性,很难用准确的传递函数来描述这一作用。实践中,采用在空间域或频域离散扫描的方法来获取离散的传输响应,即传输矩阵法[56]。
对于多模光纤来说,由于真实的像素个数可能非常庞大,可以通过测量有限个数的传输矩阵的元素来近似表征真实的光纤传输特性。将多模光纤入射方和出射方的每一个像素都看作一个通道,通过测定入射方和输出方通道之间的响应特性,再经线性叠加便可计算出多模光纤的传输矩阵。我们将一个给定波长的光学系统的传输矩阵定义为连接第m个输出自由模式的光场(振幅和相位)与第n个输入自由模式的光场的复系数kmn的矩阵K。因此,输出光场在第m个自由模态上的投影
为
(6)
其中
为第n个入射自由模态光场的复振幅[57]。
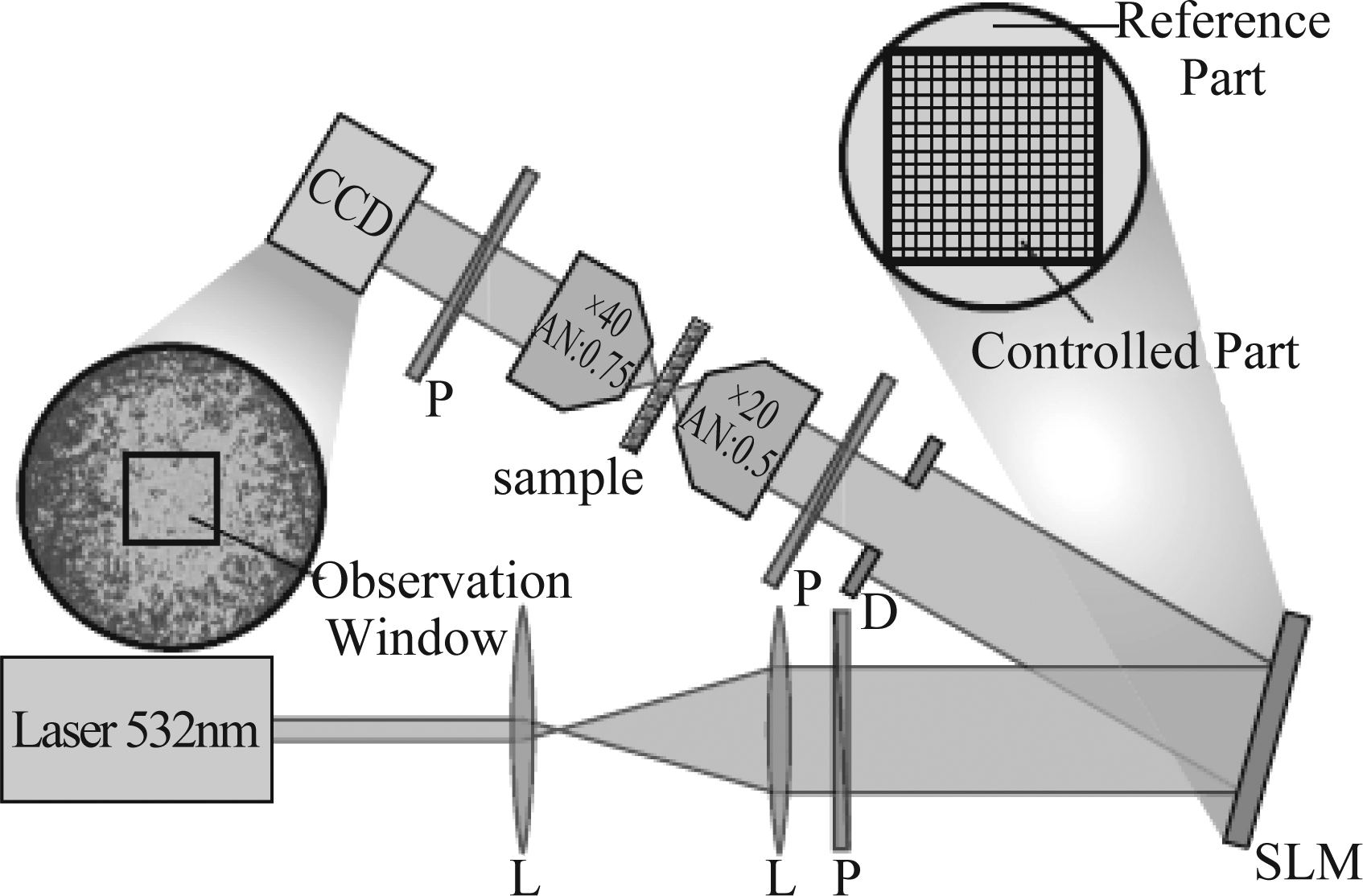
图10 传输矩阵法[57]
Fig.10 Transmission matrix method[57]
传统的多模光纤成像方法已成功地实现将多模光纤应用于内窥镜成像[58-59]、共聚焦显微镜[60]、自由扫描远场显微镜[45]、双光子成像等领域[61]。然而,以上这些技术也存在着一些不可避免的问题。首先获取传输矩阵的方法需要大量的精确校准与重复测量的过程,从而多模光纤的传输特性,通过计算补偿光纤所带来的图像畸变。这不仅提高了对精密的器件与仪器的要求,也增加了系统的硬件复杂度与成本。另外,波前整形的方法靠的是对入射多模光纤光场的相位进行操控,从而在输出端得到想要的输出。该技术需要迭代的控制与计算,而其受限于空间光调制器的调制速率,这使得成像速度无法保证。研究人员也提出了一些简化测量和计算的方法,例如通过对多模光纤模式理论计算获得其传输矩阵[62]和通过多模光纤的旋转记忆效应实现高速扫描[63], 然而这些方法的灵活性与稳定性仍然受到限制。
4.3 多模光纤成像技术发展趋势
随着计算成像技术的不断发展,人们对高分辨率、高速和低成本的内窥镜成像技术需求越来越强,压缩感知和深度学习等[64]这些被运用于散射介质成像中的技术,同时也被逐渐应用到多模光纤成像中。
(1)压缩感知技术
2018年,阿姆斯特丹大学的Amitonova L.等人将压缩感知方法与多模光纤成像相结合,提出了多模光纤压缩成像方法[65]。该方法将多模光纤产生的散斑作为一种结构光照明成像目标,用单像素成像的方法实现压缩成像,并使用数字微镜装置(DMD)对输入光纤的光场进行快速的空间调制,从而实现多次观测。实验装置如图11所示,实现了比传统方法快20倍的成像速度,提供了极限的分辨率,并且不需要复杂的波前整形设置和昂贵的空间光调制器。在这之后,Lan M.等人对该系统进行了改进,通过在光纤远端与相机之间引入准直透镜,提高了系统对成像深度的鲁棒性。除此之外,通过对弯曲光纤的模斑进行平均校准增加了成像系统对光纤弯曲的鲁棒性[66- 67]。
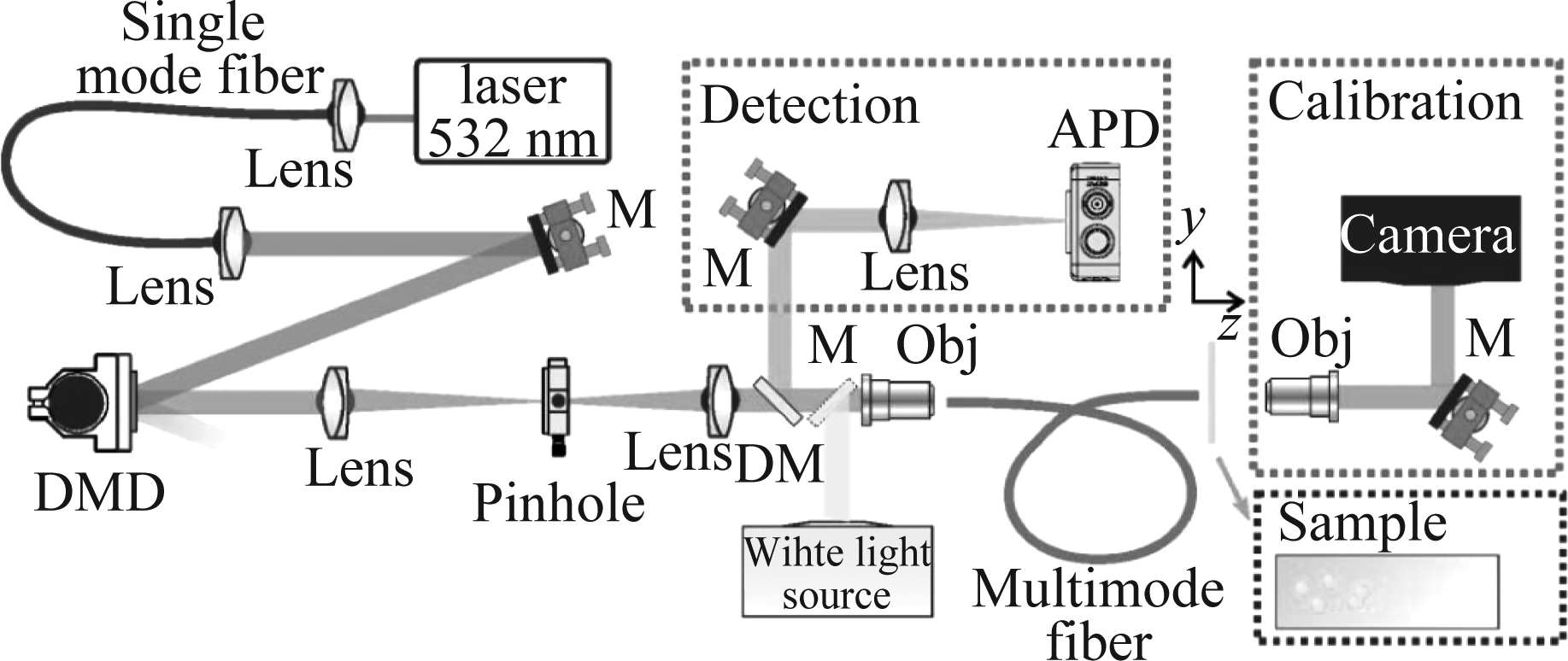
图11 压缩多模光纤成像[65]
Fig.11 Compressed multimode fiber imaging[65]
压缩成像的另一个优势是可以对场景的多维信息进行压缩采集,减小了信息存储并提高成像速度。例如基于多模光纤的颜色成像和多光谱成像系统,仅通过少量的观测得到场景的空间与光谱信息[68- 69]。
(2)深度学习技术
从多模光纤成像系统上整体来看,我们可以将多模光纤对光场的作用看作一个映射,只要找到这种映射关系的逆变换,就可以通过输出散斑来恢复输入的原始图像。最近,随着人工智能的崛起,机器学习技术成为科研与工程中新的工具。它通过学习的方式构建一种输入和输出之间的复杂映射,近几年已经被广泛研究用于求解计算成像中的逆问题。对应于多模光纤成像问题,可以用多模光纤远端得到的散斑图案和其对应的原始图像作为训练集,训练得到映射模型,从而可以对任意散斑图案进行恢复。利用深度学习可以摆脱复杂先验知识的获取,仅利用大量的数据进行分析和计算便可得到最终模型,因此逐渐发展成为多模光纤成像领域的一个新的方向。更加重要的是,多模光纤成像系统特性中的温度和弯曲影响可以加入到训练集中,从而提高系统在不同环境下的鲁棒性。
早期的研究使用简单的二层人工神经网络(ANN)来对极小数量的简单图片进行分类和重建[70-71]。近年来由于计算机性能的提升和对高维信息进行处理的需求提高,卷积神经网络(CNN)逐渐被广泛地应用于图像处理领域。卷积神经网络内部设置了专门对于矩阵的特殊操作,如卷积层,池化层等,用于挖掘图像的抽象特征,同时降低了需要网络学习的参数量。近年来,以卷积神经网络为基础的深度学习方法已经越来越多的被使用于散射介质的计算成像中[72],也逐渐被应用在多模光纤成像领域。
2018年,洛桑联邦理工学院的Borhani N.等人使用图像分割领域常用的U-net网络来恢复散斑图像[73]。他们以不同长度的渐变多模光纤为传输介质建立成像系统,使用空间光调制器(SLM)来产生强度图像和相位图像,通过CCD相机采集光纤远端散斑。图像重构的过程由一个基于U-net的深度神经网络完成[74],该网络通过16000组输入图像与输出散斑构成的数据对进行训练,输入图片采用MNIST手写数字集。其网络结构与测试结果如图12所示,该网络的优点在于融合了将多尺度特征,利用瓶颈层(Bottleneck Layer)提取深层特征,采用跳跃连接(Skip Connection)保留低阶特征。最终实现了在0.1 m的多模光纤下图像恢复的保真度为96.9%,在1 km的多模光纤下为 90.0%。
针对深度神经网络的设计和优化,北京邮电大学Zhang X.等人使用一种基于条件生成对抗网络(cGAN)的Pix2Pix框架仅使用少量训练样本得到了U-net类似的重构效果,减小了采集训练样本的成本[75-76]。Zhang R.等人利用一个简单的神经网络,实现了少模光纤图像传输和重构[77]。除此之外VGGnet[78]、ResNet[79]和预训练[80]等深度学习方法也逐渐被应用在多模光纤成像中,取得了不错的效果。
以上的方法大多只能在简单的有明显形状边缘的类MNIST数据集中奏效,对于一些复杂的自然图片却很难取得理想的效果。2019年,赫瑞瓦特大学的Caramazza P.等开发了一种基于深度复数网络(Deep Complex Networks)的方法[81- 82],实现了以更高的分辨率和帧率传输和重建更加复杂的自然场景的图像,如图13所示。实验将50000张大小为92×92的ImageNet自然场景灰度图片耦合入光纤,使用CMOS相机采集输出散斑的强度信息。
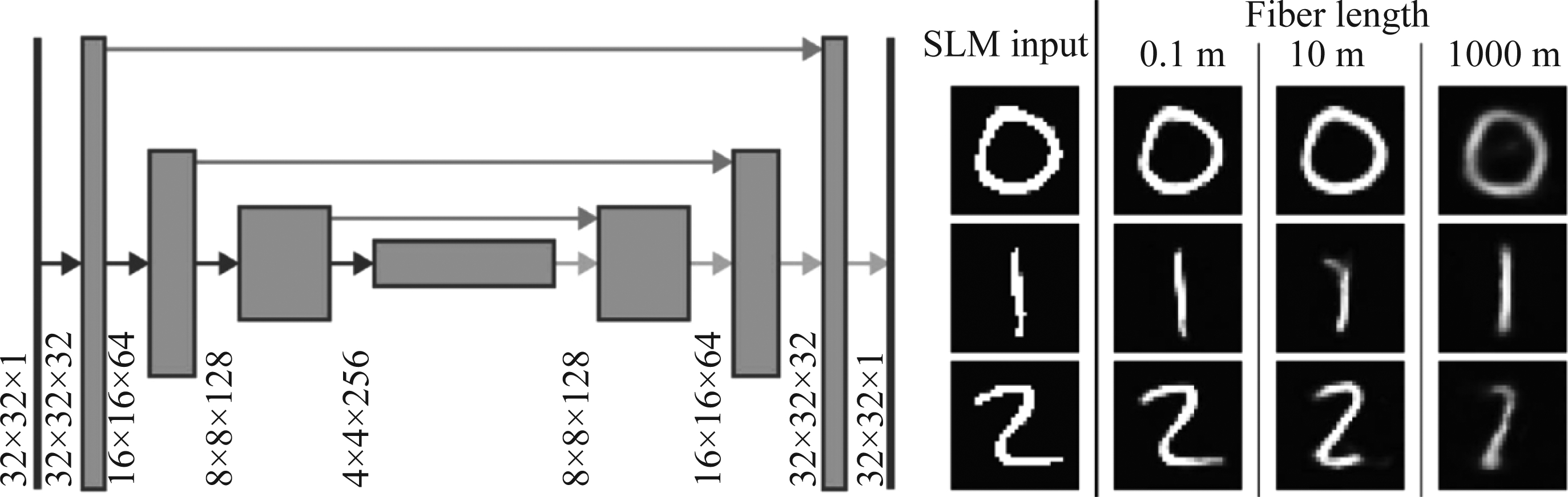
图12 基于深度神经网络的多模光纤成像:网络结构(左)与测试结果(右)[73]
Fig.12 Deep neural network for multimode fiber imaging reconstruction: network structure (left) and reconstructed results (right)[73]
图13 深度复数网络多模光纤成像重构[82]
Fig.13 Reconstruction for MMF imaging by a deep complex network[82]
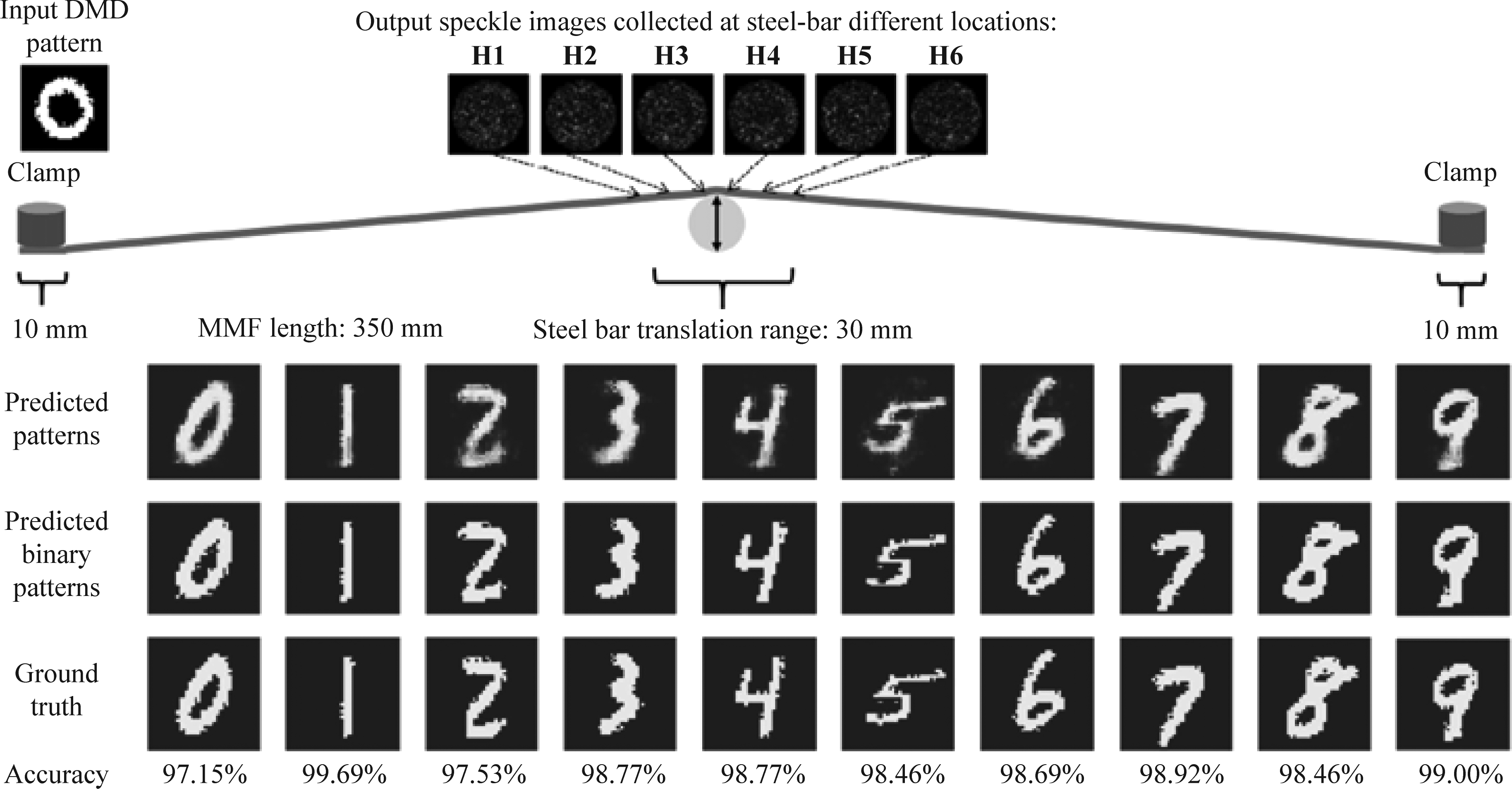
图14 深度学习恢复连续形变多模光纤成像[83]
Fig.14 Reconstruction for the continuous shape variations of MMF imaging[83]
该方法考虑了多模光纤传输矩阵的复值特性,将观测得到的散斑强度x传递给一个完全连通的复数矩阵W,等价于与复值矩阵W相乘,然后得到图像I=|Wx|2。将这张图像与实际原始图像计算一个代价函数ζ,然后使用反向传播算法,经过一定数量的循环过程,直到ζ的值收敛。然后通过重构矩阵W来将散斑图像恢复成真实图像。最终该方法在高分辨率自然场景恢复和三通道RGB图片的恢复方面初步取得了较好的效果。
由于多模光纤的传输特性对外部扰动和环境变化高度敏感,多模光纤形状和外部环境的轻微变化都会导致传输矩阵的剧变,这很大程度上制约了多模光纤成像系统的应用。而使用深度学习可以克服多模光纤的高变异性和随机性。2019年,Fan等人[83]利用机械装置使多模光纤连续弯曲,并在此过程中采集上万组散斑图案,对于一个基于U-net的深度卷积神经网络中进行训练。此方法证明神经网络可以成功地恢复受连续形状变化影响的多模光纤散斑图像,即深度学习可以克服多模光纤内部的高变异性和随机性。
4.4 多模光纤成像的总结与展望
总体来说,基于深度学习的多模光纤成像技术突破了传统成像原理,摆脱了先验知识的束缚,对周围环境的变化也有一定的鲁棒性,在实验室里对于简单图像初步取得了验证。但是对于现代医疗中对于高分辨率、高速和低成本内窥镜成像的需求,多模光纤成像技术的发展仍然具有很大的挑战性,在以下几个方面仍有进步的空间:
首先,由于多模光纤对自身弯曲或者外部环境的影响具有高度的敏感性,我们应该在应用中尽量保持多模光纤状态的稳定性,例如在应用中可以使用长度尽量短的光纤进行成像。同时,也可以使用某些性质较为稳定、不易受到外界干扰的特种光纤[84]进行成像。
其次,由于使用深度学习训练模型需要采集大量的数据,训练过程中需要大量的时间,而且目前对于复杂自然图片的恢复仍然不是很理想,需要进一步优化算法的性能,同时提高模型对于不同数据集、外部扰动的可迁移性。另外,相对于只注重统计规律而忽略了先验知识的深度学习算法,可以试着将深度学习算法与传统方法相结合。
5 光谱分析、射频谱感知及成像一体化展望
未来的信息感知与测量系统将是一个多功能、多维度和大数据的综合感知系统。高分辨率光谱测量、宽带射频谱感知以及空间图像观测是综合信息感知系统不可或缺的功能。三种功能一体化的实现具有重要意义,尤其在国防领域,三功能一体化可同时满足目标识别、无线电监测和电子侦查等多种军事需求,将极大降低军用设备的重量和体积,提高在战场中的灵活性。传统技术在各任务的实现上,存在包括硬件系统和软件算法上的区别,难以实现软硬件一体化的综合测量系统。多模光纤所具有的复杂模式特性,建立了空间到频率和时间维度的复杂联系,结合压缩感知和优化理论,使得实现一体化的多维测量系统成为可能。多模光纤具有极低的损耗和大带宽特性,可作为多维度映射的全光计算器件,理论上可以实现利用同一根多模光纤同时完成光谱分析、射频谱感知和成像三种功能。随着激光器、调制器、探测器、CCD等器件的灵敏度、响应度、集成度和稳定性的提升、深度学习算法功能的不断强大、以及三种技术的不断完善,光谱分析、射频谱感知和成像一体化系统有望在不久的将来得以实现。
6 结论
近年来,随着研究者们对多模光纤内在物理特性的研究,其应用领域从传统光通信传输时域信号已逐渐转变到测量、光计算和图像传输上。频率到空间、空间到空间的映射关系使多模光纤在光电系统中完成传输、处理、测量等任务成为可能。发挥多模光纤的宽带、无源、易于制造、低成本、便携等优势,可提高现有光电系统的性能,降低尺寸、功耗和成本。从可应用性和实用性的角度出发,与压缩感知和深度学习等技术相结合是一个重要发展趋势。更快速、更准确、更有效率将成为未来基于多模光纤的光谱测量、射频感知和成像应用的发展目标。同时,充分发挥多模光纤的高密度、低损耗和微型化的特点,推动其在多种场景下的一体化应用,并且提高其容量和稳定性,满足未来6G、空天地海一体网络、电子战场的需求,是未来多模光纤应用的重要发展方向和挑战。
[1] 赵亚军, 郁光辉, 徐汉青. 6G移动通信网络: 愿景、挑战与关键技术[J]. 中国科学: 信息科学, 2019, 49(8): 963-987.
Zhao Y J, Yu G H, Xu H Q. 6G mobile communication networks: vision, challenges, and key technologies[J]. Scientia Sinica Informationis, 2019, 49(8): 963-987.(in Chinese)
[2] Grabarnik S, Wolffenbuttel R, Emadi A, et al. Planar double-grating microspectrometer[J]. Optics Express, 2007, 15(6): 3581-3588.
[3] Xia Z, Eftekhar A A, Soltani M, et al. High resolution on-chip spectroscopy based on miniaturized microdonut resonators[J]. Optics Express, 2011, 19(13): 12356-12364.
[4] Velasco A V, Cheben P, Bock P J, et al. High-resolution Fourier-transform spectrometer chip with microphotonic silicon spiral waveguides[J]. Optics Letters, 2013, 38(5): 706-708.
[5] Yao J. Microwave photonics[J]. Journal of Lightwave Technology, 2009, 27(3): 314-335.
[6] Capmany J, Novak D. Microwave photonics combines two worlds[J]. Nature Photonics, 2007, 1(6): 319-330.
[7] Szabo V, Ventalon C, De Sars V, et al. Spatially selective holographic photoactivation and functional fluorescence imaging in freely behaving mice with a fiberscope[J]. Neuron, 2014, 84(6): 1157-1169.
[8] Redding B, Cao H. Using a multimode fiber as a high-resolution, low-loss spectrometer[J]. Optics Letters, 2012, 37(16): 3384-3386.
[9] Redding B, Popoff S M, Cao H. All-fiber spectrometer based on speckle pattern reconstruction[J]. Optics Express, 2013, 21(5): 6584- 6600.
[10] Meng Z, Li J, Yin C, et al. Multimode fiber spectrometer with scalable bandwidth using space-division multiplexing[J]. AIP Advances, 2019, 9(1): 015004.
[11] Redding B, Liew S F, Bromberg Y, et al. Evanescently coupled multimode spiral spectrometer[J]. Optica, 2016, 3(9): 956-962.
[12] Redding B, Alam M, Seifert M, et al. High-resolution and broadband all-fiber spectrometers[J]. Optica, 2014, 1(3): 175-180.
[13] Liew S F, Redding B, Choma M A, et al. Broadband multimode fiber spectrometer[J]. Optics Letters, 2016, 41(9): 2029-2032.
[14] Wan N H, Meng F, Schröder T, et al. High-resolution optical spectroscopy using multimode interference in a compact tapered fibre[J]. Nature Communications, 2015, 6(1): 1- 6.
[15] Redding B, Liew S F, Sarma R, et al. Compact spectrometer based on a disordered photonic chip[J]. Nature Photonics, 2013, 7(9): 746-751.
[16] Chakrabarti M, Jakobsen M L, Hanson S G. Speckle-based spectrometer[J]. Optics Letters, 2015, 40(14): 3264-3267.
[17] Cao H. Perspective on speckle spectrometers[J]. J.Opt., 2017, 19(060402).
[18] Piels M, Zibar D. Compact silicon multimode waveguide spectrometer with enhanced bandwidth[J]. Scientific Reports, 2017, 7: 43454.
[19] Yang T, Peng J, Li X, et al. Compact broadband spectrometer based on upconversion and downconversion luminescence[J]. Optics Letters, 2017, 42(21): 4375- 4378.
[20] Metzger N K, Spesyvtsev R, Bruce G D, et al. Harnessing speckle for a sub-femtometre resolved broadband wavemeter and laser stabilization[J]. Nature Communications, 2017, 8: 15610.
[21] Bruce G D, O’Donnell L, Chen M, et al. Overcoming the speckle correlation limit to achieve a fiber wavemeter with attometer resolution[J]. Optics Letters, 2019, 44(6): 1367-1370.
[22] Gupta R K, Bruce G D, Powis S J, et al. Deep learning enabled laser speckle wavemeter with a high dynamic range[J]. arXiv preprint arXiv: 1910.10702, 2019.
[23] Donoho D L. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289-1306.
[24] Candès E J, Wakin M B. An introduction to compressive sampling[J]. IEEE Signal Processing Magazine, 2008, 25(2): 21-30.
[25] Candes E J. The restricted isometry property and its implications for compressed sensing[J]. Comptes Rendus Mathematique, 2008, 346(9-10): 589-592.
[26] Tropp J A, Laska J N, Duarte M F, et al. Beyond Nyquist: Efficient sampling of sparse bandlimited signals[J]. IEEE Transactions on Information Theory, 2009, 56(1): 520-544.
[27] Mishali M, Eldar Y C. Xampling: Analog data compression[C]∥2010 Data Compression Conference. IEEE, 2010: 366-375.
[28] Valley G C, Sefler G A. Optical time-domain mixer[C]∥Optics and Photonics for Information Processing IV. International Society for Optics and Photonics, 2010, 7797: 77970F.
[29] Nan H, Gu Y, Zhang H. Optical analog-to-digital conversion system based on compressive sampling[J]. IEEE Photonics Technology Letters, 2010, 23(2): 67- 69.
[30] Nichols J M, Bucholtz F. Beating Nyquist with light: a compressively sampled photonic link[J]. Optics Express, 2011, 19(8): 7339-7348.
[31] Chi H, Mei Y, Chen Y, et al. Microwave spectral analysis based on photonic compressive sampling with random demodulation[J]. Optics Letters, 2012, 37(22): 4636- 4638.
[32] Valley G C, Sefler G A, Shaw T J. Compressive sensing of sparse radio frequency signals using optical mixing[J]. Optics Letters, 2012, 37(22): 4675- 4677.
[33] Chi H, Chen Y, Mei Y, et al. Microwave spectrum sensing based on photonic time stretch and compressive sampling[J]. Optics Letters, 2013, 38(2): 136-138.
[34] Valley G C, Sefler G A, Shaw T J. Sensing RF signals with the optical wideband converter[C]∥Broadband Access Communication Technologies VII. International Society for Optics and Photonics, 2013, 8645: 86450P.
[35] Bosworth B T, Foster M A. High-speed ultrawideband photonically enabled compressed sensing of sparse radio frequency signals[J]. Optics Letters, 2013, 38(22): 4892- 4895.
[36] Bosworth B T, Stroud J R, Tran D N, et al. Ultrawideband compressed sensing of arbitrary multi-tone sparse radio frequencies using spectrally encoded ultrafast laser pulses[J]. Optics Letters, 2015, 40(13): 3045-3048.
[37] Chen Y, Yu X, Chi H, et al. Compressive sensing with a microwave photonic filter[J]. Optics Communications, 2015, 338: 428- 432.
[38] Goda K, Jalali B. Dispersive Fourier transformation for fast continuous single-shot measurements[J]. Nature Photonics, 2013, 7(2): 102-112.
[39] Valley G C, Sefler G A, Shaw T J. Multimode waveguide speckle patterns for compressive sensing[J]. Optics Letters, 2016, 41(11): 2529-2532.
[40] Sefler G A, Shaw T J, Valley G C. Demonstration of speckle-based compressive sensing system for recovering RF signals[J]. Optics Express, 2018, 26(17): 21390-21402.
[41] Flusberg B A, Cocker E D, Piyawattanametha W, et al. Fiber-optic fluorescence imaging[J]. Nature Methods, 2005, 2(12): 941-950.
[42] Hughes M, Chang T P, Yang G Z. Fiber bundle endocytoscopy[J]. Biomedical Optics Express, 2013, 4(12): 2781-2794.
[43] Chen X, Reichenbach K L, Xu C. Experimental and theoretical analysis of core-to-core coupling on fiber bundle imaging[J]. Optics Express, 2009, 16(26): 21598-21607.
[44] 贺正权, 任立勇, 庄斌, 等. 单光纤成像技术[J]. 激光与光电子学进展, 2017, 54(3): 39- 47.
He Z Q, Ren L Y, Zhuang B, et al. Single Optical Fiber Imaging Technology[J]. Laser & Optoelectronics Progress, 2017, 54(3): 39- 47.(in Chinese)
[45] Choi Y, Yoon C, Kim M, et al. Scanner-free and wide-field endoscopic imaging by using a single multimode optical fiber[J]. Physical Review Letters, 2012, 109(20): 203901-203901.
[46] Oliver B M. Sparkling spots and random diffraction[J]. Proceedings of the Ieee, 1963, 51(1): 220-221.
[47] Vellekoop I M, Mosk A P. Focusing coherent light through opaque strongly scattering media[J]. Optics Letters, 2007, 32(16): 2309-2311.
[48] Mosk A P, Lagendijk A, Lerosey G, et al. Controlling waves in space and time for imaging and focusing in complex media[J]. Nature Photonics, 2012, 6(5): 283-292.
[49] Bertolotti J, Van Putten E G, Blum C, et al. Non-invasive imaging through opaque scattering layers[J]. Nature, 2012, 491(7423): 232-234.
[50] Spitz E, Werts A. Transmission des images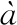 
travers une fibre optique[J]. Comptes Rendus Hebdomadaires Des Seances De L Academie Des Sciences Serie B, 1967, 264(14): 1015.
[51] Dunning G J, Lind R C. Demonstration of image transmission through fibers by optical phase conjugation[J]. Optics Letters, 1982, 7(11): 558-560.
[52] Yariv A. On transmission and recovery of three-dimensional image information in optical waveguides[J]. JOSA, 1976, 66(4): 301-306.
[53] Papadopoulos I N, Farahi S, Moser C, et al. Focusing and scanning light through a multimode optical fiber using digital phase conjugation[J]. Optics Express, 2012, 20(ARTICLE): 10583-10590.
[54] Vellekoop I M, Aegerter C M. Scattered light fluorescence microscopy: imaging through turbid layers[J]. Optics Letters, 2010, 35(8): 1245-1247.
[55] Tzang O, Caravaca-Aguirre A M, Wagner K, et al. Adaptive wavefront shaping for controlling nonlinear multimode interactions in optical fibres[J]. Nature Photonics, 2018, 12(6): 368-374.
[56] 
T, Dholakia K. Exploiting multimode waveguides for pure fibre-based imaging[J]. Nature Communications, 2012, 3(1): 1-9.
[57] Popoff S M, Lerosey G, Carminati R, et al. Measuring the transmission matrix in optics: an approach to the study and control of light propagation in disordered media[J]. Physical Review Letters, 2010, 104(10): 100601.
[58] Papadopoulos I N, Farahi S, Moser C, et al. High-resolution, lensless endoscope based on digital scanning through a multimode optical fiber[J]. Biomedical Optics Express, 2013, 4(2): 260-270.
[59] Caravaca-Aguirre A M, Piestun R. Single multimode fiber endoscope[J]. Optics Express, 2017, 25(3): 1656-1665.
[60] Loterie D, Goorden S A, Psaltis D, et al. Confocal microscopy through a multimode fiber using optical correlation[J]. Optics Letters, 2015, 40(24): 5754-5757.
[61] Morales-Delgado E E, Psaltis D, Moser C. Two-photon imaging through a multimode fiber[J]. Optics Express, 2015, 23(25): 32158-32170.
[62] Plöschner M, Tyc T, 
T. Seeing through chaos in multimode fibres[J]. Nature Photonics, 2015, 9(8): 529-535.
[63] Amitonova L V, Mosk A P, Pinkse P W H. Rotational memory effect of a multimode fiber[J]. Optics Express, 2015, 23(16): 20569-20575.
[64] Li Y, Xue Y, Tian L. Deep speckle correlation: a deep learning approach toward scalable imaging through scattering media[J]. Optica, 2018, 5(10): 1181-1190.
[65] Amitonova L V, De Boer J F. Compressive imaging through a multimode fiber[J]. Optics Letters, 2018, 43(21): 5427-5430.
[66] Lan M, Guan D, Gao L, et al. Robust compressive multimode fiber imaging against bending with enhanced depth of field[J]. Optics Express, 2019, 27(9): 12957-12962.
[67] Lan M, Xiang Y, Li J, et al. Averaging speckle patterns to improve the robustness of compressive multimode fiber imaging against fiber bend[J]. Optics Express, 2020, 28(9): 13662-13669.
[68] Shabairou N, Cohen E, Wagner O, et al. Color image identification and reconstruction using artificial neural networks on multimode fiber images: Towards an all-optical design[J]. Optics Letters, 2018, 43(22): 5603-5606.
[69] French R, Gigan S. Snapshot fiber spectral imaging using speckle correlations and compressive sensing[J]. Optics Express, 2018, 26(24): 32302-32316.
[70] Aisawa S, Noguchi K, Matsumoto T. Remote image classification through multimode optical fiber using a neural network[J]. Optics Letters, 1991, 16(9): 645- 647.
[71] Marusarz R K, Sayeh M R. Neural network-based multimode fiber-optic information transmission[J]. Applied Optics, 2001, 40(2): 219-227.
[72] Ando T, Horisaki R, Tanida J. Speckle-learning-based object recognition through scattering media[J]. Optics Express, 2015, 23(26): 33902-33910.
[73] Borhani N, Kakkava E, Moser C, et al. Learning to see through multimode fibers[J]. Optica, 2018, 5(8): 960-966.
[74] Ronneberger O, Fischer P, Brox T. U-net: Convolutional networks for biomedical image segmentation[C]∥International Conference on Medical Image Computing and Computer-assisted Intervention. Springer, Cham, 2015: 234-241.
[75] Zhang X, Yu Z, Meng Z, et al. Experimental Demonstration of a Multimode Fiber Imaging System Based on Generative Adversarial Networks[C]∥Asia Communications and Photonics Conference. Optical Society of America, 2019: T4A. 4.
[76] Isola P, Zhu J Y, Zhou T, et al. Image-to-image translation with conditional adversarial networks[C]∥Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2017: 1125-1134.
[77] Zhang R, Wang J, Song L. Image reconstruction of few-mode fiber based on deep learning[C]∥Advanced Optical Imaging Technologies. International Society for Optics and Photonics, 2018, 10816: 108160H.
[78] Kakkava E, Rahmani B, Borhani N, et al. Imaging through multimode fibers using deep learning: The effects of intensity versus holographic recording of the speckle pattern[J]. Optical Fiber Technology, 2019, 52: 101985.
[79] Kurekci S, Temur A T, Odabas M E, et al. Deep learning-based image transmission through a multi-mode fiber[C]∥Unconventional Optical Imaging II. International Society for Optics and Photonics, 2020, 11351: 1135126.
[80] Li Y, Yu Z, Chen Y, et al. Image Reconstruction Using Pre-trained Autoencoder on Multimode Fiber Imaging System[J]. IEEE Photonics Technology Letters, 2020, 32(13): 779-782.
[81] Moran O, Caramazza P, Faccio D, et al. Deep, complex, invertible networks for inversion of transmission effects in multimode optical fibres[C]∥Advances in Neural Information Processing Systems. 2018: 3280-3291.
[82] Caramazza P, Moran O, Murray-Smith R, et al. Transmission of natural scene images through a multimode fibre[J]. Nature Communications, 2019, 10(1): 1- 6.
[83] Fan P, Zhao T, Su L. Deep learning the high variability and randomness inside multimode fibers[J]. Optics Express, 2019, 27(15): 20241-20258.
[84] Zhao J, Sun Y, Zhu H, et al. Deep-learning cell imaging through Anderson localizing optical fiber[J]. Advanced Photonics, 2019, 1(6): 066001.
