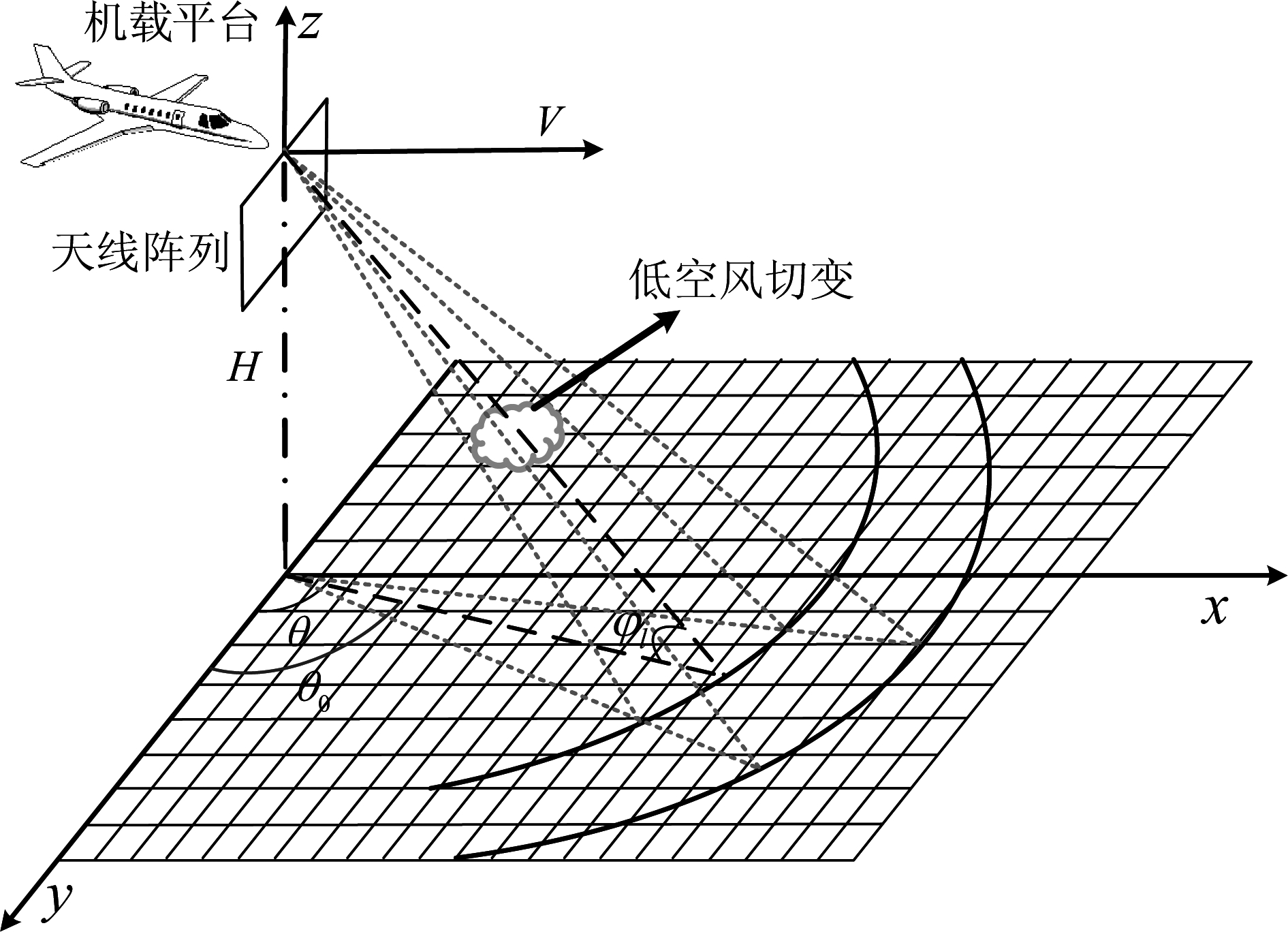
图1 机载平台探测示意图
Fig.1 Schematic diagram of airborne platform detection
Reference format: Li Hai, Liu Zhixin, Wang Jie, et al. Low-altitude Windshear Wind Speed Estimation Method Based on DDD-GMB[J]. Journal of Signal Processing, 2020, 36(1): 67-76. DOI: 10.16798/j.issn.1003- 0530.2020.01.009.
机载气象雷达可被用于探测与预警飞机前方区域的气象灾害,例如风切变、雷暴、湍流等,是飞机上保障飞行安全的重要电子设备[1]。低空风切变具有出现时间短、强度大和破坏性强等特征[2],往往发生在飞机起飞与着陆阶段,飞行员缺乏反应时间和可操作高度,极易发生坠机事故。因此低空风切变检测技术研究受到越来越多的关注。
机载气象雷达下视探测低空风切变过程中,强地杂波信号会覆盖低空风切变信号,当地杂波抑制不完全时,会造成风速无法正确估计,因此地杂波抑制是低空风切变检测的重要一环。文献[3]提出一种基于压缩感知的风速估计方法,但是仅利用了单天线数据。相控阵体制雷达[4]较传统的单天线体制雷达,有着较强的灵活性,其可以利用多阵元接收回波信号,增加了回波信号空域维度信息,在空时联合域中可以获得更好的地杂波抑制结果。文献[5]和文献[6]在利用空、时二维信息基础上,分别提出一种基于空时最优处理的风速估计方法和一种多通道联合自适应处理的风速估计方法,在抑制地杂波的同时并实现了风场速度的精确估计。然而其均是针对均匀地杂波情况,未能考虑非均匀地杂波环境所造成的估计性能的下降。在实际复杂的地面环境下,独立同分布(independent identical distribution,IID)样本缺乏,无法准确估计杂波协方差矩阵,造成地杂波抑制能力下降,进而影响风速的正确估计。因此,对于研究非均匀地杂波环境下的低空风切变风速估计方法是非常重要的。
本文提出一种针对于非均匀地杂波环境下的DDD-GMB的低空风切变风速估计方法,此方法首先直接对待检测距离单元回波数据进行低空风切变信号消除和滑窗估计杂波协方差矩阵,然后采取GMB的空时降维处理方法,组合空域相邻多个波束和时域相邻多个“波束”(即多普勒通道)进行空时自适应处理,求解得到空时降维滤波器的最优权矢量,构造得到代价函数,实现地杂波抑制与风速估计。本文方法无需利用其他参考单元估计杂波协方差矩阵,不仅在非均匀地杂波环境下杂波抑制与风速估计性能良好,而且避免了矫正机载前视阵引起的杂波非均匀(即距离依赖性),有效减少了计算复杂度和计算时间,仿真结果显示:在非均匀地杂波环境下,本文所提方法可以实现风速的精确估计。
图1是机载平台下视探测低空风切变的几何结构示意图,飞机以速度V做匀速直线运动,机载雷达的天线阵列垂直于载机飞行方向,是由N个等效阵元组成的线阵,相邻阵元的间隔d=λ/2,其中λ为雷达波长。H是机载平台所处高度,φ和θ分别是地面散射单元相对于载机的俯仰角和方位角,θ0和φl分别是低空风切变信号的水平方位角和俯仰角。假设在相干处理间隔(Coherent Processing Interval,CPI)内脉冲数为K,脉冲重复频率为fr。
图1 机载平台探测示意图
Fig.1 Schematic diagram of airborne platform detection
第l个距离单元的回波信号可表示为
Xl=Sl+Cl+n
(1)
其中,Sl代表第l个距离单元的风切变信号,n是加性高斯白噪声,Cl代表第l个距离单元的非均匀地杂波信号,且本文采用的是在Ward[7]模型基础上融合了数字高程数据和数字地表分类数据的非均匀地杂波模型。
低空风切变回波信号Sl可表示为
Sl=αl·β(ψ0, fl)=αl·[βt(fl)⊗βs(ψ0)]
(2)
其中,αl为第l个距离门风切变信号的回波幅度,ψ0是风切变信号的空间锥角,cos(ψ0)=cos(θ0)cos(φl), fl为低空风切变信号归一化多普勒频率,β(ψ0, fl)为低空风切变回波信号的空时导向矢量,βt(fl)与βs(ψ0)分别为时间导向矢量和空间导向矢量,可表示为
(3)
β(ψ0)=
(4)
其中,⊙为Hadamard积,g(σf)=[1 eΛσf ... e(K-1)Λσf]T为低空风切变信号的频率扩展函数,其中
为信号多普勒扩展,g(ψ0)=[1eσψ0Λgψ0 ... e(N-1)σψ0Λgψ0]T为低空风切变信号的角度高斯扩展函数[8],其中Λgψ0=(2πd)2σψ0/(2λ)2为信号的空域扩展,
为θ0方向上的角度扩展,σφl为φl方向上的角度扩展[9]。
本文方法中包括DDD方法估计杂波协方差矩阵与GMB方法估计风场速度,首先利用空域两阵元和时域两脉冲信号相消直接对待检测距离单元数据进行低空风切变信号消除,其次利用在空、时域滑窗得到的训练样本估计杂波协方差矩阵,最后采取GMB方法构造空时降维滤波器,求解得到最优权矢量,实现杂波抑制与风速估计。
若待检测距离单元内包含低空风切变信号,则由此距离单元数据滑窗得到的所有样本都包含低空风切变信号,此时估计该距离单元杂波协方差矩阵时,风切变信号成为干扰目标,因此为防止信号相消,需要进行风切变信号滤除。
第l个距离单元作为待检测距离单元时,其回波数据Xl表示为
Xl=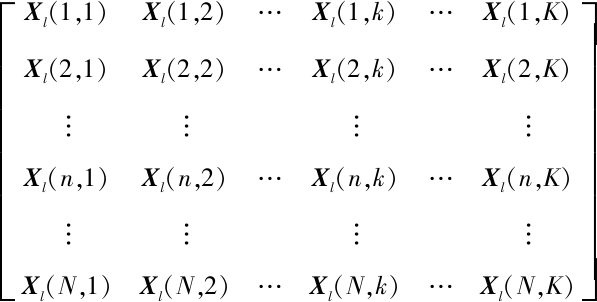
(5)
其中,Xl(n,k)表示第n个阵元第k个脉冲下的回波数据。假设低空风切变信号方位已知, fl(fl的取值范围为[-1 1])为待测距离单元内低空风切变信号的归一化多普勒频率。此时相邻脉冲之间的相位差为Zt=e-jπflΛσf,相邻阵元间的相位差为Zs=e-j2πdcos ψ0Λgψ0/λ,采用下式分别从空域、时域和空时域进行低空风切变信号滤除
(6)
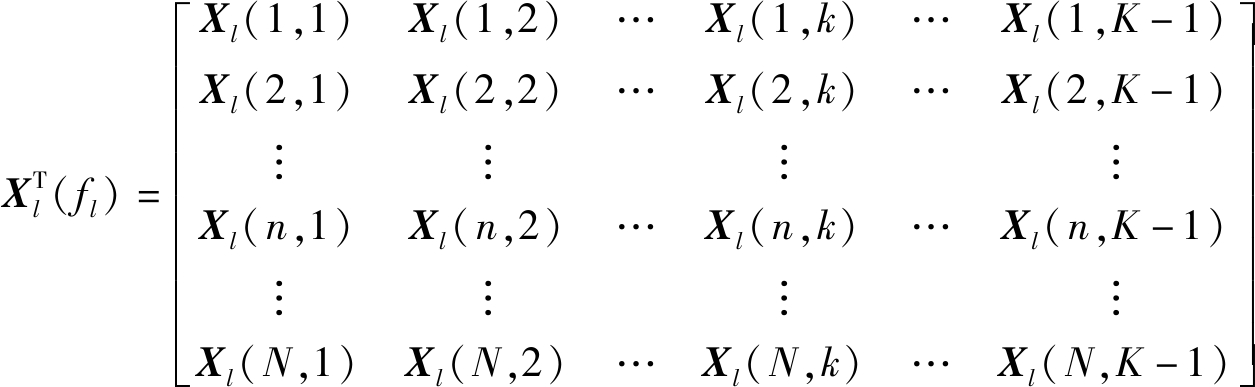
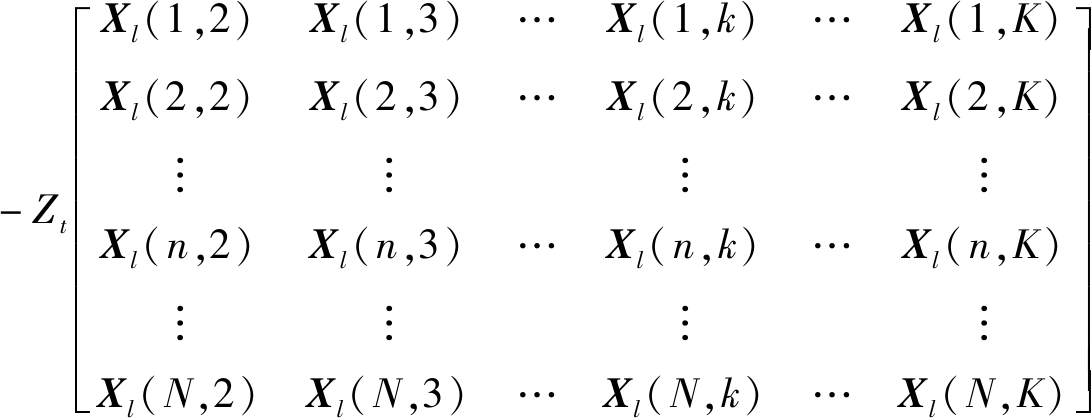
(7)
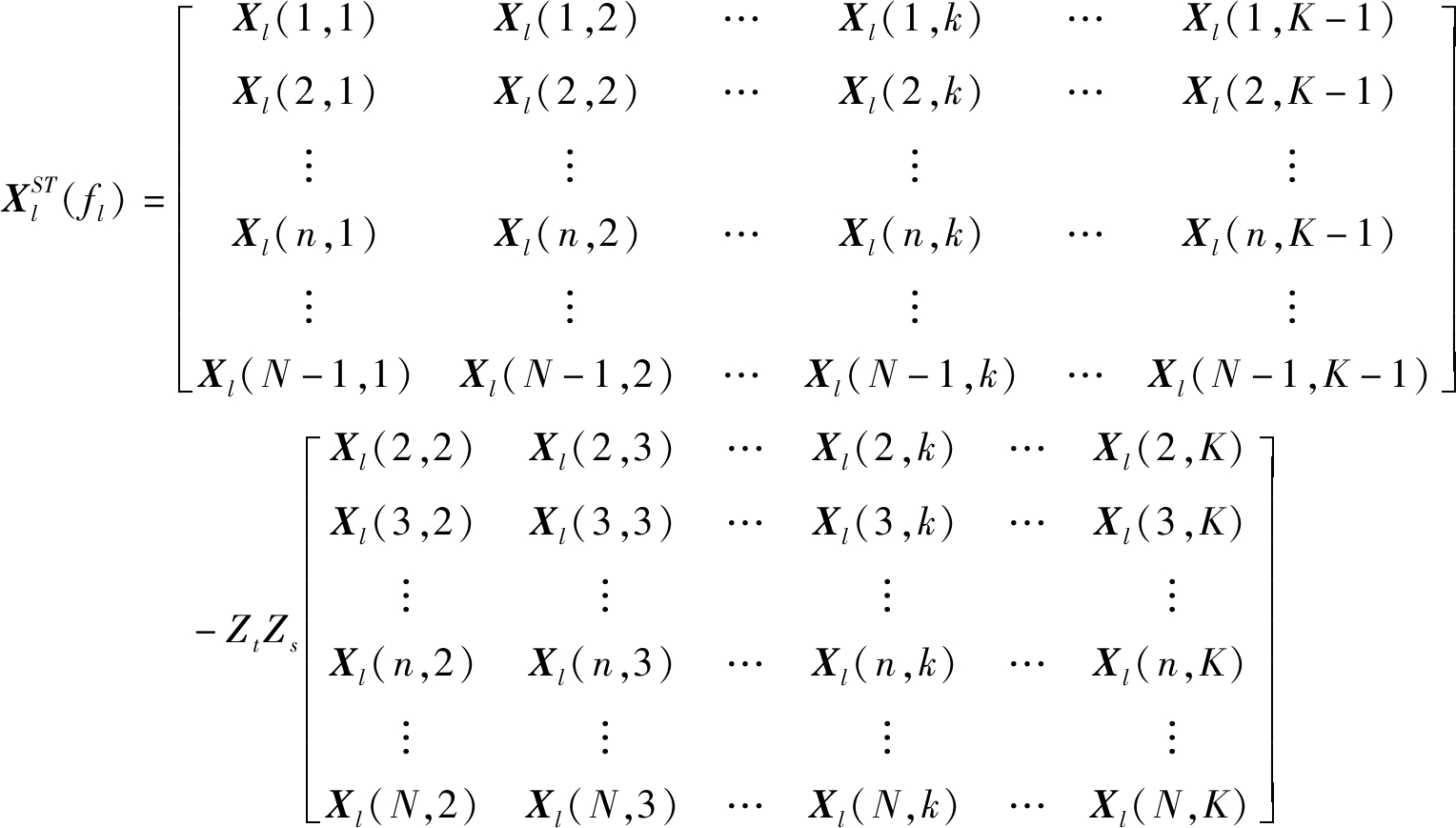
(8)
从式(6)可得在空域进行两阵元信号相消后的数据
从式(7)可得在时域进行两脉冲信号相消后的数据
从式(8)可得在空时域进行两脉冲两阵元信号相消后的数据
此时
和
仅含有地杂波与噪声项
与分别代表数据矩阵
和
是fl的函数)。
为了估计待测距离单元的杂波协方差矩阵,需要利用如图2所示的滑窗方法获取空时域训练样本,考虑对样本数的要求及RMB准则等因素[10],可确定空、时域自由度(分别表示为Nt和Kt),即滑窗大小是Nt×Kt。对数据
和
以Nt×Kt大小的固定窗口进行滑窗处理,然后将每一个窗口的数据矩阵矢量化,可表示为
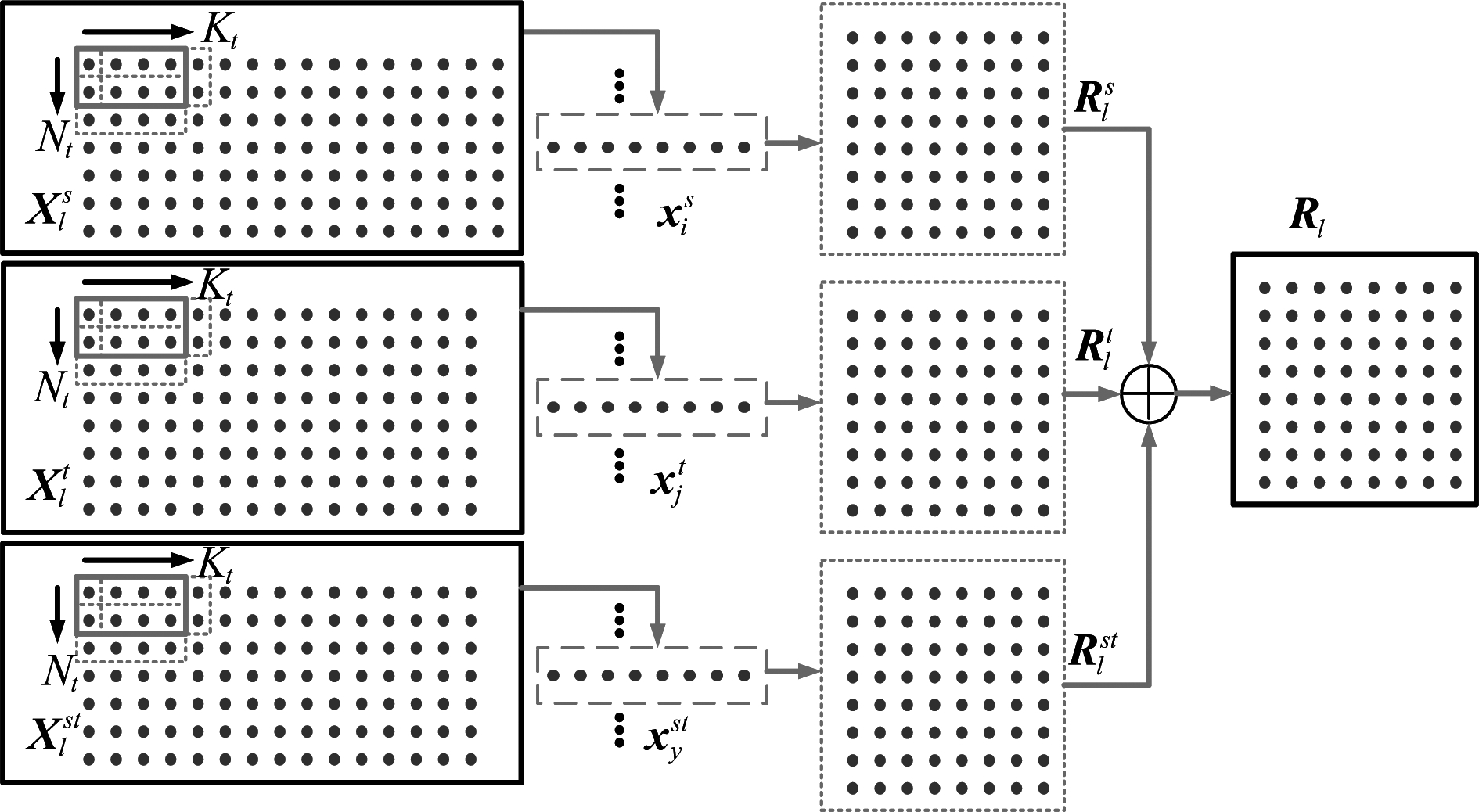
图2 滑窗估计杂波协方差矩阵示意图
Fig.2 Schematic diagram of sliding window estimation clutter covariance matrix
(9)
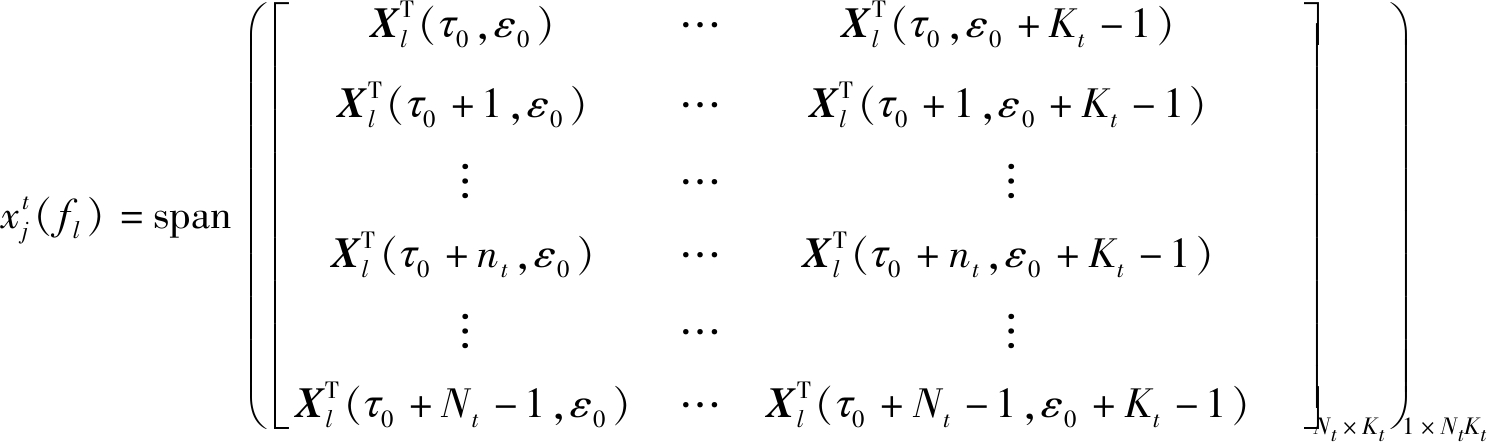
(10)
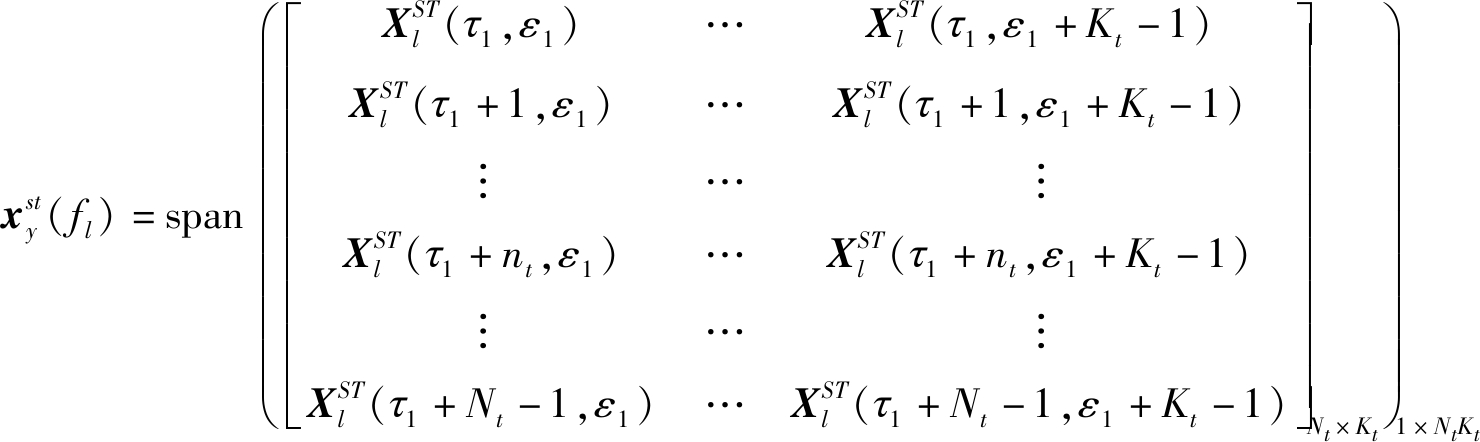
(11)
其中τ∈[1 N-Nt],ε∈[1 K-Kt+1],τ0∈[1 N-Nt+1],ε0∈[1 K-Kt],τ1∈[1 N-Nt],ε1∈[1 K-Kt]。由此,可以分别利用在空域、时域和空时域进行目标消除后的滑窗数据估计协方差矩阵,如下所示
(12)
(13)
(14)
那么待检测距离单元的杂波协方差矩阵Rl(fl),即杂波协方差矩阵Rl为fl的函数,可表示为
Rl(fl)=
(15)
其中,(N-Nt)(K-Kt+1)+(N-Nt+1)(K-Kt)+(N-Nt)(K-Kt)为训练样本总数。
在空域、时域和空时域滑窗获得样本去估计得到杂波协方差矩阵后,采用GMB空时降维自适应处理的方法进行低空风切变风速估计。如图3所示,首先由波束形成器形成p+1个空间波束,本文令p=8(即选择9个空间波束)。选择其中一个作为主波束,主波束在空间上对准风切变信号所在方向(即风切变信号空间锥角ψ0处),其余为辅助波束,然后在主波束后级联多普勒滤波器(Doppler Filter,DF),选择第q个作为检测通道(q=1,2,…,K),其余为辅助通道,在辅助波束后级联DF,选择第q个作为检测通道,其上述处理步骤可以采用一降维变换矩阵TL表示
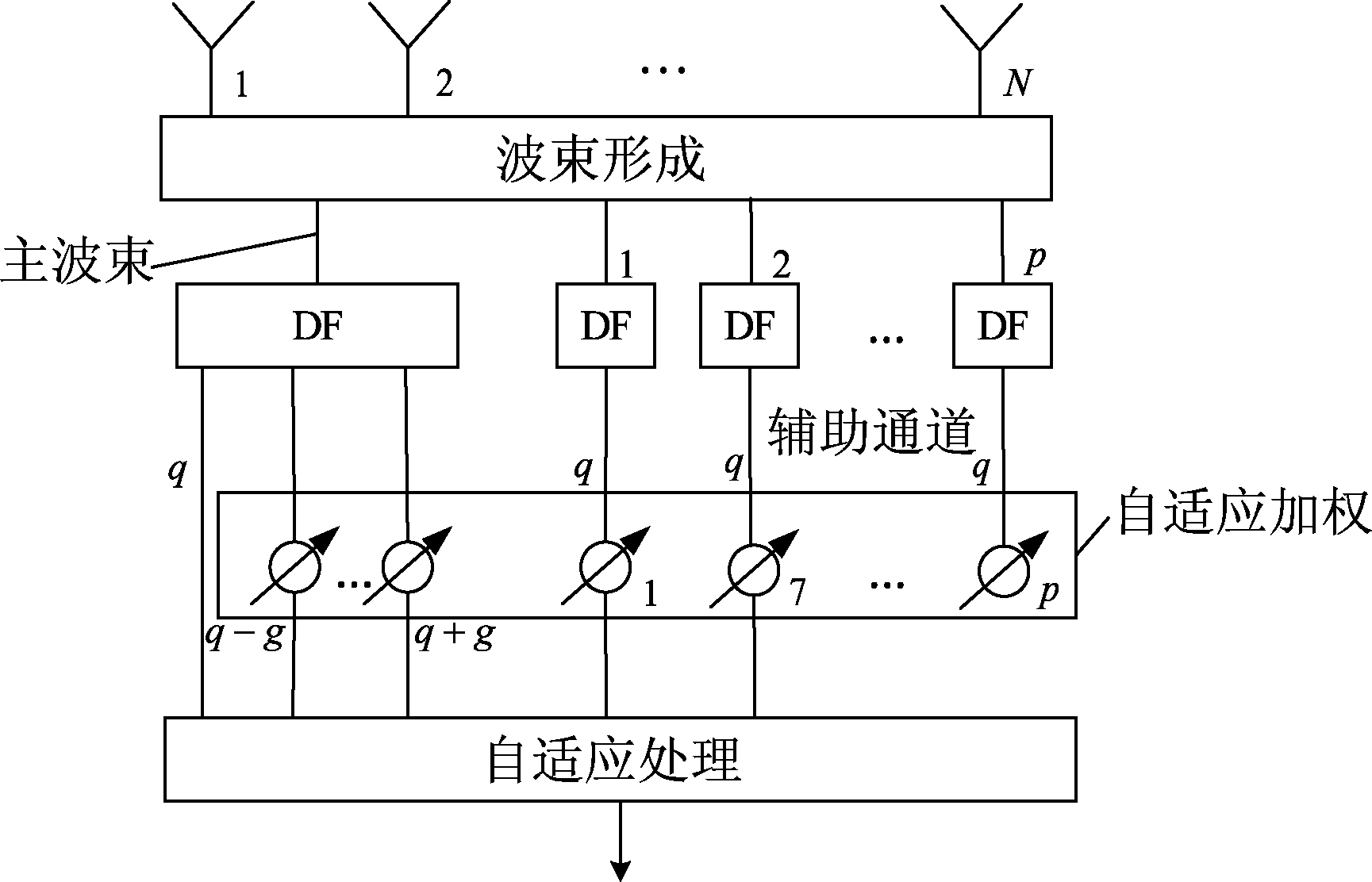
图3 GMB空时自适应处理结构图
Fig.3 structure of GMB space-time adaptive processing
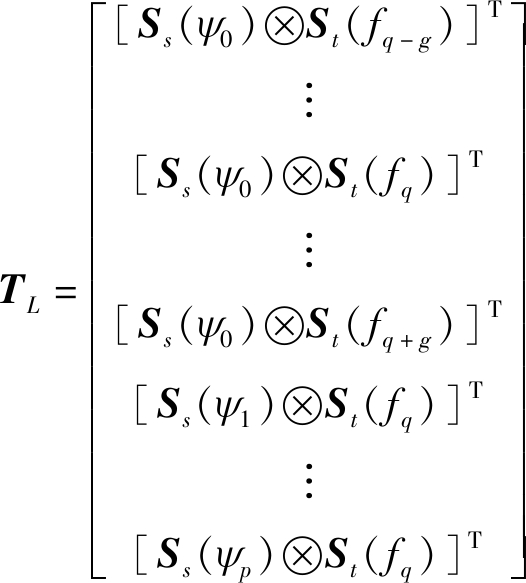
(16)
其中
Ss(ψi)|i=0,1…p=Hs⊙βs(ψi)=
(17)
St(fq)=Ht⊙βt(fq)=
(18)
Ss(ψi)|i=0,1…p为空域导向矢量,Ss(ψ0)代表主波束的空域导向矢量,其余为辅助波束空域导向矢量。St(fq)为第q个多普勒通道的时域导向矢量,St(fq-g)和St(fq+g)分别代表第q个多普勒通道左右两侧g个辅助通道的时域导向矢量,本文令g=3,即选择7个多普勒通道。fq(fq∈[-1,1])为风切变信号在第q个多普勒通道的归一化多普勒频率,
与
分别为空域和时域静态加权系数[11]。
在线性约束最小方差(Linear Constrained Minimum Variance,LCMV)准则[12]下,GMB的自适应处理部分可以描述为如下的数学优化问题
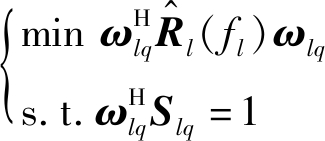
(19)
其中,ωlq为第l个距离单元第q个多普勒通道的最优权矢量,
为第l个距离单元降维变换后的杂波协方差矩阵,Rl(fl)为当低空风切变归一化多普勒频率为fl时,经过直接数据域算法处理后估计得到的杂波协方差矩阵,
为第l个距离单元第q个多普勒通道经降维变换后的低空风切变信号的空时导向矢量。那么第l个距离单元第q个多普勒通道的最优权矢量[13]为
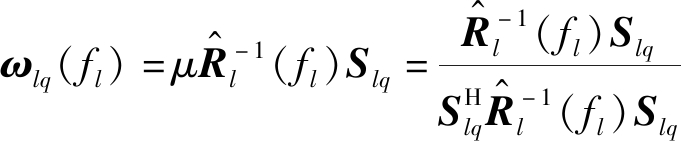
(20)
利用最优权矢量构造得到代价函数估计第l个距离单元内的多普勒频率
(21)
是降维后的回波数据,第l个距离单元的风速可以估计得到
(22)
图4所示为基于DDD-GMB的低空风切变风速估计方法的流程图。
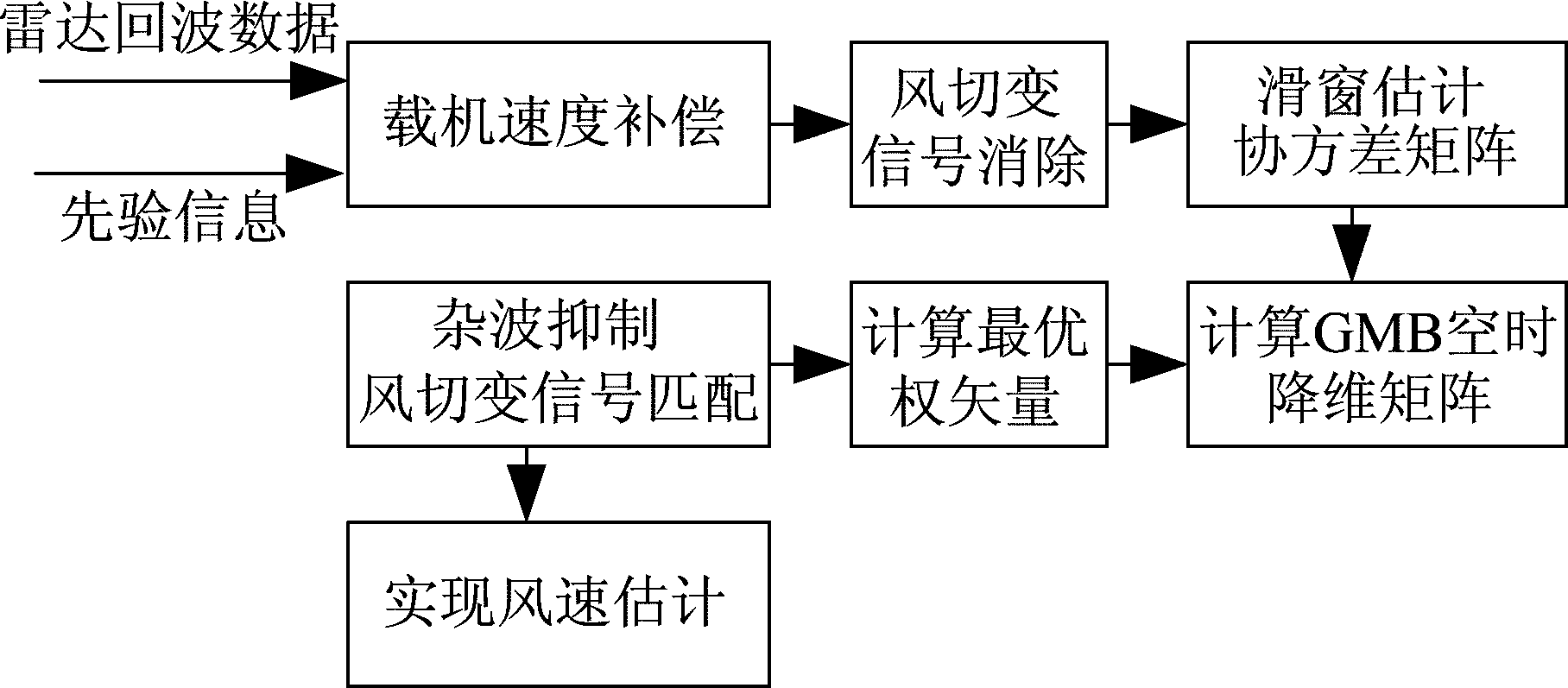
图4 DDD-GMB的低空风切变风速估计方法流程图
Fig.4 Flow chart of DDD-GMB low-altitude wind shear wind speed estimation method
本文非均匀地杂波所选区域范围为北纬45°51′～46°09′,西经112°24′～112°36′,地貌类型有4种,包括城市建筑地貌、高山地貌、水面地貌以及灌木丛地貌,数字高程模型(Digital Elevayion Model,DEM)数据分辨率为30 m。相关风切变仿真参数有:大气中雨滴与空气的质量比为0.0038,水的密度为1000 kg/m3,低空风切变场位于飞机前方8.5～16.5 km处,覆盖的距离范围是8公里,最大低空风切变原始风场速度为48.4150 m/s,最小低空风切变风场原始速度为0.1668 m/s,其他仿真参数如表1所示。
表1 仿真参数
Tab.1 Simulation parameters
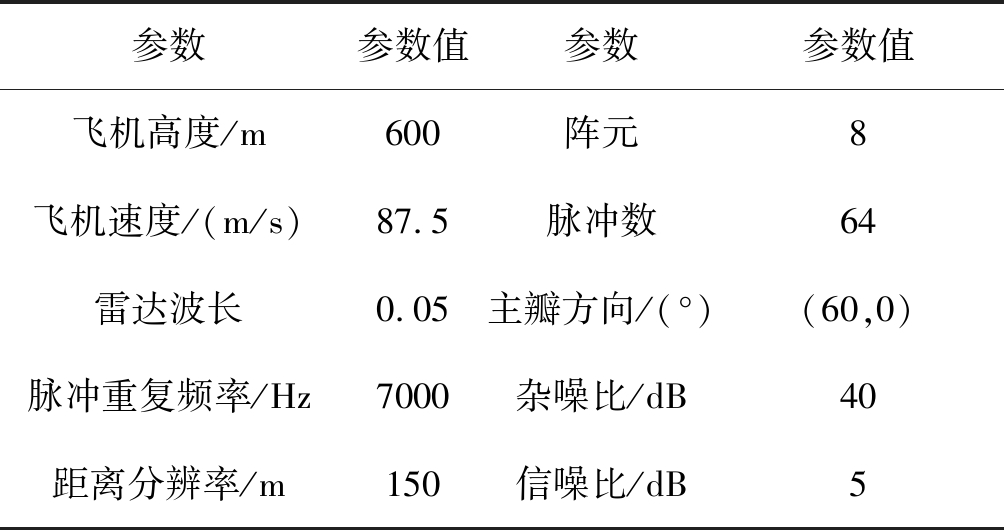
参数参数值参数参数值飞机高度/m600阵元8飞机速度/(m/s)87.5脉冲数64雷达波长0.05主瓣方向/(°)(60,0)脉冲重复频率/Hz7000杂噪比/dB40距离分辨率/m150信噪比/dB5
如图5所示为所仿真非均匀地杂波地区范围内数字高程模型数据图,此区域内海拔高度变化剧烈,地面的非均匀特性明显。如图6和图7所示分别为统计分布后向散射系数图和本文非均匀地杂波后向散射系数图,由图6与图7对比可知,本文所采用的非均匀地杂波后向散射系数复杂多变,能更好的匹配实际地形。如图8所示为机载前视气象雷达照射下地面散射单元相对于载机的擦地角信息,在均匀地杂波中,散射单元擦地角等于俯仰角,在非均匀地杂波中还与地面的地形起伏有关,由图8可知擦地角在非均匀变化,由此可以说明地杂波呈现非均匀特性。如图9所示,在非均匀地杂波回波功率随距离单元增加而变化的过程中,功率并非一直随距离增加而减少,而是上下起伏明显,并且有下降剧烈的部分,这是因为在仿真中利用了真实地形的数字高程数据和数字地表分类数据引起的。
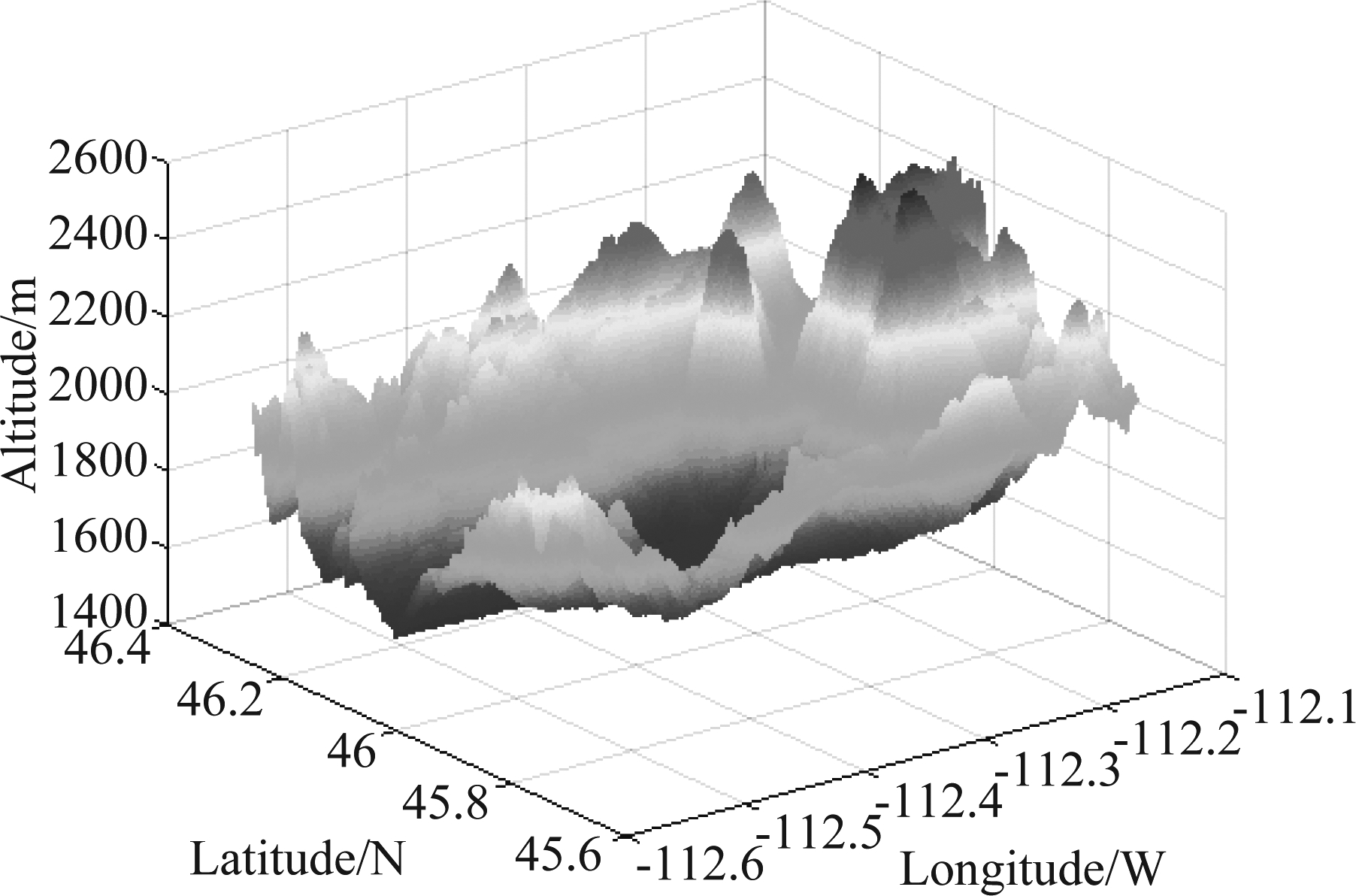
图5 数字高程模型数据图
Fig.5 Digital elevation model data chart
图6 统计分布后向散射系数图
Fig.6 Statistical distribution backscatter coefficient chart
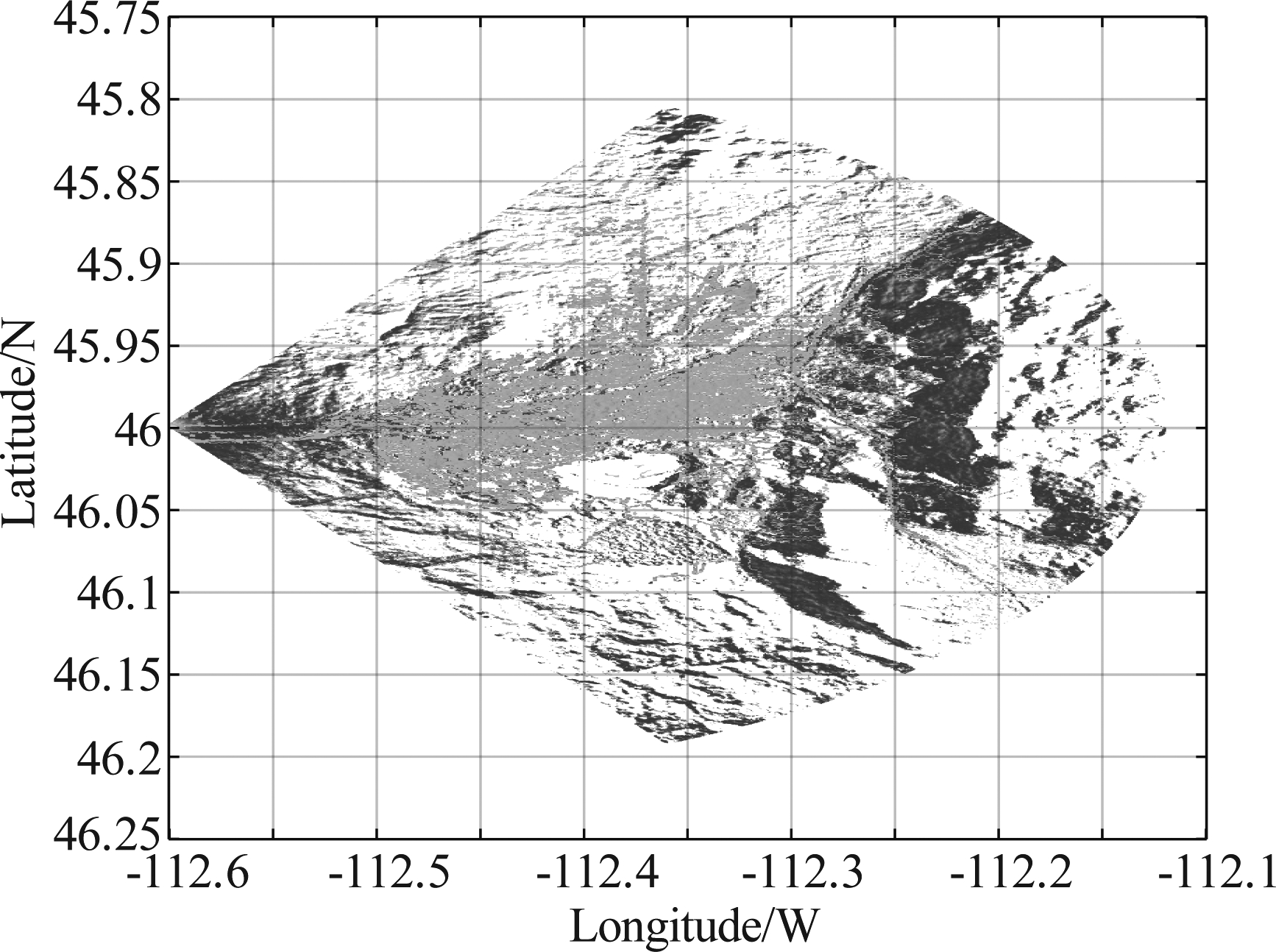
图7 本文中非均匀地杂波后向散射系数图
Fig.7 Backscatter coefficient chart for non-uniform in this paper
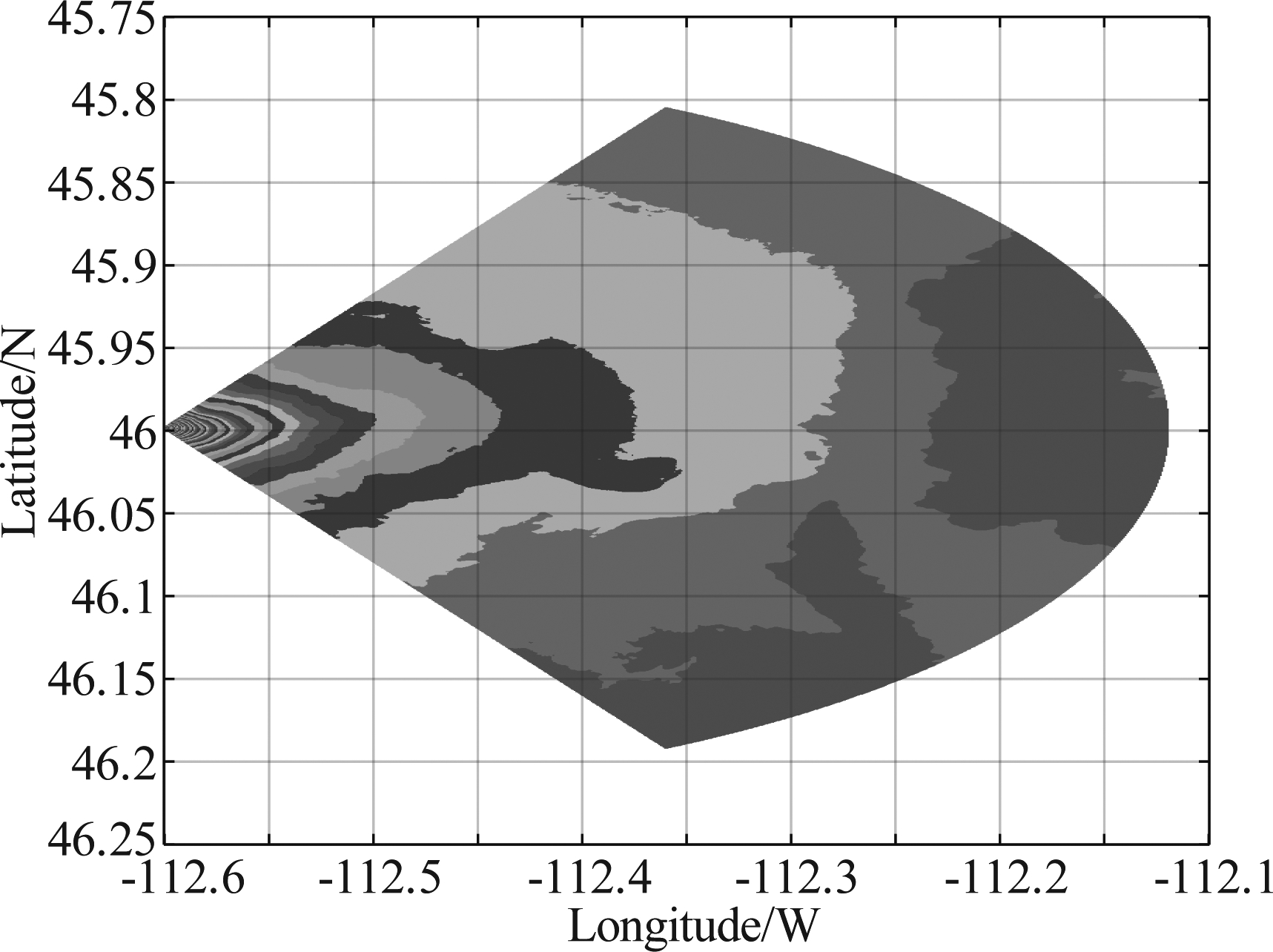
图8 散射单元相对于载机平台的擦地角信息
Fig.8 Grazing angle information of the scattering unit relative to the aircraft platform
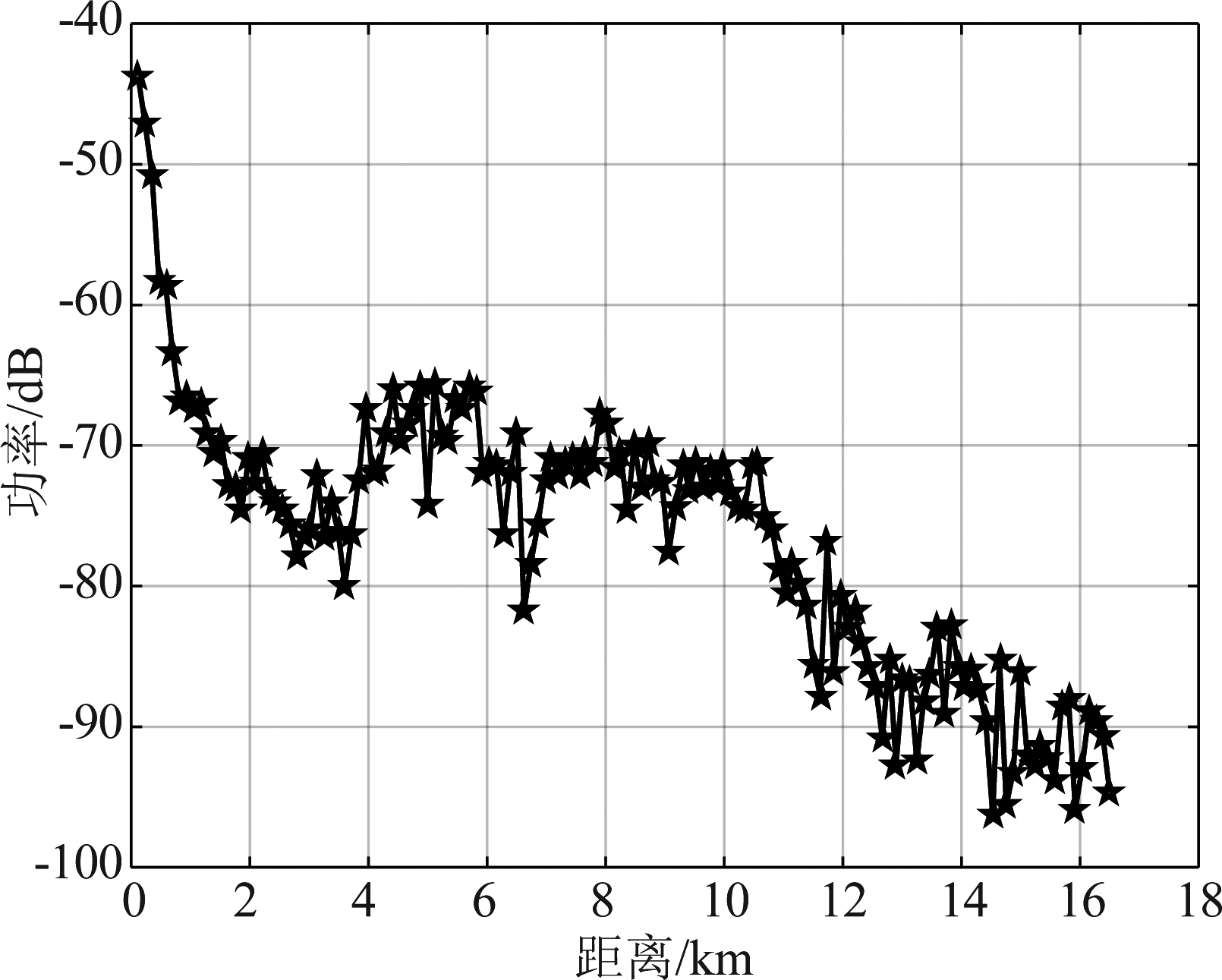
图9 非均匀地杂波回波功率随距离变化
Fig.9 Non-uniform clutter echo power varies with distance
如图10所示为补偿飞机速度后的回波信号空时二维谱,地杂波谱形状呈半圆形,这与机载前视阵雷达杂波谱的空时耦合特性相吻合。低空风切变信号空时二维谱在空时平面上呈现为一条“窄带”。另外低空风切变信号的回波功率远小于非均匀地杂波信号的功率,在空时二维谱中,地杂波信号掩盖了低空风切变信号。
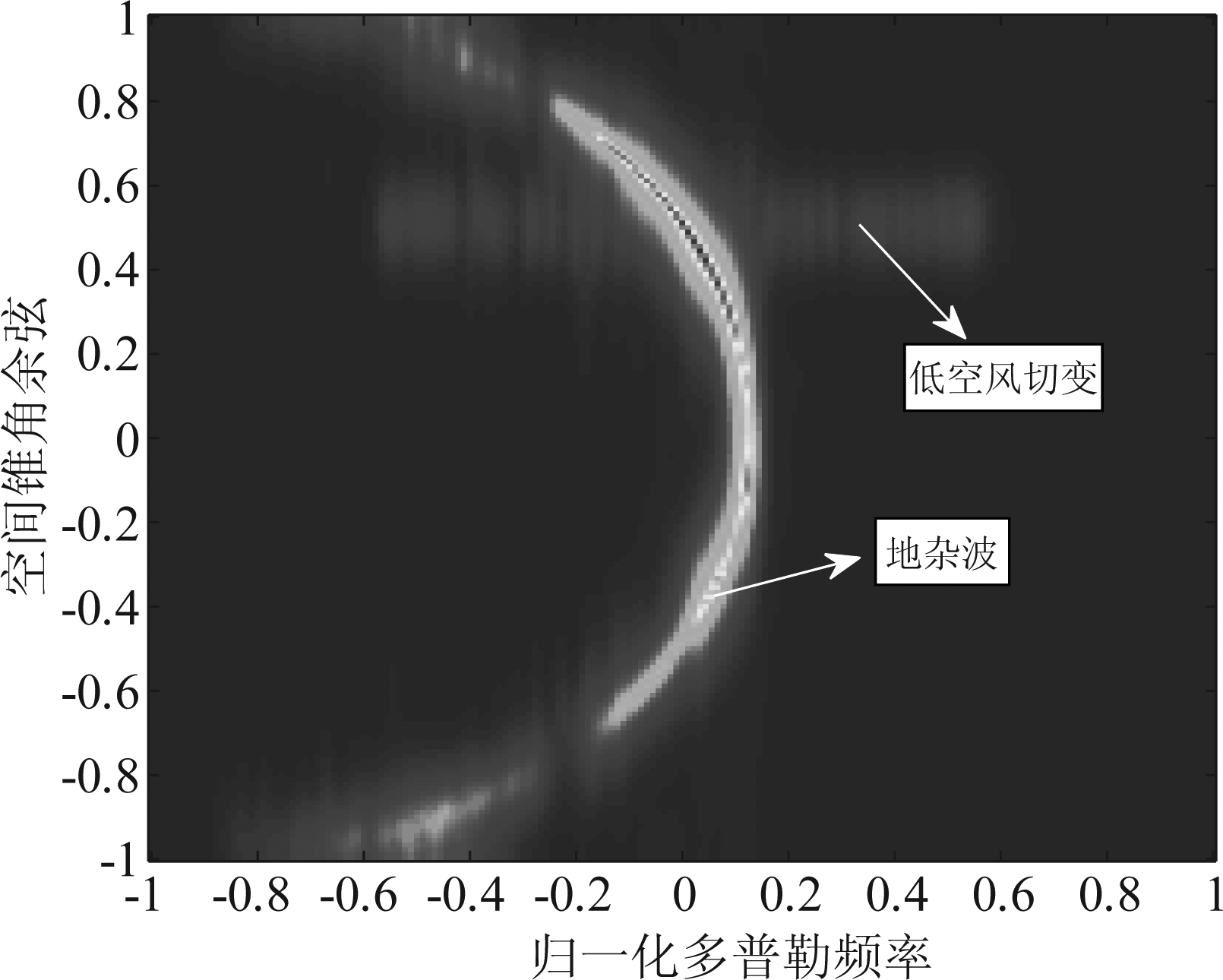
图10 回波信号空时二维谱
Fig.10 Echo signal space-time two-dimensional spectrum
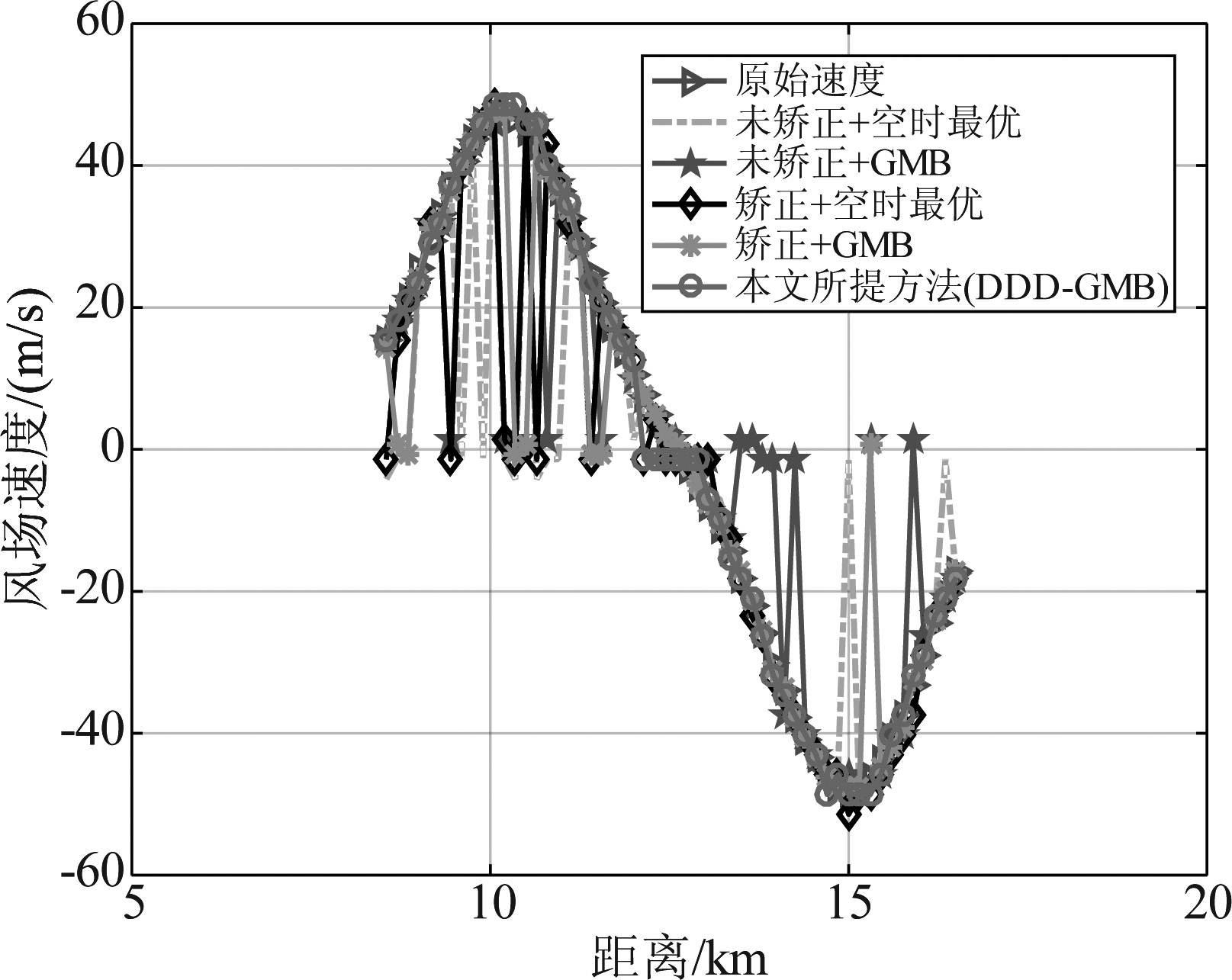
图11 风速估计对比图
Fig.11 Wind speed estimation comparison chart
图11为不同方法下的风速估计对比,机载气象雷达在前视工作状态下的地杂波存在距离依赖性,造成空时二维杂波谱在距离上呈现非均匀性,若不进行距离依赖性矫正则无法获得准确的风速估计结果,经过多普勒频移、空时插值等算法矫正后,在均匀地杂波环境下能够得到较为准确的风速估计结果,但是在非均匀地杂波环境下,依然存在距离单元功率非均匀现象,因此通过距离依赖性矫正后使用空时最优STAP方法,在非均匀地杂波背景下所需独立同分布(IID)样本无法达到RMB准则,空时最优STAP算法未能得到准确的风速估计结果,另外空时最优STAP方法运算量巨大,实时处理实现困难。经矫正后使用GMB降维STAP方法可以减少对训练样本数的要求,但是距离依赖性矫正算法计算量也是巨大的,在非均匀杂波环境下也未能得到准确的风速估计结果。本文采用DDD-GMB算法不需要利用参考距离单元估计待检测距离单元的协方差矩阵,无需进行距离依赖性的矫正,另外经滑窗处理获取训练样本,其独立同分布训练样本数较空时最优这类非降维方法大大增加,可以准确估计杂波协方差矩阵,在非均匀地杂波环境下可以准确估计得到风速。
表2给出了各方法的风速估计均方根误差计算结果,从表中可以看出在非均匀地杂波环境下本文所提方法较其他方法均方根误差最小,风速估计结果最为准确。
表2 不同风速估计方法的均方根误差
Tab.2 Root mean square error of different wind speed estimation methods
风速估计方法均方根误差/(m/s)未矫正+空时最优18.78未矫正+GMB16.44矫正+空时最优13.00矫正+GMB12.42本文所提方法2.07
图12 不同区域的非均匀地杂波数据下的风速估计结果
Fig.12 Estimation of wind speed under non-uniform clutter data in different regions
图12和表3分别为不同区域的非均匀地杂波数据下的风速估计结果和风速估计的均方根误差,其中区域A为北纬37°25′～37°55′,西经81°20′～80°50′、区域B为北纬37°30′～38°,西经80°05′～79°35′、区域C为北纬45°51′～46°09′,西经112°24′～112°36′。由图12和表3可知,在不同区域的非均匀地杂波数据下,本文所提方法仍然可以获得准确的风速估计结果。
表3 不同区域的非均匀地杂波数据下的风速估计结果均方根误差
Tab.3 Root mean square error of wind speed estimation results under non-uniform clutter data in different regions
本文所提方法在不同地区下的风速估计均方根误差/(m/s)区域A2.89区域B3.51区域C2.07
本文针对在非均匀地杂波环境下提出一种DDD-GMB的低空风切变风速估计方法,首先,此方法无需采用矫正算法矫正距离依赖性问题,其次,DDD-GMB算法直接利用待检测距离单元数据估计杂波协方差矩阵,无需利用参考距离单元,在无法获得足够IID样本的非均匀地杂波环境下杂波抑制性能优势明显,最后DDD-GMB算法构造了空时降维滤波器,减少了对训练样本数的要求,有效的抑制了地杂波,准确估计得到风速。仿真实验证明,本文方法可以在非均匀地杂波背景下实现风速的准确估计。
[1] Barber S, Paramore S, Woodell D L. Airborne Weather Radar System and Radar Display[P]. US patent: 7109913B1, 2006-09-19.
[2] 苏志刚, 陈琦, 郝敬堂. 航空器穿越低空风切变区仿真研究与实现[J]. 系统仿真学报, 2016, 28(6): 1426-1431.
Su Zhigang, Chen Qi, Hao Jingtang. Research and Implementation of Simulation for Aircraft Crossing the Low-Level Wind Shear Area[J]. Journal of System Simulation, 2016, 28(6): 1426-1431.(in Chinese)
[3] 吴仁彪, 韩雁飞, 李海. 基于压缩感知的低空风切变风速估计方法[J]. 电子与信息学报, 2013, 35(10): 2512-2517.
Wu Renbiao, Han Yanfei, Li Hai. Wind Speed Estimation for Low-attitude Wind Shear via Compressive Sensing[J]. Journal of Electronics & Information Technology, 2013, 35(10): 2512-2517.(in Chinese)
[4] 窦兴师. 相控阵雷达研究现状与发展趋势[J]. 电子测试, 2018(15): 94,100.
Dou Xingshi. Research Status and Development Trend of Phased Array Radar[J]. Electronic Test, 2018(15): 94,100.(in Chinese)
[5] 吴仁彪, 张彪, 李海, 等. 基于空时自适应处理的低空风切变风速估计方法[J]. 电子与信息学报, 2015, 37(3): 631- 636.
Wu Renbiao, Zhang Biao, Li Hai, et al. Wind Speed Estimation for Low-attitude Windshear Based on Space-time Adaptive Processing[J]. Journal of Electronics & Information Technology, 2015, 37(3): 631- 636.(in Chinese)
[6] 李海, 周盟, 陈筱浅, 等. 基于多通道联合自适应处理的微下击暴流中心风速估计方法[J]. 电子与信息学报, 2017, 39(7): 1619-1625.
Li Hai, Zhou Meng, Chen Xiaoqian, et al. Multiple Doppler Channels Joint Adaptive Processing Based Central Wind Speed Estimation for Microburst[J]. Journal of Electronics & Information Technology, 2017, 39(7): 1619-1625.(in Chinese)
[7] Ward J. Space-Time Adaptive Processing for Airborne Radar Data Systems[R]. Lexington, Massachusetts: Lincoln Laboratory of MIT, 1994. 25- 45.
[8] Boyer E, Larzabal P, Adnet C, et al. Parametric Spectral Moments Estimation for Wind Profiling Radar[J]. IEEE Transactions on Geoscience & Remote Sensing, 2003, 41(8): 1859-1868.
[9] 姚晖. 分布式信号源参数估计技术研究[D]. 郑州: 解放军信息工程大学, 2013.
Yao Hui. Research on Parameter Estimation Method for Distributed Sources[D]. Zhengzhou: PLA Information Engineering University, 2013.(in Chinese)
[10] 李明, 廖桂生, 袁晓懿. 一种有效的直接数据域地面动目标检测方法[J]. 数据采集与处理, 2010, 25(2): 133-137.
Li Ming, Liao Guisheng, Yuan Xiaoyi. Effective Direct Data Domain Method for Ground Moving Target Indication[J]. Journal of Data Acquisition and Processing, 2010, 25(2): 133-137.(in Chinese)
[11] 柳宝鹏, 解明祥. 一种稳健的降维STAP算法[J]. 电子测试, 2011(9): 21-24.
Liu Baopeng, Xie Mingxiang. Robust Approach to Reduced-dimension STAP[J]. Electronic Test, 2011(9): 21-24.(in Chinese)
[12] 冯晓宇, 谢军伟, 张晶, 等. 基于改进最速下降LCMV算法的稳健波束形成[J]. 传感器与微系统, 2018, 37(4): 108-111.
Feng Xiaoyu, Xie Junwei, Zhang Jing, et al. Robust Beam-forming Based on Improved Steepest Descent LCMV Algorithm[J]. Transducer and Microsystem Technologies, 2018, 37(4): 108-111.(in Chinese)
[13] 王永良, 彭应宁. 空时自适应信号处理[M]. 北京: 清华大学出版社, 2000: 82- 84.
Wang Yongliang, Peng Yingning. Space-Time Adaptive Processing[M]. Beijing: Tsinghua University Press, 2000: 82- 84.(in Chinese)
李 海 男, 1976年生, 天津人。中国民航大学教授、硕士生导师。研究方向为机载气象雷达信号处理及机器学习在气象雷达中的应用, 分布式目标检测与参数估计, 自适应信号处理、阵列信号处理、动目标检测与参数估计。
E-mail: elisha1976@163.com
刘志鑫 男, 1993年生, 山东潍坊人。中国民航大学硕士研究生, 研究方向为机载气象雷达信号处理。
E-mail: 582625066@qq.com
王 杰 男, 1992年生, 山东青岛人。中国民航大学硕士研究生, 研究方向为机载气象雷达信号处理。
E-mail: 9215wangjie@163.com
来 燃 男, 1990年生, 湖北随州人。中国民航大学, 助理工程师, 硕士研究生, 研究方向为极化气象雷达回波仿真, 极化气象目标检测。
E-mail: rlai@cauc.edu.cn