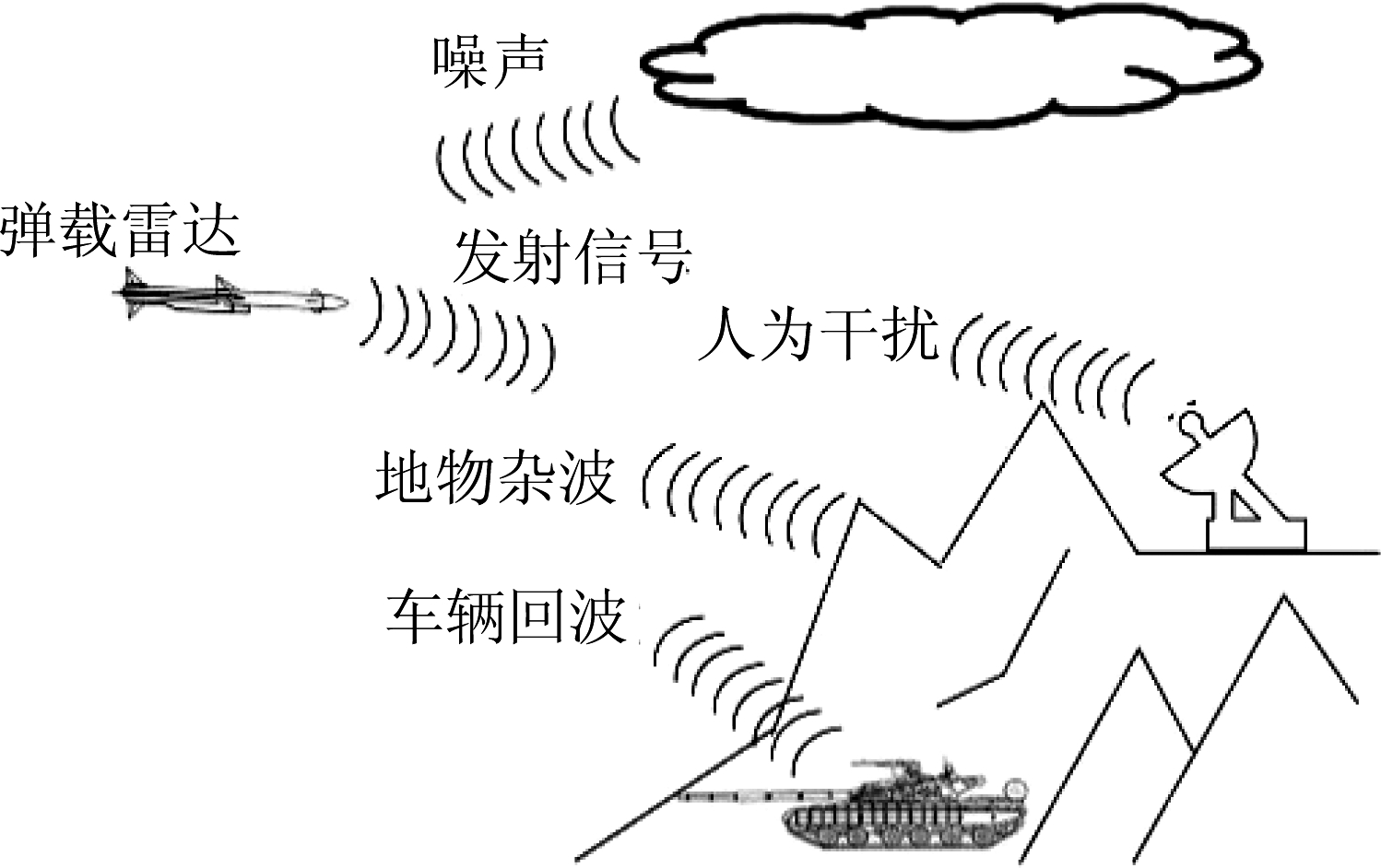
图1 弹载雷达与干扰机博弈示意图
Fig.1 Missile-borne radar and jammer game block diagram
Reference format: Wang Honglin, Li Wei, Zheng Jiayi, et al. Waveform Design of Missile-borne Radar and Jammer Based on Stackelberg Model[J]. Journal of Signal Processing, 2020, 36(1): 42- 49. DOI: 10.16798/j.issn.1003- 0530.2020.01.006.
随着电子战技术发展,雷达与干扰机间博弈日趋激烈。雷达自适应地优化发射波形,干扰机也可针对雷达波形智能地释放干扰。因此,如何在博弈条件下设计波形得到了雷达界广泛关注。
信干噪比(SINR)准则是雷达系统性能重要指标,被广泛应用于波形设计领域[1]。 Bell于1993年率先提出了能量约束下最大化互信息量(MI)和信噪比(SNR)的注水波形设计方法[2]。随后,Pillai等研究了信号相关干扰中的波形设计,提出了基于有限持续时间的发射波形和接收滤波器对的数值算法,但受杂波影响,此方法无法保证收敛到最优[3- 4]。Romero等在此基础上给出了最大化SINR的发射波形频域表达式[5]。此后,各种实际约束条件下的雷达波形设计方法得到了研究[6-9]。然而,以上波形设计方法未考虑干扰影响。自适应干扰技术一直是热点话题。文献[10]提出了通信系统中的智能干扰技术,国防科技大学王宏强团队在已知雷达波形谱条件下,提出了基于SINR和MI准则的鲁棒干扰技术[11],冯德军等提出了针对宽带雷达的相干干扰技术[12]。
近年来,雷达与干扰机间博弈现象得到了国内外学者广泛关注。康涅狄格大学的Xiufeng Song首先对MIMO雷达与干扰机间的相互博弈现象进行了研究,针对MI准则提出了基于Stackelberg博弈的波形策略[13],清华大学的张旭东团队从信息获取不完全的角度,研究了Bayesian博弈中MIMO雷达天线功率分配问题[14]。然而,他们忽略了杂波对优化过程的影响,空军工程大学李伟团队将Stackelberg模型扩展到高斯杂波环境,研究了MIMO雷达天线受损时的波形优化,发现依据信息理论的MI准则难以应用于非高斯杂波环境,可利用SINR准则进行波形设计[15]。Deligiannis基于SINR准则研究了多目标条件下雷达资源分配策略[17],但缺少对雷达波形的研究。现有MIMO雷达波形优化策略针对多个天线进行功率分配,难以适用于载荷受限的弹载雷达。
针对上述问题,本文研究杂波环境中弹载雷达与干扰机间的动态非合作博弈模型,从雷达和干扰机角度分别建立主导型Stackelberg博弈模型,基于SINR准则设计博弈波形策略,考虑功率约束条件,利用二次注水的maxmin和minmax策略对频域信号进行注水填充。仿真分析进一步表明了本文提出的博弈波形优化方法有助于提高/降低雷达检测性能。
现代战场环境日趋复杂,建立弹载雷达与干扰机间博弈模型需同时考虑多种因素影响,如图1所示。设雷达发射与接收信号分别为s(t)与y(t),信号带宽和功率约束为W与PS。目标脉冲响应h(t)为时间Th有限的随机模型,r(t)为接收滤波器脉冲响应,令H( f )与R( f )分别为h(t)与r(t)的傅里叶变换。噪声n(t)为零均值高斯信道过程,其功率谱密度PSD为Snn( f ),在W内不为零。杂波c(t)为非高斯随机过程,功率谱密度Scc( f )在W内不为常数。功率约束PJ的干扰机信号为j(t),其PSD为J( f )。图2为电子战环境下雷达信号框图。
图1 弹载雷达与干扰机博弈示意图
Fig.1 Missile-borne radar and jammer game block diagram
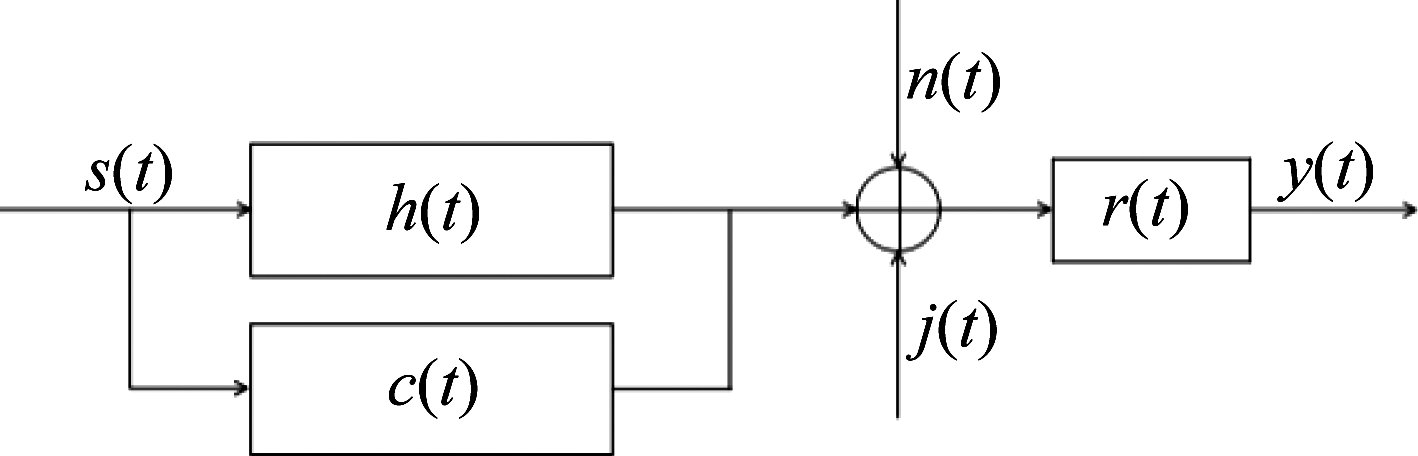
图2 雷达发射-接收信号框图
Fig.2 Radar transmit-receive signal block diagram
如图2所示,接收滤波器输出端信号y(t)表达式为
y(t)=r(t)*(s(t)*h(t)+s(t)*c(t)+n(t)+j(t))
(1)
“*”为卷积运算。令ys(t)=r(t)*(s(t)*h(t))和yj(t)=r(t)*(s(t)*c(t)+n(t)+j(t))分别为信号分量与干扰分量。则t0时刻SINR频域表达式为:
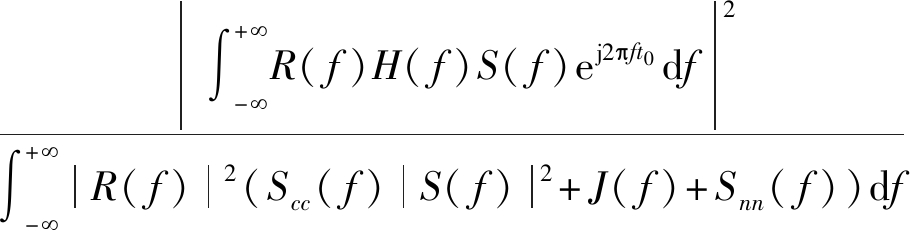
(2)
由于目标脉冲响应为时间有限随机模型,功率谱密度由能量谱方差(ESV)替代[5]:
(3)
其中μh( f )是H( f )的均值,假设为零。将式(3)带入式(2),根据施瓦兹不等式可得:
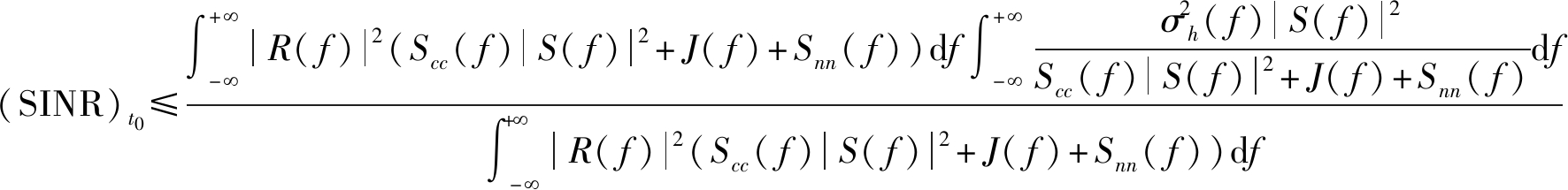
(4)
当且仅当
时,式(4)可取等号,SINR值最大,其中k为任意常数。若干扰机可精确估计雷达信号频谱,并将干扰调整至与雷达信号相同的频带内以此提升干扰有效性。此时
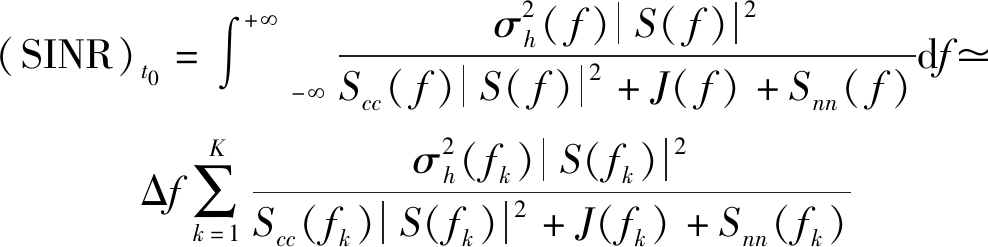
(5)
其中,K为频率采样数,Δf为频率采样间隔,KΔf=W。
根据统计判决理论,本文的雷达检测问题可定性为假设检验问题,解决该问题基本方法为经典Neyman-Pearson(NP)定理[18]。根据NP定理,雷达对目标检测问题可视为在两种假设中做出选择的二元假设检验问题:
(6)
其中H0称为零假设,H1称为备择假设。根据NP准则构建NP检测器,则雷达对目标检测概率PD为:
(7)
其中,PFA为虚警概率,
为雷达检测门限,d2为偏移系数,此节中偏移系数即SINR。对于此类检测器,检测性能完全由偏移系数确定,因此,通过求解SINR即可建立雷达信号波形与目标检测概率间的关系。
电子战环境中,雷达与干扰机相互对抗,目标函数完全对立,对抗过程中二者参数都能发生变化,变化策略依赖于前一时刻双方动作,属于动态的二元零和博弈。德国经济学家H. Von Stackelberg建立的博弈模型反映了这种动态不对称竞争[19]。Stackelberg提出将博弈论中两个参与者定义为“主导者”与“跟随者”,主导者首先行动,跟随者在观察到主导者方案后制定行动策略,主导者知晓其策略将被对手截获,决策时将跟随者的反应函数考虑在内,以最大化自身效益。由于杂波环境中博弈均衡难以收敛,本节设计了博弈条件下的二次注水波形优化方法,首先给出杂波条件下雷达与干扰单边优化策略,然后推导出雷达和干扰机分别作为Stackelberg博弈主导者时的波形策略。
基于认知理论[20],假设雷达可提前获得环境与目标的先验知识,自适应改变发射波形,基于最大化SINR准则(简称为max策略),雷达发射波形优化如下:
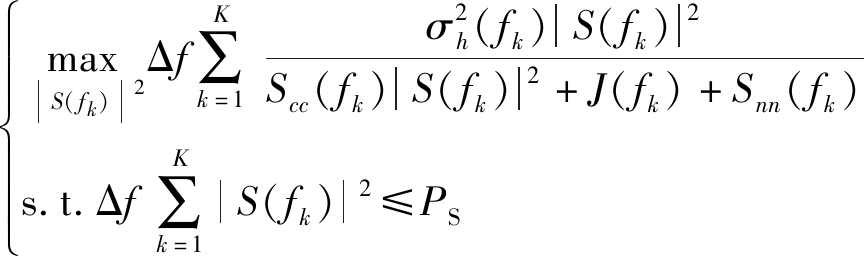
(8)
由式(8)知,目标函数是凸函数,能量约束为线性,因此,可利用拉格朗日乘子技术求解最优波形:
(9)
取式(9)对|S(fk)|2的导数并令其为零,得到最大化SINR的|S(fk)|2,利用注水定理进行频域能量重新分配[2]:
|S(fk)|2=
(10)
其中(x)+
max{0,x},λ1由
确定并决定注水位。
为降低雷达性能,减小SINR,智能干扰机可采取min策略设计干扰信号:
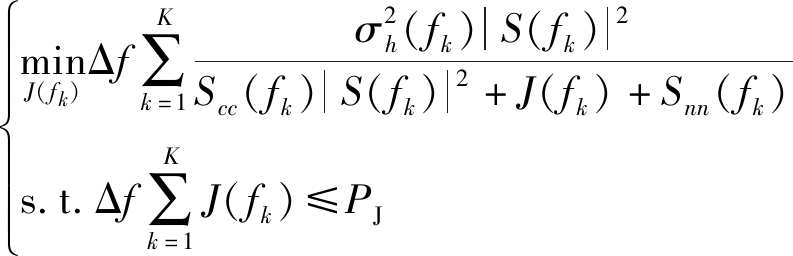
(11)
目标函数是凹函数,同理,利用注水定理确定干扰波形为
(12)
其中,γ1由功率约束
确定。
假设雷达在博弈中处于主导地位,知晓干扰机会捕获雷达信号进行干扰,且二者优化指标一致。为实现博弈均衡,雷达可设计策略最大化干扰最小化的SINR,采用二次注水maxmin方法优化波形。在我们前期工作中,已经对maxmin策略可近似于博弈纳什均衡进行了论证[15]。雷达波形设计策略如下:
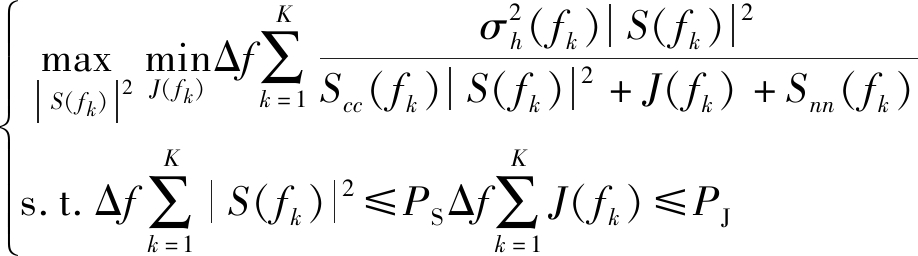
(13)
在此情况下,min策略中J(fk)可应用于第一步注水算法,波形策略根据前节定义如下:
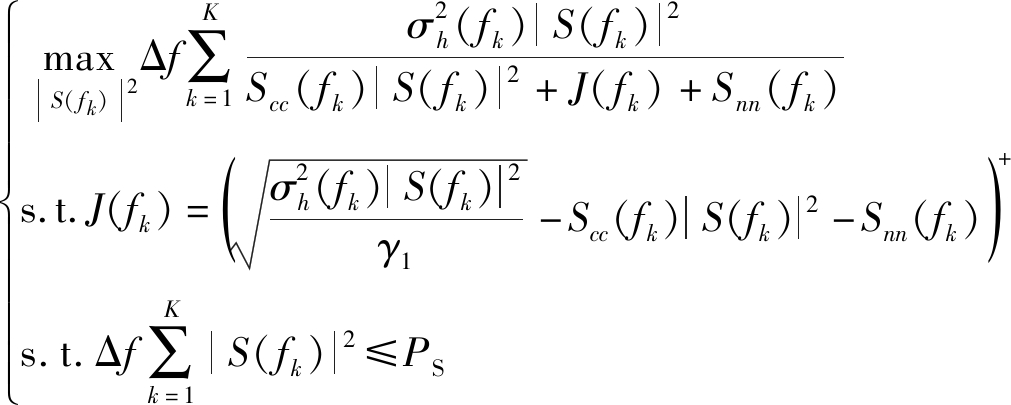
(14)
式(14)中关于|S(fk)|2的核函数仍为凸函数,构造拉格朗日方程如下:
L(|S(fk)|2,λ2,λ3)=
(15)
求解方程,通过二次注水方法重新分配频域能量,得到新的波形策略:
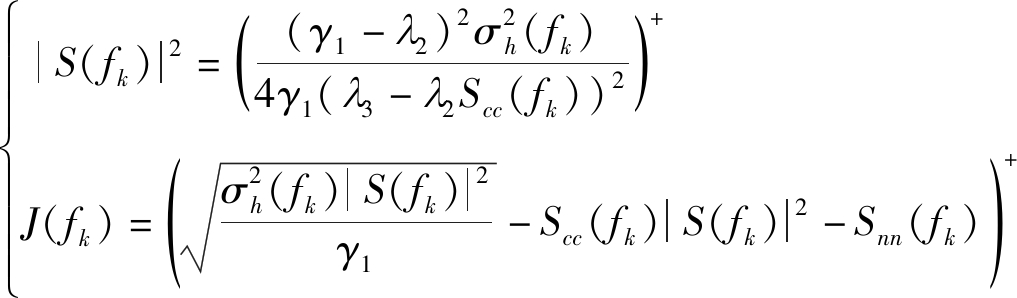
(16)
假设干扰机作为博弈主导者,知晓雷达根据干扰策略优化波形,可采取minmax策略进行对抗,即最小化雷达最大化SINR,策略如下:
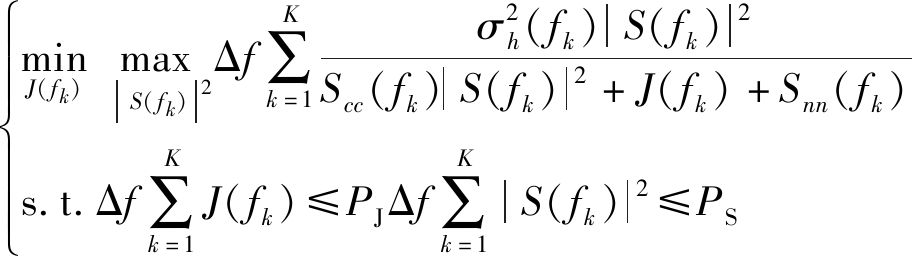
(17)
由于雷达可对目标的干扰信号做出最优反应,基于第一次注水的雷达信号,式(17)化简为
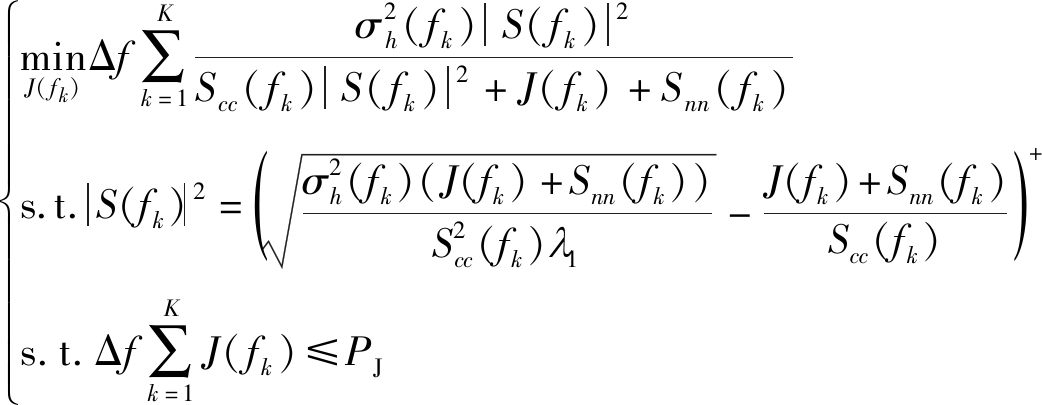
(18)
同理,可利用拉格朗日乘数法求解波形策略如下:
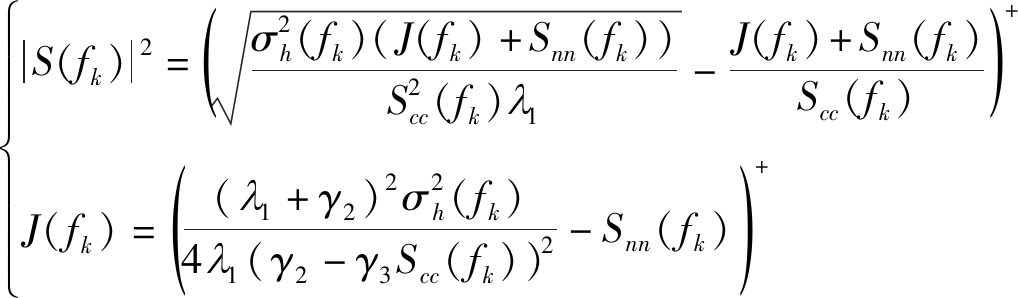
(19)
其中,注水因子由约束条件确定。
下面对本文波形策略进行仿真分析。假设某型弹载雷达发射信号参数为W=100 MHz,为简化计算,将整个频带划分为五个子频带,每个子带带宽f=20 MHz。
下标k=1,2,…,5对应五个不同子频带。定义接收机噪声Snn(fk)=1,对于实际应用场景,模拟起伏地杂波{Scc(fk)}={1.2,2,1.5,1,0.8}[12]。假设博弈主导者功率固定为20 dBw,跟随者为10～30 dBw。图3和图4显示了在max\min、maxmin以及minmax策略中雷达\干扰各频带功率分配策略随干扰\雷达总功率变化情况。
图3中,干扰功率低于20 dBw时,雷达各策略间功率分配差异较小,回波中目标冲激响应与杂波比值(TCR)对功率策略影响较大。干扰功率高于20 dBw时,各策略间的差异逐渐显现,对于max策略,雷达不考虑与干扰的博弈,各频带功率分配不变;对于maxmin策略,为最大化SINR,雷达向高TCR频段分配更多能量,如频带4,但随干扰功率的升高,
对雷达影响逐渐增加,雷达减少了TCR较高的频带5上的功率分配,向高于频带5的频带3分配更多功率;对于minmax策略,受干扰影响,回波中高TCR频带中目标响应已经被干扰覆盖,雷达难以获取信息,故雷达降低频带4、5的功率分配,提高频带1、2和3上的功率,期望在TCR相对较低的频段获取目标信息,最大化SINR。
图4中,不同于雷达信号变化特点,未进行博弈时,干扰采取min策略,最小化输出端SINR功率分配策略,如图3(a)所示;在雷达主导Stackelberg博弈条件下,干扰机对干扰功率重新分配抑制雷达性能;干扰作为博弈主导者时,随雷达功率的增加,干扰在高TCR频段分配更多的功率来抑制SINR的提高。
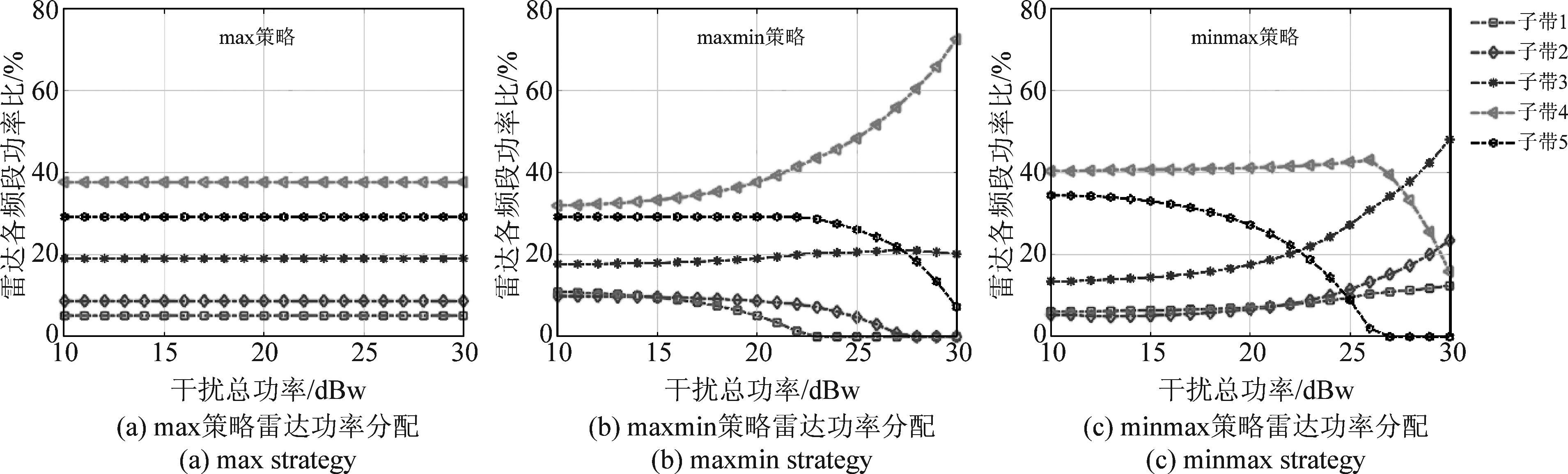
图3 雷达功率分配策略
Fig.3 Radar power allocation strategies
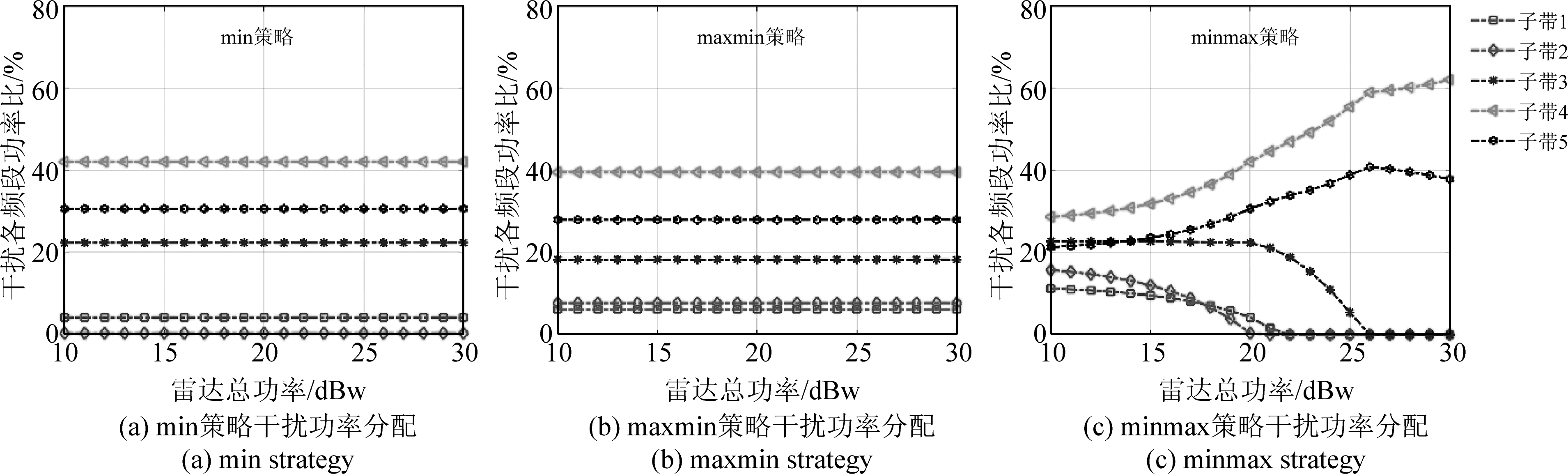
图4 干扰功率分配策略
Fig.4 Jammer power allocation strategies
图5显示了不同策略下接收端SINR随雷达及干扰功率变化情况。由图5(c)知,在雷达功率较低时,通过二次注水的maxmin方法设计的功率策略可充分利用频带资源,SINR性能较min策略有显著提升,最高可提升3.5 dB,平均性能有0.8 dB的提升;对于干扰主导的minmax策略,在雷达干扰功率相近时,有较好的干扰性能,对max策略中雷达SINR降低接近1 dB,平均可降低0.6 dB。
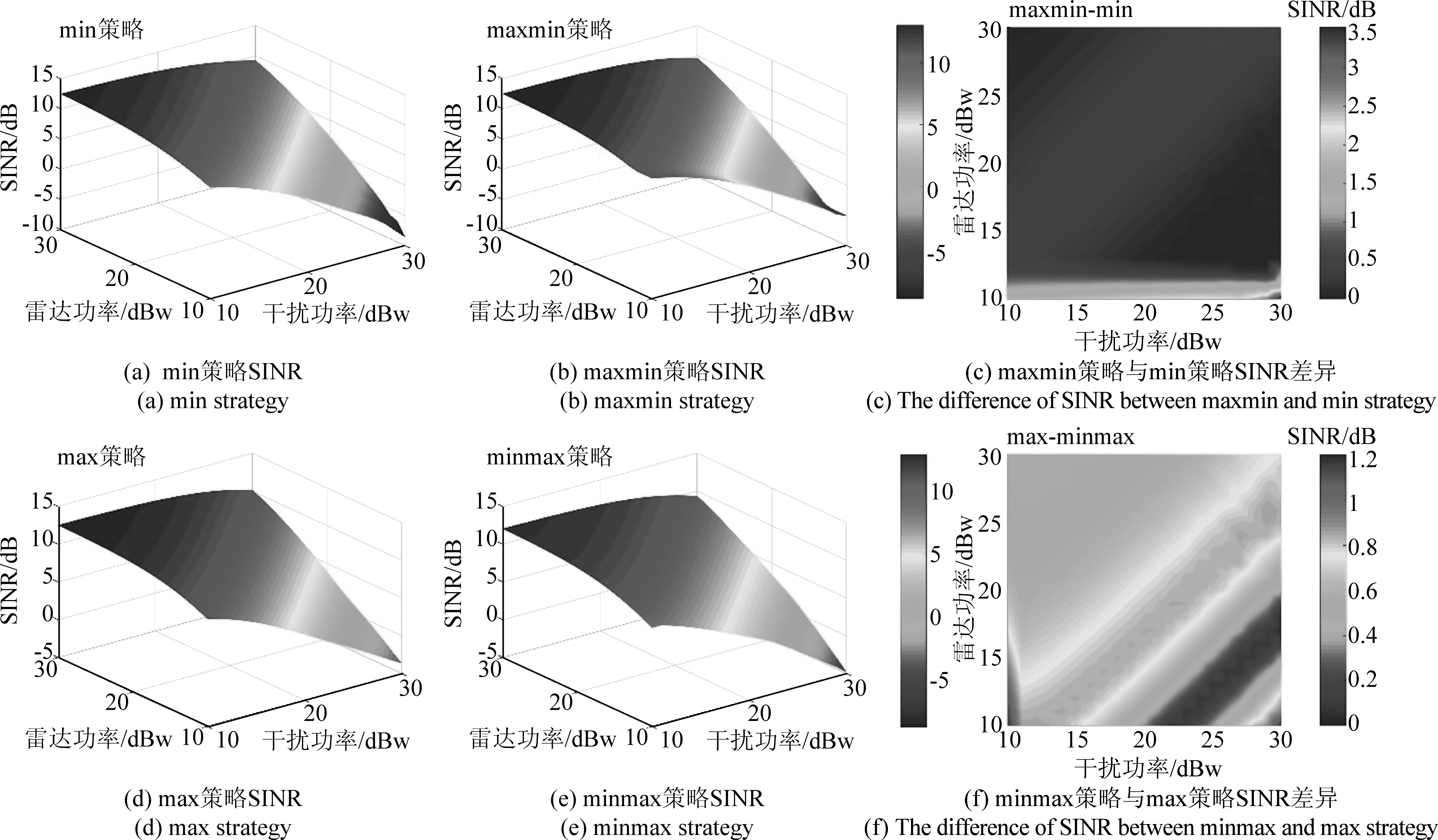
图5 不同策略条件下SINR随功率变化曲面
Fig.5 The SINR versus different strategies of the radar and the jammer
图6显示了不同策略下雷达检测性能曲线。对于雷达方,检测性能:max策略>minmax策略>maxmin策略>min策略;对于干扰方,被检测性能:min策略<minmax策略<maxmin策略<max策略。对比不同功率约束下Stackelberg博弈情况,通过二次注水的功率分配策略均能达到预期性能。在雷达主导的波形博弈中,二次注水的maxmin策略检测概率较min策略最高可提升9.17%,平均可提升4.29%;干扰主导的minmax策略较max策略,被检测概率最高可降低11.42%,平均可降低4.78%。值得注意的是,二次注水波形设计方法无需讨论复杂环境下博弈均衡解的问题,具有算法复杂度低,通用性高的优点;但若博弈一方占据绝对领导地位(二者功率非同数量级),二次注水波形策略则难以获得性能提升。
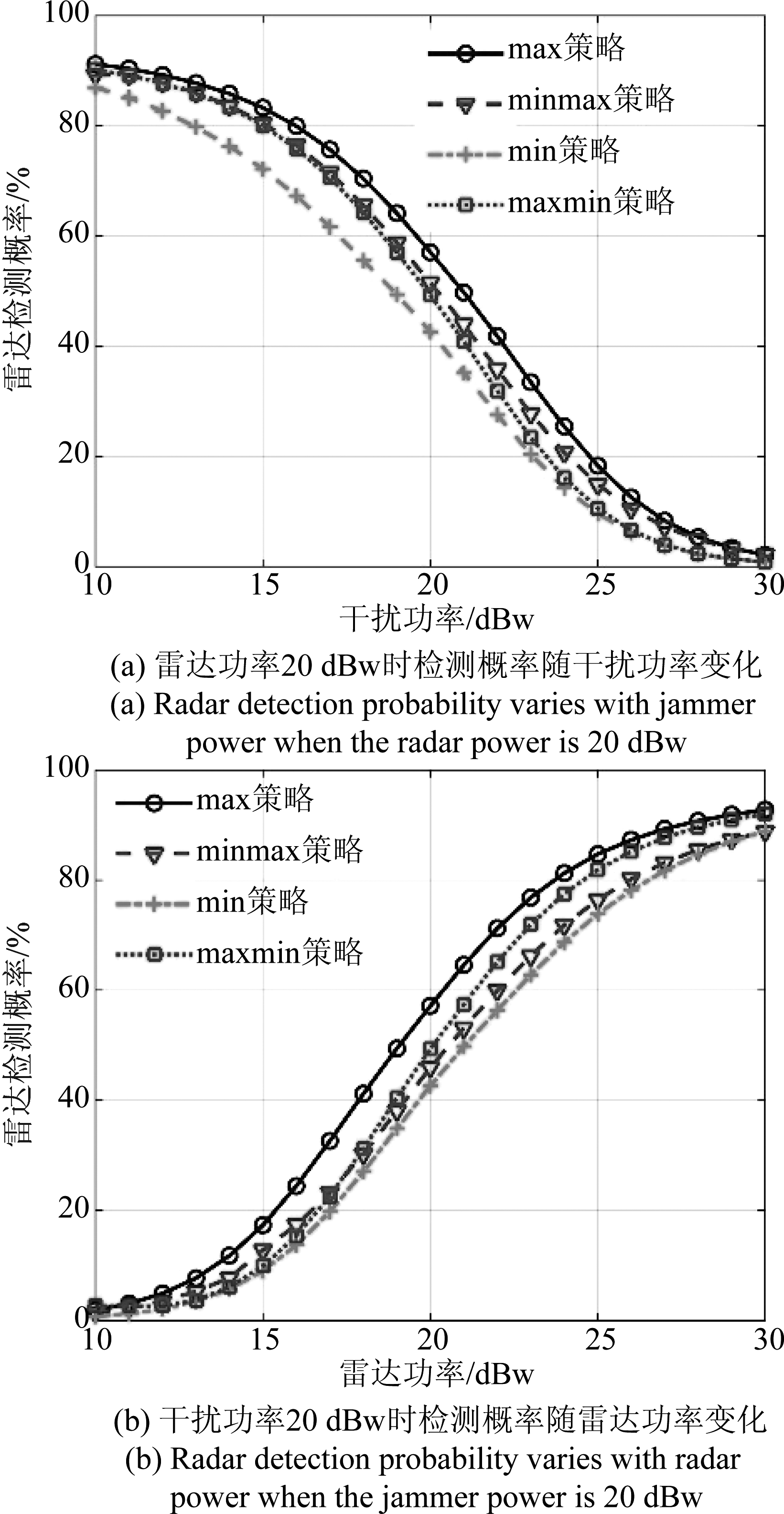
图6 雷达检测概率曲线
Fig.6 Radar detection probability curve
针对电子战条件下雷达与干扰机零和动态博弈问题,从雷达和干扰机角度分别建立Stackelberg博弈模型,基于SINR准则提出了不依赖纳什均衡的二次注水算法。在雷达主导Stackelberg博弈中,雷达通过最大化干扰最小化SINR的二次注水算法分配信号频域功率,干扰主导时,干扰机通过最小化雷达最大化SINR的二次注水算法设计干扰信号。实验仿真表明,通过二次注水的maxmin、minmax策略性能优于一次注水的min、max策略,雷达主导的maxmin策略可以提高雷达检测性能,而干扰主导的minmax策略可以降低自身被探测概率。
[1] 王璐璐, 王宏强, 王满喜, 等. 雷达目标检测的最优波形设计综述[J]. 雷达学报, 2016, 5(5): 487- 498.
Wang Lulu, Wang Hongqiang, Wang Manxi, et al. An Overview of Radar Waveform Optimization for Target Detection[J]. Journal of Radars, 2016, 5(5): 487- 498.(in Chinese)
[2] Bell M. R. Information theory and radar waveform design[J]. IEEE Transactions on Information Theory, 1993, 39(5): 1578-1597.
[3] Pillai S U, Youla D C, Oh H S, et al. Optimum transmit-receiver design in the presence of signal-dependent interference and channel noise[J]. IEEE Transactions on Information Theory, 2002, 46(5): 577-584.
[4] Kay S. Optimal signal design for detection of Gaussian point targets in stationary Gaussian clutter/reverberation[J]. IEEE Journal of Selected Topics in Signal Processing, 2007, 1(1): 31- 41.
[5] Romero R A, Bae J, Goodman N A. Theory and Application of SNR and Mutual Information Matched Illumination Waveforms[J]. IEEE Transactions on Aerospace and Electronic Systems, 2011, 47(2): 912-927.
[6] Aubry A, Demaio A, Farina A, et al. Knowledge-aided (potentially cognitive) transmit signal and receive filter design in signal-dependent clutter[J]. IEEE Transactions on Aerospace and Electronic Systems, 2013, 49(1): 93-117.
[7] Wu L, Babu P, Palomar D P. Transmit Waveform/Receive Filter Design for MIMO Radar with Multiple Waveform Constraints[J]. IEEE Transactions on Signal Processing, 2018, 66(6): 1526-1540.
[8] Imani S, Nayebi M M, Ghorashi S A. Colocated MIMO Radar SINR Maximization Under ISL and PSL Constraints[J]. IEEE Signal Processing Letters, 2018, 25(3): 422- 426.
[9] Butt F A, Naqvi I H, Riaz U. Hybrid Phased-MIMO Radar: A Novel Approach with Optimal Performance under Electronic Countermeasures[J]. IEEE Communications Letters, 2018, 22(6): 1184-1187.
[10] Guan Y, Ge X. Distributed Secure Estimation over Wireless Sensor Networks Against Random Multichannel Jamming Attacks[J]. IEEE Access, 2017, 5: 10858-10870.
[11] Wang L, Brennan P V, Wang H, et al. Minimax robust jamming techniques based on signal-to-interference-plus-noise ratio and mutual information criteria[J]. IET Communications, 2014, 8(10): 1859-1867.
[12] Feng D, Xu L, Pan X, et al. Jamming Wideband Radar Using Interrupted-Sampling Repeater[J]. IEEE Transactions on Aerospace and Electronic Systems, 2017, 53(3): 1341-1354.
[13] Song X, Willett P, Zhou S, et al. The MIMO radar and jammer games[J]. IEEE Transactions on Signal Processing, 2012, 60(2): 687- 699.
[14] Gao H, Wang J, Jiang C, et al. Equilibrium between a statistical MIMO radar and a jammer[C]∥Proceedings of 2015 IEEE Radar Conference, Johannesburg, 2015: 461- 466.
[15] Lan X, Li W, Wang X, et al. MIMO Radar and Target Stackelberg Game in the Presence of Clutter[J]. IEEE Sensors Journal, 2015, 15(12): 6912- 6920.
[16] 兰星, 李伟, 王兴亮, 等. 频率分集MIMO雷达信号优化设计[J]. 信号处理, 2015, 31(8): 1029-1034.
Lan Xing, Li Wei, Wang Xingliang, et al. Optimal Signal Design for Frequency Diversity MIMO Radar[J]. Journal of Signal Processing, 2015, 31(8): 1029-1034.(in Chinese)
[17] Deligiannis A, Lambotharan S, Chambers J A. Game theoretic analysis for MIMO radars with multiple targets[J]. IEEE Transactions on Aerospace and Electronic Systems, 2016, 52(6): 2760-2774.
[18] Steven M. Kay. 统计信号处理基础: 估计与检测理论[M]. 罗鹏飞, 张文明, 刘忠, 等, 译. 北京: 电子工业出版社, 2014: 425- 445.
Steven M. Kay. Fundamentals of Statistical Signal Processing: Estimation and Detection Theory[M]. Luo Pengfei, Zhang Wenming, Liu Zhong, et al. Translation. Beijing: Publishing House of Electronics Industry, 2014: 425- 445.(in Chinese)
[19] 朱弗登伯格, 让梯诺尔. 博弈论[M]. 黄涛, 郭凯, 龚鹏, 等, 译. 北京：中国人民大学出版社, 2010: 36- 43.
Drew F. Jean T. Game Theory[M]. Huang Tao, Guo Kai, Gong Peng, et al. Translation. Beijing: China Renmin University Press, 2010: 36- 43.(in Chinese)
[20] Haykin S. Cognitive radar: a way of the future[J]. IEEE Signal Processing Magazine, 2006, 23(1): 30.
王泓霖 男, 1995年生, 山东威海人。空军工程大学硕士研究生, 主要研究方向为雷达与电子战系统 、雷达信号处理。
E-mail: wanghonglin821@outlook.com
李 伟(通信作者) 男, 1978年生, 山东济宁人。2006年于国防科学技术大学获博士学位, 现为空军工程大学信息与导航学院副教授, 硕士生导师, 主要研究方向为新体制雷达信号处理, 目前已发表论文70余篇。
E-mail: liweichangsha@163.com
郑家毅 男, 1991年生, 河南信阳人。95019部队助理工程师, 主要研究方向为弹载雷达波形设计、雷达信号处理。
E-mail: 1416235455@qq.com
徐建业 男, 1992年生, 北京人。空军工程大学硕士研究生, 主要研究方向为信号处理、信道编码。
E-mail: xjy1236@sina.com
赵俊龙 男, 1995年生, 安徽阜阳人。空军工程大学硕士研究生, 主要研究方向为雷达信号处理、雷达波形设计。
E-mail: 1170755712@qq.com
邹 鲲 男, 1976年生, 湖北黄冈人。2005年于国防科学技术大学获博士学位, 现为空军工程大学信息与导航学院副教授, 主要研究方向为雷达信号处理、复杂电磁环境下的目标探测。
E-mail: zoukun2003@yahoo.com.cn