Reference format: Wu Sunyong, Zhao Jun, Dong Xudong, et al. DOA Tracking of Single Acoustic Vector Sensor by Multi-Bernoulli Filter in Impulse Noise[J]. Journal of Signal Processing, 2020, 36(1): 139-148. DOI: 10.16798/j.issn.1003- 0530.2020.01.017.
噪声环境下多声源波达俯仰角和方位角的检测中,定位和跟踪是信号处理中的重要课题,在室内语音增强、水下目标监视、声纳和雷达信号处理等方面有广泛的应用[1]。其中单声矢量传感器(Acoustic vector sensor, AVS)可以同时拾取声场中共点的声压和振速信息,它的出现为解决水下目标的探测、定位及识别等诸多问题提供了一种新的方法和手段。随着声矢量传感器接收模型的提出,很多经典的子空间估计算法,如旋转子空间不变法(Estimation of Signal Parameter via Rotational Invariance Techniques, ESPRIT)和多重信号分类法(Multiple Signal Classification, MUSIC)等都已经运用到声矢量传感器中,并且派生出很多基于声矢量传感器的二维ESPRIT[2]和二维MUSIC[3]算法。此外,对波达方向(Direction of arrival, DOA)跟踪估计运用较多的子空间更新算法还有近似投影子空间追踪(Projection Approximation Subspace Tracking, PAST)[4]算法。这类跟踪算法大多都先进行子空间更新,虽然通过谱峰搜索的方式进行DOA估计能降低协方差分解的计算量,但在低信噪比下跟踪效果下降明显。而且这些分析都是基于定位技术,只能使用当前量测的空间信息对静态源进行估计。现有的单声矢量DOA估计假设目标是静态的且个数已知,但是在水下和室内声学信号处理中,实际上信号是动态的,个数是不确定的,且随时间变化,此外,噪声本质上是脉冲特性。因此,在脉冲噪声环境和声源不确定的情况下,研究一种精确估计声源的单声矢量传感器DOA跟踪算法具有重要意义。
由于粒子滤波是基于状态滤波类算法中的典型代表,能够处理任何能用状态方程表示的系统,并被广泛的应用到目标跟踪问题[5-7]。在[8]中作者研究单目标DOA动态跟踪时,将MUSIC空间谱代替粒子滤波的似然函数,结果表明基于粒子滤波的跟踪算法优于传统的子空间类跟踪算法。文献[9]中提出了在高斯白噪环境下单声矢量传感器的粒子滤波跟踪算法,并详细推导了用于动态DOA贝叶斯估计的克拉美罗界,仿真结果表明所提算法优于经典的DOA估计算法。文献[10]中将粒子滤波算法和MUSIC方法相结合,采用匀速运动(Constant Velocity, CV)模型对声源运动状态进行建模,将MUSIC方法的估计函数作为粒子滤波算法中的似然函数应用于矢量水听器接收的水下运动目标数据的处理,有效地对运动目标的方位进行跟踪。虽然以上文献对目标进行了动态估计,但没有考虑噪声是脉冲的且多目标声源数目是时变的情况。
在文献[11]中描述了对称α稳定(Symmetric alpha stable, SαS)分布比高斯噪声更适合建模脉冲噪声,由于α稳定分布不具有二阶及以上的统计量,以至于二阶及高阶统计量发展的信号处理方法性能下降,基于分数低阶距的信号处理方法被广泛应用于α稳定分布的领域。在[12]中提出了在脉冲噪声条件下使用矢量水听器阵列的一种新的基于分数低阶相关的二维测向和水下二维子空间技术源定位的分数低阶相关旋转子空间不变法(FOC-ESPRIT)方法,该方法在大范围稳定分布的特征指数值下具有较强的鲁棒性。在[13]中,作者在脉冲噪声环境下,采用基于分数低阶距(Fractional Lower Order Moment, FLOM)矩阵的空间谱函数作似然函数,用粒子滤波的方法对单目标DOA的跟踪。但以上方法仍无法解决声源数目随时间变化的问题。
Mahler引入了随机有限集(Random finite set, RFS)[14]的概念用来解决多目标数目时变跟踪问题,RFS框架在多目标跟踪问题中被发现有很好的应用前景[15-17]。其中有一种是以存在概率和目标概率密度为特征把每个目标建模为伯努利RFS的方法,即多目标多伯努利滤波器(Multi-target multi-Bernoulli filter, MeMBer)[18],该滤波器的优点是对单个目标空间进行维数运算,避免了联合滤波器的计算复杂度和数据关联问题。Choppala P B等人提出将MUSIC谱函数作为MeMBer的伪似然函数[19],对相控阵列进行了有效地的DOA跟踪。然而,该算法没有考虑噪声的脉冲特性,仅用高斯噪声建模在实际应用中并不恰当。
基于以上分析,本文提出一种脉冲噪声环境下单AVS多声源的多伯努利粒子滤波跟踪算法。由于脉冲噪声环境下量测协方差矩阵不准确,故采用FLOM代替协方差矩阵,对其进行特征分解,用MUSIC空间谱代替多伯努利更新阶段中的似然函数的计算。并对此伪似然函数进行指数加权,以提高粒子权重,从而更有效重采样。与传统DOA跟踪算法相比,该算法的优点是不需要预先知道当前目标状态数目,仿真实验表明,该算法能够有效地跟踪多信源的状态和准确地估计时变声源的数目。
假设P个窄带声源sp(t),p=1,...,P,在离散时间t入射一个单AVS。第p个声源的二维DOAθp(t)=[φp(t),φp(t)]T,其中φp(t)∈(-π,π),φp(t)∈[-π/2,π/2]分别表示方位角和仰角,上标T表示转置运算。单AVS接收的声源信息可以表示为
(1)
其中Z(t)是在t时刻接收到的声源信息,n(t)为加性噪声过程,
为第p个声源的输出信号,up(t)为传感器指向声源的单位方向向量,设为
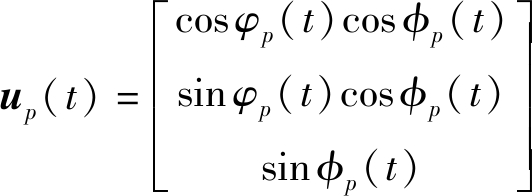
(2)
采集L次快拍,k时刻单AVS接受到的信号表示为:
(3)
其中Zk是声源接收矩阵,A(θk)=[a(θ1,k),…,a(θN,k)]∈C4×N是导向矢量,Sk=[s1(t),…,sL(t)]∈CL×N为声源矩阵,Nk=[n(t)]∈C4×1为传感器噪声向量。
对DOA估计的传统研究方法大多采用高斯噪声模型的二阶统计量。但在如雷达回波、低频大气噪声和水声信号研究中,噪声往往由持续时间短和幅度大的不规则脉冲或噪声尖峰组成,即脉冲噪声。若在脉冲噪声环境下仍然使用高斯噪声模型,算法性能将显著下降。然而,SαS能够很好地描述这类具有显著尖峰脉冲的随机信源。因此,SαS噪声模型有更好的适用性,可以用特征函数表示为:
φ(t)=exp(jδt-γ|t|α[1+jβsgn(t)
(t,α)])
(4)
其中
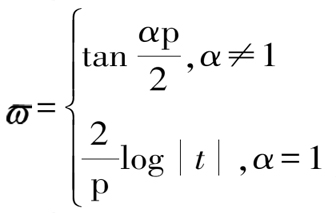
(5)
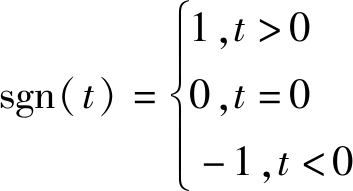
(6)
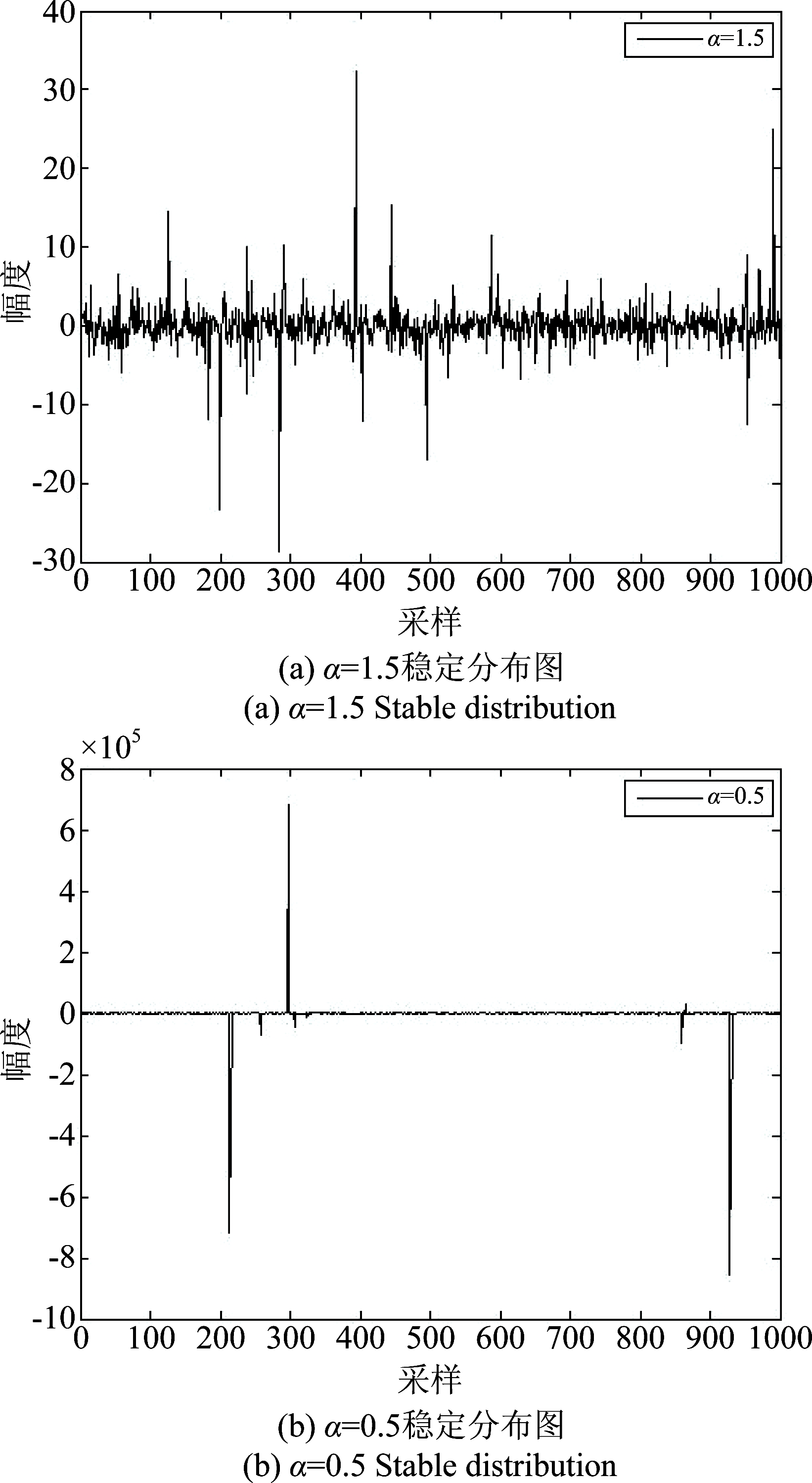
图1 特征指数α取不同值时噪声的脉冲特性
Fig.1 The impulse characteristic of noise when the characteristic exponent α is different
α是特征指数,它的大小能够影响此分布的脉冲程度,范围在0<α≤2。当α=2时的分布是高斯分布;γ是分散参数,其含义与高斯分布的方差一致;β是对称参数,当β=0时的分布为对称α稳定分布;δ是位置参数。SαS在参数选取不同时代表不同的概率密度函数。当α=2,β=0时,为高斯分布模型。当α=1,β=0时,为柯西(Cauchy)分布模型。当α=1/2,β=-1时,为皮尔逊分布模型。SαS分布中α越小,脉冲越明显;反之α越大,噪声越接近高斯噪声。高斯分布和SαS分布中重要的不同点是高斯分布具有二阶统计量,而SαS分布在0<α<2时二阶统计量不存在,则协方差就不准确。图1中分别给出了α不同值时1000个样本的脉冲噪声分布图,可以看出噪声在不定时出现脉冲特性,且α越小,脉冲越明显。
声源定位方法常见的有MUSIC算法以及ESPRIT方法都已经应用到二维DOA估计中。这些方法中,MUSIC算法是通过谱峰搜索来确定声源波达方向,假设:式(1)中的噪声是独立同分布的,零均值的复循环高斯过程,且独立于不同信号;声源信号Sk和噪声Nk是不相干的。则单AVS量测概率密度函数(PDF)可以表示为:
(7)
其中
)表示均值为μ协方差矩阵为的多变量复高斯分布。单声矢量传感器协方差矩阵Rk可以表示为:
Rk=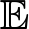
(8)
其中Q=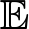
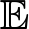是期望操作算子,diag表示对角操作,上标H表示共轭转置。信号协方差矩阵Rs=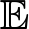
且Rk可以被近似为:
(9)
然而在实际应用中,噪声过程是非高斯的,所以上述的协方差矩阵就不够准确了。由于协方差的无界性,标准的MUSIC算法在脉冲噪声的情况下性能下降,文献[13]引入了分数低阶统计矩的新型矩阵,若已知k时刻的阵列观测矩阵Zk,则FLOM矩阵
k被定义为:
ψi, j=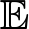
1<p<α≤2
(10)
其中ψi, j表示k的第(i, j)个元素,(·)*代表共轭。k是一个M×M的矩阵。在[20]中,作者介绍了FLOM矩阵的形式为
k=a(θk)ΛSaH(θk)+rIM
(11)
其中ΛS和r分别表示源信号和加性噪声的FLOM矩阵。由式(9)～(10)可知,第(i, j)个FLOM矩阵为
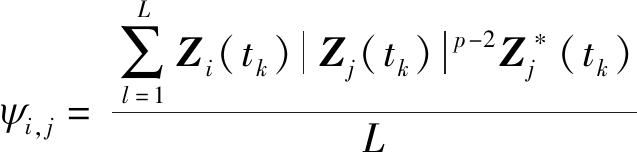
(12)
其中p是分数矩且满足1<p<α≤2。用FLOM代替信号的协方差矩阵,在MUSIC算法中再对k进行特征分解,得到噪声子空间Un,则FLOM-MUSIC空间谱估计函数[13]的形式为:
(13)
其中
表示速度;C=[1 0 1 0],使得Cxk表示信源位置信息,a(·)为空间导向矢量,ζ∈R+代表对空间谱的指数加权。通常传统的MUSIC空间谱波束形成器在脉冲噪声环境下的响应是扭曲和扩展的,这种峰值失真和频谱扩展会导致重采样步骤的性能显著下降。经过加权后,可以增强靠近真实状态的粒子数目,使得后续的重采样算法更有效地选择粒子。
在本节中,我们详细介绍多伯努利滤波器的粒子滤波实现。由文献[18 ]可知,如果k-1时刻的多目标概率密度参数集为
则k-1时刻的空间后验概率密度为:
(14)
其中
是空间后验概率密度,可以近似为加权粒子集
为粒子总数,其中
代表第i个粒子的状态,包括方位角和俯仰角,
代表权重,通常
如果k-1时刻的空间后验概率密度能够表示为则粒子滤波的预测概率密度可以表示为:
(15)
其中Jk|k-1=Jk-1+JB,k,所有的粒子可以从两部分中提取,
(16)
权重为
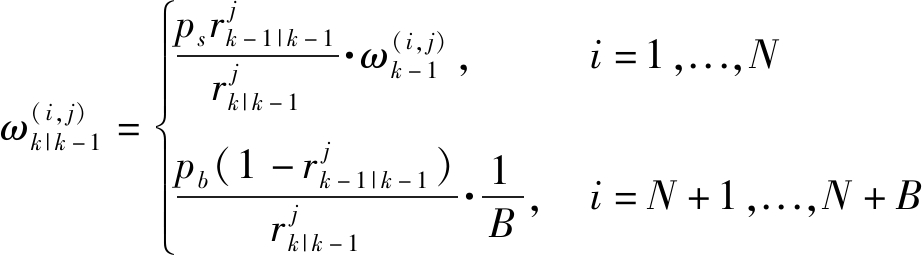
(17)
其中ps代表持续存活的概率密度,pb代表新生粒子的概率,N代表从转移概率密度fk|k-1中采样目标存活的粒子数量,B代表从建议概率密度βk中新生的粒子数量。若预测阶段的多伯努利后验概率密度在k时刻用
来表示。则更新多伯努利参数集可以表示为
权重为:
(18)
其中pD,k为检测概率,似然函数表示为
(19)
最后,采用重采样的方法,消除小权重粒子,提取权重较大的粒子。MeMBer的SMC方法实现见表1。
表1 多伯努利滤波SMC算法流程
Tab.1 MeMBer filter SMC algorithm
输入:{r jk-1,(x(i,j)k-1,ω(i,j)k-1)Nk-1i=1}Jk-1j=1,Zk。预测步骤1. 存在概率的预测:r jk|k-1=r jP,k|k-1+r jB,k|k-1。其中r jp,k|k-1=r jk-1·∑Nk-1i=1ω(i,j)k-1·Ps,k(x(i,j)k-1)表示持续存活模型的存在概率;r jB,k|k-1=(1-r jk-1)·∑Bi=1ω(i,j)k-1·Pb,k(x(i,j)k-1)表示新生模型的存在概率。2. 计算存活粒子的预测状态和构造新生目标加权粒子集:x(i,j)k|k-1～fk|k-1(xkx(i,j)k-1,Zk),i=1,...,Nk-1x(i,j)k|k-1～βk(xkZk-1),i=Nk-1+1,...,Nk-1+B3. 预测权重ω(i,j)k|k-1,i=1,...,Nk-1+B根据公式(17);
续表1
4. 联合加权粒子集:{(x(i,j)k|k-1,ω(i,j)k|k-1)Nk|k-1i=1}Jk|k-1j=1={(x(i,j)p,k-1,ω(i,j)p,k-1)Nk-1i=1}Jk-1j=1∪{(x(i,j)B,k,ω(i,j)B,k)NB,ki=1}JB,kj=1,其中Jk|k-1=Jk-1+JB,k,Nk|k-1=Nk-1+NB,k,NB,k=B。更新步骤5. 对每个粒子x(i,j)k|k-1, 计算似然函数g(Zkx(i,j)k|k-1)。(1) 通过量测信息Zk计算协方差矩阵Rk并经过特征分解得到Ek,由于本算法不需要预先估计当前信源个数,可以直接对信源跟踪,即:UN=Ek(:,SNk-1+1:END),其中SNk-1表示k-1时刻的信源个数信息。(2)对于每个粒子x(i,j)k|k-1, 根据式(19)计算似然函数g(Zkx(i,j)k|k-1)。6. 更新存在概率:r jk|k=r jk|k-1·∑Nk|k-1i=1g(Zkx(i,j)k|k-1)ω(i,j)k|k-1(x(i,j)k|k-1)1-r jk|k-1+r jk|k-1·∑Nk|k-1i=1g(Zkx(i,j)k|k-1)ω(i,j)k|k-1(x(i,j)k|k-1),其中i=1,…,Nk|k-1;j=1,…,Jk|k-1。7. 由式(18)计算更新权重,并归一化ω(i,j)k=ω～(i,j)k∑Jk|k-1j=1(∑Nk|k-1i=1ω～(i,j)k)。输出:{r jk,(x(i,j)k,ω(i,j)k)Nki=1}Jkj=1,x(i,j)k=x(i,j)k|k-1。k=k+1,重复1至7步,若k>K,K为观测时间长度,则结束。
由于传统的DOA估计方法无法解决相邻时间步长的多信源跟踪问题,本文提出了一种基于随机有限集的MeMBer跟踪仿真方法。考虑在脉冲噪声下,给出了多伯努利粒子滤波跟踪算法下采用FLOM与MUSIC空间谱相结合作为粒子的似然函数在不同条件下的数值实验结果,以下简称为MF-MUSIC算法;而直接用量测的协方差矩阵与MUSIC空间谱相结合代替多伯努利更新阶段的似然函数,称为M-MUSIC算法。广义信噪比(GSNR)定义为:
(20)
其中γ代表噪声分散参数,GSNR表示信号强度和噪声分散度的比值,GSNR越小代表信号受到的噪声影响越大。均方根误差是预测值与真实值偏差的平方与观测次数n比值的平方根,用来衡量观测值同真值之间的偏差。因此在以下仿真实验中,估计性能的评价方式为联合均方根误差(RMSE)和跟踪收敛成功概率Probability of Convergence (PROC),分别定义为:
(21)
(22)
(23)
其中
和
是第j次蒙特卡罗第i时刻仿真实验中方位角和俯仰角的估计值,P是第i时刻声源个数,MC表示蒙特卡罗实验次数。
假设源
以恒速(CV)模型运动
xk=Fkxk-1+Gνk
(24)
其中系数矩阵Fk和G分别为
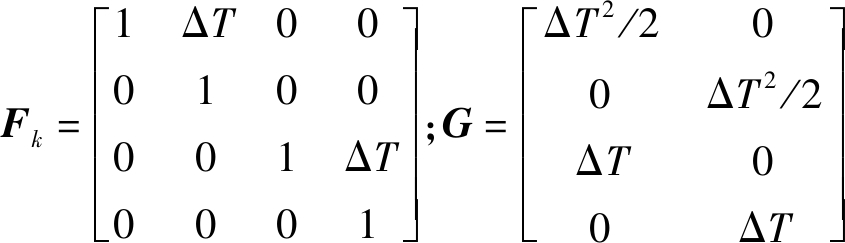
(25)
其中ΔT表示采样时间间隔,νk是服从零均值高斯过程的噪声项。即vk～N(0,k)且
实验条件如下:时间步长T=1 s,特征指数α=2表示高斯噪声环境;信源数目为2,状态时变但数目保持不变,信源初始状态为x1(0)=[20;0.1;30;0.1];x2(0)=[70;0.1;-50;0.2]。广义信噪比GSNR=10 dB,快拍数L=200,检测概率和存活概率假设为常数pD,k=0.98,pS,k=0.99;新生目标随机集可以用多伯努利参数集
来表示,其中
其中m1=[50;0;30;0],m2=[70;0;-50;0],P1=[22;0.12;22;0.32],P2=[22;0.12;22;0.82],指数加权因子ζ=3。
图2(a)是在SNR=10 dB的条件下,1次MC实验的轨迹跟踪图。图2(b)是运行100次MC实验的联合均方根误差图。从图2(a)可以看出,传统的FLOM-MUSIC跟踪算法的估计角度与真实状态偏差很大,基于随机有限集的粒子滤波(RFS-PF)跟踪算法和本文算法的估计值都在真实角度附近波动。由图2(b)可知,与RFS-PF算法相比,本文算法对目标的状态跟踪更加精确,RMSE更小。
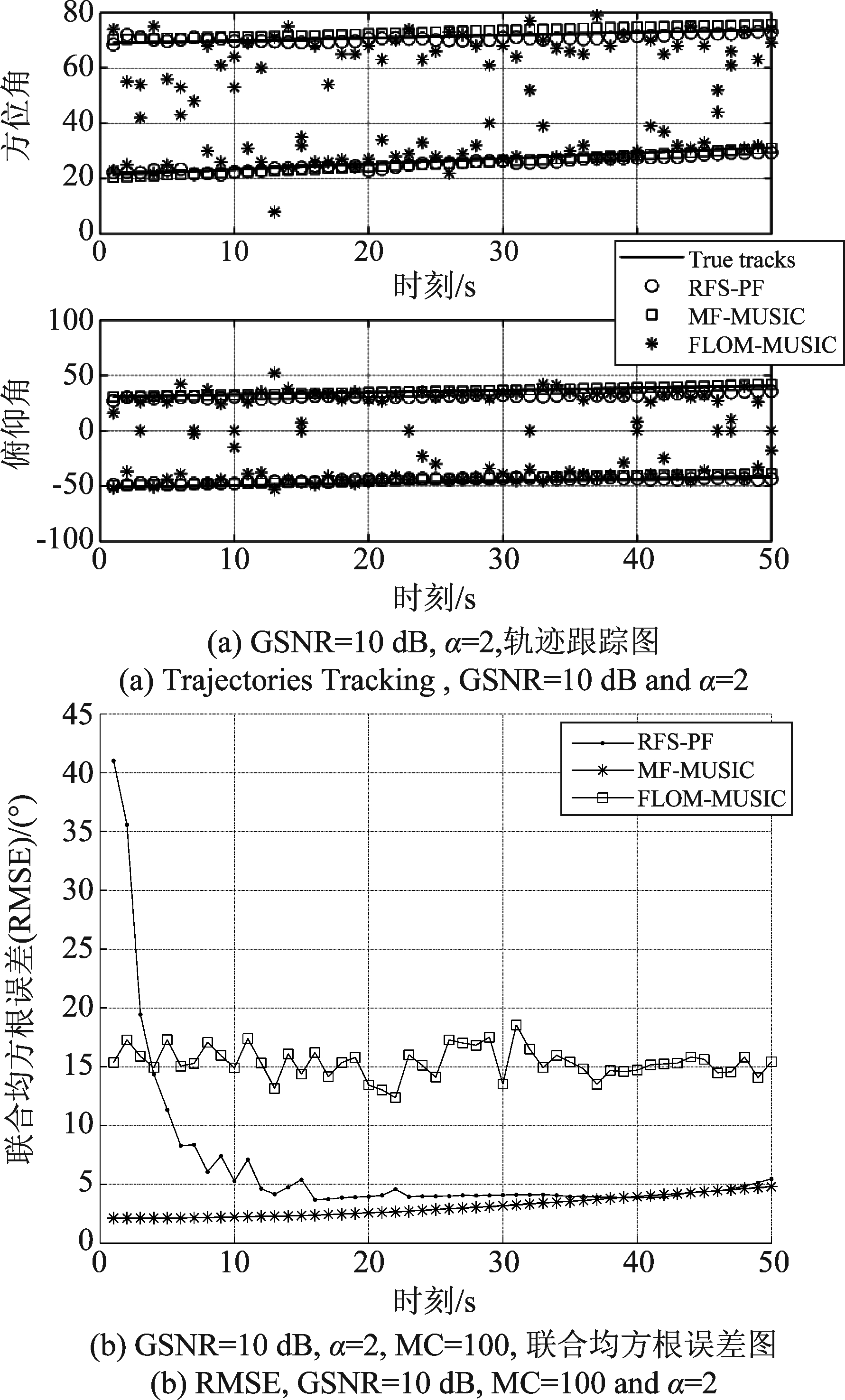
图2 GSNR=10 dB,α=2轨迹跟踪和联合均方根误差图
Fig.2 Trajectories Tracking and RMSE, GSNR=10 dB and α=2
实验条件中采样时间间隔T=1 s,跟踪总时间K=50 s。阵元个数为1,声源数目时变,声源1和声源2分别在第1和第15时刻出现,直到观测时间结束,其余实验参数同实验4.1。
由于传统DOA跟踪方法需要预先知道信源个数才能对信源进行跟踪,从而不能处理信源数目时变问题,实验4.1是建立在信源数目不发生变化情况下,将本文所提算法与传统FLOM-MUSIC跟踪算法、RFS-PF算法比较。实验4.2是考虑信源数目时变,且信源相近的情况,分析了MF-MUSIC算法的性能。在更新阶段,使用FLOM-MUSIC谱估计函数来替换似然函数。然后对粒子进行重采样,使粒子集中在高似然区域,提高了算法的可行性。由于在α=2时α稳定分布时是高斯噪声,图3(a)和(b)分别表示的是用M-MUSIC算法、RFS-PF算法和MF-MUSIC算法各运行100次MC的势估计和均方根误差效果图,从图3(a)可以看出在高斯噪声环境下三种算法均能估计目标的个数,也说明了多伯努利滤波器可以估计出AVS接收到的目标个数;图3(b)可以看出MF-MUSIC算法和M-MUSIC算法的联合均方根误差都比RFS-PF小,也说明在高斯噪声环境下直接用协方差矩阵或者通过分数协方差矩阵特征分解后与MUSIC结合的空间谱函数代替似然函数的计算是可行的。
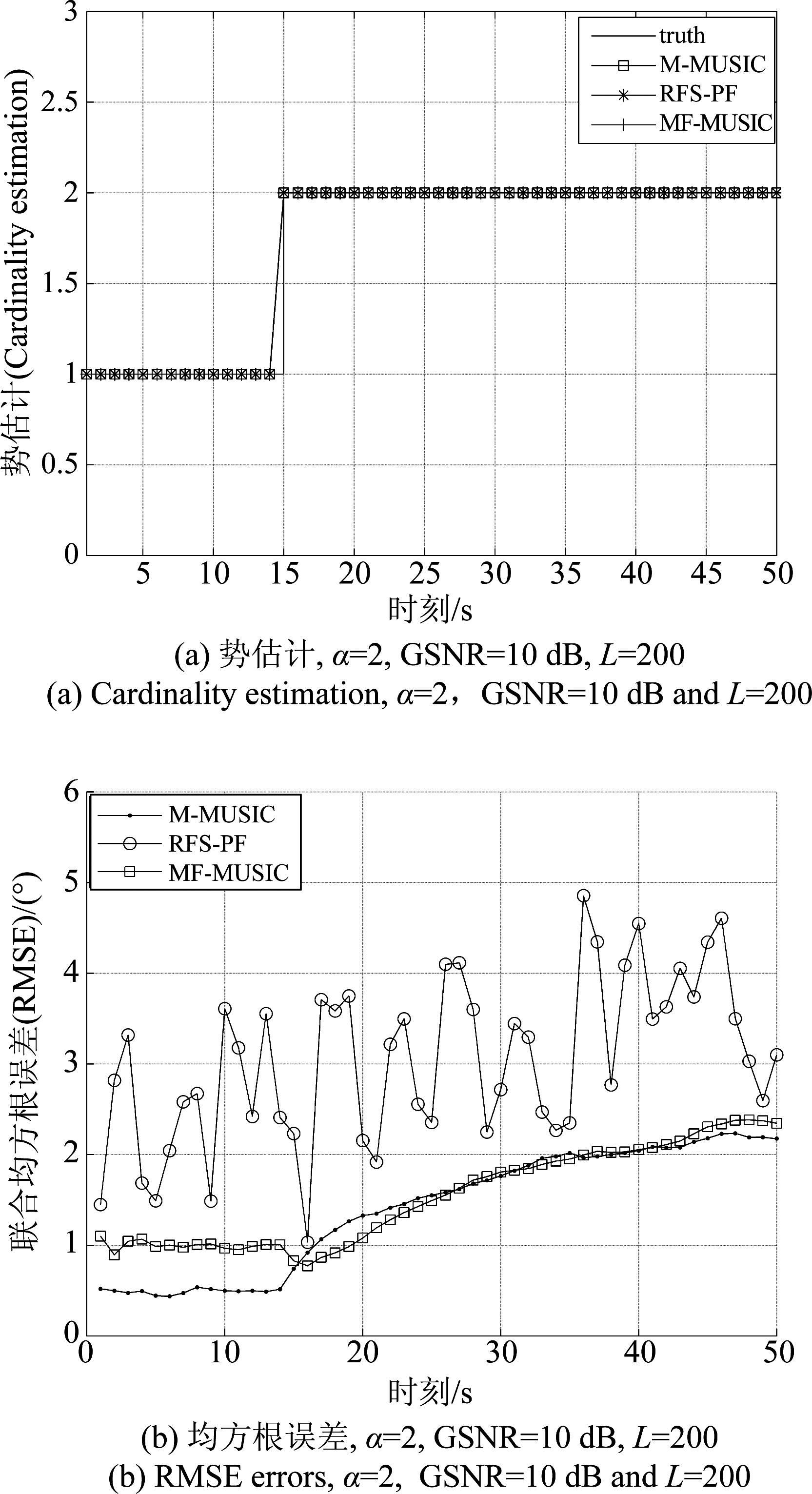
图3 GSNR=10 dB,α=2,势估计和联合均方根误差图
Fig.3 Cardinality estimation and RMSE, GSNR=10 dB and α=2
当α≠2时不是高斯噪声,图4中展示了特征指数1.1≤α≤1.9,GSNR=10 dB,L=200时M-MUSIC和MF-MUSIC算法的联合均方根误差和跟踪收敛成功概率图,其中误差门限ε=5°。从图4(a)可以看出两种算法的联合均方根误差图都随着特征指数α的增加呈现下降趋势,而当α>1.7时,由于此时α接近2,噪声的脉冲特性不会特别明显,因此两种方法的误差基本相同;从图4(b)可以看出两种算法的PROC都随着特征指数α的增加而上升,整体来看,MF-MUSIC算法跟踪收敛成功概率始终最高,且稳定性始终最高。当α>1.7时,两种方法的PROC基本都接近于1。
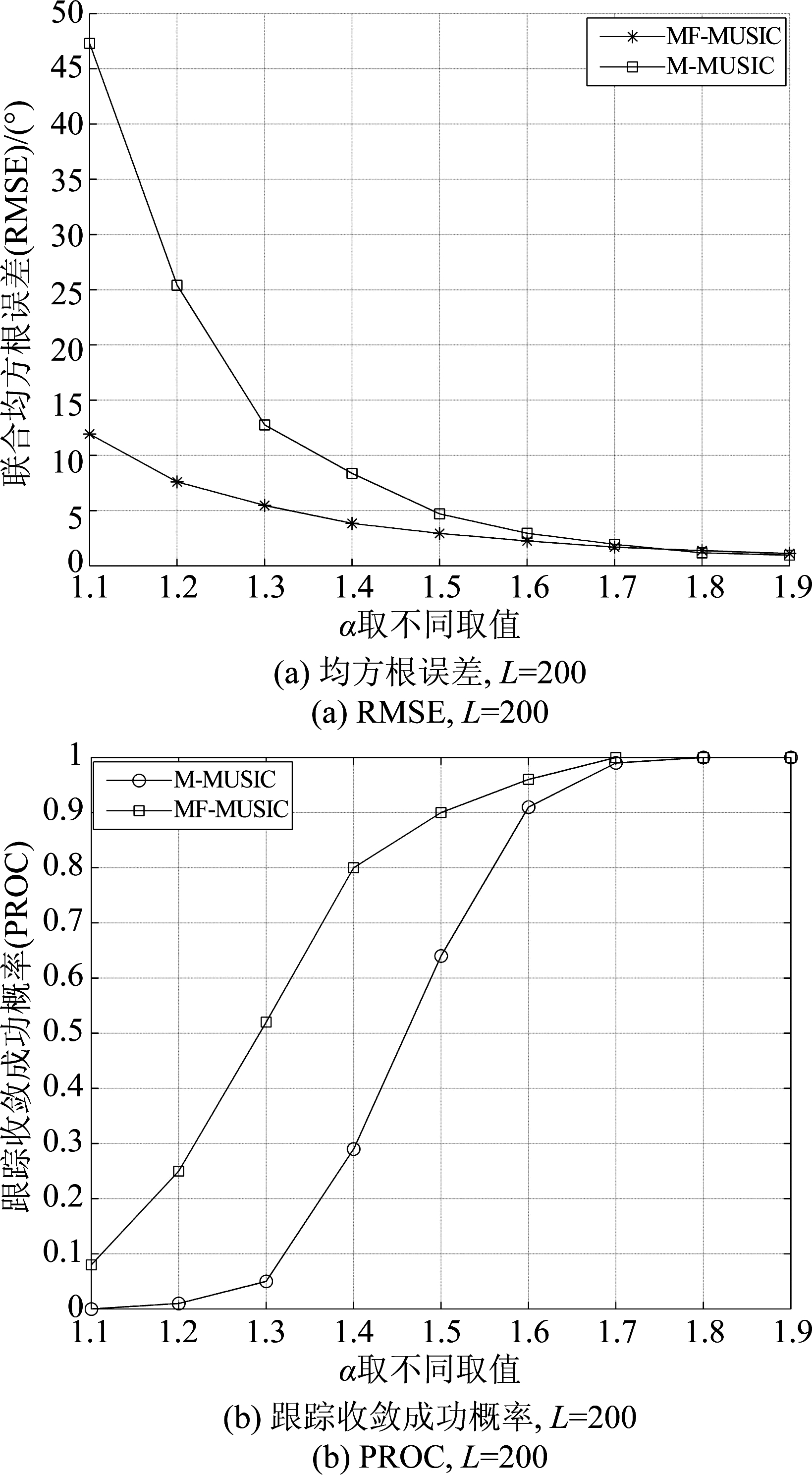
图4 α不同值时联合均方根误差和跟踪收敛成功概率图,GSNR=10 dB, L=200
Fig.4 RMSE and PROC of different α, GSNR=10 dB, L=200
在图5中展示了在具有特征指数α=1.2的α稳定分布噪声条件下,本文所提算法的单一蒙特卡罗实验跟踪轨迹图。可以看出即使在脉冲噪声环境下MF-MUSIC算法也能对目标的状态和数目进行有效跟踪,但M-MUSIC算法中却出现目标跟丢的情况,因此在脉冲噪声环境下M-MUSIC算法不能对目标精确跟踪,也说明了在脉冲噪声环境下直接用量测协方差矩阵进行似然函数的计算会使结果不准确。
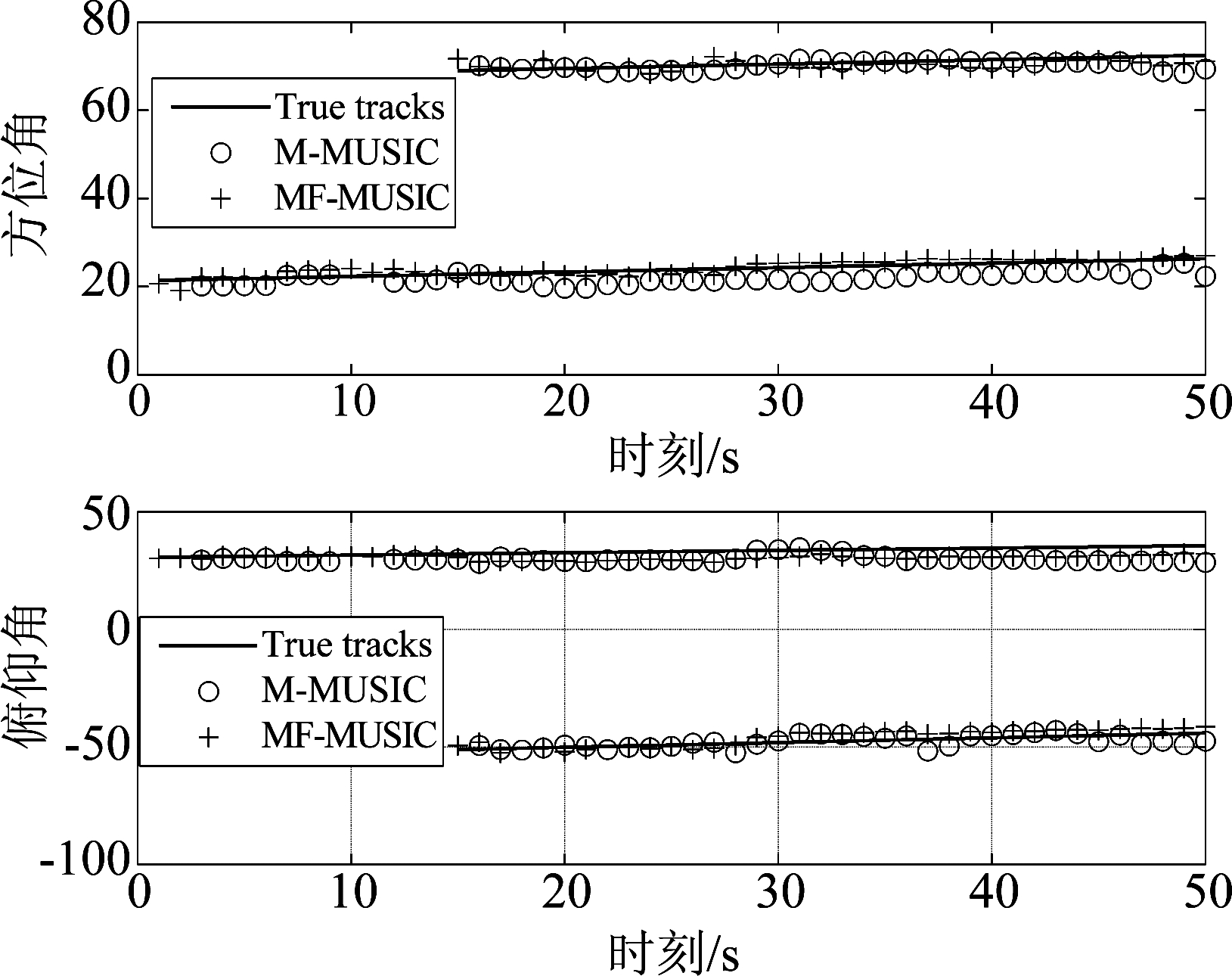
图5 声源状态估计,α=1.2, GSNR=10 dB, L=200
Fig.5 Estimation of sound source state, α=1.2, GSNR=10 dB, L=200
现考虑特征指数为α=1.2的α稳定分布噪声条件下,广义信噪比为10 dB时,用MF-MUSIC算法和M-MUSIC算法在100次MC时的均方根误差对比效果,如图6所示。可以看出MF-MUSIC算法在脉冲噪声环境下估计目标个数要比M-MUSIC算法更准确,RMSE更小。在第15个时刻由于第二个新目标的出现,势的个数会增加,会使均方根误差明显增大,但下一时刻均方根误差会迅速减小,之后均方根误差趋于平缓,从而也说明了多伯努利滤波器能迅速跟踪新生目标。
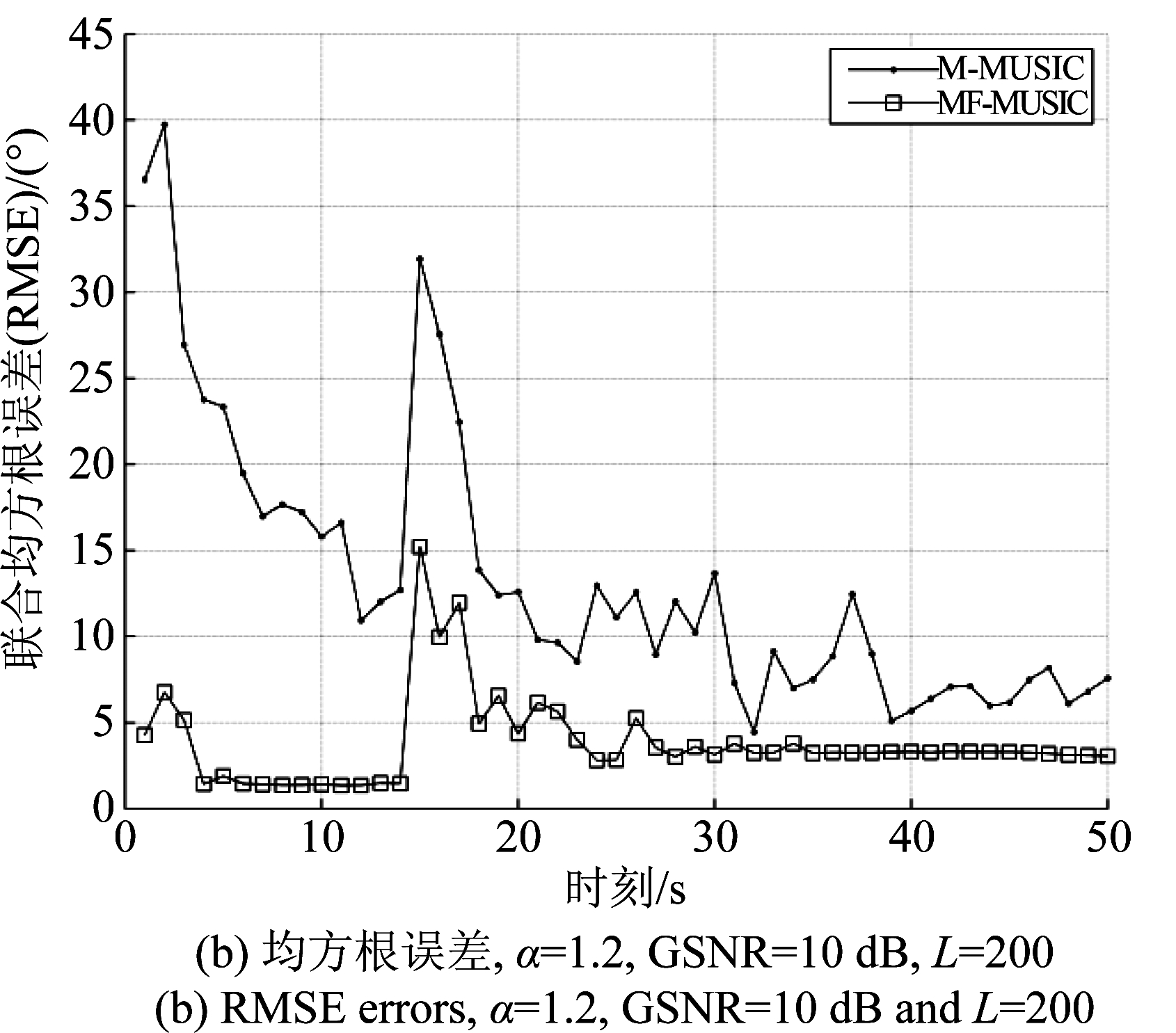
图6 GSNR=10 dB, α=1.2,势估计和联合均方根误差图
Fig.6 Cardinality estimation and RMSE, GSNR=10 dB and α=1.2
信噪比的大小反应目标受到噪声的影响,信噪比越小代表目标受到的噪声影响越大,由图7(a)可以看出在脉冲噪声环境下100次蒙特卡罗实验中MF-MUSIC算法的联合均方根误差明显比M-MUSIC算法小。随着信噪比的增加,MF-MUSIC算法均方根误差逐渐降低,当GSNR>10 dB时,MF-MUSIC算法的联合均方根误差在5°以内;从图7(b)可以看出,MF-MUSIC算法的跟踪收敛成功概率始终高于M-MUSIC算法,M-MUSIC算法在高信噪比时(10 dB以上)也没有完全跟踪上目标,如果放宽要求,可以增大ε的值来提高跟踪收敛成功概率。
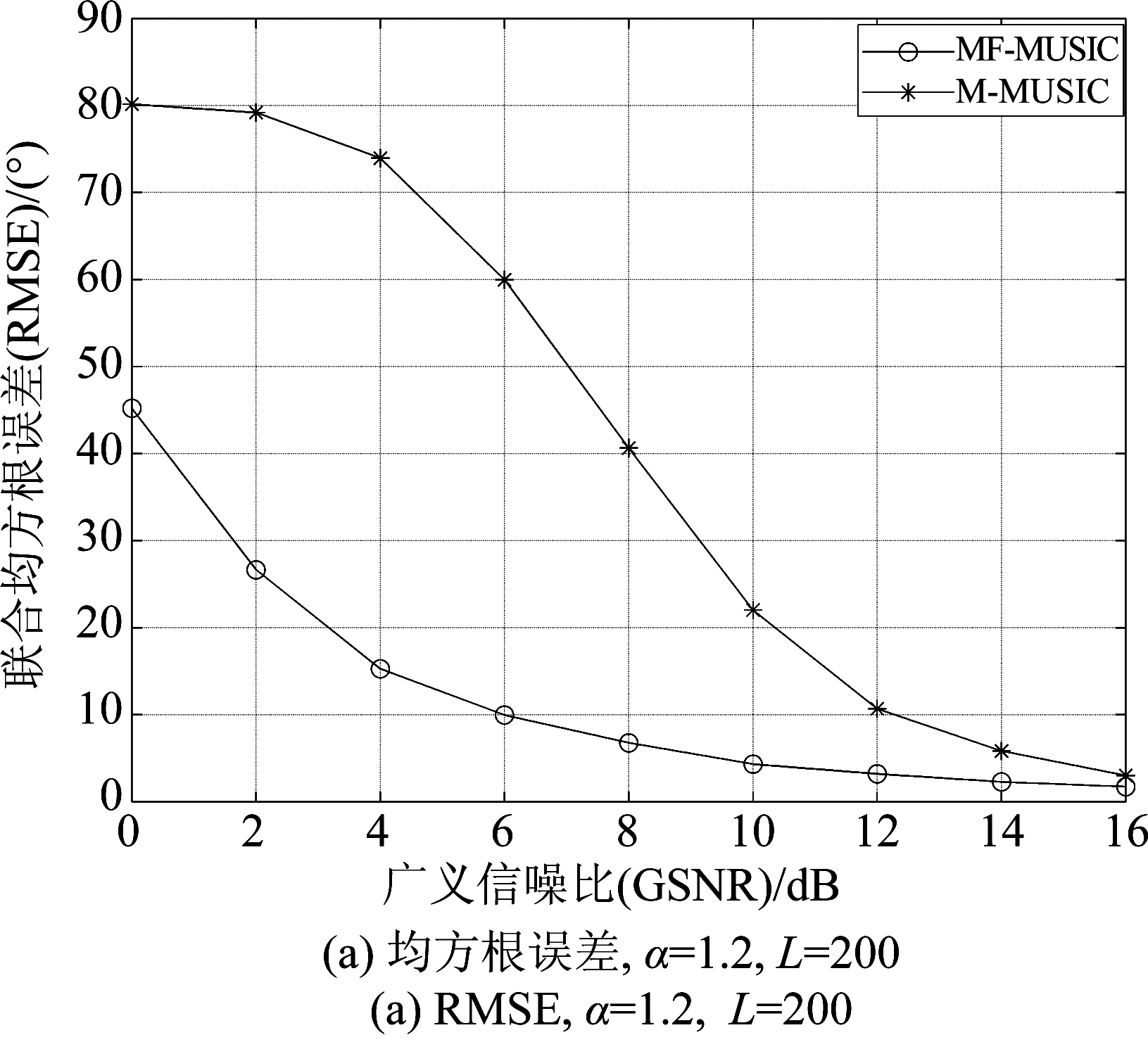
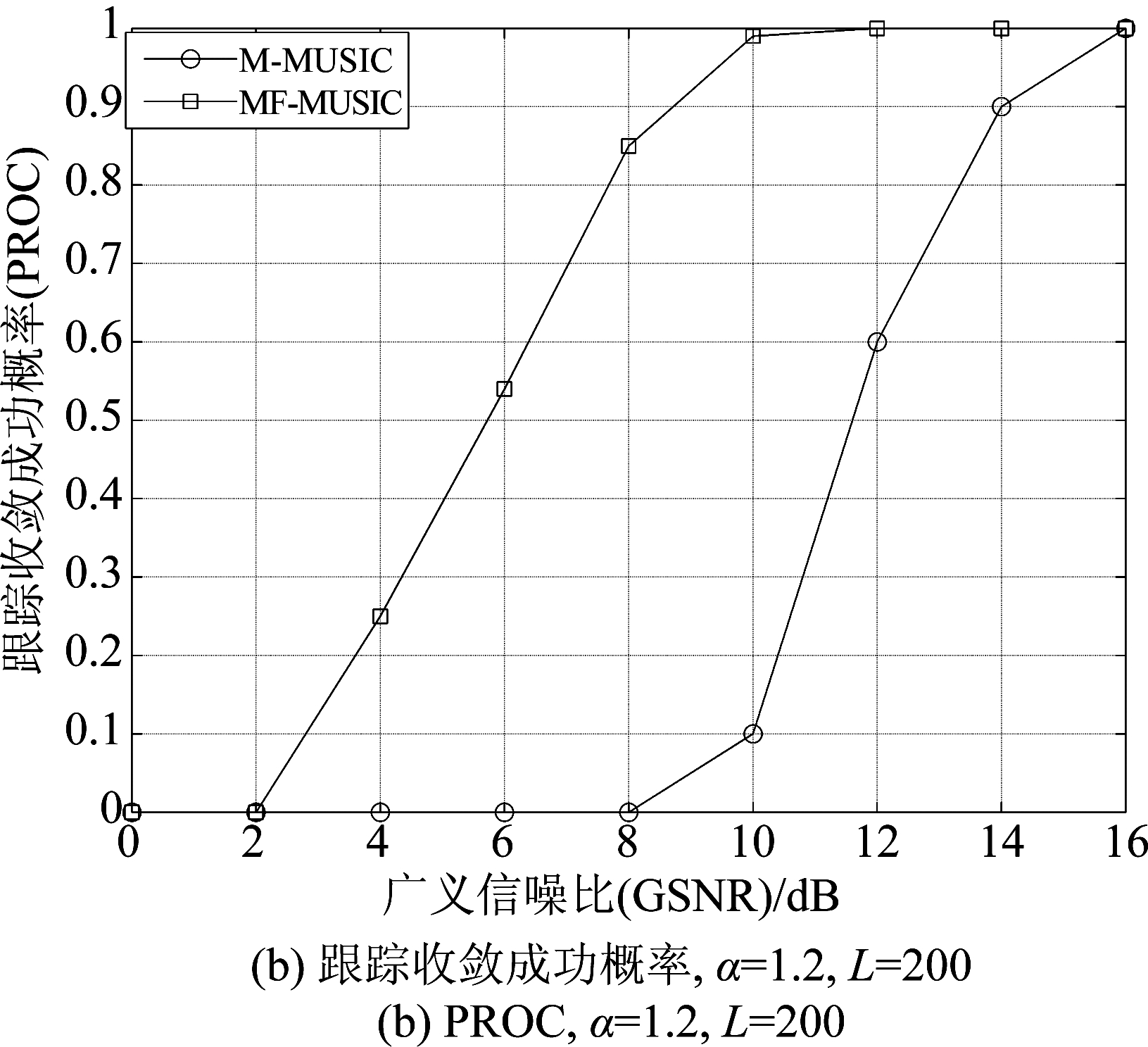
图7 不同广义信噪比的均方根误差和跟踪收敛成功概率效果图,α=1.2, L=200
Fig.7 RMSE and PROC in different GSNR, α=1.2, L=200
本文研究了一种用于脉冲噪声环境下单声矢量传感器下的多信源DOA跟踪问题,结合多伯努利随机有限集理论和粒子滤波算法思想,用分数低阶矩代替协方差矩阵,将MUSIC谱函数作为粒子的似然函数,提出了MF-MUSIC DOA跟踪算法。且计算粒子的似然函数时,进行适当指数加权,使粒子能够向后验概率密度函数的高斯然区域移动,提高粒子的权重使重采样更加有效。本文所提算法与M-MUSIC跟踪方法相比,可以在脉冲噪声环境下对当前声源有效跟踪。通过实验仿真,研究了该算法在不同信噪比下的跟踪性能,验证了所提算法的有效性。
[1] Zhong X, Premkumar A B. Particle Filtering Approaches for Multiple Acoustic Source Detection and 2-D Direction of Arrival Estimation Using a Single Acoustic Vector Sensor[J]. IEEE Transactions on Signal Processing, 2012, 60(9): 4719- 4733.
[2] Palanisamy P, Kalyanasundaram N, Swetha P M. Two-dimensional DOA estimation of coherent signals using acoustic vector sensor array[J]. Signal Processing, 2012, 92(1): 19-28.
[3] Zhang Xiaofei, Zhou Ming, Chen Han. Two-dimensional DOA estimation for acoustic vector-sensor array using a successive Music[J]. Multidimensional Systems and Signal Processing, 2014, 25(3): 583- 600.
[4] Yang B. Subspace tracking based on the projection approach and the recursive least squares method[C]∥IEEE International Conference on Acoustics, Speech & Signal Processing. IEEE Computer Society, 1993: 95-107.
[5] 昝孟恩, 周航, 韩丹, 等. 粒子滤波目标跟踪算法综述[J]. 计算机工程与应用, 2019, 55(5): 8-17.
Zan Mengen, Zhou Hang, Han Dan, et al. Survey of particle filter target tracking algorithms[J]. Computer Engineering and Applications, 2019, 55(5): 8-17.(in Chinese)
[6] 应文, 李冬海, 胡德秀, 等. 基于阵列单通道的机动目标DOA跟踪方法[J]. 信号处理, 2012, 28(4): 539-544.
Ying Wen, Li Donghai, Hu Dexiu, et al. DOA tracking of maneuvering target based on single channel array[J]. Signal Processing, 2012, 28(4): 539-544.(in Chinese)
[7] 宋德枢, 梁国龙, 王燕. 机动目标DOA跟踪粒子滤波算法[J]. 信号处理, 2014, 30(7): 861- 866.
Song Deshu, Liang Guolong, Wang Yan. Particle Filter Algorithm for DOA Tracking of Maneuvering Targets[J]. Journal of Signal Processing, 2014, 30(7): 861- 866.(in Chinese)
[8] 王芳, 李钢虎, 张雪, 等. 基于声矢量传感器的DOA跟踪[J]. 声学技术, 2018, 37(4): 176-179.
Wang Fang, Li Ganghu, Zhang Xue, et al. DOA tracking based on acoustic vector sensor[J]. Technical Acoustics, 2018, 37(4): 176-179.(in Chinese)
[9] Zhong X, Premkumar A B, Madhukumar A S. Particle Filtering and Posterior Cramér-Rao Bound for 2-D Direction of Arrival Tracking Using an Acoustic Vector Sensor[J]. IEEE Sensors Journal, 2012, 12(2): 363-377.
[10] 周彤, 宋立臣. 基于粒子滤波算法的方位跟踪方法研究[J]. 舰船科学技术, 2018, 40(11): 134-138.
Zhou Tong, Song Lichen. Research on DOA tracking technique based on particle filter algorithm[J]. Ship Science and Technology, 2018, 40(11): 134-138.(in Chinese)
[11] Shao M, Nikias C L. Signal processing with fractional lower order moments: stable processes and their applications[J]. IEEE Proceedings, 1993, 81(7): 986-1010.
[12] Zha D, Qiu T. Underwater sources location in non-Gaussian impulsive noise environments[J]. Digital Signal Processing, 2006, 16(2): 149-163.
[13] Zhong X, Premkumar A B, Madhukumar A S. Direction of arrival tracking in impulsive noise using particle filtering with fractional lower order moment likelihood[C]∥IEEE Communications & Signal Processing. IEEE, 2011: 978-981.
[14] Mahler R P S, Ebrary I. Statistical multisource-multitarget information fusion[M]. Artech House, Inc. 2007: 228-234.
[15] Vo B N, Singh S, Doucet A. Sequential Monte Carlo methods for multitarget filtering with random finite sets[J]. IEEE Transactions on Aerospace and Electronic Systems, 2005, 41(4): 1224-1245.
[16] Vo B T, Clark D, Vo B N, et al. Bernoulli Forward Backward Smoothing for Joint Target Detection and Tracking[J]. IEEE Transactions on Signal Processing, 2011, 59(9): 4473- 4477.
[17] Ristic B, Vo B T, Vo B N, et al. A Tutorial on Bernoulli Filters: Theory, Implementation and Applications[J]. IEEE Transactions on Signal Processing, 2013, 61(13): 3406-3430.
[18] Vo B T, Vo B N, Cantoni A. The cardinality balanced multi-target multi-bernoulli filter and its implementations[J]. IEEE Transactions on Signal Processing, 2009, 57(2): 409- 423.
[19] Choppala P B, Teal P D, Frean M R. Adapting the multi-Bernoulli filter to phased array observations using MUSIC as pseudo-likelihood[C]∥IEEE International Conference on Information Fusion. IEEE, 2014: 1- 6.
[20] Li S, He R, Lin B, et al. DOA Estimation Based on Sparse Representation of the Fractional Lower Order Statistics in Impulsive Noise[J]. IEEE CAA Journal of Automatica Sinica, 2018, 5(4): 98-106.
吴孙勇 男, 1981年生, 广西桂林人。桂林电子科技大学数学与计算科学学院, 教授, 博士, 主要研究方向为微弱目标检测与跟踪、阵列信号处理、粒子滤波等。
E-mail: wusunyong121991@163.com
赵 君 女, 1994年生, 河南驻马店人。桂林电子科技大学数学与计算科学学院, 硕士研究生, 主要研究方向为微弱目标检测与跟踪、阵列信号处理等。
E-mail: jun325709@163.com
董续东 男, 1995年生, 湖北武穴人。桂林电子科技大学数学与计算科学学院, 硕士研究生, 主要研究方向为微弱目标检测与跟踪、阵列信号处理等。
E-mail: 1498148536@qq.com
薛秋条 女, 1978年生, 河南三门峡人。桂林电子科技大学数学与计算科学学院, 副教授, 硕士, 主要研究方向为微弱目标检测与跟踪、阵列信号处理、粒子滤波等。
E-mail: 475561774@qq.com
廖桂生 男, 1963年生, 广西桂林人。广西信息科学实验中心, 西安电子科技大学雷达信号处理国家重点实验室, 桂林电子科技大学信息与通信工程学科“八桂学者”, 教授, 博士, 主要研究方向为自适应信号处理、阵列信号处理、信号检测与估计、智能天线信号处理技术等。
E-mail: gsliao@163.com