1 引言
由于水下无线光通信系统(UWOC)具有低蓝光/绿光窗口吸收、低延迟、宽带宽、高安全、低成本以及易于安装等优点,在商业海洋资源勘探,潜水员、无人水下航行器、潜艇、船舶、水下无线传感器网络之间的通信,以及水下军事应用等方面有着广泛的应用[1- 4]。另外,UWOC系统可以利用发光二极管(light emitting diode,LED)[5]和激光二极管(laser diode,LD)作为光源,可提供高达Gb/s量级的速率[6- 8]。这些独特的优点使UWOC技术成为比声波和射频波传输更适合于高速率水下传输的替代方案,近年来引起了人们的极大兴趣。
尽管UWOC系统有很多优点,但它也会受到一系列干扰的影响,如吸收、散射和湍流效应[1-2,9]。其中,由盐度、温度和密度等波动引起的海洋湍流是影响光束传播、引起强度波动(称为信号闪烁)的主要原因,会严重降低UWOC系统的性能。在过去几年中,研究人员提出了几种有效的技术,以减轻湍流效应对UWOC系统性能的恶化,例如空间分集传输[9-10]、信道编码技术[11]、光束整形[12-14]、调制技术[15-16]和孔径接收平均技术[2,15,17]。Yi X等人[18]观察了弱湍流信道UWOC系统采用平面波和球面波传输利用孔径平均技术时的系统性能。Muhsin C G等人[15]采用接收孔径平均技术来减轻海洋湍流的影响,并详细研究了在UWOC系统中水平通过强海洋湍流传播的球面波的闪烁系数和孔径平均因子。然而,据我们所知,在强海洋湍流条件下,还未有报道孔径平均对UWOC系统误码率性能的影响。另一方面,在UWOC系统中采用DPSK调制可以消除背景噪声[19],其BER性能也优于OOK调制下的BER[20]。本文在高斯光束通过强海湍流介质中传播的假设下,研究了孔径平均、DPSK调制、通信距离和各种海洋参数对UWOC系统的BER性能的影响。
2 理论分析
2.1 强海洋湍流下的系统模型
图1给出了DPSK调制的UWOC系统采用孔径接收的示意图。我们采用的映射方式是2进制的差分相移键控调制方式,如此就无需像常规PSK调制中需要知道绝对相位才能解调。假设信号被DPSK调制后驱动LED或LD发光,光束以高斯形式在强海洋湍流信道中传输,高斯光束的光源尺寸由αs定义,
式中,W0为1/e处的光斑半径。高斯光束到达接收端被一直径为D,焦距为FG的薄高斯透镜接收,在薄高斯透镜的焦点处放一个光电探测器(photo detector,PD)将光信号转成电信号后被DPSK解调成输出信号。
图1 DPSK调制的UWOC系统采用孔径接收示意图
Fig.1 A DPSK modulated UWOC system model with aperture averaging over oceanic turbulence channel
2.2 强海洋湍流下的闪烁系数
在强海洋湍流中传播的光波将经历辐照度波动(称为闪烁),利用修正的Rytov理论,闪烁系数
可以表示为[21]
(1)
式中,
和
分别是闪烁系数的大、小尺度部分。若采用高斯光束在强海洋湍流信道传输,到达接收端时被一孔径直径为D的透镜接收,其闪烁系数的大、小尺度部分可由下式得到
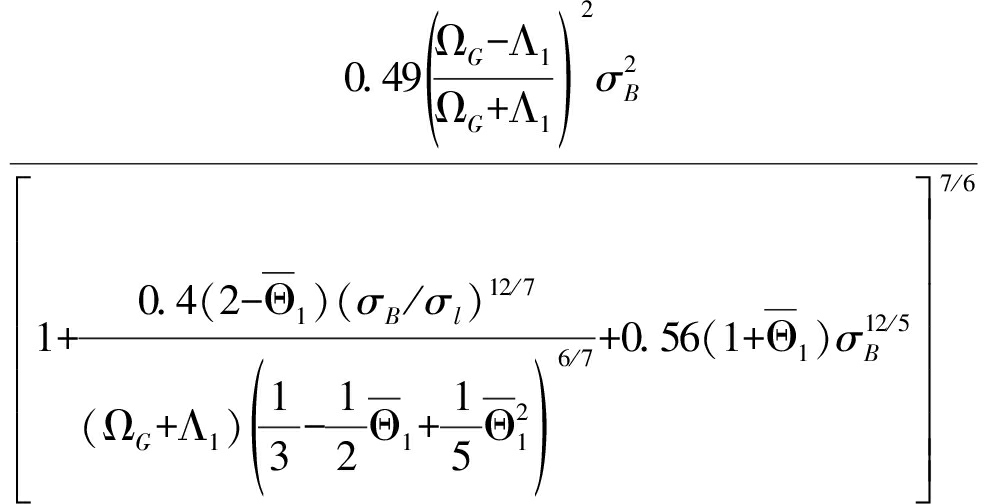
(2a)
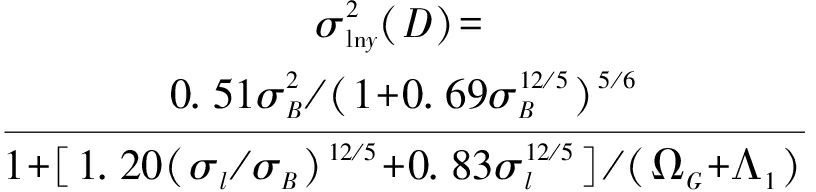
(2b)
式中,
l是光波长,L是通信距离,F0表示光束的曲率半径,
如下所示[22]:
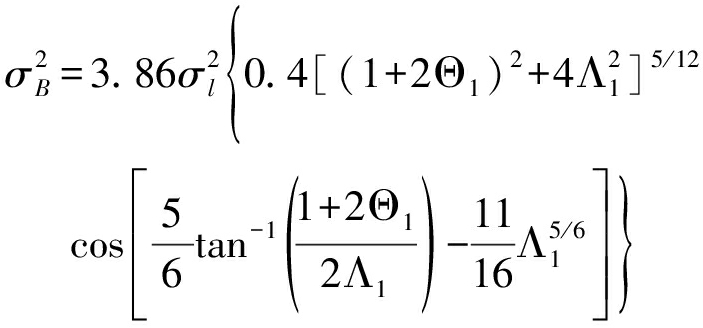
(3)
可由下式得到[23]
(4)
常数
为[23]
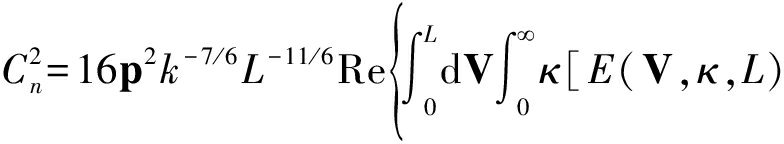
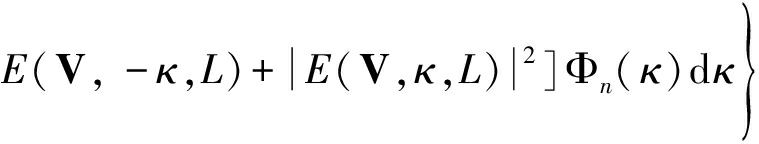
(5)
式中，
E(V,κ,L)=ik exp[-0.5iV(L-V)κ2/(kL)]
(6)
式中,V是光束传输的位置距离发送端的距离,取值范围为[0,L],κ是空间频率幅度,Φn(κ)是功率谱,在各向同性均匀湍流的海洋中,Φn(κ)由下式给出[23]
Φn(κ)=0.388×10-8ε-1/3κ-11/3(1+2.35κ2/3ν1/2ε-1/6)
ω-2χT(ω2e-ATδ+e-ASδ-2ωe-ATSδ)
(7)
式中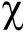
T是均方温度耗散率,其取值范围可以从10-4 K2/s到10-10 K2/s;ε是单位质量液体中的湍流动能耗散率,其数值可从10-1 m2/s3变化到10-10 m2/s3;ν是动力粘度;ω是温度和盐度波动对海洋湍流贡献的比值,为无量纲参数,ω=-5表示海洋湍流完全由温度引起,ω=0表示海洋湍流完全由盐度引起;ATS=9.41×10-3,AS=1.9×10-4,AT=1.863×10-2,δ=8.28κ4/3uε-1/3+12.978κ2u3/2ε-1/2。
需要注意的是,若D=0,则表示图1中的UWOC系统直接采用点接收器接收。当采用平面波传输时,此时式(2)简化成
(8a)
(8b)
2.3 强海洋湍流信道模型
光波在强海洋湍流中传输时的功率密度函数(power density function,PDF)可以假设成Gamma-Gamma分布,如下所示[15,20]
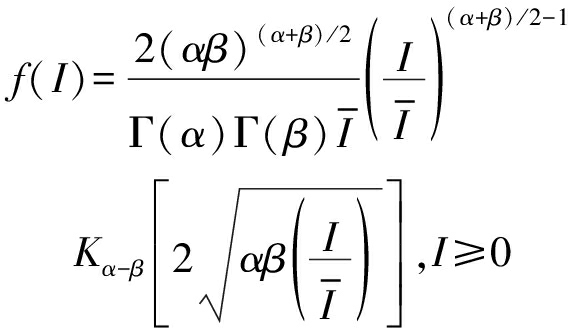
(9)
式中,
是光束在海洋中的平均光强,Km(x)是第二类修正的贝塞尔函数,Γ(x)是Gamma 函数,α和β是描述光波闪烁的外尺度和内尺度参量,其大小与闪烁系数有关[21]
(10a)
(10b)
2.4 DPSK调制的UWOC系统的BER
若UWOC系统采用DPSK调制,在强湍流信道下传输时的BER可表示成[20]
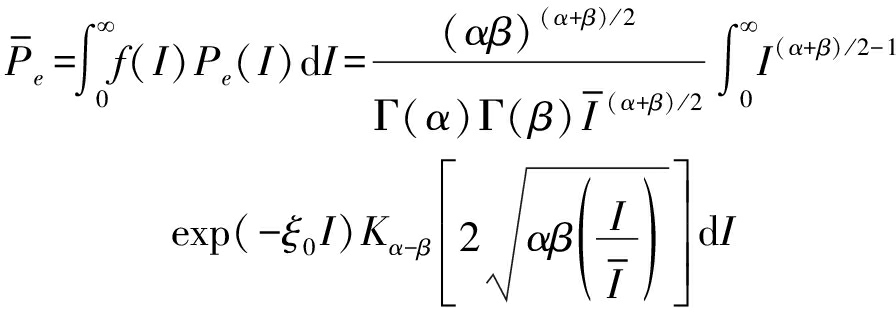
(11)
式中,ξ0=ηATb/hf,η是光电探测器的量子效率,A是接收器的接收面积,Tb是符号宽度,h是普朗克常数, f是频率。
采用如下恒等式[24]
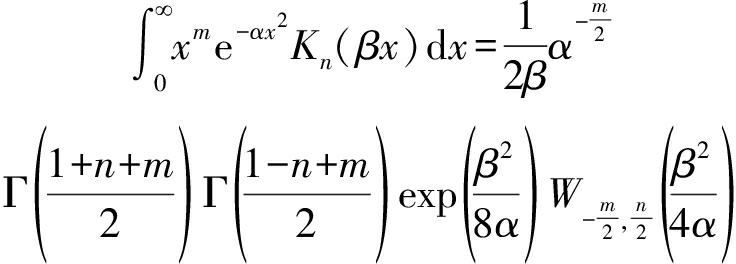
(12)
式中,
是Whittaker函数。此时,
可表示成
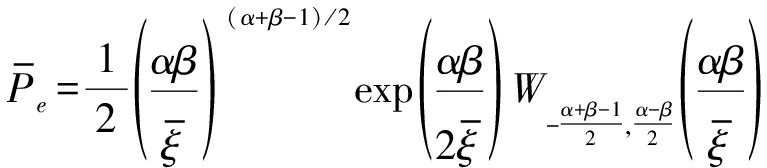
(13)
式中,
是平均信噪比(signal-to-noise ratio,SNR)。进一步地,如果α和β是非整数,利用Kummer 超几何函数[25]将Whittaker函数表示成 Whittaker M函数,可得到的另一种表达形式
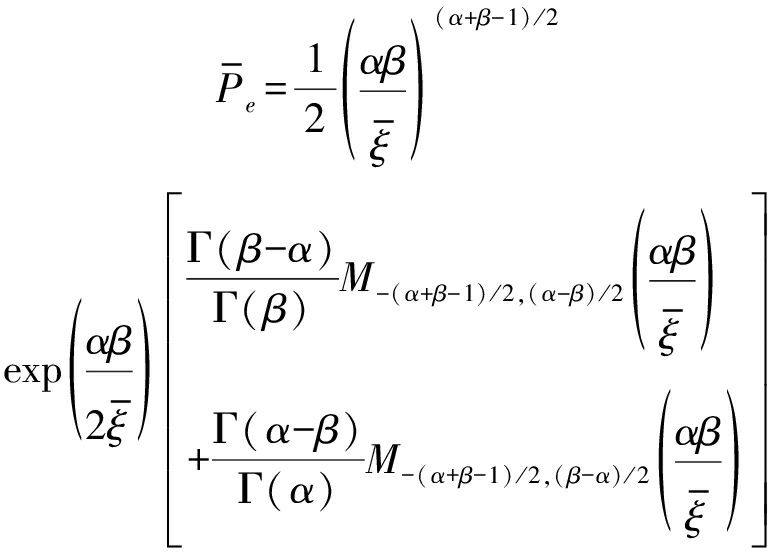
(14)
式中,M(x)是Whittaker M函数。
3 数值计算与讨论
在本节中,将观察DPSK调制的UWOC系统采用孔径接收时的系统性能,并讨论系统调制方式、孔径直径、传输距离和四种海洋湍流参数对BER性能的影响。
表1 数值仿真所用的参数
Tab.1 Parameters used for simulation
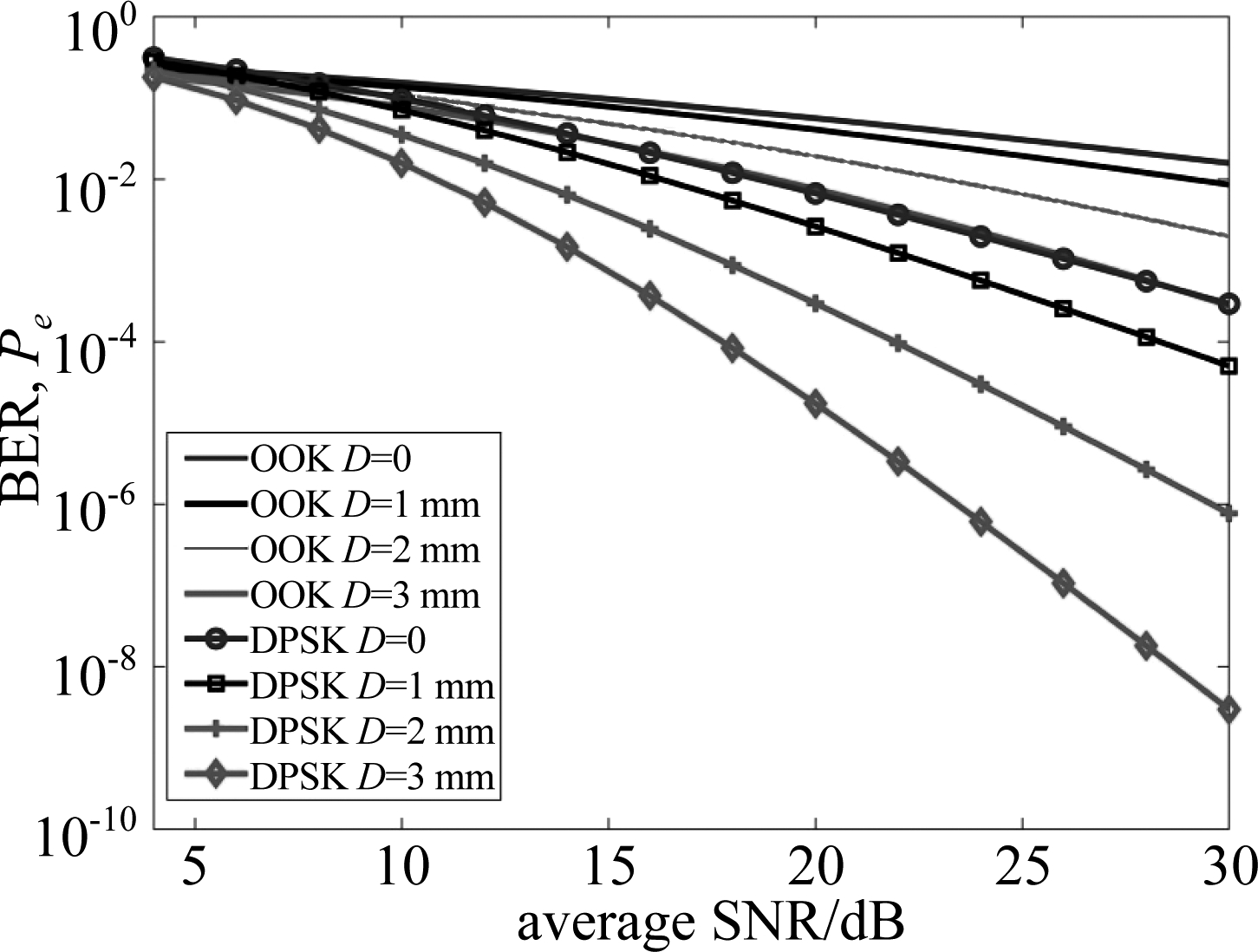
图2 DPSK调制和OOK调制的UWOC系统采用不同孔径直径D接收的BER性能
Fig.2 BER versus average SNR with OOK and DPSK modulated spherical wave for different aperture diameters D
图2观察了DPSK调制和OOK调制的UWOC系统采用不同孔径直径D接收在强湍流信道中传输的高斯光束的BER性能。计算中采用的参数见表1所示,表中F0=
表示准直光束。采用这些取值可得到Rytov方差
这对应于强海洋湍流[17]。从图2中可以观察到在同样的D和SNR下,采用DPSK调制有利于提高UWOC系统的性能。同样值得注意的是,采用孔径接收技术有利于系统性能提高,在同样的调制方式和SNR下,D最大时对应的误码率最低。这是由于采用孔径接收可消除湍流引起的畸变波前[2],从而提高了接收到的光功率,改善了系统的误码率。另外,需要说明的是,发现当D=4 mm时,在SNR比较低时(小于8 dB)时,得到的误码率将变得不正常,当SNR较大时,误码率随SNR的变化趋势将恢复正常,且D越大,BER性能也将越好。因此,我们得到孔径直径D对BER性能的改善的上限与SNR的大小有关,如果系统中的SNR较大,D可以设置得大些,但如果是在比较小的SNR环境下,D不能取得太大。其原因是,当SNR比较低时,信号受到的噪声比较大,若孔径设置成太大,将接收到更多的噪声,而湍流引起的信号波动相对接收到的噪声可以忽略,从而引起误码率的不正常变化;当SNR较大时,在接收端受到的影响主要是湍流引起的信号波动,此时采用较大直径的孔径接收来平均信号波动有利于改善BER性能。
为了深入了解海洋湍流参数对BER性能的影响,图3～图6绘制了BER随不同海洋参数,即湍流动能耗散率ε、均方温度耗散率χT、动力粘度ν和温度和盐度波动对海洋湍流贡献的比值ω的变化曲线。计算中所用的参数除了每一幅图中相应的海洋参数有变化外,其余参数同表1所示,信噪比设为20 dB。图3～图6进一步证明了,在相同的湍流环境下,孔径直径D即使只有一点点增加,BER性能都能有很明显的改善。另外,从图3中可以观察到,在同样的D下,随着ε的增加,BER数值先增加后减小,相较于D,ε对BER的影响要小得多。图4说明了χT越大,BER性能越差,这是因为χT越高对应较强的湍流,系统性能就会变差[23]。图5中,随着ν的增加,BER起初变化不大,在ν>10-4 m2/s,BER数值开始减小,即系统性能开始变好。图6说明了随着ω的增大,BER数值增加,意味着UWOC系统在盐度波动为主引起的湍流海洋中传输性能要差得多。
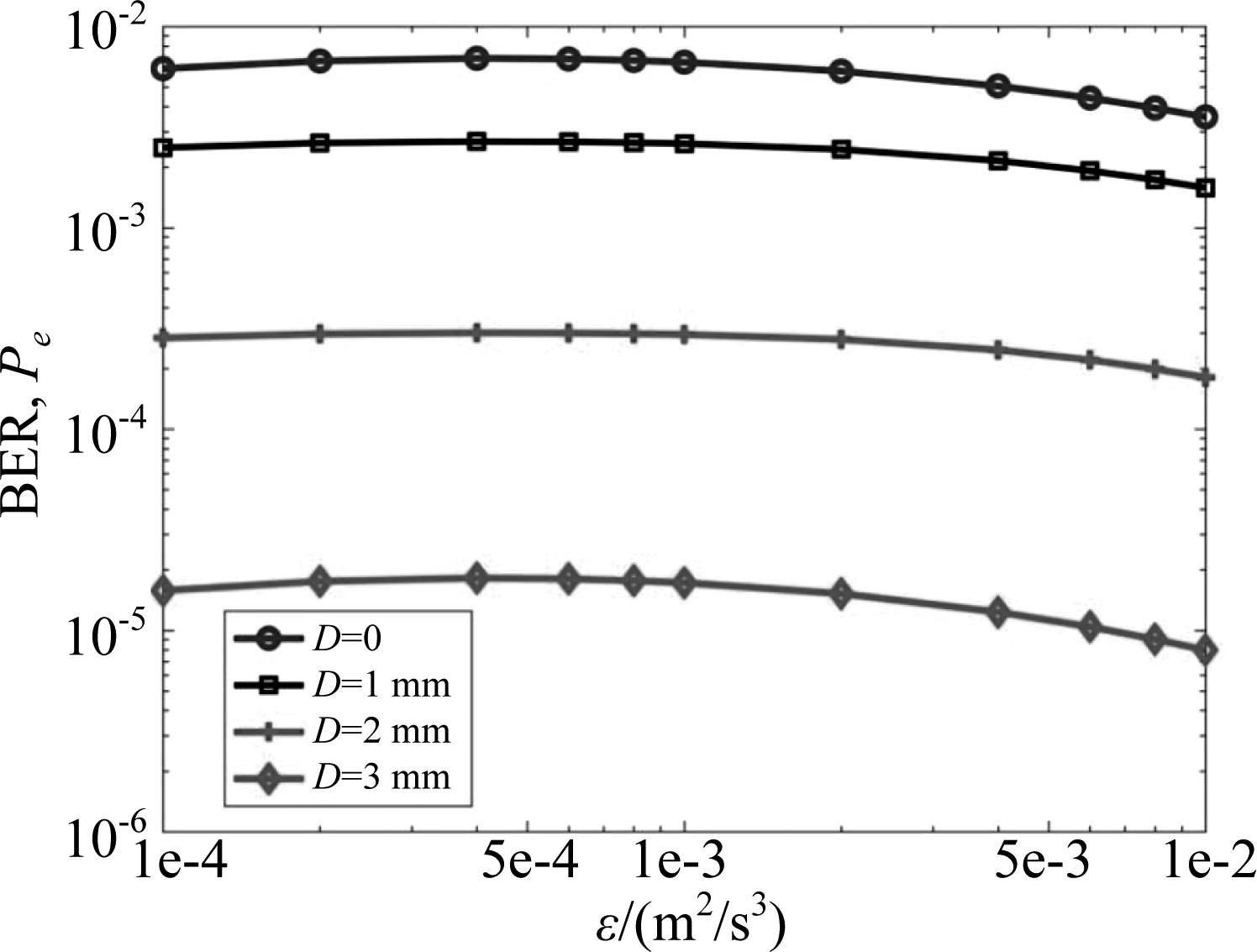
图3 不同孔径直径D下的BER随湍流动能耗散率ε的变化曲线
Fig.3 BER versus the rate of dissipation of kinetic energy per unit mass of fluid ε for different receiver aperture diameters D
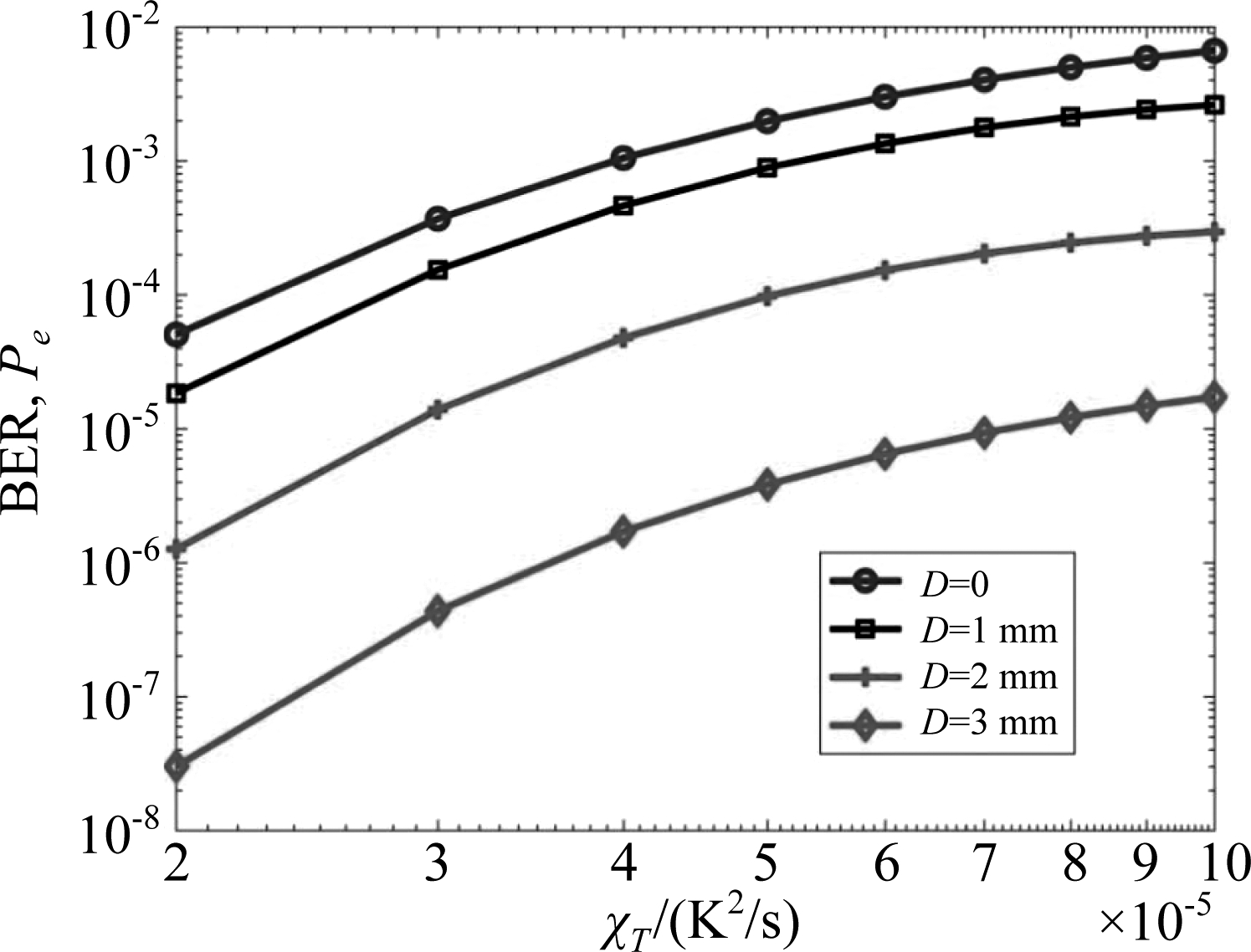
图4 不同孔径直径D下的BER随均方温度耗散率χT的变化曲线
Fig.4 BER versus the rate of dissipation of mean-squared temperature χT for different receiver aperture diameters D
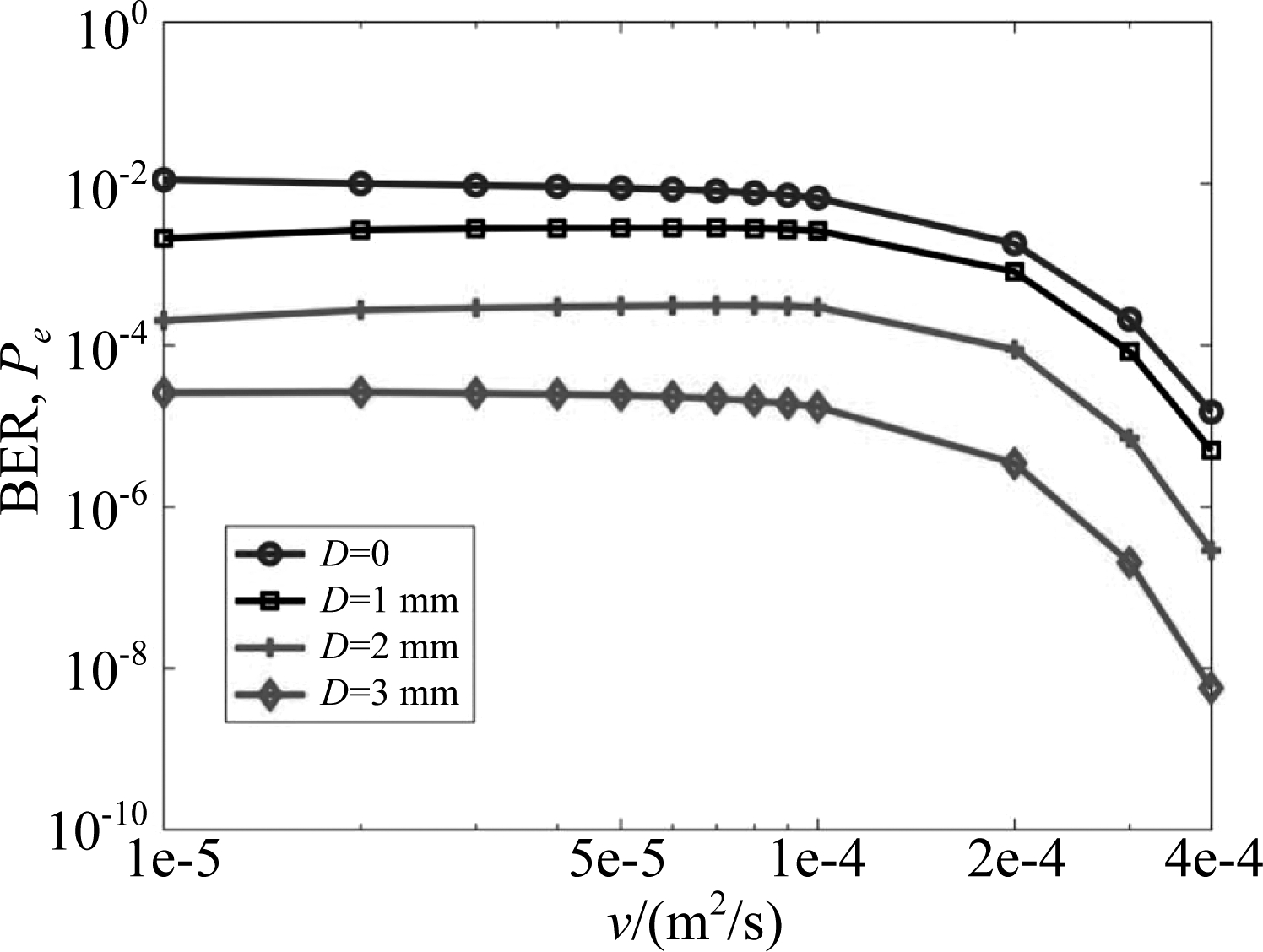
图5 不同孔径直径D下的BER随动力粘度ν的变化曲线
Fig.5 BER versus the rate of the kinetic viscosity ν for different receiver aperture diameters D
图6 不同孔径直径D下的BER随温度和盐度波动对海洋湍流贡献的比值ω的变化曲线
Fig.6 BER versus the ratio of temperature to salinity contributions to the refractive index spectrum ω for different receiver aperture diameters D
图7给出了UWOC系统传输距离对BER性能的影响,可以看出,L越大,BER性能越差。这是因为,传输距离越远,系统受到的湍流干扰越大,系统性能也就越差。
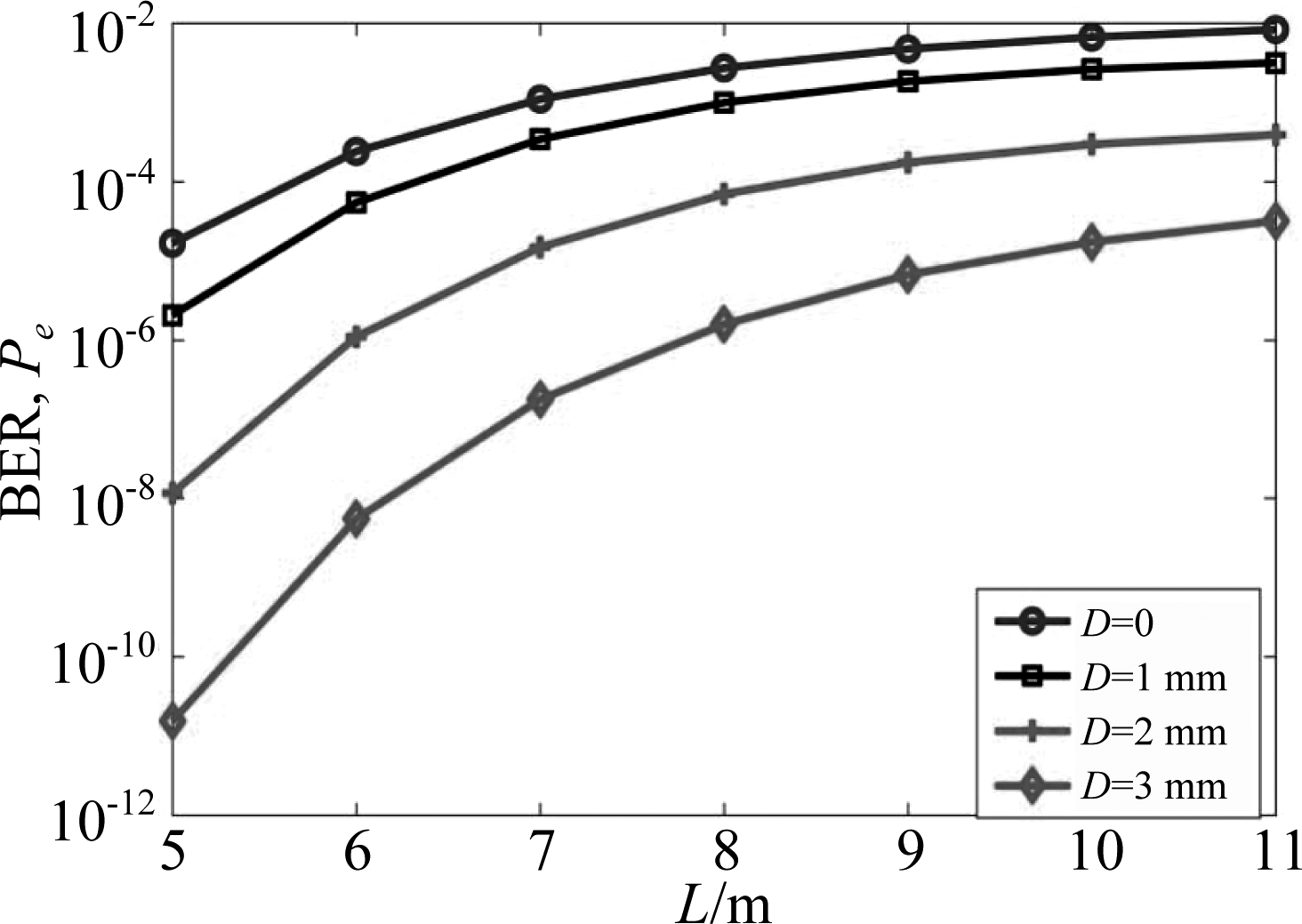
图7 不同孔径直径D下的BER随传输距离L的变化曲线
Fig.7 BER versus the transmission distance L for different receiver aperture diameters D
4 结论
基于Whittaker 和Kummer超几何函数,在假设强湍流信道为Gamma-Gamma分布的前提下,数值研究了调制方式、孔径接收直径、传输距离和四种海洋参数对UWOC系统BER性能的影响规律。结果表明,不管采用何种调制方式,在同样的海洋湍流条件下,孔径接收是一种非常有效的抑制湍流干扰技术,而且孔径直径D越大,BER性能越好。在强湍流信道中,对于同样的D接收,DPSK调制更有利于提高BER性能。另外,为了获得较高的BER性能,UWOC应该选取均方温度耗散率χT和温度和盐度波动对海洋湍流贡献的比值ω较小、动力粘度ν较大,湍流动能耗散率ε较大或较小的短距离海洋环境时进行通信。
[1] Kaushal H, Kaddoum G. Underwater optical wireless communication[J]. IEEE Access, 2016, 4: 1518-1547.
[2] Gökçe M C, Baykal Y. Aperture averaging and BER for Gaussian beam in underwater oceanic turbulence[J]. Optics Communications, 2018, 410: 830- 835.
[3] 李鑫滨, 黄志鹏, 韩松, 等. 基于博弈论的分布式水声通信网络功率分配算法[J]. 信号处理, 2017, 33(5): 758-765.
Li Xinbin, Huang Zhipeng, Han Song, et al. Power allocation algorithm for distributed underwater acoustic communication network based on game theory[J]. Journal of Signal Processing, 2017, 33(5): 758-765.(in Chinese)
[4] 傅玉青, 黄诚惕, 杜永兆. 强海洋湍流水下光通信系统误码率研究[J]. 信号处理, 2019, 35(5): 897-903.
Fu Yuqing, Huang Chengti, Du Yongzhao. Bit error rate analysis for underwater optical communication system through strong oceanic turbulence[J]. Journal of Signal Processing, 2019, 35(5): 897-903.(in Chinese)
[5] Xu J, Kong M, Lin A, et al. OFDM-based broadband underwater wireless optical communication system using a compact blue LED[J]. Optics Communications, 2016, 369: 100-105.
[6] Wu T C, Chi Y C, Wang H Y, et al. Blue laser diode enables underwater communication at 12.4 Gbps[J]. Scientific Reports, 2017, 7: 40480.
[7] Li C Y, Lu H H, Tsai W S, et al. A 5 m/25 Gbps underwater wireless optical communication system[J]. IEEE Photonics Journal, 2018, 10(3): 7904909.
[8] Fei C, Zhang G, Zhang J, et al. Demonstration of 15-meter 7.33-Gbps 450-nm underwater wireless optical discrete multi-tone transmission using post nonlinear equalization[J]. Journal of Lightwave Technology, 2018, 36: 728-734.
[9] Jamali M V, Salehi J A, Akhoundi F. Performance studies of underwater wireless optical communication systems with spatial diversity: MIMO scheme[J]. IEEE Transactions on Communications, 2017, 65(3): 1176-1192.
[10] Liu W, Xu Z, Yang L. SIMO detection schemes for underwater optical wireless communication under turbulence[J]. Photonics Research, 2015, 3(3): 48-53.
[11] Xu F, Khalighi A, Patrice Caussé, et al. Channel coding and time-diversity for optical wireless links[J]. Optics Express, 2009, 17(2): 872- 887.
[12] Baykal Y. Scintillation index of higher order mode laser beams in strong turbulence[J]. Optics Communications, 2017, 386: 53-56.
[13] Ye F, Zhang J, Xie J, et al. Propagation properties of the rotating elliptical chirped Gaussian vortex beam in the oceanic turbulence[J]. Optics Communications, 2018, 426: 456- 462.
[14] Ata Y, Baykal Y. Effect of anisotropy on bit error rate for an asymmetrical Gaussian beam in a turbulent ocean[J]. Applied Optics, 2018, 57(9): 2258-2262.
[15] Gökçe M C, Baykal Y, Ata Y. Performance analysis of M-ary pulse position modulation in strong oceanic turbulence[J]. Optics Communications, 2018, 427: 573-577.
[16] Wang W, Wang P, Cao T, et al. Performance investigation of underwater wireless optical communication system using M-ary OAMSK modulation over oceanic turbulence[J]. IEEE Photonics Journal, 2017, 9(5): 7905315.
[17] Gökçe M C, Baykal Y. Aperture averaging in strong oceanic turbulence[J]. Optics Communications, 2018, 413: 196-199.
[18] Yi X, Li Z, Liu Z. Underwater optical communication performance for laser beam propagation through weak oceanic turbulence[J]. Applied Optics, 2015, 54(6): 1273-1278.
[19] Sandalidis H G, Tsiftsis T A, Karagiannidis G K. Optical Wireless Communications With Heterodyne Detection Over Turbulence Channels With Pointing Errors[J]. Journal of Lightwave Technology, 2009, 27(20): 4440- 4445.
[20] Fu Y, Du Y. Performance of heterodyne differential phase-shift-keying underwater wireless optical communication systems in gamma-gamma-distributed turbulence[J]. Applied Optics, 2018, 57(9): 2057-2063.
[21] Andrews L C, Phillips R L, Hopen C Y, et al. Theory of optical scintillation[J]. Journal of the Optical Society of America A, 1999, 16(6): 1417-1429.
[22] Andrews L C, Phillips R L. Laser beam propagation through random media, Second Edition[M]. SPIE PRESS, Bellingham, Washington, 2005.
[23] Baykal Y. Scintillation index in strong oceanic turbulence[J]. Optics Communications, 2016, 375: 15-18.
[24] Gradshteyn I S, Ryzhik I M. In table of integrals, series, and products[M]. Academic Press, 1980.
[25] Abramowitz M, Stegun I. Handbook of mathematical functions[M]. Dover Publications, New York, 1972.
