1 引言
恒虚警(CFAR)检测是声纳检测中常用的处理方式[1-2],其基本原理是利用参考单元对背景功率水平来进行估计,使检测器保持恒定的虚警概率[3- 4],参考单元通常从检测单元两侧选取。早期人们关注的是高斯背景下的CFAR检测问题,提出了一系列具有CFAR特性的检测器[5-7]。其中文献[5]提出了单元平均(CA) CFAR检测器,在均匀高斯背景下具有准最优的检测性能,但在多目标干扰情况下性能严重下降;文献[6]提出了有序统计(OS)CFAR检测器,有效解决了该问题,但其数据排序处理耗时较长。进一步,文献[7]提出了有序统计选小(OSSO)和有序统计选大(OSGO)两种CFAR检测器,其数据排序时间仅为OS-CFAR的二分之一,且分别改善了有序统计类CFAR检测器在多目标干扰情况和杂波边缘环境下的性能[8]。
随着主动声纳分辨率的提高,混响幅度逐渐偏离高斯分布,对于非高斯分布混响统计模型的建立,一种方法采用复合高斯模型对实测数据进行拟合,该模型将混响建模为一个快变复高斯过程和一个与其独立的慢变调制过程的乘积,前者表示短相关时间的快起伏分量,后者表示待测单元内的混响功率水平,且呈现非高斯分布特征[9]。复合高斯模型中通常采用渐进最大似然估计的协方差矩阵进行目标检测,但其性能受训练样本数影响较大。为改善这一问题,文献[10]提出了基于知识辅助的贝叶斯Rao检测器, 当训练样本较少时,检测性能优于传统的非贝叶斯检测器。另一种方法采用非高斯分布对混响包络或幅度进行拟合并利用CFAR检测器进行目标检测。文献[11]证明Pareto分布是一种能够有效描述高分辨率声纳混响幅度的非高斯分布模型,该模型对实测数据的拟合效果优于Lognormal、Weibull以及K分布。近年来,该分布背景下的CFAR检测开始引起人们的重视。文献[12]证明任何分布的尾部都可以被建模为广义Pareto分布,但是文中利用极值理论所得到的检测器阈值与Pareto参数有关。文献[13]研究了Pareto分布下相干雷达检测,结果表明相干检测方案一般不具有CFAR属性。为了解决这一问题,文献[14]利用Pareto分布与指数分布关系证明了尺度参数已知情况下,OS-CFAR和CA-CFAR具有恒虚警的特性,并研究了两种检测器在均匀背景和多目标干扰情况下的检测性能;文献[15]深入讨论了OS-CFAR在Pareto杂波边缘环境下的性能。两篇文章均得到了和高斯背景相同的结论,即CA-CFAR对抗多目标干扰能力差,而OS-CFAR在杂波边缘的虚警控制能力有待提高,针对以上问题,本文研究了OSSO-CFAR和OSGO-CFAR在Pareto混响背景下的性能,证明了在尺度参数已知情况下,两种检测器均对形状参数具有恒虚警的特性。利用蒙特卡洛仿真,分析了两种检测器的性能,结果表明它们能够有效克服OS-CFAR和CA-CFAR的缺点,提高Pareto混响背景下的CFAR检测性能。
2 Pareto分布
假设随机变量X服从Pareto分布,其概率密度函数(PDF)为[14]:
(1)
对应的概率分布函数(CDF)为[14]:
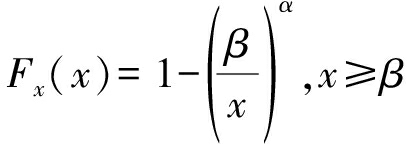
(2)
其中:α为形状参数,决定分布的拖尾情况,进而决定分布的整体形状; β为尺度参数,决定分布的起始位置,对于整体形状影响较小。鉴于文献[16]利用线性回归方法来估计数据的Pareto参数,在样本数量较少时可以精确地估计尺度参数β。因此,本文假定β为已知参数,α为未知的固定常数。
为了方便后续推导,给出Pareto分布与指数分布的关系如下[14]:
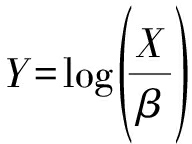
(3)
其中,Y为服从参数为α的指数分布,其PDF为[13]:
fY(y)=αe-αy
(4)
3 OSSO-CFAR和OSGO-CFAR
OSSO-CFAR和OSGO-CFAR[7]的原理框图如图1所示。其中,xCUT为检测单元,对应的随机变量为XCUT;左右分别为前、后沿参考滑窗,均包含n个参考单元,对应的样本集合分别为{x1,x2,...,xn}和{xn+1,xn+2,...,x2n}。将前、后沿滑窗样本分别按幅值从小到大进行排序,得到序列{x(1),x(2),...,x(n)}和{x(n+1),x(n+2),...,x(2n)},再分别选取序列中第k个样本得到局部估计值z1和z2,它们对应的随机变量是Z1和Z2。对于OSSO-CFAR,取z1和z2中的较小值作为混响功率水平估计 z,而对于OSGO-CFAR,z是 z1和 z2中的较大者。假设尺度参数β已知,利用z值及给定虚警概率所对应的检测阈值t可完成判决,具体判决准则在3.1和3.2节给出。
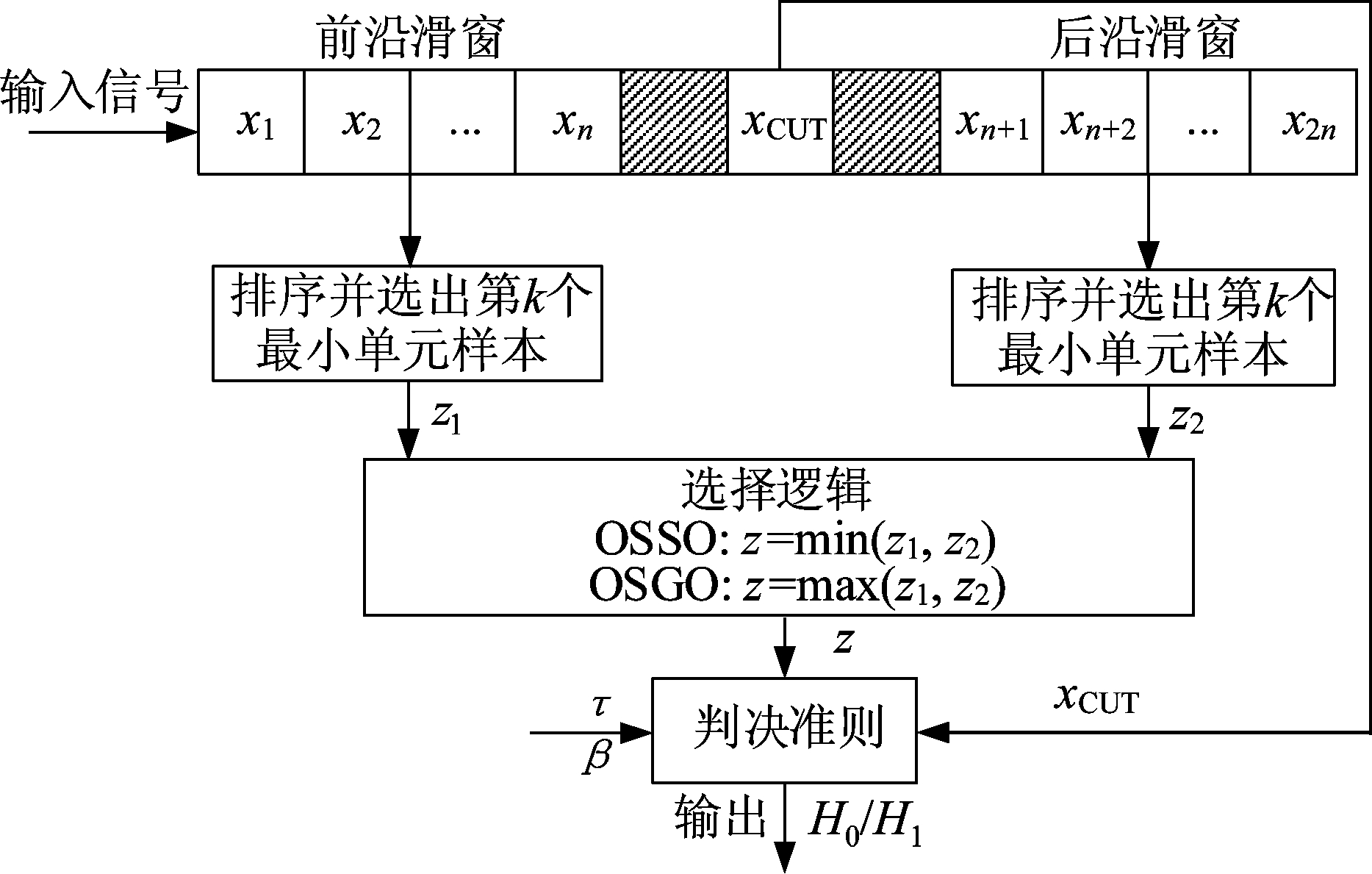
图1 OSSO-CFAR和OSGO-CFAR原理框图
Fig.1 Block diagram of OSSO-CFAR and OSGO-CFAR detector
3.1 OSSO-CFAR
由文献[14]可知,Pareto背景下OS-CFAR的判决准则为:
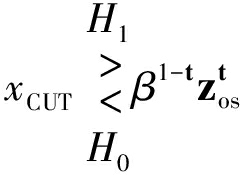
(5)
其中,zos为背景功率水平估计,它是所有2n个参考单元样本按照幅值从小到大排序后的第kos个样本值[17]。
参考式(5),Pareto背景下OSSO-CFAR的判决准则可以写为:
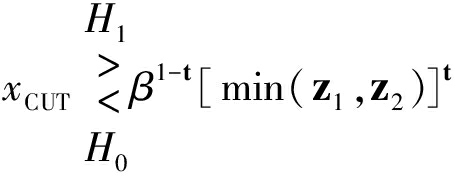
(6)
式(6)与式(5)的不同之处在于,采用min(z1,z2)替换zos作为混响背景功率水平估计。
下面推导均匀Pareto背景下OSSO-CFAR的虚警概率表达式。注意到局部估计Z1和Z2可以表示为[13]:
(7)
其中,T1,T2均服从参数为(n-k+1,k)的Beta分布,其PDF为[18]:
(8)
其CDF为[18]:
(9)
其中,B(•)为Beta函数,BT(•)为不完全Beta函数。综合式(3)、(6)和(7),OSSO-CFAR的虚警概率为:
P{eY>[max(T1,T2)]-t/α}
(10)
令Q=max(T1,T2),则随机变量Q的PDF为[8]:
fQ(q)=fT1(q)FT2(q)+ fT2(q)FT1(q)=2fT(q)FT(q)
(11)
其中, fT和FT分别由式(8)和(9)给出。利用式(8)、(9)、(10)和(11)可得:
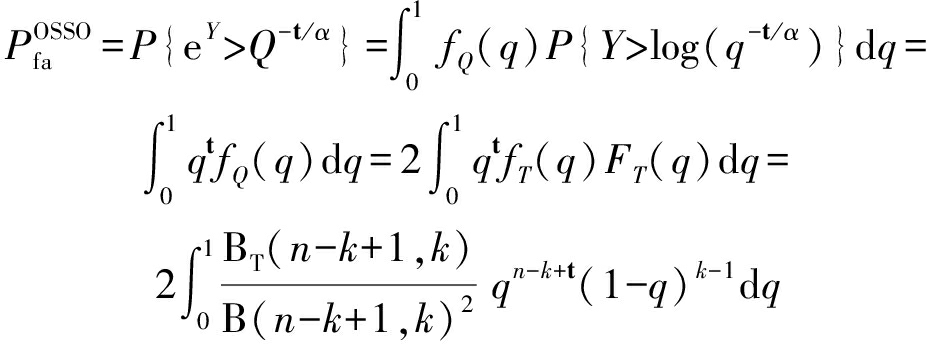
(12)
由式(12)可以看出,在尺度参数β已知情况下,OSSO-CFAR的虚警概率与形状参数α无关,所以OSSO-CFAR具有对α的恒虚警特性。
3.2 OSGO-CFAR
借鉴式(6),OSGO-CFAR的判决准则可以表示为:
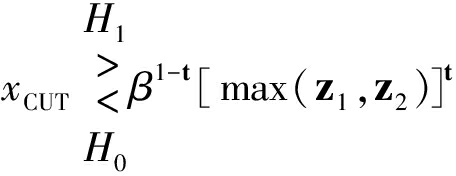
(13)
其虚警概率为:
P{eY>[min(T1,T2)]-t/α}
(14)
令Q=min(T1,T2),则随机变量Q的PDF为[8]:
fQ(q)=fT1(q)(1-FT2(q))+ fT2(q)(1-FT1(q))=
2fT(q)(1-FT(q))
(15)
利用式(8)、(9)、(14)和(15)可得:
(16)
式(16)表明,在尺度参数β已知情况下,OSGO-CFAR虚警概率与形状参数α无关,具有对α的恒虚警特性。图2(a)和(b)分别给出了k=12,n取值不同时OSSO-CFAR和OSGO-CFAR虚警概率与门限的关系。从图2可以看出,在其他参数保持不变时,前、后沿参考滑窗数量越多,相同虚警概率所对应的门限值越大。同样地,图3(a)和(b)分别给出了在n=15,k取不同值时OSSO-CFAR和OSGO-CFAR虚警概率与门限的关系。从图3可以看出,k值越大,为达到相同虚警概率所需的门限值越低,但k值过大会影响OSSO-CFAR和OSGO-CFAR抗干扰数目容限[8],因此需要根据实际情况适当选取k值。
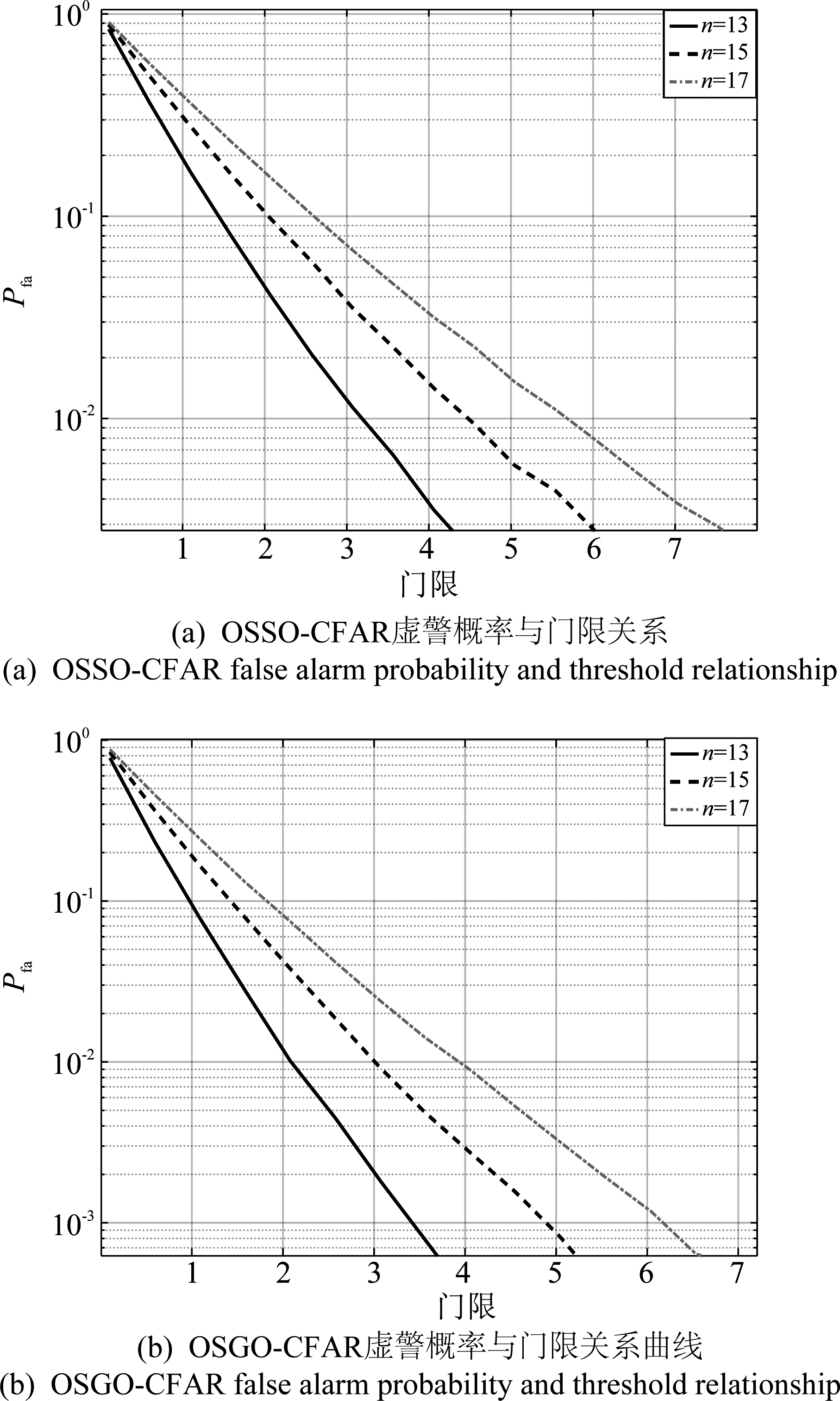
图2 不同n值时两种检测器虚警概率与门限关系
Fig.2 Two detectors false alarm probability and threshold relationship with different n
图3 不同k值时两种检测器虚警概率与门限关系
Fig.3 Two detectors false alarm probability and threshold relationship with different k
4 性能分析
为了分析OSSO-CFAR和OSGO-CFAR在Pareto分布混响背景下的性能,考虑了均匀混响背景、多目标干扰以及混响边缘环境三种情况,并与OS-CFAR进行对比。目标模型为Swerling Ⅱ型,相关参数如表1所示。其中,OS类CFAR检测器序列值通常设置为[0.8N],[·]表示不超过0.8N的最大整数[19]。对于OS-CFAR,N为全部参考单元个数;对于OSSO-CFAR和OSGO-CFAR,N为前、后沿参考单元个数。
4.1 均匀混响背景
图4给出了均匀混响背景情况下三种CFAR检测器的检测概率(Pd)与信混比(SRR)曲线,定义
其中
表示信号平均功率;
表示Pareto混响的平均功率。利用“附加损失”[20]来描述不同检测器之间检测性能的差异大小,这里指OSSO-CFAR和OSGO-CFAR相对于OS-CFAR的SRR损失。从图4可以看出,与OS-CFAR相比,OSGO-CFAR只表现出很小的检测性能下降,当检测概率为0.5 时,它的附加损失一般为0.2 dB左右,而OSSO-CFAR附加损失相对较大,一般在0.5 dB以上。
表1 仿真参数
Tab.1 Simulation parameters
参数参数值Pareto形状参数α11.39Pareto尺度参数β0.34OS序列值kOS24OSSO和OSGO序列值k12OS参考单元个数2n30OSSO和OSGO前、后参考单元个数n15虚警概率Pfa10-3
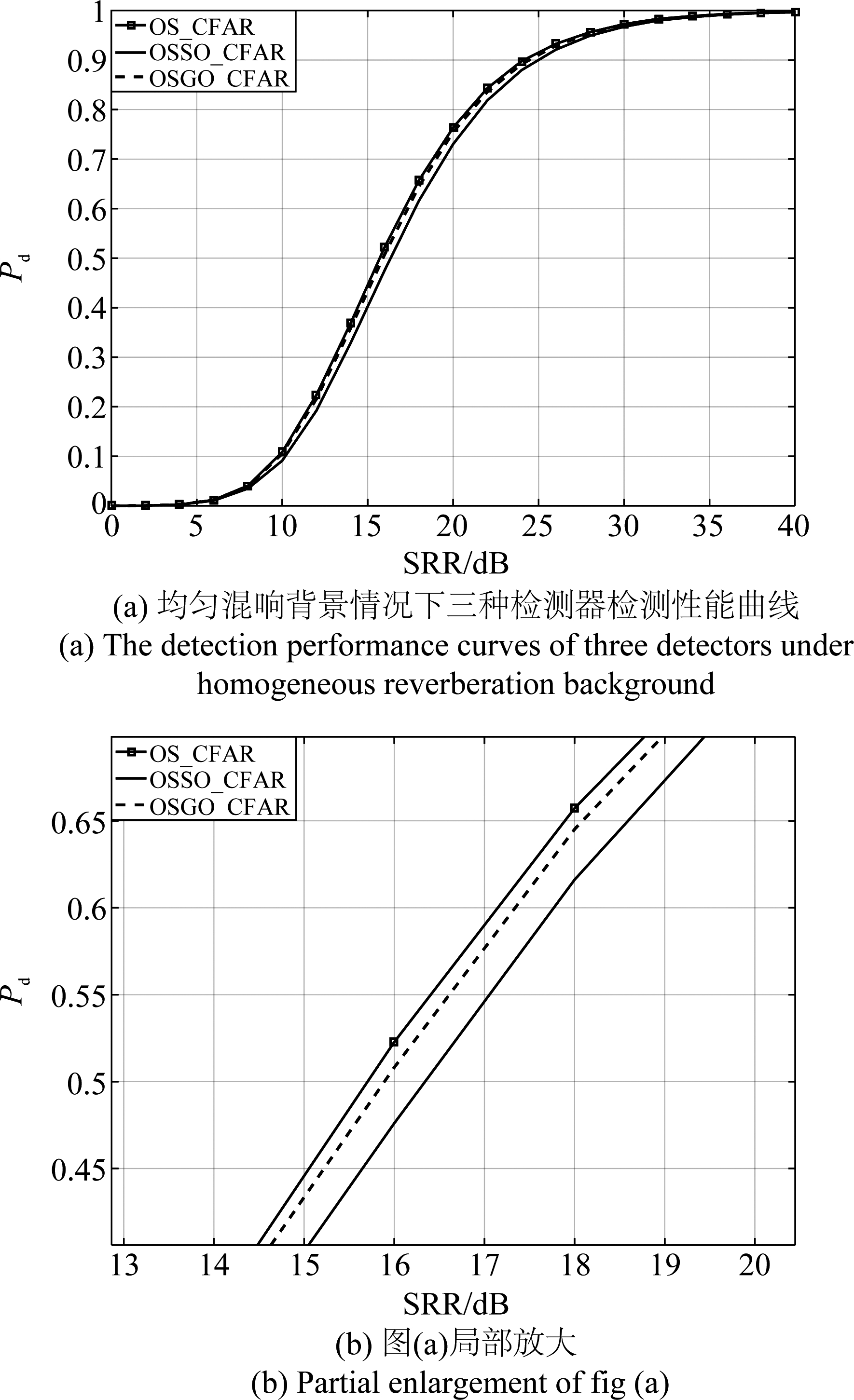
图4 均匀混响背景情况下三种检测器检测性能曲线与局部放大图
Fig.4 The detection performance curves of three detectors under homogeneous reverberation background and the partial enlargement
4.2 多干扰目标环境
本节比较了参考滑窗中存在不同数量干扰目标以及不同信干比(SIR)情况下三种检测器的检测性能。图5和图6给出了不同数量干扰目标对检测性能的影响,设置干扰目标模型为Swerling Ⅱ型,干混比(IRR)与SRR相等,定义
其中
为干扰目标的平均功率。图5考虑的是仅前沿滑窗存在干扰目标的情况,图6是前、后沿滑窗均存在干扰目标的情况。对于干扰目标仅存在于一侧滑窗的情况,OSSO-CFAR和OSGO-CFAR抗干扰目标数量容限分别为n和n-k[21]。从图5(a)可以看出,当前沿滑窗存在1个干扰目标,OS-CFAR、OSSO-CFAR和OSGO-CFAR在检测概率为0.5时所对应的SRR分别为16.17 dB、 16.78 dB和16.48 dB,三种检测器的检测性能十分相近。但是,从图5(b)可以看到,当前沿滑窗干扰目标数量超过OSGO-CFAR抗干扰容限(3个)时,其检测性能严重下降,几乎检测不到目标,而OSSO-CFAR检测性能仍比较稳定,并且当检测概率为0.5 时,OSSO-CFAR相比于OS-CFAR有6.3 dB性能的提升。
图5 前沿滑窗存在干扰目标情况下三种检测器检测性能
Fig.5 Detection performance of three detectors with interference targets in the front edge sliding window
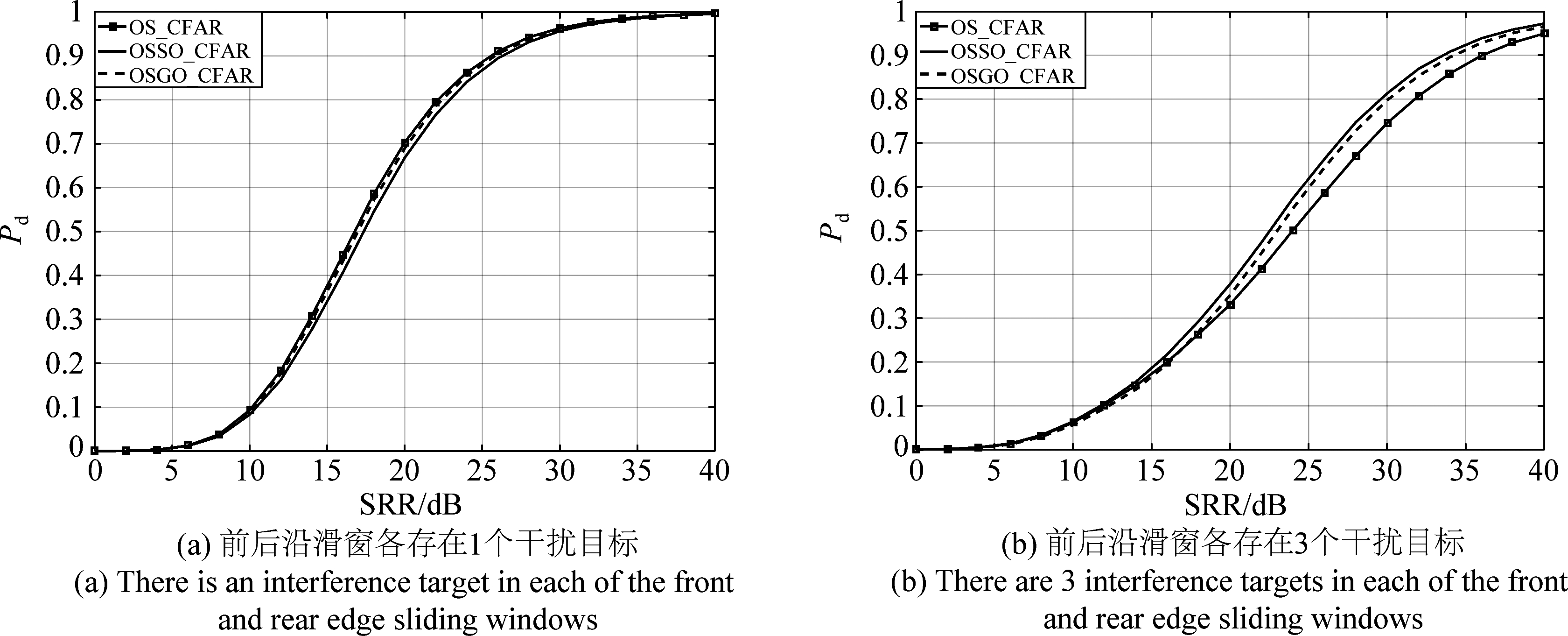
图6 前后沿滑窗存在干扰目标情况下三种检测器检测性能
Fig.6 Detection performance of three detectors with interference targets in front and rear sliding windows
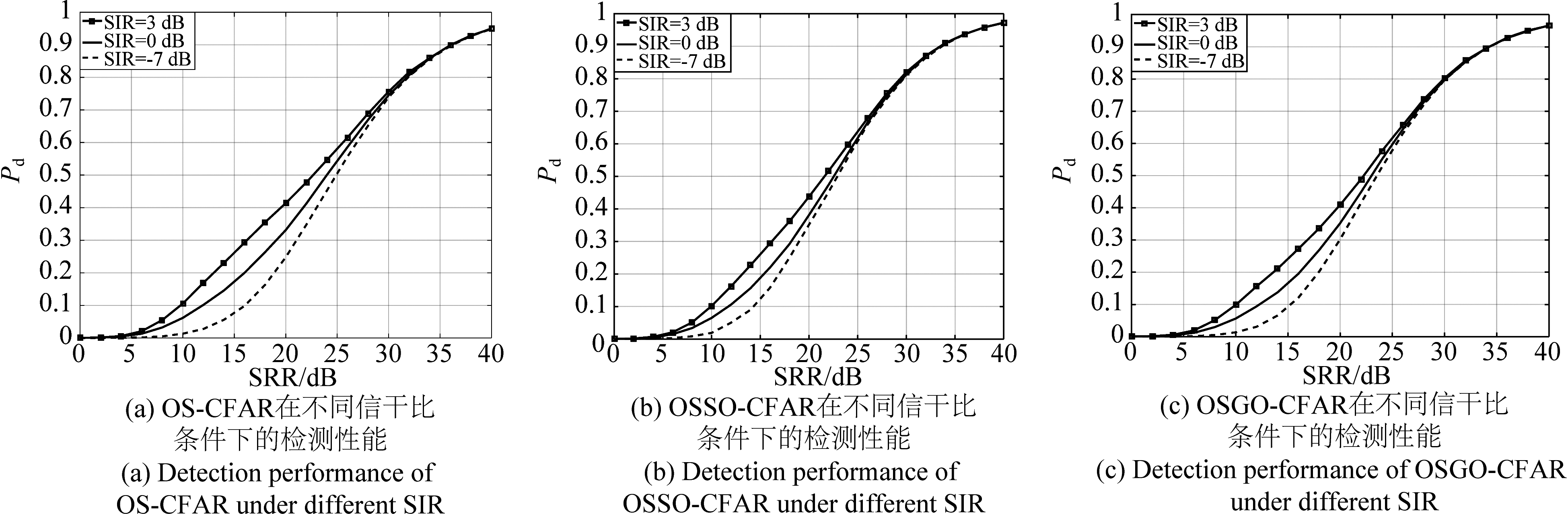
图7 三种检测器在不同信干比条件下的检测性能曲线
Fig.7 Detection performance curves of three detectors under different SIR
对于前、后沿滑窗均存在干扰目标的情况,OSSO-CFAR和OSGO-CFAR抗干扰目标数量容限均为n-k[21]。图6(a)和(b)分别为前、后沿滑窗均存在1和3个干扰目标时的检测性能曲线。由图6可以看出,当前、后沿滑窗均存在1个干扰目标时,三种检测器的检测性能相差较小;随着干扰数目的增多,它们的检测性能均有所下降,但OSSO-CFAR和OSGO-CFAR相对于OS-CFAR的检测损失逐渐减小。从图6(b)可以看到,当干扰数目达到容许限度时,OSSO-CFAR的检测性能已优于OS-CFAR和OSGO-CFAR,且当检测概率为0.5 时,OSSO-CFAR相较于OS-CFAR有近1.5 dB性能的提升。
图7给出了OS-CFAR、OSSO-CFAR和OSGO-CFAR在3组信干比(SIR=3,0和-7 dB)情况下检测性能曲线,定义
设置前、后沿滑窗均存在3个干扰目标。从图7中可以看出,随着SIR的降低,三种检测器的检测性能均有所下降。表2给出了不同SIR情况下三种检测器在检测概率为0.4 时所对应的SRR。从表2可以看到,随着SIR减小,OS-CFAR、OSSO-CFAR和OSGO-CFAR的SRR变化量(SRR-7 dB-SRR3 dB)分别为3.47 dB、1.96 dB和2.14 dB。因此,多目标情况下SIR的变化对OS-CFAR检测性能影响最大,其次是OSGO-CFAR,OSSO-CFAR影响最小。
表2 不同SIR情况下三种检测器在Pd=0.4时所对应的SRR(单位: dB)
Tab.2 SRR corresponding to three detectors atPd=0.4 under different SIR cases (unit: dB)
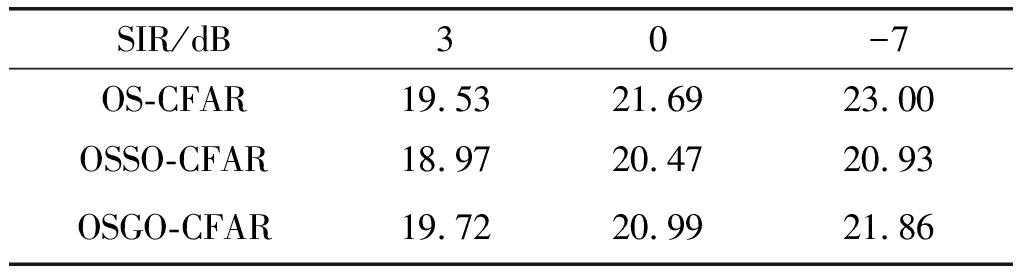
SIR/dB3 0-7OS-CFAR19.5321.6923.00OSSO-CFAR18.9720.4720.93OSGO-CFAR19.7220.9921.86
4.3 混响边缘环境
混响边缘描述的是混响从一种强度向另一种强度过渡的情况,是声纳中很常见的一种情形[21-22],例如海洋海底交界处、出现鱼群等情况。其数学模型一般考虑为在参考滑窗内混响背景功率呈现一个阶跃变化[8]。在仿真中,设置混响边缘位于参考单元数为17处,1～16为小功率混响,17～32为大功率混响。图8给出了在混响边缘功率比为5 dB时,三种检测器虚警概率的变化曲线,横坐标是参考单元数。随着参考单元数的增大,检测单元从左向右滑动,Pfa开始下降,当检测单元经过混响边缘时出现一个虚警尖峰,虚警尖峰越低,则表明检测器的虚警控制能力越强[8],由图8可以看出,在混响边缘环境下,OSGO-CFAR比其他两种检测器的虚警概率变化更小,虚警控制能力更强。
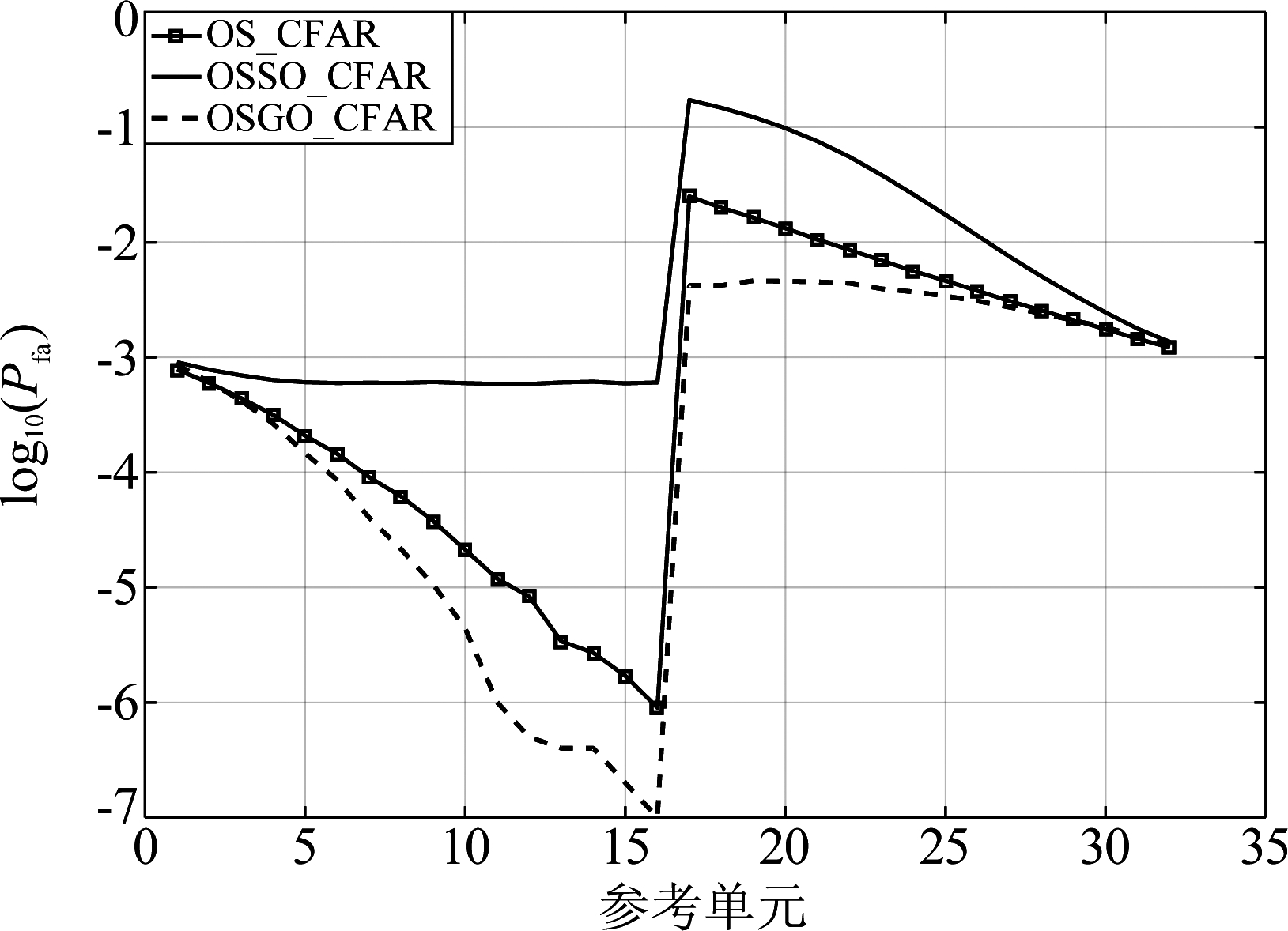
图8 混响边缘环境情况下三种检测器虚警概率
Fig.8 False alarm probability of three detectors in edge-reverberant
5 结论
Pareto分布作为一种能够有效描述高分辨率声纳混响的分布模型,以它为背景对检测器的性能进行研究有着重要意义。文章证明了在尺度参数已知情况下,OSSO-CFAR和OSGO-CFAR对形状参数具有恒虚警的特性。并进一步研究了均匀混响背景、多目标干扰以及混响边缘环境三种情况下检测器的性能,结果表明在均匀Pareto混响背景下,OSGO-CFAR与OS-CFAR的检测性能更相近;对于多目标干扰情况,在干扰目标仅存在于单侧参考滑窗时,OSGO-CFAR的抗干扰能力最差,当两侧参考滑窗均存在干扰目标时,随着干扰数目的增多,OSSO-CFAR抗干扰能力逐渐优于OS-CFAR和OSGO-CFAR,并且SIR对OSSO-CFAR检测性能影响最小;在混响边缘情况下OSGO-CFAR具有更好的虚警控制能力。值得说明的是,OSSO-CFAR和OSGO-CFAR的排序处理时间只有OS-CFAR的一半,更易于实时实现。由于本文考虑的是均匀、统计独立的Pareto分布混响,对于调制过程相关时的检测分析仍需进一步的研究。
[1] 曲超. 主动声纳恒虚警检测方法研究[D]. 北京: 中国科学院声学研究所, 2008.
Qu C. Research on Active Sonar Constant False Alarm Detection Method[D]. Beijing: The Institute of Acoustics of the Chinese Academy of Sciences, 2008.(in Chinese)
[2] 熊鹏俊, 方向红, 佘亚军, 等. Pearson分布混响下模糊CFAR检测器性能分析[J]. 舰船科学技术, 2013, 35(11): 90-95.
Xiong P J, Fang X H, She Y J, et al. Performance Analysis of Fuzzy-CFAR Detectors under Pearson-distributed Reverberation[J]. Ship Science and Technology, 2013, 35(11): 90-95.(in Chinese)
[3] 徐从安, 简涛, 何友, 等. 一种改进的VI-CFAR检测器[J]. 信号处理, 2011, 27(6): 926-931.
Xu C A, Jian T, He Y, et al. An Improved VI-CFAR Detector[J]. Signal Processing, 2011, 27(6): 926-931.(in Chinese)
[4] 关键, 张晓利, 黄勇, 等. 一种距离扩展目标的稳健检测算法[J]. 信号处理, 2011, 27(12): 1878-1883.
Guan J, Zhang X L, Huang Y, et al. A Robust Detection Method for Range-spread Targets[J]. Signal Processing, 2011, 27(12): 1878-1883.(in Chinese)
[5] Finn H M, Johnson R S. Adaptive Detection Mode with Threshold Control as a Function of Spatially Sampled Clutter-level Estimates[J]. Rca Review, 1968, 29:414- 464.
[6] Rohling H. Radar CFAR Thresholding in Clutter and Multiple Target Situations[J]. IEEE Transactions on Aerospace and Electronic Systems, 1983, 19(4): 608- 621.
[7] Eliasfuste A R, De Mercado M G G, Elias D L R D. Analysis of Some Modified Ordered Statistic CFAR: OSGO and OSSO CFAR[J]. Aerospace and Electronic Systems IEEE Transactions, 1990, 26(1): 197-202.
[8] 何友, 关键, 孟祥伟. 雷达目标检测与恒虚警处理[M]. 第2版. 北京: 清华大学出版社, 2011: 45-51.
He Y, Guan J, Meng X W. Radar Target Detection and CFAR Processing[M]. Second Edition. Beijing: Tsinghua University Press, 2011: 45-51.(in Chinese)
[9] Gao Yongchan, Liao Guisheng, Zhu Shengqi. Adaptive signal detection in compound-Gaussian clutter with inverse Gaussian texture[C]∥IRS 2013-Proceedings. Germany, 2013: 935-940.
[10] 高永婵, 廖桂生, 朱圣棋. 复合高斯噪声中知识辅助的贝叶斯Rao检测方法[J]. 西安电子科技大学学报, 2013, 40(6): 46-51, 173.
Gao Y C, Liao G S, Zhu S Q. Knowledge-aided Bayesian Rao Detection Approach in Compound Gaussian Noise[J]. Journal of Xidian University, 2013, 40(6): 46-51, 173.(in Chinese)
[11] Gelb J M, Heath R E, Tipple G L. Statistics of Distinct Clutter Classes in Midfrequency Active Sonar[J]. IEEE Journal of Oceanic Engineering, 2010, 35(2): 220-229.
[12] Piotrkowski M. Distribution Independent CFAR Detector Using Extreme Value Theory[C]∥2006 International Radar Symposium, Krakow, 2006: 1- 6.
[13] Shang X, Song H. Radar Detection Based on Compound-gaussian Model with Inverse Gamma Texture[J]. IET Radar, Sonar and Navigation, 2011, 5(3): 315-321.
[14] Weinberg, Graham V. On the Construction of CFAR Decision Rules via Transformations[J]. IEEE Transactions on Geoscience and Remote Sensing, 2016, 55(2): 1-7.
[15] Weinberg G V, Bateman L, Hayden P. Constant False Alarm Rate Detection in Pareto Type II Clutter[J]. Digital Signal Processing, 2017, 68(7): 192-198.
[16] Weinberg G V. Estimation of Pareto Clutter Parameters Using Order Statistics and Linear Regression[J]. Electronics Letters, 2013, 49(13): 845- 846.
[17] 郝程鹏, 刘斌, 陈模江, 等. 一种新的基于CA和OS的分布式模糊恒虚警检测系统[J]. 弹箭与制导学报, 2008, 28(6): 219-221.
Hao C P, Liu B, Chen M J, et al. A New Distributed Fuzzy CFAR System Based on Cell Averaging and Order Statistics[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2008, 28(6): 219-221.(in Chinese)
[18] 赵林. Beta分布与其他分布关系及其应用[J]. 安徽建筑工业学院学报:自然科学版, 2008, 16(2): 80- 81.
Zhao L. The Relation between Beta Distribution and Other Distributions as well as its Application[J]. Journal of Anhui Institute of Architecture and Industry, 2008,16(2): 80- 81.(in Chinese)
[19] Weinberg G V. Constant False Alarm Rate Detectors for Pareto Clutter Models[J]. IET Radar Sonar and Navigation, 2013, 7(2): 153-163.
[20] Hansen V G, Sawyers J H. Detectability loss due to greatest of selection in a cell averaging CFAR[J]. IEEE Tans. On AES, 1980, 16(1): 115-118.
[21] 郝程鹏, 侯朝焕, 鄢锦. OSGO-和OSSO-CFAR在K分布杂波背景下的性能分析[J]. 电子与信息学报, 2005, 27(7): 1061-1064.
Hao C P, Hou C H, Yan J. Performance Analysis of OSGO-and OSSO-CFAR in K-Distribution Clutter[J]. Journal of Electronics and Information Technology, 2005, 27(7): 1061-1064.(in Chinese)
[22] 郝程鹏, 侯朝焕. OSGO-CFAR在K分布杂波边缘中的性能分析[J]. 雷达与对抗, 2005(3): 25-29.
Hao C P, Hou C H. Performance Analysis of OSGO-CFAR Detector in K-Distribution Clutter Edge[J]. Radar and Electronic Countermeasures, 2005(3): 25-29.(in Chinese)
