1 引言
随着无人机在军事、工业、民用等众多领域的应用,基于军事及安防监管等原因,无人机防御侦察技术逐渐受到广泛关注。声学探测技术具有全向监测、不受光环境影响等优势,可有效实现目标方位角估计及特征检测与识别的优势,逐步发展成为无人机探测重要手段[1- 4]。但由于应用场景多为复杂声环境,声杂波对目标信号干扰使得实际检测中虚警率高、检测率低,限制了声学无人机检测的普及与应用。
对于低空无人机信号,可将声学检测方法与声源定位技术结合起来,实现高分辨的声源定位。传统声源定位技术中,波束形成算法[5- 6]的定位分辨率受到瑞利准则限制。要获取较高分辨率结果,需增大阵列孔径,但同时也会增加计算复杂度和测量成本,因此开发成本低、分辨率高的声源定位算法是研究的关键问题。声成像技术[6-7]基于声阵列理论对指定方向和距离的空间区域声能量进行计算,并以色图形式描述了指定空间区域的声场能量分布情况。声成像技术具有强指向性、高分辨力的优势,可应用于无人机探测问题,实现高分辨率的声源定位。2007年,荷兰NLR的P.Sijtsma[8]提出了基于同一声源产生的主瓣与旁瓣相干清除(Clean based Spatial Source Coherence, CLEAN-SC)方法。该方法通过在传统波束形成结果中反复移除与主瓣相干旁瓣来清晰化声源识别结果,因计算效率高、收敛快、旁瓣衰减能力和抗干扰能力强,成为近年来国内外学者研究的焦点。英国剑桥大学的Alexander R.Quayle[9]、中国航天空气动力技术研究院的赵小见[10]等运用该方法成功识别出了飞机气动声源。杨洋[11]等运用该方法成功开展了汽车前围板隔声薄弱部位的识别实验。而对于低空远距离无人机信号,传统波束形成算法的定位结果主瓣宽、旁瓣干扰较多,利用CLEAN-SC算法可有效减少主瓣宽度,抑制旁瓣。
常规宽带信号处理中,通常将各频率点对应数据的计算结果进行综合处理,最终实现声源定位[12]。在实际低空无人机目标定位场景中,无人机信号混有较多干扰噪声,从而影响对无人机目标的准确估计。如何在有强干扰噪声的情况下对获得的微弱无人机信号进行定位,是我们需要关注的问题。直方图是直观地对各频域结果进行统计的方法,可以根据基于直方图概率密度函数获取目标位置,但直方图估计的密度函数并不平滑,同时受到区间宽度的影响。Parzen[13]于1962年首次提出了Parzen窗估计方法,利用已知样本对总体分布概率密度进行估计,解决了直方图存在的问题。孙乃葳等[14]将Parzen窗估计方法应用于潜艇目标强度统计中,建立了符合潜艇物理结构特性的潜艇目标强度统计模型。庞菲菲等[15]提出了基于Parzen窗方位交线定位算法,改善了水下无线传感网络中节点失效情况。本文采用非参数估计模型,利用Parzen窗构造基于高分辨算法的无人机噪声能量空间分布概率模型,有效减弱了噪声干扰。
传统声阵列技术,基于完备正交信号处理理论模型,对于复杂混叠信干(干扰)条件下的信源数估计、稳定DOA估计获取等问题难以获得有效处理手段。阵列算法中在提取目标信号并加载导向矢量后,算法会得到表征频域与空间分布的空频矩阵信息(Q(ω,θ,φ)或Q(ω,x,y)), 依据目标在空间与频域的物理属性,选择适当的数据处理模型,构造合理的代价函数,采用参数、非参数及智能处理的手段优化,可以有效获得在复杂混叠环境条件下的目标特征,为后续的声源目标的检测、定位与识别提供有效参考信息。
本文基于上述思路,通过开展无人机声学检测实验,对无人机弱声源在复杂环境中的远距离检测、定位与识别问题进行了研究。本文第2节介绍了基于声成像算法的声场空频特征非参数数据建模,第3节介绍了先验频率特征建模,第4节给出了复杂环境中小型四旋翼无人机目标检测的仿真性能评估及现场实验结果,文章最后总结研究结论并做后续工作展望。
2 声场空频特征非参数融合建模
针对复杂环境条件下的声学探测问题,利用声场成像算法获取目标区域声场空间与频域分布信息,形成空频特征矩阵Φ(ω,θ,φ)。然后基于无人机的先验频率特征,建立特征频带与空间方位融合的声源目标优化判决模型。下文将对该模型做具体介绍。
目标信号模型如下:
X(ω)=A(ω)(S(ω)+O(ω))+v(ω)
(1)
其中,X(ω) 为阵列获取信号,A(ω)为阵列导向矢量,S(ω)为目标信号源,O(ω)为空间干扰噪声源,v(ω)为测量噪声源。利用声成像算法,即可获取包含全频带特征的空间声场信息矩阵:
Φ(ω,θ,φ)=A(ω,θ,φ)(S(ω)+O(ω))+N(ω)
(2)
式中Φ(ω,θ,φ)表示包含目标信号、干扰信号及噪声的空(间)频(率)等特征的声场信息函数,ω=[ω1,…,ωn,…,ωN]表示无人机信号的特征频率向量,θ=[θ1,…,θn,…,θN]和φ=[φ1,…,φn,…,φN]表示对无人机特征频率ω利用声成像算法,估计的无人机方位角向量和俯仰角向量。对于混杂信息,可通过后验估计和时空融合判决的方法建立优化模型。本研究依据无人机探测的应用需求,以频域特征与空间汇聚为依据,通过非参数融合手段,构建如下优化模型:
c(θ,φ)=argmax(p(Φ(ω,θ,φ))) s.t.T(z)>γ
(3)
式中c(θ,φ)为混杂目标的判决定位结果,p(Φ(ω,θ,φ))为宽带频率空间分布的概率密度函数。T(z)为频率假设检验中的检测统计量,γ为判定检测信号存在的阈值。本文暂不讨论S(ω)与O(ω)在信号层面区分问题,可令S′(ω)=S(ω)+O(ω)。
2.1 高分辨率声场信息获取算法
声场成像算法采用CLEAN-SC高分辨率成像算法,由m0个传声器组成的平面声阵作为接收阵列,将目标方向平面L划分为l×l′个网格点,以确认目标声源来向信息的分辨率。xm(t)和xm′(t)分别表示传声器m和m′的接收数据,其频域表达为Xm(ω)和Xm′(ω),该结果中包含有含杂声源s′(t)的频率特征与方向信息。取适合的帧长、快拍数T,即可得到式(4)所示的互谱矩阵Gmm′:
n=1,…,N
(4)
其中WL是数据窗的权重常数,ωn表示第n个无人机特征频率。记m0×1维向量a为式(1)所述的导向矢量:
a=[a1,a2,...,am0]T
(5)
其中am=exp(-j 2pωntm),tm为声源到第m个传声器相对于坐标原点的延时。
波束形成法在频率为ωn的输出结果为:
(6)
进一步采用可减小主瓣宽度、抑制旁瓣的高分辨CLEAN-SC算法。基于波束形成算法生成初始波束图,搜索波束图峰值点,反复迭代去除该峰值产生的波束旁瓣,经不断优化后获得高分辨率的声场波束图。具体迭代处理过程如下所示:
初始化阵列接收声信号的互谱矩阵D(0)=G,声源强度分布Q(0)=0,由第i次迭代计算到第i+1次迭代计算的具体步骤为:
a)根据式(6)计算第i次迭代后第j个扫描网格点
的传统波束形成输出量。
b)搜索主瓣峰值:找到声源能量的峰值
从声源能量分布中去除主瓣峰值的影响,此时式(6)可以写为
其中
得到
其中
是最大声源能量位置处
的互谱矩阵(CMS)。
c)计算声源强度分布:
其中0<β≤1是循环因子,l为设定的波束宽度函数,设定波束宽度为R, 当
时,0≤l≤1,β(0)≡0,当
时,β≡0。
d)重构i+1次迭代的互谱矩阵D(i+1)。
(7)
其中,G(i+1)为分析主瓣峰值与其他聚焦点波束形成输出量间的相干性而获得的互谱矩阵,
为相应的相干成分向量。对于任意
聚焦点,满足:
(8)
联立式(7)和(8),可得
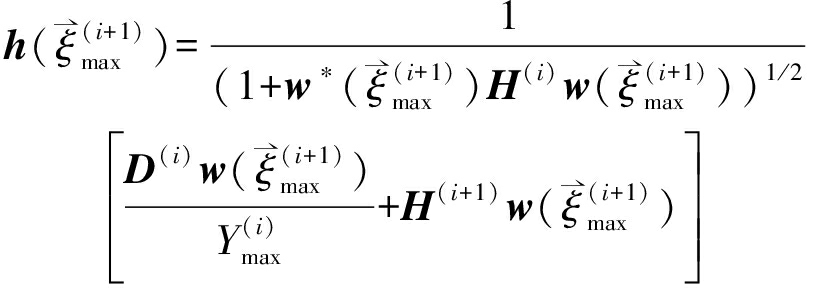
(9)
(10)
将式(9)代入式(7)重构出D(i+1)后,返回第a)步重复循环。完成I次迭代计算后,声源强度分布为
将N个特征频率ωn,n=1,…,N估计得到的方位角和俯仰角构成空频特征矩阵Φ(ω,θ,φ)。
最后,比较波束形成与高分辨CLEAN-SC算法,进一步验证CLEAN-SC算法的优越性。取300 Hz单频信号作为入射声源,声源来向为:方位角为270°,俯仰角为67°,信噪比为-10 dB。正如图1、图2所示,高分辨率CLEAN-SC算法的定位结果明显减小了主瓣宽度,并有效抑制了旁瓣。
图1 波束形成算法定位结果
Fig.1 Location results of beamforming algorithm
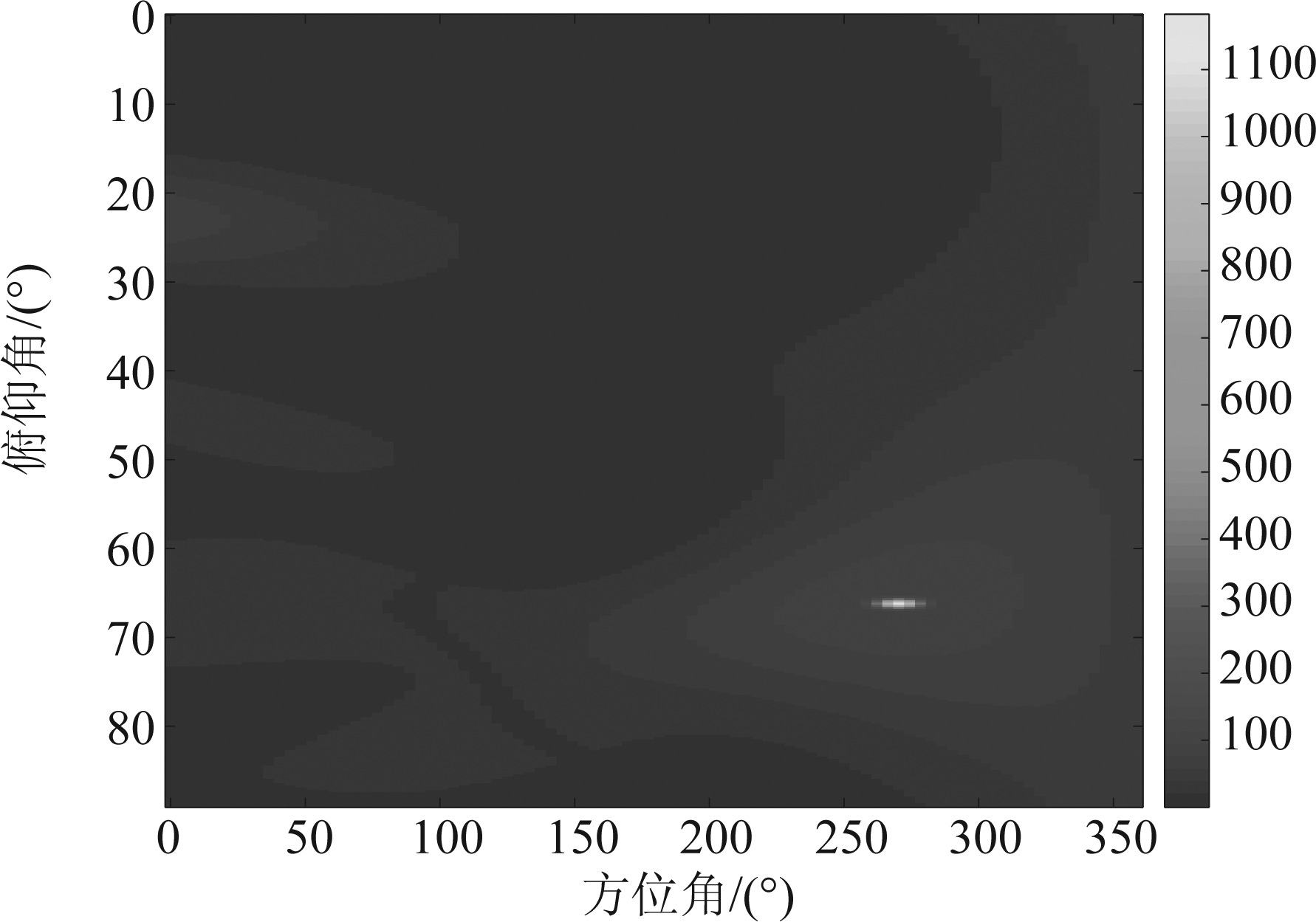
图2 CLEAN-SC算法定位结果
Fig.2 Location results of CLEAN-SC algorithm
2.2 基于非参数估计的空频融合算法
使用声探测阵列对低空无人机信号进行监测,设计基于假设检验的无人机特征谱检测手段,获取无人机先验宽谱特征。通过高分辨率声成像算法获取目标区域宽带声场信息,并根据特征频带约束去除与频带特征距离较大的干扰目标及噪声。最后采用Parzen窗空频概率密度估计方法,对获得的目标区域宽带声场分布矩阵进行处理,估计目标特征频率空间概率密度分布。通过特征频段约束及空间条件约束,利用无人机目标特征时空聚集的结果,探测无人机信号的存在及其方向信息。
2.2.1 非参数空频概率密度函数估计
依据无人机先验特征频率ω∈Ω,Ω为频率空间,采用CLEAN-SC方法获得空频特征矩阵Φ(ω,θ,φ),得到无人机宽带特征频率ω的目标方位角θ和俯仰角φ作为已知的样本集l={φ1,…,φn,…,φN},其概率密度函数表示为p(φ),考虑样本l所在空间的某个小区域R,某个随机变量落入该区域的概率为:
(11)
假设样本集l={φ1,…,φn,…,φN}是根据密度函数p(φ)独立取得N个样本点,其中有k个样本点落入到小区域R中,则其概率为:
(12)
当p(φ)连续,且小区域R的体积V足够小时,样本的密度函数可以估计为:
(13)
2.2.2 Parzen窗法
假设φ是d维特征向量,Rd是以φ为中心超立方体,h为此超立方体边长。
对CLEAN-SC算法计算获得Φ(ω,θ,φ)声场频率空间,采用式(14)给出方窗—Parzen窗函数作为核函数:
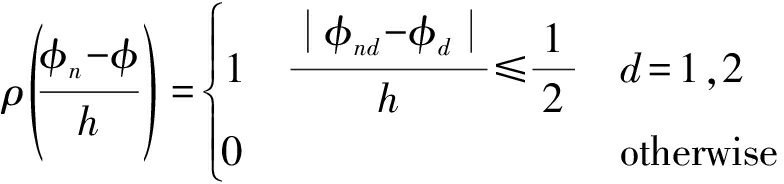
(14)
该式表示样本φn是否落入以φ为中心、h为边长的方形内。将式(14)带入式(13),通过Parzen窗法估计的概率密度函数为:
(15)
为保证
的收敛,窗函数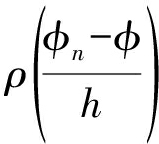
约束条件[16]为:
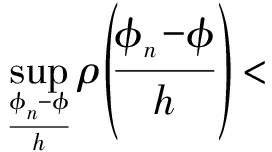
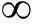
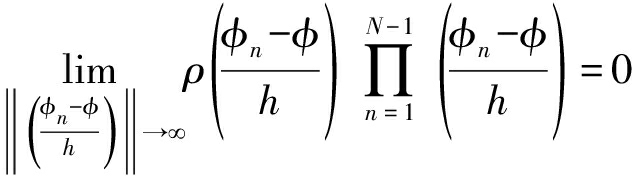
(16)
考虑到无人机信号为宽带信号,与无人机先验宽带特征匹配的候选频带容量较大。此外,估计精度、飞行环境不同可导致频点差异及存在类似特征频点干扰。而上述非参数估计手段——Parzen窗函数方法,通过对宽带频率ω利用CLEAN-SC算法得到目标的估计角度(θ,φ),利用Parzen窗函数方法计算其概率密度函数p(Φ(ω,θ,φ)),找到其峰值c(θ,φ)=argmax(p(Φ(ω,θ,φ))),即为无人机目标的位置。这种方法可解决因掺杂噪声频率导致的定位结果不精准的问题,最终实现在低信噪比条件下对无人机信号的探测。
3 先验频率特征建模方法
为了在远距离混杂环境下进行无人机的声场定位,我们需要检测出无人机的特征频率,在特征频率的基础上进行声源定位可以降低无人机的定位虚警率。对无人机频谱的检测可以采用假设检验手段,获取无人机先验特征频率。首先对无人机时域信号进行二元假设:
H0∶z(t)=ν(t) H1∶z(t)=y(t)+ν(t)
t=-…+
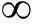
(17)
其中ν(t)是噪声的时域表示,y(t)=Asin(2pωt),其中A、ω为未知参数,分别代表无人机时域信号的幅度、频率。定义信噪比
在H0假设条件下,由于ν(t)是方差为σ2高斯白噪声,经过傅里叶变换后实部和虚部仍服从高斯分布[21]。
在H1假设条件下,对无人机信号y(t)进行傅里叶变换后表示为
无人机噪声是无人机的旋翼旋转过程中与空气摩擦振动产生的,在频域中的表现是分布着几个固有特征频率带,每一个特征频率带又服从均值为中心频率ω0的高斯分布,同时可以得到无人机先验特征频率带的范围。因此在混杂弱信号环境下,对每一个无人机频率带进行无人机特征频率检测,将式(17)时域假设转换到频域假设,以无人机信号其中一个频率带为例,其余频带类似,其二元假设为:
H0∶z(Δω)=ν(Δω)
H1∶z(Δω)=y(Δω)+ν(Δω)
(Δω=0,1,…,min(ωl-ω0,ωh-ω0))
(18)
其中Δω=ω-ω0,ω表示无人机频率,ω0表示无人机频率带中心频率,ωl表示频率带下限,ωh表示频率带上限。所以无人机频率y(Δω)服从均值为0高斯分布。
在H0假设条件下,噪声频率ν(ω)服从均值为0,方差为
的高斯分布,则ν(Δω)也服从均值为0,方差为的高斯分布。
在H1假设条件下,z(Δω)=y(Δω)+ν(ω),y(Δω)和ν(Δω)均服从均值为0的高斯分布,则z(Δω)服从均值为0,方差为
的高斯分布。共有N个Δω,第n个频率点的信号zn(Δω)表示为zn。
两种假设下的似然函数为:
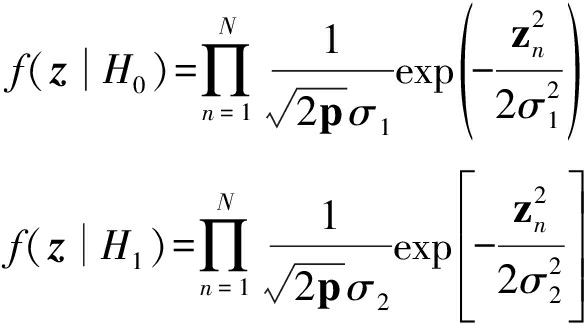
(19)
似然比为:
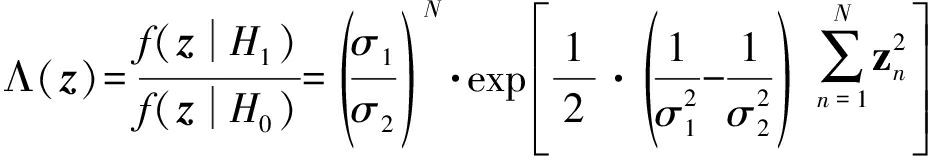
(20)
对数似然比为:
(21)
判决表达式为:
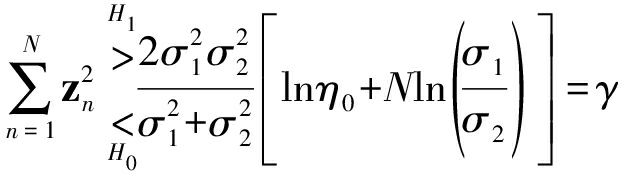
(22)
则检验统计量
服从自由度为N的χ2分布,即:
虚警概率为:
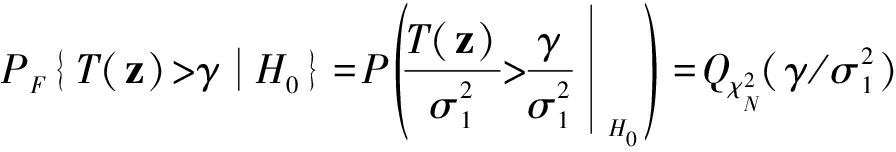
式中,
检测概率为:
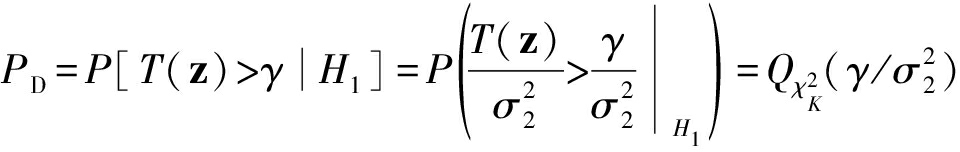
选取一段真实的无人机频域信号如图3所示。计算获得信噪比分别为-5 dB、-10 dB和-20 dB条件下的频率检测ROC曲线,如图4所示,随着信噪比的增大,检测概率PD趋向于1,说明对无人机特征频率的检测能力越来越好。图5为检测模型的检测性能曲线,反映了在给定虚警概率PF下信噪比与检测概率的关系,可得到不同信噪比条件下的最大检测概率。
图3 无人机信号的频域图
Fig.3 Frequency domain diagram of UAV signal
图4 无人机频率检测的ROC曲线
Fig.4 ROC curve of UAV frequency detection
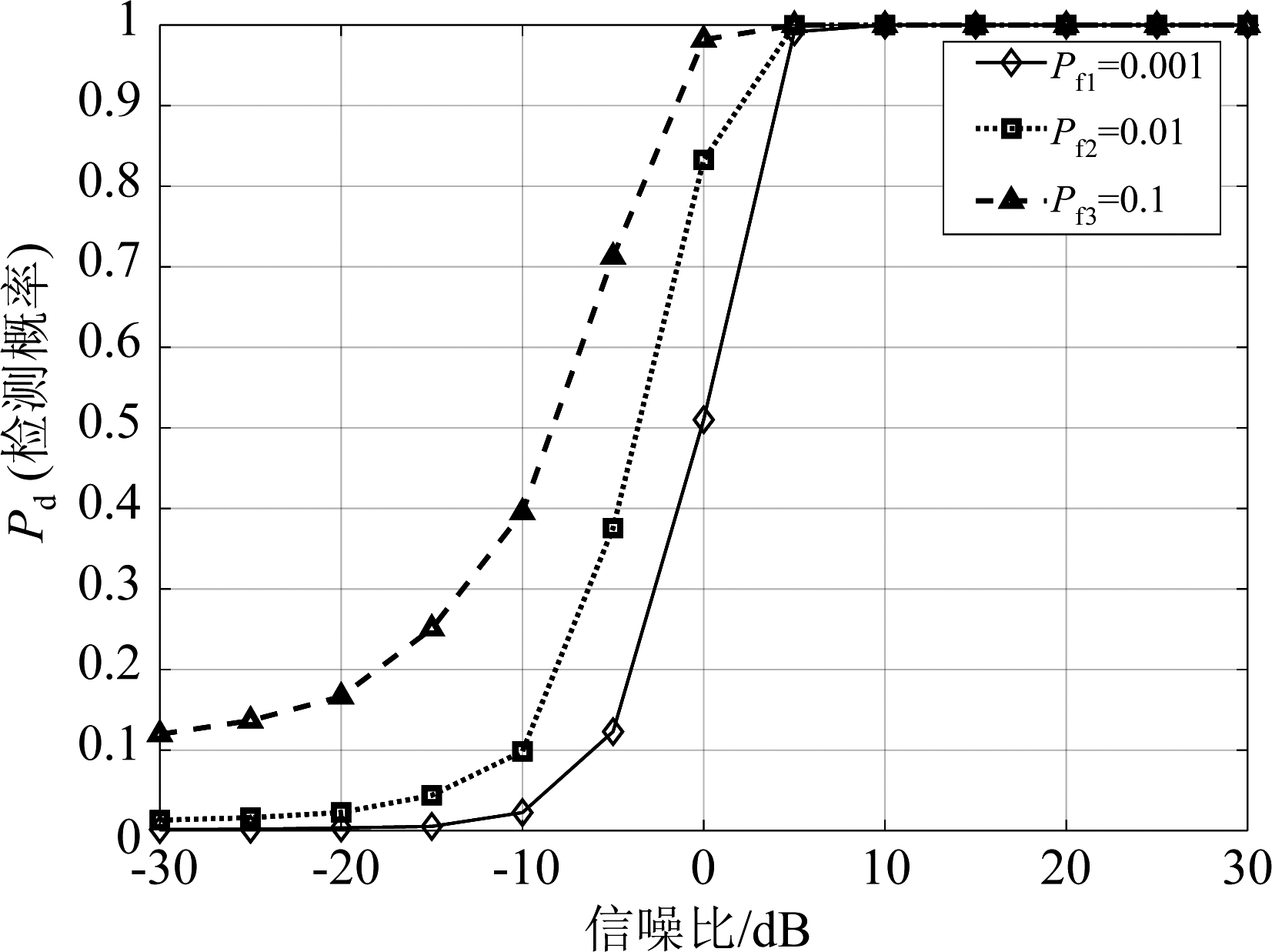
图5 检测性能曲线
Fig.5 Detection performance curve
4 性能分析及仿真验证
4.1 仿真实验
本节对提出的在多源目标混叠条件下无人机空频融合检测方法进行了仿真实验,验证了本模型的有效性。
仿真实验采用半径为0.8 m的平面阵。仿真实验利用纯净的无人机信号作为声源,方位角设为270°,俯仰角设为70°,添加高斯白噪声使其信噪比为-10 dB。首先根据无人机信号频率的先验分布找到仿真信号的无人机特征频率,随后利用CLEAN-SC算法进行空域滤波,估计每个特征频率处的空间角度位置。图6给出了无人机特征频率与其定位结果的关系。将这些定位结果的角度信息作为样本,采用Parzen窗方法对样本的概率密度进行估计,获取图7所示的概率密度函数图,从而计算得到目标的空间角度。
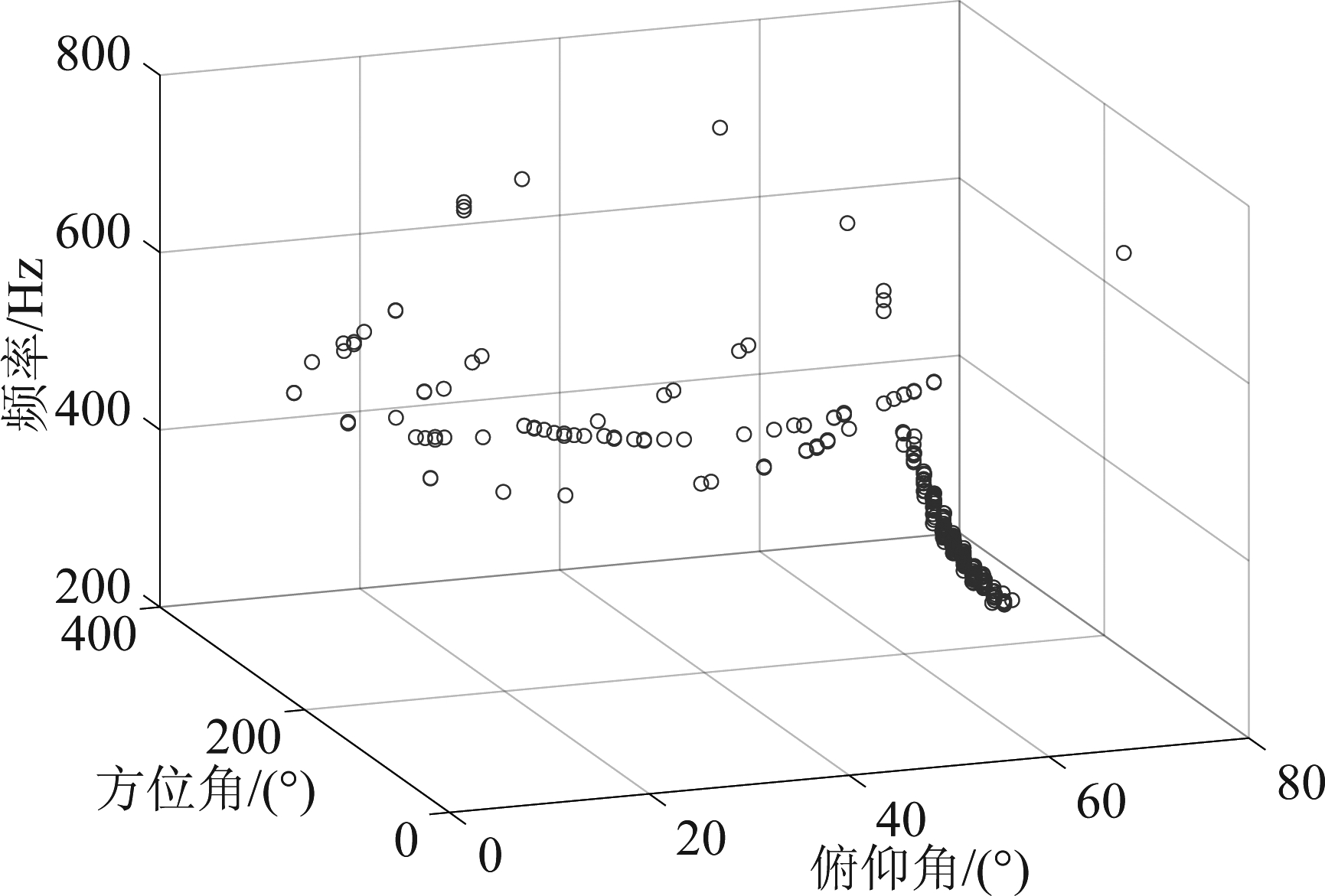
图6 无人机空间位置估计
Fig.6 UAV spatial position estimation
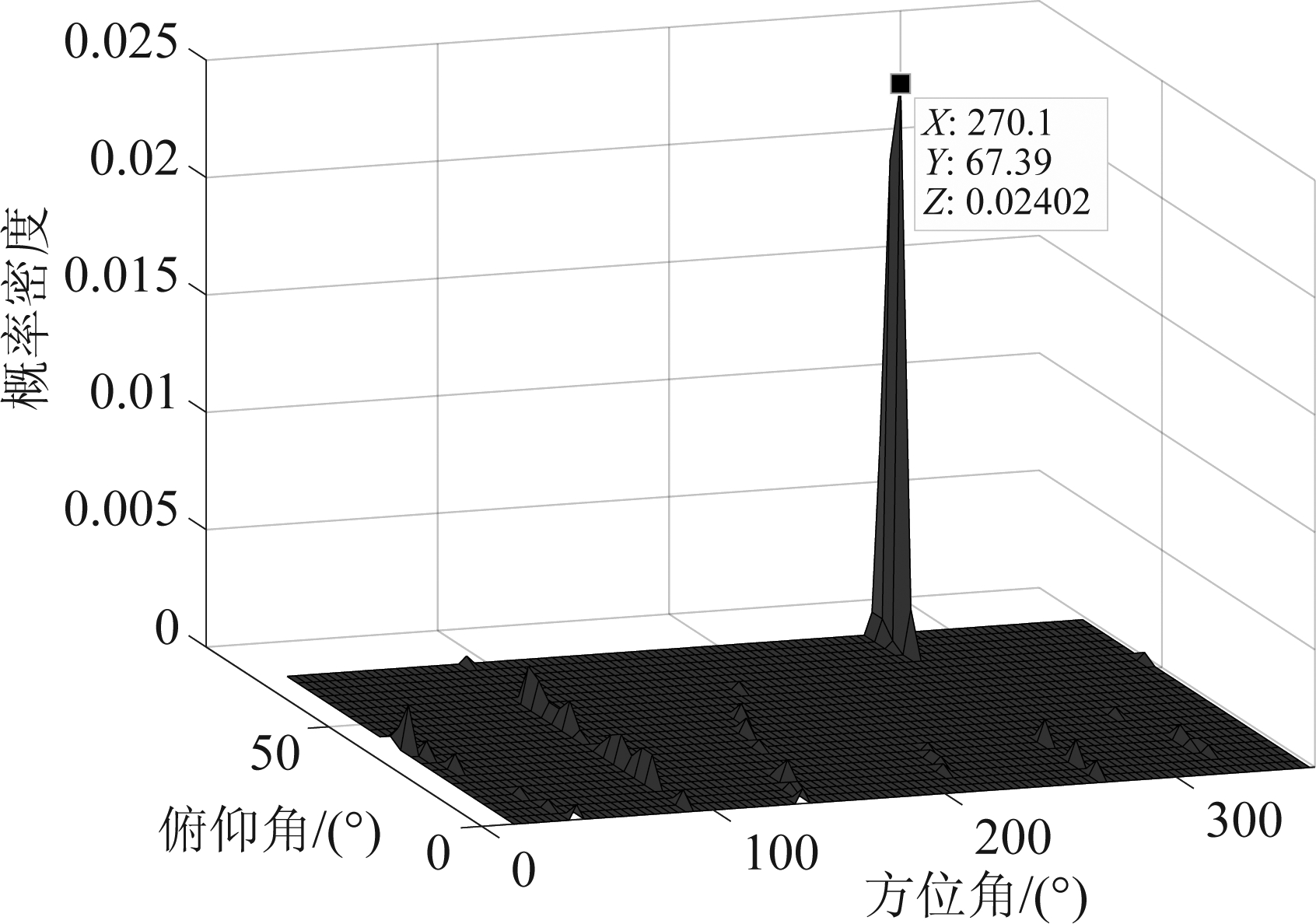
图7 Parzen窗函数估计概率密度函数的仿真图
Fig.7 Simulation diagram of probability density function estimated by Parzen window function
上述结果表明,CLEAN-SC的空间定位结果夹杂着较多伪声源位置信息,无法确定无人机真实位置。而采用Parzen窗估计空域位置的概率密度函数,可有效确定无人机的精确位置。图7中获取的目标方位角为270.1°,俯仰角为67.3°,相比于图6 所示CLEAN-SC探测的目标无人机方位结果,本文提出的方法可以有效实现对无人机目标的探测,提升了在低信噪比混杂环境下对无人机探测的准确性。本文提出的方法在下面的无人机探测实验中可以得到很好实际验证。
4.2 无人机定位实验
采用实际声阵列,开展了低空混杂环境下无人机定位实验。实验采用24元平面阵,阵列直径为1.6 m,无人机距离阵列中心水平距离为100 m,垂直高度为20 m。根据平面阵与无人机的相对位置,无人机所在的方位角、俯仰角约为277°和11.3°。图8为无人机实验场景,周围环境噪声包含鸟叫声、风声以及沿途汽车等声音。通过信噪比的公式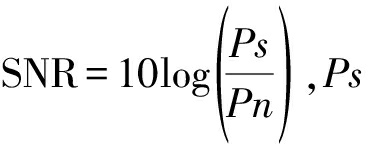
和Pn分别代表采集到的无人机信号和实验背景噪声的有效功率,计算得到此时的信噪比为-20 dB。
图8 实际实验场景
Fig.8 Actual experimental scene
实验分析中首先根据无人机先验频率特征,通过抓取局部峰值的方法得到87个无人机特征频率点,如图9中圆圈所示。利用CLEAN-SC算法计算87个频率点宽带无人机信号的方位角和俯仰角,见图10。图11为无人机87个特征频率点与其空域定位结果的关系图。可以看出图10和图11均无法直观探测无人机目标及其角度位置。利用本文提出的算法模型,通过计算Parzen窗函数估计的概率密度函数(如图12所示),可获得无人机目标的方位角为277°,俯仰角为12.5°,与真实角度相比,方位角相差0°,俯仰角相差1.2°。与CLEAN-SC算法的估计结果相比,本文所提模型可有效探测无人机的方向。
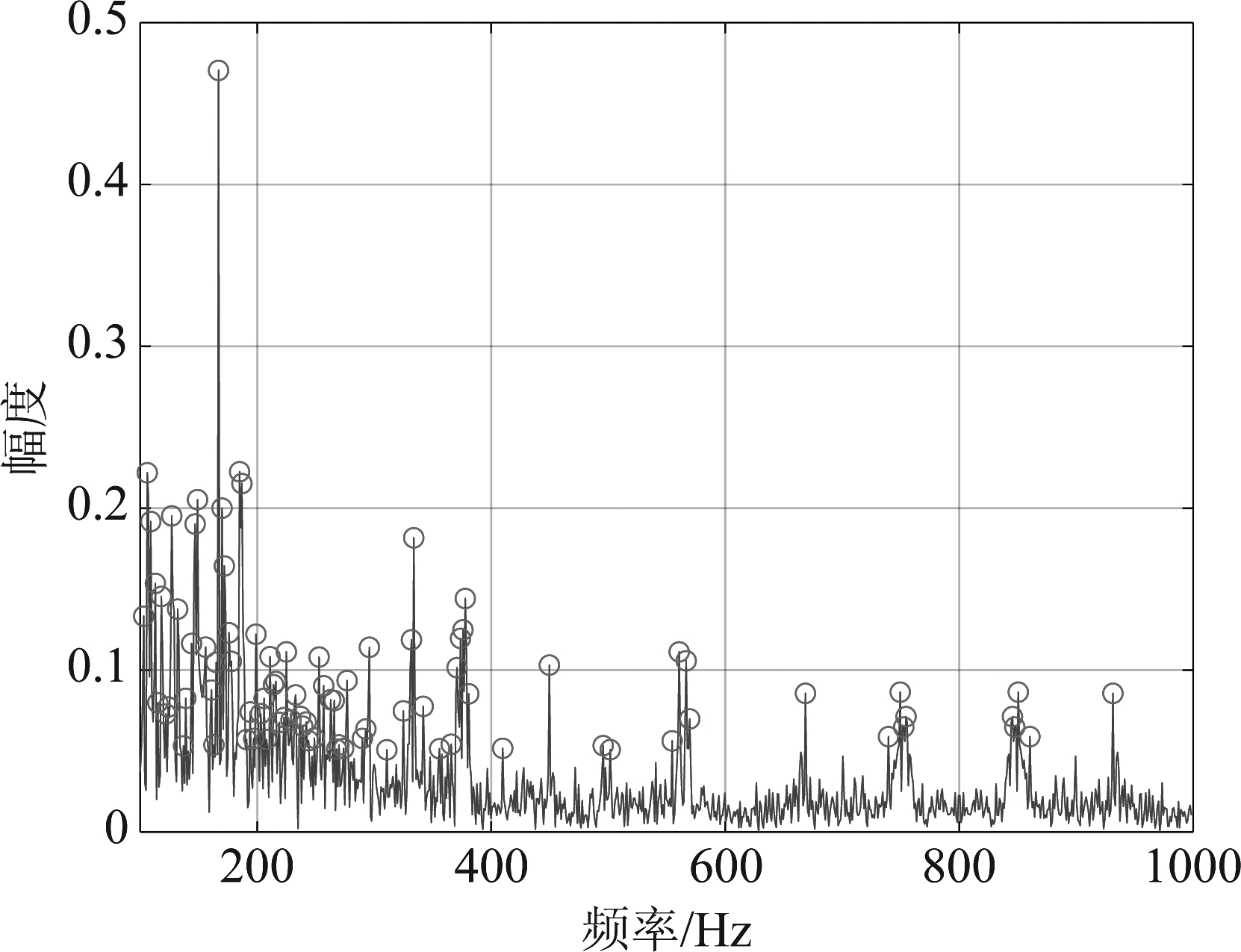
图9 无人机信号的频率图(SNR=-20 dB)
Fig.9 Frequency diagram of UAV signals(SNR=-20 dB)
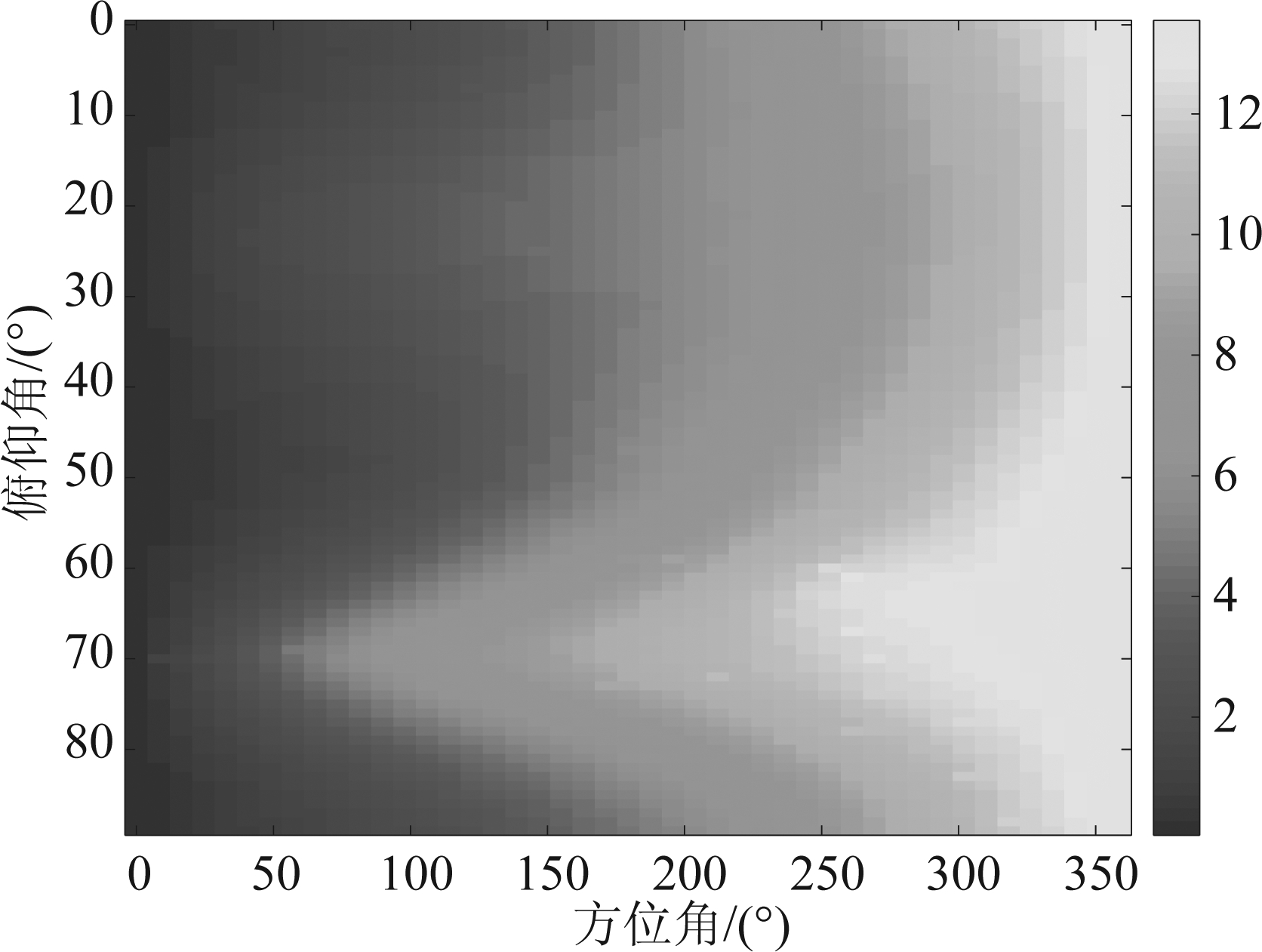
图10 CLEAN-SC定位结果图
Fig.10 CLEAN-SC positioning result diagram
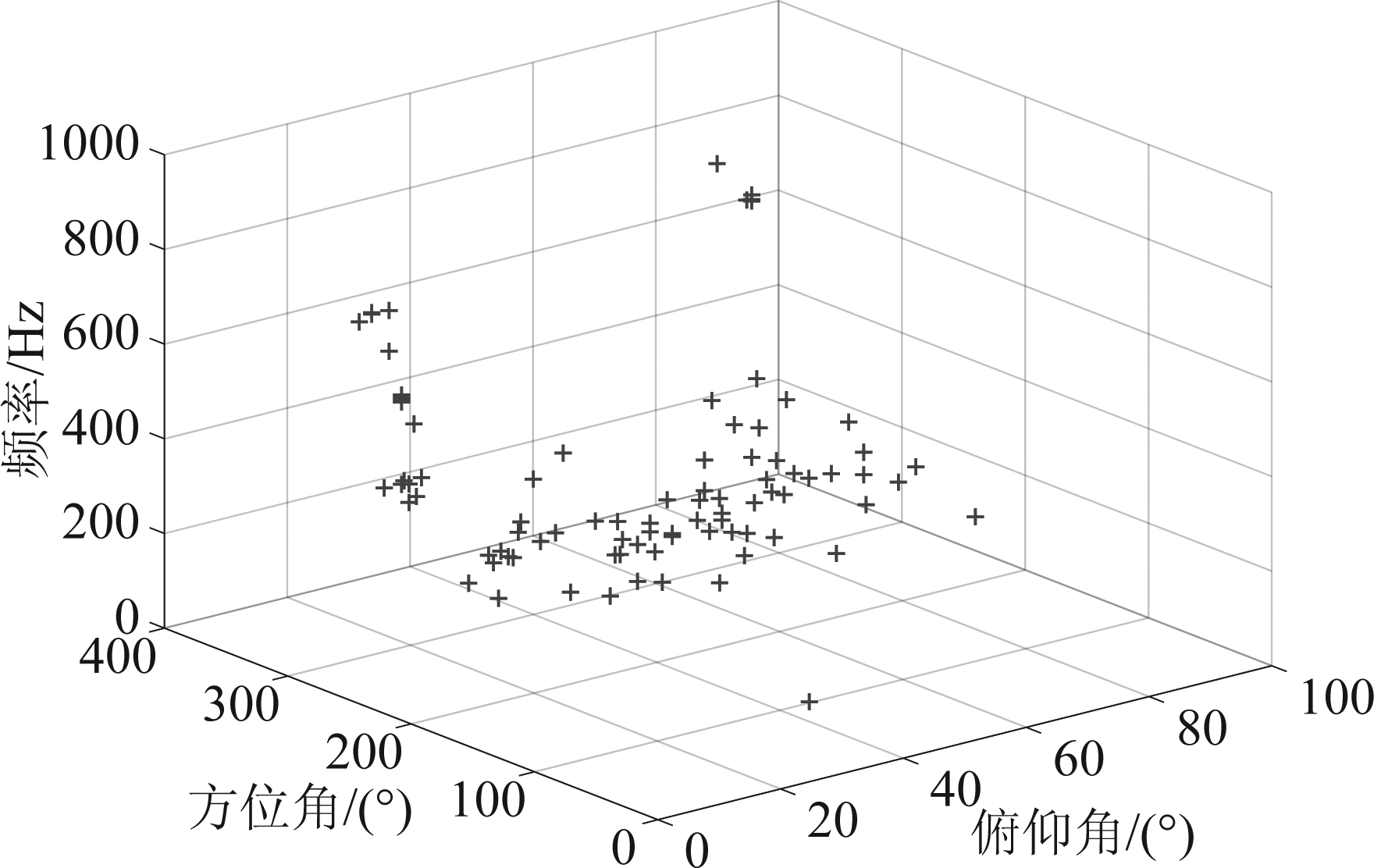
图11 无人机空间位置估计
Fig.11 UAV spatial position estimation
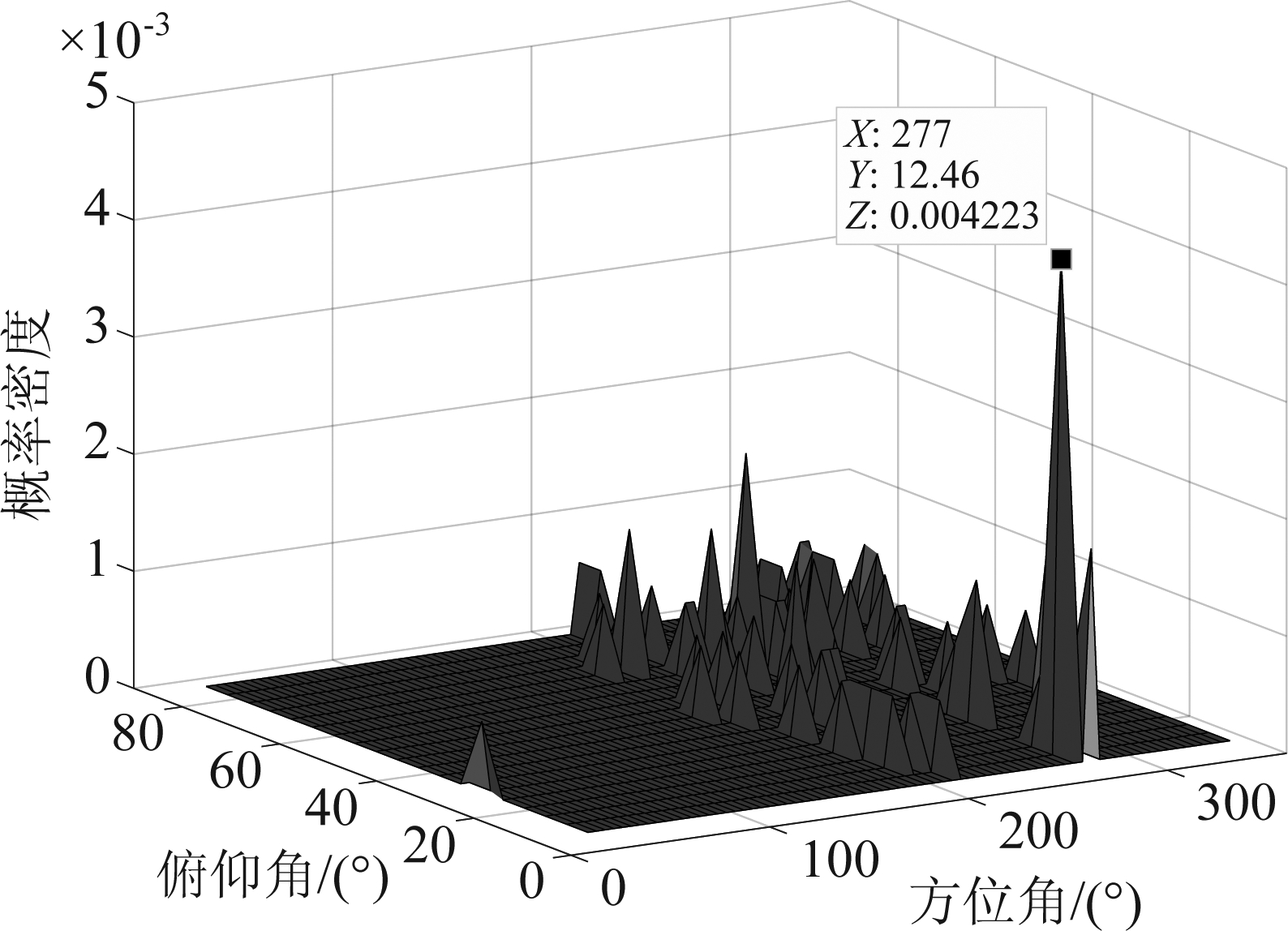
图12 Parzen窗函数估计概率密度函数图
Fig.12 Parzen window function estimation probability density function diagram
从上述结果可知,虽然CLEAN-SC算法计算效率高、收敛快、旁瓣衰减能力及抗干扰能力强,但对于远距离混杂信号,无法有效探测到无人机目标。在特征约束条件下使用高分辨率的CLEAN-SC算法,并结合非参数估计的Parzen窗方法,获得空域定位结果的概率密度函数,其最大值对应角度即为探测到的无人机目标方向。该方法可以从杂乱无章的无人机空域位置(图11所示)中确定无人机来向(图12所示),在工程上是一种行之有效的混杂环境声源探测方法。
5 结论
传统的阵列信号处理算法处理模型完备,但在复杂环境条件下,对混杂信号分离处理能力弱,本研究针对阵列中空频矩阵,采用非参数模型方法进行优化分析,对混杂无人机的检测问题建立模型,实验结果表明此方法可在混杂环境下有效实现无人机检测。
本研究工作主要贡献是面向复杂环境中多声源混叠问题,利用阵列信号处理的方法获得空间谱矩阵的闭式解，将求解目标方位过程转变为采用基于非参数估计的多维融合方法求解目标方位信息。未来的工作需重点关注后续融合处理模式,阵列信号处理模型优化改进方法以及如何建立时空频联立协同优化模型及目标特征优化建模方法在智能阵列信号处理中的应用。
[1] Deren L I, Ming L I. Research Advance and Application Prospect of Unmanned Aerial Vehicle Remote Sensing System[J]. Geomatics and Information Science of Wuhan University, 2014.
[2] 罗伦楷. 近地飞行目标的声测定向技术研究[D]. 山东: 山东科技大学, 2009. DOI: 10.7666/d.D299655.
Luo Lunkai. Technology Research of Acoustic Detetion of Low Flying Targets in the Sky[D]. Shangdong: Shandong University of Science and Technology, 2009. DOI:10.7666/d.D299655.(in Chinese)
[3] 周志文. 输电线路的无人机测距技术研究与应用[D]. 北京: 华北电力大学, 2014. DOI:10.7666/d.Y2657693.
Zhou Zhiwen. Research and application of ranging technology of Unmanned Aerial Vehicle in transmission lines[D]. Beijing: North China Electric Power University, 2014. DOI:10.7666/d.Y2657693.(in Chinese)
[4] T. Scott Brandes, Robert H. Benson. Sound source imaging of low-flying airborne targets with an acoustic camera array[J]. Applied Acoustics, 2007, 68(7): 752-765.
[5] Chiariotti Paolo, Martarelli Milena, Castellini Paolo. Acoustic beamforming for noise source localization Reviews, methodology and applications[J]. Mechanical Systems and Signal Processing, 2019, 120: 422- 448.
[6] Koyano Y, Yatabe K, Oikawa Y. Infinite-dimensional SVD for analyzing microphone array[C]∥IEEE International Conference on Acoustics. IEEE, 2017.
[7] Q. Leclère, Antonio Pereira, Christophe Bailly, et al. A unified formalism for acoustic imaging based on microphone array measurements[J]. International Journal of Aeroacoustics, 2017, 16(4-5): 431- 456.
[8] Sijtsma, Pieter. CLEAN based on spatial source coherence[J]. International Journal of Aeroacoustics, 2007, 6(4): 357-374.
[9] Quayle A R, Dowling A P, Graham W R, et al. Obtaining absolute acoustic spectra in an aerodynamic wind tunnel[J]. Journal of Sound and Vibration, 2011, 330(10): 2249-2264.
[10] 赵小见, 赵磊, 陈农. 基于相干声源CLEAN算法的常规风洞声源辨识研究[J]. 空气动力学学报, 2011, 31(2): 239-243.
Zhao Xiaojian, Zhao Lei, Chen Nong. The Study of Noise Source Identifying Clean Arithmetic Based on Spatial in Wind Tunnel with Source Coherence[J]. Acta Aerodynamica Sinica, 2011, 31(2): 239-243.(in Chinese)
[11] 杨洋, 褚志刚. 基于CLEAN-SC清晰化波束形成的汽车前围板隔声薄弱部位识别[J]. 声学技术, 2015, 34(5): 449- 456.
Yang Yang, Chu Zhigang. Weak position identification of sound insulation for car dash panel based on CLEAN-SC clearness beamforming[J]. Technical Acoustics, 2015, 34(5): 449- 456.(in Chinese)
[12] Allam M, Moghaddamjoo A. Two-dimensional DFT projection for wideband direction-of-arrival estimation[J]. IEEE Transactions on Signal Processing, 1995, 43(7): 1728-1732.
[13] Parzen E. On estimation of a probability density function and mode[J]. Ann. Math. Statis. 1962, 33(3): 1065-1076.
[14] 孙乃葳, 李建辰, 万亚民. Parzen窗估计在潜艇目标强度统计建模的应用[J]. 舰船科学技术, 2017, 39(2): 132-136. DOI:10.3404/j.issn.1672-7619.2017.02.026.
Sun Naiwei, Li Jianchen, Wan Yamin. Application of parzen window estimation in submarine target strength statistics modeling[J]. Ship Science and Technology, 2017, 29(2):132-136. DOI:10.3404/j.issn.1672-7619.2017.02.026.(in Chinese)
[15] 庞菲菲, 张群飞, 史文涛, 等. 基于Parzen窗的水下无线传感器网络目标定位方法[J]. 电子与信息学报, 2017,39(1): 45-50. DOI:10.11999/JEIT160246.
Pang Feifei, Zhang Qunfei, Shi Wentao, et al. Target Localization Method Based on Parzen Window in Underwater Wireless Sensor Network[J]. Journal of Electronics & Information Technology, 2017, 39(1): 45-50. DOI:10.11999/JEIT160246.(in Chinese)
[16] Mussa, Hamse Y, Mitchell, John B O, Afzal, Avid M. The Parzen window method: in terms of two vectors and one matrix[J]．Pattern Recognition Letters, 2015, 63: 30-35．
[17] Harvey B, Siu O’Young. Acoustic Detection of a Fixed-Wing UAV[J]. Drones, 2018, 2(1):4.
[18] Sedunov A, Salloum H, Sutin A, et al. UAV Passive Acoustic Detection[C]∥Ieee International Conference on Technologies for Homeland Security, 2018: 1- 6.10.1109/ THS.2018.8574129.
[19] Guvenc I, Ozdemir O, Yapici Y, et al. Detection, localization, and tracking of unauthorized UAS and Jammers[C]∥Ieee Aiaa Digital Avionics Systems Conference, 2017: 1-10.
[20] Farlik J, Kratky M, Casar J, et al. Multispectral Detection of Commercial Unmanned Aerial Vehicles[J]. Sensors, 2019, 19(7).
[21] 冯大航,鲍明,管鲁阳, 等.一种恒虚警线谱检测算法研究[J].声学技术,2012,31(3):304-309. DOI:10.3969/j.issn.1000-3630.2012.03.014.
Feng Dahang, Bao Ming, Guan Luyang, et al. An algorithm of line-spectrum detection with constant false alarm rate[J]. Technical Acoustics,2012, 31(3): 304-309. DOI:10.3969/j.issn.1000-3630.2012.03.014.(in Chinese)
[22] 陈银超, 杨伟. 基于Parzen窗估计的电液伺服作动器故障检测与健康评估[J]. 计算机测量与控制, 2012, 20(8): 72-73,77.
Chen Yinchao, Yang Wei. Electric Hydraulic Servo Actuator Fault Detection and Health Assessment Based on Parzen Window Estimation[J]. Computer Measurement & Control, 2012, 20(8): 72-73,77.(in Chinese)
