1 引言
恒虚警(Constant False Alarm Rate,CFAR)处理是声纳自动检测中的一个重要技术环节[1-2],其作用是使自动检测摆脱混响背景功率水平波动的影响、保持恒定的虚警概率。为达到该目的,该技术从与待检测单元相邻的参考单元中选取辅助数据,完成对背景混响平均功率的估计,从而获得可以自适应于背景环境变化的检测阈值[3]。早在上世纪六十年代,单元平均(Cell Averaging,CA)CFAR检测器由Finn和Johnson所提出,这开启了CFAR检测研究的理论先河[4]。虽然CA-CFAR是在均匀环境下的准最优检测器,但是它在多目标干扰环境中的性能严重恶化,水下的多径效应是导致该情况出现的一个主要原因。为了削弱多目标干扰对检测造成的不良影响,Trunk[5]和Rohling[6]分别在1978年和1983年提出了最小选择(Smallest Of,SO)和有序统计(Order Statistics,OS)CFAR检测器。这两种检测器的抗干扰能力相比于CA-CFAR有大幅提高,但却是以牺牲均匀背景下的检测性能为代价而换取的。为此,Farrouki和Barkat提出了自动删除单元平均(Automatic Censoring Cell Averaging,ACCA)CFAR检测器[7],该检测器通过假设检验的循环执行,可以准确地估计出环境中的干扰目标数并予以删除[8],在提高CFAR检测抗多目标干扰能力的同时,减小了在均匀背景中的性能损失。
随着声纳理论与技术的发展,高分辨声纳的距离分辨率已远小于目标尺寸,因此目标回波的能量不再局限于一个距离单元,而是在径向方向上连续地占据多个距离单元,称为“距离扩展目标”[9]。在此条件下,基于点目标假设的检测技术难以充分地利用目标回波特性,影响声纳的检测性能。因此需进一步发展和研究距离扩展目标检测技术[10-11]。近年来,高斯背景下距离扩展目标的检测已经引起国内外学者的重视。文献[12]尝试采用二进制积累来解决该问题,其选用的第一门限检测方法是OS-CFAR。文献[13]将模糊检测器应用于距离扩展目标检测研究之中,提出了模糊CFAR检测方法,相比于二进制积累,模糊检测更进一步地提高了距离扩展目标的检测性能。传统的二进制CFAR在第一门限检测步骤中被模糊CFAR代替,即采用“软”判决来替换“硬”判决;随后采用模糊积累准则对“软”判决结果进行积累,获得最终的检测统计量。虽然检测性能有所提升,但文献[13]中所采用的模糊OS-CFAR在均匀背景下的检测性能仍有待提高,其对抗干扰目标的个数也受到理论序值的限制,所以性能上还存在一定的提升空间。
为了解决上述不足,本文提出了一种新的距离扩展目标模糊CFAR检测方法,采用ACCA-CFAR作为第一门限检测方法,然后与模糊算数和、模糊代数和、模糊代数积三种模糊积累准则相结合来完成检测。值得说明的是模糊算数和积累准则是首次采用,文中推导出其虚警概率的解析表达式,为检测门限的选取提供了理论依据。仿真结果表明,新方法可实现高斯混响背景下距离扩展目标的稳健检测。
本文其余章节安排如下:第2节介绍ACCA-CFAR,第3节提出基于模糊ACCA-CFAR的距离扩展目标检测方法,第4节是仿真分析,最后一节对全文进行总结。
2 ACCA-CFAR检测器
ACCA-CFAR检测器是针对多目标干扰环境而提出的,它利用一种基于排序数据方差(Ordered Data Variability,ODV)的删除算法,通过连续的假设检验估计出干扰目标数并予以删除,对剩余样本采用CA方法进行处理。其原理框图如图1所示。
其中,D是检测单元,x1,...,xn与xn+1,...,x2n分别组成前沿、后沿参考滑窗,整个参考滑窗内的参考单元有2n个,检测单元与前后沿滑窗之间分别有一个保护单元,保障D内的信号能量不会泄漏到参考滑窗中。ACCA方法的基本工作流程是:
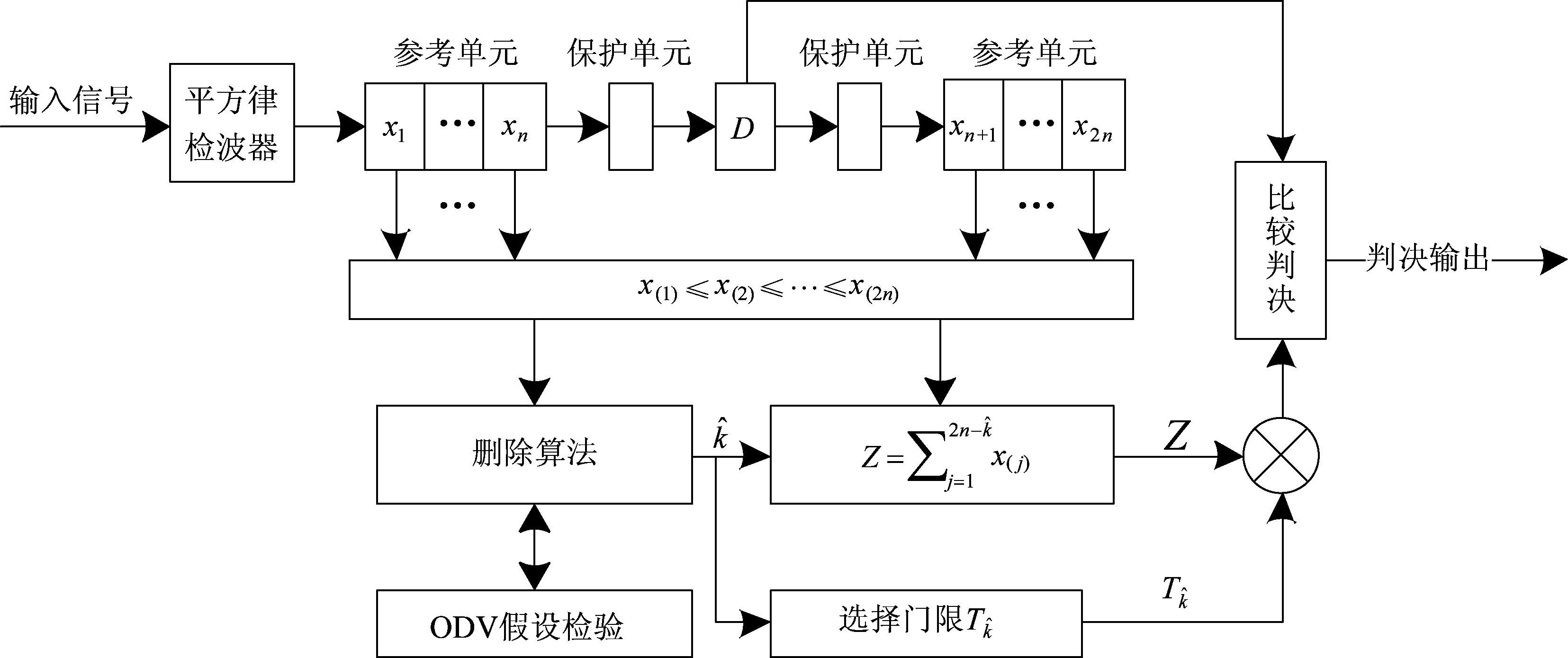
图1 ACCA-CFAR检测器原理框图
Fig.1 Principle block diagram of ACCA-CFAR detector
(1)对参考单元进行升序排序,得到序列{x(i)},x(1)≤...≤x(2n);
(2)采用基于ODV统计量的删除算法对序列{x(i)}进行操作,确定删除干扰目标数
(3)根据剩余的
个最小参考单元,采用CA方法获得混响背景功率估计Z;
(4)将检测单元与自适应阈值进行比较,判断有无目标。判决准则为
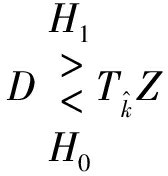
(1)
其中,H1表示目标存在,H0表示目标不存在;
是阈值因子,由期望虚警概率和
值确定。
2.1 ODV假设检验与删除算法
取升序序列{x(i)},x(1)≤...≤x(2n)中长度为m+1(m<2n)的排序子集W={x(1),x(2),...,x(m),y},得到一个ODV统计量
(2)
其中,
对式(2)求导置零后得到两个根p1=-σm,p2=μm/σm。p2代表一个局部最小值,根据σm和μm的定义,p2可以表示为
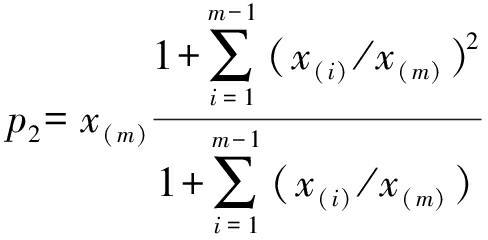
(3)
对于i=1,2,...,m-1,有x(i)/x(m)≤1,因而p2≤x(m)≤x(m+1)。由此可知,若y在区间[x(m+1),x(2n)]内递减,那么ODV(y)也是递减的。为了使删除算法能够确定出干扰目标数,需要保证假设检验的连续执行。为此,定义一个检测统计量
Yj=ODV(y)|y=x(2n-j), j=0,1,...,2n-m-1
(4)
对于j=0,1,...,2n-m-1而言,Yj是递减的,即有Y2n-m-1≤Y2n-m-2≤...≤Y1≤Y0。
对于连续的第j个假设检验,其自适应判决准则为
(5)
其中,Hnh假设为第j个排序子集W|y=x(2n-j)是非均匀的,Hh则假设其是均匀的;Sj是与Yj相对应的检测门限,由删除算法对干扰目标数的期望误检概率决定。
删除算法的基本原理是用m个最小参考单元来表示背景混响功率水平的原始估计值,删除算法中的假设检验通过如前所述的ODV统计量与自适应判决准则来重复执行;如果在第j步,算法判定子集W|y=x(2n-j)是均匀的,则子集W|y=x(2n-j)中的参考单元数据将用作背景混响功率估计。具体步骤是:
(1)令y=x(2n-j),并由升序序列{x(i)},x(1)≤...≤x(2n)获得长度为m+1的排序子集W={x(1),x(2),...,x(m),y};
(2)ODV统计量Yj由式(2)和式(4)计算获得,之后再根据式(5)执行假设检验;
(3)对于j=0,1,...,2n-m-1,重复执行步骤(1)和(2),直到W|y=x(2n-j)被判定为均匀或j=2n-m为止;
(4)由删除算法估计出的干扰目标个数即为
2.2 ACCA-CFAR的虚警概率和检测概率
根据文献[14],删除干扰目标数为
时,ACCA的矩母函数为
(6)
其中, μ是混响背景功率水平。因此,相对应的虚警概率和检测概率为
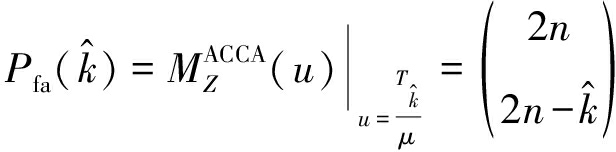
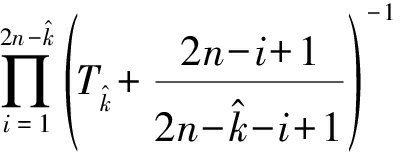
(7)
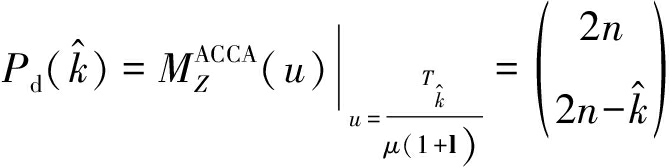
(8)
其中,l是信混比(Signal Reverberation Ratio,SRR)。对于指定的期望虚警概率值,可以得到一组不同值时的阈值因子
的总检测概率为
(9)
其中
为均匀背景情况下
的概率。
3 基于模糊ACCA-CFAR的距离扩展目标检测
本节首先推导ACCA-CFAR的模糊隶属函数,在此基础上,给出基于模糊ACCA-CFAR的距离扩展目标检测方法。对三种模糊积累准则进行讨论,首次将模糊算数和积累准则应用于距离扩展目标检测方法之中,进一步地推导出该准则虚警概率的解析表达式。并且在最后对另两种积累准则——模糊代数和、模糊代数积作简要介绍。
3.1 模糊ACCA-CFAR
由模糊检测器所定义的隶属函数ω,用来表示“无信号”与“有信号”两种假设成立与否的程度[15-16],它把所观测的空间映射成一个介于0到1之间的数值,定义为
ω(ν)=P(V>ν|H0)=1-FV(ν)
(10)
其中,ν=D/Z是单个检测单元数据D与背景混响功率估计Z之比。随机变量V定义为比值ν所对应的随机变量,FV(ν)则为V的累积分布函数。ω(ν)单调递减,强距离单元值会被赋予小的隶属值,因此,判断目标存在的条件是ω(ν)小于所设定的模糊检测门限值。由文献[17]可知,由任意连续随机变量的累积分布函数所形成的新随机变量均匀分布于区间[0,1],由式(10)可以看出,隶属函数ω(ν)也在[0,1]上服从均匀分布。根据式(10)的物理意义可得
ω(ν)=P(V>ν|H0)=pfa|T=ν=pfa(ν)
(11)
其中,pfa为检测器的虚警概率表达式。若在距离扩展目标检测方法中应用模糊检测,pfa为第一门限检测的虚警概率,因此式(11)为隶属函数与第一门限检测的虚警概率之间的关系表达式。将式(7)中的替换为ν,就可得到删除干扰目标数为时,基于ACCA的模糊检测方法的隶属函数
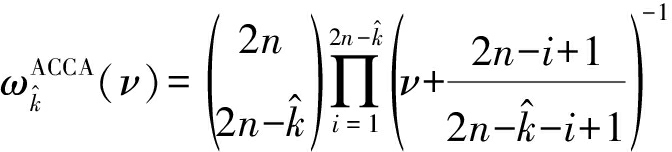
(12)
采用模糊ACCA-CFAR替换文献[13]中的模糊OS-CFAR,新的距离扩展目标检测方法得以提出,图2为其原理框图。
其中,连续的S个距离分辨单元被距离扩展目标所占据,即所需进行第一门限检测的目标距离单元有S个。对于所有的目标距离单元值Di,i=1,2,...,S,均可由式(12)转换成一个模糊隶属函数值
这S个模糊隶属函数值通过具体的模糊积累准则完成积累,从而获得最终的检测统计量。最后与所选模糊准则相对应的检测门限进行比较,输出判决结果。
3.2 模糊积累准则
模糊代数和、模糊代数积这两种常用的模糊积累准则在文献[13]中已详细研究并给出了虚警概率的推导过程,在此基础上,本文考虑另一种模糊积累准则——模糊算数和积累。
图2 基于模糊ACCA-CFAR的距离扩展目标检测方法原理框图
Fig.2 Principle block diagram of detection method based on fuzzy ACCA-CFAR for range-extended targets
(1)模糊算数和积累准则
模糊算数和准则的检测统计量和判决准则分别为
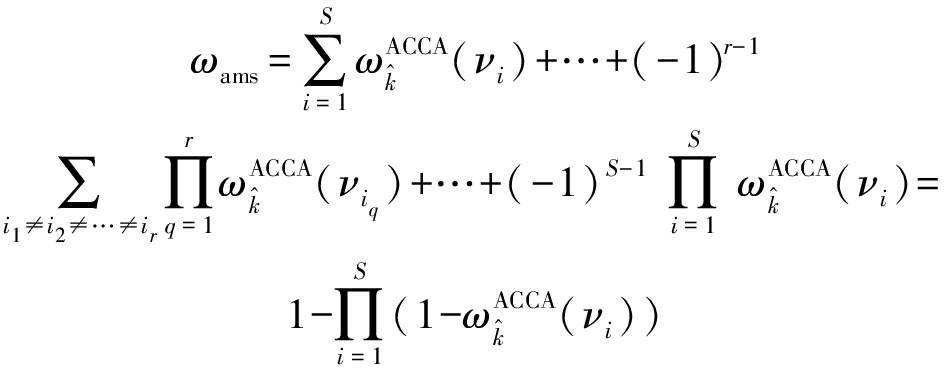
(13)
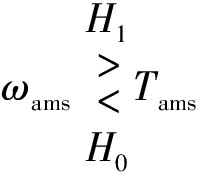
(14)
其中,Tams是模糊算数和的检测门限。由于
在均匀分布于区间[0,1],因此
也均匀分布于[0,1]。由文献[14]可知,由S个均匀分布随机变量之积所组成的新随机变量的概率密度函数为
(15)
所以,ωams的概率密度函数
(16)
因此,模糊算数和的虚警概率可表示为
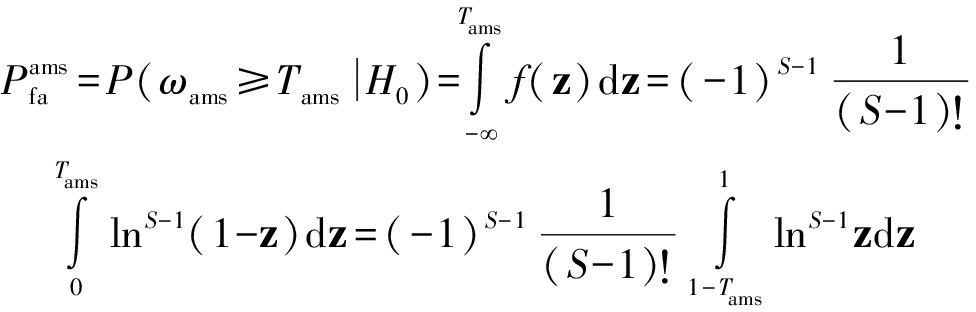
(17)
式(17)的积分部分采用分部积分法处理,从而得到
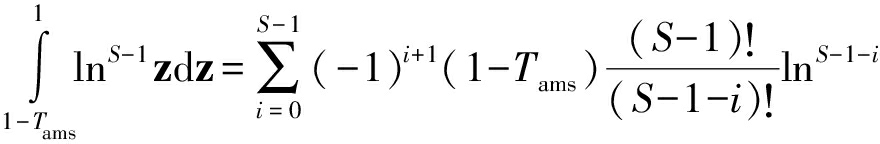
(1-Tams)-(-1)S(S-1)!
(18)
将式(18)代入式(17),可得模糊算数和准则的虚警概率解析表达式
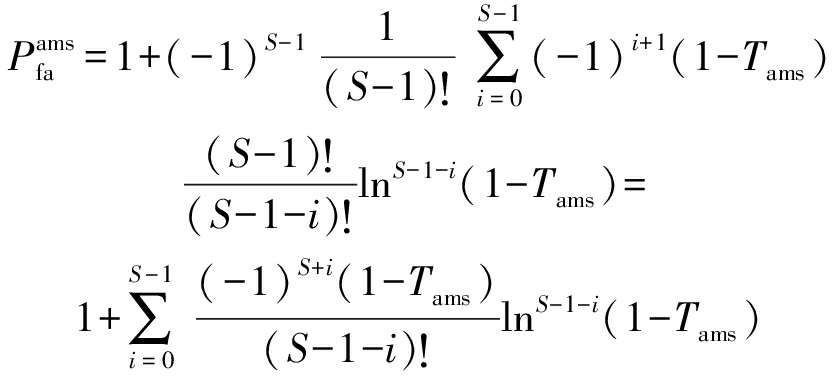
(19)
(2)模糊代数和积累准则
模糊代数和准则的判决准则为
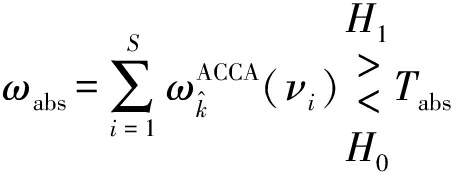
(20)
其中,Tabs是模糊代数和的检测门限。其虚警概率为[13]
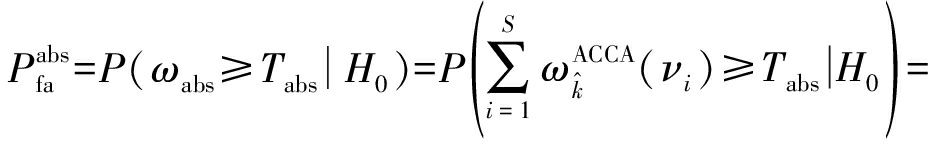
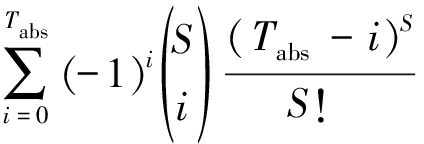
(21)
(3)模糊代数积积累准则
模糊代数积准则的判决准则为
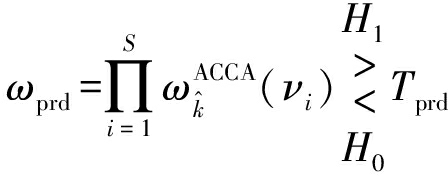
(22)
其中,Tprd是模糊代数积的检测门限。其虚警概率为[13]
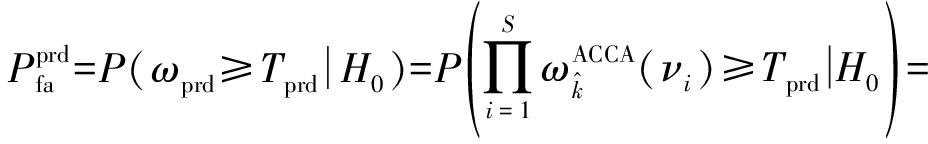
(23)
图3为三种积累准则的虚警概率与检测门限的关系曲线,三种积累准则的检测门限可由给定的期望虚警概率而确定。
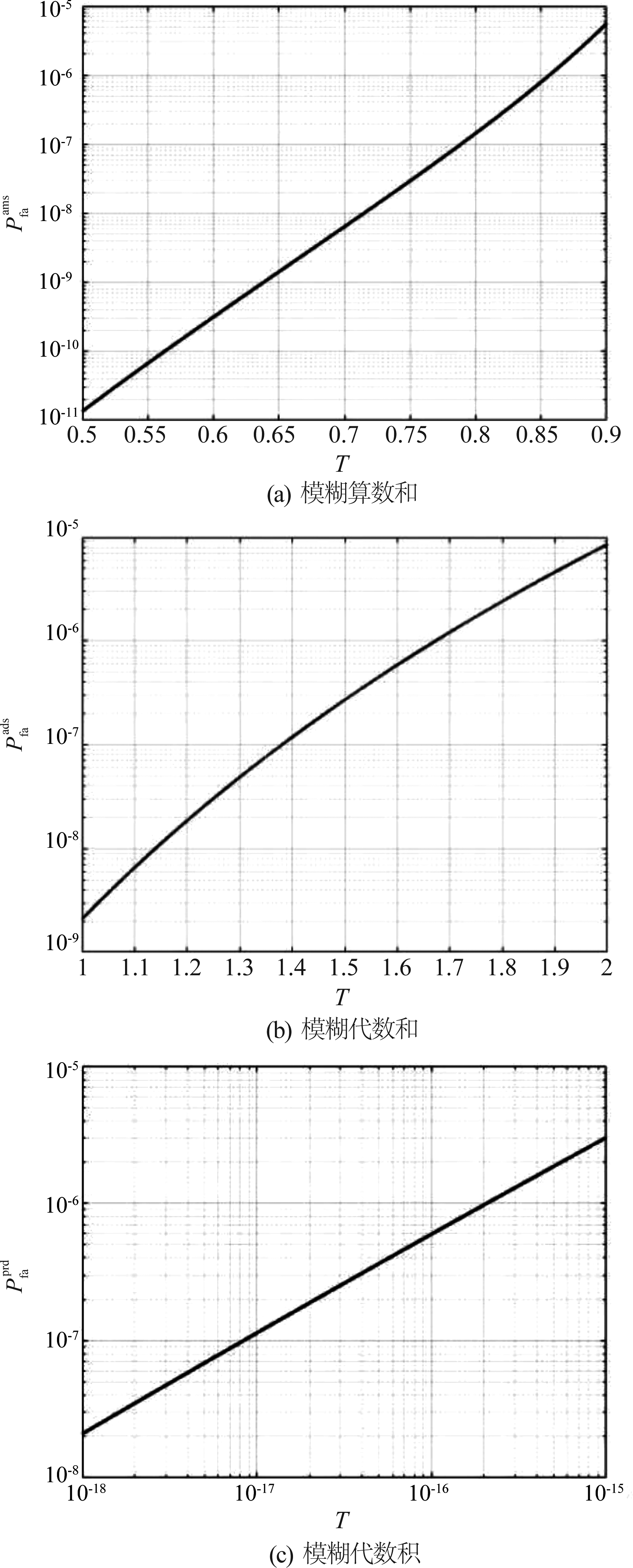
图3 虚警概率与检测门限的关系曲线
Fig.3 The relation curve between false alarm probability and detection threshold
4 性能分析
下面将分别针对非起伏目标(Swerling 0型)和起伏目标(Swerling II型)两种目标模型,通过蒙特卡洛仿真实验来分析基于模糊ACCA-CFAR的距离扩展目标检测方法在均匀混响环境和多目标干扰环境中的检测性能。为了对比分析,将其与基于模糊OS-CFAR、模糊CA-CFAR的距离扩展目标检测方法一同进行仿真实验。
4.1 非起伏目标的检测性能
采用散射点平均分布在整个距离滑窗内的Swerling 0型目标模型,具体仿真参数设置见表1,ACCA和OS均具有对抗8个干扰目标的能力。用IF和IB分别表示前沿和后沿参考滑窗中的干扰目标个数,干混比(Interference Reverberation Ratio,IRR)与信混比相同,即IRR=SRR。
表1 仿真参数
Tab.1 Simulation parameters
参数参数值参考滑窗长度32目标占据距离单元数12期望虚警概率10-6OS选择序值24ACCA初始子集长度24ACCA期望误检概率10-2蒙特卡洛次数104
图4给出的是在均匀混响环境下不同检测方法的检测性能仿真结果,表2给出了检测概率Pd=0.9时不同检测方法所需达到的信混比。结合图4与表2可以看出,对于同类第一门限检测器,模糊算数和与模糊代数和准则的积累性能较好,其中的模糊算数和略优,而模糊代数积准则性能最差。当应用同一种模糊积累准则时,在小信混比条件下,OS作为第一门限检测器的检测性能最好,随着信混比的增加,ACCA与CA的性能逐渐优于OS。ACCA与CA的性能相当,由表2可知,二者为达到检测概率0.9所需的信混比仅相差0.005 dB左右,这是由于ACCA的删除算法将此环境判定为均匀环境,从而利用所有的参考单元进行背景混响估计,等同于CA方法;而当参考单元仿真值随机出现高幅值时,ACCA将其视为干扰去掉并对剩余的样本进行平均处理,从而避免参考单元出现的个别高幅值对背景混响功率估计的影响,因此ACCA略优于CA方法。
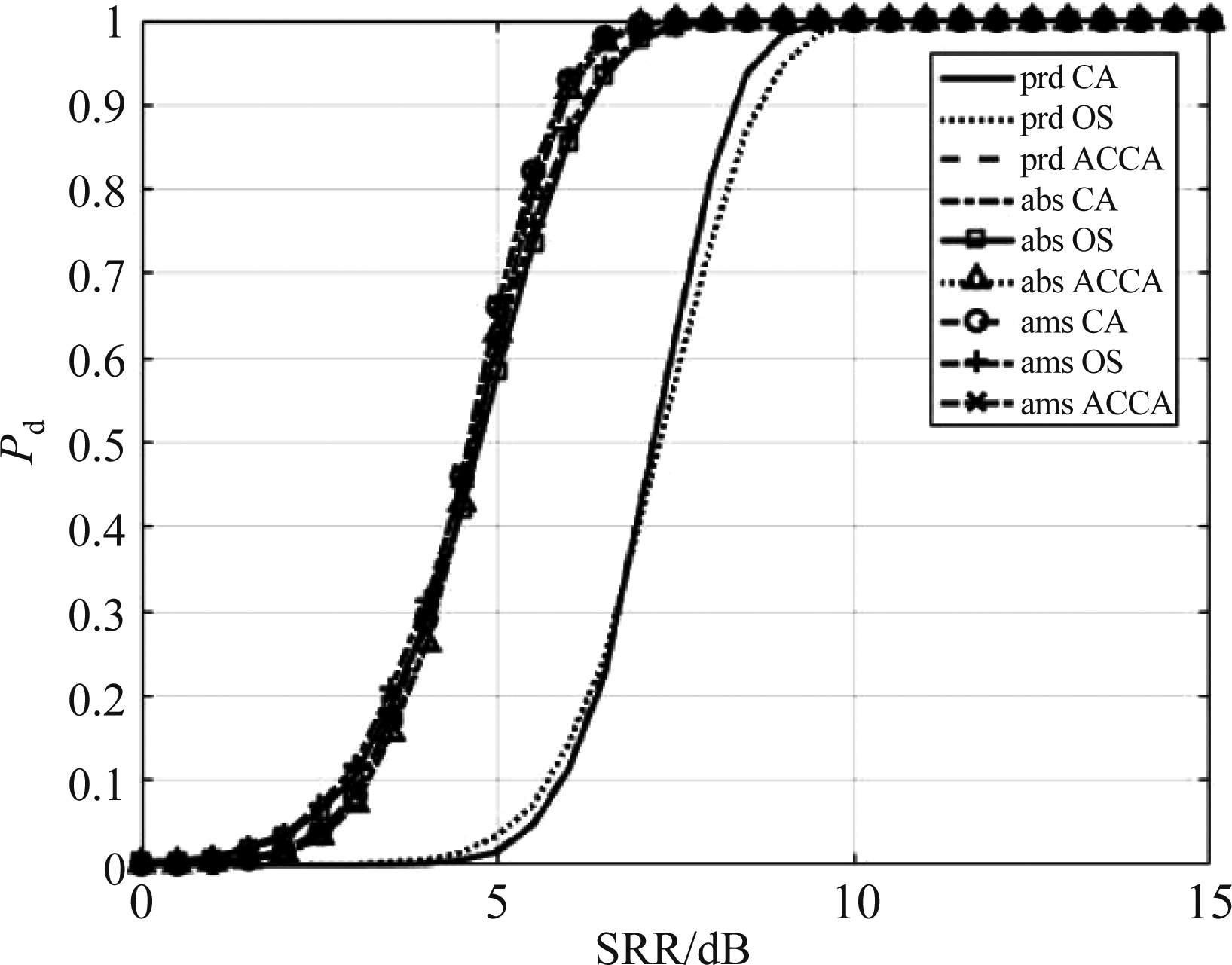
图4 均匀混响环境下不同检测方法的检测性能(非起伏目标)
Fig.4 Detection performance of different detection methods in uniform reverberation background (non-fluctuation targets)
表2 均匀混响环境下检测概率0.9时不同检测方法所需信混比(非起伏目标)
Tab.2 The SRR of different detection methods at detection probability of 0.9 in uniform reverberation background(non-fluctuation targets)
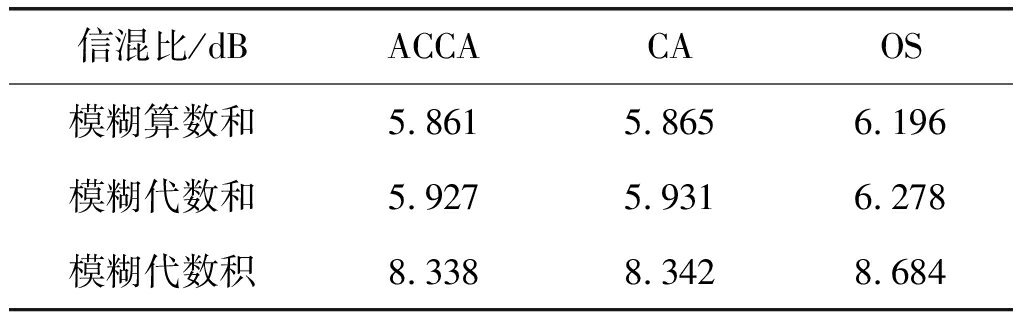
信混比/dBACCACAOS模糊算数和5.8615.8656.196模糊代数和5.9275.9316.278模糊代数积8.3388.3428.684
图5给出的是多目标干扰环境下的仿真结果,其中,图5(a)和图5(b)是参考滑窗中的干扰目标数未超过理论抗干扰数时的仿真结果,图5(c)是参考滑窗中的干扰目标数超过理论抗干扰数时的仿真结果。对于同一种模糊积累准则,因为CA方法没有抗干扰能力,所以基于模糊CA-CFAR的检测性能随干扰目标数的增加而持续下降;当参考滑窗中存在8个干扰目标时,检测方法能达到的检测概率已不足0.2。在图5(a)所示的情况即干扰目标数较少时,OS与ACCA作为第一门限检测器的检测性能相近,OS略优,达到同一检测概率所需满足的信混比相差最大不超过0.4 dB。在图5(b)所示的情况即干扰目标数较多时,随着信混比的增加,ACCA的性能优势逐渐凸显,其与OS检测性能之间的差距逐渐缩小,在信混比8.1 dB左右时二者达到的检测概率相等,随后ACCA的检测性能优于OS并逐渐将检测优势扩大。
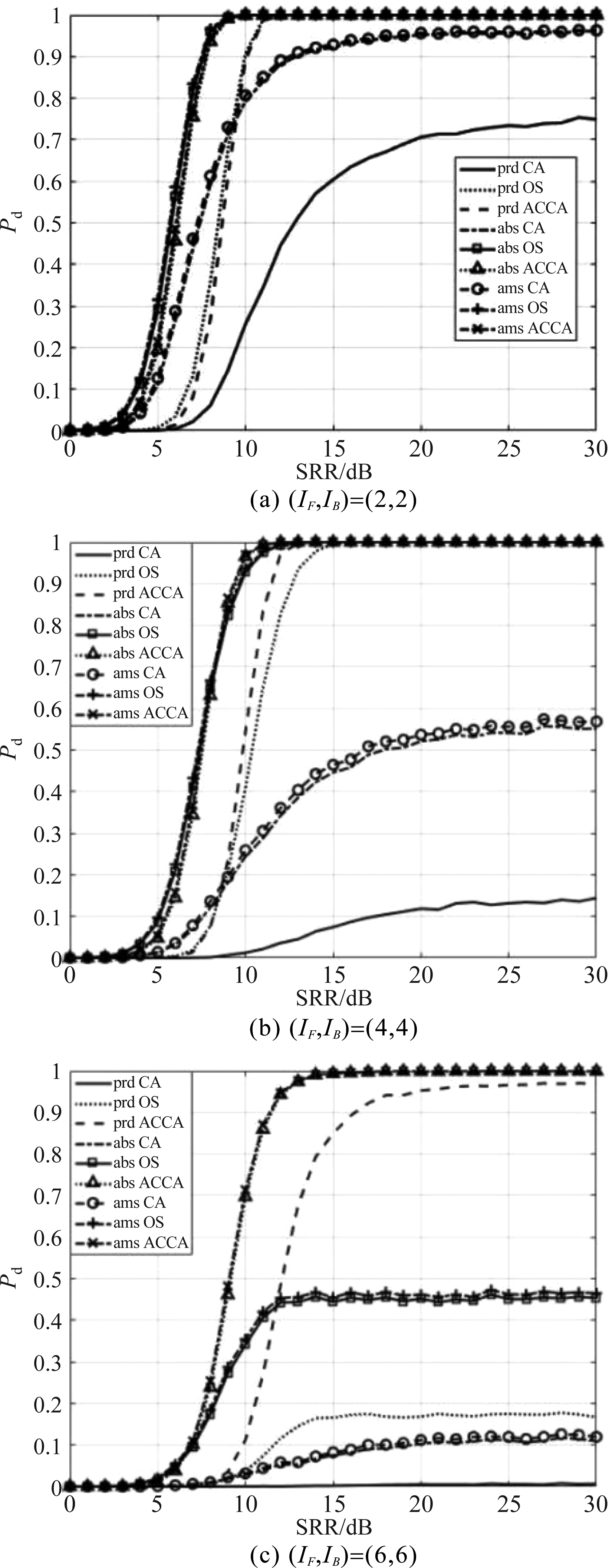
图5 多目标干扰环境下不同检测方法的检测性能(非起伏目标)
Fig.5 Detection performance of different detection methods in multi-target interference background (non-fluctuation targets)
结合图4至图5可知,对于非起伏目标模型,三种模糊积累准则积累效果由好到差依次为模糊算数和、模糊代数和、模糊代数积,其中,模糊算数和与模糊代数和性能十分相近。由图5(c)可以看出,OS检测器在实际干扰数超过理论值的情况下性能不再稳定,随着干扰目标数超出值的增加,检测性能下降。当超出理论值的干扰目标有4个时,基于模糊OS-CFAR的距离扩展目标检测方法所能达到的检测概率最高不足0.5,已不满足声纳正常工作要求。当采用模糊ACCA-CFAR时,应用模糊代数积准则的检测方法在干扰数超过理论值时性能也有所下降,但仍优于基于模糊OS-CFAR的检测性能;而应用模糊算数和或模糊代数和两种模糊积累准则时,检测方法在此情况下性能依然稳健。ACCA方法将自适应估计出的干扰目标数删除后对剩余参考单元进行单元平均处理,比OS方法更加有效利用了参考单元所提供的信息。
4.2 起伏目标的检测性能
采用散射点平均分布在整个距离滑窗内的Swerling II型目标模型,具体仿真参数设置与上节相同,如表1所示。图6是均匀混响环境下不同检测方法的检测性能仿真结果。可以看出,在起伏目标模型下,模糊代数积准则的性能最好,模糊代数和准则次优,模糊算数和最差。应用同一种积累准则时,ACCA与CA作为第一门限检测器的检测性能相当,二者均略优于OS。
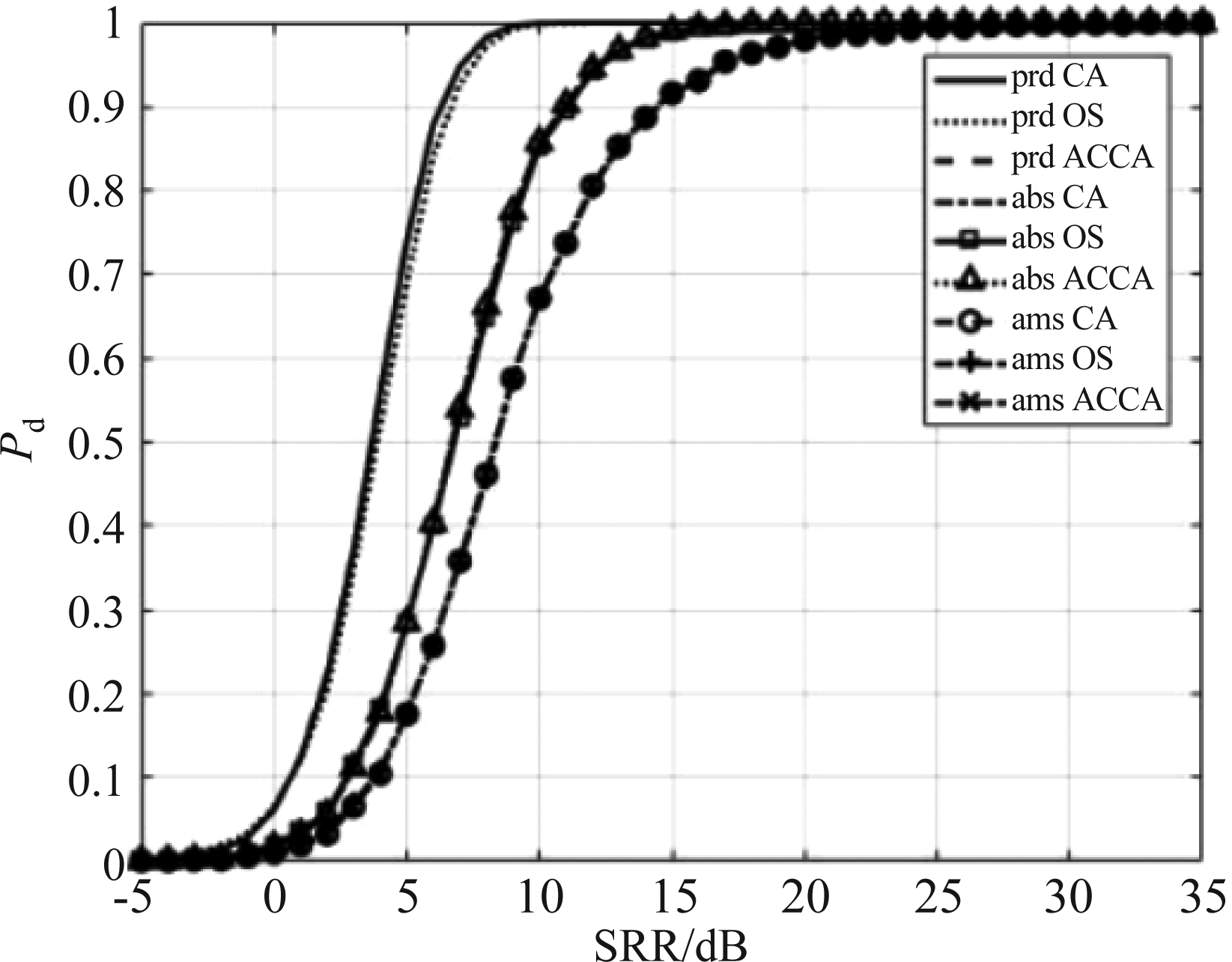
图6 均匀混响环境下不同检测方法的检测性能(起伏目标)
Fig.6 Detection performance of different detection methods in uniform reverberation background (fluctuation targets)
图7是多目标干扰环境下不同检测方法的检测性能,其中图7(a)和图7(b)为干扰数未超过理论值时的仿真结果,图7(c)为干扰数超过理论值时的仿真结果。对于同一种模糊积累准则,图7(a)即干扰目标数较少时,OS与ACCA作为第一门限检测器的检测性能相近,OS略优,达到同一检测概率所需满足的信混比相差最大不超过0.41 dB。随着干扰目标数的增多,OS和ACCA检测性能之间的差距逐渐缩小,在高信混比时,ACCA优于OS。这与上一节同等参数条件下非起伏目标模型所得结论相同。
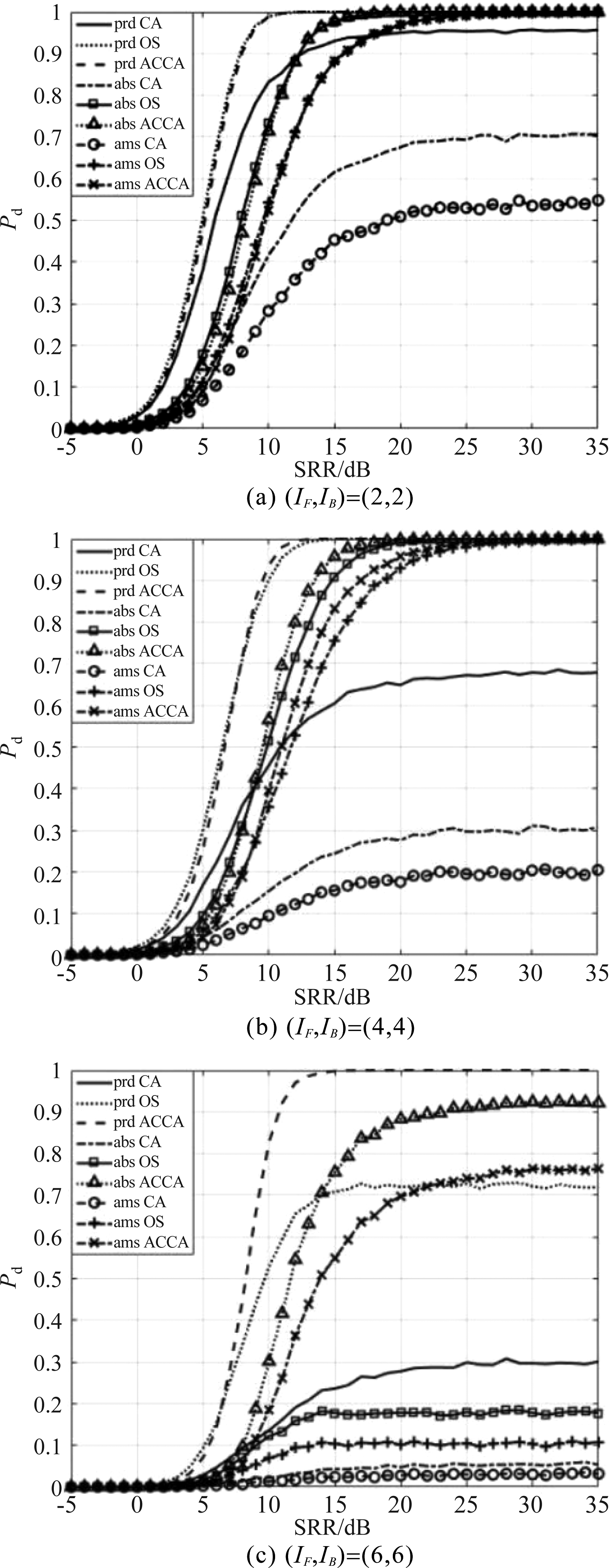
图7 多目标干扰环境下不同检测方法的检测性能(起伏目标)
Fig.7 Detection performance of different detection methods in multi-target interference background
(fluctuation targets)
在干扰数超过理论值时,OS检测器性能下降,无法得到实际工程所需的高检测概率。这一点也与非起伏目标模型结论一致。而基于模糊ACCA-CFAR的距离扩展目标检测方法在这种情况下的性能相较模糊OS-CFAR有较大提升,其中,ACCA与此目标模型下最优的模糊代数积准则相结合,所得到的检测性能依旧稳健。由此可见,基于模糊ACCA-CFAR的距离扩展目标检测方法具有更优的抗多目标干扰能力。
更直观地,在表3中给出了多目标干扰环境下,检测概率Pd=0.9时几种检测方法相对于第一门限采用最优检测的CFAR损失。只有在存在4个干扰目标的情况下,基于模糊CA-CFAR的检测方法能够达到Pd=0.9的检测概率,其在多目标干扰环境中性能下降严重。对于同一种模糊积累准则,干扰目标数越多,ACCA相较于OS的优势越明显。而在表3的后两列即干扰目标数超过理论抗干扰数时,仅有基于模糊ACCA-CFAR的距离扩展目标检测方法能够依旧稳健地工作。
表3 多目标干扰环境下不同检测方法的CFAR损失(起伏目标)
Tab.3 The CFAR loss of different detection methods in multi-target interference background (fluctuation targets)
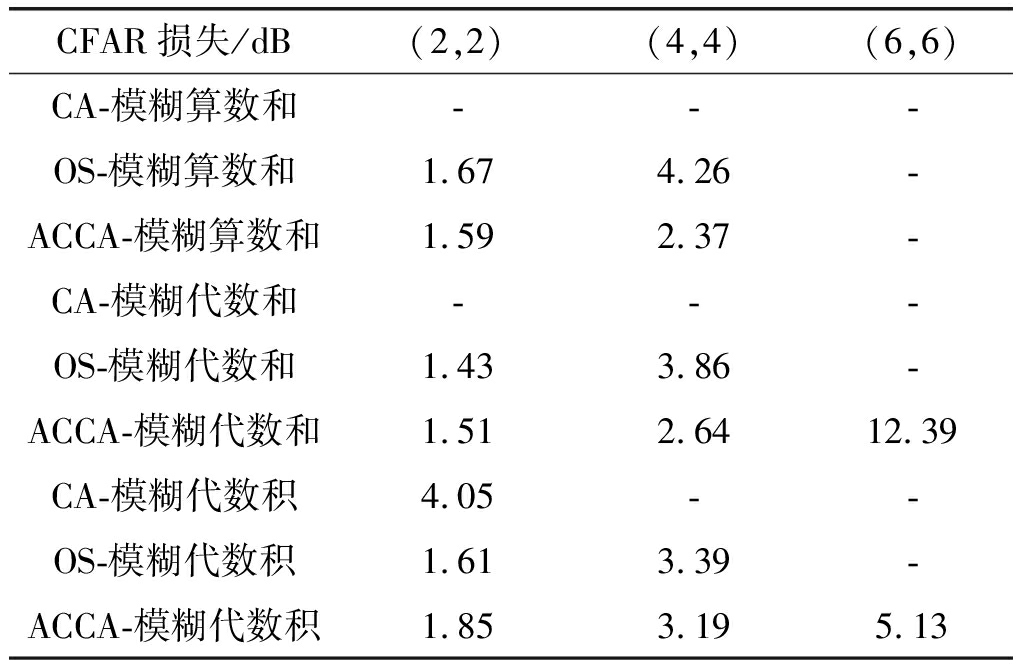
CFAR损失/dB(2,2)(4,4)(6,6)CA-模糊算数和---OS-模糊算数和1.674.26-ACCA-模糊算数和1.592.37-CA-模糊代数和---OS-模糊代数和1.433.86-ACCA-模糊代数和1.512.6412.39CA-模糊代数积4.05--OS-模糊代数积1.613.39-ACCA-模糊代数积1.853.195.13
4.3 模糊积累准则性能差异分析
为了说明在起伏目标和非起伏目标模型下模糊积累准则性能差别的原因,图8给出了S=2时上述3种模糊积累准则的二维检测空间。期望虚警概率设为
横、纵坐标分别为两个距离分辨单元相对应的模糊隶属函数值ω(ν1)、ω(ν2)。
从图8可以看出,模糊算数和与模糊代数和的检测域相近,均是模糊隶属函数值之间相差较小的区域,其中模糊算数和的检测域所允许的模糊隶属函数值差异性更小;而模糊代数积的检测域则是模糊隶属函数值之间相差较大的区域。对于起伏目标模型,ω(νi)(i=1,2,...,S)之间的差异性较大,因此模糊代数积的检测性能优于另两种模糊积累准则。对于非起伏目标模型,ω(νi)之间的差异性较小,因此模糊算数和与模糊代数和的性能均较优,二者中的模糊算数和略优。所以,对于不同的目标起伏模型,模糊积累准则存在性能差异,需要根据目标模型起伏特性的不同来择优选择最适当的模糊积累准则对隶属函数值进行积累,从而最大限度地改善距离扩展目标的检测性能。
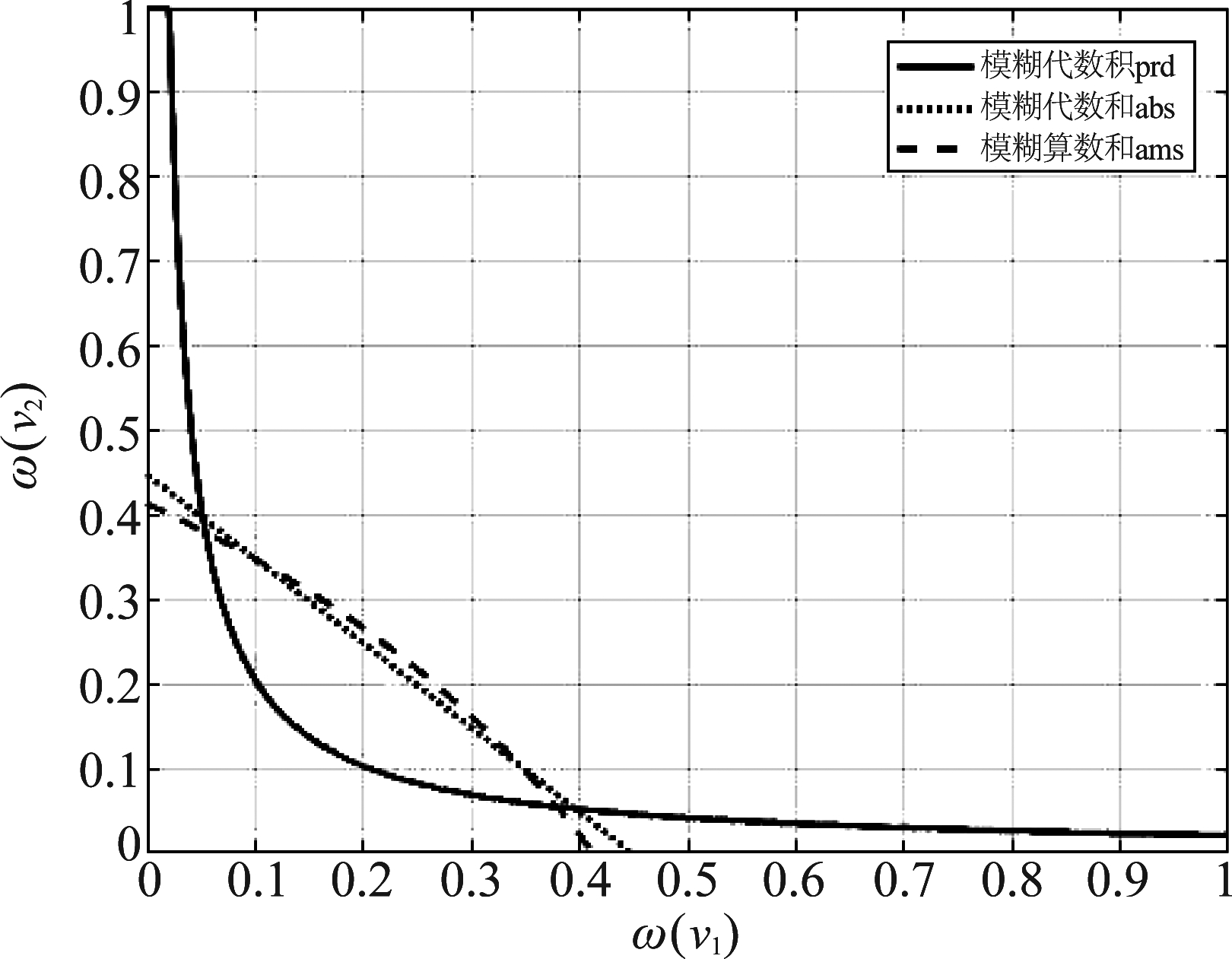
图8 模糊积累准则的二维检测空间
Fig.8 The two-dimensional detection space of fuzzy accumulation criterions
5 结论
为了进一步提高宽带高分辨率声纳对抗多目标干扰的能力,本文基于能够自适应估计出干扰目标数的ACCA-CFAR检测器,在高斯混响背景下提出了一种新的距离扩展目标CFAR检测方法。分析了ACCA作为第一门限检测,后积累分别采用模糊算数和、模糊代数和、模糊代数积三种模糊积累准则的距离扩展目标检测性能,并通过计算机仿真进行验证。结果表明,对于非起伏目标模型,模糊算数和与模糊代数和准则的性能更好;对于起伏目标模型,模糊代数积准则的性能更好。将ACCA与对应于不同目标模型下性能优越的模糊积累准则相结合,可获得较现有方法而言更优的鲁棒性和抗多目标干扰能力。
本文所提出的检测方法在均匀环境和多目标干扰环境下性能优越且稳定,但需要根据目标模型的不同来选择最合适的模糊积累准则。同时,由于ACCA方法在混响边缘环境中的性能较差,本文所提出检测方法的虚警控制能力需要进一步地展开研究。
[1] 张洋忠, 张玉, 唐波. 复合高斯杂波中自适应目标检测算法[J]. 信号处理, 2016, 32(11): 1293-1298.
Zhang Y Z, Zhang Y, Tang B. Adaptive target detection algorithm in compound Gaussian clutter[J]. Journal of Signal Processing, 2016, 32(11): 1293-1298.(in Chinese)
[2] 楼奇哲, 刘乐, 姚元. 采用卷积神经网络的海面多目标检测研究[J]. 信号处理, 2018, 34(9): 1053-1059.
Lou Q Z, Liu L, Yao Y. Multi-target detection in sea clutter with convolutional neural network[J]. Journal of Signal Processing, 2018, 34(9): 1053-1059.(in Chinese)
[3] 王楠, 许蕴山, 夏海宝, 等. 多基地雷达自适应CFAR检测融合算法[J]. 信号处理, 2018, 34(7): 818- 823.
Wang N, Xu Y S, Xia H B, et al. An adaptive fusion algorithm of CFAR detection for multisite radar[J]. Journal of Signal Processing, 2018, 34(7): 818- 823.(in Chinese)
[4] Finn H M, Johnson R S. Adaptive detection mode with threshold control as a function of spatially sampled clutter-level estimates[J]. RCA Review, 1968, 29:414- 464.
[5] Trunk G V. Range resolution of targets using automatic detectors[J]. IEEE Trans. on AES, 1978, 14(5): 750-755.
[6] Rohling H. Radar CFAR thresholding in clutter and multiple target situations[J]. IEEE Trans. on AES, 1983, 19(4): 608- 621.
[7] Farrouki A, Barkat M. Automatic censoring CFAR detector based on ordered data variability for nonhomogeneous environments[J]. IEE Proc.-Radar Sonar Navig., 2005, 152(1): 43-51.
[8] 刘贵如, 王陆林, 邹姗. 基于最大值参考单元的双剔除门限恒虚警目标检测算法[J]. 重庆邮电大学学报: 自然科学版, 2017, 29(3): 409- 415.
Liu G R, Wang L L, Zou S. Dual censoring threshold CFAR target detection algorithm based on maximal reference cell[J]. Journal of East China Normal University: Natural Science, 2017, 29(3): 409- 415.(in Chinese)
[9] 王泽玉. 雷达目标自适应检测算法研究[D]. 西安:西安电子科技大学, 2018.
Wang Z Y. Study of adaptive detection for radar targets[D]. Xi’an: Xidian University, 2018.(in Chinese)
[10] Liu W J, Liu J, Du Q L, et al. Distributed Target detection in partially homogeneous environment when signal mismatch occurs[J]. IEEE Transactions on Signal Processing, 2018, 66(14): 3918-3928.
[11] Liu W J, Liu J, Li H, et al. Multichannel signal detection based on Wald test in subspace interference and Gaussian noise[J]. IEEE Trans. on AES, 2019, 55(3): 1370-1381.
[12] 孟祥伟, 曲东才, 何友. 高斯背景下距离扩展目标的恒虚警率检测[J]. 系统工程与电子技术, 2005, 27(6): 1012-1015.
Meng X W, Qu D C, He Y. CFAR detection for range-extended target in Gaussian background[J]. Systems Engineering and Electronics, 2005, 27(6): 1012-1015.(in Chinese)
[13] 郝程鹏, 蔡龙, 陈模江. 高斯杂波中距离扩展目标的模糊CFAR检测[J]. 系统工程与电子技术, 2010, 32(4): 678- 681.
Hao C P, Cai L, Chen M J. Fuzzy CFAR detection for range-extended targets in Gaussian clutter[J]. Systems Engineering and Electronics, 2010, 32(4): 678- 681.(in Chinese)
[14] 曲超. 主动声纳恒虚警检测方法研究[D]. 北京: 中国科学院声学研究所, 2008.
Qu C. Study on CFAR detection method of active sonar[D]. Beijing: Institute of Acoustics, Chinese Academy of Sciences, 2008.(in Chinese)
[15] Leung S W, Minett J W. The use of fuzzy spaces in signal detection[J]. Fuzzy Sets Systems, 2000, 114(2): 175-184.
[16] Leung S W, Minett J W. A fuzzy approach to signal integration[J]. IEEE Trans. on AES, 2002, 38(1): 346-351.
[17] Papoulis A. Probability, random variables and stochastic processes[M]. New York: McGraw-Hill, 1991.
