1 引言
水声通信网络布放过程中,常会遇到在布放水声通信网络节点时,由于洋流,GPS,船体运动等因素,会造成设想的节点布放地点与实际的布放地点存在误差,不利于节点的维护与电池更换。水下通信节点是水声通信网络的基础。水下通信节点间的距离在一定程度上决定了水下通信网络拓扑结构。拓扑结构对水下通信网络的MAC层协议、路由协议的选择产生重要的影响,从而影响该网络的吞吐能力和能量利用率。研究节点间测距技术对水声通信网络具有重要意义。目前水声测距技术主要有:(1)多项式近似法[11];(2)平均声速法[11];(3)迭代逼近测距[1-2,11]等等。上述测距技术各有优缺点。其中平均声速测距技术的精度一般,但是由于其数学模型简单,物理意义明确,故常常被采用。平均声速测距技术通常适用于大掠射角,传播距离近的声线[12]。多项式近似法的精度很高但是受深度误差影响很大,并且在同一深度处,近程精度>中程精度>远程精度[12]。迭代逼近法的精度非常高,取决于最初设定的精度。迭代逼近法的局限在于其计算量较大并且满足不了系统实时性要求[12]。由于海洋声信道是时变,空变的,这些特点导致影响测距的各个因素都无法用严格的函数表达。所以为了得到更低的测距误差,就需要采取特殊的方式。虚源法[3- 4]被动测距技术是利用了海洋多途信道的特点来提高测距的精度,并且该算法具有抗多途干扰,计算简便,物理意义明确并且能适应介质及边界水平变化的特点。本论文将对该方法展开研究。近几十年来,对波导不变量[5- 6,13]的研究成为水声领域中的研究热点。自波导不变量的概念被提出后,众多研究人员对其展开了更深入的研究并提出了波导不变量的应用方向。本论文将虚源法结合波导不变量实现测距[7- 8,13]。即在使用虚源法测距缩小测距范围的基础上,减少波导不变量测距方法的计算量,利用波导不变量技术进行精确测距。
本文的第2部分详细描述虚源法测距原理;第3部分为结合声速补偿方法的虚源法测距仿真实现;第4部分将虚源法测距与波导不变量测距技术结合,并仿真实现;第5部分给出结论。
2 虚源法测距原理
2.1 虚源与反射声线规律
虚源是由于声波对海面或者海底发生镜面反射而产生的,是实际声源在海面或者海底上的多次镜像以及多次反射形成的。图1为虚源形成过程与声传播的多途过程。
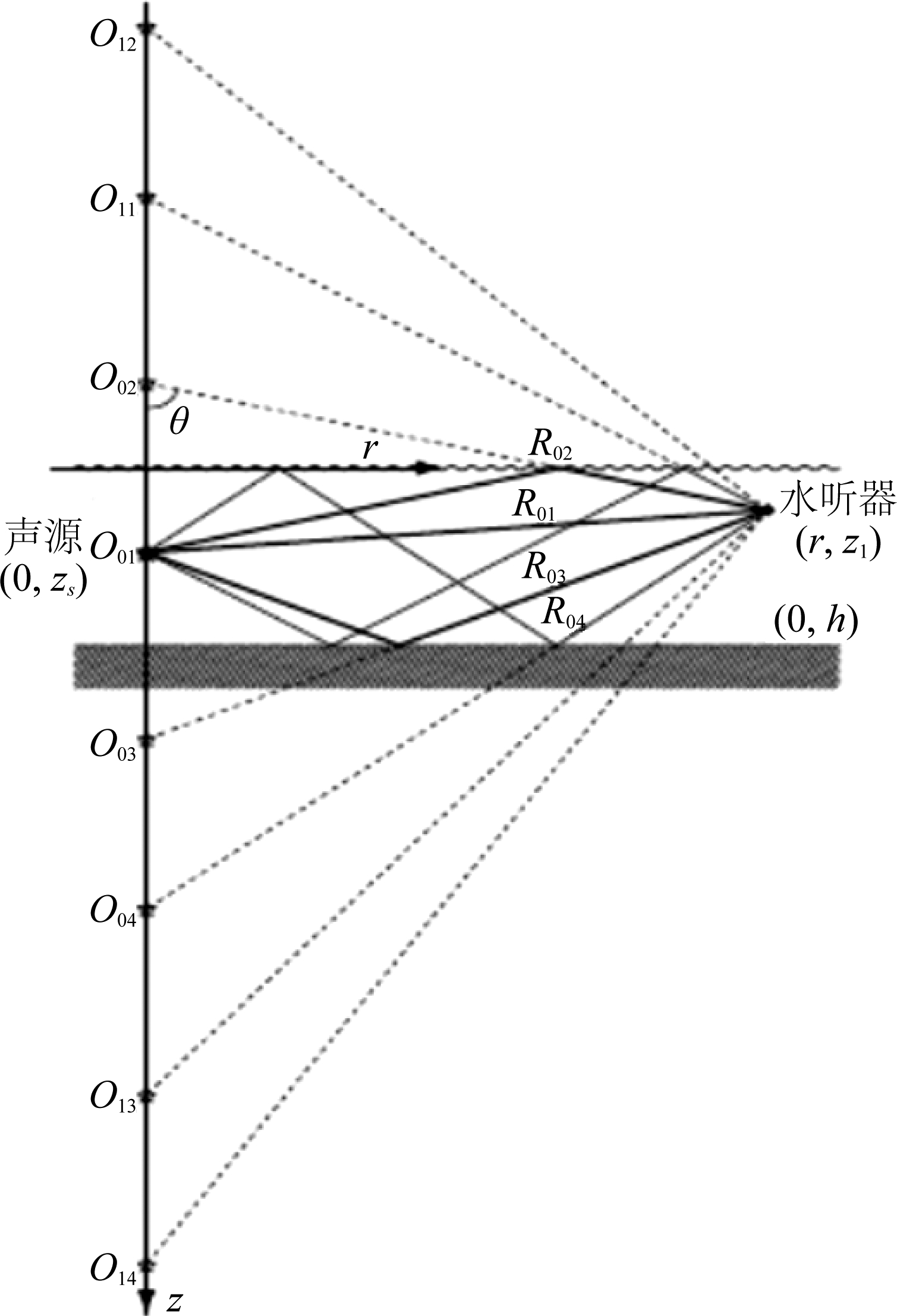
图1 声传播的多途过程
Fig.1 Multipath process of sound propagation
虚源O02,O03分别是声源O01对海面,海底产生的镜像虚源,这两个虚源又不断对海面海底镜像产生一系列虚源Ol1,Ol2,Ol3,Ol4,其中l是虚源的阶数,l=0,1,2,3…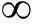
。建立如图所示坐标系roz,声源O01坐标为(0,zs),水听器位置坐标为(r,z1),声源与虚源Ol1,Ol2,Ol3,Ol4,到水听器的斜距分别为Rl1,Rl2,Rl3,Rl4,从图1中可以得出斜距与虚源阶数l的几何关系:
(1)
虚源阶数l与海面海底的关系如下图2所示。
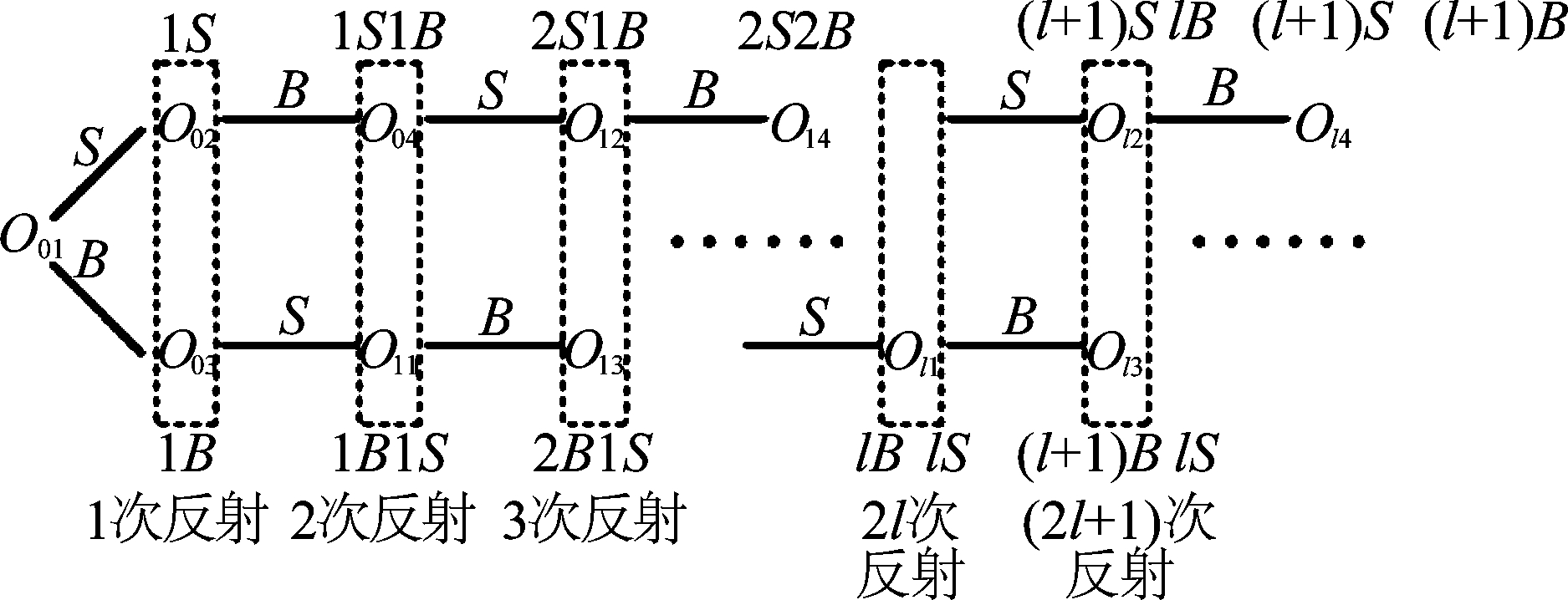
图2 虚源阶数与海底反射关系示意图
Fig.2 Schematic diagram of relation between imaginary source order and seabed reflection
图2中S表示一次海面反射,B表示一次海底反射。水听器上的接收信号为从多个虚源发出的声信号的叠加。声源发射角频率为ω的连续信号时,接收点的叠加声场为
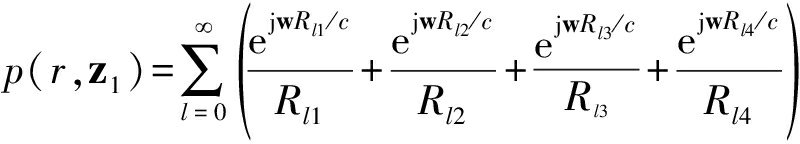
(2)
对应的信道冲激响应为:
Al3δ(t-tl3)+Al4δ(t-tl4)]
(3)
其中
Al1=1/Rl1,Al2=1/Rl2,Al3=1/Rl3,Al4=1/Rl4
tl4=Rl4/c,tl3=Rl3/c,tl2=Rl2/c,tl1=Rl1/c
(4)
分别是每个多途到达接收点的时延差与幅值。
由公式(1)可以看出斜距随着虚源阶数的增大而增大。由于几何扩展与声吸收使得反射声线衰减随着传播距离的增大而增大。故在本文中只研究了0阶虚源与1阶虚源,只采用了直达声线,一次,二次和三次反射声线,不涉及更高次的反射声。根据虚源阶数与斜距的关系,在本文中我们假设直达声与各个反射声到达接收点的顺序符合如下规律:直达声最先到达,其次到达的为一次反射声,之后到达的为二次反射声,以此类推。本文中涉及的虚源与具体反射方式对应关系如表1所示。
表1 虚源与具体反射方式对应
Tab.1 Virtual source corresponds to specific reflection mode
虚源具体反射方式0阶虚源:O01直达声0阶虚源:O02一次海面反射0阶虚源:O03一次海底反射0阶虚源:O04海面海底反射1阶虚源:O14海底海面反射1阶虚源:O12海面-海底-海面反射1阶虚源:O13海底-海面-海底反射
2.2 测距几何模型的建立
从虚源法测距原理中我们得到以下两条规律:(1)虚源阶数与具体反射方式规律;(2)斜距与具体反射方式规律。结合上述两条规律建立测距的几何模型如图3所示。图3是直达声与一次海面反射声或者一次海底反射声的几何关系示意图。
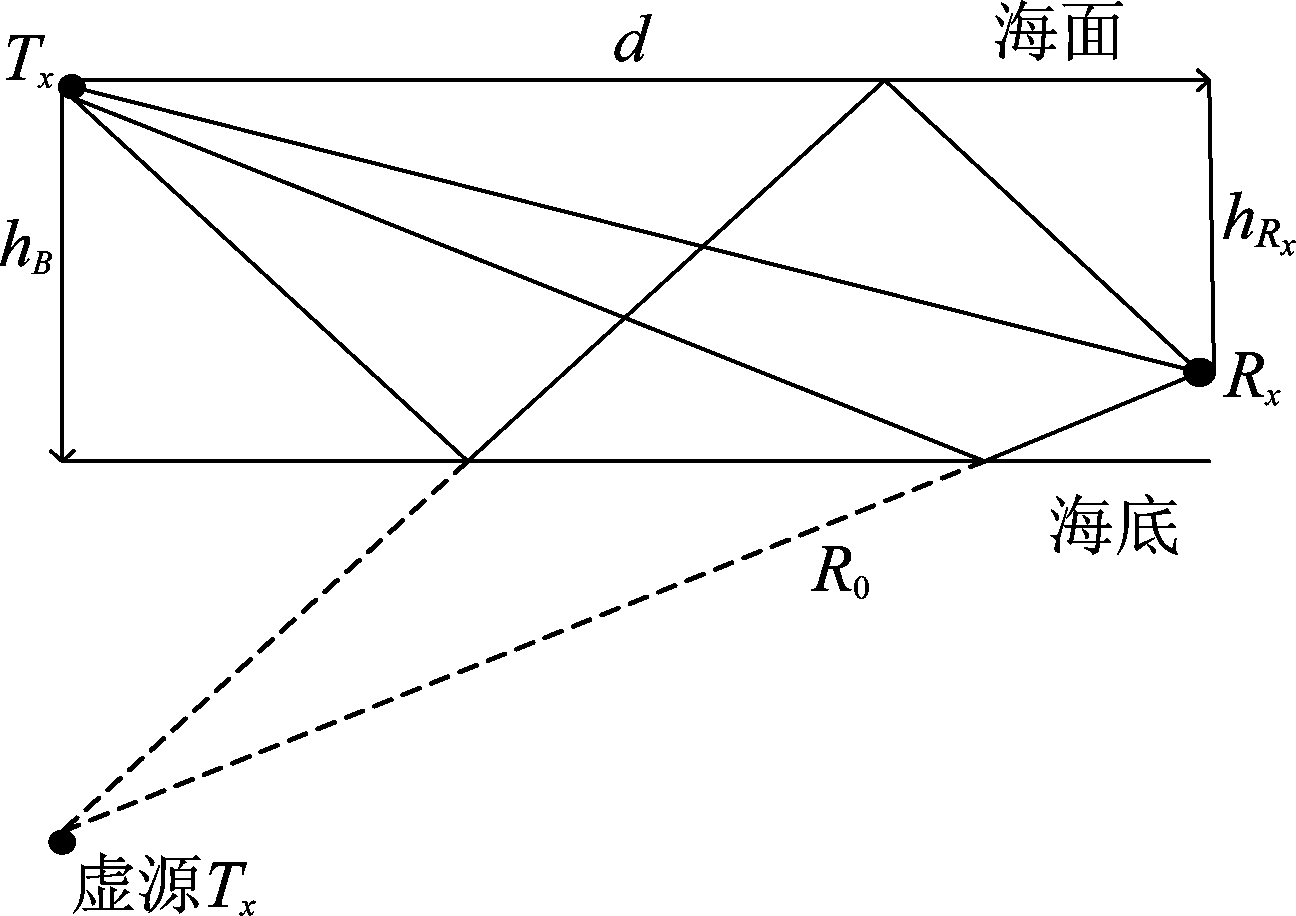
图3 直达声线与反射声线模型
Fig.3 Model of direct and reflected lines
由图3得到测距方程组:
d2=(R0+c*t01b)2-(2hB-hRx-hTx)2
d2=(R0+c*t02bs)2-(2hB-hRx+hTx)2
(5)
图3是假设锚节点Tx在海面,R0是直达声的传播距离,c是恒定声速,hRx、hTx、hB分别是Rx、Tx、海底的深度。在被动测距中由于不能确定直达声线何时到达,所以不能直接应用各个不同路径的时延信息,故利用每两个路径的时延差。应用时延差与水平距离的几何关系即可以计算出发射点与接收点的水平距离。将上述方程组(5)化简得到:
(6)
其中Δt是海底-海面反射声线与海底反射声线的时延差。上式描述了反射声线之间时延差与水平距离之间的几何关系,以下的仿真均是基于该几何关系得到的。
3 虚源法测距仿真
3.1 未进行声速补偿的虚源法测距仿真
利用上述总结的虚源法在测距上的规律:(1)虚源阶数与具体反射方式规律;(2)斜距与具体反射方式规律。在直达与一次反射声的基础上加上二次反射(包括海面-海底与海底-海面反射)与三次反射声(包括海面-海底-海面与海底-海面-海底反射)建立发射点与接收点之间的水平距离的数学模型,并用MATLAB仿真。仿真流程如图4所示。
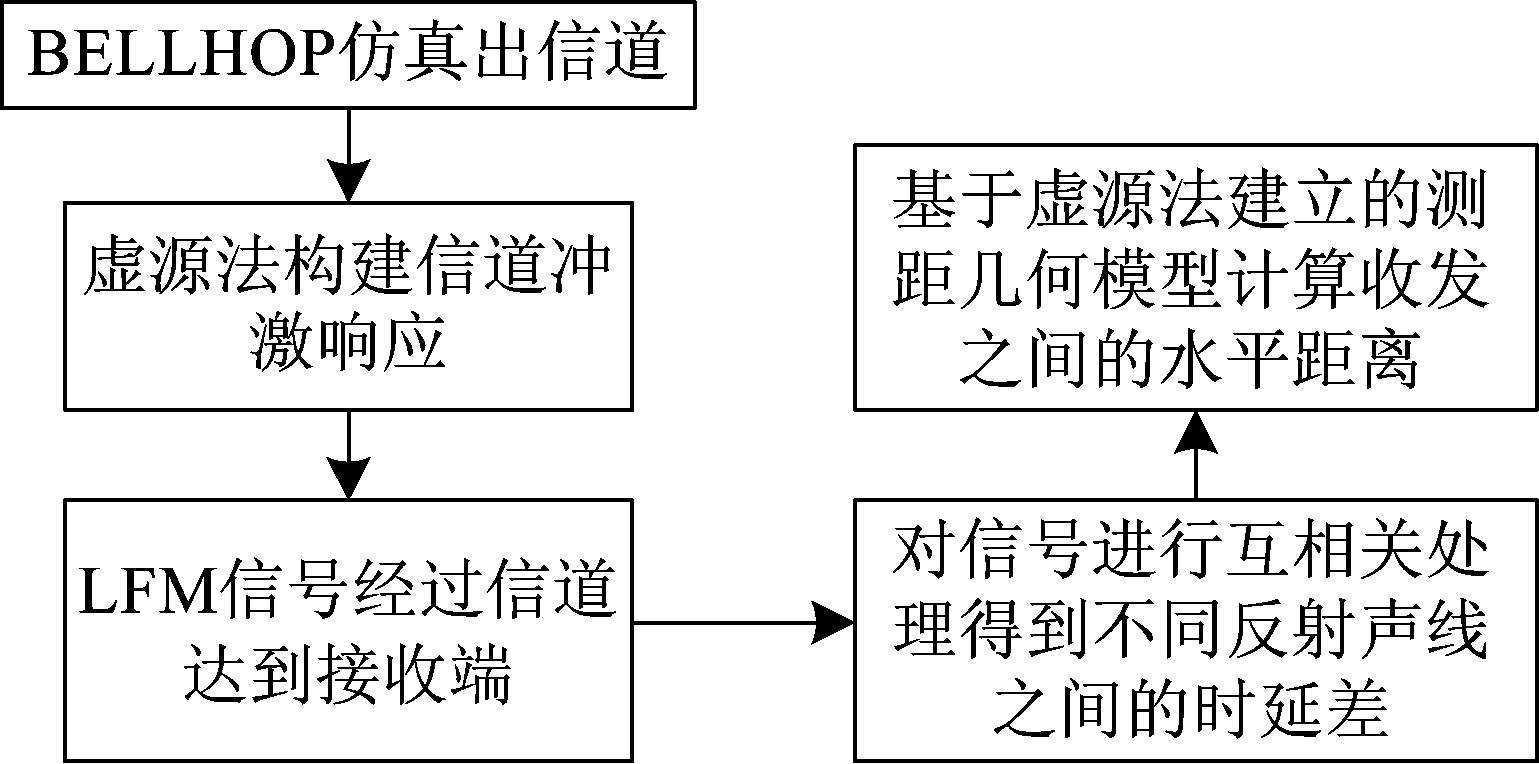
图4 仿真流程图
Fig.4 Simulation flow chart
采用线性调频信号(LFM)仿真,仿真数据如下表2所示。
表2 仿真数据
Tab.2 Simulation parameters
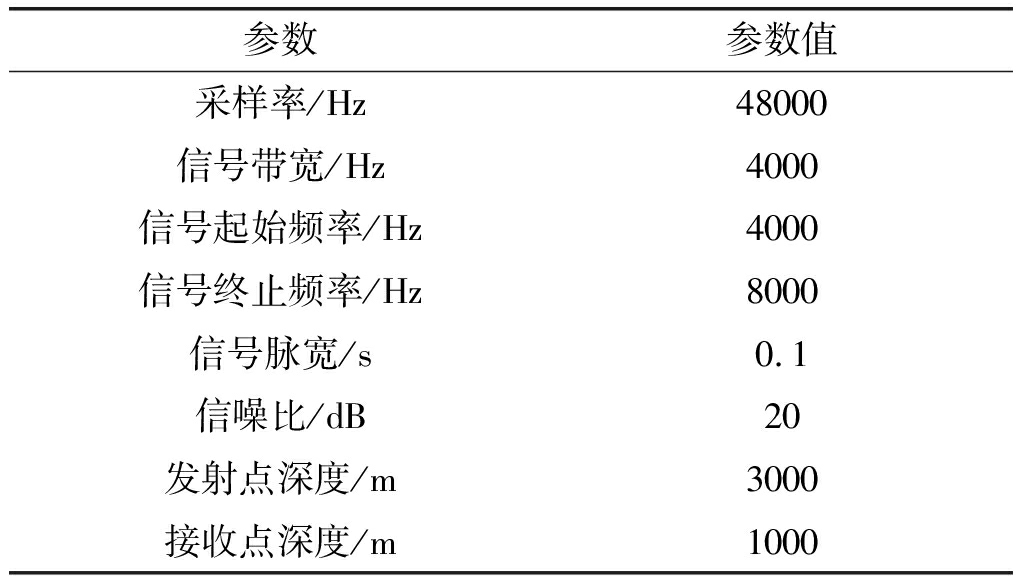
参数参数值采样率/Hz48000信号带宽/Hz4000信号起始频率/Hz4000信号终止频率/Hz8000信号脉宽/s0.1信噪比/dB20发射点深度/m3000接收点深度/m1000
在恒定声速1500 m/s时,得到的虚源法测距误差与收发点之间水平距离的关系如下图5所示。
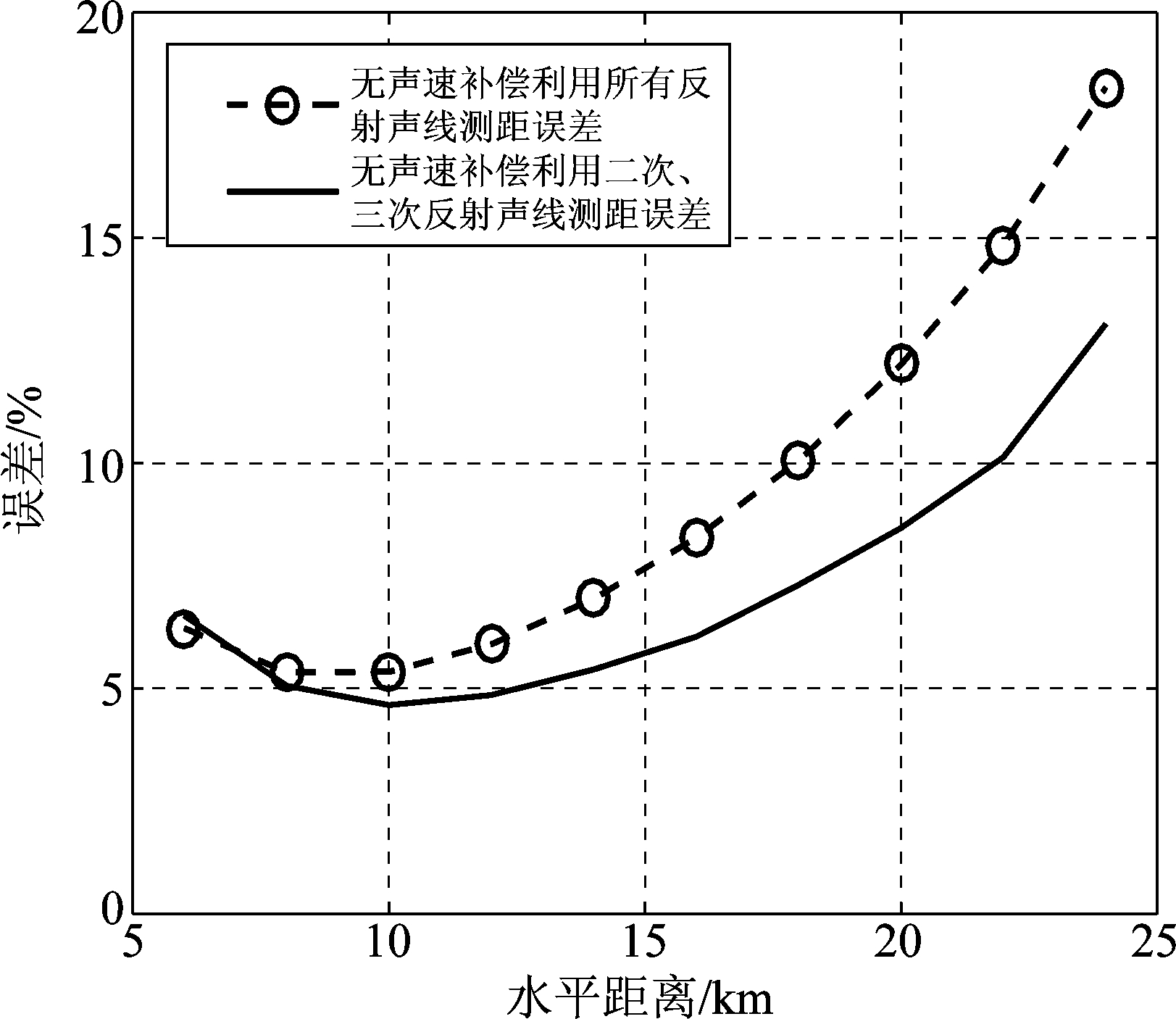
图5 无声速补偿虚源法测距误差
Fig.5 No sound velocity compensation virtual source method ranging error
图5中“利用了所有声线测距误差”是指应用了直达声线,一次反射声线(一次海面1s与一次海底1b),二次反射声线(海面-海底1s1b与海底-海面1b1s),三次反射声线(海面-海底-海面sbs与海底-海面-海底bsb)两两到达时延差;从上图可得出两个结论:(1)随着水平距离的增加,测距误差增加;(2)利用所有反射声线的测距误差大于仅利用二次与三次反射声线的测距误差。对上述两种现象进行理论分析:当水平距离较大时(大于10 km),声线历经的声速不再是恒定值,根据射线声学理论,声线会弯向声速小的区域,此时各个反射声线经历的时延较声线是直线时的时延大,且随着水平距离的增大,这种误差越大,所以随着水平距离的增加,测距误差增加。由于多次反射的声线覆盖更多声速梯度范围,故声速1500 m/s更贴近反射声线经历的平均声速。但是仅仅使用恒定声速(1500 m/s)仍会带来一定的误差。所以利用所有反射声线的测距误差大于仅利用二次与三次反射声线的测距误差。
3.2 结合声速补偿的虚源法测距仿真
通过上述仿真得出声速的误差对测距误差有一定的影响。故考虑通过声速补偿,将声速修正为更贴近声线经历的真实声速。首先对收发点所在深度的范围内的声速梯度进行线性插值,对各个声线经过的深度的声速进行加权平均得到各个声线的平均拟合声速。下面分析利用声线之间的时延差测距时使用何种声速。分析考察通过时延差计算两条路径的距离差,发现仅利用两条路径的平均拟合速度的平均值时,精度并没有得到明显提高,甚至比使用某些恒定声速值的精度更差。理论上的计算误差如下:两条路径真实距离误差:
ΔLreal=|V1t1-V2t2|=V2Δt+(V2-V1)t1
(7)
其中V1,V2分别路径1与路径2拟合的真实声速,t1,t2分别路径1与路径2的时延,Δt=t2-t1。假设:V2大于V1,t2大于t1。若仅使用平均拟合速度的平均值则结果为:
ΔLaver=(V2+V1)/2×Δt
(8)
误差为:
ΔLreal-ΔLaver=V2Δt+(V2-V1)t1-(V2+V1)/2Δt=
(V2-V1)/2Δt+(V2-V1)t1=(V2-V1)(t1+t2)/2
(9)
从上式可以看出,如果使用两条路径的拟合速度的平均值用于测距,实际路径差将与拟合速度及路径到达时间有关。又由于随着水平距离的增加,V2与V1都会收敛,但实际路径到达时间会越来越大,因此虚源法测距误差会随着距离的增加而增加。重新考察公式(7),若仅选用V2来计算路径差时,则:
ΔLν2=V2Δt
(10)
此时误差为:
ΔLreal-ΔLν2=V2Δt+(V2-V1)t1-V2Δt=(V2-V1)t1
(11)
此时误差仅与其中一根路径到达时间有关;由公式得出该种方法的误差比使用平均拟合速度的平均值要小。
虚源法结合声速补偿方法的仿真结果如下图6所示。
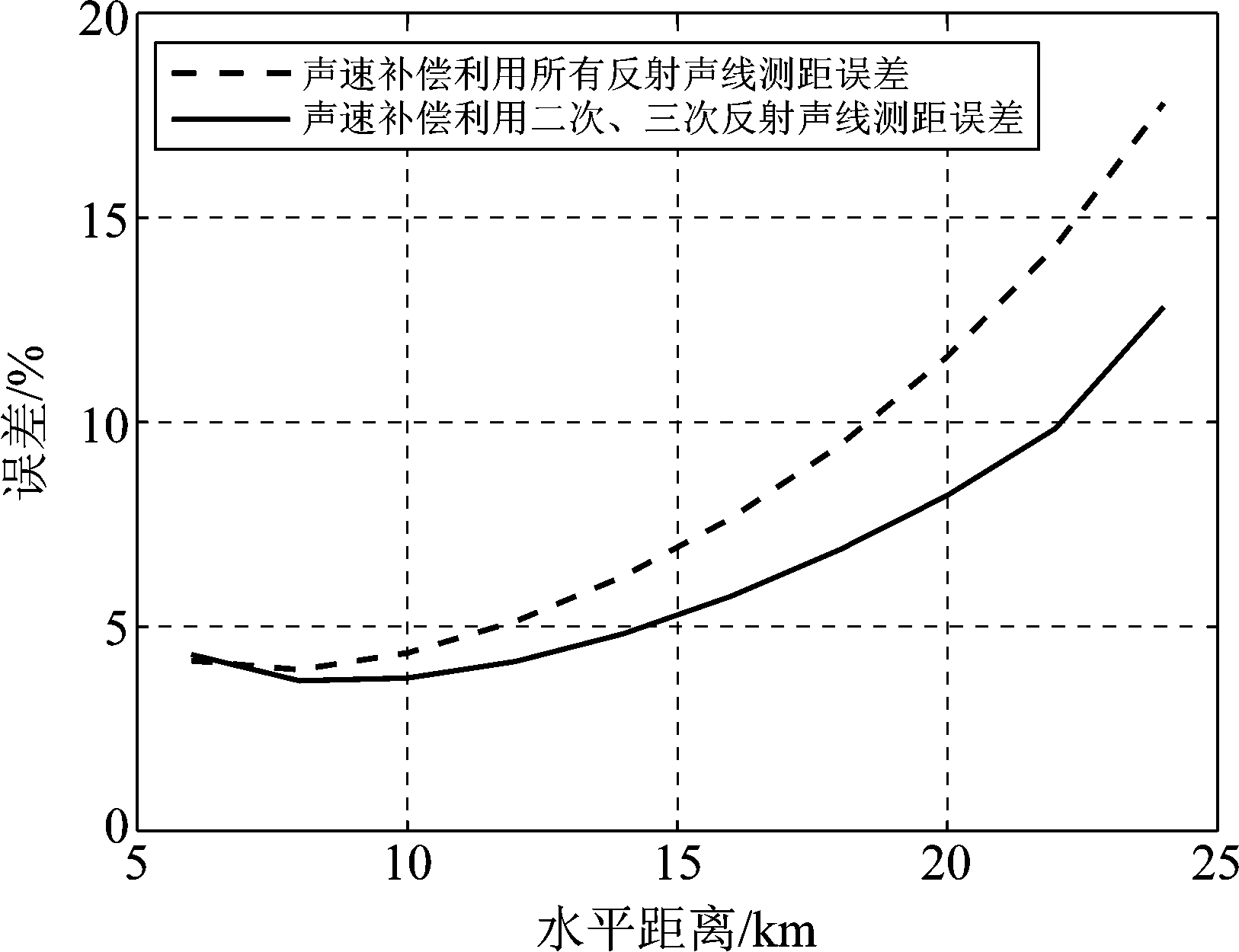
图6 结合声速补偿利用所有声线虚源法测距误差
Fig.6 Combined with sound velocity compensation, all the location errors of virtual source method are used
经过声速补偿后的测距误差与未做声速补偿的测距误差具有相同趋势。未做声速补偿的测距误差与经过声速补偿的误差比较图如下图7所示。
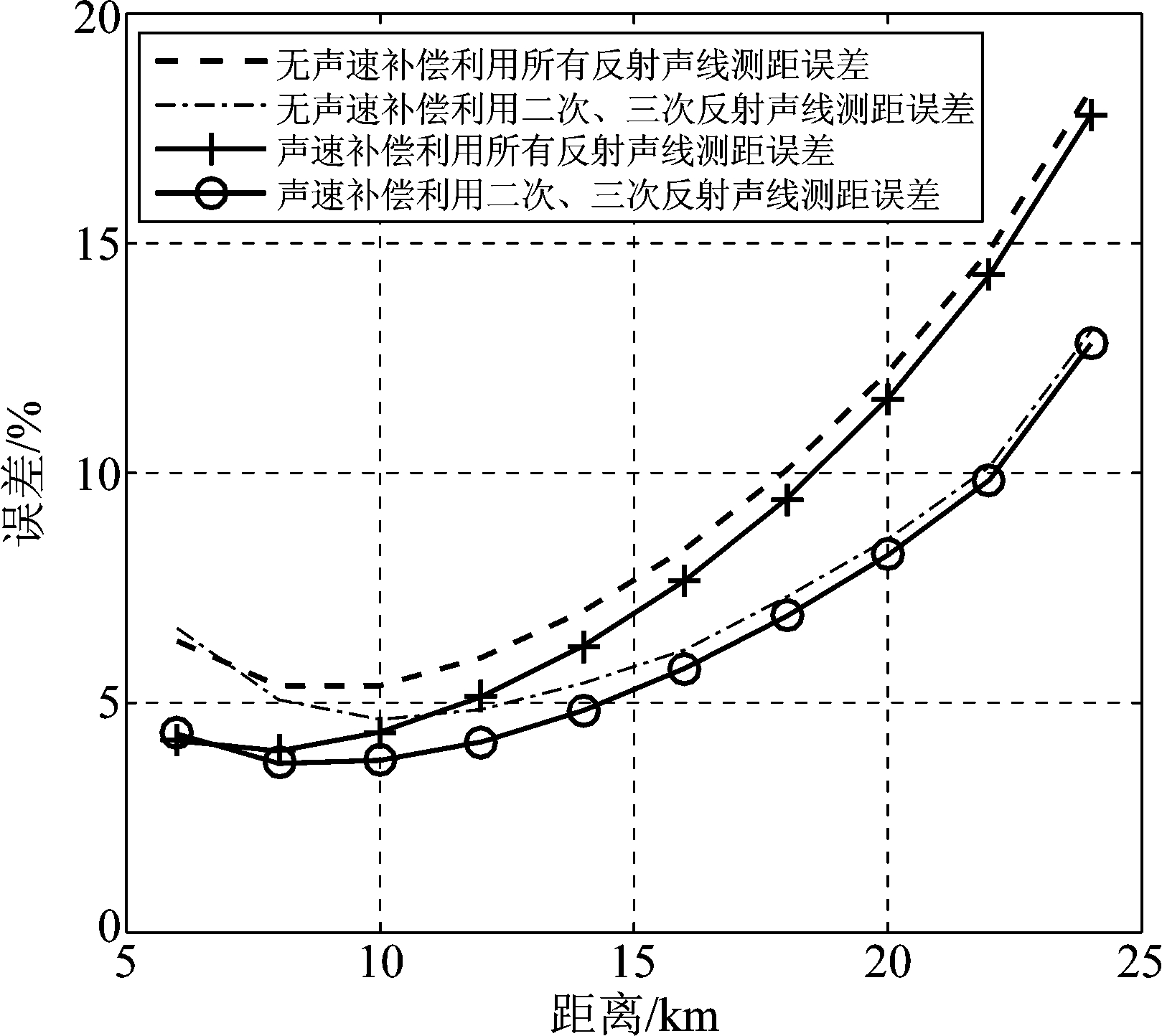
图7 结合声速测距与未结合声速补偿的测距误差比较
Fig.7 Measurement error comparison between combined sound velocity and uncombined sound velocity compensation
从图7中可以得出在水平距离低于20 km时,经过声速补偿的测距误差较未做声速补偿的测距误差低至少一个百分点。可以得出声速补偿具有一定的效果。且仅利用二次与三次反射声线结合声速补偿的测距误差是最低的。所以我们使用结合声速补偿的虚源法先确定测距范围,再通过波导不变量进行精确被动测距。
4 虚源法结合波导不变量测距技术
4.1 波导不变量测距原理
S.D.Chuprov定义了与水平距离r,声源频率ω,和r-ω平面上干涉条纹斜率有关的标量,该标量被称之为“波导不变量[16-17]”:
(12)
根据浅海简正波表达式,对于频谱为A(ω),深度为zs的点源发出的频率为ω的声信号。当接收水听器深度为z,与声源相距r时,声压用简正波表示,深度为z,距离声源r处的接收水听器处的声强为:
I(r,z,zs,ω)≡〈pp*〉=
(13)
其中A(ω)是声源的频谱,Δkmn(ω)是简正波的水平波数差:
Δkmn(ω)=km(ω)-kn(ω),m≠n
(14)
上式等号右边第一项是非相干项,第二项是干涉项,该项即能说明干涉条纹产生的原因。声源强度在r-ω平面上出现干涉条纹,等声强线满足:dI=0,其中I=I(r,ω)。推得:
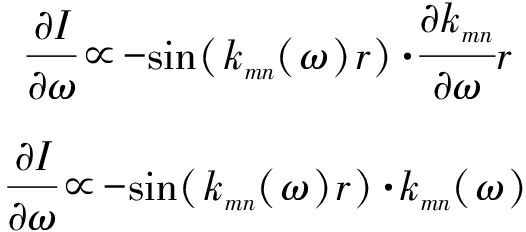
(15)
因此:
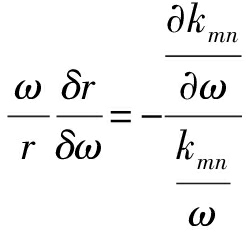
(16)
上式中的水平波数差可表示为:
(17)
是第m号简正波的“相慢度(速度的倒数称为慢度)
是第n号简正波的相慢度。
(18)
分别是第m号和第n号简正波的“群慢度”。
综上:
(19)
上式给出了第m号与第n号简正波在r-ω平面上形成的干涉条纹的斜率表达式。由以上公式可知波导不变量可由r-ω平面上的干涉条纹确定。又由于在海域环境稳定时,波导不变量变化不大,并且与r和ω无关,所以我们可以通过波导不变量测得收发点之间的水平距离[13-15]。
4.2 虚源法结合波导不变量测距仿真
利用MATLAB与BELLHOP对上述理论进行仿真。首先给出利用BELLHOP计算出的海面目标产生的典型深海声场干涉结构。参数设置如表3所示。
表3 仿真数据
Tab.3 Simulation parameters
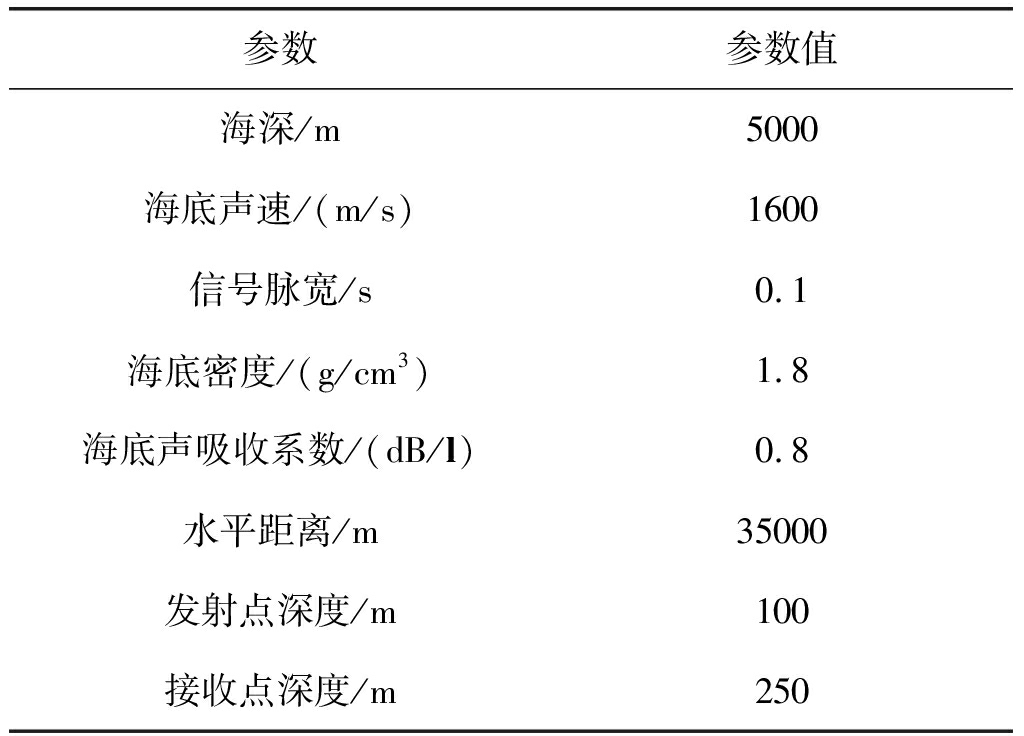
参数参数值海深/m5000海底声速/(m/s)1600信号脉宽/s0.1海底密度/(g/cm3)1.8海底声吸收系数/(dB/l)0.8水平距离/m35000发射点深度/m100接收点深度/m250
我们首先通过虚源法测距得到收发点水平距离为35 km时,测距误差为22.46%,故得到距离范围为27～43 km,使用波导不变量测距技术在这段范围内进行测距。27～43 km范围内的声场频率-距离干涉结构如图8所示。
图8 频率-干涉结构
Fig.8 Frequency-interference structure
利用BELLHOP可以计算得到一次海底反射声线与海底海面反射声线的传播时间t11和t13。根据f=m/Δt2(m=1,2,3,…),Δt2=t13-t11[9-10]可以预测声场干涉结构如图9所示。
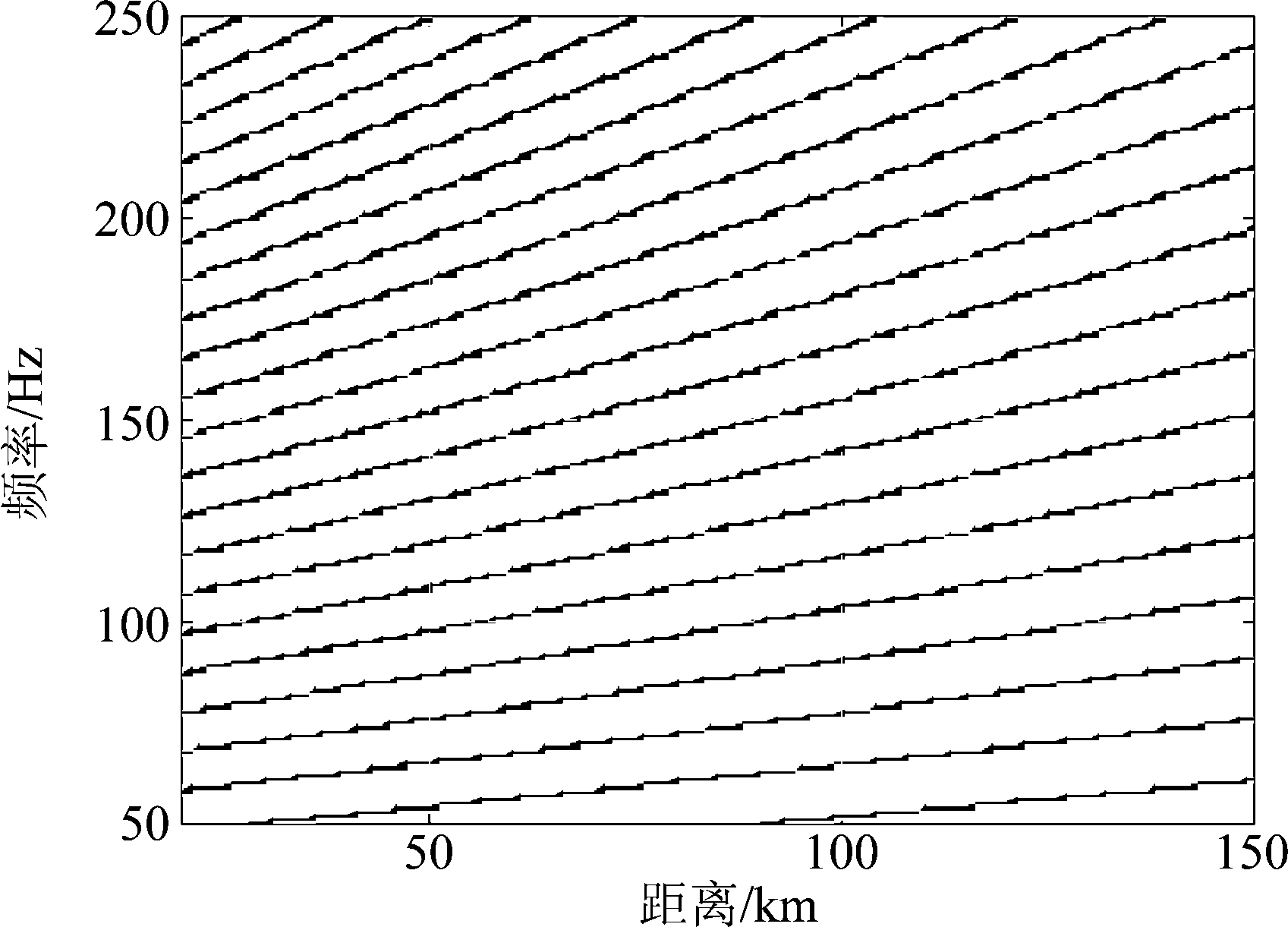
图9 声场干涉结构
Fig.9 Sound field interference structure
下图10为频域水平距离和干涉周期的关系:
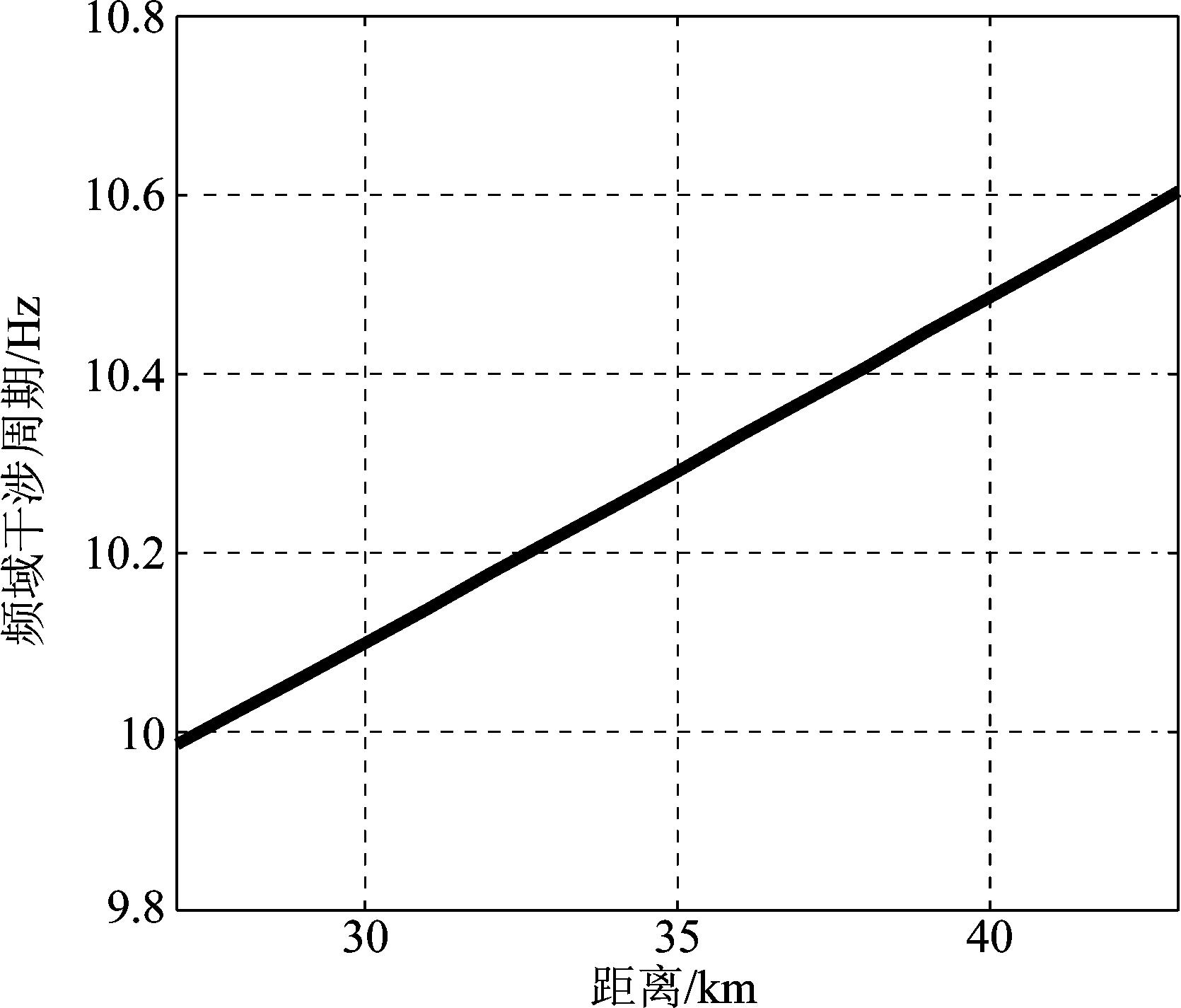
图10 距离-频域干涉周期
Fig.10 Range-frequency interference period
图10反映了频域水平距离和干涉周期的关系,结合获得的影区内声源形成的声场干涉结构的实测频域干涉周期,两者匹配则可得到声源与接收点之间的水平距离,匹配结果如图11所示(假设水平距离为35 km)。
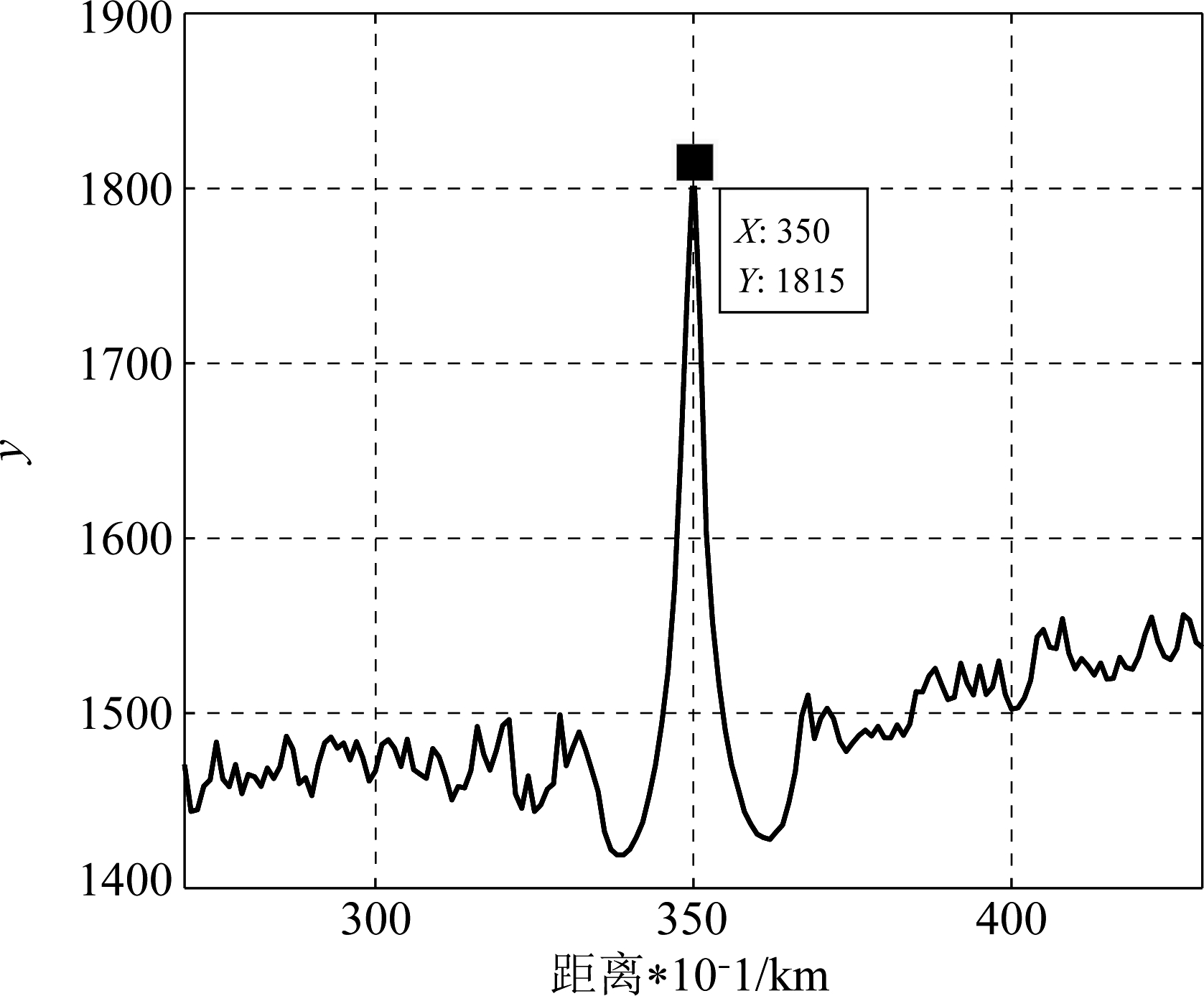
图11 匹配比对结果
Fig.11 Matching result
由上图11可知基于波导不变量测距技术的测距精度非常高。波导不变量测距技术的缺点在于计算量非常大。当不使用虚源法被动测距确定波导不变量测距范围时,需要计算0～150 km范围内的声场频率-距离干涉结构,使用虚源法测距缩小范围时,声场频率-距离干涉结构的计算范围为27～43 km,计算量为原来的1/10。故使用虚源法缩小测距范围能在很大程度上减少波导不变量测距计算量。
5 结论
结合声速补偿方法的虚源法测距技术可以明显降低测距误差。虚源法测距中利用二次与三次反射声线测距的误差较低,原因在于二次与三次反射声线中每段声线弯曲度小,更接近直线,而且二次与三次反射声线历经的声速梯度更多,我们拟合的平均声速更接近该声线经历的真实平均声速。波导不变量测距技术在结合声速补偿虚源法测距的基础上可以非常精确地测定出收发点之间的水平距离。虚源法测距与波导不变量测距方法的结合既进一步降低了测距的误差,又减少了波导不变量的计算量。
[1] 胡安平, 高锐, 张建春. 水声测距技术研究[J]. 现代导航, 2014, 2014(5): 357-361.
Hu Anping, Gao Rui, Zhang Jianchun. Study of Acoustic Underwater Ranging Technology[J]. Modern Navigation, 2014, 2014(5): 357-361.(in Chinese)
[2] 徐复. 多途信道中被动定位技术研究[D]. 哈尔滨: 哈尔滨工程大学, 2011.
Xu Fu. Research on Techniques of Passive Positioning in Multi Sea Channels Environment[D]. Harbin: Harbin Engineering University, 2011.(in Chinese)
[3] 王晋晋. 基于声传播模型的信道模拟与应用[D]. 哈尔滨: 哈尔滨工程大学, 2012.
Wang Jinjin. Underwater acoustic channel simulation and application based on propagation model[D]. Harbin: Harbin Engineering University, 2012.(in Chinese)
[4] Elizaveta Dubrovinskaya, Ivor Nissen, Paolo Casari. On the accuracy of passive multipath-aided underwater range estimation[C]∥2016 IEEE Third Underwater Communications and Networking Conference (UComms), Lerici, 2016: 1- 4.
[5] Kuperman W A, D'Spain G L. Application of waveguide invariants to analysis of spectrograms from shallow water environments that vary in range and azimuth[J]. Ocean Acoustic Interference Phenomena & Signal Processing, 1995, 106(5): 2454-2454.
[6] Young A H, Harms H A, Hickman G W, et al. Waveguide-Invariant-Based Ranging and Receiver Localization Using Tonal Sources of Opportunity[J]. IEEE Journal of Oceanic Engineering, 2019(99): 1-14.
[7] Song Xuejing, Zhao Anbang, Li Maozhen. Passive ranging technique using waveguide invariant in shallow water with thermocline[J]. Systems Engineering and Electronic Technology, 2017, 28(2): 250-250.
[8] Knut A. Sostrand. Range localization of 10-100 km explosions by means of an endfire array and a waveguide Invariant[J]. IEEE Journal of Oceanic Engineering, 2005, 30(1): 207-212.
[9] 翁晋宝, 李风华, 郭永刚. 典型深海声场频率-距离干涉结构分析及实验研究[J]. 声学学报, 2016, 41(3): 330-342.
Weng Jinbao, Li Fenghua, Guo Yonggang. The sound field frequency-range interference patterns in deep water:theory and experiment [J]. Acta Acustica, 2016, 41(3): 330-342.(in Chinese)
[10] 周士弘, 牛海强, 任云, 等. 温跃层起伏浅海中模态间干涉及其波导不变量[J]. 中国科学, 2013, 43(s1): 68-74.
Zhou Shihong, Niu Haiqiang, Ren Yun, et al. Interference characteristic between modes and its waveguide invariant in fluctuated shallow water with thermocline[J]. Science China, 2013, 43(s1):68-74.(in Chinese)
[11] 邢志刚, 封金星, 刘伯胜. 水声测距数学模型研究[J]. 哈尔滨工程大学学报, 2000, 21(3): 24-28.
Xing Zhigang, Feng Jinxing, Liu Bosheng. Study of Range Mathematical Model by Underwater Acoustics[J]. Journal of Harbin Engineering University, 2000, 21(3): 24-28.(in Chinese)
[12] 蔡龙飞, 杨蕾. 水声测距技术方法仿真研究[J]. 武汉轻工大学学报, 2015(2): 79- 82.
Cai Longfei, Yang Lei. Average speed of sound acoustic ranging study[J]. Journal of Wuhan Light Industry University, 2015(2): 79- 82.(in Chinese)
[13] 李启虎. 水下目标被动测距的一种新方法: 利用波导不变量提取目标距离信息[J]. 声学学报, 2015(2): 138-143.
Li Qihu. A new method for passive ranging for underwater target: distance information extraction based on wave guide invariant[J]. Acta Acustica, 2015(2): 138-143.(in Chinese)
[14] 祝献, 彭玲, 王忠康, 等. 利用波导不变量的水平线阵被动估距方法研究[J]. 信号处理, 2012, 28(11): 1607-1612.
Zhu Xian, Peng Ling, Wang Zhongkang, et al. Research on passive range estimation with a horizontal line array using waveguide invariant[J]. Signal Processing, 2012, 28(11): 1607-1612.(in Chinese)
[15] Thode, Aaron M. Source ranging with minimal environmental information using a virtual receiver and waveguide invariant theory[J]. The Journal of the Acoustical Society of America, 2000, 108(4): 1582-1594.
[16] Chuprov S D. Signal fluctuations during the propagation of sound in the ocean[C]∥Acoustics of the Ocean. Acoustics of the Ocean, 1975, part2: 351-394.
[17] William A. Kuperman, Gerald L. D’Spain, Hee Chun Song, et al. Applications of the waveguide invariant approach[J]. Journal of the Acoustical Society of America, 1999, 105(105): 983.
